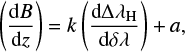| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A164 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833421 | |
| Published online | 20 November 2018 | |
Analysis of unresolved photospheric magnetic field structure using Fe I 6301 and 6302 lines
1
Jodrell Bank Centre for Astrophysics, University of Manchester, Manchester M13 9PL, UK
e-mail: mykola.gordovskyy@manchester.ac.uk
2
Department of Mathematics, Physics and Electrical Engineering, University of Northumbria, NE1 8ET, Newcastle , UK
3
Astronomical Observatory, Kyiv National University, 01053 Observatorna 3, Kyiv , Ukraine
Received:
14
May
2018
Accepted:
12
September
2018
Context.Early magnetographic observations indicated that the magnetic field in the solar photosphere has an unresolved small-scale structure. Near-infrared and optical data with extremely high spatial resolution show that these structures have scales of a few tens of kilometres, which are not resolved in the majority of solar observations.
Aims.The goal of this study is to establish the effect of the unresolved photospheric magnetic field structure on Stokes profiles observed with relatively low spatial resolution. Ultimately, we aim to develop methods for fast estimation of the photospheric magnetic filling factor and line-of-sight gradient of the photospheric magnetic field, which can be applied to large observational data sets.
Methods.We exploit 3D magnetohydrodynamic models of magneto-convection developed using the MURAM code. Corresponding profiles of Fe I 6301.5 and 6302.5 Å spectral lines are calculated using the NICOLE radiative transfer code. The resulting I and V Stokes [x, y, λ] cubes with a reduced spatial resolution of 150 km are used to calculate magnetic field values as they would be obtained in observations with the Solar Optical Telescope (SOT) onboard Hinode or the Helioseismic and Magnetic Imager (HMI) onboard the Solar Dynamic Observatory (SDO) mission.
Results. Three different methods of magnetic filling factor estimation are considered: the magnetic line ratio method, the Stokes V width method, and a simple statistical method. We find that the statistical method and the Stokes V width method are sufficiently reliable for fast filling factor estimations. Furthermore, we find that the Stokes I ± V bisector splitting gradient can be used for fast estimation of the line-of-sight gradient of the photospheric magnetic field.
Key words: Sun: photosphere / Sun: magnetic fields / techniques: imaging spectroscopy
© ESO 2018
1. Introduction
Early observational studies indicated that the photospheric magnetic field is very non-uniform on scales smaller than the spatial resolution of optical instruments. Magnetographic observations showed that the magnetic field strengths measured using two Fraunhofer lines with similar characteristics but different magnetic sensitivity (i.e. different Lande factor g) can differ by a factor of up to 2.5 (Howard & Stenflo 1972; Stenflo 1973). This has been interpreted as evidence of strong horizontal field inhomogeneity. It has been suggested that most of the photospheric magnetic flux is carried by numerous intense small-scale magnetic fluxtubes, and the photospheric magnetic filling factor can be as low as 10% (Frazier & Stenflo 1972). Despite very significant progress in achieving high spatial resolution in solar observations, most existing optical solar instruments do not resolve the smallest scales in the photospheric magnetic field (see e.g. Solanki 1993; Lozitska & Lozitsky 1994; Solanki & Schüssler 2004; de Wijn et al. 2009, for review).
Obviously, direct high-resolution observations are the most reliable way of studying photospheric fine structure. However, very high spatial resolution (50–100 km or even less) can be achieved only in some observations using advanced instrumentation as well as advanced data-processing techniques, which are often computationally expensive. Direct high-resolution observations of small-scale photospheric magnetic elements were performed using speckle interferometry in the Fe I 5250.2 Å line by Keller & von der Lühe (1992), Keller (1992). They found magnetic elements with a field strength of a few kilo-Gauss and estimated their sizes at 100–200 km. Lin (1995) observed Stokes profiles in magneto-sensitive near-infrared Fe I lines 15648 Å and 15652 Å and showed that there are two types of small-scale magnetic elements: stronger elements with a field of 1.4 kG and diameters of 100–1000 km located in the network boundaries, and weaker ones with fields of about 500 G and diameters of about 70 km, located inside granulation cells. Lagg et al. (2010), using IMaX magnetograph1 on-board Sunrise balloon mission, have achieved spatial resolutions of about 100 km in all Stokes components. They were able to detect small magnetic elements with the filling factor equal to 1 (i.e. no unresolved structure), which have been interpreted as individual photospheric fluxtubes. The sizes of these elements are 100–500 km.
Inversion of Stokes profiles observed using a moderate spatial resolution (a few 100 km) can be an alternative to high-resolution observations (e.g. Viticchie et al. 2011). However, inversion algorithms are computationally expensive and can be applied only to rather small patches of the photosphere. Furthermore, most inversion codes oversimplify the magnetic field structure by assuming the same magnetic filling factor at different heights.
Forward-modelling is another way of studying small-scale photospheric magnetic field. Three-dimensional (3D) models of magneto-convection in the photosphere developed using high-resolution 3D magnetohydrodynamic (MHD) simulations offer a unique opportunity to investigate photospheric magnetic field structure unresolved by normal solar telescopes. Combined with radiative transfer calculations, these models make it possible to link characteristics of the small- and large-scale magnetic field 3D structure with parameters inferred directly from solar observations with limited spatial and spectral resolution.
Recently, Smitha & Solanki (2017) used MHD models of magneto-convection combined with radiative transfer calculations in order to investigate the Stokes profiles of several photospheric lines. The focus was on using various pairs of lines for measuring photospheric field using the magnetic line ratio (MLR) approach. This approach makes it possible to evaluate the actual field value based on the ratio of magnetic field values measured using two lines with similar thermodynamic characteristics (and, hence, similar formation depths) but different Lande factors, unlike single line measurements that yield average field (or magnetic flux) values (see Sect. 4). This study identified two new pairs of lines, one visible and another in the near-infrared, as effective diagnostic tools for magnetic field measurements using the MLR approach.
In the present study, we investigate the effect of magnetic field filling factor (in a plane perpendicular to the line-of-sight (LOS)) and vertical field gradient on Stokes I and V profiles observed with relatively low spatial resolution. We deploy techniques very similar to Smitha & Solanki (2017), however, we focus specifically on the unresolved structure of the photospheric field, both in horizontal and vertical (i.e. line-of-sight) directions. Most importantly, in addition to the magnetic line ratio method, we consider two other methods (Stokes V width method and the statistical method). The ultimate goal is to find a simple, empirical way of estimating these two parameters using large field-of-view spectropolarimetric data from telescopes such as Hinode, Gregor, and future DKIST2.
2. Methodology and definitions
In this paper, we use a combination of MHD and radiative transfer simulations in order to investigate Stokes profiles of the Fe I 6301.5 and 6302.5 Å lines produced by the photospheric magnetic field. A comparison of synthetic Stokes profiles calculated with high and low spatial resolution for the same areas of the model photosphere makes it possible to link characteristics of the low-resolution Stokes profiles with intrinsic physical characteristics of photospheric magnetic field.
The 6301–6302 Å line pair is not the best for the magnetic line ratio method (see analysis in Khomenko et al. 2005; Khomenko & Collados 2007; Smitha & Solanki 2017). However, the 6301–6302 pair is currently the most used and most widely-available pair, thanks to Hinode SOT and a few other instruments, and that is why this specific pair is chosen.
Both lines are formed within a relatively large height interval (400–500 km), however, the average formation height of the 6301 Å line is 80–150 km higher than that of the 6302 Å line (depending on thermodynamic conditions). This difference is substantial compared to other pairs: the classical 5247–5250 Å pair has a formation height difference of about 50 km, while for the near-infrared pair 15648–15652 Å it is less than 20 km (see e.g. Fig. 5 in Khomenko & Collados 2007). At the same time, the difference in the formation heights of the 6301 and 6302 lines is substantially smaller than the height intervals over which the lines are formed and, hence, this pair can still be used in the MLR method, although one should expect relatively large errors.
By “high-resolution data”, we mean the original data from MHD simulations, which has a horizontal spatial resolution of 6.25 km (see Sect. 3). By “low resolution data”, we mean data degraded to a spatial resolution of about 150 km, which is typical for most optical solar observations (Table 1), and by “effective” we mean parameters obtained using this low-resolution data (see Sect. 5). By “small-scale” or “sub-telescopic” structures, we mean structures with length scales smaller than ∼100 km, that is, those that are resolved in the high-resolution data but unresolved in the low-resolution data. By intrinsic magnetic field, we mean the value of the vertical component of magnetic field Bz averaged in the height interval between −100 and 300 km.
Spatial resolution around 6300Å and pixel size for three optical solar imaging spectrographs and for the synthetic degraded Stokes cubes used in this study (Kosugi et al. 2007; Volkmer et al. 2010; Tritschler et al. 2016).
We assume that the observed photospheric areas are close to the disk centre and, therefore, by vertical or LOS direction, we mean the z-direction in the MHD model. The velocity sign is defined as in spectroscopy: positive velocities correspond to the motion away from the observer (i.e. downflows, Doppler shift to longer wavelengths), and negative velocities correspond to the motion towards the observer (i.e. upflows, Doppler shift to shorter wavelengths).
In this paper we use standard definitions of commonly used parameters, unless stated otherwise; some of them are shown in the line profile sketch in Fig. 1. The amplitude and the full width at half-maximum (FWHM) of the Stokes I profile are denoted as I and WI. However, it should be noted that by line width we mean FWHM of I ± V, unless otherwise stated. The amplitude and width of the Stokes V profile are the amplitude and FWHM of the blue peak of the line’s Stokes V profile; they are denoted as V and WV, respectively. The bisector splitting function is defined as ΔλH (δ λC), where ΔλH is the splitting of the Stokes I + V and I − V bisectors at a certain intensity level, and ΔλC is the full width of the profile at that intensity level. The bisector splitting gradient (BSG) is defined as 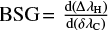 . The MLR is defined as the ratio of the Stokes V amplitude of the line with lower Lande factor to that of the line with higher Lande factor. Namely,
. The MLR is defined as the ratio of the Stokes V amplitude of the line with lower Lande factor to that of the line with higher Lande factor. Namely, ![$MLR = \frac{V[6301]}{V[6302]}$](/articles/aa/full_html/2018/11/aa33421-18/aa33421-18-eq2.gif) , where V[6301] and V[6302] are amplitudes of the blue peaks of the Stokes V profiles of these lines.
, where V[6301] and V[6302] are amplitudes of the blue peaks of the Stokes V profiles of these lines.
 |
Fig. 1. Sketch of a line profile, showing Stokes I profile (panel a), Stokes V (panel b), and Stokes I ± V profiles (panel c) with some of their parameters used in this paper. |
In order to measure the amplitude and width of the blue wing of the Stokes V profile, we locate positive and negative extrema for each line. The extremum located at shorter wavelength is assumed to be the blue peak; its amplitude and FWHM are V[630x] and WV[630x], respectively.
Effective values (i.e. those corresponding to the low resolution) of the magnetic field, velocity, and Stokes I and V profile widths are obtained using spatially-averaged Stokes profiles. Degraded Stokes cubes ID(x′,y′,λ) and VD(x′,y′,λ) are calculated by convolving the original Stokes cubes with a two-dimensional (2D) Gaussian point spread function (PSF) and adding random noise as follows:
where S(x, y, λ) is the original and SD(x, y, λ) is the degraded Stokes (I or V) profiles, respectively. Coordinates (x, y) and (x′, y′) correspond to the original and sparse grids, respectively, and β = rPSF/4. Here rPSF = 100 km is, effectively, the spatial resolution, and the step of the sparse grid is rPSF/2. The function ξ(x′, y′) adds random noise with normal distribution and σ = 10−3.
3. Magnetic field structure obtained using magneto-convection simulations
Three-dimensional models of the photospheric magneto-convection have been developed using the radiative MHD code MURAM (see Schüssler et al. 2003; Shelyag et al. 2004; Vögler et al. 2005). Simulations have been performed using a box with a uniform grid of 960 × 960 × 400 elements with dimensions 6000 × 6000 × 2000 km. The upper boundary of the domain corresponds to the temperature minimum level. The simulation starts with a well-developed low-resolution (240 × 240 × 160 grid cells) non-magnetic photospheric convection model. At this point, a uniform vertical magnetic field is added. The model is then run for about five convective timescales (corresponding to 50 min of physical time). After this initial stage, the model is interpolated onto a grid with doubled resolution and run for 10 min of physical time. The process is repeated twice to reach the resolution of 6.25 × 6.25 × 5 km3 per grid cell.
In this study we use three snapshots from two different models. Snapshot A corresponds to the model with the initial field 100 G, while snapshots B and C correspond to the model with the initial field 200 G. Snapshot B represents a stage when the magnetic structure still shows some changes, while A and C represent quasi-stationary states: although small-scale elements keep varying, the large-scale structure and, most importantly, the magnetic field spectrum do not change. The magnetic field map for snapshot C is shown in Fig. 2a.
 |
Fig. 2. Magnetic field in snapshot C at different spatial resolutions. Panel a: magnetic field measured using Stokes V amplitudes of the 6301 line with high spatial resolution (not calibrated). Panel b: map of Beff[6301], magnetic field from the same model snapshot, but representing low-resolution data. |
The evolution of the considered models has been described in detail by Vögler et al. (2005). After magnetic field is added to the domain, it quickly becomes very non-uniform: convective motions redistribute it so the field becomes concentrated at the boundaries of granulation cells, forming the photospheric network. The field strength is amplified by almost an order-of-magnitude; thus, in the model with initial field of 200 G, when the network is fully developed, the maximum field is around 1800–2000 G. Horizontal magnetic field structure appears to be formed of thin walls and larger blobs. The field is non-uniform at scales as small as 10 km (close to horizontal resolution of the computational grid, 6.25 km). Importantly, this scale-length is well below the typical resolution of existing optical solar telescopes (50–100 km).
Histograms of magnetic field values for all three model snapshots are shown in Fig. 3. It shows that magnetic field distribution is not “turbulent”: its spectrum is not a monotonically decreasing, nearly power-law function. Instead, snapshots B and C reveal two peaks: one at B = 0 and another around B ≈ 1 kG. It should be noted that Vögler et al. (2005) show that the weak field peak is located around a few tens of Gauss, that is, the magnetic field is non-zero everywhere in the domain, although most of the model photosphere is permeated by very weak field. In other words, the intrinsic photospheric magnetic field is represented by two distinct populations: strong small-scale elements found mostly in the network boundaries embedded into ambient weak field. As far as the weaker initial field model is concerned (Model A), its field histogram does not show two clear peaks. However, it appears that it still has a multi-component field structure, which will be discussed in Sect. 5.2.
 |
Fig. 3. Magnetic field distribution function in snapshots A, B, and C (panels a, b, and c, respectively). The black dashed lines correspond to the actual field taken from the high-resolution MHD simulations. Solid blue lines with squares correspond to the magnetic field measured with high resolutions using Stokes V amplitudes of the 6301 line. Blue bars correspond to the effective magnetic field Beff[6301] (see Sect. 5). |
A two-component field model has been used as a simplification necessary to reduce the parametric space in many studies (see e.g. Gordovskyy & Lozitsky 2014). Furthermore, most inversion algorithms (SIR, NICOLE) characterise local magnetic field only by two parameters, strength and filling factor, effectively assuming the two-component small-scale field structure. However, these MHD models of magneto-convection show that, indeed, the intrinsic photospheric magnetic field has at least two distinct components: a strong kilo-Gauss field mixed with an ambient field B < 50−100 G. The data from MHD simulations of magneto-convection is used to calculate corresponding I and V Stokes profiles of the Fe I 6301.51 and 6302.49 Å lines. Stokes I(x, y, λ) and V(x, y, λ) cubes are calculated using the radiative transfer code NICOLE Socas-Navarro et al. 2000; Socas-Navarro 2011), assuming that the system is in local thermodynamic equilibrium (LTE), and ignoring possible horizontal scattering (in other words, radiative transfer is fully one-dimensional). The wavelength interval is 6301–6303 Å with the step 5 mÅ. The excitation potentials are V = 3.65 eV and V = 3.686 eV, log(gf) = −0.59 and log(gf) = −1.13 for the 6301 Å and 6302 Å lines, respectively.
Now, let us discuss the parameters required for a quantitative description of the magnetic field inhomogeneity. Vertical inhomogeneity of the magnetic field in the simplest case can be described using the average field gradient dBz/dz. Horizontal inhomogeneity is normally described using the magnetic filling factor α. It is assumed that the field consists of two components – strong field and background field – and α is the fraction of the surface area penetrated by the strong field. However, it is not obvious how to determine α in case of an arbitrary magnetic field strength spectrum.
A possible definition of the filling factor can be based on the fraction of the area occupied by 50% of the flux carried by the strongest field. The magnetic field distribution within area Stot can be defined as dS/dB = f(B), with the total area 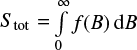 , and the total magnetic flux
, and the total magnetic flux 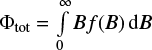 . There is a value of magnetic field B1 such that
. There is a value of magnetic field B1 such that  . The corresponding area
. The corresponding area 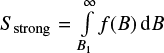 will be equal
will be equal 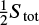 if the magnetic field is uniform (f(B) = δ(B −B1); otherwise
if the magnetic field is uniform (f(B) = δ(B −B1); otherwise 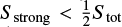 and it will be smaller, the more inhomogeneous the magnetic field. Therefore, the filling factor can be introduced as
and it will be smaller, the more inhomogeneous the magnetic field. Therefore, the filling factor can be introduced as
where B1 is the field value satisfying
It is easy to show that when the magnetic field is two-component with the strong component B1 and zero background field, the formula for the filling factor would reduce to
4. Calibration curves obtained with analytical field configurations
There are several parameters that can be potentially used as proxies of the magnetic flux, magnetic field strength, and filling factor. In the presence of horizontal field inhomogeneity, a Stokes profile is a convolution of the field distribution dS/dB and corresponding Stokes profiles (I(B; λ) or V(B; λ)). If the field is two-component with nearly zero ambient field, the resulting Stokes profiles can be expressed as simple linear combinations:
Hence, the amplitudes of Stokes V will be reduced by the filling factor α, while the ratio of Stokes V peak amplitudes as well as the peak widths should remain the same. In other words, if the magnetic field has two components with nearly zero ambient field, then the average field is Beff = α Breal, with the measured Stokes V amplitudes representing the average field Beff. At the same time, the MLR V[6301] / V[6302] should not be affected by α and would represent the real magnetic field value. Similarly, Stokes V widths WV, which also depend on the magnetic field, are not affected by the filling factor and should represent the real field value. This is demonstrated by Figs. 3–5. Thus, the histograms of magnetic field measured using V[6301] (Fig. 3) significantly change when spatial resolution changes. At the same time, the histograms of the MLR and Stokes V widths (Figs. 4 and 5) change only slightly. That is why MLR is commonly used as a proxy for the real field value, although the Stokes V width method approach is almost unknown. These two methods will be compared in Sect. 5.
 |
Fig. 4. MLR value spectra from snapshots A, B, and C (panels a, b, and c, respectively). The line corresponds to MLR measured with the original MHD model resolution, while the bars correspond to MLR measured using Stokes V amplitudes obtained with low spatial resolution. |
Measuring both the average and real field values, one can estimate the filling factor as
In the present study we use both MLR and the Stokes V width to estimate the filling factor.
The MLR approach is a well-studied method that has been extensively used before. Different line pairs, including the 6301–6302 pair, have been shown as reliable tools for estimating the intrinsic magnetic field values (e.g. Stenflo 1973; Sanchez Almeida et al. 1988; Khomenko & Collados 2007; Smitha & Solanki 2017). Analysis of Stokes V profile widths is not a commonly used method, although Stokes V width is used in some solar and stellar magnetic field measurements (e.g. Donati & Landstreet 2009). In this study, we compare these two methods for the magnetic filling factor estimation.
Calibration curves for Veff[6301](B), Veff[6302](B), ![$\left[\frac{V_\mathrm{eff}[6301]}{V_\mathrm{eff}[6302]}\right](B),$](/articles/aa/full_html/2018/11/aa33421-18/aa33421-18-eq17.gif) and WV[6301](B) have been calculated using the NICOLE code (Socas-Navarro et al. 2000; Socas-Navarro 2011) for different values of uniform magnetic field from -2000 to 2000 G embedded into the Harvard-Smithsonian Reference Atmosphere (HSRA). Line width has been varied by the introduction of microturbulence with the amplitude from 0 to 6 km s−1.
and WV[6301](B) have been calculated using the NICOLE code (Socas-Navarro et al. 2000; Socas-Navarro 2011) for different values of uniform magnetic field from -2000 to 2000 G embedded into the Harvard-Smithsonian Reference Atmosphere (HSRA). Line width has been varied by the introduction of microturbulence with the amplitude from 0 to 6 km s−1.
Figure 6 shows the calibration curves V[6301](B) and V[6302](B), as well as actual Stokes V amplitudes obtained from the magneto-convection model. It can be seen that, on average, the actual values of V are similar to the calibration curves, although they seem to saturate faster at B > 1 kG. Most importantly, the actual V values show a very significant spread, which cannot be explained by different profile widths. This is not surprising, taking into account strong vertical magnetic field and velocity gradients, as well as the correlation of magnetic field and LOS velocities.
 |
Fig. 6. Panel a: calibration curves for the considered Fe I lines. Black and red lines are for the 6301.5 and 6302.5 Å lines, respectively. Solid and dashed lines are for line widths of 0.12 and 0.23, respectively. Panel b: Stokes V amplitudes taken from the MURAM-NICOLE simulations. Blue and orange dots are for the 6301.5 and 6302.5 Å lines, respectively. Black and red lines show sliding averages for the 6301.5 and 6302.5 Å lines, respectively. |
In the present study, we use the calibration curves V[6301](B) to measure the average magnetic field. This is done using calibration function Beff[6301] = G(V[6301], WI ± V[6301]), where G is tabulated for a range of input parameters.
Figure 7 shows calibration curves of MLR Veff[6301]/Veff[6302] and Stokes V widths of the 6301 Å line, WV[6301]. Different curves in Fig. 7 correspond to different widths of the I + V profile of the 6301.5 Å line. We intentionally use the I + V width, unlike in other studies using the Stokes I width; this is because the latter appears to be strongly affected by the magnetic field value, not only by macroturbulence velocity. It can be seen that both MLR and Stokes V width can be used for Breal estimations. The MLR is most efficient (i.e. has the highest derivative values) at moderate field values and saturates at 1200–1300 G. At the same time, the Stokes V width is efficient above 200–300 G, with WV[6301](Breal) being nearly flat at Breal < 250 G. Another benefit of using WV[6301] is that it appears to be less affected by line broadening compared to MLR. Thus, at Breal = 1000 G, the change of I ± V profile width from 0.15 to 0.25 Å (corresponding to the macroturbulent velocities of 0 and 4.5 km s−1) results in a change of MLR from 0.96 to 1.18, equivalent to a difference of about 600 G at constant width, while Stokes V width changes from 0.68 to 0.75, equivalent to a difference of less than 200 G.
 |
Fig. 7. Panel a: calibration curves for MLR. Panel b: calibration curves for Stokes V widths of the 6301.5 Å line. In both panels different lines correspond to different widths of the I ± V profile of the 6301.5 Å line: the lowest line corresponds to 0.12 Å and the highest line corresponds to 0.23 Å. Green dots show MLR values (left panel) and Stokes V widths (right panel) taken from the MURAM-NICOLE simulations. Values below 100 G are ignored. |
The MLR and Stokes V width calibration curves are used to estimate the real magnetic field values using calibration functions Breal = K(Veff[6301]/Veff[6302], WI ± V[6301]) and Breal = L(WV[6301], WI ± V[6301]), with the functions K and L tabulated for a range of input parameters. Therefore, the filling factor can be estimated either as
or as
5. Synthetic Stokes profiles calculated with low spatial resolution
5.1. Degraded Stokes profiles
In this section we investigate degraded synthetic I and V Stokes profiles. We recover the filling factor and vertical magnetic field gradient values using degraded synthetic profiles and compare them with those derived using actual magnetic field distributions in the MHD models.
Table 1 compares spatial resolution and the pixel size of Hinode/SOT, GREGOR Fabry-Prot Interferometer (GFPI), and Visible Spectro-Polarimeter (ViSP, part of DKIST) instruments. The chosen spatial resolution for degraded synthetic data is similar to the three instruments. It is two times higher than in Hinode/SOT and approximately two times lower than in Gregor and DKIST. We do not expect that spatial resolutions differing by a factor of two would make a substantial difference to the results discussed below and, therefore, our analysis should be applicable to the widely used Hinode/SOT, as well as future DKIST/ViSP.
A map of effective magnetic field Beff[6301] is shown in Fig. 2b. The field distribution is much smoother, it is impossible to see any sharp details on the convective scales. Unlike high-resolution maps, degraded maps do not show thin magnetic walls. As a result, it looks like the magnetic field consists of numerous blobs in the granulation cell boundaries. Most importantly, the statistical distribution of Beff[6301] values is different to that of the intrinsic field. The former does not have kilo-Gauss peaks, it is a smooth, monotonically-decreasing function. This can be explained by a horizontally non-uniform field structure with a wide range of filling factor variation.
Figure 8 shows values of Beff[6301] plotted against α, with red and blue colours indicating positive and negative LOS velocities. In snapshots B and C these plots reveal two quite distinct populations. The first has low magnetic field values (<100 G) and mostly positive LOS velocities. This population represents the weak magnetic field inside granulation cells. Another population has much stronger magnetic field (up to few kilo-Gauss) and mostly positive Doppler velocities. Hence, this population corresponds to the intergranulation network. The magnetic field values in this population are nearly proportional to the filling factor, Beff ∼ α, although the coefficient of proportionality is different for different snapshots. This effect can be easily explained by the two-component structure of photospheric magnetic field with nearly constant intrinsic field. Indeed, in this case Beff ∼ α B becomes Beff ∼ const α. Snapshot A, corresponding to the model with weaker initial field, reveals a slightly more complicated picture: it seems that the magnetic flux in this model is carried by few magnetic field components, which appear as separate strands in Fig. 8a. The fact that the effective magnetic field values are determined primarily by the filling factor is clearly demonstrated by the maps of α (Fig. 9a–c). Thus, the low-resolution magnetic field map for the snapshot C (Fig. 2b) is very similar to the distribution of α for the same snapshot (Fig. 9c).
 |
Fig. 8. Magnetic field values corresponding to low spatial resolution against the filling factor values in snapshots A, B, and C (panels a, b, and c, respectively). Red and blue dots correspond to positive and negative LOS velocities (positive and negative Doppler shifts). |
 |
Fig. 9. Magnetic filling factor α maps for snapshots A (left panels), B (middle panels), and C (right panels). Panels a–c show α calculated using actual field (i.e. using Formula (1) and MHD data), panels d–f, g–i, and j–l show α calculated using the MLR method (Eq. (6)), Stokes V width method (Eq. (7)), and statistical method (Eq. (8)), respectively. Magnetic filling factor values in pixels with magnetic field |B| < 100 G are ignored. |
5.2. Estimation of the filling factor using low-resolution data
Based on the calibration curves discussed in Sect. 3 and on the low-resolution data analysis discussed in Sect. 4, we can propose three methods to estimate the filling factor assuming a two-component magnetic field. Firstly, this can be done using Formula Eq. (6), with the intrinsic magnetic field estimated using the MLR approach. Secondly, this can be done using Formula Eq. (7) with the intrinsic field estimated using the width of Stokes V peaks. Finally, the filling factor can be estimated statistically, assuming that the intrinsic field is constant within a reasonably small area of the photosphere (up to a few square megameters). Indeed, for strong magnetic field > 100 G, the filling factor can be approximated as α ≈ κBeff + α0, where 1/κ should approximately be equal to the maximum Beff within the sample area. In order to reduce the error in κ evaluation, it is calculated as
where Beff, mean max is the average of the top 10% of field values. The best linear fit for the available data is provided by α0 = 0.215 and κ0 = 0.78. Maps of the filling factor estimated using different methods are shown in Fig. 9d–l.
Generally, all three methods, on average, seem to yield values close to the actual ones. However, it is difficult to compare the reliability of these methods based on the maps in Fig. 9. Hence, in Fig. 10 “recovered” values of the filling factor are plotted against their actual values. Because filling factor values are based on the intrinsic field estimations, these plots also demonstrate the reliability of Breal estimations using different methods.
 |
Fig. 10. Comparison of estimated values of the magnetic filling factor with real values. Left panels are for snapshot A, middle panels are for snapshot B, and right panels are for snapshot C. Panels a–c, d–f, and g–i correspond to the MLR method, Stokes V width method, and statistical method, respectively. Only pixels with magnetic field |B| > 100 G are shown here. |
It can be seen that using the MLR method (as per Eq. (6)) yields a very substantial spread as well as significantly underestimating filling factor values. In fact, this can also be seen in Fig. 9d–f. Using the Stokes V widths appears to yield more reliable results. This method slightly underestimates α below 0.5 and slightly overestimates it at higher values, however, it provides much better α estimations compared with using the MLR method. Finally, using the statistical approach (Eq. (8)) appears to provide the best estimations for the filling factor in snapshots B and C: this method seems to give values closest to the α = αreal line in Fig. 10g–i, as well as the smallest spread compared to the two other methods. At the same time, the statistical method does not work well for snapshot A; there are too many pixels with substantially underestimated α values. This can be explained by the multi-component field structure in snapshot A (see Fig. 8), with the statistical method requiring the intrinsic magnetic field to be nearly constant within the considered photospheric area.
It should be noted that it is practically possible to estimate the filling factor values only where the magnetic field is significantly above the noise level (approximately 50 G). In Figs. 9 and 10, values of α are calculated only for B > 100 G.
5.3. Estimation of vertical field gradient using low-resolution data
We now discuss the effect of vertical magnetic field inhomogeneity. It is well known that different parts of line profiles are sensitive to different heights in the photosphere: the core is more sensitive to higher layers, close to the temperature minimum, while wings are more sensitive to hotter, deeper photospheric layers. Therefore, the vertical distribution of physical parameters in the photosphere can be studied using the shapes of the Stokes profile bisectors (e.g. Rimmele 1995; Tritschler et al. 2004; Sankarasubramanian & Rimmele 2002). Figure 11 shows values of the bisector splitting gradient (BSG) plotted against vertical magnetic field gradient separately for positive (network) and negative (cells) LOS velocities. Both snapshots clearly show a strong correlation between these values, with dΔλH/dδ λ nearly linearly changing with dB/dz. Best linear fits have been calculated using the data from different snapshots added together, however, they have been calculated separately for positive and negative velocities (dashed lines in Fig. 11). Regions with positive velocities (photospheric network) show mostly negative field gradients (field becomes stronger with depth), while regions with negative velocities (granulation cells) show predominantly positive field gradients. This also can be seen from the maps of dB/dz (Fig. 12a–c). This is in agreement with the widely-accepted model of the magnetic field in the solar atmosphere (see e.g. review by Wedemeyer-Böhm et al. 2009).
 |
Fig. 11. Bisector splitting gradients of I ± V profiles versus vertical gradients of magnetic field for snapshots A, B, and C (panels a, b, and c, respectively). Red and blue dots correspond to pixels with positive (downflow) and negative (upflow) Doppler velocities, respectively. Dashed lines show corresponding best linear fits. |
 |
Fig. 12. Maps of vertical magnetic field gradients measured directly from the model and reconstructed using BSG. The left, middle, and right panels are for snapshots A, B, and C, respectively. Panels a–c: show real gradients (measured from the MHD model), and panels d–f show constructed field gradient values. The colour scale is in units of 10−3 G m−1. Magnetic field gradient values on panels d–f are calculated only for pixels with magnetic field |B| > 100 G. |
The linear fits for the diagrams in Fig. 11 are
where k is −1.37 × 10−4 and −1.83 × 10−4, and a is −5.97 × 10−5 and −5.30 × 10−6 for positive and negative velocities, respectively. In this formula, 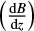 is in units of G m−1 and
is in units of G m−1 and 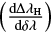 is dimensionless (Å/Å). This simple formula can be used to recover values of magnetic field gradient using degraded Stokes profiles. Maps of actual and recovered values of magnetic field gradient are compared in Fig. 12. Generally, they are in good agreement, both qualitatively and quantitatively, although the recovered gradient maps are more noisy and have several patches where negative gradient values are significantly overestimated. Most likely this is because the linear approximation used for gradient evaluation fails below dBz/dz < −0.0010 G m−1, which is clearly seen in Fig. 12b and c. Using higher order polynomials would improve the reliability of the method, while making it more computationally expensive, which may be a problem for large field-of-view data analysis.
is dimensionless (Å/Å). This simple formula can be used to recover values of magnetic field gradient using degraded Stokes profiles. Maps of actual and recovered values of magnetic field gradient are compared in Fig. 12. Generally, they are in good agreement, both qualitatively and quantitatively, although the recovered gradient maps are more noisy and have several patches where negative gradient values are significantly overestimated. Most likely this is because the linear approximation used for gradient evaluation fails below dBz/dz < −0.0010 G m−1, which is clearly seen in Fig. 12b and c. Using higher order polynomials would improve the reliability of the method, while making it more computationally expensive, which may be a problem for large field-of-view data analysis.
6. Summary
In this study, we analyse synthetic I and V Stokes profiles of Fe I 6301.5 and 6302.5 Å lines derived using a magneto-convection model of the photospheric magnetic field, as well as calibration curves derived for these lines. Based on this analysis, three different methods of estimating the intrinsic magnetic field and the magnetic filling factor in the solar photosphere are compared. For this pair of lines we show that:
The Stokes V width method appears to be quite reliable for the intrinsic magnetic field and filling factor estimations above 200–300 G and does not show any saturation up to at least 2 kG. Moreover, Stokes V widths seem to be less sensitive to the line width. Therefore, this method appears to be the best for the Breal and α estimation using the 6301 line.
The statistical approach can be very efficient for estimating α values within a small patch of the photosphere when the intrinsic field is likely to be nearly constant. Obviously, it cannot be applied to large or very inhomogeneous, active photospheric areas.
-
The magnetic line ratio method can be used for intrinsic magnetic field and the filling factor using the 6301–6302 Å pair. However, it appears to be the least reliable method because of the formation height difference and saturation. Furthermore, MLR is more sensitive to the line width (Sect. 4), and hence an error in evaluating the line width would increase the error in derived Breal values. This, in turn, would translate to an even higher error in estimated Beff/Breal values.
However, it should be noted that the MLR approach can be very efficient for Breal and α estimations using other line pairs, which do not saturate in a wider magnetic field range (see Khomenko & Collados 2007; Smitha & Solanki 2017, and references therein). Finally, we find that BSG correlates with the LOS gradient of the magnetic field. Linear calibration functions dB/dz(BSG) calculated separately for lines with positive and negative Doppler shifts provide quite reliable maps of the photospheric magnetic field gradient.
Acknowledgments
MG and PKB are funded by Science and Technology Facilities Council (UK), grant ST/P000428/1. Simulations have been performed using the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility.
References
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 114, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Frazier, E. N., & Stenflo, J. O. 1972, Sol. Phys., 27, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., & Lozitsky, V. G. 2014, Sol. Phys., 289, 3681 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., & Stenflo, J. O. 1972, Sol. Phys., 22, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U. 1992, Nature, 359, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U., & von der Lühe, O. 1992, A&A, 261, 321 [NASA ADS] [Google Scholar]
- Khomenko, E., & Collados, M. 2007, ApJ, 659, 1726 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., Shelyag, S., Solanki, S. K., & Voegler, A. 2005, A&A, 442, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H. 1995, ApJ, 446, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Lozitska, N. I., & Lozitsky, V. G. 1994, Sol. Phys., 151, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmele, T. R. 1995, A&A, 298, 260 [NASA ADS] [Google Scholar]
- Sanchez Almeida, J., Solanki, S. K., Collados, M., & del Toro Iniesta, J. C. 1988, A&A, 196, 266 [NASA ADS] [Google Scholar]
- Sankarasubramanian, K., & Rimmele, T. 2002, ApJ, 576, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A., & Solanki, S. K. 2003, ApJ, 597, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Schüssler, M., Solanki, S. K., Berdyugina, S. V., & Vögler, A. 2004, A&A, 427, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smitha, H. N., & Solanki, S. K. 2017, A&A, 608, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J. & Ruiz Cobo, B. 2000. ApJ, 544, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2011, A&A, 529, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Schüssler, M. 2004, ASP Conf. Ser., 325, 105 [NASA ADS] [Google Scholar]
- Spruit, H. C. 1974, Sol. Phys., 34, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1973, Sol. Phys., 32, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., Schlichenmaier, R., Bellot Rubio, L. R., et al. 2004, A&A, 415, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tritschler, A., Rimmele, T. R., Berukoff, S., et al. 2016, Astron. Nachr., 337, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchie, B., Sanchez Almeida, J., Del Moro, D., & Berrilli, F. 2011, A&A, 526, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volkmer, R., von der Lühe, O., Denker, C., Solanki, S. K., et al. 2010, Astron. Nachr., 331, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer-Böhm, S., Lagg, A., & Nordlund, A. 2009, Space Sci. Rev., 144, 317 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spatial resolution around 6300Å and pixel size for three optical solar imaging spectrographs and for the synthetic degraded Stokes cubes used in this study (Kosugi et al. 2007; Volkmer et al. 2010; Tritschler et al. 2016).
All Figures
 |
Fig. 1. Sketch of a line profile, showing Stokes I profile (panel a), Stokes V (panel b), and Stokes I ± V profiles (panel c) with some of their parameters used in this paper. |
| In the text | |
 |
Fig. 2. Magnetic field in snapshot C at different spatial resolutions. Panel a: magnetic field measured using Stokes V amplitudes of the 6301 line with high spatial resolution (not calibrated). Panel b: map of Beff[6301], magnetic field from the same model snapshot, but representing low-resolution data. |
| In the text | |
 |
Fig. 3. Magnetic field distribution function in snapshots A, B, and C (panels a, b, and c, respectively). The black dashed lines correspond to the actual field taken from the high-resolution MHD simulations. Solid blue lines with squares correspond to the magnetic field measured with high resolutions using Stokes V amplitudes of the 6301 line. Blue bars correspond to the effective magnetic field Beff[6301] (see Sect. 5). |
| In the text | |
 |
Fig. 4. MLR value spectra from snapshots A, B, and C (panels a, b, and c, respectively). The line corresponds to MLR measured with the original MHD model resolution, while the bars correspond to MLR measured using Stokes V amplitudes obtained with low spatial resolution. |
| In the text | |
 |
Fig. 5. Same as in Fig. 4 but for the Stokes V width values. |
| In the text | |
 |
Fig. 6. Panel a: calibration curves for the considered Fe I lines. Black and red lines are for the 6301.5 and 6302.5 Å lines, respectively. Solid and dashed lines are for line widths of 0.12 and 0.23, respectively. Panel b: Stokes V amplitudes taken from the MURAM-NICOLE simulations. Blue and orange dots are for the 6301.5 and 6302.5 Å lines, respectively. Black and red lines show sliding averages for the 6301.5 and 6302.5 Å lines, respectively. |
| In the text | |
 |
Fig. 7. Panel a: calibration curves for MLR. Panel b: calibration curves for Stokes V widths of the 6301.5 Å line. In both panels different lines correspond to different widths of the I ± V profile of the 6301.5 Å line: the lowest line corresponds to 0.12 Å and the highest line corresponds to 0.23 Å. Green dots show MLR values (left panel) and Stokes V widths (right panel) taken from the MURAM-NICOLE simulations. Values below 100 G are ignored. |
| In the text | |
 |
Fig. 8. Magnetic field values corresponding to low spatial resolution against the filling factor values in snapshots A, B, and C (panels a, b, and c, respectively). Red and blue dots correspond to positive and negative LOS velocities (positive and negative Doppler shifts). |
| In the text | |
 |
Fig. 9. Magnetic filling factor α maps for snapshots A (left panels), B (middle panels), and C (right panels). Panels a–c show α calculated using actual field (i.e. using Formula (1) and MHD data), panels d–f, g–i, and j–l show α calculated using the MLR method (Eq. (6)), Stokes V width method (Eq. (7)), and statistical method (Eq. (8)), respectively. Magnetic filling factor values in pixels with magnetic field |B| < 100 G are ignored. |
| In the text | |
 |
Fig. 10. Comparison of estimated values of the magnetic filling factor with real values. Left panels are for snapshot A, middle panels are for snapshot B, and right panels are for snapshot C. Panels a–c, d–f, and g–i correspond to the MLR method, Stokes V width method, and statistical method, respectively. Only pixels with magnetic field |B| > 100 G are shown here. |
| In the text | |
 |
Fig. 11. Bisector splitting gradients of I ± V profiles versus vertical gradients of magnetic field for snapshots A, B, and C (panels a, b, and c, respectively). Red and blue dots correspond to pixels with positive (downflow) and negative (upflow) Doppler velocities, respectively. Dashed lines show corresponding best linear fits. |
| In the text | |
 |
Fig. 12. Maps of vertical magnetic field gradients measured directly from the model and reconstructed using BSG. The left, middle, and right panels are for snapshots A, B, and C, respectively. Panels a–c: show real gradients (measured from the MHD model), and panels d–f show constructed field gradient values. The colour scale is in units of 10−3 G m−1. Magnetic field gradient values on panels d–f are calculated only for pixels with magnetic field |B| > 100 G. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



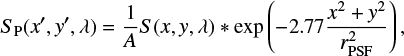

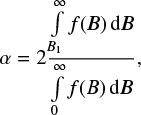
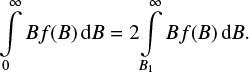



![$$ \begin{equation} \alpha = \frac{G({V_{\rm eff}}[6301])}{K({V_{\rm eff}}[6301]/V_{\rm{eff}}[6302])} \end{equation} $$](/articles/aa/full_html/2018/11/aa33421-18/aa33421-18-eq18.gif)
![$$ \begin{equation} \alpha = \frac{ G({V_{\rm eff}}[6301]) }{L({W_{\rm V}}[6301]) }\cdot \end{equation} $$](/articles/aa/full_html/2018/11/aa33421-18/aa33421-18-eq19.gif)