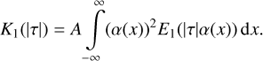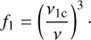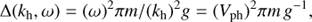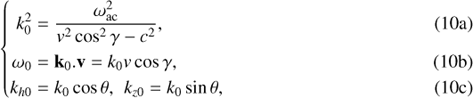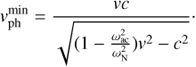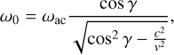| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201832896 | |
| Published online | 08 November 2018 | |
Lost and found sunquake in the 6 September 2011 flare caused by beam electrons
1
E.A. Milne Centre for Astrophysics, School of Mathematics and Physical Sciences, Hull University, Kingston upon Hull, HU6 7RX, UK
e-mail: s.zharkov@hull.ac.uk
2
Northumbria University, Department of Mathematics, Physics and Electrical Engineering, Newcastle upon Tyne NE1 8ST, UK
3
Stockholm University, Department of Astronomy, 106 91 Stockholm, Sweden
4
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
5
Institute for Space and Astronautical Science, Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 252-5210, Japan
Received:
23
February
2018
Accepted:
16
July
2018
The active region NOAA 11283 produced two X-class flares on 6 and 7 September 2011 that have been well studied by many authors. The X2.1 class flare occurred on September 6, 2011 and was associated with the first of two homologous white light flares produced by this region, but no sunquake was found with it despite the one being detected in the second flare of 7 September 2011. In this paper we present the first observation of a sunquake for the 6 September 2011 flare detected via statistical significance analysis of egression power and verified via directional holography and time–distance diagram. The surface wavefront exhibits directional preference in the north-west direction We interpret this sunquake and the associated flare emission with a combination of a radiative hydrodynamic model of a flaring atmosphere heated by electron beam and a hydrodynamic model of acoustic wave generation in the solar interior generated by a supersonic shock. The hydrodynamic model of the flaring atmosphere produces a hydrodynamic shock travelling with supersonic velocities toward the photosphere and beneath. For the first time we derive velocities (up to 140 km s−1) and onset time (about 50 s after flare onset) of the shock deposition at given depths of the interior. The shock parameters are confirmed by the radiative signatures in hard X-rays and white light emission observed from this flare. The shock propagation in the interior beneath the flare is found to generate acoustic waves elongated in the direction of shock propagation, that results in an anisotropic wavefront seen on the solar surface. Matching the detected seismic signatures on the solar surface with the acoustic wave front model derived for the simulated shock velocities, we infer that the shock has to be deposited under an angle of about 30° to the local solar vertical. Hence, the improved seismic detection technique combined with the double hydrodynamic model reported in this study opens new perspectives for observation and interpretation of seismic signatures in solar flares.
Key words: Sun: flares / Sun: X-rays, gamma rays / Sun: helioseismology / radiative transfer / hydrodynamics
© ESO 2018
1. Introduction
Sunquakes are localised flare-induced acoustic waves first predicted by Wolff (1972) and later observed by Kosovichev & Zharkova (1998). They are often seen as ripples radially emanating from a point source from 20–30 min to up an hour after a flare onset. These ripples are suggested (Kosovichev & Zharkova 1998; Zharkov et al. 2013a) to be the reflections from the solar surface of acoustic (in some cases, magneto-acoustic) waves induced by a sharp deposition of momentum (and energy) on the solar surface.
Sunquakes are detected on the solar surface using helioseismic methods such as time–distance (TD) diagram analysis (Kosovichev & Zharkova 1998) and acoustic holography (Donea et al. 1999, 2000; Lindsey & Braun 1999, 2000; Donea & Lindsey 2005). TD diagram analysis is an observationally direct method that uses Dopplergram data where a surface wavefront is identified by an apparent ridge in a time–distance diagram. Acoustic holography uses a model of the solar interior to estimate acoustic sources and sinks from the observed Dopplergram series. The sunquake origin is normally indicated by a compact bright (source) kernel peaking during the flare verified by statistical tests (Matthews et al. 2011). TD diagrams and acoustic holography have been shown to be complementary (Zharkov et al. 2011b, 2013a,b; Buitrago-Casas et al. 2015).
The occurrence of sunquakes is often accompanied by strong high-energy emission in HXR, extreme ultra-violet (EUV) and white light (WL) wavelengths (Matthews et al. 2015). Sunquakes have been detected in X-class (see, for example Kosovichev & Zharkova 1998; Zharkova & Zharkov 2007; Moradi et al. 2007), M-class (Donea et al. 2006) and even in C-class (Sharykin et al. 2015) flares, while the most powerful sunquakes are associated with M-class flares (Donea 2011). In addition, during some flares there are also essential changes in the photospheric magnetic field often observed well above the noise levels – both on short timescales of minutes (impulsive phase) and longer timescales of hours (Kosovichev & Zharkova 2001; Zharkova & Gordovskyy 2005; Sudol & Harvey 2005; Petrie 2016). The magnetic field changes in flare locations can be as large as several hundred Gauss, well above the background noise of any instruments (Zharkova & Gordovskyy 2005). Recently Green et al. (2017) explored the role of an active regions magnetic field topology in establishing the conditions leading to the production of sunquakes. They determined that some localised magnetic configurations appear to be more effective in channeling the energy and momentum to the lower atmosphere. This variety of complex sunquake signatures and their association with flares poses the key unresolved questions about a physical mechanism, or mechanisms, responsible for their initiation and subsequent development.
The first of the mechanisms proposed for generating sunquakes is a hydrodynamic response of flaring atmospheres to the injection of energetic particle beams, which reveals strong hydrodynamic shocks travelling downward toward photospheric levels (Zharkova & Zharkov 2007, 2015; Somov et al. 1981; Fisher et al. 1985a,b; Allred et al. 2005). Hydrodynamic shocks in flares are generally found to be generated by energetic particles (electrons or protons) accelerated in a current sheet produced during a flare by interacting magnetic loops. These particles precipitate into the loop footpoints and deliver to the photosphere the energy and momentum gained by these particles during a magnetic reconnection process. Authors have considered either energetic electrons (Kosovichev & Zharkova 1998; Donea & Lindsey 2005; Kosovichev 2006) or proton or mixed electron-proton beams (Zharkova & Zharkov 2007, 2015)asthe agents capable of delivering this energy.
Some authors have suggested radiative back-warming as a source of pressure transients that can produce acoustic waves (Donea et al. 2006; Donea 2011). However, observations show that not all sunquakes are associated with WL emission, with some found in the locations with little or no HXR and white-light emission (Matthews et al. 2011; Buitrago-Casas et al. 2015; Zharkov et al. 2011a). Based on the complex magnetic picture of flaring events, another driving mechanism is proposed to be related to the Lorentz force. While many sunquakes are seen to be associated with the variations of longitudinal magnetic fields of flares (Hudson et al. 2008; Fisher et al. 2012) and magneto-acoustic wave conversion (Cally 2006; Hansen et al. 2016), the precise role of Lorentz force transients remains to be fully established. The common element for all of these mechanisms is magnetic reconnection initiating a solar flare and, in many cases, an associated eruption. However, the question about which of these mechanisms is the main driver of seismic responses occurring during flaring processes remains open and needs further investigation.
The hydrodynamic processes in solar flares are normally tested by observations of blue shifts in coronal lines caused by evaporation of the chromospheric plasma into the corona (Zharkova & Zharkov 2007; Somov et al. 1981; Fisher et al. 1985a,b; Allred et al. 2005) and red shifts in the optical hydrogen emission in Hα and other lines (Ichimoto & Kurokawa 1984; Wuelser & Marti 1989). This red-shifted Hα emission often leads to a disappearance of Hα emission in the line core and reappearance again 10−20 s later (Druett & Zharkova 2018). In addition, precipitation of energetic electrons in solar flares leads to strong nonthermal plasma ionisation and prolonged white-light (WL) emission (Buitrago-Casas et al. 2015; Zharkova 2008; Kuhar et al. 2016; Kawate et al. 2016).
Recently, using a joint hydrodynamic (Zharkova & Zharkov 2007, 2015) and full non-LTE model Druett et al. (2017) produced the first quantitative interpretation of the EUV emission recorded by AIA instrument onboard SDO and associated Hα line profiles with large redshifts recorded by the Swedish Solar Telescope (SST) at the onset of a C1.5-class solar flare. The line shifts were shown to be caused by the chromospheric evaporation combined with shocks generated by hydrodynamic response to the injection of beam electrons. This provided the first explanation of the past Hα observations with large red shifts and even the disappearance of this emission for up to 30 s reported for the past three decades (Ichimoto & Kurokawa 1984; Wuelser & Marti 1989). The success of this interpretation of EUV and Hα emission highlighted the effect of hydrodynamic shocks on a flaring atmosphere induced by electron beams, which are shown to deliver a noticeable part of energy toward lower atmospheric levels.
This motivated us to investigate the effects of hydrodynamic shocks on the solar interior in an attempt to find some quantified characteristics of the shocks derived from optical emission and to test whether their energy is sufficient to account for signatures of sunquakes. In this paper we applied a modified technique to detect a sunquake in the flare of 6 September 2011, which was previously reported not to have any (Liu et al. 2014). Subsequently, we provide interpretation of this sunquake properties (timing, directionality) using a hydrodynamic model for plasma heating by beam electrons as an input for the hydrodynamic model for acoustic wave propagation in the solar interior. This allows us to produce the first successful quantitative interpretation of the simultaneous seismic and optical signatures recorded for this flare.
The observations of this flare are reported in Sect. 2, the models of a flaring atmosphere are described in Sect. 3, probing these models with optical observations is shown in Sect. 4, the model of acoustic wave propagation and its comparison with seismic observations is discussed in Sect. 5 and conclusions are drawn in Sect. 6.
2. Observations
2.1. Active region with X2.1 flare of 6 September 2011
Active region (AR) NOAA 11283 produced two X-class flares that have been well studied by many authors, including the properties of associated flare emission (Xu et al. 2014), the observed magnetic field changes (Liu et al. 2014; Petrie 2016) and flare energetics (Feng et al. 2013). The X2.1 class flare occurred on September 6, 2011 and was the first of two WL homologous flares produced by this region, with an X1.8 class flare produced on the following day (not studied in this work). Both the X2.1 and X1.8 flares are seen to be morphologically similar (Liu et al. 2014), but only the X1.8 event appeared to produce a sunquake (Zharkov et al. 2013a). At the time of X2.1 flare studied herein, the AR had a βγ – βδ configuration containing one δ spot.
Observationally, the X2.1 flare starts with the activation of an S-shaped sigmoid, representing a flux rope, as seen in the 94 Å AIA data (Fig. 1a). During flare onset (22:18:37 UT) one observes two flaring loops and a circular Hα ribbon (Fig. 1b), similar to that reported by Kawate et al. (2016). NOAA 11283 undergoes a period of flux emergence prior to the September 6 flare leading to fan-spine reconnection initiating the flare (Jiang et al. 2014). This process leads to repeated eruptions with a stronger eruption occurring to the south at 22:19 UT, followed by the ribbons that form a circular structure, as expected from a reconnection at the null point of the fan-spine configuration (Janvier et al. 2016). Using NLFFF extrapolation and MHD simulations, the sigmoid eruption was shown to proceed due to the torus instability (Jiang et al. 2013). This flux rope eruption signalled the possible occurrence of a sunquake as first noted by Zharkov et al. (2011a) for the flare of 15 February 2011.
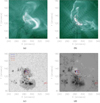 |
Fig. 1. AIA 94 Å images at 22:10 UT with an s-shaped sigmoid and flux rope prior to flare onset (panel a) and the two flaring loops and circular ribbon formed during the flare (22:18:37 UT) (panel b). Red and black contours denote 500 and −500 Gauss LOS magnetic field respectively. HXR emission at 50−100 keV (solid contours) highlights two closely spaced sources in panel b, with TD source (black cross) located close to the northern HXR source. The context images of both HMI continuum and LOS magnetogram at 22:18:37 UT are given in panels c and d, with detected source location contours from the statistical test on full-angle egression power maps. Regions of a significant acoustic signal are given for the 4–7 mHz pass bands, in addition to the location of the time– distance source origin. HXR emission is represented as dashed contours in panels c and d for clarity. |
2.2. X-rays, Hα and white light (WL) flare emission
GOES observations indicate flare onset occurred at 22:13 UT, with two close HXR peaks between 22:18 and 22:19 UT (Fig. 2, HXR) and SXR peaking at 22:20 UT (Fig. 2, SXR). Figure 2 (LOS B, WL) shows the variations in the spatially averaged LOS magnetic field and continuum intensity at the quake location. WL intensity begins to rise prior to the quake onset peaking at 7% following the quake, while, in general, for flares the maximum WL enhancement can reach up to 20% (Xu et al. 2014) and slowly, over 15 min, fades to the pre-flare level. We observe magnetic field variations showing the signs of global restructuring (associated with a magnetic reconnection) settling eventually at lower than pre-flare levels, reducing the LOS magnetic field magnitude by ~30–40 gauss.
There are also the transient magnetic field changes observed during the flare onset indicating to a presence of energetic electrons (Zharkova & Zharkov 2007). Negative polarity kernel 1 is located in the northern positive umbra and a smaller positive transient is recorded in the south kernels. These kernels are situated on either side of the polarity inversion line (PIL), with the stronger magnetic transient located in the northern positive umbra. These magnetic field features suggest that the flare is initiated by a magnetic field reconstruction leading to the rope eruption, which, in turn, led to the occurrence of relativistic electrons confirmed by the magnetic transients.
There are two closely separated sources of 50−100 keV HXR emission during the flare, co-spatial to the observed WL kernels. However, it is the northern kernel with weaker emission where we detect the acoustic source (Figs. 1c and 1d). These observations agree with the two 30−80 keV sources observed by Kuhar et al. (2016) for this flare (see their Fig. 1).
In order to extract HXR parameters required for modelling the hydrodynamic response, spectral fitting across the flare duration is carried out using Object Spectral Executive (OSPEX) for RHESSI data from all collimators bar 2 and 7. To retrieve an initial electron flux and spectral index we select the time period 22:18:16–22:18:36 UT, during the quake onset (interval 20, see Fig. 2, right top plot), and fit using a variable thermal (green) and thick-target bremsstrahlung (yellow) component. The resultant two-component fit (red) is made over the energy range 12– 270 keV, dictated by the detector’s attenuator state and the drop off to background levels of photon flux. Background levels are determined from RHESSI nighttime prior to the event. From the fit displayed in Fig. 2, we extract the following initial parameters: the initial energy flux F0 = 4.3 × 1011 erg cm−2 s−1 and spectral index γ = 3.5. The second HXR peak occurred at ≈22:19:20 UT, where a similar fitting procedure provides the following parameters: F0 = 3.7 × 1011 erg cm−2 s−1 and spectral index γ = 4.0.
Moreover, in these two regions there is enhanced WL emission (WL kernels 1 and 2) observed during the flare onset, or its impulsive phase, which is co-spatial with the velocity and LOS magnetic field transients (Fig. 1d). The WL kernel brightenings appear at chromospheric and photospheric levels at 22:10 UT (Xu et al. 2014) quickly evolving into flare ribbons that grow to full-length by 22:18 UT (Figs. 1a and 1b). As the two ribbons evolve almost perpendicularly to each other, another circular ribbon encircles the two ribbon structure (Janvier et al. 2016; Kawate et al. 2016). Averaging over the seismic source location one can see that all the transients and WL emission are co-temporal with one another, situated prior to SXR peak and between the dual HXR peaks (Fig. 2).
 |
Fig. 2. Left plots: light curves of RHESSI 100−300 keV HXR (HXR), GOES (1.0−8.0 Å) SXR (SXR), integrated HMI LOS magnetogram (LOS B), WL continuum (WL) and egression power (EGR). The HMI data products are integrated over the seismic signal. Black vertical dotted line denotes the sunquake onset time (22:18:37 UT) from time–distance diagrams (Fig. 3d). Continuum emission shows a peak emission at 22:18:37 UT, coincident with quake onset and LOS magnetogram transient. Egression power, normalised with respect to quiet sun levels, peaks above a defined detection threshold (red horizontal line) of the local mean (yellow) plus 5σ within the flare window (blue vertical lines). Right plots: photon flux spectrum for the time interval 22:18:16–22:19:12 UT with variable thermal (green) and thick-target bremstrahlung (green) fitting giving the total fit (red) over the 12−270 keV energy range (bounded in black; top) and respective residuals of fitting (bottom). |
2.3. Detecting a missing sunquake
Helioseismic analysis requires four hour datacubes of full-disc HMI/SDO (Schou et al. 2012) dopplergrams, intensity continuum and LOS magnetograms, which are obtained using the JSOC database. Remapping and de-rotating at the region of interest is carried out using Postel projection and Snodgrass differential rotation rate. The resultant spatial resolution is then 0.04° per pixel, or 0.486 Mm per pixel, with 45 s cadence. In this work, for detection of the missing sunquake both time–distance and helioseismic holography combined statistical significance analysis of egression power are applied. Additionally, the egression power from acoustic holography has been treated directionally, in order to analyse anisotropy of the source.
2.3.1. Time–distance diagram
Time–distance diagrams (Kosovichev & Zharkova 1998; Zharkov et al. 2013a,b) aim to measure and to interpret travel times of acoustic waves on the solar surface. They are computed by choosing a central point source location, then rewriting the observed velocity signal at the surface into polar co-ordinates, and applying an azimuthal transformation as follows:
over a full circle or over a selected arc (if the ripples are directional). After about 20 s from a flare onset the surface wavefront can be seen as ripples travelling with an increasing speed from the flare site. In the time–distance diagram the locations of ripples are plotted versus the times that is presented as a ridge describing the ripple travel, which can be compared with a theoretical ray path. This ridge can be extrapolated back in time allowing for more precise determination of the onset time of the acoustic source. Not all flares show discernible ripples despite some of them still having seismic signatures detected with a helioseismic holography.
2.3.2. Acoustic holography
Helioseismic holography is the phase-coherent computational reconstruction of the acoustic field into the solar interior, in order to produce stigmatic images of the subsurface sources generating the disturbance (Braun & Lindsey 2000). Central to calculating egression is the Green’s function, which describes acoustic wave propagation from a point source in order to backtrack the observed surface signal. Generally, these functions can be constructed through ray theory (Lindsey & Braun 2000; Zharkov et al. 2011a) for a monochromatic point source, as used in this work, or through wave theory (Lindsey & Braun 2004). Egression is calculated from the Green’s function, G+(|r − r′|, ν), as such in the temporal Fourier domain (Zharkov et al. 2013a,b):
where 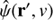 represents the surface signal obtained from the HMI data, r and θ are polar coordinates around the sources as in Eq. (1), whilst a and b define the dimensions of the holographic pupil. Taking the inverse Fourier transform one can obtain:
represents the surface signal obtained from the HMI data, r and θ are polar coordinates around the sources as in Eq. (1), whilst a and b define the dimensions of the holographic pupil. Taking the inverse Fourier transform one can obtain:
Egression power is then calculated by integrating the modulus squared over time as such:
Sunquakes are usually identified as localised enhanced emission coincident with the flare spatially and temporally, with the acoustic egression kernels usually identified on egression power snapshots around the time of the flare, P(r, tflare), via a suitable threshold.
In this paper we use directional holography, splitting the pupil into arcs, that is the azimuthal angle, θ integration in Eq. (2) between 0 and 2π is instead, carried out over an arc of, for example, 0 to π/2. Dividing by the total power will then supply a fraction of egression power from acoustic waves that have travelled in the selected direction. Therefore, this allows for a quantitative consideration of source anisotropy, or simply, directional distribution of of the acoustic power emitted from a source.
Helioseismic egression is computed from the single frame running difference SDO/HMI dopplergrams, with a pupil size of 10−80 Mm. Frequency ranges are chosen from the acoustic spectrum as 1 mHz bands, incrementally increasing from 2.5−3.5 mHz to 9.5−10.5 mHz – denoted from here on in as the central frequency of each band. To note: the band size selection induces a limit to egression time resolutions of Δt = 1/1 mHz = 1000 s.
To account for weak and dispersed sunquake sources that may be obscured by stochastic noise, even within acoustically damped sunspot features, we have developed a reliable semi-automated statistical method allowing confident detection of a sunquake. In order to detect a significant seismic signal above the background noise the following procedures are to be carried out:
Firstly, apply a 21 × 21 pixel (10.2 × 10.2 Mm) box smoothing to the full datacube.
Choose temporal window encompassing impulsive phase of the flare in which to search for signal. This ensures the testing occurs only in the time frame where one expects a source to appear, as well as to avoid any strong signal being included in the calculation of statistical parameters.
A boundary of 50 pixels (24.3 Mm) from each box edge is established to exclude the data input from the datacube edges, which can suffer from anomalies induced during the egression computation. As remapping is carried out to the centre of a flare location, this does not affect the resultant detections.
Now, for all pixels within the selection parameters and in each frequency band, a signal-to-noise test is applied with a threshold of 5σ. Through the analysis of known seismic events, we find a threshold of 5σ can be only exceeded by the acoustic signals driven by a flare impulse, and rarely exceeded by the stochastic emission.
Similar to egression kernels described above, we define statistical kernels as smoothed egression regions where signal is above 5σ threshold of the statistical significance level.
As a result of the application of this technique, we expect that a significant signal in any frequency band will exceed the 5σ threshold above the local mean of the background signal (Zharkov et al. 2011a). This, however, is an insufficient definition, as occasionally we see stochastically driven noise, in for example the quiet sun, exceed this threshold in low frequency bands (which are more susceptible to stochastic noise). Therefore, we enforce a number of additional constraints for the seismic detection described below.
Initially, for a proven seismic signal, we require a successful detection in the 6 mHz band. The lower end of the acoustic spectrum (2−5 mHz) exhibits increased ambient noise due to convection (p-modes, for example) which can compete unfavourably with acoustic emission (Donea et al. 2006). As the sub-photosphere is an effective specular reflector, low frequency waves will undergo a number of surface skips whilst retaining coherency (Donea et al. 2000), meaning that emission in the vicinity of a pupil centre is in part comprised of p-mode energy reflection from elsewhere (Lindsey & Braun 1999). Oppositely, at frequencies above 5 mHz, the quiet sun photosphere reflectivity becomes a close to perfect absorber, thereby inducing a limit of a single surface skip (Lindsey & Braun 1999; Donea et al. 2000).
In addition, the acoustic waves of these frequencies offer finer diffraction limit and improved depth discrimination (Donea et al. 2000). Therefore, signals appearing in 6 mHz egression power images can be attributed as more likely seismic sources due to the decreased, p-mode induced, background noise level, which is lower by more than an order of magnitude (Donea & Lindsey 2005; Donea et al. 2006). Strong seismic events show kernel brightening across the acoustic spectrum. Thus, we crucially expect further seismic signatures to be visible in the multiple frequency bands above and below this frequency of 6 mHz. Naturally, these detections will be both co-spatial and co-temporal with the 6 mHz signal, appearing as the signal overlaps.
2.3.3. Detection results – holography
Helioseismic egression is computed from a single frame running difference of the SDO/HMI Dopplergrams (Schou et al. 2012), with a pupil size of 10−80 Mm. We run a semi-automated statistical testing, as described in the section above, on a flare window of 22:09:37–22:29:07 UT in all the frequency bands. Significant signals are detected in 1 mHz frequency ranges around 4, 5, 6 and 7 mHz. The detected statistical egression kernel is bounded by red solid contours in the 6 mHz egression snapshot in Fig. 3a, located around 284″×129″– 6 mHz is typically where the strongest acoustic sources are observed. Another 6 mHz source (Fig. 3a) and a 7 mHz source are highlighted in Figs. 1c and 1d, away from the detected sunquake source. These detections do not pass the necessary conditional tests to be verified as seismic sources, therefore, they are ignored. We note that the statistical kernels have different properties when compared to the egression kernels usually used in acoustic holography. For instance, apart from the capability to detect diluted signals, another clear difference would be smudging of a (usual) compact egression kernel due to the integration used in the statistical procedure.
In order to provide a spatial reference, Fig. 1c displays the source location contours, as determined by the detection code, for frequency bands 4–7 mHz over intensity continuum at 22:18:37 UT. It is clearly seen that the source is located in the penumbra to the north of the AR. In comparisons with LOS magnetogram reference at 22:18:37 UT, we see the source to be located in the parasitic positive polarity region of the AR (Fig. 1d), in close vicinity to the umbral transient perturbation seen at the time of the flare – where we see WL emission peak and LOS magnetogram step change. Following methodology described by Zharkov et al. (2013a,b), we estimate the acoustic energy emitted from the source region into the 10–80 Mm pupil through 3–10 mHz frequency bands to be 8.26 × 1027 erg.
Directional egressions (calculated from the selected arcs of the input pupil (see the previous section), highlight the anisotropy of the seismic source, with the enhanced acoustic brightening observed within the source location in the input arc of 0°−90° in Fig. 3b. Here, 0° is defined as the west on the solar disc, progressing anti-clockwise. This source is highlighted using the overplot 6 mHz statistical test result from Fig. 3a, where it is centred at 284″ × 129″(black cross). By plotting the value of directional egression power, in terms of local nonflaring levels, at 284″ × 129″against arc starting angle (Fig. 3c), the anisotropy of the source becomes clear, with peaking egression power between the starting angles 330° and 0° – essentially covering first bounce wave propagation between angles 330° and 90°.
Due to temporal smearing, intrinsic to the helioseismic egression measured using finite frequency bypass (Donea & Lindsey 2005), the egression source appears much earlier and fades much later than the seismic impulse physically lasts (see the egression light curve, Fig. 2). Such effect is introduced by the choice of bandwidth Δv = 1 mHz, pertaining to temporal smearing of Δt = 1/(Δv) = 1/(1 mHz) = 1000 s. Therefore, it is not straight forward to extract accurate timings from the egression measurements alone, only detect the peaks within the flare time window. The TD diagrams in this case provide a more reliable quake onset time due to avoidance of temporal filtering, thereby avoiding the 1000 s time smearing.
 |
Fig. 3. Helioseismic analysis snapshots of both full-angle (panel a) and directional 6 mHz egression power (panel b) at the time of quake onset (22:18:37 UT) highlights the presence of a detected acoustic kernel within statistical detection contour for the 6 mHz frequency band. We see acoustic emission to be reduced within the sunspot (penumbral boundary represented with white dashed contour), where magnetic fields damp stochastic effects. Directional egression computed with a displayed pupil arc highlights the acoustic kernel centred at 284″ × 129″. Value of the egression directional power is calculated at the location 284″ × 129″ and normalised to the local nonflaring levels is given in panel c, where angle denotes the starting angle of a 60° arc progressing anti-clockwise. TD diagram (panel d), is presented for the source centred at 284″×129″using arc of 0°−90°. A distance is in Mm and time is given in minutes starting at 22:11:07 UT. Fitting of the theoretical curve (right – black curve) yields an onset time of +7.5 min, or 22:18:37 UT. |
2.3.4. Detection results – time–distance diagram
TD diagrams are computed from the surface signal centred on 284″ × 129″as determined through directional egressions (see Fig. 3b), over a 90° arc, starting at 60°. For detailed description of TD diagram procedure see the Methods section. In order to enhance visibility of the surface wavefront, surface remapping is carried out on a running difference of four dopplergram frames (three minute time difference). The resultant time–distance array is then thresholded to account for the perturbations at the flare location where the surface seismic transient is observed.
The results are presented in Fig. 3d (left), where we see an accelerating TD ridge become visible 20 min into the selected time range (starting with 0 min at 22:11:07 UT). This ridge is highlighted Fig. 3d (right) with an overplot theoretical ray path. Manual fitting of the ray path to the signal ridge indicates the onset time for the quake of +7.5 min, giving the sunquake start time at 22:18:37 UT. This is in agreement with the times of observable LOS magnetogram transient peak, as well as WL emission peak and about 20 s later than HXR emission onset (see the light curves, Fig. 2).
3. Hydrodynamic and radiative models of a flaring atmosphere heated by an electron beam
3.1. Hydrodynamic response of a flaring atmosphere
Based on the observations of strong hard X-ray emission in the flaring event associated with the sunquake, we assume that flare emission is produced by injection of sub-relativistic electron beams with power-law energy distributions (Syrovatskii & Shmeleva 1972) into the chromosphere of the quiet Sun (QS) from the primary energy release point in the corona. The beam electrons are assumed to heat the cold ambient chromospheric plasma, sweeping it as a piston to deeper atmospheric levels (Syrovatskii & Shmeleva 1972). This heating prompts a hydrodynamic response of the ambient plasma turning the QS chromosphere into a flaring atmosphere (Somov et al. 1981; Zharkova & Zharkov 2007). The simulation of a hydrodynamic response provides column depth distributions of the kinetic temperature, density and macrovelocities of the ambient plasma for different instances after the beam onset. The method for calculation of the hydrodynamic response in a flaring atmosphere to injection of power-law beam electrons is described in detail in the previous papers (Somov et al. 1981; Zharkova & Zharkov 2007; Druett et al. 2017).
The plasma is heated by an electron beam precipitating from the top boundary with the heating function derived from continuity equation (Syrovatskii & Shmeleva 1972). Plasma cooling is caused by the viscosity, or motion between electrons and ions (Somov et al. 1981; Zharkova & Zharkov 2007). We consider the radiative energy losses in the corona (Cox & Tucker 1969) and by hydrogen emission in the chromosphere (Zharkova & Kobylinskii 1993). The duration of beam injection is chosen as 10 s, the initial energy flux of a beam varies as a triangular function in time, with maximum at five seconds (Zharkova & Zharkov 2007).
After solving the system of four partial differential equations with the initial and boundary conditions for precipitating electron beam with given parameters (initial energy flux F0 and spectral index γ) we obtain time-dependent distributions of electron Te and ion Ti temperatures, ambient plasma density T and macrovelocities, v.
The temperature in a flaring corona heated by beam electrons, with the parameters derived from RHESSI, is found to be increased to ten million Kelvin compared to the initial chromospheric temperature of 6700 K (Fig. 4a). At the same time the ambient number density (Fig. 4b) is significantly reduced in the flaring corona, from the initial QS chromospheric magnitude (1010 cm−3) to 109−108 cm−3, to form a new corona of the flaring atmosphere (Somov et al. 1981). These trends are similar to the hydrodynamic models heated by electron beams with the same parameters reported by Fisher et al. (1985a,b).
The upward motion of the flaring plasma is reflected in the macrovelocity plots (Fig. 4c), showing evaporation of chromospheric plasma upwards to the newly formed corona at the column depths between 1017 and 1019 cm−2. This evaporation lasts for a hundred seconds, expanding with increasing velocities upwards for a few thousand seconds even after the beam is stopped (Somov et al. 1981; Fisher et al. 1985b). The evaporation velocities range from a few tens of km s−1 (at 1 s) up to 1400 km s−1 (at 20–100 s). Higher magnitudes of the evaporation velocities, though observed by the SMM mission (Antonucci et al. 1990), are larger than the observations with the modern instruments (Hinode/EIS, for example). This reflects the fact that modern instruments typically observe lower temperature lines occurring in the lower corona where the macrovelocity is restricted to 500 km s−1 while the higher velocities above 1000 km s−1 occur at the top of the flaring corona.
The beam energy deposition leads to the formation of a low temperature condensation in the flaring chromosphere seconds after beam injection begins with a slightly increased temperature up to 104 K. This condensation moves as a shock toward the photosphere and interior (Zharkova & Zharkov 2015) starting with velocities of 30−35 km s−1 (reached 1 second after the beam onset) and approaching up to 100 km s−1 after five seconds of the beam injection (Fig. 4c). The plasma density of this shock is a factor of 1013 cm−3 (Fig. 4b).
 |
Fig. 4. Simulated hydrodynamic responses to beam electron injection. The simulated hydrodynamic responses of a flaring atmosphere to the injection of a beam with the initial flux of 4.3 × 1011 erg cm−2 s−1 and spectral index of 3.9 obtained from the conversion of a spectral index of HXR emission to that of electron beam Zharkova & Gordovskyy (2006) showing the column depth dependencies of electron kinetic temperature, K (panel a), the plasma density, cm−3 (panel b), plasma macrovelocity, km s−1 (panel c) and linear heights (panel d). |
3.2. Simulated radiative signatures of a flaring atmosphere
Based on the hydrodynamic models calculated above and taking into account that the characteristic hydrodynamic time is about 30 s (Shmeleva & Syrovatskii 1973; Somov et al. 1981), which is much longer than the characteristic radiative time of a fraction of a second (Shmeleva & Syrovatskii 1973), we can apply the radiative models for hydrogen emission to the hydrodynamic models calculated for each second. The hydrogen emission in a flaring atmosphere was calculated using the second part of HYDRO2GEN code utilising a full non-LTE approach for a five level plus continuum hydrogen model atom (Druett & Zharkova 2018). We consider hydrogen atom excitation and ionisation by thermal and beam electrons as well by external and diffusive radiation.
For nonthermal hydrogen excitation and ionisation rates by beam electrons the analytical formulae by Zharkova & Kobylinskii (1993) were used. Stimulated photoexcitation, de-excitation, and ionisation rates by external sources were also taken from Zharkova & Kobylinskii (1993).
Steady state equations are considered for all the transitions in a five level plus continuum hydrogen atom model. For the lines and Lyman continuum, which are optically thick, the radiative transfer equations are solved in the integral form, as follows:
where S is the source function for the line or continuum, τ is an optical depth in the line centre or the continuum head, λ is the survival probability of a scattered photon, and S∗ is the initial source function, calculated without diffusive radiation. The integral was calculated over all the optical depths up to its maximum value for each different wavelength, τ0.
The kernel functions, K1, in the lines and Lyman continuum are given by the following equations:
Lyman continuum:
Lines:
The absorption profile in the Lyman continuum, f1, is defined as follows:
F(T ) is a normalisation coefficient of the kernel functions for the Lyman continuum, and A is the one for the lines. T is the kinetic temperature of the plasma, ν is the frequency of the radiation and ν1c the frequency in the Lyman continuum head. E1(x) is the exponential integral of the first kind. The absorption profiles in the lines, α(x), were assumed to have the form of a Voigt function, where x is a dimensionless wavelength measured in Doppler half widths from the line central wavelength. The effective Doppler half widths of spectral lines, ΔνD, defined by thermal motion of hydrogen atoms are calculated for the temperature profiles from the hydrodynamic model for every instant of beam injection by considering the contribution of the relevant Doppler widths from each layer weighed by the layer thickness. For Balmer lines the Stark’s effect induced by strong electric fields caused by ionisation of the ambient plasma, was also considered.
The radiative transfer and statistical equilibrium equations were solved simultaneously defining the source functions in each atomic transition and ionisation degree of hydrogen atoms in the atmosphere at any given instant of a hydrodynamic response. The solutions of the radiative transfer Eq. (5) were found using the L2 approximation introduced by Ivanov & Serbin (1984). The simulated Hα line intensities are calculated from the source function between levels 3 and 2 using Voigt’s absorption profiles (Druett & Zharkova 2018).
4. Probing the models with Hα and white light observations
4.1. Hα line emission
The simulated Hα line profiles (Figs. 5a and 5b) were calculated using a full non-LTE approach for a five level plus continuum hydrogen atom considering radiative, thermal and nonthermal excitation and ionisation processes as described in the section above and the Method section of Druett et al. (2017). Nonthermal excitation and ionisation is produced by injection of an electron beam with the initial flux of 4.3×1011 erg cm−2 s−1 (4.3F11 model) and spectral index obtained from from observations (see Fig. 2). For calculation of Hα line profiles the full NLTE problem was solved for the simulated hydrodynamic models obtained for each 100 s after the beam onset (for more details on the method see also Druett & Zharkova 2018).
The radiative simulations clearly show that in the very first seconds after the beam onset, Hα becomes an emission line (see Fig. 5). Hα profiles reveal a strong increase of the central and wing emission caused by enhanced ionisation and excitation induced by the electron beams recently highlighted by Druett et al. (2017). Furthermore, in the very first seconds, Hα line profiles become strongly redshifted because they are dominated by the downward motion of a hydrodynamic shock generated in the response to the injection of beam electrons (Fig. 4). For this flaring event heated by a beam with a high initial energy flux of 4.3×1011 erg cm−2 s−1, the downward velocity approaches up to 138 km s−1, resulting in the redshift of Hα line intensity central peak from the line centre to the red wing by 3 Å(Fig. 5).
After the beam is switched off, the ambient plasma remains strongly ionised for a very long time (order of tens of minutes) due to the recombination rates being two orders of magnitude lower than the nonthermal ionisation rates by the beam electrons and radiative transfer of the optically thick Lyman continuum radiation governing this recombination. In this period, the excitation by thermal electrons, and slow recombination of the ambient electrons, with hydrogen atoms sustains the high excitation level of hydrogen atoms for up to 100 s – as reflected in the Hα profiles (see the burgundy and blue profiles in Fig. 5a). Although, there is a continuous decrease of the red wing intensity over the subsequent 60 s (Fig. 5a). At later times, beyond 60 s, the simulated Hα emission returns back to standard thermal profiles without red shifts but with self-absorption caused by radiative transfer of the emission with high opacity.
Our simulation produces the line profiles and intensities of Hα line emission from a flaring atmosphere within the spectral range (±3.0 Å from a central wavelength) that is broader than the observational range (±1.5 Å) measured by the spectral filter of the FISCH instruments (marked by the vertical lines in Fig. 5a). Hence, for a comparison of temporal variations of the integrated Hα intensities with the FISCH observations the integration of Hα line intensity has been adjusted within the spectral limits defined by the filter (±1.5 Å).
The redshift in the simulated Hα line profile reaches a maximum at (or just after) 5 s, post beam onset, when the downward velocity in a hydrodynamic model is maximal – approaching 138 km s−1 (Fig. 4c), similar to those reported previously (Ichimoto & Kurokawa 1984; Wuelser & Marti 1989). The Hα line profile is shown to be strongly red-shifted by around 3 Å from the central wavelength (λ0 = 6563 Å), corresponding to a Doppler velocity of 138 km s−1 (Fig. 5a).
The total intensity calculated for the spectral window of 3 Å(marked by the vertical lines in Fig. 5a), plotted in Fig.5b, reflects the dynamics of the Hα emission. However, during the flare onset FISCH instrument suffered saturation of the Hα intensity at about 1.6 times of the intensity of the quiet Sun, so the whole increase of Hα-line intensity shown for the impulsive phase during the flare onset was missed.
Here we can only discuss the simulated temporal variations of the total Hα line intensity reflecting the reduction of this intensity, or dip, caused by the redshift by 3 Å of the whole Hα line profile reported in the previous observations Ichimoto & Kurokawa (1984), Wuelser & Marti (1989). This red shift can explain a dip in the Hα line intensity integrated in the observational window appearing approximately 4−6 s after the beam onset because of the line red shift and lasting up to a few minutes (Fig. 5b) until the flaring plasma returns back to the preflare status. So, if the spectral interval used by any Hα instrument is ±1.5 Å, then the whole Hα line becomes shifted to the red wing, and only the blue wing of the line can be observed in the line window (the second vertical line in Fig. 5a) until the beam stops and the flaring atmosphere cools off.
 |
Fig. 5. Temporal variations of Hα line profiles (panel a) Hα total intensities (panel b) the temporal variations of total Hα line intensity (blue line) simulated for 100 s of the hydrodynamic models heated by an electron beam. We note that a strong increase of Hα intensity in this flare caused by beam electrons, as shown in (panel b), led to the blackout for a few minutes of the FISCH sensors during the flare onset. |
4.2. White-light emission
From the FISCH observations by Kawate et al. (2016) of white light emission in this flare we present a close up of the WL kernel 1 in the Northern umbra observed with FISCH (Fig. 6a), within which the sunquake is detected. Similarly to Druett & Zharkova (2018), the white light emission in this flare was interpreted with temporal variations of Paschen contiuum of hydrogen atoms affected by beam electrons calculated using the non-LTE model (see Sect. 3.2) for the hydrodynamic models described in Sect. 3.1 at different times after the beam onset.
The simulated intensities of Paschen continuum seen in white light were then compared with the observed temporal variations of the emission in the WL kernel (Fig. 6b) associated with the sunquake. In order to understand the sources causing the increase of WL emission, we also plot in the bottom row of Fig. 6 the contribution functions of Paschen emission from different layers of a flaring atmosphere for 5 s corresponding to the maximum flux of the beam during its injection (Figs. 6c and 6d). Figure 6d reflects the contribution function caused only by thermal electrons and radiation, whilst Fig. 6c shows the contribution function caused by both the beam and thermal electrons, as well as radiation.
The contribution function clearly shows (compare Fig. 6c with 6d) that Paschen continuum, which is seen as white light emission, is strongly affected by the ionisation and excitation caused by the beam electrons. The injection of beam electrons is followed by a strong nonthermal ionisation of hydrogen atoms from all the atomic levels leading to the increased Paschen continuous emission in the chromosphere, in addition to the WL emission for the quiet Sun seen normally at the photosphere only (Zharkova 2008). This additional hydrogen ionisation in a flaring atmosphere is maintained for a very long time (up to 30–40 min) by the radiative transfer in Lyman continuum (Druett & Zharkova 2018). This expains the long duration of white light emision in many flares and in this one under the investigation. Evidently, beam electrons are the agents producing the main contribution for white light emission in this flaring event (Druett & Zharkova 2018), as a comparison of the simulated and observed WL temporal curves (Fig. 6b) demonstrates.
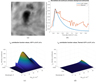 |
Fig. 6. Top plots: panel a: close-up of the white light (WL) kernel 1 observed with the FISCH instrument Kawate et al. (2016) where the first HXR peak and sunquake occurred (see Fig. 1). Panel b: WL temporal profiles observed with the FISCH instrument Kawate et al. (2016) versus simulated from the hydrodynamic model presented in Fig. 4. Bottom plots: contribution functions of Paschen continuum simulated for the joint effect of thermal and nonthermal (beam) electrons 5 s after their injection onset (panel c) and for thermal electron only (panel d). |
5. Interpretation of helioseismic results with the combined hydrodynamic model
5.1. Hydrodynamic response of the solar interior
Hydrodynamic shocks from the flaring atmosphere above the solar interior can be used as the initial condition for another hydrodynamic model developed for the acoustic wave propagation in the solar interior (Zharkov et al. 2013a,b). As the initial hydrodynamic shock terminates within relatively shallow depths and with strongly supersonic velocities, the generated waves are formed at the point of deposition as a closed cone around the velocity vector in the solar interior, which, in accordance to Fermat’s principle, propagates deeper into the interior refracting due to the increasing temperature and reflecting back to the photosphere (Fig. 8).
Using sound speed and Lamb’s acoustic cut-off frequency from the solar interior model, one can solve the equation for acoustic wave propagation in the interior either analytically for a polytrope (Zharkov et al. 2013a,b) or numerically (Shelyag et al. 2009) for the Christensen-Dalsgaard numeric model S (Christensen-Dalsgaard et al. 1996). Thus, using the analytic solution for a polytrope model (Zharkov et al. 2013a,b) we can evaluate the parameters of acoustic wave packets generated in the interior and the condition of their detection from Doppler observations on the solar surface, while the numeric model can help to obtain more realistic acoustic signatures. As shown by Zharkov et al. (2013a,b), the vertical shock perturbation moving with a supersonic velocity can generate a set of multiple acoustic waves, or rays, from which only the waves with the phase speed exceeding a certain threshold (see Eq. (5.8) in Zharkov et al. 2013a,b) can reproduce the observed signatures of acoustic waves.
An individual ray, characterised by a constant frequency, ω, and horizontal wavenumber, kh, initialised at a given depth, propagates into the solar interior and, generally will have, at least, two, upper and lower, turning points (see Fig. 1 in Zharkov et al. 2013a,b). The lower turning point indicates where the wave moving to the interior is reflected back to the surface by changing its direction of its motion because of Fermat’s principle. The first upper turning point along the ray defines the first surface appearance of the acoustic wave (as a first ripple), or the first bounce. Then the propagating ripples correspond to a sequence of the first bounces of the source-generated acoustic rays from the packet reaching in succession their first upper turning points. This reflection of acoustic waves from the solar surface creates a visible motion of ripples on this surface from the flare site.
The source of the deposited impulse, depending on its properties, generates a family of the rays that provides a solution to the ray equations in the phase space and defines the generated wave front. As the source is located in the interior, the first ray (out of all generated by the source) to reach its upper turning point defines the minimal distance where the ripple is formed. This distance will depend on the momentum deposited by the source. The depth where this momentum is deposited and the interior model are described below.
For a near-surface source, that is for the ray initiated near its upper turning point, the first surface appearance, or the minimal distance, can be approximated by the ray’s skip distance, Δ, the distance between its surface bounces. This distance depends on the ray’s horizontal phase speed, ω/kh (see, for example Zharkov et al. 2013a,b; Christensen-Dalsgaard et al. 1996). For the polytrope model of the solar interior, used by Zharkov et al. (2013a,b), the minimal skip distance, Δ, or the distance from the point of the initial impulse deposition to the first ripple occurrence, is derived from Eq. (A1) of Zharkov et al. (2013a,b) as follows:
where g is the gravitational constant, g = 2.67 × 10−4 Mm s−2, m is the polytrope index, Vph = w/kh is the horizontal speed of wave propagation.
If the (non-oscillatory) source moves in the interior with a supersonic velocity, the waves of the packet are generated in a cone around the velocity vector (Zharkov et al. 2013a,b), with the ray frequencies depending on the angle between the velocity vector and each ray, γ :
where c is the sound speed, ωac acoustic cut-off frequency, all measured at the source depth, k0 is the initial wave-vector with horizontal and vertical components, kh0 and kz0, respectively.
In this case, the acoustic rays are generated at the source depth with frequencies above the acoustic cut-off frequency. Thus, the observations of high-frequency waves will be limited by the Nyquist frequency and cadence of the series (8.33 mHz for MDI, 11.11 mHz for SDO/HMI). For instance, the waves with high-frequency above Nyquist frequency, ωN, may not be observed, imposing further restrictions on the conditions for observable ripples, e.g ω ≤ ωN holds.
This leads to the threshold condition for the minimal phase speed, 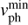 , defining the condition for registering the first ripples on the surface by the following relation (see Eq. (5.8) in Zharkov et al. 2013a,b):
, defining the condition for registering the first ripples on the surface by the following relation (see Eq. (5.8) in Zharkov et al. 2013a,b):
Propagation of acoustic waves (or rays) generated by a supersonic source moving with the velocity of 120 km s−1 at depth zs = 65 km is shown in Fig. 8. The abscissa defines a horizontal distance in Mm of the ray propagation about the location of a deposition of supersonic disturbance (shock) and the ordinate shows a propagation depth, z, under the photosphere.
5.2. Probing the sunquake properties with the combined hydrodynamic models
Hydrodynamic modelling of a flaring atmosphere response to electron beam injection (Fig. 7) discussed in Sect. 3.1 shows that the hydrodynamic shock formed in the flaring atmosphere enters the solar interior (or crosses at the surface a linear depth of zero) with the velocity above the local sound speed, with the vertical velocities of v(zs) = 120 km s−1 at zs = 65 km s−1 (Fig. 7c), and propagates in the interior for 40−50 s before termination at 2.5Mm (Fig. 7b). Hence, the hydrodynamic shock generated by atmospheric response enters the photospheric layers at a supersonic speed (Figs. 7a and 7b) as is clearly seen from comparing these plots of the hydrodynamic shock velocities with the sound speed plot shown in Fig. 7c.
Moreover, this shock remains supersonic down to the depths of 500–2000 km as it is shown by Figs. 7a and 7b where the red and orange curves in both plots are supersonic and travel for 45 s down to the interior before their velocties are reduced below the local sound speed marked by dashed lines. This is a very important development because the hydrodynamic calculations of acoustic wave propagation show, that if the shock velocity is higher than a local acoustic speed, then it generates acoustic waves in the solar interior (Zharkov et al. 2013a,b). Therefore, the shock parameters supply the initial condition for the hydrodynamic model simulating acoustic wave propagation in the solar interior (see Sect. 5.1) and define the shape of acoutic waves.
Since the propagation of the surface ripples from a source can be determined by the phase speed of acoustic waves (Zharkov et al. 2013a,b), the minimal skip distance, Δ, can be estimated for a polytrope from Eq. (9) after a substitution of the minimal phase speed given in Eq. (11). The skip distance is where these acoustic waves are reflected by the surface (the upper turning point) and observed as surface ripples. Zharkov et al. (2013a,b) showed that for horizontal velocities from 15−45 km s−1, as reported for the first sunquake (Kosovichev & Zharkova 1998), the first bounce came to the surface at a skip distance of about Δ = 25 Mm corresponding to20−25 minafter theinitial impulsedeposition. For this event the TD diagram in Fig. 3 shows a first bounce of 15−20 Mm (at 22:23:40 UT), which corresponds to a ray with the initial phase velocity of about 45−50 km s−1.
For acoustic-wave propagation modelling we use Model S of Christensen-Dalsgaard et al. (1996) with the source parameters described above. The profiles of acoustic cutoff frequency and sound speed in this model are shown in Fig. 7c. In addition, we introduced an inclination of γ = 60° to the surface for the direction where the hydrodynamic shock from the atmosphere is deposited (estimated from HMI vector magnetogram field inclination at the seismic source). The acoustic cut-off frequency, ωac/(2π), and sound speed, c, at this depth are then 9.9 mHz and 8.4kms−1 (see Fig. 7c). Therefore, it follows from (10a–10b) that
the acoustic waves generated at this depth are above 9.9 mHz.
Examples of generated rays and wavefronts at different times are shown in Fig. 8 for wavevectors in the same plane as velocity, that is if ϕ = 0 in notation of Sect. 5.21 of Zharkov et al. (2013a,b). At 1.83 min after initial shock injection, we see that uppropagating rays from the source escape into the solar atmosphere as they are above acoustic cut-off. Also some fraction of down-propagating rays from the source show similar behaviour, seen at 8.5 min and later snapshots, especially, to the left hand side (LHS) of the source. Rays with the upper turning points that turn back to the interior first produce the ripples on the surface at about 20 min after the impact at the distance approaching 10–20 Mm from the source, in close agreement with the skip distance derived from TD diagrams. Given a rather high ratio of the source velocity to a local sound speed, the wave-packet generated at this depth is expected to be wide as only the rays with θ > 86° become evanescent for ϕ = 180°. However, it seems that only ripples generated by 6 mHz waves are detectable in the TD diagrams (Fig. 3) 20 min after the momentum deposition at the distance of 15–18 Mm because these waves have the strongest acoustic energy (see Fig. 3c).
As the shock travels deeper in the interior, its velocity decreases, the acoustic cut off frequency drops and the sound speed grows (Fig. 7c), making wave packets generated at larger depths lower frequency and more narrow. The fact that we have observed holographic signatures at low frequencies such as 3 mHz indicates that the shock must have travelled to at least 500 km below the surface (as predicted by the atmospheric hydrodynamic model), which is also in a very good agreement with the acoustic ray’s modelling (see Fig. 8).
 |
Fig. 7. Top plots: velocity profiles of simulated hydrodynamic shocks plotted versus linear depths under the quiet Sun (QS) photosphere for different times after beam injection (panel a) and versus time after the beam onset for different linear depths in the solar interior under the QS photosphere (panel b). Zero in the X-axis indicates the position of the QS photosphere, positive height is above and negative height is below the QS photosphere. The horizontal dashed lines in panel b represent the sound speed at 0.1, 0.5, 1 and 2 Mm. Bottom plot: distributions over depth z in the solar interior of a model acoustic cut-off frequency (top) and a sound speed (bottom) taken from Chirstensen-Dalsgaard’s model S (Christensen-Dalsgaard et al. 1996). |
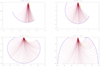 |
Fig. 8. The individual acoustic rays (generated at the depth of 65 km and travelling to the bottom of the plot) by a moving supersonic source, v = 120 km s−1, depositing a momentum below the photosphere (the origin) under 30° angle to the right hand side (RHS) from the local vertical for the times shown above the plots. The rays are computed numerically for parameters extracted from model S and shown in Fig. 7c. The rays are colour-coded in the range 3–11 mHz with 3 corresponding to the darkest shade. The photosphere is denoted by the top line, the X-axis denotes a distance in Mm from the point of momentum deposition. The points of ray reflection from the photosphere are observed as ripples on the surface, or a sunquake, generated about and propagating outward the central point of the momentum deposition. |
6. Discussion and conclusions
The evolution of the active region which produced the September 6th 2011 flare, is driven by a new flux emergence leading to the fan-spine reconnection initiating the flare (Jiang et al. 2014). The X2.1 flaring event is associated with a strong eruption to the south at 22:19 UT, followed by formation of ribbons that form a circular structure, as expected from reconnection at the null point of the fan-spine configuration (Janvier et al. 2016). This proximity to the ends of the erupting flux rope structure is similar to the scenarios reported for the flares of 15 February 2011 (Zharkov et al. 2011a) and 7 September 2011 (Zharkov et al. 2013b), where the flux rope eruption leads to the formation of two flare ribbons and sunquakes. However, for the X2.1 event presented in this study, a seismic signature was not originally found in the previous studies (Liu et al. 2014).
In this paper we report a detection of the seismic signatures in one of footpoints related to the 6 September 2011 X2.1 flare using statistical analysis of egression power combined with directional holography and time–distance diagram. Similar to the September 7 event that occurred on the following day (Liu et al. 2014), we observe magnetic field variations that are consistent with the presence of a significant Lorentz-force perturbation asociated with magnetic field restructuring (Petrie 2016). This is in agreement with the idea that the main energy in flares comes from Lorentz force during a magnetic reconnection as proposed by Zharkova (2008), Hudson et al. (2008) and Fisher et al. (2012). The magnetic reconnection process is assumed to energise beam electrons to relativistic energies with a power-law energy distribution (see for example Zharkova et al. 2011, and the references therein).
These electrons precipitate into the flare footpoints while heating and sweeping the ambient plasma from the top to the photospheric levels and beneath. This process produces a strong hydrodynamic shock travelling to the photosphere and the interior combined with chromospheric plasma evaporation back to the flaring corona (Somov et al. 1981; Zharkova & Zharkov 2007; Druett et al.2017). At the same time, these beam electrons strongly excite and ionise nearly all the ambient hydrogen atoms at lower atmospheric depths causing strong diffusive radiation in Lyman, Balmer and Paschen continua. This leads to a strong increase of Paschen continuous emission seen in white light over all atmospheric depths from the chromosphere to the photosphere (Druett & Zharkova 2018) shown in Sect. 4.2 that can account for the occurrence of a white light flare in this (and many other) events. Its long duration up to 20 min is governed by a large (up to 106) opacity of the radiation in Lyman continuum and its exchange with the other hydrogen continua (Druett & Zharkova 2018) that explains a close link between HXR and white light emission and their joint link to a seismic response in the flare as discussed below.
The hydrodynamic shock induced in a flaring atmosphere by the energy deposted by beam electrons and travelling with a supersonic velocity in the solar interior generates the acoustic wave packets in the solar interior. These waves travel down to the lower turning points in the interior and return back to the solar surface to reach their upper turning points (or the first bounce) observed as ripples on the solar surface (Zharkov et al. 2013a,b) as described in Sect. 5.1. This hypothesis is supported by the seismic source timing and location within the vicinity of cospatial WL and peak HXR emission combined with energy estimates as indicated in Sect. 5.2. Acoustic energy, 8.26 × 1027 erg, is a fraction of the estimated kinetic energy originating from chromospheric evaporation, 5.1 × 1029 ergs (Feng et al. 2013) and nonthermal electron energies, 2.09 × 1029 erg s−1 calculated from the spectral RHESSI data.
Due to the diluted egression signal, the past studies (Liu et al. 2014) have missed the seismic signals concluding that there was no seismic response present in this event. However, we noted the peculiarity in the analogous X1.8 flare occurred on the following day and the fact that it did generate a seismic response (Zharkov et al. 2013a). The flare had two WL kernels observed in HMI and FISCH, as is often seen in large flares, it also had significant disturbances to both LOS magnetic field and velocity dopplergrams during the impulsive phase of the flare. These disturbances to the surface indicated the photospheric impacts in two locations.
This motivated us to investigate the 6 September 2011 using a revised helioseismic holography technique based on an enhanced statistical analysis of the holography egression data computed from the HMI data. This technique helped to reveal a significant acoustic signature located in the penumbra immediately west of the northern WL kernel, in the parasitic positive polarity umbra. The new technique shows great potential for developing the tool for automated detection of seismic signatures.
A time–distance diagram was used for defining a starting time of the quake from fitting the theoretical ray path to the detected surface ridge. This provided the quake initiation time of 22:18:37 (±45 s) UT (Fig. 3d). Our estimations of the quake properties from the TD diagram show that the wavefront appeared at 15−20 Mm from the deposition point in the flare, and the phase velocity of ripple propagation on the photosphere is close to the estimation of the skipping distance for acoustic waves generated by a supersonic shock in the shallow depth of 500–600 km beneath the photosphere, while its vertical speed is higher than the local sound speed.
Directional egression and time–distance diagrams display high anisotropy of the seismic source indicating that the shock was deposited under some angle to the local solar vertical. The wavefront is strongest in the north-west direction (Figs. 3b and 3c) and, similarly to the September 7th X1.8 event, is co-directional to the WL kernel drift. However, unlike the X1.8 event, the direction of wavefront propagation is away from the sunspot. This anisotropy indicates that the shock was deposited at an angle of about 30° to the local vertical, thereby explaining the location of the first bounce and the average phase speed of ripples on the photosphere.
Therefore, in summary we can conclude that in this paper we show for the first time that a combination of the two hydrodynamic models (for a flaring atmosphere heated by electron beam and for production of acoustic waves by the shock deposition in the solar interior) provides the first quantitative interpretation of the seismic signatures in a flare. We show that all the observed signatures in this flare can be logically accounted for by the complex dynamic processes in the atmosphere and interior caused by the injection of an electron beam. The hydrodynamic model of a flaring atmosphere allowed us to closely fit the white light observations in this flare, seen in the same location as the sunquake, with the simulated emission of the hydrogen Paschen continuum. We demonstrate with the radiative NLTE simulations that WL emission can only be produced by the additional excitation and ionisation of hydrogen atoms by beam electrons. The proposed interpretation links all the models suggested for a generation of sunquakes into a unified model involving simultaneously Lorentz force, hydrodynamic shocks and white light emission, all produced by the magnetic energy released during the flare and its conversion into energetic particles (electrons) with their further effects on a flaring atmosphere and the interior.
Acknowledgments
The authors acknowledge that HMI and AIA images are available by courtesy of NASA/SDO and the AIA, EVE, and HMI science teams. C. Macrae and S. Zharkov would like to thank the University of Hull for providing the studentship for this research. M. Druett and V. Zharkova wish to acknowledge the PhD studentship support from Northumbria University via the University Research Development Fund at Research Councils UK (RCUK). S. Matthews acknowledges a financial support from STFC via the Consolidated Grant ST/N000722/1. S. Zharkov and V. Zharkova acknowledge the funding for this research provided by the US Air Force grant PRJ02156.
References
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, E., Dodero, M. A., & Martin, R. 1990, ApJS, 73, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D., & Lindsey, C. 2000, Sol. Phys., 192, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago-Casas, J., Martinez Oliveros, J., Lindsey, C., et al. 2015, Sol. Phys., 290, 3151 [NASA ADS] [CrossRef] [Google Scholar]
- Cally, P. S. 2006, Phil. Trans. R. Soc. London, Ser. A, 364, 333 [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., et al. 1996, Science, 272, 1286 [CrossRef] [Google Scholar]
- Cox, D. P., & Tucker, W. H. 1969, ApJ, 157, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Donea, A. 2011, Space Sci. Rev., 158, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Donea, A., & Lindsey, C. 2005, ApJ, 630, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Donea, A.-C., Braun, D. C., & Lindsey, C. 1999, ApJ, 513, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Donea, A.-C., Lindsey, C., & Braun, D. C. 2000, Sol. Phys., 192, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Donea, A.-C., Besliu-Ionescu, D., Cally, P. S., Lindsey, C., & Zharkova, V. V. 2006, Sol. Phys., 239, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Druett, M., Scullion, E., Zharkova, V. V., et al. 2017, Nat. Commun., 8, 15905 [NASA ADS] [CrossRef] [Google Scholar]
- Druett, M., & Zharkova, V. 2018, A&A, 610, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, L., Wiegelmann, T., Su, Y., et al. 2013, AJ, 765, 37 [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985a, ApJ, 289, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985b, ApJ, 289, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Bercik, D. J., Welsch, B. T., & Hudson, H. S. 2012, Sol. Phys., 277, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Valori, G., Zuccarello, F. P., et al. 2017, ApJ, 749, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. C., Cally, P. S., & Donea, A.-C. 2016, MNRAS, 456, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H., Fisher, G., & Welsch, B. 2008, ASP Conf. Ser., 383, 221 [NASA ADS] [Google Scholar]
- Ichimoto, K., & Kurokawa, H. 1984, Sol. Phys., 93, 105 [NASA ADS] [Google Scholar]
- Ivanov, V. V., & Serbin, V. M. 1984, Sov. Astron., 28, 405 [NASA ADS] [Google Scholar]
- Janvier, M., Savcheva, A., Pariat, E., et al. 2016, A&A, 591, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, C., Feng, X., Wu, S. T., & Hu, Q. 2013, ApJ, 771, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C., Wu, S. T., Feng, X., & Hu, Q. 2014, ApJ, 780, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Kawate, T., Ishii, T. T., Nakatani, Y., et al. 2016, ApJ, 833, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G. 2006, Sol. Phys., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Zharkova, V. V. 1998, Nature, 393, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Zharkova, V. V. 2001, ApJ, 550, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhar, M., Krucker, S., Martínez Oliveros, J. C., et al. 2016, ApJ, 816, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Braun, D. C. 1999, ApJ, 510, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Braun, D. 2000, Sol. Phys., 192, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsey, C., & Braun, D. 2004, ApJS, 155, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Deng, N., Lee, J., et al. 2014, ApJ, 795, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, S. A., Zharkov, S., & Zharkova, V. V. 2011, ApJ, 739, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, S. A., Harra, L. K., Zharkov, S., & Green, L. M. 2015, ApJ, 812, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Moradi, H., Donea, A.-C., Lindsey, C., Besliu-Ionescu, D., & Cally, P. S. 2007, MNRAS, 374, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, G. J. D. 2016, Sol. Phys., 291, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Scherrer, P., Bush, R., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Sharykin, I. N., Kosovichev, A. G., & Zimovets, I. V. 2015, ApJ, 807, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Zharkov, S., Fedun, V., Erdélyi, R., & Thompson, M. J. 2009, A&A, 501, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shmeleva, O. P., & Syrovatskii, S. I. 1973, Sol. Phys., 33, 371 [Google Scholar]
- Somov, B. V., Spektor, A. R., & Syrovatskii, S. I. 1981, Sol. Phys., 73, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Sudol, J. J., & Harvey, J. W. 2005, AJ, 635, 647 [Google Scholar]
- Syrovatskii, S. I., & Shmeleva, O. P. 1972, Sov. Astron., 16, 273 [NASA ADS] [Google Scholar]
- Wolff, C. 1972, ApJ, 176, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Wuelser, J.-P., & Marti, H. 1989, ApJ, 341, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Jing, J., Wang, S., & Wang, H. 2014, ApJ, 787, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S. 2013, MNRAS, 431, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S., Green, L. M., Matthews, S. A., & Zharkova, V. V. 2011a, ApJ, 741, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S., Zharkova, V. V., & Matthews, S. A. 2011b, ApJ, 739, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S., Green, L. M., Matthews, S. A., & Zharkova, V. V. 2013a, J. Phys. Conf. Ser., 440, 012046 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S., Green, L. M., Matthews, S. A., & Zharkova, V. V. 2013b, Sol. Phys., 284, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V. 2008, Sol. Phys., 251, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, MNRAS, 356, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2006, ApJ, 651, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Kobylinskii, V. A. 1993, Sol. Phys., 143, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Zharkov, S. I. 2007, ApJ, 664, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Zharkov, S. I. 2015, Sol. Phys., 290, 3163 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Arzner, K., Benz, A. O., et al. 2011, Space Sci. Rev., 159, 357 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. AIA 94 Å images at 22:10 UT with an s-shaped sigmoid and flux rope prior to flare onset (panel a) and the two flaring loops and circular ribbon formed during the flare (22:18:37 UT) (panel b). Red and black contours denote 500 and −500 Gauss LOS magnetic field respectively. HXR emission at 50−100 keV (solid contours) highlights two closely spaced sources in panel b, with TD source (black cross) located close to the northern HXR source. The context images of both HMI continuum and LOS magnetogram at 22:18:37 UT are given in panels c and d, with detected source location contours from the statistical test on full-angle egression power maps. Regions of a significant acoustic signal are given for the 4–7 mHz pass bands, in addition to the location of the time– distance source origin. HXR emission is represented as dashed contours in panels c and d for clarity. |
| In the text | |
 |
Fig. 2. Left plots: light curves of RHESSI 100−300 keV HXR (HXR), GOES (1.0−8.0 Å) SXR (SXR), integrated HMI LOS magnetogram (LOS B), WL continuum (WL) and egression power (EGR). The HMI data products are integrated over the seismic signal. Black vertical dotted line denotes the sunquake onset time (22:18:37 UT) from time–distance diagrams (Fig. 3d). Continuum emission shows a peak emission at 22:18:37 UT, coincident with quake onset and LOS magnetogram transient. Egression power, normalised with respect to quiet sun levels, peaks above a defined detection threshold (red horizontal line) of the local mean (yellow) plus 5σ within the flare window (blue vertical lines). Right plots: photon flux spectrum for the time interval 22:18:16–22:19:12 UT with variable thermal (green) and thick-target bremstrahlung (green) fitting giving the total fit (red) over the 12−270 keV energy range (bounded in black; top) and respective residuals of fitting (bottom). |
| In the text | |
 |
Fig. 3. Helioseismic analysis snapshots of both full-angle (panel a) and directional 6 mHz egression power (panel b) at the time of quake onset (22:18:37 UT) highlights the presence of a detected acoustic kernel within statistical detection contour for the 6 mHz frequency band. We see acoustic emission to be reduced within the sunspot (penumbral boundary represented with white dashed contour), where magnetic fields damp stochastic effects. Directional egression computed with a displayed pupil arc highlights the acoustic kernel centred at 284″ × 129″. Value of the egression directional power is calculated at the location 284″ × 129″ and normalised to the local nonflaring levels is given in panel c, where angle denotes the starting angle of a 60° arc progressing anti-clockwise. TD diagram (panel d), is presented for the source centred at 284″×129″using arc of 0°−90°. A distance is in Mm and time is given in minutes starting at 22:11:07 UT. Fitting of the theoretical curve (right – black curve) yields an onset time of +7.5 min, or 22:18:37 UT. |
| In the text | |
 |
Fig. 4. Simulated hydrodynamic responses to beam electron injection. The simulated hydrodynamic responses of a flaring atmosphere to the injection of a beam with the initial flux of 4.3 × 1011 erg cm−2 s−1 and spectral index of 3.9 obtained from the conversion of a spectral index of HXR emission to that of electron beam Zharkova & Gordovskyy (2006) showing the column depth dependencies of electron kinetic temperature, K (panel a), the plasma density, cm−3 (panel b), plasma macrovelocity, km s−1 (panel c) and linear heights (panel d). |
| In the text | |
 |
Fig. 5. Temporal variations of Hα line profiles (panel a) Hα total intensities (panel b) the temporal variations of total Hα line intensity (blue line) simulated for 100 s of the hydrodynamic models heated by an electron beam. We note that a strong increase of Hα intensity in this flare caused by beam electrons, as shown in (panel b), led to the blackout for a few minutes of the FISCH sensors during the flare onset. |
| In the text | |
 |
Fig. 6. Top plots: panel a: close-up of the white light (WL) kernel 1 observed with the FISCH instrument Kawate et al. (2016) where the first HXR peak and sunquake occurred (see Fig. 1). Panel b: WL temporal profiles observed with the FISCH instrument Kawate et al. (2016) versus simulated from the hydrodynamic model presented in Fig. 4. Bottom plots: contribution functions of Paschen continuum simulated for the joint effect of thermal and nonthermal (beam) electrons 5 s after their injection onset (panel c) and for thermal electron only (panel d). |
| In the text | |
 |
Fig. 7. Top plots: velocity profiles of simulated hydrodynamic shocks plotted versus linear depths under the quiet Sun (QS) photosphere for different times after beam injection (panel a) and versus time after the beam onset for different linear depths in the solar interior under the QS photosphere (panel b). Zero in the X-axis indicates the position of the QS photosphere, positive height is above and negative height is below the QS photosphere. The horizontal dashed lines in panel b represent the sound speed at 0.1, 0.5, 1 and 2 Mm. Bottom plot: distributions over depth z in the solar interior of a model acoustic cut-off frequency (top) and a sound speed (bottom) taken from Chirstensen-Dalsgaard’s model S (Christensen-Dalsgaard et al. 1996). |
| In the text | |
 |
Fig. 8. The individual acoustic rays (generated at the depth of 65 km and travelling to the bottom of the plot) by a moving supersonic source, v = 120 km s−1, depositing a momentum below the photosphere (the origin) under 30° angle to the right hand side (RHS) from the local vertical for the times shown above the plots. The rays are computed numerically for parameters extracted from model S and shown in Fig. 7c. The rays are colour-coded in the range 3–11 mHz with 3 corresponding to the darkest shade. The photosphere is denoted by the top line, the X-axis denotes a distance in Mm from the point of momentum deposition. The points of ray reflection from the photosphere are observed as ripples on the surface, or a sunquake, generated about and propagating outward the central point of the momentum deposition. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



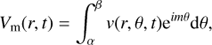
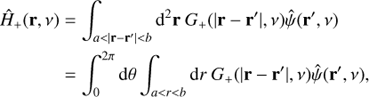
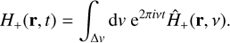
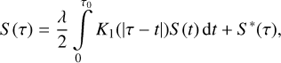
![$${K_1}(|\tau |) = F(T)\int\limits_{{\nu _{{\rm{1c}}}}}^\infty {{f_1}} {\nu ^2}{\rm{exp}}\left[ { - {{h(\nu - {\nu _{{\rm{1c}}}})} \over {kT}}} \right]{E_1}(|\tau |{f_1}){\mkern 1mu} {\rm{d}}\nu $$](/articles/aa/full_html/2018/11/aa32896-18/aa32896-18-eq7.gif)