| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201732259 | |
| Published online | 05 November 2018 | |
Interpreting GRB170817A as a giant flare from a jet-less double neutron star merger
1
Università degli Studi di Milano-Bicocca, Dip. di Fisica “G. Occhialini”, Piazza della Scienza 3, 20126 Milano, Italy
e-mail: omsharan.salafia@brera.inaf.it; omsharan.salafia@gmail.com
2
INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
3
INFN – Sezione di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
Received:
8
November
2017
Accepted:
6
August
2018
We show that the delay between GRB170817A and GW170817 is incompatible with de-beamed emission from an off-axis relativistic jet. The prompt emission and the subsequent radio and X-ray observations can instead be interpreted within a giant-flare-like scenario, being the result of a relativistic outflow driven by the ultra-strong magnetic field produced by magnetohydrodynamic amplification during the merger of the progenitor double neutron-star binary. Within such a picture, the data indicate that the outflow must be endowed with a steep velocity profile, with a relatively fast tail extending to Γ ∼ 8. Since the conditions for the launch of such an outflow are relatively general, and the presence of a velocity profile is a natural expectation of the acceleration process, most neutron star binary mergers should feature this quasi-isotropic, hard X-ray emission component, that could be a powerful guide to the discovery of additional kilonovae associated to relatively nearby gravitational wave events.
Key words: relativistic processes / gamma-ray burst: individual: GRB170817A / stars: neutron / gravitational waves
© ESO 2018
1. Introduction
Before 17 August 2017, events like GRB170817A have probably been detected several times by instruments such as Fermi/GBM and possibly Swift/BAT without attracting too much attention. Due to the low flux and fluence, this kind of burst usually does not become a candidate for a follow-up aimed at searching for the afterglow and identifying the host galaxy. These events simply end up populating the highly incomplete part of the “log N–log S” (the fluence distribution of the sample), and are usually taken out of the flux-limited samples used for population studies.
The association with the gravitational wave (GW) event GW170817 reveals, however, that at least some of these low-flux events might offer extremely precious information about one of the most interesting astrophysical events: a binary neutron star (NS–NS) merger (Abbott et al. 2017a,b,c).
The fact that such an association entered the scene so early is astonishing from many points of view: even though NS–NS mergers have been among the best candidate short gamma-ray burst (SGRB) progenitors for a long time now (Eichler et al. 1989), the most recent predictions based on available observational data (Ghirlanda et al. 2016; Wanderman & Piran 2015) indicate a very small probability for the detection of an SGRB located within the Advanced LIGO/Virgo network range during the first and second run. Moreover, all measurements of SGRB half-opening angles to date (Soderberg et al. 2006; Nicuesa Guelbenzu et la. 2011 Fong et al. 2012, 2013; Troja et al. 2016) point to narrow jets (θjet ≲ 10° – even though serious selection effects could be at play), implying that the probability of an on-axis or slightly off-axis jet associated with the very first GW from a NS–NS merger is very small. Last but not least, several studies (e.g. Ruiz & Shapiro 2017; Murguia-Berthier et al. 2017b; Margalit et al. 2015) seem to indicate that not all NS–NS mergers are capable of producing a jet, making the association even more unlikely.
It could certainly be the case that all or some of the above expectations and prejudices about SGRB jets are simply incorrect. On the other hand, many features of GRB170817A suggest quite naturally that it does not belong to the SGRB population we are used to. Its isotropic equivalent energy is several orders of magnitude below the least energetic SGRB known so far, despite the spectral peak energy being only moderately low with respect to the known population (Nava et al. 2011; Zhang et al. 2018). Indeed, these facts have been taken by many as hints that GRB170817A is an ordinary or structured SGRB jet seen off-axis (e.g. Pian et al. 2017; Ioka & Nakamura 2018; Burgess et al. 2017; Zhang et al. 2018; Lamb & Kobayashi 2018; He et al. 2018; Kathirgamaraju et al. 2017), while others interpret GRB170817A as emission from the jet cocoon (e.g. Kasliwal et al. 2017; Bromberg et al. 2018; Piro & Kollmeier 2018; Gottlieb et al. 2018; Lazzati et al. 2017b).
In this work, we explore whether GRB170817A can be interpreted as emission from an isotropic fireball powered by the strong magnetic field produced during the progenitor NS–NS merger, as already proposed in (Salafia et al. 2018; Paper I hereafter).
2. Observational properties of GRB170817A
The GRB triggered Fermi/GBM on 2017-08-17 12:41:06, just 1.74 s after the estimated merger time of GW170817 (Abbott et al. 2017c). A corresponding signal was also detected by INTEGRAL/SPI-ACS (Savchenko et al. 2017), providing important confirmation. The duration of the burst has been estimated as T90 = 2.0 ± 0.5 s. The 64 ms peak flux in the 10–1000 keV band was 3.7 ± 0.9 ph cm−2 s−1, and the fluence was (2.8 ± 0.2) × 10−7 erg cm−2. Detailed analysis (Goldstein et al. 2017; Zhang et al. 2018) indicates the possible presence of two components: a non-thermal component dominating the early part of the light curve, whose spectrum is fit by a power-law with an exponential cut-off with Epeak = 185 ± 62 keV, and has a fluence of (1.8 ± 0.4) × 10−7 erg cm−2; and a thermal component visible in the tail of the light curve, which can be fit by a blackbody with kBT = 10.3±1.5 keV (where kB is the Boltzmann’s constant) and a fluence of (0.61 ± 0.12) × 10−7 erg cm−2, which corresponds to an isotropic equivalent energy (1.20 ± 0.23) × 1046 erg at dL ≈ 40 Mpc (i.e. the distance to the host galaxy NGC 4993, Hjorth et al. 2017; Im et al. 2017). According to Goldstein et al. (2017), the thermal component could be present since the beginning, masked initially by the non-thermal emission.
Multi-wavelength follow-up of the event (Abbott et al. 2017c) resulted in several important detections. In the ultraviolet (UV), optical, and near infrared (NIR) during the week following the merger, a relatively bright optical transient was discovered (Coulter et al. 2017; Valenti et al. 2017) and extensively observed (e.g. Andreoni et al. 2017; Arcavi et al. 2017; Chornock et al. 2017; Covino et al. 2017; Díaz et al. 2017; Drout et al. 2017, Evans et al. 2017; Hallinan et al. 2017; Pian et al. 2017; Pozanenko et al. 2018; Smartt et al. 2017; Utsumi et al. 2017). Its nature is established (e.g. Pian et al. 2017; Cowperthwaite et al. 2017; Gall et al. 2017; Kilpatrick et al. 2017; McCully et al. 2017; Nicholl et al. 2017; Smartt et al. 2017) as being nuclear-decay-powered emission from the expanding NS–NS merger ejecta (i.e. a kilonova, Li & Paczyński 1998; Metzger et al. 2010; Metzger 2017).
Another transient, which we interpret as a GRB-related afterglow, has been detected in X-rays by Chandra (Troja et al. 2017, 2018; Margutti et al. 2017, 2018; Haggard et al. 2017) and XMM-Newton (D’Avanzo et al. 2018) in the Optical by HST (Lyman et al. 2018; Margutti et al. 2018) and in radio by several facilities (Hallinan et al. 2017; Mooley et al. 2017; Margutti et al. 2018; Dobie et al. 2018). Observations between 9 and 150 days after GRB170817A show a spectrum which is consistent with a single power law extending from a few gigahertz to the X-ray band (Margutti et al. 2018). The luminosity during that period kept rising approximately as t0.8 (Mooley et al. 2017). Observations in the optical (Margutti et al. 2018), X-rays (D’Avanzo et al. 2018) and radio (Dobie et al. 2018) around 150 days started to show some signs of a flattening in the light curve, and a peak at approximately 160 days was later confirmed (Alexander et al. 2018). When interpreted as synchrotron emission from a blast wave in a constant-density interstellar medium (ISM), these observations indicate (Nakar & Piran 2018) that the emitting material is mildly relativistic (Γ ∼ a few).
3. The time delay between GW170817 and GRB170817A: relatively short for an off-axis jet
As discussed in Salafia et al. (2016) and Murguia-Berthier et al. (2017a) for example, the observed duration of a GRB should not depend on the viewing angle. Individual pulses that constitute the light curve become longer with increasing viewing angle, but their separation remains unchanged. The result is a smoother pulse shape when the jet is seen off-axis, but without significant change in the total duration (provided that single pulses are much shorter than the total duration of the burst).
The delay with respect to the jet launch time (and thus the merger time in our case), instead, increases with the viewing angle. We show in what follows that it is hard to reconcile a delay of ∼2 s with emission from a jet seen under a large viewing angle (somewhat similar arguments are outlined in Shoemaker & Murase 2018).
In order to emit gamma-rays, the jet must expand enough to become transparent. We estimate the transparency radius Rt as (e.g. Daigne & Mochkovitch 2002)
where σT is the Thomson cross-section, mp is the proton mass, and we are assuming an electron fraction of unity. LK, iso in this expression is the isotropic equivalent kinetic luminosity of the outflow, that is, LK, iso = ΓṀisoc2. If we assume that the jet is launched a short time (≪1 s) after the merger, the arrival time difference between the latest gravitational waves and the first photons is
This accounts for the fact that fluid elements on the jet border must travel up to Rt at a speed of βc before being able to emit the gamma-ray photons (see Fig. 1).
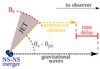 |
Fig. 1. If the gamma-ray prompt emission is due to an off-axis jet, the arrival time difference between the last gravitational waves and the first gamma-ray photons is dominated by the time it takes for the jet to become transparent in the observer frame. |
We can relate the kinetic luminosity of the jet to the on-axis gamma-ray luminosity by assuming that 10% of the kinetic luminosity is converted into photons, that is, Liso(θv = 0) = 0.1 LK,iso (as in e.g. Kathirgamaraju et al. 2017, see also Beniamini & Granot 2016 who show that this is a typical conversion efficiency). We compute the corresponding off-axis luminosity Liso(θv) using Eq. (11) of Salafia et al. (2016). If we require that Liso(θv) = 1047 erg s−1 as in GRB170817A (Goldstein et al. 2017), and we assume a jet half-opening angle θjet, we can compute the corresponding on-axis luminosity Liso(0) and arrival time delay tγ − tGW for various combinations of the bulk Lorentz factor Γ and off-axis viewing angle θv = θjet. Figure 2 shows the contours of these quantities for θjet = 0.2 rad = 11.5° (the figure would be very similar for θjet = 0.1 rad or θjet = 0.3 rad). The red solid contour corresponds to the actual 1.7 s delay time as observed in GRB170817A, while the dotted contours represent the on-axis luminosities. The figure shows that a “standard” jet with a large Lorentz factor Γ ≳ 70 and an on-axis luminosity Liso(0)∼1051 erg s−1 is formally compatible with the observed time delay, but it requires fine-tuning of the viewing angle, which implies an extremely small probability. Moreover, the line of sight being only slightly off the jet border, the jet afterglow should have turned very bright after a few days, which would conflict with the stringent early X-ray upper limits set by Swift and NuSTAR during the first week after GW170817 (see e.g. Evans et al. 2017). A “slow” fireball with a Lorentz factor around Γ ≲ 7 and a much smaller energy, instead, would give the correct time delay both if seen on-axis or a few degrees off-axis. For these reasons, we believe that GRB170817A is more naturally explained by slow material moving towards the observer (which is the case both for the jet cocoon – Lazzati et al. 2017a,b – and for the isotropic giant flare described in Paper I) than by a fast off-axis jet. The cocoon explanation, on the other hand, still requires the presence of a jet. Since the launch of a jet in the post-merger phase is not guaranteed (e.g. Ruiz & Shapiro 2017; Murguia-Berthier et al. 2017b), while the conditions leading to the giant flare seem to be typical for double neutron-star mergers (Zrake & MacFadyen 2013; Giacomazzo et al. 2015), the latter seems to be the most natural, and below we show that indeed both the prompt and the afterglow emission of GRB170817A can be understood within such a jet-less picture. Future observations of double neutron-star mergers and their electromagnetic counterpart will certainly provide the necessary evidence to discern between the possible scenarios outlined here and help to assess their relative frequency.
 |
Fig. 2. Solid red and dashed brown lines represent contours of the gamma-ray photon arrival time delay with respect to the last gravitational waves for a given jet bulk Lorentz factor Γ and off-axis viewing angle θv = θjet. The dotted lines represent contours of the on-axis jet luminosity Liso(0) corresponding to an off-axis luminosity of Liso(θv) = 1047 erg s−1. |
4. Interpreting the GRB as an isotropic fireball
4.1. The scenario
Let us briefly summarise the scenario described in Paper I: during the inital phase of the merger, the magnetic field is quickly amplified to B ∼ 1016 G (Price 2006; Zrake & MacFadyen 2013; Giacomazzo et al. 2015). If such a strong magnetic field transfers part of its energy to a small amount of plasma surrounding the merger, for example by reconnection or by impulsive magnetic acceleration (Contopoulos 1995; Granot et al. 2010; Lyutikov 2011), a relativistic fireball can be produced. The fireball, whose initial radius is R0, promptly expands and accelerates to relativistic velocities under its own pressure1. The acceleration ends when most of the initial internal energy E0 has been transformed into kinetic energy, at a radius (we employ the usual notation Qx ≡ Q/10x incgs units),
The thickness of the fireball at this point is of the order of the initial radius R0, but its intrinsic velocity profile (developed during the initial acceleration phase, e.g. Piran et al. 1993) causes it to spread2 as the expansion proceeds. The effect becomes significant only beyond a “spreading” radius Rs ∼ Γ2R0 (e.g. Mészáros et al. 1993), after which the fireball thickness is given by R/Γ2. The opacity κ of the fireball to high-energy photons is dominated by Thomson scattering, and thus
where Ye = ne/(np + nn) is the electron fraction. In what follows, we take Ye = 0.5, which is expected for relativistic, pair-dominated outflows (Beloborodov 2003). The photospheric radius of a thin shell is given by (e.g. Mészáros 2006)
Once the fireball becomes transparent, relic photons from the initial radiation-dominated phase are liberated. Assuming the energy to be initially completely thermal and confined in a spherical volume of radius R0, the photospheric temperature can be estimated as
where β = (1 − Γ−2)1/2 ≈ 1, producing a thermal pulse containing an energy of
The duration of the pulse is approximately given by the angular timescale (e.g. Salafia et al. 2016)
The above timescale is equal to the transverse timescale (e.g. Piran 2005), corresponding to the delay in the observer frame between the fireball formation and the arrival time of the first photons, which in our case should be equal to the time delay between GW170817 and GRB170817A.
As discussed in Paper I, dissipation of kinetic or magnetic energy within the outflow can give rise to additional emission, just as in GRBs.
Constraints from observations.
A first constraint to the simple model outlined above is set by the 1.74 s delay between the GW chirp and the start of the GRB. Taking Γ1 ≲ 1 as suggested by the arguments in Sect. 3, and setting tang = 1.74 s in Eq. (8), we have
The initial energy release in our scenario must happen in the vicinity of the merging neutron stars, for example within the light cone of the system, which is located at ∼100 km for a system rotating at an angular frequency of Ω = 3000 rad s−1. We then see from Eqs. (7) and (6) that the energy content of GRB170817A and its temperature are not fully explained by photospheric emission, and we therefore need some form of energy dissipation in the outflow to explain the GRB in our scenario. On the other hand, if afterglow observations are to be interpreted as synchrotron emission from the external shock that forms as the shell decelerates in the ISM, the energy in the ejecta (assumed isotropic) is of the order of ∼1050 erg (Nakar & Piran 2018; Huang & Li 2018), meaning that inequality (Eq. (9)) would be violated, that is, the shell was still optically thick at the time at which it should have produced the GRB. As we show in the following section, this seemingly unsolvable tension can be addressed differently if the ejecta velocity profile is taken into account.
4.2. The velocity profile
Several authors (e.g. Vitello & Salvati 1976; Piran et al. 1993; Mészáros et al. 1993; Bisnovatyi-Kogan & Murzina 1995) studied the hydrodynamics of an expanding relativistic fireball in spherical symmetry. Asymptotic scalings of the main quantities are established, but the details of the profile are only accessible by numerical integration of the relativistic Euler equations. Nevertheless it seems clear that, regardless of the initial conditions, during its initial accelerated expansion the fireball undergoes a rearrangement and develops a velocity profile (Piran et al. 1993), with a Lorentz factor spread ΔΓ ∼ Γ across the pulse (Piran et al. 1993; Mészáros et al. 1993). The same holds also if the shell is launched by impulsive magnetic acceleration (Contopoulos 1995; Granot et al. 2010; Lyutikov 2011). The presence of such a profile is indeed a natural outcome of the shell acceleration. The transparency condition in this case becomes simply
where M(> Γ) is the mass in ejecta moving with a Lorentz factor larger than Γ. This is usually neglected in GRBs because the time (in the observer frame) it takes for the photosphere to recede from 2Γ to Γ is small if Γ ≳ 100, but in our mildly relativistic case this effect can make the difference. The idea is therefore that the prompt emission is produced at a time when only a fraction of the ejecta is transparent. Let us assume that the kinetic energy dissipation in the outflow, independently from its nature, has an efficiency of η ≲ 0.1, that is, only a relatively small fraction of the ejecta kinetic energy is converted into prompt radiation. We therefore require that the fraction of the ejecta that is transparent at an observer time 1.74 s contains an energy larger than η−1 times the GRB energy, namely E(> Γ) ≳ Eiso/η = 6 × 1047 erg. Several authors (e.g. Mooley et al. 2017; Huang & Li 2018) have shown that a power-law energy profile E(> Γ) = E⋆(Γβ)−α with α ∼ 5 − 7 is consistent with the observed afterglow, so let us adopt this parametrization. We have M(> Γ) ∼ E(> Γ)/Γc2, and therefore
Assuming β ∼ 1, the requirement that at tang(Γ) = (tγ − tGW) the transparent part of the ejecta have E(> Γ) > Eiso/η is satisfied as long as
where the numerical values are given hereafter for α = 6. Since we are assuming no upper Lorentz factor cut in the energy profile, we should also invert Eq. (11) to check what the Lorentz factor is at the photosphere at tang = 1.74 s. We obtain
which shows that the ejecta must possess a relatively high-speed tail.
A consistency check is that the total energy in the ejecta must be a fraction of the magnetic energy developed during the merger amplification, which is ∼1051 erg (Giacomazzo et al. 2015). In order to check that, we introduce a minimum velocity βmin in the velocity profile (which corresponds to the inner rarefaction wave), below which no significant energy is present, just as in D’Avanzo et al. (2018): the total ejecta energy is therefore Etot ∼ E⋆(Γminβmin)−α. Such minimum velocity can be related to the time of the afterglow peak, which is approximately tpeak ∼ 160 d (Alexander et al. 2018), as follows. We assume the afterglow to be synchrotron emission from the forward shock that forms as the ejecta decelerate in the ISM. The radius of the shock is found (Hotokezaka et al. 2016) by solving the energy balance equation (assuming a uniform ISM density),
where n is the ISM number density and mp is the proton mass. The afterglow luminosity keeps rising as long as slower ejecta inject their energy into the shocked region, and it therefore peaks when the ejecta with minimum velocity βmin reach the shock. Taking the observer time to be tobs ∼ R/βΓ2c, we obtain
The total energy in the ejecta is therefore roughly
The actual energy requirement is further reduced if the outflow is not totally isotropic, but is instead ejected along the polar direction within an effective half-opening angle θ0. Since the region close to the equatorial plane of the binary is likely filled with tidal ejecta, this is actually the most likely case. If θ0 ∼ 45°, the afterglow would be essentially unaffected, while the total energy would be lowered by a factor (1 − cos θ0)−1 ∼ 3.
We can therefore conclude that, in the presence of a mechanism capable of extracting ∼10% of the energy contained in the amplified magnetic field during the initial part of the merger (e.g. reconnection close to the light cylinder, or impulsive magnetic acceleration in the low-density polar regions), and in the presence of a form of energy dissipation within the outflow (e.g. internal shocks, or further magnetic reconnection within the outflow) able to dissipate ∼10% of such energy, we can still interpret GRB170817A and its afterglow within the giant-flare-like scenario proposed in Paper I.
5. Discussion
The fact that GRB170817A has been associated to the first GW from a NS–NS merger is exciting and somewhat surprising given expectations based on the rate and geometry of SGRBs (e.g. Ghirlanda et al. 2016; Wanderman & Piran 2015). Indeed, the vast majority of the GRB community seems to agree that some new ingredient must be added to the usual recipe (i.e. the traditional narrow, uniformly ultrarelativistic jet with sharp borders) in order to explain this burst. In Sect. 3 we outlined an argument against de-beamed emission from an ultrarelativistic jet seen off-axis, showing that the short time delay between GW170817 and GRB170817A would require fine-tuning of the viewing angle. This makes such a scenario unlikely, and points instead to a picture where the gamma-ray emission comes from material moving towards the observer with a relatively small Lorentz factor Γ ≲ 10. This is well accommodated in the jet cocoon emission scenario proposed by Lazzati et al. (2017a,b) and supported by, for example, Kasliwal et al. (2017), Bromberg et al. (2018), Gottlieb et al. (2018), Piro & Kollmeier (2018), Margutti et al. (2018), Lyman et al. (2018), Troja et al. (2018) and D’Avanzo et al. (2018), but these scenarios require the presence of a jet, which may not always be produced in NS–NS mergers. In this work we showed that the alternative explanation of the gamma-ray burst and of its afterglow light curve as a sort of giant flare powered by the magnetic field amplified during the NS–NS merger, as described in Paper I, is still possible, provided that the outflow is endowed with a velocity profile.
During the preparation of this work, a preprint was posted by Mooley et al. (2018), which argues that VLBI radio observations of the source show superluminal motion indicating that the external shock still moves with Γ ∼ 4 around 200 days after GW170817, thereby supporting the presence of a successful jet. If their conclusions are correct, then our proposed mechanism is likely unimportant for this source. Nevertheless, given that the conditions to produce our giant flare could be common to all NS–NS mergers, future observations of these events will provide new testing grounds for this scenario.
Acknowledgments
We thank the anonymous referee for helping us to significantly improve the original manuscript. We also thank Albino Perego for insightful discussions and useful suggestions.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, ApJ, 848, L12 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017c, ApJ, 848, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, K. D., Margutti, R., Blanchard, P. K., et al. 2018, ApJ, 863, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Andreoni, I., Ackley, K., Cooke, J., et al. 2017, Publ. Astron. Soc. Aust., 34, e069 [Google Scholar]
- Arcavi, I., McCully, C., Hosseinzadeh, G., et al. 2017, ApJ, 848, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2003, ApJ, 585, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., & Granot, J. 2016, MNRAS, 459, 3635 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Murzina, M. V. A. 1995, Phys. Rev. D, 52, 4380 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Tchekhovskoy, A., Gottlieb, O., Nakar, E., & Piran, T. 2018, MNRAS, 475, 2971 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M., Greiner, J., & Begue, D. 2017, ArXiv e-prints [arXiv:1710.05823] [Google Scholar]
- Chornock, R., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, J. 1995, ApJ, 450, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Coulter, D. A., Foley, R. J., Kilpatrick, C. D., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S., Wiersema, K., Fan, Y. Z., et al. 2017, Nat. Astron., 1, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Cowperthwaite, P. S., Berger, E., Villar, V. A., et al. 2017, ApJ, 848, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 2002, MNRAS, 336, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P., Campana, S., Salafia, O. S., et al. 2018, A&A, 613, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, M. C., Macri, L. M., Lambas, D. G., et al. 2017, ApJ, 848, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Dobie, D., Kaplan, D. L., Murphy, T., et al. 2018, ApJ, 858, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Piro, A. L., Shappee, B. J., et al. 2017, Science, 358, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Cenko, S. B., Kennea, J. A., et al. 2017, Science, 358, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Margutti, R., et al. 2012, ApJ, 756, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Metzger, B. D., et al. 2013, ApJ, 780, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gall, C., Hjorth, J., Rosswog, S., Tanvir, N. R., & Levan, A. J. 2017, ApJ, 849, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Salafia, O. S., Pescalli, A., et al. 2016, A&A, 594, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacomazzo, B., Zrake, J., Duffell, P. C., MacFadyen, A. I., & Perna, R. 2015, ApJ, 809, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, ApJ, 848, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, O., Nakar, E., Piran, T., & Hotokezaka, K. 2018, MNRAS, 479, 588 [NASA ADS] [Google Scholar]
- Granot, J., Komissarov, S., & Spitkovsky, A. 2010, MNRAS, 411, 1323 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haggard, D., Nynka, M., Ruan, J. J., et al. 2017, ApJ, 848, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Corsi, A., Mooley, K. P., et al. 2017, Science, 358, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- He, X. B., Thomas Tam, P. H., & Shen, R. F. 2018, Res. Astron. Astrophys., 18, 043 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Levan, A. J., Tanvir, N. R., et al. 2017, ApJ, 848, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hotokezaka, K., Nissanke, S., Hallinan, G., et al. 2016, ApJ, 831, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y., & Li, Z. 2018, ApJ, 862, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Yoon, Y., Lee, S.-K. J., et al. 2017, ApJ, 849, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ioka, K., & Nakamura, T. 2018, Prog. Theor. Exp. Phys., 2018, 043E02 [Google Scholar]
- Kasliwal, M. M., Nakar, E., Singer, L. P., et al. 2017, Science, 358, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Kathirgamaraju, A., Duran, R. B., & Giannios, D. 2017, MNRAS, 473, L121 [Google Scholar]
- Kilpatrick, C. D., Foley, R. J., Kasen, D., et al. 2017, Science, 358, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, G. P., & Kobayashi, S. 2018, MNRAS, 478, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Deich, A., Morsony, B. J., & Workman, J. C. 2017a, MNRAS, 471, 1652 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., López-Cámara, D., Cantiello, M., et al. 2017b, ApJ, 848, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [Google Scholar]
- Lyman, J. D., Lamb, G. P., & Levan, A. J. 2018, Nat. Astron., 2, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2011, MNRAS, 411, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Margalit, B., Metzger, B. D., & Beloborodov, A. M. 2015, Phys. Rev. Lett., 115, 171101 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Berger, E., Fong, W., et al. 2017, ApJ, 848, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Alexander, K. D., Xie, X., et al. 2018, ApJ, 856, L18 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Hiramatsu, D., Howell, D. A., et al. 2017, ApJ, 848, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2006, Rep. Prog. Phys., 69, 8 [Google Scholar]
- Mészáros, P., Laguna, P., & Rees, M. J. 1993, ApJ, 415, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2017, Liv. Rev. Rel., 20, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Martínez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Nakar, E., Hotokezaka, K., et al. 2017, Nature, 554, 207 [Google Scholar]
- Mooley, K. P., Deller, A. T., & Gottlieb, O. 2018, Nature, 561, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Murguia-Berthier, A., Ramirez-Ruiz, E., Kilpatrick, C. D., et al. 2017a, ApJ, 848, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Murguia-Berthier, A., Ramirez-Ruiz, E., Montes, G., et al. 2017b, ApJ, 835, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Piran, T. 2018, MNRAS, 478, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nicholl, M., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Nicuesa Guelbenzu, A., Klose, S., Rossi, A., et al. 2011, A&A, 531, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pian, E., D’Avanzo, P., Benetti, S., et al. 2017, Nature, 551, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2005, Rev. Mod. Phys., 76, 1143 [Google Scholar]
- Piran, T., Shemi, A., & Narayan, R. 1993, MNRAS, 263, 861 [NASA ADS] [Google Scholar]
- Piro, A. L., & Kollmeier, J. A. 2018, ApJ, 855, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Pozanenko, A. S., Barkov, M. V., Minaev, P. Y., et al. 2018, ApJ, 852, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J. 2006, Science, 312, 719 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ruiz, M., & Shapiro, S. L. 2017, Phys. Rev. D, 96, 084063 [NASA ADS] [CrossRef] [Google Scholar]
- Salafia, O. S., Ghisellini, G., Pescalli, A., Ghirlanda, G., & Nappo, F. 2016, MNRAS, 461, 3607 [NASA ADS] [CrossRef] [Google Scholar]
- Salafia, O. S., Ghisellini, G., & Ghirlanda, G. 2018, MNRAS: Lett., 474, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Kuulkers, E., et al. 2017, ApJ, 848, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Shoemaker, I. M., & Murase, K. 2018, Phys. Rev. D, 97, 083013 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Chen, T.-W., Jerkstrand, A., et al. 2017, Nature, 551, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Berger, E., Kasliwal, M., et al. 2006, ApJ, 650, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Sakamoto, T., Cenko, S. B., et al. 2016, ApJ, 827, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Piro, L., van Eerten, H., et al. 2017, Nature, 551, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Piro, L., Ryan, G., et al. 2018, MNRAS: Lett., 478, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Utsumi, Y., Tanaka, M., & Tominaga, N. 2017, Publ. Astron. Soc. Japan, 69, 101 [Google Scholar]
- Valenti, S., Sand, D. J., Yang, S., et al. 2017, ApJ, 848, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Vitello, P., & Salvati, M. 1976, Phys. Fluids, 19, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Wanderman, D., & Piran, T. 2014, MNRAS, 448, 3026 [Google Scholar]
- Zhang, B.-B., Zhang, B., Sun, H., et al. 2018, Nat. Commun., 9, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Zrake, J., & MacFadyen, A. I. 2013, ApJ, 769, L29 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. If the gamma-ray prompt emission is due to an off-axis jet, the arrival time difference between the last gravitational waves and the first gamma-ray photons is dominated by the time it takes for the jet to become transparent in the observer frame. |
| In the text | |
 |
Fig. 2. Solid red and dashed brown lines represent contours of the gamma-ray photon arrival time delay with respect to the last gravitational waves for a given jet bulk Lorentz factor Γ and off-axis viewing angle θv = θjet. The dotted lines represent contours of the on-axis jet luminosity Liso(0) corresponding to an off-axis luminosity of Liso(θv) = 1047 erg s−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



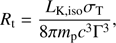
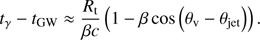
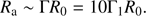
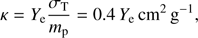
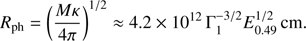
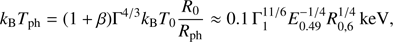
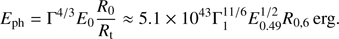
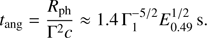
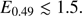
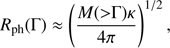
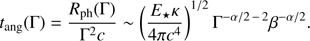
![$$ \begin{aligned} \begin{array}{l} E_\star >\left[4\pi c^4(t_\gamma -t_{\mathrm{GW} })\right]^{-\alpha /5}\left(E_{\mathrm{iso} }/\eta \right)^{\alpha /5\,+\,1}\\ \quad \,\,=1.6\times 10^{53}\,\eta _{-1}^{-11/5}\,{\mathrm{erg} }, \end{array} \end{aligned} $$](/articles/aa/full_html/2018/11/aa32259-17/aa32259-17-eq12.gif)
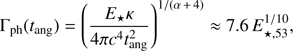
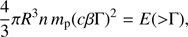
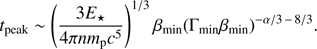
![$$ \begin{aligned} \begin{array}{l} E_{\mathrm{tot} }\sim \left[\frac{4\pi }{3}nm_{\mathrm{p} }c^5t_{\mathrm{peak} }^{3}E_\star ^{8/\alpha }\right]^{\alpha /(8\,+\,\alpha )}\\ \quad ~~~\approx 2\times 10^{50}\,n_{-4}^{3/7}E_{\star ,53}^{4/7}\,{\mathrm{erg.} }\\ \end{array} \end{aligned} $$](/articles/aa/full_html/2018/11/aa32259-17/aa32259-17-eq16.gif)