| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833354 | |
| Published online | 17 October 2018 | |
The CARMENES search for exoplanets around M dwarfs
A Neptune-mass planet traversing the habitable zone around HD 180617*
1
Landessternwarte, Zentrum für Astronomie der Universtät Heidelberg,
Königstuhl 12,
69117 Heidelberg, Germany
e-mail: A.Kaminski@lsw.uni-heidelberg.de
2
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117 Heidelberg, Germany
3
Centro de Astrobiología (CSIC-INTA), ESAC campus, Camino Bajo del Castillo s/n,
28692 Villanueva de la Cañada,
Madrid, Spain
4
Institut de Ciències de lEspai (ICE, CSIC), Campus UAB, c/ de Can Magrans s/n,
08193 Bellaterra,
Barcelona, Spain
5
Institut dEstudis Espacials de Catalunya (IEEC),
08034 Barcelona,
Spain
6
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077 Göttingen, Germany
7
Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n,
18008 Granada, Spain
8
School of Geosciences, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University,
Tel Aviv 6997801, Israel
9
Université Grenoble Alpes, CNRS, IPAG,
38000 Grenoble, France
10
Observatoire de Genève, Université de Genève,
51 ch. des Maillettes,
1290 Sauverny, Switzerland
11
Departamento de Astronomía, Universidad de Concepción,
Casilla 160-C,
Concepción, Chile
12
Instituto de Astrofísica de Canarias,
Vía Láctea s/n,
38205 La Laguna,
Tenerife, Spain
13
Departamento de Astrofísica, Universidad de La Laguna,
38206 La Laguna,
Tenerife, Spain
14
Departamento de Astrofísica y Ciencias de la Atmósfera, Facultad de Ciencias Fcas, Universidad Complutense de Madrid,
28040 Madrid, Spain
15
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778 Tautenburg, Germany
16
Hamburger Sternwarte,
Gojenbergsweg 112,
21029 Hamburg, Germany
17
Centro Astronómico Hispano-Alemán (CSIC-MPG), Observatorio Astronómico de Calar Alto, Sierra de los Filabres,
04550 Gérgal,
Almería, Spain
Received:
3
May
2018
Accepted:
14
July
2018
Despite their activity, low-mass stars are of particular importance for the search of exoplanets by the means of Doppler spectroscopy, as planets with lower masses become detectable. We report on the discovery of a planetary companion around HD 180617, a bright (J = 5.58 mag), low-mass (M = 0.45M⊙) star of spectral type M2.5 V. The star, located at a distance of 5.9 pc, is the primary of the high proper motion binary system containing vB 10, a star with one of the lowest masses known in most of the twentieth century. Our analysis is based on new radial velocity (RV) measurements made at red-optical wavelengths provided by the high-precision spectrograph CARMENES, which was designed to carry out a survey for Earth-like planets around M dwarfs. The available CARMENES data are augmented by archival Doppler measurements from HIRES and HARPS. Altogether, the RVs span more than 16 yr. The modeling of the RV variations, with a semi-amplitude of K = 2.85-0.25+0.16 m s-1, yields a Neptune-like planet with a minimum mass of 12.2-1.4+1.0 M⊕ on a 105.90-0.10+0.09 d circumprimary orbit, which is partly located in the host star’s habitable zone. The analysis of time series of common activity indicators does not show any dependence on the detected RV signal. The discovery of HD 180617 b not only adds information to a currently hardly filled region of the mass-period diagram of exoplanets around M dwarfs, but the investigated system becomes the third known binary consisting of M dwarfs and hosting an exoplanet in an S-type configuration. Its proximity makes it an attractive candidate for future studies.
Key words: planetary systems / stars: late-type / stars: low-mass / stars: individual: HD 180617
The RV data (Table C.1) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A115
© ESO 2018
1 Introduction
The search for exoplanets by means of Doppler spectroscopy has significantly advanced since the first confirmed discoveries at the end of the last century (e.g., Mayor & Queloz 1995). The development in instrumentation within this field led to detection limits on the order of meters per seconds, as has been demonstrated, for example, by HIRES at the Keck Observatory (Vogt et al. 1994), HARPS at the La Silla Observatory (Mayor et al. 2003), HARPS-N at El Roque de Los Muchachos Observatory (Cosentino et al. 2014), or the Automated Planet Finder at the Lick Observatory (Radovan et al. 2014). Still, the choice of the parent stars is crucial. It allows pushing the boundaries with respect to the exoplanet parameter space, and exoplanet programs targeting M dwarfs have become of major interest (e.g., Charbonneau et al. 2008; Zechmeister et al. 2009; Bonfils et al. 2013). Because of their low masses, M dwarfs are particularly suitable for Doppler surveys, since the semi-amplitude of a radial velocity (RV) signal induced by a companion increases with decreasing stellar mass. Thus, lower mass planets are more easily detectable around low-mass stars. M dwarfs have luminosities between 10−4 and 10−1L⊙ and producesignificantly less flux than their more massive counterparts. Consequently, their habitable zones (HZs) are located closer to their host stars at distances of about 0.05–0.4 au (e.g., Joshi et al. 1997; Tarter et al. 2007; Kopparapu et al. 2014; Dressing &Charbonneau 2015). However, the intrinsic stellar activity of M dwarfs can hinder the search for exoplanets around these stars. Signatures of stellar activity such as active regions on the stellar surface and their cyclic variability can mimic radial velocity signals that have previously been misinterpreted as arising from a planetary companion. Since the strength of such activity-related signals has been shown to be wavelength dependent (e.g., Desort et al. 2007; Reiners et al. 2010), a wide wavelength coverage in RV measurements can help distinguish planetary signals from those due to activity (e.g., Sarkis et al. 2018).
The high-resolution fiber-fed spectrograph CARMENES1, which is installed at the 3.5 m telescope at the Calar Alto Observatory in Spain, was specifically designed with a broad wavelength coverage. It consists of two spectrograph channels, which together cover wavelengthsfrom 520 to 1710 nm, with a resolution of 94 600 in the visual and 80 500 in the near-infrared channel (Quirrenbach et al. 2014, 2016). The instrument has been operating since January 2016 and is performing a search for exoplanets around M dwarfs. More than 300 targets that have been selected from the CARMENES input catalog Carmencita (Caballero et al. 2016a; Reiners et al. 2018b) are regularly monitored for this purpose. The capability of the visual channel of achieving an RV precision of 1–2 m s−1 has been demonstrated by Seifert et al. (2016), Trifonov et al. (2018), and the first CARMENES exoplanet discovery byReiners et al. (2018a).
In this paper we analyze the RV data of HD 180617, one of the M dwarfs monitored by CARMENES. The measurements indicate the presence of a planet with a minimum mass comparable to Neptune on an orbit partly located within the habitable zone of the host. In Sect. 2 we characterize the observed star, followed by a short description of the RV data compilation in Sect. 3. The results from the RV analysis are presented in Sect. 4, and we conclude in Sect. 5.
2 Host star HD 180617 (GJ 752 A)
The star HD 180617 is a well-investigated early-M dwarf. Discovered from Königstuhl almost one century ago by Wolf (1919), HD 180617 is known particularly for being the primary of the common (high) proper motion pair that also contains the M8.0 V dwarf vB 10 (V1298 Aql). The pair, first reported as a binary by van Biesbroeck (1944), received the code LDS 6334 in the Washington Double Star catalog (Mason et al. 2001), and is separated by about 76 arcseconds. With its mass near the hydrogen-burning limit at 0.07 M⊙, vB 10 was the least massive star known for almost four decades (van Biesbroeck 1944; Herbig 1956; Kumar 1964; Kirkpatrick et al. 1991). Pravdo & Shaklan (2009) proposed that vB 10 might host a giant planet, which made “vB 10 b” the first putative exoplanet around an ultracool dwarf and the first such object discovered astrometrically. However, this hypothesis was soon after refuted by means of precise radial velocity and astrometric measurements (Bean et al. 2010; Anglada-Escudé et al. 2010; Lazorenko et al. 2011).
The actual exoplanet host is the primary star HD 180617. Although it displays Ca II H&K in emission (Lippincott 1952) and is listed as a flaring star by Simbad, it is rather inactive. In spite of its M2.5 V spectral type, it displays Hα in absorption (Jeffers et al. 2018) and very faint X-ray emission (González-Álvarez 2014). With parallactic distance and proper motions from the Gaia Data Release 2 (DR2; Gaia Collaboration 2018) and radial velocity from Reiners et al. (2018b), we computed Galactocentric space velocities UV W as in Montes et al. (2001), which within errors agree with Delfosse et al. (1998), and we conclude as Cortés-Contreras (2016) did that it is kinematically separated from the young stellar population in the thin disk. The star exhibits a solar-like metallicity (Passegger et al. 2018), and its most probable age therefore lies in the wide range between 1 and 10 Gyr. The extremely young age derived by Tetzlaff et al. (2011) for HD 180617 is apparently incorrect.
The basic information on the star is given in Table 1. The tabulated values are in general consistent with previous determinations, when available (e.g., radial velocities by Nidever et al. 2002, Nordström et al. 2004, and Soubiran et al. 2013; spectral type by Joy & Abt 1974 and Henry et al. 2002; photospheric parameters by Soubiran et al. 2008, Rojas-Ayala et al. 2012, and Gaidos & Mann 2014).
To determine new stellar parameters, we first collected broadband photometry from several surveys covering the whole spectral energy distribution (SED) of all CARMENES GTO targets (Caballero et al. 2016a). In order to determine the stellar luminosity L, we used theVirtual Observatory SED Analyzer (Bayo et al. 2008), the Gaia parallactic distance, and photometry from the following catalogs: SDSS (Ahn et al. 2012), UCAC4 (Zacharias et al. 2013), Tycho-2 (Høg et al. 2000), Gaia DR2 (Gaia Collaboration 2018), CMC15 (Muiños & Evans 2014), 2MASS (Skrutskie et al. 2006), and AllWISE (Cutri & et al. 2013). In the GALEX passbands (Bianchi et al. 2011) and SDSS u, the M-dwarf photometry is dominated by chromospheric emission. Using this luminosity together with the spectroscopic Teff from Passegger et al. (2018) and the Stefan-Boltzmann law, we calculated the radius R. To derive the stellar mass M, we did not use the surface gravity, as we find the large uncertainty that is introduced by the error propagation unacceptable. Instead, we applied the empirical linear M⋆ –R⋆ relation determined by Schweitzer et al. (in prep.), which is similar to other determinations in the literature (e.g., Torres 2013and references therein). Based on data from Pojmański (2002; ASAS), we list a rotational period of Prot = 46.04 ± 0.20 d measured by Díez Alonso et al. (2017; DA17). The reported rotational period was determined by standard means of signal search with the Lomb-Scargle periodogram of the time series of 389 observations, spread over 8 yr. It is almost identical to the period derived by Suárez Mascareño et al. (2016; SM16), as both determinations are based on the same data set. There are differences between amplitudes (8 mmag in DA17, 4.5 mmag in SM16) and false-alarm probabilities (FAP; 2.0% in DA17; <0.1% in SM16), however. The period also agrees with the one estimated from the stellar 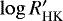 of –5.07, PHK = 47 ± 4 d (Astudillo-Defru et al. 2017).
of –5.07, PHK = 47 ± 4 d (Astudillo-Defru et al. 2017).
More than 700 citations are collected for HD 180617 and vB 10 together, but numerous misidentifications of the secondary still abound in public catalogs because of its low Galactic latitude (b ≈ –3 deg) and the resulting high stellar density in the area. Furthermore, Cortés-Contreras et al. (2014) noted that WDS tabulated only three epochs from 1942 to 1999, and the last epoch (2MASS) was incorrect. In Table 2 we provide angular separations, position angles, epochs, and the sources of the relative astrometry determined by us. With the 33-yr time baseline, and in spite of the saturation of the primary in the photographic plates (particularly from the Quick-V Northern survey), we double the number of published astrometric visits for this system and confirm that there is no measurable orbital variation. The pair is separated by ρ = 75.20 ± 0.22 arcsec, which translates into a projected physical separation of 444.6 ± 1.3 au. The expected orbital period is about 104 yr (Cortés-Contreras et al. 2014).
Using CARMENES data, Reiners et al. (2018b) tabulated the first precise determination of the absolute radial velocity of vB 10 to V r = +35.699 km s−1. This is almost identical to that of HD 180617 (see Table 1), as expected from their common proper motion and distance (Gaia DR2 tabulates d = 5.918 ± 0.005 pc for vB 10). In spite of numerous deep searches (Oppenheimer et al. 2001; Carson et al. 2005; Jódar et al. 2013; Ward-Duong et al. 2015), no additional stellar or substellar member in the system could be confirmed to date.
Basic information on the host star.
Astrometric measurements of the wide pair HD 180617 + vB 10 (WDS 19169+0510, LDS 6334).
3 Radial velocity data
We initially considered the RVs from both CARMENES channels for HD 180617. However, Reiners et al. (2018b) showed that the intrinsic precision (i.e., RV content) of the near-infrared channel velocities is about four times lower than that of the visual channel for targets of M2–3 spectral type. Given the low amplitude of the RV signal and the small contribution of the near-infrared RVs to improving the model parameters, we decided to use only the CARMENES visual channel data for our analysis. A complete characterization of the near-infrared channel and its performance will be carried out in a broader context of the survey. It is work in progress and beyond the scope of this particular publication.
All exposures used for this work comprise the spectral information of both the stellar target and the calibration source, which is a temperature-stabilized Fabry–Pérot etalon (Schäfer & Reiners 2012) that monitors any instrument drifts during the night. These drifts are typically below 10 m s−1 and are determined with a precision below 1 m s−1. Together with the standard dusk and dawn calibration sequences, which contain exposures of U-Ar, U-Ne, and Th-Ne hollow cathode lamps, an accurate wavelength reference is provided for each observation. The wavelength solution, described inBauer et al. (2015), is encapsulated into the standard data processing, carried out by the CARACAL pipeline (Caballero et al. 2016b). The software also performs standard corrections such as bias subtraction and flat-fielding.
From the order-by-order extracted spectra, the radial velocities are then derived by the RV pipeline SERVAL (SpEctrum Radial Velocity AnaLyser; Zechmeister et al. 2018). The RV computation is based on least-squares fitting, where the RVs are determined against a template with a high signal-to-noise ratio (S/N) that is constructed by coadding all available spectra of the target. They are corrected for barycentric motion (Wright & Eastman 2014), as well as for secular acceleration, which is important for stars with high proper motions (Zechmeister et al. 2009).
In addition, a nightly zero-point (NZP) correction was applied in order to achieve the highest RV precision at the 1m s −1 level. For each night, the NZPs were determined from RV measurements of the survey’s “RV-quiet” stars, which in general show only little RV variability. This correction, whose values for the observation nights of HD 180617 were on average about 3 m s−1, was verified and described in more detail by Trifonov et al. (2018).
We supplemented the CARMENES RV measurements by data available from the HARPS spectrograph in Chile and the HIRES spectrograph in Hawai’i. Consequently, our final Keplerian models were applied to the combined data sets. The HIRES data were taken from Butler et al. (2017), while the HARPS RVs were calculated by us using the ESO archival spectra that were reprocessed by SERVAL. We combined 124 CARMENES RV measurements taken over 622 days, 138 HARPS measurements over 4470 days, and 158 HIRES RVs spanning 4849 d. One data point (at JD = 2457258.622) was removed from the HARPS data set, as it is an obvious outlier with an offset of more than 10 m s−1. The full data set of 421 measurements spans 6037 days. There is some overlap in time between the HIRES and HARPS measurements, and also between the HARPS and CARMENES RVs. The typical RV precisions of the instruments are estimated from the medians of the RV uncertainties at 2.10 ms−1 for HIRES, 0.76 ms−1 for HARPS, and 1.42 ms−1 for CARMENES. Compared to the HARPS RVs determined by SERVAL, those determined by the standard HARPS-DRS pipeline in the case of HD 180617 show lower errors with a median of 0.43 ms−1. This is most likely explained by the different error treatment of the two distinct software packages, and does not in general imply a difference in accuracy. We found that our results (see Sect. 4.2) agree very well with those obtained together with the HARPS DRS RVs.
4 Analysis and results
4.1 Periodogram analysis
In Fig. 1 we provide generalized Lomb-Scargle (GLS) periodograms (Zechmeister & Kürster 2009) for the individual data sets (CARMENES, HARPS, and HIRES) as well as the combined data. Three levels of FAPs at 0.1, 1 and 10% are also depicted. They were assessed over the whole frequency range by means of bootstrapping, for which 1000 randomly reordered time series were created from the original data.
The most significant peak in the CARMENES periodogram appears at a period of P ≈ 104 d (f ≈ 0.00961 d−1) with an FAP below 0.1%. Three other signals are visible at periods of around 134, 184 (FAPs below 0.1%), and 300 days (FAP below 1%), which translates into frequencies of 0.00744, 0.00543, and 0.00334 d−1. Since the four signals seem equidistant with Δ f ≈ 0.00209 d−1 in frequency space, and the sampling function of the CARMENES RVs shows a prominent peak close to Δ f at around f ≈0.00233 d−1 (428 d), one might assume that the three peaks with longer periods are aliases of the most significant signal. However, when the dominant peak at 104 d is subtracted from the data, only the signal at 134 d vanishes. The other two remain, and the peak at around 300 d becomes the most significant. Subtracting a simultaneous fit to the two signals at 104 d and 300 d from the data eliminates all of the four peaks. The same applies to a simultaneous fit to the signals at 104 d and 184 d. We therefore conclude that the signal at 134 d is an alias of the 104 d peak and that the signals at 184 d and at about 300 d are also correlated. It is unclear which of the latter two is the true signal, which an alias, and where they come from. The 300 d signal is only visible in the periodogram of the CARMENES data, although HARPS shows a signal with an FAP below 1% at around 600 d. While the time span of the CARMENES measurements is currently too short for properly sampling such a long period, the 300 d peak could be a harmonic of it. On the other hand, the peak at 184 d, which is apparent also in the model residuals, is close to four times the rotation period of the star and might be correlated to some activity signals we find (see below). In addition to the most significant peak at P ≈ 106 d with a power of around 38 and the peak at around P ≈ 600 d, the HARPS periodogram shows further signals that can be attributed to modulations that are due to the sampling function. The latter shows dominant peaks at f1 ≈ 0.00271 d−1 (369 d) and at f2 ≈ 0.00033 d−1 (3005 d). Consequently, aliases appear at about fa = f ± fs (0.00668 and 0.01210 d−1). These aliases, as well as the main signal, come in packages, where the peaks are separated by Δ f ≈ f2. The HIRES periodogram does not exhibit any significant peak. There is subtle power (FAP around 10%) at 106 d, as well as at around 0.01754 d−1 (57 d). The latter is not easily explained by the sampling function, which shows dominant peaks at periods of one year and one month only. Therefore its nature remains unclear.
In the GLS periodogram of the combined data set, the signal in question is highly significant (FAP < 0.002%), with a refined period value of around 106 d. Since all additional peaks of significance are understood, mainly due to the sampling of the HARPS time series, we focused on the dominant peak alone for the further modeling.
 |
Fig. 1 GLS periodograms of the RV data for HD 180617. Upper three panels: individual instruments, followed by the combined data set. Lowermost panel: periodogram of the residuals of the best-fit solution. The horizontal lines (dotted, dash-dotted, and dashed) illustrate FAP levels of 10, 1, and 0.1%. The best-fit period at Pb = 105.9 d is highlighted by the vertical red line. |
4.2 Keplerian modeling
For the subsequent analysis we applied a Keplerian model to the combined data set. It included the following free parameters: semi-amplitude K, orbital period P, eccentricity e, mean anomaly M (valid for JD = 2452061.959, the first observational RV epoch), longitude of periastron ϖ, and RV offsets γ for each individual instrument. The HARPS instrument underwent an upgrade in May 2015, during which new optical fibers were implemented (Lo Curto et al. 2015). In order to take this into account, we divided the HARPS data into two subsets, and applied two different RV offsets for the pre- and post-upgrade epochs, respectively. Although HIRES also was upgraded in August 2004, when it received a new CCD, we did not subdivide its data, as Butler et al. (2017) showed that the upgrade did not produce a significant RV offset.
All free parameters were determined by minimizing the negative logarithm of the model likelihood, based on the Nelder Mead simplex algorithm (Nelder & Mead 1965). The resulting quantities, the time of transit ttrans., and the instrument-dependent RV jitter variances that were modeled simultaneously during the parameter optimization following Baluev (2009) are listed in Table 3. The 1σ uncertainties were estimated from the posterior distributions derived by Markov chain Monte Carlo (MCMC) sampling (see Fig. A.1). The same free parameters as in the Keplerian model, together with flat priors, were employed for the MCMC analysis, for which we made use of the open-source affine-invariant ensemble sampler emcee (Foreman-Mackey et al. 2013). Plots of the RV time series are shown in Fig. 2.
In combination with the stellar parameters in Table 1, the measured semi-amplitude 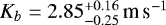 and the period of
and the period of 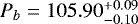 d translate into a planet with a minimum mass of
d translate into a planet with a minimum mass of  M⊕, a semi-major axis of ab =
M⊕, a semi-major axis of ab = 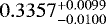 au, and an eccentricity of
au, and an eccentricity of 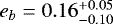 . The errors of the mass and the semi-major axis take the uncertainty of the stellar mass into account. The eccentricity is not well constrained and has a high uncertainty toward lower values. This is illustrated in the posterior distrubutions from the MCMC analysis. The distribution of eb is concentrated at lower values with a mean of
. The errors of the mass and the semi-major axis take the uncertainty of the stellar mass into account. The eccentricity is not well constrained and has a high uncertainty toward lower values. This is illustrated in the posterior distrubutions from the MCMC analysis. The distribution of eb is concentrated at lower values with a mean of 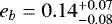 . According to Kopparapu et al. (2014), the best-fit solution places the planet at the outer edge of the conservative estimate of the liquid water habitable zone for its host star, 0.19 au ≤ a ≤ 0.36 au. If the eccentricity is non-zero, the planet is inside the HZ for about half of the orbit, near periastron, while it is outside for the other half, near apastron (see Fig. 3).
. According to Kopparapu et al. (2014), the best-fit solution places the planet at the outer edge of the conservative estimate of the liquid water habitable zone for its host star, 0.19 au ≤ a ≤ 0.36 au. If the eccentricity is non-zero, the planet is inside the HZ for about half of the orbit, near periastron, while it is outside for the other half, near apastron (see Fig. 3).
The stellar irradiance at the top of the planet atmosphere varies between Smax ≈ 0.41S0 and Smin ≈ 0.22S0, where the solar constant S0 = 1360.8 W m−2 is the solar irradiance at the distance of 1 au.
For CARMENES and the HARPS data sets, the total RV jitter is comparable at ≲ 2 m s−1, while it is 5.62 m s−1 for the HIRES data. With 1.77 m s−1, the root mean square of the residuals of the model fits is lowest for the HARPS post-upgrade data, followed by the HARPS pre-upgrade (2.15 m s−1) and the CARMENES (2.66 m s−1) data. Again, HIRES shows the highest value, with 6.02 m s−1. Compared to the formal uncertainties of the measurements (see Sect. 3), this means a factor of around three for HIRES and the HARPS pre-upgrade, and a factor of two for the HARPS post-upgrade and the CARMENES data.
The GLS periodogram of the residuals does not show any significant signals (lower panel Fig. 1). However, there is some power at periods around 45 days and its overtones. This can be attributed to the rotation period Prot = 46.04 d of the host star. Moreover, the strongest peak at around P ≈ 190 d nearly reaches the 1% FAP level. The source of this signal is currently unknown, although the activity indicators hint at stellar activity. We also analyzed the residuals for possible long-term structures, but found the results inconclusive. While the entire data set shows only a negligible drift term of 0.03 ms−1yr−1, it is more significant for the residuals of the most recent RV measurements. A linear fit to the combined residuals from the HARPS post-upgrade epoch together with the CARMENES data gives a slope of around 0.5 ms−1yr−1. This could be an indication for an additional long-term signal, which in the HIRES data might be obscured by the comparably high scatter.
In order to investigate the robustness of our fit results against possible contributions from correlated noise and additional RV or activity signals, we studied five additional models, using the concepts of moving averages (MA) and Gaussian process (GP) regression. The results from this analysis and their discussion can be found in Appendix. B. They agree with the orbital parameters reported here.
Best-fit parameters with the corresponding 1σ errors for HD180617 b.
 |
Fig. 2 Unfolded (left) and phase-folded (right) RV measurements of the individual instruments for HD 180617, together with the best fit overplotted. |
4.3 Activity analysis
Periodic variability in RV measurements can also be introduced by stellar activity. Chromospheric emission, chromatic dependence of the RVs, and changes in line profiles are indicative of stellar activity. In Fig. 4 we provide GLS periodograms for some of these quantities, derived from the available CARMENES spectra. The Hα index, the chromatic index (CRX), and the differential line width (dLW), shown in the three uppermost panels, are derived from the time series of activity indicators directly provided by SERVAL (Zechmeister et al. 2018). While the chromatic index reflects wavelength dependencies of the measured RVs in the different échelle orders, which can result from the temperature surface structure onthe star (spots or faculae), the differential line width serves as another measure for variations in the shape of the line profiles. In addition, we evaluated the full width at half-maximum (FWHM) of the cross-correlation function (CCF). We show periodograms of the CCF-FWHM, the contrast, and the bisector span. The latter is defined as the difference between the average bisector values in the two CCF regions from 90 to 60% and from 40 to 10%.
There is no significant power at any of these indicators at the orbital period Pb = 105.90 d. The highest peak in the GLS periodogram of Hα is at a period of P ≈ 196 d (f ≈ 0.00510 d−1) and an FAP of nearly 0.1%. This period is consistent with a peak found in the periodogram of the RV residuals after subtracting the best-fit planet solution. The second highest peak at around 140 d (f ≈ 0.00716 d−1) and an FAP around 1% is an alias. It disappears after subtracting a fit to the 196 d period. Thesampling function (not plotted) shows a strong signal at around 436 days (fs ≈ 0.00229 d−1). Together with that sampling frequency fs, the signal at f ≈0.00510 d−1 could produce an alias at around fa = f + fs. The indicators sensitive to line profile variations also show some power at around 200 days. Peaks (FAP ~ 10%) at around 50 d, which is close to the rotation period of the star, are evident in the periodograms of CCF-FWHM and CCF contrast.
We also investigated the activity indicators from the other instruments. For HARPS we analyzed the time series of the Hα and CRX indices, the dLW, the CCF-FWHM, and the bisector span. The HIRES data provided time series of the S-index and the H-index, two further chromospheric activity indicators (Gomes da Silva et al. 2011; Butler et al. 2017). Signatures from the stellar rotation are obvious in HARPS Hα data with an FAP below 0.1% around the period of 50 d and recognizable although insignificant (FAP ~ 10%) in the CCF-FWHM periodogram. The same is true for the HIRES indices. In the GLS of the S-index the rotational period of the star was recovered from a signal with an FAP below 1%, while a forest of peaks with low significance (FAP ≳ 10%) was found in the H-index data. Furthermore, the periodograms of the H-index and the dLW from HARPS also showed some power at periods between 185 and 195 d and some significant power excess was found in the GLS of the S-index at around 3500 d, which might imply a long-term magnetic cycle. However, none of these additional indicators showed any significant signal at the planetary period, and we conclude that the RV signal at 105.90 d is due to the stellar reflex motion caused by a planetary companion rather than stellar activity. We found no correlation between any of the activity indicators and the RV model residuals either.
 |
Fig. 3 Orbital plot for HD 180617 b around its host star. The red ellipse corresponds to the best-fit solution, while the dashed ellipses represent the orbits at the upper and lower 1σ uncertainty levels of the eccentricity. The conservative liquid water habitable zone according to Kopparapu et al. (2014), shaded in green, is given by 0.19 au ≤ a ≤ 0.36 au. Separations are in units of astronomical units. |
 |
Fig. 4 GLS periodograms of activity indicators derived from the CARMENES spectra of HD 180617 with lines (dotted, dash-dotted, and dashed) at FAP levels of 10, 1, and 0.1%. The vertical red and black lines represent the best-fit planet period at Pb = 105.9 d, and the rotation period of the star at Prot = 46.04 d, respectively. No significant power is found at the planetary period. |
5 Summary and concluding remarks
We presented radial velocity time series of the inactive early-M dwarf HD 180617 using RV measurements from the visual channel of the high-resolution spectrograph CARMENES in addition to HARPS and HIRES archival data. The combined data sets indicate the existence of a planet with a minimum mass of 12.2 M⊕ on a 105.9 d orbit around its stellar host. Our investigation of periodicities in the activity indicators for Hα emission, RV chromaticity, and line profile variations shows no obvious indication that the planetary signal is due to activity-induced RV variability. The orbit of the Neptune-like planet, with semi-major axis a = 0.3357 au and eccentricity e = 0.16, is partly located in its host star’s liquid water habitable zone. Under the condition of an edge-on view onto the system, the semi-amplitude astrometric signature at Earth’s distance is estimated to be about 4.6 μas. With decreasing orbital inclination, the planetary mass and therefore the astrometric signature increase, therefore this is only a lower limit and the astrometric orbit could potentially be observed by Gaia. Because of the proximity of HD 180617 (d = 5.9 pc), the angular separation of the planet from its host star is rather large, comparable to the ~ 50 mas inner working angle of a high-performance coronograph on a 4 m class space telescope. While the mass of HD 180617 b is too high to be considered a close Earth analog, it is thus nevertheless a prime target for future missions – such as the HabEx concept (Mennesson et al. 2016) – aimed at studying the atmospheres of potentially life-bearing planets, or ESO’s ground-based Extremely Large Telescope (Gilmozzi & Spyromilio 2007).
Only 15 closer stars, 10 of which are M dwarfs, are currently known to have an exoplanet. Within this group, HD 180617 is the seventh brightest in the V band. Moreover, it is the primary of the wide binary containing the low-mass star vB 10. We provide new measurements on the binary separation and new determinations of the primary mass, radius, luminosity, and Galactocentric space motion. Of the 88 currently confirmed binary systems that host exoplanets, only a handful possess an M dwarf as the primary (Schwarz et al. 2016). Except for Gliese 676 A/B and Gliese 15 A/B, the system investigated in this work is the third of this kind with an exoplanet in an S-type2 configuration (Rabl & Dvorak 1988), which means that the planet is in a close orbit around only one of the systems’ stars. Because of the wide separation (s ≥ 450 au) between the system’s stellar components (more than 1300 times larger than the semi-major axis of HD 180617 b), the perturbation of vB 10 on the formation and dynamical evolution of the planet is expected to be negligible (e.g., Whitmire et al. 1998; Quintana et al. 2007; Quintana 2008). In this configuration, the gravitational pull from the host star on the planet is about 107 times stronger than from the secondary. Furthermore, given the very low luminosity of 425 ± 4 × 10−6 L⊙ of the M8.0 V companion (Cifuentes 2017), the presence of vB 10 is not expected to affect the radiative equilibrium of HD 180617 b. Consequently, in this particular case, binarity does not affect habitability.
In line with HD 147379 b, the first exoplanet discovery by CARMENES (Reiners et al. 2018a), our work demonstrates the potential and capability of the instrument of finding exoplanets within the mass range of Neptunes and mini-Neptunes within the habitable zones of M dwarfs. Both HD 180617 b and HD 147379 b have orbital periods of about 100 d. Although dozens of exoplanets with lower masses on shorter orbits around M dwarfs are known, these two discoveries belong to only a few known Neptunes at longer orbits with periods ≳ 100 d. While they improve the sampling within this barely filled region of the exoplanet parameter space, even longer periods for exoplanets of similar masses around M dwarfs are becoming accessible as a result of the steadily increasing time baselines and the improved precision of current and future instruments.
Acknowledgements
CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Science through projects AYA2016-79425-C3-1/2/3-P, ESP2016-80435-C2-1-R, and AYA2015-69350-C3-2-P, the German Science Foundation through the Major Research Instrumentation Programme and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. Based on data from the CARMENES data archive at CAB (INTA-CSIC). N. A. D. acknowledges support from FONDECYT #3180063. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme(s) 072.C-0488(E), 183.C-0437(A), 191.C-0873(A), 191.C-0873(B), 191.C-0873(D), 191.C-0873(E), 191.C-0873(F). Some of the data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation. We made use of the corner.py package (Foreman-Mackey 2016). We thank the anonymous referee for useful comments that improved the paper.
Appendix A MCMC analysis
 |
Fig. A.1 Posterior distributions from the MCMC analysis on HD 180617 b. The best-fit solution is indicated by red lines and the contours define uncertainty levels of 1, 2, and 3σ with respectto the mean. |
Appendix B Model comparison
In orderto investigate the influence of the spurious RV and activity signals on the estimation of the orbital parameters, we applied five additional models to the full data set for comparison. First, a moving-average (MA) noise model (Tuomi et al. 2013a,b) was used to assess the effect of correlated noise. By the means of two additional parameters, an amplitude and a correlation length, this method accounts for the influence of consecutive data points on each another. In our second approach, the possible contributions were modeled by Gaussian process (GP) regressions, which are now widely used within the community (e.g., Rajpaul et al. 2015; Dumusque et al. 2017), and for which we used two different packages. The first was the python library george3 developed by D. Foreman-Mackey (Ambikasaran et al. 2015). Here the covariance matrix was calculated over a quasi-periodic kernel, which consists of four hyperparameters. They are commonly translated into an RV amplitude h, a rotational period Θ, a weighting factor w, and a timescale λ, which can be associated with the corresponding signal’s lifetime, or in particular cases with the lifetime of its underlying process, like an active region within the stellar photosphere (e.g., Perger et al. 2017). An MCMC analysis was applied to estimate the uncertainties. The second package was the fast and scalable GP regression package celerite4, which makes use ofa damped harmonic oscillator as its kernel (Foreman-Mackey et al. 2017). This GP model is characterized by the natural oscillator frequency, or period P0, damping time τ, and peak height S0, which scaleswith the power at the corresponding frequency. The GP model can either be constrained by the RV data alone or by supplementary data, like in our case the time series of the activity indicator Hα from the CARMENES data.
Results from different models to the combined RV time series.
Within all of the models we accounted for the RV offsets between the instruments and for RV jitter terms. The likelihood ln L was calculated as an indicator for the significance of the different approaches. The results from all the different methods are summarized in Table B.1. Model 1 lists the results from our original Keplerian fit (see Sect. 4.2). Model 2 with MA accounts for correlated noise, as well as for the planet via an additional Keplerian term. Within their errors, the determined orbital parameters agree with the parameters from model 1. Models 3 and 4, using george, and models 5 and 6, using celerite, are based on GP regressions. In model 3, only the correlated noise is modeled, and the period of the dominant RV signal (Pb = 105.9 d) is fairly recovered. The long timescale λ = 502.54 d indicates that the RV variation is stable over the time of the observations, as expected from a planet. High attention should be given to models 4–6, which all account for the planet and for correlated noise. Like model 2, they all agree with our original results from model 1. The parameter showing the highest dispersion is the eccentricity, which is quasi-zero in model 6, which was additionally constrained by the Hα data. However, it is also the parmameter with the highest relative errors, and it has been discussed before that it is not well constrained in model 1, with a high uncertainty in particular toward low values. Within the hyperparameters of the GP models 4 and 5, the rotational period of the star is recovered.
Altogether, from the comparison of the different approaches, we conclude that the reported results for the orbital parameters in Sect. 4.2 are robust against and not significantly affected by the additional signals in the RV time series. Therefore, although the lnL is increased for the models that take correlated noise into account, we consider the results from the traditional approach sufficiently reliable.
Appendix C RV data
The RV data, corrected for barycentric motion and secular acceleration, are only available at the CDS (see title footnote on page 1).
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Floriano, F. J., Morales, J. C., Caballero, J. A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Transactions on Pattern Analysis and Machine Intelligence,38, 2 [Google Scholar]
- Anglada-Escudé, G., Shkolnik, E. L., Weinberger, A. J., et al. 2010, ApJ, 711, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Astudillo-Defru, N., Delfosse, X., Bonfils, X., et al. 2017, A&A, 600, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baluev, R. V. 2009, MNRAS, 393, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bean, J. L., Seifahrt, A., Hartman, H., et al. 2010, ApJ, 711, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, L., Efremova, B., Herald, J., et al. 2011, MNRAS, 411, 2770 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Cortés-Contreras, M., Alonso-Floriano, F. J., et al. 2016a, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 148 [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016b, in Proc. SPIE, Observatory Operations: Strategies, Processes, and Systems VI, 9910, 99100E [Google Scholar]
- Carson, J. C., Eikenberry, S. S., Brandl, B. R., Wilson, J. C., & Hayward, T. L. 2005, AJ, 130, 1212 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Irwin, J., Nutzman, P., & Falco, E. E. 2008, BAAS, 40, 44.02 [Google Scholar]
- Cifuentes, C. 2017, MSc Thesis, Universidad Complutense de Madrid, Spain [Google Scholar]
- Cortés-Contreras, M. 2016, PhD Thesis, Universidad Complutense de Madrid, Spain [Google Scholar]
- Cortés-Contreras, M., Caballero, J. A., & Montes, D. 2014, The Observatory, 134, 348 [NASA ADS] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2014, in Proc. SPIE, Ground-based and Airborne Instrumentation for Astronomy V, 9147, 91478C [Google Scholar]
- Cutri, R. M., et al. 2013, VizieR Online Data Catalog: II/328 [Google Scholar]
- Delfosse, X., Forveille, T., Perrier, C., & Mayor, M. 1998, A&A, 331, 581 [NASA ADS] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díez Alonso, E., Montes, D., de Cos Juez, F. J., et al. 2017, in Highlights on Spanish Astrophysics IX, eds. S. Arribas, A. Alonso-Herrero, F. Figueras, et al., 502 [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Borsa, F., Damasso, M., et al. 2017, A&A, 598, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D. 2016, The Journal of Open Source Software, 1 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Agol, E., Angus, R., & Ambikasaran, S. 2017, AJ, 154, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaidos, E., & Mann, A. W. 2014, ApJ, 791, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmozzi, R., & Spyromilio, J. 2007, The Messenger, 127, 11 [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Álvarez, E. 2014, MSc Thesis, Universidad Complutense de Madrid, Spain [Google Scholar]
- Henry, T. J., Walkowicz, L. M., Barto, T. C., & Golimowski, D. A. 2002, AJ, 123, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1956, PASP, 68, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Jeffers, S. V., Schöfer, P., Lamert, A., et al. 2018, A&A, 614, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jódar, E., Pérez-Garrido, A., Díaz-Sánchez, A., et al. 2013, MNRAS, 429, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, M. M., Haberle, R. M., & Reynolds, R. T. 1997, Icarus, 129, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, A. H., & Abt, H. A. 1974, ApJS, 28, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Henry, T. J., & McCarthy, D. W. Jr. 1991, ApJS, 77, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Ramirez, R. M., SchottelKotte, J., et al. 2014, ApJ, 787, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, S. S. 1964, The Observatory, 84, 18 [NASA ADS] [Google Scholar]
- Lazorenko, P. F., Sahlmann, J., Ségransan, D., et al. 2011, A&A, 527, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lippincott, S. L. 1952, ApJ, 115, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mennesson, B., Gaudi, S., Seager, S., et al. 2016, Proc. SPIE, 9904, 99040L [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Muiños, J. L., & Evans, D. W. 2014, Astron. Nachr., 335, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, The Computer Journal, 7, 308 [Google Scholar]
- Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., & Vogt, S. S. 2002, ApJS, 141, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppenheimer, B. R., Golimowski, D. A., Kulkarni, S. R., et al. 2001, AJ, 121, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- Passegger, V. M., Reiners, A., Jeffers, S. V., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perger, M., Ribas, I., Damasso, M., et al. 2017, A&A, 608, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pojmański, G. 2002, Acta Astron., 52, 397 [Google Scholar]
- Pravdo, S. H.,& Shaklan, S. B. 2009, ApJ, 700, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Quintana, E. V. 2008, ASP Conf. Ser., 398, 201 [NASA ADS] [Google Scholar]
- Quintana, E. V., Adams, F. C., Lissauer, J. J., & Chambers, J. E. 2007, ApJ, 660, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Proc. SPIE, Ground-based and Airborne Instrumentation for Astronomy V, 9147, 91471F [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, in Proc. SPIE, Ground-based and Airborne Instrumentation for Astronomy VI, 9908, 990812 [Google Scholar]
- Rabl, G., & Dvorak, R. 1988, A&A, 191, 385 [NASA ADS] [Google Scholar]
- Radovan, M. V., Lanclos, K., Holden, B. P., et al. 2014, in Proc. SPIE, Ground-based and Airborne Telescopes V, 9145, 91452B [Google Scholar]
- Rajpaul, V., Aigrain, S., Osborne, M. A., Reece, S., & Roberts, S. 2015, MNRAS, 452, 2269 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Ribas, I., Zechmeister, M., et al. 2018a, A&A, 609, L5 [Google Scholar]
- Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018b, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sarkis, P., Henning, T., Kürster, M., et al. 2018, AJ, 155, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Schäfer, S., & Reiners, A. 2012, in Proc. SPIE, Ground-based and Airborne Instrumentation for Astronomy IV, 8446, 844694 [CrossRef] [Google Scholar]
- Schwarz, R., Funk, B., Zechner, R., & Bazsó, Á. 2016, MNRAS, 460, 3598 [NASA ADS] [CrossRef] [Google Scholar]
- Seifert, W., Xu, W., Stahl, O., et al. 2016, in Proc. SPIE, Ground-based and Airborne Instrumentation for Astronomy VI, 9908, 990865 [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, A&A, 480, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soubiran, C., Jasniewicz, G., Chemin, L., et al. 2013, A&A, 552, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., & González Hernández J. I. 2016, A&A, 595, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tarter, J. C., Backus, P. R., Mancinelli, R. L., et al. 2007, Astrobiology, 7, 30 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tetzlaff, N., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 410, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2013, Astron. Nachr., 334, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Anglada-Escudé, G., Gerlach, E., et al. 2013a, A&A, 549, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013b, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Biesbroeck, G. 1944, AJ, 51, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in Proc. SPIE, Instrumentation in Astronomy VIII, eds. D. L. Crawford & E. R. Craine, 2198, 362 [Google Scholar]
- Ward-Duong, K., Patience, J., De Rosa, R. J., et al. 2015, MNRAS, 449, 2618 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmire, D. P., Matese, J. J., Criswell, L., & Mikkola, S. 1998, Icarus, 132, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M. 1919, Astron. Nachr., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., & Eastman, J. D. 2014, PASP, 126, 838 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
All Tables
Astrometric measurements of the wide pair HD 180617 + vB 10 (WDS 19169+0510, LDS 6334).
All Figures
 |
Fig. 1 GLS periodograms of the RV data for HD 180617. Upper three panels: individual instruments, followed by the combined data set. Lowermost panel: periodogram of the residuals of the best-fit solution. The horizontal lines (dotted, dash-dotted, and dashed) illustrate FAP levels of 10, 1, and 0.1%. The best-fit period at Pb = 105.9 d is highlighted by the vertical red line. |
| In the text | |
 |
Fig. 2 Unfolded (left) and phase-folded (right) RV measurements of the individual instruments for HD 180617, together with the best fit overplotted. |
| In the text | |
 |
Fig. 3 Orbital plot for HD 180617 b around its host star. The red ellipse corresponds to the best-fit solution, while the dashed ellipses represent the orbits at the upper and lower 1σ uncertainty levels of the eccentricity. The conservative liquid water habitable zone according to Kopparapu et al. (2014), shaded in green, is given by 0.19 au ≤ a ≤ 0.36 au. Separations are in units of astronomical units. |
| In the text | |
 |
Fig. 4 GLS periodograms of activity indicators derived from the CARMENES spectra of HD 180617 with lines (dotted, dash-dotted, and dashed) at FAP levels of 10, 1, and 0.1%. The vertical red and black lines represent the best-fit planet period at Pb = 105.9 d, and the rotation period of the star at Prot = 46.04 d, respectively. No significant power is found at the planetary period. |
| In the text | |
 |
Fig. A.1 Posterior distributions from the MCMC analysis on HD 180617 b. The best-fit solution is indicated by red lines and the contours define uncertainty levels of 1, 2, and 3σ with respectto the mean. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


