| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201832815 | |
| Published online | 12 October 2018 | |
A phylogenetic approach to chemical tagging
Reassembling open cluster stars
1
Observatoire de Genève, Université de Genève, 1290
Versoix, Switzerland
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
e-mail: sblancocuaresma@cfa.harvard.edu
3
Univ. Grenoble Alpes, CNRS, IPAG, Grenoble, France
e-mail: didier.fraix-burnet@univ-grenoble-alpes.fr
Received:
12
February
2018
Accepted:
10
July
2018
Context. The chemical tagging technique is a promising approach to reconstructing the history of the Galaxy by only using stellar chemical abundances. Multiple studies have undertaken this analysis and they have raised several challenges.
Aims. Using a sample of open cluster stars, we wish to address two issues: minimize chemical abundance differences whose origin is linked to the evolutionary stage of the stars and not their original composition and evaluate a phylogenetic approach to group stars based on their chemical composition.
Methods. We derived differential chemical abundances for 207 stars, belonging to 34 open clusters, using the Sun as reference star (classical approach) and a dwarf plus a giant star from the open cluster M 67 as reference (new approach). These abundances were then used to perform two phylogenetic analyses: cladistics (maximum parsimony) and neighbor joining, together with a partitioning unsupervised classification analysis with k-means. The resulting groupings were finally confronted to the true open cluster memberships of the stars.
Results. We successfully reconstruct most of the original open clusters when carefully selecting a subset of the abundances derived differentially with respect to M 67. We find a set of eight chemical elements that yield the best result and discuss the possible reasons for these elements to be good tracers of the history of the Galaxy.
Conclusions. Our study shows that unraveling the history of the Galaxy by only using stellar chemical abundances is greatly improved provided that i) we perform a differential spectroscopic analysis with respect to an open cluster instead of the Sun, ii) select the chemical elements that are good tracers of the history of the Galaxy, and iii) use tools that are adapted to detect evolutionary tracks such as phylogenetic approaches.
Key words: stars: abundances / stars: evolution / open clusters and associations: general / methods: data analysis / methods: statistical / techniques: spectroscopic
© ESO 2018
1. Introduction
Stars are known to form in large numbers within molecular clouds, which generally have a homogeneous chemical composition (Bland-Hawthorn et al. 2010; Feng & Krumholz 2014). The newly born stars may rest gravitationally bound for very long periods of time (e.g., the open clusters that we observe today), but most of the stellar aggregates dissolve owning to gravitational interactions. The stars may end up with very different kinematics and their original chemical composition is the main clue that can help us identify a family of stars born together or, at least, at similar periods of time (Freeman & Bland-Hawthorn 2002).
To distinguish and cluster the different families by individually tagging stars, we need to consider a rich set of individual chemical abundances derived homogeneously and apply clustering techniques. Such multivariate clustering (unsupervised classification) approaches have already been performed by several studies such as Blanco-Cuaresma et al. (2015) using the k-means technique applied on several principal component analysis components, Hogg et al. (2016) with a k-means technique on 15 abundances, and Smiljanic (2018) with a hierarchical clustering technique.
The resulting clustering showed how challenging the problem is even with very homogeneous spectroscopic analysis and high quality observations. The chemical composition of the stars is altered with time as a consequence of stellar evolution (e.g., atomic diffusion), which at the same time is different depending on the original stellar mass. The simplifications and assumptions that our current models incorporate also affect the results in different ways depending on the stellar evolutionary stage (e.g., NLTE effects). At the very least, these effects need to be minimized to improve the results generated by classification algorithms. In additional, however, the clustering techniques used by previous studies may not be the most suitable for solving the problem.
The most important caveat of these partitioning (such as k-means) and hierarchical techniques is that they are based on similarities, they are thus adapted to detect distinct and more or less compact structures in the multivariate parameter (here abundance) space. This could be a valid approach if all the surface chemical abundances, i.e., the abundances we can derive from spectroscopy, do not change with time. In that case, each open cluster would always define a cloud of stars in parameter space defined by the chemical abundances. But this is not the case since stars of the same family evolve differently according to their mass, leading each family of stars to be distributed along elongated structures for which partitioning and hierarchical techniques are not designed.
In addition, partitioning techniques require the number of groups to be input a priori. In other words we have to guess the number of families in advance, which is impossible in practice when applying the chemical tagging technique to field stars. There are a number of statistical criteria that can be used for this purpose, but this is often not very conclusive as we briefly discuss in this paper.
The multivariate methods used so far are thus not well adapted to be used in the context of the chemical tagging technique. However, it has been shown that phylogenetic approaches are able to reconstruct the evolutionary tracks of stars from abundances (Fraix-Burnet et al. 2016). At first glance, stellar evolution does not appear to be a good case for a phylogenetic study since there seems to be no direct transmission of properties between stars. But, firstly, the evolution of a star depends on mainly two parameters, their initial mass and metallicity; identical stars at different ages are related together because their relationships are represented by the evolutionary track. Secondly, the enriched gas expelled through the explosions or winds of the most massive stars form the new generation of stars. For instance, this is the basis of the well-known Populations I, II, and III in galaxies. This is a typical transmission with modification process between different families of stars, which can be representing as a branching pattern linking the different evolutionary tracks.
For evolutionary tracks, the transformation driver is the age of the stars, such that each family of stars is characterized by the same initial set of chemical abundances and mass. While when trying to identify stars born together during the same period of time via chemical tagging, the transformation driver within each open cluster is mass and not age. To avoid confusion with the traditional evolutionary tracks of stars most often shown on the Hertzsprung-Russell diagram, we refer to the paths followed by stars born together as family tracks. Such family tracks are exactly the equivalent of those used to determine the age of stellar populations in globular and open clusters (i.e., isochrones) except that in this case we are in a p-dimension space (the p abundances).
A first phylogenetic analysis of real stars in our Galaxy was performed by Jofré et al. (2017). Their goal was not to classify stars following the chemical tagging objectives, that is to group stars that were born together, but to obtain an evolutionary scenario for stars in the solar neighborhood. These authors used a neighbor joining (hereafter NJ) technique, which like cladistics (maximum parsimony; hereafter MP), is a phylogenetic tool seeking to establish relationships between the objects under study (see for instance Fraix-Burnet et al. 2015 and Appendix A). From the relationships depicted by their resulting tree, they drew conclusions about the star formation rate in the thick and thin disk and investigated the impact of processes such as radial migration and disk heating. This confirms the usefulness of phylogenetic approaches for stellar astrophysics.
In the present paper, we use the relationships to reconstruct the different families but we do not seek to discuss the relationships between them. We want to test the ability of phylogenetic approaches to group stars applying the chemical tagging technique on a sample of open cluster stars. One key element of our study is that phylogenetic reconstructions rely on characters that are descriptors, for example observables, parameters, variables, or properties; in our case these include chemical abundances that act as tracers of the history of the Galaxy (see Appendix A). As a consequence, it is often counter-productive to use all available observables blindly, and we show in this paper that limiting the analysis to a selection of certain chemical abundances leads to a much better result.
This paper is organized as follows. The data are presented in Sect. 2 and the methods in Sect. 3. The cladistics (MP) results are shown in Sect. 4, together with the results from NJ and k-means. We discuss some possible explanations for the selected set of abundances Sect. 5 and conclude in Sect. 6. Appendix A presents a detailed description of the methods used and Appendix B contains the contingency tables for the four biggest open clusters.
2. Data
To obtain high-precision chemical abundances it is necessary to use high-resolution stellar spectra with a good signal-to-noise ratio (S/N). The dataset presented in Blanco-Cuaresma et al. (2015) is very convenient for this work because it contains 2121 spectra of FGK stars observed with the following three different instruments:
-
NARVAL: ∼300–1100 nm and an average resolution of ∼80 000;
-
HARPS: ∼378–691 nm with a gap between chips that affects the region from 530 to 533 nm and a resolution of ∼115 000;
-
UVES: ∼476–683 nm with a small gap between 580 and 582 nm and a minimal resolution of ∼47 000.
After co-adding all the spectra corresponding to the same star and observed with the same instrument/setup, the dataset is composed of 446 stellar spectra. We discarded the stars with radial velocities 2.5 km s−1 higher or lower than the reference radial velocity of each cluster (Blanco-Cuaresma et al. 2015) or with errors higher than 1.5 km s−1. The final dataset is composed of 371 stellar spectra.
Following the method described in Blanco-Cuaresma & Soubiran (2016), we derived atmospheric parameters (i.e., effective temperature, surface gravity, and metallicity) and individual absolute chemical abundances for all the stars and the Sun. Then, we computed two different sets of line-by-line differential abundances using different reference stars: firstly, with respect to the Sun, discarding stars with surface gravities between 3.00 and 4.00 dex to be coherent with the M 67 set and secondly, with respect to the open cluster M 67, using the star No164 for giants (i.e., log(g)< 3.00 dex) and No1194 for dwarfs (i.e., log(g)> 4.00 dex).
For certain stars, we had more than one observation made with different instruments, i.e., they could not be co-added. In these cases we selected the spectrum with higher S/N. This process left us with a dataset of chemical abundances for 207 stars when compared to the Sun and 180 stars when compared to M 67. The former corresponds to 34 open clusters, while the latter to 33 as shown in Table 1.
From this analysis we cannot obtain the exact same number of chemical elements for all the stars. There are targets and reference stars that do not show reliable absorption lines for certain elements. Hence, we measure up to 29 chemical abundances in total but we cannot derive all these abundances for all the stars in the dataset. We could limit the analysis to the minimum common set, but the classification technique explored in this study can deal with a reasonably low number of unknown values.
Hereafter, when we refer to a chemical element symbol we mean its chemical abundance relative to the iron abundance of the same star (e.g., references to Ti represent [Ti/Fe]), except for iron, which is relative to hydrogen (i.e., [Fe/H]). All of these are averaged from the differentially line-by-line calculation with respect to a reference star, i.e., the Sun or M 67 depending on the dataset as explained above. The differential individual chemical abundances computed in this work for each star are used as input variables for the methods explained in Sect. 3, the average values and dispersion per open cluster when using M 67 as reference are summarized in Tables C.1 – C.3 and discussed in Sect. 5.
Cluster names, number of stars per cluster, and index of cluster used on some figures.
3. Method
3.1. Phylogenetic and partitioning analyses
Phylogenetic techniques look for the relationships between objects (stars in this work), minimizing a path through all the objects of the sample, providing a graph representation of the simplest scenario for transforming any object into any other one by changing their descriptors (individual chemical abundances in this case). The result of a phylogenetic analysis is thus a tree. Each family of stars is supposedly spread along a track, which appears as a substructure (bunches of branches) on the tree.
Cladistics, also called MP, is the simplest and most general phylogenetic technique. Among all the possible tree arrangements of the sample objects, we select that which possess the least number of changes on all its branches. These changes are counted from the discretized input variables (i.e., chemical abundances) with a simple L1-norm (Manhattan distance). This approach has been explained in detail in many astrophysics papers (Fraix-Burnet et al. 2006a,b; Fraix-Burnet et al. 2015; Fraix-Burnet et al. 2016) and is summarized in Appendix A.1.
The MP analyses were performed with the software PAUP 4.0a1542 (Swofford 2003). The quality of the family reconstruction was estimated by eye with the help of the representation shown on Fig. 1. Because of the hierarchical nature of the phylogeny, there is some arbitrariness when defining the families. We decided to remain conservative by selecting the largest structures that the tree suggests without going too much into subdivisions (see gray boxes in Fig. 1), placing ourselves in a real life situation in which we would know nothing about the families. The tree structures chosen and shown in Fig. 1 were established independently of the real cluster membership and correspond to visually obvious groups of branches. Naturally, this grouping can be especially disputed for the many small clusters (i.e., composed by very few stars) for which any global quantitative measures of the similarity between two data clusterings such as the adjusted rand index is not informative; i.e., it would be equally possible to choose different breakpoints in the graph and make different boxes. This is not the case for the four biggest open clusters M 67, NGC 6705, IC 4651, and NGC 2632 for which we compute quantitative estimates of our results.
The trees resulting from MP analyses are unrooted, i.e., there is no evolutionary direction, unless some common ancestorship is chosen. The analysis does not depend on this choice, such that rooting a tree only modifies its graphical representation and therefore may somewhat impact the groupings from its structure and the associated interpretation. For convenience in this paper, we have rooted all the trees with the stars that have the lowest surface gravity values.
For comparison and reliability estimation, we also performed a phylogenetic analysis with a different technique, the NJ tree estimation algorithm, and a partitioning analysis with the well-known k-means method using the function kmeans of the package stats and njs of the package ape in the R environment. These two techniques are explained in Appendices A.2 and A.3. The following papers provide more details on these methods: MacQueen (1967); Ghosh et al. (2010); Saitou & Nei (1987); Gascuel & Steel (2006); Blanco-Cuaresma et al. (2015); Fraix-Burnet et al. (2015); Jofré et al. (2017).
 |
Fig. 1. Cladograms obtained for 207 stars from 34 clusters calibrated using the Sun and with abundances from 25 elements (left panel), for 180 stars from 33 clusters calibrated using M 67 with abundances from 29 elements (middle panel) and with abundances from 8 elements (right panel). Red points and blue triangles correspond to red giant and dwarf stars, respectively. The horizontal axis gives the stellar cluster index, as given in Table 1, in decreasing order of the number of stars. The gray boxes indicate the structures on the tree that could be defined as groups. They also serve as a visual aid: the more the stars are stacked together vertically and the better they belong to the same gray box, the better is the phylogenetic reconstruction of the stellar clusters. |
Groups of selected chemical elements tested with the various methods presented in this work.
3.2. Selection of the chemical elements
As we show in the following, the result obtained by the MP technique with all the derived abundances for all the analyzed chemical elements is already satisfactory. We however tried to improve it by selecting a subset of the chemical elements since, as explained in the Appendix A, the success of phylogenetic analyses relies on the descriptors being good tracers of the history of the Galaxy. For this purpose we used several tools, such as principal component analysis, independent component analysis, multivariate clustering of input variables, and many trial and error runs. We note that these tools allow a better understanding of the data, but they do not reveal anything about the phylogenetic interest of the abundances. Only trial and error MP analyses give the correct information, or, ideally, some theoretical arguments that we presently lack.
At the end, our best subset is made of eight elements: Al, Ba, Co, Fe, Mg, Mn, Sc, and Ti. It is the best we have found, but we cannot exclude that there could be still a better one. We note that we have found another subset that yields very close results: Ba, C, Ca, Fe, Mg, Mn, Si, Ti, and Y. In this paper, we thus consider three samples (Table 2): Sfull, which is calibrated from the Sun with all 25 abundances, Mfull and Msel, which are calibrated from M 67 with 29 and 8 abundances, respectively.
4. Results
4.1. Maximum parsimony analysis
The results of the MP analyses of Sfull, Mfull, and Msel are shown in Fig. 1. The dwarfs and red giants are shown with given different colors and symbols, and the gray boxes underline substructures of the tree that are identified to the families of stars. The open clusters are ranked on the abscissa in decreasing number of stars as given in Table 1. Ideally, for a given open cluster, all the stars should be stacked together vertically and correspond to a unique substructure on the tree.
On the Sfull tree (Fig. 1, left), the dwarf and red giant stars are perfectly separated irrespective of the true families. Because of the gap in our sample between dwarf and red giants stars, even in the abundance space, the MP analysis naturally finds that the shortest route is to connect first each category separately. Even if some families are partially gathered in few groups, it would be difficult in practice to recognize that these groups indeed belong to the same family. This result is thus not satisfactory.
Performing differential abundance analysis for dwarfs and giants separately improves the result very significantly (Mfull, Fig. 1, middle) because families much better match substructures on the tree; the differences due to different evolutionary stages mentioned before are minimized. For all clusters, dwarfs and giants are better mixed up, even if this is not perfect (see for instance cluster 3, which is IC 4651). The differential calibration considering the evolutionary stage of the stars thus seems to be a necessary procedure.
The selection of elements (Msel, Fig. 1, right) still improves the result: this selection is almost perfect for clusters 2 and 4, and for the largest part of cluster 1. Cluster 3 is more problematic and we never managed to get a better result for it. Interestingly, as can be already noticed on the Mfull result and much more clearly on the Msel result, this cluster (IC 4651) is mixed with cluster 1 (M 67) on the same substructures of the tree. This means that we are not able to separate these two open clusters, indicating that they probably have very similar chemical compositions (see Sect. 5). Many smaller groups are also well reconstructed clearly better than for Mfull.
To quantify the quality of the classifications and compare them, we present in Appendix B contingency tables with recall and precision estimators for the four biggest open clusters M 67, NGC 6705, IC 4651, and NGC 2632. The other clusters have less than 8 members so that these indicators are not very much reliable. The recall (or sensitivity) is the fraction of stars of an open cluster (true class) that are retrieved in the same group. The precision is the fraction of stars of a group that are members of the same open cluster. Since we are interested in reconstituting families of stars belonging to the same open cluster, our main criterion is the recall estimator.
There are more stars of the biggest open cluster outside the defined groups (situated at individual branches) for Sfull (Table B.1) than for Msel (Table B.3) or Mfull (Table B.2) because in this case (Sfull) the chemical abundances were not computed to minimize differences due to the evolutionary stages; dwarfs and giants from the same open clusters end up in different families as shown in the Sfull tree in Fig. 1. This is reflected in the recall values, which are higher for Msel. The precision is more difficult to interpret. For instance the group corresponding to the open cluster M 67 contains more stars of other open clusters (not shown in the Tables) in Msel than in Sfull, even though it has most of its stars in Msel. However, the precision looks slightly better for Msel than for Sfull and Mfull seems even slightly better. Globally, we want to maximize recall and precision values and Msel seems to have the best balance.
 |
Fig. 2. Tree obtained with the NJ tree estimation method for 183 stars from 33 clusters calibrated using M 67 with abundances from 8 elements. Otherwise same as Fig. 1. |
4.2. Neighbor joining result
We have performed a NJ analysis to test the robustness of the presence of a phylogenetic signal. Theoretically, when the phylogeny is perfect, the trees from NJ and MP are identical (e.g., Fraix-Burnet et al. 2015). Even though this ideal situation is never met in real life, at least this is a safe check. We show in Fig. 2 only the NJ result for Msel since the selected elements are supposedly the most suited to reconstruct the phylogeny.
The NJ family reconstruction is rather good and is very comparable to the MP tree for Msel (Fig. 1). Maybe the biggest cluster M 67 is better reconstructed in the MP analysis, otherwise this is globally similar for the smaller groups. This is confirmed by the contingency table (Table B.4) that is similar to that for Msel (Table B.3) with very close recall and precision values with a significantly higher recall for M 67 in Msel. This indicates that the trees are very close to each other, giving strong support to the MP analysis and more importantly, confirms that the selected elements bear a real phylogenetic signal.
4.3. K-Means result
We also performed a k-means analysis for Msel. The big problem of this partitioning technique is the a priori choice of the number of clusters, which in practice is unknown. Another problem is that it cannot take unknown values, hence we replaced two unknown Al abundances in the Msel dataset by the mean of this parameter in this sample. We used the package NbClust from the R environment in which many techniques can be used to infer the best number of groups present in the data. The majority of the tests find either 2 or 30 as the optimal number of groups. We chose 30 groups, which is remarkably close to the real number of open clusters, but somewhat surprising owing to the very small number of stars in many of the clusters. We show the correspondence between the groups and the true families in Fig. 3 in a similar way as the other figures except that the vertical order of the k-means clusters is arbitrary.
None of the biggest open clusters are correctly reconstructed, i.e., each family is split into several k-means groups, confirming that partitioning techniques are not adapted to the chemical tagging objectives, even with the subset of elements selected on a phylogenetic basis. The contingency table (Table B.5) has more groups (15) than all other results except for Sfull, and the recall values are clearly the worst of all. The precision values seem high, but NGC 6705 and NGC 2632 cannot be identified with a single group (groups 2 and 3 for the first cluster, groups 5 and 6 for the second cluster).
 |
Fig. 3. K-Means correspondence plot for 30 groups (Sect. 4.3) in the same presentation as the other figures. The vertical order of the k-means groups represented by the gray boxes is arbitrary. |
5. Discussion
The two different phylogenetic techniques agree with each other and yield a very satisfactory reconstruction, especially for the biggest stellar clusters. In both cases, there is some arbitrariness in the precise definition of the families particularly for the smallest clusters, for which no robust quantitative estimates are possible. However, we remained rather conservative and consider only visually obvious substructures of the trees. In a real scenario, a subsequent analysis, not done in this paper, of the kinematics of the stars would provide significant information to assess and justify the results.
We conclude that the phylogenetic approaches can essentially improve the chemical tagging family reconstruction provided calibration of dwarfs and red giants are made properly and a proper element selection is carried out. We discuss in the following possible explanations for the chemical element subset we found.
We showed that the selection of the chemical elements, being in any case a necessary step for phylogenetic analyses, improves considerably the reconstruction of the stellar families. We found by trials and errors a very satisfactory subset of eight elements. An important question is why we found this subset.
The first idea is that this is an artifact from the data. In particular, the abundances for these elements could be more reliable because they have lower uncertainties. This is however not true for our sample. Inspecting the standard deviation per cluster for this selection of elements (Table C.1) shows a low dispersion that can also be found in some of the non-selected elements (Tables C.2 and C.3).
The second possibility is that these elements are less affected by stellar evolution, in the sense that they better probe the true chemical composition of the star at the time of observation. But when we verify the relation between the abundances and evolutionary stage using the Spearman rank-order correlation coefficient, the results for this set of elements are not particularly different from the rest of the abundances.
The third and more exciting possibility is that, based on the differential approach with respect to M 67 that we followed, these elements are better tracers of subsequent generation of stars. These elements could constitute the equivalent of the DNA of living organisms used to build the “Tree of Life” (e.g., Dress et al. 2010; de Vienne 2016). We do not claim that this is the absolute best combination of elements. Future works should apply this phylogenetic analysis to bigger datasets of stars and chemical elements, thereby improving data quality and analysis techniques when possible. There is a delicate equilibrium between how much phylogenetic information a chemical element provides and how much noise it introduces because of difficulties measuring its abundance from stellar spectra. Some of the selected elements could be replaced by counterparts with which they are correlated and for which more precise abundance measurements are possible; some other elements could be included if the abundance determination is improved. These factors have the potential to reshape the selection of elements and, for instance, in Sect. 3.2 we already indicate that a different set of elements yields close results.
This subset of elements cover difference nucleosynthetic processes. Iron (mainly created via explosive nucleosynthesis) is a key element that traditionally has been used to represent the overall metallicity evolution of stars. It is expected to be part of the selected elements since it contains a lot of information and the rest of abundances have been expressed relative to it. All the elements except aluminum and barium (i.e., Fe, Sc, Mn, Co, Ti, and Mg) are fundamentally synthesized during the core-collapse phase of a core-collapse massive star supernova or during a thermonuclear explosion involving a less massive star. Aluminum is mainly synthesized in the interior of the stars from Ne and C burning. Barium is the only element in this group that is synthesized owing to neutron capture processes such as s-processes (mainly) and r-processes (Anders & Grevesse 1989; Arlandini et al. 1999). It is expected that good proxies for the history of the Galaxy should contain a set of elements with decoupled synthesis rates (as is the case for this subset) because it maximizes the information needed to distinguish between families of stars.
When comparing to the second subset with close results (Sect. 3.2), both groups have Ba, Fe, Mg, Mn, Si, and Ti in common and Co and Al are replaced by C, Ca, and Y. Cobalt is one of the elements mainly created by explosive nucleosynthesis as is calcium. Aluminum is synthesized in the interior of the stars as is carbon. Finally, yttrium is a neutron capture element and that nucleosynthetic process is already represented by barium. This confirms the idea that other subsets of elements may be found with slight variations and this work demonstrates how phylogenetic techniques can be used to identify the best set.
The quality of the data and the uncertainties naturally limit our ability to distinguish families. In our sample, the uncertainties are sometimes as large as the spread within the sample. Our result is remarkably good taking this into consideration, and this might indicate that phylogenetic approaches may be more tolerant to uncertainties.
Another important limitation to chemical tagging can appear if stars born from the same molecular cloud do not share a unique abundance pattern as suggested by Smiljanic (2018), based on an experiment in which a hierarchical clustering technique was used. If we assume that this hypothesis is true, then it seems that our phylogenetic approach is less sensitive to this level of abundance discrepancies, or the open clusters in our sample happen to be sufficiently homogeneous and the spectroscopic analysis succeeded in reducing evolutionary effects using a differential approach with respect to M 67.
Several distinct molecular clouds may also have similar initial chemical compositions. As a consequence, from the phylogenetic point of view, a family of stars does not necessarily mean a single open cluster. For instance, this could be the reason why we were not able to reconstruct correctly the group IC 4651, which appears to be mixed with M 67 on our Msel tree (Fig. 1). It happens that the chemical signature of IC 4651 was already identified as very similar to that of M 67 (Blanco-Cuaresma & Soubiran 2016). This is probably not an issue for the study of the chemical history of star formation within our Galaxy, but this is definitively an issue if we are also interested in the spatial origin of these stars. In the latter case, it would be necessary to include dynamical studies based on spatial positions and motions in conjunction to the phylogenetic analysis based on abundances.
Some of the previous limitations could explain the difficulties for some of the smaller clusters, but their very low statistics prevents any further investigation. This raises again the importance of future phylogenetic analysis with a greater number of stars.
6. Conclusions
We have shown that phylogenetic analysis is a very promising tool to reconstitute families of stars born from similar molecular clouds (i.e., chemical tagging). Based on the requirement by this technique that the input variables (i.e., chemical abundances) must be good tracers of the history of the Galaxy, we conclude that a careful selection of the chemical elements must be made. We show that this improves considerably the quality of the result. We also proved that using a differential spectroscopic analysis with respect to an open cluster, in particular for this study, a dwarf, and a giant star from M 67, is a better strategy than the traditional approach of using the Sun as reference.
Questions arise concerning why the subset of chemical elements we have found is well suited for the phylogenetic chemical tagging study. We explored the idea that they may be intrinsic marks of families of stars, being somewhat a proxy for the DNA of stars. Other good proxies could be eventually found with some variations on the selected elements, further investigation will be needed using a greater sample of stars. This works opens a new approach to studying the history of star formation in our Galaxy based on the stellar chemical signatures.
Acknowledgments
This work would not have been possible without the support of Dr. Laurent Eyer (University of Geneva). The authors thank Paula Jofré for contributing interesting and different points of view regarding chemical tagging and phylogenetic studies, and Carine Babusiaux for interesting discussions. We thank the anonymous referee for suggesting significant improvements to a first version of this paper. This research has made use of NASA’s Astrophysics Data System.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco-Cuaresma, S., & Soubiran, C. 2016, in SF2A-2016: Proc. Ann. Meeting French Soc. Astron. Astrophys., eds. C. Reylé, J. Richard, L. Cambrésy, et al. 333 [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Heiter, U., et al. 2015, A&A, 577, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bland-Hawthorn, J., Krumholz, M. R., & Freeman, K. 2010, ApJ, 713, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Charrad, M., Ghazzali, N., Boiteau, V., & Niknafs, A. 2014, J. Stat. Softw., 61, 1 [CrossRef] [Google Scholar]
- de Vienne, D. M. 2016, PLOS Biol., 14, e2001624 [CrossRef] [Google Scholar]
- Dress, A., Moulton, V., Steel, M., & Wu, T. 2010, J. Theor. Biol., 265, 535 [CrossRef] [Google Scholar]
- Fakcharoenphol, J., Rao, S., & Talwar, K. 2003, Proc. of the 35th Annual ACM Symp. on Theory of Computing , 448 [Google Scholar]
- Felsenstein, J. 1984, in Cladistics: Perspectives on the Reconstruction of Evolutionary History, eds. T. Duncan, & T. Stuessy (New York: Columbia University Press), 169 [Google Scholar]
- Feng, Y., & Krumholz, M. R. 2014, Nature, 513, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Fraix-Burnet, D. 2016, in Statistics for Astrophysics: Clustering and Classification, eds. D. Fraix-Burnet, & S. Girard (EDP Sciences), EAS Pub. Ser., 77, 221 [Google Scholar]
- Fraix-Burnet, D., & Thuillard, M. 2014, unpublished https://hal.archives-ouvertes.fr/hal-01703341 [Google Scholar]
- Fraix-Burnet, D., Choler, P., Douzery, E., & Verhamme, A. 2006a, J. Classif., 23, 31 [CrossRef] [MathSciNet] [Google Scholar]
- Fraix-Burnet, D., Douzery, E., Choler, P., & Verhamme, A. 2006b, J. Classif., 23, 57 [CrossRef] [MathSciNet] [Google Scholar]
- Fraix-Burnet, D., Thuillard, M., & Chattopadhyay, A. K. 2015, Front. Astron. Space Sci., 2, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Gascuel, O., & Steel, M. 2006, Mol. Bio. Evol., 23, 1997 [Google Scholar]
- Ghosh, J., & Liu, A. 2010, in The Top Ten Algorithms in Data Mining, eds. X. Wu, & V. Kumar (Taylor& Francis), 21 [Google Scholar]
- Hogg, D. W., Casey, A. R., Ness, M., et al. 2016, ApJ, 833, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Das, P., Bertranpetit, J., & Foley, R. 2017, MNRAS, 467, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- MacQueen, J. B. 1967, in Proc. 5th Berkeley Symp. Math. Stat. Prob. , 281 [Google Scholar]
- R Core Team. 2014, R: A Language and Environment for Statistical Computing (Vienna, Austria: R Foundation for Statistical Computing) [Google Scholar]
- Saitou, N., & Nei, M. 1987, Mol. Biol. Evol., 4, 406 [Google Scholar]
- Smiljanic, R., et al. (Gaia-ESO Survey Consortium), 2018,IAU Symp., 334, 128 [Google Scholar]
- Sugar, C. A., & James, G. M. 2003, J. Am. Stat. Assoc., 98, 750 [CrossRef] [Google Scholar]
- Swofford, D. L., 2003, PAUP*: Phylogenetic Analysis Using Parsimony (*and Other Methods), [Google Scholar]
- Tajunisha, S., & Saravanan, V. 2010, Int. J. Artif. Intell. Appl. (IJAIA), 1, 44 [Google Scholar]
Appendix A
Methods used in this paper
A general presentation of several unsupervised classification methods that has been used in extragalactic astronomy can be found in Fraix-Burnet et al. (2015). We present in this section some excerpts regarding the three methods used in this paper.
There are two main categories of phylogenetic methods: distance-based and character-based. The so-called characters are traits, descriptors, observables, parameters, variables, or properties, which can be assigned at least two states characterizing the evolutionary stage of the objects for that character. For continuous variables, these states can be obtained through discretization. The most popular method for character-based approaches is cladistics (or MP) and for the distance-based approaches it is NJ.
A detailed explanation of MP can be found in Fraix-Burnet et al. (2016) and a detailed illustration of its application on stellar evolutionary tracks is presented in an unpublished paper (Fraix-Burnet & Thuillard 2014).
A.1. Cladistics or maximum parsimony
Cladistics when applied to domain outside of biology, such as astrocladistics, refers more generally to the classification of objects by a rooted or an unrooted tree. In that case, the tree represents possible relationships between objects (or classes of objects). In the 1980s cladistics was associated with the search of a MP tree. Maximum parsimony is a powerful approach to find tree-like arrangements of objects. The drawback is that the analysis must consider all possible trees before selecting the most parsimonious tree. The computation complexity depends on the number of objects and character states, such that samples that are too large (more than a few thousand) cannot be analyzed.
In the standard approach to parsimony, the score s
p of a tree corresponds, after labeling of the internal nodes, to the minimum number of edges (u, ν), where c(u) ≠ c(ν), c(u) is the character state at node u. The tree with the minimum score is searched for with some heuristics (Felsenstein et al. 1984). The MP approach can be directly extended to continuous characters or values. To each internal node is associated a real value f(u). The score s of a tree equals the sum over all edges of the absolute difference between those values, i.e.,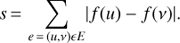 (A.1)
(A.1)
The success of a cladistics analysis much depends on the behavior of the input variables. In particular, it is sensitive to redundancies, incompatibilities, too much variability (reversals), and parallel and convergent evolutions. It is thus a very good tool for investigating whether a given set of input variables can lead to a robust and pertinent diversification scenario.
We wish to point out that MP is based on the variables, not on pairwise distances such as hierarchical clustering techniques or other phylogenetic approaches such as NJ described in Appendix A.2.
A.2. Neighbor joining
Among distance-based approaches, NJ is the most popular approach to construct a phylogenetic tree. The NJ tree estimation (Saitou & Nei 1987; Gascuel & Steel 2006) is based on a distance (or dissimilarity) matrix. In this paper, we have taken the Euclidean distance to compute this matrix. This method is a bottom-up hierarchical clustering methods. It starts from a star tree (unresolved tree). A corrected distance Q(i, j) between objects i and j from the dataset of n objects, is computed from the distances d(i, j),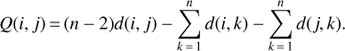 (A.2)
(A.2)
The branches of the two objects with the lowest Q(i, j) are linked together by a new node u on the tree. This node replaces the pair (i, j) in the subsequent iterations through the distance to any other object k ,![$ \begin{aligned} d(u,k)\,{=}\,\frac{1}{2}\left[d(i,k)-d(i,u)\right]\,{+}\,\frac{1}{2}\left[d(j,k)-d(j,u)\right] . \end{aligned} $](/articles/aa/full_html/2018/10/aa32815-18/aa32815-18-eq3.gif) (A.3)
(A.3)
Neighbor joining minimizes a tree length, according to a criteria that can be viewed as a balanced minimum evolution (Gascuel & Steel 2006). For a tree metrics, NJ furnishes a simple algorithm to reconstruct a tree from the distance matrix. There is a large amount of literature on how to best approximate a metrics by a tree metrics (see for instance Fakcharoenphol et al. 2003).
K-Means
The k-means algorithm (MacQueen 1967; Ghosh et al. 2010) is not a phylogenetic tool, rather it is a partitioning approach that is simple and can be very efficient in some cases.
The algorithm starts with k centroids, where k corresponds to the number of clusters given a priori. It then assigns each data point to the closest (as measured by an Euclidean distance measure) centroid and when the clusters are built, the new k centroids are computed and the process iterates until convergence. The result depends very much on the initial centroids, such that repeating the analysis with several initial choices (1000 in this paper) is thus necessary. However, consistency is not guaranteed if the data do not contain distinguishable and roughly spherical clusters. Some strategies have been devised to guess the best initial choice for the centroids (e.g., Sugar & James 2003; Tajunisha & Saravanan 2010) and many indices are available in the package NbClust (Charrad et al. 2014) of R (R Core Team 2014).
Appendix B
Contingency tables
In this appendix we present the contingency tables for the four biggest open clusters (M 67, NGC 6705, IC 4651, and NGC 2632; see Table 1) corresponding to the five clustering analyses performed in this paper: Sfull, Mfull, and Msel with MP (Sect. 4.1), Msel with NJ (Sect. 4.2), and k-means (Sect. 4.3).
Each tables provides the number of stars of each open cluster that are members of the groups given in the left column. The group index is arbitrary, ordered according to the best correspondence with the four open clusters and to their total number of stars for these clusters.
The precision and recall (sensitivity) of the classification is also computed in the tables for the four main open clusters. The precision gives the proportion of stars in a given group that belong to the same open cluster. The latter is supposed to be the cluster that has the largest number of stars in the given group. The precision is computed using all the open clusters (not shown in the tables). The recall gives the proportion of stars among a given open cluster that belong to the group having most of its members.
Contingency table for the MP analysis on Sfull (Sect. 4.1) for the four biggest open clusters.
Same as Table B.1 for the MP analysis of Mfull (Sect. 4.1 and Fig. 1).
Same as Table B.1 for the MP analysis of Msel (Sect. 4.1 and Fig. 1).
Same as Table B.1 for the NJ analysis of Msel (Sect. 4.2 and Fig. 2).
Same as Table B.1 for the k-means analysis of Msel (Sect. 4.3 and Fig. 3).
Additional tables
Differential abundances with respect to M 67 for the Msel set of elements.
Differential abundances with respect to M 67 for the rest of elements not included in Msel.
Differential abundances with respect to M 67 for the rest of elements not included in Msel.
All Tables
Cluster names, number of stars per cluster, and index of cluster used on some figures.
Groups of selected chemical elements tested with the various methods presented in this work.
Contingency table for the MP analysis on Sfull (Sect. 4.1) for the four biggest open clusters.
Differential abundances with respect to M 67 for the rest of elements not included in Msel.
Differential abundances with respect to M 67 for the rest of elements not included in Msel.
All Figures
 |
Fig. 1. Cladograms obtained for 207 stars from 34 clusters calibrated using the Sun and with abundances from 25 elements (left panel), for 180 stars from 33 clusters calibrated using M 67 with abundances from 29 elements (middle panel) and with abundances from 8 elements (right panel). Red points and blue triangles correspond to red giant and dwarf stars, respectively. The horizontal axis gives the stellar cluster index, as given in Table 1, in decreasing order of the number of stars. The gray boxes indicate the structures on the tree that could be defined as groups. They also serve as a visual aid: the more the stars are stacked together vertically and the better they belong to the same gray box, the better is the phylogenetic reconstruction of the stellar clusters. |
| In the text | |
 |
Fig. 2. Tree obtained with the NJ tree estimation method for 183 stars from 33 clusters calibrated using M 67 with abundances from 8 elements. Otherwise same as Fig. 1. |
| In the text | |
 |
Fig. 3. K-Means correspondence plot for 30 groups (Sect. 4.3) in the same presentation as the other figures. The vertical order of the k-means groups represented by the gray boxes is arbitrary. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


