| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201833065 | |
| Published online | 12 September 2018 | |
14N/15N ratio measurements in prestellar cores with N2H+: new evidence of 15N-antifractionation⋆,⋆⋆
1
Centre for Astrochemical Studies, Max-Planck-Institut für Extraterrestrische Physik, Gießenbachstraße 1, 85749 Garching bei München, Germany
e-mail: eredaelli@mpe.mpg.de, bizzocchi@mpe.mpg.de, caselli@mpe.mpg.de
2
Department of Physics, University of Helsinki, PO Box 64, 00014, Finland
3
Istituto de Astrofísica e Ciências do Espaço, Universidade de Lisboa, OAL, Tapada da Ajuda, 1349-018 Lisboa, Portugal
4
Dipartimento di Chimica “G. Ciamician”, Università di Bologna, Via F. Selmi 2, 40126 Bologna, Italy
Received:
21
March
2018
Accepted:
31
May
2018
Context. The 15N fractionation has been observed to show large variations among astrophysical sources, depending both on the type of target and on the molecular tracer used. These variations cannot be reproduced by the current chemical models.
Aims. Until now, the 14N/15N ratio in N2H+ has been accurately measured in only one prestellar source, L1544, where strong levels of fractionation, with depletion in 15N, are found (14N/15N ≈ 1000). In this paper, we extend the sample to three more bona fide prestellar cores, in order to understand if the antifractionation in N2H+ is a common feature of this kind of source.
Methods. We observed N2H+, N15NH+, and 15NNH+ in L183, L429, and L694-2 with the IRAM 30 m telescope. We modelled the emission with a non-local radiative transfer code in order to obtain accurate estimates of the molecular column densities, including the one for the optically thick N2H+. We used the most recent collisional rate coefficients available, and with these we also re-analysed the L1544 spectra previously published.
Results. The obtained isotopic ratios are in the range 580–770 and significantly differ with the value, predicted by the most recent chemical models, of ≈440, close to the protosolar value. Our prestellar core sample shows a high level of depletion of 15N in diazenylium, as previously found in L1544. A revision of the N chemical networks is needed in order to explain these results.
Key words: ISM: clouds / ISM: molecules / ISM: abundances / radio lines: ISM / stars: formation
This work is based on observations carried out with the IRAM 30 m Telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
The reduced spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/617/A7
© ESO 2018
1. Introduction
In the last two decades, the chemistry of nitrogen, the fifth most abundant element in the Universe, has raised interest in the context of understanding the formation of interstellar materials and of our own solar system. In particular, the isotopic ratio 14N/15N seems to represent an important diagnostic tool to follow the evolutionary process from the primitive solar nebula (where measurements indicate 14N/15N ≈ 440–450, Marty et al. 2011; Fouchet et al. 2004) up to present. The materials of the solar system, from meteorites to the Earth’s atmosphere, are enriched in 15N, with the exception of Jupiter’s atmosphere. Measurements of N2 in the terrestrial atmosphere led to the result of 14N/15N ≈ 272 (Nier 1950), and carbonaceous chondrites show isotopic ratios as low as 50 (Bonal et al. 2010), suggesting that at the origin of the solar system, multiple nitrogen reservoirs were present (Hily-Blant et al. 2017).
The nitrogen isotopic ratio has been measured also in different cold environments of the interstellar medium (ISM), and the results show a remarkable spread. Gerin et al. (2009) found 14N/15N = 350–810 in NH3 in a sample of low-mass dense cores and protostars, while, using HCN, Hily-Blant et al. (2013) found 14N/15N = 140–360 in prestellar cores1. Using N2H+, Bizzocchi et al. (2013) report a value of 14N/15N = 1000 ± 200 in L1544. In high-mass star-forming regions, the ratio spans a range from 180 up to 1300 in N2H+ (Fontani et al. 2015), and from 250 to 650 in HCN and HNC (Colzi et al. 2018a)2.
From the theoretical point of view, these results, and especially the very high ratio of L1544, are difficult to explain. The first chemical models addressing the N-fractionation (Terzieva & Herbst 2000) suggested that diazenylium (N2H+) should experience a modest enrichment in 15N through the ion-neutral reactions: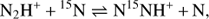 (1)
(1)
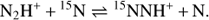 (2)
(2)
A further development of the chemical network made by Charnley and Rodgers led to the so-called superfractionation theory. According to this, extremely high enhancements in 15N are expected in molecules such as N2H+ or NH3, when CO is highly depleted in the gas phase (Charnley & Rodgers 2002; Rodgers & Charnley 2008). Recently, however, based on ab initio calculations, Roueff et al. (2015) suggested that the reactions (1) and (2) do not occur in the cold environments due to the presence of an entrance barrier. As a consequence, no fractionation is expected and the 14N/15N ratio in diazenylium should be close to the protosolar value of ≈440, which is assumed to be valid in the local ISM, according to the most recent results (e.g. Colzi et al. 2018a,b). This value, however, can be considered as an upper limit, since other recent works suggest a lower value for the elemental N-isotopic ratio in the solar neighbourhood (e.g. 14N/15N ≈ 300, Kahane et al. 2018, or 14N/15N ≈ 330, Hily-Blant et al. 2017). None of these values are consistent with the anti-fractionation seen for instance by Bizzocchi et al. (2013). More recently, Wirström & Charnley (2018) included the newest rate coefficients from Roueff et al. (2015) in a chemical model that also takes into account spin-state reactions, but their predictions fail in reproducing high depletion levels, as well as the high fractionation measured in HCN and HNC.
So far, the observational evidence of anti-fractionation in low-mass star forming regions has been sparse due to the difficulty of such investigations, which require very long integration times (≳8 h). Diazenylium presents a further complication. Often, the N2H+ (1–0) emission is optically thick and presents hyperfine excitation anomalies that deviate from the local thermodynamic equilibrium (LTE) conditions (Daniel et al. 2006, 2013). Therefore, a fully non-LTE radiative transfer approach must be adopted, requiring knowledge of the physical structure of the observed source. This method has thus far been applied to only a few sources at early stages, besides L1544. One is the core Barnard 1b, in which isotopic ratios of 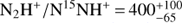 and N2H+/15NNH+ > 600 were measured by Daniel et al. (2013). A second study was performed in the L16923E core in L1689N, and resulted in
and N2H+/15NNH+ > 600 were measured by Daniel et al. (2013). A second study was performed in the L16923E core in L1689N, and resulted in 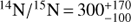 (Daniel et al. 2016). These two sources, however, are not truly representative of the prestellar phases. Barnard 1b hosts two extremely young sources with bipolar outflows (Gerin et al. 2015). 16293E in turn is located very close to the Class 0 protostar IRAS 16293-2422, and is slightly warmer than typical prestellar cores (T
dust = 16 K, Stark et al. 2004). We can therefore say that the L1544 14N/15N ratio in N2H+ appears peculiarly high, raising the doubt that it could represent an isolated and pathological case.
(Daniel et al. 2016). These two sources, however, are not truly representative of the prestellar phases. Barnard 1b hosts two extremely young sources with bipolar outflows (Gerin et al. 2015). 16293E in turn is located very close to the Class 0 protostar IRAS 16293-2422, and is slightly warmer than typical prestellar cores (T
dust = 16 K, Stark et al. 2004). We can therefore say that the L1544 14N/15N ratio in N2H+ appears peculiarly high, raising the doubt that it could represent an isolated and pathological case.
In this paper, we present the analysis of three more objects: L183, L429, and L694-2. These are all bona fide prestellar cores according to Crapsi et al. (2005), due to their centrally peaked column density profiles and high level of deuteration. As in the case of L1544, we modelled their physical conditions and used a non-LTE code for the radiative transfer of N2H+, N15NH+, and 15NNH+ emissions. Our results confirm the depletion of 15N in diazenylium in this kind of source.
2. Observations
The observations towards the three prestellar cores L183, L429, and L694-2 were carried out with the Institut de Radioastronomie Millimétrique (IRAM) 30 m telescope, located at Pico Veleta (Spain), during three different sessions. The telescope pointing was checked frequently on planets (Uranus, Mars, Saturn) or a nearby bright source (W3OH), and was found to be accurate to within 4″. We used the EMIR receiver in the E090 configuration mode. The tuning frequency for the three observed transitions are listed in Table 1. The hyperfine rest frequencies of 15NNH+ and N15NH+ were taken from Dore et al. (2009). The single pointing observations were performed using the frequency-switching mode. We used the VESPA backend with a spectral resolution of 20 kHz, corresponding to 0.06 km s−1 at 90 GHz. We observed the vertical and horizontal polarizations simultaneously, and averaged them to obtain the final spectra.
Rest frequencies of the observed transitions and 1σ uncertainties.
L694-2 was observed in good weather condition during July 2011, integrating for 1.15 h for the N2H+ (1–0) transition, for 8.9 h for N15NH+ (1–0), and for 9.0 h for 15NNH+ (1–0). L183 was observed in July 2012 in good to excellent weather conditions. The total integration times were 11.25 min (N2H+) and 4.3 h (N15NH+). L429 was observed during two different sessions (July 2012 and July 2017) in average weather conditions. We integrated for a total of 23 min for N2H+ (1–0) and 5.7 h on N15NH+ (1–0). We also observed for 1.2 h at the 15NNH+ (1–0) frequency, but we not detect any signal. For all the sources, we pointed at the millimetre dust peak (Crapsi et al. 2005). The core coordinates, together with their distances and locations, are summarised in Table 2.
Sources’ coordinates, distances, and locations.
Complementary Herschel SPIRE data, used to obtain the density maps of the sources (see Sect. 4.1), were taken from the Herschel Science Archive. The observation IDs are: 1342203075 (L183), 1342239787 (L429), and 1342230846 (L694-2). We selected the highest-processing-level data, already zero-point calibrated and imaged (SPG version: v14.1.0). Figure 1 shows the three cores as seen with the Herschel SPIRE instrument at 350 μm, as well as the positions of the single-pointing observations performed with IRAM.
 |
Fig. 1. The three prestellar cores as seen in dust thermal emission at 350 μm with Herschel SPIRE camera, in units of MJy sr−1. From top to bottom panel: L183, L429, L694-2. The scale bar is indicated in the bottom-right corner of each panel. The white circles represent the positions of the IRAM pointings and the size of the beam. |
3. Results
The obtained spectra are shown in the left panels of Fig. 2 (L183), Fig. 3 (L429), and Fig. 4 (L694-2). The data were processed using the GILDAS3 software, and calibrated in main beam temperature TMB using the telescope efficiencies (Feff = 0.95 and ηMB = 0.80, respectively) at the observed frequencies. The typical rms is 10–20 mK for N2H+ (1–0), and 3–4 mK for the spectra of the rarer isotopologues, resulting in good-to high-quality detections. The minimum signal-to-noise ratio (S/N) is ≈8, whilst the maximum is ≈150.
 |
Fig. 2. Observed (black) and modelled (red) spectra in L183, for N2H+ (top panels) and N15NH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4. The left panels show the entire acquired spectra, while the right ones are a zoom-in of the grey shaded velocity range. |
 |
Fig. 3. Observed spectra (black) and modelled ones (red) in L429, for N2H+ (top panels) and N15NH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4, and includes the infall velocity profile. The left panels show the entire acquired spectra, while the right ones are zoom-ins of the grey shaded velocity range. |
 |
Fig. 4. Observed (black) and modelled (red) spectra in L694-2, for N2H+ (top panels), N15NH+ (middle panels), and 15NNH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4. The left panels show the entire acquired spectra, while the right ones are zoom-ins of the grey shaded velocity range. |
The CLASS package of GILDAS was first used to spectrally fit the data. We used the HFS fitting routine, which models the hyperfine structure of the analysed transition assuming local thermodynamic equilibrium (LTE). Especially in the case of the N2H+ (1–0) line, this routine is not able to reproduce the observed data, due to the fact that the LTE conditions are not fulfilled. This is not due only to optical depth effects, which are taken into account in CLASS routines, but also to the fact that the excitation temperature is not the same for all the hyperfine transitions. A more refined approach that uses non-LTE analysis is therefore needed to compute reliable column densities, and will be discussed later (see Sect. 4). Nevertheless, the CLASS analysis provides reliable results for the local standard of rest velocity (VLSR), whose values are summarised in Table 3. Different isotopologues give generally consistent results, within 3σ, for each source. The values derived from N2H+ (1–0) are also in agreement with the literature ones (Crapsi et al. 2005). Table 3 also summarises the total line width (full width at half maximum – FWHM) obtained with the CLASS fitting routine.
VLSR estimated from the CLASS HFS fitting routine.
4. Analysis
Our aim is to derive the column density of the different isotopologues, and to compute from their ratios the values of the corresponding 14N/15N, assuming that they are tracing the same regions. For the reasons mentioned above, this is not possible using a standard LTE analysis (such as the one presented in Appendix A of Caselli et al. 2002), as already shown for instance in the analysis of L1544 by Bizzocchi et al. (2013). Therefore, we used a non-LTE method based on the radiative transfer code MOLLIE (Keto 1990; Keto et al. 2004). MOLLIE can produce synthetic spectra of a molecule arising from a source with a given physical model. In particular, it is able to treat the case of overlapping transitions, and therefore can properly model the crowded N2H+ (1–0) pattern. In what follows, we first describe the construction of the core models, and then present the analysis of the observed spectra using MOLLIE. The case of L429, which presents peculiar issues, is treated separately.
4.1. Source physical models
MOLLIE is able to treat genuine three-dimensional (3D) source models. Nevertheless, for the sake of simplicity, we chose to model the cores in our sample as spherically symmetric (One-dimensional – 1D). As one can see in Fig. 1, this assumption holds reasonably well for the densest parts of all cores4. For L183, a more sophisticated, two-dimensional (2D) model has already been developed in our team (Lattanzi et al., in prep.). This consists of a cylinder, with the axis lying on the plane of sky. In order to be consistent with the analysis of the other two cores, we decided to average this model in concentric annuli on the plane of sky to obtain a 1D profile.
The simplest 1D model consists of a volume density radial profile and a temperature radial profile. We therefore assume that the gas kinetic temperature and the dust temperature are equal. This is strictly true only when gas and dust are coupled (n > 104−5 cm−3, Goldsmith 2001), but we do not have enough information on the spatial distribution of the gas temperature for all the sources, which would require maps of NH3 (1, 1) and (2, 2) with JVLA (see Crapsi et al. 2007). On the other hand, the available continuum data allow us to determine reliable values for the dust temperature with a resolution of ≈40″.
The volume density profile is derived from the analysis of the Herschel SPIRE maps at 250 μm, 350 μm, and 500 μm, as follows. Since we are interested in the core properties, we filtered out the contribution of the diffuse, surrounding material with a background subtraction. We computed the average flux of each map in the surrounding of the cores, at a distance of ≈500–800″. This was assumed to be the background contribution, and was subtracted from the SPIRE images pixel by pixel. Then, the background-subtracted SPIRE maps were fitted simultaneously using a modified black body emission, in order to obtain the dust column density map of the source (for a complete description of the procedure, see for example Appendix B of Redaelli et al. 2017). We adopted the optically thin approximation, and a gas-to-dust ratio of 100 (Hildebrand 1983) to derive the H2 column density. The dust opacity is assumed to scale with the frequency as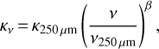 (3)
(3)
where κ250 μm = 0.1 cm2 g−1 is the reference value at 250 μm (Hildebrand 1983), and β = 2.0, a suitable value for low-mass star-forming regions (Chen et al. 2016; Chacón-Tanarro et al. 2017; Bracco et al. 2017). From this procedure, one also gets the line-of-sight averaged dust temperature map of each source. These data, however, were not used in the following analysis.
The obtained column density map was averaged in concentric annuli starting from the densest pixel, and then a Plummer profile was fitted to the obtained points according to:![$$ N{(r)}=\frac{N{({\mathrm H}_2)}_\text{peak}}{{\left[1+{(\frac r{r_0})}^2\right]}^\frac{p-1}2}. $$](/articles/aa/full_html/2018/09/aa33065-18/aa33065-18-eq6.gif) (4)
(4)
The obtained best-fit values of the free parameters (the characteristic radius r0, the power-law parameter p and the central column density N(H2)peak) can be used to derive the volume density profile n(r), according to Arzoumanian et al. (2011), following:![$$ n{(r)}=\frac{n_0}{{\left[1+{\left(\frac r{r_0}\right)}^2\right]}^\frac{p}2}. $$](/articles/aa/full_html/2018/09/aa33065-18/aa33065-18-eq7.gif) (5)
(5)
Table 4 summarises the best fit values of the Plummer-profile fitting of each source. The values obtained for the p exponent are in the range ≈2–3.5, relatively consistent with those found for other cores using similar power-law profile shapes (e.g. in Tafalla et al. 2004; Pagani et al. 2007). The profiles obtained with this method typically show n0 ≲ a few 105 cm−3, and fall below 105 cm−3 within the central ≈3500 AU. They thus fail to reach the high volume densities typical of prestellar cores centres. In fact, the integrated n(r) profiles along the line of sight result in column density values lower by a factor of 2–4 compared to the results of Crapsi et al. (2005), although the dust opacity value used in that work is consistent with ours within 15%. This is due to the poor angular resolution of the SPIRE maps, which were all convolved to the beam size of the 500 μm map (≈38″). The central regions of dense cores are in fact better traced with millimetre dust emission observations performed with large telescopes, which allow to better see their cold and concentrated structure. In order to correct for this, we artificially increased the density in the central part (5–10% of the total core radius rc), until the column density derived from this profile is consistent with the value obtained from 1.2 mm observations. The inserted density profile was taken from the central part of the profile developed through hydrodynamical simulations for L1544 in Keto et al. (2015), a model known to work well to reproduce the prestellar core properties.
Summary of the best fit values for the parameters of the Plummer profiles, for each source.
The volume density profile derived in the previous paragraph is used as an input for the continuum radiative transfer code (CRT; Juvela et al. 2001; Juvela 2005) to derive the dust temperature (Tdust) profile. The CRT is a Monte Carlo code that computes the emerging emission and the dust temperature, given a background radiation field. For the latter, we used the standard interstellar radiation field of Black (1994). Since we want to model cores embedded in a parental cloud, the background radiation field has to be attenuated. Our team has the tabulated values for the Black (1994) model with an attenuation corresponding to a visual extinction of AV = 1, 2, and 10 mag. We tested all three options, and found that generally the first two provide overly warm temperatures. We therefore decided to assume that radiation impinging on the cores is attenuated by an ambient cloud, whose thickness corresponds to a visual extinction of AV = 10 mag. The external radiation field can still be multiplied by a factor k, in order to correctly reproduce the emitted surface brightness. To determine this parameter, we tested a number of values in the range k = 0.5–5.0, and for each one we computed the synthetic flux emitted at the SPIRE wavelengths at the cores’ centres. We adopted the model that provides the best agreement with the observations5. Typically, we needed to increase the external radiation field by a factor of 2–3, suggesting that the assumed thickness of the ambient cloud was too large, and that the real, correct attenuation is somewhere in between 2 and 10 mag. This assumption is reasonable, as the H2 column density derived from the SPIRE maps around the cores is usually ≈5 × 1021 cm−2, although we do not know the 3D structure of the cloud. The dust opacities are taken from Ossenkopf & Henning (1994) for unprocessed dust grains covered by thin icy mantles. This choice is made so that the dust opacity values used in this part are consistent with the one from Hildebrand (1983), used for fitting the SPIRE maps. Fig. 5 shows the volume density and temperature profiles derived for each source.
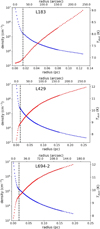 |
Fig. 5. Volume density profile (blue dots) and the dust temperature profile (red dots) for the three cores (from top panel to bottom panel: L183, L429, L694-2), as a function radius in both pc and arcsec. The vertical, dashed lines represent the radius within which the density was artificially increased (see text for details). |
The models built so far are static, that is, the velocity field is zero everywhere. However, we know that many cores show hints of infall or expansion motions (Lee et al. 2001). The velocity field can heavily impact the spectral features, and, when possible, it must be taken into account. For L183, in Sect. 4.2 we will show that the static model is good enough to properly reproduce the observations. For L694-2, we used the infall profile derived in Lee et al. (2007) using high-spatial-resolution HCN data. L429 represents a more difficult case, and will be accurately treated in the following subsections.
4.2. Spectral modelling with MOLLIE
The physical models developed in Sect. 4.1 are used as inputs for MOLLIE. The structure of each core is modelled with three nested grids of increasing resolution towards the centre, each composed of 48 cells, onto which the physical quantities’ profiles are interpolated. The collisional coefficients used are from Lique et al. (2015), who computed them for the main isotopologue and the most abundant collisional partner, p-H2. The o-H2 is therefore neglected, which is a reasonable assumption given that the orto-to-para ratio (OPR) in dense cores is expected to be very low (in L1544, OPR ≈ 10−3, Kong et al. 2015). The collisional coefficients for N15NH+ and 15NNH+ have been derived from those of N2H+ following the method described in Appendix A.
Our fit procedure has two free parameters, the turbulent velocity dispersion, σturb, and the molecular abundance Xst with respect to H2, assumed to be radially constant. Since MOLLIE requires very long computational times to fully sample the parameter space and find the best-fit values, we proceeded with a limited parameter space sampling. We first set the σturb value, testing ≈5 values on the N2H+ (1–0) spectra. This value is kept fixed also for the N15NH+ and 15NNH+ (1–0) lines. We then produced eight synthetic spectra for each transition, varying the initial abundance each time, and convolving them to the 27″ IRAM beam. The results were compared to the observations using a simple χ2 analysis, that is, computing: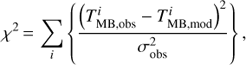 (6)
(6)
where 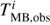 and
and 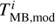 are the main beam temperature in the ith velocity channel for the observed spectrum and the modelled one, respectively, and σobs is the rms of the observations. The sum is computed excluding signal-free channels. In order to evaluate the uncertainties, we fitted a polynomial function to the χ2 distribution and set the lower/upper limits on Xst according to χ2 variations of ≈20% for the N2H+ (1–0) spectra and ≈15% for the other isotopologues. We chose these two different limits due to different opacity effects. In fact, the N2H+ (1–0) lines are optically thick, and therefore changes in the molecular abundance lead to smaller changes in the resulting spectra compared to the optically thin 15NNH+ and N15NH+ lines. Since the χ2 distribution is usually asymmetric, so are the error bars. In order to evaluate the column densities, we integrated the product n(H2) · Xst (convolved to the IRAM beam) along the line of sight crossing the centre of the model sphere. In Appendix B, we report the curves for the χ2 in the analysed sources.
are the main beam temperature in the ith velocity channel for the observed spectrum and the modelled one, respectively, and σobs is the rms of the observations. The sum is computed excluding signal-free channels. In order to evaluate the uncertainties, we fitted a polynomial function to the χ2 distribution and set the lower/upper limits on Xst according to χ2 variations of ≈20% for the N2H+ (1–0) spectra and ≈15% for the other isotopologues. We chose these two different limits due to different opacity effects. In fact, the N2H+ (1–0) lines are optically thick, and therefore changes in the molecular abundance lead to smaller changes in the resulting spectra compared to the optically thin 15NNH+ and N15NH+ lines. Since the χ2 distribution is usually asymmetric, so are the error bars. In order to evaluate the column densities, we integrated the product n(H2) · Xst (convolved to the IRAM beam) along the line of sight crossing the centre of the model sphere. In Appendix B, we report the curves for the χ2 in the analysed sources.
Figures 2 and 4 show the best fit spectra (in red), obtained as described above, in comparison with the observed ones (black curve) for L183 and L694-2, respectively. The overall agreement is good, and most of the spectral features are well reproduced, as seen in the right panels, which show a zoom-in of the main component.
4.3. Analysis of L429
L429 represents a more difficult case to model. As one can see in Fig. 3 and from the last column of Table 3, the N2H+ (1–0) line is almost a factor of two broader than in the other two sources. This may be due to the fact that this core is located in a more active environment, the Aquila Rift, but could also be a hint of multiple components along the line of sight. Moreover, concerning its velocity field, Lee et al. (2001) listed L429 among the “strong infall candidates” while in Sohn et al. (2007) the analysed HCN spectra show both infall and expansion features. A full charachterisation of the dynamical state of the source and its velocity profile would require high-quality, high-spatial-resolution maps of molecular emission, which are beyond the scope of this paper. At the first stage, we tried to fit the observed spectra first increasing σturb. The static model is however unable to reproduce the hyperfine intensity ratios, and therefore we adopted the infall profile of L694-2. The agreement with the observations increased significantly, meaning that a velocity field is indeed required to model the spectra. Due to the difficulties in analysing this source, the χ2 analysis previously described is not suitable, because it presents an irregular shape and its minimum corresponds to a clearly incorrect solution, due to the fact that it is not possible to simultaneously reproduce the intensity of all the hyperfine components. We therefore determined Xst in the same way as for σturb, testing multiple values. We then associated the uncertainty to this value using the largest relative uncertainties found in the other two sources (24% for N2H+ (1–0) and 25% for N15NH+ (1–0)).
4.4. Obtained results
Table 5 summarises the values of σturb, Xst, and column density Nmol for each line in the observed sample. For a consistency check, since the rare isotopologue transitions are optically thin and do not present intensity anomalies, we derived their molecular densities using the LTE approach of Caselli et al. (2002), focusing on the main component only. The results of this analysis are shown in the sixth column of Table 5
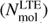 . One can note that these values are consistent with the ones derived through the non-LTE method. The L183 physical structure and N2H+ emission have previously been modelled by Pagani et al. (2007). It is interesting to notice that their best fit profiles for both density and temperature are close to ours, even though their model is warmer in the outskirts of the source. Furthermore, despite a different abundance profile, their derived N2H+ column density is consistent with our value.
. One can note that these values are consistent with the ones derived through the non-LTE method. The L183 physical structure and N2H+ emission have previously been modelled by Pagani et al. (2007). It is interesting to notice that their best fit profiles for both density and temperature are close to ours, even though their model is warmer in the outskirts of the source. Furthermore, despite a different abundance profile, their derived N2H+ column density is consistent with our value.
Parameters and results of the modelling with MOLLIE.
With the values for the molecular column densities found with the fully non-LTE analysis, we can infer the isotopic ratio dividing the main isotolopogue column densities from those of the corresponding rare isotopologue. Uncertainties are propagated using standard error calculation. The results are summarised in the last column of Table 5.
5. Discussion
Figure 6 shows a summary of the obtained isotopic ratios. Since from the analysis of Bizzocchi et al. (2013) the collisional rates for the N2H+ system have changed, we re-modelled the literature data for this source. The new results are: 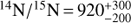 (using N15NH+) and
(using N15NH+) and 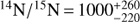 (using 15NNH+). They are also shown in Fig. 6. These values are perfectly consistent with the already mentioned literature value of 14N/15N = 1000 ± 200 of Bizzocchi et al. (2013). More recently, De Simone et al. (2018) computed again the nitrogen isotopic ratio from diazenylium in L1544, and found 14N/15N = 228–408, a result inconsistent with ours. The IRAM data analysed by those authors, though, have a spectral resolution of 50 KHz (more than twice as coarse as ours). Furthermore, the authors used a standard LTE analysis, which is not suitable for this case, as already mentioned. This point has been studied in detail in Daniel et al. (2006, 2013), where the authors showed that in typical core conditions (T ≈ 10 K, n ≈ 104−6 cm−3) the hypothesis of identical excitation temperature for all hyperfine components in the N2H+ (1–0) transition is not valid. Due to radiative trapping effects, in fact, the hyperfine intensity ratios deviate from the ones predicted with LTE calculations.
(using 15NNH+). They are also shown in Fig. 6. These values are perfectly consistent with the already mentioned literature value of 14N/15N = 1000 ± 200 of Bizzocchi et al. (2013). More recently, De Simone et al. (2018) computed again the nitrogen isotopic ratio from diazenylium in L1544, and found 14N/15N = 228–408, a result inconsistent with ours. The IRAM data analysed by those authors, though, have a spectral resolution of 50 KHz (more than twice as coarse as ours). Furthermore, the authors used a standard LTE analysis, which is not suitable for this case, as already mentioned. This point has been studied in detail in Daniel et al. (2006, 2013), where the authors showed that in typical core conditions (T ≈ 10 K, n ≈ 104−6 cm−3) the hypothesis of identical excitation temperature for all hyperfine components in the N2H+ (1–0) transition is not valid. Due to radiative trapping effects, in fact, the hyperfine intensity ratios deviate from the ones predicted with LTE calculations.
 |
Fig. 6. 14N/15N values obtained in the sample presented in this paper and re-computed for L1544 with errorbars, determined with the method described in the main text. Red points refer to measurements of N15NH+, while blue ones of 15NNH+. The solid line represents the average value found in the whole sample (=770), while the dashed curve is the proto-solar nebula value (440). |
Figure 6 shows that the computed values are consistent within the source sample. Due to the large uncertainties, we can conclude that the isotopic ratios are only marginally inconsistent with the value of 440, representative of the protosolar nebula (black, dashed curve). Nevertheless, the trend is clear. Despite the fact that L1544 still present the highest values in the sample, its case is now clearly not an isolated and pathological one. This larger statistics therefore supports the hypothesis that diazenylium is 15N-depleted in cold prestellar cores. Instead of “super-fractionation” predicted by some chemistry models, N2H+ seems to experience “anti-fractionation” in these objects. As already stressed out, this trend cannot be understood within the frame of current chemical models. Roueff et al. (2015) predict that the 14N/15N should be close to the protosolar value (≈400). Wirström & Charnley (2018) came to very similar conclusions. In both chemical networks, the physical model assumes a temperature of 10 K for the gas, whichis up to 40% higher than the values found for the central parts of the cores (6–7 K). However, further calculations have shown that lowering the temperature by 2–3 K does not produce significant differences in the results (Roueff, priv. comm.). Visser et al. (2018) highlighted how isotope-selective photodissociation is a key mechanism to understand the nitrogen isotopic chemistry in protoplanetary disks. We can speculate that different levels of selective photodissociation in different environments could reproduce the variety of N-isotopic ratios that are observed. Further investigation of this point from both an observational and a theoretical point of view is merited.
From the L1544 and L694-2 results, there seems to be tentative evidence that N15NH+ is more abundant than 15NNH+. This can be explained by the theory according to which the proton transfer reaction,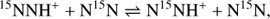 (7)
(7)
tends to shift the relative abundance of the two isotopologues, slightly favouring N15NH+ due to the fact that N15NH+ zero-point energy is lower than that of 15NNH+ by 8.1 K (see reaction RF2 in Wirström & Charnley 2018). It is interesting that the same trend is found also in a very different environment such as OMC-2 FIR4, a young protocluster hosting several protostellar objects. In this source, Kahane et al. (2018) measured lower values for the isotopic ratio, but in agreement with our result found that 15NNH+ is less abundant than N15NH+. However, we emphasise that higher-quality observations and those with better statistics are needed to confirm this point.
6. Conclusions
We have analysed the diazenylium isotopologues’ spectra in three prestellar cores, L183, L429 and L694-2 in order to derive nitrogen isotopic ratios. Since LTE conditions are not fulfilled, especially for the N2H+ (1–0) transition, we have used a fully non-LTE radiative transfer approach, implemented in the numerical code MOLLIE. We have carefully derived the physical models of the sources, computing their volume density and dust temperature profiles. With these, we were able to produce synthetic spectra to be compared with our observations, in order to derive the best-fit values for the molecular abundances and column densities. Using the same method, we have also recomputed the isotopic ratio of L1544. The difference with the literature value of Bizzocchi et al. (2013), due to changes in the molecular collisional rates, is well within the uncertainties.
In our sample of four cores, we derived 14N/15N values in the range 580–1000. Within the confidence range given by our uncertainties estimation, all our results are inconsistent with the value ≈400, predicted by the current theoretical models. L1544 still presents higher depletion levels than the other sources, but in general all the cores are anti-fractionated. The theoretical bases of such a trend are at the moment not understood. A deep revision of our knowledge of the nitrogen chemistry is required in order to understand the chemical pathways that lead to such low abundances of N15NH+ and 15NNH+ compared to the main isotopologue.
The reader must be aware that isotopic ratios measured using HCN (or HNC) depends on the value assumed for the 12C/13C ratio (Roueff et al. 2015).
A summary of the measured isotopic ratios can be found in Wirström et al. (2016).
Available at http://www.iram.fr/IRAMFR/GILDAS/
L694-2 was modelled as an elongated cylinder with the axis almost along the line of sight by Harvey et al. (2003a,b), but for the sake of simplicity, and given the relative roundness of the source at high density (shown in Fig. 1), we adopted a 1D model.
In order to be consistent with the formalism employed in collision studies (e.g., Daniel et al. 2005; Lique et al. 2015), in this appendix the lower-case symbol j is used for the quantum number of the molecule end-over-end rotation.
Acknowledgments
We thank the anonymous referee, whose comments helped to improve the quality of the manuscript.
References
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Bizzocchi, L., Caselli, P., Leonardo, E., & Dore, L. 2013, A&A, 555, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H. 1994, in The First Symposium on the Infrared Cirrus and Diffuse Interstellar Clouds, eds. R. M. Cutri, & W. B. Latter, ASP Conf. Ser., 58, 355 [NASA ADS] [Google Scholar]
- Bonal, L., Huss, G. R., Krot, A. N., et al. 2010, Geochim. Cosmochim. Acta, 74, 6590 [NASA ADS] [CrossRef] [Google Scholar]
- Bracco, A., Palmeirim, P., André, P., et al. 2017, A&A, 604, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buffa, G., Dore, L., & Meuwly, M. 2009, MNRAS, 397, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ, 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Cludi, L., Buffa, G., & Puzzarini, C. 2012, ApJ, 203, 11 [Google Scholar]
- Chacón-Tanarro, A., Caselli, P., Bizzocchi, L., et al. 2017, A&A, 606, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnley, S. B., & Rodgers, S. D. 2002, ApJ, 569, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M. C.-Y., Di Francesco, J., Johnstone, D., et al. 2016, ApJ, 826, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Colzi, L., Fontani, F., Caselli, P., et al. 2018a, A&A, 609, 129 [Google Scholar]
- Colzi, L., Fontani, F., Rivilla, V. M., et al. 2018b, MNRAS, 478, 3693 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daniel, F., Dubernet, M.-L., & Meuwly, M. 2004, J. Chem. Phys., 121, 4540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Daniel, F., Dubernet, M.-L., Meuwly, M., Cernicharo, J., & Pagani, L. 2005, MNRAS, 363, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Cernicharo, J., & Dubernet, M.-L. 2006, ApJ, 648, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Gérin, M., Roueff, E., et al. 2013, A&A, 560, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daniel, F., Faure, A., Pagani, L., et al. 2016, A&A, 592, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Simone, M., Fontani, F., Codella, C., et al. 2018, MNRAS, 476, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Dore, L., Bizzocchi, L., Degli Esposti, C., & Tinti, F. 2009, A&A, 496, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Palau, A., Bizzocchi, L., & Ceccarelli, C. 2015, ApJ, 808, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchet, T., Irwin, P. G. J., Parrish, P., et al. 2004, Icarus, 172, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Pety, J., Fuente, A., et al. 2015, A&A, 577, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Harvey, D. W. A., Wilner, D. J., Lada, C. J., Myers, P. C., & Alves, J. F. 2003a, ApJ, 598, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, D. W. A., Wilner, D. J., Myers, P. C., & Tafalla, M. 2003b, ApJ, 597, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013, Icarus, 223, 582 [Google Scholar]
- Hily-Blant, P., Magalhaes, V., Kastner, J., et al. 2017, A&A, 603, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M. 2005, A&A, 440, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Padoan, P., & Nordlund, Å. 2001, ApJ, 563, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Kahane, C., Jaber Al-Edhari, A., Ceccarelli, C., et al. 2018, ApJ, 852, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. R. 1990, ApJ, 355, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., Rybicki, G. B., Bergin, E. A., & Plume, R. 2004, ApJ, 613, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., Caselli, P., & Rawlings, J. 2015, MNRAS, 446, 3731 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, S., Caselli, P., Tan, J. C., Wakelam, V., & Sipilä, O. 2015, ApJ, 804, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 2001, ApJS, 136, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S. H., Park, Y.-S., Sohn, J., Lee, C. W., & Lee, H. M. 2007, ApJ, 660, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., Daniel, F., Pagani, L., & Feautrier, N. 2015, MNRAS, 446, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Nier, A. O. 1950, Phys. Rev., 77, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pagani, L., Bacmann, A., Motte, F., et al. 2004, A&A, 417, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redaelli, E., Alves, F. O., Caselli, P., et al. 2017, ApJ, 850, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2008, MNRAS, 385, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sohn, J., Lee, C. W., Park, Y.-S., et al. 2007, ApJ, 664, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, R., Sandell, G., Beck, S. C., et al. 2004, ApJ, 608, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., Bruderer, S., Cazzoletti, P., et al. 2018, A&A, 615, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wirström, E. S., & Charnley, S. B. 2018, MNRAS, 474, 3720 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Adande, G., Milam, S. N., Charnley, S. B., & Cordiner, M. A. 2016, IAU Focus Meeting, 29, 271 [Google Scholar]
Appendix A: New hyperfine rate coefficients for the N2H+/p-H2 collisional system
Recently, Lique et al. (2015) published a new set of theoretically computed hyperfine rate coefficients of N2H+ (X1 Σ+) excited by p-H2 (j = 0). The scattering calculation is based on a high-level ab initio potential energy surface (PES), from which state-to-state rate coefficients between the low-lying hyperfine levels were derived for temperatures ranging from 5 to 70 K. These new results provided the first genuine description of the N2H+/p-H2 collisional system, much improving the one based on previously published studies (Daniel et al. 2004, 2005) which used the He atom as collision partner. Indeed, the dissimilar polarizability of H2 and He has a sizeable effect on the longrange electrostatic interaction and produces A marked difference in the corresponding collision cross sections. Lique et al. (2015) found discrepancies up to a factor of ~3 (N2H+/p-H2 being the larger), indicating that the commonly used scaling factor of 1.37 (based on reduced masses) is not appropriate for these systems.
In a previous non-LTE analysis of N2H+ emission in L1544 (Bizzocchi et al. 2013), a J-dependent scaling relation based on HCO+–H2 and HCO+–He rate coefficients was adopted. This scheme produced factors in the 1.4–3.2 interval with an average ratio of ~2.3 for 1 ≤ j ≤ 4, and therefore allowed for a more reliable modelling of the N2H+ collisional excitation in the ISM6. However, the newly computed set of genuine N2H+/p-H2 collision data clearly supersedes the one derived through this procedure. The RT modellings presented in this paper were therefore performed inserting the N2H+/p-H2, N15NH+/p-H2, and 15NNH+/p-H2 rate coefficients derived from Lique et al. (2015) into MOLLIE.
Hyperfine de-excitation rate coefficients for the main isotopologue have been made available through the BASECOL7 database (Dubernet et al. 2013). They are derived from a Maxwellian average over the corresponding hyperfine crosssections σαβ (Lique et al. 2015)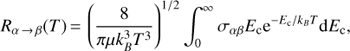 (A.1)
(A.1)
where μ is the reduced mass of the collision system, Ec is the collision energy, and α, β are the initial and final levels, respectively, each labelled with the j, F1, F quantum numbers. These are obtained by coupling the rotational angular momentum with the two 14N nuclear spins, for example F1 = j + I1, and F = F1 + I2. The cross sections are, in turn, obtained by the recoupling technique starting from the “spinless” opacity tensor elements PK(j → j′):![$$ \begin{align} \sigma_{jF_1F\,{\rightarrow}\, j^{\prime}F^{\prime}_1F^{\prime}} &= \frac{\pi}{k_j^2}[F_1\,F^{\prime}_1\,F^{\prime}] \sum_K \left\{ {\begin{array}{lllllllllllllll}{{F_1}}&{F_1^\prime }&K\\{{F^\prime }}&F&{{I_2}}\end{array}} \right\}^2 \left\{ {\begin{array}{lllllllllllllll}j&{{j^\prime }}&K\\{F_1^\prime }&{{F_1}}&{{I_1}}\end{array}} \right\}^2 P^K(j\,{\rightarrow}\, j^{\prime}).\end{align} $$](/articles/aa/full_html/2018/09/aa33065-18/aa33065-18-eq47.gif) (A.2)
(A.2)
Here, kj is the wave-vector for the energy channel Ec, 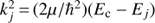 ; the terms in brace parentheses are the Wigner-6 j symbols, and the notation [xy …] is a handy shorthand for the product (2x + 1)(2y + 1) ….
; the terms in brace parentheses are the Wigner-6 j symbols, and the notation [xy …] is a handy shorthand for the product (2x + 1)(2y + 1) ….
Hyperfine cross-sections for the N15NH+, and 15NNH+ isotopic variant (one 14N nucleus) are not included in the basecol compilation. They can however be obtained, to a very good approximation, by summing Eq. (A.2) over the final F′ states. Using the orthogonality property of the 6 j symbols it holds:![$$ \underset{F'}{\mathrm\Sigma}{[F']}{\left\{ {\begin{array}{lllllllllllllll}{{F_1}}&{F_1^\prime }&K\\{{F^\prime }}&F&{{I_2}}\end{array}} \right\}}^2={[F_1]}^{-1}, $$](/articles/aa/full_html/2018/09/aa33065-18/aa33065-18-eq49.gif) (A.3)
(A.3)
because the triads (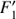 , F1, K) and (I2, F′,) satisfy the triangular condition by definition (Daniel et al. 2004). Hence, one has the equality:
, F1, K) and (I2, F′,) satisfy the triangular condition by definition (Daniel et al. 2004). Hence, one has the equality:![$$ \begin{align} \sum_{F^{\prime}} \sigma_{jF_1F\,{\rightarrow}\, j^{\prime}F^{\prime}_1F^{\prime}} &= \frac{\pi}{k_j^2}[F^{\prime}_1] \left\{ {\begin{array}{lllllllllllllll}j&{{j^\prime }}&K\\{F_1^\prime }&{{F_1}}&{{I_1}}\end{array}} \right\}^2 P^K(j\,{\rightarrow}\, j^{\prime})\nonumber\\ &= \sigma_{jF_1\,{\rightarrow}\, j^{\prime}F^{\prime}_1}, \end{align} $$](/articles/aa/full_html/2018/09/aa33065-18/aa33065-18-eq51.gif) (A.4)
(A.4)
which, inserted in the (A.1) yields, to a very good approximation: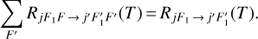 (A.5)
(A.5)
The 15N-bearing isotopologues contain only one quadrupolar nucleus and the appropriate angular momentum addition scheme is F = j + I. Therefore, in the right-hand term of (A.5), the quantum number F1 can be replaced by the new F to give the hyperfine coefficients for the N15NH+/p-H2 and 15NNH+/p-H2 collisions. In this treatment, we neglected the isotopic dependence of the cross sections, which is expected to be negligible for the 14N↔15N substitution (see for example Buffa et al. 2009).
The excitation rates, which are also required in MOLLIE, are derived through the detailed balance relations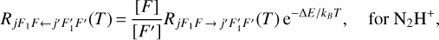 (A.6)
(A.6)
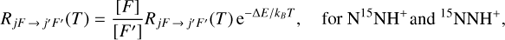 (A.7)
(A.7)
where ΔE represents the energy difference between the hyperfine levels (jF1F) and 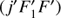 or (jF) and (j′ F′).
or (jF) and (j′ F′).
Appendix B: χ2 analysis
In this appendix, we show the χ2 values used to determine the best-fit value for the abundance (and therefore for the column density) of each molecule, together with their uncertainties, in L183, L694-2 and L1544 (Figs. B.1–B.3). The χ2 is evaluated according to Eq. (6). L429 is not present due to the difficulties of its modelling. See the main text for more details.
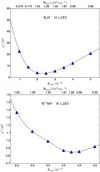 |
Fig. B.1. The χ2 values for different abundance values (and corresponding column densities) in L183, for N2H+ (upper panel) and N15NH+ (lower panel). The black curve is the one used to estimate the uncertainties, according to what said in Sect. 4.2. |
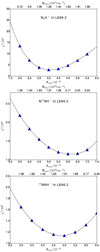 |
Fig. B.2. The χ2 values for different abundance values (and corresponding column densities) for L694-2. From top panel to bottom panel: N2H+, N15NH+, 15NNH+. The black curve is the one used to estimate the uncertainties, as explained in Sect. 4.2. |
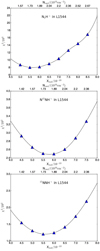 |
Fig. B.3. The χ2 values obtained for different abundance values (and corresponding column densities) in L1544. From top panel to bottom panel: N2H+, N15NH+, 15NNH+. The black curve is the one used to estimate the uncertainties, as explained in Sect. 4.2. |
All Tables
Summary of the best fit values for the parameters of the Plummer profiles, for each source.
All Figures
 |
Fig. 1. The three prestellar cores as seen in dust thermal emission at 350 μm with Herschel SPIRE camera, in units of MJy sr−1. From top to bottom panel: L183, L429, L694-2. The scale bar is indicated in the bottom-right corner of each panel. The white circles represent the positions of the IRAM pointings and the size of the beam. |
| In the text | |
 |
Fig. 2. Observed (black) and modelled (red) spectra in L183, for N2H+ (top panels) and N15NH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4. The left panels show the entire acquired spectra, while the right ones are a zoom-in of the grey shaded velocity range. |
| In the text | |
 |
Fig. 3. Observed spectra (black) and modelled ones (red) in L429, for N2H+ (top panels) and N15NH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4, and includes the infall velocity profile. The left panels show the entire acquired spectra, while the right ones are zoom-ins of the grey shaded velocity range. |
| In the text | |
 |
Fig. 4. Observed (black) and modelled (red) spectra in L694-2, for N2H+ (top panels), N15NH+ (middle panels), and 15NNH+ (bottom panels). The modelling was performed with MOLLIE as described in Sect. 4. The left panels show the entire acquired spectra, while the right ones are zoom-ins of the grey shaded velocity range. |
| In the text | |
 |
Fig. 5. Volume density profile (blue dots) and the dust temperature profile (red dots) for the three cores (from top panel to bottom panel: L183, L429, L694-2), as a function radius in both pc and arcsec. The vertical, dashed lines represent the radius within which the density was artificially increased (see text for details). |
| In the text | |
 |
Fig. 6. 14N/15N values obtained in the sample presented in this paper and re-computed for L1544 with errorbars, determined with the method described in the main text. Red points refer to measurements of N15NH+, while blue ones of 15NNH+. The solid line represents the average value found in the whole sample (=770), while the dashed curve is the proto-solar nebula value (440). |
| In the text | |
 |
Fig. B.1. The χ2 values for different abundance values (and corresponding column densities) in L183, for N2H+ (upper panel) and N15NH+ (lower panel). The black curve is the one used to estimate the uncertainties, according to what said in Sect. 4.2. |
| In the text | |
 |
Fig. B.2. The χ2 values for different abundance values (and corresponding column densities) for L694-2. From top panel to bottom panel: N2H+, N15NH+, 15NNH+. The black curve is the one used to estimate the uncertainties, as explained in Sect. 4.2. |
| In the text | |
 |
Fig. B.3. The χ2 values obtained for different abundance values (and corresponding column densities) in L1544. From top panel to bottom panel: N2H+, N15NH+, 15NNH+. The black curve is the one used to estimate the uncertainties, as explained in Sect. 4.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


