| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832873 | |
| Published online | 19 September 2018 | |
The bivariate luminosity and mass functions of the local HRS galaxy sample
The stellar, dust, and gas mass functions⋆
1
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
e-mail: pandrean@eso.org
2
Laboratoire d’Astrophysique de Marseille – LAM, Université d’Aix-Marseille & CNRS, UMR7326, 38 rue F. Joliot-Curie, 13388 Marseille Cedex 13, France
3
Chip Computers Consulting s.r.l., Viale Don L. Sturzo 82, S. Liberale di Marcon, 30020 Venice, Italy
4
International Centre for Radio Astronomy Research, The University of Western Australia, 35 Stirling Hwy, Crawley, WA 6009, Australia
5
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia
6
Nobeyama Radio Observatory, NAOJ, Nobeyama, Minamimaki, Minamisaku, 384-1305 Nagano, Japan
7
NAOJ, Osawa, 181-8588 Mitaka, Tokyo, Japan
Received:
22
February
2018
Accepted:
28
May
2018
Aims. We discuss the results of the relationships between the K-band and stellar mass, FIR luminosities, star formation rate, and the masses of the dust and gas of nearby galaxies computing the bivariate K-band-luminosity function (BLF) and bivariate K-band-mass function (BMF) of the Herschel Reference Survey (HRS), a volume-limited sample with full wavelength coverage.
Methods. We derive the BLFs and BMFs from the K-band and stellar mass, FIR luminosities, star formation rate, dust and gas masses cumulative distributions using a copula method, which is outlined in detail. The use of the computed bivariate taking into account the upper limits allows us to derive a more solid statistical ground for the relationship between the observed physical quantities.
Results. The analysis shows that the behaviour of the morphological (optically selected) subsamples is quite different. A statistically meaningful result can be obtained over the whole HRS sample only from the relationship between the K-band and the stellar mass, while for the remaining physical quantities (dust and gas masses, far-infrared luminosity, and star formation rate), the analysis is distinct for late-type (LT) and early-type galaxies (ETG). However, the number of ETGs is small to perform a robust statistical analysis, and in most of the case results are discussed only for the LTG subsample. The luminosity and mass functions (LFs, MFs) of LTGs are generally dependent on the K-band and the various dependencies are discussed in detail. We are able to derive the corresponding LFs and MFs and compare them with those computed with other samples. Our statistical analysis allows us to characterise the HRS which, although non-homogeneously selected and partially biased towards low IR luminosities, may be considered as representative of the local LT galaxy population.
Key words: galaxies: luminosity function / mass function / methods: statistical / methods: data analysis
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/617/A33
© ESO 2018
1. Introduction
We try to understand galaxy evolution through the comparison of simulations, both hydrodynamics and semi-analytical, with the physical and statistical properties extracted from the observed galaxy samples. One extremely useful tool is abundance matching between a theoretical Galactic halo mass function and the observed luminosity and mass functions (LFs, MFs, respectively) of a given population of objects, which provide stringent constrains on the fraction of baryonic mass converted into stars (see e.g. Shankar et al. 2006).
Operationally, LFs and MFs are defined as the mean space density of objects per unit luminosity or mass interval (Binggeli et al. 1988; Blanton et al. 2001; Bell et al. 2003; Hill et al. 2010; Johnston 2011, and references therein). A key issue is then to obtain galaxy samples with well defined extracted statistical and physical properties whose selection biases are well under control. Such samples are difficult to build and require a large investment in terms of observing time and in the interpretation of the extracted physical observables.
In the past decades many authors have used local samples selected at various wavelengths to estimate the local LFs and MFs of galaxies and their redshift evolution. These estimates (and correspondingly the total star formation rates and the local luminosity or mass density) contain some significant uncertainties mainly derived from the lack of either the imaging of large fields, or the required multi-wavelength homogeneous coverage and complete redshift information.
Any astronomical sample is affected by selection effects and systematic biases, therefore any statistically meaningful inference of the LF and MF needs a careful analysis of these issues. Even with the best data sets the accurate construction of the LF/MF remains a tricky pursuit, since the presence of observational selection effects due to for example detection thresholds in apparent magnitude, colour, surface brightness, or some combination thereof can make any given galaxy survey incomplete and thus introduce biases in the LF/MF estimates. This is particularly critical by investigating the LFs at other wavelengths than that used as the primary selection criterium of the sample. In this latter case, the use of the bivariate luminosity functions (BLFs), and in the case of the bivariate mass functions (BMFs), if the statistical assumptions are correctly defined, may provide a powerful method of studying the LFs at wavelengths different from the one used for selection.
The Herschel1 Reference Survey (HRS) is a Herschel guaranteed time key project, performing photometric observations with the Spectral and Photometric Imaging Receiver (SPIRE) cameras towards HRS galaxies (Boselli et al. 2010). The HRS is a volume-limited sample (i.e. 15 < D < 5 Mpc) including late-type galaxies (LTGs; Sa and later) with Two Micron All Sky Survey (2MASS) K-band magnitude ≤12 mag and early-type galaxies (ETGs; S0a and earlier) with ≤8.7 mag. The survey selection criteria (magnitude- and volume-limited, see Sect. 2), size and multi-wavelength coverage (from UV to radio wavelengths both in spectroscopy and photometry) together with the Herschel results in the far-infrared (FIR), sensitive to dust mass down to 104 M⊙, have shown that the HRS can be considered as a “reference” sample to carry out statistical analysis in the Local Universe (Boselli et al. 2010). Its use as a reference sample has been key to compare the predicted scaling relations (dust-to-stellar mass ratios and gas fraction; McKinnon et al. 2016; Davé et al. 2017) to provide additional constraints on feedback mechanisms and other physical processes of galaxy formation in cosmological simulations (i.e. Lagos et al. 2016).
With the above in mind, we use in this paper the HRS sample to investigate the BLFs and the BMFs derived in the various frequency bands. The HRS sample is K-band selected and a direct derivation of the LF can be carried out only at this wavelength (Boselli et al. 2010; Andreani et al. 2014), although with a small statistical significance because of the small number of sources. At wavelengths different from that of the selection there is no way to unbiasedly derive a LF or a MF (for a complete discussion see Johnston 2011).
In this paper we exploit the knowledge of the K-band LF, which is well established (Cole et al. 2001; Kochanek et al. 2001) and use the BLF as a statistical tool in the presence of upper limits, which provides results that lie on more solid statistical ground than any other simpler tool such as a linear regression test. The HRS is relative small to achieve this aim and limited in statistics but it is the only sample with complete and accurate multi-wavelength coverage.
Andreani et al. (2014) have already determined the BLF of the HRS sample but restricted to the monochromatic cases: K-band – 250 μm, K-band – 350 μm, and K-band – 500 μm. Meanwhile with the collection and the analysis of a larger multi-wavelength data set (Boselli et al. 2013, 2014a, 2015; Ciesla et al. 2014; Cortese et al. 2012a) we are able to extend our analysis. We make use of the total infrared (IR) and the Hα luminosities, the stellar, dust, and gas masses to derive the bivariate functions with respect to the K-band luminosity, which is the band at which the sample is complete (Andreani et al. 2014). Our analysis is statistically clean because of the accuracy of the employed statistical method and of the use of the whole data sets including the upper limits on the observed fluxes (and therefore on the derived quantities from these fluxes).
We compare the derived functions to the ones computed for other local samples to understand how the selection criteria affect the outcomes. These latter must be taken into account when comparing simulations with observations. The distribution functions in Hα, HI, and H2 have been already studied in dedicated works (Boselli et al. 2014b, 2015) and their properties and differences with respect to other local samples discussed in those papers.
This paper is organised as follows. The sample is briefly described in Sect. 2. The mathematical tools and the method used to compute the luminosity functions are described in Sect. 3. Results are described in Sect. 4 and discussed in Sect. 5. Conclusions are summarised in Sect. 6.
2. The data
The HRS is a volume-limited sample (i.e. 15 < D < 25 Mpc) including late-type galaxies (LTGs; Sa and later) with 2MASS K-band magnitude ≤12 mag and early-type galaxies (ETGs; S0a and earlier) with ≤8.7 mag. Additional selection criteria are high Galactic latitude (b > +55°) and low Galactic extinction (AB < 0.2 mag, Schlegel et al. 1998). The sample includes 322 galaxies (260 LTGs and 62 ETGs), and the total volume over an area of 3649 sq.deg. is 4539 Mpc3. The selection criteria are fully described in Boselli et al. (2010).
The multi-wavelength data used in this work have been taken from Boselli et al. (2011, 2013, 2015), Ciesla et al. (2012), Cortese et al. (2012a, 2014). Morphological types and distances are taken from Cortese et al. (2012a).
This huge data set has been extensively used to derive and discuss the main physical properties of this sample. In this work we make use of the stellar masses, determined from Li and g−i (Cortese et al. 2012a) following the prescription of Zibetti et al. (2009) based on the i-band luminosity and g − i mass-to-light ratio. For galaxies without Sloan Digital Sky Survey (SDSS) g and i-band data, stellar masses have been computed using the prescription of Boselli et al. (2009) based on the H-band luminosity and B − H mass-to-light ratio. The stellar mass range covered by this sample is 8 < log(Mstar/M⊙) < 12. The total FIR luminosity and the dust masses are derived from the spectral energy distrbution (SED) fit (Ciesla et al. 2014), the gas masses from CO and HI observations, and the molecular mass given in Table 2 is determined using a luminosity dependent value as explained in detail in Boselli et al. (2014a,b). A constant XCO factor, usually employed to convert the CO luminosity to molecular gas mass, underestimates the molecular content at stellar masses below 1010 M⊙. Star Formation Rates (SFR) are taken from Boselli et al. (2015) and are the average of the values derived from Hα luminosities (from Boselli et al. 2015) corrected using the Balmer decrement (from Boselli et al. 2013) or the FIR emission at 24 μm (from Bendo et al. 2012; Ciesla et al. 2014), from GALEX FUV luminosities (from Cortese et al. 2012b) still corrected for dust attenuation using the FIR emission at 24 μm, and from 20 cm radio luminosities (collected mainly from the NVSS (see Boselli et al. 2015). The choice of using different tracers has been done to minimise the observational errors and the uncertainty on the dust attenuation correction and to have at least one measurement for each galaxy (not all data are available for the whole sample). Details on the adopted calibrations and corrections can be found in Boselli et al. (2015).
Because the stellar masses have been computed using a Chabrier Initial Mass Function (IMF), to use consistent values for stellar masses and SFR we convert the SFR, which have been derived using a Salpeter IMF, to values compatible with a Chabrier IMF, dividing the first SFR by 1.58. The sample has a very limited luminosity coverage; the maximum observed luminosity at 250 μm is 109 L⊙, and it contains the Virgo cluster, which might introduce two biases: (1) Morphology segregation effect (Dressler 1980): clusters are dominated by ETGs compared to the field. The HRS contains a higher fraction of ETGs than one would normally find in a “blindly generated” sample, like for instance the H-ATLAS (Vaccari et al. 2010) and the HerMES survey (Marchetti et al. 2016), where the fraction of cluster galaxies is only a few percent. (2) The LTGs in clusters are different compared to those in the field for multiple reasons. For instance they have a reduced star formation and therefore a reduced FIR emission because they are poorer in gas (Boselli & Gavazzi 2006, 2014; Boselli et al. 2014c,d). Cortese et al. (2010, 2012b) have shown that the HRS LTGs in the Virgo cluster have truncated dust discs and lower dust masses. This might introduce a non-homogenous K-band distribution for LTGs because of the presence of two types of LTs: cluster and field galaxies. However, as already shown in Boselli et al. (2010) and in Andreani et al. (2014), the K-band LF computed on the HRS sample agrees within the errorbars with the LFs computed on the parent sample (the 2MASS) (Kochanek et al. 2001; Cole et al. 2001) despite the limited range in luminosities spanned from the HRS. Additional information about this sample may be found in Boselli et al. (2010, 2015) and Cortese et al. (2012a).
3. Estimation of a bivariate luminosity and mass function using a semi-parametric approach
To estimate the bivariate probability distribution function (PDF), ψ(x, y), Andreani et al. (2014) used a procedure based on the copulas (see Schmidt 2007, for the mathematical definition). The PDF is derived from a given a set of N observed quantities 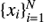 and
and  such that ψ(x, y)dxdy is the probability that a random variable (in this case the luminosity or the mass) takes values in the range [x, x + dx] and [y, y + dy].
such that ψ(x, y)dxdy is the probability that a random variable (in this case the luminosity or the mass) takes values in the range [x, x + dx] and [y, y + dy].
The method requires the computation of the cumulative distribution function (CDF) of the PDFs ϕ(x) and θ(y) (hereafter called marginals), defined from the equations
 (1)
(1)
 (2)
which are distributed according to a uniform distribution that takes values in the range [0, 1]. Defining ux = Φ(x) and uy = Θ(y), and if G−1(uz) is the inverse function of the standard Gaussian CDF G(z), the quantities zx and zy,
(2)
which are distributed according to a uniform distribution that takes values in the range [0, 1]. Defining ux = Φ(x) and uy = Θ(y), and if G−1(uz) is the inverse function of the standard Gaussian CDF G(z), the quantities zx and zy,
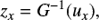 (3)
(3)
 (4)
are distributed according to a standard Gaussian PDF, g(z); that is, they are Gaussian variables. In other words, by means of Eqs. (1)–(4) the random variables x and y are “Gaussianised”. It is assumed that the joint PDF gΣ(zx, zy) of zx and zy is the bivariate Gaussian PDF with covariance matrix Σ given by
(4)
are distributed according to a standard Gaussian PDF, g(z); that is, they are Gaussian variables. In other words, by means of Eqs. (1)–(4) the random variables x and y are “Gaussianised”. It is assumed that the joint PDF gΣ(zx, zy) of zx and zy is the bivariate Gaussian PDF with covariance matrix Σ given by
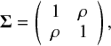 (5)
where ρ is the linear correlation coefficient of the two random variables zx and zy (see Takeuchi 2010).
(5)
where ρ is the linear correlation coefficient of the two random variables zx and zy (see Takeuchi 2010).
The copula CΣ(ux, uy) of gΣ(zx, zy) is defined from the equation by (Schmidt 2007)
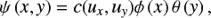 (6)
where x = Φ−1(ux) and y = Θ−1(uy) and
(6)
where x = Φ−1(ux) and y = Θ−1(uy) and
 (7)
(7)
We recall that a d-dimensional copula C: [0, 1]d → [0, 1] is a CDF with uniform marginals. Copulas are used to describe the dependence between random variables, and their main use is to disentangle marginals and the dependence structure. In particular, with the Gaussian copula the dependence structure is parametrised by a single parameter, the correlation coefficient.
It is possible to see that
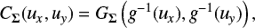 (8)
where the GΣ is the CDF of the bivariate Gaussian with covariance matrix Σ. From Eq. (7) it is
(8)
where the GΣ is the CDF of the bivariate Gaussian with covariance matrix Σ. From Eq. (7) it is
![$$ {c_{\bf{\Sigma }}}({u_x},{u_y}) = \frac{1}{{|{\bf{\Sigma }}|}}\exp \left\{ { - \frac{1}{2}\left[ {{{\bf{G}}^{ - {\rm{T}}}}({{\bf{\Sigma }}^{ - 1}} - {\rm{I}}){\rm{ }}{{\bf{G}}^{ - 1}}} \right]} \right\}. $$](/articles/aa/full_html/2018/09/aa32873-18/aa32873-18-eq12.gif) (9)
Here, G−1 ≡ (G−1(ux), G−1(uy))T, G−T is the transpose of G−1, I is the identity matrix, and |Σ| is the determinant of Σ. In summary, to obtain a full description of the two variables, two ingredients are needed: the marginals and the type of interrelation.
(9)
Here, G−1 ≡ (G−1(ux), G−1(uy))T, G−T is the transpose of G−1, I is the identity matrix, and |Σ| is the determinant of Σ. In summary, to obtain a full description of the two variables, two ingredients are needed: the marginals and the type of interrelation.
Using the above results, a procedure for estimating the bivariate PDF ψ(x, y) in the presence of possible left-censored data (upper limits) is the following.
Estimation of the marginals
 and
and 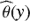 ;
;Computation of the uniform random variates
 ,
, 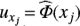 ,
,  and
and  by means of Eqs. (1) and (2);
by means of Eqs. (1) and (2);Computation of the standard Gaussian variates zxi, zxj, zyk, and zyl by means of Eqs. (3) and (4);
Maximum likelihood estimation of the linear correlation coefficient and then of matrix Σ;
Computation of ψ(x, y) for specific values of x and y by means of Eqs. (6)–(9).
The copula related to zxi, zxj, zyl, and zyk is the same as the one related to xi, xj, yk, and yl. This is due to the invariance property of copulas by which the dependence captured by a copula is invariant with respect to increasing and continuous transformations of the marginal distributions (see page 13 in Trivedi & Zimmer 2005). The procedure of this method, with its semi-parametric solution, as outlined in detail above, is extensively discussed in Andreani et al. (2014).
4. The bivariate luminosity and mass functions
The first step in the above procedure is the estimation of the marginals. In the absence of any a priori knowledge of the analytical form of 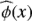 and
and  , a possible approach is represented by the system of three families, say SU, SB, and SL, introduced by Johnson (1949) according to the fact that a random variable is unbounded (SU), bounded above and below (SB), or bounded only below (SL). A detailed description of such families as well as of their use in practical applications is given in Vio et al. (1994). Here, it is sufficient to say that the members of this system are characterised by four free parameters that allow them great flexibility in reproducing most of the classical PDFs. As described in Vio et al. (1994), a robust method to select the specific family and to estimate the corresponding parameters for a given set of data is based on the percentiles of their empirical distribution. In the present case, this method indicates the SB family
, a possible approach is represented by the system of three families, say SU, SB, and SL, introduced by Johnson (1949) according to the fact that a random variable is unbounded (SU), bounded above and below (SB), or bounded only below (SL). A detailed description of such families as well as of their use in practical applications is given in Vio et al. (1994). Here, it is sufficient to say that the members of this system are characterised by four free parameters that allow them great flexibility in reproducing most of the classical PDFs. As described in Vio et al. (1994), a robust method to select the specific family and to estimate the corresponding parameters for a given set of data is based on the percentiles of their empirical distribution. In the present case, this method indicates the SB family
![$$ \begin{equation} f(x) = \frac{\eta}{\sqrt{2 \pi}} \frac{\lambda}{(x-\epsilon)(\lambda-x+\epsilon)} \exp{-\left\{\frac{1}{2}\left[ \gamma + \eta \ln\left(\frac{x-\epsilon}{\lambda - x + \epsilon}\right) \right]^2\right\}} \label{SB} \end{equation} $$](/articles/aa/full_html/2018/09/aa32873-18/aa32873-18-eq21.gif) (10)
with ϵ ≤ x ≤ λ + ϵ as the most suited to reproduce the PDF of the observed data. Table 1 shows the estimated parameters and Fig. 1 the corresponding PDFs versus the experimental histograms. Finally, Figs. 3–8 show the corresponding bivariate PDF obtained by means of Eq. (6).
(10)
with ϵ ≤ x ≤ λ + ϵ as the most suited to reproduce the PDF of the observed data. Table 1 shows the estimated parameters and Fig. 1 the corresponding PDFs versus the experimental histograms. Finally, Figs. 3–8 show the corresponding bivariate PDF obtained by means of Eq. (6).
 |
Fig. 1. Histograms of the data in Table 1 and corresponding fitted Johnson PDF. In all cases the SB family has been selected. The best fit parameters of Eq. (10) are reported on Table 1. These PDFs have been used to estimate the bivariate PDF shown in Figs. 3–8. |
It is important to stress here that, as explained in detail in Andreani et al. (2014), we have considered several PDFs to fit the K-band luminosities. All of them have a support of type Lmin < L < ∞ (or Mmin < M < ∞), a steep slope for L → Lmin (or M → Mmin), and the possibility that ϕ(L), ϕ(M) → ∞. However, since the Lmin (or Mmin) is unknown, the three-parameters version of such a PDF has to be used. The fit of this kind of PDF is a difficult problem since the maximum likelihood approach fails if ϕ(L), ϕ(M) → ∞ when L → Lmin (or M → Mmin). This problem has been solved with the method described in Appendix A in Andreani et al. (2014).
4.1. Analysis of the bivariate LFs
Before discussing the outcomes of our analysis of the bivariate PDFs shown in Figs. 3–8 we examine the distribution of the physical quantities listed in Table 1 and plotted in Fig. 2.
 |
Fig. 2. Scatterplots and histograms for the data. Blue dots correspond to the objects with morphological type ≤3 (ET), green dots to objects with morphological type ≥3 (LT). Because of the lack of data at some wavelengths the various panels contain a different number of points. |
Galaxies are split in objects as LT and ET according to the classification in Cortese et al. (2012a). The original classification was a NED-based morphological type classification (Boselli et al. 2010), which has been modified for several galaxies after revision based on more recent literature and visual inspection as discussed in Cortese et al. (2012a). The diagonal inlayings contain the histograms of the two populations. The first result is that the histograms are quite distinct and clearly show in most of the cases the existence of two distinct distributions for LTGs and ETGs. The two populations cover different values of luminosities and masses. Atomic, molecular, and total gas masses, infrared luminosities, and SFR are much larger in LTGs, while the K-band luminosity and the stellar masses are larger in the ETGs. The distribution of the dust mass is similar in LTGs and ETGs, but the distribution is shifted to a lower value in ETGs of 0.5 dex. The relations between these variables are not affected by the luminosity-distance relation, because the HRS is a volume-limited sample. The values of the correlation coefficients are listed in the sixth column of Table 1.
The analysis of the correlations implies that a correct statistical analysis for many physical quantities can only be carried over a subset of the sample: either containing only ET or only LT. We then computed the bivariate functions over the whole sample only in one case (stellar mass) for which we cannot distinguish the behaviour of the two populations. In the following we compute most of the bivariates for LTGs and, because of the limited statistics, only the overall trends are discussed for the ETGs in the sample. Errorbars are computed with a bootstrap technique, iteratively extracting the values of the marginal functions (see Sect. 4 above) when the variable changes within its errorbar.
4.2. The bivariate L(K)−Mstar
Both Fig. 2 and the bivariate LF LK−Mstar in Fig. 3 highlight the tight relation between the K-band luminosity and the stellar mass (Gavazzi et al. 1996). The correlation coefficient is 0.965. This is not surprising as the stellar masses are derived from the i-band luminosity and g−i colour, close to the K-band (Cortese et al. 2012a; Boselli et al. 2009). Both ETGs and LTGs follow the same correlation, with the former objects containing larger stellar masses. A few sources can be identified as outliers both in Figs. 2 and 3 because they deviate from the tight correlation. This deviation is clearly visible in Fig. 3 where the values are on a linear scale.
 |
Fig. 3. Panel a: bivariate PDF LK−Mstar: estimated bivariate PDF shown in linear scale (and enlarged in the inset) for the K-band with the stellar masses. Contour lines correspond to levels 0.1, 0.3, 0.5, 0.7, and 0.9. These values correspond to the fraction of the peak value of the BLF that is set to one. Panel b: reconstructed stellar mass function of the HRS sample (red line) shown together with the best fit of the Galactic mass function given by Baldry et al. (2012) for the GAMA survey (blue line). |
The K-band magnitude of the HRS sample is taken from the 2MASS survey and these outliers may lack well derived values of the K-band magnitude due to their complex morphology and low surface brightness (Kochanek et al. 2001), and their closeness to the completion limit of the survey (Jarrett et al. 2000). Indeed, the errorbars on the photometry for the extended (and more nearby) and low surface brightness galaxies are more affected by sky fluctuations on a large scale (see discussion in Appendix A in Kochanek et al. 2001).
Overall this correlation confirms a well-known result that the K-band magnitude is a fair tracer of the stellar mass. Figure 3 shows the marginal function used to compute the bivariate in Sect. 3 representing the stellar mass distribution. This can be retrieved from the analytical form of Eq. (10) using the parameters in Table 2. Bearing in mind that a strict comparison with previous works on the stellar mass function (SMF) of the Local Universe is not straightforward because of our different way of computing this function, we draw in Fig. 3, together with our derived marginal, the Schechter (Schechter 1976) functions whose parameters are extracted from the best fit of the SMFs by Baldry et al. (2012). These authors characterised the SMF at z ∼ 0 down to M = 108 M⊙ using data from the Galaxy and Mass Assembly (GAMA) surveys, fitted their data with a double Schechter (Schechter 1976) function with a single value for the break mass, and provided a good fit to the data for M > 108 M⊙. They claim that this is approximately the sum of a single Schechter (Schechter 1976) function for the blue population and double Schechter function for the red population.
The deviation of the marginal derived in this work with the SMFs computed by Baldry et al. (2012) at stellar mass lower than ∼3 × 109 M⊙ simply highlights the incompleteness of the HRS sample at low stellar mass, that is, the lack of galaxies with low stellar mass in the HRS sample. The HRS sample covers a small volume and lacks the necessary depth to detect K-band magnitude faint and/or low surface brightness galaxies. The low end of the mass function is dominated by disc galaxies, the LTGs, (Thanjavur et al. 2016), which the HRS misses as discussed above.
The high-mass end of the SMF is in agreement amongst the different samples and confirms previous findings that it is dominated by spheroidal galaxies. Thanjavur et al. (2016) show that at masses lower than log(M/M⊙) = 10.3 there is a preponderance of disc galaxies, whereas when galaxy stellar mass increases, this disc dominance gradually decreases with a corresponding increase in the spheroidal contribution. Although the SMF of the disc components shows a steep increase at the faint end, their contribution to the total galaxy stellar mass density is only 37 per cent. This gradual change of the SMF from disc-dominated to spheoridal-dominated galaxies is linked to the physics and environmental processes that drive the build-up of stellar mass in these two principal galaxy components (Thanjavur et al. 2016). The lack of small disc galaxies could be also due to the environment and this could well be the case for the HRS sample (Boselli et al. 2014a, 2016). Changes in the shape of the local SMF (and in the value of M⋆) in the highest density environments, which contain an enhancement of massive galaxies, are discussed in Blanton & Moustakas (2009).
4.3. The bivariate L(K)−L(IR)
The relation between the IR luminosity and the K-band luminosity clearly highlights a dichotomy between the two morphological types (ET) and (LT); the relation is almost linear in logarithmic scale (L(K) ∼ α · L(IR), with α ∼ 10,1000 for LT and ET respectively). The IR luminosity is fainter in ETGs, while LTGs have fainter values of K-band luminosity. A closer look at the K-band/IR luminosity relation in Fig. 2 shows that one tenth of the objects have properties in between the relations defined for ET and LT respectively. The majority of these objects host a weak Active Galactic Nucleus (AGN) and/or are classified as “retired galaxy” by Gavazzi et al. (2018). These galaxies have been star-forming in the past and, although the nucleus is sterilised, there are still remnants of star formation in the outer region. They share most of the properties of the ETGs, with less gas and very low specific SFR. The lower left part of the L(K)−L(IR) plane is occupied mostly by objects classified as LTGs dominated by HII regions (Gavazzi et al. 2018).
Because of the low number of ET objects and the distinct behaviour of the ET and LT galaxies with respect to the IR Luminosity, Fig. 4 shows the BLF for LTGs only. In spite of the relative good correlation measured (0.79), the BLF shows a spread at large values of the IR and K-band luminosities. The objects responsible for this spread are galaxies of the Virgo cluster and host a weak AGN and/or are classified as “retired galaxy” by Gavazzi et al. (2018). These objects might be in migration from the blue cloud (star-forming) to the green valley (post-starburst) and eventually to the red sequence. Particulary those in the Virgo cluster lose gas (mainly atomic) through ram pressure stripping and have more compact discs because of the further loss of dust and molecular gas (Boselli et al. 2014c, 2016).
 |
Fig. 4. Panel a: bivariate PDF L(K)−L(IR) for LTGs only: estimated bivariate PDF shown in linear scale (and enlarged in the inset) for the K-band with the infrared luminosities. Contour lines correspond to levels 0.1, 0.3, 0.5, 0.7, and 0.9. These values correspond to the fraction of the peak value of the BLF that is set to one. Panel b: reconstructed IR luminosity function of the HRS sample (red line) shown together with the LF computed over local blind IR surveys (blue line) by Marchetti et al. (2016). Error bars are estimated through a bootstrapping technique. |
In Andreani et al. (2014) a similar BLF was computed limited to the monochromatic luminosities in the FIR (in the SPIRE bands at 250, 350 and 500 μm). Andreani et al. (2014) discussed how for LTGs the dependence L(K)−L(IR) can be interpreted as a physical connection between the cold component of the dust – closely related to the galaxy dust mass – and the stellar mass – inferred from the K-band absolute luminosity –, which is a tracer of the mass of the old stellar population.
Figure 4 shows the analytical form (the marginal) computed in Sect. 3 of the local IR luminosity function. To locate this finding in the context of other authors’ results, Fig. 4 reports the best fit of the modified Schechter function derived by Marchetti et al. (2016) using the Herschel HerMES survey. This latter is the most recent version of the local IR LF based on blind FIR-submillimetre surveys (Vaccari et al. 2010; Negrello et al. 2013; Clemens et al. 2013; Wang et al. 2016) and computed using the total FIR (3–1000 μm) luminosity combined with models.
The agreement shown in Fig. 4 is good with small deviations at low and large luminosities. While at large luminosities the HRS is statistically not complete because of the small surveyed area, the discrepancy at low IR luminosities can be attributed to the ways these samples have been selected: the HRS sample is K-band selected and may miss very low IR luminosity objects, which are more easily detected in blind FIR surveys. There might be an additional factor related to the definition of morphology or colour in the infrared and in the optical. Marchetti et al. (2016) interpret the shape of the local FIR LF as due to the contributions of red (possibly ET) and blue (possibly LT) galaxy populations, with their different Schechter forms, rapidly evolving already at low redshifts. However, the cut-off line between red and blue galaxies in this context is less sharp than in the optical classification of the galaxy morphology, as in the HRS sample, where among red galaxies there are red spiral galaxies that could be the result of their highly inclined orientation and/or a strong contribution of the old stellar population (see also Dariush et al. 2016).
4.4. The bivariate dust mass function (DMF), L(K)−Mdust, and the relation Mdust−Mstar
As shown in Fig. 2 the variation of the K-band luminosity in ETGs is roughly constant with respect to the dust mass and, considering also the upper limits, there is no correlation between the star luminosity and the dust emission. For this reason and for the low statistical significance of the number of ETGs we compute the bivariate PDF LK−Mdust shown in Fig. 5 only for LTGs. The dependence of the K-band luminosity and the dust mass shows a very tight relation, with a correlation coefficient of 0.849, slightly stronger than that between L(K)−L(IR). This is expected as dust thermal emission is the main contributor of IR luminosities.
 |
Fig. 5. Panel a: bivariate PDF L(K)−Mdust, same as Fig. 4 for the K-band luminosity and the dust mass. Panel b: reconstructed dust mass function of the HRS sample (red line) shown together with the DMFs computed over local blind IR surveys: Dunne et al. (2011; green), Beeston et al. (2018; blue), Clemens et al. (2013; purple and grey). |
Stellar and dust masses seem to be in tight relationship, which could be interpreted as a relationship between the stellar mass, the cold dust mass, and the FIR luminosity in LTGs. This tightness could also be due to the presence of old stars that dominate the stellar mass and at the same time produce the dust in their stellar winds (Dwek 1998; Zhukovska et al. 2008, 2016). What is clear is that the distribution of the cold dust in the galaxy discs follows that of the stars.
The spread of this relation, due to the objects with larger dust mass and low K-band luminosity (small stellar mass), can be ascribed to the fact that lower (stellar) mass galaxies have higher dust mass fractions than their more massive counterparts (Cortese et al. 2012b; Clemens et al. 2013).
From this function, using Eq. (10) and Table 1, we can derive the DMF, which is shown in Fig. 5. In the same figure we plot the DMFs obtained by Dunne et al. (2011), the best-fit model by Clemens et al. (2013), and the recent one by Beeston et al. (2018). Dunne et al. (2011) and Beeston et al. (2018) compute the DMF over a sample of Herschel selected galaxies, while Clemens et al. (2013) over a sample selected from the Planck source catalogue. Clemens et al. (2013) claim agreement with the Dunne et al. (2011) values because of the large uncertainties on the derivations of the dust masses, which are mainly linked to the assumed physical properties of the dust (see also De Vis et al. 2017). All these models make use of SED fitting templates to derive the physical parameters of the galaxies (therefore also the value of the dust mass). The mostly used MAGPHYS package (Clemens et al. 2013; Beeston et al. 2018; Driver et al. 2018) combines black bodies with different temperatures, keeping the energy balance between UV/optical and NIR, while for HRS Ciesla et al. (2014) fitted the Draine and Li models only on the IR part.
Although the accuracy of the dust mass values mainly depends on the quality of the fit (i.e. the number of photometric points), it also largely depends on the dust model, which assumes dust absorption coefficient differing up to a factor of two; among the different models, other uncertainties may arise from the selection criteria and systematics, which are not perfectly under control. To overcome some of the discrepancies we make use of the recomputed values reported in Beeston et al. (2018) who have rescaled the DMFs at the same value as the dust absorption coefficient. These rescaled DMFs are those shown in Fig. 5.
The DMF computed for the HRS sample lies in between the DMF given by Clemens et al. (2013) and those derived by Dunne et al. (2011) and Beeston et al. (2018). We do not want to overinterpret this result because of the difference in the dust models, the difference in the selection wavelengths (250 μm and 500 μm), and the difference in the catalogues (Herschel/SPIRE and Planck). We can claim that the local DMF derived from the HRS is consistent with the values found for FIR/submm galaxies. We need to keep in mind, however, that the HRS may miss a number of dusty galaxies because it targets K-band selected objects.
Herschel galaxy samples contain red galaxies, which may correspond to the optical classification of both LTGs and ETGs (i.e. contain part of the ETGs of the HRS sample), with dust masses similar to the blue objects, that is, normal spiral and star-forming systems. Some red ETGs keep the properties of optical ETGs (lower mean dust-to-stellar mass ratios, lower mean star-formation/specific-star-formation rates) but a population of ETGs exists containing a significant level of cold dust similar to that observed in blue and star-forming galaxies. The origin of dust in such ETGs is still unclear. It could be of external origin (e.g. fuelled through mergers and tidal interactions, Dariush et al. 2016) or have existed for a long time in galaxy discs, with recent results favouring this latter interpretation (Bassett et al. 2017; see also Gomez et al. 2010; Cortese et al. 2012b; Smith et al. 2012; Agius et al. 2015; Eales et al. 2018).
The tight relation between the K-band luminosity and the stellar mass (see Figs. 2 and 3) allows us also to explore the relation between the dust and the stellar masses. This latter is very tight for the LTGs, while no clear connection is detected in ET objects. This is expected as about half of the ETGs remain undetected in the Herschel bands (Cortese et al. 2012b; Smith et al. 2012) and the corresponding IR luminosity and derived dust masses have to be considered as upper limits (Ciesla et al. 2014). Cortese et al. (2012b) show that the spread in the relation between stellar and dust masses in the HRS may be attributed to the variation of the dust content as a function of the environment and of the HI content more than to the morphological (late versus early) type.
4.5. The bivariate L(K)−SFR
The SFR BLF is displayed in Fig. 6. The computed bivariate function shows a slight relation between the SFR and the K-band luminosity, with this latter, as highlighted in Fig. 2 and in Sect. 4.2, strongly linked to the stellar mass. Figure 6 displays the SFR functions derived in this work from the BLF and compares the SFR function with the values obtained from other samples. The comparison is not straightforward because of the way the SFR has been computed in the different samples. The HRS SFR is the average value amongst those derived from the dust-corrected Hα luminosity, the far-UV dust-corrected luminosity, and the radio emission at 20 cm (Boselli et al. 2015). SFR values in other samples have been obtained either from the Hα measurements alone (Bothwell et al. 2011; Gunawardhana et al. 2013) or translating the IR luminosity to SFR (Clemens et al. 2013). It is straightforward to see that the SFR function is a strong function of the sample selection criteria. While the SFR function extracted from the Hα is significantly lower than that computed from the IR luminosities, the behaviour of the HRS SFR function misses large values of the SFR.
 |
Fig. 6. Panel a: bivariate PDF L(K)−SFR, same as Fig. 4 for the K-band luminosity and the SFR. Panel b: reconstructed SFR LF for the HRS sample (red) compared with that of (Gunawardhana et al. 2013; blue), and (Clemens et al. 2013; purple). |
We are not at all astonished to see a large difference at high star formation rates with the Planck-derived Clemens et al. (2013) LF, which includes FIR selected starbursts known to be totally absent in the Local Universe (within 25 Mpc the most extreme case is M 82, with ∼10 M⊙ yr−1) and might be limited and biased by confusion. Furthermore, the difference in the several published Hα selected SFR LF is huge (see Fig. 11 Boselli et al. 2015), even within the same work once different samples are used. Gunawardhana et al. (2013) published two different SFR LFs derived from Hα, the first from SDSS data and the second from GAMA data, which is higher at least at low SFR values. Boselli et al. (2016) have compared these Hα LF (GAMA and SDSS) to the one derived using NUV data in the Virgo cluster periphery and they match pretty well. This means that the observed differences in the SFR LF between HRS and Gunawardhana et al. (2013) are mainly due to the sample and not to the method of deriving the SFR.
In the past two decades a great number of works have investigated the link between the SFR and the stellar mass (e.g. Eales et al. 2017, and references therein). Our interpretation of the SFR bivariate function is that the relation between the SFR and Mstar is a combination of at least two factors. On the one hand, there is an effect due to the environment. Boselli et al. (2016) link the decrease in the star formation activity in the main sequence relation to HI-deficiency, which may be due to ram pressure stripping (Boselli et al. 2015, 2016). The location of the galaxy main sequence is different for objects that do show signs of perturbation from the main sequence drawn by unperturbed systems. Many of the HRS galaxies show signs of perturbation due to the environment and a large infall rate of star forming systems is observed in Virgo.
On the other hand, there is a selection effect. The HRS sample contains most of the stellar mass in a specific volume of the Local Universe and, as discussed above in Sect. 4.4, it should not be biased towards galaxies with high star formation rates. However, it contains optically classified red galaxies that are red not only because of the old stellar population but because of a fraction of dust and gas, which show that they are still forming stars. Thirty per cent of the red population classified as ET still contain a fraction of dust and have a residual star formation rate (Eales et al. 2017). For very red objects, those with the lowest values of the SFR, the redness is due to an old population and not to dust reddening and the values of the ratio 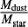 are < 10−4.
are < 10−4.
We are not able to investigate this issue further using the BLF. The number of objects is too low to split the sample and compute the BLF differently for the galaxies belonging to the cluster and to the fields.
4.6. The bivariates L(K)−Mgas, atomic and molecular gas
In Figs. 2, 7, and 8, we report the values of the distributions of the atomic gas, the molecular gas masses, and the bivariate mass functions. The amount of atomic and molecular gas is a strong function of the morphological type, where most of the ETGs are undetected in atomic and molecular gas (Boselli et al. 2014a).
 |
Fig. 7. Panel a: bivariate PDF L(K)−M(HI), same as Fig. 4 for the K-band luminosity and the atomic gas mass. Panel b: reconstructed atomic gas mass function of the HRS sample (red curve) shown together with the gas mass computed in the Local Universe by Martin et al. (2010), and Zwaan et al. (2005; blue and green curves respectively) and models by Popping et al. (2014), and Lagos et al. (2011; purple and grey points/lines). |
 |
Fig. 8. Panel a: bivariate PDF L(K)−M(H2), same as Fig. 4 for the K-band luminosity and the molecular gas mass. Panel b: reconstructed molecular gas mass function of the HRS sample shown together with the predicted ones by (Lagos et al. 2011; green and grey lines), and the molecular mass function derived from the L′(CO) function from (Saintonge et al. 2017; blue line). |
The derived atomic gas function for LTGs only and those obtained by HI dedicated surveys (Zwaan et al. 2005; Martin et al. 2010; Hoppmann et al. 2015; Jones et al. 2018) are shown in Fig. 7. Overplotted are also the predictions by Popping et al. (2014) and Lagos et al. (2011). The M(HI)−MF derived from the HRS data differs substantially at values M(HI) > a few × 109 M⊙. The weak correlation of the HI mass with the K-band luminosity (see Fig. 7a and Table 2) does not allow us to strongly constrain the bivariate and as a consequence the construction of the atomic gas mass function is poorly determined. This may explain the strong difference in shape observed in the HI MF.
The deficiency of large mass objects can be explained by two factors: the HRS is K-band luminosity selected, while the HI dedicated surveys blindly select HI emitting galaxies (Zwaan et al. 2005; Martin et al. 2010; Hoppmann et al. 2015; Jones et al. 2018). The HRS sample therefore may misses most of the HI-massive galaxies. Secondly, the HRS contains more HI deficient objects than normal field galaxies (roughly half of the sample). This fact is attributed to the presence of the Virgo cluster and its gravitational effect on the gas. Through direct stripping of the ISM from the disc (e.g. ram pressure) the galaxy disc loses its atomic gas content as widely discussed in the various HRS follow-up papers (Boselli et al. 2014c; Cortese et al. 2016).
At variance with the HI mass, the BLF of the H2 mass is relatively strongly correlated with the K-band luminosity (see Fig. 8 and Table 2). The correlation shown in Fig. 8 reflects the relation between the stellar mass and the molecular gas mass within the sample, with the scatter due to the HI-deficient galaxies (Boselli et al. 2014b). Boselli et al. (2014c) used the M(H2) versus stellar mass, Mstar, scaling relation to define the H2-deficiency parameter as the difference, on the logarithmic scale, between the expected and observed molecular gas mass for a galaxy of given stellar mass. This molecular hydrogen deficiency is considered as a proxy for galaxy interactions with the surrounding cluster environment. The molecular gas and the extension of the molecular disc are also affected by the presence of the cluster galaxies and on average these galaxies have a lower molecular content than galaxies in the field. A similar finding is reported by Fumagalli et al. (2009) who find that molecular deficient galaxies form stars at a lower rate or have dimmer far infrared fluxes than gas rich galaxies, as expected if the star formation rate is determined by the molecular hydrogen content. A different view has been proposed by Mok et al. (2016) who argue that Virgo galaxies have longer molecular gas depletion times compared to group galaxies, due to their higher H2 masses and lower star formation rates, and suggest that the longer depletion times may be a result of heating processes in the cluster environment or differences in the turbulent pressure. This issue requires further study and is not settled yet.
Figure 8 displays the H2 MF derived from the BLF (Fig. 8) compared with the predictions by Lagos et al. (2011). At masses lower than 108 M⊙ the HRS sample may miss galaxies with low molecular hydrogen content. However, very few samples in the Local Universe are complete in molecular hydrogen and the data of galaxies with very low molecular content in unbiased samples are still scanty (Bothwell et al. 2016). Previous molecular MFs of nearby galaxies have been derived from the CO MF. Keres et al. (2003) used an incomplete CO sample based on a FIR selection and exploiting the correlation with the 60 μm luminosity. The resulting CO MF is, therefore, biased towards gas rich galaxies. An updated estimate of the H2 MF, based on an empirical and variable CO-H2 conversion factor, was presented by Obreschkow & Rawlings (2009). We use in Fig. 8 the molecular mass function derived from the L′(CO) luminosity distribution of Saintonge et al. (2017) from the COLD GASS (CO legacy data base for GASS; Saintonge et al. 2011) survey. This last survey, although biased towards massive galaxies (stellar mass, Mstar > a few 109 M⊙, Saintonge et al. (2011, 2017); therefore it might not sample a sufficiently large dynamic range in Mstar to trace a fair distribution) is at present the only survey with a large enough database to allow a fair reconstruction of the L′(CO) luminosity distribution. However, this sample too is not unbiased, since it is not CO-selected.
The comparison shown in Fig. 8 of the molecular mass function derived from the HRS and that from the COLD GASS sample is only indicative. In addition to the issues discussed above we lack the information about the galaxy properties to apply the luminosity dependent conversion factor between L′(CO) and M(H2) equal to the one used by Boselli et al. (2014b). We show in Fig. 8 our derived H2 MF using a constant conversion factor (αCO = 3.6 M⊙/(K km s−1 pc2). Moreover, the completeness at low molecular masses is for both samples very poor and below log(M(H2)) = 8.4 M⊙ nothing can be inferred.
5. Discussion
The fundamental goal for theoretical models of galaxy formation and evolution is reproducing the observed statistical distributions (such as LFs, and stellar and cold gas MFs) of the global properties of the galaxy populations at different cosmic epochs. On the one hand, most of the models are not able to reconstruct the whole spectrum of data, commonly used to fix the parameters and to predict evolution at larger redshifts. Because of the large uncertainties in the theory associated with the physics of the SF, stellar and AGN feedback, and environmental effects, tuning the multi-parameter space by fitting the observed physical properties of the galaxies in the Local Universe is key. In addition, many free parameters are frequently degenerate with each other, and the tuned recipes make these models more or less successful in predicting galaxy evolution over cosmic time. On the other hand, from the observational side, the building up of samples sufficiently large to be statistically meaningful and with a wide wavelength range to cover the whole spectrum of observed properties is laborious. However, this would be the only way to allow a fair comparison with models and to keep biases and systematics fully under control.
We have discussed extensively the limitations of the HRS sample and constrained its biases and selection effects while discussing the individual mass and luminosity functions. The sample is strongly limited in statistical significance by the small number of sources, which does not allow us to fully constrain the properties of the various functions. However, it is the only local sample that has a large coverage in wavelengths for which many physical properties can be simultaneously studied. The large number of observations and the original well defined selection in the K-band have been used to define several LFs and MFs presented in this work, which can be used to constrain the galaxy formation models.
The BLF and BMF that we estimate are fairly comparable to those derived in the literature, given that the wide variety of functions published are not always consistent with one another. Just as an example, the SFR LF seems to be the most different from those derived in the literature. It is clear that the SMF and the atomic gas MF are better determined in much larger local samples, but in the cases of the dust and the molecular MF, for which data are either scanty or not well constrained, the functions determined from the HRS show good quality and at the same level or even better than those found in the literature.
Furthermore, the HRS is composed of galaxies located in a wide range of environments, from the general field to the core of the Virgo cluster, the largest concentration of galaxies in the nearby universe. It is thus ideally defined to study in great detail environmental effects on the different Galactic components (stars, gas, dust). Thanks to its proximity (∼20 Mpc) and to the quality of the multi-frequency data gathered so far, this sample is a unique laboratory for studying the role of mass and environmental quenching and feedback on galaxy evolution down to sub kiloparsec scales.
5.1. The local LFs, the IR luminosity, and the SFR densities
The IR LF derived from the bivariate PDF LK − LIR is in good agreement with that extracted from blind FIR survey, it deviates mainly at low-IR luminosity where the HRS likely misses low luminosity galaxies. The selection in the K-band, as discussed in Sect. 4.3, may miss low surface density objects, faint optical galaxies, and galaxies with IR luminosity larger than that expected for a given K-band luminosity. Overall the agreement with the caveats mentioned above is good.
The present derivation of the luminosity functions allow us to derive the local extragalactic luminosity density. This latter is computed integrating the functional form of the LFs within the limits where the function is defined L(IR) = 2 × 108 ÷ 6 × 1010 L⊙. The density of the IR luminosity in the Local Universe, measured from the HRS IR LF shown in Fig. 4, turns out to be 1.5 × 107 L⊙ Mpc−3, a factor of five lower than that reported in Marchetti et al. (2016), who reported 8.3 × 107 L⊙ Mpc−3. The HRS misses starburst galaxies because of the small sampled volume.
The SFR function derived from the bivariate PDF LK−SFR as discussed in Sect. 4.5 shows very different behaviour from those derived from Hα surveys and from blind IR surveys mainly at large values of the SFRs. This reflects two problems. First, the large difference in sampling the local SFR from optical and IR samples and second the inference of the SFR from the observables with the optical values that are largely affected by the uncertainties in the attenuation correction factors. These latter depend on parameters such as stellar mass and dust temperature and on our poor understanding of the relation between the IRX ratio (L(IR)/L(UV)) and the UV spectral slope (see for extensive discussion, Wang et al. 2016).
Probably because the HRS SFR function misses large values of the SFR, due to the lack of starburst galaxies, the local SFR density computed on this sample is a factor of two below that determined from other local surveys. The SFR density is inferred integrating the derived SFR function shown in Fig. 6 (within the integration limits SFR = 0.01 ÷ 15 M⊙ yr−1) and turns out to be (1.6 ± 0.4) 10−3 M⊙ yr−1 Mpc−3, which is a factor two lower than that derived from other optical surveys (Gunawardhana et al. 2013) and five to ten times lower than that derived from IR surveys (see Clemens et al. 2013; Marchetti et al. 2016, and reference therein). This is not surprising as a large scatter in the local Star Formation Rate Density (SFRD) estimates using different SFR diagnostics is seen. In addition galaxies in the Virgo cluster show a reduced SFR. The Hα measurements present the largest scatter among different published results (see Fig. 11 in Boselli et al. 2015; Marchetti et al. 2016, and reference therein).
5.2. The local mass functions and local mass densities
As discussed in Sect. 4.2, the SMF of the HRS shows a deficit of small galaxies due to the limit in the original selection in the K-band and to the poor sampling of low surface brightness galaxies. The computed local stellar mass density of the HRS (integrating the functional form over the range Mstellar = 109 ÷ 2 × 1011 M⊙) turns out to be 2.25 × 108 M⊙ Mpc−3, within a factor of two from that computed integrating the best fit of the SMF given by Baldry et al. (2012).
The dust mass function of the HRS sample follows closely the same behaviour as those derived from other blind IR surveys. The large scatter shown among the different functions reflects the uncertainties related to the physical and chemical properties of the dust grains. The derived local dust mass density has a value consequently in between the value derived with the mass functions from Dunne et al. (2011), Beeston et al. (2018) and Clemens et al. (2013). The dust mass local density ∼8 × 104 M⊙ Mpc−3, obtained by integrating the functional form (Eq. (10)) over the range 105 ÷ 5 × 108 M⊙, agrees within the uncertainties with those derived from the other DMFs computed so far and rescaled by Beeston et al. (2018) at the same value of the dust absorption coeffecient, ∼1.5 × 105 M⊙ Mpc−3. Driver et al. (2018) report from their analysis on the GAMA survey an average value of the local dust mass density of ∼1.4 × 105 M⊙ Mpc−3.
Figure 7 shows the atomic gas function and highlights that HI−MF derived from the HRS data differs substantially at values M(HI) > a few × 109 M⊙. This is due to the very weak correlation between the HI mass and the K-band luminosity (see Fig. 7 and Table 1), which does not allow us to strongly constrain the bivariate and as a consequence the construction of the atomic gas mass function is poorly determined. In particular we find a deficiency of large mass objects in the HRS survey because its selection in the K-band misses galaxies with large values of the atomic gas found in HI dedicated blind surveys (Zwaan et al. 2005; Martin et al. 2010; Hoppmann et al. 2015; Jones et al. 2018). Moreover, the HRS contains more HI deficient objects than normal field galaxies, due to the presence of the Virgo cluster and the likely direct stripping of ISM from the disc (e.g. ram pressure, Cortese et al. 2016; Boselli et al. 2014c).
The molecular mass function reported in Fig. 8 is the first function built on a complete sample, although the completeness is in the K-band. The H2 mass is relatively strongly correlated with the K-band luminosity, due to relation between the stellar mass and the molecular gas mass within the sample and the scatter due to the HI-deficient galaxies. The derived H2 MF, when compared with the predictions by Lagos et al. (2011), shows a deficit at masses lower than 108 M⊙ where the HRS sample may miss galaxies with low molecular hydrogen content.
We have derived a very rough molecular mass function from the best fit of the CO luminosity distribution by Saintonge et al. (2017) and compare this function to the one computed over the HRS sample. The comparison is only indicative. It shows an overall good agreement but at small molecular mass where neither the HRS nor the COLD GASS sample are complete and therefore we cannot infer any meaningful conclusion. The molecular mass local density turns out to be 107 M⊙ Mpc−3. Table 3 summarises the values of the local luminosity and mass density derived from our analysis.
Local luminosity and mass densities.
6. Conclusions
By using the bivariate function based on the K-band luminosity we have constructed the LFs and MFs of the HRS sample. We have discussed the LFs and MFs derived from the HRS and compared these with the same LFs and MFs derived from local samples selected in completely different ways. This comparison highlights the limits and biases inherent to the HRS but also its strength as a representative sample of the Local Universe.
The analysis shows that the behaviour of the morphological (optically selected) subsamples is quite different and a statistically meaningful result can be obtained over the whole HRS sample only from the relationship between the K-band and the stellar mass. The same analysis with the other physical quantities (dust and gas masses, FIR luminosity and star formation rate) has to be restricted to the late-type galaxy (LTG) subsample. The LFs and MFs of LTGs are generally dependent on the K-band and the various dependencies are discussed in detail. We are able to derive the corresponding LFs and MFs and compare with those computed with other samples and with results from galaxy formation simulations.
The analysis reported in this paper represents a fundamental local benchmark to compare with models of galaxy evolution. The HRS is designed to provide a concise view of the large galaxies in our Local Universe. The results found in this work could therefore be representative for late type galaxies. The derived relations can be applied to a larger set of local galaxies and can be compared with a similar analysis at higher redshift.
Acknowledgments
This research has made use of data from the HRS project. HRS is a Herschel Key Programme utilising guaranteed time from the SPIRE instrument team, ESAC scientists, and a mission scientist. The HRS data was accessed through the Herschel Database in Marseille (HeDaM − http://hedam.lam.fr) operated by CeSAM and hosted by the Laboratoire d’Astrophysique de Marseille. We acknowledge financial support from the Programme National de Cosmologie and Galaxies (PNCG) of CNRS/INSU, France. Parts of this research were conducted by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. P.A. warmly thanks Ken Tatematsu-san for his kind invitation to Japan and his hospitality at the Nobeyama Observatory. She warmly thanks NAOJ-Chile for her stay at Mitaka where this work was completed. We thank the anonymous referee whose help greatly improved the readability of the paper.
References
- Agius, N. K., di Serego Alighieri, S., Viaene, S., et al. 2015, MNRAS, 451, 3815 [NASA ADS] [CrossRef] [Google Scholar]
- Andreani, P., Spinoglio, L., Boselli, A., et al. 2014, A&A, 566, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Bassett, R., Bakkik, K., Cortese, L., et al. 2017, MNRAS, 470, 1991 [NASA ADS] [CrossRef] [Google Scholar]
- Beeston, R. A., Wright, A.H., Maddox, S.C., et al. 2018, MNRAS, 479, 1077 [NASA ADS] [Google Scholar]
- Bendo, G., Galliano, F., Maddox, S.C., et al. 2012, MNRAS, 423, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B. A., Sandage, A., & Tamman, G. A. 1988, ARA&A, 26, 509B [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., & Moustakas, J. 2009, ARA&A, 47, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Dalcanton, J., Eisenstein, D., et al. 2001, AJ, 121, 2358B [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. R., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2014, A&ARv, 22, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2009, ApJ, 706, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Eales, S., & Cortese, L. 2010, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Heinis, S., et al. 2011, A&A, 528, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Hughes, T. M., Cortese, L., Gavazzi, G., & Buat, V. 2013, A&A, 550, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., & Boquien, M., 2014a, A&A, 564, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014b A&A, 564, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014c, A&A, 564, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Voyer, E., Boissier, S., et al. 2014d, A&A, 570, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Fossati, M., Gavazzi, G., et al. 2015, A&A, 579, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Roehlly, Y., Fossati, M., et al. 2016, A&A, 596, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Kenicutt, R. C., Johnson, B. D. J., et al. 2011, MNRAS, 415, 1815 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Maiolino, R., Peng, Y., et al. 2016, MNRAS, 455, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boselli, A., Smith, M. W. L., et al. 2012, A&A, 543, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciesla, L., Boquien, M. A., Boselli, A., et al. 2014, A&A 565, A128 [Google Scholar]
- Ciesla, L., Boselli, A., Elbaz, D., et al. 2016, A&A, 585, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clemens, M. S., Negrello, M., De Zotti, G., et al. 2013, MNRAS, 433, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Norberg, P., Baugh, C. M., et al. 2001, MNRAS, 393, 681 [Google Scholar]
- Cortese, L., Bendo, G. J., Boselli, A., et al. 2010, A&A, 518, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Ciesla, L., Boselli, A., et al. 2012a, A&A, 540, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Boissier, S., Boselli, A., et al. 2012b, A&A, 544, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Fritz, J., Bianchi, S., et al. 2014, MNRAS, 440, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Bekki, K., Boselli, A., et al. 2016, MNRAS, 459, 3574 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Dib, S., Hony, S., et al. 2016, MNRAS, 456, 2221 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Rafieferantsoa, M. H., Thompson, R. J., & Hopkins, P. F. 2017, MNRAS, 467, 115 [NASA ADS] [Google Scholar]
- Davidzon, I., Cucciati, O., Bolzonella, M., et al. 2016, A&A, 586, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Vis, P., Gomez, H. L., Schofield, S. P., et al. 2017, MNRAS, 471, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Gomez, H. L., da Cunha, E., et al. 2011, MNRAS, 417, 1510 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S., de Vis, P., Smith, M. W. L., et al. 2017, MNRAS, 465, 3125 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S., Smith, D., Bourne, N., et al. 2018, MNRAS, 473, 3507 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Krumholz, M. R., Prochaska, J. X., Gavazzi, G., & Boselli, A. 2009, ApJ, 697, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [NASA ADS] [Google Scholar]
- Gavazzi, G., Consolandi, G., Belladitta, S., Boselli, A., & Fossati, M. 2018, A&A 615, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomez, H. L., Baes, M., Cortese, L., et al. 2010, A&A, 518, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Bland-Hawthorn, J., et al. 2013, MNRAS, 433, 27641 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, D. T., Driver, S. P., Cameron, E., et al. 2010, MNRAS, 404, 1215 [NASA ADS] [Google Scholar]
- Hoppmann, L., Staveley-Smith, L., Freudling, W., et al. 2015, MNRAS, 452, 3726 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, N. L. 1949, Biometrika, 36, 149 [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Johnston, R. 2011, A&ARv, 19, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. G., Haynes, M. P., Giovanelli, R., & Moorman, C. 2018, MNRAS, 477, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Keres, D., Yun, M. S., & Young, J. S. 2003, ApJ, 582, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Pahre, M. A., Falco, E. E., et al. 2001, ApJ, 560, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Baugh, C. M., Lacey, C. G., et al. 2011, MNRAS, 418, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Theuns, T., Schaye, J., et al. 2016, MNRAS, 459, 2632 [NASA ADS] [CrossRef] [Google Scholar]
- Marchetti, L., Vaccari, M., Franceschini, A., et al. 2016, MNRAS, 456, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, A. M., Papastergis, E., Giovanelli, R., et al. 2010, ApJ, 723, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, R., Torrey, P., & Vogelsberger, M. 2016, MNRAS, 457, 3775 [NASA ADS] [CrossRef] [Google Scholar]
- Mok, A., Wilson, C. D., Golding, J., et al. 2016, MNRAS, 456, 4384 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Coil, A. L., Aird, J., et al. 2013, ApJ, 767, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Clemens, M., Gonzalez-Nuevo, J., et al. 2013, MNRAS, 429,1309 [NASA ADS] [CrossRef] [Google Scholar]
- Obreschkow, D., & Rawlings, S. 2009, MNRAS, 394, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Popping, G., Somerville, R. S., & Trager, S. C. 2014, MNRAS, 442, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Kramer, C., et al. 2011, MNRAS, 415, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Catinella, B., Tacconi, L. J., et al. 2017, ApJS, 233, 22 [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJS, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, T. 2007, in Copulas: From Theory to Application in Finance, ed. J. Rank (Risk Books) [Google Scholar]
- Shankar, F., Lapi, A., Salucci, P., De Zotti, G., & Danese, L. 2006, ApJ, 643, 14 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Smith, D. J. B., Dunne, L., da Cunha, E., et al. 2012, MNRAS, 427, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T. T. 2010, MNRAS, 406, 1830 [NASA ADS] [Google Scholar]
- Thanjavur, K., Simard, L., Bluck, A. F. L., & Mendel, T. 2016, MNRAS, 459, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Trivedi, P. K., & Zimmer, D. M. 2005, Copula Modelling: An Introduction for Practitioners (Hanover, USA: now Publishers Inc.) [Google Scholar]
- Vaccari, M., Marchetti, L., Franceschini, A., et al. 2010, A&A, 518, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vio, R., Fasano, G., Lazzarin, M., & Lessi, O. 1994, A&A, 289, 640 [NASA ADS] [Google Scholar]
- Wang, L., Norberg, P., Bethermin, M., et al. 2016, A&A, 592, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, M., Meyer, M. J., Staveley-Smith, L., & Webster, R. L. 2005, MNRAS, 359, L30 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Histograms of the data in Table 1 and corresponding fitted Johnson PDF. In all cases the SB family has been selected. The best fit parameters of Eq. (10) are reported on Table 1. These PDFs have been used to estimate the bivariate PDF shown in Figs. 3–8. |
| In the text | |
 |
Fig. 2. Scatterplots and histograms for the data. Blue dots correspond to the objects with morphological type ≤3 (ET), green dots to objects with morphological type ≥3 (LT). Because of the lack of data at some wavelengths the various panels contain a different number of points. |
| In the text | |
 |
Fig. 3. Panel a: bivariate PDF LK−Mstar: estimated bivariate PDF shown in linear scale (and enlarged in the inset) for the K-band with the stellar masses. Contour lines correspond to levels 0.1, 0.3, 0.5, 0.7, and 0.9. These values correspond to the fraction of the peak value of the BLF that is set to one. Panel b: reconstructed stellar mass function of the HRS sample (red line) shown together with the best fit of the Galactic mass function given by Baldry et al. (2012) for the GAMA survey (blue line). |
| In the text | |
 |
Fig. 4. Panel a: bivariate PDF L(K)−L(IR) for LTGs only: estimated bivariate PDF shown in linear scale (and enlarged in the inset) for the K-band with the infrared luminosities. Contour lines correspond to levels 0.1, 0.3, 0.5, 0.7, and 0.9. These values correspond to the fraction of the peak value of the BLF that is set to one. Panel b: reconstructed IR luminosity function of the HRS sample (red line) shown together with the LF computed over local blind IR surveys (blue line) by Marchetti et al. (2016). Error bars are estimated through a bootstrapping technique. |
| In the text | |
 |
Fig. 5. Panel a: bivariate PDF L(K)−Mdust, same as Fig. 4 for the K-band luminosity and the dust mass. Panel b: reconstructed dust mass function of the HRS sample (red line) shown together with the DMFs computed over local blind IR surveys: Dunne et al. (2011; green), Beeston et al. (2018; blue), Clemens et al. (2013; purple and grey). |
| In the text | |
 |
Fig. 6. Panel a: bivariate PDF L(K)−SFR, same as Fig. 4 for the K-band luminosity and the SFR. Panel b: reconstructed SFR LF for the HRS sample (red) compared with that of (Gunawardhana et al. 2013; blue), and (Clemens et al. 2013; purple). |
| In the text | |
 |
Fig. 7. Panel a: bivariate PDF L(K)−M(HI), same as Fig. 4 for the K-band luminosity and the atomic gas mass. Panel b: reconstructed atomic gas mass function of the HRS sample (red curve) shown together with the gas mass computed in the Local Universe by Martin et al. (2010), and Zwaan et al. (2005; blue and green curves respectively) and models by Popping et al. (2014), and Lagos et al. (2011; purple and grey points/lines). |
| In the text | |
 |
Fig. 8. Panel a: bivariate PDF L(K)−M(H2), same as Fig. 4 for the K-band luminosity and the molecular gas mass. Panel b: reconstructed molecular gas mass function of the HRS sample shown together with the predicted ones by (Lagos et al. 2011; green and grey lines), and the molecular mass function derived from the L′(CO) function from (Saintonge et al. 2017; blue line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


