| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731822 | |
| Published online | 25 September 2018 | |
Cross section of curvature radiation absorption
1
INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
e-mail: locatelli@ira.inaf.it, nicola.locatelli@brera.inaf.it
2
Univ. di Milano Bicocca, Dip. di Fisica G. Occhialini, Piazza della Scienza 3, 20126 Milano, Italy
3
Univ. Alma Mater Studiorum, Dip. di Fisica e Astronomia DIFA, via Piero Gobetti 93/2, 40129 Bologna, Italy
4
Istituto di Radio Astronomia (IRA) sede di Bologna, via Piero Gobetti 101, 40129 Bologna, Italy
Received:
24
August
2017
Accepted:
5
June
2018
When treating the absorption of light, it is instructive to focus on the absorption coefficient related to the probability of photons to survive while traversing a layer of material. From the point of view of particles doing the absorption, however, the elementary interaction of the particle with the photon is best described by the corresponding cross section. We revisit curvature radiation in order to find the absorption cross section for this process, making use of the Einstein coefficients and their relations with spontaneous and stimulated emission and true absorption. We derive the cross section as a function of the emission angle ψ (i.e. the angle between the instantaneous velocity vector and the direction of the photon) and the cross section integrated over angles. Both are positive, contrary to the synchrotron case for which the cross section can be negative for large ψ. Therefore, it is impossible to have curvature radiation masers. This has important consequences for sources of very large brightness temperatures that require a coherent emission process, such as pulsars and fast radio bursts.
Key words: masers / radiation mechanisms: non-thermal / radio continuum: general
© ESO 2018
1. Introduction
When dealing with the absorption process in general, we are usually interested in the absorption coefficient, namely the resulting intensity and spectrum of the radiation. But there is a complementary view, namely the electron point of view. In this case we are interested in the absorbing electron gain or loss of energy and momentum as a result of the total absorption rate, which includes stimulated emission. The latter view is best captured by the concept of cross section. As in the synchrotron case, this helps to treat the problem of energy exchange between particles (both protons and electrons) eventually leading to their thermalization. If the absorbed radiation carries some linear momentum, a fraction of this momentum lets the absorbing particles acquire a pitch angle and emit by synchrotron radiation, while the component along the magnetic field line accelerates the absorbing particle in that direction.
Curvature radiation is very similar to synchrotron radiation, in which the Larmor radius takes the place of the curvature radius of the magnetic field (see e.g. Jackson 1962). The absorption cross section of synchrotron radiation, in some special cases, can become negative, and therefore a synchrotron maser is possible (Ghisellini & Svensson 1991; hereafter GS91). Given the similarities between the synchrotron and curvature emission processes, we wonder if a curvature maser is possible. This would have a great impact on the studies of the emission process of fast radio bursts (FRBs), helping to explain the large observed brightness temperatures, requiring coherent radiation.
Jackson (1962, see also the 1999 edition) gives the classical treatment for curvature emission, but not absorption. Coherent absorption by a bunch of particles was considered by Cocke & Pacholczyk (1975). Twiss (1958) and Blandford (1975) found that the absorption coefficient is positive in general, but can be negative in specific cases and geometries. However, Melrose (1978) argued against this conclusion, finding the impossibility of a curvature maser even in the presence of ambient particles. Later, Zheleznyakov & Shaposhnikov (1979) found instead results in agreement to Blandford (1975). The issue is therefore not completely clear and we would like to explain the absorption process at the elementary level, resorting to the Einstein coefficients and their relations. In other words, we would like to compute the probability for true absorption or stimulated emission of the single electron of a given energy when interacting with a photon of energy h ν.
We leave the construction of a more complex scenario, involving a realistic dipole field around a neutron star, its rotation, and the acceleration of particles along divergent field lines, to a future paper concerning pulsars (see the review by e.g. Usov 2000 and Lyutikov et al. 1999a,b). Although our main aim is to find the cross section for curvature absorption, we revisit concepts and formulae that are well known, but that we re-use with our notation.
2. Curvature cross section
When deriving the absorption cross section, we are dealing with a particle at some energy level γmc2 (for simplicity, we call this level 2) and an incoming photon of energy hν. The particle can absorb it, jumping to a higher energy level (level 3, with energy γmc2 + hν), or can emit another photon of same energy, phase, and direction of the incoming photon, through stimulated emission. In this case it jumps to level 1 (of energy γmc2 − hν). Both these processes are related to the spontaneous process of emitting a photon of the same energy hν, through the Einstein coefficients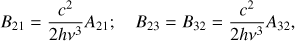 (1)
(1)
where B21 and B32 are the Einstein coefficients for stimulated emission, while B12 and B23 are the coefficients for true absorption, and A21 and A32 correspond to spontaneous emission. The probability that the particle initially in level 2 absorbs the photon (B23) depends on the spontaneous emissivity in level 3 (A32), while the probability to have induced emission (B21) depends on the spontaneous emissivity in level 2 (A21).
We set ϵ ≡ hν/(mc2), and measure the particle energy in units of mc2, and momentum p in units of mc. We then have γ1 = γ2 − ϵ and γ3 = γ2 + ϵ.
Consider the emissivity of the single particle (in erg s−1 Hz−1 ster−1) for a small emission angle ψ between the (instantaneous) velocity of the particle and the direction of the produced photon. At the two energies γ2 and γ3 = γ2 + ϵ the emissivity can be written as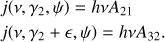 (2) The differential cross section for true absorption (dσta/dΩ) and stimulated emission (dσse/dΩ) can then be written as (see GS91)
(2) The differential cross section for true absorption (dσta/dΩ) and stimulated emission (dσse/dΩ) can then be written as (see GS91)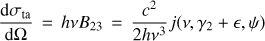 (3)
(3)
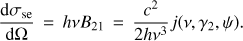 (4)
(4)
We note that the above formulae implicitly assume that the momentum of the particle, after having absorbed the photon, is still along the magnetic field line, even for ψ ≠ 0. This is different from the synchrotron case, for which a phase space factor (∝ γp) given by all the possible final states of the momentum of the free particle should also be considered in Eqs. (2)–(5), (see GS91 for comparison). The net absorption cross section is the difference between the two, very similar, cross sections. When ϵ ≪ γ we can write![$ \begin{aligned} {\mathrm{d}\sigma \over \mathrm{d}\Omega } \, =\, {\mathrm{d}\sigma _\mathrm{ta} \over \mathrm{d}\Omega } - {\mathrm{d}\sigma _\mathrm{se} \over \mathrm{d}\Omega } = \frac{1}{2m\nu ^2} \frac{\partial }{\partial \gamma }\left[ j(\nu , \gamma , \psi ) \right] . \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq5.gif) (5)
(5)
The differential cross sections in Eqs. (3) and (4) refer to one particular direction ψ of the incoming photon. This direction coincides with the corresponding emission angle for the emissivity. If the particles emits a photon in front of it, the corresponding cross section is for an incoming photon at the same angle (i.e. the photon is coming from behind the particle). In general, if the energy of the particle increases, so does its emissivity.
In the synchrotron case, however, there are special cases where the emissivity for specific directions decreases when the particle energy is increased. This occurs when the incoming photon arrives at an angle larger than the characteristic beaming angle 1/γ. GS91 have shown that when ψ > 1/γ, the increase of γ makes the synchrotron emissivity decrease, possibly even more than the increase of the phase space factor γp, which multiplies the emissivity in the synchrotron case.
The stimulated emission becomes larger than the true absorption, the total cross section becomes negative, and there is the possibility to have a maser or laser.
Following Jackson (1999), we report the single particle emissivity for curvature radiation as a function of the emission angle ψ. First let us introduce the notation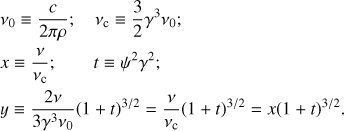 (6)
(6)
which is valid for γ ≫ 1 and ψ ≪ 1. Ka(y) is the modified Bessel function of order a. It is instructive to compare this emissivity with the synchrotron emissivity, i.e.![$ \begin{aligned} j_\mathrm{s}(\nu , \gamma ,\psi )& = {3 \over 4\pi ^2} \, { e^2 \over r_\mathrm{L} } x_\mathrm{s}^2 \gamma ^2\, (1+t) \nonumber \\& \quad \times \, \left[ (1+t) K^2_{2/3}(y_\mathrm{s}) +t K^2_{1/3}(y_\mathrm{s}) \right], \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq8.gif) (8)
(8)
where rL is the Larmor radius, rL = γβmc2/(eB), xs = ν/νs = 2ν/(3γ2νL sin θ), and the Larmor frequency νL = eB/(2πmc). The argument of the Bessel functions ys is the same as in Eq. (6), but with xs replacing x. As expected, the functional forms are the same. We note that
-
the curvature emissivity does not depend on the mass of the particle, contrary to the synchrotron emissivity (via the Larmor radius and frequency);
-
the typical frequency for curvature radiation is νc = (3/2)γ3c/(2πρ) ∝ γ3. Here ρ is independent of γ, contrary to the Larmor radius that is instead ∝γ, which makes νs = (3/2)γ3c/(2πrL) ∝ γ2. The overall dependence from the particle energy is thus different from the curvature to the synchrotron case.
![$ \begin{aligned} {\mathrm{d}\sigma _\mathrm{c} \over \mathrm{d}\Omega } (\nu , \gamma , \psi )& = {4 \over 3 } {e^2\over m c^2} \, {\rho \over \gamma ^5 } \,\, \{ 3y [(1+t)K_{2/3}(y)K_{5/3}(y) \nonumber \\& \quad +\,\,t K_{1/3}(y)K_{4/3}(y) ] -4(1+t) K^2_{2/3}(y) \nonumber \\& \quad -\,\,2tK^2_{1/3}(y) \}. \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq9.gif) (9)
(9)
As shown below, this cross section is positive for all values of ψ. Figure 1 shows dσc/dΩ as a function of ψ for different values of γ. For each curve we assume ν = νc = (3/2)ν0γ3. The circles correspond to ψ = 1/γ, i.e. t = 1.
 |
Fig. 1. Top panel: curvature absorption cross section as a function of the emission angle ψ for different values of γ. We assume a curvature radius ρ = 106 cm and a frequency ν = νc = (3/2)ν0γ3. Bottom panel: single electron emissivity as a function of ψ for different values of γ, as labelled. The circles in both panels correspond to ψ = 1/γ. |
2.1. Impossibility of curvature maser
To understand why dσc/dΩ is always positive, we consider the emissivity (Eq. (7)) as a function of ν, as shown in the top and middle panels of Fig. 2. The emission angles are 0.125∘ (left) and 5∘ (right). The plotted curves correspond to different values of γ, as labelled. The top panels shows that increasing γ, the emissivity increases both for small and large angles ψ. This contrasts the behaviour of the synchrotron emissivity, shown in the bottom panels. In this case, for large angles ψ > 1/γ, and at high frequencies, the emissivity decreases increasing γ. For small ψ, the behaviour is similar to the curvature radiation.
 |
Fig. 2. Top panels: curvature emissivity as a function of frequency ν for different γ (labelled) and for two values of the emission angle ψ, 0.125∘ (left column) and 5∘ (right column). We can see that at large ψ the emission at high frequencies is quenched, but that the emissivity at larger γ is always greater than the emissivity at lower γ. Bottom panels: the same, multiplied by the phase space factor γp, for the synchrotron case. Contrary to the curvature case, for large γ the emissivity can be smaller than the one at lower γ. A magnetic field B = 1 G was considered in calculations for comparison. |
The reason for this difference lies in the difference between the Larmor radius, proportional to γ, and the curvature radius, that is constant. This is the reason why the total power emitted by the single particle (integrated over angle) is ∝ γ2 for synchrotron and ∝ γ4 for curvature emission. The latter dependence is so strong that at large ψ the received radiation is still larger for increasing γ, even if the beaming cone (of semi-aperture angle 1/γ) becomes narrower.
2.2. Total cross section
The emissivity integrated over the emission angles (see e.g. Jackson 1999) gives the power per unit frequency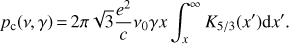 (10)
(10)
We can then find the cross section integrated over angles using, in Eq. (5), the above emissivity instead of j(ν, γ, ψ). We obtain![$ \begin{aligned} \sigma _\mathrm{c} (\nu ,\gamma )\,{=}\,{1 \over 2 \sqrt{3}}\, {e^2\over mc^2} \, {\rho \over \gamma ^6 } \left[ K_{5/3}(x) - \frac{2}{3x} \int _x^\infty K_{5/3}( y)\,\mathrm{d}{ y} \right] .\end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq11.gif) (11)
(11)
The top panel of Fig. 3 shows the behaviour of σc(ν, γ) as a function of ν/ν0 for different values of γ, while the bottom panel shows the corresponding power emitted by the single particle.
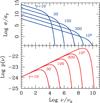 |
Fig. 3. Top panel: curvature absorption cross section, normalized to the scattering Thomson cross section σT, as a function of ν/ν0 for different values of γ. A curvature radius ρ = 106 cm has been assumed. For ν/ν0 = 1, σc is of the order of ρ/(reγ) (namely a factor ∼ 1019/γ) larger than σT. Bottom panel: single electron emissivity, again as a function of ν/ν0 for different values of γ, as labelled. |
We can find the asymptotic behaviour of of Eq. (11) for low frequencies (i.e. x ≪ 1), using Ka(x) → 2a − 1Γ(a)x−a. Furthermore, let us consider electrons, and thus e2/(mec2) is equal to the classical electron radius re. In this case,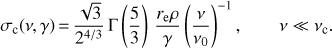 (12)
(12)
This is the maximum value of the cross section and it is equivalent to a physical surface of the order of the classical electron radius times the curvature radius divided by γ. We note that ρ/γ is the actual segment of arc travelled by the electron illuminating the observer.
3. Self absorption frequency and brightness temperature
In the Appendix we derive the emissivity and absorption coefficient αc(ν) for a particle distribution N(γ) = N0γ−n between γmin and γmax. We can then derive the self-absorption frequency for a power law distribution of particles emitting and absorbing curvature radiation.
The absorption optical depth of a layer of length R is τν = Rαc(ν). The self-absorption frequency νt is defined through τνt = 1. For N(γ) = N0γ−n, with γmin ∼ 1, we have![$ \begin{aligned} \nu _\mathrm{t} = \nu _0\left[ C(n){e^2\over mc^2} \rho R N_0 \right]^{3/(n+5)} , \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq14.gif) (14)
(14)
Typical values for C(n) are C(1) = 0.38, C(2) = 0.42, C(3) = 0.52, C(4) = 0.7.
Using ρ = R = 106 cm, n = 3, and N0 = 1015 cm−3, we derive νt ∼ 1 GHz. The large particle density is just a fraction of the order of the Goldreich & Julian (1969) density nGJ close to the surface of a rapidly spinning magnetar,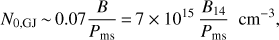 (15)
(15)
where Pms is the period of the magnetar measured in milliseconds.
The brightness temperature is defined by equating the monochromatic intensity to the Raleigh–Jeans part of the black-body intensity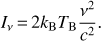 (16)
(16)
In our case, TB is maximized at the self-absorption frequency νt. Using the source function (Eq. (A.6)) at νt and derive![$ \begin{aligned} T_\mathrm{B,max}& = { S_\mathrm{c}(\nu _\mathrm{t}) \over 2 k_\mathrm{B} } \, {c^2\over \nu ^2_\mathrm{t}} \nonumber \\ \,& = {2\pi ^2 D(n)\over C(n) ^{(n+4)/(n+5)} } {mc^2\over k_\mathrm{B}} \left[ {e^2\over mc^2 } \rho R N_0 \right]^{1/(n+5)} ,\end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq18.gif) (17)
(17)
where D(n) is given by Eq. (A.4). With R = ρ = 106 cm and n = 3, we have TB, max = 1.8 × 1012(N0/1015 cm−3)1/8 K.
4. Conclusions
We have revisited the process of curvature radiation in order to calculate the absorption cross section between the particle and an incoming photon. In general, the concept of cross section allows us to consider the basic process of the particle–photon interaction from the point of view of the electron. Therefore it can be useful when considering the momentum and energy gained by the particles absorbing radiation through the radiative process under consideration. All this has been already considered for the synchrotron process (by e.g. GS91), but it was never derived before for curvature radiation.
The derived cross section can be several orders of magnitude larger than the scattering Thomson cross section. Thus the absorption of relatively low energy photons by a generic electron moving along a magnetic field line may easily become the leading photon–particle interaction. Exchange of energy between different emitting and absorbing particles proceeds via the exchange of photons, and this can thermalize the particles even in the absence of Coulomb collisions in rarefied, hot and magnetized plasma, similar to the thermalization that can occur in synchrotron sources (Ghisellini et al. 1998). Comparing the cross sections for Thomson scattering, synchrotron absorption, and absorption of curvature radiation we have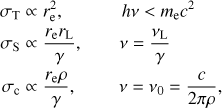 (18)
(18)
where we evaluated σS at the fundamental harmonic νB = νL/γ. We note that σT ∝ 1/me2, σc ∝ 1/me while σS is independent of the mass of the particle (at the fundamental frequency).
The absorption of curvature radiation can be particularly relevant for large values of the magnetic fields, like those in the vicinity of the surface of neutron stars ad magnetars, where strong synchrotron losses make the particles rapidly lose their initial pitch angle, while leaving unaltered the momentum along the magnetic field lines. Furthermore, along these lines, the particles could accelerate through the process of magneto-centrifugally driven acceleration (see e.g. Rieger & Mannheim 2000; Osmanov et al. 2007; Rieger & Aharonian 2008), using the spin of the neutron star. In the self-absorbed regime, this acceleration process is not limited by radiative cooling (the absorption balances the emission), and this makes the particle distribution to have a relatively large low energy cut-off γmin.
The other crucial difference between the synchrotron and curvature cross sections is the impossibility of maser for the curvature radiation. This result is particularly relevant for the origin of the huge brightness temperature seen in pulsars (see e.g. the review by Usov 2000) and FRBs (TB > 1034 K; see e.g. the review by Katz 2016) requiring coherent radiation. If the millisecond pulses seen in FRB are indeed due to curvature radiation, then coherence cannot be associated with maser action without taking into account effect such as Cherenkov–curvature or Cherenkov–drift instabilities (Lyutikov et al. 1999a,b). Whenever the conditions for their action are not satisfied, coherence must necessarily be due to the bunching of particles contained in one wavelength (e.g. Kumar et al. 2017) and not to a maser. This, together with the large absorption cross section derived in this work, poses the problem of how to avoid the self-absorption of the produced curvature radiation, even in the coherent case. We plan to investigate possible solutions to this problem in a future paper.
Acknowledgments
We thank Sergio Campana, Luca Zampieri, Giancarlo Ghirlanda and Fabrizio Tavecchio for discussions. We thank the anonymous referees for critical comments that helped to improve the paper. NL acknowledges financial contribution from the ERC Starting Grant “MAGCOW”, no.714196.
References
- Abramowitz, M., & Stegun, I. A. 1974, Handbook of Mathematical Functions, National Bureau of Standards Applied Mathematics Series, 55 [Google Scholar]
- Blandford, R. D. 1975, MNRAS, 170, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Cocke, W. J., & Pacholczyk, A. G. 1975, ApJ, 195, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Svensson, R. 1991, MNRAS, 252, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Haardt, F., & Svensson, R. 1998, MNRAS, 297, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. D. 1962, Classical Electrodynamics, first edition (New York: Wiley) [Google Scholar]
- Jackson, J. D. 1999, Classical Electrodynamics, third edition (New York: Wiley) [Google Scholar]
- Katz, J. I. 2016, Mod. Phys. Lett. A, 31, 1630013 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Lu, W., & Bhattacharya, M. 2017, MNRAS, 468, 2726 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., Blandford, R., & Machabeli, G. 1999a, MNRAS, 305, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., Machabeli, G., & Blandford, R. 1999b, ApJ, 512, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1978, ApJ, 225, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Osmanov, Z., Rogava, A., & Bodo, G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieger, F. M., & Aharonian, F. 2008, A&A, 479, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieger, F. M., & Mannheim K. 2000, A&A, 353, 473 [NASA ADS] [Google Scholar]
- Twiss, R. K. 1958, Aust. J. Phys., 11, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Usov, V. V. 2000, ASP Conf. Ser., 202, 417 [NASA ADS] [Google Scholar]
- Westfold, K. C. 1959, ApJ, 130, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Shaposhnikov, V. E. 1979, Aust. J. Phys., 32, 49 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Emissivity and absorption coefficient
The emissivity  of particles distributed as a power law for a source with tangled magnetic field is
of particles distributed as a power law for a source with tangled magnetic field is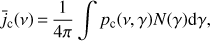 (A.1)
(A.1)
where N(γ) = N0γ−n and pc(ν, γ) is given by Eq. (10). The 4π factor implies that we are assuming an isotropic emission. Using Eq. (35) in Westfold (1959)
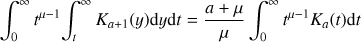 (A.2)
(A.2)
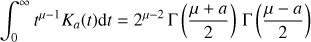 (A.3)
(A.3)
which coincides with Cocke & Pacholczyk (1975) apart from the factor (n + 3)/(n + 1), that is missing from their Eq. (5).
Comparing with synchrotron emissivity made by the same particle distribution, 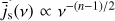 , we can see that curvature emissivity has a steeper spectrum.
, we can see that curvature emissivity has a steeper spectrum.
The absorption coefficient for curvature radiation can be simply derived by integrating the cross section over the energy distribution of electrons. For a power law, N(γ) = N0γ−n between γmin ∼ 1 and γmax ≫ 1, we have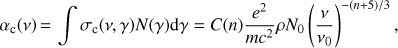 (A.5)
(A.5)
where C(n) is given in Eq. (14), and where we used again Eq. (A.3) (see also Eq. (11.4.22) of Abramowitz & Stegun 1974).
We note the ν7/3 slope, unlike the self–absorbed synchrotron spectrum, that has a ν5/2 slope.
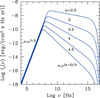 |
Fig. A.1. Specific intensity of curvature radiation for different spectral indexes n of the electron distribution. The other parameters are ρ = 106 cm, R = 104 cm, N0 = 1015 cm−3, γmax = 2 × 104. Note the ν7/3 behaviour in the self–absorbed part. |
Figure A.1 shows how the specific intensity changes by changing the low energy cut-off γmin of the electron distribution.
All Figures
 |
Fig. 1. Top panel: curvature absorption cross section as a function of the emission angle ψ for different values of γ. We assume a curvature radius ρ = 106 cm and a frequency ν = νc = (3/2)ν0γ3. Bottom panel: single electron emissivity as a function of ψ for different values of γ, as labelled. The circles in both panels correspond to ψ = 1/γ. |
| In the text | |
 |
Fig. 2. Top panels: curvature emissivity as a function of frequency ν for different γ (labelled) and for two values of the emission angle ψ, 0.125∘ (left column) and 5∘ (right column). We can see that at large ψ the emission at high frequencies is quenched, but that the emissivity at larger γ is always greater than the emissivity at lower γ. Bottom panels: the same, multiplied by the phase space factor γp, for the synchrotron case. Contrary to the curvature case, for large γ the emissivity can be smaller than the one at lower γ. A magnetic field B = 1 G was considered in calculations for comparison. |
| In the text | |
 |
Fig. 3. Top panel: curvature absorption cross section, normalized to the scattering Thomson cross section σT, as a function of ν/ν0 for different values of γ. A curvature radius ρ = 106 cm has been assumed. For ν/ν0 = 1, σc is of the order of ρ/(reγ) (namely a factor ∼ 1019/γ) larger than σT. Bottom panel: single electron emissivity, again as a function of ν/ν0 for different values of γ, as labelled. |
| In the text | |
 |
Fig. A.1. Specific intensity of curvature radiation for different spectral indexes n of the electron distribution. The other parameters are ρ = 106 cm, R = 104 cm, N0 = 1015 cm−3, γmax = 2 × 104. Note the ν7/3 behaviour in the self–absorbed part. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$ \begin{aligned} j_\mathrm{c}(\nu , \gamma ,\psi )& = {3 \over 4\pi ^2} \, { e^2 \over \rho } x^2 \gamma ^2\, (1+t) \nonumber \\& \quad \times \, \left[ (1+t) K^2_{2/3}(y) +t K^2_{1/3}(y) \right] , \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq7.gif)
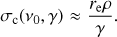
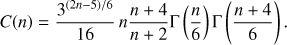
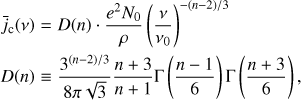
![$ \begin{aligned}& S_\mathrm{c}(\nu )\equiv {\bar{j}_\mathrm{c}(\nu )\over \alpha _\mathrm{c}(\nu )} = B(n) {mc^2\over \rho ^2} \left( \nu \over \nu _0 \right)^{7/3} \nonumber \\&B(n)={D(n) \over C(n)} = {2\over 3^{1/3}\pi n} {(n+3)(n+2) \over (n+1)(n+4)}\, {\Gamma [{n-1\over 6}] \, \Gamma [{n+3\over 6}] \over \Gamma [{n\over 6}] \, \Gamma [{n+4\over 6}]}\cdot \end{aligned} $](/articles/aa/full_html/2018/09/aa31822-17/aa31822-17-eq27.gif)