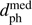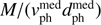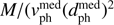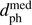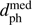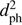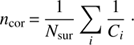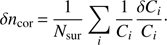| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833456 | |
| Published online | 13 August 2018 | |
New stellar encounters discovered in the second Gaia data release⋆
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: calj@mpia.de
Received:
19
May
2018
Accepted:
19
June
2018
Passing stars may play an important role in the evolution of our solar system. We search for close stellar encounters to the Sun among all 7.2 million stars in Gaia DR2 that have six-dimensional phase space data. We characterize encounters by integrating their orbits through a Galactic potential and propagating the correlated uncertainties via a Monte Carlo resampling. After filtering to remove spurious data, we find 694 stars that have median (over uncertainties) closest encounter distances within 5 pc, all occurring within 15 Myr from now. 26 of these have at least a 50% chance of coming closer than 1 pc (and 7 within 0.5 pc), all but one of which are newly discovered here. We confirm some and refute several other previously-identified encounters, confirming suspicions about their data. The closest encounter in the sample is Gl 710, which has a 95% probability of coming closer than 0.08 pc (17 000 AU). Taking mass estimates obtained from Gaia astrometry and multiband photometry for essentially all encounters, we find that Gl 710 also has the largest impulse on the Oort cloud. Using a Galaxy model, we compute the completeness of the Gaia DR2 encountering sample as a function of perihelion time and distance. Only 15% of encounters within 5 pc occurring within ±5 Myr of now have been identified, mostly due to the lack of radial velocities for faint and/or cool stars. Accounting for the incompleteness, we infer the present rate of encounters within 1 pc to be 19.7 ± 2.2 per Myr, a quantity expected to scale quadratically with the encounter distance out to at least several pc. Spuriously large parallaxes in our sample from imperfect filtering would tend to inflate both the number of encounters found and this inferred rate. The magnitude of this effect is hard to quantify.
Key words: Oort Cloud / methods: analytical / methods: statistical / astrometry / solar neighborhood / surveys
Full Tables 2 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/616/A37
© ESO 2018
1. Introduction
The first convincing evidence for relative stellar motion came from Edmund Halley in 1718. Since then – if not well before – people have wondered how close other stars may come to our own. Several studies over the past quarter century have used proper motions and radial velocities to answer this question (Matthews 1994; Mülläri & Orlov 1996; García-Sánchez et al. 1999, 2001; Dybczyński 2006; Bobylev 2010a, b; Jiménez-Torres et al. 2011; Bailer-Jones 2015a; Dybczyński & Berski 2015; Mamajek et al. 2015; Berski & Dybczyński 2016; Bobylev & Bajkova 2017; Bobylev 2017; Bailer-Jones 2018).
Other than being interesting in their own right, close encounters may have played a significant role in the evolution of our solar system, in particular of the Oort cloud. This may also have had implications for the development of life, since a strong perturbation of the Oort cloud by an encountering star could push comets into the inner solar system. An ensuing collision with the Earth could be catastrophic enough to cause a mass extinction. Such a fate probably befell the dinosaurs 65 Myr ago. Studies of stellar encounters and comet impacts on the Earth can also be used to learn about the general hazards for life on exoplanets.
The recent publication of the second Gaia data release (Gaia DR2; Gaia Collaboration 2018) is a boon to encounter studies. It contains six-dimensional (6D) kinematic data – position, parallax, proper motion, and radial velocity – for 7.2 million stars. This is 22 times larger than our previous encounter study using TGAS in the first Gaia data release. Furthermore, TGAS contained no radial velocities, so these had to be obtained by cross matching to external catalogues.
Here we report on results of looking for close encounters in Gaia DR2. Our approach follows very closely that taken by Bailer-Jones (2015a; hereafter paper 1) for HIPPARCOS and Bailer-Jones (2018; hereafter paper 2) for TGAS. The main differences here are:
-
We use only Gaia data. This avoids the complications of having to obtain radial velocities from several different catalogues, which resulted in some data heterogeneity and duplicate sources.
-
Using mass estimates from multiband photometry and Gaia DR2 astrometry in Fouesneau et al. (in prep), we estimate the momentum transfer from an encountering star to Oort cloud comets for essentially every encounter.
-
We account for the incompleteness of our encounter sample by sampling from a self-consistent spatial and kinematic Galaxy model. This is more realistic that the analytic model developed in paper 2.
The main limitation in the number of encounter candidates in this study is still the availability of radial velocities. While Gaia DR2 contains five-parameter astrometry for 1.33 billion stars, only 7.2 million have published radial velocities. These are predominantly brighter than G = 14 mag, and are also limited to the approximate Teff range of 3550 < Teff/K < 6900 (Katz et al. 2018). This is simply the temperature range of the templates used. Teff estimates in Gaia DR2 are described in Andrae et al. 2018.
In Sect. 2 we describe how we select our sample and infer the distribution of the encounter parameters for each candidate. We analyse the results in Sect. 3, discussing new (and dubious) cases, and highlighting disagreement with earlier results. Issues of spurious data and imperfect filtering we discuss in subsections 2.2 and 3.2. In Sect. 4 we introduce the new completeness model and use this to derive the completeness-corrected encounter rate. We conclude in Sect. 5 with a brief discussion.
2. Identification and characterization of close encounters
2.1. Initial selection and orbital integration
We searched the Gaia archive for all stars which would approach within 10 pc of the Sun under the assumption that they move on unaccelerated paths relative to the solar system (the so-called “linear motion approximation”, LMA, defined in paper 1). The archive ADQL query for this is in Appendix A. This yielded 3865 encounter candidates, which we call the unfiltered sample. In both this selection and the orbital integration used later, we estimate distance using inverse parallax rather than doing a proper inference (Bailer-Jones 2015b; Bailer-Jones et al. 2018). This is acceptable here, because for the filtered sample we define later, 95% have fractional parallax uncertainties below 0.08 (99% below 0.14; the largest is 0.35), meaning the simple inversion is a reasonably good approximation.
The Gaia data are used as they are, other than we added 0.029 mas to the parallaxes to accommodate the global parallax zeropoint Lindegren et al. (2018). (Neglecting this would remove 83 sources from the unfiltered sample.) There is no evidence for a proper motion zeropoint offset (Arenou et al. 2018). While there may be a systematic difference between the Gaia radial velocities and other catalogues of up to 0.5 km s−1, the origin of this is unclear (Katz et al. 2018). This is of the order of the gravitational redshifts which are also not corrected for. None of the Gaia uncertainties have been adjusted to accommodate a possible over- or underestimate of their values (e.g. missing RMS systematics).
To get more precise encounter parameters for the set of candidates, we integrated the orbits of the unfiltered sample through a smooth Galactic potential forward and backwards in time. (It was shown in paper 1 that the deviation of an orbit due to perturbations by individual stars can be neglected.) We use the same procedure and model as described in paper 2. The Galactic potential, described in detail in paper 1, is a three-component axisymmetric model. The bar and spiral arms are not included, partly because their properties are not well determined, but mostly because using the same potential as in our previous studies eases comparison of results. As the orbit segments up to encounter are generally short compared to the scale lengths in the model, the exact choice of potential will have only a small impact on the encounter parameters for most stars.
In order to accommodate and propagate the uncertainties in the data, we draw 2000 samples from the 6D covariant probability density function (PDF) over the data – position, parallax, proper motion, and radial velocity – for each star and integrate the orbits of each of these “surrogates” through the potential. The distribution of the perihelion time, distance, and speed over the surrogates for each star is used to characterize the encounter (in the next section). Comparisons of encounter parameters computed with the LMA, orbital integration of the nominal data, and orbital integration of the surrogates were shown in paper 1 and paper 2. Due to the nonlinear transformation from astrometric measurements to perihelion parameters, neglecting the full PDF can lead to erroneous results (and not just erroneous uncertainties), in particular for stars with long travel times.
2.2. Filtering on astrometric solution quality metrics
There are many reasons why astrometric solutions in Gaia DR2 may be “wrong” for some stars, in the sense that the reported uncertainties may not be representative of the true uncertainties. The main reasons are: neglect of accelerated motions (i.e. unseen companions); cross-matching errors leading to the inclusion of observations of other sources (spurious data); a poor correction of the so-called “DOF bug” (see Appendix A of Lindegren et al. 2018). These can lead to erroneous estimates of the quantities or their uncertainties.
Various metrics on the astrometric solution are reported in Gaia DR2 to help identify good solutions. Lindegren et al. (2018) discuss some of these and give an example of a set of cuts which may be used to define a conservative sample, i.e. an agressive removal of poor solutions (e.g. in their Fig. C.2). This is not appropriate for our work, however, because we are looking to determine the encounter rate, not just find the most reliable encounters. While quantiles on the various metrics are easily measured, there is no good model for the expected distribution of these for only non-spurious results. Concepts like “the reduced χ 2 should be about one” are simplistic at best (and statistically questionable), and also don’t tell us whether deviations from this are “wrong” or just have mildly deviant astrometry or slightly underestimated uncertainties. Even a highly significant astrometric excess noise of a few mas may be of little consequence if the parallax and proper motion are large. It is therefore difficult to make a reliable cut. The main quality metric of interest here is the “unit weight error”, defined in Appendix A of Lindegren et al. (2018) as u = (χ2/ν)1/2, where χ2 is the metric astrometric_chi2_al and ν is the degrees of freedom, equal to astrometric_n_good_obs_al−5. For our unfiltered sample, u correlates quite strongly with the astrometric_excess_noise and reasonably well, but less tightly, with astrometric_excess_noise_sig. There is no correlation between u and visibility_periods_used. Figure C.2 of Lindegren et al. (2018) plots u against G. We see u increasing for brighter sources, albeit it with a lot of scatter. The full range of u in our unfiltered sample is 0.63 to 122, and the brighest star in our unfiltered sample (Gaia DR2 5698015743040715264 = rho Puppis) has G = 2.67 mag. This corresponds to u < 35 for the selection in Figure C.2, so we only retain sources with u < 35. This moderately liberal cut reduces the sample size to 3465. Rho Puppis itself has u = 29, astrometric_excess_noise = 2.4 mas, and astrometric_excess_noise_sig = 2458, yet its parallax and proper motion in Gaia DR2 agree with those from HIPPARCOS-2 (van Leeuwen 2007) to within about 2%. A more agressive cut would clearly be removing genuine solutions. To ensure that the astrometric solutions are reasonably overdetermined, we further require that visibility_periods_used is at least 8. According to Arenou et al. (2018), this should help to remove the most spurious proper motions. This cuts the sample down to 3379.
Large uncertainties in the data, provided they are representative of the true uncertainty, are not a problem per se because they are accommodated by the resampling we used to map the PDF of the perihelion parameters. We will also accommodate this PDF when we compute the completeness and encounter rate in Sect. 4. We therefore do not filter out sources due to large uncertainties.
One should be very careful about filtering out extreme values of the data just because they are extreme. Gaia DR2 is known to include sources with implausibly large parallaxes. For example, there are 21 sources with ϖ > 1000 mas (which would place them all nearer than Proxima Centauri). However, as they all have G > 19 mag none of them appear in any of our selections. Other, less extreme, spurious values are impossible to identify without using additional information. Spuriously large proper motions are less of a problem, because close encounter stars generally have relatively small proper motions (unless they are currently very close to encounter). In contrast, stars which come close tend to be those that currently have large radial velocities (compared to their transverse velocities). The radial velocity processing for Gaia DR2 may have produced spuriously large radial velocities (the pipeline can produce values up to ±1000 km s−1). Katz et al. (2018) report they were hard to verify due to the absence of observations of standards with radial velocities larger than 550 km s−1. They further state that the precisions are lower for stars with |νr| > 175 km s−1, but not that the radial velocities themselves are problematic. Moreover, they visually inspected all results with |νr| > 500 km s−1 and removed suspicious results. At this point in the filtering we have only seven stars with |νr| > 500 km s−1, six of which were determined by just two focal plane transits (rv_nb_transits = 2; the minimum for inclusion in Gaia DR2) whereas the median number for this sample is 8. They do not have particularly large uncertainties, because Gaia DR2 only includes stars for which |σ(νr)| < 20 km s−1. It is tempting to filter out stars with a small number of transits, but this also removes valid measurements, such as that for the closest known encounter, Gl 710, which has two transits and a radial velocity consistent with non-Gaia measurements. We do not filter on rv_nb_transits.
We define the remaning set of 3379 stars as the filtered sample. It comprises all stars that approach within 10 pc of the Sun according to the LMA (but not necessarily the orbital integration) and which satisfy the filters u < 35 and visibility_periods_used ≥ 8. When it comes to considering the completeness-corrected encounter rate (Sect. 4.3), we shall further limit this sample to stars with G < 12.5 mag, which contains 2522 stars.
3. Close encounters found in Gaia DR2
We first look at the overall results, then discuss individual stars found approaching within 1 pc, and finally those close encounters from papers 1 and 2 not found in the present study.
3.1. Overall results
The perihelion for each star is described by the distribution of the 2000 surrogates in the perihelion time, tph, distance, dph, and speed νph. The distribution for one particular star is shown in Fig. 1. As in papers 1 and 2 we summarize these using the median, and characterize their uncertainty using the 5th and 95th percentiles (which together form a 90% confidence interval, CI). The number of stars coming within various perihelion distances is shown in Table 1 (see also Fig. 10 later). Summary perihelion data for those stars with 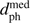 < 1 pc are shown in Table 2 (the online table at CDS reports higher numerical precisions for the whole filtered sample). Negative times indicate past encounters. The magnitude, colour, and quality metrics from Gaia DR2 are shown in Table 3. Some of these encounters we have cause to disregard (discussed later).
< 1 pc are shown in Table 2 (the online table at CDS reports higher numerical precisions for the whole filtered sample). Negative times indicate past encounters. The magnitude, colour, and quality metrics from Gaia DR2 are shown in Table 3. Some of these encounters we have cause to disregard (discussed later).
 |
Fig. 1. Distribution of the perihelion parameters for the 2000 surrogates used to characterize the encounter of Gl 710 = Gaia DR2 4270814637616488064. |
Number of stars in the filtered sample found by the orbit integration to have 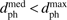 (for any
(for any 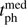 ).
).
Figure 2 plots the perihelion times and distances. (This and other plots do not remove bogus cases.) The stars were selected by the LMA to come within 10 pc of the Sun, but some of the orbit integrations result in much larger median perihelion distances. Similarly, our list will be missing those stars which would have had 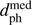 < 10 pc had they been subject to the orbital integration, but were never selected because they had d
ph > 10 pc from the LMA. This latter omission will in principle lead to an underestimate of the derived encounter rate. However, as shown in both papers 1 and 2, this mostly affects stars that will encounter further in the past/future and/or nearer to the edge of the 10 pc distance limit. As stars at such large distances can hardly be considered encountering, we will only be interested in encounters within 5 pc from now on. Moreover, when we later compute the (completeness-corrected) encounter rate, we will limit the sample to a narrower time window.
< 10 pc had they been subject to the orbital integration, but were never selected because they had d
ph > 10 pc from the LMA. This latter omission will in principle lead to an underestimate of the derived encounter rate. However, as shown in both papers 1 and 2, this mostly affects stars that will encounter further in the past/future and/or nearer to the edge of the 10 pc distance limit. As stars at such large distances can hardly be considered encountering, we will only be interested in encounters within 5 pc from now on. Moreover, when we later compute the (completeness-corrected) encounter rate, we will limit the sample to a narrower time window.
 |
Fig. 2. Perihelion times and distances computed by orbit integration for the filtered sample (278 points lie outside the plotting range). Open circles show the median of the perihelion time and distance distributions. The error bars show the limits of the 5% and 95% percentiles. |
The encounters with 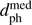 < 5 pc are shown in Fig. 3. We see a strong drop in the density of encounters with increasing |tph|. This is primarily a consequence of the magnitude limit in the sample (95% brighter than G = 13.4 mag): Encounters that would occur further in the past/future generally correspond to stars that are currently more distant, and so more likely to be below the limiting magnitude. The effective time limit of this study is 5–10 Myr. Comparing this with Fig. 3 of paper 2, we see that while Gaia DR2 has found many more encounters than our TGAS study (by a factor of about seven within 5 pc), Gaia DR2 does not allow us to probe much further into the past/future, because of the similar magnitude limits on the samples.
< 5 pc are shown in Fig. 3. We see a strong drop in the density of encounters with increasing |tph|. This is primarily a consequence of the magnitude limit in the sample (95% brighter than G = 13.4 mag): Encounters that would occur further in the past/future generally correspond to stars that are currently more distant, and so more likely to be below the limiting magnitude. The effective time limit of this study is 5–10 Myr. Comparing this with Fig. 3 of paper 2, we see that while Gaia DR2 has found many more encounters than our TGAS study (by a factor of about seven within 5 pc), Gaia DR2 does not allow us to probe much further into the past/future, because of the similar magnitude limits on the samples.
 |
Fig. 3. As Fig. 2, but just showing the 694 stars with |
We also see in Fig. 3 a slight reduction in the density of encounters very close to the present time. (The effect is not quite as strong as first appears, as it is partly an illusion produced by the shorter error bars.) This was also seen with in paper 2, where we argued this was due to two things: missing bright stars in the Gaia catalogue; and the ever smaller volume available for encounters to occur at arbitrarily near times. Both of these apply for Gaia DR2, although we argue later that this is also a consequence of the limited Teff range for stars with radial velocities in Gaia DR2.
The uncertainties in tph and dph are correlated. This can be seen in Fig. 4, where we plot the individual surrogates instead of the summary median and axis-parallel error bars. Each star is generally represented as an ellipsoidal shape pointing roughly towards tph = 0, dph = 0.
 |
Fig. 4. As Fig. 3, but now showing the individual surrogates from the orbital integrations (but just plotting 100 per star rather than all 2000 per star). Surrogates from stars with median perihelion parameters outside the plotting range (and so not shown in Fig. 3) are shown here. |
The perihelion speeds for encounters with 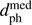 < 5 pc are shown in Fig. 5. 90% have
< 5 pc are shown in Fig. 5. 90% have 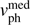 < 100 km s−1. The very fast encounters are almost entirely due to stars with large radial velocities.
< 100 km s−1. The very fast encounters are almost entirely due to stars with large radial velocities.
 |
Fig. 5. Median perihelion velocities from the orbit integrations for those encounters shown in Fig. 3 The velocity axis is a logarithmic scale. |
The masses of the encountering stars are listed in Table 2. The 5th, 50th, and 95th quantiles of the mass distribution over the entire filtered sample are 0.53, 0.91, and 1.64 M⊙ respectively. The lack of massive stars in the sample is a consequence of the Teff filtering on radial velocities published in Gaia DR2.
Perihelion parameters for all stars with a median perihelion distance (median of the samples; 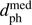 ) below 1 pc, sorted by this value.
) below 1 pc, sorted by this value.
Close encounters are interesting not least because they perturb the Oort cloud. The degree of perturbation, or rather the impulse which comets can receive, depends not only on the distance of the encountering star, but also on its speed and the mass. According to the simple impulse approximation (Öpik 1932; Oort 1950; Rickman 1976; Dybczynski 1994) the impulse transfer is given by 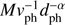 where α is 1 for very close encounters (on the order of the comet–Sun separation), and 2 otherwise. The impulse of the encountering stars is visualized in Figs. 6 and 7 for equal to 1 and 2 respectively. Regardless of which impulse approximation we use, it is the closest encounters which have the greatest impact.
where α is 1 for very close encounters (on the order of the comet–Sun separation), and 2 otherwise. The impulse of the encountering stars is visualized in Figs. 6 and 7 for equal to 1 and 2 respectively. Regardless of which impulse approximation we use, it is the closest encounters which have the greatest impact.
3.2. Colour-magnitude diagram
Figure 8 shows the colour-absolute magnitude diagram (CMD) for the close encounters on the assumption of zero interstellar extinction. The upper panel shows the 26 non-bogus encounters with 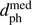 < 1 pc from Table 2. Eleven of these have unit weight error u > 10 (the others have u < 2) and lie some way below and left of the main sequence (MS), yet well above the white dwarf (WD) sequence. The dimensionless quantity u measures how well the five-parameter solution describes the astrometric data (see Sect. 2.2). If we assumed that all the encounters were single main sequence stars, then one interpretation of this diagram is that the parallaxes of these 11 sources are wrong; specifically that they are all overestimated by one or two orders of magnitude (i.e. the sources should be much further away). This seems unlikely, although it is the case that a search for encounters will preferentially include sources with spuriously large parallaxes rather than sources with spuriously small parallaxes (because the former are more likely to have apparent close encounters). As we see a smaller proportion of sources between the MS and WDs among nearby stars (blue points in Fig. 8), it at first seems unlikely that we would get such a large proportion of such sources among the closest encounters (upper panel). The magnitude of this selection effect is impossible to estimate without knowing which parallaxes are actually spurious. On the other hand, if we look instead at all encounters (lower panel), then we find that just 14% of all encounters within the plotted range lie below the MS, whereas this figure is 24% for the nearby stars. In other words, there is in fact a decreased tendency for encounters to be below the MS compared to nearby stars. This comparison is not ideal, however, because some of these nearby stars are WDs – essentially absent from the encountering sample due to the magnitude limit – and the encounters are drawn from a much larger volume.
< 1 pc from Table 2. Eleven of these have unit weight error u > 10 (the others have u < 2) and lie some way below and left of the main sequence (MS), yet well above the white dwarf (WD) sequence. The dimensionless quantity u measures how well the five-parameter solution describes the astrometric data (see Sect. 2.2). If we assumed that all the encounters were single main sequence stars, then one interpretation of this diagram is that the parallaxes of these 11 sources are wrong; specifically that they are all overestimated by one or two orders of magnitude (i.e. the sources should be much further away). This seems unlikely, although it is the case that a search for encounters will preferentially include sources with spuriously large parallaxes rather than sources with spuriously small parallaxes (because the former are more likely to have apparent close encounters). As we see a smaller proportion of sources between the MS and WDs among nearby stars (blue points in Fig. 8), it at first seems unlikely that we would get such a large proportion of such sources among the closest encounters (upper panel). The magnitude of this selection effect is impossible to estimate without knowing which parallaxes are actually spurious. On the other hand, if we look instead at all encounters (lower panel), then we find that just 14% of all encounters within the plotted range lie below the MS, whereas this figure is 24% for the nearby stars. In other words, there is in fact a decreased tendency for encounters to be below the MS compared to nearby stars. This comparison is not ideal, however, because some of these nearby stars are WDs – essentially absent from the encountering sample due to the magnitude limit – and the encounters are drawn from a much larger volume.
 |
Fig. 8. Colour–magnitude diagram for stellar encounters coloured according to the unit weight error u in Table 3. The vertical axis equals MG assuming extinction is zero. For orientation, the grey lines are unreddened solar metallicity PARSEC isochrones for 1 Gyr (solid) and 10 Gyr (dashed) from Marigo et al. (2017), the grey points are white dwarfs within 20 pc of the Sun identified by Hollands et al. (2018) (many lie outside the range of the plot), and the small blue dots show all sources in Gaia DR2 with ϖ > 50 mas (plotted on the bottom layer, so most are obscured by coloured and grey points, especially in the lower panel). The upper panel shows all reliable (non-bogus) encounters with |
We noted in Sect. 2.2 that a large value of u does not mean the parallax is wrong. Indeed, a relatively poor fit of the five-parameter solution is in principle expressed by larger values of the astrometric uncertainties (and these are quite correlated with u). Here, the 11 sources in the upper panel of Fig. 8 have σ(ϖ) between 0.5 and 1.1 mas, whereas the other 15 have σ(ϖ) < 0.06 mas. We have already accommodated the uncertainties in the identification of the close encounters. Furthermore, although the parallax uncertainties are larger, they produce uncertainties in the absolute magnitude of no more than 0.08 mag, which is smaller than the size of the points plotted in Fig. 8. Contamination of the astrometric solution by nearby (sub-arcsecond) sources is possible, and although most of the sources are near to the Galactic plane (as are unquestioned sources), they are all bright, so less likely to be affected by crowding. Visual inspection of non-Gaia images of these targets shows no obvious contaminants. They do generally have fewer visibility periods in the solutions, however: 9, 10, or 11, as opposed to 8–18 for the sources lying near the main sequence.
Given their location in the CMD, it is possible that some or all of these 11 sources are subdwarfs or MS-WD binaries. The latter, of which many have been discovered (e.g. Rebassa-Mansergas et al. 2016), can in principle lie in much of the region between the MS and WD sequence. Such binarity could potentially explain elevated values of u, although only if the periods were short enough and the amplitudes large enough to be detectable over Gaia DR2’s 22-month baseline. Even then the parallax should be reasonably accurate, because the different astrometric displacements at different times should not create a large bias (Lennart Lindegren, private communication). Furthermore, four of the 11 sources have much larger radial velocity uncertainties than the other encounters in Table 2 (>14 km s−1 as opposed to <6 km s−1). As this uncertainty is computed from the standard deviation of measurements at different epochs (Eq. (1) of Katz et al. 2018), this could be an indication of binarity.
In conclusion, the correlation of the CMD location with u is suspicious, and would be consistent with a selection effect that preferentially includes spuriously large parallaxes in a search for stellar encounters. On the other hand, we do not have specific evidence to claim that these stars have spurious solutions or unaccounted for errors, and it is quite possible that some or all are MS-WD binaries. Spectroscopy may help identify the nature of these sources, and astrometry over a longer timebase (e.g. from Gaia DR3) should help to determine if the astrometric solutions are good.
3.3. Individual encounters found to be coming within 1 pc
We find 31 stars with 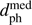 < 1 pc. All have been visually checked against 2MASS, DSS, PS1, and AllWISE images in Aladin and all are confirmed as real sources. Some have moderately high values of u, astrometric_excess_noise and/or astrometric_excess_noise_sig, as can be seen in Table 3. Only one of the encounters has been discovered by the previous studies listed in the introduction. 21 do not have HIPPARCOS or Tycho IDs, so could not have been discovered in papers 1 or 2. Of the remaining nine stars, seven have obvious Tycho matches but were not found in paper 2 for reasons discussed below. The last two stars are problematic and are also discussed below.
< 1 pc. All have been visually checked against 2MASS, DSS, PS1, and AllWISE images in Aladin and all are confirmed as real sources. Some have moderately high values of u, astrometric_excess_noise and/or astrometric_excess_noise_sig, as can be seen in Table 3. Only one of the encounters has been discovered by the previous studies listed in the introduction. 21 do not have HIPPARCOS or Tycho IDs, so could not have been discovered in papers 1 or 2. Of the remaining nine stars, seven have obvious Tycho matches but were not found in paper 2 for reasons discussed below. The last two stars are problematic and are also discussed below.
The closest approaching star, and the only one to have been found already, is Gaia DR2 4270814637616488064, better known as Gl 710 (Tyc 5102-100-1, Hip 89825). This is a K7 dwarf known from many previous studies to be a very close encounter. In paper 1 we found a median encounter distance of 0.267 pc (90% CI 0.101–0.444 pc). A much smaller – and more precise – proper motion measured by TGAS gave a closer encounter, with a median distance of 0.076 pc (90% CI 0.048–0.104 pc) (paper 2 and Berski & Dybczyński 2016). Gaia DR2 has slightly decreased this distance – 0.0676 pc (13 900AU) – and has narrowed the uncertainty – 90% CI 0.0519–0.0842 pc (10 700–17 400AU) – although this is statistically consistent with the TGAS result. This is well within the Oort cloud. Due to the slightly more negative radial velocity published in Gaia DR2 than used in the earlier studies, the encounter time is slightly earlier (but no more precisely determined). We note, however, that the radial velocity in Gaia DR2 comes from just two Gaia focal plane transits, the minimum for a value to be reported in the catalogue. Despite its low mass, Gl 710 imparts the biggest impulse according to either impact approximation (Figs. 6 and 7), in part because of its low velocity. Using the same data, de la Fuente Marcos & de la Fuente Marcos (2018) get a slightly closer mean (and median) distance of 0.052 pc (with a symmetric standard deviation of 0.010 pc). Their estimate is close to what one gets for a constant gravitational potential, namely 0.0555 pc (computed by propagating the set of surrogates using the LMA and taking the mean). This suggests they used a very different potential from ours. Note that ignorning the parallax zeropoint and/or ignoring the astrometric correlations changes the estimate by less than 0.0001 pc, so these are not the cause of the difference.
The second closest approach in Table 2, Gaia DR2 955098506408767360, is also the one with the second largest impulse. It is one of the most massive of the closest encounters, with a perihelion in the relatively recent past. Four fainter 2MASS sources lie within 8″, but there is no good reason to think these have interfered with the Gaia solution. The most recent reliable encounter in the table is Gaia DR2 3376241909848155520, which has a 50% chance of having passed within 0.5 pc, around 450 kyr ago.
Among the 21 sources without Tycho matches, most have matches to 2MASS (and a couple of others to other surveys). A few of these are in very crowded regions (e.g at low Galactic latitude) and have close companions, but in all but one case these companions are much fainter, and there is no specific evidence to suggest a problem with the Gaia measurements. The one exception is Gaia DR2 5700273723303646464, which has a companion 4″ away that is just 1.6 mag fainter in the J-band (the best match to this in Gaia DR2 is 0.7 mag fainter in the G band, and has a completely different parallax and proper motion). This is a borderline case. Its measurements are not suspicious, but some of the quality metrics make it questionable. We decide to flag this as bogus.
There are seven encounters with obvious Tycho matches that were not found as encounters in paper 2, either because they lacked a radial velocity, or because their astrometry has changed substantially from TGAS to Gaia DR2. These are as follows (with notes on the problematic cases).
-
Gaia DR2 510911618569239040 = TYC 4034-1077-1.
-
Gaia DR2 154460050601558656 = TYC 1839-310-1. This is rather faint, G=15.37 mag, and has a rather high radial velocity based on just 3 transits. It also has no BP-RP colour and a large astrometric_excess_noise_sig of 360, so we consider this encounter to be bogus.
-
Gaia DR2 1791617849154434688 = TYC 1662-1962-1.
-
Gaia DR2 1949388868571283200 = TYC 2730-1701-1. The large radial velocity is based on just two transits, so we consider this to be bogus.
-
Gaia DR2 3972130276695660288 = TYC 1439-2125-1 = GJ 3649.
-
Gaia DR2 2926732831673735168 = TYC 5960-2077-1.
-
Gaia DR2 2929487348818749824 = TYC 5972-2542-1.
The final two sources have ambiguous matches. Simbad lists four objects within 5″ of Gaia DR2 5231593594752514304 (G = 12.03 mag), although in reality these four are probably just two or three unique sources. Gaia DR2 itself identifies one of these as Gaia DR2 5231593599052768896, which with G = 9.12 mag is almost certainly Hip 53534 with V = 9.21 mag. Whichever other star our close encounter is, its RVS spectrum is surely contaminated by this much brighter star just a few arcseconds away, suggesting that the whoppingly large radial velocity of −715 km s−1 measured by RVS is in fact spurious. We therefore consider this encounter to be bogus.
Finally, Gaia DR2 939821616976287104 would appear to match with TYC 2450-1618-1. However the 2MASS image clearly shows this to be a double star, and this surely has contaminated the RVS spectrum. In that case we do not trust the high radial velocity reported (568 km s−1) and conservatively consider this to be a bogus encounter too.
3.4. Individual encounters coming within 1 pc in papers 1 and 2, but not found in the present study
In paper 2 we found two stars with 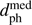 < 1 pc, one of which was Gl 710, discussed above. The other was Tyc 4744-1394-1 which is in Gaia DR2 but without a radial velocity. The astrometry is consistent with that from TGAS, confirming the reality of that encounter also.
< 1 pc, one of which was Gl 710, discussed above. The other was Tyc 4744-1394-1 which is in Gaia DR2 but without a radial velocity. The astrometry is consistent with that from TGAS, confirming the reality of that encounter also.
In paper 1 we found 14 stars coming within 1 pc. One was Gl 710. The other 13 are not found in the present study for various reasons. We briefly discuss each of these cases. The match in Gaia DR2 was found by searching for sources within about 30″ using Simbad, and identifying the one with the closest magnitude. In all cases but one the match was unambiguous, and in none of these is there anything to suggest the Gaia DR2 data are problematic.
Hip 85605. This was the closest encounter found in paper 1 at 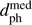 = 0.103 pc (90% CI 0.041–0.205 pc). It was deemed dubious due to the inconsistency of its magnitude and HIPPARCOS parallax with its apparent spectral type. This suspicion is confirmed with Gaia DR2, which has a much smaller parallax of 1.822 ± 0.027 mas compared to 146.84 ± 29.81 in HIPPARCOS-2 (the proper motions and radial velocities are consistent within 1σ). This now places the closest approach at 420 pc. It was conjectured in paper 1 that the cause for the incorrect parallax is a binary companion at a very problematic separation for the HIPPARCOS detectors.
= 0.103 pc (90% CI 0.041–0.205 pc). It was deemed dubious due to the inconsistency of its magnitude and HIPPARCOS parallax with its apparent spectral type. This suspicion is confirmed with Gaia DR2, which has a much smaller parallax of 1.822 ± 0.027 mas compared to 146.84 ± 29.81 in HIPPARCOS-2 (the proper motions and radial velocities are consistent within 1σ). This now places the closest approach at 420 pc. It was conjectured in paper 1 that the cause for the incorrect parallax is a binary companion at a very problematic separation for the HIPPARCOS detectors.
Hip 63721. Its best match, Gaia DR2 1459521872495435904, has a parallax of 5.99 ± 0.04 mas, compared to 216.62 ± 56.53 mas in HIPPARCOS. This HIPPARCOS solution was doubted in paper 1 on the grounds of inconsistency with spectral type and it being a double star.
Hip 91012. The parallax and proper motion of its best match, Gaia DR2 4258121978471892864, are consistent with HIPPARCOS, but the Gaia DR2 radial velocity is now much smaller, at −16.27 ± 0.61 km s−1, compared to the RAVE value of −364.1 ± 22.4 adopted in paper 1.
Hip 23311. This matches to Gaia DR2 3211461469444773376. It is a high proper motion (>1000 mas yr−1) nearby (113 mas) star – Gaia DR2 and HIPPARCOS agree – but the Gaia DR2 radial velocity is much smaller: 21.38 ± 0.15 km s−1 compared to the implausibly large value of −813.7 ± 48.6 from RAVE that led it to being flagged as dubious in paper 1.
Hip 85661. The parallax and radial velocity used in paper 1 agree with the best match star, Gaia DR2 4362793767434602752, but the Gaia DR2 proper motion is much larger (8.5 ± 0.2 mas yr−1 versus 0.5 ± 0.6 mas yr−1), meaning it no longer comes near to the Sun.
Hip 55606. The proper motion of its best match, Gaia DR2 3590767623539652864, is consistent with HIPPARCOS (parallax less so), but the Gaia DR2 radial velocity is now much smaller, at −18.12 ± 0.70 km s−1, compared to the implausibly large value of −921.0 ± 91.9 from RAVE that led it to being flagged as dubious in paper 1.
Hip 75159. Its counterpart, Gaia DR2 6251546901899531776, has no radial velocity in Gaia DR2. The Gaia DR2 astrometry agrees within 2σ of the HIPPARCOS astrometry (which was rather imprecise, with a proper motion consistent with zero). Using the (large) RAVE radial velocity of 368 km s−1 from paper 1 with the Gaia DR2 astrometry, the LMA gives a closest approach of 2.1 pc 660 kyr in the past.
Hip 103738 (gamma Microscopii). This G6 giant was the potentially most massive encounter coming within 1 pc in paper 1, found to have 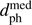 = 0.83 pc (90% CI 0.35–1.34 pc) based on the HIPPARCOS-2 proper motion of 1.78 ± 0.35 mas yr−1. (A second entry in the catalogue based on the larger Tycho-2 proper motion put it at 3.73 pc; 90% CI 2.28–5.22 pc) This star is Gaia DR2 6781898461559620480 with G = 4.37 mag. The proper motion in Gaia DR2 is ten times (17σ) larger, 17.7 ± 0.9 mas yr−1, with no suggestion from the quality metrics that this is a poor solution. (Both the parallaxes and radial velocities agree to within 1σ.) Either there is a significant, unaccounted for acceleration, or the proper motion in HIPPARCOS-2 or Gaia DR2 (or both) is wrong. Using the Gaia DR2 data we find the encounter to be at
= 0.83 pc (90% CI 0.35–1.34 pc) based on the HIPPARCOS-2 proper motion of 1.78 ± 0.35 mas yr−1. (A second entry in the catalogue based on the larger Tycho-2 proper motion put it at 3.73 pc; 90% CI 2.28–5.22 pc) This star is Gaia DR2 6781898461559620480 with G = 4.37 mag. The proper motion in Gaia DR2 is ten times (17σ) larger, 17.7 ± 0.9 mas yr−1, with no suggestion from the quality metrics that this is a poor solution. (Both the parallaxes and radial velocities agree to within 1σ.) Either there is a significant, unaccounted for acceleration, or the proper motion in HIPPARCOS-2 or Gaia DR2 (or both) is wrong. Using the Gaia DR2 data we find the encounter to be at 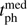 = − 3440 kyr (90% CI −3630 to −3260 kyr),
= − 3440 kyr (90% CI −3630 to −3260 kyr), 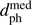 = 20.3 pc (90% CI 18.0–22.9 pc).
= 20.3 pc (90% CI 18.0–22.9 pc).
Hip 71683 (α Centauri A). This is not in Gaia DR2 on account of its brightness.
Hip 71681 (α Centauri B). This is not in Gaia DR2 on account of its brightness.
Hip 70890 (Proxima Centauri). This is Gaia DR2 5853498713160606720. It has no radial velocity in Gaia DR2, but the parallax and proper motion agree with HIPPARCOS to within 2σ. Given their high precision, the perihelion parameters using the new astrometry together with the old radial velocity are consistent with the result in paper 1 (now more precise).
Hip 3829 (van Maanen’s star). This is Gaia DR2 2552928187080872832. It has no radial velocity in Gaia DR2, but the parallax and proper motion agree with HIPPARCOS to better than 1σ. Given their high precision, the perihelion parameters using the new astrometry with the old radial velocity are consistent with the result in paper 1 (now more precise).
Hip 42525. Two Gaia DR2 sources with the same parallax, proper motion, and radial velocity as each other (within their uncertainties) match this. They are Gaia DR2 913394034663258752 and Gaia DR2 913394034663259008. The proper motion and radial velocity agree with the data used in paper 1, but the Gaia DR2 parallax of 6.1 ± 0.8 mas is quite different from the HIPPARCOS-2 value of 68.5 ± 15.5 mas adopted in paper 1. It was noted in that paper, however, that the HIPPARCOS-2 parallax was almost certainly corrupted by a close companion, and that the HIPPARCOS-1 solution of 5.1 ± 4.3 mas was more plausible. This value is in fact consistent with the new Gaia DR2 one, which is five times more precise. It is (they are) no longer a close encounter.
4. Completeness correction and the encounter rate
4.1. Principle of the completeness model
Gaia DR2 does not identify all encounters, primarily because of its faint-end magnitude limit for radial velocities. To compute an encounter rate over a specified time and distance window we must correct for this. This was done in paper 2 using a simple analytic model. Although insightful and easy to work with, that model made severe assumptions of isotropic spatial and homogeneous velocity distributions. Here we take the same conceptual approach to building a completeness map, but replace the analytic model with a more realistic Galaxy simulation, in which the spatial and kinematic distributions are also self-consistent. We first simulate the positions and velocities of all stars in the nearby Galaxy (“mock full Galaxy”), and trace the orbits backwards and forwards in time (with LMA) to determine the distribution of encounters in perihelion coordinates. Call this Fmod(tph, dph), the number of encounters per unit perihelion time and distance. We then repeat this including only the stars which would have full 6D kinematic information in Gaia DR2 (“mock Gaia-observed Galaxy”), then trace orbits to give Fexp(tph, dph). The ratio of these two distributions gives the completeness map, C(tph, dph), which can be interpreted as the fraction of encounters at a specific perihelion time and distance that will actually be observed (in our sample).
4.2. The model
To generate our mock full Galaxy we use Galaxia (Sharma et al. 2011) to sample stars following a Besancon-like (Robin et al. 2003) model distribution of the Galaxy, in a similar way to how we generated the mock Gaia DR2 catalogue described in Rybizki et al. (2018). The main difference is that we now apply no magnitude cut, but instead a distance cut, to keep the computations manageable. We use 3 kpc, as only stars with radial velocities above 200 km s−1 would reach the Sun within 15 Myr. (Our final completeness-corrected encounter rate only uses the model out to 5 Myr, so only mock stars beyond 3 kpc with radial velocities above 600 km s−1 will be neglected.) We checked on a subsample of the data that increasing this limit to 10 kpc made negligible difference to the distribution of encounters. We then computed the perihelion parameters of all stars using the LMA. Although the LMA is not an accurate model for long paths in the Galaxy, the inaccuracy introduced by this for the distribution as a whole will be small. The impact is further diminished given that we are ultimately interested only in the ratio of the two encounter distributions from these two models.
Figure 9 shows the positions in perihelion parameter space of individual stars from the sampled mock full Galaxy. The density of encounters shows essentially no dependence on tph over the range shown. This is different from what was found from the model in paper 2 which showed a drop off to large |tph|. This was in part due to the spatial distribution adopted (and its inconsistency with the velocity distribution adopted). In the present model we also do not see the drop in density towards tph = 0. The encounter density in Fig. 9 does show a strong dependency on dph. Closer inspection shows that the number of encounters per unit distance varies linearly with dph, i.e. the number of encounters within dph varies as 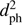 . This is what the simple model in paper 2 predicts (see Sect. 4.2 of that paper, which also explains why it does not vary as
. This is what the simple model in paper 2 predicts (see Sect. 4.2 of that paper, which also explains why it does not vary as 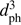 , as one may initially expect). To construct the completeness map we therefore replace the 2D distribution in Fig. 9 with a 1D distribution Fexp(tph, dph) = a dph, where the constant a is fit from the simulated data. The distribution of the real encounters also shows this linear variation out to several pc, as shown in Fig. 10.
, as one may initially expect). To construct the completeness map we therefore replace the 2D distribution in Fig. 9 with a 1D distribution Fexp(tph, dph) = a dph, where the constant a is fit from the simulated data. The distribution of the real encounters also shows this linear variation out to several pc, as shown in Fig. 10.
 |
Fig. 9. Perihelion times and distances for star samples from the mock full Galaxy (no Gaia selection). Each star is represented by a single sample. |
 |
Fig. 10. Variation of the number of observed encounters per unit perihelion distance as a function of perihelion distance (for the filtered sample for all tph). The open circles count the encountering stars discretely, using |
To produce the mock Gaia-observed Galaxy we query the mock catalogue of Rybizki et al. (2018) using the following ADQL query
SELECT parallax, pmra, pmdec, radial_velocity
FROM gdr2mock.main
WHERE phot_g_mean_mag <= 12.5
AND teff_val > 3550 AND teff_val < 6900
The Teff limit simulates the limit on the radial velocities published in Gaia DR2 (Katz et al. 2018), and the magnitude limit is the selection we will apply to the observed encounter sample to compute the completeness-corrected encounter rate below. We do not specifically account for the incompleteness at the bright end in Gaia DR2 because it is poorly defined. There are so few bright stars in the model that this is anyway a minor source of error. This above query delivers 4.4 million stars. (As a comparison, the number of stars in Gaia DR2 with complete 6D kinematic data brighter than G = 12.5 mag is 3.6 million.)
Given the nonlinear relationship between the 6D kinematic data and the perihelion parameters for a star, symmetric (Gaussian) errors in the former can lead to asymmetric distributions in the latter. In other words, measurement errors in the real Gaia observations can lead to stars being preferentially scattered into or out of some part of the perihelion parameter space. We accommodate this in our model by replacing each star in the mock Gaia-observed Galaxy with a set of 100 noise-perturbed samples generated using a simple error model. For this we use a 4D-Gaussian PDF (the Gaia-uncertainties on RA and Declination are negligible), with the following standard deviations, obtained from inspection of the Gaia DR2 uncertainties shown in Lindegren et al. (2018): σ(ϖ) = 0.068 mas; σ(μα*) = 0.059 mas yr−1; σ(μδ) = 0.041 mas yr−1; σ(νr) = 0.8 km s−1. We neglect correlations as there is no reliable model for these. Just as was done with the surrogates for the real data, the orbits of each of the samples are traced (but here using LMA rather than a potential).
Figure 11 shows the resulting positions in perihelion parameter space of the samples from the mock Gaia-observed Galaxy. In principle this is a model for the observations shown in Fig. 4. They are not the same due to shot noise, imperfect modelling of the (complex) Gaia DR2 selection function, and in particular the fact that Galaxia is not an exact model of our Galaxy. A particular difference is that the mock catalogue shows more encounters at larger perihelion times. There are several possible causes for this. One possibility is differing velocity distributions: if stars in the mock catalogue were generally slower, then the most distant visible stars would arrive at larger perihelion times. An identical reproduction of the observational distribution is not necessary, however, because the completeness is dependent primarily on the change from the mock full Galaxy to the mock Gaia-observed Galaxy.
 |
Fig. 11. Perihelion times and distances for star samples from the mock Gaia-observed Galaxy. Each star is represented by 100 samples. This is just a window on a much larger set of encounters, so includes samples of stars which are predominantly outside the range shown (e.g. the median perihelion position is outside). |
As an aside, we can use the mock Gaia-observed simulation to try to explain features in the observed perihelion distribution (e.g. Fig. 3). In particular, the gap at small |tph| might be explained by the Teff cut. This cut removes cool M dwarfs, which are also intrinsically faint. To be observable now, they must therefore be relatively near, in which case they will all encounter relatively soon (past or future). M dwarfs are highly abundant, so would dominate the encounters at small |tph|. Yet they have been removed by the Teff cut. A similar argument in principle also applies to the brightest stars – many of which are bright because they are close by, and thus near to encounter now – which are also missing in Gaia DR2, but these are fewer, so their net contribution is smaller.
We can now build the completeness map. We bin the distribution in Fig. 11, and divide by the number of samples, to get a binned distribution of the (fractional) number of encountering stars per bin. We then divide this by the expected (continuous) distribution from the mock full Galaxy, which was just Fexp(tph, dph) = a dph, to give our completeness map. This is shown in Fig. 12. The map was computed and fitted over the range −15 to +15 Myr and 0 to 10 pc to improve the fit to Fexp(tph, dph) (by reducing the shot noise), but is only shown over a smaller dph range (and will only be used over a narrower tph range too). The completeness ranges between nearly zero and 0.48, with an average value (over the bins) of 0.09 for |tph| < 10 Myr and 0.14 for |tph| < 5 Myr. The binning of Fig. 11 resulted in some cells with no encounters, which would lead to zero completeness (and thus a divide-by-zero when we come to use it). We overcame this by replacing zero-valued cells with the mean of their neighbours. We experimented with producing a smoother map via kernel density estimation or fitting a smoothing spline, but the results were too sensitive to the fitting parameters and suffered from edge effects (which could be mitigated by expanding the grid, but at the expense of sensitivity to low completeness values at larger times).
 |
Fig. 12. The completeness map, C(tph, dph), which can be interpreted as the probability of observing an encounter in the selected Gaia DR2 sample as a function of its perihelion time and distance. “Selected” here means for G < 12.5 mag in the filtered sample. |
4.3. An estimate of the encounter rate
If a star is observed to be encountering at position tph, dph, then the completeness-corrected (fractional) number of encounters corresponding to this is simply 1/C(tph, dph). When each star is instead represented by a set of Nsur surrogates, the completenesses at which are {Ci}, the completeness-corrected number of encounters is
This same expression applies when we have a set of stars represented by surrogates over some range (“window”) of tph and dph with corresponding completenesses {Ci}. Nsur is still the number of surrogates per stars. ncor is then the completeness-corrected number of encounters in the window.
Random errors in ncor come from two main sources: (i) Poisson noise from the finite number of encounters observed; (ii) noise in the completeness map. The first source is easily accommodated. The fractional number of encounters observed in a window, nenc, is just the sum of the fraction of all surrogates per star which lie in that window. The signal-to-noise ratio in this is 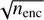 , so the standard deviation in ncor due to this alone would be ncor/
, so the standard deviation in ncor due to this alone would be ncor/ 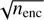 . This does not include any noise due arising from the original sample selection (e.g. from changes in the filtering). The second source can be treated with a first order propagation of errors in Eq. (1)
. This does not include any noise due arising from the original sample selection (e.g. from changes in the filtering). The second source can be treated with a first order propagation of errors in Eq. (1)
In practice it is difficult to determine δCi. We have experimented with varying the approach to constructing the completeness map. We approximate the uncertainties arising thereby as a constant fractional uncertainty of fc = δCi/Ci = 0.1. In that case Eq. (2) can be written δncor = fcncor. Combining this with the Poisson term for (i) we may approximate the total random uncertainty in ncor as
To compute nenc we use just the filtered encounter sample with G < 12.5 mag – 2522 stars – as this is what was also used to build the completeness model. We do not remove bogus encounters, as their number is small. (Identifying them is a laborious, manual process that we have only done for the 31 encounters out to 1 pc.) Within the window |tph| < 5 Myr, dph < 5 pc we have nenc = 463.4 (the sum in Eq. 1 is over 926 736 surrogates), which is an uncorrected rate of 46 encounters per Myr within 5 pc. This compares to 639 stars with 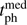 and
and 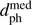 in this range (i.e. neglecting the uncertainties gives an uncorrected rate of 64 stars per Myr within 5 pc.) Applying the completeness correction as outlined above yields ncor = 4914 ± 542 encounters, which corresponds to 491 ± 54 encounters per Myr within 5 pc. We could calculate the corrected rates for smaller upper limits on dph, but such results are sensitive to the use of fewer bins in the completeness map and are more affected by the scattering of the surrogates. We instead scale the value found for 5 pc using the expectation that the number of encounters within some distance grows quadratically with distance. (Figure 10 shows that out to 5 pc the scaling is as expected, unaffected by the drop-off near to 10 pc.) This gives encounter rates of 78.6 ± 8.7 per Myr within 2 pc, and 19.7 ± 2.2 per Myr within 1 pc. We adopt these as our final encounter rates.
in this range (i.e. neglecting the uncertainties gives an uncorrected rate of 64 stars per Myr within 5 pc.) Applying the completeness correction as outlined above yields ncor = 4914 ± 542 encounters, which corresponds to 491 ± 54 encounters per Myr within 5 pc. We could calculate the corrected rates for smaller upper limits on dph, but such results are sensitive to the use of fewer bins in the completeness map and are more affected by the scattering of the surrogates. We instead scale the value found for 5 pc using the expectation that the number of encounters within some distance grows quadratically with distance. (Figure 10 shows that out to 5 pc the scaling is as expected, unaffected by the drop-off near to 10 pc.) This gives encounter rates of 78.6 ± 8.7 per Myr within 2 pc, and 19.7 ± 2.2 per Myr within 1 pc. We adopt these as our final encounter rates.
In paper 2, using TGAS and an analytic completeness correction, we derived an encounter rate within 5 pc of 545 ± 59 per Myr (which scales to 21.8 ± 2.4 per Myr within 1 pc). This is consistent with what we find here. García-Sánchez et al. (2001) obtained a rate of 11.7 ± 1.3 per Myr within 1 pc using HIPPARCOS. Possible reasons for this discrepancy are discussed in paper 2.
Choosing a smaller time window, |tph| < 2.5 Myr and dph < 5 pc, we have nenc = 319.4 and a completeness-corrected encounter rate of 373 ± 44 per Myr within < 5 pc. This is 1.5σ times smaller than that obtained with the larger time window. This may suggest some time variability in the encounter rate, although this is hard to distinguish given the difficulty of propagating all the uncertainties. It is also clear that Eq. 1 is rather sensitive to small values of the completeness. Over the window |tph| < 5 Myr and dph < 5 pc, 3462 of the 926736 surrogates (0.4%) have Ci < 0.01. It is an unfortunate and unavoidable fact that it is the low completeness regions which contribute the largest uncertainty to any attempt to correct the encounter rate.
5. Conclusions
We have identified the closest stellar encounters to the Sun from among the 7.2 million stars in Gaia DR2 that have 6D phase space information. Encounters were found by integrating their orbits in a smooth gravitational potential. The correlated uncertainties were accounted for by a Monte Carlo resampling of the 6D likelihood distribution of the data and integrating a swarm of surrogate particles. The resulting distributions over perihelion time, distance, and speed are generally asymmetric, and are summarized by their 5th, 50th, and 95th percentiles.
We find 31, 8, and 3 stars which have come – or which will come – within 1 pc, 0.5 pc, and 0.25 pc of the Sun, respectively. These numbers drop to 26, 7, and 3 when we remove likely incorrect results (“bogus encounters”) following a subjective analysis (including visual inspection of images). Quality metrics in the Gaia catalogue are not calibrated and are hard to use to identify sources with reliable data. Thus some of the stars in our encounter list are sure to be bogus, and we are sure to have missed some others for the same reason. In particular, a number of encounters with unexpected positions in the CMD have large values of the astrometric unit weight error. These are not necessarily poor astrometric solutions. At least some could be main sequence-white dwarf binaries.
The closest encounter found is Gl 710, long known to be a close encounter, now found to come slightly closer and with slightly better determined perihelion parameters. Most of the other encounters found are discovered here, including 25 within 1 pc. Using newly available masses for 98% of the sample computed by Fouesneau et al. (in preparation) from Gaia astrometry and multiband photometry, we compute the impulse transfer to the Oort cloud using the impulse approximation. For both the 1/dph or 1/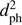 dependencies, Gl 710 induces the largest impulse. Berski & Dybczyński (2016) studied the impact of this star on the Oort cloud in some detail using the encounter parameters from the first Gaia data release. They found that it would inject a large flux of Oort cloud comets toward the inner solar system. Given that the encounter parameters are not significantly changed in Gaia DR2, this conclusion still holds. It remains to be studied what the cumulative effect is of the many more encounters found in our study.
dependencies, Gl 710 induces the largest impulse. Berski & Dybczyński (2016) studied the impact of this star on the Oort cloud in some detail using the encounter parameters from the first Gaia data release. They found that it would inject a large flux of Oort cloud comets toward the inner solar system. Given that the encounter parameters are not significantly changed in Gaia DR2, this conclusion still holds. It remains to be studied what the cumulative effect is of the many more encounters found in our study.
The main factors limiting the accuracy of our resulting perihelion parameters are: for most stars, the accuracy of the radial velocities; for distant stars, the accuracy of our potential model; and for some stars, the neglect of possible binarity.
Our sample is not complete. The main limitation is the availability of radial velocities in Gaia DR2. 99% of the stars (whether in the unfiltered or filtered sample) are brighter than G = 13.8 mag. Published radial velocities are also limited to stars in the approximate Teff range 3550–6900 K, thereby limiting the number of (numerous) late-type stars as well as massive stars. Both Teff and G should be extended in subsequent Gaia data releases. Correcting for this incompleteness using a model based on the Galaxia simulation, we infer the encounter rate averaged over the past/future 5 Myr to be 491 ± 54 Myr−1 within 5 pc. When scaled to encounters within 1 pc, this is 19.7 ± 2.2 Myr−1. We caution, however, that the accuracy of this rate is limited by the completeness model assumptions and fitting the resulting completeness map, as well as the distribution of the actual encounters. It may also be overestimated if there is a large fraction of sources with spuriously large parallax values that are not accounted for by their formal uncertainties.
The other source of incompleteness is missing bright stars in Gaia DR2. Bright stars saturate even with the shortest CCD gate on Gaia, making them harder to calibrate. Astrometry for these will only be provided in later data releases. Although few in number (and therefore acceptably neglected by our completeness correction), some bright stars are currently nearby and/or massive, so encounter parameters more accurate than those obtained with HIPPARCOS could ultimately reveal some important encounters. The case of gamma Microscopii – no longer a close encounter in Gaia DR2 – has already been discussed. Another case is the A2 dwarf zeta Leporis, computed in paper 1 to have 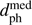 = 1.30 pc 850 kyr ago. It is in Gaia DR2 but without a radial velocity. Using the old radial velocity we find its perihelion parameters to be rather similar (
= 1.30 pc 850 kyr ago. It is in Gaia DR2 but without a radial velocity. Using the old radial velocity we find its perihelion parameters to be rather similar (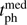 = −860 kyr,
= −860 kyr, 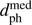 = 1.43 pc). Sirius, Altair, and Algol are not in Gaia DR2.
= 1.43 pc). Sirius, Altair, and Algol are not in Gaia DR2.
There are no doubt many more close – and probably closer – encounters to be discovered in future Gaia data releases.
Acknowledgments
This work is based on data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. We thank Lennart Lindegren for discussions about the Gaia astrometric solution and Ted von Hippel for discussions about white dwarfs. This work was funded in part by the DLR (German space agency) via grant 50 QG 1403. We are grateful for the availability of the Simbad object database and Aladin sky atlas, both developed and provided by CDS, Strasbourg.
References
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Bailer-Jones, C. A. L. 2015a, A&A, 575, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L. 2015b, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L. 2018, A&A, 609, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Berski, F., & Dybczyński, P. A. 2016, A&A, 595, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobylev, V. V. 2010a, Astron. Lett., 36, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Bobylev, V. V. 2010b, Astron. Lett., 36, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Bobylev, V. V. 2017, Astron. Rep., 61, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bobylev, V. V. & Bajkova, A. T. 2017, Astron. Lett., 43, 559 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, R. & de la Fuente Marcos, C. 2018, Res. Notes AAS, 2, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczynski, P. A. 1994, Celest. Mech. Dyn. Astron., 58, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczyński, P. A. 2006, A&A, 449, 1233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dybczyński, P. A. & Berski, F. 2015, MNRAS, 449, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.). 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Sánchez, J., Preston, R. A., Jones, D. L., et al. 1999, AJ, 117, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- García-Sánchez, J., Weissman, P. R., Preston, R. A., et al. 2001, A&A, 379, 634 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollands, M. A., Tremblay, P. E., Gaensicke, B. T., Gentile-Fusillo, N. P., & Toonen, S. 2018, MNRAS, submitted [arXiv:1805.12590] [Google Scholar]
- Jiménez-Torres, J. J., Pichardo, B., Lake, G., & Throop, H. 2011, MNRAS, 418, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, D., Sartoretti, P., Cropper, M., et al. 2018, A&A, submitted [arXiv:1804.09372] [Google Scholar]
- Lindegren, L., Hernandez, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., Barenfeld, S. A., Ivanov, V. D., et al. 2015, ApJ, 800, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, R. A. J. 1994, QJRAS, 35, 1 [NASA ADS] [Google Scholar]
- Mülläri, A. A. & Orlov, V. V. 1996, Earth Moon Planet., 72, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H. 1950, Bull. Astron. Inst. Neth., 11, 91 [Google Scholar]
- Öpik, E. 1932, Proc. Am. Acad. Arts Sci., 67, 169 [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Ren, J. J., Parsons, S. G., et al. 2016, MNRAS, 458, 3808 [NASA ADS] [CrossRef] [Google Scholar]
- Rickman, H. 1976, Bull. Astr. Inst. Czechosl., 27, 92 [NASA ADS] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybizki, J., Demleitner, M., Fouesneau, M., et al. 2018, PASP, 130, 074101 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, S., Bland-Hawthorn, J., Johnston, K. V., & Binney, J. 2011, ApJ, 730, 3 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F., ed. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library, 350 [Google Scholar]
Appendix A
Gaia archive query
Below is the ADQL query used to select stars from Gaia DR2 which have perihelion distances less than 10 pc according to the linear motion approximation (specified by equation 4 in paper 1).
SELECT source_id, ra, dec, parallax, pmra, pmdec,
radial_velocity, ra_error, dec_error, parallax_error,
pmra_error, pmdec_error, radial_velocity_error,
ra_dec_corr, ra_parallax_corr, ra_pmra_corr,
ra_pmdec_corr, dec_parallax_corr, dec_pmra_corr,
dec_pmdec_corr, parallax_pmra_corr, parallax_pmdec_corr,
pmra_pmdec_corr, visibility_periods_used,
phot_g_mean_mag, bp_rp, astrometric_chi2_al,
astrometric_n_good_obs_al, astrometric_excess_noise,
astrometric_excess_noise_sig, rv_nb_transits, l, b
FROM gaiadr2.gaia_source
WHERE (parallax IS NOT NULL) AND (parallax > -0.029)
AND (radial_velocity IS NOT NULL) AND
(
(
( 1000*4.74047*sqrt(power(pmra,2)+power(pmdec,2))
/ power(parallax+0.029,2)
)
/ sqrt( (power(pmra,2)+power(pmdec,2))
* power(4.74047/(parallax+0.029),2)
+ power(radial_velocity,2)
)
) < 10
)
All Tables
Number of stars in the filtered sample found by the orbit integration to have 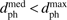 (for any
(for any 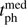 ).
).
Perihelion parameters for all stars with a median perihelion distance (median of the samples; 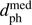 ) below 1 pc, sorted by this value.
) below 1 pc, sorted by this value.
All Figures
 |
Fig. 1. Distribution of the perihelion parameters for the 2000 surrogates used to characterize the encounter of Gl 710 = Gaia DR2 4270814637616488064. |
| In the text | |
 |
Fig. 2. Perihelion times and distances computed by orbit integration for the filtered sample (278 points lie outside the plotting range). Open circles show the median of the perihelion time and distance distributions. The error bars show the limits of the 5% and 95% percentiles. |
| In the text | |
 |
Fig. 3. As Fig. 2, but just showing the 694 stars with |
| In the text | |
 |
Fig. 4. As Fig. 3, but now showing the individual surrogates from the orbital integrations (but just plotting 100 per star rather than all 2000 per star). Surrogates from stars with median perihelion parameters outside the plotting range (and so not shown in Fig. 3) are shown here. |
| In the text | |
 |
Fig. 5. Median perihelion velocities from the orbit integrations for those encounters shown in Fig. 3 The velocity axis is a logarithmic scale. |
| In the text | |
 |
Fig. 6. As Fig. 3, but now plotting each star as a circle, the area of which is proportional to M/( |
| In the text | |
 |
Fig. 7. As Fig. 3, but now plotting each star as a circle, the area of which is proportional to M/ |
| In the text | |
 |
Fig. 8. Colour–magnitude diagram for stellar encounters coloured according to the unit weight error u in Table 3. The vertical axis equals MG assuming extinction is zero. For orientation, the grey lines are unreddened solar metallicity PARSEC isochrones for 1 Gyr (solid) and 10 Gyr (dashed) from Marigo et al. (2017), the grey points are white dwarfs within 20 pc of the Sun identified by Hollands et al. (2018) (many lie outside the range of the plot), and the small blue dots show all sources in Gaia DR2 with ϖ > 50 mas (plotted on the bottom layer, so most are obscured by coloured and grey points, especially in the lower panel). The upper panel shows all reliable (non-bogus) encounters with |
| In the text | |
 |
Fig. 9. Perihelion times and distances for star samples from the mock full Galaxy (no Gaia selection). Each star is represented by a single sample. |
| In the text | |
 |
Fig. 10. Variation of the number of observed encounters per unit perihelion distance as a function of perihelion distance (for the filtered sample for all tph). The open circles count the encountering stars discretely, using |
| In the text | |
 |
Fig. 11. Perihelion times and distances for star samples from the mock Gaia-observed Galaxy. Each star is represented by 100 samples. This is just a window on a much larger set of encounters, so includes samples of stars which are predominantly outside the range shown (e.g. the median perihelion position is outside). |
| In the text | |
 |
Fig. 12. The completeness map, C(tph, dph), which can be interpreted as the probability of observing an encounter in the selected Gaia DR2 sample as a function of its perihelion time and distance. “Selected” here means for G < 12.5 mag in the filtered sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.