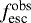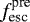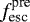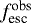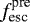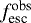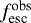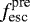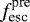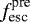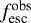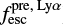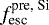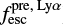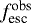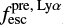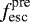| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201832758 | |
| Published online | 08 August 2018 | |
Accurately predicting the escape fraction of ionizing photons using rest-frame ultraviolet absorption lines
1
Observatoire de Genève, Université de Genève,
51 Ch. des Maillettes,
1290
Versoix,
Switzerland
e-mail: John.Chisholm@unige.ch
2
Johan Bernoulli Institute, University of Groningen,
PO Box 407,
9700
AK
Groningen,
The Netherlands
3
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV Groningen,
The Netherlands
4
KVI-Center for Advanced Radiation Technology (KVI-CART), University of Groningen,
Zernikelaan 25,
Groningen
9747 AA,
The Netherlands
5
CNRS, IRAP,
14 Avenue E. Belin,
31400
Toulouse,
France
6
Observational Cosmology Lab, NASA Goddard Space Flight Center,
8800 Greenbelt Rd.,
Greenbelt,
MD
20771,
USA
7
MIT Kavli Institute for Astrophysics and Space Research,
77 Massachusetts Ave.,
Cambridge,
MA
02139,
USA
8
Department of Astronomy, University of Michigan,
500 Church St.,
Ann Arbor,
MI
48109,
USA
9
Department of Astronomy & Astrophysics, University of Chicago,
5640 S. Ellis Ave.,
Chicago,
IL
60637,
USA
10
Kavli Institute for Cosmological Physics, University of Chicago,
5640 S. Ellis Ave.,
Chicago,
IL
60637,
USA
11
Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029, Blindern,
0315
Oslo,
Norway
Received:
2
February
2018
Accepted:
20
March
2018
The fraction of ionizing photons that escape high-redshift galaxies sensitively determines whether galaxies reionized the early Universe. However, this escape fraction cannot be measured from high-redshift galaxies because the opacity of the intergalactic medium is large at high redshifts. Without methods to measure the escape fraction of high-redshift galaxies indirectly, it is unlikely that we will know what reionized the Universe. Here, we analyze the far-ultraviolet (UV) H I (Lyman series) and low-ionization metal absorption lines of nine low-redshift, confirmed Lyman continuum emitting galaxies. We use the H I covering fractions, column densities, and dust attenuations measured in a companion paper to predict the escape fraction of ionizing photons. We find good agreement between the predicted and observed Lyman continuum escape fractions (within 1.4σ) using both the H I and ISM absorption lines. The ionizing photons escape through holes in the H I, but we show that dust attenuation reduces the fraction of photons that escape galaxies. This means that the average high-redshift galaxy likely emits more ionizing photons than low-redshift galaxies. Two other indirect methods accurately predict the escape fractions: the Lyα escape fraction and the optical [O III]/[O II] flux ratio. We use these indirect methods to predict the escape fraction of a sample of 21 galaxies with rest-frame UV spectra but without Lyman continuum observations. Many of these galaxies have low escape fractions (fesc ≤ 1%), but 11 have escape fractions >1%. Future studies will use these methods to measure the escape fractions of high-redshift galaxies, enabling upcoming telescopes to determine whether star-forming galaxies reionized the early Universe.
Key words: dark ages, reionization, first stars / galaxies: irregular / galaxies: ISM / galaxies: starburst
© ESO 2018
1 Introduction
In the local Universe, gas between galaxies is mostly highly ionized (Fan et al. 2006), but it has not always been that way. Hydrogen recombined at z = 1090 and remained neutral until z ~ 7−9 (Planck Collaboration XLVII 2016). This is most easily observed by the absorption blueward of rest-frame Lyα (1216 Å) in the spectra of z > 6 quasars (the “Gunn-Peterson trough”; Gunn & Peterson 1965; Becker et al. 2001). Some mechanism must have produced copious ionizing photons to reionize the Universe.
The source of reionization is one of the core questions that future large observatories, such as the James Webb Space Telescope (JWST) and extremely large telescopes (ELT), aim to answer. One possibility is that active galactic nuclei (AGN) provided the ionizing photons. However, current observed AGN luminosity functions indicate that there were not enough AGN to reionize the early Universe (Hopkins et al. 2008; Willott et al. 2010; Fontanot et al. 2012; Ricci et al. 2017; Onoue et al. 2017).
An alternative source of ionizing photons is the first generation of high-mass stars. For these stars to matter to reionization, the emissivity of ionizing photons (ṅion) escaping high-redshift galaxies must exceed the recombination rate. Commonly, ṅion is expressed as
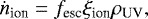 (1)
(1)
where ξion is the intrinsic number of ionizing photons emitted by stars, ρUV is the total ultraviolet (UV) luminosity density, and fesc is the absolutefraction of ionizing photons that escape galaxies. More generally, the quantities in Eq. (1) depend on the UV magnitude, MUV, and the total ṅion is found by integrating over the UV luminosity function. While highly dependent on clumping and redshift, the estimated Ωmatter from Λ cold dark matter indicates that the Universe is reionized when log(ṅion[photons s−1 Mpc−3]) is near 50−51 (Madau et al. 1999; Meiksin 2005; Bolton & Haehnelt 2007; Ouchi et al. 2009; Kuhlen & Faucher-Giguère 2012; Robertson et al. 2013, 2015).
In principle, whether or not stars reionized the Universe is an observable question. The parameter ξion is related to the observed Hα emission and depends on the metallicity and star formation rate of the galaxies (Leitherer & Heckman 1995; Bruzual & Charlot 2003). Recent studies constrain ξion at z = 6−8 (Dunlop et al. 2012; Bouwens et al. 2012b; Robertson et al. 2013; Harikane et al. 2018). Similarly, deep Hubble Space Telescope (HST) observations have pushed the UV luminosity functions down to fainter MUV at high redshifts (Bouwens et al. 2006, 2015; Ouchi et al. 2009; Oesch et al. 2014, 2018; Finkelstein et al. 2015; Livermore et al. 2017). While requiring extraordinary observations, these studies are beginning to constrain ξion and ρUV during the epoch of reionization.
These observational constraints suggest that fesc ~ 0.1−0.2 if stars reionized the Universe (Ouchi et al. 2009; Robertson et al. 2013, 2015; Bouwens et al. 2015; Dressler et al. 2015; Ishigaki et al. 2018). Whether fesc reaches these values has not been observationally confirmed. First, the opacity of the intergalactic medium (IGM) is, on average, too large to observe LyC photons above z ~ 4 (Worseck et al. 2014). Therefore, a direct detection of ionizing photons escaping from a single galaxy during the epoch of reionization is statistically unlikely. Alternatively, studies focused on lower redshift galaxies where the Lyman continuum (LyC; < 912Å) is directly observable. However, directly detecting ionizing photons at low redshift is still challenging. It requires deep observations of intrinsically faint emission in the very far-UV, which is a notoriously hard regime for high-sensitivity detectors. Only ten individual z < 0.4 galaxies have spectroscopically confirmed fesc > 0 (Bergvall et al. 2006; Leitet et al. 2011; Borthakur et al. 2014; Izotov et al. 2016a,b, 2018; Leitherer et al. 2016). Additionally, four such galaxies at z ~ 3 − 4 have been confirmed (Vanzella et al. 2015, 2016, 2018; de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017), after accounting for foreground contamination (e.g., Vanzella et al. 2010). To constrain fesc during the epoch of reionization, indirect fesc probes available at both high (to measure galaxies in the epoch of reionziation) and low redshifts (to confirm the predicted fesc values) are required.
We present a new analysis of the rest-frame UV properties of nine confirmed low-redshift galaxies that emit ionizing photons and have publicly available far-UV observations. We use the fits of the stellar continua, interstellar medium (ISM) metal absorption lines, and ISM H I absorption lines (the Lyman series) from Gazagnes et al. (2018; hereafter Paper I) to constrain the neutral gas and dust attenuation properties. Since the H I and dust are the major sinks of ionizing photons, these measurements allow us to accurately predict fesc. These new methods can be used to efficiently select low-redshift galaxies that emit ionizing photons or for future telescopes (such as JWST or ELTs) to constrain ṅion of galaxies reionizing the Universe.
The structure of this paper is as follows. Section 2 introduces the observations of the nine publicly available LyC emitters and summarizes how Paper I fit the Lyman series absorption lines. We use these fits to predict fesc (Sect. 3) and explore what fit parameters contribute to the observed fesc values (Sect. 4). We then test using the Si II absorption lines (Sect. 5.1), Lyα escape fractions (Sect. 5.2), and the [O III]/[O II] ratios (Sect. 5.3) to indirectly predict fesc. In Sect. 6 we apply these indirect methods to galaxies without Lyman series observations to demonstrate how these methods can be used for high-redshift galaxies. Our main conclusions are summarized in Sect. 7.
2 Data and absorption line analysis
2.1 Rest-frame far-UV observations
2.1.1 The Lyman continuum emitting sample
In this paper, we predominantly use the rest-frame far-UV spectra of the nine publicly available known LyC emitters (hereafter called the Lyman continuum emitting sample; Borthakur et al. 2014; Izotov et al. 2016a,b; Leitherer et al. 2016) taken with the Cosmic Origins Spectrograph (COS; Green et al. 2012) on the HST. We note that Izotov et al. (2018) recently discovered a tenth Lyman continuum emitter that we do not include in this paper because it is not publicly available (but see Sect. 6.4). As summarized in Chisholm et al. (2017), these nine galaxies have low stellar masses (108 −1010 M⊙), high star formation rates (3− 77 M⊙ yr−1), and moderately low gas-phase metallicities (12 + log(O/H) = 7.9−8.7). Table 1 lists the galaxies in the Lyman continuum emitting sample and their observed Lyman continuum (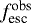 ; Chisholm et al. 2017) and Lyα (
; Chisholm et al. 2017) and Lyα (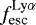 ; Verhamme et al. 2017) escape fractions. Two galaxies, Tol 0440 − 381 and Mrk 54, have the COS detector gap over the Lyα feature. Therefore, their
; Verhamme et al. 2017) escape fractions. Two galaxies, Tol 0440 − 381 and Mrk 54, have the COS detector gap over the Lyα feature. Therefore, their 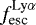 values are not measured.
values are not measured.
Eight of these nine galaxies were observed with the low-resolution G140L grating (nominal resolution of R ~ 1500) on HST/COS, while J0921+4509 was observed with the high-resolution G130M and G160M gratings (R ~ 15 000). These setups observed the rest-frame Lyman series and Si II 1260 Å absorption lines of each galaxy. Each galaxy also has rest-frame optical observations, such that extinction-corrected [O III] 5007 Å/[O II] 3727 Å flux ratios (O32) are measured (last column of Table 1; Verhamme et al. 2017).
The HST/COS G140L data were reduced using the methods outlined in Worseck et al. (2016). Special attention was paid to the pulse heights and extraction apertures of each individual spectrum. The pulse heights and apertures used were outlined in Chisholm et al. (2017). We placed the galaxy into the rest frame using the redshifts from the Sloan Digital Sky Survey (Ahn et al. 2014). We then corrected each spectrum for foreground reddening using the values from Schlegel et al. (1998) and the Milky Way reddening law (Cardelli et al. 1989).
Measured properties of the Lyman continuum emitting sample from Gazagnes et al. (2018) in order of decreasing 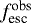 .
.
2.1.2 Low-redshift galaxies with unobserved LyC emission
In Sect. 5.3 we extend the Lyman continuum emitting sample to include the full sample from Paper I with measured O32 (see Table 2). This full sample includes four low-redshift galaxies that do not have observations of the Lyman continuum, but have observations of the Lyman series. The full sample includes three Green Pea galaxies (Henry et al. 2015) and one Lyman Break Analog (Heckman et al. 2011; Heckman et al. 2015; Alexandroff et al. 2015; Heckman & Borthakur 2016). These four galaxies were also observed with HST/COS and the G130M grating. The data were reduced following the methods outlined in Wakker et al. (2015). These galaxies do not have LyC observations, consequently we predict their LyC escape fractions but we cannot confirm them. In Sect. 5.3 we use the Lyman series observations of the full sample to predict the relation between fesc and O32.
Measured properties for the 7 galaxies from Gazagnes et al. (2018) without observed Lyman continuum escape fractions.
2.1.3 High-redshift galaxies from MEGaSaURA
Similarly, in Sect. 6 we focus on 14 z > 2 lensed galaxies from The Magellan Evolution of Galaxies Spectroscopic and Ultraviolet Reference Atlas (MEGaSaURA; Rigby et al. 2018). These lensed galaxies have spectra taken with the MagE spectrograph (Marshall et al. 2008) on the Magellan telescopes. The data were reduced using D. Kelson’s pipeline1 and placed into the observed frame using the redshifts measured from the UV emission lines (Rigby et al. 2018). Two of these galaxies have Lyman series and O32 observations, thus they are included in the full sample (Table 2). The other 12 galaxies do not have Lyman series or O32 observations, and we apply our indirect methods to these spectra in Sect. 6. These high-redshift galaxies do not have measured Lyman continuum escape fractions, but their rest-frame UV spectra test the methods presented in this paper.
2.2 Lyman series fitting
To predict the fraction of ionizing photons that escape a galaxy, we determined the H I properties from the Lyman series absorption lines between 920 and 1025 Å. These measurements describe the quantity and porosity of H I along the line of sight. Paper I describes this procedure in detail; here we summarize the process and further details are provided in that paper.
We fit the observed flux density (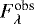 ) using a linear combination of fully theoretical, STARBURST99 stellar continuum models (
) using a linear combination of fully theoretical, STARBURST99 stellar continuum models (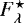 ; Leitherer et al. 1999). We created these stellar continuum models using the Geneva stellar evolution tracks (Meynet et al. 1994) and the WM-BASIC method (Leitherer et al. 2010), assuming an initial mass function with a high (low) mass exponent of 2.3 (1.3) and a high-mass cutoff at 100 M⊙. These models have a spectral resolution of R ~ 2500. The final
; Leitherer et al. 1999). We created these stellar continuum models using the Geneva stellar evolution tracks (Meynet et al. 1994) and the WM-BASIC method (Leitherer et al. 2010), assuming an initial mass function with a high (low) mass exponent of 2.3 (1.3) and a high-mass cutoff at 100 M⊙. These models have a spectral resolution of R ~ 2500. The final 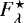 is a linear combination of 10 single-age stellar continuum models each with an age between 1 and 40 Myr. The stellar continuum metallicity was chosen as the model closest to the measured gas-phase metallicity. We fit for the linear coefficient multiplied by each single-aged STARBURST99 model that best matches the data using MPFIT (Markwardt 2009).
is a linear combination of 10 single-age stellar continuum models each with an age between 1 and 40 Myr. The stellar continuum metallicity was chosen as the model closest to the measured gas-phase metallicity. We fit for the linear coefficient multiplied by each single-aged STARBURST99 model that best matches the data using MPFIT (Markwardt 2009).
We simultaneously reddened 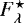 to account for a uniform foreground dust screen using the attenuation law (kλ) from Reddy et al. (2016a) and a fitted stellar attenuation value (EB−V). In Sect. 3.2 we discuss the implications for the assumed dust geometry.
to account for a uniform foreground dust screen using the attenuation law (kλ) from Reddy et al. (2016a) and a fitted stellar attenuation value (EB−V). In Sect. 3.2 we discuss the implications for the assumed dust geometry.
Finally, we measured the H I and metal ISM absorption line properties by including Lyman series, O VI, O I, C II, C III, and Si II absorption features. Wefit for the observed Lyman series absorption lines using the radiative transfer equation, assuming an overlapping covering fraction (Cf; Barlow & Sargent 1997; Hamann et al. 1997), which has a functional form of
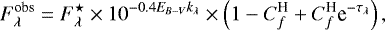 (2)
(2)
where we fit for EB−V, the intrinsic stellar continuum (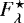 ), the optical depth (τ = σNHI), and the H I covering fraction (
), the optical depth (τ = σNHI), and the H I covering fraction (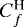 ). As discussed in Paper I, the H I lines are saturated (τλ ≫ 1), but not damped. Consequently, NHI cannot be accurately determined. Therefore, we measured the H I column density from the unsaturated O I 1039 Å line, and converted this column density into NHI using the observed 12 + log(O/H). One galaxy, J0925+1403, does not have a O I 1039 Å detection, therefore we used the fitted NHI value and the large associated errors. The fits of Eq. (2) constrain the stellar population, dust and NHI properties of the LyC emitters. The Lyman series fits for all of the galaxies are shown in the Appendix of Paper I.
). As discussed in Paper I, the H I lines are saturated (τλ ≫ 1), but not damped. Consequently, NHI cannot be accurately determined. Therefore, we measured the H I column density from the unsaturated O I 1039 Å line, and converted this column density into NHI using the observed 12 + log(O/H). One galaxy, J0925+1403, does not have a O I 1039 Å detection, therefore we used the fitted NHI value and the large associated errors. The fits of Eq. (2) constrain the stellar population, dust and NHI properties of the LyC emitters. The Lyman series fits for all of the galaxies are shown in the Appendix of Paper I.
Since the Lyman series is always found to be optically thick (Paper I), we find that 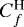 is most robustly measured by taking the median of
is most robustly measured by taking the median of
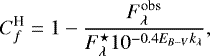 (3)
(3)
in a region that we visually selected near each Lyman series line. To calculate the  errors of the individual Lyman series transitions, we varied the observed flux by a Gaussian distribution centered on zero with a standard deviation equal to the flux error. We then measured
errors of the individual Lyman series transitions, we varied the observed flux by a Gaussian distribution centered on zero with a standard deviation equal to the flux error. We then measured  from this altered flux array and tabulated the result. We repeated the process 1000 times to produce a distribution of
from this altered flux array and tabulated the result. We repeated the process 1000 times to produce a distribution of  values. We then took the median and standard deviation of this distribution as the
values. We then took the median and standard deviation of this distribution as the  estimate and uncertainty. After we measured
estimate and uncertainty. After we measured 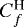 for each transition, we took the weighted median and standard deviation of all observed Lyman series lines as the
for each transition, we took the weighted median and standard deviation of all observed Lyman series lines as the  estimate and error (see Table 1). We used this method because it does not rely on assumptions about how the
estimate and error (see Table 1). We used this method because it does not rely on assumptions about how the 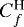 changes with velocity, and we could control for the impact of nearby Milky Way absorption lines.
changes with velocity, and we could control for the impact of nearby Milky Way absorption lines.
2.3 Si II observations
Finally, we measured the Si II covering fraction (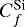 ) in two ways. First, we measured
) in two ways. First, we measured 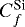 of the Si II 1260 Å line with Eq. (3). This method assumes that the strong Si II 1260 Å line, with an oscillator strength of 1.22, is saturated. Second, we calculated
of the Si II 1260 Å line with Eq. (3). This method assumes that the strong Si II 1260 Å line, with an oscillator strength of 1.22, is saturated. Second, we calculated 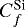 from the Si II 1190 Å doublet, which accounts for low Si II optical depths. We took the average and standard deviation of these two values as the
from the Si II 1190 Å doublet, which accounts for low Si II optical depths. We took the average and standard deviation of these two values as the 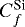 values and errors, respectively. We note that both estimates of
values and errors, respectively. We note that both estimates of 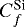 are largely equivalent to each other, implying that the Si II 1260 Å line is saturated (see Paper I). Now we have measured the ingredients to predict the Lyman continuum escape fractions.
are largely equivalent to each other, implying that the Si II 1260 Å line is saturated (see Paper I). Now we have measured the ingredients to predict the Lyman continuum escape fractions.
3 Predicting the Lyman continuum escape fraction with the Lyman series
3.1 Predicting the Lyman continuum escape fraction
The absolute Lyman continuum escape fraction, fesc, is defined as the ratio of the observed ionizing flux to the intrinsic ionizing flux produced by stars,
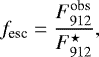 (4)
(4)
where 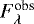 is defined in Eq. (2). Since ionizing photons can be absorbed by dust or H I, fesc is predicted from the fits to the Lyman series and the dust attenuation as
is defined in Eq. (2). Since ionizing photons can be absorbed by dust or H I, fesc is predicted from the fits to the Lyman series and the dust attenuation as
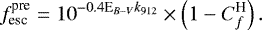 (5)
(5)
The Lymancontinuum is optically thick at H I column densities above 1017.7 cm−2. For column densities below this column density, the gas is optically thin and the escape fraction increases because unabsorbed light escapes. However, in Paper I we used the O I column densities to demonstrate that the NH in these galaxies is larger than 1018.63 cm−2. Therefore, we neglected the last term of Eq. (2) when calculating 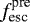 . To calculate
. To calculate 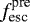 , we used k912 = 12.87 from the attenuation curve of Reddy et al. (2016a). The errors on
, we used k912 = 12.87 from the attenuation curve of Reddy et al. (2016a). The errors on 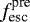 were calculated by propagating the errors of EB−V and
were calculated by propagating the errors of EB−V and 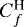 through Eq. (5).
through Eq. (5).
The value 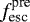 closely follows
closely follows 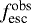 for the nine galaxies in the Lyman continuum emitting sample (Fig. 1). The normalized absolute difference between
for the nine galaxies in the Lyman continuum emitting sample (Fig. 1). The normalized absolute difference between 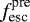 and
and 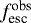 (|
(|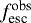 –
– 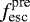 |/
|/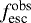 ) is 48%. The median
) is 48%. The median 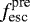 is within 1.4σ of
is within 1.4σ of 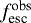 (i.e., within the 95% confidence interval). This assumes a uniform distribution because the reported
(i.e., within the 95% confidence interval). This assumes a uniform distribution because the reported 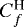 and EB−V errors are highly non-Gaussian. The value
and EB−V errors are highly non-Gaussian. The value 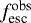 heavily depends on the modeling of the stellar population. Table 9 of Izotov et al. (2016b) demonstrates that the median
heavily depends on the modeling of the stellar population. Table 9 of Izotov et al. (2016b) demonstrates that the median 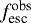 varies by 0.01 (10–20%) if different stellar population models are used. This error, while not accounted for in the standard
varies by 0.01 (10–20%) if different stellar population models are used. This error, while not accounted for in the standard 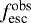 error bars, would improve the quoted statistics.
error bars, would improve the quoted statistics.
Two galaxies have 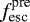 more than 3σ from
more than 3σ from 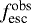 : Tol 1247−232 and J1503+3644. For Tol 1247−232,
: Tol 1247−232 and J1503+3644. For Tol 1247−232, 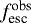 is challenging to measure because it is a low-redshift galaxy with possible geocoronal Lyα contamination (Chisholm et al. 2017). Other studies, which used the same observations but different reductions and handling of geocoronal Lyα, have measured
is challenging to measure because it is a low-redshift galaxy with possible geocoronal Lyα contamination (Chisholm et al. 2017). Other studies, which used the same observations but different reductions and handling of geocoronal Lyα, have measured 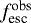 = 0.045 ± 0.012 and 0.015 ± 0.005 (Leitherer et al. 2016; Puschnig et al. 2017, respectively), whereas Chisholm et al. (2017) have measured
= 0.045 ± 0.012 and 0.015 ± 0.005 (Leitherer et al. 2016; Puschnig et al. 2017, respectively), whereas Chisholm et al. (2017) have measured 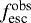 = 0.004 ± 0.002. These values are more consistent with the derived
= 0.004 ± 0.002. These values are more consistent with the derived 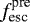 = 0.049 ± 0.008. In reality, it is remarkable that
= 0.049 ± 0.008. In reality, it is remarkable that 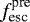 and
and 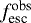 are at all similar. Regardless, we conclude that Eq. (5) accurately reproduces the observed LyC escape fractions to within 1.4σ, on average.
are at all similar. Regardless, we conclude that Eq. (5) accurately reproduces the observed LyC escape fractions to within 1.4σ, on average.
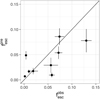 |
Fig. 1 Observed Lyman continuum escape fraction ( |
3.2 Effect of the assumed geometry on fesc
The fesc is measured along the line of sight from a star-forming region to the observer and line-of-sight geometric effects could impact fesc. To estimate 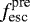 , we assumed a uniform dust screen (Eq. (5)). This posits that the dust is uniformly distributed along the line of sight to the galaxy. It is worth exploring the effect this assumed geometry has on
, we assumed a uniform dust screen (Eq. (5)). This posits that the dust is uniformly distributed along the line of sight to the galaxy. It is worth exploring the effect this assumed geometry has on 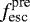 . Detailed discussions on this issue are also provided elsewhere (Zackrisson et al. 2013; Vasei et al. 2016; Reddy et al. 2016b; Gazagnes et al. 2018).
. Detailed discussions on this issue are also provided elsewhere (Zackrisson et al. 2013; Vasei et al. 2016; Reddy et al. 2016b; Gazagnes et al. 2018).
A simple alternative geometry is that the dust only resides within clumpy neutral gas clouds. Between these neutral clouds are dustless and gasless holes, which we call a clumpy geometry. This geometry alters the radiative transfer equation (Eq. (2)) to become
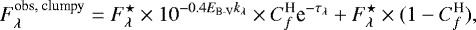 (6)
(6)
and the ionizing escape fraction is
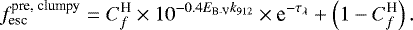 (7)
(7)
We note that the clumpy and uniform geometries treat the dust differently. In the clumpy geometry, the dust attenuation acts only on the e−τλ term. To remain at the same 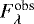 (or fesc), the
(or fesc), the 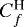 and EB−V of the clumpy geometry must be larger than the uniform geometry. This is because unattenuated light passes through holes in clumpy geometry, forcing the attenuation within the clumps to be stronger, and the holes to be smaller, to match the observed flux.
and EB−V of the clumpy geometry must be larger than the uniform geometry. This is because unattenuated light passes through holes in clumpy geometry, forcing the attenuation within the clumps to be stronger, and the holes to be smaller, to match the observed flux.
To test the effect of the geometry, in Paper I we refit 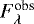 from J1152+3400 and J0921+4509, a large and a small
from J1152+3400 and J0921+4509, a large and a small 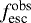 galaxy, with the clumpy model (Eq. (6)). We find that
galaxy, with the clumpy model (Eq. (6)). We find that 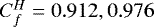 and EB−V = 0.239 and 0.236, respectively. Both are larger than the uniform dust screen model (Table 1). However, these values and Eq. (7) lead to
and EB−V = 0.239 and 0.236, respectively. Both are larger than the uniform dust screen model (Table 1). However, these values and Eq. (7) lead to 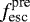 = 0.088 and 0.024, statistically consistent with
= 0.088 and 0.024, statistically consistent with 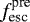 using the uniform screen (0.08 and 0.016 respectively).
using the uniform screen (0.08 and 0.016 respectively).
The fitted values (EB−V, 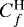 ) change to match
) change to match 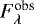 based on the assumed geometry. Therefore, parameters such as
based on the assumed geometry. Therefore, parameters such as 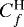 and EB−V are model dependent. However, fesc is model independent because the best combination of the model and the parameters are fit to match the data (as discussed in Paper I). The geometry must be accounted for – and remembered – when comparing and interpreting Cf and EB−V, but the fesc values do not strongly depend on the assumed geometry.
and EB−V are model dependent. However, fesc is model independent because the best combination of the model and the parameters are fit to match the data (as discussed in Paper I). The geometry must be accounted for – and remembered – when comparing and interpreting Cf and EB−V, but the fesc values do not strongly depend on the assumed geometry.
4 Parameters contributing to the predicted escape fractions
The previous section showed that the fits to the observed flux accurately predict the escape fraction of ionizing photons. H I column density, H I covering fraction, and dust attenuation determine these fits. The natural question is which parameters contribute to the predicted escape fractions? In the next three subsections, we explore the contribution of each estimated parameter to the predicted escape fractions. We note that the following analysis does not refit the data to maximize the contributionof each parameter, rather it uses the previous fits to answer which parameters contribute to the predicted escape fractions.
4.1 H I column density
The first parameter that we discuss is NHI. If NHI is low enough, ionizing photons pass through the ISM unabsorbed (a “density-bounded” region; Jaskot & Oey 2013; Zackrisson et al. 2013; Nakajima & Ouchi 2014). The escape fraction of ionizing photons only due to NHI is
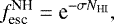 (8)
(8)
where σ is the photoionization cross section (6.3 × 10−18 cm2). We set 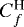 = 1 and EB−V = 0 in Eq. (5). The
= 1 and EB−V = 0 in Eq. (5). The 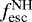 values are too low to match
values are too low to match 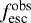 (red circles in Fig. 2). This implies that the H I along the line of sight is optically thick (see the discussion in Paper I).
(red circles in Fig. 2). This implies that the H I along the line of sight is optically thick (see the discussion in Paper I).
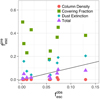 |
Fig. 2 Observed Lyman continuum escape fraction ( |
4.2 Covering fraction
The second parameter, the covering fraction, implies that ionizing photons escape through holes in the H I gas (Heckman et al. 2011). If we assumed no attenuation from dust (EB−V = 0) and that H I is optically thick, the predicted escape fractions are
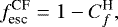 (9)
(9)
which is greater than 0 for the nine Lyman continuum emitters (green squares in Fig. 2). However, these 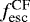 values are substantially higher than
values are substantially higher than 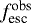 . If holes in the H I were solely responsible for the escape of ionizing photons, and there was no dust, the escape fractions would be much higher than observed.
. If holes in the H I were solely responsible for the escape of ionizing photons, and there was no dust, the escape fractions would be much higher than observed.
Several previous studies have used 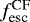 to estimate fesc, but overestimated the fesc values (Quider et al. 2009; Heckman et al. 2011; Jones et al. 2012, 2013; Leethochawalit et al. 2016; Vasei et al. 2016). For example, Quider et al. (2009) obtained
to estimate fesc, but overestimated the fesc values (Quider et al. 2009; Heckman et al. 2011; Jones et al. 2012, 2013; Leethochawalit et al. 2016; Vasei et al. 2016). For example, Quider et al. (2009) obtained 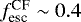 for the Cosmic Horseshoe, but this disagrees with the upper limit of the absolute fesc < 0.02 derived with HST imaging by Vasei et al. (2016). However, Quider et al. (2009) did not account for dust attenuation when deriving fesc. In Sect. 6.1 we show that accounting for dust leads to fesc values that are consistent with the HST observations of the Cosmic Horseshoe.
for the Cosmic Horseshoe, but this disagrees with the upper limit of the absolute fesc < 0.02 derived with HST imaging by Vasei et al. (2016). However, Quider et al. (2009) did not account for dust attenuation when deriving fesc. In Sect. 6.1 we show that accounting for dust leads to fesc values that are consistent with the HST observations of the Cosmic Horseshoe.
4.3 Dust attenuation
The final contributor to the escape of ionizing photons in our fits is dust. Dust heavily impacts the observed stellar continuum at 912 Å: even small EB−V values lead to large attenuations. J1152+3400, with the smallest EB−V in the Lyman continuum emitting sample, has an A912 = 1.7 mag (τ912 = 1.5). Consequently, even small dust attenuation removes significant amounts of ionizing photons.
The effect of dust is maximized in the idealistic case where there is only dust and no H I along the line of sight (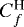 =1 and τ = 0). In this case, dust regulates the escape of ionizing photons. The contribution to the escape fraction solely from dust (
=1 and τ = 0). In this case, dust regulates the escape of ionizing photons. The contribution to the escape fraction solely from dust (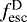 ) is calculated as
) is calculated as
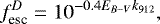 (10)
(10)
where 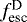 values are the closest to
values are the closest to 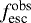 of the three parameters (cyan diamonds in Fig. 2). Nonetheless,
of the three parameters (cyan diamonds in Fig. 2). Nonetheless, 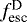 is still too high to match
is still too high to match 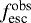 , and the combination of dust and
, and the combination of dust and 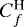 are required to match the modeled
are required to match the modeled 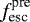 (see purple triangles in Fig. 2).
(see purple triangles in Fig. 2).
The individual values of EB−V and 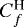 change depending on the assumed geometry (Sect. 3.2; Paper I). However, this does not diminish the contribution of either dust or
change depending on the assumed geometry (Sect. 3.2; Paper I). However, this does not diminish the contribution of either dust or 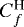 to
to 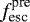 . In an alternative geometry, the clumpy geometry (Eq. (6)), the observed flux far from optically thick H I lines (at wavelengths where τλ is small) is heavily influenced by the product of
. In an alternative geometry, the clumpy geometry (Eq. (6)), the observed flux far from optically thick H I lines (at wavelengths where τλ is small) is heavily influenced by the product of 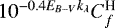 . Since most of the fitted wavelengths are actually in the small τλ regime, the attenuation significantly influences the fitted
. Since most of the fitted wavelengths are actually in the small τλ regime, the attenuation significantly influences the fitted 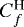 value. While the exact contribution of dust and covering fraction are model dependent,
value. While the exact contribution of dust and covering fraction are model dependent, 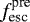 depends on both.
depends on both.
4.4 Connecting low attenuation to high-redshift leakers
We find that dust attenuation strongly contributes to the predicted escape fractions. Consequently, low-mass – or equivalently low-metallicity – galaxies are ideal targets to emit ionizing photons. These properties are similar to the host galaxy properties of known local emitters (Izotov et al. 2016b; Chisholm et al. 2017). Galaxies in the early Universe should naturally have these properties (Bouwens et al. 2012a; Madau & Dickinson 2014) and may have higher fesc than local galaxies. Schaerer & de Barros (2010) found that typical < 1010 M⊙ galaxies at z = 6 − 8 have AV < 1. This implies that 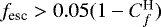 for galaxies expected to reionize the Universe. Using the median
for galaxies expected to reionize the Universe. Using the median 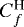 from the Lyman continuum emitting sample (
from the Lyman continuum emitting sample (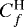 = 0.64), z = 6−8 galaxies should have fesc > 0.02, much higher than the average galaxy at z = 0. Further, all of the z ~ 3−4 confirmed LyC emitters have EB−V < 0.11 mag, or
= 0.64), z = 6−8 galaxies should have fesc > 0.02, much higher than the average galaxy at z = 0. Further, all of the z ~ 3−4 confirmed LyC emitters have EB−V < 0.11 mag, or 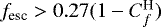 (de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017). Using the median
(de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017). Using the median 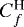 from our Lyman continuum emitting sample, this corresponds to fesc > 0.1, which agrees with the fesc required to reionize the Universe at z = 6−8. Galaxies in the epoch of reioniziation likely have low dust attenuations, which makes them ideal candidates to emit a high fraction of their ionizing photons.
from our Lyman continuum emitting sample, this corresponds to fesc > 0.1, which agrees with the fesc required to reionize the Universe at z = 6−8. Galaxies in the epoch of reioniziation likely have low dust attenuations, which makes them ideal candidates to emit a high fraction of their ionizing photons.
5 Indirectly predicting the Lyman continuum escape fraction
Directly measuring 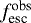 requires deep rest-frame far-UV observations. This means that only a dozen galaxies are confirmed LyC emitters at any redshift. While the Lyman series accurately predicts the escape fraction (Fig. 1), the Lyman series is also not observable at high redshifts because the opacity of the circum-galactic medium is large. Therefore, we explored ancillary, indirect methods that can predict the fesc of high-redshift galaxies. First we explored using the Si II covering fraction to predict the escape fraction. Then we used the observed Lyα escape fraction to approximate fesc. Finally, we used the ratio of the optical oxygen emission lines (O32 = [O III] 5007 Å/[O II] 3727 Å). In Sect. 6, we illustrate how these three methods predict
requires deep rest-frame far-UV observations. This means that only a dozen galaxies are confirmed LyC emitters at any redshift. While the Lyman series accurately predicts the escape fraction (Fig. 1), the Lyman series is also not observable at high redshifts because the opacity of the circum-galactic medium is large. Therefore, we explored ancillary, indirect methods that can predict the fesc of high-redshift galaxies. First we explored using the Si II covering fraction to predict the escape fraction. Then we used the observed Lyα escape fraction to approximate fesc. Finally, we used the ratio of the optical oxygen emission lines (O32 = [O III] 5007 Å/[O II] 3727 Å). In Sect. 6, we illustrate how these three methods predict 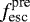 for galaxies that are not in our full sample because they do not have publicly available Lyman series observations.
for galaxies that are not in our full sample because they do not have publicly available Lyman series observations.
5.1 Using Si II absorption
Si II has multiple absorption lines in the rest-frame far-UV, including the 1190 Å doublet and 1260 Å singlet. The ionization potential of Si II (16 eV) means that it probes partially neutral gas, and many studies have used it to diagnose LyC emitters (Heckman et al. 2011; Jones et al. 2012, 2013; Alexandroff et al. 2015; Chisholm et al. 2017). In Paper I, we showed that 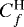 and the Si II covering fraction (
and the Si II covering fraction (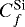 ) are linearly related, but not equal. We fit the relationship between
) are linearly related, but not equal. We fit the relationship between 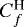 and
and 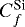 as
as
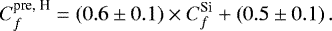 (11)
(11)
This relationship is significant at the 3σ significance level (p-value <0.001). This relation is statistically consistent with the relationship between Si II 1260 Å and H I found for z ~ 3 galaxies in Reddy et al. (2016b). In Paper I, we posited that this relation arises because metals do not completely trace the same gas as H I, and 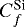 must be corrected to account for this differential covering. A multiple linear regression demonstrates that the constant in Eq. (11) (0.6) depends on the gas-phase metallicity of the galaxy. This indicates that at lower metallicities the Si II traces a lower fraction of the H I.
must be corrected to account for this differential covering. A multiple linear regression demonstrates that the constant in Eq. (11) (0.6) depends on the gas-phase metallicity of the galaxy. This indicates that at lower metallicities the Si II traces a lower fraction of the H I.
We predicted the escape fraction of ionizing photons using the Si II absorption lines as
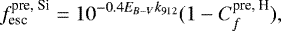 (12)
(12)
where we used k912 = 12.87, the observed EB−V, and 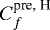 from Eq. (11). The value
from Eq. (11). The value 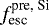 is consistent with
is consistent with 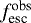 for the nine known Lyman continuum emitters (left panel of Fig. 3). The difference between
for the nine known Lyman continuum emitters (left panel of Fig. 3). The difference between 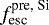 and
and 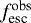 is 46% of the measured
is 46% of the measured 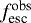 values. Similarly, the median
values. Similarly, the median 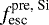 is within 1.2σ of
is within 1.2σ of 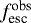 . Using the Si II absorption predicts the observed escape fractions with similar accuracy as the Lyman series.
. Using the Si II absorption predicts the observed escape fractions with similar accuracy as the Lyman series.
 |
Fig. 3 Left panel: observed Lyman continuum escape fraction ( |
5.2 Using Lyα escape fractions
Ionizing photons and Lyα photons are related because H I gas absorbs or scatters both (Verhamme et al. 2015). The Lyα escape fraction is calculated as
![\begin{equation*} f_{\text{esc}}^{\text{Ly}\alpha} = \frac{\left(F[\text{Ly}\alpha]/F[\text{H}\alpha]\right)_{\text{obs}}}{\left(F[\text{Ly}\alpha]/F[\text{H}\alpha]\right)_{\text{int}}},\end{equation*}](/articles/aa/full_html/2018/08/aa32758-18/aa32758-18-eq114.png) (13)
(13)
where ![$\left(F[\text{Ly}\alpha]/F[\text{H}\alpha]\right)_{\text{obs}}$](/articles/aa/full_html/2018/08/aa32758-18/aa32758-18-eq115.png) is the observed ratio of the Lyα flux to the extinction-corrected Hα flux, and
is the observed ratio of the Lyα flux to the extinction-corrected Hα flux, and ![$\left(F[\text{Ly}\alpha]/F[\text{H}\alpha]\right)_{\text{int}}$](/articles/aa/full_html/2018/08/aa32758-18/aa32758-18-eq116.png) is the theoretical intrinsic flux ratio (which has a value of 8.7 for Case B recombination and a temperature of 104 K). The
is the theoretical intrinsic flux ratio (which has a value of 8.7 for Case B recombination and a temperature of 104 K). The 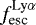 measures the fraction of Lyα photons that escape and does not directly depend on how the Lyα photons escapes. Consequently, we assumed that the only difference between fesc and
measures the fraction of Lyα photons that escape and does not directly depend on how the Lyα photons escapes. Consequently, we assumed that the only difference between fesc and 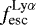 is the dust attenuation, and used the Lyα escape fraction to predict the LyC escape fraction (
is the dust attenuation, and used the Lyα escape fraction to predict the LyC escape fraction (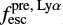 ) as
) as
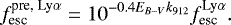 (14)
(14)
This implies that the LyC and Lyα escape fractions are similar, but that the LyC escape fraction is lower because the dust attenuation is larger at 912 Å than at 1216 Å. Consequently, Eq. (14) effectively extinction corrects the Lyα escape fraction to predict fesc. These values are consistent with 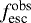 for the seven galaxies with measured
for the seven galaxies with measured 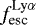 (right panel of Fig. 3). The average relative difference between
(right panel of Fig. 3). The average relative difference between 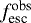 and
and 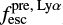 is 55% of
is 55% of 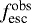 , and
, and 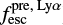 is, on average, within 1.8σ of
is, on average, within 1.8σ of 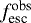 . The consistency of
. The consistency of 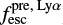 is comparable to the two previous
is comparable to the two previous 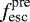 measurements.
measurements.
The similar 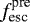 and
and 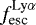 values are driven by the similar attenuations because the attenuation dominates
values are driven by the similar attenuations because the attenuation dominates 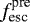 (Sect. 4). The difference in calculating
(Sect. 4). The difference in calculating 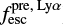 and
and 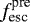 are the
are the 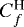 and
and 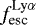 values (compare Eq. (5) and Eq. (14)). This implies that
values (compare Eq. (5) and Eq. (14)). This implies that 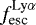 and
and 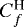 are causally related (Dijkstra et al. 2016; Verhamme et al. 2017).
are causally related (Dijkstra et al. 2016; Verhamme et al. 2017).
5.3 Using O32
Historically, it was challenging to find galaxies emitting ionizing photons. A breakthrough came by selecting samples based on the [O III] 5007 Å/[O II] 3727 Å flux ratio (O32), compactness, and large Hβ equivalent widths. Izotov et al. (2016a,b, 2018) found six out of six galaxies with O32 > 4 had 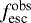 > 0.05. This selection technique appears to efficiently select galaxies that emit ionizing photons based on their easily observed rest-frame optical properties. If this selection criteria is universally applicable, it is a powerful technique to select LyC emitting galaxies. It enabled Faisst (2016) to extend local O32 scaling relations to high redshifts to predict that z > 6.5 galaxies could reionize the Universe.
> 0.05. This selection technique appears to efficiently select galaxies that emit ionizing photons based on their easily observed rest-frame optical properties. If this selection criteria is universally applicable, it is a powerful technique to select LyC emitting galaxies. It enabled Faisst (2016) to extend local O32 scaling relations to high redshifts to predict that z > 6.5 galaxies could reionize the Universe.
To test the effect of O32 on the ionizing escape fraction, we used the full sample of 15 galaxies with predicted 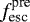 using the Lyman series (Eq. (5)) and O32 measurements from Paper I. The Cosmic Eye and J1429+0643 are excluded because they do not have measured O32, and GP 0303−0759 is excluded due to Milky Way contamination. By including these six galaxies, with unobserved LyC emission, we extended the O32 dynamic range and derived a relationship between O32 and
using the Lyman series (Eq. (5)) and O32 measurements from Paper I. The Cosmic Eye and J1429+0643 are excluded because they do not have measured O32, and GP 0303−0759 is excluded due to Milky Way contamination. By including these six galaxies, with unobserved LyC emission, we extended the O32 dynamic range and derived a relationship between O32 and 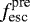 (Fig. 4).
(Fig. 4).
We first explored whether O32 scales with 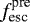 . We tested avariety of models for the scaling of the two variables: linearly, quadratically, or as a logarithm of each (or both) variable. We maximized the F-statistic for a model where the variables scale as
. We tested avariety of models for the scaling of the two variables: linearly, quadratically, or as a logarithm of each (or both) variable. We maximized the F-statistic for a model where the variables scale as 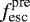 -
-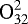 . This relationship is significant at the 3σ significance (p-value < 0.001; R2 = 0.61; Fig. 4). A linear regression (see the line in Fig. 4, with the shaded 95% confidence region) gives a relationship of
. This relationship is significant at the 3σ significance (p-value < 0.001; R2 = 0.61; Fig. 4). A linear regression (see the line in Fig. 4, with the shaded 95% confidence region) gives a relationship of
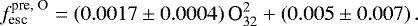 (15)
(15)
This predicts fesc using easily observed rest-frame optical emission lines.
Figure 4 also shows the empirical relationship from Faisst (2016). The two relations are discrepant at O32 values corresponding to fesc > 0.05. Equation (15) predicts that more than 10% of the ionizing photons escape galaxies when O32 > 5.7. Using the extrapolation of O32 with redshift from Faisst (2016), the average galaxy does not have fesc = 0.1 until z ~ 11. z ~ 11 is marginally consistent with the 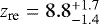 redshift of instantaneous reionization derived from the combination of the Planck lensing and polarization studies (Planck Collaboration XLVII 2016).
redshift of instantaneous reionization derived from the combination of the Planck lensing and polarization studies (Planck Collaboration XLVII 2016).
Figure 4 also compares Eq. (15) to a similar trend found by Izotov et al. (2018). These authors used a recently discovered galaxy, J1154+2443 with an exceptionally high 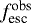 = 0.46 to derive a relationship between O32 and
= 0.46 to derive a relationship between O32 and 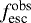 (the dot-dashed green curve in Fig. 4). Many of our
(the dot-dashed green curve in Fig. 4). Many of our 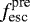 values agree with the Izotov et al. (2018) relation and the two relationships are consistent for
values agree with the Izotov et al. (2018) relation and the two relationships are consistent for 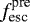 values up to fesc ~ 0.1. However, the Izotov et al. (2018) relationship increases more rapidly at higher O32 and
values up to fesc ~ 0.1. However, the Izotov et al. (2018) relationship increases more rapidly at higher O32 and 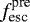 values than Eq. (15) does. This is apparent from the galaxy J1154+2443, which has O32 = 11.5 ± 1. The expected
values than Eq. (15) does. This is apparent from the galaxy J1154+2443, which has O32 = 11.5 ± 1. The expected 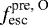 , 0.26 ± 0.06, is nearly 3σ lower than
, 0.26 ± 0.06, is nearly 3σ lower than 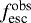 . This suggests that Eq. (15) may steepen at larger O32, but the steep portion of the Izotov et al. (2018) trend is largely driven by the one high
. This suggests that Eq. (15) may steepen at larger O32, but the steep portion of the Izotov et al. (2018) trend is largely driven by the one high 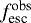 galaxy. If Eq. (15) steepens at higher O32 then the redshift required for galaxies to emit 10% of their ionizing photons would be lower than z ~ 11. Further observations, probing a uniform and large range of O32, are required to refine Eq. (15).
galaxy. If Eq. (15) steepens at higher O32 then the redshift required for galaxies to emit 10% of their ionizing photons would be lower than z ~ 11. Further observations, probing a uniform and large range of O32, are required to refine Eq. (15).
Studies often use low NHI values to explain the correlation between fesc and O32 (so-called “density-bounded” regimes; Jaskot & Oey 2013; Zackrisson et al. 2013; Nakajima et al. 2013). However, O32 arises both from high ionization parameter (as required in the density-bounded regime) and from low metallicities (Nagao et al. 2006; Nakajima & Ouchi 2014; Shapley et al. 2015; Sanders et al. 2016; Chisholm et al. 2017; Strom et al. 2017). As shown in Paper I and Fig. 2, LyC photons escape because the H I covering fraction and dust attenuation are low, not because the H I column density is low. Rather, the low attenuation likely connects O32 and fesc. Low attenuation could be related to high ionization parameters (dust is destroyed) and/or low metallicities (dust is not created). In this scenario, the lower dust content could mean that there are not enough metals to uniformly fill the gas, or that there are not enough metals to efficiently cool the gas. Both result in channels with little dust or H I along the line of sight, allowing for more ionizing photons to escape the galaxy. We find a 2σ trend between O32 and EB−V in our sample. Thus, the correlation between fesc and O32 may reflect the low dust attenuation of LyC emitters. However, further observations, spanning a large range of O32, and more theoretical work are required to confirm and understand this observed correlation.
 |
Fig. 4 Predicted Lyman continuum escape fraction ( |
5.4 Usingmultiple methods to predict fesc
Above, we demonstrated that the Si II absorption lines, 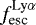 , and O32 consistently predict
, and O32 consistently predict 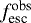 , but the O32 method needs further data to verify. These three prediction methods have similar deviations from
, but the O32 method needs further data to verify. These three prediction methods have similar deviations from 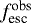 as using the H I absorption lines. However, the individual methods do not always precisely reproduce
as using the H I absorption lines. However, the individual methods do not always precisely reproduce 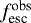 . If the LyC cannot be directly observed, then
. If the LyC cannot be directly observed, then 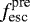 should be calculated using as many of the three methods as possible. The mean and standard deviation of the three different methods then approximates
should be calculated using as many of the three methods as possible. The mean and standard deviation of the three different methods then approximates 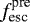 . As an example, Tol 1247−232 has a largely discrepant
. As an example, Tol 1247−232 has a largely discrepant 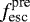 , but when the average of
, but when the average of 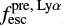 ,
, 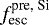 , and
, and 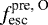 are taken
are taken 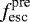 = 0.038 ± 0.022, which is consistent, within 2σ, with
= 0.038 ± 0.022, which is consistent, within 2σ, with 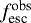 . Estimating fesc with multiple methods reduces the systematic errors of individual observations and produces more consistent fesc predictions. We illustrate this in the next section with observations of both high- and low-redshift galaxies.
. Estimating fesc with multiple methods reduces the systematic errors of individual observations and produces more consistent fesc predictions. We illustrate this in the next section with observations of both high- and low-redshift galaxies.
It is important to produce a statistical sample of predicted fesc values with all of the different methods to determine the systematics of each method. For instance, direct observations of the LyC, as well as fesc inferred from the Lyman series, Lyα, and Si II lines are all line-of-sight geometry dependent estimates of fesc, such that the inferred value substantially changes whether the orientation is through a hole in the H I or through an H I cloud. Conversely, the O32 ratio depends less on the geometry because the ISM is relatively optically thin to the [O III] and [O II] emission. These effects may be imprinted on the different predicted fesc values, and variations in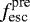 may illustrate physical geometric variations in LyC emitting galaxies.
may illustrate physical geometric variations in LyC emitting galaxies.
6 Predicting the Lyman continuum escape fractions of galaxies without Lyman series observations
The relations presented in the previous section enable estimation of fesc, even if the Lyman continuum or Lyman series are not observable. This is especially important for z > 4 galaxies because the IGM transmissionof the LyC is <38% at z> 4 (Songaila 2004), making LyC detections even more challenging. The three indirect probes in the previous section may be the only way to estimate the emissivity of high-redshift galaxies reionizing the Universe (Eq. (1)). We test the methods of Sect. 5 by fitting the rest-frame UV spectra between 1200−1500Å of a few test cases in the same manner as we did in Sect. 5. These test cases are the Cosmic Horseshoe, the MEGaSaURA sample, Haro 11, a recently discovered strong LyC emitter from Izotov et al. (2018), and high-redshift confirmed LyC emitters. Because of the uncertainty of the O32 relation (see Sect. 5.3), we only comment on what the observed O32 values imply for 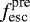 . Table 3 lists the parameters used to predict the escape fractions for each galaxy.
. Table 3 lists the parameters used to predict the escape fractions for each galaxy.
Predicted Lyman continuum escape fractions for the 8 galaxies with predicted escape fractions higher than 0.01, but without Lyman series or Lyman continuum observations.
6.1 The Cosmic Horseshoe
The Cosmic Horseshoe (Belokurov et al. 2007) is an ideal test case for these methods. At z = 2.38, it is one of the best-studied gravitationally lensed galaxies. However, from the methods presented in Sect. 5, we would not expect the Cosmic Horseshoe to strongly emit ionizing photons. Restframe UV spectra from the MEGaSaURA sample (Fig. 5; Rigby et al. 2018) show a young stellar population with relatively deep Si II absorption lines (i.e., large 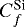 ). Similarly, Lyα observations from the Echellette Spectrograph and Imager on the KECK II telescope only find
). Similarly, Lyα observations from the Echellette Spectrograph and Imager on the KECK II telescope only find 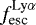 = 0.08 (Quider et al. 2009). Moreover, the Cosmic Horseshoe has a relatively small extinction-corrected O32 (2; Hainline et al. 2009). The suspicions of low fesc are confirmed by deep HST LyC imaging that measures an upper limit of the absolute escape fraction of
= 0.08 (Quider et al. 2009). Moreover, the Cosmic Horseshoe has a relatively small extinction-corrected O32 (2; Hainline et al. 2009). The suspicions of low fesc are confirmed by deep HST LyC imaging that measures an upper limit of the absolute escape fraction of 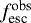 < 0.02 (Vasei et al. 2016). Vasei et al. (2016) noted that there was a 20% chance that the low
< 0.02 (Vasei et al. 2016). Vasei et al. (2016) noted that there was a 20% chance that the low 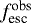 arises from IGM attenuation. While the IGM attenuation has a low probability of impacting the
arises from IGM attenuation. While the IGM attenuation has a low probability of impacting the 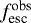 , proper simulations of the IGM opacity can quantify the impact of the IGM opacity at higher redshifts (Shapley et al. 2016).
, proper simulations of the IGM opacity can quantify the impact of the IGM opacity at higher redshifts (Shapley et al. 2016).
From the stellar continuum fit in Fig. 5 (red line), we measured an EB−V of 0.16 mag, consistent with Quider et al. (2009). The Si II 1260 Å profile has a 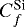 of 0.77 (corresponding to a H I covering fraction of
of 0.77 (corresponding to a H I covering fraction of 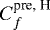 = 0.94 using Eq. (11)). The escape fraction predicted using
= 0.94 using Eq. (11)). The escape fraction predicted using 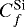 and Eq. (12) is
and Eq. (12) is 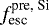 = 0.009. The measured
= 0.009. The measured 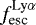 = 0.08 leads to a LyC escape fraction of
= 0.08 leads to a LyC escape fraction of 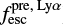 = 0.012 (Eq. (13)). Finally, the extinction-corrected O32 is small, such that Eq. (15) implies a low
= 0.012 (Eq. (13)). Finally, the extinction-corrected O32 is small, such that Eq. (15) implies a low 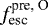 =0.011 (Eq. (15)).
=0.011 (Eq. (15)).
Combining the two robust estimates of 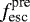 (the Si II and Lyα values), we derive a mean estimate of
(the Si II and Lyα values), we derive a mean estimate of 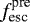 = 0.011 ± 0.002 (Table 4). This result is also consistent with the escape fraction predicted by the O32 scaling relation. The
= 0.011 ± 0.002 (Table 4). This result is also consistent with the escape fraction predicted by the O32 scaling relation. The 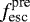 satisfies the upper limit of the absolute escape
satisfies the upper limit of the absolute escape 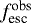 < 0.02 from the HST imaging (Vasei et al. 2016).
< 0.02 from the HST imaging (Vasei et al. 2016).
 |
Fig. 5 Top panel: rest-frame UV spectra between 1150 and 1400Å of the Cosmic Horseshoe, a z = 2.38 gravitationally lensed galaxy from the MEGaSaURA sample (Rigby et al. 2018). Overplotted in red is the best-fit STARBURST99 stellar continuum fit. This fit measures EB−V = 0.16 mag. The error spectrum is included underneath in dark green. Bottom panels: Si II 1190 Å doublet (left) and Si II 1260 Å singlet (right). The corresponding |
Observed properties of SGAS J0900+2234.
6.2 Other MEGaSaURA galaxies
The Cosmic Horseshoe is one of 14 galaxies within the MEGaSaURA sample (three are included in the full sample in Table 2; Rigby et al. 2018). We also predicted the escape fraction for the full MEGaSaURA sample. Fitting the stellar continua and Si II 1260 Å covering fractions of the sample predicts that only six (42%) have 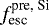 > 0.01 (Table 3 gives the predicted escape fractions of these six galaxies). Two MEGaSaURA galaxies with low
> 0.01 (Table 3 gives the predicted escape fractions of these six galaxies). Two MEGaSaURA galaxies with low 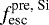 < 0.01, SGAS J1226+2152 and SGAS J1527+0652, also have low O32 values of 1.4 and 1.6, respectively (Table 2; Wuyts et al. 2012). These low O32 values correspond to
< 0.01, SGAS J1226+2152 and SGAS J1527+0652, also have low O32 values of 1.4 and 1.6, respectively (Table 2; Wuyts et al. 2012). These low O32 values correspond to 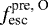 < 0.01, consistent with their low
< 0.01, consistent with their low 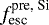 . No MEGaSaURA galaxy has
. No MEGaSaURA galaxy has 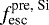 > 0.1. This is consistent with the nondetection of LyC photons in the individual spectra (Rigby et al. 2018).
> 0.1. This is consistent with the nondetection of LyC photons in the individual spectra (Rigby et al. 2018).
SGAS J0900+2234, a z = 2.03 lensed galaxy, is the second best MEGaSaURA test case. First, combining the rest-frame optical observations from Bian et al. (2010) with the MEGaSaURA data estimates the Lyα escape fraction to be 0.09 (Table 4). This 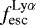 leads to
leads to 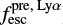 = 0.025, consistent with the
= 0.025, consistent with the 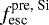 = 0.026 (Table 3). There are no literature [O II] 3727 Å observations for this galaxy. Consequently, we predicted
= 0.026 (Table 3). There are no literature [O II] 3727 Å observations for this galaxy. Consequently, we predicted 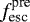 = 0.026 ± 0.001.
= 0.026 ± 0.001.
This lensed galaxy has both LyC (F218W; rest-frame central wavelength of 734 Å; PID: 13349; PI: X. Fan; Bian et al. 2017) and rest-frame FUV (F475W; rest-frame central wavelength of 1566 Å; PID: 11602; PI: S. Allam) HST imaging. Bian et al. (2017) have not detected significant LyC photons from this lensed galaxy, but the HST images provide weak constraints on 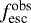 . Following Eq. (1) from Leitet et al. (2013), we estimated
. Following Eq. (1) from Leitet et al. (2013), we estimated 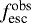 as
as
![\begin{equation*} f^{\text{obs}}_{\text{esc}} = \frac{(F[1500]/F[900])_{\text{int}}}{(F[1500]/F[900])_{\text{obs}}} 10^{-0.4 E_{B-V} k_{1500}},\end{equation*}](/articles/aa/full_html/2018/08/aa32758-18/aa32758-18-eq196.png) (16)
(16)
where we took k1500 from the Reddy et al. (2016a) attenuation law and EB−V from the STARBURST99 stellar continuum fit. The intrinsic flux ratio is measured from the STARBURST99 stellar population fit to the spectra (Table 4), and is similar to values from Izotov et al. (2016b) for an instantaneous 7 Myr stellar population (the fitted stellar age). ![$(F[1500]/F[900])_{\text{obs}}$](/articles/aa/full_html/2018/08/aa32758-18/aa32758-18-eq197.png) is the observed ratio of the flux at 1500 Å and 900 Å, respectively. The F[1500] and F[900] values are measured from the exact same regions in the F475W and F218W images. F[900] has a low significance (1.3σ; Table 4), which led Bian et al. (2017) to not report a significant LyC detection. We measured
is the observed ratio of the flux at 1500 Å and 900 Å, respectively. The F[1500] and F[900] values are measured from the exact same regions in the F475W and F218W images. F[900] has a low significance (1.3σ; Table 4), which led Bian et al. (2017) to not report a significant LyC detection. We measured 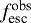 = 0.015 ± 0.012, consistent, within 1σ, with
= 0.015 ± 0.012, consistent, within 1σ, with 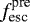 (Table 3).
(Table 3).
6.3 Haro 11
Haro 11, a nearby star-forming galaxy has a measured 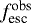 = 0.033 ± 0.007 from Far-Ultraviolet Spectroscopic Explorer (FUSE) observations (Bergvall et al. 2006; Leitet et al. 2011). A recent HST/COS spectrum of Knot C in Haro 11 covers rest-frame 1130–1760 Å (Heckman et al. 2011; Alexandroff et al. 2015). We measured EB−V = 0.124 mags and
= 0.033 ± 0.007 from Far-Ultraviolet Spectroscopic Explorer (FUSE) observations (Bergvall et al. 2006; Leitet et al. 2011). A recent HST/COS spectrum of Knot C in Haro 11 covers rest-frame 1130–1760 Å (Heckman et al. 2011; Alexandroff et al. 2015). We measured EB−V = 0.124 mags and 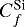 = 0.60 from this COS spectrum (Chisholm et al. 2016). This
= 0.60 from this COS spectrum (Chisholm et al. 2016). This 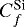 value agrees with the recent value from Rivera-Thorsen et al. (2017) and leads to
value agrees with the recent value from Rivera-Thorsen et al. (2017) and leads to 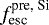 = 0.036. Keenan et al. (2017) have measured the O32 of Haro 11 using HST/WFC3 imaging. While the imaging makes it challenging to robustly subtract the stellar continuum, the O32 ratio is between 2 and 4 for Knot C. This corresponds to a
= 0.036. Keenan et al. (2017) have measured the O32 of Haro 11 using HST/WFC3 imaging. While the imaging makes it challenging to robustly subtract the stellar continuum, the O32 ratio is between 2 and 4 for Knot C. This corresponds to a 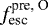 = 0.01−0.03 (Eq. (15)). Both
= 0.01−0.03 (Eq. (15)). Both 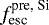 and
and 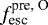 are broadly consistent, within 1σ, with
are broadly consistent, within 1σ, with 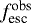 .
.
6.4 J1154+2443
Izotov et al. (2018) have recently discovered a new low-redshift LyC emitter, J1154+2443, with HST/COS spectra. At 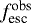 = 0.46 ± 0.02, it has the highest observed escape fraction in the local Universe. Izotov et al. (2018) have listed properties of J1154+2443 that nicely align with those that we suggest lead to a high
= 0.46 ± 0.02, it has the highest observed escape fraction in the local Universe. Izotov et al. (2018) have listed properties of J1154+2443 that nicely align with those that we suggest lead to a high 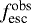 : low metallicity (12 + log(O/H) = 7.65), low extinction (Av= 0.145, or EB−V = 0.06 using their Rv = 2.4), high
: low metallicity (12 + log(O/H) = 7.65), low extinction (Av= 0.145, or EB−V = 0.06 using their Rv = 2.4), high 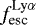 (
(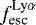 = 0.98), and large O32 (O32 = 11.5). Using the
= 0.98), and large O32 (O32 = 11.5). Using the 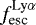 and converting the attenuation measured with the Cardelli et al. (1989) curve to an attenuation using the Reddy et al. (2016a) relation, we predict that J1154+2443 would have
and converting the attenuation measured with the Cardelli et al. (1989) curve to an attenuation using the Reddy et al. (2016a) relation, we predict that J1154+2443 would have 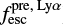 = 0.48 (Table 3). This is consistent with
= 0.48 (Table 3). This is consistent with 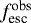 found by Izotov et al. (2018). In Sect. 5.3 we found the O32 relation under-predicts the
found by Izotov et al. (2018). In Sect. 5.3 we found the O32 relation under-predicts the 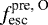 of this galaxy by 3σ. This suggests that more observations are required to better constrain the O32 relation at large O32.
of this galaxy by 3σ. This suggests that more observations are required to better constrain the O32 relation at large O32.
6.5 High-redshift LyC emitters
While mostof the confirmed LyC detections have come at low redshift (z < 0.4), four z ~ 3−4 galaxies have confirmed 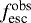 (Vanzella et al. 2015, 2018; de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017). These galaxies are typically more extreme LyC emitters than the z ~ 0 galaxies (
(Vanzella et al. 2015, 2018; de Barros et al. 2016; Shapley et al. 2016; Bian et al. 2017). These galaxies are typically more extreme LyC emitters than the z ~ 0 galaxies (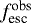 = 0.2−0.7) and have characteristics that Sect. 5 suggests lead to high
= 0.2−0.7) and have characteristics that Sect. 5 suggests lead to high 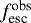 : low EB−V, weak Si II absorption lines, and strong Lyα. Ion2 (Vanzella et al. 2015) is the only high-redshift galaxy with literature limits for O32 or
: low EB−V, weak Si II absorption lines, and strong Lyα. Ion2 (Vanzella et al. 2015) is the only high-redshift galaxy with literature limits for O32 or 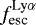 , while no high-redshift galaxy has a published
, while no high-redshift galaxy has a published 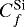 . Ion2 has an extreme
. Ion2 has an extreme 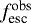
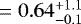 , an upper limit of O32 > 15, a very low dust extinction upper limit (EB−V < 0.04 mag), a large lower limit of
, an upper limit of O32 > 15, a very low dust extinction upper limit (EB−V < 0.04 mag), a large lower limit of 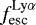 > 0.78, and a nondetected Si II 1260 Å absorption line (de Barros et al. 2016). Using the methods in Sect. 5, we predict
> 0.78, and a nondetected Si II 1260 Å absorption line (de Barros et al. 2016). Using the methods in Sect. 5, we predict 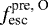 > 0.39 and
> 0.39 and 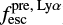 > 0.49. These predicted lower limits of the LyC escape fraction are consistent with
> 0.49. These predicted lower limits of the LyC escape fraction are consistent with 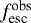 = 0.64 from de Barros et al. (2016).
= 0.64 from de Barros et al. (2016).
6.6 Prospects for the epoch of reionization
The above examples indicate that the methods from Sect. 5 can powerfully predict the fesc of high-redshift galaxies. JWST and ELTs will observe the rest-frame UV of field and lensed z = 6−8 galaxies to estimate 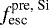 . Additionally, optical emission lines will be redshifted to 3.5–4.5 μm, such that the NIRSpec instrument on JWST will measure Hα and O32. These observations will estimate
. Additionally, optical emission lines will be redshifted to 3.5–4.5 μm, such that the NIRSpec instrument on JWST will measure Hα and O32. These observations will estimate 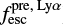 and
and 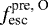 . Combined, the three methods predict fesc values that are broadly consistent with the observed escape fractions of local Lyman continuum emitting galaxies. The escape fractions, the total number of ionizing photons, and the luminosity functions will then describe whether star-forming galaxies reionized the z = 6−8 Universe.
. Combined, the three methods predict fesc values that are broadly consistent with the observed escape fractions of local Lyman continuum emitting galaxies. The escape fractions, the total number of ionizing photons, and the luminosity functions will then describe whether star-forming galaxies reionized the z = 6−8 Universe.
7 Summary
We analyzed the rest-frame UV spectra of nine low-redshift (z < 0.3) star-forming galaxies that emit ionizing photons. In a companion paper (Gazagnes et al. 2018), we fit the stellar continuum, dust attenuation, Lyman series absorption lines (H I absorption lines blueward of Lyα), and ISM metal absorption lines. Here, we combined the H I column densities and covering fractions with the dust attenuations to predict the fraction of ionizing photons that escape local galaxies. The Lyman continuum and Lyman series both directly trace the escape of ionizing photons, but neither are observable at redshifts greater than 4. Therefore, we tested three indirect ways of estimating fesc: the Si II absorption lines (Sect. 5.1), the Lyα escape fraction (Sect. 5.2), and the [O III]/[O II] flux ratio (Sect. 5.3). We then used these methods to predict the escape fractions of galaxies without Lyman series observations to illustrate how these indirect methods can estimate the escape fractions of high-redshift galaxies (Sect. 6).
The major results of this study are as follows:
- 1.
The radiative transfer equation (Eq. (5)), along with the fits to the dust attenuation, H I covering fraction, and H I column density reproduce the observed fesc to within 1.4σ (Fig. 1). The Lyman series absorption properties accurately predict the escape fraction of ionizing photons.
- 2.
As shown in Gazagnes et al. (2018), the observed H I column densities indicate that the Lyman continuum is optically thick. Instead, ionizing photons escape because the covering fraction is less than one (Fig. 2).
- 3.
The covering fraction alone overpredicts the escape fraction. While geometry dependent (see the discussion in Sect 3.2), dust attenuation is a key ingredient for the escape of ionizing photons (Fig. 2). Estimating the escape fraction as (1 – Cf) will overestimate the true escape fraction.
- 4.
Indirect methods also provide accurate estimates of the escape fraction of ionizing photons. The Si II absorption line and extinction-corrected Lyα escape fraction predicts fesc with similar accuracy as the Lyman series (Fig. 3), while the square of the [O III]/[O II] flux ratio scales strongly with fesc (3σ significance; Fig. 4). The [O III]/[O II] relation agrees with previous studies for low [O III]/[O II] values, but underpredicts the fesc of higher [O III]/[O II] values. This suggests that a larger sample of large [O III]/[O II] galaxies is required to constrain the full trend.
- 5.
We applied the indirect methods to galaxies without Lyman series observations to illustrate how these methods predict fesc (Table 3). In all cases, the fesc values predicted with indirect methods are consistent with either the observed fesc or upper limits of fesc. Most (58%) of the z = 1.7−3.6 MEGaSaURA galaxies have low escape fractions (fesc ≤ 1%), while the remaining galaxies have predicted fesc ~ 1−8% (Sect. 6.2). Additionally, the predicted escape fraction of J1154+2443, a recently discovered local galaxy with a high escape fraction (0.46), agrees with the observed value. Overall, the predicted fesc values are consistent with the observed escape fractions.
This analysis presents new methods to measure and analyze the escape fractions of galaxies in the epoch of reionization using JWST and future ELT (Sect. 6.6). Deep rest-frame UV and optical spectroscopy of these high-redshift galaxies may determine whether high-redshift galaxies emit sufficient ionizing photons to reionize the Universe or if other sources are required.
Acknowledgements
We would like to thank the anonymous referee for helpful and constructive suggestions that strengthened the scope and content of this paper.
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Alexandroff, R. M., Heckman, T. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 810, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, T. A., & Sargent, W. L. W. 1997, AJ, 113, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., Fan, X., White, R. L., et al. 2001, AJ, 122, 2850 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Evans, N. W., Moiseev, A., et al. 2007, ApJ, 671, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bergvall, N., Zackrisson, E., Andersson, B.-G., et al. 2006, A&A, 448, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, F., Fan, X., Bechtold, J., et al. 2010, ApJ, 725, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, F., Fan, X., McGreer, I., Cai, Z., & Jiang, L. 2017, ApJ, 837, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2007, MNRAS, 382, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Borthakur, S., Heckman, T. M., Leitherer, C., & Overzier, R. A. 2014, Science, 346, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., & Franx, M. 2006, ApJ, 653, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012a, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012b, ApJ, 752, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chisholm, J., Tremonti, C. A., Leitherer, C., Chen, Y., & Wofford, A. 2016, MNRAS, 457, 3133 [NASA ADS] [CrossRef] [Google Scholar]
- Chisholm, J., Orlitová, I., Schaerer, D., et al. 2017, A&A, 605, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Barros, S., Vanzella, E., Amorín, R., et al. 2016, A&A, 585, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dijkstra, M., Gronke, M., & Venkatesan, A. 2016, ApJ, 828, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Henry, A., Martin, C. L., et al. 2015, ApJ, 806, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Robertson, B. E., et al. 2012, MNRAS, 420, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L. 2016, ApJ, 829, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L., Ryan, Jr. R. E., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Cristiani, S., & Vanzella, E. 2012, MNRAS, 425, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Gazagnes, S., Chisholm, J., Schaerer, D., et al. 2018, A&A, 616, A29 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, J. C., Froning, C. S., Osterman, S., et al. 2012, ApJ, 744, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Hainline, K. N., Shapley, A. E., Kornei, K. A., et al. 2009, ApJ, 701, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., Barlow, T. A., Junkkarinen, V., & Burbidge, E. M. 1997, ApJ, 478, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ouchi, M., Ono, Y., et al. 2018, PASJ, 70, S11 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Borthakur, S. 2016, ApJ, 822, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Borthakur, S., Overzier, R., et al. 2011, ApJ, 730, 5 [Google Scholar]
- Heckman, T. M., Alexandroff, R. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 809, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, A., Scarlata, C., Martin, C. L., & Erb, D. 2015, ApJ, 809, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M., Kawamata, R., Ouchi, M., et al. 2018, ApJ, 854, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Orlitová, I., Schaerer, D., et al. 2016a, Nature, 529, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Thuan, T. X., et al. 2016b, MNRAS, 461, 3683 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Worseck, G., et al. 2018, MNRAS, 474, 4514 [NASA ADS] [CrossRef] [Google Scholar]
- Jaskot, A. E., & Oey, M. S. 2013, ApJ, 766, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T., Stark, D. P., & Ellis, R. S. 2012, ApJ, 751, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. A., Ellis, R. S., Schenker, M. A., & Stark, D. P. 2013, ApJ, 779, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. P., Oey, M. S., Jaskot, A. E., & James, B. L. 2017, ApJ, 848, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhlen, M., & Faucher-Giguère, C.-A. 2012, MNRAS, 423, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Leethochawalit, N., Jones, T. A., Ellis, R. S., Stark, D. P., & Zitrin, A. 2016, ApJ, 831, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Leitet, E., Bergvall, N., Piskunov, N., & Andersson, B.-G. 2011, A&A, 532, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitet, E., Bergvall, N., Hayes, M., Linné, S., & Zackrisson, E. 2013, A&A, 553, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., & Heckman, T. M. 1995, ApJS, 96, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Hernandez, S., Lee, J. C., & Oey, M. S. 2016, ApJ, 823, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Livermore, R. C., Finkelstein, S. L., & Lotz, J. M. 2017, ApJ, 835, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Haardt, F., & Rees, M. J. 1999, ApJ, 514, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Analysis Software and Systems XVIII, Astronomical Data, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marshall, J. L., Burles, S., Thompson, I. B., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701454 [CrossRef] [Google Scholar]
- Meiksin, A. 2005, MNRAS, 356, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakajima, K., & Ouchi, M. 2014, MNRAS, 442, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2013, ApJ, 769, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2014, ApJ, 786, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., Labbé, I., & Stefanon, M. 2018, ApJ, 855, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Onoue, M., Kashikawa, N., Willott, C. J., et al. 2017, ApJ, 847, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ono, Y., Egami, E., et al. 2009, ApJ, 696, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XLVII., et al. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschnig, J., Hayes, M., Östlin, G., et al. 2017, MNRAS, 469, 3252 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Pettini, M., Shapley, A. E., & Steidel, C. C. 2009, MNRAS, 398, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., & Bogosavljević, M. 2016a, ApJ, 828, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., Bogosavljević, M., & Shapley, A. E. 2016b, ApJ, 828, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, F., Marchesi, S., Shankar, F., La Franca, F., & Civano, F. 2017, MNRAS, 465, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J. R., Bayliss, M. B., Sharon, K., et al. 2018, AJ, 155, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Thorsen, T. E., Östlin, G., Hayes, M., & Puschnig, J. 2017, ApJ, 837, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Furlanetto, S. R., Schneider, E., et al. 2013, ApJ, 768, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016, ApJ, 816, 23 [Google Scholar]
- Schaerer, D., & de Barros, S. 2010, A&A, 515, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Reddy, N. A., Kriek, M., et al. 2015, ApJ, 801, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Strom, A. L., et al. 2016, ApJ, 826, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A. 2004, AJ, 127, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, A. L., Steidel, C. C., Rudie, G. C., et al. 2017, ApJ, 836, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Grazian, A., Hayes, M., et al. 2010, A&A, 513, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzella, E., de Barros, S., Castellano, M., et al. 2015, A&A, 576, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzella, E., de Barros, S., Vasei, K., et al. 2016, ApJ, 825, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Nonino, M., Cupani, G., et al. 2018, MNRAS, 476, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Vasei, K., Siana, B., Shapley, A. E., et al. 2016, ApJ, 831, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Orlitová, I., Schaerer, D., & Hayes, M. 2015, A&A, 578, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Orlitová, I., Schaerer, D., et al. 2017, A&A, 597, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakker, B. P., Hernandez, A. K., French, D. M., et al. 2015, ApJ, 814, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Delorme, P., Reylé, C., et al. 2010, AJ, 139, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Prochaska, J. X., O’Meara, J. M., et al. 2014, MNRAS, 445, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Prochaska, J. X., Hennawi, J. F., & McQuinn, M. 2016, ApJ, 825, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, E., Rigby, J. R., Gladders, M. D., et al. 2012, ApJ, 745, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., Inoue, A. K., & Jensen, H. 2013, ApJ, 777, 39 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Measured properties of the Lyman continuum emitting sample from Gazagnes et al. (2018) in order of decreasing 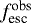 .
.
Measured properties for the 7 galaxies from Gazagnes et al. (2018) without observed Lyman continuum escape fractions.
Predicted Lyman continuum escape fractions for the 8 galaxies with predicted escape fractions higher than 0.01, but without Lyman series or Lyman continuum observations.
All Figures
 |
Fig. 1 Observed Lyman continuum escape fraction ( |
| In the text | |
 |
Fig. 2 Observed Lyman continuum escape fraction ( |
| In the text | |
 |
Fig. 3 Left panel: observed Lyman continuum escape fraction ( |
| In the text | |
 |
Fig. 4 Predicted Lyman continuum escape fraction ( |
| In the text | |
 |
Fig. 5 Top panel: rest-frame UV spectra between 1150 and 1400Å of the Cosmic Horseshoe, a z = 2.38 gravitationally lensed galaxy from the MEGaSaURA sample (Rigby et al. 2018). Overplotted in red is the best-fit STARBURST99 stellar continuum fit. This fit measures EB−V = 0.16 mag. The error spectrum is included underneath in dark green. Bottom panels: Si II 1190 Å doublet (left) and Si II 1260 Å singlet (right). The corresponding |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.