| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732353 | |
| Published online | 21 August 2018 | |
Energy conversion in cometary atmospheres
Hybrid modeling of 67P/Churyumov–Gerasimenko
1
Department of Physics, Umeå University,
Umeå,
Sweden
e-mail: jesper.lindkvist@umu.se
2
Royal Belgian Institute for Space Aeronomy (BIRA-IASB),
Brussels,
Belgium
3
Swedish Institute of Space Physics,
Kiruna,
Sweden
4
Department of Physics, University of Oslo,
Oslo,
Norway
5
Department of Electronics and Nanoengineering, Aalto University,
Espoo,
Finland
6
Department of Physics and Technology, University of Tromsø,
Tromsø,
Norway
7
School of Electrical Engineering, KTH Royal Institute of Technology,
Stockholm,
Sweden
Received:
23
November
2017
Accepted:
30
May
2018
Aims. We wish to investigate the energy conversion between particles and electromagnetic fields and determine the location where it occurs in the plasma environment of comets.
Methods. We used a hybrid plasma model that included photoionization, and we considered two cases of the solar extreme ultraviolet flux. Other parameters corresponded to the conditions of comet 67P/Churyumov–Gerasimenko at a heliocentric distance of 1.5 AU.
Results. We find that a shock-like structure is formed upstream of the comet and acts as an electromagnetic generator, similar to the bow shock at Earth that slows down the solar wind. The Poynting flux transports electromagnetic energy toward the inner coma, where newly born cometary ions are accelerated. Upstream of the shock-like structure, we find local energy transfer from solar wind ions to cometary ions. We show that mass loading can be a local process with a direct transfer of energy, but also part of a dynamo system with electromagnetic generators and loads.
Conclusions. The energization of cometary ions is governed by a dynamo system for weak ionization, but changes into a large conversion region with local transfer of energy directly from solar wind protons for high ionization.
Key words: comets: individual: 67P/Churyumov–Gerasimenko / Sun: UV radiation / solar wind / methods: numerical / plasmas / acceleration of particles
© ESO 2018
1 Introduction
Comets show a highly variable interaction with their environments as their distance to the Sun changes. Sublimated and emitted material from the comet forms a neutral cloud that becomes partially ionized by solar extreme ultraviolet (EUV) radiation and other processes. Far from the Sun, the solar wind directly impacts the surface of the comet nucleus in an asteroid-like interaction, while at smaller heliospheric distances, the ionized cometary atmosphere (coma) becomes an obstacle to the solar wind. For high outgassing rates, the coma can become dense enough to form plasma boundaries, creating a cometary magnetosphere (Johnstone et al. 1993; Szegö et al. 2000; Cravens & Gombosi 2004).
These magnetospheres have been observed in situ by spacecraft flybys (Giotto, ICE, Vega1, Vega2, Suisei, Deep Space 1) or spacecraft impacting (Deep Impact, Stardust) comets of varying activities and sizes, such as 1P/Halley, 26P/Grigg–Skjellerup, 19P/Borrelly, and 21P/Giacobini–Zinner (Neugebauer et al. 1990; Coates & Jones 2009). The Rosetta mission rendezvoused with comet 67P/Churyumov–Gerasimenko, a weakly active Jupiter-family comet, for the first time. Rosetta orbited the comet throughout its perihelion passage in 2014–2016 (Glassmeier et al. 2007). Rosetta made continuous in situ observations of the plasma environment with a suite of five dedicated plasma instruments (Carr et al. 2007).
One of the objectives of the Rosetta mission was to understand the formation of boundary structures within the cometary atmosphere, and how they evolve with the comet activity (Simon Wedlund et al. 2016; Glassmeier 2017). The cometary atmosphere becomes ionized by EUV radiation, and locally mass-loads the solar wind. These particles, consisting mostly of water-group ions, are accelerated by the solar wind convective electric field, transferring energy and momentum from the solar wind to the coma. As momentum is transferred to the newly ionized water ions, the solar wind protons are deflected in the opposite direction. For weak mass-loading, when the ambient electromagnetic fields are mostly undisturbed, modeling shows that water ions will accelerate along the solar wind electric field and E-cross-B drift with a gyroradius much larger than the water ion source region (Kallio & Jarvinen 2012; Lindkvist et al. 2017). The picked-up electrons, however, have a gyroradius much smaller than the source region and will therefore behave more fluid-like. Charge separation between electrons and cometary ions will occur (Nilsson et al. 2015b; Behar et al. 2016b). This charge separation could build up a self-polarization of the coma for low-activity comets in the same way as that of a plasmoid penetrating a magnetic barrier (Brenning et al. 1991, 2005).
Energy will be exchanged from the solar wind particles to the cometary ions via the electromagnetic fields. The energy budget of an interaction can be seen from the Poynting theorem, which describes the conservation of electromagnetic energy. When the displacement current is neglected, the change of electromagnetic energy density over time is given by
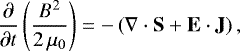 (1)
(1)
where 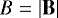 is the magnetic field magnitude, and S = E × B ∕μ0 is the Poynting flux, with μ0 as the permeability of vacuum. The left-hand side of Eq. (1) describes the change in electromagnetic energy density over time, and it is zero at steady state. At steady state, the power density (rate of work done by the electric field) is balanced by the divergence of the Poynting flux (the transfer of electromagnetic energy to or from that region).
is the magnetic field magnitude, and S = E × B ∕μ0 is the Poynting flux, with μ0 as the permeability of vacuum. The left-hand side of Eq. (1) describes the change in electromagnetic energy density over time, and it is zero at steady state. At steady state, the power density (rate of work done by the electric field) is balanced by the divergence of the Poynting flux (the transfer of electromagnetic energy to or from that region).
Energy transfer in magnetized plasmas has been studied at Earth’s magnetospheres (also at Venus by, e.g., Saunders & Russell 1986) by considering the power density, P = E ⋅J, where E is the electric field and J is the current density. The power density is the rate at which the electromagnetic fields do work on charged particles. A generator, E ⋅ J < 0, stores energy in the fields, while a load, E ⋅J > 0, transfers energy to particles. In the Earth’s magnetosphere, loads and generators have been identified in the magnetotail plasma sheet (Hamrin et al. 2011) as well as in the regions along the magnetopause (Rosenqvist et al. 2008). Earth’s bow shock drives subsolar reconnection on the dayside magnetopause for southward-oriented interplanetary magnetic field (Siebert & Siscoe 2002), acting as a generator and slowing down the solar wind flow. Identifying similar regions at comets will tell us where the energy dispersion takes place.
Hybrid plasma models are adequate tools for resolving the heavy ion kinetics in cometary atmospheres. The draping of the magnetic fields and investigation of the diamagnetic cavity has been reported by Koenders et al. (2015), for instance. Later, Simon Wedlund et al. (2016) used hybrid models to study the effect that different processes (e.g., charge exchange with solar wind helium) have on the size and shape of the cometary atmosphere. Comparisons between magnetohydrodynamics (MHD) and hybrid models show distinctive shortcomings in MHD when modeling a weak comet (Rubin et al. 2014) because these models are not able to resolve the extremely large gyroradius of the cometary ions. In the hybrid approximation, the electron motion is averaged over one gyroperiod and therefore does not resolve wave phenomena at electron scales.
We here use a hybrid model to study the energy transfer between particles and electromagnetic fields for comet 67P/Churyumov–Gerasimenko (67P). We consider the conditions at the heliocentric distance 1.5 AU (when 67P was at the orbit of Mars) for two extreme conditions of solar EUV radiation. We isolate and identify the regions of energy conversion in the cometary atmosphere, and compare the two cases.
2 Model
To model the interaction between comet 67P and the solar wind plasma, we used a self-consistent hybrid plasma model in which we included the production of cometary ions. In the hybrid approximation, ions are treated as particles and electrons as a massless charge-neutralizing fluid. Below we present the governing equations for the solver and the comet model. We refer to Holmström (2010, 2013) for more information about the solver.
The trajectory of a particle, 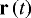 , with velocity,
, with velocity, 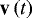 , charge, q, and mass, m, is given by the solution of the equation of motion with the Lorentz force, F:
, charge, q, and mass, m, is given by the solution of the equation of motion with the Lorentz force, F:
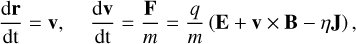 (2)
(2)
where 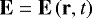 is the electric field,
is the electric field, 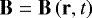 is the magnetic field, η is the resistivity, and
is the magnetic field, η is the resistivity, and 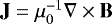 is the current density from the radiation-free Ampère law (Darwin limit). The resistive term, ηJ, is used as a tool to dampen numerical oscillations in the electromagnetic fields of the collisionless plasma and is removed in the Lorentz force to prohibit the electron fluid from transferring momentum to the ions (Bagdonat & Motschmann 2002).
is the current density from the radiation-free Ampère law (Darwin limit). The resistive term, ηJ, is used as a tool to dampen numerical oscillations in the electromagnetic fields of the collisionless plasma and is removed in the Lorentz force to prohibit the electron fluid from transferring momentum to the ions (Bagdonat & Motschmann 2002).
The electric field is calculated from the electron momentum conservation equation assuming quasi-neutrality and massless electrons, resulting in Ohm’s law:
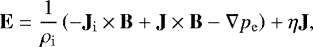 (3)
(3)
where ρi is the ion charge density, Ji is the ion current density, pe is the electron pressure, and η is the resistivity. The electron current, Je, is known at all times as Je = J −Ji.
The gradient of the electron pressure is calculated by imposing quasi-neutrality and a polytropic index, γe, giving ∇pe = γekBTe ∇ne, with the electron temperature as 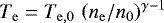 . We here approximated electron processes as adiabatic with three degrees of freedom, corresponding to γe = 5∕3. For this study, the electron pressure gradient term in Ohm’s law (Eq. (3)) is small, but it will play a major role close to the comet nucleus for cases of higher activity (water production).
. We here approximated electron processes as adiabatic with three degrees of freedom, corresponding to γe = 5∕3. For this study, the electron pressure gradient term in Ohm’s law (Eq. (3)) is small, but it will play a major role close to the comet nucleus for cases of higher activity (water production).
Faraday’s law is used to advance the magnetic field in time,
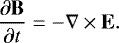 (4)
(4)
In the limit of a physical vacuum, Faraday’s law behaves as a diffusion equation with a resistivity going toward infinity (Hewett 1980). In the model, we define vacuum regions as cells without enough simulated particles (macroparticles) for statistical purposes to solve Ohm’s law in Eq. (3). In order to numerically solve Ohm’s law, we set 1∕ρi = 0 and η = ηv in Eq. (3) when the charge density in a cell is lower than what corresponds to half a macroparticle. The numerical parameter ηv is the vacuum resistivity and is chosen to be as large as possible. Faraday’s law is reduced to solving the magnetic diffusion equation,
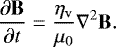 (5)
(5)
A constraint on the time step is being inferred since the field cannot diffuse more than one cell per time step,
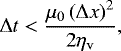 (6)
(6)
where Δt is the time step and Δx is the cell size. The time step is for moving the particles (ions). The electromagnetic fields can be updated more frequently (subcycled) since it is usually computationally cheaper to update the fields than to move all the particles.
When gravity is neglected and a constant outflow velocity is assumed, the total flux of non-collisional water vapor in a comet will be constant through any spherical shell around the nucleus at distance r. This is called the Haser model (Haser 1957), and is described below.
The number density of water vapor, n, as a function of the distance, r, from the comet nucleus is
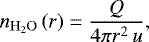 (7)
(7)
where Q is the production rate of water vapor, and u is the meanvelocity of water vapor in the radial direction. However, if losses are accounted for (they are mainly due to photodissociation), the flux will decrease exponentially with time, t = r∕u, as the molecules move outward from the nucleus, and we obtain
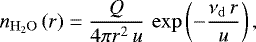 (8)
(8)
where νd is the photodestruction rate of water vapor, which includes all possibilities of photodissociation, photoionization, and dissociative photoionization.
The water vapor is ionized at a certain ionization rate, νi, creating water ions, H2 O+. The water ion production rate as a function of distance then becomes
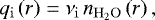 (9)
(9)
where, in the implementation, the number density of water, 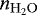 , is taken at the center of each grid cell for each time step, generating the prescribed amount of ions at random positions in that cell.
, is taken at the center of each grid cell for each time step, generating the prescribed amount of ions at random positions in that cell.
When the neutral daughter molecules of water via photodestruction are not considered, the charge density due to cometary ions is slightly underestimated (see Simon Wedlund et al. 2017).
2.1 Coordinate system and simulation box
We used a body-centered right-handed coordinate system in the hybrid model. It is centered on the middle of the nucleus of comet 67P. This is the frame in which we expect the system to reach the solution with the highest steady state, keeping the partial time derivative ofPoynting’s theorem (Eq. (1)) close to zero.
The ambient convective electric field is given by E0 = − u0×B0, where u0 is the undisturbed solar wind bulk velocity flowing in the negative x direction, and B0 is the interplanetary magnetic field (IMF), which is initially homogeneous everywhere. We assumed that the IMF has a Parker spiral configuration, with components in the xy plane such that the ambient convective electric field is along the z axis.
The simulation domain was given by − 12 000 km < x < 6000 km, |y| < 12 000 km, |z| < 18 000 km, and the cubic cell size was Δx = 100 km. Initially, the domain was filled with eight solar wind proton macroparticles randomly distributed in each cell. The simulations were run for 100 s. The magnetic fields were updated 16 times for each time step, Δ t =8.2 × 10−3.
To dampen numerical oscillations, we set the plasma resistivity to ηp = 6.8 × 103 Ω m. We assumed a vacuum resistivity of ηv = 5.7 × 105 Ω m, which is used when solving the diffusion equation of Faraday’s law (Eq. (5)) for regions with a charge density lower than ρmin = e n0∕16, where n0 is the ambient solar wind proton/electron number density, and e is the elementary charge. To summarize:
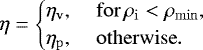 (10)
(10)
2.2 Physical parameters
To model the change in solar wind interaction with the comet at the heliocentric distance of 1.5 AU, we used two cases of solar conditions that only differed by the change in EUV flux. In the first case, the conditions were weakly ionizing, and in the other case, they were highly ionizing, corresponding to the quiet and active conditions in Huebner & Mukherjee (2015), respectively. These two cases are summarized in Table 1. The Rosetta mission was active during a weak solar maximum, with low EUV fluxes. In the model, we used typical solar wind conditions from Slavin & Holzer (1981) scaled to the heliocentric distance, R, of comet 67P. They can be compared with similar cases previously modeled by Behar et al. (2016a).
The water production rate of a comet changes with its distance from the Sun. We used a production rate (s−1) of Q = 2.59 × 1028 R−5.18, where R is a unitless parameter given by theheliocentric distance in terms of AU (Hansen et al. 2016). The neutral water vapor expansion speed is observed to be relatively constant around u = 700 m s−1 (Gulkis et al. 2015), but a more precise formula by Hansen et al. (2016) has been found to be
![\begin{equation*} u = \left[ -55.5 \, R + 771 \right] \cdot \left[ 1 + 0.171 \, \exp \left( - \frac{ R - 1.24 }{0.13} \right) \right], \vspace*{1.5pt}\end{equation*}](/articles/aa/full_html/2018/08/aa32353-17/aa32353-17-eq19.png) (11)
(11)
given in (m s−1), based on combined observations from experiments on board Rosetta during the comet’s inbound orbital phase.
Water ions are produced in the simulation according to Eq. (9). For the photoionization and photodestruction rates we used scaled values with heliocentric distances from Huebner & Mukherjee (2015). Quiet solar conditions give a photoionization rate of νi,q = 3.31 × 10−7 R−2 s−1 and a photodestruction rate of νd,q = 1.206 × 10−5 R−2 s−1. Active solar conditions give a photoionization rate of νi,a = 8.28 × 10−7 R−2 s−1 and a photodestruction rate of νd,a = 2.203 × 10−5 R−2 s−1.
The undisturbed solar wind plasma parameters are a bulk velocity of u0 = 430 km s−1 along 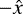 (neglecting aberration), where
(neglecting aberration), where 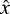 denotes the unit vector in the x direction. The number density of protons is n0 = 7 R−2 cm−3, and the temperatures of protons and electrons are Tp = 8 × 104 R−2∕3 K and Te = 15 × 104 R−1∕3 K, respectively. The IMF has a magnitude of
denotes the unit vector in the x direction. The number density of protons is n0 = 7 R−2 cm−3, and the temperatures of protons and electrons are Tp = 8 × 104 R−2∕3 K and Te = 15 × 104 R−1∕3 K, respectively. The IMF has a magnitude of 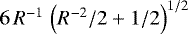 nT, with a Parker spiral angle of
nT, with a Parker spiral angle of 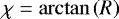 . The proton temperature was used to generate macroparticle protons at the inflow boundary according to a Maxwellian velocity distribution, whereas the electron temperature can be solved at all points in space and describes the width of the Maxwellian electron fluid velocity distribution. No water ion temperature was given as an initial condition, since macroparticle water ions were generated via Eq. (9).
. The proton temperature was used to generate macroparticle protons at the inflow boundary according to a Maxwellian velocity distribution, whereas the electron temperature can be solved at all points in space and describes the width of the Maxwellian electron fluid velocity distribution. No water ion temperature was given as an initial condition, since macroparticle water ions were generated via Eq. (9).
Solar wind conditions and cometary parameters used in the model.
3 Results
We first present an overview of the solar wind interaction with comet 67P at a heliocentric distance of 1.5 AU for weakly ionizing conditions and highly ionizing conditions, corresponding to the two cases in Table 1. We then present the energy conversion of the interaction: where and how much energy is transferred between particles and the electromagnetic fields.
 |
Fig. 1 Cuts through the planes y = 0 and z = 0 for comet 67P at 1.5 AU during weakly ionizing solar conditions. Shown in color of panels a, b is the magnetic field magnitude relative to the ambient solar wind value, B0. The vector field in panel b marks the direction and size of the magnetic field. In panels c, d the color shows the solar wind proton number density relative to its ambient value, n0, and the vector fields mark the velocity of the solar wind protons. In panels e, f the cometary water ion number density relative to the ambient solar wind proton number density. The comet nucleus is marked by white crosshairs. The local geometry for each row of panels is shown to the right of the figure. |
3.1 Weakly ionizing case
Figure 1a and b shows the magnetic field magnitude in the xz plane, which is perpendicular to the IMF, and in the plane of the IMF (xy), respectively.The magnetic field magnitude is normalized to the ambient solar wind value, B0 = 3.4 nT. In Fig. 1a, the magnetic field piles up upstream (to the right) of the comet nucleus, and directly downstream of the nucleus. The high concentration of water ions of cometary origin is the result of the magnetic field downstream of the comet nucleus being frozen-in to the almost stationary plasma, and thus cannot diffuse to relax the field. Several sharp and thin arcs of magnetic field increase are shown in the lower part of panel a. The upper part of the same panel shows a more diffusemagnetic field increase in a large region. The disturbed solar wind magnetic field forms a cone in the xz plane with asudden increase (jump) in the magnetic field. We refer to the jump at the front of the cone as a shock-like structure. What exactly this boundary corresponds to cannot be investigated further here because we lack spatial resolution at the shock-like structure.
In Fig. 1b, the magnetic field is shown in the plane of the IMF. The IMF is draped around the comet, forming a shock-like structure. Since the IMF is tilted in a Parker-spiral configuration, the upper part of the panel shows a quasi-perpendicular shock-like interaction. Multiple arcs of increased magnetic field are seen inside the shock-like structure for x ≲ −3 × 103 km and y ≳ 3 × 103 km. The lower part of the panel shows a quasi-parallel shock-like interaction, which enables wave propagation and backflow of ions (and electrons) at the boundary.
The draped field lines shown in Fig. 1b are generally referred to as Alfvén wings, which are Alfvén waves propagating along the magnetic field lines away from either a conducting or mass-loading obstacle (Russell et al. 2016). For the simulation parameters of Table 1, we note that the Alfvén speed of the undisturbed solar wind, vA ≈ 42 km s−1, is lower than the magnetosonic wave speed, vMS ≈ 67 km s−1. A compressional wave moving perpendicular to the magnetic field is thus expected to move faster than a shear Alfvén wave along the magnetic field. Therefore, the shock-like structure is a broader cone in Fig. 1a, where the magnetic field points into the plane, than the structure visible in Fig. 1b, where the magnetic field is located in the plane.
Figure 1c and d shows the solar wind proton number density in color, normalized to its ambient value, n0 = 3.1 cm−3, for two planes perpendicular to the solar wind flow. The cell-averaged velocity is shown as a vector field with an arrow length proportional to its magnitude. In Fig. 1e and f, the water ion number density is shown in color, also normalized to the ambient solar wind proton density.
In Fig. 1e, the water ions close to the comet nucleus are accelerated by the convective electric field of the solar wind (toward positive z). However, the water ion concentration is high enough to considerably alter the local electromagnetic fields, causing the solar wind protons to transfer much of their momentum to the water ions, which deflects the solar wind in the opposite direction of the electric field (toward negative z). This causes the shock-like structure of increased solar wind proton density visible in Fig. 1c; this has been discussed previously by Behar et al. (2016a,b, 2017).
The upper part of Fig. 1c shows a swirl of solar wind protons traveling downstream. In the time evolution of the simulations, these protons show that the comet system does not arrive at a steady state, but rather has instabilities on the positive z side. The shock-like structure in the lower part of the same panel is connected throughout the entire distance to the comet nucleus, which means that the solar wind is present in the vicinity of the comet nucleus. Several arcs of increased solar wind proton density are present farther downstream, corresponding to the magnetic field increase shown in Fig. 1a. These arcs are seperated by around λA ≈ 500 km. The ion inertial length of protons in the undisturbed solar wind is  km. Similar arcs are visible in the magnetic field at the top of Fig. 1b.
km. Similar arcs are visible in the magnetic field at the top of Fig. 1b.
In the weak mass-loading limit, the water ions have cycloidal trajectories with a large gyroradius (~ 2 × 104 km). The water ion number density in Fig. 1e and f shows that water is instead transported downstream into the tail. Along the arcs in the lower panel in Fig. 1a, there are almost no water ions, showing that the arc structure is due to the solar wind proton dynamics. These arcs are the effect of gyrating solar wind protons and resemble what is known as an overshoot in supercritical collisionless bow shocks, where the magnetic field is oscillating downstream of such a shock (Heppner et al. 1967; Greenstadt et al. 1968; Russell et al. 1982).
3.2 Highly ionizing case
Figure 2 shows the same plasma parameters as Fig. 1, but for the highly ionizing case summarized in Table 1. In the lower part of Fig. 2a, showing the magnetic field magnitude in color in the plane ofthe ambient solar wind electric field, the magnetic field is bunched together in striations, just as we showed earlier for the weakly ionizing case of Fig. 1a. In the upper part of the same panel (x = 0, z = 103 km), the magnetic field is strongly piled up. This is where the water ions and solar wind meet head on. In Fig. 2b, showing the magnetic field magnitude and vector field in the plane of the IMF, the magnetic field is shown to be draped around the comet, resulting in a current sheet downstream at y = 0. The magnetic field magnitude does not drop to zero, and hence no diamagnetic cavity is present in either case.
The solar wind proton number density is shown in color in Fig. 2c and d. The solar wind flows around the comet and is absent at the comet nucleus. We therefore call the outermost sudden jumps in density and magnetic field strength “a detached shock-like structure”, in analogy to the attached shock-like structure visible in Fig. 1. The observed “shock jump” of 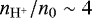 corresponds to the hypersonic limit shock jump from the Rankine–Hugoniot conditions for a polytropic index of γ = 5∕3 (Cravens 1997).
corresponds to the hypersonic limit shock jump from the Rankine–Hugoniot conditions for a polytropic index of γ = 5∕3 (Cravens 1997).
The water ion number density is shown in Fig. 2e and f. An almost spherically symmetric water ion cloud is formed close to the nucleus, in contrast to the weakly ionizing case shown in Fig. 1e and f. In Fig. 2e, the ion cloud is shown to be slightly elongated along the ambient solar wind electric field. In Fig. 2f, the ion cloud is elongated downstream of the comet nucleus, which corresponds to the current sheet mentioned in the magnetic field structure above. The water ion number density color scale is saturated in Fig. 2e and f close to the nucleus; it reaches a maximum value of 40 n0 within the simulation. Here, the water ions are much more numerous than the solar wind protons, and the electric field within the water ion cloud is close to zero (not shown).
The shock-like structure in Fig. 1a and b is shaped like a bow instead of a cone, as in the weakly ionizing case in Fig. 1a and b. For the highly ionizing case, the part of the water ion cloud that has higher charge densities than the solar wind has a larger extent than the arc separation distance of λA ≈ 500 km. This means that the source of the waves (i.e., the water ion obstacle) cannot be considered point-like in nature, as is the case for a low ionization.
 |
Fig. 3 Shown in color is the total power density (panels a, b), the divergence of the Poynting flux (panels c, d), and the time derivative of the electromagnetic energy density (panels e, f), for the y = 0 and z = 0 planes around the comet at 1.5 AU during weakly ionizing solar conditions. The Poynting theorem states that the sum of these three quantities should be zero for all points. The arrows in (panels c, d) mark the direction of the Poynting flux, S = E ×B∕μ0, and their sizes are proportional to the magnitude. The comet nucleus is marked by black crosshairs. The local geometry for each rowof panels is shown to the right of the figure. |
3.3 Energy conversion
The energy balance for the electromagnetic fields is described by the Poynting theorem introduced in Eq. (1). Each term of the Poynting theorem is shown in color in Fig. 3 for weakly ionizing conditions and in Fig. 4 for highlyionizing conditions.
In Fig. 3a and b, the power density, P = E ⋅J, is shown in color, and it is well balanced by the divergence of the Poynting flux, shown in color in Fig. 3c and d, where the Poynting flux vector, S = E ×B∕μ0, is shown as a vector field. Figure 3e and f shows that the time derivative of the electromagnetic energy density, ∂∕∂t(B2∕2μ0), is smaller the other terms, which implies steady state, meaning that the power density is well balanced by the Poynting flux transport. This reasoning also applies to the highly ionizing condition shown in Fig. 4.
The rate of work (or power) done by the electromagnetic fields on a charged particle can be expressed directly from the Lorentz force in Eq. (2) as F ⋅v. Summing over all ion species “s” in a volume gives the rate of energy transferred between electromagnetic energy and kinetic energy for that charged species, and is in the model given by the power density, Ps = (E − ηJ) ⋅Js, where Js = ρsus, with ρs being the charge density and us the bulk velocity.
The total power density can be expressed as a sum of the contributions from each ion species, s, and the electron fluid,
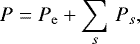 (12)
(12)
where Pe is the power density for the electron fluid. The electron fluid power density is calculated from the other terms, which is written as
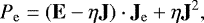 (13)
(13)
where the first term is non-dissipative, and the second term is dissipative (depends on the numerical resistivity, η). As mentioned before, the electron current is known at all times and is given by Je = J −Ji.
The power density for all species including the electrons is shown in Fig. 5 for weakly ionizing conditions, for cuts in the plane perpendicular to the IMF in the upper panels, and for the plane of the IMF in the lower panels. In Fig. 5a and b, the power density, E ⋅J, is shown in color. Panels c and d of the same figure show the power density for the electron fluid, panels e and f show the power density for solar wind protons, and panels g and h show the power density for the cometary water ions.
In Fig. 5a, the shock-like structure at z < 0 (in blue) acts as an electromagnetic generator, E ⋅J < 0, that slows down the solar wind and piles up the magnetic field, resulting in a higher field energy there. Arcs are present downstream of this structure and are related to secondary acceleration of solar wind protons. The power density depends on the direction of the total current density, which alternates its direction (not shown). The upper part of Fig. 5a does not reach steady state along the shock-like structure, and has regions where the power density flips sign (e.g., x = 0, z = 3 × 103 km). Downstream of the comet nucleus (to the left) around z = 0, there is a large load of electromagnetic energy (in red), E ⋅J > 0, where the water ions are being accelerated. The power density for electrons (not shown), E ⋅ Je, is close to zero outside the shock-like structure, and it is somewhat lower than the other power densities elsewhere. In Fig. 5b, the electromagnetic generator (in blue) is along the shock-like structure with an electromagnetic load (in red) close to y = 0 downstream of the comet nucleus, where most water ions are located (compare with the water ion density in Fig.1f).
The Poynting flux shown as the vector field in Fig. 3c and d transports the electromagnetic energy from the shock-like structure toward y= 0 and in the 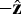 direction. Most water ions are accelerated close to y = 0 where
direction. Most water ions are accelerated close to y = 0 where 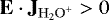 . There, the acceleration acts as an electromagnetic load, E ⋅J > 0.
. There, the acceleration acts as an electromagnetic load, E ⋅J > 0.
When we compare the four panels Fig. 5e–h, we see that the solar wind protons are mostly slowed down along the shock-like structure, 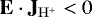 . Electromagnetic energy is tranferred by Poynting flux toward y = 0, where most water ions are accelerated,
. Electromagnetic energy is tranferred by Poynting flux toward y = 0, where most water ions are accelerated, 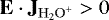 (red).
(red).
The energy conversion for the comet at the heliocentric distance 1.5 AU for highly ionizing conditions is shown in Fig. 6, with the same figure structure as Fig. 5. The energy transfer regions can be identified in a similar way to the weakly ionizing case, but with major differences. In Fig. 6a and b the shock-like structure acts as a generator. Secondary acceleration of protons is present downstream of the shock-like structure, and it is correlated in location with the arcs. However, there is no strong electromagnetic load close to y = 0 downstream of the nucleus for this case.
When we compare the four panels in Fig. 6e–h, we see that most energy is transferred locally fromsolar wind protons to water ions in regions outside the shock-like structure where E ⋅ J ≈ 0, but where 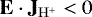 and
and 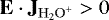 .
.
The acceleration of water ions in the highly ionizing case is noted to be more homogeneous than the weakly ionizing case, where acceleration predominantly occurred in the y = 0 plane.
 |
Fig. 5 Total power density (panels a, b), which is the sum of the electron power density (panels c, d), the solar wind proton power density (panels e, f), and the cometary water ion power density (panels g, h). We show cuts for the y = 0 and z = 0 planes around the comet at 1.5 AU during weakly ionizing solar conditions. Red (E ⋅ J > 0) is where the electromagnetic field exerts work on charged particles, while blue (E ⋅ J < 0) shows the opposite. The comet nucleus is marked by black crosshairs. The local geometry for each row of panels is shown to the right of the figure. |
3.4 Comparison with observations
Observations by the Rosetta spacecraft are the key to understand the model results. In the two cases we analyzed, a void formed in solar wind particles, a solar wind cavity, just as in the observations reported by Behar et al. (2017) and Nilsson et al. (2017). In the weakly ionizing case, the solar wind cavity extends only about 100 km upstream of the nucleus, whereas in the high-activity case, it is located at about 500 km distance upstream. The latter is in approximate agreement with observations, as Rosetta was within the solar wind cavity around comet 67P from about mid-April 2015 until December 2015. Rosetta performed a dayside excursion when it was at a heliocentric distance of 1.4 AU out to a comet distance of 1500 km, but still did not leave the solar wind cavity. The size of the solar wind cavity must thus have been at least 1500 km, close to perihelion. During the return from the dayside excursion, faint fluxes of solar wind ions were seen during an extreme space-weather event (Edberg et al. 2016), indicating that the solar wind cavity was significantly compressed during the event, enough so for solar wind particles to become visible. Thus, it seems that Rosetta could have been near the boundary of the solar wind cavity.
Throughout the mission, when the solar wind was observed, it was apparently not shocked, and the energy of the solar wind ions did not change significantly. At the same time, the solar wind ions were significantly deflected as a result from a direct interaction with the local water ions (Behar et al. 2016a,b). This seems to be best captured by the high-activity model as well. Our model results imply that the interaction of solar wind with comet atmosphere can behave in different ways for different ionization rates. The diffuser more direct interaction of the highly ionizing case, which also leads to a large solar wind cavity, is closest to what was observed by instruments on the Rosetta spacecraft at comet 67P. In the model, however, photoionization rates may suffer from uncertainties that are due to the changing nature of the Sun’s EUV spectrum. Time-dependent models of the photoionization, in quiet and more extreme conditions, may help elucidate the local composition and dynamics of the cometary plasma.
4 Summary and conclusions
We analyzed the energy conversion at comet 67P/Churyumov–Gerasimenko using a hybrid plasma model at a heliocentric distance of 1.5 AU for two extremes of solar ultraviolet radiation. These two cases correspond to scenarios where in the weakly ionizing case the solar wind can reach the comet nucleus, while this is not true for the highly ionizing case.
The modeling shows that a shock-like structure is formed upstream of the comet, but this is not the traditional bow shock seen at Earth since there is a large region outside the shock structure where energy is transferred locally from solar wind protons to cometary water ions.
For the weakly ionizing case, the shock-like structure acts as an electromagnetic generator, similar to the bow shock at Earth (Lopez et al. 2011), and this is where the solar wind slows down and the protons lose most of their energy to the ambient cometary plasma and electromagnetic fields. The electromagnetic energy is transported with a Poynting flux toward the inner coma, where most of the water ions are accelerated. The highly ionizing case has the same dynamo mechanism, but most energy is transferred locally from solar wind protons to water ions, upstream of the shock-like structure.
This leads us to speculate that the acceleration of cometary heavy ions can be both a local process with direct transfer of energy, and a dynamo system with generators and loads, depending on the solar activity conditions. For a comet approaching the Sun, acceleration of cometary ions is dominated by local transfer close to the nucleus, which first evolves into a dynamo system, and finally evolves into a large region with a local transfer of energy.
Acknowledgements
The software used in this work was in part developed by the DOE NNSA-ASC OASCR Flash Center at the University of Chicago. The hybrid solver is part of the openly available FLASH code and can be downloaded from http://flash.uchicago.edu/. The simulation results are available from the corresponding author upon request. This research was conducted using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N), Umeå University, Sweden. J.L. and M.H. are funded by the Swedish National Space Board (SNSB project 201/15). H.G. was supported by the Belgian Science Policy Office through the Solar-Terrestrial Centre of Excellence, and by PRODEX/ROSETTA/ROSINA PEA 4000107705.H.N. was supported by the Swedish National Space Board under contract 112/13 and by the Swedish Research Council under contract 2015-04187. C.S.W. is supported by the Research Council of Norway grant No. 240000. I.M. was supported by the Research Council of Norway grant No. 262941.
References
- Bagdonat, T., & Motschmann, U. 2002, J. Comput. Phys., 183, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., Lindkvist, J., Nilsson, H., et al. 2016a, A&A, 596, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Behar, E., Nilsson, H., Stenberg Wieser, G., et al. 2016b, Geophys. Res. Lett., 43, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., Nilsson, H., Alho, M., Götz, C., & Tsurutani, B. 2017, MNRAS, 469, stx1871 [Google Scholar]
- Brenning, N., Kelley, M. C., Providakes, J., Stenbaaek-Nielsen, H. C., & Swenson, C. 1991, J. Geophys. Res., 96, 9735 [NASA ADS] [CrossRef] [Google Scholar]
- Brenning, N., Hurtig, T., & Raadu, M. A. 2005, Phys. Plasmas, 12, 012309 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, C, Cupido, E. Lee, C. G. Y., et al. 2007, Space Sci. Rev., 128, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Coates, A. J., & Jones, G. H. 2009, Planet. Space Sci., 57, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E. 1997, Physics of Solar System Plasmas (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Cravens, T. E., & Gombosi, T. I., 2004, Adv. Space Res., 33, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Edberg, N. J. T., Alho, M., André, M., et al. 2016, MNRAS, 462, stw2112 [Google Scholar]
- Glassmeier, K-H. 2017, Phil. Trans. R. Soc. A, 375, 20160256 [NASA ADS] [CrossRef] [Google Scholar]
- Glassmeier, K-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, Space Sci. Rev., 128, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstadt, E. W., Green, I. M., Inouye, G. T., et al. 1968, J. Geophys. Res., 73, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, aaa0709 [Google Scholar]
- Hamrin, M., Marghitu, O., Norqvist, P., et al. 2011, J. Geophys. Res., 116, A00K08 [CrossRef] [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Haser, L. 1957, Bull. Cl. Sci. Acad. R. Belg., 43, 740 [Google Scholar]
- Heppner, J. P., Sugiura, M., Skillman, T. L., Ledley, B. G., & Campbell, M. 1967, J. Geophys. Res., 72, 5417 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, D. W. 1980, J. Comput. Phys., 38, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Holmström, M. 2010, in Hybrid Modeling of Plasmas (Berlin: Springer), Proceedings of ENUMATH, the 8th European Conference on Numerical Mathematics and Advanced Applications, 451 [Google Scholar]
- Holmström, M. 2013, Handling Vacuum Regions in a Hybrid Plasma Solver, ASP Conf. Ser., 474, 202 [Google Scholar]
- Huebner, W. F., & Mukherjee, J. 2015, Planet. Space Sci., 106, 11 [Google Scholar]
- Johnstone, A. D., Coates, A. J., Huddleston, D. E., et al. 1993, A&A, 273, L1 [NASA ADS] [Google Scholar]
- Kallio, E., & Jarvinen, R. 2012, Earth Planets Space, 64, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Koenders, C., Glassmeier, K.-H., Richter, I., Ranocha, H., & Motschmann, U. 2015, Planet. Space Sci., 105, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lindkvist, J., Holmström, M., Fatemi, S., Wieser, M., & Barabash, S. 2017, Geophys. Res. Lett., 44, 2070 [NASA ADS] [Google Scholar]
- Lopez, R. E., Merkin, V. G., & Lyon, J. G. 2011, Ann. Geophys., 29, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, M., Coates, A. J., Neubauer, F. M. 1990, J. Geophys. Res., 95, 18745 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., & Behar, E. 2015, A&A, 583, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2017, MNRAS, 469, stx1491 [Google Scholar]
- Rosenqvist, L., Vaivads, A., Retinò, A., et al. 2008, Geophys. Res. Lett., 35, L08104 [NASA ADS] [Google Scholar]
- Rubin, M., Koenders, C., Altwegg, K., et al. 2014, Icarus, 242, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, C. T., Hoppe, M. M., & Livesey, W. A. 1982, Nature, 296, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, C. T., Luhmann, J. G., & Strangeway, R. J. 2016, Space Physics (Cambridge: Cambridge University Press) [Google Scholar]
- Saunders, M. A., & Russell, C. T. 1986, J. Geophys. Res., 91, 5589 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, K. D., & Siscoe, G. L. 2002, J. Geophys. Res., 107, 1095 [CrossRef] [Google Scholar]
- Simon Wedlund, C., Kallio, E., Alho, M., et al. 2016, A&A, 587, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon Wedlund, C., Alho, M., Gronoff, G., et al. 2017, A&A, 604, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, J. A., & Holzer, R. E. 1981, J. Geophys. Res., 86, 11401 [NASA ADS] [CrossRef] [Google Scholar]
- Szegö, K., Glassmeier, K.-H., Bingham, R., et al. 2000, Space Sci. Rev., 94, 429 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cuts through the planes y = 0 and z = 0 for comet 67P at 1.5 AU during weakly ionizing solar conditions. Shown in color of panels a, b is the magnetic field magnitude relative to the ambient solar wind value, B0. The vector field in panel b marks the direction and size of the magnetic field. In panels c, d the color shows the solar wind proton number density relative to its ambient value, n0, and the vector fields mark the velocity of the solar wind protons. In panels e, f the cometary water ion number density relative to the ambient solar wind proton number density. The comet nucleus is marked by white crosshairs. The local geometry for each row of panels is shown to the right of the figure. |
| In the text | |
 |
Fig. 2 Same form as Fig. 1, but for highly ionizing solar conditions. |
| In the text | |
 |
Fig. 3 Shown in color is the total power density (panels a, b), the divergence of the Poynting flux (panels c, d), and the time derivative of the electromagnetic energy density (panels e, f), for the y = 0 and z = 0 planes around the comet at 1.5 AU during weakly ionizing solar conditions. The Poynting theorem states that the sum of these three quantities should be zero for all points. The arrows in (panels c, d) mark the direction of the Poynting flux, S = E ×B∕μ0, and their sizes are proportional to the magnitude. The comet nucleus is marked by black crosshairs. The local geometry for each rowof panels is shown to the right of the figure. |
| In the text | |
 |
Fig. 4 Same form as Fig. 3, but for highly ionizing solar conditions. |
| In the text | |
 |
Fig. 5 Total power density (panels a, b), which is the sum of the electron power density (panels c, d), the solar wind proton power density (panels e, f), and the cometary water ion power density (panels g, h). We show cuts for the y = 0 and z = 0 planes around the comet at 1.5 AU during weakly ionizing solar conditions. Red (E ⋅ J > 0) is where the electromagnetic field exerts work on charged particles, while blue (E ⋅ J < 0) shows the opposite. The comet nucleus is marked by black crosshairs. The local geometry for each row of panels is shown to the right of the figure. |
| In the text | |
 |
Fig. 6 Same form as Fig. 5, but for highly ionizing solar conditions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


