| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731808 | |
| Published online | 24 August 2018 | |
Comparing the asteroseismic properties of pulsating pre-extremely low mass white dwarf and δ Scuti stars
1
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: jsanchez@fcaglp.unlp.edu.ar
2
Instituto de Astrofísica La Plata, CONICET-UNLP, Argentina
3
Instituto de Física, Universidade Federal do Rio Grande do Sul, 91501-900 Porto-Alegre, RS, Brazil
e-mail: alejandra.romero@ufrgs.br
4
Stellar Astrophysics Centre, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
5
Instituto Argentino de Radioastronomía, CCT-La Plata, CONICET, C.C. Nro. 5, 1984 Villa Elisa, Argentina
Received:
21
August
2017
Accepted:
17
April
2018
Context. Pulsating extremely low-mass pre-white dwarf stars (pre-ELMV), with masses between ~0.15 M⊙ and ~0.30 M⊙, constitute a new class of variable stars showing g- and possibly p-mode pulsations with periods between 320 and 6000 s (frequencies between 14.4 and 270 c/d), driven by the κ mechanism operating in the second He ionization zone. On the other hand, main sequence δ Scuti stars, with masses between 1.2 and 2.5 M⊙, pulsate in low-order g and p modes with periods in the range [700–28 800] s (frequencies in the range [3–123] c/d), driven by the κ mechanism operating in the He II ionization zone and the turbulent pressure acting in the HI ionization layer. Interestingly enough, the instability strips of pre-ELM white dwarf and δ Scuti stars nearly overlap in the Teff vs. log g diagram, leading to a degeneracy when spectroscopy is the only tool to classify the stars and pulsation periods only are considered.
Aims. Pre-ELM white dwarf and δ Scuti stars are in very different stages of evolution and therefore their internal structure is very distinct. This is mirrored in their pulsational behavior, thus employing asteroseismology should allow us to distinguish between these groups of stars despite their similar atmospheric parameters.
Methods. We have employed adiabatic and non-adiabatic pulsation spectra for models of pre-ELM white dwarfs and δ Scuti stars, and compare their pulsation periods, period spacings, and rates of period change.
Results. Unsurprisingly, we found substantial differences in the period spacing of δ Scuti and pre-ELM white dwarf models. Even when the same period range is observed in both classes of pulsating stars, the modes have distinctive signature in the period spacing and period difference values. For instance, the mean period difference of p-modes of consecutive radial orders for δ Scuti model are at least four times longer than the mean period spacing for the pre-ELM white dwarf model in the period range [2000–4600] s (frequency range [18.78–43.6] c/d). In addition, the rate of period change is two orders of magnitudes larger for the pre-ELM white dwarfs compared to δ Scuti stars. In addition, we also report the discovery of a new variable star, SDSSJ075738.94+144827.50, located in the region of the Teff versus log g diagram where these two kind of stars coexist.
Conclusions.The characteristic spacing between modes of consecutive radial orders (p as well as g modes) and the large differences found in the rates of period change for δ Scuti and pre-ELM white dwarf stars suggest that asteroseismology can be employed to discriminate between these two groups of variable stars. Furthermore, we found that SDSSJ075738.94+144827.50 exhibits a period difference between p modes characteristic of a δ Sct star, assuming consecutive radial order for the observed periods.
Key words: asteroseismology / stars: evolution / stars: interiors / stars: oscillations / stars: variables: delta Scuti / white dwarfs
© ESO 2018
1. Introduction
A significant number of pulsating stars were discovered by the COnvection ROtation and planetary Transits (COROT) satellite (Auvergne et al. 2009), the NASA’s Kepler space telescope (Borucki 2016), and by the Kepler’s second mission: K2 (Van Cleve et al. 2016). Moreover, the upcoming NASA Transiting Exoplanet Survey Satellite (TESS) will provide excellent photometric precision and long intervals of uninterrupted observations of of almost the entire sky (Ricker et al. 2015). These observations will rapidly increase the population of the Hertzsprung–Russell (HR) diagram with new families of variable stars and therefore a proper classification of the observed objects is essential. In particular, there is a region in the Teff– log g diagram which is being particularly rapidly populated and in which two very different families of variable stars coexists: main sequence (MS) δ Scuti (δ Sct) stars and the pulsating extremely low-mass pre-white dwarf stars (pre-ELMV). These two families of variable stars share very similar atmospheric characteristics, which makes it difficult to distinguish them from spectroscopy alone. The main goal of this work is to provide asteroseismic tools to enable their correct classification and to increase the number of known pre-ELMVs in order to study their very interesting evolution and stellar structure.
Pulsating stars in the lower part of the classical instability strip are associated with early stages of evolution, the pre-MS, MS, and the immediate post-MS. The most numerous pulsator class among them are known as δ Sct stars showing low to intermediate radial order pressure, mixed and gravity modes.
In smaller numbers, we also have other types of pulsators such as the γ Doradus (γ Dor) stars, that pulsate in high radial order gravity modes. Because the instability strip of γ Dor and δ Sct stars overlap, we can also find stars showing both δ Sct and γ Dor pulsations, also known as hybrid pulsators. A third group of pulsators in this region are the rapid oscillating (roAp) stars, which show periods on the order of ten minutes and display strong magnetic fields.
Recently, two new classes of pulsating white dwarfs (WD) stars were found in a similar region of the Teff–log g diagram, known as extremely low mass variable (ELMV) stars and their evolutionary precursors, the pre-ELMV stars. The ELM WD stars are characterized by stellar masses ≲0.3 M⊙ (Brown et al. 2010), and are thought to be the result of strong mass–transfer events at the red giant stage of low-mass stars evolution in close binary systems (see e.g., Istrate et al. 2014, 2016b; Althaus et al. 2013). A single star of such a low mass would take more than the age of the Universe to evolve into the WD stage clearly implying binary evolution. In 2012, the first ELMV WD star was discovered (Hermes et al. 2012), opening the prospect for probing the internal structure of this kind of stars.
Pre-ELMV stars are thought to be the progenitors of the ELMV stars. The pre-ELMVs show pulsations with periods compatible with low order radial and non-radial p and g modes. The excitation mechanism is the κ–γ mechanism acting mainly in the zone of the second He ionization (HeII layer) (Córsico et al. 2016; Gianninas et al. 2016; Istrate et al. 2016b). Their effective temperatures are similar to those of ELMVs, but they are less compact, showing lower surface gravities. The location of the pre-ELMV WDs in the Teff–log g diagram is one of our main interests in this paper, since it partially overlaps with the classical instability strip.
Observations show that not only the instability strip for both δ Sct stars and pulsating pre-ELM WDs overlap in the Teff–log g plane, but they also share a common range of excited periods, thus making the correct identification of each class more difficult. One way to distinguish the δ Sct from pre-ELM WD stars is by knowing their mass, of course. As mentioned, pre-ELM WD stars have stellar masses ≲0.3 M⊙ while δ Sct stars have masses between 1.5 and 2.5 M⊙. Also, the stellar radius characteristic of a MS star is two to three times the radius of a pre-ELM WD star. The surface gravity depends on both the stellar mass and radius, there is a degeneracy in the surface gravity, which means we cannot determine both parameters independently using only spectroscopy. However, we can estimate the radius of the star if we know its distance. The Gaia satellite will measure parallaxes, and thus distances, for most of the stars in the Milky Way, giving rise to a very detail map of our Galaxy (Gaia Collaboration et al. 2016a, 2016b). The first data release was published by Gaia Collaboration et al. (2016a), consisting of astrometry and photometry for over one billion sources brighter than magnitude 20.7, and DR2 is scheduled for April 2018. However, most of the ELM and pre-ELM WD stars are in binary systems and are usually found by looking for high proper motion objects, since they are intrinsically faint and must be close by to be observed (Pelisoli et al. 2017). In addition, approximately 50% of δ Sct stars, can be found in binary systems as well. A more complex data reduction is necessary for some of this objects with high proper motions, in binary systems and showing photometric variabilities and therefore most of the parallax and distances measures will only be available after Gaia finishes with the observations. This shows the need to find other tools to correctly separate MS δ Sct from pre-ELM variable stars that do not rely on spectroscopy or parallax measures.
In this work we present such tools, by taking advantage of the pulsating nature of MS δ Sct and pre-ELM variable stars. We address a comparison of the pulsational properties of both MS δ Sct stars and pre-ELM WD stars, aiming at providing asteroseismic tools for their correct classification. Specifically, we present the period and frequency spacings (ΔΠ = Πk+1 − Πk and Δv = vk+1 − vk, respectively, k being the radial order) and the rate of the period changes (dΠ /dt) as tools to distinguish MS δ Sct stars from pre-ELMV WDs. The differences expected in these two quantities allow us to shed light on the nature of both classes of stars and to classify them without the knowledge of their masses and radii. To this end, we have considered two different regions in the Teff–log g plane where pulsating objects are currently observed and can be confused with δ Sct or pre-ELMV stars. A cool region with a characteristic effective temperature of δ Sct stars (Teff ~ 7500 K) where pre-ELMV are predicted to lie and a hot region at Teff ~ 9600 K where δ Sct and pre-ELMV stars can be confused if we consider the external uncertainties in log g (0.25 dex) and Teff (up to 5%) of the pulsating objects found in this region (Kepler et al. 2016; Pelisoli et al. 2018). For each region, we have analyzed the pulsational properties of stellar models for MS δ Sct stars computed by Sánchez Arias et al. (2017) and pre-ELM WD models computed by Córsico et al. (2016). All stellar models are computed using the stellar evolutionary code LPCODE (Althaus et al. 2005, 2009, 2013), that calculates the full evolution of low- and intermediate-mass stars from the zero age main sequence (ZAMS). For each stellar model, we analyzed the period range of adiabatic pulsation modes, the period and frequency spacings, and the evolutionary rates of period change for p and g modes, and also study the pulsational instability through non-adiabatic pulsation computations.
The paper is organized as follows. In Sect. 2 we describe in detail the observational properties of the variables in lower part of the classical instability strip and pre-ELMV pulsators. In Sect. 3 we describe the numerical tools employed in building the models considered in our analysis. Section 4 is devoted to the analysis and comparison of the pulsational properties of MS δ Sct (hereinafter δ Sct) and pre-ELMV stars, highlighting their similarities and differences. The non-adiabatic pulsational properties, in particular the instability of the pulsation modes, is presented in Sect. 5. In Sect. 6 we apply the analysis described in Sect. 4 to a new pulsating star, J075739.94+144827.5 and the stars J173001.94+070600.25 and J145847.02+070754.46 reported in Corti et al. (2016). Finally, we summarize our results in Sect. 7.
2. Observational properties
The δ Sct stars are variables of spectral type between A3 and F5, lying on the extension of the Cepheid instability strip toward effective temperatures between 6700 K and 8500 K and with stellar masses in the interval 1.2–2.5 M⊙. Pulsation periods can be between ~700 s and ~28 800 s (frequencies between 3 c/d and 123 c/d; Table 2; see, e.g., Breger et al. 2012; Uytterhoeven et al. 2011; Grigahcène et al. 2010), corresponding to radial and non-radial low and intermediate order p and g modes, mainly driven by the κ mechanism operating in the He II partial ionization zone (see, e.g., Dupret et al. 2005) and the turbulent pressure acting in the hydrogen ionization zone (Antoci et al. 2014). δ Sct stars are subdivided into many categories (e.g., Breger 2000), including the sub-classes of Population I and II stars. The latter are also known as SX Phe stars, they are usually blue straggler stars presumably formed by the merger of two MS stars (Aerts et al. 2010) and their belonging to the MS is today an open question. SX Phe stars are usually connected with low metallicities. However, recently Nemec et al. (2017) have discovered SX Phe stars with near solar metallicity.
The γ Dor stars are variable stars with spectral types of A7–F5 located near the cool border of the classical instability strip, encompassing regions in the HR diagram with effective temperatures between 6900 K and 7700 K and stellar masses in the interval 1.3–1.8 M⊙. They pulsate in non-radial high order g modes with periods between 26 000 s and 260 000 s (frequencies between 0.3 c/d and 3.3 c/d), reaching up to 12 342 s (7 c/d) when rapid rotation is involved (see, e.g., Bouabid et al. 2013; Ouazzani et al. 2017). These modes are driven by a convective flux blocking mechanism operating in the base of their convective envelope (Guzik et al. 2000).
The instability strips of δ Sct and γ Dor stars partially overlap in a region in which we find the so-called hybrid δ Sct-γ Dor stars. These stars show pulsations typical for both δ Sct stars and g-mode variables (see, e.g., Sánchez Arias et al. 2017).
The roAp stars are also located close to the MS where δ Sct lies. They are strongly magnetic Population I stars with a peculiar chemical surface composition caused by atomic diffusion. They exhibit high-order low-degree p modes pulsations, with periods in the range 339–1272 s (frequencies in the range 67– 254 c/d; Aerts et al. 2010).
The number of ELM WDs has increased in recent years thanks to large scale surveys, like the Sloan Digital Sky Survey (Brown et al. 2010; Bell et al. 2017). Pulsations in some ELM WDs have been reported from 2012 onward (Hermes et al. 2012, 2013a,b; Kilic et al. 2015; Bell et al. 2017). They oscillate in non-radial g modes, with periods typically in the range [1000–6300] s (Córsico et al. 2017) and some of them may also exhibit p modes, which are not common to observe in a WD star (Hermes et al. 2013b). Their effective temperatures and surface gravities are in the ranges 7000 ≲ Teff ≲ 10 000 K and 6 ≲ log g ≲ 7 respectively.
To date, five objects identified as variable pre-ELM WD stars are known (Gianninas et al. 2016; Maxted et al. 2013, 2014). They are characterized by surface gravities and effective temperatures in the theoretical ranges 3 ≲ log g ≲ 5.5 and 6000 ≲ Teff ≲ 12 000 K respectively, a region of the log g − Teff plane that partially overlaps with the region where some variable stars in the classical instability strip are usually found. The excitation mechanism is the κ–γ mechanism acting in the HII ionization zone (Córsico et al. 2016; Gianninas et al. 2016; Istrate et al. 2016a). According to Gianninas et al. (2016), the pre-ELMV objects J0756+6704, J1141+3850 and J1157+0546 are classified as p-mode pulsators with periods between 320 and 590 s. On the other hand, the other two pre-ELMVs known, WASP J0247−25B and WASP J1628+10B reported in Maxted et al. (2013, 2014) seem to have a non-radial and radial mixed modes. Besides these well-known five pre-ELMVs, there are three more objects reported in Corti et al. (2016) and Zhang et al. (2016) as possible pre-ELMV with periods that reaches 6000 s (frequencies above 14.4 c/d).
In Tables 1 and 2 we summarize the atmosphere parameters and observed period and frequency range of the different classes of variable stars described in this section.
In Fig. 1 we display the position of the different classes of variable stars analyzed in this work in the Teff–log g plane. δ Sct stars, depicted with white circles, are from Uytterhoeven et al. (2011), Bradley et al. (2015) and Bowman et al. (2016). SX Phe are those from Balona & Nemec (2012), depicted by magenta circles. The error bars for the δ Sct stars and the SX Phe stars are depicted outside the δ Sct and SX Phe region in black and magenta, respectively. With blue diamonds we show the position of the known pre-ELMVs (Maxted et al. 2013, 2014; Gianninas et al. 2016), while the ELMVs are depicted with light green triangles (Hermes et al. 2012, 2013a,b; Kilic et al. 2015; Bell et al. 2015). The new pulsating J0757+1448 reported for the first time in this article is depicted with a cyan diamond and the cyan squares indicate the position of the two stars reported by Corti et al. (2016), J1730+0706 and J1458+0707. We have also included theoretical evolutionary tracks for low mass He-core WDs from Althaus et al. (2013; dotted black lines in Fig. 1) and Serenelli et al. (2001; dashed black line in Fig. 1). Black numbers correspond to the values of the stellar mass of low mass He-core WD evolutionary tracks. In the same figure we illustrate MS evolutionary tracks (with red lines), for different values of metallicity (Z), mass (M⊙) and overshooting parameter (αOV) from Sánchez Arias et al. (2017). The red numbers indicate different combinations of these parameters which are summarized in Table 3. Up and down triangles show the position of two sets of models (see Sect. 4). The obvious differences in the MS evolutionary tracks are due to the different values of stellar mass, metallicity and core overshooting parameter adopted. The occurrence of the overshooting phenomena extends the track of the stellar model toward lower values of log g and Teff, resulting ultimately in a notable broadening of the MS. This is because extra mixing leads to a larger amount of H available for burning in the stellar core which of course prolongs the MS lifetime. Note that unlike metallicity, overshooting does not change the location of the ZAMS in the HR diagram.
 |
Fig. 1. Teff–log g diagram showing the location of ELMV stars (light green triangles), pre-ELMV stars (blue diamonds), δ Sct stars (white circles) including SX Phe stars (magenta circles). The atmospheric parameters are extracted from different works detailed in the main text. Also, we included the theoretical evolutionary tracks of low mass He-core WDs (black dotted and dashed lines) from Althaus et al. (2013) and Serenelli et al. (2001), and of MS evolutionary tracks (red lines) from Sánchez Arias et al. (2017). Black numbers correspond to different values of the stellar mass of the low mass Hecore WDs, whereas red numbers are associated to the values of the mass, the metallicity and the overshooting parameter (see Table 3). Orange triangles show the position of the template models (see Sect. 4). The cyan squares indicate the position of the two stars reported by Corti et al. (2016), J1730+0706 and J1458+0707, and the cyan diamond represents the position of a new pulsating star, J0757+1448. These three objects will be analyzed in Sect. 6. |
From Fig. 1 we note that the region where pre-ELMVs are located overlaps with the region occupied by the δ Sct stars. It is important to mention that the percentage of pre-ELM and ELM WDs “polluting” this region of the diagram (6000 < Teff < 12 000 K and 3 < log g < 7) is approximately 7% in a sample of subdwarf A-type (sdA) stars commonly observed in this region (Pelisoli et al. 2018). Note that the physical nature of sdAs stars is still an open issue. Possible explanations include metal poor main sequence A–F stars (see, e.g., Brown et al. 2017), and binary byproducts such as ELMs, pre-ELMs and blue stragglers (e.g., Pelisoli et al. 2018).
Finally, we show in Fig. 1 the location of the theoretical blue edge and the empirical red edge of the δ Sct instability strip extracted from Pamyatnykh (2000), and also the blue edge of the pre-ELMV instability strip computed by Córsico et al. (2016). We note that both instability strips overlap for 3 ≲ log g ≲ 4.4. In addition, the observed period ranges showed by all the variable stars mentioned also overlap between 400 and 12 000 s (or between 7.2 c/d and 216 c/d in frequencies) (see Table 2). However, the nature of the pulsation modes would not be the same for δ Sct and pre-ELM WD stars. For δ Sct pulsators most of those periods would correspond to radial modes or non-radial p modes, while for pre-ELM WDs only g-modes can have long periods in that range. Thus, it would be possible to distinguish δ Sct and pre-ELMVs by analyzing the pulsational properties of these two classes of variable stars. This is the main goal of the present study.
Among all types of variable stars described in this section, we have analyzed in particular the δ Sct stars and pre-ELMV classes, since they are found in the same region of the log g − Teff plane and they share a common range of observed periods. γ Dor stars are found within the δ Sct instability strip, but they exhibit pulsation periods that are too long as compared to the periods usually observed in ELMVs and pre-ELMVs (see Table 2). This is also the case for hybrid δ Sct-γ Dor stars. The period ranges of roAp stars partially overlaps with that of pre-ELMV WDs, but roAp stars show an overabundance of rare earth elements and strong magnetic fields and both characteristics, easily detected, are not observed in pre-ELMV stars. Finally, ELMV stars are characterized by surface gravities (log g ≳ 6) larger than for pre-ELMVs and δ Sct stars. Therefore, we exclude δ Doradus, hybrid δ Sct-γ Dor, roAp and ELMV stars from our analysis.
Spectroscopic parameters of the different groups of variable stars described in the text.
Period and frequency ranges usually observed of the different variable stars described in the text.
Stellar parameters of the MS evolutionary sequences.
3. Numerical tools
The pulsation analysis presented in this work has made use of full stellar evolution models computed with the LPCODE stellar evolution code. LPCODE computes the complete evolution of low- and intermediate-mass stars, from the ZAMS, through the core H-burning phase, the He-burning phase, and thermally pulsing asymptotic giant branch (AGB) to the WD stage. Details of the LPCODE can be found in Althaus et al. (2005, 2009, 2013), Renedo et al. (2010) and Romero et al. (2015) and references therein. Here, we comment on the main input physics relevant for this work. Further details can be found in those papers.
To account for convection we adopted the mixing length theory with the free parameter α = 1.66 for the MS phase. Note that the calibration of α depends on the effective temperature and surface gravity and therefore change with the evolution as shown in Trampedach et al. (2014). Although a non-constant treatment of α should be used during the evolution in the MS, we selected α = 1.66 with which we have reproduced the present luminosity and effective temperature of the Sun, L⊙ = 3.842 × 1033 erg s−1 and log Teff = 3.7641, when Z = 0.0164 and X = 0.714 are adopted, according to the Z/X value of Grevesse & Noels (1993). For the WD phase we adopted the MLT in its ML2 flavor, with α = 1.0. We include radiative opacities from the OPAL project Iglesias & Rogers (1996) complemented at low temperatures with the molecular opacities from Ferguson et al. (2005). For the WD regime an updated version of the Magni & Mazzitelli (1979) equation of state was employed. In the present work, we considered pre-WD stellar models without element diffusion (i.e., radiative levitation, thermal and chemical diffusion and gravitational settling). In this way, it is assumed that pre-ELMV stars preserve the outer H/He homogeneous chemical structure resulting from the previous evolution. The presence of He in the envelopes of pre-ELMVs plays a fundamental role for exciting pulsation modes (Córsico et al. 2016; Istrate et al. 2016a), and has been observed in the atmosphere of three pre-ELMVs reported in Gianninas et al. (2016).
We treated the extra-mixing (overshooting) as a time-dependent diffusion process by assuming that the mixing velocities decay exponentially beyond each convective boundary with a diffusion coefficient given by D = D0 exp(−2z/ f Hp), where D0 is the diffusive coefficient near the edge of the convective zone, z is the geometric distance of the considered layer to this edge, Hp is the pressure scale height at the convective boundary, and f is the overshooting parameter also named as αOV (Herwig et al. 1997; Herwig 2000). In this study we selected a δ Sct model with extreme overshooting parameter value of αOV = 0.03. Finally, the metallicity is taken to be Z = 0.01 for this selected model. In the sake of simplicity, the impact of stellar rotation on the equilibrium models and on the pulsation spectra has been neglected in this work. Nevertheless, we include a brief discussion about the effect of stellar rotation in the next section.
The pulsation computations employed in this work were carried out with the adiabatic and non-adiabatic versions of the LP-PUL pulsation code described in detail in Córsico & Althaus (2006) and Córsico et al. (2006), respectively. Briefly, the adiabatic version of the LP-PUL pulsation code is based on the general Newton–Raphson technique to solve the fourth order system of equations and boundary conditions that describe linear, adiabatic, non-radial stellar pulsations, following the dimensionless formulation of Dziembowski (1971). For the non-adiabatic computations, the code solves the sixth-order complex system of linearized equations and boundary conditions as given by Unno et al. (1989).
4. Asteroseismic comparison
In this section we analyze and compare the pulsational properties of two groups of stellar models. The δ Sct models were taken from Sánchez Arias et al. (2017), while the models of pre-ELM stars are from Córsico et al. (2016). The pre-ELMV models employed in this work were computed considering a solar metallicity progenitor, typical of Population I stars. We note that some pre-ELM WDs actually could belong to the halo population, and so they would come from low-metallicity progenitors. In that case, the H content of the pre-ELM WDs would be larger than that characterizing pre-ELM WDs coming from solar metallicity progenitors (see, e.g., Istrate et al. 2016b). It is interesting to note that pre-ELMVs and evolved δ Sct stars show low radial order p and g modes which, strictly speaking, are mixed modes (e.g., Lenz et al. 2010; Córsico et al. 2016). However, for simplicity, we call them conventional p and g modes.
In our analysis, we consider non-radial p and g modes with pulsation periods in the ranges ~400–50 000 s and ~100– 10 000 s for the δ Sct model and the pre-ELMV model respectively (frequencies in the ranges ~1.72–216 c/d and ~8.64–864 c/d respectively), with harmonic degrees ℓ = 1 and ℓ = 2. We selected two sets of two models, one for δ Sct stars and the other one for a pre-ELM WD star, both models being characterized by similar atmospheric parameters. The atmospheric parameters along with other parameters for the models are listed in Tables 4 and 5. The first set of stellar models is in a cool region of the Teff–log g plane with an effective temperature typically of δ Sct stars and where pre-ELMV are predicted to lie. This cool set of stellar models is characterized by log g ~ 4.08 and Teff ~ 7650 K (Table 4), and is indicated with an orange triangle up symbol in Fig. 1. The second set of stellar models is in a hot region of the Teff–log g diagram in which δ Sct stars and pre-ELMV WDs can be confused if we consider the external uncertainties in Teff and log g of the pulsating objects usually finds in this region. This hot set is characterized by log g ~ 4.23 and Teff ~ 9670 K (Table 5), and is indicated as a triangle down symbol in Fig. 1. Note that there are usually no δ Sct stars at such high effective temperature and this is consistence with the non-adiabatic analysis for this model (not included) which do not predict any unstable period. Nevertheless, the next adiabatic analysis provides tools to distinguish between the two kinds of stars in this region of the Teff–log g diagram.
Parameters characterizing our set of cool models.
Parameters characterizing our set of hot models.
4.1. Chemical profiles and propagation diagrams
We begin by analyzing the internal structure of the δ Sct and pre-ELMV models. In Figs. 2 and 3 we show the inner chemical abundances of H and He and the propagation diagram as a function of the radius for our “cool” and “hot” models, respectively. Top panels correspond to the δ Sct models, while bottom panels correspond to the pre-ELMV models. The δ Sct models show a H-dominated envelope and a H/He core, consistent with stars in the H-burning stage. The specific H/He ratio at the stellar core depends on the stellar mass and the age of the model. Since our cool δ Sct is older than the hot δ Sct model, the He abundances in the former is higher, leading to a He-dominated core star. The pre-ELM WD models, on the other hand, have a pure He-core since those models already depleted all the H in the core but did not reach the core temperature necessary to start the He burning in the core. These objects are consider as He-core stars.
 |
Fig. 2. Abundances by mass of He and H as a function of the normalized radius (top panels), and propagation diagrams (the run of the logarithm of the squared Brunt–Väisälä and Lamb frequencies, lower panels) corresponding to the δ Sct model (upper panel), and to the pre-ELMV model (lower panel) indicated as a triangle up symbol in Fig. 1. |
 |
Fig. 3. Same as in Fig. 2, but for the set of hot models, indicated as a triangle down symbol in Fig. 1. |
As shown in Figs. 2 and 3, the presence of internal density gradients associated to the He/H chemical transition regions leave strong signatures in the Brunt–Väisälä (B–V) frequency. For instance, considering the cool model showed in Fig. 2, the bump in the B–V frequency for the δ Sct model (at r/R ~ 0.1) is higher and wider than for the pre-ELM model, indicating a wide chemical transition region for δ Sct stars. In addition, the B–V frequency is zero in convective regions. This can be seen for the δ Sct model, at the convective core region and the outer convective layers. Note that, for the δ Sct model, the B–V frequency takes non-null values in an external layer of the core (at 0.08 ≲ r/R ≲ 0.1) with overshooting. In the case of the pre-ELMV model, the B–V frequency is zero only at the outer convective zone. In addition, the B–V and the Lamb frequencies take both higher values for the pre-ELMV model than for the δ Sct model, especially in the inner region. We note that the radius for the δ Sct model is approximately three times larger than for the pre-ELM model and the density for δ Sct star is much lower than for pre-ELM WDs. This increase the value of B–V frequency for pre-ELM star leading to a significant reduction of the mean period spacings of g modes compared with mean period spacing of theoretical g modes for the δ Sct model, which are usually associated with mixed modes.
4.2. Periods and period spacings
In this section we analyze and compare the period ranges of dipole (ℓ = 1) p and g modes for both, the pre-ELMV and δ Sct models. It is important to mention that not all modes are excited in δ Sct stars, which complicates mode identification and often hampers unique modeling. This mode selection mechanism is unfortunately still unclear (see review e.g., Smolec 2014). In addition, modes with ℓ = 0, 2, 3, … are also excited in these stars. We have explored the case of ℓ = 2 and we have found similar results, thus we restrict ourselves to show the results for ℓ = 1 only and we focus our analysis in the adiabatic pulsation spectra.
The theoretical adiabatic periods in the usually observed period range for p and g dipole modes of the cool and hot models are depicted in Figs. 4 and 5. From these figures, we can see that the δ Sct and pre-ELMV models share a common range of periods. However, even if the period values are the same, the properties of the modes are not. For instance, in Fig. 4 we can see that the period range of p modes for the δ Sct model overlaps with the period range of p and g modes for the pre-ELM WD model, while the periods of g modes are much longer. Periods in the range 4 579–5 748 s 15–19 c/d) belong exclusively to the g modes of the pre-ELMV model. Depending on the period value itself, the mode can be associated with a p mode or a g mode. For example, if an observed mode has a period of ~2 000 s (~43.2 c/d), then it can be a g mode if it belongs to a pre-ELMV star, but it could alternatively be a p mode if the object is actually a δ Sct star. However, for periods shorter than ~1 000 s or larger than ~5 700 s (frequencies larger that 86.4 c/d or shorter than 15.15 c/d), the modes will correspond to p modes or g modes, respectively, for both types of stars. Furthermore, by taking into account the usual range of observed periods in δ Sct—which extends from ~700 s onward—modes with periods below 700 s belong exclusively to pre-ELMV stars (equivalently modes with frequencies above 123.42 c/d belong exclusively to pre-ELMV stars). The values of the periods and frequencies for dipole g and p modes for the cool models depicted in Fig. 4 are listed in Tables A.1–A.4 of the Appendix, along with their corresponding radial orders.
 |
Fig. 4. Adiabatic periods in the usually observed ranges computed for the cool δ Sct and pre-ELMV selected models, depicted with a triangle up symbol in Fig. 1. The upper strips represent p and mixed g modes (in red and black, respectively) for the pre-ELMV model. The bottom strips represent p and mixed modes for the δ Sct model. |
In order to decipher the nature of the observed periods, we need additional information, such as an estimation of the period spacing for g-modes(ΔΠ = Πk+1 − Πk) and the frequency spacing for p-modes (Δv = vk+1 − vk, k being the radial order). For high radial orders and for a given small value of ℓ, the period spacing for g modes tends to a constant value with no rotation or abrupt transitions in the stellar interior. Similarly, for k ≫ l the large frequency separation (for p modes) will also be constant, allowing to distinguish between p and g modes. Despite some stars showing high radial orders (e.g., Antoci et al. 2011), δ Sct and pre-ELMV stars rather exhibit pulsation in low to intermediate radial order. This means that is not completely adequate to use the asymptotic period spacing or the asymptotic frequency spacing to characterize the nature of the star. For this reason we focus on period spacings, frequency spacings, the mean period spacings (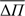 ) and mean frequency spacings (
) and mean frequency spacings (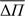 ), as defined below. The differences in these quantities along with the rate of the period change allow to distinguish between pre-ELMV and δ Sct stars.
), as defined below. The differences in these quantities along with the rate of the period change allow to distinguish between pre-ELMV and δ Sct stars.
We clarify that we use ΔΠ and 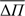 for p modes only as math tools, to mimic the possible confusion between p and g modes, but they are not real seismic tools. The same applies for Δv and
for p modes only as math tools, to mimic the possible confusion between p and g modes, but they are not real seismic tools. The same applies for Δv and 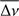 for g modes. We assume no additional information other than the Teff and log g values, and the observed pulsation modes, for which we have no prior knowledge concerning their nature. In order to properly distinguish between the well-known frequency and period spacings from Δv for g modes and ΔΠ for p modes, we name the last two quantities as the frequency difference (of g modes) and period difference (of p modes) respectively. Note that these four quantities are computed for modes with consecutive radial order.
for g modes. We assume no additional information other than the Teff and log g values, and the observed pulsation modes, for which we have no prior knowledge concerning their nature. In order to properly distinguish between the well-known frequency and period spacings from Δv for g modes and ΔΠ for p modes, we name the last two quantities as the frequency difference (of g modes) and period difference (of p modes) respectively. Note that these four quantities are computed for modes with consecutive radial order.
In Fig. 6 we show the period spacing, ΔΠ , as a function of the periods, for the cool (blue) and hot (black) δ Sct (upper panel) and pre-ELM (bottom panel) template models. We include the asymptotic period spacing for g modes, depicted with thin horizontal continuous and dashed red lines for the cool and hot models, respectively, as a reference. Let us consider the mean period spacing, defined as 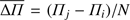 , where N is the number of consecutive radial orders modes with periods between Πi and Πj. For theoretical g modes, which are usually associated with mixed modes, the value of
, where N is the number of consecutive radial orders modes with periods between Πi and Πj. For theoretical g modes, which are usually associated with mixed modes, the value of 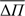 for the δ Sct model is larger than that for the pre-ELMV model in the usually range of observed periods for each kind of star. In particular, for the cool models,
for the δ Sct model is larger than that for the pre-ELMV model in the usually range of observed periods for each kind of star. In particular, for the cool models, 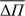 for the δ Sct model is ~3000 s (similar to the asymptotic period spacing) while for the pre-ELMV model the mean period spacing is more than an order of magnitude shorter, around ~90 s. Regarding the period spacing for g modes for the δ Sct models, ΔΠ ranges from 2300 to 3500 s approximately, while for the pre-ELMV model it ranges from ~50 to 110 s. For p-modes, we also measured the
for the δ Sct model is ~3000 s (similar to the asymptotic period spacing) while for the pre-ELMV model the mean period spacing is more than an order of magnitude shorter, around ~90 s. Regarding the period spacing for g modes for the δ Sct models, ΔΠ ranges from 2300 to 3500 s approximately, while for the pre-ELMV model it ranges from ~50 to 110 s. For p-modes, we also measured the 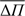 value and it ranges from 50 to 300 s, depending on the range of periods (Πi and Πj) considered for the δ Sct model, while it shows a more restricted range for the pre-ELM WD model, between 10 and 30 s. Besides, ΔΠ ranges from 10 to 1200 s for the δ Sct model, while it takes smaller values for pre-ELMV model, from 10 to 75 s. A similar trend is found for the hot models. We point out that the deviations from a constant value of ΔΠ for g modes in Fig. 6 are of course related with the chemical gradient and therefore with the profile of the B–V frequency. For a given star with a convective core, the numbers of minima in the period spacing increase as the star evolves on the MS due to the widening of the H/He chemical transition region (e.g., Miglio et al. 2008).
value and it ranges from 50 to 300 s, depending on the range of periods (Πi and Πj) considered for the δ Sct model, while it shows a more restricted range for the pre-ELM WD model, between 10 and 30 s. Besides, ΔΠ ranges from 10 to 1200 s for the δ Sct model, while it takes smaller values for pre-ELMV model, from 10 to 75 s. A similar trend is found for the hot models. We point out that the deviations from a constant value of ΔΠ for g modes in Fig. 6 are of course related with the chemical gradient and therefore with the profile of the B–V frequency. For a given star with a convective core, the numbers of minima in the period spacing increase as the star evolves on the MS due to the widening of the H/He chemical transition region (e.g., Miglio et al. 2008).
 |
Fig. 6. Period spacing versus period for p modes (circles) and g modes (squares) corresponding to the δ Sct models (upper panel), and to the pre-ELMV models (lower panel). The asymptotic period spacing for g modes is depicted as a reference with thin horizontal continuous and dashed lines for the cool and hot models, respectively. Selected periods with consecutive radial orders are marked with magenta squares. They correspond to p modes for the δ Sct model, and to g modes for the pre-ELMV model (see text for details). |
In Fig. 7 we show the frequency spacing (Δv) versus frequency for the δ Sct models (upper panel) and the pre-ELMV models (lower panel). Horizontal continuous and dashed red lines correspond to the asymptotic frequency spacing for p modes for the cool and hot model, respectively, included as a reference. The frequency spacing reflects the same trend that has been described for the period spacing. For example, considering the cool models, we can see that the mean frequency spacing (defined as 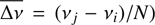 ) for p modes of the δ Sct model is 6.56 c/d, while for the pre-ELMV model is 21.74 c/d. Furthermore, Δv ranges between 1.32 and 5.46 c/d for the δ Sct model and from 2.59 to 8.64 c/d approximately for the pre-ELM model. For low order g-modes,
) for p modes of the δ Sct model is 6.56 c/d, while for the pre-ELMV model is 21.74 c/d. Furthermore, Δv ranges between 1.32 and 5.46 c/d for the δ Sct model and from 2.59 to 8.64 c/d approximately for the pre-ELM model. For low order g-modes, 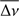 is 2.06 c/d for the δ Sct model while for the pre-ELMV model it is 1.07 c/d. In addition, for low order g modes ranges from 0.59 to 4.61 c/d for the δ Sct model and from 0.2 to 4.32 c/d for the pre-ELMV model.
is 2.06 c/d for the δ Sct model while for the pre-ELMV model it is 1.07 c/d. In addition, for low order g modes ranges from 0.59 to 4.61 c/d for the δ Sct model and from 0.2 to 4.32 c/d for the pre-ELMV model.
 |
Fig. 7. Same as Fig. 6, but for the frequency spacings. Horizontal continuous and dashed lines correspond to the asymptotic frequency spacing for p modes for the cool and hot models, respectively. |
Note that if the observed periods belong to modes with the same ℓ and are consecutive radial orders, then the ΔΠ value and its behavior can also help to distinguish δ Sct from pre-ELMV stars, even if the observed modes have the same nature for both classes of pulsating stars. To illustrate this point, let us consider the g-mode periods corresponding to k = 1 and k = 2 for the δ Sct model, depicted with magenta squares in the upper panel of Fig. 6, and the periods corresponding to k = 9 and k = 10 for the pre-ELMV model, depicted with magenta squares in the lower panel of the same figure. The period spacing for the selected periods of the δ Sct model is 2543 s, while for the pre-ELMV model it is 89 s, it is almost two orders of magnitude smaller.
By taking a closer look at the cool models in Fig. 6 we can note that for periods between 1000 and 4600 s (18.78–86.4 mHz) the low radial order p modes corresponding to the δ Sct model overlap with the pre-ELMV g-modes. In particular, for the δ Sct model (see the magenta squares in upper panel of Fig. 6), the p modes from k = 1 to k = 5 have periods between 2500 and 4600 s (18.86 and 34.15 c/d), with a mean period difference of ~510 s (or mean frequency spacing of 3.05 c/d). In this same period interval, the mean period spacing for periods corresponding to high radial order g modes for the pre-ELMV model (modes with radial order from k = 20 to k = 41) is ~100 s (or mean frequency difference of 0.72 c/d). This difference of ~400 s allows us to easily distinguish between consecutive low-radial order p modes and high-radial order g modes, and thus δ Sct stars from pre-ELMV stars. On the other hand, for p modes with k = 6 to k = 15 for the δ Sct model, the periods are in the range [1000–2500] s (34.56–86.4 c/d) and the mean period difference is ~132 s (mean frequency spacing of 5 c/d). In the same period range, g-mode periods of low radial order from k = 1 to k = 19 of the pre-ELMV model show a mean period spacing of 75 s (mean frequency difference of 2.29 c/d). Then, the difference in 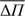 is ~60 s, which still could allow to distinguish between p modes and g modes.
is ~60 s, which still could allow to distinguish between p modes and g modes.
We point out that δ Sct stars are moderate to rapid rotators, showing projected rotational velocities (V sin i) around 110 km s−1 (see e.g., Solano & Fernley 1997). On the other hand the only calculated V sin i values for pre-ELMVs are 30 km s−1 and 24 km s−1 for J0247−25B and WASP1628+10B respectively. Rotation induces to rotational splitting of the frequencies in the pulsation spectra. Considering rigid rotation and a first order perturbation theory we can estimate the maximum velocity (Vmax) beyond which the difference between the frequency of the m = 0 component and the m = ±1 component of the rotational multiplet (δv) is greater than the mean frequency spacing. Using this expression for the cool models: 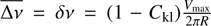 we calculate the velocity Vmax at which the rotational splitting mimic the frequency spacing. For the Sct model we obtain ~Vmax = 634 km s−1 for p-modes and Vmax = 411 km s−1 for low order g modes. Note that the break up velocity for this δ Sct model is ~ 394 km s−1, therefore the rotational splitting will not mimic the frequency spacing of consecutive radial order modes. On the the other hand, for the pre-ELMV model we obtained Vmax = 693 km s−1 for p-modes and Vmax = 50 km s−1 for g modes. The break up velocity for this model is 230 km s−1, therefore the splitting in p modes will not be confused with the frequency spacing of consecutive radial order p modes at any possible velocity. On the contrary, the rotational splitting of g modes could be confused with the frequency separation if i ≲ 37° considering V sin i = 30 km s−1 for the pre-ELMV model. We conclude that this phenomena should be taken into account, in general cases, specially when a mode identification is required.
we calculate the velocity Vmax at which the rotational splitting mimic the frequency spacing. For the Sct model we obtain ~Vmax = 634 km s−1 for p-modes and Vmax = 411 km s−1 for low order g modes. Note that the break up velocity for this δ Sct model is ~ 394 km s−1, therefore the rotational splitting will not mimic the frequency spacing of consecutive radial order modes. On the the other hand, for the pre-ELMV model we obtained Vmax = 693 km s−1 for p-modes and Vmax = 50 km s−1 for g modes. The break up velocity for this model is 230 km s−1, therefore the splitting in p modes will not be confused with the frequency spacing of consecutive radial order p modes at any possible velocity. On the contrary, the rotational splitting of g modes could be confused with the frequency separation if i ≲ 37° considering V sin i = 30 km s−1 for the pre-ELMV model. We conclude that this phenomena should be taken into account, in general cases, specially when a mode identification is required.
4.3. Rate of period change
In this section we analyze the values of the temporal rate of period change, dΠ /dt. For the two cool template models, we estimated the dΠ /dt corresponding to a pulsation mode with a period of ~966 s (89.44 c/d). From Tables A.3 and A.4 we see that such a mode, emphasized in bold, corresponds to a p mode with radial order k = 16 and k = 2 for the δ Sct and the pre-ELMV models, respectively. For the mode corresponding to the δ Sct model (with a period of 966.95 s and a frequency of 89.35 c/d) we obtain a rate of period change of dΠ /dt = 5.45 × 10−5 s yr−1. For the period corresponding to the pre-ELMV model (963.715 s or 89.65 c/d) the result is dΠ /dt = −1.42 × 10−3 s yr−1. Then, for the selected modes, the absolute value of the rate of period change for the pre-ELMV mode is two orders of magnitude higher than for the δ Sct model. These results are in agreement with Breger & Pamyatnykh (1998) regarding δ Sct stars, and Calcaferro et al. (2017) in connection with pre-ELMV stars. Therefore, the rate of period change is a potential tool with which to distinguish the two kinds of stars.
We mention here that in the frame of the Kepler and K2 missions and the upcoming TESS mission, the rate of the period change is a powerful tool that could help to improve the classification of the stars observed by these mission. Given that is possible to measure dΠ /dt for δ Sct stars with approximately four years of observations, the 351 days of the continuous viewing zone of the TESS Satellite should be enough to measure dΠ /dt for pre-ELMV WDs since these objects evolve more than one thousand times faster than δ Sct stars. It is important to note that unlike the measure of the ΔΠ or Δv, the rate of the period change is independent of mode identification which makes it a powerful tool to distinguish between δ Sct and pre-ELM pulsators.
5. Non-adiabatic analysis
In this section we present the results from non-adiabatic pulsation computations for the cool set of models. As mentioned, the calculations were carried out using the non-adiabatic version of the LP-PUL pulsation code described in detail in Córsico et al. (2006). Figure 8 shows the normalized growth rate η (≡ −ℑ(σ)/ℜ(σ)) in terms of the pulsation periods Π for ℓ = 1 modes corresponding to the δ Sct (depicted with black squares) and pre-ELM WD template model (depicted with red circles). ℑ(σ) and ℜ(σ) are the imaginary and the real part, respectively, of the complex eigenfrequency (σ). If η > 0, then the mode is pulsationally unstable, and could reach observable amplitudes, while modes with η < 0 are stable.
 |
Fig. 8. Normalized growth rates η for p and g modes in terms of the pulsation periods corresponding to the selected models. Modes corresponding the δ Sct model are depicted with square symbols and continuous black line, while modes corresponding to the pre-ELM WD model are depicted with circle symbols and continuous red lines. A value of η > 0 (η < 0) implies unstable (stable) modes. In frequencies, the band of excited modes for the δ Sct model is 10.16 ≲ v ≲ 34.56 c/d and for the pre-ELMV model is 17.28 ≲ v ≲ 24.68 c/d. |
We can observe in Fig. 8 that the band of excited modes for the δ Sct model is 2500 ≲ Π ≲ 8 500 s (10.16 ≲ v ≲ 34.56 c/d) which correspond to low-order g and p modes. Overlapping this period interval, we found the unstable modes for the pre-ELMV model, spreading from 3500 s to 5000 s (17.28 c/d–24.68 c/d), which are g modes with relatively high radial orders. This means, for these particular models, that if we find excited modes in the ranges 2 500 ≲ Π ≲ 3 500 s and 5 000 ≲ Π ≲ 8 500 s ( 24.68 ≲ v ≲ 34.56 c/d and 10.16 ≲ v ≲ 17.28 s), they will correspond to a δ Sct star. In the case of having observed periods only in the interval 3 500 ≲ Π ≲ 5 000 s (17.28 ≲ v ≲ 24.68 c/d), it is not possible to discern whether these observed periods correspond to a δ Sct star or a pre-ELMV star with this analysis only since the periods of excited modes of both stars overlap in this region and the period spacing analysis described previously should be done with the aim of properly classify the star. We consider the case of ℓ = 1 and these ranges might be increased if modes with l = 0, 2, … are also taken into account.
6. Testing the technique
In this section we present a new variable star, J075738.94+144827.5, with spectroscopic values of Teff and log g in the region where the instability strips of pre-ELMV and δ Sct stars overlap (see Table 6). The atmospheric parameters were determined by fitting the optical spectra to DA local thermodynamic equilibrium (LTE) grids of synthetic nonmagnetic spectra derived from model atmospheres with metals in solar abundances from Koester (2010; see also Pelisoli et al. 2018). We analyze the nature of this star in the frame of the previous discussion, considering the external uncertainties in log g and Teff, which are approximately 0.25 dex and 5–10% respectively.
The variable star J075738.94+144827.5 was observed in the Southern Astrophysical Research (SOAR) telescope for 4.6 h during the night of 04 April 2016 as part of the project SO2016A-006 – Photometry of Extremely-Low Mass White Dwarf Candidates. It was observed with the Goodman HTS with an integration time of 10 s and the S8612 blue filter. The CCD region of interest was set to 800 × 800, resulting on a read out time of about 3.8 s. The light curve and Fourier transform are shown on Fig. 9. Four pulsation periods were found above a 3σ limit of detection, where σ is the mean amplitude of the Fourier transform. Three periods are between 2000 and 3000 s (28.8 and 43.2 c/d), and one period is shorter (802.90 s or 107 c/d) and with smaller amplitude. The spectroscopic parameters along with the observed periods corresponding to this object are listed in Table 6. The position of the star in the Teff–log g diagram on Fig. 1 is represented as a cyan full diamond.
 |
Fig. 9. Top panel: light curve for J075738.94+144827.5. Error bars are shown in gray and a smoothed light curve is shown in red. Bottom panel: original Fourier transform in gray, and the subsequent Fourier transforms, subtracting periods above the 3 ~ σ detection limit, in different colors. The final detection limit, above which no further periods were found, is shown in red. |
Regarding the nature of J075738.94+144827.5, and considering the p and g mode period ranges of the δ Sct and pre-ELMV models (Tables A.2 and A.3), there are two possible scenarios. Specifically, the star could be a δ Sct star with four p modes, or it could be a pre-ELMV star with three g modes and one p mode (the one with a period of 802.90 s or 107.6 c/d) as well. If we assume that the periods between 2000 and 3000 s (28.8 and 43.2 c/d) have consecutive radial orders, then the observed period difference is between 380 and 546 s (frequency difference ~6.53). These values are similar to the period difference values corresponding to p-modes of the δ Sct model in the range 2000–3000 s, i.e., ~300 s (mean frequency spacing of ~3.6. Note that the mean period spacing for a pre-ELMV model in the same range of periods is of only ~80 s (mean frequency difference of ~1.1 c/d). Then we conclude that J075738.94+144827.5 is most likely a δ Sct star with four observed p modes, if we consider the external uncertainties in the atmospheric parameters of this object.
In addition, two interesting variable stars have recently been reported in Corti et al. (2016): J145847.02+070754.46 and J173001.94+070600.25. Their location in the HR diagram (log g = 4.25 and Teff ≈ 7950 K) along with the lack of information about theirs masses make their classification difficult. Furthermore, the observed periods are compatible with those corresponding to δ Sct star and pre-ELMV WDs simultaneously. In the case of J173001.94+070600.25, the star shows only one period of 3367.1 s (25.66 c/d), which is in the period range where both Sct and pre-ELMV stars show variability. However, as can be seen from Fig. 4, the observed period corresponds to a p mode or a g mixed mode, depending on the type of star. The detection of additional pulsation periods could allow us an estimate of the period spacing. A similar situation occurs for J145847.02+070754.46 which shows two periods of 1633.9 s and 3278.7 s (52.9 c/d and 26.35 c/d). According to those periods, these modes would correspond to p modes if the star is a δ Sct star, and g modes if the star is a pre-ELMV star. The difference between the two periods is ~1645 s (~26.55 c/d), which is too large for the periods to have consecutive radial orders, either if the pulsating object is a δ Sct star or a pre-ELMV star. The rate of period change would help to classify these three stars. Unfortunately, these objects were observed during a short period and it is not possible to measure the rate of period change for them. We conclude that further observations are needed in order to allow a safe classification of these two stars on the basis of their pulsation properties.
Spectroscopic parameters and periods of J075738.94 +144827.50.
7. Conclusions
Pulsating pre-ELM stars and δ Sct are found roughly in the same region in the log g–Teff diagram, corresponding to an effective temperature in the range 6000 ≲ Teff ≲ 11 000 K and surface gravity in the range 3.5 ≲ log g ≲ 5.5, as can be seen from Fig. 1. Specifically, theoretical models predict that pre-ELMV stars can be found in the δ Sct region (6000 ≲ Teff ≲ 9000 and 3.25 ≲ log g ≲ 4.4) making it rather difficult to distinguish between the two groups from atmospheric parameters alone. In this paper, we performed a detailed analysis of the pulsational properties of δ Sct and pre-ELMV stars, aiming to use the differences in those properties to achieve a better classification. From the evolutionary and pulsation models of Sánchez Arias et al. (2017) and Córsico et al. (2016), we have considered adiabatic and non-adiabatic pulsations for ℓ = 1 p, g and mixed modes with periods between ~400 s and ~10 000 s (~8.64 c/d and ~216 c/d) for the pre-ELMV model, and between ~400 s and ~300 000 (~0.28 c/d and ~216 c/d) for the δ Sct model. Two sets of models for each class of stars were chosen to cover different regions in the Teff– log g diagram where pulsating objects are currently observed and can be confused with δ Sct stars or pre-ELM WDs. The cool set is characterized by atmosphere parameters of Teff ~ 7 650 K– log g ~ 4.08 representative of δ Sct stars and also predicted for pre-ELMV WDs. The hot set, with Teff ~ 9 670 K–log g ~ 4.23, is very close to the lower part of the classical instability strip, in a region where δ Sct and pre-ELMV can be confused if we consider the external uncertainties measured in these parameters. For each model, we analyzed the period range, period spacing and rates of period change. In addition, we analyze the pulsational stability of modes for the cool model. Finally, we compared the pulsational properties of both δ Sct and pre-ELMV stars, looking for differences and similarities in their pulsational properties. As mentioned above, we have assumed no additional information other than the Teff and log g values, and the observed periods, for which we have no mode identification. Therefore we used ΔΠ and 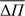 for p modes only as math tools and the same applies for Δv and
for p modes only as math tools and the same applies for Δv and 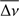 for g modes. Our main tools shown in this paper are the following:
for g modes. Our main tools shown in this paper are the following:
-
The values of periods of δ Sct and pre-ELMV stars overlap, meaning that the observed mode may originate from either star. However, the nature of the mode (either p or g mode classification), can be different, depending on the nature of the star and the pulsation period.
-
In the case of low radial orders and short periods (~1000 s and frequencies ~86.4 c/d), pulsation modes are p modes for both kinds of stars. A similar situation is found for mixed modes with periods larger than ~5700 s (frequencies shorter than 15.15 c/d), that correspond to g mode pulsations. On the other hand, periods between ~1000 s and ~5700 s (~15.15 c/d and 86.4 c/d) are associated to p modes if the star is a δ Sct star, while they are consistent with g modes if the star is a pre-ELMV star. Once discovered, the different nature of the observed modes can be used to distinguish δ Sct from pre-ELMV stars if the periods are between ~1000 s and ~5700 s (~15.15 c/d and 86.4 c/d).
-
The mean period difference for the δ Sct model is at least four times longer than that for the pre-ELMVs models in the period range between 2500 and 4600 s (18.78 and 34 c/d). This difference, that amounts to ~400 s, allows us to distinguish between consecutive low-radial order p modes and high-radial order g modes, and thus δ Sct stars from pre-ELMV stars. A longer period difference for δ Sct stars is not surprising, since those stars have radii between 1.5 and 3.5 R⊙ typical of MS stars, while pre-ELMV with the same log g have a radius of ~0.6 R⊙.
-
The rate of period change shows a large difference between δ Sct and pre-ELMV stars. For the cool models, the rate of period change for a mode with a period of ~965 s is dΠ /dt = 5.453 × 10−5 s yr−1 for the δ Sct model, while for the pre-ELM model it is dΠ /dt = −1.42 × 10−3 s yr−1. Note that δ Sct stars are evolving at MS rates of ~Gyrs, while pre-ELMV stars are in a giant star stage forced by the residual H burning before entering the WD cooling curve for the first time, evolving more than one thousand times faster than δ Sct stars.
-
Our preliminary non-adiabatic exploration indicates that for δ Sct and pre-ELMV stars, the ranges of unstable periods for the cool models overlap.
-
We present a new pulsating star, J075738.94+144827.5, with four detected periods and spectroscopic parameters within the overlap region. We tried to determine the class of variable stars to which it belongs. The star could either be a δ Sct star with four p modes, or it could be a pre-ELMV star with three g modes and one p mode as well. If we assume that the periods between 2000 and 3000 s (28.8 and 43 c/d) have consecutive radial orders, then the observed period difference is compatible with the period difference values corresponding to p-modes of the δ Sct stars, but not with the mean period spacing of the pre-ELMV model in the same range of periods. We conclude that J075738.94+144827.5 is most likely a δ Sct star, if we consider the external uncertainties in the atmospheric parameters of this object.
The strong differences found in the period spacing of g and p modes, and in the rate of period change for δ Sct and pre-ELMV stars suggest that asteroseismology could be employed to discriminate between δ Sct and pre-ELMV stars. The Kepler/K2, TESS and PLATO missions will provide further observations needed to increase the number of pulsation modes, and to estimate the period and frequency spacing and/or the rate of period change in order to be able to distinguish between these two very different classes of pulsating stars. Finally, we will be able to confirm our results once the Gaia mission provides parallaxes for those objects with an unclear nature.
Acknowledgments
We thank our anonymous referee for their very relevant comments and suggestions that largely improved the content of the paper. JPSA especially thanks to Stellar Astrophysics Center and their funding provided by The Danish National Research Foundation (Grant agreement no.: DNRF106) for supporting this work. JPSA also thanks to the Henri Poincare Junior Fellowship during which this paper was finish. Part of this work was also supported by CNPq-Brazil and AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, by the PIP 112-200801-00940 grant from CONICET. Part of this work has been done with observations from the Southern Astrophysical Research (SOAR) telescope, which is a joint project of the Ministério da Ciência, Tecnologia, e Inovação (MCTI) da República Federativa do Brasil, the U.S. National Optical Astronomy Observatory (NOAO), the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU). This research has made use of NASA’s Astrophysics Data System.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology, 68, 36 [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Panei, J. A., Miller Bertolami, M. M., et al. 2009, ApJ, 704, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoci, V., Handler, G., Campante, T. L., et al. 2011, Nature, 477, 570 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antoci, V., Cunha, M., Houdek, G., et al. 2014, ApJ, 796, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balona, L. A., & Nemec, J. M. 2012, MNRAS, 426, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. J., Kepler, S. O., Montgomery, M. H., et al. 2015, in 19th European Workshop on White Dwarfs, eds. P. Dufour, P. Bergeron, & G. Fontaine, ASP Conf. Ser., 493, 217 [NASA ADS] [Google Scholar]
- Bell, K. J., Gianninas, A., Hermes, J. J., et al. 2017, ApJ, 835, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J. 2016, Rep. Prog. Phys., 79, 036901 [NASA ADS] [CrossRef] [Google Scholar]
- Bouabid, M.-P., Dupret, M.-A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 2000, Baltic Astron., 9, 149 [NASA ADS] [Google Scholar]
- Breger, M., & Pamyatnykh, A. A. 1998, A&A, 332, 958 [NASA ADS] [Google Scholar]
- Breger, M., Fossati, L., Balona, L., et al. 2012, ApJ, 759, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allende Prieto, C., & Kenyon, S. J. 2010, ApJ, 723, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., & Gianninas, A. 2017, ApJ, 839, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Calcaferro, L. M., Córsico, A. H., & Althaus, L. G. 2017, A&A, 600, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., & Miller Bertolami, M. M. 2006, A&A, 458, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Serenelli, A. M., et al. 2016, A&A, 588, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Calcaferro, L. M., et al. 2017, in 20th European White Dwarf Workshop, eds. P.-E. Tremblay, B. Gaensicke, & T. Marsh, ASP Conf. Ser., 509, 289 [NASA ADS] [Google Scholar]
- Corti, M. A., Kanaan, A., Córsico, A. H., et al. 2016, A&A, 587, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A. 1971, Acta Astron., 21, 289 [NASA ADS] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gianninas, A., Curd, B., Fontaine, G., Brown, W. R., & Kilic, M. 2016, ApJ, 822, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Grigahcène, A., Uytterhoeven, K., Antoci, V., et al. 2010, Astron. Nachr., 331, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Winget, D. E., et al. 2012, ApJ, 750, L28 [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Gianninas, A., et al. 2013a, MNRAS, 436, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Winget, D. E., et al. 2013b, ApJ, 765, 102 [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Istrate, A. G., Tauris, T. M., & Langer, N. 2014, A&A, 571, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Istrate, A. G., Fontaine, G., Gianninas, A., et al. 2016a, A&A, 595, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Istrate, A. G., Marchant, P., Tauris, T. M., et al. 2016b, A&A, 595, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2016, MNRAS, 455, 3413 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Hermes, J. J., Gianninas, A., & Brown, W. R. 2015, MNRAS, 446, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D. 2010, Mem. Soc. Astron. It., 81, 921 [NASA ADS] [Google Scholar]
- Lenz, P., Pamyatnykh, A. A., Zdravkov, T., & Breger, M. 2010, A&A, 509, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Maxted, P. F. L., Serenelli, A. M., Miglio, A., et al. 2013, Nature, 498, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maxted, P. F. L., Serenelli, A. M., Marsh, T. R., et al. 2014, MNRAS, 444, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Balona, L. A., Murphy, S. J., Kinemuchi, K., & Jeon, Y.-B. 2017, MNRAS, 466, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Pamyatnykh, A. A. 2000, in IAU Colloq. 176: The Impact of Large-Scale Surveys on Pulsating Star Research, eds. L. Szabados, & D. Kurtz, ASP Conf. Ser., 203, 443 [NASA ADS] [Google Scholar]
- Pelisoli, I., Kepler, S. O., Koester, D., & Romero, A. D. 2017, in 20th European White Dwarf Workshop, eds. P.-E. Tremblay, B. Gaensicke, & T. Marsh, ASP Conf. Ser., 509, 447 [NASA ADS] [Google Scholar]
- Pelisoli, I., Kepler, S. O., & Koester, D. 2018, MNRAS, 475, 2480 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Campos, F., & Kepler, S. O. 2015, MNRAS, 450, 3708 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Arias, J. P., Córsico, A. H., & Althaus, L. G. 2017, A&A, 597, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A. M., Althaus, L. G., Rohrmann, R. D., & Benvenuto, O. G. 2001, MNRAS, 325, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Smolec, R. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 265 [NASA ADS] [Google Scholar]
- Solano, E., & Fernley, J. 1997, A&AS, 122, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., & Asplund, M. 2014, MNRAS, 445, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Cleve, J. E., Howell, S. B., Smith, J. C., et al. 2016, PASP, 128, 075002 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X. B., Fu, J. N., Li, Y., Ren, A. B., & Luo, C. Q. 2016, ApJ, 821, L32 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A
Tables
Tables with the periods and frequencies of the cool set of models are presented below.
Radial orders (k), periods in seconds and frequencies in units of mHz and c/d for the g modes of the cool δ Sct model (triangle up symbol in Fig. 1).
Same as in Table A.1, but for the g modes of the cool pre-ELMV model (triangle down symbol in Fig. 1).
Same as in Table A.1, but for p modes of the cool δ Sct model (triangle up symbol in Fig. 1).
Same as in Table A.1, but for p modes of the cool pre-ELMV template model (triangle down symbol in Fig. 1).
All Tables
Spectroscopic parameters of the different groups of variable stars described in the text.
Period and frequency ranges usually observed of the different variable stars described in the text.
Radial orders (k), periods in seconds and frequencies in units of mHz and c/d for the g modes of the cool δ Sct model (triangle up symbol in Fig. 1).
Same as in Table A.1, but for the g modes of the cool pre-ELMV model (triangle down symbol in Fig. 1).
Same as in Table A.1, but for p modes of the cool δ Sct model (triangle up symbol in Fig. 1).
Same as in Table A.1, but for p modes of the cool pre-ELMV template model (triangle down symbol in Fig. 1).
All Figures
 |
Fig. 1. Teff–log g diagram showing the location of ELMV stars (light green triangles), pre-ELMV stars (blue diamonds), δ Sct stars (white circles) including SX Phe stars (magenta circles). The atmospheric parameters are extracted from different works detailed in the main text. Also, we included the theoretical evolutionary tracks of low mass He-core WDs (black dotted and dashed lines) from Althaus et al. (2013) and Serenelli et al. (2001), and of MS evolutionary tracks (red lines) from Sánchez Arias et al. (2017). Black numbers correspond to different values of the stellar mass of the low mass Hecore WDs, whereas red numbers are associated to the values of the mass, the metallicity and the overshooting parameter (see Table 3). Orange triangles show the position of the template models (see Sect. 4). The cyan squares indicate the position of the two stars reported by Corti et al. (2016), J1730+0706 and J1458+0707, and the cyan diamond represents the position of a new pulsating star, J0757+1448. These three objects will be analyzed in Sect. 6. |
| In the text | |
 |
Fig. 2. Abundances by mass of He and H as a function of the normalized radius (top panels), and propagation diagrams (the run of the logarithm of the squared Brunt–Väisälä and Lamb frequencies, lower panels) corresponding to the δ Sct model (upper panel), and to the pre-ELMV model (lower panel) indicated as a triangle up symbol in Fig. 1. |
| In the text | |
 |
Fig. 3. Same as in Fig. 2, but for the set of hot models, indicated as a triangle down symbol in Fig. 1. |
| In the text | |
 |
Fig. 4. Adiabatic periods in the usually observed ranges computed for the cool δ Sct and pre-ELMV selected models, depicted with a triangle up symbol in Fig. 1. The upper strips represent p and mixed g modes (in red and black, respectively) for the pre-ELMV model. The bottom strips represent p and mixed modes for the δ Sct model. |
| In the text | |
 |
Fig. 5. Same as Fig. 4, but for the hot models depicted with a triangle down symbol in Fig. 1. |
| In the text | |
 |
Fig. 6. Period spacing versus period for p modes (circles) and g modes (squares) corresponding to the δ Sct models (upper panel), and to the pre-ELMV models (lower panel). The asymptotic period spacing for g modes is depicted as a reference with thin horizontal continuous and dashed lines for the cool and hot models, respectively. Selected periods with consecutive radial orders are marked with magenta squares. They correspond to p modes for the δ Sct model, and to g modes for the pre-ELMV model (see text for details). |
| In the text | |
 |
Fig. 7. Same as Fig. 6, but for the frequency spacings. Horizontal continuous and dashed lines correspond to the asymptotic frequency spacing for p modes for the cool and hot models, respectively. |
| In the text | |
 |
Fig. 8. Normalized growth rates η for p and g modes in terms of the pulsation periods corresponding to the selected models. Modes corresponding the δ Sct model are depicted with square symbols and continuous black line, while modes corresponding to the pre-ELM WD model are depicted with circle symbols and continuous red lines. A value of η > 0 (η < 0) implies unstable (stable) modes. In frequencies, the band of excited modes for the δ Sct model is 10.16 ≲ v ≲ 34.56 c/d and for the pre-ELMV model is 17.28 ≲ v ≲ 24.68 c/d. |
| In the text | |
 |
Fig. 9. Top panel: light curve for J075738.94+144827.5. Error bars are shown in gray and a smoothed light curve is shown in red. Bottom panel: original Fourier transform in gray, and the subsequent Fourier transforms, subtracting periods above the 3 ~ σ detection limit, in different colors. The final detection limit, above which no further periods were found, is shown in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


