| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732349 | |
| Published online | 31 July 2018 | |
Solar barycentric dynamics from a new solar-planetary ephemeris
1
Comisión de Investigaciones Científicas, Provincia de Buenos Aires (CIC) – Universidad Tecnológica Nacional (UTN), Colón 332, San Nicolás, Buenos Aires, Argentina
e-mail: gcionco@frsn.utn.edu.ar
2
Institute of Applied Astronomy of the Russian Academy of Sciences (IAA RAS), nab. Kutuzova 10, St. Petersburg 191187 Russia
e-mail: dpavlov@iaaras.ru
Received:
23
November
2017
Accepted:
18
April
2018
Aims. The barycentric dynamics of the Sun has increasingly been attracting the attention of researchers from several fields, due to the idea that interactions between the Sun’s orbital motion and solar internal functioning could be possible. Existing high-precision ephemerides that have been used for that purpose do not include the effects of trans-Neptunian bodies, which cause a significant offset in the definition of the solar system’s barycentre. In addition, the majority of the dynamical parameters of the solar barycentric orbit are not routinely calculated according to these ephemerides or are not publicly available.
Methods. We developed a special version of the IAA RAS lunar–solar–planetary ephemerides, EPM2017H, to cover the whole Holocene and 1 kyr into the future. We studied the basic and derived (e.g., orbital torque) barycentric dynamical quantities of the Sun for that time span. A harmonic analysis (which involves an application of VSOP2013 and TOP2013 planetary theories) was performed on these parameters to obtain a physics-based interpretation of the main periodicities present in the solar barycentric movement.
Results. We present a high-precision solar barycentric orbit and derived dynamical parameters (using the solar system’s invariable plane as the reference plane), widely accessible for the whole Holocene and 1 kyr in the future. Several particularities and barycentric phenomena are presented and explained on dynamical bases. A comparison with the Jet Propulsion Laboratory DE431 ephemeris, whose main differences arise from the modelling of trans-Neptunian bodies, shows significant discrepancies in several parameters (i.e., not only limited to angular elements) related to the solar barycentric dynamics. In addition, we identify the main periodicities of the Sun’s barycentric movement and the main giant planets perturbations related to them.
Key words: astrometry / ephemerides / planets and satellites: general / Sun: general / solar-terrestrial relations
© ESO 2018
1. Introduction
Extrasolar planetary systems are natural laboratories for learning about new features and provide insights on stars and planetary interactions. These new traits include evidence of photospheric signatures associated with a possible magnetic star–planet interaction (Lanza 2013), and axial tilt variations in a young star due to magnetic torques (Chang et al. 2012; both mechanisms involve close-in hot-Jupiter exoplanets. Interestingly, our solar system might also provide empirical evidence (whose interpretation has been framed in theoretical explanations) on a possible subtle interaction between the Sun and the solar system bodies. We refer to the hypothetical modulating effect of planetary gravitation on the solar magnetic activity (the solar cycles), which has been discussed since long ago and recently has also been taken into account in the context of the extrasolar planetary systems (Perryman & Schulze-Hartung 2011). From the field of astronomy and astrophysics, but fundamentally from geosciences, several authors have taken into consideration some dynamical parameters of the Sun’s orbit around the solar system barycentre. Diverse orbital dynamical parameters of the Sun have been used for this task, but most were obtained from very different sources or methods, including synthetic planetary theories, two-body calculations, numerical simulations, unpublished data and ephemerides, and standard high-precision ephemerides.
The first description of what is known as solar inertial motion was reported by Jose (1965; see also Wood & Wood 1965), using orbital integrations of giant planets by Eckert, Brouwer and Clemence published in 1951. Jose analysed the solar motion in the period 1610–2010, and described the orbital loops and some dynamical parameters of the Sun as its barycentric range r (the magnitude of the barycentric position) and the variation T of the modulus L of the orbital angular momentum (T = dL/dt). He noted basic periodicities coming from Jupiter and Saturn, and the pacemaker effect of the alignment of the giant planets on the barycentric dynamical parameters studied with a certain periodicity that we call the Jose-period, that is, the series of dynamical parameters that seem to repeat with a periodicity estimated by Jose of ~179 yr. Nevertheless, the period of this repetition is variable and we identify this quantity just with a nominal Jose-period. Fairbridge & Shirley (1987) and Charvátová (1988) also found that very definite patterns in solar inertial motion are repeated every Jose-period, in which the Sun alternates between a trefoliar-like (quasi-symmetric) orbit and a lapse of “disordered” motion. The first orbital phase was arbitrarily determined over an ~50 yr period, which is dominated by the first harmonic of the Jupiter–Saturn synodic period (JS period), that is, JS/2, ~9.93 yr, with the remaining portion with a period of about 120 yr (Charvátová 2009). These findings (directly or indirectly) have motivated the wide use of solar barycentric dynamics, especially (but not limited to) the analysis of the long-term solar magnetic cycle variability and the development of theoretical mechanisms capable of explaining them. Whatever the underlying physical mechanism present in this issue, if any, it seems clear that it must be looked for in relation to a dynamical theory which should be based on solar barycentric dynamical quantities.
Solar barycentric position, r, velocity, ν, and acceleration, a, are routinely calculated in high-precision ephemerides: the JPL DE series (Folkner et al. 2014), the Institut de Mécanique Céleste et de Calcul des Éphéméides INPOP series (Fienga et al. 2008), and the Institute of Applied Astronomy EPM series (Pitjeva & Pitjev 2014). Modern versions of the DE, INPOP, and EPM ephemerides apply similar dynamical models of the Sun’s barycentric motion that treat the Sun as a regular body in the solar system. They use the relativistic definition of the barycentre, take into account not only Newtonian forces between major planets, but also relativistic terms, the non-uniform gravitational potential of the Sun (J2 term only), the Earth and Moon (main harmonics), the influence of asteroids and dwarf planets, etc. However, there is no 100% correspondence between the formulations used at different institutions. Because of the inclusion of these more complete models, we prefer to name the solar movement around the solar system’s barycentre, solar barycentric motion (SBM), to describe a more accurate modelling of the solar movement than just the inertial reaction to punctual planetary N-body forces.
The Sun’s barycentric r and ν are easily obtained through different means such as web services associated with these ephemerides; however, other solar dynamical parameters such as acceleration or orbital angular momentum, with all high-precision ephemerides, L, are not. In addition, the time span covered by high-precision ephemerides is, in general, short on geophysical timescales. As an exception, the JPL DE431 ephemeris covers about 30 kyr as a whole, from the year 13201 BC to the year 17191 AD, hence it includes all of the Holocene (the recent post-glacial geological period from about −12 kyr to the present). To date, DE431 is the only high-precision ephemeris officially published that covers such a long time span. While the above-mentioned high-precision ephemerides are in good agreement with each other, the EPM series has an important difference from DE and INPOP: the EPM model includes the 30 largest trans-Neptunian objects (TNOs) in addition to Pluto, which cause a significant offset in the definition of the solar system barycentre (Pitjeva 2010; Pitjeva & Pitjev 2013, 2014). The drift induced by the TNOs in the calculation of the solar system barycentre is about 6 km in just one decade (Pitjeva 2010). This difference with respect to the other existing high-precision ephemerides can be seen (on timescales covering 100–150 yr) as a quasi-constant offset in the location of the solar system barycentre in the ephemeris comparison performed by the IAU WG41. In addition to the 30 largest TNOs, the EPM model includes a uniform TNO ring that causes a smaller change in the Sun’s position with respect to the solar system barycentre (hereafter the barycentre).
The impact of the differences in the barycentre determination on solar movement is an important issue that must be addressed. This barycentric offset may produce important differences in SBM angular quantities and orientation changes in vectorial quantities regarding inertial and non-inertial directions. In addition, changes in the magnitudes of the derived solar dynamical parameters (e.g., orbital angular momentum), are also expected because TNO bodies produce significant torque on SBM due to their heliocentric distances. We are also aware that accessing long-term planetary ephemerides and the posterior calculations of associated solar dynamical parameters can be a difficult task for users who are not experts in dynamical astronomy. A standardized tool for this kind of study for widespread use in solar physics and geosciences is lacking, specifically a reconstruction of the solar barycentric dynamics for the whole Holocene, a time period of great geophysical importance. Our aim is thus twofold: first, to produce a tool for the full Holocene, which is publicly available, analysed in terms of the dynamical astronomy and second, to present and describe the results for a wide scientific audience.
2. EPM2017H, a new long-term high-precision ephemeris
Until recently, the last ephemeris released by IAA RAS was EPM2015 (see for details Pitjeva & Pitjev 2013, 2014). EPM2015 covers the period from 1787 to 2014. A new version of EPM has recently been released: EPM20172. The most important differences with previous versions are the inclusion of the Lense–Thirring acceleration; definition of the relativistic barycentre; modelling of the acceleration of the Sun as a regular body (in previous versions the Sun was explicitly placed to keep the barycentre at the origin); models of the asteroid belt and the Kuiper belt not as a uniform annulus and ring, but as 180 and 160 uniformly distributed point-masses, respectively (which in turn allows their influence on the orbit of the Sun to be modelled). Also, some recent observations of spacecraft and lunar laser ranging normal points that appeared after EPM2015 were included in the EPM2017 solution. We develop a special version of EPM2017 to cover the whole Holocene and 1 kyr into the future. We call it EPM2017H, and it covers the time span from 10107 BC to AD 3036. Two exclusive modifications were made to the EPM2017H model. First, the latest formulation for the precessional quantities of the Earth valid over thousands of years was included (Vondrák et al. 2011). This formulation, in addition to the standard IAU theory of nutation IAU2000A, enables us to also obtain the Milanković astro-climatic elements for the Earth taking into account short-term perturbations (Cionco & Soon 2017). Second, the lunar model of EPM2017H does not have friction between crust and core in order to avoid exponential growing of the angular velocity of the lunar core in the past. The lunar parameters of the solution were then re-fitted back to the EPM2017H model.
As usual, we date the Holocene from about 12 kyr ago, so we start our study of SBM from about 10 000 BC; exactly, from 1/1/−9999, JD = −1931076.0 (in barycentric dynamical time, TDB); approximate Julian epoch −9998.9624, to AD 3000, JD = 2816795.0; with a time step of 1 d. The date expressed in years, as a real number, for a corresponding Julian day (JD) is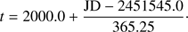 (1)
(1)
In what follows, when we mention “time in years” we refer to this Julian epoch (in TDB timescale) given by Eq. (1) as the independent variable of the dynamics.
The longest solar-planetary high-precision ephemeris is DE431, which has been available since mid-20133. As mentioned above, DE431 is in good agreement, inside the corresponding temporal lapse, with all high-precision ephemerides, that is, INPOP4 and also the EPM ephemerides. A first comparison DE431-EPM2017H is performed defining the percentage difference, in position, velocity, and barycentric acceleration of the Sun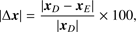 (2)
(2)
where vector x ∈ to the set {r, ν, a} and sub-indexes D and E refer to each ephemerides, respectively. In addition, we also explored the percentage difference of magnitude, in position, velocity, and barycentric acceleration, where the magnitudes of the corresponding vectors were used in turn. The result of this set of comparisons shows differences smaller than 1.7%, 0.0039%, and 0.0036% in |Δr|, |Δν|, and |Δa|, respectively. No significant secular growth can be seen on these comparisons. As expected, the differences in magnitude values are smaller. The most interesting result is on velocity where, except for a minute drift, the ~550 yr period of dwarf planet Eris can be detected by simple inspection (Fig. 1).
 |
Fig. 1. Percentage differences in the solar barycentric velocity vectors between DE431 and EPM2017H (Eq. (2)) for the indicated years (one datum per Julian year). The ~550 yr oscillation due to dwarf planet Eris can be clearly seen. |
3. SBM from EPM2017H
3.1. General description
Due to the mass and semi-major axis of Jupiter, SBM is performed at a mean barycentric range of ~5 × 10−3 au, as can be seen in Fig. 2, where we have selected a period of time related to a trefoliar-like solar orbit after Charvátová (2009). To present our results, we use the solar system invariable plane (IP) as reference plane. This plane is the most natural reference for long-term dynamics and it is normal to the total angular momentum of the solar system. SBM is performed in the proximities of the IP, following the movement of the giant planets, which mostly produces the total solar system’s angular momentum (see Appendix A for further details).
 |
Fig. 2. Trefoliar, particularly quasi-closed ~60 yr pattern of SBM for the indicated interval. The first JS period is marked as a thick line. The interval corresponds to the closest approximation to the initial position on the IP. The x-axis of the figure coincides with the nodal line equator-IP (see Appendix A for further information). |
Charváitová identified these trefoliar orbits over ~50 yr period as the most symmetrical patterns trying to find a distinctive solar orbit related to solar Grand Minima events5; instead, we adopted a ~60 yr period, which is more meaningful from a dynamical point of view, because it corresponds to a quasi-complete Jupiter–Saturn synodic cycle of oppositions-conjunctions (each synodic configuration is advanced by approximately 120° at each JS period). More specifically, this period corresponds to the second most important perturbation over orbital longitudes in the Jupiter–Saturn pair, produced by the trigonometric argument λJ − 2 λS, where λJ and λS represent the corresponding mean orbital longitudes of both planets, or in short, the (1, −2) “inequality” (see Sect. 4). Each inner equilateral closed loop in Fig. 2 corresponds to Jupiter–Saturn JS/2 period. The first complete loop of JS period, ~19.86 yr, is marked with a thick line. In Fig. 2, after a ~60 yr period (between the years 1723.4716 and 1783.2745) the projection of the Sun’s movement on the IP tends to occupy the same position after that time span, with a magnitude of the difference in spatial position of 3.4 × 10−5 au, that is, less than 51 000 km. Not all ~60 yr trefoliar orbits are so closed, however.
In Fig. 3, we plot the magnitudes of barycentric position r, velocity ν, and acceleration a, for two Jose-periods starting around the year 1366 after a Jupiter–Saturn opposition (when the difference in orbital longitudes between Jupiter and Saturn, ΔλJS, is 0°). The corresponding trefoliar (quasi-closed) 60 yr periods of each Jose-period are indicated (dotted lines). Each Jupiter– Saturn opposition corresponds to peaks in ν and ν plots. Then, after a Jose-period of 177 yr (the timing in the repetition of the kinematics parameters can be highly variable regarding the mean ~179 yr period found by Jose), the trefoliar orbit and the series of kinematics elements seem to be repeated, although more important changes can appear in the kinematics series trough time. We note that the non-Keplerian nature of SBM is evidenced by the fact that the longer/shorter the barycentric range, the higher/lower the orbital speed. Nevertheless, there is a lag between the extrema in r and ν series; for example, the big drop in solar velocity around the year 1672 occurs about one year after the drop in barycentric distance. The shortest recognizable periodicity in velocity and acceleration parameters, 1.5–1.6 yr, is due to the Venus–Earth synodic period.
 |
Fig. 3. Basic dynamical parameters for two Jose-periods of 177 yr (continuous line). The intervals of trefoliar 60 yr orbits are indicated (dotted lines). All the quantities are reckoned in astronomical units and days. The “form” of the series seems to be repeated, although more important changes can appear in the kinematics series trough time. For example, the double peaks in r series inside “disordered” motion intervals change to two valleys, for example, between the years 2100 and 2500 (result not shown). |
Although the successive JS periods of conjunction-oppositions rules the cyclicity of extrema values of these time series, after the finalization of the 60 yr period the series show an apparent change in their evolution (coincident with the Sun entering in periods of disordered motion after the Charvátová 2009 nomenclature), for example, double peaked variations in r series. We can explain these features as follows: when the Sun ends a trefoliar 60 yr movement (after a Jupiter–Saturn opposition) Jupiter is rapidly situated near quadrature with Saturn (ΔλJS = |λJ − λS| ~ 90°). In addition, the Uranus–Neptune centre of mass (CM) tends to be aligned and in conjunction with Saturn, i.e. |λCM − λS| = ΔλCMs ~ 180° (where λCM is the orbital longitude of the Uranus–Neptune centre of mass), producing an important redistribution of mass, which is expressed as a variation of the orbital torque for which the Sun reacts to keep the barycentre at rest. Nevertheless, a sine qua non condition for these changes is that both icy giant planets are at near conjunction with Saturn, which is expressed in the additional condition ΔλUN ≲ 90°, where ΔλUN is the difference in orbital longitudes of both planets. These giant planet configurations can be seen in Fig. 4 where, in addition to r series, differences in orbital Jupiter–Saturn longitudes, and differences in longitudes between the Uranus–Neptune centre of mass and the Saturn position are plotted. The filled dots mark the difference of longitudes between Uranus and Neptune when ΔλCMs ≃ 180°. It can also be noted that the “disturbances” in r series occur when ΔλCMs ~ 180°, but only if ΔλUN ≲ 90°.
 |
Fig. 4. Relative position of icy and gaseous giant planets and their effect on r over two Jose-periods. The disordered orbits begin when Saturn and the Uranus–Neptune pair tend to be aligned (near conjunction) being Jupiter near quadrature. All the quantities are reckoned in astronomical units, days, and sexagesimal degrees. Hollow circles around 1632 indicate a particular planetary quasi-alignment which produces a solar retrograde motion (see Sect. 3.2). |
Indeed, a disturbance in r series begins to occur when ΔλUNis near 90° as in the years 1430 or 1610. Then the ordered motion changes to disordered when the Sun–Jupiter–Saturn movement is highly perturbed by the Saturn–Uranus–Neptune alignment. Uranus and especially Neptune produce significant torque over the solar motion, owing to their distance from the barycentre. In particular, Neptune produces very distinctive features in solar orbital torque, as can be seen in Cionco & Abuin (2016). The double peaked effect in r series persists over one Saturn–Uranus synodic period (SU period), ~45.36 yr. Then, we wanted to determine whether another quasi-closed or quite symmetrical (projected) orbital pattern related to these repeated features could be expected. We find, after the first double-peaked pair and lasting for approximately one SU period, a quite symmetrical and quasi-closed orbital pattern, between the years 1474.245 and 1519.0856 (being the magnitude of difference in position ~8000 km). This particular pattern is repeated for several Jose-periods, and it is shown in Fig. 5 for the indicated temporal interval. Then, the pattern is modified, when the inner “lemon-like” loop begins progressively to rotate. In the case of the SBO shown in Fig. 5, the Sun passes at a distance shorter than 15 000 km from its initial position (less than 295 km in the x–y plane). Close approaches of the Sun to the same barycentric position occur continuously, following the basic periodicities involved in SBM (JS, JS/2, SU, etc.). The most closed orbit occurs at the year −7654.3272, after a Saturn–Neptune synodic period (SN period), ~35.87 yr, with a difference in position of 6.6 × 10−7 au, about 99 km. A very close approach to the barycentre around the year 1632 can be seen in r panel (Fig. 4, open dots). This is produced by a superior quasi-conjunction of Jupiter with the other giants. As a result, the Sun fails to loop the barycentre, entering in a retrograde motion mode, and this change is consistent with a momentary inversion of the SBO.
 |
Fig. 5. Quite symmetric and quasi-closed projected (on the IP) pattern of SBM for ~SU period, associated disordered motion interval. The x-axis of the figure coincides with the nodal line equator-IP. An approximate value for the Sun’s radius is indicated. After that time span the Sun returns to less than 15 000 km of its initial position. |
3.2. Retrograde solar motion
Lapses of retrograde solar motion around the barycentre were detected by the changing sign of the z-component, Lz, of the orbital angular momentum (Jose 1965; Javaraiah 2005), which produces a brief clockwise SBM. Retrograde solar motion and also variations in angular momentum were linked to possible solar cycle mechanisms (see e.g., Landscheidt 1999; Juckett 2003; Javaraiah 2005; Perryman & Schulze-Hartung 2011; Cionco & Soon 2015), especially Grand Minima events and their possible periodicity over the time.
We searched for all the retrograde motion lapses (on a daily basis) in this studied period and their durations (Table 1). Negative Lz values depend on the reference system used (see Appendix A for graphical descriptions). Nevertheless, an estimation using the equinox-ecliptic of J2000.0 as reference plane yields few days of difference in the duration of these events. Clearly, orbital inversions are not periodic phenomena in terms of the Jose-period, they appear in irregular ways, in groups of three to nine events. In turn, these retrograde motion intervals appear with a bimillennial cycle (six cycles inside the studied period) of, on average, 13 kyr/6 ~2.2 kyr. Moreover, inside these bimillennial periods of retrograde motion, they do not happen regularly at the Jose-period. Some intervals of retrograde motion are separated by about 140 yr, for example between the years 2168 and 2308 or between −2458 and −2318. In this last case, the retrograde intervals of the bimillennial “wave” beginning at the year −2994, appear at each Jose-period until the year −2458. Although the Jose-period beginning at −2458 is maintained, with another orbital inversion occurring at −2279, an intermediate lapse of retrograde motion takes place at the year −2318, that is, 39.26 yr before the expected event of the year −2279. Notably, before the retrograde interval of the year −2994, all orbital inversions inside each bimillennial cycle occur at the Jose-period. The explanation of these shorter periods is simple. At each Jose-period, which is strongly related to the Uranus–Neptune synodic period (UN period) of ~171 yr, a quasi-conjunction between Jupiter and the other giants tends to occur. These quasi-alignments are not always able to produce a solar retrograde motion because of the ever changing planetary positions and velocities at these particular events. One Jose-period (as already noted by Jose) is ~9 × JS ~179 yr; sometimes, ~2 × JS ~40 yr before a Jose-period, that is, ~7 × JS ~139 yr after an earlier inversion event, giant planets are already quasialigned and able to produce a retrograde motion. In brief, JS period, as will be also shown in Sect. 4, is the fundamental period in this problem. Nevertheless, significant differences in periodic barycentric phenomena can be produced by the simple fact that the planetary periods are not commensurable among themselves, that is “the planets are not trapped in mean motion resonances”.
This bimillennial wave of orbital inversions (whose possible origin is related to the long-term dynamics of Uranus and Neptune; see Sect. 4) can be seen quite clearly by the simple inspection of almost all the dynamical quantities analysed, for example the SBO inclination (Fig. 6). The above-mentioned SBO was calculated following Cionco & Compagnucci (2012), determining the inclination, iS, and the ascending node, ΩS, of the SBO regarding the IP reference system. In addition, we also determined the Sun’s positional angle on its SBO, uS (the argument of latitude), reckoned from the nodal line equator-IP. The SBO allows us to describe the Sun’s acceleration from a co-orbital reference system, owing to the projection of the Sun’s acceleration onto the solar orbital plane (see Appendix A for graphical descriptions). This coplanar acceleration, aπ, shows the impulsive changes in acceleration due to the giant planets quasi-alignments, a dynamical feature that cannot be seen in the usual Cartesian representation of a. The magnitude of aπ, aπ, is also plotted in Fig. 6. Consistent with the retrograde motion intervals, it is observed that the Sun’s orbital inclination overpasses 90° at these moments and the coplanar acceleration increases impulsively its magnitude. These impulses are only produced by the giant planets. It is interesting to note that planetary alignments have also been considered regarding the solar cycles, and these extrema values could be relevant in this regard (McCracken et al. 2014). The coplanar acceleration is obtained by the decomposition of the Cartesian acceleration in a co-orbital reference system, following the radial, transversal, and normal6 directions associated with the SBO, that is, 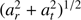 , being ar and at the components of the radial and transversal accelerations, respectively (see Figs. A.2, A.3 and A.4). The positive radial direction is taken from the barycentre pointing towards the Sun. The most common situation in this N-body system is thus that the “orbital centre of force” is near the barycentre, and in its “normal” prograde motion the Sun loops the barycentre with negative values of ar (Figs. 2 and 5). As was shown in Cionco & Compagnucci (2012), the impulsive changes induced by the giant planet alignments produce positive values of radial acceleration. Nevertheless, analysing the fine structure of these impulses at this level of precision, we can see that radial acceleration is not always positive at retrograde lapses (Fig. 7). The process can be explained as follows: when an alignment of giant planets is produced, the transversal acceleration oscillates rapidly, causing a variation in the orbital torque, and the Sun fails to loop the barycentre (see e.g., Perryman & Schulze-Hartung 2011, Fig. 2); hence, the centre of curvature of the SBO leaves the barycentre “outside” the orbit, and positive values of radial acceleration (i.e. in the barycentre–Sun sense) are expected. Nevertheless, the effect of the Earth–Venus pair in the acceleration (evidenced in the ~1.6 yr peaks also visible in Fig. 7) causes a momentary change in the sign of ar: the expected positive values change, momentarily, to negative. This can be seen in the embedded plots of Fig. 7, when a lapse of ar < 0 can be observed in addition to Lz < 0 values.
, being ar and at the components of the radial and transversal accelerations, respectively (see Figs. A.2, A.3 and A.4). The positive radial direction is taken from the barycentre pointing towards the Sun. The most common situation in this N-body system is thus that the “orbital centre of force” is near the barycentre, and in its “normal” prograde motion the Sun loops the barycentre with negative values of ar (Figs. 2 and 5). As was shown in Cionco & Compagnucci (2012), the impulsive changes induced by the giant planet alignments produce positive values of radial acceleration. Nevertheless, analysing the fine structure of these impulses at this level of precision, we can see that radial acceleration is not always positive at retrograde lapses (Fig. 7). The process can be explained as follows: when an alignment of giant planets is produced, the transversal acceleration oscillates rapidly, causing a variation in the orbital torque, and the Sun fails to loop the barycentre (see e.g., Perryman & Schulze-Hartung 2011, Fig. 2); hence, the centre of curvature of the SBO leaves the barycentre “outside” the orbit, and positive values of radial acceleration (i.e. in the barycentre–Sun sense) are expected. Nevertheless, the effect of the Earth–Venus pair in the acceleration (evidenced in the ~1.6 yr peaks also visible in Fig. 7) causes a momentary change in the sign of ar: the expected positive values change, momentarily, to negative. This can be seen in the embedded plots of Fig. 7, when a lapse of ar < 0 can be observed in addition to Lz < 0 values.
 |
Fig. 6. Extrema in Lz values, coplanar acceleration magnitude, and SBO inclination for the whole studied period showing the bimillennial wave of impulsive effects of giant planets. When the SBM is retrograde, the iS is larger than 90°. All the quantities are reckoned in astronomical units, days, and degrees. |
 |
Fig. 7. Evolution of radial and transversal accelerations and Lz around the retrograde interval of the year 1990. Contrary to what was expected, radial acceleration points towards the barycentre (i.e. it is negative) during brief moments when Lz < 0, marked with arrows and depicted in the embedded plots. They are produced by Venus–Earth synodic period perturbations. All the quantities are reckoned in astronomical units and days. |
Retrograde solar motion intervals (Lz < 0) regarding the solar system’s invariable plane.
3.3. Differences in derived dynamical quantities
To evaluate the differences between EPM2017H and DE431 in the SBM derived dynamical parameters, we compare the values of key angular and orbital torque related quantities. First, we calculate the differences in uS and iS angles. Also, we estimate the differences in the positional angle θ, which we define as the angular distance (reckoned in the SBO plane) between aπ and the radial direction (the barycentre–Sun direction, see Fig. A.4). The results for uS and θ angles are shown in Fig. 8, absolute values are larger than 1° are plotted. For iS the differences (not shown) are much smaller (about 6° at most) and are simply related to retrograde motion epochs (differences in orbital inclinations larger than 1° occur just 172 times in the whole period). It seems clear that these differences in iS are explained by the impulsive nature of these retrograding events when the Sun is very near the barycentre. The same applies to θ angle, for which the larger differences are all associated with orbital inversion intervals. In turn, the larger differences in uS angle are not related to orbital inversion epochs, neither related to the largest values in r or ν. Nevertheless, the big differences seen around 1672.6, for example, seem to be associated with very small values of orbital speed (see Fig. 3). In addition to these angular quantities, we also compare L, the torque T, and the norm of the orbital (vectorial) torque Γ, Γ. The differences in L are in general less than 6%, with their largest values related to the close approaches to the barycentre. The absolute value of the percentage differences DE431-EPM2017H in T and Γ quantities larger than 5% (0.32% of the total) are shown in Fig. 9. Of these, the biggest values are all related to orbital inversion epochs. Furthermore, they seem to be clumped every ~500 yr, which is produced by dwarf planet Eris, more massive than Pluto, orbiting between ~38.8 and 97.4 au (Santos-Sanz et al. 2012). Orbital simulations by numerical integrations using just the major planets and the major planets plus Eris (result not shown) clearly show this oscillation and approximately the same dispersion in the corresponding torque differences as observed in Fig. 9. Then, as expected, Eris produces a detectable difference in the solar orbital torque quantities. The differences can be very large, especially in T, one of the most commonly used parameters in the applications to solar-terrestrial relation studies. These T value differences are sensibly larger than Γ differences, which is easily explained by the fact that T = Γ cos(L, Γ), hence this parameter also takes into account the angular differences between L and the vectorial planetary torque. These directional differences are amplified at the retrograde motion intervals, when the Sun’s orbital angular momentum rotates rapidly by about 180°.
 |
Fig. 8. Differences in uS and θ angles determined from DE431 and EPM2017H ephemerides. Just the differences whose absolute values are larger than 1° are plotted. They are a small fraction of the total (0.45% and 0.02%, respectively), but are not necessarily related to the impulsive events of retrograde motion (see Sect.3.3). The largest differences in uS (e.g. around 1672.6) are related to low values of solar velocity. |
 |
Fig. 9. Absolute values of percentage differences larger than 5% in T and Γ magnitudes determined from DE431 and EPM2017H ephemerides (see Sect. 3.3 for details). The differences are clumped every ~ 500 yr and related to dwarf planet Eris, which produces a detectable torque because of its mass and mean distance to the Sun. |
4. Harmonic analysis of SBM
The determination of the main periodicities present in SBM was another issue attracting attention, regarding the different short- and long-term modulating periods detected in the solar cycles (see e.g., Soon et al. 2014; Beer et al. 2018). Several authors have determined orbital periodicities from the SBM dynamical parameters and further identification of these spectral peaks came from the evident synodic and orbital periods, or simple combinations of planetary mean motions, trying to find numeric relationships as multiples or “resonant harmonics” of more basic periods (see e.g., McCracken et al. 2014; Scafetta et al. 2016). It is important to note that we can find an arbitrary number of combinations between integers and mean motions very close to zero, but it is not an indication of resonance, as a well-defined and strong dynamical phenomenon. An arbitrary combination of integers and mean motions can be identified with a certain periodicity, but this does not assure its dynamical relevance (as a periodic effect) in the system under study. Moreover, the periodicity of that supposed “perturbation” to the SBM must be highly variable in order to be easily evidenced in the corresponding harmonic analysis. In this work, we have also been identifying particular periodicities with meaningful combinations of integers and planetary mean motions that do produce significant effects in terms of perturbative methods, and we are going to clarify this relationship. It is also worth noting that basic planetary dynamics (heliocentric distance, velocity, etc.) depend on non-linear combinations of the orbital elements. As a result, a certain spectral peak in SBM could be a direct measure of the involved periodic planetary perturbations, and also the result of a non-linear mixing of several perturbing periodicities present in the variations of these elements. In addition, if a periodic perturbation is important (i.e., of significant amplitude) for certain orbital elements, it is not necessarily relevant for other dynamical parameters. Our search for periodicities in SBM and their relationship with planetary perturbations is far from exhaustive, but provides a basic guideline on how this topic should be addressed.
4.1. Theoretical estimates
The physical analysis of the main giant planets perturbations can be very easily performed using VSOP2013 planetary theory Simon et al. (2013), where planetary perturbations are expressed as Poisson series. In that development, the purely periodic part is obtained as a trigonometric series in terms of planetary orbital longitudes. Then, for the giant planets, the periodic variations in the orbital element X along time, ΔXper(t), have the form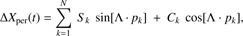 (3)
(3)
where Λ = (λ5, λ6, λ7, λ8) is the vector of mean orbital longitudes ranging from Jupiter (5) to Neptune (8), and pk = (p5, p6, p7, p8) is a particular combination of integers. The mean orbital longitude for planet i is written as λi = ni (t − t0) + λi0, where ni is the mean motion of the planet and λi0 is an initial phase related to the reference time t0. Therefore, the period of the k-perturbation is 2π/(n · pk), where n is the vector of planetary mean motions. For example, a particular periodic perturbation on orbital longitudes will produce a difference or “inequality” regarding the nominal Keplerian mean motion. Hence, with a slight abuse of the language, we are referring to the perturbation by its cause: the (1, −2, 0, 0) term for Jupiter’s longitude corresponds to the perturbing periodic effect given by Eq. (3) (with the corresponding amplitudes for Jupiter’s longitude) with the argument λJ − 2 λS, or in short, the (1, −2) inequality. Then, the strength or “importance” of that perturbation can be obtained by the combination of both amplitudes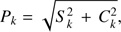 (4)
(4)
which permits the establishment of the relative intensity of the thousands of perturbations considered here. Following this procedure, not only are we able to arrange the perturbations over a particular planetary orbital element from the strongest to the weakest, but also to identify the mean motion combination which produces such a physical perturbation. Hence, taking into account the reordered series, the k-order of a perturbation corresponds now to its position in the ranking (1st, 2nd, etc.). In Table 2 we present (based on VSOP2013 constants) the nominal periods of some inequalities discussed in the text, characterized by its respective k-order for the semi-major axis and longitude of Jupiter and Neptune (kJ or kN), respectively. We have only considered the giant planet perturbations. Nevertheless, the Theory of the Outer Planets, TOP2013 (Simon et al. 2013), is more accurate than VSOP2013 over several thousands of years, with a different Fourier series representation in Poisson’s expansion. Using this representation, as suggested by the reviewer, we can also estimate the possible variations in the periodicities of these inequalities, comparing their corresponding TOP2013/VSOP2013 values.
Selected inequalities and their periods from the VSOP2013 theory.
4.2. Spectral analysis
In order to determine the main periodicities present in our modelling of SBM, we use the multi-taper method (MTM) and Lomb (normalized) periodogram (Ghil et al. 2002; Press et al. 1992). We find the Lomb periodogram to be the best choice because it gives a sharper determination of the longer periodicities (>200 yr). The time span considered comprises all 13 063 yr over which the SBM analysis was performed. We have used one value per year, hence we cannot resolve periods shorter than 2 yr, according to the Nyquist theorem. First of all, we found the basic and shorter periodicities, which are easier to determine. The results for the magnitude of the velocity and barycentric range correspond well with each other and are shown in Fig. 10. The giant planet periods, and the periodicities of several inequalities already shown in Table 2, are present. Neptune’s orbital period, N, is clearly involved in the majority of the main periodicities present in the corresponding spectral bands (e.g., decadal, centennial), such that the JN periodicity, for example, is stronger than Jupiter’s orbital period, J. Those periods are imprinted even more strongly than the Jupiter–Saturn (1, −2) inequality, detected at 60.9 yr, which is virtually coincident with its nominal value. The percentage difference TOP2013/VSOP2013 (hereafter T/V) of this periodicity is just −0.09% (i.e., its TOP2013 period is 60.89 yr). The periods of the (0, 1, 0, −1) and (0, 1, −2) inequalities, which appeared with relatively low intensity for Jupiter in Table 2, are also clearly detected. In the spectral band related to the Jose-period, the largest power corresponds to the N and UN periods. A spectral peak coincident with the nominal Jose-period, or related to the (0, 0, 2, −3) inequality which is also an important perturbation for Neptune, was not clearly identified. Around the UN period there are many side-lobes associated with it. We think that these periodicities could be present, but masked by these spectral power variations.
 |
Fig. 10. Main short-term periodicities detected in barycentric range, r (raw periodogram over 13 036 yr). The (1, −2) inequality of periodicity of 60.9 yr is clearly seen (indicated with its numerical value). We note the participation of Neptune on important peaks. J, S, U, and N are the giant planets’ orbital periods. This result is similar to the corresponding velocity spectrum. |
The MTM and the periodogram also show, for solar r, wide bands in the range ~2–5 kyr, significant at the 95–99% confidence level; nevertheless, these longer periodicities can be more easily specified in other parameters such as aπ, L, Γ, etc. In particular, the acceleration aπ, shows clear long-term periods (but with relatively low power and low confidence level in the Lomb-periodogram), even in the raw power spectrum (Fig. 11). Notably, spectral bands around 2.2–2.3 kyr (with a measurable peak at 2266 yr) and around 4.3 kyr are easily found with any kind of filtering (no sampling). The MTM applied to this parameter shows a ~2 kyr band significant at the 95% confidence level. We relate the first mentioned band with the bimillennial wave discussed in Sect. 3.2. These bands, we think, are mainly produced by the most important inequalities found at these frequencies: the Uranus–Neptune (0, 0, 1, −2) great inequality Simon et al. (1992; kN = 1 for Neptune longitude), and its first harmonic, (0, 0, 2, −4), with periodicities of 4233.14 yr and 2116.57 yr, respectively, for VSOP2013. The T/V difference of these inequalities is ~3%. In particular, TOP2013 shows that (0, 0, 1, −2) is the only inequality with period ~4.3 kyr. Around 2–2.5 kyr, the VSOP2013 and TOP2013 theories show us the existence of some inequalities with significant relative amplitudes, especially in orbital longitudes, for both Jupiter and Neptune: (4, −11, 3), (2, −6, 4, −2), both exhibit important differences in their periodicities of 26.4% and −14.9% (2496.54 yr/1975.15 yr and 2184.48 yr/2566.51 yr for the TOP2013 and VSOP2013 theories, respectively). The (1, −3, 1, 1) inequality is also present in this spectral zone, with a −5.8% (2184.5 yr and 2319.93 yr) T/V difference. Other shorter periodicities that can be identified are near the N and UN peaks, namely the 186 yr period, which closely coincides with the period of the inequality (1, −3, 0, 2). This period is also coincident with an important perturbation for Neptune’s longitudes, (0, 0, 3, −5), kN = 29. In addition, a sharp peak is observed at 159 yr that is coincident with the period of the (1, −3, 2) inequality.
 |
Fig. 11. Main long-term periodicities detected in aπ acceleration. Spectral bands coincident with the bimillennial wave and the great inequality (0, 0, 1, −2) between Uranus and Neptune are detected at low confidence level in this parameter. Other indicated inequalities are discussed in the text. |
Power spectra of L, T, and Γ are quite similar and we present themas the averaged (previously normalized) periodogram of these three parameters. The result in Fig. 12 shows the ~2.3 kyr and ~4.3 kyr spectral bands. The bimillennial band is detected at low confidence levels in these parameters. Other bands around 1.0–1.5 kyr can be seen. There are many inequalities related to these bands in the VSOP2013 theory, especially (2, −5, −1, 2), (1, −3, 0, 3), and (2, −6, 3). In addition, (2, −6, 3) presents a ~9% T/V difference in its periodicity. Also, the second harmonic of the Uranus and Neptune great inequality, (0, 0, 3, −6), kN = 13 for Neptune’s longitude, has a ~1411 yr periodicity. The Jupiter– Saturn great inequality (GI), (2, −5) of 883.3 yr (VSOP2013) or 919.8 yr (TOP2013) of nominal periodicities never appears with distinctive power on these raw spectra. The GI is the most important perturbation for the Jupiter longitude and it is kJ = 4 for Jupiter’s semi-major axis. Nevertheless, as was pointed out by the reviewer, following the TOP2013 theory, the contribution of the GI to solar r is negligible: it is the 2841th term.
 |
Fig. 12. Main long-term periodicities detected in the averaged raw power spectra of L, T , and Γ (over 13036 years). Numerical values of several periods detected are indicated and explained in the text. |
A notable spectral band around 516 yr (also visible in Fig. 11) is found, which is virtually coincident with the most important band detected in the calculation of the modelled torque over the solar tachocline zone, performed by Abreu et al. (2012). The (0, 1, −2, −2) inequality, has a quite stable periodicity of around 500 yr, but far from the 516 yr period. TOP2013 just detects one perturbation around that periodicity, of 513.99 yr, equivalent to the period of (4, −10, −1, 2) of 493.08 yr for VSOP2013 (see Table 2). Another band/peak around 767 yr (Fig. 12) is quite prominent in its spectral zone, and it is also present in the spectrum of Fig. 11, but with low relative power. The (0, 1, −5, 4) inequality is especially related to this band, with a period of ~760 yr, following the TOP2013 theory. We also find two notable spectral peaks at 214 yr and 240 yr. We find (2, −6, 0, 5), with a period of 211.22 yr and 213.12 yr for VSOP2013 and TOP2013, respectively. Also, (1, −4, 5, −2), the ~243 yr period of VSOP2013, but with Ȉ246 yr in TOP2013. The inequality (4, −10, −1, 3), with quite low amplitudes in VSOP2013, has a ~243 yr period in TOP2013.
5. Conclusions
To date, EPM2017H is the most complete high-precision solar-planetary ephemeris accounting for the SBM during the whole Holocene. The positioning of the SBM was done using a reference system defined by the solar system’s IP. The released files with the SBM data are stored in the repository PANGAEA data publisher. The improvement in the solar orbit calculation is evident when comparing the SBM in EPM2017H and DE431 ephemerides. Although they are very consistent ephemerides, the differences in certain important dynamical quantities of SBM (and not only in angular quantities) obtained from both ephemerides can be very significant. The differences in torque related quantities are clearly imprinted by the dynamics of dwarf planet Eris, which is included in the modelling of the TNOs region performed in EPM2017H. In this sense, it is clear that undiscovered massive bodies beyond the Kuiper belt would have a non-negligible effect on the SBM, even on the inclination of the solar spin axis with respect to the IP (Bailey et al. 2016). Therefore, significant differences in SBM parameters could also be expected in EPM2017H regarding a more accurate model that includes massive planets that are farther away.
The periodicities present in the SBM were analysed for the first time in terms of the main physical planetary perturbations involving the giant planets. We emphasize that a simple combination of mean motions does not produce a “resonance” in the system, and does not guarantee the dynamical importance or strength of that inequality7 in the SBM. This is particularly pertinent in the periodicity of the solar retrograde motion intervals, which seem to be far from a regular metric. Particular long-term periods in the solar cycles, such as the 2.2–2.3 kyr cycle (known as the Hallstatt cycle, see e.g., Beer et al. 2018) were also related in the past to SBM using different arguments. We show cyclic variations in key dynamical parameters of SBM with that bimillennial periodicity, and confirm the existence of a ~2.3 kyr spectral band in SBM, although with varying spectral power (i.e., at different confidence levels). We are not arguing that the Hallsttat cycle is produced by or is connected to this bimillennial period. We propose the origin of this spectral band in SBM, taking into account the important periodic perturbation, is the inequality (0, 0, 2, −4). In this sense, statements such as those of Scafetta et al. (2016) regarding a “stable resonance” produced by the inequality (1, −3, 1, 1) as the specific origin of this bimillennial periodicity, just because of the periodicity coincidence, are very vulnerable to criticism. In addition, the TOP2013 period of this inequality is 2184.5 yr.
The most important periods are detected with different confidence levels according to each parameter studied. We have not used stringent criteria of statistical confidence levels to reject low power periodicities because we are analysing a theoretical model of the solar system. Although it is not a purely periodic model, the use of high-level semi-analytical theories (VSOP2013/TOP2013) enables us to determine a physical root to the bands/peaks, even if they are of small amplitude. The application of very precise semi-analytical theories is fundamental in order to identify possible perturbations contributing to some spectral band of the SBM. Moreover, a full treatment of this problem implies the application of these theories to obtain the orders of the specific inequalities in each dynamical parameter studied. Another important long-term inequality clearly present (but with low confidence levels in some analysed parameters) is the great inequality (0, 0, 1, −2) between Uranus and Neptune. The relevance of Neptune (with more than 30% of the contribution of Uranus to the solar system’s angular momentum) is evident in the spectral analysis. Periodicities like the nominal Jose-period or that belonging to the TNO bodies, such as the dwarf planet Eris, are not detected (even at a low confidence level) in the raw power spectra presented here.
Acknowledgments
Part of this work was supported by the grant PID-UTN 4362 (2017–2018) of UTN. The authors acknowledge the reviewer, Jean Louis Simon, for his comments that improved this work. RGC especially acknowledges him for correcting an early claim that the observed variations in the periodicities were the main cause of the lack of some inequalities in SBM. The authors are indebted to Elena Pitjeva for useful discussions regarding the new EPM2017 planetary model. RGC thanks William Folkner for an open discussion of the DE431 ephemeris at an earlier stage of this work, and for encouraging him to address several topics. RGC especially thanks Willie Soon for the very important discussions, and José Valentini and Luciana Andrín for their help in the editing process.
A word intensively used by Laplace to address the departures of the observed planetary motions from the Keplerian elliptic motion; see e.g., Wilson (1985).
References
- Abreu, J. A., Beer, J., Ferriz-Mas, A., McCracken, K. G., & Steinhilber, F. 2012, A&A, 548, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, E., Batygin, K., & Brown, M. E. 2016, AJ, 152, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Beer, J., Tobias, S. M., & Weiss, N. O. 2018, MNRAS, 473, 1596 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y.-L., Bodenheimer, P. H., & Gu, P.-G. 2012, ApJ, 757, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Charvátová, I. 1988, Adv. Space Res., 8, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Charvátová, I. 2009, New Ast., 14, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Cionco, R. G., & Abuin, P. 2016, Adv. Space Res., 57, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Cionco, R. G., & Compagnucci, R. H. 2012, Adv. Space Res., 50, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Cionco, R. G., & Soon, W.-H. 2015, New Ast., 34, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Cionco, R. G., & Soon, W.-H. 2017, Earth-Sci. Rev., 166, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Fairbridge, R. W., & Shirley, J. H. 1987, Sol. Phys., 110, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014, Interplanet. Network Prog. Rep., 196, 1 [Google Scholar]
- Ghil, M., Allen, M. R., Dettinger, M. D., et al. 2002, Rev. Geophys., 40, 3 [Google Scholar]
- Javaraiah, J. 2005, MNRAS, 362, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Jose, P. D. 1965, AJ, 70, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Juckett, D. 2003, A&A, 399, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landscheidt, T. 1999, Sol. Phys., 189, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2013, A&A, 557, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, K. G., Beer, J., & Steinhilber, F. 2014, Sol. Phys., 289, 3207 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M., & Schulze-Hartung, T. 2011, A&A, 525, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pitjeva, E. V. 2010, IAU Symp., 263, 93 [NASA ADS] [Google Scholar]
- Pitjeva, E. V., & Pitjev, N. P. 2013, MNRAS, 432, 3431 [NASA ADS] [CrossRef] [Google Scholar]
- Pitjeva, E. V., & Pitjev, N. P. 2014, Celest. Mech. Dyn. Astron., 119, 237 [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1992, Numerical recipes in Fortran (Cambridge: Cambridge University Press) [Google Scholar]
- Santos-Sanz, P., Lellouch, E., Fornasier, S., et al. 2012, A&A, 541, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scafetta, N., Milani, F., Bianchini, A., & Ortolani, S. 2016, Earth-Sci. Rev., 162, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. -L., Joutel, F., & Bretagnon, P. 1992, A&A, 265, 308 [NASA ADS] [Google Scholar]
- Simon, J.-L., Francou, G., Fienga, A., & Manche, H. 2013, A&A, 557, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soon, W., Herrera, V. M. V., Selvaraj, K., et al. 2014, Earth-Sci. Rev., 134, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Souami, D., & Souchay, J. 2012, A&A, 543, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vondrák, J., Capitaine, N., & Wallace, P. 2011, A&A, 534, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, C. 1985, Arch. Hist. Exact Sci., 33, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, R. M., & Wood, K. D. 1965, Nature, 208, 129 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional information
The SBO for the whole studied time interval (4747872 Julian days) and its dynamical parameters are stored in PANGAEA web8. There are six self-explanatory files with labels over each saved quantity and a README file.
The EPM ephemerides, including EPM2017H, are oriented to the International Conventional Reference System (ICRS) (with accuracy of ≈0:2 milliarcseconds; Pitjeva 2017, priv. comm.) which uses the equator as reference plane. As explained in Sect. 2, we transform the solar coordinates obtained from EPM2017H to a reference frame attached to the solar system's IP. We take into account the estimated orientation between the IP frame and the materializing frame of ICRS, ICRF, following Souami & Souchay (2012), i.e. using two orientation angles, namely, the inclination I = 23°0′31ʺ̣9 and the ascending node ω = 3°51′9ʺ̣4 (see Fig. A.1)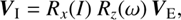 (A.1)
(A.1)
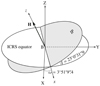 |
Fig. A.1. Reference systems associated with the ICRS and IP. The angles I and ω are used to transform the solar coordinates from the ICRS to the IP system. With H we depict the solar system's total angular momentum (always normal to the IP). B is the solar system's barycentre. |
where the vector VE is defined in the EPM2017H reference system and VI is the corresponding vector with components in the IP system, i.e. defined with the x-axis towards the nodal line equator-IP and the z-axis coincident with the direction of the total angular momentum of the solar system.
The geometry of the co-orbital system can be seen in Figs. A.2 and A.3; the geometry of the θ angle is shown in Fig. A.4. The transformation from the IP system to the co-orbital system is performed by applying three rotation matrices, namely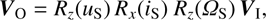 (A.2)
(A.2)
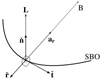 |
Fig. A.2. Non-inertial co-orbital system defined by the radial r̆, transversal t̆, and normal direction n̆ to the SBO. The symbol ⊙ marks the Sun's position on its orbit, B is the barycentre. The solar movement is anti-clockwise, prograde, regarding B. L is the Sun's orbital angular momentum, is parallel to n̆. The vector ar is the Sun's acceleration decomposed in the radial direction (ar < 0). |
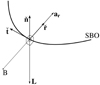 |
Fig. A.3. Non-inertial co-orbital system defined (as in Fig. A.2) for a retrograde Sun. Now L is anti-parallel to n̆. The solar movement is clockwise regarding B(ar > 0). |
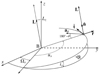 |
Fig. A.4. Relationship between the IP system and the co-orbital system (prograde Sun). It is materialized by the three angles uS, iS, and ΩS. The xy-plane is the IP. The aπ vector is the projection of the Sun's acceleration onto the instantaneous SBO plane. The θ angle is the polar angle which positions aπ from the radial direction. The z-component of the orbital solar angular momentum vector, L = Ln̆, is Lz = L cos iS. |
where now VO is the corresponding vector with defined components in the co-orbital, non-inherital system.
All Tables
Retrograde solar motion intervals (Lz < 0) regarding the solar system’s invariable plane.
All Figures
 |
Fig. 1. Percentage differences in the solar barycentric velocity vectors between DE431 and EPM2017H (Eq. (2)) for the indicated years (one datum per Julian year). The ~550 yr oscillation due to dwarf planet Eris can be clearly seen. |
| In the text | |
 |
Fig. 2. Trefoliar, particularly quasi-closed ~60 yr pattern of SBM for the indicated interval. The first JS period is marked as a thick line. The interval corresponds to the closest approximation to the initial position on the IP. The x-axis of the figure coincides with the nodal line equator-IP (see Appendix A for further information). |
| In the text | |
 |
Fig. 3. Basic dynamical parameters for two Jose-periods of 177 yr (continuous line). The intervals of trefoliar 60 yr orbits are indicated (dotted lines). All the quantities are reckoned in astronomical units and days. The “form” of the series seems to be repeated, although more important changes can appear in the kinematics series trough time. For example, the double peaks in r series inside “disordered” motion intervals change to two valleys, for example, between the years 2100 and 2500 (result not shown). |
| In the text | |
 |
Fig. 4. Relative position of icy and gaseous giant planets and their effect on r over two Jose-periods. The disordered orbits begin when Saturn and the Uranus–Neptune pair tend to be aligned (near conjunction) being Jupiter near quadrature. All the quantities are reckoned in astronomical units, days, and sexagesimal degrees. Hollow circles around 1632 indicate a particular planetary quasi-alignment which produces a solar retrograde motion (see Sect. 3.2). |
| In the text | |
 |
Fig. 5. Quite symmetric and quasi-closed projected (on the IP) pattern of SBM for ~SU period, associated disordered motion interval. The x-axis of the figure coincides with the nodal line equator-IP. An approximate value for the Sun’s radius is indicated. After that time span the Sun returns to less than 15 000 km of its initial position. |
| In the text | |
 |
Fig. 6. Extrema in Lz values, coplanar acceleration magnitude, and SBO inclination for the whole studied period showing the bimillennial wave of impulsive effects of giant planets. When the SBM is retrograde, the iS is larger than 90°. All the quantities are reckoned in astronomical units, days, and degrees. |
| In the text | |
 |
Fig. 7. Evolution of radial and transversal accelerations and Lz around the retrograde interval of the year 1990. Contrary to what was expected, radial acceleration points towards the barycentre (i.e. it is negative) during brief moments when Lz < 0, marked with arrows and depicted in the embedded plots. They are produced by Venus–Earth synodic period perturbations. All the quantities are reckoned in astronomical units and days. |
| In the text | |
 |
Fig. 8. Differences in uS and θ angles determined from DE431 and EPM2017H ephemerides. Just the differences whose absolute values are larger than 1° are plotted. They are a small fraction of the total (0.45% and 0.02%, respectively), but are not necessarily related to the impulsive events of retrograde motion (see Sect.3.3). The largest differences in uS (e.g. around 1672.6) are related to low values of solar velocity. |
| In the text | |
 |
Fig. 9. Absolute values of percentage differences larger than 5% in T and Γ magnitudes determined from DE431 and EPM2017H ephemerides (see Sect. 3.3 for details). The differences are clumped every ~ 500 yr and related to dwarf planet Eris, which produces a detectable torque because of its mass and mean distance to the Sun. |
| In the text | |
 |
Fig. 10. Main short-term periodicities detected in barycentric range, r (raw periodogram over 13 036 yr). The (1, −2) inequality of periodicity of 60.9 yr is clearly seen (indicated with its numerical value). We note the participation of Neptune on important peaks. J, S, U, and N are the giant planets’ orbital periods. This result is similar to the corresponding velocity spectrum. |
| In the text | |
 |
Fig. 11. Main long-term periodicities detected in aπ acceleration. Spectral bands coincident with the bimillennial wave and the great inequality (0, 0, 1, −2) between Uranus and Neptune are detected at low confidence level in this parameter. Other indicated inequalities are discussed in the text. |
| In the text | |
 |
Fig. 12. Main long-term periodicities detected in the averaged raw power spectra of L, T , and Γ (over 13036 years). Numerical values of several periods detected are indicated and explained in the text. |
| In the text | |
 |
Fig. A.1. Reference systems associated with the ICRS and IP. The angles I and ω are used to transform the solar coordinates from the ICRS to the IP system. With H we depict the solar system's total angular momentum (always normal to the IP). B is the solar system's barycentre. |
| In the text | |
 |
Fig. A.2. Non-inertial co-orbital system defined by the radial r̆, transversal t̆, and normal direction n̆ to the SBO. The symbol ⊙ marks the Sun's position on its orbit, B is the barycentre. The solar movement is anti-clockwise, prograde, regarding B. L is the Sun's orbital angular momentum, is parallel to n̆. The vector ar is the Sun's acceleration decomposed in the radial direction (ar < 0). |
| In the text | |
 |
Fig. A.3. Non-inertial co-orbital system defined (as in Fig. A.2) for a retrograde Sun. Now L is anti-parallel to n̆. The solar movement is clockwise regarding B(ar > 0). |
| In the text | |
 |
Fig. A.4. Relationship between the IP system and the co-orbital system (prograde Sun). It is materialized by the three angles uS, iS, and ΩS. The xy-plane is the IP. The aπ vector is the projection of the Sun's acceleration onto the instantaneous SBO plane. The θ angle is the polar angle which positions aπ from the radial direction. The z-component of the orbital solar angular momentum vector, L = Ln̆, is Lz = L cos iS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


