| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 15 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201116836 | |
| Published online | 28 July 2011 | |
La2010: a new orbital solution for the long-term motion of the Earth⋆
1
ASD, IMCCE-CNRS UMR8028, Observatoire de Paris, UPMC, 77 Av. Denfert-Rochereau, 75014 Paris, France
e-mail: laskar@imcce.fr
2
Observatoire de Besançon–CNRS UMR6213, 41bis Av. de l’Observatoire, 25000 Besançon, France
Received: 5 March 2011
Accepted: 3 May 2011
We present here a new solution for the astronomical computation of the orbital motion of the Earth spanning from 0 to −250 Myr. The main improvement with respect to our previous numerical solution La2004 is an improved adjustment of the parameters and initial conditions through a fit over 1 Myr to a special version of the highly accurate numerical ephemeris INPOP08 (Intégration Numérique Planétaire de l’Observatoire de Paris). The precession equations have also been entirely revised and are no longer averaged over the orbital motion of the Earth and Moon. This new orbital solution is now valid over more than 50 Myr in the past or into the future with proper phases of the eccentricity variations. Owing to the chaotic behavior, the precision of the solution decreases rapidly beyond this time span, and we discuss the behavior of various solutions beyond 50 Myr. For paleoclimate calibrations, we provide several different solutions that are all compatible with the most precise planetary ephemeris. We have thus reached the time where geological data are now required to discriminate between planetary orbital solutions beyond 50 Myr.
Key words: chaos / methods: numerical / celestial mechanics / ephemerides / planets and satellites: dynamical evolution and stability / Earth
The solutions are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/532/A89
© ESO, 2011
1. Introduction
Owing to gravitational planetary perturbations, the elliptical elements of the orbit of the Earth are slowly changing in time, as is the orientation of the planet’s spin axis. As described by Milankovitch (1941) these changes induce variations in the insolation received on the Earth’s surface that are at the origin of large climatic changes. Since the work of Hays et al. (1976), which established a correlation between astronomical forcing and the δ18O records over the past 500 kyr, there has been a increasing need for a precise long-term ephemeris for the Earth orbital and rotational evolution (see Laskar et al. 2004 for a more detailed historical account).
For paleoclimate studies, the most widely used orbital solutions are nowadays either the averaged solution of Laskar (1988) and Laskar et al. (1993b) or the numerical solution of Laskar et al. (2004).
The first long-term direct numerical integration (without averaging) of a realistic model of the Solar System, together with the precession and obliquity equations, was performed by Quinn et al. (1991) over 3 Myr. Over its range, this solution presents only small differences with the secular solutions of Laskar (1988, 1990) (see Laskar et al. 1992). The orbital motion of the full Solar System was computed over 100 Myr by Sussman & Wisdom (1992) using a symplectic integrator with mixed variables (Wisdom & Holman 1991), confirming the chaotic behavior found by Laskar (1989, 1990). Following the improvement of computer technology, long-term integrations of realistic models of the Solar System have improved (Varadi et al. 2003; Laskar et al. 2004), but the main limitation remains the exponential divergence of nearby orbits resulting from the chaotic motion of the Solar System (Laskar 1989, 1990, 1999). Although it is now possible to integrate the motion of the Solar System over time periods of more than 5 Gyr, which is comparable to its age or expected lifetime (Laskar & Gastineau 2009), it is clear that the chaotic behavior of the solution will still limit its validity to a few tens of Myr.
The present paper is a continuation of the work that has been conducted for decades in our group to obtain the most precise solution for the past evolution of the orbit and rotational state of the Earth, specifically aimed to paleoclimate studies.
The numerical integrator is the same symplectic integrator of Laskar & Robutel (2001) that was used in the La2004 solution (Laskar et al. 2004), but it was entirely rewritten in C in order to access the extended precision of the Intel architecture. The tidal model has been largely modified, and is now similar to the one used in the JPL planetary ephemeris DE405 (Standish 1998b) or in our new planetary ephemeris INPOP (Fienga et al. 2008, 2009). The precession equations for the evolution of the spin axis of the Earth are also new (Boué & Laskar 2006). We no longer average over the orbital motion of the planets, which allows a precise computation of the evolution of the Earth spin axis that can be compared to the most precise model adopted by the IAU (Soffel et al. 2003) (see Fienga et al. 2008).
In previous long-term solutions (Laskar 1988; Quinn et al. 1991; Laskar et al. 1993a; Varadi et al. 2003; Laskar et al. 2004), the initial conditions of the solutions were obtained either directly from a high precision planet ephemeris, or by performing a fit over its full time span (as in La2004) that was still limited to a few thousands of years. It was also difficult to monitor the real uncertainty in the adopted ephemeris.
In the present work, we have removed these limitations. In the past few years, we have build the new high precision planetary ephemeris INPOP that has been fitted to all available planetary and Lunar observations (Fienga et al. 2008, 2009). This ephemeris that has already been released in two versions (INPOP06 and INPOP08) is thus equivalent to the JPL ephemerides DE used to determine the initial conditions of the previous long-term solutions. In addition, we have removed in INPOP all time limitations and carefully designed the numerical integrator. We could thus extend the integration of INPOP06 and INPO08 over 1 Myr with the full ephemeris model. The initial conditions of the present long-term ephemeris could then be fitted over an extended interval of several hundreds of thousands of years before being extended to 250 Myr. By doing so, we were able to take into account the full precision of the ephemeris, such that it now appears that the limitations are no longer those of the model but those of the planetary observations themselves.
The first sections of this paper (Sects. 2–6) describe successively the La2010 numerical model, its link with the INPOP ephemeris, the various La2010 solutions, and their comparison with the high precision INPOP ephemeris and the previous La2004 solution. The following sections (Sects. 7–9) are focussed on the long-term cycles that are present in the eccentricity solution and their stability. This topic is of essential importance to attempts to establish an astronomically calibrated geological timescale (see Pälike & Hilgen 2008). The La2004 solution (Laskar et al. 2004) has been successfully used for the astronomical calibration of the Neogene period ( ≈ 23 Myr) (Lourens et al. 2004), which is included in the most recent standard timescale GTS2004 (Gradstein et al. 2004). There has been a continuous effort to improve this timescale and to extend the astronomical calibration to the full Cenozoic period ( ≈ 65 Myr) through the Earthtime and Earthtime-eu projects1. To do so, the length of validity of the orbital solution has to be extended by more than 20 Myr. Because of the chaotic behavior of the solution (Laskar 1989), this corresponds to improving the precision of the model and parameters by two orders of magnitude, and the present work represents a step in this direction.
Beyond the horizon of predictibility of the orbital solution, it is tempting to use the recorded geological information to provide constraints on the orbital motion of the Solar System (Lourens et al. 2001; Pälike et al. 2004). Owing to the lack of precision of the geological data over very early periods of time, this can only be done by studying some macroscopic aspects of the orbital solution. The analysis of the secular resonance g4 − g3 − 2(s4 − s3) (Sect. 8) is devoted to this problem. In particular, we show how the analysis of the modulation of the amplitude of the 405 kyr eccentricity term can discriminate between various orbital solutions and thus provide feedback from geological data into astronomical models.
In the present work, we focus on the orbital solution of the Earth, and more specifically on the long period terms in the eccentricity that are of crucial importance for a better understanding of the geological data. We discuss here neither the precessing motion nor obliquity evolution of the spin axis of the Earth for which we refer to the La2004 solution (Laskar et al. 2004). We also refer to this previous work for the evolution of the Lunar orbit that was not improved in the present work, owing to the large uncertainties that remain in the evolution of the tidal dissipation in the Earth-Moon system (see Laskar et al. 2004).
2. Numerical model
The orbital solutions La90-93 (Laskar 1990; Laskar et al. 1993a) were obtained by a numerical integration of the averaged equations of the Solar System, including the main general relativity and Lunar perturbations. As computer technology now allows us to integrate directly precise models of the evolution of the Solar System over several hundreds of Myr, we have decided since La2004 (Laskar et al. 2004) to use direct integrations without any averaging.
The dynamical model and numerical integrators are very close to the ones of La2004. We thus refer to Laskar et al. (2004) for a detailed description of these models, and only report here the elements that are different in the present model and integration.
2.1. Dynamical model
The orbital model comprises the Sun, all eight planets of the Solar System, Pluto, and the Moon. The post-Newtonian general relativity corrections of order 1/c2 due to the Sun are included following Saha & Tremaine (1994). The Moon is treated as a separate object. To obtain a realistic orbital evolution of the Earth-Moon system, we also take into account the most important coefficient of the gravitational potential (J2) of both the Earth and the Moon, and the tidal dissipation in the Earth-Moon System (Laskar et al. 2004). In contrast to La2004, the precession and obliquity are now integrated without averaging over the orbital periods, following Boué & Laskar (2006). In the final runs, as in the DE and INPOP ephemerides, we also added the contribution of the three main asteroids Ceres, Pallas, and Vesta, as well as those of Iris and Bamberga, which both exert strong perturbations on Mars (Standish 1998a; Kuchynka et al. 2010). These five asteroids are then treated in the same way as the planets. As in La2004 (Laskar et al. 2004), some small corrections to the orbital precession motions are made to take into account the average effect of the remaining asteroids or other unmodelized parameters.
2.2. Numerical integrator
As in La2004, the numerical integration was performed with the symplectic integrator scheme SABAC4 of Laskar & Robutel (2001), including a correction step for the integration of the Moon. This integrator is particularly adapted to perturbed systems where the Hamiltonian governing the equations of motion can be written as the sum of an integrable part (the Keplerian equations of the planets orbiting the Sun and the Moon orbiting the Earth), and a small perturbing potential representing the interactions among the planets.
The step size used in the integration is in general τ = 5 × 10-3 yr = 1.82625 days, while for La2010a, τ = 10-3 yr = 0.36525 days. The initial conditions of the integration were least squares adjusted to a special version of INPOP that was extended in time over 1 Myr. Depending on the solution, this fit was performed over either 1 Myr or 580 kyr (see Table 2).
In La2004, the integration was made in double precision, with machine Epsilon εM ≈ 2.22 × 10-16. Here, we integrated the solutions in extended precision on Xeon Intel processors, which allows arithmetics in 80 bits instead of 64 bits in double precision. The machine Epsilon then becomes  .
.
The integration time for our complete model, including five asteroids and the Moon as a separate object with τ = 5 × 10-3 yr is about one day per 3 Myr in extended precision, and one day per 6 Myr in double precision on a Intel Xeon E5462 2.8 Ghz workstation. When the step size is decreased to τ = 10-3 yr, for the nominal solution La2010a, the requested time is 5 days for 3 Myr, and more than one year for the whole integration.
2.3. Numerical error
As in La2004, the numerical error is estimated by comparing two integrations with the same model but slightly different step sizes. For the nominal solution, we use τ = 5 × 10-3 yr, and for the alternate solution τ∗ = 4.8828125 × 10-3 years. This special value is chosen such that our output time span h = 1000 years corresponds to an integer number (204 800) of steps, to avoid any interpolation problems when checking the numerical accuracy. With τ = 10-3 yr, we then have τ∗ = 0.9765625 × 10-3 yr (Table 2).
2.3.1. Rotational evolution
In contrast to La2004, the precession equations are no longer averaged over the orbital motion of the planets or the Moon, but are treated in a vectorial manner, following Boué & Laskar (2006). Following (Darwin 1880; Mignard 1979), we assume that the torque resulting from tidal friction is proportional to the time lag Δt needed for the deformation to reach the equilibrium. This time lag is supposed to be constant, and the angle between the direction of the tide–raising body and the direction of the high tide is proportional to the rotation speed. Such a model is called “viscous”, and corresponds to the case in which 1/Q is proportional to the tidal frequency.
Various small additional dissipative effects such as core–mantle friction (Poincaré 1910; Rochester 1976; Lumb & Aldridge 1991; Correia et al. 2003), atmospheric tides (Chapman & Lindzen 1970; Volland 1978; Correia & Laskar 2003), mantle convection (Forte & Mitrovica 1997), climate friction (Rubincam 1990, 1995; Bills 1994; Ito et al. 1995; Levrard & Laskar 2003), were discussed in La2004, but their effects are considered to be too small and uncertain to be added to the model, as was the case in La2004.
3. The numerical ephemeris INPOP
The initial conditions of La2004 were obtained by a fit to the JPL numerical ephemeris DE406 (Standish 1998a) over the full range of DE406, that is from −5000 yr to +1000 yr from the present date. DE406 is itself adjusted to planetary observations.
With this procedure, we were limited by the range of the available ephemeris, and in general, the latest ephemeris is not always computed over a long time interval. For example, the most recent ephemeris from JPL, DE421 (Folkner et al. 2008), has only been provided for the time interval [1900,2050] yr. Moreover, it is difficult to estimate the true uncertainty in the provided ephemeris. Most often, this uncertainty is only revealed with the publication of the new ephemeris which can then be the compared with the previous one. To overcome these limitations, our research group has undertaken the construction of high precision planetary and lunar ephemerides. After five years of work, two successive versions have been published: INPOP06 (Fienga et al. 2008) and INPOP08 (Fienga et al. 2009). The detailed information about the dynamical models and fit to available observations can be found in the related publications.
In the construction of these ephemerides, we removed all elements that would limit the length of validity of the solutions. In particular, we did not use some precession formulae for the evolution of the spin axis of the Earth. We instead integrated together with the full ephemeris, a precession model for the Earth that is obtained after averaging over the rotation period of the Earth, but not over the orbital period of either the Earth or the Moon (Fienga et al. 2008).
The full ephemeris could then be extended over 1 Myr using extended precision 80 bit arithmetic with the Adams integrator of INPOP. This integration took about four month of CPU time on an itanium 9040 1.6 Ghz workstation. This process was first made for INPOP06, and then for INPOP08, when the final version of this latest ephemeris (Fienga et al. 2009) was finally made available. These highly accurate ephemerides are then used for the calibration and evaluation of the long-term models La2010.
We refer to Fienga et al. (2008, 2009) for a precise description of INPOP06 and INPOP08. With respect to INPOP06, the more recent INPOP08 benefitted from several additional sets of observations. The Mars Express and Venus Express ranging data provided very precise measures of Earth–Mars and Earth-Venus distances with a precision of a few meters (Fienga et al. 2009). For Mars, this was a continuation of a long sequence of very precise measurements that had been acquired with the Martian spacecrafts since the first Viking landers on Mars, but for Venus, the new ranging data processed by ESOC were the first highly accurate estimates of the Earth-Venus distance, whose uncertainty was thus reduced from a few hundred meters to a few meters (Fienga et al. 2009). Another improvement in INPOP08 consists of the use of some Cassini normal points (Folkner et al. 2008) that also help us to constrain the position of Saturn. In INPOP08, the Lunar orbit was also fitted to Lunar laser ranging data in a consistent way, while in INPOP06, the fit of the Lunar ephemeris was only made with respect to Lunar distances given by DE405 (Standish 1998a).
It is always difficult to estimate the true uncertainty of an ephemeris. In Fienga et al. (2009), this estimate is obtained by comparison with INPOP06 and DE421 over 10 and 100 years. The differences between INPOP08 and DE421 are in general smaller, but comparable with the differences INPOP08-INPOP06, with the notable exception of the positions of Saturn, where the differences INPOP08-DE421 are one order of magnitude smaller than the differences INPOP08-INPOP06. This is certainly the consequence of the use in both DE421 and INPOP08 of the new Cassini data which tightly constrain the position of Saturn.
After 100 yr, the differences INPOP08-DE421 in barycentric positions range from a few kilometers for the inner planets to a few thousand kilometers for the outer planets, and only 40 km for Saturn (Fienga et al. 2009, Table 6). This is several orders of magnitude more than the error in the numerical integration (Fienga et al. 2008, Table 1) which reaches only a few micrometers after the same range, and less than a few meters after 10 000 yr. It can thus be assumed that after one million years, the numerical error in the integration of INPOP will still be smaller than the propagation of the uncertainty in the model and parameters, obtained by the fit to planetary positions.
Maximum difference between INPOP06 and INPOP08 over 1 Myr (top). and between INPOP08 (computed in extended precision) and INPOP08d, a version of INPOP08 computed in double precision, over 1 Myr (bottom).
We thus extended the two INPOP ephemeris (INPOP06 and INPOP08) over 1 Myr to use these solutions as a starting point for the long-term ephemeris. The accuracy of these solutions after 1 Myr is then evaluated by comparing INPOP06 with INPOP08, assuming that the real uncertainty in INPOP08 is smaller than the difference INPOP08-INPOP06 (Table 1). In Table 1, we also provide the differences in the two integrations of INPOP08 made in both double and extended precision, to evaluate the numerical precision of the integration. From the comparisons made in Fienga et al. (2008), we can assume that the error in the integration of INPOP08 made in extended precision is several orders of magnitude smaller than the differences reported in this table.
4. Successive versions of La2010
The process leading to a long-term solution is long, as we had to wait first for the INPOP solution to be ready over 1 Myr, and then only we could make the fit of the long-term model. After that, the integration of the long-term model over 250 Myr in extended precision still required about three months of CPU time, and more than one year when the step size is reduced to 10-3 yr. We therefore computed several versions of these long-term ephemeris, which could be used for comparisons, and also to study the stability of the solution with respect to improvements in the INPOP ephemeris. As the INPOP08 ephemeris was finished only very recently, some of the solutions fitted to INPOP08 have been fitted only over 580 kyr instead of 1 Myr for INPOP06. This did not however make a large difference, and the solutions are still at the end compared to INPOP08 over 1Myr as the integration of INPOP08 has now reached 1Myr. The various models that were selected are summarized in Table 2.
The solution La2010d was fitted to INPOP06 over 1 Myr, while the more recent solutions La2010a, La2010b, La2010c, and their associated solutions La2010a*, La2010b*, La2010c*, were fitted to INPOP08, over 580 kyr for the solutions with index a,b, and over 1 Myr for La2010c and La2010c*. All these models, except La2010c and La2010c* comprise the five major asteroids, Ceres, Vesta, Pallas, Iris, and Bamberga.
In all cases, the parameters are taken from the corresponding INPOP ephemeris, as well as the starting value of the initial conditions. To take into account the differences in the models, we then perform a fit of the semi-major axis, and add a small precessing term that can be thought as representative of the average contribution of the minor planets that have not been taken into account in our simplified models. In these solutions, the Moon is integrated as a separate object, taking into account the tidal dissipation in the Earth-Moon system. The step size is then 5 × 10-3 yr for La2010b,c,d and 10-3 yr for the nominal solution La2010a.
To check the numerical accuracy of the solution, we also integrated these solutions with an alternate step size of τ∗ = 4.8828125 × 10-3 yr for b and c, and τ∗ = 0.9765625 × 10-3 yr for La2010a*. These values are different, but close to the nominal step size. They are taken in such a way that 1024 × τ∗ = 1000 × τ, where τ is the nominal step size of the corresponding solution. In Fig. 1, the difference in the eccentricity of the Earth for two solutions La2010x and La2010x* are plotted over time for 100 Myr for x = a,b,c. Because of the exponential divergence of the solutions resulting from chaotic behavior, the difference is nearly zero for a very long time, of more than 50 Myr, and then grows rapidly to their maximal value, as the two solutions become out of phase.
Variants of the La2010 solutions.
 |
Fig. 1 Estimate of the numerical precision of the solutions La2010a,b,c. The estimate is obtained by the difference in the eccentricity of the Earth obtained with the integration of two solutions La2010x and La2010x* for x = a,b,c (see Table 2). |
This is an external way of evaluating the precision of the numerical integration, but it is in fact a pessimistic view. Indeed, we have fitted the solutions La2010a,b,c to INPOP08, but the initial conditions of La2010x* is the same as for La2010x. The difference in step size will then induce a difference in the reference Hamiltonian of the symplectic integration of the system, which should explain most of the difference that is observed here. This is why for a reduced step size, as in the case of La2010a, the differences between La2010a and La2010a* are smaller.
Nevertheless, although pessimistic, this experiment shows that the numerical error can be neglected over 55 Myr for La2010b,c and 60 Myr for La2010a. This is why we selected La2010a as our nominal solution.
5. Comparison with INPOP08
The solution La2004 was fitted to DE406 over its full range, that is over the interval [−5000: +1000] yr from now. In 2004, there was no possibility of comparing it to an accurate ephemeris over a longer time. With the construction of the new INPOP ephemerides, this is now possible, as we have extended INPOP06 and INPOP08 over 1 Myr. Since the set of observation used in INPOP08 is significantly larger than that of INPOP06, we use INPOP08 as the reference ephemeris, representing the best knowledge of the long-term orbital motion of the Solar System that we can achieve at present.
We thus compared La2004 to INPOP08, as well as INPOP06 and the new computed solutions of the Earth eccentricity for La2010a,b,c,d (Fig. 2). From Fig. 2 (top), it is clear that the new solution La2010a represents a significant improvement with respect to La2004. The difference La2010a-INPOP08 (Fig. 2 (a3) and (b3)) is indeed nearly 15 times smaller than the difference La2004-INPOP08 (Fig. 2 (a1)).
 |
Fig. 2 Differences in the eccentricity of the Earth-Moon barycenter over 1 Myr for various solutions as follows: a1 = La2004-INPOP08; a2 = La2010d-INPOP08; a3 =b3= La2010a – INPOP08; a4=INPOP06-INPOP08; b1 = La2010b – INPOP08; b2 = La2010c -INPOP06. We note that the vertical scale is enlarged ten times in the bottom plot. All solutions are compared to INPOP08. In the top figure, La2010d (a2) and INPOP06 (a4) are almost superimposed. This is because La2010d was adjusted over INPOP06. |
In Fig. 2, we can see that La2010d-INPOP08 (a2) is almost superimposed on INPOP06-INPOP08 (a4). This is because La2010d has been adjusted to INPOP06. It is also clear from this plot that the differences between a long-term solution and its reference ephemeris are now much smaller than those of two consecutive versions of the high resolution planetary ephemeris (such as INPOP06 and INPOP08).
Maximum difference between the La2010 solutions and INPOP08 over 1 Myr. Top: maximum difference ast5AL08cx -INPOP08 over 1 Myr. Bottom: maximum difference ast5SL08ax -INPOP08 over 1 Myr.
Maximum difference between the La2010 solutions and INPOP06 over 1 Myr. Top: maximum difference ast5ALix -INPOP06 (both solutions are in extended precision) over 1 Myr. Bottom: maximum difference ast5ALh -INPOP06 over 1 Myr.
The main result of these comparisons, are also displayed in Tables 3 and 4, for the various solutions that we selected. The differences between the long-term “simplified” model that we use here and the most precise planetary ephemerides are now much smaller than the difference between two consecutive planetary ephemeris (INPOP06-INPOP08), which can be considered as representative of the true uncertainty in the ephemeris. The main limitation of the precision of the long-term planetary solution then resides in the precision of the planetary ephemeris, that is in the planetary observations. In Tables 3 and 4, the differences between the values of the eccentricity and inclination of the Moon are much larger than for the planets. This is largely due to the offset in the longitudes of perihelion and node that result from the rapid precessing motion of the Lunar orbit. As seen in these tables, this has nevertheless a very limited effect on the EMB orbit.
6. Comparison with La2004
After comparing the solutions over 1 Myr with the most precise planetary ephemeris, we now compare the various solutions La2010a,b,c,d to the former solution La2004 over the whole expected range of validity of these solutions, that is over a few tens of million of years.
 |
Fig. 3 Eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d). In the interval [ − 40: − 30] Myr, the four solutions are virtually identical, but before − 45 Myr, La2004 begins to depart significantly from the La2010 solutions. We have then plotted again the time interval [ − 50: − 40] Myr (bottom), removing La2004 to allow a clearer comparison of the La2010 solutions. Over this interval, these three solutions are very similar. |
In Fig. 3, we present the variation in the eccentricity of the EMB from − 30 Myr to − 50 Myr for the La2004 solution and the four La2010a,b,c,d new solutions. The interval [ − 30:0] Myr is not represented because all five solutions practically coincide over this time interval. Some discrepancies between La2004 and the new La2010 solutions only appear within the time interval [ − 40: − 30], although most of the time the solutions remain very similar, and the small differences that can be seen in Fig. 3 will most probably not lead to any significant change in the paleoclimate records. We can even consider that the solution La2004 remains in good agreement with the new solutions until − 45 Myr. This is in good agreement with the expected precision forecasted in (Laskar et al. 2004).
Beyond − 45 Myr, noticeable differences start to appear, and the solution La2004 becomes significantly different from the La2010 solutions. We have thus made an additional plot of the [ − 50: − 40] Myr interval in Fig. 3, for only the solutions La2010a,b,c,d. These latest solutions closely agree across this time interval, despite the variations in the models or initial conditions among these new solutions. We can thus consider that the present new solutions are at least valid over 50 Myr.
Frequency decomposition of z = eexpiϖ for the Earth on the time interval [ − 15, + 5] Myr (Laskar et al. 2004).
Beyond −50 Myr, the situation is less clear as the solutions La2010a,b,c,d differ significantly (Fig. 4). Nevertheless, from Fig. 4, it can be seen that if moderate precision only is required, the solution could be used up to −60 Myr. In particular, the solutions are still well in phase around −55 Myr. This date is of particular interest, as it corresponds to specific climatic events that have been well documented in the paleoclimate records: the Paleocene-Eocene Thermal Maximum (PETM) that is dated around 55.53–56.33 Ma2 (Westerhold et al. 2007, 2008), and the Elmo Thermal Maximum (ETM) dated at 53.7–54.5 Ma (Lourens et al. 2005; Westerhold et al. 2007, 2008).
 |
Fig. 4 Eccentricity of the Earth for the solutions La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from −50 to −65 Myr. Although the various solution begin to diverge beyond 53 Ma, it is remarkable that the minima of eccentricity at 51.75 Ma, 56.25 Ma, and 58.25 Ma (in grey) correspond in all various solutions. |
From Fig. 4, it is however quite clear that the solutions La2010a,b,c,d cannot be used beyond 60 Ma, as the solutions differ substantially in the interval [−65: −60] Myr. It should thus be stressed that in this time interval, the direct use of the eccentricity solution of the Earth for geological calibration should be used with utmost care.
Practically speaking, if one wishes to use these solutions beyond 50 Myr, for a geological calibration for example, one should only use the features of the solutions that remain the same in the four La2010 solutions. This provides a measure of the stability of such a calibration with respect to the uncertainty in the La2010 solutions.
7. Long-term cycles
Main secular frequencies gi and si of La2004 and La2010a determined over 20 Ma for the four inner planets, and over 50 Ma for the five outer planets (in arcsec yr-1).
The complete eccentricity solution of the Earth allows a direct adjustment of paleoclimate data to the oscillations of about 95 kyr and 124 kyr in the eccentricity (see Laskar et al. 2004), but for ancient records, this signal may not be clearly visible in the sediments. However, the 405 kyr oscillation with argument g2 − g5, where gi (Table 6) are the secular frequencies3 of the Solar System (see Laskar et al. 2004), is very often present in the sedimentary records. This term is the largest term in a quasi-periodic approximation of the eccentricity of the Earth (see Laskar et al. 2004, Table 6), and is less influenced by the chaotic diffusion present in the Solar System than the shorter period terms around 100 kyr (Laskar 1990; Laskar et al. 2004).
 |
Fig. 5 In a), we present the spectrum of the eccentricity over 65 Myr from the La2010a solution, limited to the interval [0,5′′/yr] (period > 259.2 kyr). In b), the same spectrum is plotted for a solution build with only the 5 main terms of z3 (Table 5). The main peaks are then easily identified and thus also the main peaks of the full eccentricity a). |
In recent works, the modulation of the 405 kyr component, which is caused by the beat g3 − g4 of period ≈ 2.4 Myr, has also been identified in the sedimentary records, and is thought to be a key factor in the onset of special climate events (Lourens et al. 2005; Pälike et al. 2006; van Dam et al. 2006). There have also been been many searches for long-term cycles in the sedimentary records and attempts to use them to relate the sedimentary data to the eccentricity computations (Olsen & Kent 1996; Lourens et al. 2005; Westerhold et al. 2007, 2008; Jovane et al. 2010). In Fig. 5a, we plot the spectrum of the nominal solution La2010a, limited to the range [0,5]′′/yr (periods larger than 260 kyr). As there is a gap at about 2.2′′/yr in this spectrum, we filtered the eccentricity data for all various solutions in the range [0,2.2]′′/yr (Figs. 6 and 7).
Here again, it is clear that all of the solutions La2004 and La2010a,b,c,d are practically identical over [ − 30:0] Myr, and very similar up to –45 Myr, where La2004 starts to differ notably from the new solutions La2010, which still behave in a similar manner up to about –50 Myr where the situation becomes more confused.
7.1. The modulation of the g2–g5 405 kyr cycle
In order to examine more closely the long-term cycles in the Earth eccentricity, we identified the origin of the main spectral terms in the eccentricity spectrum of Fig. 5a. To do so, a synthetic eccentricity curve is build along the same time range using only the five terms of eexp(iϖ) provided by the frequency decomposition of the solution La2004 over the time interval [−15,+5] Myr, taken from (Laskar et al. 2004). The plot of the spectrum of the eccentricity function that is obtained with this purely quasiperiodic signal with frequencies limited to the linear terms g1,g2,g3,g4, and g5 (Table 5) is plotted in Fig. 5b.
As this synthetic model is quasiperiodic with only five main frequencies, the identification of the main spectral terms of the eccentricity are then obtained unambiguously with a spectral analysis over 65 Myr as described in Fig. 5b. These terms are easily related to the corresponding peaks of the full eccentricity spectrum of Fig. 5a.
This exercise, which in some sense complements a full quasiperiodic decomposition of the eccentricity as in (Laskar et al. 2004, Table 6), allows us to better understand the behavior and origin of the main long-term cycles observed by the practitioners in the context of geological data (Olsen & Kent 1996; Lourens et al. 2005; Westerhold et al. 2007, 2008; Jovane et al. 2010; Hilgen et al. 2010).
The leading periodic term is the well-known 405 kyr term g2 − g5, but this term is surrounded by the two terms (g2 − g5) − (g4 − g3) and (g2 − g5) + (g4 − g3), which will induce with g2 − g5 a modulation of the 405 kyr eccentricity term of frequency g4 − g3, corresponding to a 2.4 Myr period. An obvious consequence is that when analyzing geological data to search for the 405 kyr term, one needs to use a spectral window that includes these two side terms, that is a window similar to the [2.2,4.3]′′/yr window used in Fig. 8. In addition, the two terms g1 − g5 of period ≈ 1 Myr, and g2 − g1 of period ≈ 688 kyr are also of strong amplitude in the eccentricity spectrum.
7.2. The g4–g3 2.4 Myr cycle
Moreover, g4 − g3 also appears directly as a main periodic term of the eccentricity (Fig. 5a,b). The same 2.4 Myr cycle can thus be directly retrieved from the eccentricity curve. Indeed, in Fig. 8, we have plotted both the filtered eccentricity in the interval [2.2,4.3]′′/yr (ea) (in red) and as well the filtered eccentricity with a [0,0.1]′′/yr window (eb) (in blue). It can then be seen that the envelope (in green) of ea is almost identical to the opposite of eb (Fig. 8).
As a consequence, the two components ea and eb of the eccentricity need to be added to really evaluate the component of the 2.4 Myr term (Fig. 9). In the resulting ea + eb curve, the variations in the maxima are then attenuated, while the minima variations are increased to about 0.02. The variations in the minima are in phase with the g4 − g3 term (plotted in blue in Fig. 9).
The large size of these variations then makes it understandable that a signature of these variations could be recorded in the sedimentary paleoclimate signal. Indeed, although the global mean annual insolation on Earth varies as e2 and thus is not strongly influenced by eccentricity variations, this is not the case for seasonal variations. If one considers a black body with uniform temperature at distance d of a star, using Stefan’s law for the emission of a black body, one finds that its surface temperature T is proportional to d − 1/2. In this case, the difference δT between perihelion and aphelion temperature will be given by 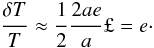 (1)A change of 0.02 in the eccentricity thus corresponds in this simplified model to a change of about 0.02 × 300 = 6 K in the difference between perihelion and aphelion temperatures.
(1)A change of 0.02 in the eccentricity thus corresponds in this simplified model to a change of about 0.02 × 300 = 6 K in the difference between perihelion and aphelion temperatures.
 |
Fig. 6 Filtered eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from + 10 to − 30 Myr. The solution is filtered in the interval [0:2.2′′/yr], that is for periods in [589, + ∞ [ kyr. |
 |
Fig. 7 Filtered eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from − 30 to − 70 Myr. The solution is filtered in the interval [0:2.2′′/yr], that is for periods in [589, + ∞ [ kyr. |
Because of the increasing importance of this 2.4 Myr component in some of the analyses of sedimentary records, we have added here a detailed comparison of the filtered solution in the [0,1.1]′′/yr interval in Fig. 10 for the time intervals of [ − 55, − 40] and [ − 65, − 50] Myr. We note that it is not necessary to compare the various orbital solutions in the [ − 40,0] Myr time interval as they are practically identical in this range.
 |
Fig. 8 Filtered eccentricity around the 405 kyr period for La2010a. In red is ea, the filtered eccentricity in the band [2.2,4.3]′′/yr ( [301,589] kyr period), while eb, the filtered eccentricity in the band [0,1.1]′′/yr ( period > 1.18 Myr) is plotted in blue. The opposite (in pink) of the maximum enveloppe of ea (in green) nearly coincides with eb. |
 |
Fig. 9 ea + eb (see Fig. 8) for the La2010a solution is plotted in red. Its minimum are in phase with eb, the filtered eccentricity in the band [0,1.1]′′/yr ( period > 1.18 Myr) is plotted in blue. |
 |
Fig. 10 Filtered eccentricity in the band [0,1.1]′′/yr (period > 1.18 Myr) for La2004 and La2010a,b,c,d. |
As in the previous discussion, we can see that all curves are very similar until −45 Myr, while La2004 differs significantly beyond −45 Myr. This is why this solution is no longer plotted in the bottom plot of Fig. 10, which is displayed for the [−65,−50] time interval. This range is particularly critical, as it corresponds to the location of both the PETM (at about −55 Myr) and the K/P boundary (at about −66 Myr) (Lourens et al. 2005; Westerhold et al. 2007, 2008). The various solutions begin to differ significantly beyond −53 Myr, but it can be seen that the two maxima at about −57.3 Myr and −59.3 Myr agree for all four La2010 solutions, although they largely differ around − 55 Myr. One could thus use these three peaks to attempt to fit a geological timescale beyond –50 Myr, in the [−60,−50] Myr time interval.
In the La2010a solution, the g4 − g3 argument has a period of about 2π/2.664 ≈ 2.36 Myr in the interval [−45,0] Myr, but beyond −45 Myr, this period changes because of chaotic diffusion (Fig. 11). As this occurs at the border of the validity range of the solution, it is still difficult to be sure of the real behavior of the g4 − g3 argument beyond −45 Myr, and it will be necessary to compare these data to geological records to confirm the behavior of the Solar System eccentricity solution.
 |
Fig. 11 Argument (in radians) related to g4 − g3 − 2.664 T versus T (in Myr) for La2010a (top). Argument (in radians) related to s4 − s3 − 2 × 2.664 T versus T (in Myr) for La2010a (bottom). |
8. Resonant angles
8.1. Secular resonances
The previous discussion demonstrates the importance of the behavior of the g4 − g3 argument in the macroscopic aspect of the variations in the Earth’s eccentricity, and thus its possible relation to the past climate on Earth.
Using the secular equations, Laskar (1990, 1992) demonstrated that the chaotic behavior of the Solar System arises from multiple secular resonances in the inner Solar System, and in particular, from the critical argument associated with  (2)where g3,g4 are related to the precession of the perihelion of the Earth and Mars, and s3,s4 are related to the precession of the node of the same planets. This argument is presently in a librational state, but can evolve in a rotational state, and even move to libration in a new resonance, namely
(2)where g3,g4 are related to the precession of the perihelion of the Earth and Mars, and s3,s4 are related to the precession of the node of the same planets. This argument is presently in a librational state, but can evolve in a rotational state, and even move to libration in a new resonance, namely 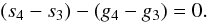 (3)The argument θ as well as the other important resonant argument (σ = (g1 − g5) − (s1 − s2)) identified by Laskar (1990, 1992) as the origin of the chaotic behavior of the inner planets are plotted in figure 12 for all solutions La2004, La2010a,b,c,d. In all cases, transition from libration to circulation appears around − 50 Myr, leaving some uncertainty in the behavior of the solution beyond this date.
(3)The argument θ as well as the other important resonant argument (σ = (g1 − g5) − (s1 − s2)) identified by Laskar (1990, 1992) as the origin of the chaotic behavior of the inner planets are plotted in figure 12 for all solutions La2004, La2010a,b,c,d. In all cases, transition from libration to circulation appears around − 50 Myr, leaving some uncertainty in the behavior of the solution beyond this date.
 |
Fig. 12 Resonant arguments (in radians versus time in Myr) σ = (g1 − g5) − (s1 − s2) (top) and θ = (s4 − s3) − 2(g4 − g3) (middle and bottom) for the different solutions La2004, La2010a,b,c,d. In the bottom plot, θ is displayed on a greater scale. One can see that the La2010 solutions are very close up to 50 Myr. |
8.2. Searching for some geological evidence of chaos
The transition from libration to circulation of the resonant argument related to θ = (s4 − s3) − 2(g4 − g3) is directly linked to the chaotic diffusion of the orbital trajectories. Searching for and identifying in the geological records evidence of such transitions would thus provide observational confirmation of the past chaotic evolution of the Solar System.
As it appears from the previous sections, it becomes more and more difficult to obtain by numerical computations only the date of the first transition from libration to circulation for this resonant argument (Fig. 12). The direct observation of the individual arguments related to g3,g4,s3,s4 is certainly out of reach. The argument θ, however corresponds to a 2:1 resonance between the two secular terms g4 − g3 and s4 − s3, both terms being present in the sedimentary records. We have discussed the importance of the g4 − g3 beat in the eccentricity solution. In a similar way, s4 − s3 appears as a beat of about 1.2 million of years in the solution of the obliquity, as the result of the beat between the p + s4 and p + s3 components of the obliquity, where p is the precession frequency of the axis (see Laskar et al. 2004, Fig. 7).
With the occurrence of these beats, the detection of the resonant state in the geological data becomes possible. The modulation of 1.2 Myr in the obliquity indeed clearly appears in the spectral analysis of the paleoclimate record from the Ocean Drilling Program Site 926, (Zachos et al. 2001). Moreover, using the ODP legs 154 and 199, Pälike et al. (2004) were able to find some evidence that the critical argument of θ did not show a transition to circulation at 25 Myr, as in La93, but remained in libration over 30 Myr, as in the La2004 solution.
Searching for a transition of the (s4 − s3) − 2(g4 − g3) resonance to the (s4 − s3) − (g4 − g3) resonance, as displayed in Fig. 12) is difficult, as it requires us to obtain both a good signal in eccentricity (or precession) and in obliquity. It may be more direct to search only for a modulation of the g4 − g3 (or s4 − s3) period, as it appears in Fig. 11. The change in La2010a at − 45 Myr of the g4 − g3 slope, from a period of about 2.4 Myr to a period of about 2 Myr also reflects the same chaotic transition.
This change can be directly seen in the eccentricity record (Figs. 9, 10), as it induces a change in the time interval from two maxima in the filtered eccentricity (Fig. 10) from a 2.4 Myr period to a 2 Myr period. If the 405 kyr g2 − g5 signal is clearly present in the geological data, this then becomes a macroscopic feature that can be detectable. A local timescale can indeed be established using the 405 kyr signal, and the modulation period of this signal should be the g4 − g3 term. The transition is then obtained as a transition from six periods per beat to five periods per beats. Such geological data could then be used to discriminate between the various La2010 solutions (Fig. 13). It is therefore important to search for good sedimentary sections where the 405 kyr signal is clearly determined.
 |
Fig. 13 Argument (in radians) related to g4 − g3 − 2.664 T versus T (in Myr) for various orbital solutions (top). Argument (in radians) related to s4 − s3 − 2 × 2.664 T versus T (in Myr) for various orbital solutions (bottom). |
9. Stability of the g2–g5 405 kyr cycle
As stressed above, the g2 − g5 405 kyr argument is of particular importance to a long-term geological calibration, as it is present in many sedimentary records and its good stability (Laskar 1990) allows one to use it as a reference timescale. This argument is indeed visible in many sedimentary records of the Early Mesozoic (Olsen & Kent 1999, and references therein). As in Laskar et al. (2004), we tested the stability of this argument over the full period of our integrations, that is over 250 Myr by comparing its evolution with all retained La2010 solutions and La2004 (14). The present values of g2 − g5 do not differ significantly from the value of La2004 (Laskar et al. 2004). The frequency g2 − g5 is thus kept to its La2004 value 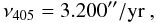 (4)which corresponds exactly to a period
(4)which corresponds exactly to a period 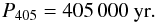 (5)As seen in Fig. 14, the maximum deviation obtained by comparing all solutions is about 2π over 250 Myr, which corresponds to a full cycle of 405 kyr after 250 Myr, as was already written in (Laskar et al. 2004).
(5)As seen in Fig. 14, the maximum deviation obtained by comparing all solutions is about 2π over 250 Myr, which corresponds to a full cycle of 405 kyr after 250 Myr, as was already written in (Laskar et al. 2004).
 |
Fig. 14 405 kyr term in eccentricity. Maximum difference (in radians) of the argument θg2 − g5(t) − θg2 − g5(0) of g2 − g5 in all solutions La2004, La2010a,b,c,d with respect to the linear approximation θ0(t) = 3.200′′ t where t is in yr. |
10. Discussion and future work
The new orbital solutions of the Earth that are presented here can be used for paleoclimate computations over 50 Myr. Beyond that time interval, the precision of the solution cannot be guaranteed but we nevertheless provide the solution over 250 Myr on our Web site4 and at the CDS as reference, and for possible use, with caution, over the full Paleogene period (up to 65 Myr).
To allow practitioners to test the stability of the solution and the deduced calibration, we decided to provide the four solutions that have been discussed here, La2010a,b,c,d, where La2010a is the nominal solution.
It should be stressed that La2010a is chosen as the nominal solution because of its higher numerical accuracy, but there is no strong evidence that La2010a is more appropriate than the other solutions. Before −50 Myr, they all behave in practically identical ways. Beyond −50 Myr, the robustness of a fit could be tested by changing the solutions. Alternatively, in the presence of convincing geological records, one may conclude that one solution is more probable than another. This will be in some sense a feedback from geology to celestial mechanics.
In contrast to Laskar et al. (1993a) and Laskar et al. (2004), we have provided here only the eccentricity solution. Although the model for the Earth rotational evolution has been improved, the main uncertainty linked to the evolution of the tidal dissipative effect in the past is still the main unknown parameter for the precession and obliquity evolution. We thus do not believe that a new rotational solution would provide more insight than La2004, unless a full analysis of the geophysical effects were made, in confrontation with the geological records, an analysis that is beyond the scope of the present paper. We thus refer to La2004 for precession and obliquity.
In addition, we soon plan to release a full high-precision, non-averaged solution of the rotation and precession of the Earth over 1 Myr, as computed from the INPOP model.
After the publication of the La2004 solution (Laskar et al. 2004), our goal was to search for an improved solution that is valid over the full cenozoic era. We must say that we have not reached this goal. Although the present solution represents a significant improvement with respect to La2004, it is only valid over about 50 Myr.
The main improvement in the present solution was to use a 1 Myr version of the INPOP ephemeris (Fienga et al. 2008, 2009) to fit the initial conditions and parameters of the model. As future versions of INPOP appear (Fienga et al. 2011), we will be able to evaluate more accurately the true accuracy of our model.
At this point, it is still difficult to say whether it will be possible to obtain a precise solution over 65 Myr for the eccentricity of the Earth. In the present solution, we used a more complex model, by adding the five main asteroids in the orbital computation, but this also added some instabilities to the system, and although we increased the numerical accuracy of the algorithm by using extended precision instead of double precision, we were unable to reach a higher numerical accuracy than in La2004. We intend to improve on this point, and increase the numerical accuracy of the solution, as we would like to be sure that the numerical precision is not the limiting factor in the final precision of the solution. To do so, we will also need to improve at the same time on the speed of the algorithm, as the present version of our nominal solution La2010a took nearly 18 months to complete.
With the present solution (La2010), we have reached the limit of the observational data, and the limit of predictability for a precise solution of the orbital evolution of the Earth. We have thus decided to provided several possible outcomes instead of a single one as usual. The solutions La2010a,b,c,d are all available on our Web site5 and at the CDS.
Practitioners can thus check which of these solutions more closely fits their data beyond −50 Myr. Moreover, it becomes clear that the long periodic terms related to g4 − g3 in the eccentricity, which also appears as a modulation of the 405 kyr term in the eccentricity, and the equivalent s4 − s3 term in the inclination, are some key macroscopic features of the orbital solution that are imprinted in the geological record. Their precise recovery can thus provide some clues about the past chaotic diffusion of the orbital motion of the Earth.
The secular frequencies are the frequencies of the slow precessing motion of the orbit in its plane (precession of perihelion) and of the slow motion of the plane of the orbit in space (precession of the node). These slow precessing motions are due to the gravitational perturbations of the other planets in the Solar System.
Acknowledgments
This work was supported by ANR-ASTCM. It benefitted from support from INSU-CNRS, PNP-CNRS, and CS, Paris Observatory.
References
- Bills, B. G. 1994, Geophys. Res. Lett., 21, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Boué, G., & Laskar, J. 2006, Icarus, 185, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S., & Lindzen, R. S. 1970, Atmospheric Tides [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003, Icarus, 163, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Laskar, J., & de Surgy, O. N. 2003, Icarus, 163, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Darwin, G. H. 1880, Philos. Trans. R. Soc. London, 171, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Laskar, J., Morley, T., et al. 2009, A&A, 507, 1675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fienga, A., Manche, H., Kuchynka, P., Laskar, J., & Gastineau, M. 2011, Planetary and Lunar ephemerides, INPOP10A [arXiv:1011.4419v1] [Google Scholar]
- Folkner, W.M., Williams, J.G., Boggs, D.H., 2008, in The Planetary and Lunar Ephemeris DE 421, JPL IOM 343R-08-003 [Google Scholar]
- Forte, A. M., & Mitrovica, J. X. 1997, Nature, 390, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Gradstein, F. M., Ogg, J. G., & Smith, A. G. 2004, A Geologic Time Scale, 589p (Cambridge, New York, Melbourne: Cambridge University Press) [Google Scholar]
- Hays, J. D., Imbrie, J., & Shackleton, N. J. 1976, Science, 194, 1121 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hilgen, F., Kuiper, K., & Lourens, L. 2010, Earth and Planetary Sci. Lett., 300, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Ito, T., Masuda, K., Hamano, Y., & Matsui, T. 1995, J. Geophy. Res., 100 [Google Scholar]
- Jovane, L., Sprovieri, M., Coccioni, R., et al. 2010, Earth and Plan. Sci. Lett., 298, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchynka, P., Laskar, J., Fienga, A., & Manche, H. 2010, A&A, 514, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, J. 1988, A&A, 198, 341 [NASA ADS] [Google Scholar]
- Laskar, J. 1989, Nature, 338, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1992, IAU Symp., 1, 152 [Google Scholar]
- Laskar, J. 1999, Roy. Soc. London Philos. Trans. Ser. A, 357, 1735 [Google Scholar]
- Laskar, J., & Robutel, P. 2001, Celestial Mechanics and Dynamical Astronomy, 80, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., & Gastineau, M. 2009, Nature, 459, 817 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Laskar, J., Quinn, T., & Tremaine, S. 1992, Icarus, 95, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Joutel, F., & Boudin, F. 1993a, A&A, 270, 522 [NASA ADS] [Google Scholar]
- Laskar, J., Joutel, F., & Robutel, P. 1993b, Nature, 361, 615 [Google Scholar]
- Laskar, J., Robutel, P., Joutel, F., et al. 2004, A&A, 428, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levrard, B., & Laskar, J. 2003, Geophy. J. Inter., 154, 970 [Google Scholar]
- Lourens, L. J., Wehausen, R., & Brumsack, H. J. 2001, Nature, 409, 1029 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lourens, L., Hilgen, F., Laskar, J., Shackleton, N., & Wilson, D. 2004, in A Geological Timescale 2004, ed. F. Gradstein, J. Ogg, & A. Smith, 409 [Google Scholar]
- Lourens, L. J., Sluijs, A., Kroon, D., et al. 2005, Nature, 435, 1083 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lumb, L. I., & Aldridge, K. D. 1991, J. Geomag. Geoel., 43, 93 [Google Scholar]
- Mignard, F. 1979, The Moon and the Planets, 20, 301 [Google Scholar]
- Milankovitch, M. 1941, Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitenproblem (Spec. Acad. R. Serbe, Belgrade) [Google Scholar]
- Olsen, P. E., & Kent, D. V. 1996, Palaeogeography, Palaeoclimatology, Palaeoecology, 122, 1 [CrossRef] [Google Scholar]
- Olsen, P. E., & Kent, D. V. 1999, Roy. Soc. London Philos. Trans. Ser. A, 357, 1761 [NASA ADS] [CrossRef] [Google Scholar]
- Pälike, H., & Hilgen, F. 2008, Nature Geoscience, 1, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Pälike, H., Laskar, J., & Shackleton, N. J. 2004, Geology, 32, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Pälike, H., Norris, R. D., Herrle, J. O., et al. 2006, Science, 314, 1894 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Poincaré, H. 1910, Bull. Astron., 27, 321 [Google Scholar]
- Quinn, T. R., Tremaine, S., & Duncan, M. 1991, AJ, 101, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Rochester, M. G. 1976, Geophys. J. R. Astron. Soc., 46, 109 [Google Scholar]
- Rubincam, D. P. 1990, Science, 248, 720 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rubincam, D. P. 1995, Paleoceanography, 10, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, P., & Tremaine, S. 1994, AJ, 108, 1962 [NASA ADS] [CrossRef] [Google Scholar]
- Soffel, M., Klioner, S. A., Petit, G., et al. 2003, AJ, 126, 2687 [NASA ADS] [CrossRef] [Google Scholar]
- Standish, E. M. 1998a, JPL Interoffice Memorandum, 98 [Google Scholar]
- Standish, E. M. 1998b, JPL Planetary and Lunar Ephemerides [Google Scholar]
- Sussman, G. J., & Wisdom, J. 1992, Science, 257, 56 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dam, J. A., Aziz, H. A., Sierra, M. Á. Á., et al. 2006, Nature, 443, 687 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Varadi, F., Runnegar, B., & Ghil, M. 2003, AJ, 592, 620 [Google Scholar]
- Volland, H. 1978, Earth’s Rotation from Eons to Days, 62 [Google Scholar]
- Westerhold, T., Röhl, U., Laskar, J., et al. 2007, Paleoceanography, 22, 2201 [NASA ADS] [CrossRef] [Google Scholar]
- Westerhold, T., Röhl, U., Raffi, I., et al. 2008, Palaeogeography, Palaeoclimatology, Palaeoecology, 257, 377 [CrossRef] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Zachos, J. C., Shackleton, N. J., Revenaugh, J. S., Pälike, H., & Flower, B. P. 2001, Science, 292, 274 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Maximum difference between INPOP06 and INPOP08 over 1 Myr (top). and between INPOP08 (computed in extended precision) and INPOP08d, a version of INPOP08 computed in double precision, over 1 Myr (bottom).
Maximum difference between the La2010 solutions and INPOP08 over 1 Myr. Top: maximum difference ast5AL08cx -INPOP08 over 1 Myr. Bottom: maximum difference ast5SL08ax -INPOP08 over 1 Myr.
Maximum difference between the La2010 solutions and INPOP06 over 1 Myr. Top: maximum difference ast5ALix -INPOP06 (both solutions are in extended precision) over 1 Myr. Bottom: maximum difference ast5ALh -INPOP06 over 1 Myr.
Frequency decomposition of z = eexpiϖ for the Earth on the time interval [ − 15, + 5] Myr (Laskar et al. 2004).
Main secular frequencies gi and si of La2004 and La2010a determined over 20 Ma for the four inner planets, and over 50 Ma for the five outer planets (in arcsec yr-1).
All Figures
 |
Fig. 1 Estimate of the numerical precision of the solutions La2010a,b,c. The estimate is obtained by the difference in the eccentricity of the Earth obtained with the integration of two solutions La2010x and La2010x* for x = a,b,c (see Table 2). |
| In the text | |
 |
Fig. 2 Differences in the eccentricity of the Earth-Moon barycenter over 1 Myr for various solutions as follows: a1 = La2004-INPOP08; a2 = La2010d-INPOP08; a3 =b3= La2010a – INPOP08; a4=INPOP06-INPOP08; b1 = La2010b – INPOP08; b2 = La2010c -INPOP06. We note that the vertical scale is enlarged ten times in the bottom plot. All solutions are compared to INPOP08. In the top figure, La2010d (a2) and INPOP06 (a4) are almost superimposed. This is because La2010d was adjusted over INPOP06. |
| In the text | |
 |
Fig. 3 Eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d). In the interval [ − 40: − 30] Myr, the four solutions are virtually identical, but before − 45 Myr, La2004 begins to depart significantly from the La2010 solutions. We have then plotted again the time interval [ − 50: − 40] Myr (bottom), removing La2004 to allow a clearer comparison of the La2010 solutions. Over this interval, these three solutions are very similar. |
| In the text | |
 |
Fig. 4 Eccentricity of the Earth for the solutions La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from −50 to −65 Myr. Although the various solution begin to diverge beyond 53 Ma, it is remarkable that the minima of eccentricity at 51.75 Ma, 56.25 Ma, and 58.25 Ma (in grey) correspond in all various solutions. |
| In the text | |
 |
Fig. 5 In a), we present the spectrum of the eccentricity over 65 Myr from the La2010a solution, limited to the interval [0,5′′/yr] (period > 259.2 kyr). In b), the same spectrum is plotted for a solution build with only the 5 main terms of z3 (Table 5). The main peaks are then easily identified and thus also the main peaks of the full eccentricity a). |
| In the text | |
 |
Fig. 6 Filtered eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from + 10 to − 30 Myr. The solution is filtered in the interval [0:2.2′′/yr], that is for periods in [589, + ∞ [ kyr. |
| In the text | |
 |
Fig. 7 Filtered eccentricity of the Earth for the solutions La2004 (L04), La2010a (L10a), La2010b (L10b), La2010c (L10c), and La2010d (L10d) from − 30 to − 70 Myr. The solution is filtered in the interval [0:2.2′′/yr], that is for periods in [589, + ∞ [ kyr. |
| In the text | |
 |
Fig. 8 Filtered eccentricity around the 405 kyr period for La2010a. In red is ea, the filtered eccentricity in the band [2.2,4.3]′′/yr ( [301,589] kyr period), while eb, the filtered eccentricity in the band [0,1.1]′′/yr ( period > 1.18 Myr) is plotted in blue. The opposite (in pink) of the maximum enveloppe of ea (in green) nearly coincides with eb. |
| In the text | |
 |
Fig. 9 ea + eb (see Fig. 8) for the La2010a solution is plotted in red. Its minimum are in phase with eb, the filtered eccentricity in the band [0,1.1]′′/yr ( period > 1.18 Myr) is plotted in blue. |
| In the text | |
 |
Fig. 10 Filtered eccentricity in the band [0,1.1]′′/yr (period > 1.18 Myr) for La2004 and La2010a,b,c,d. |
| In the text | |
 |
Fig. 11 Argument (in radians) related to g4 − g3 − 2.664 T versus T (in Myr) for La2010a (top). Argument (in radians) related to s4 − s3 − 2 × 2.664 T versus T (in Myr) for La2010a (bottom). |
| In the text | |
 |
Fig. 12 Resonant arguments (in radians versus time in Myr) σ = (g1 − g5) − (s1 − s2) (top) and θ = (s4 − s3) − 2(g4 − g3) (middle and bottom) for the different solutions La2004, La2010a,b,c,d. In the bottom plot, θ is displayed on a greater scale. One can see that the La2010 solutions are very close up to 50 Myr. |
| In the text | |
 |
Fig. 13 Argument (in radians) related to g4 − g3 − 2.664 T versus T (in Myr) for various orbital solutions (top). Argument (in radians) related to s4 − s3 − 2 × 2.664 T versus T (in Myr) for various orbital solutions (bottom). |
| In the text | |
 |
Fig. 14 405 kyr term in eccentricity. Maximum difference (in radians) of the argument θg2 − g5(t) − θg2 − g5(0) of g2 − g5 in all solutions La2004, La2010a,b,c,d with respect to the linear approximation θ0(t) = 3.200′′ t where t is in yr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


