| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A173 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201731659 | |
| Published online | 07 August 2018 | |
Abundances of Mg and K in the atmospheres of turn-off starsin Galactic globular cluster 47 Tucanae⋆
1
Institute of Theoretical Physics and Astronomy, Vilnius University, Saul˙etekio al. 3, Vilnius, 10222, Lithuania
e-mail: algimantas.cerniauskas@tfai.vu.lt
2
Department of Astronomy and Astronomical Observatory, Odessa National University and Isaac Newton Institute of Chile Odessa branch, Shevchenko Park, 65014 Odessa, Ukraine
3
Crimean Astrophysical Observatory, Nauchny
298409, Crimea
4
GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92190 Meudon, France
5
Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
6
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received:
27
July
2017
Accepted:
4
April
2018
Aims. We determined abundances of Mg and K in the atmospheres of 53 (Mg) and 75 (K) turn-off (TO) stars of the Galactic globular cluster 47 Tuc. The obtained abundances, together with those of Li, O, and Na that we had earlier determined for the same sample of stars, were used to search for possible relations between the abundances of K and other light elements, Li, O, Na, and Mg, as well as the connections between the chemical composition of TO stars and their kinematical properties.
Methods. Abundances of Mg and K were determined using archival high resolution VLT FLAMES/GIRAFFE spectra, in combination with the one-dimensional (1D) non-local thermodynamic equilibrium (NLTE) spectral synthesis methodology. Spectral line profiles were computed with the MULTI code, using 1D hydrostatic ATLAS9 stellar model atmospheres. We also utilized three-dimensional (3D) hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres for computing 3D–1D LTE abundance corrections for the spectral lines of Mg and K, in order to assess the influence of convection on their formation in the atmospheres of TO stars.
Results. The determined average abundance-to-iron ratios and their root mean square variations due to star-to-star abundance spreads were 〈[Mg/Fe]〉1D NLTE = 0.47 ± 0.12, and 〈[K/Fe]〉1D NLTE = 0.39 ± 0.09. Although the data suggest the possible existence of a weak correlation in the [K/Fe]–[Na/Fe] plane, its statistical significance is low. No statistically significant relations between the abundance of K and other light elements were detected. Also, we did not find any significant correlations or anti-correlations between the [Mg/Fe] and [K/Fe] ratios and projected distance from the cluster center. Similarly, no relations between the absolute radial velocities of individual stars and abundances of Mg and K in their atmospheres were detected. The 3D–1D abundance corrections were found to be small (≤0.1 dex) for the lines of Mg and K used in this study, thus indicating that the influence of convection on their formation is small.
Key words: globular clusters: individual: NGC 104 / stars: late-type / stars: atmospheres / stars: abundances / techniques: spectroscopic / convection
© ESO 2018
1. Introduction
During the last decade studies of Galactic globular clusters (GGCs) opened a new chapter when it was discovered that GGCs may consist of multiple stellar generations. The first strong evidence in favor of this paradigm came from spectroscopic observations, which lead to the discovery of large star-to-star variation in the light element abundances within a given GGC (Kraft 1994; Gratton et al. 2004), and, then, to the detection of various (anti-)correlations between the abundances of these elements, such as Na–O (Carretta et al. 2009a) and Li–O (Pasquini et al. 2005; Shen et al. 2010) correlations, and Na–Li (Bonifacio et al. 2007) and Mg–Al (Carretta et al. 2009a) anti-correlations. It is worth mentioning that these abundance trends are not seen in Galactic halo field stars. Further photometric observations have revealed the existence of multiple subsequences in the cluster color-magnitude diagrams (CMDs), all the way from the main sequence (MS) and up to the tip of the red giant branch (RGB; Piotto et al. 2007; Milone et al. 2012). All these findings suggest that stars in the GGCs may have formed during two or more star formation episodes (see, e.g., Gratton et al. 2012), thus contradicting the earlier notion that GGCs are perfect examples of simple stellar populations.
The most popular theories are that either massive asymptotic giant branch (AGB) stars (e.g., Ventura et al. 2001) or fast-rotating massive stars (e.g., Decressin et al. 2007) could have enriched the second-generation stars in Na and Al, and depleted them in O and Mg. Other scenarios, such as enrichment by binary stars (de Mink et al. 2009) and early disk accretion (Bastian et al. 2013) have been discussed, too. However, none of them can explain, for example, all observed abundance (anti-)correlations simultaneously (see discussion in, e.g., Bastian et al. 2015). From the theoretical point of view, new ideas regarding the possible polluters are needed. From the observational side, it would be desirable to identify new chemical elements that would allow us to discern between the different already proposed self-enrichment scenarios of the GGCs or, possibly, help to suggest new ones.
Potentially, new clues in this context may come from the investigations of potassium abundance. Since K is synthesized mainly via oxygen burning in high-mass stars, it is unlikely that the atmospheric K abundance would undergo any appreciable changes during the course of the stellar evolution of the low-mass stars in the GGCs. Mucciarelli et al. (2012) presented an analysis of RGB stars in NGC 2419 ([Fe/H] = −2.09) in which the first hints of K–Mg anti-correlation and bimodal distribution of [Mg/Fe] ratio were detected. The authors also confirmed an unusually large (≈2 dex) spread and depletion (to ≈−1 dex) in the magnesium abundance. A more recent study of NGC 2808 ([Fe/H] = −1.1) by Mucciarelli et al. (2015) has revealed the existence of statistically significant correlations of the [K/Fe] abundance ratio with [Na/Fe] and [Al/Fe], and anti–correlations with [O/Fe] and [Mg/Fe]. A fraction of the stars in both clusters is strongly enhanced in helium, with Y = 0.34 in NGC 2808 (Marino et al. 2014) and Y = 0.42 in NGC 2419 (di Criscienzo et al. 2011). These values are much higher than those observed in other GGCs (Milone et al. 2014). Mucciarelli et al. (2015) suggested a self-enrichment model proposed by D’Ercole et al. (2012) as one of the possible explanations of [K/Fe]–[Mg/Fe] anti-correlation. In this scenario, Mg-poor/K- rich (extreme population) stars formed from the ejecta of AGB and super-AGB stars. However, this scenario still requires some fine tuning in the nuclear reaction cross-sections and burning temperatures to explain the observed trends satisfactorily.
In their recent study of 144 RGB stars in 47 Tuc, Mucciarelli et al. (2017) claimed a detection of a mild [K/Fe]–[Na/Fe] correlation and [K/Fe]–[O/Fe] anti-correlation. This is in contrast with the results of our recent study of Na, Mg, and K abundances in the atmospheres of RGB stars in 47 Tuc, where we found no statistically significant relations between either the abundances of different elements, or the abundances and kinematical properties of the cluster stars (Černiauskas et al. 2017, hereafter Paper I). It is conceivable, however, that non-detection in our case could be due to a smaller sample of RGB stars studied: 32 in our work versus 144 in the study of Mucciarelli et al. (2017). Apart from these two studies, the only other investigation of K abundances in 47 Tuc was done by Carretta et al. (2013) who determined K abundances in three turn-off (TO) and nine subgiant branch (SGB) stars. Obviously, the sample size used in the latter study was too small to search for possible relations between the elemental abundances among little-evolved stars.
Given this somewhat ambiguous situation, investigation of K abundances in the atmospheres of TO stars in 47 Tuc could be very interesting, especially if based on a larger sample of stars than that used by Carretta et al. (2013). It is well know that the cores of unevolved low-mass stars do not reach temperatures high enough for Ne−Na and/or Mg−Al cycles to operate. Moreover, their convective envelopes are not deep enough to bring up to the surface the products of proton-capture reactions. Therefore, the atmospheres of these stars should have retained their primordial chemical composition, unless their atmospheres have been contaminated by accreted chemical elements synthesized in other stars. In the present study we therefore determine abundances of Mg and K in the atmospheres of 53 and 75 (TO) stars in 47 Tuc, respectively (abundances of both elements were obtained in 44 stars). We then use this data to search for possible relations between the abundances of K and Mg, and those of other light elements, Li, O, and Na (with their abundances taken from Dobrovolskas et al. 2014), as well as relations between the elemental abundances and kinematical properties of TO stars.
The paper is structured as follows. In Sect. 2 we present spectroscopic data used in our study and outline the procedures used to determine abundances of Mg and K using one-dimensional (1D) non-local thermodynamic equilibrium (NLTE) methodology. Analysis and discussion of the obtained results is presented in Sect. 3, while the main findings of this paper and final conclusions are outlined in Sect. 4.
2. Methodology
Abundances of Mg and K were determined using 1D hydrostatic ATLAS9 model atmospheres and 1D NLTE abundance analysis methodology. Additionally, we also utilized three-dimensional (3D) hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres to compute the 3D–1D abundance corrections using the assumption of LTE (see Sect. 2.3.3 for details). This was done in order to study the importance of convection in the formation of the spectral lines of Mg I and K I used in this study, though the obtained corrections were not applied to determine 3D-corrected elemental abundances (see Sect. 2.3.3 for details). A brief description of all steps involved in the abundance analysis is provided below.
2.1. Spectroscopic data
In this work we used the same sample of TO stars of 47 Tuc as in D’Orazi et al. (2010) and Dobrovolskas et al. (2014). We note that in the two previous studies abundances of Mg and K in the atmospheres of these stars were not determined.
In the abundance analysis we utilized high-resolution archival VLT FLAMES/GIRAFFE spectra of TO stars that were reduced by and used in Dobrovolskas et al. (2014, programme ID: 081.D-0287(A), PI: Shen). The spectra were obtained in Medusa mode using HR 18 setup (746.8–788.9 nm, R = 18400). In total, 116 fibers were dedicated to target stars and 16 were used for sky spectra. The continuum normalization procedure was completed using IRAF (Tody 1986) continuum task (see Dobrovolskas et al. 2014, for details).
Effective temperatures and surface gravities of the sample TO stars were taken from Dobrovolskas et al. (2014). The former were determined by fitting the wings of Hα line profiles, while the latter were obtained using the classical relation between the surface gravity, mass, effective temperature, and luminosity.
2.2. Model atmospheres
We used two types of 1D hydrostatic model atmospheres, ATLAS9 and LHD, and 3D hydrodynamical CO5BOLD model atmospheres:
-
ATLAS9: for the atmospheric parameters of each individual sample star we computed a 1D hydrostatic model atmosphere using the ATLAS9 code (Kurucz 1993; Sbordone 2005). The model atmospheres were calculated using ODFNEW [M/H] = −1.0 opacity tables (Castelli & Kurucz 2003), with the α−element enhancement of [α/Fe] = +0.4. The mixing length parameter was set to αMLT = 1.25 and the overshooting was switched off. These model atmospheres were used in the 1D NLTE abundance analysis of Mg and K for synthesizing spectral line profiles with the MULTI code (see Sect. 2.3);
-
LHD: the 1D hydrostatic LHD models were computed using the LHD model atmospheres code (Caffau et al. 2008), which utilises chemical composition, equation of state, and opacities identical to those used in the 3D hydrodynamical CO5BOLD model atmospheres (see below). In order to compute the 3D–1D abundance corrections for magnesium and potassium (see Sect. 2.3.3), atmospheric parameters of the LHD models were matched to those of the CO5BOLD model atmospheres;
-
CO5BOLD: the 3D hydrodynamical CO5BOLD model atmosphere code solves time-dependent equations of hydrodynamics and radiation transfer on a Cartesian grid (Freytag et al. 2012). We used four 3D hydrodynamical model atmospheres from the CIFIST grid (Ludwig et al. 2009), which we utilised for computing the 3D–1D abundance corrections. Atmospheric parameters of the CO5BOLD models are provided in Table 1. The CO5BOLD and LHD models were computed using an identical chemical composition, equation of state, opacities, and radiative transfer scheme.
Parameters of the 3D hydrodynamical CO5BOLD model atmospheres used in this work.
2.3. Determination of 1D NLTE abundances of Mg and K
The 1D NLTE abundances of Mg and K were determined using the MULTI code (Carlsson 1986) modified by Korotin et al. (1999). The code computes theoretical line profiles using 1D ATLAS9 model atmospheres and a model atom of a given chemical element (Sect. 2.3.1). Atomic parameters of the spectral lines that were used in our study are provided in Table 2. In the case of Mg, line parameters were taken from the Vienna atomic line database (VALD-3) database (Piskunov et al. 1995; Kupka et al. 2011). For K, log gf value was taken from Morton (1991) while the line broadening constants are from VALD-3. We stress that in the case of K, the NLTE approach in the abundance analysis is critical since for this element 1D NLTE–LTE abundance corrections are typically very large, reaching from −0.5 to −0.7 dex (Takeda et al. 2002). Besides, they tend to be larger for the latetype stars and increase with decreasing metallicity (Andrievsky et al. 2010).
Abundances of each element were determined by fitting theoretical line profiles to those observed in a given TO star. A typical example of the obtained best fit is shown in Fig. 1. During the fitting procedure, we used a fixed microturbulence velocity of 1.0 km s−1 for all sample stars, while the macroturbulence velocity was varied during each iteration as a free parameter to obtain the best match to the observed line profile. The macroturbulence velocities of stars in our sample were in the range of 1–5 km s−1. A fixed value of [Fe/H]1D LTE = −0.76 from Carretta et al. (2009a) was used throughout this study. We verified that the determined abundances show no dependence on the effective temperature (Fig. 2).
 |
Fig. 1. Typical fits of synthetic Mg and K line profiles (solid blue lines) to those in the observed GIRAFFE spectrum (filled red circles) of the target TO star 47Tuc45982 (Teff = 5707 K, log g = 4.00). We also provide the abundances determined from each observed line, A(X), together with their errors (see Sec. 2.3.4). Thin gray lines show synthetic line profiles computed with the abundances altered by ±0.2 dex. |
 |
Fig. 2. [Mg/Fe] (top) and [K/Fe] (bottom) abundance ratios determined in the sample of TO stars in 47 Tuc and plotted versus the effective temperature of individual stars. Error bars show uncertainties that were computed as described in Sect. 2.3.4. |
Atomic parameters of the spectral lines used in the abundance determinations of Mg and K. Natural (γ
rad), Stark 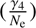 , and van der Waals
, and van der Waals 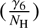 broadening constants computed using classical prescription are provided in the last three columns.
broadening constants computed using classical prescription are provided in the last three columns.
2.3.1. Model atoms of Mg and K
The model atoms of Mg and K that were used in our study are briefly described below; for more details see Paper I and references therein. In the case of Mg, we used the model atom from Mishenina et al. (2004). It consisted of 84 levels of Mg I, 12 levels of Mg II, and the ground state of Mg III. In the computation of departure coefficients, radiative transitions between the first 59 levels of Mg I and ground level of Mg II were taken into account.
The model atom of K was taken from Andrievsky et al. (2010) and consisted of 20 levels of K I and the ground level of K II. In addition, another 15 levels of K I and seven levels of K II were used to ensure particle number conservation. The total number of bound-bound radiative transitions taken into account was 62 (see Andrievsky et al. 2010, for further details).
2.3.2. 1D NLTE abundances of Mg and K in the atmospheres of TO stars in 47 Tuc
Before the determination of Mg and K abundances, Mg I and K I lines in the spectra of all stars studied were carefully inspected for blends and/or possible contamination by telluric lines (to remind, we had only one spectral line per element available for the abundance determination in the spectrum of each TO star). This inspection revealed significant star-to-star variation in terms of the line quality. In order to take this into account, we grouped Mg I and K I lines into three classes according to their quality, the latter determined by visual inspection using the following criteria:
-
A-class: strong or moderately strong lines with well-resolved line profiles;
-
B-class: lines that are moderately blended with telluric lines, or lines that were insufficiently resolved in the line wings;
-
C-class: lines with weak and/or poorly defined profiles, or significantly blended lines.
These quality flags are marked by different colors in Fig. 3. The line of Mg I and the line of K I in the spectrum of each star were always assigned to their individual quality classes. As a consequence, even in the spectrum of the same star, Mg I and K I lines could belong to different quality classes, for example, Mg line to A-class, K line to C-class. This explains why both Mg and K could not be determined in all the stars, because for some stars only one of the two lines was suitable for abundance determination.
 |
Fig. 3. Abundance-to-iron ratios of Li, O, Na, Mg, and K in the sample of TO stars, shown in various abundance-abundance planes. Colors on the left and right sides of the symbols correspond to the quality (symbols denoting different quality classes are shown in the top-left panel) of spectral lines used to determine abundances of the light elements in a given star plotted on the y and x axes, respectively (see Sect. 2.3.2 for details). The values of two-tailed probabilities, p, computed using Pearson’s parametric correlation coefficients (with and without abundance errors, p witherrors and p withouterrors, respectively), Spearman’s, and Kendall’s non-parametric rank-order correlation coefficients are given in the corresponding panels (see Sect. 3.2). |
To verify that the spectral lines used in our study are not seriously affected by telluric lines, such as telluric A band in the vicinity of the K I 769.89 nm line, we used (a) telluric lines identified in the spectrum of fast-rotating O6.5 III spectral type star HD94963, which was taken from the UVES POP spectral library (Bagnulo et al. 2003); and (b) a synthetic spectrum of the atmospheric transmission computed with the TAPAS tool (Bertaux et al. 2014) for the dates when the observations were done.
The 1D NLTE abundances of Mg and K were then determined by fitting synthetic spectral line profiles to those observed in the spectra of TO stars.
The iron abundance among the stars in 47 Tuc is very homogeneous: from 147 stars observed with GIRAFFE Carretta et al. (2009a) found [Fe/H] = −0.743 ± 0.003 (stat) ± 0.026 (syst) and from 11 stars observed with UVES, Carretta et al. (2009b) determined [Fe/H] = −0.768 ± 0.016 (stat) ± 0.031 (syst), in both cases with the assumed iron abundance A(Fe) = 7.54 from Gratton et al. (2003). In our GIRAFFE spectra we can measure about 20 Fe I lines, which are of poor quality, due to the low signal-to-noise ratios (S/N) of the spectra and contamination from telluric lines. As a consequence, the line to line scatter is 0.2 dex or larger for our stars. We therefore consider it more robust to assume for each star the mean Fe abundance of the cluster that we take as the average of the measurements from the UVES spectra by Carretta et al. (2009b) and the GIRAFFE spectra by Carretta et al. (2009a): [Fe/H] = −0.76. Solar Mg and K abundances, 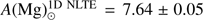 and
and 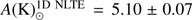 , were determined in this work (see Appendix A). The 1D NLTE abundance ratios of [Li/Fe], [O/Fe], and [Na/Fe] were taken from Dobrovolskas et al. (2014) where authors determined them using the same [Fe/H] value as utilized in the present study. More information about the procedure of Li, O, and Na abundance determination see Sects. 5.2.2, 5.2.3, and 5.3 in Dobrovolskas et al. (2014).
, were determined in this work (see Appendix A). The 1D NLTE abundance ratios of [Li/Fe], [O/Fe], and [Na/Fe] were taken from Dobrovolskas et al. (2014) where authors determined them using the same [Fe/H] value as utilized in the present study. More information about the procedure of Li, O, and Na abundance determination see Sects. 5.2.2, 5.2.3, and 5.3 in Dobrovolskas et al. (2014).
The determined average element-to-iron abundance ratios in the sample of TO stars are 〈[Mg/Fe]〉1D NLTE = 0.47 ± 0.12 (53 objects) and 〈[K/Fe]〉1D NLTE = 0.39±0.09 (75 objects; numbers after the ± sign are root mean square (RMS) abundance variations due to star-to-star scatter). In Fig. 3 we show [K/Fe], [Mg/Fe], [Na/Fe], [O/Fe], and [Li/Fe] abundance ratios plotted in various abundance-abundance planes.
2.3.3. 3D–1D abundance corrections for Mg and K
To assess the role of convection in the formation of Mg and K lines in the atmospheres of TO stars, we used 3D hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres (Sect. 2.2). The two types of model atmospheres were used to compute 3D–1D LTE abundance corrections for the spectral lines of Mg I and K I utilized in our study (corrections for the lines of O I and Na I were computed earlier in Dobrovolskas et al. 2014). Spectral line synthesis computations were carried out with the Linfor3D spectral synthesis package.1
The procedure used to compute the 3D–1D LTE abundance corrections, Δ3D−1D LTE, was identical to that utilized in Paper I. Since the abundance corrections of Mg and K showed little variation with the spectral line strength, in case of each element they were computed for two values of line equivalent width, W (corresponding to “weak” and “strong” spectral lines) that bracketed the range measured in the observed spectra of the sample TO stars. Equivalent widths used for the weakest lines were 4 pm and 15 pm, while for the strongest lines we used 7 pm and 18 pm, in the case of Mg, and K, respectively. Microturbulence velocity in the 3D model atmosphere was determined by applying Method 1 described in Steffen et al. (2013) and was subsequently used in the spectral line synthesis with the LHD model atmospheres (see Paper I for details).
The obtained 3D–1D LTE abundance corrections, Δ3D−1D LTE, are provided in Table 3. For both lines, they do not exceed 0.09 dex, which allows us to conclude that the influence of convection on the formation of Mg I and K I lines in the atmospheres of TO stars is minor.
We note that the obtained abundance corrections were not used for obtaining 3D-corrected abundances which, in principle, could be done by adding the 3D–1D LTE corrections to the determined 1D NLTE abundances of Mg and K. Such a procedure was avoided for two reasons. First, abundances obtained in this way would be generally different from those that would be obtained using the full 3D NLTE approach (see, e.g., Klevas et al. 2016). Second, the determined 3D–1D abundance corrections are small, therefore applying them would result in a small and nearly uniform shift of the abundances determined in all our sample stars. In fact, only in the case of K is the difference in the 3D–1D abundance corrections obtained for weak and strong lines somewhat larger, 0.06 dex, while for Mg this difference is only 0.01 dex. Our tests have shown that if these (small) 3D–1D abundance corrections are taken into account, our conclusions regarding the intrinsic abundance spreads and possible existence of different relations between, for example, the abundance of K and those of other light elements, remain unaltered (see Sect. 3).
3D–1D abundance corrections, Δ3D−1D LTE, computed for different strengths of Mg I and K I lines used in this work (see text for details).
2.3.4. Uncertainties in the determined abundances of Li, O, Na, Mg, and K
The uncertainties in the determined abundances occur for two main reasons: (i) inaccurate determination of atmospheric parameters (effective temperature, surface gravity, and microturbulence velocity); and (ii) uncertainties in the spectral line profile fitting (due to the choice of continuum level and inaccurate spectral line profile fit). Individual contributions to the total uncertainty in the determined abundances of O, Na, Mg, and K arising from the different error sources were estimated in the following way:2
σ(Teff) (Table 4, Col. 4). Effective temperatures that were used in our study were obtained in Dobrovolskas et al. (2014) using the Hα line profile fitting. The authors estimated that the uncertainty in their determined effective temperatures was ±100 K. We used this value to evaluate the influence of the uncertainty in Teff on the determined elemental abundances, σ(Teff);
σ(log g) (Table 4, Col. 5). The error in the surface gravity, log g, ±0.04 dex, was obtained from the individual components: error in the effective temperature (±100 K), error in luminosity (±0.03 L⊙), estimated from the photometric error in MV, and stellar mass (±0.01 M⊙, obtained from the isochrones). However, the error in surface gravity obtained in this way was, in our view, unrealistically low. Therefore, to estimate the resulting errors in the determined abundances, σ(log g), a more conservative error of ±0.1 dex was used;
σ(ξt) (Table 4, Col. 6). The error in the microturbulence velocity was estimated by evaluating the slope uncertainty in the [Fe/H]−W plane (W is line equivalent width). In this procedure we used six TO stars for which we were able to determine Fe abundance using individual Fe I lines. The average slope error determined in this way was ±0.001 dex pm−1, which corresponds to the error in ξt of ±0.29 km s−1. This value was used as a representative uncertainty in ξt to estimate the resulting abundance errors, σ(ξt);
σ(cont) (Table 4, Col. 7). The error in continuum determination was estimated in the same way as in Paper I, by measuring the dispersion at the continuum level in the spectral windows expected to be free of spectral lines, both of stellar and telluric origin (see Paper I for details). The continuum was then shifted by the amount of this uncertainty to obtain the resulting error in the determined abundance, σ(cont);
σ(fit) (Table 4, Col. 8). To estimate the errors in the line profile fitting, we computed RMS deviation between the observed and synthetic line profiles, which were converted into the uncertainties in the line equivalent width, W, and, finally, into the errors in the determined abundances, σ(fit) (see Paper I for details).
Individual errors were added in quadratures to obtain the total error in the determined abundances of O, Na, Mg, and K (Col. 9 in Table 4). The obtained total errors were further used in Sect 2.3.5 to estimate the possible intrinsic spreads in the obtained elemental abundances (see Sect. 2.3.5 for details). We stress that they only provide a lower limit for the uncertainties in the determined abundances since they do not account for various systematic uncertainties that are unavoidable in the abundance analysis procedure.
In the case of Li, the procedure was similar except for the following two points:
-
Li abundances in Dobrovolskas et al. (2014) were determined by using the A(Li)–W interpolation formula from Sbordone et al. (2010) and W was determined by fitting synthetic line profiles. Therefore, the line profile fitting errors were estimated by measuring RMS deviation between the observed and best-fit Gaussian profiles;
-
an error in the determined Li abundance stemming from the use of the interpolation formula was taken into account by using an estimated uncertainty of ±0.01 dex (Sbordone et al. 2010).
The determined uncertainties are provided in Table 4.
Errors in the abundances of Li, O, Na, Mg, and K determined in TO stars of 47 Tuc.
2.3.5. Maximum-likelihood testing of the intrinsic spread in elemental abundances
In order to estimate the size of the possible intrinsic spread in the 1D NLTE abundances of Li, O, Na, Mg, and K, we followed the procedure used in Paper I, which is based on the prescription of Mucciarelli et al. (2012, 2015) that the authors applied to study the K abundance spreads in NGC 2419 and NGC 2808, and, later, also in 47 Tuc (Mucciarelli et al. 2017). In the present work, the maximum-likelihood (ML) technique was utilized to evaluate the mean abundance ratio, 〈[A/B]〉, of elements A and B, as well as intrinsic spread, σint, in the determined [A/B] abundance ratio. Here, we used [Li/Fe], [O/Fe], [Na/Fe], [Mg/Fe], and [K/Fe] abundance ratios in the TO stars, with the former three taken from Dobrovolskas et al. (2014) and the latter two determined in this study. The obtained mean abundance ratio, 〈[Xi/Fe ]〉, and its uncertainty, as well as the total dispersion due to star-to-star abundance spread, σ[Xi/Fe], and the determined intrinsic abundance variation, 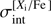 , in the abundance of element Xi are provided in Table 5.
, in the abundance of element Xi are provided in Table 5.
Results of the maximum-likelihood testing of the intrinsic spread in the abundances of Li, O, Na, Mg, and K.
3. Results and discussion
3.1. Average abundances and intrinsic abundance spreads in 47 Tuc
To our knowledge, the only studies of K abundance in 47 Tuc that have been carried out until now are those by Carretta et al. (2013) and Mucciarelli et al. (2017). The average 1D NLTE potassium-to-iron abundance ratios obtained by Carretta et al. (2013) in three TO and nine SGB stars were 〈[K/Fe]〉TO = 0.19 ± 0.07 and 〈[K/Fe]〉SGB = 0.12 ± 0.12, respectively (the error is RMS deviation due to star-to-star abundance variation). These values are compatible with the average 1D NLTE abundance ratios obtained using RGB stars in Paper I, 〈[K/Fe]〉RGB = 0.05 ± 0.13. However, the average potassium-to-iron abundance ratio determined using TO stars in the present study, 〈[K/Fe]〉TO = 0.39 ± 0.09, is 0.2 dex higher than that obtained using three TO stars by Carretta et al. (2013). We found that two stars are common to both samples. For them, the average abundance ratios obtained by Carretta et al. (2013) and determined in our study are 〈[K/Fe]〉TO = 0.18 and 〈[K/Fe]〉TO = 0.32 (the 1D NLTE–LTE abundance corrections and microturbulence velocities used for these stars in the two studies are nearly identical). When corrected for the difference in iron abundance used by Carretta et al. (2013, [Fe/H] = −0.65) and us (−0.76), the two values become nearly identical, with our [K/Fe] ratio being only 0.03 dex higher. We therefore conclude that the difference in [K/Fe] ratios obtained in the TO samples by Carretta et al. (2013) and us is mostly due to the different [Fe/H] values used to compute [K/Fe] ratios. In addition, a substantial difference in the sample sizes may also lead to slightly different average [K/Fe] ratios.
The sample-averaged K abundance obtained in the study of 144 RGB stars in 47 Tuc by Mucciarelli et al. (2017), 〈[K=Fe]〉1D NLTE = −0.12 ± 0.08, is somewhat lower than that determined in Paper I, 〈[K/Fe]〉RGB = 0.05 ± 0.13. This difference may be a result of the different microturbulent velocties used in the two studies: the sample-averaged value in Mucciarelli et al. (2017) is ξt = 1.66 km s−1 while in our analysis we used 1.5 km s−1. Our tests show that the difference of 0.16 km s−1 in ξt would lead to an ~0.13 dex decrease in the average [K/Fe] ratio determined in Paper I using RGB stars. With this taken into account, abundances obtained in the two studies would become very similar.
The origin of the significant difference between the average [K/Fe] ratios obtained by us in the TO and RGB stars, 0.34 dex, is not entirely clear, however. One possibility is that the value of microturbulent velocity used in our analysis of TO stars was in fact too low. We checked this using the six TO stars mentioned in Sect. 2.3.4 where we determined their iron abundances and microturbulence velocities using individual Fe I lines. The average microturbulence velocity obtained in this way for the six stars was ξt = 1.22 ± 0.07 km s−1, where error is RMS star-to-star variation. This value is significantly higher than the one used in the present study, 1.0 km s−1. With the higher value of ξt, the average abundance obtained in our sample of TO stars would become ≈0.1 dex lower. Still, this would still leave a difference of ≈0.25 dex between the values obtained using TO and RGB stars. On the other hand, it may also be that the microturbulence velocity used in our analysis of RGB stars, 1.5 km s−1, was slightly too low. For example, the ξt − log g calibration of Kirby et al. (2009) that was also used in Mucciarelli et al. (2017) would predict the average microturbulence velocity of 1.66 km s−1 for the gravity range of our RGB stars. Unfortunately, we could not obtain a reliable constraint on ξt in our RGB stars using spectroscopic means, due to an insuffcient number of iron lines available in their spectra (see Černiauskas et al. 2017). Nevertheless, the increase in ξt in both TO and RGB star samples would reduce the average abundance but the difference between two samples would remain almost the same.
Nevertheless, analysis of the six TO stars mentioned above revealed that star-to-star scatter in the determined microturbulence velocities was ≈±0.07 km s−1. In terms of the determined K abundances, this would lead to a scatter of ≈0.03 dex. Such star-to-star variation should have no detectable effect on various possible (anti-)correlations between the light element abundances. Therefore, our conclusions obtained in Sect. 3.2 below should remain unaffected.
The intrinsic abundance spreads of Li, O, Na, Mg, and K determined in our analysis are provided in Table 5. In the case of K, we find zero intrinsic spread, 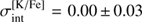 , identical to what was determined in Paper I using RGB stars,
, identical to what was determined in Paper I using RGB stars, 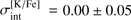 , and obtained by Mucciarelli et al. (2017),
, and obtained by Mucciarelli et al. (2017), 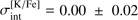 . While the intrinsic spread of [Mg/Fe] in TO stars is similar to that determined by us in RGB stars,
. While the intrinsic spread of [Mg/Fe] in TO stars is similar to that determined by us in RGB stars, 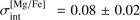 (Paper I), in the present work we obtain considerably larger intrinsic spread in [Na/Fe],
(Paper I), in the present work we obtain considerably larger intrinsic spread in [Na/Fe], 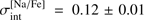 (TO) versus
(TO) versus 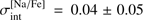 (RGB, Paper I). The latter difference may be due to the lower quality of the RGB spectra, which led to larger abundance errors obtained using RGB stars and, thus, smaller intrinsic abundance spread. An intrinsic scatter of similar size was obtained in the case of Li and O for TO stars,
(RGB, Paper I). The latter difference may be due to the lower quality of the RGB spectra, which led to larger abundance errors obtained using RGB stars and, thus, smaller intrinsic abundance spread. An intrinsic scatter of similar size was obtained in the case of Li and O for TO stars, 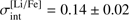 and
and 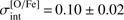 .
.
3.2. Relations between the abundances of light elements and evolutionary properties of TO stars in 47 Tuc
As in our previous study, Paper I, we used Student’s t-test to verify the validity of the null hypothesis, that is, that the Pearson’s correlation coefficient is equal to zero and, thus, there is no correlation in the abundance–iron and/or abundance–abundance planes (for simplicity, hereafter we will refer to the abundance ratios as abundances; we note that all abundance-to-iron ratios were obtained by scaling abundances of individual elements by the same constant value of [Fe/H]). For this, using each x − y dataset shown in the panels of Fig. 3, we computed the two-tailed probability, p, that the t-value in the given dataset could be equal or higher than its attained value when there is no correlation in the given x − y plane. In all panels Pearson’s correlation coefficients were computed by taking errors on both x and y axes into account. The obtained p-values are listed in Table 6.
Our results suggest that there is no statistically significant relations in the [K/Fe]−[O/Fe] (p = 0.99) and [K/Fe]−[Na/Fe] (p = 0.99) planes. Similarly, we find no evidence for statistically significant relations in the [K/Fe]−[Li/Fe] (p = 0.99), [K/Fe]−[Mg/Fe] (p = 0.99), and [K/Fe]−[Na/O] (p = 0.99) planes. We only found statistically significant relation in the [Mg/Fe]−[Na/Fe] plane (p < 0.0001), which may suggest that the null hypothesis can be formally rejected on a high significance level (see below, however)3.
In Fig. 4 we show the determined [Mg/Fe] and [K/Fe] abundance ratios plotted versus the normalized distance from the cluster center, r/rh, were r is the projected distance from the cluster center and rh is the half-light radius of 47 Tuc taken from Trager et al. (1993, rh = 174″). In both planes the obtained probabilities are p ≥ 0.55 indicating that there are no statistically significant relations between the two abundance ratios and the projected distance from the cluster center.
 |
Fig. 4. Abundance-to-iron ratios of Mg and K plotted versus the projected distance from the cluster center, r/rh (small filled circles; rh is a half-mass radius of 47 Tuc, rh = 174″, taken from Trager et al. 1993). Symbol color denotes quality (class) of the spectral lines from which the abundance was determined. Large open circles are average abundance ratios computed in non-overlapping Δr/rh = 1 wide distance bins (marked by the vertical dashed lines; RMS scatter of the abundance ratios in a given bin is shown by the black vertical error bars). Black solid lines are linear fits to the data of individual stars, with the p-values obtained using different tests (see text) marked in the corresponding panels. |
Following Kučinskas et al. (2014) and Paper I, we also investigated whether there are any significant relations between the kinematical properties of TO stars and the abundances of Mg and K in their atmospheres. For this we used absolute radial velocities of TO stars computed in Kučinskas et al. (2014), |Δνr| ≡ |νrad − 〈νrad〉clust|, where νrad is the radial velocity of the individual star and 〈νrad〉clust = −18.6 km s−1 is the mean radial velocity of the sample. As the p-values of the t-test indicate (see Table 6), there are no statistically significant relations between the abundances of Mg and K and radial velocities.
These findings support our earlier results obtained in the analysis of Na, Mg, and K abundances in 32 RGB stars in Paper I, where we found no statistically significant relations in the abundance-abundance, abundance-distance, and abundanceabsolute radial velocity planes. On the other hand, a study of 144 RGB stars in 47 Tuc by Mucciarelli et al. (2017) revealed statistically significant [K/Fe]−[Na/Fe] correlation and [K/Fe]−[O/Fe] anti-correlation (in the same study, such correlations were also detected in the globular cluster NGC 6752). In their analysis, Mucciarelli et al. (2017) used Spearman’s non-parametric rank-order correlation coefficients, rs, and computed the two-tailed probability, p, that in a given dataset rs could attain a value that is equal to or larger than its measured value.
We therefore also performed non-parametric Spearman’s and Kendall’s τ rank-correlation tests using the data in our Figs. 3–5. We also computed p-values using Pearson’s correlation coefficients calculated without taking abundance errors into account. The p-values determined in all tests are provided in Table 6 and in the corresponding panels of Figs. 3–5.
Except for the [Mg/Fe]−[Na/Fe] plane, the p-values computed using the Pearson’s, Spearman’s, and Kendall’s correlation coefficients are all very similar but, at the same time, are significantly smaller than the p-values obtained using Pearson’s coefficients computed with errors. In two planes, [K/Fe]−[Mg/Fe] and [K/Fe]−[Na/Fe], the obtained p-values are now sufficiently small to indicate the possible existence of weak correlations. In the [K/Fe]−[Mg/Fe] plane, however, the result may be influenced by the three stars with highest K abundances (for one of them K abundance and for two of them Na abundances were poorly determined as they were obtained from lines of quality classes B and C). When these points were removed from the analysis, Spearman’s and Kendall’s p-values became significantly larger, p = 0.22 and 0.21, respectively. Therefore, despite the relatively small p-values obtained in this plane using all data, we cannot reject with certainty the possibility that these small values are in fact a spurious result. In the [Mg/Fe]−[Na/Fe] plane, the p-values obtained in all three additional tests are significantly larger than the one determined by taking abundance errors into account. This may indicate that the very small p-value obtained by us in the analysis, when errors on both the x and y axes were taken into account, was spurious. Therefore, we conclude that also in this case the null hypothesis cannot be rejected. Finally, no statistically significant relations were detected between abundances (see Figs. 4 and 5).
 |
Fig. 5. Absolute radial velocities of TO stars in 47 Tuc, |Δνr|, plotted versus [Mg/Fe] and [K/Fe] abundance ratios measured in their atmospheres. Other symbols and notations are as in Fig. 4. |
The possible existence of the weak correlation in the [K/Fe]−[Na/Fe] plane may be seen as being compatible with the result obtained by Mucciarelli et al. (2017) who detected a correlation in the [K/Fe]−[Na/Fe] plane with Spearman’s p = 0.017. Although our Spearman’s and Kendall’s p-values are larger than those computed by Mucciarelli et al. (2017), the difference at least in part may be due to different sample sizes used in the two studies. Nevertheless, the null hypothesis, that there is no correlation between the two abundance ratios, cannot be rejected with confidence based alone on the p-values obtained in our Spearman and Kendall tests. We note that the analysis performed on subsamples of stars selected according to the quality class of spectral lines did not reveal any significant relations in any of the data planes studied above.
Pearson’s, Spearman’s, and Kendall’s two-tailed p-values for various abundance-abundance, abundance-r/rh, and |Δνr|-abundance velocity planes.
4. Conclusions
We performed abundance analyses of Mg and K in the turnoff stars of the Galactic globular cluster 47 Tuc. Abundances were determined using archival VLT FLAMES/GIRAFFE spectra that were obtained in HR 18 setup (746.8–788.9 nm, R = 18 400). Spectroscopic data were analyzed using 1D ATLAS9 model atmospheres and 1D NLTE abundance analysis methodology. One-dimensional NLTE spectral line synthesis was performed with the MULTI package, using up-to-date model atoms of Mg and K. We also used 3D hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres to compute 3D–1D abundance corrections for the spectral lines of Mg I and K I utilized in this study. The obtained abundance corrections were small, in all cases <0.1 dex, indicating that the influence of convection on the formation of these spectral lines in the atmospheres of TO stars in 47 Tuc should be minor.
The determined sample-averaged abundance ratios are 〈[Mg/Fe]〉1D NLTE = 0.47 ± 0.12 and 〈[K/Fe]〉1D NLTE = 0:39 ± 0.09 (numbers after the ± sign are RMS abundance variations due to star-to-star scatter). In the case of Mg we find small but significant intrinsic star-to-star scatter in the [Mg/Fe] abundance ratio, 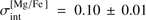 . No intrinsic scatter was found for K. Both results are in line with our earlier findings obtained using RGB stars in 47 Tuc (Paper I). Abundances of another three light elements, Li, O, and Na, that were determined in our sample stars earlier by Dobrovolskas et al. (2014), also show intrinsic scatter on levels similar to that of Mg,
. No intrinsic scatter was found for K. Both results are in line with our earlier findings obtained using RGB stars in 47 Tuc (Paper I). Abundances of another three light elements, Li, O, and Na, that were determined in our sample stars earlier by Dobrovolskas et al. (2014), also show intrinsic scatter on levels similar to that of Mg, 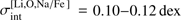 dex.
dex.
Although our data suggest the existence of a weak correlation in the [K/Fe]−[Na/Fe] plane, its statistical significance is not high enough to claim its existence with confidence. We also detected no statistically significant correlations or anti-correlations between [Mg/Fe] and [K/Fe] abundance ratios and projected distance from the cluster center. Finally, we found no relations between the absolute radial velocities of individual stars and abundances of Mg and K in their atmospheres.
The absence of statistically significant relations between abundances of different light elements, as well as those between their abundances and the kinematical properties of the host stars, is in good agreement with the results obtained in our previous analysis of RGB stars in 47 Tuc (Paper I). The results of the present analysis may be seen to support the existence of a possible relation in the [K/Fe]−[Na/Fe] plane, as found in Mucciarelli et al. (2017), albeit at a lower level of significance. However, we find no statistically significant relation in the [K/Fe]−[O/Fe] plane. Differences in the statistical significance levels obtained in the two studies may in part be due to the factor of two difference in the sample sizes used. Therefore, further homogeneous analyses of larger stellar samples using higher quality spectroscopic data may be needed to shed further light on this controversial issue.
Acknowledgments
We would like to thank the anonymous referee for constructive comments and suggestions that have helped to improve the paper. This work was supported by grants from the Research Council of Lithuania (MIP-089/2015, TAP LZ 06/2013). The study was based on observations made with the European Southern Observatory telescopes obtained from the ESO/ST-ECF Science Archive Facility.
An identical error determination procedure was also used in Paper I. In this procedure errors due to uncertainties in the atomic line parameters, as well as various systematic errors, were ignored. Apart from the uncertainties for Mg and K, for consistency we also re-derived the errors for Li, O, and Na, which had their abundances determined in Dobrovolskas et al. (2014).
To test whether adding 3D–1D abundance corrections may change our conclusions regarding the possible relations in different abundance-abundance planes, we also computed Student’s t-values using 3D+NLTE abundances instead of those determined in 1D NLTE. In all planes involving different abundance ratios, the obtained p-values were only slightly different from those determined earlier, thereby confirming the findings obtained in the 1D NLTE case.
References
- Andreasen, D. T., Sousa, S. G., Delgado Mena, E., et al. 2016, A&A, 585, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2010, A&A, 509, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Bastian, N., Lamers, H. J. G. L. M., de Mink, S. E., et al. 2013, MNRAS, 436, 2398 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., et al. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Pasquini, L., Molaro, P., et al. 2007, A&A, 470, 153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M. 1986, Upps. Astron. Obs. Rep., 33 [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Gratton, R., Bragaglia, A., et al. 2013, ApJ, 769, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Černiauskas, A., Kučinskas, A., Klevas, J., et al. 2017, A&A, 604, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Ercole, A., D'Antona, F., Carini, R., Vesperini, E., & Ventura, P. 2012, MNRAS, 423, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- di Criscienzo, M., D'Antona, F., Milone, A. P., et al. 2011, MNRAS, 414, 3381 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Bonifacio, P., et al. 2014, A&A, 565, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Orazi, V., Lucatello, S., Gratton, R., et al. 2010, ApJ, 713, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comp. Phys., 231, 919 [Google Scholar]
- Gratton, R. G., Carretta, E., Claudi, R., Lucatello, S., & Barbieri, M. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Villanova, S., Lucatello, S., et al. 2012, A&A, 544, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K.,Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A, eds. K. Hinkle, L. Wallace, J. Valenti, & D. Harmer (San Francisco: ASP) [Google Scholar]
- Jofré, P., Heiter, U, Soubiran, C. et al. 2015, A&A, 582, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirby, E. N., Guhathakurta, P., Bolte, M. et al. 2009, ApJ, 705, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Klevas, J., Kučinskas, A., Steffen, M. et al. 2016, A&A, 586, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., & Luck, R. E. 1999, A&A, 351, 168 [NASA ADS] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 55 [Google Scholar]
- Kučinskas, A., Dobrovolskas, V., & Bonifacio, P. 2014, A&A, 568, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Dubernet, M.-L., & VAMDC Collaboration 2011, Balt. Astron., 20, 503 [Google Scholar]
- Kurucz, R. L. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s−1 Grid, CD-ROM No. 13 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Kurucz, R. L. 2006, ArXiv e-prints [arXiv:astro-ph/0605029] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. It., 80, 711 [NASA ADS] [Google Scholar]
- Marino, A. F., Milone, A. P., Przybilla, N., et al. 2014, MNRAS, 437, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Dotter, A., et al. 2014, ApJ, 785, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T. V., Soubiran, C., Kovtyukh, V. V., & Korotin, S. A. 2004, A&A, 418, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, D. C. 1991, ApJS, 77, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2012, MNRAS, 426, 2889 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Bellazzini, M., Merle, T., et al. 2015, ApJ, 801, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Merle, T., & Bellazzini, M. 2017, A&A, 600, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Bonifacio, P., Molaro, P., et al. 2005, A&A, 441, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, 53 [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Ramírez, I., & Allende Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Z.-X., Bonifacio, P., Pasquini, L., & Zaggia, S. 2010, A&A, 524, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steffen, M., Caffau, E., & Ludwig, H.-G. 2013, Mem. Soc. Astron. It. Supp., 24, 37 [Google Scholar]
- Takeda, Y., Zhao, G., Chen, Y.-Q., Qiu, H.-M., & Takada-Hidai, M. 2002, PASJ, 54, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, Proc. SPIE, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Djorgovski, S. G., & King, I. R. 1993, ASP Conf. Ser., 50, 347 [Google Scholar]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A
Determination of Mg and K abundances in the Sun and Arcturus
To verify the adopted model atoms and atomic parameters of Mg I and K I lines that were used in our study of TO stars in 47 Tuc, we used the MULTI code to compute their synthetic 1D NLTE line profiles and determined abundances of these elements in the Sun and Arcturus. The obtained solar abundances were also used to compute element-to-iron abundance ratios in the sample of TO stars (Sect. 2.3.2).
A.1. Observed spectra and abundance determination
For Mg and K 1D NLTE abundance determination in the Sun, we used the re-reduced Kitt Peak Solar Flux atlas from Kurucz (2006). The spectrum covers a range of 300–1000 nm, with R = 523 000, and S/N ~4000 in the infrared part of the spectrum. A solar model atmosphere computed with the ATLAS9 code was used in the abundance determination. The model atmosphere was computed using Teff = 5777 ± 10K and log g = 4.43 ± 0.02 (Andreasen et al. 2015). The value of solar microturbulence velocity used in the abundance determination, ξt = 1.01 ± 0.06 km s−1, was also taken from Andreasen et al. (2015).
In the case of Arcturus, we used a spectral atlas from Hinkle et al. (2000). The spectrum covers a wavelength range of 372.7–930.0 nm, has a resolution of R = 150 000, and S/N ~ 1000 in the near-infrared part of the spectrum. For the abundance determination we computed an ATLAS9 model atmosphere using the atmospheric parameters from Ramírez & Allende Prieto (2011): Teff = 4286 ± 30 K, log g = 1.66 ± 0.05, and [Fe/H] = −0.52 ± 0.04. The value of microturbulent velocity, νt = 1.58 ± 0.12 km s−1, was taken from Jofré et al. (2015). The fits of Mg and K line profiles in the spectra of the Sun and Arcturus are shown in Figs. A.1 and A.2.
 |
Fig. A.1. Potassium line profiles in the spectra of the Sun and Arcturus. Gray dots show the observed spectra and the blue solid lines are theoretical 1D NLTE line profiles computed using the MULTI code. |
 |
Fig. A.2. Magnesium line profiles in the spectra of the Sun and Arcturus. Gray dots show the observed spectra and the blue solid lines are theoretical 1D NLTE line profiles computed using the MULTI code. |
A.2. Errors in the determined abundances of Mg and K
To estimate errors in the determined K and Mg abundances in the Sun and Arcturus, we used the same methodology that was employed to obtain abundance determination errors for TO stars (Sect. 2.3.4). The determined individual errors arising due to inaccuracies in the determined effective temperature, gravity, microturbulence velocity, continuum placement, and the line profile fit, as well as the total error in the determined abundance, are provided in Cols. 3–8 of Table A.1.
Errors in the determined abundances of Mg and K in the atmospheres of the Sun and Arcturus, σ(A)tot, obtained by changing various atmospheric parameters by their errors.
A.3. Abundances of Mg and K in the Sun and Arcturus
The determined solar 1D NLTE abundance of potassium is 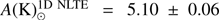 . The obtained 1D LTE potassium abundance is
. The obtained 1D LTE potassium abundance is 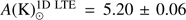 , which is slightly lower than
, which is slightly lower than 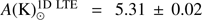 obtained by Ramírez & Allende Prieto (2011). In the case of magnesium, we determined
obtained by Ramírez & Allende Prieto (2011). In the case of magnesium, we determined 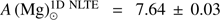 and
and 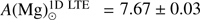 . The latter value is slightly larger than
. The latter value is slightly larger than 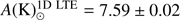 determined by Ramírez & Allende Prieto (2011).
determined by Ramírez & Allende Prieto (2011).
For Arcturus, we determined A(K)1D NLTE = 4.41 ± 0.11. The 1D LTE potassium abundance, A(K)1D LTE = 5.01 ± 0.11, agrees very well with A(K)1D LTE = 4.99 ± 0.07 obtained by Ramírez & Allende Prieto (2011). For magnesium, we obtained A(Mg)1D NLTE = 7.36 ± 0.05. In the case of 1D LTE abundances, again, we obtained a good agreement between our 1D LTE abundance, A(Mg)1D LTE = 7.46 ± 0.05, and A(Mg) = 7.47 ± 0.03 from Ramírez & Allende Prieto (2011).
Appendix B
Abundances of Mg and K in the atmospheres of TO stars of 47 Tuc
The 1D NLTE [Mg/Fe] and [K/Fe] abundance ratios determined in the sample of TO stars in 47 Tuc are provided in Table B.1. A detailed description of the methodology used to determine elemental abundances is given in Sect. 2.3.
Target TO stars in 47 Tuc, their atmospheric parameters, and determined [Mg/Fe] and [K/Fe] abundance ratios.
The sample-averaged values of the determined abundance ratios and their RMS values are provided in the last two lines of Table B.1.
All Tables
Parameters of the 3D hydrodynamical CO5BOLD model atmospheres used in this work.
Atomic parameters of the spectral lines used in the abundance determinations of Mg and K. Natural (γ
rad), Stark 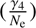 , and van der Waals
, and van der Waals 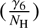 broadening constants computed using classical prescription are provided in the last three columns.
broadening constants computed using classical prescription are provided in the last three columns.
3D–1D abundance corrections, Δ3D−1D LTE, computed for different strengths of Mg I and K I lines used in this work (see text for details).
Errors in the abundances of Li, O, Na, Mg, and K determined in TO stars of 47 Tuc.
Results of the maximum-likelihood testing of the intrinsic spread in the abundances of Li, O, Na, Mg, and K.
Pearson’s, Spearman’s, and Kendall’s two-tailed p-values for various abundance-abundance, abundance-r/rh, and |Δνr|-abundance velocity planes.
Errors in the determined abundances of Mg and K in the atmospheres of the Sun and Arcturus, σ(A)tot, obtained by changing various atmospheric parameters by their errors.
Target TO stars in 47 Tuc, their atmospheric parameters, and determined [Mg/Fe] and [K/Fe] abundance ratios.
All Figures
 |
Fig. 1. Typical fits of synthetic Mg and K line profiles (solid blue lines) to those in the observed GIRAFFE spectrum (filled red circles) of the target TO star 47Tuc45982 (Teff = 5707 K, log g = 4.00). We also provide the abundances determined from each observed line, A(X), together with their errors (see Sec. 2.3.4). Thin gray lines show synthetic line profiles computed with the abundances altered by ±0.2 dex. |
| In the text | |
 |
Fig. 2. [Mg/Fe] (top) and [K/Fe] (bottom) abundance ratios determined in the sample of TO stars in 47 Tuc and plotted versus the effective temperature of individual stars. Error bars show uncertainties that were computed as described in Sect. 2.3.4. |
| In the text | |
 |
Fig. 3. Abundance-to-iron ratios of Li, O, Na, Mg, and K in the sample of TO stars, shown in various abundance-abundance planes. Colors on the left and right sides of the symbols correspond to the quality (symbols denoting different quality classes are shown in the top-left panel) of spectral lines used to determine abundances of the light elements in a given star plotted on the y and x axes, respectively (see Sect. 2.3.2 for details). The values of two-tailed probabilities, p, computed using Pearson’s parametric correlation coefficients (with and without abundance errors, p witherrors and p withouterrors, respectively), Spearman’s, and Kendall’s non-parametric rank-order correlation coefficients are given in the corresponding panels (see Sect. 3.2). |
| In the text | |
 |
Fig. 4. Abundance-to-iron ratios of Mg and K plotted versus the projected distance from the cluster center, r/rh (small filled circles; rh is a half-mass radius of 47 Tuc, rh = 174″, taken from Trager et al. 1993). Symbol color denotes quality (class) of the spectral lines from which the abundance was determined. Large open circles are average abundance ratios computed in non-overlapping Δr/rh = 1 wide distance bins (marked by the vertical dashed lines; RMS scatter of the abundance ratios in a given bin is shown by the black vertical error bars). Black solid lines are linear fits to the data of individual stars, with the p-values obtained using different tests (see text) marked in the corresponding panels. |
| In the text | |
 |
Fig. 5. Absolute radial velocities of TO stars in 47 Tuc, |Δνr|, plotted versus [Mg/Fe] and [K/Fe] abundance ratios measured in their atmospheres. Other symbols and notations are as in Fig. 4. |
| In the text | |
 |
Fig. A.1. Potassium line profiles in the spectra of the Sun and Arcturus. Gray dots show the observed spectra and the blue solid lines are theoretical 1D NLTE line profiles computed using the MULTI code. |
| In the text | |
 |
Fig. A.2. Magnesium line profiles in the spectra of the Sun and Arcturus. Gray dots show the observed spectra and the blue solid lines are theoretical 1D NLTE line profiles computed using the MULTI code. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


