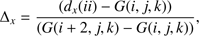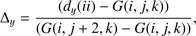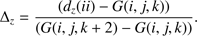| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201730580 | |
| Published online | 09 July 2018 | |
Nonlocal heat flux effects on temperature evolution of the solar atmosphere
1
Instituto Nacional de Pesquisas Espaciais (INPE), São José dos Campos, SP, Brazil
e-mail: suzana.seas@gmail.com
2
Universidade Tecnológica Federal do Parana (UTFPR), Curitiba, PR, Brazil
3
Max Planck Institut für Sonnensystemforschung (MPS), Göttingen, NDR, Germany
Received:
8
February
2017
Accepted:
20
December
2017
Context. Heat flux is one of the main energy transport mechanisms in the weakly collisional plasma of the solar corona. There, rare binary collisions let hot electrons travel over long distances and influence other regions along magnetic field lines. Thus, the fully collisional heat flux models might not describe transport well enough since they consider only the local contribution of electrons. The heat flux in weakly collisional plasmas at high temperatures with large mean free paths has to consider the nonlocality of the energy transport in the frame of nonlocal models in order to treat energy balance in the solar atmosphere properly.
Aims. We investigate the impact of nonlocal heat flux on the thermal evolution and dynamics of the solar atmosphere by implementing a nonlocal heat flux model in a 3D magnetohydrodynamic simulation of the solar corona.
Methods. We simulate the evolution of solar coronal plasma and magnetic fields considering both a local collision dominated and a nonlocal heat flux model. The initial magnetic field is obtained by a potential extrapolation of the observed line-of-sight magnetic field of AR11226. The system is perturbed by moving the plasma at the photosphere. We compared the simulated evolution of the solar atmosphere in its dependence on the heat flux model.
Results. The main differences for the average temperature profiles were found in the upper chromosphere/transition region. In the nonlocal heat transport model case, thermal energy is transported more efficiently to the upper chromosphere and lower transition region and leads to an earlier heating of the lower atmosphere. As a consequence, the structure of the solar atmosphere is affected with the nonlocal simulations producing on average a smoother temperature profile and the transition region placed about 500 km higher. Using a nonlocal heat flux also leads to two times higher temperatures in some of the regions in the lower corona.
Conclusions. The results of our 3D MHD simulations considering nonlocal heat transport supports the previous results of simpler 1D two-fluid simulations. They demonstrated that it is important to consider a nonlocal formulation for the heat flux when there is a strong energy deposit, like the one observed during flares, in the solar corona.
Key words: Sun: corona / Sun: atmosphere / magnetohydrodynamics (MHD)
© ESO 2018
1. Introduction
One of the problems of simulating the solar atmosphere is to find an appropriate heat flux model that describes well the thermal transport properties of the weakly collisional plasma of the transition region and the solar corona. Therefore, it is of interest to compare existing formulations for the heat flux in order to find a proper description for the thermal evolution of those regions. When describing the transport of energy in the solar atmosphere, it is common to use collision-dominated models for the heat flux as calculated by Spitzer & Härm (1953; hereafter SH). Their derivation describes the heat flux in terms of local temperature gradient,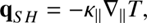 (1)
(1)
where T is the plasma temperature and κ∥ is the parallel component of a thermal conduction tensor. This thermal diffusion model is valid for a considerable range of plasma parameters. However, Gray & Kilkenny (1980) have shown that the approximation used by Spitzer & Härm (1953) applies only to 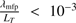 , where
, where 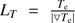 is the electronic temperature scale height and λmfp is the electron mean free path. Typical values for the ratio λmfp/LT for the quiet Sun and flare conditions are summarized in Table 1. The values for quiet sun conditions were calculated from the initial data profile used in the code GOEMHD3D (Skála et al. 2015). The values for the flaring atmosphere were obtained from the results of numerical simulations of Abbett & Hawley (1999). In the dense and collisional plasma of the chromosphere the ratio λmfp/LT is within the limit allowing the SH thermal conductivity. However, for the upper transition region and corona the SH approach is no longer valid, in particular during solar flares. Steep temperature gradients in the transition region (TR) and the low plasma density in the corona lead to a longer electron mean free path and larger electron temperature scale heights.
is the electronic temperature scale height and λmfp is the electron mean free path. Typical values for the ratio λmfp/LT for the quiet Sun and flare conditions are summarized in Table 1. The values for quiet sun conditions were calculated from the initial data profile used in the code GOEMHD3D (Skála et al. 2015). The values for the flaring atmosphere were obtained from the results of numerical simulations of Abbett & Hawley (1999). In the dense and collisional plasma of the chromosphere the ratio λmfp/LT is within the limit allowing the SH thermal conductivity. However, for the upper transition region and corona the SH approach is no longer valid, in particular during solar flares. Steep temperature gradients in the transition region (TR) and the low plasma density in the corona lead to a longer electron mean free path and larger electron temperature scale heights.
Ratio of the electron mean-free-path, Lmfp, to the electronic temperature scale height, LT.
Ljepojevic & MacNeice (1989) tried to obtain a heat flux under more general conditions and considering departures from a Maxwellian velocity distribution function. They derived the heat flux from a distribution function obtained by solving the Landau equation. For low velocities the distribution function was approximated by the SH method, while they considered the high velocity form of the Landau equation to obtain the distribution at higher velocities. For typical electron temperature and density of active regions and flaring atmosphere, their results indicate that the SH model fails to properly describe the energy balance in the upper TR and low corona. Lie-Svendsen et al. (1999) used a test particle model against a Maxwellian background and applied density and electron temperatures expected to be found in the TR with a thickness of 50 Mm. They have shown that there will be contributions coming from the free streaming coronal electrons to the heat flux for a low density TR (1012–1013 particles m−3). In that case, Lie-Svendsen et al. (1999) demonstrate that a considerable portion of the heat flux would come from particles in the tail of distribution function. For higher TR density (1014 particles m−3), they concluded that the contributions for the heat flux would come basically from the core of the distribution function. Therefore, the classical collisional model would give good approximations for high densities and low temperature gradients. From kinetic model results, Vocks et al. (2016) suggest that the electronic velocity distribution in the TR have a considerable deviation from the Maxwellian. Therefore, the SH model may not be an appropriate choice to describe thermal conduction in TR.
The possible breakdown of the collisional model according to SH requires, therefore, looking for a more appropriate description of the transport. A better model for the heat flux in coronal plasmas would be a nonlocal (NL) treatment, as suggested by the results of Ljepojevic & MacNeice (1989). Strictly speaking, this would mean computing the contributions of energetic electrons in a way that the heat flux is no longer solely determined by the local gradient of temperature. Since there is no available NL transport theory, many authors have considered a linear perturbation approach including higher orders in the kinetic theory derivation of the heat flux. By means of kinetic simulations, Luciani et al. (1983) were able to mimic an NL behavior in the electron heat flux by expressing it as a convolution integral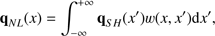 (2)
(2)
where w(x, x′) is the delocalization kernel.
The kernel, w(x, x′), acts by weighting the influence of the x′ points along the magnetic field line on the x position in the field line. Different delocalization kernels have been tested in the literature. Most of the suggested kernels were obtained assuming plasma conditions not applicable in the upper solar atmosphere (Brantov & Bychenkov 2013). However, Luciani et al. (1983) derived a kernel under assumptions that are not far from the conditions found in the corona (Karpen & DeVore 1987):![$$ \begin{equation}w(x,x')= \frac{1}{2\lambda(x')} \exp \left[ - \left| \int_{x'}^{x} {\rm d}x'' \frac{n(x'') }{\lambda(x') n(x')} \right| \right].\end{equation} $$](/articles/aa/full_html/2018/07/aa30580-17/aa30580-17-eq5.gif) (3)
(3)
Here λ(x′) is the effective distance which electrons at a temperature T (x′) can reach. It can be written in terms of the electron mean free path as (Luciani et al. 1983)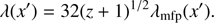 (4)
(4)
This delocalized heat flux has been applied before to study 1D models of the solar atmosphere. Karpen & DeVore (1987) and Karpen et al. (1989) performed a 1D two-fluid simulation of a flaring solar atmosphere along a loop considering optically thin radiation and volumetric heating. Their results indicate significant differences in the plasma behavior in dependence on the heat flux model, especially in the pre-peak phase of a flare. The main differences were a smoother transition region, higher coronal temperatures, and lower upflow velocities in comparison with the classical model results. The work of Ciaravella et al. (1991) indicates that the differential emission measure, D, can be increased by a factor of 2 in the temperature range of 2 × 104 K < T < 5 × 104 K when considering the NL heat flux model. Their results indicate that an NL heat flux model leads to changes in D values both at the base and near the top of the loops.
In the following section we discuss the numerical aspects of our work and the data used to build the initial magnetic field conditions. In Sect. 3, we analyze the effects of heat flux models on the average temperature and velocity vertical profiles, followed by the investigation of their effects along a specific magnetic field line in Sect. 4.
2. Data and methodology
We used the code GOEMHD3 (Skála et al. 2015) to simulate the solar corona. The code solves the following set of MHD equations: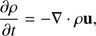 (5)
(5)
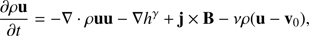 (6)
(6)
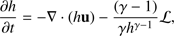 (7)
(7)
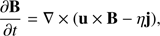 (8)
(8)
where the variables ρ, η, u, v 0, B, and j stand for the normalized plasma density, resistivity, velocity, neutral gas velocity, magnetic field, and current density. The normalization parameters are listed in Table 2. The variable h represents the enthalpy and it is related to the thermal pressure p by h = (p/2)1/γ, where γ= 5/3 is used for the ratio of specific heats. The variable ν stands for the collision coefficient between the plasma and the neutral gas. The collision with neutrals is only used to set plasma into motion at the bottom of the simulation box.
Normalization parameters.
The variable ℒ is the energy loss function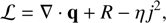 (9)
(9)
where the heat flux transport along the magnetic field lines is given by ∇ · q, and q was substituted by either the SH or NL model expressions. We have considered an anomalous plasma resistivity to describe the heating by current dissipation. This resistivity can be justified by the physical processes that explain current dissipation in low collisional plasma (Büchner & Elkina 2005, 2006). Our plasma resistivity is constant in time and uniform in the xy-plane. It was modeled according to Bingert & Peter (2011) in the TR and corona in order to mimic the heating deposit expected from nanoflare heating. In the lower part of the domain, the resistivity was decreased to classical values, which helped to keep the numerical stability.
The general loss rate by thermal emission, R, was described by an optically thin plasma approximated by Cook et al. (1989) as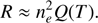 (10)
(10)
In our work we used the Q(T) obtained by interpolating the values from the curve given by CHIANTI (Del Zanna et al. 2015).
For the simulations, the bottom of the box was located in the chromosphere, with 49.0 Mm in the x and y directions, and it extended 40.0 Mm in the vertical direction (z) up to the lower corona. The mesh used in the model is uniform in the x and y directions. It is refined in the z direction with maximum resolution close to the bottom of the simulation box in order to cope with the large gradients of temperature and density in the TR (see Fig. 1). The mesh has 258 grid points in the z direction and 1462 points in the xy-plane. The horizontal resolution is about 336 km and the maximum resolution in the z direction is approximately 100 km.
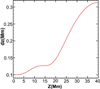 |
Fig. 1. Grid resolution in the z direction as a function of height Z above the photosphere layer. |
We ran the simulations with initial conditions established from observations of active region AR11226. The initial magnetic field was obtained by a potential magnetic field extrapolation (Otto et al. 2007) of the line-of-sight (LOS) component of the photospheric magnetic field measured by the Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamics Observatory (SDO) satellite. Before the extrapolation, the LOS photospheric magnetic field was Fourier-filtered in order to retain only the first 16 modes. This procedure removes small gradients that cannot be resolved by the computational grid. Figure 2a shows the LOS component of the magnetic field observed on 7 June 2011 at 05:40:00 UT, and Fig. 2b the filtered magnetogram used for the extrapolation.
 |
Fig. 2. Line-of-sight magnetogram before (panel a) and after (panel b) Fourier filtering. |
The plasma is perturbed by coupling it with a moving neutral gas via the collision term in the momentum equation. The collisions with neutrals in the simulation domain are imposed only in the lower part of the simulation box (H < 1 Mm). This is done by setting ν as a function of height decreasing exponentially from ν = 3 at H = 0 to zero at H = 1 Mm. The perturbation is maintained throughout the whole simulation modeling the effects of footpoint displacement in the photosphere. The neutral gas velocity field (u0) was approximated by a horizontal incompressible vortex and has no vertical component. Figure 3 displays the neutral gas velocity pattern used in the simulations.
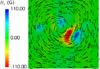 |
Fig. 3. Neutral gas horizontal velocity pattern, u0, which corresponds to an incompressible vortex; it is used to perturb plasma and magnetic field. The color-code shows the values of the z-component of the magnetic field. |
The plasma pressure was considered initially uniform over the entire domain and the plasma density profile was set as described by Skála et al. (2015) to mimic a stratified atmosphere in a model that does not consider gravity. The normalized coronal density is defined as ρc = 1 and the chromospheric density as ρch = 100ρc. The height profiles of the initial normalized temperature and density are displayed in Fig. 4. We used the perfect gas law to obtain an initial temperature profile that is in accordance with the Vernazza et al. (1981) model for the temperature of the solar atmosphere. We defined the solar atmospheric regions in our model based on the temperature range. The chromosphere was defined as the region where T ≤ 2 × 104 K, and the corona as the region where plasma has a temperature equal to or higher than a million Kelvin. The TR is located between these regions and the lower (upper) part of the TR in our model is considered to be in the temperature range of 2 × 104 K < T < 5 × 105 K (5 × 105 K ≤ T < 1 × 106 K).
 |
Fig. 4. Height profiles of normalized temperature (T0 = 104 K) and normalized density, n0, used as initial condition in the MHD model. |
To compute the NL heat flux we needed to know the density and pressure along the magnetic field lines. For this sake we traced for each grid point a magnetic field line path l by integrating forward and backward along the direction of the magnetic field: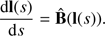 (11)
(11)
Figure 5a illustrates the process. For a starting grid point (yellow), we obtain the selected points along the magnetic line path (blue) by integrating Eq. (11). We have considered a resolution of Δl = 0.1dzmin for the magnetic field integration.
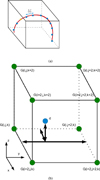 |
Fig. 5. Panel a: Tracing of the magnetic field for the whole domain starting at the yellow grid point and moving through the blue points. Panel b: Mesh points, G, in green used to interpolate the variables at the blue point at a distance d from the origin of the Cartesian grid. |
To compute the variables at the points along the field line, we performed a trilinear interpolation using the information obtained from the grid points around it. Since the GOEMHD3 is parallelized using message passing interface (MPI), the values at the grid points in other partitions are not directly available. Therefore, those values had to be communicated among the partitions. A MPI communication of every grid point would be computationally too expensive. In order to reduce computation time, only half of the points in each partition were communicated. Therefore, the interpolation was performed with information from every other point in our domain. This is illustrated in Fig. 5b, where the green points are the communicated mesh points and the blue point is a point located along the magnetic field line path that is being traced and where the properties are going to be interpolated. The vector position 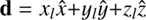 denotes the distance of the blue point to the origin of the coordinate system. The value of the variable ϕ at the blue point is obtained by
denotes the distance of the blue point to the origin of the coordinate system. The value of the variable ϕ at the blue point is obtained by![$$\begin{aligned} \phi ( ii)&= ([ \varphi _{i,j, k}(1-\Delta _x) + \varphi _{i+1,j , k } \Delta _x ] (1-\Delta _y) \\ \nonumber&\quad + [ \varphi _{i, j+1,k }(1- \Delta _x) +\varphi _{i+1,j+1,k } \Delta _x] \Delta _y ) (1- \Delta _z)\\ \nonumber&\quad + ([\varphi _{i,j , k+1 }(1-\Delta _x) + \varphi _{i+1,j , k+1 } \Delta _x ](1-\Delta _y) \\ \nonumber&\quad + [ \varphi _{i, j+1,k+1 }(1- \Delta _x) + \varphi _{i+1,j+1,k +1 } \Delta _x] \Delta _y ) \Delta _z , \end{aligned}$$](/articles/aa/full_html/2018/07/aa30580-17/aa30580-17-eq17.gif) (12)
(12)
The interpolation (Eq. (12)) calculates the values of ϕ by means of a weighted average of the values in the grid points using Δx,y,z as the weights. Although the interpolation was done using every other point, the final result was able to replicate the profiles for density and temperature, as can be seen in Fig. 6a. The computation of the NL heat flux costs three times the computation of the classical heat flux for the mesh used here. The corresponding initial divergence of heat flux along a field line, according to the two heat flux models, is displayed in Fig. 6b. The height of the loop (H) is normalized by the apex loop height (Ha). If we decrease the number of points used in the interpolation, the final result is not able to reproduce those profiles with the same accuracy.
 |
Fig. 6. Panel a: Initial temperature and density profiles along a magnetic field line through grid point (i = 70, j = 70, k = 100). Panel b: Initial divergence heat flux profile along a field line for classical formulation (green curve) and NL (red curve). The height of the loop, H, was normalized by the apex loop height, Ha |
3. Average profiles
We performed two simulations starting from exactly the same initial conditions but for different heat flux formulations (NL and SH). Figure 7 shows the vertical profile of the averaged over the xy-plane temperature obtained at three different instants of time (20 s, 410 s, and 820 s) for the SH (black dashed line) and NL (solid green line) models. The vertical red lines denote the beginning of TR (TR-line) and the base of corona (C-line). As the differences in height for the position of the TR and corona are less than 1 Mm between the models, we only plot the lines for the NL heat flux simulations. The vertical bars in the plots are for the standard deviation and the simulation results are in black for SH and in green for NL.
 |
Fig. 7. Average temperature T(K) over the xy-plane as a function of height (H) obtained using the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, and (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
The temporal evolution of the temperature profile shows that the temperature in the lower corona decreases, while it increases in the TR and upper chromosphere. These temperature variations move the base of TR to lower heights and smooth the existing temperature gradients in the upper part of TR, T > 5×105 K. The base of the TR moves from the initial 3.5 Mm to around 1.7 Mm. Both models predict the base of corona starting at greater heights as we have defined the base of the corona as the height where T = 106 K. The SH model predicts the base of the corona around 300 km and 500 km higher than the NL model for the times t = 410 s and t = 820 s, respectively. This indicates that the SH model predicts more conductive cooling for the plasma in the base of the corona.
Figure 8 shows a closer view of the upper chromosphere and TR. It is possible to identify the main differences between the two models of the temperature of the TR. The NL model results in a smoother TR with final temperatures lower than those obtained using the classical collisional SH formulation. The temperature in the upper TR is lower in the NL model and the base of the upper TR (T = 5 × 105 K) is located 500 km higher than in the SH model. The upper chromosphere starts to be heated earlier in the NL formulation as an effect of the delocalization mechanism. Figure 9 shows the relative percentage difference in the temperature profile between the NL and SH models using the temperature obtained with SH as reference. There it can be clearly seen that the main differences between the two heat flux models are found in the TR. In the NL formulation the TR is less heated, thus the lower temperatures found using NL model.
 |
Fig. 8. Average temperature, T (K), over the xy-plane as a function of height in the lower part of the atmosphere, H ≤ 8 Mm, for the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
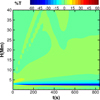 |
Fig. 9. Temporal evolution of the height distribution of relative percentage difference for temperature using SH values as reference. |
The profiles of the vertical plasma flows is shown in Fig. 10. Positive values indicate upflows and negative values indicate plasma downflows. At the beginning of the simulation, t = 20 s, plasma downflows at the lower corona and upflows at the TR produce a mix of plasma coming from both regions. The flows obtained with the SH model are on average up to 50% higher than those obtained with the NL model. The mixed flow pattern is later substituted by a general upflow starting at H ~ 2 Mm and extending up to the top boundary of the simulation box. The resulting flows are very similar in both models with the NL formulation producing slightly lower velocities at the lower TR and higher velocities in the upper TR.
 |
Fig. 10. Average vertical velocity, Uz, over the xy-plane as a function of height (H) for the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
The results for the temperature and vertical flows can be understood if we look at the vertical profiles of the divergence of the heat flux obtained using the SH and NL formulations. Figure 11 shows these results where the negative (positive) values of the divergence means energy gain (loss) by heat flux transport. At t = 20 s the peaks of energy deposition for NL and SH are in the same position. However, the conductive heating obtained in the NL model is less intense and broader than that of SH, reaching lower heights and heating the base of the TR more efficiently due the delocalization mechanism. This conductive heating is responsible for the shift of the base of the TR to lower altitudes in both models and for the upflows observed in the lower TR at the early stages of the simulation. For H > 4 Mm, the heat flux mechanism is responsible for the energy loss in the higher TR and the peaks of energy removal for the SH and NL models no longer coincide. The energy removal for the SH model peaks at higher altitudes and it is more intense than that obtained from the NL simulations. This shifts the base of the corona upwards and causes the downward plasma flows observed at the higher TR. From the profiles for the average flux divergence at t = 410 s and 820 s, we observed that the conductive heating of the lower TR is maintained, but the peaks of SH and NL model no longer coincide. The energy gain in the SH model is more intense and occurs at lower altitudes than that obtained with the NL model. This conductive heating pattern sustains the upflows starting at the lower TR observed at later times.
 |
Fig. 11. Average heat flux divergence, ∇ · q, over the xy-plane as a function of height, H, for three different times: (a) t = 20 s, (b) t = 410 s, and (c) t = 820 s. Standard deviations for SH (NL) heat flux model are shown using black (green) vertical bars. |
4. Local effects
In this section, we investigate the evolution of the plasma along a field line that connects to a maximum temperature region in the solar corona. Figure 12 shows the temporal variation of the peak temperature found in the simulation domain as a function of time for the SH and NL models. We verify that the NL model results in higher peak temperatures than the SH model. The peak temperature starts to rise very early and is increased dramatically after 400 s, mainly in the NL heat flux model. This indicates that different heat flux models predict different thermal evolutions on the solar atmosphere, consequently affecting the temperature peak values.
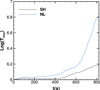 |
Fig. 12. Temporal evolution of the peak temperature found in the simulation domain as a function of time for SH (dash-dot-dot) and NL (dotted) models. |
Figure 13 shows two snapshots of the simulation at t = 820 s with the magnetic field lines color-coded by the temperature and the bottom slice by the z-component of the magnetic field. The first snapshot, Fig. 13a, shows the isosurface regions where the plasma temperatures were higher than 1.5 million Kelvin at t = 820 s. Since both models predict approximately the same locations for plasma heating, we only show the snapshot for the NL simulation. Figure 13b displays the selected field line for the investigation. This field line has its apex at the chromosphere at the beginning of the simulation and rises towards the corona as the simulation evolves, stabilizing around Ha ~ 10 Mm after t = 600 s (see Fig. 14).
 |
Fig. 13. Simulation box for t = 820 s showing (a) the isosurfaces of T > 1.5 × 106 K (in red) and the magnetic field lines, color-coded according to temperature; and (b) the selected field line color-coded according to temperature. The horizontal plane is color-coded by the z-component of the magnetic field. |
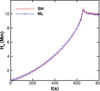 |
Fig. 14. Height of the loop apex, Ha, as a function of time. |
In our simulations, the increase in temperature is caused in part by current dissipation. Figure 15 shows the temporal evolution of the current dissipation (CD) along the selected magnetic field line for the simulation with SH model (Fig. 15a) and NL model (Fig. 15b). We verify that current dissipation is relevant after t = 600 s and is qualitatively very similar for both simulation cases. The contribution from current dissipation is especially strong in the range 0.1 ≤ H/Ha ≤ 0.7, which covers the region going from the upper TR up to the lower corona. The peak for CD is located around H/Ha = 0.25 in both cases. The NL heat flux leads to CD around 20% higher in the interval 0.3 − 0.4H/Ha (bottom corona) compared to the prediction from SH model for the same region. In the range 0.5–0.55 H/Ha (upper corona), the CD is around 10% higher for the SH case.
 |
Fig. 15. Temporal evolution of the current dissipation (CD) term for the selected field line in the (panel a) SH and (panel b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
The heat flux also contributes to the thermal energy redistribution. Figure 16 shows the temporal evolution of the heat flux along the investigated magnetic field line for SH (Fig. 16a) and NL (Fig. 16b) cases. Negative values show where energy is being deposited and positive values show where the energy is removed by heat flux. In both cases, the heat flux acts to transport thermal energy towards the base of the loop. Close to the end of the simulation, most of the energy is being deposited in the height range 0.15 ≤ H/Ha ≤ 0.3. In the NL case, a considerable quantity of energy is also being deposited in even lower regions, 0.10 ≤ H/Ha ≤ 0.15. The main difference between the simulations is from where the energy is removed. In the SH model, the thermal energy is removed from heights in the range 0.3 ≤ H/Ha ≤ 0.6, whereas in the NL case the energy is transported from a region closer to the top of the loop (~0.8H/Ha). Another significant difference is the quantity of energy transported from the corona. The SH heat flux takes considerably more energy from the corona than the NL heat flux model.
 |
Fig. 16. Temporal evolution of the divergent of heat flux (HF) term for the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
The combination of these mechanisms produces the thermal profiles shown in Fig. 17. As the field line goes up and the plasma along the loop is slowly heated, the upper part of the loop starts to present higher temperatures. Around t = 500 s, the upper part of the loop reaches the temperature expected in the solar corona. After t = 600 s, the dramatic rise in the contribution from the heating mechanisms leads to temperatures above one million Kelvin. The NL formulation, Fig. 17b, reveals 2.5 times higher temperatures at heights between 40% and 80% of the field line apex. The differences between the NL and SH temperature profiles, Fig. 17a, cannot be explained solely by the differences in heat flux and current dissipation profiles. Therefore, the heat flux model may also affect other mechanisms appearing in the energy equation leading to differences in plasma heating in general.
 |
Fig. 17. Temporal evolution of the logarithm of the temperature (T) for the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
The temporal evolution of the vertical velocity along the field line is quite similar between the two models, as can be seen in Fig. 18. At the beginning, upflows from the chromosphere-TR and downflows from the lower corona mix the plasma between these two regions. Then, after t = 500 s, this mixed up/down flow pattern is substituted by a general upflow. The classical SH model reveals higher upflow velocities than NL model at heights around 20% of the fluxtube apex height. This is due to the higher energy input of SH in the upper TR, which leads to greater heating and consequently higher upflow velocities.
 |
Fig. 18. Temporal evolution of the vertical velocity along the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
5. Summary and conclusions
We have presented the results of 3D MHD simulations comparing the influence of different heat flux models on the plasma temperature and velocity vertical profile in the solar atmosphere above an active region. The average temperature and velocity vertical profiles obtained by assuming NL transport differ slightly from the prediction of the collisional transport model. The main differences are found in the upper chromosphere/TR. Both models act to transport energy from the corona to the TR and lower chromosphere. However, in the NL heat transport model case, due to the delocalization mechanism, thermal energy is transported more efficiently to lower altitudes contributing to an earlier heating of the upper chromosphere and lower TR. The heat deposition in the lower parts of the solar atmosphere causes a plasma upflow from the upper chromosphere/lower TR towards the corona. At the same time, the cooling of the upper TR/lower corona causes a plasma downflow from the corona to lower altitudes. These mixed up/down flows are later substituted by a general upflow pattern in both simulations. This all affects the structure of the TR, with the nonlocal simulations producing a smoother temperature profile at the TR, and lower final temperatures. This temperature distribution affects the position of the TR, with a difference of about 500 km between the models. The delocalization mechanism, present in the NL model, also contributes to less energy losses in the corona. During the simulation, the maximum difference in the average temperature profiles between the two models reached 55%. Locally, the temperature difference was considerably higher for certain regions of the lower corona where the temperature peaks gave values two times higher for the NL heat flux model.
The differences found for the heat flux models in our simulations indicate that is important to consider the contributions from fast electrons, as suggested by Vocks et al. (2016). In addition, our results point out that those contributions can be significant for the TR since we observed considerable differences between temperature profiles for that region. Regarding the results from Lie-Svendsen et al. (1999), they concluded that these contributions are only important for low densities in the TR. Our results have demonstrated that there are considerable contributions from the electrons in the tail of the distribution function even in the case of a TR with a higher density plasma. The discrepancy between their conclusions and ours is due to the difference in the thickness of the TR in each study. Lie-Svendsen et al. (1999) have considered a TR that is fifty times thicker than that in our initial condition. A greater thickness for the TR leads to lower temperature gradients, and therefore may underestimate the values for classical heat flux there. Thus, the differences between the SH model and any other model that considers the contribution from the fast electrons will be considerably smaller. Observations have shown that in flaring conditions, the TR is sharp (Reale 2010) and therefore there will be contributions from the tail electrons. The importance of these contributions can only be completely understood when considering other mechanisms that influence the shape of the TR, for example, a better description of the ionization and excitation process in the chromosphere and other microphysical mechanisms that have not been considered in our model.
The results of our 3D MHD simulations considering NL heat transport are in agreement with the results of the simpler 1D two-fluid simulations performed in the past (Karpen & DeVore 1987). They show that in order to treat the upper chromosphere/TR properly, it is important to consider the contributions from fast electrons by implementing an NL formulation for the heat flux. This is even more important when strong energy dissipation, like the one observed during flares, occurs in the solar corona. The NL heat flux will transport this energy more efficiently along the magnetic field lines, depositing it in the upper chromosphere/TR and affecting all the dynamics of the plasma there.
Acknowledgments
This work was supported by CAPES under the project CAPES-process 99999.004487/2014-01. The simulations were performed on the HYDRA cluster at MPG, Germany, and on the GAUSS cluster at CE-SUP, Brazil. We thank Patrick Killian, Luiz A.C.A. Schiavo, and Jan Skála for initial discussions on this work. S.S.A.S. acknowledges the International Max Planck Research School (IMPRS) and a stipend from the Max-Planck society.
References
- Abbett, W. P., & Hawley, S. L. 1999, ApJ, 521, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 530, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brantov, A., & Bychenkov, V. 2013, Plasma Phys. Rep., 39, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Büchner, J., & Elkina, N. 2005, Space Sci. Rev., 121, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Büchner, J., & Elkina, N. 2006, Phys. Plasmas, 13, 082304 [NASA ADS] [CrossRef] [Google Scholar]
- Ciaravella, A., Peres, G., & Serio, S. 1991, Sol. Phys. J., 132, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, J. W., Cheng, C. C., Jacobs, V. L., & Antiochos, S. K. 1989, ApJ, 338, 1176 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. R., & Kilkenny, J. D. 1980, Plasma Phys., 22, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., & DeVore, C. R. 1987, ApJ, 320, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Cheng, C.-C., Doschek, G. A., & DeVore, C. R. 1989, ApJ, 338, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Lie-Svendsen, Ø., Holzer, T. E., & Leer, E. 1999, ApJ, 525, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Ljepojevic, N. N., & MacNeice, P. 1989, Phys. Rev. A, 40, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Luciani, J. F., Mora, P., & Virmont, J. 1983, Phys. Rev. Lett., 51, 1664 [NASA ADS] [CrossRef] [Google Scholar]
- Otto, A., Büchner, J., & Nikutowski, B. 2007, A&A, 468, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reale, F. 2010, Liv. Rev. Sol. Phys., 7, 5 [Google Scholar]
- Skála, J., Baruffa, F., Büchner, J., & Rampp, M. 2015, A&A, 580, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJ, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Vocks, C., Dzifčáková, E., & Mann, G. 2016, A&A, 596, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Ratio of the electron mean-free-path, Lmfp, to the electronic temperature scale height, LT.
All Figures
 |
Fig. 1. Grid resolution in the z direction as a function of height Z above the photosphere layer. |
| In the text | |
 |
Fig. 2. Line-of-sight magnetogram before (panel a) and after (panel b) Fourier filtering. |
| In the text | |
 |
Fig. 3. Neutral gas horizontal velocity pattern, u0, which corresponds to an incompressible vortex; it is used to perturb plasma and magnetic field. The color-code shows the values of the z-component of the magnetic field. |
| In the text | |
 |
Fig. 4. Height profiles of normalized temperature (T0 = 104 K) and normalized density, n0, used as initial condition in the MHD model. |
| In the text | |
 |
Fig. 5. Panel a: Tracing of the magnetic field for the whole domain starting at the yellow grid point and moving through the blue points. Panel b: Mesh points, G, in green used to interpolate the variables at the blue point at a distance d from the origin of the Cartesian grid. |
| In the text | |
 |
Fig. 6. Panel a: Initial temperature and density profiles along a magnetic field line through grid point (i = 70, j = 70, k = 100). Panel b: Initial divergence heat flux profile along a field line for classical formulation (green curve) and NL (red curve). The height of the loop, H, was normalized by the apex loop height, Ha |
| In the text | |
 |
Fig. 7. Average temperature T(K) over the xy-plane as a function of height (H) obtained using the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, and (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
| In the text | |
 |
Fig. 8. Average temperature, T (K), over the xy-plane as a function of height in the lower part of the atmosphere, H ≤ 8 Mm, for the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
| In the text | |
 |
Fig. 9. Temporal evolution of the height distribution of relative percentage difference for temperature using SH values as reference. |
| In the text | |
 |
Fig. 10. Average vertical velocity, Uz, over the xy-plane as a function of height (H) for the SH and NL heat flux models for three different instants of time: (a) t = 20 s, (b) t = 410 s, (c) t = 820 s. Standard deviations for the SH (NL) heat flux model are shown using black (green) vertical bars. |
| In the text | |
 |
Fig. 11. Average heat flux divergence, ∇ · q, over the xy-plane as a function of height, H, for three different times: (a) t = 20 s, (b) t = 410 s, and (c) t = 820 s. Standard deviations for SH (NL) heat flux model are shown using black (green) vertical bars. |
| In the text | |
 |
Fig. 12. Temporal evolution of the peak temperature found in the simulation domain as a function of time for SH (dash-dot-dot) and NL (dotted) models. |
| In the text | |
 |
Fig. 13. Simulation box for t = 820 s showing (a) the isosurfaces of T > 1.5 × 106 K (in red) and the magnetic field lines, color-coded according to temperature; and (b) the selected field line color-coded according to temperature. The horizontal plane is color-coded by the z-component of the magnetic field. |
| In the text | |
 |
Fig. 14. Height of the loop apex, Ha, as a function of time. |
| In the text | |
 |
Fig. 15. Temporal evolution of the current dissipation (CD) term for the selected field line in the (panel a) SH and (panel b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
| In the text | |
 |
Fig. 16. Temporal evolution of the divergent of heat flux (HF) term for the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
| In the text | |
 |
Fig. 17. Temporal evolution of the logarithm of the temperature (T) for the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
| In the text | |
 |
Fig. 18. Temporal evolution of the vertical velocity along the selected field line in the (a) SH and (b) NL simulations. The horizontal axis shows the time, in seconds, and the vertical axis the height of the loop normalized by the loop apex. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.