© ESO 2018

1 Introduction

In recent years, several papers by various authors have been devoted to investigating the properties of the out-of-plane equilibrium points, which are located outside the orbital plane of the oblate primary bodies in the restricted three-body problem. This research is mainly based on Douskos & Markellos (2006), which first reported the existence of out-of-plane equilibrium points caused by the J₂ term perturbation.

Intuitively, in the Z direction perpendicular to the orbital plane (O − XY), only gravitational forces from both primaries produce an acceleration towards the O − XY plane and no other force can balance such acceleration. Therefore, the existence of such out-of-plane equilibrium points is doubtful. We notice that even Douskos and Markellos suspected that the existence of such points is only a mathematical illusion due to the truncation of the potential.

For the case of oblate ellipsoidal primaries, we analytically show in this report that such equilibrium points proposed by Douskos & Markellos (2006) are located just inside the Brillouin sphere, where the potential function adopted therein is invalid. These equilibrium points do not exist in the physical point of view.

2 Estimation of the equilibrium

Just as in Douskos & Markellos (2006), let us consider the circular restricted three-body problem, in which a massless body P moves under the gravitational force exerted by an oblate ellipsoid m₁ and a point mass m₂. We choose the distance between these two primaries as the unit of length, the total mass (m₁ + m₂) as the unit of mass, and the unit of time is chosen so as to make the gravitational constant G = 1. The motion of the massless body in the synodic frame (see Fig. 1) can be described as 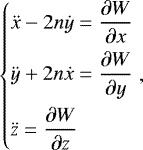$$\{\begin{array}{l}\ddot{x}-2n\dot{y}=\frac{\partial W}{\partial x}\hfill \\ \ddot{y}+2n\dot{x}=\frac{\partial W}{\partial y}\hfill \\ \ddot{z}=\frac{\partial W}{\partial z}\hfill \end{array},$$(1)

where W is the potential function given by $$\begin{array}{lll}W\hfill & =\hfill & \frac{1}{2}{n}^2(x^2+y^2)+\frac{{\mu }_1}{r_1}\left[1+\frac{A}{2r_1^2}\left(1-\frac{3z^2}{r_1^2}\right)\right]+\frac{{\mu }_2}{r_2},\hfill \\ {\mu }_1\hfill & =\hfill & m_1/(m_1+m_2), {\mu }_2=1-{\mu }_1,\hfill \\ r_1^2\hfill & =\hfill & {(x+{\mu }_1)}^2+y^2+z^2, r_2^2={(x-{\mu }_2)}^2+y^2+z^2.\hfill \end{array}$$(2)

The angular velocity n depends on the oblateness of m₁ and in this case 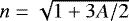$n=\sqrt{1+3A/2}$. The dimensionless quantity A indicates the oblateness of m₁ which is defined as 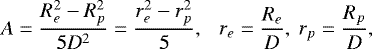$$A=\frac{R_e^2-R_p^2}{5D^2}=\frac{r_e^2-r_p^2}{5}, r_e=\frac{R_e}{D}, r_p=\frac{R_p}{D},$$(3)

where D is the distance between two primaries, while R_e (r_e) and R_p (r_p) are the real (normalized) equatorial and polar radii of the ellipsoid m₁, respectively. It is worth noting that the potential of m₁ in W is the truncation up to the J₂ term of the spherical harmonics expansion of the potential function.

Since we are only interested in the out-of-plane equilibrium points, we focus on the Z direction, where the equilibrium is attained when ∂W∕∂z = 0, i.e., $$\frac{\partial W}{\partial z}=-\frac{{\mu }_2}{r_2^3}z-\frac{{\mu }_1}{r_1^3}\left[1+\frac{3A}{2r_1^2}\left(3-\frac{5z^2}{r_1^2}\right)\right]z=0.$$(4)

Obviously the gravitational force from the point mass m₂ (the first term) and the main part of m₁ always pointtowards the XY plane, thus only the component generated by the J₂ term of m₁ may balance the acceleration towards the XY plane. For any out-of-plane point z≠0, Eq. (4) can be possibly satisfied only if the latter term is negative for some r₁, i.e., 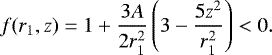$$f(r_1,z)=1+\frac{3A}{2r_1^2}\left(3-\frac{5z^2}{r_1^2}\right)<0.$$(5)

Actually, z² can take any value from 0 to 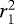$r_1^2$, and thus the minimum value of f(r₁, z) for arbitrary fixed r₁ can be reached at z = ±r₁, i.e., 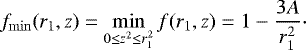$$f_{\min }(r_1,z)=\underset{0\le z^2\le r_1^2}{\min }f(r_1,z)=1-\frac{3A}{r_1^2}\cdot$$(6)

It is necessary to have f_min(r₁, z) < 0 to make the inequity Eq. (5) true, which gives the estimation of r₁, that is 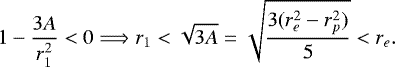$$1-\frac{3A}{r_1^2}<0\Rightarrow r_1<\sqrt{3A}=\sqrt{\frac{3(r_e^2-r_p^2)}{5}}<r_e.$$(7)

The inequality r₁ < r_e in Eq. (7) means that any out-of-plane equilibrium points obtained by solving Eq. (4) must be located inside the Brillouin sphere around m₁.

If the rotational ellipsoid satisfies some usual constrains, we can further show that such artificial equilibrium points are even located inside the rotational ellipsoid. Suppose a rotational ellipsoid meets the following conditions: 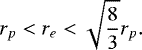$$r_p<r_e<\sqrt{\frac{8}{3}}{r}_p.$$(8)

We first introduce a function g(r₁, z) as follows: $$\begin{array}{lll}g(r_1,z)\hfill & =\hfill & \left[\frac{{(x+{\mu }_1)}^2}{r_e^2}+\frac{y^2}{r_e^2}+\frac{z^2}{r_p^2}\right]-1\hfill \\ \hfill & =\hfill & \frac{(r_1^2-z^2)}{r_e^2}+\frac{z^2}{r_p^2}-1,\hfill \end{array}$$(9)

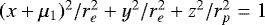where ${(x+{\mu }_1)}^2/r_e^2+y^2/r_e^2+z^2/r_p^2=1$ indicates the surface of the ellipsoid. Then, obviously 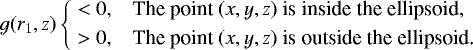$$g(r_1,z)\{\begin{array}{ll}<0,\hfill & \text{The point }(x,y,z)\text{ \& is inside the ellipsoid,}\hfill \\ >0,\hfill & \text{The point }(x,y,z)\text{ \& is outside the ellipsoid.}\hfill \end{array}$$(10)

From Eq. (5), we obtain 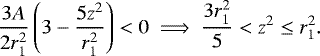$$\frac{3A}{2r_1^2}\left(3-\frac{5z^2}{r_1^2}\right)<0 \Rightarrow \frac{3r_1^2}{5}<z^2\le r_1^2.$$(11)

Thus, for any fixed r₁, the maximum of g(r₁, z) is attained when 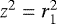$z^2=r_1^2$, and thus 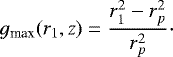$$g_{\text{max}}(r_1,z)\text{\&}=\frac{r_1^2-r_p^2}{r_p^2}\cdot$$(12)

Since here g_max depends only on r₁ but not z, the estimation given in Eq. (7) shall be taken into account, resulting in 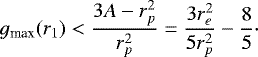$$g_{\text{max}}(r_1)<\frac{3A-r_p^2}{r_p^2}=\frac{3r_e^2}{5r_p^2}-\frac{8}{5}\cdot$$(13)

Because any equilibrium point must satisfy Eqs. (5) and (11), when Eq. (8) is fulfilled, we have for any equilibrium point 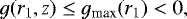$$g(r_1,z)\le g_{\text{max}}(r_1)<0,$$(14)

that is, the equilibrium points are inside the ellipsoid. Apparently, such rotational ellipsoid satisfying Eq. (8) is ubiquitous. This gives the counterexamples for the existence of out-of-plane equilibrium because the potential function adopted in Douskos & Markellos (2006) is obviously invalid inside the ellipsoid.

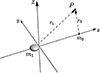Fig. 1 Illustration of the circular restricted three-body problem with oblateness. The origin of the synodic coordinate is in the barycentre. The primary m1 is the rotational ellipsoid whose coordinate is (−μ2, 0, 0), while m2 is the point mass located at (μ1, 0, 0).

3 Discussion

Base on the force balance in the Z direction, we have analytically shown that the out-of-plane equilibrium points found in Douskos & Markellos (2006) are located inside the Brillouin sphere of the oblate primary or even below the surface of the ellipsoidal primary body. Since the spherical harmonics expansion of the potential function is not valid at this point, we believe that the existence of these out-of-plane equilibrium points is caused by the improper application of the potential function. In fact, using the closed form of potential function, wecan also prove that the acceleration produced by an ellipsoidal asteroid will always point towards to the O − XY plane, such that no out-of-plane balance point can exist. Surely, this conclusion holds for the case that both primaries are oblate.

Acknowledgements

We thank the anonymous referee for very helpful comments. This work has been supported by the National Natural Science Foundation of China (NSFC, Grants No.11473016 & No.11333002).

References

All Figures

	Fig. 1 Illustration of the circular restricted three-body problem with oblateness. The origin of the synodic coordinate is in the barycentre. The primary m1 is the rotational ellipsoid whose coordinate is (−μ2, 0, 0), while m2 is the point mass located at (μ1, 0, 0).
In the text