| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201732215 | |
| Published online | 22 June 2018 | |
A new solution to the plasma starved event horizon magnetosphere
Application to the forked jet in M87
1
ICRANet, Piazza della Repubblica 10 Pescara, 65100, Italy
2
ICRA, Physics Department, University La Sapienza, Roma, Italy
e-mail: brian.punsly@cox.net
3
Centre for Astrophysics Research, School of Physics, Astronomy and Mathematics, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
4
Mizusawa VLBI Observatory, National Astronomical Observatory of Japan, Osawa, Mitaka, Tokyo 181-8588, Japan
Received:
31
October
2017
Accepted:
10
January
2018
Very Long Baseline Interferometry observations at 86 GHz reveal an almost hollow jet in M87 with a forked morphology. The detailed analysis presented here indicates that the spectral luminosity of the central spine of the jet in M87 is a few percent of that of the surrounding hollow jet 200–400 μ as from the central black hole. Furthermore, recent jet models indicate that a hollow “tubular” jet can explain a wide range of plausible broadband spectra originating from jetted plasma located within ~30 μ as of the central black hole, including the 230 GHz correlated flux detected by the Event Horizon Telescope. Most importantly, these hollow jets from the inner accretion flow have an intrinsic power capable of energizing the global jet out to kiloparsec scales. Thus motivated, this paper considers new models of the event horizon magnetosphere (EHM) in low luminosity accretion systems. Contrary to some models, the spine is not an invisible powerful jet. It is an intrinsically weak jet. In the new EHM solution, the accreted poloidal magnetic flux is weak and the background photon field is weak. It is shown how this accretion scenario naturally results in the dissipation of the accreted poloidal magnetic flux in the EHM not the accumulation of poloidal flux required for a powerful jet. The new solution indicates less large scale poloidal magnetic flux (and jet power) in the EHM than in the surrounding accretion flow and cannot support significant EHM driven jets.
Key words: black hole physics / galaxies: active / galaxies: jets / accretion, accretion disks / quasars: general
© ESO 2018
1 Introduction
Large scale poloidal magnetic flux that threads the event horizon (EH) of a rotating black hole (BH) forms an event horizon magnetosphere (EHM) that is a viable source of BH driven jets. Since the BH cannot be a source of plasma, the EHM is charge starved (lacks a supply of charge that is required to support a frozen-in magnetosphere, everywhere) and strong analogies with pulsar driven winds have been made (Blandford & Znajek 1977). A large distinction between these two environments is that the neutron star (NS) is a superconductor and supports magnetic fields with the largest field strengths in the known Universe (~108 G–1014 G), whereas the BH cannot support its own magnetic field, since the field must be produced outside of the EH (Punsly 2008). This distinction has not been considered in depth in previous treatments of EHM jets. This paper discusses plausible astrophysical circumstances in which this distinction has a crucial effect on the physics of the system.
The EHM is located within the vortex of the accretion flow and requires plasma injection in order to maintain a jetted system (Blandford & Znajek 1977). In seminal efforts, two viable options for producing the plasma in the EHM were postulated. The first was drawn directly from pulsar theory. In the charge starved limit, various types of vacuum gaps and null (zero density) surfaces can exist in principle. As in pulsar theory, the semi-vacuum electric field in these gaps can accelerate leptons to very high energy thereby powering multi-stage pair creation scenarios that seed the magnetosphere with an ideal magnetohydrodynamic (MHD) plasma (Sturrock 1971; Cheng et al. 1986). Analogously, EHM gap models always assume that a background magnetic field is already present (Beskin et al. 1992; Hirotani & Okamoto 1998; Hirotani & Pu 2016; Broderick & Tchekhovskoy 2015; Ptitsyna & Neronov 2016; Levinson 2000; Levinson & Rieger 2011). The other idea, unique to BHs, is that the ambient γ-ray field (presumably from the accretion flow) can produce enough electron-positron pairs to seed the EHM. This study considers these scenarios in the context of creating (as opposed to perpetuating) an EHM in realistic astrophysical environments. In particular, in any BH time evolution problem a causal temporal order of events is required to establish the initial state. Without this key element as part of the solution, it is not clear that a physical solution is attained.
In Sect. 2, the details of the scenario in which the EHM is created by a slow accumulation of thin, weak, isolated magnetic flux tubes that are transported to the EH by an accretion flow is explored. This assumed model of the seeding of the EHM is the basis of the analysis of the charge starved limit discussed in this paper. By “thin, weak, isolated magnetic flux tubes” it is meant:
-
thin: the dimensions of the flux tubes are very narrow compared to the dimensions of the disk and BH;
-
isolated: the large scale poloidal flux that extends above or below the disk consists of a few strands of flux that extend off to infinity as opposed to closing as loops back into the disk. They accrete sporadically as opposed to a nearly uniform, continual deposition of flux tubes into the EHM;
-
weak: the field lines are readily deformed by the surrounding disk atmosphere. The field strength is less than that which is required to initiate a pair cascade.
The EHM solution considered here is evaluated in the charge starved limit. Without sufficient plasma, it is shown that the accreted poloidal magnetic flux readily dissipates in the EHM. The dissipation is rapid relative to the rate that plausible accretion scenarios can replenish the flux. Thus, a highly magnetized EHM is not created.
The radio galaxy, M87, appears to be an ideal candidate for the new EHM solution. It has a very low luminosity accretion flow with arguably too low a photon flux to support significant pair creation on weak accreting flux tubes in the EHM. Furthermore, new high resolution Very Long Baseline Interferometry (VLBI) 86 GHz VLBI observations resolve the jet in M87 on scales much closer to the central BH than has been accomplished for any other radio loud active galactic nucleus (AGN; Kim et al. 2016; Hada et al. 2016). These images reveal a jet with an unexpected forked topology that seems to represent a hollow jet (see Sect. 4). There is no evidence of significant jet emission along the central spine above the EH in agreement with the new EHM solution to be presented in this paper. The new EHM solution is particularly relevant in the context of recent models of hollow jets emanating from the inner regions of an accretion flow that can describe a very wide range of plausible broadband spectra (mm wavelengths to UV) of the base of the jet in M87 on scales ~ 15− 30 μ as. In addition to explaining broadband emission from the region that produces the correlated 230 GHz flux detected by the EH Telescope (EHT), the jet base has sufficient power to energize the entire jet out to kiloparsec scales (Punsly 2017). There is no need to invoke a powerful invisible spine jet driven by the EHM in order to power the jet (Moscibrodzka et al. 2016). This supports the most direct interpretation of the 86 GHz VLBI images: the jet is hollow because the EHM jet is intrinsically weak in accord with the model presented here. Thus motivated, much of the discussion to follow is focused on the example of M87.
The paper is organized as follows. Section 2 is a discussion of the details of the time evolution of weak, isolated fluxtubes in the completely charge starved limit. This section assumes negligible plasma injection into the EHM in order to describe the new solution of the EHM that is proposed here. Without plasma injection from the external environment or a particle creation gap in the weak flux tubes, currents cannot be maintained. Flux is dissipated, not accumulated, if it accretes to the EHM. In Appendices A–C, the details of the dissipation of the poloidal magnetic flux transported within the charged starved, accreting flux tube is explored by means of approximate solutions to Maxwell’s equations in curved spacetime. The lack of a reservoir for accreted flux in the EHM indicates a weak EH driven jet.
The second part of the paper focuses on the application of the model to M87. The new model of the magnetosphere is predicated on the mode of accretion and inefficient pair creation. It is shown in Appendix D that for any plausible model there is some minimum field strength below which the posited accreted flux tubes will not produce a potential difference across the vacuum gap large enough to initiate a pair cascade. Thus, pair production in an external γ-ray field would be required to seed the EHM with plasma and would determine the maximum sustainable magnetic field and jet power in the EHM. In Sect. 3, the observational evidence that bounds the γ-ray luminosity of the inner accretion flow, from above, in M87 is discussed. No γ-ray telescope can resolve the inner accretion flow. The highest resolution observations of the hard photon spectrum are with the Chandra X-ray telescope. The core flux within 0.67 arcsec of the nucleus is extracted. This is combined with broadband hard photon spectra of AGN from INTEGRAL in order to give bounds on the γ-ray luminosity from the nucleus. This in turn implies an upper bound on the maximum sustainable magnetic field strength in the EHM and the resultant maximum Poynting flux that can be delivered by an EHM jet in M87. It is concluded that M87 is likely an example of a source with a weak γ-ray field near the EH that is incapable of producing enough pairs to support the currents required for an astrophysically significant EHM. In Sect. 4, it is noted that the results of Sects. 2 and 3 and Appendix C indicate that M87 is a possible example in which the EHM is so charge starved that any jet produced in this region will be very weak. It is shown that HSA (High Sensitivity Array) observations at 86 GHz support the new EHM model. There is a profound nadir of emissivity along the central spine at the jet base above the putative EHM that is consistent with this basic consequence of the new EHM solution. In the following, it is assumed that M = 6 × 109 M⊙ (8.4 × 1014 cm in geometrized units) appropriate for M87 (Gebhardt et al. 2011).
2 The creation of an EHM by accretion
This study considers a possible new EHM solution that might occur in some astrophysical black hole accretion systems. It is predicated on a particular mode of accretion onto a rotating (Kerr) BH described by a mass, M, and an angular momentum per unit mass, a. The context is the initial seeding of the BH magnetosphere with large scale poloidal flux. This is the initial state for the time of evolution of the EHM. The specific details of how an EHM is established are not known, and the processes involved are on too small a scale to be observed directly, even if one were to be observing during the initial stages. Thus any scheme for establishing the EHM must rely on assumptions. It is known that the flux must be delivered from the external environment since the Kerr BH does not support a magnetic field in isolation. A plausible method of creating a significant EHM is the radiatively inefficient accretion of weak poloidal magnetic flux from large distances over a long period of time (Igumenshchev 2008; Beckwith et al. 2009; McKinney et al. 2012). Similar ideas have been proposed for protostellar systems (Lery et al. 1999). It has been suggested that the large scale magnetic flux near a black holehas its origins in the advection of the weak large scale patchy magnetic field in the intergalactic medium or from a magnetized stellar wind or a tidal disruption event of a nearby magnetized star (McKinney et al. 2012). This is the scenario considered in this model of the EHM and it is the fundamental assumption of this paper.
Note that the charge starved limit and the assumed pair creation in an EHM violates perfect MHD. There are no existing numerical simulations that can study this limit. Perfect MHD numerical experiments involving accreting mass always end with the code crashing before the charge-starved limit is approached (see Koide et al. (2002) and references therein). Thus, numerical simulations artificially insert a non-MHD mass floor that perpetuates the solution (De Villiers et al. 2003; McKinney & Gammie 2004). One can distinguish these from ideal MHD simulations by denoting them as SFMHD+MF (single fluid MHD plus mass floor) in the following. A numerical simulation that utilizes a mass floor is not an acceptable device if one is considering the time evolution of a charge depleted system as is the case here. Thus, the dynamics of the charge starved accretion into the EHM will be described in what follows by approximate analytic arguments.
The dynamics take place in the background spacetime of a rotating black hole, the Kerr solution. In Boyer–Lindquist coordinates, the Kerr metric,gμν, is given by the line element in geometrized units
![\begin{eqnarray*} &&\mathrm{d}s^{2} \equiv g_{\mu\nu}\, \mathrm{d}x^{\mu}\mathrm{d} x^{\nu}= -\left (1-\frac{2Mr}{\rho^{2}}\right) \mathrm{d}t^{2}+\rho^{2}\mathrm{d}\theta^{2} \nonumber \\ && +\left(\frac{\rho^{2}}{\Delta}\right)\mathrm{d}r^{2} -\frac{4Mra}{\rho^{2}}\sin^{2}\theta\, \mathrm{d}\phi \, \mathrm{d}t \nonumber \\ && +\left [(r^{2}+a^{2})+\frac{2Mra^{2}}{\rho^{2}}\sin^{2} \theta\right ] \sin^{2} \theta \, \mathrm{d}\phi^{2}, \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq1.png) (1)
(1)
where ρ2 = r2 + a2 cos2θ and
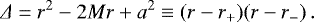 (2)
(2)
There are two EHs given by the roots of the equation Δ = 0. The outer horizon at r+ is of physical interest
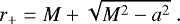 (3)
(3)
In order to simplify the calculations, one can compute quantities in a hypersurface orthogonal, orthonormal frame. There exists an orthonormal, Zero Angular Momentum Observers (ZAMO) frame associated with each coordinate pair, (r, θ). The ZAMOs can be used to express, locally, the electromagnetic field in terms of electric and magnetic (observer-dependent) fields. There are three main benefits of calculating in the ZAMO frames. The orthonormality condition is beneficial for utilizing many results and techniques from special relativity. By contrast, the Boyer–Lindquist coordinates are curvilinear and not even orthogonal. Thus, a physical interpretation of the covariant and contravariant quantities near the black hole is far from trivial. Secondly, unlike other orthonormal frames, being hypersurface orthogonal, the ZAMO frame provide an unambiguous definition of the electromagnetic field that is integrable (Punsly 2008). Most importantly, as shown in Appendix B, one can rotate the poloidal direction to always be along the local poloidal magnetic field direction. This greatly simplifies the interpretation of the electromagnetic quantities. Even though calculations are much clearer in the rotated ZAMO basis, ultimately we need to express the results in terms of the Boyer–Lindquist coordinates associated with the stationary observers at asymptotic infinity. Thus, we describe the transformation between frames. The ZAMO basis vectors are
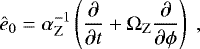
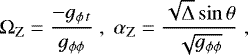
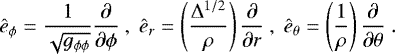 (4)
(4)
The lapse function, αZ, is the gravitational redshift of the ZAMOs as measured by the stationary observers at asymptotic infinity (i.e., astronomers on earth). Note that

Similarly, ΩZ, is the angular velocity of the ZAMOs as viewed by stationary observers at asymptotic infinity.
Boyer–Lindquist evaluated quantities are distinguished from ZAMO evaluated quantities by the use of a “tilde” on the variables. Both formalisms will be utilized in the description of the flux evolution.
 |
Fig. 1 Accretion of weak flux tubes into the EHM occurs in the SFMHD+MF simulation of Beckwith et al. (2009; left hand frame). Right hand frame: isolated flux tubes in the 3D radiatively inefficient simulations of (Igumenshchev 2008) and (Punsly et al. 2009). The strength of the vertical poloidal magnetic field is color coded. Dark blue is no field and red is a strong field (near equipartition with the gas pressure). The inner calculational boundary is a circle of radius 2M. Notice the weaker, green, small patches of vertical flux in the inner accretion flow. See the text for more details. |
2.1 Weak isolated flux tubes in the EHM
The conceptof a weak isolated magnetic flux tube is introduced by means of SFMHD+MF simulations. In the initial state there is no large scale poloidal flux that threads the event horizon. There needs to be a mechanism that can transport large scale poloidal flux to the EHM. The accretion flow is the natural place to look for such a source. Attempts to spontaneously create the flux from the accretion flow itself by means of the magneto-rotational instability (MRI) proved to be unsuccessful (Beckwith et al. 2009). A simulation requires a net poloidal flux in the accretion flow in order to build up a significant EHM (Igumenshchev 2008; Beckwith et al. 2009). When the simulation starts there is a transient state when the first flux tubes approach the EH. It will look similar to the t=1500M snapshot from a SFMHD+MF simulation of Beckwith et al. (2009), depicted in Fig. 1. The magnetic flux is clearly weaker in the EHM than in the disk and a single field line is separated by a large gap from the magnetic field in the disk. This is an accreted isolated flux tube created in the early stages of a SFMHD+MF simulation. All transient early stages of SFMHD+MF simulations create an EHM by beginning with the arrival of a first weak flux tube, unless the initial state is unphysical and posits large amounts of flux in the initial state in the EHM proper or adjacent to the EHM. This is true even if a saturated magnetosphere is attained at large times (McKinney et al. 2012).
The right hand frame of Fig. 1 shows a different depiction of isolated flux tubes in the 3D radiatively inefficient simulation of (Igumenshchev 2008) and (Punsly et al. 2009). This frame is from the online movies of the latter reference. The strength of the vertical poloidal magnetic field is color coded. Dark blue is no field and red is a strong field (near equipartition with the gas pressure of the surrounding accretion flow). Notice that the field accumulates in isolated patches. Even though it was definitely not the intent of this simulation, in this image there are small patches of weak field near the inner boundary (a circle of radius 2M). The greenish-yellow patches have a magnetic pressure ~ 2%–10% of equipartition with the gas pressure of the surrounding gas. These are examples of weak isolated flux tubes. It is important to note that in this simulation they formed as a consequence of the amalgamation of a steady influx of very weak field from the outer calculation boundary. The flux reservoir at the outer boundary is axisymmetric, but the accretion flow is not. The 3D accretion flow is driven by the MRI as in the Beckwith et al. (2009) simulations. However, these simulations have a much larger reservoir of flux at the outer boundary. If there is a large reservoir of poloidal flux, condensations of vertical flux will naturally occur as a consequence of the MRI driven turbulence. In general the isolated flux tubes are more magnetized in other time snapshots. However, these simulations suggest that weak isolated vertical flux tubes might be natural in an accretion flow. The patches of vertical magnetic flux near the black hole should be weaker and more isolated if the reservoir of flux is a weak patchy intergalactic magnetic field as opposed to a constant flood of flux as in the simulation in Fig. 1.
2.2 Relevant assumptions of SFMHD+MF simulations
In this paper, the early time behavior of a nascent EHM is analyzed after abandoning some major assumptions of the SFMHD+MF simulations. In particular:
-
The notion of a mass floor is dropped. Physically, this equates to a black hole accretion system in which there is no efficient plasma injection mechanism to support the flux in the EHM.
-
There is no large reservoir of magnetic flux that persistently deposits flux into the EHM. It is instead assumed that the flux deposits into the EHM on astronomically large time scales. For example, the jet propagation speeds indicate a jet lifetime of >106 years for many radio loud AGN (Willott et al. 1999). This is >108 light travel times across the black hole in M87. Even a small fraction of this time scale is not computer resource efficient for SFMHD+MF simulations, so a more compact flux source is assumed in those numerical models. However, a compact source is not a valid assumption if the rate that flux accretes is dynamically important as in this section and Appendix C.
-
It is alsonot assumed that the distant flux reservoir is uniform, but is composed of small distinct patches of isolated flux.
By dropping assumption 1), there will be insufficient plasma to support MHD. In the low or zero pair creation limit, it is shown in Appendix C that the magnetic flux will dissipate in the EHM on a timescale, tdis. that is estimated. Dropping assumption 3) allows for an non uniform deposition of flux into the EHM over time. This naturally produces temporal gaps between episodes in which isolated patches of accreted flux are deposited in the EHM. The dynamical timescale to deposit more flux, tdyn, can exceed tdis allowing theflux tube to dissipate before an accumulation of flux can occur.
2.3 Maxwell’s Equations description of a weak isolated flux tube
Figure 2 shows an idealized isolated, large scale, poloidal flux tube accretion scenario. There are two components of the magnetic field in the accretion flow since the system is in rotation with the plasma, Bϕ and BP, azimuthal and poloidal respectively. In the thin flux tube limit (so thin that cross-field gradients in the current and field are negligible compared tothe gradients at the boundaries), the electromagnetic sources are approximately surface currents. To quantify this for flux tubes that emanate from the accretion disk, a cylindrical coordinate system in flat space is chosen for demonstrative purposes, (ρcyl, ϕ, z). The inner boundary of the flux tube is 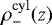 and the outer boundary is
and the outer boundary is 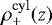 , where axisymmetry is assumed for simplicity. The thin flux tube limit is defined for small ϵ > 0 by the conditions,
, where axisymmetry is assumed for simplicity. The thin flux tube limit is defined for small ϵ > 0 by the conditions,
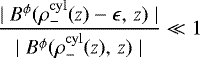 (8)
(8)
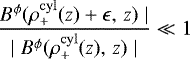 (9)
(9)
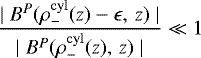 (10)
(10)
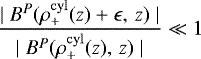 (11)
(11)
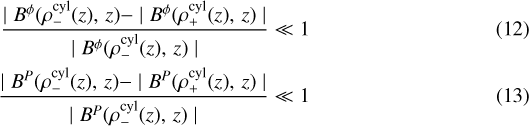
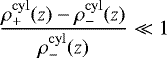 (14)
(14)
The fact that the slowly accreting isolated flux tubes have a B field much stronger than that of the plasma on both sides of the flux tube means that the surface current will change the field strength from approximately zero to B in Ampere’s law at the inner face of the flux tube. Similarly, the surface current will change the field from B to near zero at the outer face of the flux tube. Since the flux tube accretes with the plasma in the disk, it essentially spirals with the Keplerian velocity with a relatively slow inward radial drift (Sadowski 2011). Thus, to first approximation, one can ignore displacement current in Amperes’s law for the field inside the axisymmetric flux tube. Let K designate a surface current. In the approximately cylindrical configuration. by Ampere’s Law and Eqs. (8)–(14),
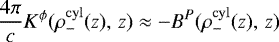 (15)
(15)
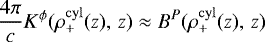 (16)
(16)
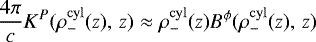 (17)
(17)
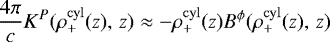 (18)
(18)
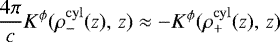 (19)
(19)
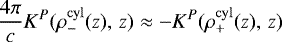 (20)
(20)
The integralof KP over an orthogonal cross-section of either the inner or outer boundary of the flux tube (the total poloidal current) is approximately conserved from the disk to asymptotic infinity in the axisymmetric, magnetically dominated limit and a conserved value represents electromagnetic angular momentum flux conservation in the flux tube (Punsly 2008). Kϕ is set by the poloidal magnetic flux conservation condition from the accretion flow to asymptotic infinity in each flux tube. The corresponding curved spacetime versions of these surface current equations are derived in Appendix B in the ZAMO frames.

These equations are required near the black hole. The Boyer–Lindquist coordinates, (rin, θin) indicates a point on the inner boundary of the flux tube and (rout, θout) indicates a point on the outer boundary of the flux tube.
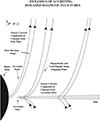 |
Fig. 2 Dynamics of the accretion of weak flux into the EHM is depicted above. The accretion flow in this image is likely much thinner than what occurs in M87. The concepts that are illustrated are not a consequence of the accretion flow thickness. |
2.4 The dynamics of accreted weak isolated flux tubes
During the inflow through the disk, the source of the charges that create the currents that sustain the magnetic flux is in the base of the flux tube that is frozen into the accretion flow. Plasma is shot outward by magneto-centrifugal forces in the rotating flux tube and dragged inward near the base (accretion) by gravity (Igumenshchev 2008). The plasma that is shot outward is provided by the accretion flow before the flux tube enters the EHM.
Figure 2 shows that the dynamic that existed in the flux tube in the accretion disk persists as it enters the EHM. In particular, plasma is still shot outward by magneto-centrifugal forces in the rotating flux tube and still dragged inward (accretion) by gravity (Koide et al. 2002; Semenov et al. 2004). At the flow division surface, the flow divides into an accretion flow and an outgoing wind (Phinney 1983). Due to gravitational redshifting and frame dragging, the plasma in the flux tube near the EH is out of causal contact with the large scale poloidal flux (Punsly 2008). In this discussion, it is assumed that there is no external plasma injection mechanism such as pair production (see Appendix D and Sect. 3 for the likelihood of this possibility in M87). Plasma that is already threaded on the flux tube must provide the outgoing plasma and the currents supporting the magnetic field.1 There is a finite amount of plasma in the flux tube and the plasma quickly becomes tenuous. The plasma starts to drain from the flow divisionsurface producing a vacuum gap as depicted in Fig. 3. The figure is a schematic diagram that shows the split that occurs in the distribution of plasma, not the field lines, as the vacuum gap begins to expand. Initially, the field lines are not severed in the vacuum gap. However, the poloidal magnetic field is not uniform in this region. The poloidal field bulges outward and inward as fringing effects become pronounced. A laboratory example of this effect would occur if one split a long solenoid in the middle, then pulled the two halves away from each other along the axis of symmetry. A non-uniformbulging field occurs in the gap between the two coils. At later times, the fringing fields associated with the spreading vacuum gap expand and can approach other fringing field lines along circles (due to axisymmetry) of X-type reconnection points. This reconnection process can change the topology of the poloidal magnetic field.
In Appendix C, we discuss a model of an accreted flux tube in which there are insufficient charges to maintain the source currents in the EHM–charge starved. The lower portion of the flux tube contracts toward the black hole by gravity and the outer is slung out by magneto-centrifugal forces. Evaluating Maxwell’s equations as the inner portion of the flux tube approaches the EH indicates that the large scale poloidal magnetic field in the EHM will approximately be a decaying magnetic dipole (see Fig. C.2). Since the calculation is very long and involved, we only summarize the logic and results in the main text.
-
Equations (21)–(24) are used to describe the current distribution in the ingoing portion of the severed flux tube as two nested, coaxial helical surface currents distributions, one in each hemisphere.
-
In Appendix C.1, it is shown that due to gravitational redshift as these helical current flows accrete close to the EH they seem to be frozen in corotation with the horizon, hovering just above it, as viewed by external observers. Thus, these axisymmetric electromagnetic source are approximately time stationary to the external observers (e.g. in Boyer–Lindquist coordinates) that would be affected by the large scale poloidal magnetic field. Therefore, Laplace’s equations can be used to accurately depict the large scale poloidal magnetic field for these sources at any given Boyer–Lindquist time, t (Punsly & Coroniti 1989).
-
In Appendix C.2, it is shown that at late times in the accretion, near the event horizon, the large scale poloidal magnetic field from the helical current sources can be approximated as the large scale poloidal magnetic field due to 4 azimuthal current rings that are located near the black hole (see Fig. C.1).
-
In Appendix C.3, the large scale poloidal magnetic field produced by the four current loops is calculated by means of Laplace’s equations in curved spacetime and the results plotted in Fig. C.2. The large scale poloidal magnetic field is approximately a decaying magnetic dipole.
-
In Appendix C.4, it is estimated that the flux tube dissipates (magnetic dipole decays) on a time scale, t < 10 M, after thevacuum gap starts to spread apart. This time scale is much less than any time scale of the accretion flow. Thus, for the accretion scenario posited in this section, the flux will dissipate before more flux can accumulate in the EHM. A highly magnetized EHM will not form.
-
In Appendix C.4, based on Fig. C.2, it is argued that surface currents induced in the disk during the field decay do not prevent accreted, thin, isolated flux tubes in a charge starved EHM from dissociating. These currents are decaying and are of the wrong sign to maintain the accreted flux within the EHM.
This suggests that an interesting new dynamic can exist in the EHM if the EHM is charge starved: no vacuum gap pair cascades and weak γ-ray pair production. Thus motivated, standard vacuum gap pair production in the EHM are considered in Appendix D and γ-ray pair production is discussed in the case of M87 in the next section.
 |
Fig. 3 In the charge-starved limit, a vacuum gap will spread outward from the flow division surface if there is no substantive pair injection mechanism as is quite possibly the case in M87. In this charge starved limit, the surrounding magnetosphere is a semi-vacuum. The only significant source of electromagnetic fields is within the flux tube. The very tenuous stray charges have trajectories that are affected by these fields, but the number density is too small to provide a source for a significant perturbation to these fields. Charges can only flow inward across the charge horizon (Komissarov 2004; Punsly 2004). |
3 The γ-ray induced pair creation in the EHM of M87
In the weak field limit, proposed in the last section, the EHM will not be able to sustain pair creation in a vacuum gap (see Appendix D for more elaboration). Thus, pair creation in an external γ-ray field is required in order to provide plasma to the accreted flux tubes and this will determine the maximum sustainable magnetic field strength in the EHM. This particle injection mechanism is considered in the context of the accretion scenario of Sect. 2 in the environment of M87.
γ-rays from the jet in M87 are produced relatively far away and beamed away from the EH and do not contribute to EHM pair production. However, the γ-ray field of the accretion flow can produce electron-positron pairs in the EHM. In this section, the available data related to the hard photon spectrum of M87 is considered in order to make as precise as possible any constraints that can be imposed on the γ-ray luminosity. The resolution of telescopesin the γ-ray band is many orders of magnitude too low to be of any use. However, the low energy region of the hard photon spectrum can be resolved to within 0.67 arcsec by Chandra. This information is used in consort with what is known about the hard photon spectra of other AGN (in particular, the cutoff energy) in order to constrain the γ-ray luminosity in M87. Even though it will be concluded that the Chandra flux is likely from the jet itself, this detection still provides a useful andnon-arbitrary bound on the hard photon spectrum from the accretion flow.
The number density of created pairs from a background γ-ray field can be estimated by balancing the infall (free-fall) rate with the pair creation rate (Phinney 1983)
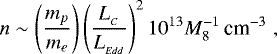 (25)
(25)
where 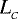 is the luminosity of γ-rays > 1 MeV from the accretion flow,
is the luminosity of γ-rays > 1 MeV from the accretion flow, 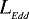 is the Eddington luminosity and M8 is the mass of the black hole in units of 108 M⊙. If the pair creation process can produce a charge density in excess of the Goldreich-Julian density,
is the Eddington luminosity and M8 is the mass of the black hole in units of 108 M⊙. If the pair creation process can produce a charge density in excess of the Goldreich-Julian density,  , then the growth of the electric field in the vacuum gap can be quenched and the surface current flow sustained on the flux tube (Goldreich & Julian 1969). One can estimate
, then the growth of the electric field in the vacuum gap can be quenched and the surface current flow sustained on the flux tube (Goldreich & Julian 1969). One can estimate 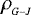 near the EH
near the EH
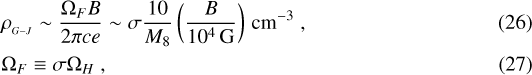
where ΩF and ΩH are the angular velocity of the magnetic field and the EH angular velocity as viewed from asymptotic infinity, respectively. For a given γ-ray field, the condition, 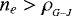 , determines the maximum sustainable B field in a thin accreting magnetic flux tube in the EHM.
, determines the maximum sustainable B field in a thin accreting magnetic flux tube in the EHM.
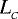 in M87 is constrained by revisiting the estimate of the accretion flow X-ray luminosity, Lx, from Hardcastle et al. (2009), with a smaller extraction region (correcting for the PSF outside the region) of 0.67 arcsec (versus 1 arcsec) to avoid contamination from the knot, HST-1, in the Chandra data (Harris et al. 2003). No detectable X-ray excess above a single unabsorbed power law flux density was observed: αx =1.1, LE ∝ E−αx, where E is photon energy and Lx = 2.9 × 1040erg s−1 from 2–10 keV. The nucleus is a continuation of the large scale X-ray jet with similar values of Lx and αx to those of the knots in the jet (Wilson & Yang 2002). Mid-IR and optical studies conclude that there is no hidden strong accretion source, but just a synchrotron nuclear source in M87 (Whysong & Antonucci 2004; Chiaberge et al. 1999). Broadband correlations amongst the nuclear synchrotron and X-ray fluxes in many Fanaroff-Riley I (FRI) radio galaxies such as M87 also imply a jet origin for X-rays (Hardcastle & Worrall 2000; Hardcastle et al. 2009).
in M87 is constrained by revisiting the estimate of the accretion flow X-ray luminosity, Lx, from Hardcastle et al. (2009), with a smaller extraction region (correcting for the PSF outside the region) of 0.67 arcsec (versus 1 arcsec) to avoid contamination from the knot, HST-1, in the Chandra data (Harris et al. 2003). No detectable X-ray excess above a single unabsorbed power law flux density was observed: αx =1.1, LE ∝ E−αx, where E is photon energy and Lx = 2.9 × 1040erg s−1 from 2–10 keV. The nucleus is a continuation of the large scale X-ray jet with similar values of Lx and αx to those of the knots in the jet (Wilson & Yang 2002). Mid-IR and optical studies conclude that there is no hidden strong accretion source, but just a synchrotron nuclear source in M87 (Whysong & Antonucci 2004; Chiaberge et al. 1999). Broadband correlations amongst the nuclear synchrotron and X-ray fluxes in many Fanaroff-Riley I (FRI) radio galaxies such as M87 also imply a jet origin for X-rays (Hardcastle & Worrall 2000; Hardcastle et al. 2009).
An upper bound for 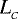 due to accretion can be estimated in two ways from the Chandra data. First, consider the limiting scenario (although itis unlikely considering the discussion above) that the Chandra nuclear flux is from the accretion flow. This estimate is performed in order to establish the most conservative limit on the upper bound on
due to accretion can be estimated in two ways from the Chandra data. First, consider the limiting scenario (although itis unlikely considering the discussion above) that the Chandra nuclear flux is from the accretion flow. This estimate is performed in order to establish the most conservative limit on the upper bound on 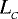 , Secondly, it is assumed that the accretion X-ray source is hidden by an attenuating column of neutral hydrogen, 1022 cm−2 < NH < 1023 cm−2 and αx = 0.7 (Hardcastle et al. 2009). Note that there is no evidence of such a large NH in M87. In this case, an intrinsic Lx < 1.9 × 1039erg s−1 from 2–10 keV with 90% confidence is estimated. These are “worst case”, not necessarily likely, scenarios for producing upper bounds on
, Secondly, it is assumed that the accretion X-ray source is hidden by an attenuating column of neutral hydrogen, 1022 cm−2 < NH < 1023 cm−2 and αx = 0.7 (Hardcastle et al. 2009). Note that there is no evidence of such a large NH in M87. In this case, an intrinsic Lx < 1.9 × 1039erg s−1 from 2–10 keV with 90% confidence is estimated. These are “worst case”, not necessarily likely, scenarios for producing upper bounds on 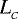 .
.
The wideband Lx(wb) from accretion in AGN and Galactic compact objects is typically approximated by a cutoff power law, Lx (wb) ∝ E−αxe-E/Ec, where Ec is the cutoff energy (Malizia et al. 2014). It is assumed that the spectral index, αx, is constant from keV to MeV energies in the following calculations. However, the upper bounds that are computed below are valid as long as the power law does not flatten at higher energies. Figure 4 contains plots of three upper bounds as functions of Ec for both scenarios: 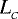 , the associated maximum sustainable Poynting flux from the EHM and the maximum sustainable value of B from Eqs. (25)–(27). The B plot assumes the seminal value of σ = 0.5 from Blandford & Znajek (1977) and a∕M = 0.9. The range of Ec appropriate to the putative accretion source of Lx(wb) is motivated by INTEGRAL observations indicating an average Ec = 125 keV for type I AGN and radio loud AGN in which Lx(wb) is not of blazar (jet) origin (Malizia et al. 2014). The MHD Poynting flux in the magnetically dominated limit is
, the associated maximum sustainable Poynting flux from the EHM and the maximum sustainable value of B from Eqs. (25)–(27). The B plot assumes the seminal value of σ = 0.5 from Blandford & Znajek (1977) and a∕M = 0.9. The range of Ec appropriate to the putative accretion source of Lx(wb) is motivated by INTEGRAL observations indicating an average Ec = 125 keV for type I AGN and radio loud AGN in which Lx(wb) is not of blazar (jet) origin (Malizia et al. 2014). The MHD Poynting flux in the magnetically dominated limit is
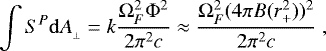 (28)
(28)
where Φ is the total magnetic flux enclosed within the jet (through the EH), 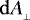 is the cross-sectional area element (surface area element of EH) and k is a geometrical factor that equals 1 for a uniform highly collimated jet (Punsly 2008). Using the fact that ΩH = a∕(2Mr+) and Eqs. (25)–(28), the upper bound on the approximate Poynting flux is independent of BH spin and the jet model for σ over a wide range: 0.4 < a < 0.95 and 0.1 < σ < 1.
is the cross-sectional area element (surface area element of EH) and k is a geometrical factor that equals 1 for a uniform highly collimated jet (Punsly 2008). Using the fact that ΩH = a∕(2Mr+) and Eqs. (25)–(28), the upper bound on the approximate Poynting flux is independent of BH spin and the jet model for σ over a wide range: 0.4 < a < 0.95 and 0.1 < σ < 1.
Figure 4 shows that the Chandra data likely imply a γ-ray accretion source in M87 that is insufficient to support even a 1G field in a charge-starved EHM. Furthermore, the largest upper bounds on Poynting flux are more than three to four orders of magnitude less than the estimated jet power of ~ 1043ergs s−1–1044ergs s−1 (McNamara et al. 2011; Stawarz et al. 2006).
 |
Fig. 4 Upperlimits on LC and the maximum sustainable Poynting flux from the EHM for M87 as a function of Ec for two cases, Lx is entirely from accretion or Lx from accretion is attenuated by an absorbing screen, NH. The maximum sustainable magnetic field in the EHM assuming that a∕M = 0.9 is also plotted. |
4 Evidence for a hollow jet in M87
This section considers possible evidence in support of the posited model of the EHM for the particular case of M87. New data reductions from high sensitivity 86 GHz VLBI are provided that indicate a much larger deficit of luminosity along the jet spine at the base of the jet in M87 than has been previously demonstrated at lower resolution. This result is combined with lower resolution data in order to examine the details of the new EHM model and previous explanations of limb brightening.
The fundamental testable consequence of this model of the EHM is the existence of a jet with a base that is wider than the EH (i.e., driven from the accretion flow) that will have a dearth of intrinsic emissivity along its central spine, above the EH. The jet in M87 is likely optically thin since the flux density, Fν ∝ ν−0.8 (Hada et al. 2016). If the jet is hollow to first order, lines of sight (LOS) that are nearly parallel (or anti–parallel) to the tangent to the circumference of the jet will intersect larger column densities of optically thin plasma than a LOS through the middle of the jet. Thus, one expects a limb brightened appearance in two places, one where the LOS is parallel and one where it is anti-parallel to the tangent of the jet circumference if the jet is hollow to first order as predicted by the new EHM model. In order to test this prediction, consider the HSA image at 86 GHz in Fig. 5 (Hada et al. 2016). The flux nadir along the center of the jet is resolved within 56 M (0.2 mas) of the EH and is not transient, occurring in multiple epochs (Kim et al. 2016). The flux nadir from 0.2 mas to 0.4 mas can be described quantitatively in terms of the integrated flux density. The total 86 GHz flux density of the central flux nadir in the region 0.2 mas–0.4 mas from the black hole is ≈ 6% of the flux density of the surrounding outer sheath jet (hollow jet).
Patches of enhanced surface brightness are clearly detected in the central void (“the spine”) at 0.5 mas in Fig. 5 and beyond 1.5 mas in multiple epochs with increasing prominence downstream (Mertens et al. 2016). In particular, the velocity field of the inner jet in M87 has been mapped by means of a 43 GHz VLBA wavelet analysis (Mertens et al. 2016). Even though, the data is from 2007, seven years before the HSA observations, the components line up reasonably well with the ridges seen in the 86 GHz image between 0.5 mas and 1.5 mas. The 43 GHz wavelet analysis is consistent with new 22 GHz VLBI data from 2014 (Hada et al. 2017). Within 1.5 mas, the wavelet based apparent velocities are similar to the values obtained by Hada et al. (2016) for the HSA observation, ~ 0.1c–0.4c, quite subluminal. The 43-GHz analysis also provides valuable evidence of the dynamics of the spine beyond 1.5 mas from the core. The apparent velocity, vapp, of the individual components of the spine, at the smallest displacements from the core for which the signal to noise of the spine is sufficient for such estimates (1.5 mas–2 mas from the core), is vapp ∕∕c = 1.33 ± 0.63 and vapp ∕∕c = 1.16 ± 0.77 for the surrounding limbs (Mertens et al. 2016). The similarity of the velocity field for the spine and the limbs suggests that the spine is gradually being filled by plasma that originates in the surrounding sheath and slowly spreads inward towards the central axis, as would be expected in the model in which the spine is empty at the jet base. In other words, the vapp distribution and increased spine prominence downstream is well explained in terms of a weak EHM jet surrounded by a hollow jet that slowly fills in the relative void with kinematically similar plasma as it propagates.
We consider a few possible alternative models for the observations.
4.1 Bifurcating obstacle
There could be an obstacle ≤ 120 M downstreamfrom the black hole. When the jet collides with this obstacle, it would bifurcate, rendering the central parts of the jet empty without it being intrinsically so. However, the jet has the hollow morphology in multiple epochs (Kim et al. 2016). So there needs to be a quasi-stationary feature hovering ≤ 120 M above the black hole. We know of no physical mechanism that could create such a quasi-equilibrium above the black hole.
 |
Fig. 5 Top frame: central flux nadir of the jet near its base is apparent in the 86 GHz HSA image from Hada et al. (2016; restored with a 0".0001 beam). Bottom frame: surface brightness cross-sections from the image above. The central flux nadir is resolved within 56 M (0".0002) of the EH. The central flux nadir surface brightness is ~ 4%–8% of the average surface brightness on the limbs, 56 M–112 M from the EH and ~ 20–30% of the average surface brightness of the limbs at 140 M. |
4.2 Doppler suppression
The central spine could be of similar emissivity to the observed sheath, but have a much higher speed, so that Doppler suppression reduces the observed spine surface brightness. Given the Doppler factor for the approaching jet ![${\cal D} = 1/({\rm{\Gamma}}[1-\beta\cos\theta])$](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq38.png) , where Γ is the bulk Lorentz factor, it can easily be shown that Doppler suppression takes place for angles to the line of sight
, where Γ is the bulk Lorentz factor, it can easily be shown that Doppler suppression takes place for angles to the line of sight ![$\theta > \cos^{-1}[({\rm{\Gamma}} -1)/({\rm{\Gamma}}^2-1)^{1/2}]$](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq39.png) . For example, the bulk Lorentz factors (Γ ~ 10–50) often implied by observations of superluminal motion in blazars, Lister et al. (2016), Doppler suppression will take place unless the angle to the line of sight is smaller than a critical angle in the range ~ 25°~10°. While this model cannot be ruled out in principle, we regard the observed similar apparent velocities in the sheath and spine region as evidence against it; in such a model we might expect to see higher apparent speeds in the center of the jet.
. For example, the bulk Lorentz factors (Γ ~ 10–50) often implied by observations of superluminal motion in blazars, Lister et al. (2016), Doppler suppression will take place unless the angle to the line of sight is smaller than a critical angle in the range ~ 25°~10°. While this model cannot be ruled out in principle, we regard the observed similar apparent velocities in the sheath and spine region as evidence against it; in such a model we might expect to see higher apparent speeds in the center of the jet.
4.3 Ghost jet
The central spine could have the same speed as the observed sheath, but have a low emissivity because the energy density of the particles is low (Moscibrodzka et al. 2016), forming a “ghost jet”. However, it is not obvious that the Poynting flux core can be protected from an infusion of high energy particles, if it is surrounded by an energetic outflow of protonic material from the surrounding disk/corona accretion system. There are three significant sources of high energy particles.
First, the accretion vortex in numerical simulations of radiatively inefficient accreting systems is not the ordered force-free environment envisioned in theoretical treatments when the putative Poynting jet does exist in the EHM. In the simulations of Krolik et al. (2005), it was found that the EHM and the jet base are very unsteady and the accretion vortex appeared to be a cauldron of strong MHD waves rather than what would be expected of a force-free structure (even though the energy density of the particles is much less than the energy density of the electromagnetic field). This appears to be the case in the simulations of Tchekhovskoy et al. (2012), as well, based on the supporting online movies in which the field lines in the vortex whip around chaotically. As these strong MHD waves crash against the bounding sheath jet, fast magnetosonic shocks are created. Even though, in this magnetically dominated limit, these shocks are not highly effective at accelerating plasma to high energy (see Kennel & Coroniti 1984), there would be many such shocks. This would be expected to imbue the Poynting flux core with a back-flow of particles from the high energy tail of the plasma that is energized at the shock front.
Secondly, it is difficult to keep the sheath plasma from mixing into the jet, if it is there. Near the base of the jet, it was found in 3D numerical simulations that the corona/jet interface is unsteady with large fingers of hot gas being injected into the Poynting jet on scales of ~ 20 M–30 M from the BH (Punsly 2007). To accurately model such mixing of corona and jet gas requires an accurate numerical scheme. For example, codes like HARM which is used in Tchekhovskoy et al. (2012); McKinney et al. (2012) do not utilize the contact discontinuity in their Riemann solver. The absence of the contact discontinuity tends to numerically dissipates effects associated with abrupt density gradients (Punsly et al. 2016). Furthermore, a recent study of Howson et al (2017) showed that the typical numerical resistivity in MHD simulations is large enough that mixing modes such as the Kelvin–Helmholtz instability (associated with a strong magnetic coronal loop) are highly suppressed. Thus, it is an open question how much the corona and sheath will seed a putative strong Poynting jet core with high energy plasma.
Thirdly, the chaotic behavior in the accretion vortex and the large toroidal twisting of the field lines is not conducive to maintaining an ordered, untangled field. Field tangling is often called braiding in solar physics. Braided fields are believed to release the extra energy of tangling as they relax to a more simplified state by reconnection (Wilmot-Smith et al. 2010). Reconnection of the braided fields in the jet can also provide high energy plasma to the jet and the fields are strongest near its base (Wilmot-Smith et al. 2010; Blandford et al. 2015).
Based on the fact that the putative ghost jet would support a pair cascade of high energy particles in the accretion vortex, Broderick & Tchekhovskoy (2015), and the three plausible sources of high energy plasma described above, it is not at all clear that the energy density of the jet can be maintained low enough to keep it invisible or extremely weak at mm wavelengths. Thus, the study of alternative scenarios that require fewer assumptions, such as a weak EHM jet, is worthwhile.
5 Conclusion
This paper considers an EHM that is built up by the accumulation of accreted weak, isolated strands of magnetic flux over a long period of time. In the absence of a significant background photon field, an analysis based on Maxwell’s equations incurved spacetime that was developed in Appendices A–C indicates that the magnetic flux will readily dissipate in the EHM instead of accumulate in the EHM. In this accretion scenario, the resultant weak field that can be sustained in the EHM is determined by the pair creation rate in the γ-ray field of the accretion disk/corona. In Sect. 3, evidence that M87 appears to have a weak γ-ray accretion source was presented based on the Chandra X-ray spectrum of the nucleus and the high energy cutoffs of other AGN derived form INTEGRAL observations. The derived upper bounds on the γ-ray luminosity renders the EHM of M87 ineffectual for jet launching. In Sect. 4, it is shown that 86 GHz HSA observations reveal a bizarre forked jet 50M–400M from the black hole. This is a manifestation of the weak central spine of the jet above the EH that is expected as a consequence of the new solution of the EHM. Many other FRI and some FRII radio galaxies also appear to have weak accretion X-ray emission and likely weak γ-ray emission as well (Hardcastle et al. 2009). Thus, a weak or absent EHM might be common to radio galaxies with radiatively inefficient accretion such as M87. It is tempting to speculate that jet bases with a forked morphology might occur in other radiatively inefficient radio galaxies.
The EHM solution is consistent with recent hollow jet models from the inner accretion flow of M87 (Punsly 2017). The models are able to fit an extremely wide range of plausible spectra of broadband emission emanating from 15–30 μ as scales including the 230 GHz correlated flux detected by the EHT. For high spin black holes, a∕M = 0.99, the jet transports 1043 –1044ergs sec−1 if the poloidal magnetic field is 8–15 G in the inner accretion flow. Thus, these models can supply the entire jet power of M87 that has been estimated from the analysis of large scale features (McNamara et al. 2011; Stawarz et al. 2006). The accord with constraints based on broadband spectra and jet power is achieved with a magnetic field strength that is consistent with assumption 1) of Sect. 2. In particular, based on Appendix D, 8–15 G is ≪ than the ~ 225 G that would be required for a self-sustaining pair creation mechanism on an accreted flux tube in the EHM in the absence of a significant ambient soft photon flux. Thus, the key assumption of the EHM solution presented here, a weak accreted magnetic field, is a property of a wide range of high spin BH, hollow jets models of M87 that have both a plausible mm wavelength to UV spectrum and a jet power of 1043 –1044ergs sec−1.
The EHM solution described in this article could be used to argue that a steady accretion of weak axisymmetric flux would also dissipate in a charge starved EHM. But, more importantly, the flux dissipation does not depend on the assumption of axisymmetry. Even for non-axisymmetric flux tubes, as in the right hand frame of Fig. 1, the charges will drain off without a plasma source in the EHM and the flux will be dissipated. Even though an axisymmetric disk was used in the models of the broadband luminosity of the jet in Punsly (2017), this is not necessary to drive the jet from the inner accretion flow. In the quasar jet launching study of Punsly (2015a), the jets are considered to originate in isolated flux tubes (magnetic islands), as in the right hand frame of Fig. 1, within the innermost accretion flow. In this case, the jet Poynting flux is altered slightly from our Eq. (28). Instead of the jet power from the inner disk scaling as 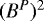 as in Eq. (28), it scales as
as in Eq. (28), it scales as 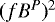 , where f is the fillingfraction of the disk threaded by isolated flux tubes with a vertical field strength, BP. It should be noted that in general (more realistically) there would be a bivariate distribution of field strengths and filling fractions. In the example of M87, as noted above, for a∕M = 0.99 the broadband spectrum and jet power was fit in Punsly (2017) with an inner accretion disk field strength of 8–15 G. For a filling factor, f ~50%, this corresponds to BP ~ 15–30 G in order to reproduce the jet power.
, where f is the fillingfraction of the disk threaded by isolated flux tubes with a vertical field strength, BP. It should be noted that in general (more realistically) there would be a bivariate distribution of field strengths and filling fractions. In the example of M87, as noted above, for a∕M = 0.99 the broadband spectrum and jet power was fit in Punsly (2017) with an inner accretion disk field strength of 8–15 G. For a filling factor, f ~50%, this corresponds to BP ~ 15–30 G in order to reproduce the jet power.
The EHM solution described in this article provides an alternative to assuming a powerful invisible (or highly under-luminous) ghost jet along the central spine on sub-mas scales that is also posited to be the primary power source for the large scale jet on kpc scales. Being under-luminous, by assumption, a powerful jet cannot be directly verified by any observation on sub-mas or mas scales. It can only be ascertained indirectly with deductive reasoning or it must dissipate violently farther out in the jet, thereby revealing its intrinsic power. Evidence of this second alternative, would be a spine that far out shines the limbs over an extended region. Putative spine emission on larger scales falls far short of satisfying this requirement (Hada 2017). The heretofore only posited deductive argument is that a powerful spine is required to energize regions of enhanced emission such as the knot HST-1 nearly 1 arcsec from the BH (Stawarz et al. 2006; Mertens et al. 2016). However, in this context, it was shown in Punsly (2017) that a hollow jet from the inner accretion flow not only explains a multitude of plausible spectra of broadband emission emanating from 15–30 μ as scales, but also supports ~1044ergs s−1 of jet power. Thus, a powerful ghost jet is not required to power the large scale jet (including energizing the knot HST-1). This renders deductive arguments that the ghost jet must be powerful in order to meet global energy requirements untenable. In summary, a powerful ghost jet is not indicated directly by any observation nor is it required to explain any of the observations.
By contrast, there are two very extreme properties in M87 that are observed near the nucleus. Both are fundamental elements of the new EHM solution. There is the extreme central flux nadir in the base of the jet near the EH. There is also the extraordinarily weak high energy luminosity of the accreting gas given the large central black hole mass. The EHM solution presented here implies that these two extreme circumstances might not be coincidental in M87. If the new EHM solution applies to M87 then a luminous jet should extend back towards its source in the inner accretion disk as in the hollow jet models (Punsly 2017). The detection of a luminous forward jet on scales <30 μ as by futureEHT imaging would be direct evidence of a powerful hollow jet connecting the accretion flow to kpc scales and the compatible new EHM solution. This is in contrast to models of ghost jets surrounded by a luminous sheath that predict no strong forward jet emission at 230 GHz–370 GHz on scales < 40 μ as (Dexter et al. 2012; Moscibrodzka et al. 2016). Future EHT imaging might be able to discriminate between these two models.
Acknowledgements
We would like to thank Robert Antonucci for many valuable comments. This paper also benefitted from the insightful review of an anonymous referee.
Appendix A Laplace’s Equation in the kerr spacetime
In Punsly & Coroniti (1989); Punsly (2008) and Appendix C, it is shown that the poloidal magnetic field of axisymmetric electromagnetic sources near the EH can be accurately described by Laplace’s Equation as a consequence of gravitational redshifting. Thus, Laplace’s Equations will be used in Appendix C.3 to compute the late time behavior of the poloidal magnetic field of the spreading vacuum gap scenario illustrated in Fig. 3. This appendix presents axisymmetric solutions to Laplace’s Equation.
In orderto solve Laplace’s Equation in the Kerr Spacetime, it is customary to work with the spin coefficients of the field, ϕ0, ϕ1, ϕ3, instead of the Faraday tensor, 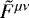 (tildes are used in the following to designate Boyer–Lindquist evaluated quantities), since Maxwell’s equations are separable in the Newman-Penrose spin coefficients. One can explicitly expand
(tildes are used in the following to designate Boyer–Lindquist evaluated quantities), since Maxwell’s equations are separable in the Newman-Penrose spin coefficients. One can explicitly expand 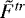 in terms of thespin coefficients Punsly (2008):
in terms of thespin coefficients Punsly (2008):
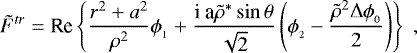
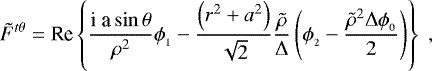
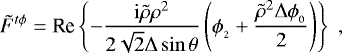
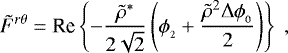
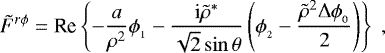
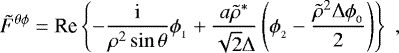 (A.1)
(A.1)
Thus, knowledge of the spin coefficients is sufficient to determine the electromagnetic field in Boyer-Lindquist coordinates. A normalization change on the spin coefficients leads to simpler solutions,
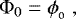
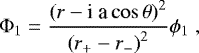 (A.3)
(A.3)
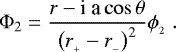
Define ±1Y lm as spin weighted spherical harmonics. Also define,
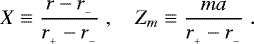 (A.4)
(A.4)
The general solution to Laplace’s equation in the Kerr space–time for a source located between r1 and r2, with 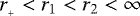 is presented (Bicak & Dvorak 1976; Punsly 2008). In the region between the source and the horizon,
is presented (Bicak & Dvorak 1976; Punsly 2008). In the region between the source and the horizon, 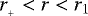 :
:
![\begin{eqnarray*} {\rm{\Phi}}_0 &=& \sum_{l,m} a_{lm} \, 2 [l(l+1)]^{-1} \left( 1 -\frac{1}{X} \right)^{- \textrm{i} \textrm{Z}_{\textrm{m}}} \nonumber\\ &&\times \frac{{\rm{d}}^2}{{\rm{d}} \textrm{X}^2} \left[ \,^2 y_{{lm}}^{(I)} \right] \,_{+1} Y_{lm} (\theta,\phi) \; ,\\[4pt] \nonumber \\ {\rm{\Phi}}_1 &=& \frac{\sqrt{2} \left( r_{_+} - r_{_-} \right)} { \left( r - \textrm{i a} \cos \theta \right)^2 }\nonumber\\ && \times \sum_{l,m} a_{lm} \, [l(l+1)]^{-1} \left( 1 - \frac{1}{X} \right)^{- \textrm{i Z}_{\textrm{m}}} \left\{ \left[l(l+1)\right]^{1/2} \right. \nonumber \\[4pt] && \times \left[ \left( r - \textrm{i a} \cos \theta \right) \frac{\textrm{d}}{\textrm{d X}} \left( \,^2 y_{{lm}}^{(I)} \right) - \left( r_{_+} - r_{_-} \right) \left( \,^2 y_{{lm}}^{(I)} \right) \right] \,_0 Y_{lm} (\theta,\phi) \nonumber \\[4pt] && \hspace{.1 in} \left. - \textrm{i a} \sin \theta \frac{\textrm{d}}{\textrm{d X}} \left( \,^2 y_{{\ell m}}^{(I)} \right) \,_{+1} Y_{\ell m} (\theta,\phi) \right\} + \frac{E_a}{ \left( r - \textrm{i a} \cos \theta \right)^2 } \; ,\\[4pt] {\rm{\Phi}}_2 &=& \frac{\left( r_{_+} - r_{_-} \right)^2} { \left( r - \textrm{i a} \cos \theta \right)^2 } \nonumber\\ &&\times \sum_{l,m} a_{lm} \left( 1 - \frac{1}{X} \right)^{- \textrm{i Z}_{\textrm{m}}} \left( \,^2 y_{{lm}}^{(I)} \right) \,_{-1} Y_{lm} (\theta,\phi) \; .\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq58.png)
The solutions of most interest are those at r > r2.
![\begin{eqnarray} {\rm{\Phi}}_0 &=& \sum_{l,m} b_{lm} \, 2 [l(l+1)]^{-1} \left( 1 - \frac{1}{X} \right)^{- \textrm{i Z}_{\textrm{m}}} \nonumber\\ &&\times \frac{\textrm{d}^2}{\textrm{d X}^2} \left[ \,^2 y_{{lm}}^{(II)} \right] \,_{+1} Y_{lm} (\theta,\phi) \; ,\nonumber \\[-6pt] && \\ {\rm{\Phi}}_1 &=& \frac{\sqrt{2} \left( r_{_+} - r_{_-} \right)} { \left( r - \textrm{i a} \cos \theta \right)^2 } \nonumber\\ &&\times \sum_{l,m} b_{lm} \, [l(l+1)]^{-1} \left( 1 - \frac{1}{X} \right)^{- \textrm{i Z}_{\textrm{m}}} \left\{ \left[l(l+1)\right]^{1/2} \right.\nonumber \\[3pt] && \hspace{-0.1 in}\times \left[ \left( r - \textrm{i a} \cos \theta \right) \frac{\textrm{d}}{\textrm{d X}} \left( \,^2 y_{{lm}}^{(II)} \right) - \left( r_{_+} - r_{_-} \right) \left( \,^2 y_{{lm}}^{(II)} \right) \right] \,_0 Y_{lm} (\theta,\phi) \nonumber \\[3pt] && \left. - \textrm{i a} \sin \theta \frac{\textrm{d}}{\textrm{d X}} \left( \,^2 y_{{\ell m}}^{(II)} \right) \,_{+1} Y_{\ell m} (\theta,\phi) \right\} + \frac{E_b}{ \left( r - \textrm{i a} \cos \theta \right)^2 } \; , \\ && \rule{0 in}{.1 in} \nonumber \\ {\rm{\Phi}}_2 &=& \frac{\left( r_{_+} - r_{_-} \right)^2} { \left( r - \textrm{i a} \cos \theta \right)^2 }\nonumber\\ && \times \sum_{l,m} b_{lm} \left( 1 - \frac{1}{X} \right)^{- \textrm{i Z}_{\textrm{m}}} \left( \,^2 y_{{lm}}^{(II)} \right) \,_{-1} Y_{lm} (\theta,\phi) \; .\end{eqnarray}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq59.png)
The constants alm, blm, Ea, and Eb are determined by the nature of the source. The radial functions satisfy
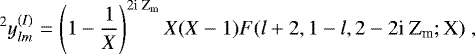 (A.11)
(A.11)
The symbol,“F”, stands for the hypergeometric function. Each charge neutral solution is determined by the coefficients alm and blm which result from the spinorial current, 2Jlm(ξ).
![\begin{eqnarray*} a_{lm} &=& - \frac{ 4 \pi (l+1)! \; \; {\rm{\Gamma}} \left( l + 1 - 2 \textrm{i Z}_{\textrm{m}} \right)} { (2l+1)! \; \; {\rm{\Gamma}} \left( 2 - 2 \textrm{i Z}_{\textrm{m}} \right)} \nonumber \\ &&\times \int_{X_1 - \epsilon}^{X_2 + \epsilon} \frac{ \left( \,^2 J_{lm} (\xi) \right) \left( \,^2 R_{lm}^{(II)} (\xi) \right) }{ \xi (\xi-1) } \textrm{d} \xi \, ,\quad \nonumber \\ && \,^2 R_{lm}^{(II)} \equiv \Bigg[1-\frac{1}{X}\Bigg]^{-iZ_m}\left[ \,^2 y_{{lm}}^{(II)} \right] \, , \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq62.png) (A.13)
(A.13)
![\begin{eqnarray*} b_{lm} &=& - \frac{ 4 \pi (l+1)! \; \; {\rm{\Gamma}} \left( l + 1 - 2 \textrm{i Z}_{\textrm{m}} \right)} { (2l+1)! \; \; {\rm{\Gamma}} \left( 2 - 2 \textrm{i Z}_{\textrm{m}} \right)}\nonumber \\ && \times \int_{X_1 - \epsilon}^{X_2 + \epsilon} \frac{ \left( \,^2 J_{lm} (\xi) \right) \left( \,^2 R_{lm}^{(I)} (\xi) \right) }{ \xi (\xi-1) } \textrm{d} \xi \, ,\quad\nonumber \\ && \,^2 R_{lm}^{(I)} \equiv \Bigg[1-\frac{1}{X}\Bigg]^{-iZ_m}\left[ \,^2 y_{{lm}}^{(I)} \right] \, .\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq63.png) (A.14)
(A.14)
The current source 2Jlm(r) is rather complicated:
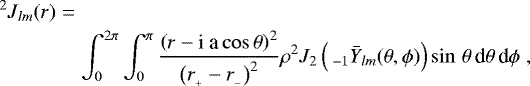 (A.15)
(A.15)
A particularly relevant solution is for the external electromagnetic field of an uncharged azimuthal current loop in the equatorial plane (Bicak & Dvorak 1976),
![\begin{eqnarray*} b_{\ell m}&=&\frac{\delta_{m0} 4 \pi^{2}I^{\phi}(\ell+1)!\ell!}{\sqrt{2}(r_{+}-r_{-})(2\ell +1)!}\sqrt{\frac{{\rm{\Delta}}(r_o)}{\rho(r_o)^{2}}}\nonumber\\* &&\times \Bigg[\textrm{i}\frac{\textrm{r}_{\textrm{o}}^{2}+\textrm{a}^{2}}{\textrm{r}_{+}-\textrm{r}_{-}}\,_{-1}\bar{\textrm{Y}}_{\ell 0} \left(\frac{\pi}{2},0\right)F(\ell +1,-\ell,1;\textrm{X}_{o}) \nonumber\\* &&+\left(\textrm{i}\textrm{r}_{\textrm{o}}\,_{-1}\bar{\textrm{Y}}_{\ell 0}\left(\frac{\pi}{2},0\right)-a\sqrt{\ell(\ell+1)}\,_{0}\bar{\textrm{Y}}_{\ell 0}\left(\frac{\pi}{2},0\right)\right) \nonumber \\* && \times \left(X_{o}(X_o-1)F(\ell+2,1-\ell,2;X_{o})\right)\Bigg] \nonumber\\* E_{a}=E_{b}=0 \;,\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq67.png) (A.19)
(A.19)
where, Iϕ, is the azimuthal current in the current loop evaluated in the ZAMO frames. Equation (A.19) determines the solution at r larger than the radial coordinate of the current ring at ro.
Equation (A.19) ignored the effects of charge and in general a current ring in a rotating environment will have an induced charge from a motional electromotive force. The motivation for segregating the uncharged ring is that the charge contributionto the poloidal magnetic flux is negligible in the calculation of Appendix C. If a ring has a charge q then there are two additional terms that need to be added to Eq. (A.19) for the source of the charged current loop (Bicak & Dvorak 1976)
![\begin{eqnarray*} b_{\ell m}&=&\frac{\delta_{m0} 2 \pi q(l\ell+1)!\ell !}{\sqrt{2}(r_{+}-r_{-})^{3}(2\ell +1)!}\frac{{\rm{\Delta}}(r_o)\rho(r_o)^{2}}{r_{o}g_{\phi\,\phi}(r_{o})}\nonumber\\ &&\times\Bigg[{\rm{-i}}ar_{o}^{2}(r_{+}-r_{-})\,_{-1}\bar{Y}_{\ell0} \left(\frac{\pi}{2},0\right)F(\ell +1,-\ell,1;X_{o}) \nonumber\\ &&+\Bigg(2{\rm{i}}Mar_{o}^{2}\,_{-1}\bar{Y}_{\ell0}\left(\frac{\pi}{2},0\right)-\big([r_{o}^{2}+a^{2}]^{2}-{\rm{\Delta}}(r_{o})\rho(r_{o})^{2}\big) \nonumber \\ && \times \sqrt{\ell (\ell+1)}\,_{0}\bar{Y}_{\ell0}\left(\frac{\pi}{2},0\right)\Bigg)F(\ell+ 2,l-\ell,2;X_{o})\Bigg] \nonumber \\ E_{a}&=&E_{b}=\frac{1}{2}q \;.\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq68.png) (A.20)
(A.20)
The 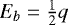 term yields the Kerr Newman field of a charged rotating black hole for a net charge near the black hole. The blm is the source from the azimuthal current produced by the charge set into rotation by the frame dragging of spacetime. Notice that the blm term dies off like Δ(ro) for the charged contribution to the external field in Eq. (A.20) and only dies off like
term yields the Kerr Newman field of a charged rotating black hole for a net charge near the black hole. The blm is the source from the azimuthal current produced by the charge set into rotation by the frame dragging of spacetime. Notice that the blm term dies off like Δ(ro) for the charged contribution to the external field in Eq. (A.20) and only dies off like 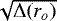 for the uncharged current ring in Eq. (A.19).
for the uncharged current ring in Eq. (A.19).
The interior solution, Eq. (A.7), for the uncharged current ring is given by the source term (Bicak & Dvorak 1976)
![\begin{eqnarray*} a_{\ell m}&=&\frac{\delta_{m0} 4 \pi^{2}I^{\phi}(\ell +1)!\ell!}{\sqrt{2}(r_{+}-r_{-})(2\ell +1)!}\sqrt{\frac{{\rm{\Delta}}(r_o)}{\rho(r_o)^{2}}}(-X_{o}^{-\ell})\nonumber\\ &&\hspace{-0.1in}\times \Bigg[{\rm{i}}\frac{r_{o}^{2}+a^{2}}{r_{+}-r_{-}}\,_{-1}\bar{Y}_{\ell 0} \left(\frac{\pi}{2},0\right)\frac{\ell}{X_{o}}F(\ell +1,\ell + 1,2\ell + 2;X_{o}^{-1}) \nonumber \\ &&+\left({\rm{i}}r_{o}\,_{-1}\bar{Y}_{\ell 0}\left(\frac{\pi}{2},0\right)-a\sqrt{\ell(\ell+1)}\,_{0}\bar{Y}_{\ell 0}\left(\frac{\pi}{2},0\right)\right) \nonumber \\ && \times \left(F(\ell,\ell+1,2\ell +2;X_{o}^{-1})\right)\Bigg] \nonumber \\ E_{a}&=&E_{b}=0 \;.\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq71.png) (A.21)
(A.21)
Appendix B Surface currents in the ZAMO frames
Near the black hole, Eqs. (15)–(20) for the surface current approximation to the thin flux tube needs to be formulated in a general relativistic context. This will be done by integrating Maxwell’s equations in the ZAMO frame across the boundary of the flux tube. One of the computational advantages of the ZAMO orthonormal frame is that it is defined only up to a rotation in the 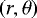 plane. In the study of winds it is useful to define a rotated ZAMO basis in which the unit vector ê 1 is parallel to the poloidal component of the magnetic field, BP (Punsly 2008). In terms of the Maxwell tensor in the ZAMO frames,
plane. In the study of winds it is useful to define a rotated ZAMO basis in which the unit vector ê 1 is parallel to the poloidal component of the magnetic field, BP (Punsly 2008). In terms of the Maxwell tensor in the ZAMO frames,
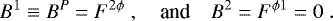 (B.1)
(B.1)
The basis vectors in the 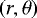 plane become
plane become
![\begin{eqnarray*} \left[ \begin{array}{c} \hat{e}_{1} \medskip \\ \hat{e}_{2} \end{array} \right] = \frac{1}{\left| B^P \right|} \left[ \begin{array}{cc} F^{\theta \phi} & F^{\phi r} \medskip \\ -F^{\phi r} & F^{\theta \phi} \end{array} \right] \left[ \begin{array}{c} \hat{e}_r \medskip \\ \hat{e}_{\theta} \end{array} \right] \; .\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq75.png) (B.2)
(B.2)
Using Br = Fθϕ and Bθ = Fϕr, the basis covectors in the rotated ZAMO frame are (note: 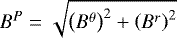 )
)
![\begin{eqnarray*} \left[ \begin{array}{c} \omega^1 \medskip \\ \omega^2 \end{array} \right] = \frac{1}{\left| B^P \right|} \left[ \begin{array}{cc} B^r& B^{\theta} \medskip \\ -B^{\theta} & B^r \end{array} \right] \left[ \begin{array}{c} \omega^r \medskip \\ \omega^{\theta} \end{array} \right] \; .\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq77.png) (B.3)
(B.3)
This basis is more conducive to studying flux tubes. Partial derivatives in the rotated ZAMO basis are found from (B.2) to be
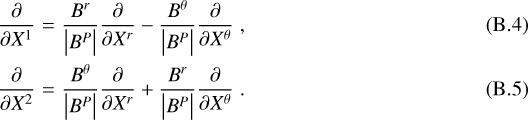
In the rotated ZAMO basis, the poloidal component of Ampere’s Law is found in Punsly (2008):
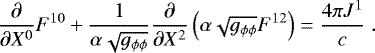 (B.6)
(B.6)
One can construct a local coordinate system that is momentarily at rest with respect to the rotated ZAMO basis at any point in spacetime (ro, θo),
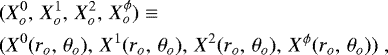 (B.7)
(B.7)
where the last step means to evaluate the metric coefficients at (ro, θo) and treat them as constants. Thus, the coordinate system is orthonormal only at the origin. Then integrate Eq. (B.6) across the thin boundary layer at the edge of the flux tube. Namely integrate over 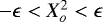 and take the limit of ϵ goes to zero,
and take the limit of ϵ goes to zero,
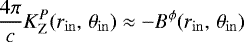 (B.8)
(B.8)
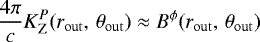 (B.9)
(B.9)
The azimuthal component of Ampere’s law does not simplify so nicely in the rotated ZAMO basis. The ZAMO expression from Punsly (2008) is
![\begin{eqnarray*} \frac{\partial}{\partial X^0} F^{\phi 0} &+&\frac{1}{\alpha \sqrt{g_{\theta\theta}}} \frac{\partial}{\partial X^r} \left[ \alpha \sqrt{g_{\theta\theta}} F^{\phi r} \right]\nonumber \\ && +\frac{1}{\alpha \sqrt{g_{rr}}} \frac{\partial}{\partial X^{\theta}} \left[ \alpha \sqrt{g_{rr}} F^{\phi \theta} \right] \nonumber \\ && \quad+ 2 \left( {\rm{\Gamma}}^{\phi} \smallskip_{0r} F^{0r} + {\rm{\Gamma}}^{\phi} \smallskip_{0\theta} F^{0\theta} \right) = \frac{4 \pi J^{\phi}}{c} \; ,\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq84.png) (B.10)
(B.10)
where the connection coefficients are
![\begin{eqnarray*} {\rm{\Gamma}}^{\phi} \smallskip_{0r} &=&- \frac{ Ma \sin \theta } { \rho^3 \left[ \left(r^2+a^2\right) \rho^2 + 2Mra^2 \sin^2 \theta \right] } \nonumber \\ && \times \left[ \left(r^2 - a^2\right) a^2 \cos^2 \theta + r^2 \left( 3r^2 + a^2 \right) \right]\\ {\rm{\Gamma}}^{\phi} \smallskip_{0\theta} &=& - \frac{ 2Mra^3 \sin^4 \theta \cos \theta }{ \rho^5 g_{\phi \phi} } \left( r^2 + a^2 - 2Mr \right)^{1/2} \;. \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq85.png)
Both connection coefficients are well behaved at the horizon. The poloidal derivatives in Eq. (B.10) can be rewritten in terms of derivatives in the rotated ZAMO basis using the inverse of Eqs. (B.4) and (B.5). Then, integrate Eq. (B.10) over 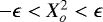 and take the limit of ϵ goes to zero (with X1 held fixed) to obtain
and take the limit of ϵ goes to zero (with X1 held fixed) to obtain
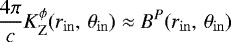 (B.13)
(B.13)
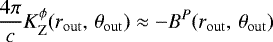 (B.14)
(B.14)
Appendix C Flux dissipation in a semi-vacuum magnetosphere
Without a pair creation mechanism to quench the vacuum gap, at later times, the gap between the ingoing and outgoing flows becomes larger and larger. The inner current sources experience gravitational accretion toward the EH. The outer current sources are still unbound and are driven off to infinity by magneto-centrifugal forces in the flux tube. There is nothing that will stop the semi-vacuum gap from spreading open.
Contrast this spreading gap with the familiar configuration in a pulsar. Pulsar pair creation models (see Appendix D) utilize the voltage drop across the magnetic field (see Eq. (D.2)) as the particle accelerating mechanism that initiates pair cascades. Some of this voltage can be dropped along the length of the gap, thereby accelerating particles in the gap. Is this a valid mechanism for a weak accreted flux tube in isolation? The notion that there is a voltage drop along the gap length is rooted in our experience of the strong fields from super-conducting neutron stars in pulsars. In Fig. 3, if the field line angular velocity, ΩF, is equal on both sides of the vacuum gap when the gap starts to spread apart (and there is no reason it should not be, since it was an instant before) then the voltage drop across the field lines is equal above and below the gap by Eq. (D.2). Applying Faraday’s law to a vacuum gap that starts to spread apart there is a transient parallel poloidal electric field, EP, in the gap that is associated with the radiative decay of Bϕ in the gap. The poloidal electromagnetic field in the spreading gap is composed of this transient displacement current and decaying fringing poloidal magnetic fields. By Faraday’s law, the sum of the voltage drops around a closed poloidal loop near the center of the gap will tend to zero in time. There is no residual voltage drop along the field lines that increases as the gap spreads: and there is no electromagnetic force that prevents the plasma below and above the gap from moving off towards the horizon and infinity, respectively.
By contrast, in a pulsar, if the gap grows in time, the voltage drop in the gap increases in time as well and so will the propensity for particle acceleration in the gap. The fundamental difference is that the sources of the gap magnetic field in the weak accreting flux tube are not fixed in time and space. Conversely, the poloidal magnetic field and the rotational EMF in the gap are persistent in the pulsar; this dynamic is imposed by the star (not the magnetospheric plasma as for the weak, accreting, magnetic flux tubes). Thus, one cannot justify the use of the voltage drop in the gap as the source of a pair cascade in the case of weak, accreting, isolated flux tubes in the charge starved limit.
In the semi-vacuum region that forms between the sources, the electromagnetic field transforms from MHD to radiative in nature. The poloidal magnetic field topology changes as the current disappears in the rapidly expanding vacuum gap. Initially, the topology of the polodial field (in a flat spacetime analogy) in the accreting thin flux tube resembles that of two coaxial solenoids that extend to infinity in each hemisphere (see Eqs. (15)–(20)). As the gap grows between the ingoing and outgoing current sources, in each hemisphere of the EHM, the poloidal magnetic field of the outgoing disconnected segment of the flux tube starts to resemble that of two semi-infinite coaxial solenoids in each hemisphere. The poloidal magnetic field of the ingoing segment near the EH starts to resemble that of two short coaxial solenoids in each hemisphere (see Fig. C.1).
In this Appendix, the field configuration from the inner portion of the severed flux tube on the background of a semi-vacuum in the surrounding EHM is estimated. The charge is considered so tenuous that it does not modify the vacuum fields from the inner flux tube segment. The background charges move in response to these fields, but are of insufficient quantity to create currents strong enough to non-negligibly modify these fields. The entire exact electromagnetic evolution is complicated. However, large simplifications occur at late times as the outer flux tube moves far out of the central vortex of the accretion flow and the inner portion of the severed flux tube approaches the EH. This section explores the large scale poloidal field from the inner severed flux tubes. The analysis follows from the freezing of the flow and the gravitational redshifting of axisymmetric current sources near the EH that are quantified in the next section.
C.1 The effects of gravitational redshift on Maxwell’s Equations
Gravitational redshift results in the freezing of the flow near the EH
![\begin{eqnarray*} \frac{\textrm{dr}}{\textrm{dt}}=-\frac{{\rm{\Delta}}}{r_{+}^{2}+a^{2}}\left[1+\textrm{O}(\alpha_{\rm{Z}}^{2})\right] \; , \, r\gtrsim r_{+}\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq89.png) (C.1)
(C.1)
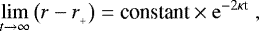 (C.2)
(C.2)
where 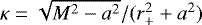 is the surface gravity (Punsly 2008). Equation (C.2) indicates that as viewed from asymptotic infinity all plasma approaches the black hole at a rate that slows down exponentially, never actually reaching the event horizon. In the remainder of this Appendix, the freezing of the flow condition in Eq. (C.1) will be used to estimate the time evolution of the fields from the contracting severed flux tube.
is the surface gravity (Punsly 2008). Equation (C.2) indicates that as viewed from asymptotic infinity all plasma approaches the black hole at a rate that slows down exponentially, never actually reaching the event horizon. In the remainder of this Appendix, the freezing of the flow condition in Eq. (C.1) will be used to estimate the time evolution of the fields from the contracting severed flux tube.
 |
Fig. C.1 At t ≈ 4M (in geometrized units) after the time snapshot in Fig. 3, the outgoing severed flux tube segment has been magneto-centrifugally slung out to large distances. The ingoing portion of the severed flux tube has contracted toward the event horizon. The particular case has a∕M = 0.9 and the top boundary of the severed flux tube is at r = 1.08r+. The compact size suggests replacing the azimuthal surface current source of BP in Eqs. (21) and (22) with small azimuthal current rings. This configuration defines the calculation that produces the field line plot in the top frame of Fig. C.2. |
The quantity of interest for jet power from an EHM is the large scale poloidal flux. The entire exact electromagnetic evolution is complicated. There is electromagnetic radiation from decaying fields and this radiation reflects off of the disk and the centrifugal potential (Hod 2000; Gleiser et al. 2008). However, after these transients have decayed, and the current sources are near the event horizon, the situation is simplified. The freezing of the flow and the gravitational redshifting of the source term in Maxwell’s equations greatly simplifies the solution for the large scale poloidal field from the severed flux tube at late times in the semi-vacuum EHM. As first noted in Punsly & Coroniti (1989), for axisymmetric sources, one can implement the time stationary version of Maxwell’s equations in curved spacetime to achieve accurate solutions to the large scale poloidal magnetic fields. To paraphrase the logic, as r → r+, by the freezing of the flow all electromagnetic sources seem to just corotate with the EH as seen by all external observers. For axisymmetric sources there is no change except for a slow poloidal advance toward the black hole given by Eqs. (C.1) and (C.2). For axisymmetric sources, the time dependent fields that are detected by external observers can be approximated by treating the fields of the sources near the horizon as changing adiabatically slowly and are approximately time stationary. Thus, the time evolution of the large scale fields in the semi-vacuum EHM arising from axisymmetric sources near the horizon can be evaluated in terms of solutions to Laplace’s equations in Boyer-Lindquist. Equivalently, as r →r+, 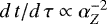 , where τ is the proper time (Punsly 2008). Thus, all time derivatives reflect the gravitational redshift by being weighted by a factor
, where τ is the proper time (Punsly 2008). Thus, all time derivatives reflect the gravitational redshift by being weighted by a factor 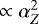 relative to the time derivatives in the proper frame. For axisymmetric sources of Maxell’s equations, as r →r+, this equates to an
relative to the time derivatives in the proper frame. For axisymmetric sources of Maxell’s equations, as r →r+, this equates to an 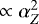 contributionfrom displacement currents in Boyer-Lindquist coordinates. Hence, time variability and displacement currents will not affect the computation of the large scale poloidal magnetic fields.
contributionfrom displacement currents in Boyer-Lindquist coordinates. Hence, time variability and displacement currents will not affect the computation of the large scale poloidal magnetic fields.
Appendix A is a review of the mathematical tools needed to study Laplace’s equations in the Kerr spacetime. The fundamental elements of the field are the spin coefficients Eqs. (A.8)–(A.10), from which algebraic combinations produce the Faraday field strength tensor in Boyer-lIndquist coordinates by means of Eqs. (A.1) and (A.3). For external fields (those at larger radius than the source), the source is expressed by the coefficients blm that are determined in (A.14). These calculations are in general rather labor intensive. For simplicity, the axisymmetric approximations is adopted. As an axisymmetric charge neutral source contracts toward the black hole (Punsly 2008)
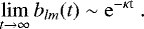 (C.3)
(C.3)
The source term is gravitationally redshifted away and this result is known as the “No-Hair Theorem” for charge neutral, axisymmetric, electromagnetic sources.
C.2 A current source description of the ingoing severed flux tube
In the simulations of Hawley & Krolik (2006); Krolik et al. (2005), the flow division point in the EHM ~ 1.4r+ − 1.5r+ for rapidly spinning black holes. This will be taken as the starting location for the vacuum gap in the following analysis. In Figs. C.1 and C.2, the black hole has a∕M = 0.9. From Eq. (3), the EH is located at r+ = 1.436M.
The inward spread of the vacuum gap is approximated by Eq. (C.1) with the  correction set equal to zero. This is a very crude approximation during the initial spreading of the gap. Initially, α2 ≈ 0.14, so the correction terms are not necessarily negligible. However, at late times. as in Fig. C.2, the top of the ingoing severed flux tube is at α2 = 2.7 × 10−2 in the top frame and α2 = 3.2 × 10−3 in the bottom frame. Thus, we expect Eq. (C.1), without correction terms, to be very accurate in this part of the inflow. Even at the late times of interest, there is an offset, to, to the infall times associated with the error in using Eq. (C.1), without correction terms, as the equation of motion at the beginning of the inflow. Below the flow division point, the electromagnetic force,
correction set equal to zero. This is a very crude approximation during the initial spreading of the gap. Initially, α2 ≈ 0.14, so the correction terms are not necessarily negligible. However, at late times. as in Fig. C.2, the top of the ingoing severed flux tube is at α2 = 2.7 × 10−2 in the top frame and α2 = 3.2 × 10−3 in the bottom frame. Thus, we expect Eq. (C.1), without correction terms, to be very accurate in this part of the inflow. Even at the late times of interest, there is an offset, to, to the infall times associated with the error in using Eq. (C.1), without correction terms, as the equation of motion at the beginning of the inflow. Below the flow division point, the electromagnetic force,  is directed inward (Punsly 2008). The ingoing force means that the magnitude of the ingoing radial velocity obtain from Eq. (C.1), without correction terms, is underestimated. Thus, the infall times computed without the correction terms from the start of the gap spreading to the configuration in the top frame of Fig. C.2 are overestimated and the offset, to < 0. Since the infall time to reach the configuration in the top frame of Fig. C.2 computed from Eq. (C.1), without the correction terms, is 4M, and the total infall time must be positive, the offset error is constrained to be to ~ M. This does not affect the conclusions drawn from the infall times in Appendix C.4 for two reasons. First, its magnitude is relatively small and secondly we are using the infall times as a maximum time for the flux tube to dissipate and decreasing this time only strengthens the argument.
is directed inward (Punsly 2008). The ingoing force means that the magnitude of the ingoing radial velocity obtain from Eq. (C.1), without correction terms, is underestimated. Thus, the infall times computed without the correction terms from the start of the gap spreading to the configuration in the top frame of Fig. C.2 are overestimated and the offset, to < 0. Since the infall time to reach the configuration in the top frame of Fig. C.2 computed from Eq. (C.1), without the correction terms, is 4M, and the total infall time must be positive, the offset error is constrained to be to ~ M. This does not affect the conclusions drawn from the infall times in Appendix C.4 for two reasons. First, its magnitude is relatively small and secondly we are using the infall times as a maximum time for the flux tube to dissipate and decreasing this time only strengthens the argument.
At t ≈ 4M, after the vacuum gap starts to spread open, the top boundary of the inner severed accretion flow will be at r ≈ 1.08r+ = 1.55M or by Eq. (4), αZ = 0.163. In Figs. C.1 and C.2, it is evident that the inner severed flux tube is very short and the  source for BP in Eqs.(21) and (22) can be well approximated by azimuthal current loops. This approximation does not include the affects of
source for BP in Eqs.(21) and (22) can be well approximated by azimuthal current loops. This approximation does not include the affects of 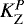 , which wouldsource a local toroidal magnetic field near the loops and inwards towards the horizon. It would also not accurately depict fringing fields and fringing displacement currents near the severed end of the flux tube. However, the interest here is the large scale poloidal magnetic field. Based on the discussion of Appendix C.1, due to the freezing of the flow in Eqs. (C.1) and (C.2), this source model in Laplace’s equations will produce representative magnetic fields near the accretion disk and it will approximate the background magnetic field in most of the semi-vacuum EHM (Punsly & Coroniti 1989).. The current loops carry an equal and opposite azimuthal current. However, the outer current loop at r = rout has a larger enclosed area than the current loop at the inner boundary, r = rin, and therefore the magnitude of the magnetic moment is larger (see the full general relativistic calculational description in Eqs. (C.9)–(C.13)). Thus, there is a net magnetic dipole moment.
, which wouldsource a local toroidal magnetic field near the loops and inwards towards the horizon. It would also not accurately depict fringing fields and fringing displacement currents near the severed end of the flux tube. However, the interest here is the large scale poloidal magnetic field. Based on the discussion of Appendix C.1, due to the freezing of the flow in Eqs. (C.1) and (C.2), this source model in Laplace’s equations will produce representative magnetic fields near the accretion disk and it will approximate the background magnetic field in most of the semi-vacuum EHM (Punsly & Coroniti 1989).. The current loops carry an equal and opposite azimuthal current. However, the outer current loop at r = rout has a larger enclosed area than the current loop at the inner boundary, r = rin, and therefore the magnitude of the magnetic moment is larger (see the full general relativistic calculational description in Eqs. (C.9)–(C.13)). Thus, there is a net magnetic dipole moment.
In order to solve for the global field of the four current loops in Fig. C.1, first note that Iϕ, the azimuthal current in the ZAMO frame, used in the discussion of the current loop in the Appendix satisfies from Eqs. (21) and (22),
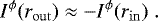 (C.4)
(C.4)
Even though it is customary to use a ZAMO evaluated azimuthal current in such calculations, Chitre & Vishveshwara (1975); Bicak & Dvorak (1976), it is necessary to understand if a well behaved ZAMO current provides any pathological(unphysical) scalings near the EH. The meaningful condition is that the globally defined, coordinate independent, magnetic flux has no pathological behavior near the EH. Implementing the rotated ZAMO basis (one poloidal basis vector field is along the poloidal field direction and the other poloidal basis vector field is orthogonal to the poloidal field direction) from Eq. (B.3), the flux in the flux tube is (Punsly 2008)
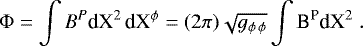 (C.5)
(C.5)
The surface current in Eq. (22) is related to Iϕ by
![\begin{equation*} K^{\phi}_{\rm{Z}}(r_{\rm{out}}, \, \theta_{\rm{out}}) = I^{\phi} \delta [X^{2} -X^{2}(r_{\rm{out}}, \, \theta_{\rm{out}})]\;,\end{equation*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq102.png) (C.6)
(C.6)
where X2 is a the poloidal coordinate orthogonal to the local poloidal field direction defined in a coordinate system that is instantaneously at rest with the ZAMO at (rout, θout). Inserting this into Eqs. (22) and (C.5), shows that the flux scales with Iϕ and is only well behaved if Iϕ is well behaved. It is therefore concluded that the ZAMO frame is suitable for evaluating the azimuthal current in this study.
The inner flux tube at t = 4M in Fig. C.1 is approximated by 4 current loops that are located near the equatorial plane. Using Eq. (C.4), the current loop source term (A.19) evaluated at r ≳ r+ is approximated to find the net source term.
![\begin{eqnarray*} b_{\ell m}&\approx& 2\frac{\delta_{m0} 4 \pi^{2}I^{\phi}(\ell+1)!\ell!}{\sqrt{2}(r_{+}-r_{-})(2\ell+1)!}\sqrt{\frac{{\rm{\Delta}}(r_{\rm{out}})}{\rho(r_{\rm{out}})^{2}}}\nonumber\\ &&\times\left[{\rm{i}}\frac{\textrm{r}_{\textrm{out}}^{2}+\textrm{a}^{2}}{\textrm{r}_{+}-\textrm{r}_{-}}\,_{-1}\bar{\textrm{Y}}_{\ell0}\left(\frac{\pi}{2},0\right)\textrm{F}(\ell+1,-\ell,1;\textrm{X}_{\rm{out}})\right] \nonumber\\ &&- 2\frac{\delta_{m0} 4 \pi^{2}I^{\phi}(\ell+1)!\ell!}{\sqrt{2}(r_{+}-r_{-})(2\ell+1)!}\sqrt{\frac{{\rm{\Delta}}(r_{\rm{in}})}{\rho(r_{\rm{in}})^{2}}}\nonumber\\ &&\times\left[\textrm{i}\frac{\textrm{r}_{\textrm{in}}^{2}+\textrm{a}^{2}}{\textrm{r}_{+}-\textrm{r}_{-}}\,_{-1}\bar{\textrm{Y}}_{\ell0}\left(\frac{\pi}{2},0\right)\textrm{F}(\ell+1,-\ell,1;\textrm{X}_{\rm{in}})\right]\;, \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq103.png) (C.7)
(C.7)
where by Eq. (A.4), X = 1 at the EH, thus making two of the terms that would have arisen from (A.19) negligible. The neglect of these terms means that the fringing fields near the horizon are not accurately depicted. This greatly simplifies the algebra and does not affect the global poloidal magnetic field calculation in the EHM which is the quantity of interest. 2
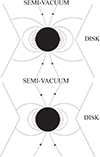 |
Fig. C.2 Ingoing portion of the severed flux tube has contracted toward the EH to r = 1.08r+ in the top frame at t = 4M after thevacuum gap starts to spread open. The large scale poloidal magnetic field is plotted in Boyer–Lindquist coordinates. The nature of the disk is very uncertain and it is represented symbolically by a simple wedge. In the bottom frame, the severed flux tube has contracted to r = 1.001r+ at t = 15M after the vacuum gap starts to spread open. Note that the large scale field is contracting towards the black hole. In the top (bottom) frame the poloidal magnetic field in the disk is ≈ 2% (≈ 0.4%) of the poloidal field strength in the original flux tube when it entered the EHM. The bottom frame indicates that poloidal magnetic flux is almost completely dissipated on a timescale of one half of the rotational period of the ISCO. |
Further simplification at r ≳ r+ yields
![\begin{eqnarray*} b_{\ell m}&\approx& 2\frac{\delta_{m0} 4 \pi^{2}I^{\phi}(\ell+1)!\ell!}{\sqrt{2}(r_{+}-r_{-})(2l+1)!}\nonumber\\ && \times \left[\frac{\sqrt{{\rm{\Delta}}(r_{\rm{out}})}(r_{\rm{out}}^{2}+a^{2})}{r_{\rm{out}}}-\frac{\sqrt{{\rm{\Delta}}(r_{\rm{in}})}(r_{\rm{in}}^{2}+a^{2})}{r_{\rm{in}}}\right]\nonumber\\ &&\times\left[\textrm{i}\frac{1}{\textrm{r}_{+}-\textrm{r}_{-}}\,_{-1}\bar{\textrm{Y}}_{\ell0}\left(\frac{\pi}{2},0\right)\textrm{F}(\ell+1,-\ell,1;0.5(\textrm{X}_{\rm{out}}+\textrm{X}_{\rm{in}}))\right] \nonumber\\\end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq104.png) (C.8)
(C.8)
C.3 The large scale poloidal magnetic field of the ingoing severed flux tube
The resultant external large scale poloidal magnetic field is derived by inserting Eq. (C.8) into Eqs. (A.8)–(A.12) to solve for the spin coefficients. Then using (A.1) and (A.3) the spin coefficients determine the Boyer-Lindquist evaluated fields.
The result is plotted in Fig. C.2. There is an intersection of a weak field line with the disk that is not indicated since there is an uncertain interaction. The field strength at the disk in the top frame is < 2% of the original weak field strength of the accreted flux tube, thus no significant interacting is expected. There is an important simplification of the large scale poloidal field when the ingoing severed flux tube is located near the EH due to the term in the numerator of Eq. (C.8),
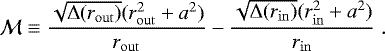 (C.9)
(C.9)
From Eqs. (4) and (6) this corresponds to a difference in lapse function. The lapse function is significantly smaller (the gravitational redshift is significantly larger) for the inner current loops than the outer current loops. For example, in Fig. C.1, the inner current loops are located at αZ = 0.08 and the outer current loops are located at αZ = 0.14. Thus, the outer current loops contributes almost two times as much to the large scale poloidal field as the inner loops. This effect becomes more pronounced as the severed inner flux tube (current loops in the approximation) contracts closer to the EH. The current loop configuration in Fig. C.1 is used as a source of Laplace’s equations to compute the magnetic field configuration in the top frame of Fig. C.2. The resultant field line plots are computed by the same methods employed by Bicak & Dvorak (1980). Field line plots have been traditionally used to show the behavior of the large poloidal magnetic field as a current source is moved closer to a black hole and are well suited for our purposes. The particular choice of current loops in Fig. C.1 at r = 1.02r+ and r = 1.06r+ actually produces a resultant source term in Eq. (C.8) that is equivalent to a single current loop at r = 1.05r+ in the equatorial plane. The field line plot was produced by Tomas Ledvinka and generously supplied to Punsly (2008) as Fig. 4.9.
The bottom frame of Fig. C.2 is the same calculation with the poloidal field of the severed flux tube analyzed at t ≈ 15M after the vacuum gap starts to spread. The top boundary of the severed flux tube is now at r = 1.001r+ or αZ = 0.057. The poloidal magnetic field strength at the disk is ≈ 0.37% of the original field strength of the accreted flux tube. Comparing the top frame and bottom frames of Fig. C.2 illustrates the No-Hair Theorem for axisymmetric charge neutral sources in the Kerr spacetime for this particular example. Comparing the top frame in Fig. C.2 to the bottom frame of Fig. C.2 shows that the poloidal magnetic field is being contracted into a circular set of O-points where the magnetic flux is dissipated. Furthermore. this circular set of O-points is slowly contracting toward the EH. This is manifested on global scales by the factor of 5 reduction ofthe poloidal field strength at the accretion disk in the bottom frame. The global poloidal magnetic field from the ingoing portion of the severed flux is redshifted away. The point of the approximate calculation is not to find the exact field at a given time and point in space. It is to show that the effects of gravitational redshift are overwhelming and the inner accreting severed flux tube will quickly have its large scale fields redshifted away.
Express the Boyer-Lindquist magnetic field plotted in the top frame of Fig. C.2 in the orthonormal ZAMO frame at large r
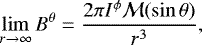 (C.10)
(C.10)
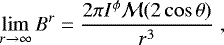 (C.11)
(C.11)
where 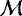 was defined in Eq. (C.9). These are the poloidal magnetic field components of a magnetic dipole with a net magnetic moment is
was defined in Eq. (C.9). These are the poloidal magnetic field components of a magnetic dipole with a net magnetic moment is 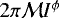 . The net magnetic dipole moment is the sum of the two larger dipole moments from the outer current loops, each with a magnetic moment, mout,
. The net magnetic dipole moment is the sum of the two larger dipole moments from the outer current loops, each with a magnetic moment, mout,
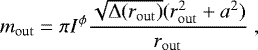 (C.12)
(C.12)
minus the sum of the two smaller dipole moments from the inner current loops, each with a magnetic moment, min,
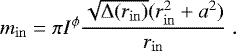 (C.13)
(C.13)
Since Δ tends to zero as r → r+, min attains a significantly smaller value than mout, more so than would be expected from a pure flat space analogy as a consequence of gravitational redshifting.
In order to make this approximation scheme for the complicated calculation complete, a discussion of the effects of rotational induced charge on the solution must be included. Since this is a rotating system there will be a rotationally induced cross field potential drop and associated electric field that is orthogonal to the poloidal magnetic field direction. In the rotated ZAMO basis of Appendix B, this electric field has a very simple form (Punsly 2008)
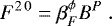 (C.14)
(C.14)
where 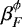 is the angular velocity of the local field as measured by the local ZAMO. By Gauss’s law there msut be a surface charge density on the walls of the flux tube. The field lines begin on one wall of the flux tube and end on the opposite wall. The net charge on one flux tube wall, q, is equal and opposite that, − q on the otherwall in order to source and sink the field lines. Now consider the contributions due to a net charge on the current loop in the ZAMO frame as shown in Equation (A.20). There are two terms, in addition to Equation (A.19), that contribute to the large scale poloidal magnetic field. The dominant term is the Kerr–Newman field term from Eb. For a charge near the EH, this term creates the electromagnetic field of a Kerr–Newman (charged, rotating) black hole. If one computes Gauss’s law on a closed surface just outside the severed flux tubes in Fig. C.1, then the net rotationally induce charge on the flux tubes will identically cancel. Thus, for the total configuration, the total charge is zero and Eb = 0 (Bicak & Dvorak 1976). Thus, there is no large scale Kerr–Newman poloidal magnetic field.
is the angular velocity of the local field as measured by the local ZAMO. By Gauss’s law there msut be a surface charge density on the walls of the flux tube. The field lines begin on one wall of the flux tube and end on the opposite wall. The net charge on one flux tube wall, q, is equal and opposite that, − q on the otherwall in order to source and sink the field lines. Now consider the contributions due to a net charge on the current loop in the ZAMO frame as shown in Equation (A.20). There are two terms, in addition to Equation (A.19), that contribute to the large scale poloidal magnetic field. The dominant term is the Kerr–Newman field term from Eb. For a charge near the EH, this term creates the electromagnetic field of a Kerr–Newman (charged, rotating) black hole. If one computes Gauss’s law on a closed surface just outside the severed flux tubes in Fig. C.1, then the net rotationally induce charge on the flux tubes will identically cancel. Thus, for the total configuration, the total charge is zero and Eb = 0 (Bicak & Dvorak 1976). Thus, there is no large scale Kerr–Newman poloidal magnetic field.
There isanother term in Eq. (A.20) that is from the rotational motion of the charge and the current that it produces
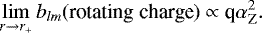 (C.15)
(C.15)
By comparison from Eqs. (A.19), (C.5) and (C.6), the charge neutral current source
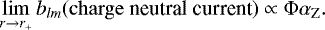 (C.16)
(C.16)
Thus, combining Eqs. (C.15) and (C.16)
 (C.17)
(C.17)
Since q and Φ are well behaved and frame independent, the charge neutral term will dominate near the EH. This approximation was used in the computation of the field lines in Fig. C.2.
With the approximation of ignoring the charge contribution to the large scale poloidal flux, the field line configuration is completed in Fig. C.2, by choosing a compatible source term for the interior solution for r+ < r < ro, alm. This interior solution is that of the uncharged current rings only in Eq. (A.21). Even though this creates continuous poloidal magnetic field lines, it should be noted that this simplification does not yield an accurate depiction of the interior solution near the EH. However, as has been repeatedly emphasized, this complicated detail is not relevant to the study of the large scale poloidal magnetic flux.
C.4 Results in the context of global accretion
Another item to consider is the time scale for a flux tube to dissipate, tdis, compared to the dynamical time scale, tdyn, in which a new weak patch of poloidal flux is fed into the EHM. Based on the physical assumptions 2) and 3) expressed in Sect. 2.2, this analysis does not consider a constant flood of magnetic flux as the physical state of flux deposition. Flux deposition occurs over long periods of time and since it is not a constant flood of magnetic field, but the occasional deposition of a flux tube, tdyn would be longer than the inflow time of the disk plasma. The shortest possible dynamical time scale of the accretion flow is the orbital period of the innermost stable orbit (ISCO). In Boyer-Linquist coordinates, there is a slow radial inward drift near the ISCO, but the plasma motion is mainly rotational as it completes many revolutions as it approaches the ISCO (Sadowski 2011). The Keplerian angular velocity as viewed in the stationary frames at asymptotic infinity is
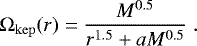 (C.18)
(C.18)
For a∕M = 0.9, the ISCO is at r = 2.32M, corresponding to an orbitalperiod of T = 28M. Thus, from Figs. C.1 and C.2, the flux tube dissipates in less than half an orbital period of the ISCO. Thusbased on assumptions 2) and 3) any reasonable dynamical time for flux deposition would satisfy
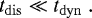 (C.19)
(C.19)
This does not mean that the magnetic flux is identically zero in the EHM. Small amounts of flux could exist (especially episodically) based on the dissipation rate and inflow rate of magnetic flux balance even in the absence of efficient pair creation. The main idea is that since the flux dissipates on time scales that are much less than any dynamical scale of the accretion disk, in the charge starved limit, flux will not build up in the EHM. Old flux will dissipate faster than new flux is deposited. The EHM is a sink for flux not a reservoir. Thus, flux never builds up to the point that a pair creation scenario would be effective (as discussed in Appendix D). This also does not mean that mathematically based models in which one floods the EHM with strong poloidal field would not sustain itself through pair creation. However, it is unclear if that assumed dynamic is relevant to low luminosity accretion systems.
Finally, it is noted that the time evolution does not support the idea that the flux tube will induce a surface current on the inner disk that will in turn be the source of the flux tube and maintain the flux. The tangential magnetic field does induce a surface current on the inner wall of the accretion disk. However, this field is transient and decays as the extent of the severed region grows (see Fig. C.2). Furthermore, based on Fig. C.2, the sign of the surface current is the opposite of what is required to maintain the flux. In summary, surface currents in the disk do not prevent accreted, thin, isolated flux tubes in a charge starved EHM from dissociating. Accreted weak flux is dissipated in the EHM, not accumulated.
C.5 Summary of the results of the calculation
In this Appendix, we calculated multiple items. Some were required to established the relevant approximations (these can be useful for future calculations performed by other researchers as well) and some relate directly to the dynamics of the weak accreted flux tubes in the EHM. The last items are the most important to this research and we list these first.
-
Using a very elaborate spin coefficient formalism that is described in the Appendix A, it is shown that coaxial helical current flows that contract toward the EH in each hemisphere will produce a large scale poloidal magnetic field that decays to very small values as the horizon is approached. This is shown graphically in Fig. C.2. Quantitatively, when the top end of the accreted coaxial solenoids is at ~1.08r+ (~1.001r+) the field at the accretion disk is ≈2% (≈0.37%) of the original field strength in the accreted flux tube.
-
In Appendix C.4, it is demonstrated that time scale for the fields to decay in the EHM is much shorter than any plausible dynamical time scale in the accretion flow and flux will dissipate faster than it will accumulate. This prevents the growth of a significant EHM.
-
In Fig. C.2 and Appendix C.4, it is demonstrated that as a charge starved flux tube dissipates in the EHM, it does not induce a current on the inner wall of the accretion disk that can sutain the flux within the EHM.
-
In Appendix C.2, Equations (C.5) and (C.6), it is shown that the ZAMO evaluated azimuthal current used by other researchers for similar calculations is an appropriate current to consider for studying the global changes in the poloidal magnetic field as sources approach the EH.
-
It is shown in Appendix C.3, Eq. (C.17), that the charge (Kerr–Newman) contribution to the contracting current loop configuration is lower order and can be neglected near the EH.
-
In Appendix C.3, Eqs. (C.12) and (C.13), it is shown that the magnetic moment of an azimuthal current source is reduced by gravitational redshift near the EH.
The first point is critical for our understanding of the dynamics of weak accreted flux tubes in the EHM in the charge starved limit. In a charge starved EHM, without plasm injection, the large scale current system supporting an isolated accreted flux tube severs at the flow division point. In the lower segment, the plasma and its currents will then accrete toward the horizon. The flux tube near the horizon is not aware of the severing due to causality. As long as charges are being supplied from upstream, the lower portions of the flux tube are unaffected. The top end of the flux tube is therefore treated as a contact discontinuity that signals the change to the lower section of the flux tube. The ingoing flow from the charge depleted region below the vacuum gap makes the inner severed flux tube appear like two contracting coaxial solenoids in each hemisphere. Thus, the calculation presented in this section indicates that at late times. the large scale poloidal magnetic field of the charge depleted inner flux tube will approximately be an ever weakening dipolar magnetic field.
Appendix D Vacuum gap induced pair cascades on weak accreted flux tubes
This appendix discusses standard pair creation models in the EHM with two additional considerations that are germane to the new model of the EHM. First, the notion that the magnetosphere is not fully developed is incorporated and one is considering the deposition of isolated weak flux tubes in the EHM. Secondly, the implications of the very low luminosity of the accretion flow in M87 is studied. In any vacuum gap pair creation model, if the magnetic field in each accreted flux tube is sufficiently weak, the electric field in the gap is incapable of producing enough pairs to seed the currents and prevent further gap growth (Blandford & Znajek 1977). This is in contrast to rapidly rotating neutron stars (NSs) with strong magnetic fields in pulsars. It is more analogous to weaker field NSs which cannot support pulsars that are below (far below in this case) the pulsar death line (Chen & Ruderman 1993; Harding et al. 2002). The electric field that accelerates particles to high energy and initiates a pair cascade ultimately arises from the electromotive force induced by the rotation of the magnetic field. This is proportional to the poloidal magnetic field strength, B. Thus, regardless of the pair creation mechanism, there exists a B small enough that the threshold electric field for pair production is not attained. For any pair creation scenario envisioned, one can assume that B for the accreted flux tubes is below this threshold. However, before making this assumption, pair creation models are considered in detail in the EHM. In spite of the detailed discussion to follow, it is important to remember that the assumption is the accretion of weak magnetic flux with field strengths lying far below the effective pair creation death line. Furthermore, one should not lose sight of the fact that the field strength of accreted flux is unknown in the example of M87 and estimates depend on many assumptions (Kino et al. 2014, 2015; Hada et al. 2016).
As noted in the references in the Introduction, many pair cascade models based on vacuum gaps have been posited in the literature. They depend on different assumptions and Hirotani & Pu (2016) provide an in depth comparison and contrast of a few of these. In order to make the statements concrete these models are referenced to the context of M87.
D.1 Pair cascades based on inverse compton scattering
A possible model of pair creation is one in which inverse Compton (IC) scattering of the soft photon field by seed electrons accelerated in the semi-vacuum gap can initiate pair creation. It is a two step process.
-
First, the high energy electrons up-scatter the soft photons to γ-ray energies.
-
Next, these high energy γ-rays scatter off the soft photon field, producing the electron-positron pairs that fill the magnetosphere.
These models were motivated by radiatively efficient accretion scenarios in which there is a strong soft photon field. However, there is no detection of the soft photon field in the example of M87. The broadband spectrum based on high spatial resolution observations is consistent with that of a synchrotron emitting jet (Whysong & Antonucci 2004; Leipski et al. 2009; Prieto et al. 2016). Thus, observations can not provide an estimate of the soft photon flux from the inner accretion flow that would support a putative IC based pair cascade. It is pointed out in the setup of the IC based cascade model of Broderick & Tchekhovskoy (2015) that it is “unclear” what the soft photon flux would be in M87 and that the number density produced by the cascade strongly depends on the soft photon flux. Furthermore, an IC based pair cascade “gap solution ceases to exist” if the soft photon flux is sufficiently small (Hirotani & Pu 2016). Thus, transferring the IC based gap models to inefficient accretion flow environments, such as that in M87, is not straightforward. It is assumed that the soft photon flux is too small for the process to operate and the following analysis concentrates on models that assume that curvature radiation is the source of the high energy γ-rays that initiate pair production. This does not have the ambiguity of invoking an undetected soft photon flux.
D.2 Curvature radiation based gap models
This section is a review of curvature pair production processes in the context of EHM formation by the accretion of isolated, weak, strands of flux as opposed to pair production in a fully developed magnetosphere. One curvature radiation based gap model is introduced for the purpose of an example only (Chen & Ruderman 1993). This pulsar gap model has been adapted to Kerr–Newman black holes (Punsly 1998). Even though other pair creation models have proven to have better predictive power for γ-ray emission than Chen & Ruderman (1993), such as Higgins & Henriksen (1997), it is beyond the burden and scope of this paper to compare and contrast the different gap models. This is already actively debated in the literature (see the references in the Introduction). This burden is circumvented by assuming that the field strength of an accreting, isolated, thin flux tube is weaker than that which is required to initiate a cascade. Note, there is no claim that the Chen & Ruderman (1993) method is the best model of a gap for M87. It is chosen because it is straightforward to compute analytically.
The only required ingredients of the Chen and Ruderman model are rotation and a magnetic field that is not purely radial. This process does not depend on the unknown weak soft photon flux. In this model, it is the rotationally induced voltage drop across the magnetic field lines, ΔV, that is the energy source for the pair cascade. The condition for pair creation is
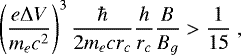 (D.1)
(D.1)
where me is the mass of the electron, rc is the radius of curvature of the magnetic field, h is the gap height, Bg = 4.4 × 1013 G is the critical magnetic field strength and B is the EHM poloidal magnetic field near the EH. The voltage drop across a thin flux tube, rotating with a field line angular velocity, ΩF, and a total flux δΦ is (Punsly 2008)
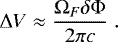 (D.2)
(D.2)
Consider a flux tube that threads a fraction, 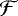 , of the total surface area of a hemisphere of the EH. From the expression for the hemispheric surface area of the EH, SAEH, in Punsly (2008), one can write the more convenient expression,
, of the total surface area of a hemisphere of the EH. From the expression for the hemispheric surface area of the EH, SAEH, in Punsly (2008), one can write the more convenient expression,
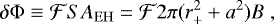 (D.3)
(D.3)
where the radius of the EH is 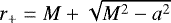 . The analog of
. The analog of 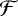 in the standard pulsar model is the fraction of the neutron star surface area, near the polar cap, that comprises the open field lines of the magnetosphere (Chen & Ruderman 1993). A field line angular velocity intermediate between the seminal value of Blandford & Znajek (1977) and the numerical values of McKinney et al. (2012) is chosen,
in the standard pulsar model is the fraction of the neutron star surface area, near the polar cap, that comprises the open field lines of the magnetosphere (Chen & Ruderman 1993). A field line angular velocity intermediate between the seminal value of Blandford & Znajek (1977) and the numerical values of McKinney et al. (2012) is chosen,
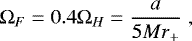 (D.4)
(D.4)
where ΩH = a∕(2Mr+) is the EH angular velocity as viewed by stationary observers at asymptotic infinity.
For illustrative purposes, one can use the simulated field lines such as those from Beckwith et al. (2009) in Fig. 1 in order to estimate rc. The minimum value occurs juxtaposed to the EH, rc ≳ 8r+. The value approximates the flux tube out to ≈ 2.5r+. Thus, rc ≈ 8r+ is chosen. To be quantitative, this analysis is applied to M87, thus all numbers are based on the value of M for M87. A value of h ≈ 0.5r+ is also chosen. The gap height choice is similar in terms of the radius of the compact object to that obtained in a pulsar dipolar field (Chen & Ruderman 1993). Choosing rc and h is somewhat subjective. Beyond ~ 5r+ of the EH, rc >> r+. Thus, if the gap grows large,  will decrease and the pair creation threshold value of B must increase to compensate in equation (D.1). A value of
will decrease and the pair creation threshold value of B must increase to compensate in equation (D.1). A value of  is chosen (see Fig. 2). Based on these pulsar models, Equations (D.1)–(D.4) imply a death-line (insufficient electromotive force to drive pair creation) if B ~ 225 G (B ~ 1440 G) for a∕M = 0.99 (a∕M ~ 0.1).
is chosen (see Fig. 2). Based on these pulsar models, Equations (D.1)–(D.4) imply a death-line (insufficient electromotive force to drive pair creation) if B ~ 225 G (B ~ 1440 G) for a∕M = 0.99 (a∕M ~ 0.1).
The original analysis in Blandford & Znajek (1977) for the curvature radiation process, Equation (2.8), is similar to the analysis for pulsars (Chen & Ruderman 1993). It is consistent with the minimum B-field analysis above although they obtain a smaller number due to different assumptions. They consider a fully established 2π steradian hemispheric magnetosphere as an initial state as opposed to a thin flux tube, their characteristic angular frequency is 5 times the value in equation (D.4) and the radius of curvature is simply M. Making these adjustments reconciles the two estimates.
D.3 Discussion
The vacuum gap analysis considered here is consistent with the analysis of the assumptions provided in the seminal model of Blandford & Znajek (1977) in which it was stated upfront that “If the field strength is large enough, the vacuum is unstable to a cascade production of electron-positron pairs and a surrounding force-free magnetosphere will be established”. In other words, there is a minimum field strength for the cascade models to work.
The pulsar-based analysis in Appendix C.2 is for demonstration purposes only. Other gap models can produce different minimum field strengths. The example demonstrates the fact that any pair creation scenario must rely on estimating the parametric details. This introduces a significant uncertainty in any method. Based on the crude guide provided by the pulsar-based estimates, it is clear that there is some field strength (which, given the uncertainties, could be below the limit derived from this calculation) which will be too low to allow an accreted flux tube to sustain itself through pair production in the vacuum gap. The new EHM model consider the dynamics if the accreted flux tubes have field strengths this low.
References
- Beckwith, K., Hawley, J., & Krolik, J. 2009, ApJ, 707, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., & Zheltoukhov, A. A. 2013 Astron. Lett., 39, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., Istomin, Y. N., & Parev, V. I. 1992, Sov. Ast., 36, 642 [Google Scholar]
- Bicak, J., & Dvorak L., 1976, Gen. Rel. and Grav., 7, 959 [CrossRef] [Google Scholar]
- Bicak, J., & Dvorak L., 1980, Phys. Rev. D, 22, 2293 [CrossRef] [Google Scholar]
- Blandford, R.,& Znajek, R. 1977 MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., East, W., Nalewajko, K., Yuan, Y., & Zrake, J. 2015, arXiv e-prints [arXiv:1511.07515] [Google Scholar]
- Broderick, A. E., & Tchekhovskoy A. 2015, ApJ, 809, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, K., & Ruderman, M. 1993 ApJ, 402, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 1999, A&A, 349, 77 [NASA ADS] [Google Scholar]
- Chiaberge, M., Macchetto, F. D., Sparks, W. B., et al. 2002, ApJ, 571, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Chitre, D., & Vishveshwara, C. 1975, Phys. Rev. D, 12, 1538 [CrossRef] [Google Scholar]
- De Villiers, J-P., Hawley, J., Krolik 2003, ApJ, 599, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., McKinney, J. C., & Agol, E. 2012, MNRAS, 421, 151 [Google Scholar]
- Gebhardt, K., Adams, J., Richstone, D., Lauer, T. R., & Faber, S. M., 2011, ApJ, 729, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Giroletti, M., Hada, K., Giovannini, G., et al. 2012, A&A, 538, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, & , W. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gleiser, R., Price, R. & Pullin, J. 2008, Claas. Qunat. Grav., 25, 072001 [CrossRef] [Google Scholar]
- Hada, K. 2017, Galaxies, 5, 2 [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Hada, K., Park, J., Kino, M., et al. 2017, PASJ, 69, 71 [CrossRef] [Google Scholar]
- Hardcastle, M., & Worrall, D. 2000, MNRAS, 314, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M., Evans, D. & Croston, J. 2009, MNRAS, 396, 1929 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A., Muslimov, A., & Zhang, B. 2002, ApJ, 576, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Biretta, J. A., Junor, W., et al. 2003, ApJ, 586, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley J., & Krolik J., 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Higgins, M., & Henriksen, R. 1997, MNRAS, 292, 034 [CrossRef] [Google Scholar]
- Hirotani, K., & Okamoto, I. 1998, ApJ, 497, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K., & Pu, H.-Y. 2016, ApJ, 818, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hod, S. 2000, Phys. Rev. Lett., 84, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howson, T., De Moortel, I., & Antolin, P. 2017, A&A, 602, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Igumenshchev, I. V. 2008, ApJ, 677, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Kennel, C., Coroniti, F. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-Y., Lu, R.-S., Krichbaum, T., 2016 et al., Galaxies, 4, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Kino, M., Takahara, F., Hada, K., & Doi, A. 2014, ApJ, 786, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Kino, M., Takahara, F., Hada, K., et al. 2015, ApJ, 803, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Koide, S., Shibata, K., Kudoh, T., & Meier, D. L. 2002, Science, 285, 1688 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Komissarov, S. 2004, MNRAS, 350, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, K., Hawley, J., & Hirose, S. 2005, ApJ, 622, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Leipski, C., Antonucci, R., Ogle, P., Whysong, D. 2009, ApJ, 701, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Lery, T., Henriksen, R., Fiege, J. 1998, A&A, 350, 254 [Google Scholar]
- Levinson, A. 2000, Phys. Rev. Lett., 85, 912 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levinson, A., & Rieger, F. 2011, ApJ, 730, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z.-Y., Chiueh, T., & Begelman, M. 1992, ApJ, 394, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., & Blandford, R. 1985, ApJ, 295, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M., Aller, M. & Aller, H. et al. 2016, AJ, 152, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Molinal, M., Bassanil, L., et al. 2014, ApJ, 782, 25 [Google Scholar]
- McKinney, J., & Gammie, C. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J., Tchekhovskoy, A., & Blandford, R. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B., Rohanizadegan, M., & Nulsen, P. 2011, ApJ, 727, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Mertens, F., Lobanov, A., Walker, R., & Hardee, P. 2016, A&A, 595, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moscibrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen F. N., Eilek J. A., & Kassim N. E. 2000, ApJ, 543, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Phinney, E. S. PhD 1983, Dissertation University of Cambridge [Google Scholar]
- Prieto, M. A., Fernandez-Ontiveros, J. A., Markoff, S., Espada, D., & Gonzalez-Martin, O. 2016, MNRAS, 457, 3801 [NASA ADS] [CrossRef] [Google Scholar]
- Ptitsyna, K., & Neronov, A. 2016, A&A, 593, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Punsly, B. 1998, ApJ, 498, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Punsly, B. 2004, ApJ, 612, 41 [CrossRef] [Google Scholar]
- Punsly, B. 2007, MNRAS, 381, L79 [CrossRef] [Google Scholar]
- Punsly, B. 2008, Black Hole Gravitohydromagnetics, 2nd edn. (New York: Springer-Verlag) [Google Scholar]
- Punsly, B. 2015a, in The Formation and Disruption of Black Hole Jets, eds. I. Contopoulos, D. Gabuzda, & N. Kylafis, Astrophys. Space Sci. Lib., 414, 149 [Google Scholar]
- Punsly, B. 2015b, ApJ, 806, 47 [CrossRef] [Google Scholar]
- Punsly, B. 2017, ApJ, 850, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Punsly, B., & Coroniti, F. 1989, Phys. Rev. D, 40, 3834 [CrossRef] [Google Scholar]
- Punsly, B., Igumenshchev, I. V., & Hirose, S. 2009, ApJ, 704, 1065 [CrossRef] [Google Scholar]
- Punsly, B., Balsara, D., Kim, J., & Garain, S. 2016, Comput. Astrophys. Cosmol., 3, 5 [CrossRef] [Google Scholar]
- Sadowski, A. 2011, A&A, 527, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, V., Dyadechkin, S., & Punsly, B. 2004, Science, 305, 978 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stawarz, L., Aharonian, J., & Kataoka, J. et al. 2006, MNRAS, 370, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Sturrock, P. A. 1971, ApJ, 164, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., McKinney, & J. 2012, MNRAS Lett., 423, 55 [Google Scholar]
- Teukolsky, S. 1973, ApJ, 185, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, K., Price, R., & Macdonald, D. 1986 Black Holes: The Membrane Paradigm (New Haven: Yale University Press) [Google Scholar]
- Whysong, D., & Antonucci, R. 2004, ApJ, 602, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., Pontin, D. I., & Hornig, G. 2010, A&A, 516, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willott, C., Rawlings, S., Blundell, K., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S., & Yang, Y. 2002, ApJ, 568, 122 [Google Scholar]
These smaller terms are included in the final field plot in Fig. C.2. This is done to make the field solution vary smoothly near the EH, but it should be remembered that due to the numerous approximations in this discussion that the field configuration near the EH is not accurate
All Figures
 |
Fig. 1 Accretion of weak flux tubes into the EHM occurs in the SFMHD+MF simulation of Beckwith et al. (2009; left hand frame). Right hand frame: isolated flux tubes in the 3D radiatively inefficient simulations of (Igumenshchev 2008) and (Punsly et al. 2009). The strength of the vertical poloidal magnetic field is color coded. Dark blue is no field and red is a strong field (near equipartition with the gas pressure). The inner calculational boundary is a circle of radius 2M. Notice the weaker, green, small patches of vertical flux in the inner accretion flow. See the text for more details. |
| In the text | |
 |
Fig. 2 Dynamics of the accretion of weak flux into the EHM is depicted above. The accretion flow in this image is likely much thinner than what occurs in M87. The concepts that are illustrated are not a consequence of the accretion flow thickness. |
| In the text | |
 |
Fig. 3 In the charge-starved limit, a vacuum gap will spread outward from the flow division surface if there is no substantive pair injection mechanism as is quite possibly the case in M87. In this charge starved limit, the surrounding magnetosphere is a semi-vacuum. The only significant source of electromagnetic fields is within the flux tube. The very tenuous stray charges have trajectories that are affected by these fields, but the number density is too small to provide a source for a significant perturbation to these fields. Charges can only flow inward across the charge horizon (Komissarov 2004; Punsly 2004). |
| In the text | |
 |
Fig. 4 Upperlimits on LC and the maximum sustainable Poynting flux from the EHM for M87 as a function of Ec for two cases, Lx is entirely from accretion or Lx from accretion is attenuated by an absorbing screen, NH. The maximum sustainable magnetic field in the EHM assuming that a∕M = 0.9 is also plotted. |
| In the text | |
 |
Fig. 5 Top frame: central flux nadir of the jet near its base is apparent in the 86 GHz HSA image from Hada et al. (2016; restored with a 0".0001 beam). Bottom frame: surface brightness cross-sections from the image above. The central flux nadir is resolved within 56 M (0".0002) of the EH. The central flux nadir surface brightness is ~ 4%–8% of the average surface brightness on the limbs, 56 M–112 M from the EH and ~ 20–30% of the average surface brightness of the limbs at 140 M. |
| In the text | |
 |
Fig. C.1 At t ≈ 4M (in geometrized units) after the time snapshot in Fig. 3, the outgoing severed flux tube segment has been magneto-centrifugally slung out to large distances. The ingoing portion of the severed flux tube has contracted toward the event horizon. The particular case has a∕M = 0.9 and the top boundary of the severed flux tube is at r = 1.08r+. The compact size suggests replacing the azimuthal surface current source of BP in Eqs. (21) and (22) with small azimuthal current rings. This configuration defines the calculation that produces the field line plot in the top frame of Fig. C.2. |
| In the text | |
 |
Fig. C.2 Ingoing portion of the severed flux tube has contracted toward the EH to r = 1.08r+ in the top frame at t = 4M after thevacuum gap starts to spread open. The large scale poloidal magnetic field is plotted in Boyer–Lindquist coordinates. The nature of the disk is very uncertain and it is represented symbolically by a simple wedge. In the bottom frame, the severed flux tube has contracted to r = 1.001r+ at t = 15M after the vacuum gap starts to spread open. Note that the large scale field is contracting towards the black hole. In the top (bottom) frame the poloidal magnetic field in the disk is ≈ 2% (≈ 0.4%) of the poloidal field strength in the original flux tube when it entered the EHM. The bottom frame indicates that poloidal magnetic flux is almost completely dissipated on a timescale of one half of the rotational period of the ISCO. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



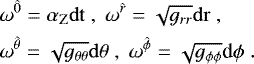
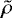
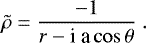
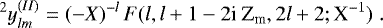
![\begin{eqnarray*} J_2 &=& \frac{-{\rm{\Delta}}}{2 \sqrt{2} \rho^2 \left( r - \textrm{i a} \cos \theta \right)^2 }\nonumber \\ &&\times \left[ \sqrt{2} \left( \frac{\partial}{\partial r} - \frac{a}{{\rm{\Delta}}} \frac{\partial}{\partial \phi} + \frac{1}{r - \textrm{i a} \cos \theta} \right) \left( r - \textrm{i a} \cos \theta \right) J_{\bar{m}} \right. \nonumber \\ && \hspace{-0.1 in} \left. + 2 \left( \frac{\partial}{\partial \theta} - \frac{\textrm{i}}{\sin \theta} \frac{\partial}{\partial \phi} + \frac{\textrm{i a} \sin \theta}{r - \textrm{i a} \cos \theta} \right) \frac{\rho^2 \left( r - \textrm{i a} \cos \theta \right)}{{\rm{\Delta}}} J_n \right] \; ,\nonumber\\ && \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq65.png)
![\begin{eqnarray*} J_{\bar{m}} &=& \left[ \sqrt{2} (r - \textrm{i a} \cos \theta)\right]^{-1}\nonumber \\[3pt] && \times \left[ - \textrm{i a} \cos \theta \tilde{J}^t - \rho^2 \tilde{J}^{\theta} + \textrm{i} (\textrm{r}^2 + \textrm{a}^2) \sin \theta \tilde{J}^{\phi}\right] \; ,\\[3pt] && J_n = \frac{1}{2} \left[ \frac{{\rm{\Delta}}}{\rho^2} \tilde{J}^t + \tilde{J}^r - \frac{a {\rm{\Delta}}}{\rho^2} \sin^2 \theta \tilde{J}^{\phi} \right] \; . \end{eqnarray*}](/articles/aa/full_html/2018/06/aa32215-17/aa32215-17-eq66.png)