| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 12 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201732093 | |
| Published online | 07 June 2018 | |
A revised distance to IRAS 16293-2422 from VLBA astrometry of associated water masers
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
e-mail: sdzib@mpifr-bonn.mpg.de
2
Humboldt Fellow,
Berlin, Germany
e-mail: gortiz@mpifr-bonn.mpg.de
3
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México,
Morelia
58089, Mexico
e-mail: a.hernandez@irya.unam.mx
4
IRAP, Université de Toulouse, CNRS, UPS, CNES,
Toulouse, France
5
Instituto de Astronomía, Universidad Nacional Autónoma de México,
Apartado Postal 70-264,
CdMx
C.P. 04510,
Mexico
6
National Radio Astronomy Observatory,
PO Box 0,
Socorro,
NM
87801, USA
Received:
12
October
2017
Accepted:
8
February
2018
IRAS 16293-2422 is a very well-studied young stellar system seen in projection towards the L1689N cloud in the Ophiuchus complex. However, its distance is still uncertain; there is a range of values from 120 pc to 180 pc. Our goal is to measure the trigonometric parallax of this young star by means of H2O maser emission. We use archival data from 15 epochs of VLBA observations of the 22.2 GHz water maser line. By modeling the displacement on the sky of the H2O maser spots, we derived a trigonometric parallax of 7.1 ± 1.3 mas, corresponding to a distance of 141−21+30 pc. This new distance is in good agreement with recent values obtained for other magnetically active young stars in the L1689 cloud. We relate the kinematics of these masers with the outflows and the recent ejections powered by source A in the system.
Key words: astrometry / masers / stars: formation / stars: individual: IRAS 1629-2422 / techniques: interferometric
© ESO 2018
1 Introduction
As a result of the development and improvement of Very Long Base Interferometry (VLBI) techniques in recent decades, it has become possible to measure the trigonometric parallax of deeply embedded young stellar objects (YSOs) with very high accuracy. This information is crucial for the determination of some of the most fundamental stellar parameters, such as age, luminosity, and mass. Low-mass YSOs with nonthermal emission (such as gyrosynchrotron or synchrotron emission) are good candidates to be observed with VLBI since they have a high surface brightness over a few solar radii (e.g. Loinard et al. 2008; Dzib et al. 2016; Ortiz-León et al. 2017). However, VLBI observations of Class 0 objects, the youngest stars, are more complicated because their nonthermal emission can suffer strong free-free absorption effects from the ionized winds that they typically power.
Emission from water masers has been observed in a variety of objects and has been used to determine their trigonometric parallax and hence their distance (e.g., Imai et al. 2007; Hirota et al. 2008; Reid et al. 2009; Sanna et al. 2017b). Although water masers can vary on short timescales (Claussen et al. 1996), and their structure can be resolved at angular resolutions of VLBI instruments in nearby regions (Imai et al. 2007), they are a fundamental tool used to determine distances to far away star-forming regions. Recent VLBI observations of strong water masers have provided an accurate determination of the distance to a star-forming region at 20 kpc from the Sun (Sanna et al. 2017b).
Water maser emission has been observed towards IRAS 16293-2422 (hereafter I16293), a very well-studied young stellar system located to the north of the Lynds 1689 (L1689) cloud, in the Ophiuchus complex (Fig. 1). This system is comprised of two main sources, A and B, identified from interferometric observations at centimeter wavelengths (Wootten 1989; Mundy et al. 1992) that are separated by 5″ and have properties of Class 0 objects, i.e., YSOs in very early evolutionary phases. Source A itself is resolved into two subsources, A1 and A2, separated by 0.″3 (Chandler et al. 2005; Loinard et al. 2007). Recently, other continuum sources associated with an episodic ejection from A were observed with the VLA (Loinard et al. 2007; Pech et al. 2010; Loinard et al. 2013). Source A seems to power two outflows in the E-W and NW-SE directions observed through the emission of CO and SiO lines (Mizuno et al. 1990; Girart et al. 2014). There is also a compact outflow extending along the axis between sources A and B in the SE-NW direction. Since I16293 is an interesting laboratory for studying the kinematics and dynamics of clustered star formation, it is of crucial importance to determine its distance very precisely and, therefore, to infer its physical parameters correctly. Furthermore, relating the small-scale kinematics of the water masers with those of the larger scale outflows would be interesting.
Previously, Imai et al. (2007) reported on the emission of H2O masers observed with the VLBI Exploration of Radio Astrometry (VERA) array towards this source and obtained an annual parallax for a maser feature of 5.6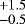 mas, corresponding to a distance of 178
mas, corresponding to a distance of 178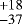 pc. On the other hand, Loinard et al. (2008) measured the distance to the core of the Ophiuchus complex (also known as Lynds 1688 or L1688) from VLBA observations of nonthermal emission from two YSOs and found a distance of
pc. On the other hand, Loinard et al. (2008) measured the distance to the core of the Ophiuchus complex (also known as Lynds 1688 or L1688) from VLBA observations of nonthermal emission from two YSOs and found a distance of 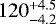 pc. This distance is now commonly used in the literature as the distance to I16293. More recently, Ortiz-León et al. (2017) measured the distance to the L1689 streamer using VLBA observations of three stellar systems, finding a mean parallax of 6.79 ± 0.16 mas, which corresponds to a distance of 147.3 ± 3.4 pc. They also revisited the mean distance to the Ophiuchus core and found a mean parallax of 7.28 ± 0.06 mas, corresponding to a distance of 137.3 ± 1.2 pc. As the distance to I16293 measured by Imai et al. (2007) is significantly larger than that to other stars in the L1689 cloud, it is not yet clear whether it is a background object seen along the line of sight to L1689. However, it is hard to think that such a deeply embedded young star should not be part of a cloud when it appears in projection on the densest part of that cloud (see Fig. 1). It is clear that the distance to I16293 needs to be revisited.
pc. This distance is now commonly used in the literature as the distance to I16293. More recently, Ortiz-León et al. (2017) measured the distance to the L1689 streamer using VLBA observations of three stellar systems, finding a mean parallax of 6.79 ± 0.16 mas, which corresponds to a distance of 147.3 ± 3.4 pc. They also revisited the mean distance to the Ophiuchus core and found a mean parallax of 7.28 ± 0.06 mas, corresponding to a distance of 137.3 ± 1.2 pc. As the distance to I16293 measured by Imai et al. (2007) is significantly larger than that to other stars in the L1689 cloud, it is not yet clear whether it is a background object seen along the line of sight to L1689. However, it is hard to think that such a deeply embedded young star should not be part of a cloud when it appears in projection on the densest part of that cloud (see Fig. 1). It is clear that the distance to I16293 needs to be revisited.
In this paper, we present high-sensitivity VLBI observations of H2 O masers towards I16293. From these observations, we were able to identify the positions of several masers spots and perform a precise astrometry, finding a distance to I16293 that is in good agreement with the recent measured values to other young stars in the Ophiuchus complex.
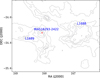 |
Fig. 1 Molecular cloud of Ophiuchus traced by optical extinction obtained as part of the COMPLETE project (Ridge et al. 2006). The location of I16293, the core (L1688), and Lynds 1689 (L1689) are indicated. The contours corresponds to AV = 4, 7, 10, and 13. |
2 Observations and data calibration
We analyzed a series of 18 observations of water masers at 22.2 GHz carried out with the Very Long Baseline Array (VLBA) as part of project BC152 (PI: M. Claussen). These observations cover a period of eight months from 2005 August 2 to 2006 April 13 (see Table 1), and were taken at intervals of about 15 days. Each epoch consisted of cycles switching between I16293 and the quasar J1625-2527 ( ~1.°8 away), with two minutes of integration time on the target and one minute on the quasar. Data were taken in right and left circular polarizations with four baseband channels (BBCs) of 8 MHz bandwidth each. The BBC containing the maser line, which was centered at 22.2371 GHz, was also correlated with a channel separation of 15.6250 kHz (corresponding to a velocity resolution of 0.215 km s−1) to produce 512 spectral channels. Throughout the whole data analysis, we only considered the BBC containing the maser emission.
The strong quasar 3C345 was observed at the beginning and at the end of each epoch and was used asa fringe finder. In total, three hours of observation were spent on I16293 during each observation1 , which was correlated at position αJ2000 = 16h32m22.s889 and δJ2000 = −24°28′36.″25.
Data calibration and imaging were performed using the Astronomical Image Processing System (AIPS; Greisen 2003). First, we removed the delays introduced by the ionospheric content; then we applied corrections to the Earth Orientation Parameters used by the correlator, and corrections for voltage offsets in the samplers. Instrumental single-band delays were then determined and removed using fringes detected on 3C345. Amplitude calibration was done using the provided gain curves and system temperatures to derive the System Equivalent Flux Density (SEFD) of each antenna. At this stage, the bandpass shape calibration, which was obtained from the scans on 3C345, was applied to the data. In order to set the velocity information for I16293, we used the radio velocity definition and adopted a line rest frequency of 22.23508 GHz. Then we corrected the data for the Doppler shift due to the rotation of the antennas with the Earth around the Sun during observations. Finally, global fringe fitting was run on J1625-2527 in order to find residual phase rates and delays; the solutions from this final step were then applied to the maser line data. Due to poor weather conditions or technical faults at some antennas of the array, the first three epochs presented very poor data quality and were discarded from the analysis.
We found strong maser emission at an LSR velocity, vLSR, of ≈ 6.1 km s −1 (channel 252; see Fig. 2 for an example) in all the 15 remaining epochs. Images were produced for this velocity channel (see Sect. 3.1) using a pixel size of 50 μas and a weighting scheme intermediate between natural and uniform (ROBUST = 0 in AIPS). The emission from this channel was found to be offset from the phase centerby ~1.″2. Therefore, the phase center was shifted (using the task UVFIX in AIPS) to the position of the emission and then used to produce our final images, shown in Fig. 3. The resulting r.m.s. noises in these images are given in Table 1.
The final images were exported to FITS format for further analysis using the CASA software package. This software provides more flexibility for fitting multiple Gaussians in regions containing a large number of pixels (task IMFIT in CASA versus task JMFIT in AIPS). The Gaussian fittings were used to determine the position and flux of the water masers spots. We compared the fitted positions from the two software tools and found that they agree within 1σ. JMFIT and IMFIT provide an estimate of the position errors based on the expected theoretical astrometric precision of an interferometer (Condon 1997). The barycentric coordinates of the Earth and the Julian date of each observation, which are necessary for the astrometric fits, were calculated using the NOVAS routines distributed by the US Naval Observatory.
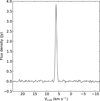 |
Fig. 2 Observed spectrum of the water emission toward the brightest spot in epoch M (also called spot 2 in Sect. 3.2). |
Main parameters of all images obtained for each VLBA observation data set.
Other water maser features detected toward I16293 with the VLBA.
3 Results
3.1 Structure and properties of the emission
Maser emission is detected at radial velocities vLSR ~ 1.9, 2.1, 2.8, 4.0, and 6.1 km s−1. These velocities are very similar to the systemic LSR velocity of I16293 A, for which Jørgensen et al. (2011) give +3.2 km s−1. Only the emission at 6.1 km s−1 is detected in all of the 15 epochs, while emission at the other velocities is not seen in more than two epochs (see Table 2). For this reason, we focus our analysis on the persistent emission at 6.1 km s−1. We note that Imai et al. (2007) also detected emission in their VERA observations from 2005 to 2006, at a velocity of vLSR = 6.0 km s−1 with Sν ~ 2 Jy, which may correspond to the emission detected here.
For the astrometric analysis we only consider the spots detected in the maps for this velocity channel (channel 252). In general, several spots are detected at each epoch. Some spots show an elongated structure, just as was previously reported by Imai et al. (2007). As noticed by these authors, the brightness distribution of the emission is spatially resolved and variable. The brightest spot at one epoch is not necessarily the brightest one in the other epochs and many of them were detected in one epoch only. For all these reasons, choosing the correct positions for the astrometry implies a careful analysis of the images.
3.2 Selection of positions for astrometry
In order to perform accurate and reliable astrometry, the position of the same object needs to be measured at several consecutive epochs. For compact objects, such as stellar nonthermal continuum sources, there is little or even null confusion of the source position from epoch to epoch: it is the position of the emitting star. However, the case of water masers in nearby star-forming regions is much more complex. Due to their variability and motions, it is not easy to associate different spots even between contiguous epochs, especially when the emission is heavily resolved. The water maser shocks are located at the base of YSOs outflows (Torrelles et al. 2003; Sanna et al. 2012). Their motion on the plane of the sky is the result of the superposition of a proper motion plus a reflex motion introduced by the parallax. Especially important is their movement in the right ascension (R.A.) direction, since their position in this direction is better determined and allows better determinations of the trigonometric parallax (Reid et al. 2009).
To select the spots we made the following assumptions: (i) all the spots lie at the same distance, (ii) they have similarproper motions, and (iii) their radial velocity is constant at the different epochs. According to these assumptions, we expect that the position angle and projected angular distance between two different spots do not significantly change in a time interval of 15 days. With this in mind, we can identify individual spots between consecutive epochs as shown in Fig. 4. In the left panel, we superpose the maser emission detected in epochs D–G, which were observed from 2005 September to November. We can clearly identify a spot that is detected in these four epochs and that shows a coherent motion toward the southwest of the map. We refer to this spot as “spot 1”. In the right panel of Fig. 4, we now show the detected emission in epochs M–R, which were taken from 2006 January to April. In these epochs, the structure of the emission is much more complex. We can still distinguish two spots with coherent motions, also toward the southwest. Both emission spots are detected in epochs O, P, Q, and R. These two spots show a similar position angle and angular separation (of about 2.5 mas) in the four epochs. We call them “spot 2” and “spot 3” (see Fig. 4). Spot 2 is also detected in epoch M, but not in epoch N, and, conversely, spot 3 is detected in epoch N but not in epoch M. We discarded epochs H–L because the maser emission shows multiple blended peaks, which cannot be distinguished unambiguously. The positions of spots 1, 2, and 3 are listed in Table 3, and they are used in Sect. 3.3 to estimate the parallax of I16293.
It is clear from this analysis that the spots are very variable and that their associated emission lasts for only a few months. A second approach for the determination of the trigonometric parallax is to track the motion of the shock front, which is traced by the collection of several spots at each epoch, and then fit the positions of this shock front in the RA direction. We adopted the mean position of the spots associated with it, which were identified by their proximity in the maps, as the position of the shock front at each epoch. These positions are listed in Table 4 and are shown as blue strips in Fig. 3. In the epochs where we see a lot of structure in the emission (for example in epochs N and P) we only consider the spots at the expected positions according to the advancing motion of the shock front.
Having identified three main spots that persisted in at least four epochs and the mean positions of the shock front, we now proceed with the astrometric fits. For this purpose, we apply the single value decomposition (SVD) fitting scheme described by Loinard et al. (2007).
 |
Fig. 3 Watermasers detected in our VLBA images above 10σ at each epoch. The images show the emission from the channel at vLSR = 6.1 km s−1. Contour levels are 0.3, 0.4, 0.5, 0.65, 0.80, and 0.95 times the peak level on the images, which are given in Table 1. The blue strips indicate the RA position with error bars of the shock front (see Sect. 3.2.) |
 |
Fig. 4 Superposition of the detected spots. For clarity and to guide the eye, left panel: spots detected in the first four epochs (epoch D–G; see Table 1). Right panel: spots detected from epochs M to R. The contour levels are 0.3, 0.4, 0.5, 0.65, 0.80, and 0.95 times the peak flux of each image. Triangles indicate the emission peaks of spot 1; squares and circles correspond to spot 2 and 3, respectively. |
3.3 Astrometry
In radio astrometry, the source positions are commonly registered at multiple epochs spanning long periods, usually of one-year duration, in order to trace the full parallax sinusoid. The observations presented here cover only a time period of seven months. However, the first and last data were taken close to the time when the maximum parallax angle is reached, i.e., in September and March. Radio astrometry has been performed with similar time spans for other star-formingregions with good determination of parallaxes (e.g., Hirota et al. 2008; Kim et al. 2008). As described in Sect. 3.2, only three spots are detected in four or five epochs each (see Table 3), with time spans of only 2 to 3 months. The shock front, on the other hand, is tracked over the full seven months. We can compare the astrometry derived from the individual spots to that derived from the positions of the shock front.
We first fit each of the three maser spots separately (Fig. 5, first panel). The resulting values of the trigonometric parallaxanddistance from these fits are given in Table 5. Since the results from the three fits are consistent with each other within 1σ, we simultaneously fit the three maser spots by requiring a single parallax, and allowing the proper motions to vary between the different spots. The parallax obtained in this case is 7.4 ± 1.1 mas, corresponding to a distance of 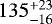 pc. The values of the proper motions do not significantly change when compared to those derived from the individual fits.
pc. The values of the proper motions do not significantly change when compared to those derived from the individual fits.
We note that if we extrapolate the positions of spot 1 to the epochs when spot 2 is detected (by using the best models from the previous two fits), then their corresponding positions are consistent within the errors. This suggests that these two spots are related and may indeed correspond to the same gas condensation (or cloudlet; Sanna et al. 2017a). To test this hypothesis, we perform a simultaneous fit to both spots and consider that there is a positional offset between them. The resulting astrometric parameters from this fit are also given in Table 5 and are shown in Fig. 5 (bottom left). The best-fit parallax yields a distance of 141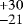 pc. It is important to mention that the resulting positional offset is relatively small and the proper motions of the spots are consistent within errors (see Table 5). Thus, an additional fit was done by assuming that spots 1 and 2 trace the motion of the same cloudlet. From this fit, we found that the parallax uncertainty is at least a factor of two lower than that obtained in the previous fits. However, given the strong variability of the maser emission, the spots could be bright at different times, and thus we consider the fit with nonzero positional offset to be more robust.
pc. It is important to mention that the resulting positional offset is relatively small and the proper motions of the spots are consistent within errors (see Table 5). Thus, an additional fit was done by assuming that spots 1 and 2 trace the motion of the same cloudlet. From this fit, we found that the parallax uncertainty is at least a factor of two lower than that obtained in the previous fits. However, given the strong variability of the maser emission, the spots could be bright at different times, and thus we consider the fit with nonzero positional offset to be more robust.
Second, we performed an astrometric fit to the mean position of the shock front and derive a trigonometric parallax of π = 6.6 ± 0.6 mas, corresponding to a distance of 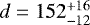 pc. We show the parallax sinusoid from this fit in Fig. 6, and give the resulting parameters in Table 5. The values of the parallax derived from the fits to the three main spots are in good agreement with that obtained from the fit to the R.A. motion of the shock front.
pc. We show the parallax sinusoid from this fit in Fig. 6, and give the resulting parameters in Table 5. The values of the parallax derived from the fits to the three main spots are in good agreement with that obtained from the fit to the R.A. motion of the shock front.
The correlation coefficient matrices for all fits are shown in Appendix A. From these matrices we noticed a high (anti-) correlation between the parallax and the other fitted parameters in all the fits, as is expected given the short timescale covered by the observations. To check the reliability of our results, in view of these high correlations, we performed a series of Monte Carlo simulations which are presented in Appendix B. The result from these simulations is that, given the statistical and systematic errors in our measurements, the true astrometric parameters can be recovered from our fits even when the observations cover a period of only 3–7 months. The worst case is the individual fit to spot 1; this spot was only detected in four epochs and, consequently, the uncertainties on the fitted parameters are significantly larger.
Detected epochs and positions of the different maser spots used for the astrometry.
 |
Fig. 5 Resulting fits to the water maser spots detected toward I16293 (see Table 5). The black, red, and yellow lines show the best fits for spot 1, 2, and 3, respectively. The solid squares with the error bars indicate measured positions and their corresponding uncertainties. The solid circles mark the expected positions from the fits at the observing epochs. Top left: individual fits to each of the three maser spots. Top right: simultaneous fit assuming that the parallax is the same for the three spots. Bottom left: simultaneous fit to positions of Spot 1 and 2, by allowing them to have a positional offset and different proper motions. Bottom right: simultaneous fit to spots 1 and 2, assuming that they belong to the same cloudlet. |
Observed epochs and RA positions of the water maser shock front.
Parameters obtained from the astrometric fits. The systematic errors that were added quadratically are also presented.
4 Discussion
4.1 Distance to I16293
As we mentioned in the introduction, Imai et al. (2007) obtained a distance of 178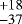 pc to I16293 by measuring the trigonometric parallax of water masers associated with this YSO. Imai et al. (2007) mentioned that the most severe factor causing their modest astrometric accuracy was the temporal variation in the brightness structure of the maser spots they detected. If water masers have short lifetimes of a few months, as is the case with water masers in I16293, it is possible to misidentify maser spots even from one epoch to the next. Taking into account this possibility, these authors performed several fits by using different combinations of observed positions. By excluding the oddest positions, they obtained an upper limit to the trigonometric parallax of 7.1 mas (corresponding to a lower limit in the distance of d = 141 pc). In the following, we discuss the differences between our analysis and that of Imai et al. (2007).
pc to I16293 by measuring the trigonometric parallax of water masers associated with this YSO. Imai et al. (2007) mentioned that the most severe factor causing their modest astrometric accuracy was the temporal variation in the brightness structure of the maser spots they detected. If water masers have short lifetimes of a few months, as is the case with water masers in I16293, it is possible to misidentify maser spots even from one epoch to the next. Taking into account this possibility, these authors performed several fits by using different combinations of observed positions. By excluding the oddest positions, they obtained an upper limit to the trigonometric parallax of 7.1 mas (corresponding to a lower limit in the distance of d = 141 pc). In the following, we discuss the differences between our analysis and that of Imai et al. (2007).
The first difference comes from their criterion for the selection of maser spots. They assumed that the brightest peak always traces the same spot, and used its measured positions for the astrometric fits. As we can see in Fig. 4, this assumption is not valid, for instance from epoch M to epoch N. Additionally, the radial velocities of their spots vary from one epoch to the other by ~ 1 km s−1, suggesting that they are not tracing the same gas (e.g., Moscadelli et al. 2006). Finally, the time intervals between their observed epochs range from 22 days up to three months, whereas our measurements are spaced 15 days apart, on average. This higher cadence improves our ability to trace the same maser spots and, particularly, the shock front in time.
The estimated trigonometric parallaxes from all our fits agree with the lower limit of 141 pc obtained by Imai et al. (2007). However, the fits that exhibit the smallest parallax errors may be affected by the assumptions we made regarding the associations between the detected spots (see Sects. 3.2 and 3.3). The most conservative result is thus the fit “With offset” (Table 5) since it allows the spots to have non-identical positions and also spans the longest period of observation (7 months). The resulting trigonometric parallax from this fit is 7.1 ± 1.3 mas, corresponding to a conservative value of 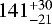 pc for the distance. This result also agrees within 1σ with a recent value of 147.3 ± 3.4 pc measured to three other systems in Lynds 1689 (Ortiz-León et al. 2017).
pc for the distance. This result also agrees within 1σ with a recent value of 147.3 ± 3.4 pc measured to three other systems in Lynds 1689 (Ortiz-León et al. 2017).
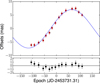 |
Fig. 6 Parallax fit to the mean positions of the shock front. Top: parallax sinusoid from the best fit to these data (blue line). The red squares are the mean positions of the shock front. In both cases, we have subtracted the proper motion and the RA position at JD 2453731.31 (the mean epoch from our observations) from the best fit. Bottom: residuals in right ascension. |
 |
Fig. 7 Stellar system I16293. Left: continuum map at 22 GHz taken with the VLA on 2006 February 10. The noise level of this image is 47 μJy beam−1, and the contour levels are −4, 4, 6, 10, 15, 20, and 30 times this value. Right: zoom-in on source A. Shown are the sources composing this system: A1, A2, and the ejecta A2α. Also shown are the directions of the three outflows (blue and red arrows). The colored crosses represent the positions of the maser spots detected at different velocities (see Table 2). The magenta cross indicates the position of the masers at 6.1 km s−1 and the magenta arrow arising from it shows the mean proper motion direction, while the green arrow indicates the proper motion direction of the maser spot at 2.1 km s−1 identified on epochs I and J. The blue cross indicates the position of the maser emission detected in epoch R at 1.9 km s−1, very close to source A1, and the red cross marks the position of the maser spot at 2.8 km s−1 close to source A2 and detected in epoch F. The position of the maser spot detected in epoch R at 4.0 km s−1 is shown with a purple cross. The arrow lengths do not represent velocity magnitudes, but only the direction of the outflows and the proper motions of the masers. Also included is a reference of the physical scale on both images. |
4.2 Relationship between water maser emission and molecular outflows in I16293
In Fig. 7 we show a radio continuum map of the I16293 system at 22.46 GHz, as observed with the VLA on 2006 February 10 (and previously reported by Pech et al. 2010). This image shows the sources A and B that were introduced in Sect. 1. On the right side of this figure we zoom in on source A and show its two components, A1 and A2, and the A2α ejecta as well. In Fig. 7 the magenta cross shows the position of the persistent water maser peak observed at vLSR = 6.1 km s−1.
The proper motions of the continuum sources A1 and A2 are ( − 3.0 ± 0.4, − 27.9 ± 0.8) mas yr−1 and ( − 7.8 ± 0.6, − 21.8 ± 0.5) mas yr−1, respectively (Hernández-Gómez et al., in prep.). To convert proper motions into transverse velocities we use the relation 1 mas ≡ 0.67 km s−1, which is appropriate for a distance of 141 pc. Here, we have measured a proper motion of ( − 39 ± 2, − 13 ± 1) mas yr−1 for the persistent maser cloudlet (Spots 1 and 2). The proper motion in declination of this cloudlet is similar in magnitude and direction to that of source A2, but is significantly larger in the R.A. direction. After subtracting the velocity vector of source A2, we found that the intrinsic proper motion of the spot is ( − 31.2 ± 2.1, 8.8 ± 1.1) mas yr−1 = ( − 20.9 ± 1.4, 5.9 ± 0.7) km s−1, i.e., toward the northwest of the continuum source. It is indicated with the magenta arrow in Fig. 7.
Another maser spot at a radial velocity of 2.1 km s−1 was detected in the consecutive epochs I and J and is indicated in Fig. 7 with a green cross. We measured its positions and corrected for the trigonometric parallax in order to arrive at a proper motion of (43.6 ± 0.9, 7.5 ± 1.9) mas yr−1. Thus, its relative proper motion with respect to source A2 is (51.4 ± 0.9, 29.3 ± 2.0) mas yr−1 = (34.5 ± 0.7, 19.7 ± 1.3) km s−1, i.e., toward the northeast of the continuum source, as indicated by the green arrow in Fig. 7. The maser spots at other radial velocities were only detected once, and their positions are shown in Fig. 7 as crosses of different colors. We note that two of them are close to source A2 and the other is close to source A1.
As mentioned before, several molecular outflows have been observed towards I16293 (see, e.g., Mizuno et al. 1990; Loinard et al. 2013; Girart et al. 2014). There are two bipolar outflows arising from source A with position angles (P.A.) of approximately 60° and 110°. There is also a third outflow in the SE-NW direction extending between sources A and B. The red- and blueshifted lobes have radial velocities between 6 and 20 km s−1, and − 10 and 2 km s−1, respectively (Mizuno et al. 1990). The direction of the lobes of these three outflows are also indicated in Fig. 7. The water masers in I16293 are at the starting point of these much larger scale outflows. Given that the water maser shocks are usually found at the base of YSOs outflows (Torrelles et al. 2003; Sanna et al. 2012), we suggest that the maser emission at 2.1 km s−1 and at 6.1 km s−1 are associated with these outflows. In particular, the radial velocity, position, and proper motions of the spot at 6.1 km s−1 suggest that this is directly related to the redshifted lobe of the outflow with PA = 110°. The radial velocity of the maser spot at 2.1 km s−1 suggests that it may be associated with a blueshifted lobe, possibly with the outflow with PA = 110°. However, the direction of its proper motions are similar to the redshifted lobe of the outflow with PA = 60°. Thus, we cannot unambiguously associate the maser emission with a specific flow.
5 Conclusions
We analyzed 15 archival VLBA observations at 22.2 GHz to measure the trigonometric parallax of water masers associated with the YSO I16293 in the Ophiuchus molecular cloud, and to determine its distance. In our analysis the main source of uncertainty is the maser variability and the short time span covered by the observations.
After a careful analysis of the maps, we identified three maser spots, and fitted their displacement on the plane of the sky as being due to a linear motion and the reflex motion of the trigonometric parallax. Additionally, we also tracked the position of the shock front and fitted its motion in the RA direction. All our fits agree within the errors, and suggest a distance of around 140 pc. Our most conservative approach yields a trigonometric parallax of 7.1 ± 1.3 mas, corresponding to a distance of 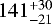 pc.
pc.
This distance estimate is smaller than that reported by Imai et al. (2007) by nearly 40 pc, but the two results are consistent within 1σ. Our value for the I16293 distance is also 21 pc larger than the 120 pc obtained by Loinard et al. (2008) based on two objects in L1688 (theirresults were later corrected by Ortiz-León et al. (2017), who derived greater distances for both objects). Furthermore, our measured distance is in good agreement with recent measurements by Ortiz-León et al. (2017) of trigonometric parallaxes of magnetically active YSOs in the Ophiuchus complex, and especially in the L1689 cloud at a distance of 147.3 ± 3.4 pc. Thus, our results support the widely held view that I16293 is a member of the L1689 cloud in Ophiuchus.
The radial velocities and direction of the relative proper motions of the water masers (with respect to source A2), agrees with those of the outflow emission previously reported in this system. In the case of the water masers with vLSR = 6.1 km s−1 it was possible to associate them with the redshifted lobe of the outflow with a PA = 110°.
Acknowledgements
We would like to acknowledge the referee Mark Reid for his comments and suggestions that improved the manuscript. G.-N.O.L acknowledges support from the Alexander von Humboldt Foundation in the form of a Humboldt Fellowship. A.H.-G. and L.L. acknowledge the financial support of DGAPA, UNAM (project IN112417), and CONACyT, México. The Long Baseline Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
Appendix A Correlation matrices
The purpose of this appendix is to show the correlations matrices for all the fits made to our data. In the following subsections we keep the name of the fits as they were introduced in Table 5.
A.1 Individual
A.2 Simultaneous
A.3 With offset
A.4 Spot 1 & 2
A.5 Shock front
Appendix B Monte Carlo simulations
To test the reliability of our results, particularly in relation to the short observing time span, we performed the following simulations. We created new data sets consisting of simulated observed positions at the epochs when the spots 1, 2, and 3 were detected. We then evaluated their positions following the equations appropriated for a particle moving with a linear proper motion (μ) plus the trigonometric parallax (π) as
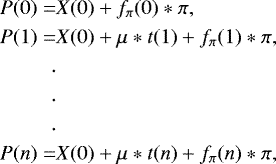 (B.1)
(B.1)
where the parameter are as follows: P(n) is the simulated position at the epoch n; the start position, X(0), is the position of our detected water maser spots in their first detection; and fπ (n) is the projection of the parallactic ellipse at epoch n (e.g., Urban & Seidelmann 2013).
To each simulated position we added a random error drawn from a normal distribution of mean equal to zero and standard deviations of 0.4 mas and 0.8 mas in R.A. and Dec., respectively. These values are similar to the maximum values of our systematic errors (Esys; see Table 5). Each data set was then fitted using the same scheme that we used for the actual observations.
We created 10 000 realizations of the simulated positions and then calculated the mean and standard deviation of the resulting distributions of the astrometric parameters. The input values used in the simulation and the resulting values are given in Table B.1. As an example, a distribution histogram of one of the simulation sets is presented in Fig. B.1.
Input and output parameters of the Monte Carlo simulations.
 |
Fig. B.1 Distribution histogram of the simulation set corresponding to the Simultaneous 1 set, at the input distance 147.3 pc. |
References
- Chandler, C. J., Brogan, C. L., Shirley, Y. L., & Loinard, L. 2005, ApJ, 632, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Claussen, M. J., Wilking, B. A., Benson, P. J., et al. 1996, ApJS, 106, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Dzib, S. A., Ortiz-León, G. N., Loinard, L., et al. 2016, ApJ, 826, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Estalella, R., Palau, A., Torrelles, J. M., & Rao, R. 2014, ApJ, 780, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Greisen, E. W. 2003, Information Handling in Astronomy – Historical Vistas, 285, 109 (Netherlands: Springer) [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Bushimata, T., Choi, Y. K., et al. 2008, PASJ, 60, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, H., Nakashima, K., Bushimata, T., et al. 2007, PASJ, 59, 1107 [NASA ADS] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Nguyen Luong, Q., & Takakuwa, S. 2011, A&A, 534, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, M. K., Hirota, T., Honma, M., et al. 2008, PASJ, 60, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Chandler, C. J., Rodríguez, L. F., et al. 2007, ApJ, 670, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., & Rodríguez, L. F. 2008, ApJ, 675, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Zapata, L. A., Rodríguez, L. F., et al. 2013, MNRAS, 430, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Fukui, Y., Iwata, T., Nozawa, S., & Takano, T. 1990, ApJ, 356, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Moscadelli, L., Testi, L., Furuya, R. S., et al. 2006, A&A, 446, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mundy, L. G., Wootten, A., Wilking, B. A., Blake, G. A., & Sargent, A. I. 1992, ApJ, 385, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Kounkel, M. A., et al. 2017, ApJ, 834, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Pech, G., Loinard, L., Chandler, C. J., et al. 2010, ApJ, 712, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2009, ApJ, 693, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Ridge, N. A., Di Francesco, J., Kirk, H., et al. 2006, AJ, 131, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Reid, M. J., Carrasco-González, C., et al. 2012, ApJ, 745, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Moscadelli, L., Surcis, G., et al. 2017a, A&A, 603, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Reid, M. J., Dame, T. M., Menten, K. M., & Brunthaler, A. 2017b, Science, 358, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Torrelles, J. M., Patel, N. A., Anglada, G., et al. 2003, ApJ, 598, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Urban, S., & Seidelmann, P. 2013, The Explanatory Supplement to the Astronomical Almanac (California, USA: University Science Books) [Google Scholar]
- Wootten, A. 1989, ApJ, 337, 858 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Detected epochs and positions of the different maser spots used for the astrometry.
Parameters obtained from the astrometric fits. The systematic errors that were added quadratically are also presented.
All Figures
 |
Fig. 1 Molecular cloud of Ophiuchus traced by optical extinction obtained as part of the COMPLETE project (Ridge et al. 2006). The location of I16293, the core (L1688), and Lynds 1689 (L1689) are indicated. The contours corresponds to AV = 4, 7, 10, and 13. |
| In the text | |
 |
Fig. 2 Observed spectrum of the water emission toward the brightest spot in epoch M (also called spot 2 in Sect. 3.2). |
| In the text | |
 |
Fig. 3 Watermasers detected in our VLBA images above 10σ at each epoch. The images show the emission from the channel at vLSR = 6.1 km s−1. Contour levels are 0.3, 0.4, 0.5, 0.65, 0.80, and 0.95 times the peak level on the images, which are given in Table 1. The blue strips indicate the RA position with error bars of the shock front (see Sect. 3.2.) |
| In the text | |
 |
Fig. 4 Superposition of the detected spots. For clarity and to guide the eye, left panel: spots detected in the first four epochs (epoch D–G; see Table 1). Right panel: spots detected from epochs M to R. The contour levels are 0.3, 0.4, 0.5, 0.65, 0.80, and 0.95 times the peak flux of each image. Triangles indicate the emission peaks of spot 1; squares and circles correspond to spot 2 and 3, respectively. |
| In the text | |
 |
Fig. 5 Resulting fits to the water maser spots detected toward I16293 (see Table 5). The black, red, and yellow lines show the best fits for spot 1, 2, and 3, respectively. The solid squares with the error bars indicate measured positions and their corresponding uncertainties. The solid circles mark the expected positions from the fits at the observing epochs. Top left: individual fits to each of the three maser spots. Top right: simultaneous fit assuming that the parallax is the same for the three spots. Bottom left: simultaneous fit to positions of Spot 1 and 2, by allowing them to have a positional offset and different proper motions. Bottom right: simultaneous fit to spots 1 and 2, assuming that they belong to the same cloudlet. |
| In the text | |
 |
Fig. 6 Parallax fit to the mean positions of the shock front. Top: parallax sinusoid from the best fit to these data (blue line). The red squares are the mean positions of the shock front. In both cases, we have subtracted the proper motion and the RA position at JD 2453731.31 (the mean epoch from our observations) from the best fit. Bottom: residuals in right ascension. |
| In the text | |
 |
Fig. 7 Stellar system I16293. Left: continuum map at 22 GHz taken with the VLA on 2006 February 10. The noise level of this image is 47 μJy beam−1, and the contour levels are −4, 4, 6, 10, 15, 20, and 30 times this value. Right: zoom-in on source A. Shown are the sources composing this system: A1, A2, and the ejecta A2α. Also shown are the directions of the three outflows (blue and red arrows). The colored crosses represent the positions of the maser spots detected at different velocities (see Table 2). The magenta cross indicates the position of the masers at 6.1 km s−1 and the magenta arrow arising from it shows the mean proper motion direction, while the green arrow indicates the proper motion direction of the maser spot at 2.1 km s−1 identified on epochs I and J. The blue cross indicates the position of the maser emission detected in epoch R at 1.9 km s−1, very close to source A1, and the red cross marks the position of the maser spot at 2.8 km s−1 close to source A2 and detected in epoch F. The position of the maser spot detected in epoch R at 4.0 km s−1 is shown with a purple cross. The arrow lengths do not represent velocity magnitudes, but only the direction of the outflows and the proper motions of the masers. Also included is a reference of the physical scale on both images. |
| In the text | |
 |
Fig. B.1 Distribution histogram of the simulation set corresponding to the Simultaneous 1 set, at the input distance 147.3 pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha\quad & \quad\delta \quad & \quad \mu_{\alpha}\cos(\delta) \quad & \quad \mu_{\delta} \quad & \quad \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha\\ \delta\\ \mu_{\alpha}\cos(\delta)\\ \mu_{\delta}\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.21 & -0.55 & 0.16 & 0.68 \\ -0.21 & 1.00 & 0.31 & 0.82 & -0.31 \\ -0.55 & 0.31 & 1.00 & -0.23 & -0.99 \\ 0.16 & 0.82 & -0.23 & 1.00 & 0.24 \\ 0.68 & -0.31 & -0.99 & 0.24 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq11.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha\quad & \quad\delta \quad & \quad \mu_{\alpha}\cos(\delta) \quad & \quad \mu_{\delta} \quad & \quad \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha\\ \delta\\ \mu_{\alpha}\cos(\delta)\\ \mu_{\delta}\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.07 & -0.27 & -0.07 & -0.93\\ -0.07 & 1.00 & -0.01 & -0.94 & 0.07 \\ -0.27 & -0.01 & 1.00 & -0.01 & -0.10 \\ -0.07 & -0.94 & -0.01 & 1.00 & 0.08 \\ -0.93 & 0.07 & -0.10 & 0.08 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq12.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha\quad & \quad\delta \quad & \quad \mu_{\alpha}\cos(\delta) \quad & \quad \mu_{\delta} \quad & \quad \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha\\ \delta\\ \mu_{\alpha}\cos(\delta)\\ \mu_{\delta}\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.23 & -0.79 & -0.08 & -0.97\\ -0.23 & 1.00 & 0.15 & -0.92 & 0.23 \\ -0.79 & 0.15 & 1.00 & 0.05 & 0.62\\ -0.08 & -0.92 & 0.05 & 1.00 & 0.08\\ -0.97 & 0.23 & 0.62 & 0.08 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq13.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha[1]\quad & \quad\delta [1]\quad & \quad{\displaystyle \mu_{\alpha}\cos(\delta) [1]} &\mu_{\delta} [1]\quad & \quad\alpha [2]\quad & \quad\delta [2]\quad & \quad\mu_{\alpha}\cos(\delta) [2] &\mu_{\delta} [2]\quad & \quad\alpha [3]\quad & \quad\delta [3]\quad & \quad\mu_{\alpha}\cos(\delta) [3] &\mu_{\delta} [3] &\pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha[1]\\ \delta [1]\\ {\displaystyle \mu_{\alpha}\cos(\delta) [1]}\\ \mu_{\delta} [1]\\ \alpha [2]\\ \delta [2]\\ \mu_{\alpha}\cos(\delta) [2]\\ \mu_{\delta} [2]\\ \alpha [3]\\ \delta [3]\\ \mu_{\alpha}\cos(\delta) [3]\\ \mu_{\delta} [3] \\ \pi \end{array}} & \left( \begin{array}{*{20}{c}} 1.00 & -0.11 & -0.74& -0.04& -0.18& 0.07& 0.70& -0.05& 0.79& -0.05& 0.07& -0.06& -0.88\\ -0.11 & 1.00& 0.04& -0.95& 0.03& -0.01& -0.10& 0.01& -0.11& 0.01& -0.01& 0.01& 0.12\\ -0.74& 0.04& 1.00& 0.01& 0.07& -0.03& -0.28& 0.02& -0.32& 0.02& -0.03& 0.02& 0.35\\ -0.04& -0.95& 0.01& 1.00& 0.01& -0.00& -0.03& 0.00& -0.04& 0.00& 0.00& 0.00& 0.04\\ -0.18& 0.03& 0.07& 0.01& 1.00& -0.02& 0.41& 0.01& -0.19& 0.01& -0.02& 0.01& 0.21\\ 0.07& -0.01& -0.03& -0.00& -0.02& 1.00& 0.06& 0.96& 0.07& 0.00& 0.01& 0.00& -0.07\\ 0.70& -0.10& -0.28& -0.03& 0.41& 0.06& 1.00& -0.04& 0.72& -0.05& 0.07& -0.05& -0.8\\ -0.05& 0.01& 0.02& 0.00& 0.01& 0.96& -0.04& 1.00& -0.05& 0.00& 0.00& 0.00& 0.06]\\ 0.79& -0.11& -0.32& -0.04& -0.19& 0.07& 0.72& -0.05& 1.00& -0.06& -0.34& -0.06& -0.90\\ -0.05& 0.01& 0.02& 0.00& 0.01& 0.00& -0.05& 0.00& -0.06& 1.00& -0.01& -0.94& 0.06\\ 0.07& -0.01& -0.03& 0.00& -0.02& 0.01& 0.07& 0.00& -0.34& -0.01& 1.00& -0.01& -0.08\\ -0.06& 0.01& 0.02& 0.00& 0.01& 0.00& -0.05& 0.00& -0.06& -0.94& -0.01& 1.00& 0.06\\ -0.88& 0.12& 0.35& 0.04& 0.21& -0.07& -0.80& 0.06& -0.90& 0.06& -0.08& 0.06& 1.00 \end{array} \right) \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq14.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha [1] & \mu_{\alpha}\cos(\delta) [1] & \mu_{\alpha}\cos(\delta) [2] & \textrm{Offset}(\alpha) & \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha [1] \\ \mu_{\alpha}\cos(\delta) [1]\\ \mu_{\alpha}\cos(\delta) [2]\\ \textrm{Offset}(\alpha)\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.90 & -0.09 & -0.93 & -0.98\\ -0.90 & 1.00 & 0.08 & 0.82 &-0.83 \\ -0.09 & 0.08 & 1.00 & -0.26 & -0.09\\ -0.93 & -0.82 & 0.26 & 1.00 & -0.93\\ -0.98 & -0.83 & -0.09 & -0.93 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq15.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \delta [1] & \mu_{\delta} [1] & \mu_{\delta} [2] & \textrm{Offset}(\delta) & \pi \end{array}}\\ {\begin{array}{*{20}{c}} \delta [1] \\ \mu_{\delta} [1]\\ \mu_{\delta} [2]\\ \textrm{Offset}(\delta)\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.75 & -0.78 & -0.84 & -0.98\\ -0.75 & 1.00 & 0.52 & 0.63 &-0.65 \\ -0.78 & 0.52 & 1.00 & 0.33 & 0.80\\ -0.84 & 0.63 & 0.33 & 1.00 & 0.82 \\ -0.98 & -0.65 & 0.80 & 0.82 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq16.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha & \delta & \mu_{\alpha}\cos(\delta) &\mu_{\delta} & \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha\\ \delta\\ \mu_{\alpha}\cos(\delta)\\ \mu_{\delta}\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & -0.01 & -0.27 & 0.07 & 0.22\\ -0.01 & 1.00 & 0.04 & -0.21 & -0.04\\ -0.27 & 0.04 & 1.00 & -0.30 & -0.96\\ 0.07 & -0.21 & -0.30 & 1.00 & 0.31\\ 0.22 & -0.04 & -0.96 & 0.31 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq17.png)
![\[ \begin{array}{*{20}{c}} {}& {\begin{array}{*{20}{c}} \alpha & \mu_{\alpha}\cos(\delta) & \pi \end{array}}\\ {\begin{array}{*{20}{c}} \alpha\\ \mu_{\alpha}\cos(\delta)\\ \pi \end{array}}&{\left( {\begin{array}{*{20}{c}} 1.00 & 0.56 & -0.60\\ 0.56 & 1.00 & -0.94\\ -0.60 & -0.94 & 1.00 \end{array}} \right)} \end{array} \]](/articles/aa/full_html/2018/06/aa32093-17/aa32093-17-eq18.png)