| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201731908 | |
| Published online | 27 June 2018 | |
Propagation of a global coronal wave and its interaction with large-scale coronal magnetic structures
1
The Institute of Solar-Terrestrial Physics of the Siberian Branch of the Russian Academy of Sciences,
PO Box 291,
Lermontov St. 126A,
Irkutsk
664033, Russia
e-mail: afa@iszf.irk.ru
2
Centre for mathematical Plasma Astrophysics, Department of Mathematics,
KU Leuven,
Leuven, Belgium
3
Solar-Terrestrial Centre of Excellence - SIDC, Royal Observatory of Belgium,
Brussels, Belgium
e-mail: Andrei.Zhukov@sidc.be
4
Skobeltsyn Institute of Nuclear Physics, Moscow State University,
Moscow, Russia
Received:
7
September
2017
Accepted:
9
February
2018
Context. Global coronal waves associated with solar eruptions (the so-called EIT waves) often encounter coronal holes and solar active regions and interact with these magnetic structures. This interaction leads to a number of observed effects such as wave reflection and transmission.
Aims. We consider the propagation of a large-scale coronal shock wave and its interaction with large-scale non-uniformities of the background magnetic field and plasma parameters.
Methods. Using the Lare2d code, we performed 2.5-dimensional simulations of the interaction of a large-scale single-pulse fast-mode magnetohydrodynamic shock wave of weak-to-moderate intensity with the region of enhanced Alfvén speed as well as with that of reduced Alfvén speed. We analysed simple models of non-uniformity and the surrounding plasma to understand the basic effects in wave propagation.
Results. We found the reflected waves of plasma compression and rarefaction, transmitted waves that propagate behind or ahead of the main part of the wave, depending on properties of the plasma non-uniformity, and secondary wave fronts. The obtained results are important to the correct interpretation of the global coronal wave propagation in the solar corona, understanding of theoretical aspects of the interaction of large-scale coronal shock waves with large-scale coronal magnetic structures, and diagnostics of coronal plasma parameters.
Key words: Sun: corona / waves / magnetohydrodynamics (MHD) / Sun: activity / methods: numerical
© ESO 2018
1 Introduction
Solar eruptions are often accompanied by large-scale coronal wave-like phenomena observed at extreme ultraviolet (EUV) wavelengths (e.g. Thompson et al. 1999), the so-called EIT waves1. Many of these wave-like phenomena can be confidently interpreted in terms of fast magnetoacoustic shock waves (e.g. Zhukov 2011; Liu & Ofman 2014; Warmuth 2015; Long et al. 2017). A number of numerical simulations have confirmed this interpretation (e.g. Wu et al. 2001; Downs et al. 2011, 2012; Vršnak et al. 2016). However, also various non-wave interpretations for some EIT wave observations have been discussed (Chen et al. 2002; Zhukov & Auchère 2004).
Propagating coronal shock waves are often observed to encounter various large-scale non-uniformities of the background magnetic field and plasma parameters (e.g. Gopalswamy et al. 2009; Grechnev et al. 2011; Olmedo et al. 2012; Li et al. 2012; Shen et al. 2013; Yang et al. 2013). The non-uniformities can be associated, in particular, with coronal holes and solar active regions and represent regions of enhanced Alfvén speed. As a consequence of the interaction of coronal waves with such magnetic structures, a number of effects such as wave reflection, transmission, or more generally, generation of secondary wavefronts can be observed in EUV images of the Sun. Using Solar Terrestrial Relations Observatory (STEREO) data, Gopalswamy et al. (2009) revealed the reflected wavefronts emitted backwards and sideways from a coronal hole. Grechnev et al. (2011) confirmed the wave reflection observed in the event reported by Gopalswamy et al. (2009), using the non-subtracted images, and explained the slower speed of the reflected wave as a result of the plasma flow behind the incident wave front. The wave transmitted through the coronal hole and reflected waves were reported by Olmedo et al. (2012). Li et al. (2012) found that the wave was not seen while propagating through an active region, but it re-emerged at its distant boundary. Shen et al. (2013) also observed the interaction of global EUV waves with active regions and interpreted the wave behaviour, invoking wave diffraction, refraction, and reflection effects.
Physically, the appearance of secondary wavefronts is believed to be due to sharp gradients of the background plasma density, temperature, and magnetic field strength at the boundaries of solar magnetic structures. Initially, the coronal plasma can be in the state of equilibrium owing to the balance of the total pressure, and no waves are emitted by magnetic structures. However, as an incident wave encounters a non-uniformity, sharp gradients of the background plasma parameters cause significant variations in wave propagation conditions, which results in reflection and transmission of incident waves. Sharp variations can be treated analytically as jump-like changes in the background parameters, and therefore this case is the opposite limit to the case of weakly non-uniform media, which could be analysed using the method of geometrical acoustics (cf. Uchida 1968; Afanasyev & Uralov 2011). In addition, the shock wave interaction with plasma non-uniformities is significantly complicated by nonlinear properties of waves and geometrical factors of the problem, so this requires numerical analysis of the problem.
Numerical magnetohydrodynamic (MHD) simulations of the fast-mode MHD wave interaction with large-scale magnetic structures were performed in a number of studies. Ofman & Thompson (2002) performed three-dimensional numerical MHD simulations of the fast magnetoacoustic wave interaction with a bipolar active region, revealing the appearance of secondary waves and flows and paying special attention to triggering secondary coronal mass ejections and flares. The reflected and transmitted waves in thevicinity of a coronal hole were obtained by Schmidt & Ofman (2010). They used the photospheric data to reconstruct a potential magnetic field in the solar corona, and modelled the overall eruption process on 19 May 2007 up to 24 solar radii to obtain the EIT wave propagating along the solar surface. The authors identified the EIT wave as a fast-mode MHD wave in their simulations and revealed the wave reflection and transmission at the boundaries of the coronal hole. However, the results of their numerical simulations were difficult to interpret and to perform further applications because of the very complicated model of the background coronal plasma parameters, which incorporated real observational data. It would be useful and important for the understanding of underlying physical processes to carefully analyse the wave interaction with large-scale plasma non-uniformities using simple models.
The basic aim of our study is to understand theoretically how the large-scale wave reflection and transmission occur in the plasma of the solar corona. We perform numerical MHD simulations of the fast-mode MHD wave interaction with large-scale magnetic structures. In the presentation of our results, we emphasise density variations. Such an approach is justified since we aim at applying our results to the interpretation of global coronal wavefronts observed in EUV, which are believed to be due to plasma density variations. The paper is organised as follows. Section 2 gives details of numerical simulations. In Sect. 3 we present results of the simulations performed and discuss them. We draw conclusions in Sect. 4.
 |
Fig. 1 Details of the coronal hole model. Initial profiles at the y = 0 plane are shown. Panel a: plasma number density measured in 108 cm−3 (solid line) and magnetic field in G (dashed); panel b: characteristic speeds in the plasma in km s−1, sound speed (solid line) and Alfvén speed (dashed), and magnetoacoustic (MAC) speed in the transverse direction (dotted); and panel c: plasma β* values. See the exact values of parameters of the model in the text. |
 |
Fig. 2 Details of the coronal plume model. The notations are the same as in Fig. 1. See the exact values of parameters of the model in the text. |
2 Method and model
We performed MHD numerical simulations to analyse the shock wave interaction with coronal magnetic structures. We applied the Lare2d numerical code developed by Arber et al. (2001). This is a Lagrangian remap code for solving the full set of nonlinear MHD equations in two dimensions. The Lare2d code is of the second order accuracy in space and time and uses gradient limiters, allowing thecode to be applicable to shock calculations. It has been tested in many problems of solar physics (see e.g. the review by Pascoe 2014).
We considered two simple models of the background plasma. One model includes a region of the enhanced Aflvén speed. We refer to this model as the coronal hole model. Indeed, it is recognised that coronal holes are usually less dense and have enhanced magnetic field in comparison with their environment. For the sake of completeness, the other model includes a region of the reduced Aflvén speed, which is hereinafter referred to as the coronal plume model, although it is not straightforward to associate such a large-scale structure with a real plume or group of plumes.
Let us introduce the coordinate system with x and y axes in the plane of the computational box, and z axis directed outwards the plane. In fact, we analysed a 2.5-dimensional problem, assuming that there is no dependence of the MHD variables on the z coordinate, however, the z component of the magnetic field vector does not drop to zero. The other components of the magnetic field vector (in x and y directions) are equal to zero, so the magnetic field is perpendicular to the computational box. The plasma number density n and temperatureT are distributed as
![\begin{eqnarray*} \hspace*{-4pt} n = n_{\mathrm{out}} - (n_{\mathrm{out}} - n_{\mathrm{ins}}) \exp \left[ - \left( \frac{r}{d} \right) ^8 \right],\nonumber \\ T = T_{\mathrm{out}} - (T_{\mathrm{out}} - T_{\mathrm{ins}}) \exp \left[ - \left( \frac{r}{d} \right) ^8 \right],\end{eqnarray*}](/articles/aa/full_html/2018/06/aa31908-17/aa31908-17-eq1.png) (1)
(1)
where r is the distance from the centre of the plasma non-uniformity, d is its characteristic size, nout and Tout, and nins and Tins are the number density and temperature values outside and inside the non-uniformity, respectively. The initial equilibrium in the models used is achieved by assuming the balance of the total pressure of the plasma, pT, namely that the sum of the gas pressure pgas and magnetic pressure is constant throughout the computational box
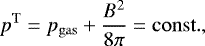 (2)
(2)
where B is the z component of the magnetic field vector. Equation (2) determines the magnetic field, given that its value outside the plasma non-uniformity, Bout, has been defined. Figure 1 presents the details of the coronal hole model with the following values: Bout = 4.0 G, nout = 1.0 × 109 cm−3, nins = 1.0 × 108 cm−3, Tout = 1.5 MK, and Tins = 1.0 MK, d = 150 Mm. Figure 2 presents the details of the coronal plume model with the following values: Bout = 3.0 G, nout = 1.0 × 108 cm−3, nins = 1.0 × 109 cm−3, Tout = 1.5 MK, and Tins = 1.0 MK, d = 100 Mm. We define plasma β* as the squared ratio of the sound speed to the Alfvén speed without any coefficients.
We analysed the wave propagation in a computational box of size of 1024 × 1024 cells. Its physical sizeis 2000 × 2000 Mm. We imposed the periodic boundary conditions at the top and bottom boundaries of the box and assume the open boundary at the right boundary. At the left boundary, a pulse driver acts to generate a plane incident wave. We considered the incident wave to be a single-pulse nonlinear disturbance of the fast magnetoacoustic nature. In order to drive the fast magnetoacoustic mode, we perturbed only the x component of the plasma velocity, leaving other components to be zero.
Figure 3 shows the used time profiles of the wave driver. We considered a piston-like wave profile that has longer duration (in comparison with triangle-shaped blast-like wave profiles) and a part of nearly constant amplitude. This kind of wave profile couldcorrespond better to real global coronal shock waves produced by coronal mass ejections, which push coronal plasma like magnetic pistons. The panels in the figure show wave profiles used for the coronal hole model and coronal plume model. The Mach number for the incident disturbances can be estimated to be 1.15−1.19. These values can be approximately calculated both from the simulation data and from driver profiles. The incident wave is seen to be of weak to moderate intensity, which is in a good agreement with observations of large-scale coronal waves (Thompson et al. 1999; Veronig et al. 2010; Warmuth 2015).
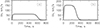 |
Fig. 3 Velocity profiles of the wave driver acting at the left boundary of the computational box. Panel a corresponds to the wave profile used for the coronal hole model and panel b corresponds to the wave profile used for the coronal plume model. |
 |
Fig. 4 Plasma number density snapshot at simulation time t = 7.40 and two one-dimensional profiles taken along the dashed lines. Because of the interaction of the shock wave with the coronal hole, the transmitted and reflected waves appear. They are shown by arrows in the snapshot. The cut-off at level 8 × 108 cm−3 is applied toincrease the contrast of wave fronts in the snapshot. |
 |
Fig. 5 Interaction of a shock wave with the coronal hole plasma non-uniformity. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 8 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
3 Simulation results and discussion
First, we should clarify the terminology we use to describe shock wave propagation. Figure 4 shows an example of the individual snapshot of the plasma number density for the case of the coronal hole model at simulation time t = 7.40 and the plasma number density profiles taken along the dashed lines at the snapshot. Simulation times are output in dimensionless units throughout the paper; the normalisation coefficient is about 500 s. The dark spot atthe centre of the snapshot represents the non-uniformity of reduced density (a coronal hole). The visible leading part of the disturbance after the apparent passage through the coronal hole is referred to as the transmitted wave, while the reflected wave is a quasi-circular wave emitted backwards and sideways from the plasma non-uniformity. We also consider the main wave front, whichcan be readily identified in the snapshot as the incident wave front propagating towards the right boundary.
Figure 5 contains a set of the simulated plasma number density snapshots, demonstrating the propagation of a shock wave in the coronal hole model (Eqs. (1) and (2)) with the following parameters: Bout = 4.0 G, nout = 1.0 × 109 cm−3, nins = 1.0 × 108 cm−3, Tout = 1.5 MK, and Tins = 1.0 MK, d = 150 Mm. The initially planar incident wave front is significantly distorted by the plasma non-uniformity, and the transmitted and reflected waves appear. Owing to the enhanced Alfvén speed inside the coronal hole, the wave propagates very fast there, and its amplitude is very low inside the coronal hole; see density profiles at different instants in Fig. 6. This resembles the wave leaking through the regions of sharp gradients (of density and magnetoacoustic speed) at the boundary of the plasma non-uniformity.
The wave reflected backwards is a wave of rarefaction. This fact is very intriguing because it has been observed that the reflected waves are bright disturbances (e.g. Gopalswamy et al. 2009; Olmedo et al. 2012), which implies the plasma compressioneffect is present. The waves reflected sideways are bright, hence they are compressive disturbances. However, we should keep in mind that the brightness variation in solar EUV images is a complex function of plasma density and temperature (see e.g. Zhukov 2011), so the brightening can also be due to the temperature response of the channel. The amplitudes of the waves reflected sideways are higher than those of other waves in each snapshot, which, along with the curved shape of the fronts moving around the non-uniformity, is most likely due to wave diffraction effects. In particular, significantly enhanced amplitudes of waves reflected sideways could be interpreted as diffraction caustics effects of propagation (cf. the caustics effects due to wave refraction in Afanasyev & Uralov 2012). We also note that the back edge of the rarefaction wave propagating in the negative x direction could be interpreted as a propagating front of the trailing weak plasma compression (noticeable in Figs. 5 and 6) if the size of the rarefaction is large enough. The rarefaction size appears to depend on the parameters of the plasma non-uniformity, and we will carefully investigate this issue in a future paper.
The transmitted wave overtakes the main wave front, however, its amplitude is lower than that of the main wave front. Therefore, the distance between the main wave front and transmitted wave progressively decreases owing to the nonlinear nature of the shock wave and the wave front tends to recover a quasi-planar shape (e.g. at t = 9.00 in Fig. 5).
Figure 6 shows the evolution of wave, providing the number density profiles taken along the lines x = 0 and y = 0. Different colours correspond to different simulation times. The amplitude of the wave reflected backwards decreases due to the geometrical divergence of its wavefront. After the reflected rarefaction wave, a weak compression wave propagates (see violet and brown lines) in the backwards direction. The orange profile demonstrates the low magnitude of the perturbation inside the coronal hole during the passage of the wave. We also note that the incident shock wave pushes the coronal hole towards the direction of its propagation; we do not include the line-tying effect of the photosphere in our model because of its 2.5 dimensions. The shift in the location of the coronal hole before and after the interaction with the wave depends strongly on the amplitude of the shock wave and on its duration and profile shape; this shift is larger for more intense and longer waves.
The interaction of a shock wave with the plasma non-uniformity of the coronal plume type is shown in Fig. 7. The following parameters of the model (Eqs. (1) and (2)) were used: Bout = 3.0 G, nout = 1.0 × 108 cm−3, nins = 1.0 × 109 cm−3, Tout = 1.5 MK, Tins = 1.0 MK, and d = 100 Mm. In this case, the wave propagates more slowly inside the non-uniformity, therefore the transmitted wave lags behind the main wave front. The wave front is distorted as well and tends to recover its quasi-planar shape due to nonlinearity. Unlike the case of the coronal hole, the wave reflected backwards is a wave of plasma compression. Also, multiple secondary wave fronts of quasi-circular shape are emitted. The first secondary front is seen in last three snapshots of Fig. 7. The extended simulations performed have shown that the amplitudes of emitted secondary fronts decrease with time.
Figure 8 shows the number density profiles taken along the lines x = 0 and y = 0. Different colours correspond to different simulation times. The black and red profiles show the wave before the interaction, while the orange and green profiles show the superposition of the incident wave and the wave reflected backwards; see the different shapes of the trailing slopes of the red and green curves, for instance. After the passage of the reflected wave in the negative x direction, the number density drops below the background value, producing a weak plasma rarefaction.
The coronal plume model contains a region of reduced Alfvén speed, which acts as a resonator for fast magnetoacoustic waves, capturing the wave energy. Figure 9 shows how the captured disturbance travels inside the non-uniformity, generating secondary wave fronts. The simulations presented for this case were performed on a grid with double resolution. The corresponding number density profiles are shown in Fig. 10. The capturing effect somewhat resembles the “resonance of a coronal hole” discussed by Schmidt & Ofman (2010). It is of interest that according to their simulated maps of the phase speed of fast magnetoacoustic waves, the plasma non-uniformity generating the reflected wavefront corresponds rather to the region of the weakly reduced phase speed. However, it is difficultto say from their paper whether plasma compression or rarefaction was obtained in the reflected wave.
In both cases described above, we considered incident shock waves having the pulse lengths of the order of the plasma non-uniformity size, which is in a good agreement with observations. We also studied the interaction of a shock wave with plasma non-uniformities, when their sizes are several times larger than the pulse length of the shock wave. However, we have not found any additional specific effects there.
 |
Fig. 6 Density profiles at y = 0 (left) and x = 0 (right) for different simulation times in the case of wave interaction with the coronal hole. Black, red, orange, green, blue, violet, and brown colours correspond to t = 4.1, 5.0, 5.9, 6.8, 7.7, 8.6, 9.5, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
 |
Fig. 7 Interaction of a shock wave with the plasma non-uniformity of the coronal plume type. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 1.3 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
 |
Fig. 8 Density profiles at y = 0 (left) and x = 0 (right) for different simulation times in the case of wave interaction with a coronal plume. Black, red, orange, green, blue, violet, and brown colours correspond to t = 1.6, 2.1, 2.6, 3.1, 3.6, 4.1, 4.6, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
4 Summary
Observations of the solar corona in the EUV band revealed that global coronal waves can encounter and interact with coronal holes and solar active regions. In this paper, we have considered the propagation of global coronal shock waves and their interaction with large-scale non-uniformities of the background magnetic field and plasma parameters. More specifically, we analysed the interaction of a large-scale single-pulse fast-mode MHD shock wave of weak-to-moderate intensity with the region of enhanced Alfvén speed (coronal hole) and the region of reduced Alfvén speed (coronal plume).
We found the transmitted and reflected waves and the generation of secondary emitted waves. The initial wave front is significantly distorted by the plasma non-uniformity. The transmitted wave overtakes the main wave front in the case of a coronal hole non-uniformity, while in the case of a coronal plume, the transmitted wave lags behind.Then wave fronts tends to recover the original planar shape due to their nonlinear nature and wave diffraction effects. The wave reflected backwards is a rarefaction wave in the case of a coronal hole, while in the case of a coronal plume it is a compression wave. This result could be used for plasma diagnostics in the solar corona.
The region of the reduced Alfvén speed, the coronal plume, acts as a resonator for fast-mode waves and captures the wave energy, emitting several subsequent fronts of secondary waves of progressively decreasing amplitudes. In contrast, the region of the enhanced Alfvén speed, the coronal hole, does not capture wave energy.
It should be noted that the present study addresses a case that is different from the well-recognised case of weakly non-uniformmedium, in which fast-mode MHD waves propagate into regions of reduced Alfvén speed and therefore tend to avoid active regions and coronal holes (e.g. Uchida 1974; Wang 2000; Afanasyev et al. 2013). The latter case can be described using the ray approximation, and there is no wave reflection and transmission because waves gradually propagate away from non-uniformities of the enhanced Alfvén speed. In the case under study, the characteristic scale of an incident wave (its pulse length) is much larger than the non-uniformity scale (the width of its boundary). Therefore, the boundaries of magnetic structures look like rather thin interface regions, which results in the wave reflection and transmission. This corresponds well to observations, in particular, to the work by Olmedo et al. (2012), who first reported the wavefront transmitted through a coronal hole.
The simple models used allowed us to demonstrate the basic effects of shock wave propagation in the plasma with large-scale non-uniformities, analyse their nature, and draw an interpretation. True coronal large-scale magnetic structures have significant extent above the solar surface and are restricted by the dense solar chromosphere from below. Moreover, emission of global wavefronts in EUV appears to come from relatively low heights in the solar corona (several tens of Mm, or at least up to one density scale height), where the coronal plasma is the densest. Therefore, the problem is expected to have effectively 2.5 dimensions, as considered in this study. The gravity effect should not seriously impact the derived conclusions since we analysed the propagation of a large-scale wave pulse. The global stratification of the plasma due to gravity leads to refraction effects and variations inthe wave kinematics in the quiet Sun regions (see e.g. Afanasyev & Uralov 2011). Taking into account more realistic models of the solar corona, we could obtain dispersion and dissipation of global shock wave pulses in the quiet Sun regions due to small-scale plasma non-uniformities (see e.g. Yuan et al. 2015). These effects, which are essential for the evolution of global waves, however, do not seem to affect significantly the interaction under study in this paper. However, full three-dimensional simulations (perhaps combined with a forward modelling technique) could shed some additional light on the nature of global coronal wave interaction with large-scale magnetic structures.
In an upcoming work, we plan to consider in detail which parameters affect the wave reflection and transmission and pay special attention to the interpretation of real observations, varying and making the models more sophisticated.
 |
Fig. 9 Wave captured by the plasma non-uniformity of the coronal plume type, which acts like a resonator with the reduced Alfvén speed. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 6.0 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
 |
Fig. 10 Density profiles at y = 0 (left) and x = 0 (right) in the non-uniformity region for different simulation times in the case of wave interaction with a coronal plume. Black, red, orange, green, blue, violet, and brown colours correspond to t = 2.6, 3.0, 3.4, 3.8, 4.2, 4.6, 5.0, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
Acknowledgements
We thank Dr. A.M. Uralov and Dr. V.V. Grechnev for helpful discussions. We are grateful to the anonymous referee for valuable comments. A.N.A. acknowledges support from the Russian Science Foundation under grant 17–72–10076 (numerical simulations, analysis of results). A.N.Z. acknowledges support from the Belgian Federal Science Policy Office through the ESA–PRODEX programme. Numerical simulations were performed with the Academician V.M. Matrosov HPC cluster of the Irkutsk Supercomputer Center of the SB RAS (http://hpc.icc.ru) and at KU Leuven under support of the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 724326). The work was motivated by discussions at the XIVth Hvar Astrophysical Colloquium in 2016 under support of the Russian Foundation of Basic Research (grant agreement 16-32-00315 mol_a). A.N.A. also thanks the SOC of the XIVth Hvar Astrophysical Colloquium for supporting his participation.
References
- Afanasyev, A. N., & Uralov, A. M. 2011, Sol. Phys., 273, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Afanasyev, A. N., & Uralov, A. M. 2012, Sol. Phys., 280, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Afanasyev, A. N., Uralov, A. M., & Grechnev, V. V. 2013, Astron. Rep., 57, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Wu, S. T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., et al. 2011, ApJ, 728, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N., & Sokolov, I. V. 2012, ApJ, 750, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N., Yashiro, S., Temmer, M., et al. 2009, ApJL, 691, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Uralov, A. M., Chertok, I. M., et al. 2011, Sol. Phys., 273, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T., Zhang, J., Yang, S., & Liu, W. 2012, ApJ, 746, 13 [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Long, D. M., Bloomfield, D. S., Chen, P. F., et al. 2017, Sol. Phys., 292, 7 [Google Scholar]
- Ofman, L., & Thompson, B. J. 2002, ApJ, 574, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Olmedo, O., Vourlidas, A., Zhang, J., & Cheng, X. 2012, ApJ, 756, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J. 2014, Res. Astron. Astrophys., 14, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, J. M., & Ofman, L. 2010, ApJ, 713, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., et al. 2013, ApJ, 773, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, B. J., Gurman, J. B., Neupert, W. M., et al. 1999, ApJ, 517, 151 [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1974, Sol. Phys., 39, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M., & Vršnak B. 2010, ApJ, 716, L57 [Google Scholar]
- Vršnak, B., Žic, T., Lulić, S., Temmer, M., & Veronig, A. M. 2016, Sol. Phys., 291, 89 [Google Scholar]
- Wang, Y.-M. 2000, ApJ, 543, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Warmuth, A. 2015, Liv. Rev. Sol. Phys., 12, 3 [Google Scholar]
- Wu, S. T., Zheng, H., Wang, S., et al. 2001, J. Geophys. Res., 106, 25089 [Google Scholar]
- Yang, L., Zhang, J., Liu, W., Li, T., & Shen, Y. 2013, ApJ, 775, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., Pascoe, D. J., Nakariakov, V. M., Li, B., & Keppens, R. 2015, ApJ, 799, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukov, A. N. 2011, J. Atmos. Sol. Terr. Phys., 73, 1096 [Google Scholar]
- Zhukov, A. N., & Auchère, F. 2004, A&A, 427, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
See discussion about terminology in Zhukov (2011); Liu & Ofman (2014).
All Figures
 |
Fig. 1 Details of the coronal hole model. Initial profiles at the y = 0 plane are shown. Panel a: plasma number density measured in 108 cm−3 (solid line) and magnetic field in G (dashed); panel b: characteristic speeds in the plasma in km s−1, sound speed (solid line) and Alfvén speed (dashed), and magnetoacoustic (MAC) speed in the transverse direction (dotted); and panel c: plasma β* values. See the exact values of parameters of the model in the text. |
| In the text | |
 |
Fig. 2 Details of the coronal plume model. The notations are the same as in Fig. 1. See the exact values of parameters of the model in the text. |
| In the text | |
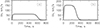 |
Fig. 3 Velocity profiles of the wave driver acting at the left boundary of the computational box. Panel a corresponds to the wave profile used for the coronal hole model and panel b corresponds to the wave profile used for the coronal plume model. |
| In the text | |
 |
Fig. 4 Plasma number density snapshot at simulation time t = 7.40 and two one-dimensional profiles taken along the dashed lines. Because of the interaction of the shock wave with the coronal hole, the transmitted and reflected waves appear. They are shown by arrows in the snapshot. The cut-off at level 8 × 108 cm−3 is applied toincrease the contrast of wave fronts in the snapshot. |
| In the text | |
 |
Fig. 5 Interaction of a shock wave with the coronal hole plasma non-uniformity. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 8 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
| In the text | |
 |
Fig. 6 Density profiles at y = 0 (left) and x = 0 (right) for different simulation times in the case of wave interaction with the coronal hole. Black, red, orange, green, blue, violet, and brown colours correspond to t = 4.1, 5.0, 5.9, 6.8, 7.7, 8.6, 9.5, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
| In the text | |
 |
Fig. 7 Interaction of a shock wave with the plasma non-uniformity of the coronal plume type. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 1.3 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
| In the text | |
 |
Fig. 8 Density profiles at y = 0 (left) and x = 0 (right) for different simulation times in the case of wave interaction with a coronal plume. Black, red, orange, green, blue, violet, and brown colours correspond to t = 1.6, 2.1, 2.6, 3.1, 3.6, 4.1, 4.6, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
| In the text | |
 |
Fig. 9 Wave captured by the plasma non-uniformity of the coronal plume type, which acts like a resonator with the reduced Alfvén speed. The plasma number density (in 108 cm−3) maps are plotted. The cut-off at level 6.0 × 108 cm−3 is applied toincrease the contrast of wave fronts. |
| In the text | |
 |
Fig. 10 Density profiles at y = 0 (left) and x = 0 (right) in the non-uniformity region for different simulation times in the case of wave interaction with a coronal plume. Black, red, orange, green, blue, violet, and brown colours correspond to t = 2.6, 3.0, 3.4, 3.8, 4.2, 4.6, 5.0, respectively. The grey shading shows the initial position of the plasma non-uniformity and its size characterised by parameter d. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


