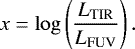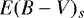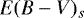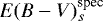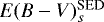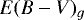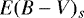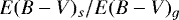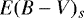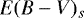| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731865 | |
| Published online | 16 May 2018 | |
Spatially resolved star formation and dust attenuation in Mrk 848: Comparison of the integral field spectra and the UV-to-IR SED
1
Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, CAS,
80 Nandan Road,
Shanghai
200030, PR China
e-mail: yuanft@shao.ac.cn
2
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR7326,
13388
Marseille, France
3
Universidad de Antofagasta, Unidad de Astronomía, Facultad Cs. Básicas,
Av. U. de Antofagasta 02800,
Antofagasta, Chile
4
Institute of Astronomy & Astrophysics, Academia Sinica,
Taipei
10617, Taiwan
Received:
31
August
2017
Accepted:
5
January
2018
We investigate the star formation history and the dust attenuation in the galaxy merger Mrk 848. Thanks to the multiwavelength photometry from the ultraviolet (UV) to the infrared (IR), and MaNGA’s integral field spectroscopy, we are able to study this merger in a detailed way. We divide the whole merger into the core and tail regions, and fit both the optical spectrum and the multi-band spectral energy distribution (SED) to models to obtain the star formation properties for each region respectively. We find that the color excess of stars in the galaxy E(B-V)sSED measured with the multi-band SED fitting is consistent with that estimated both from the infrared excess (the ratio of IR to UV flux) and from the slope of the UV continuum. Furthermore, the reliability of the E(B-V)sSED is examined with a set of mock SEDs, showing that the dust attenuation of the stars can be well constrained by the UV-to-IR broadband SED fitting. The dust attenuation obtained from optical continuum E(B-V)sspec is only about half of E(B-V)sSED. The ratio of the E(B-V)sspec to the E(B-V)g obtained from the Balmer decrement is consistent with the local value (around 0.5). The difference between the results from the UV-to-IR data and the optical data is consistent with the picture that younger stellar populations are attenuated by an extra dust component from the birth clouds compared to older stellar populations which are only attenuated by the diffuse dust. Both with the UV-to-IR SED fitting and the spectral fitting, we find that there is a starburst younger than 100 Myr in one of the two core regions, consistent with the scenario that the interaction-induced gas inflow can enhance the star formation in the center of galaxies.
Key words: dust, extinction / galaxies: interactions / galaxies: evolution
© ESO 2018
1 Introduction
Galaxy mergers play an important role in the formation and evolution of galaxies. Many studies have confirmed that the merging event is responsible for the elevated star formation activity in (ultra)luminous infrared galaxies (Sanders et al. 1988; Melnick & Mirabel 1990), and the interaction between two galaxies can enhance the star formation activity in these galaxies (e.g., Barton Gillespie et al. 2003; Sánchez & González-Serrano 2003; Alonso et al. 2004; Ellison et al. 2008; Xu et al. 2010; Zhang et al. 2010; Taniguchi et al. 2012; Yuan et al. 2012; Wild et al. 2014). However, the enhanced star formation rate (SFR) compared to non-interacting galaxies and its dependence on merging stages are still quantitatively uncertain. Moreover, the spatial extent of star formation in interacting galaxies is still under debate. Some observational and theoretical studies have shown that the star formation triggered in mergers is widespread in tidal tails and bridges (e.g., Mirabel et al. 1998; Alonso-Herrero et al. 2000; Elmegreen et al. 2006; Renaud et al. 2014; Wild et al. 2014), whereas there are also works arguing that for most cases the enhanced star formation is restricted to the central region of the galaxy (Di Matteo et al. 2007; Schmidt et al. 2013; Moreno et al. 2015). Besides the current SFR, the star formation history (SFH) of a merger is also important for constraining the merging stages and the effect of the interaction. However, estimating the SFH of galaxies suffers from several uncertainties. Especially, due to the complication of the interaction, the SFH of mergers is difficult to reconstruct (Pforr et al. 2012; Conroy 2013; Buat et al. 2014; Boquien et al. 2014; Smith & Hayward 2015).
One of the uncertainties to determine the star formation properties is the dust attenuation. In the optical wavelengths, the dust attenuation is degenerated with the stellar age. It is better estimated when introducing ultraviolet-to-infrared multiwavelength data, as the ultraviolet (UV) and infrared (IR) bands are more sensitive to the dust properties. Methods that measure the dust attenuation include (1) fitting the stellar populations and the dust attenuation together for the spectra or the spectral energy distribution (SED), (2) estimating from the IR to UV ratio (infrared excess, IRX) and (3) calculating from the slope of the UV continuum (β). All these methods can give the attenuation for the stars in galaxies. When there are IR data, the dust attenuation can be estimated more reliably since the IR data provide additional constraints on the dust emission.
If the optical spectra are available, the Balmer decrement can also be used to derive the dust attenuation. The Balmer decrement gives the attenuation for nebular emission, and then the dust attenuation for stars is taken as a factor f of that for the nebular emission. The classical value of f for galaxies is 0.44 (Calzetti et al. 2000). However, recent studies have shown that the value can vary from 0.44 to 0.93 (e.g., Kashino et al. 2013; Kreckel et al. 2013; Price et al. 2014; Puglisi et al. 2016), indicating that the dust attenuation for stars estimated from Balmer decrement may be underestimated. The complexity of dust attenuation in gas and stars suggests that the commonly used one-component dust model in the stellar population synthesis may not be suitable, and a more sophisticated model of dust should be used. The two-component dust model proposed by Charlot & Fall (2000) contains a dust component for the diffuse interstellar medium (ISM) where old stars are located and a second dust component with larger optical depth for birth clouds where young stars are born. The age-dependent dust model has already been adopted in several works (e.g., Brinchmann et al. 2004; Noll et al. 2009; Buat et al. 2011; Wild et al. 2011; Lo Faro et al. 2017). The typical time scale for a birth cloud is about 10 Myr (Blitz & Shu 1980; Charlot & Fall 2000). For normal galaxies, the stellar population younger than 10 Myr makes up only a negligible fraction of the total mass, and therefore the two-component dust model gives similar results to the one-component dust model (Tojeiro et al. 2009). However, for more complicated cases like starbursts/mergers, because the young stellar population is not negligible, and the young stellar population may take longer to escape from the birth clouds (Silva et al. 1998; Panuzzo et al. 2007), using the two-component dust model might be necessary.
With the development of observational techniques, more and more data with wavelength coverage from UV to IR are available to constrain the star formation and dust attenuation properties in galaxies at a spatially resolved level. Especially, the development of the integral field unit (IFU) provides us with a large amount of spatially resolved spectra in the optical band, which contains much more information than either the photometry data or the one dimensional spectra. Based on these data, some studies have been done focusing on the star formation properties and the dust attenuation in interacting galaxies (e.g., Rich et al. 2011; Wild et al. 2014). However, a comparison between the results derived from the optical IFU data and those from the photometric data (UV to IR) has yet to be made. Also, previous studies only focus on the distribution of the current SFR in interacting galaxies, but few attempts have been made to study the SFH for interacting galaxies.
We report the dust attenuation and the SFH of the core and tail parts of the merger Mrk 848 using both the IFU spectra and the UV-to-IR photometry data. Due to its merger nature, Mrk 848 has been extensively observed across multiwavelengths, including photometric data from UV (GALEX) to IR (Spitzer). It has also been observed by the SDSS-IV/MaNGA project (Mapping Nearby Galaxies at APO, Bundy et al. 2015; Drory et al. 2015; Law et al. 2015; Yan et al. 2016). The existence of both the photometric and IFU data of Mrk 848 provides a unique opportunity to derive spatially resolved dust attenuation and SFH using different methods. Through the comparison of the results from different methods, we attempt to decipher how the calculation of the dust attenuation affects the estimation of the SFH, and whether a two-component dust model is better for this case. The derived SFH for the core and tail regions can also provide some constraints on the spatial extent of the interaction-triggered star formation and the time scale of the merging process.
In Sect. 2, we present the photometric and IFU data of Mrk 848. In Sect. 3, we compare the dust attenuation derived from UV-to-IR photometric data and from the optical IFU data, and discuss the possible physical mechanism for the different results of these methods. In Sect. 4, we examine the SFH and SFR obtained given different dust attenuation. We summarize the work in Sect. 5.
 |
Fig. 1 Regions (cores: R3 and R4, tails: R1, R2, R5 and R6) of Mrk 848 used for analysis in this work, overplotted on the r band image of SDSS. The radius of each region is 5″. This image is rotated north-up. |
Center coordinates of each region and the signal-to-noise ratio (S/N) of the binned MaNGA spectra in each region.
2 Data
Mrk 848 is a major merger of two galaxies with stellar masses log (M*∕M⊙) = 10.44 and 10.30 (Yang et al. 2007) in the nearby Universe (z = 0.041). Its morphologies, with obvious tidal tails, indicate strong interaction between the two galaxies. In Fig. 1, we divide Mrk 848 into six regions according to its tail and core features. The radius of each region is 5″, which is chosen according to the size of the cores. The center coordinates of each region are listed in Table 1. We analyze the star formation and dust properties using the IFU and broadband SED data in each region. For all the data, the Galactic extinction has been corrected using the SFD map (Schlegel et al. 1998) and the Galactic extinction curve of Cardelli et al. (1989).
2.1 MaNGA integral field data
MaNGA is an IFU program to survey 10 000 nearby galaxies using the BOSS spectrographs (Smee et al. 2013) on the 2.5-meter SDSS telescope (Gunn et al. 2006; Blanton et al. 2017). The wavelength coverage of MaNGA spectra is from 3600 to 10 000 Å, with a spectral resolution R ~ 2000. The diameters of MaNGA IFUs range from 12′′ to 32″, composed of 19 to 127 fibers. The angular resolution (the FWHM of the fiber-convolved PSF) of MaNGA data is about 2.5′′ (Yan et al. 2016). Mrk 848 (MaNGA 12-193481) is selected as one of the commissioning targets of MaNGA integral field spectra survey. It is observed by one of the largest IFU bundles with 127 fibers and a diameter of 32″. With this size, the IFU fully covers R3, R4, and R5, and partially covers R2 and R6. R1 is not covered by the IFU. The coverage of MaNGA IFU bundle is shown in Fig. 2.
Figure 2 also shows the S/N of each spaxel. For each region, the binned spectra are obtained by taking the average of all valid spaxels in that region. The errors are added quadratically with a modifying term accounting for the covariance. The S/N after binning are shown in Table 1.
 |
Fig. 2 Left panel: coverage of MaNGA IFU bundle on Mrk 848. Right panel: S/N distribution of MaNGA spectra. |
2.2 Multiwavelength photometric data
We analyze the UV to IR photometric data to obtain the panchromatic SED of each region. The observations, effective wavelengths, and resolution of the photometric data used in this work are listed in Table 2. The UV data are taken from GALEX All Imaging Survery (Martin et al. 2005), including the FUV image at 1528 Å and the NUV image at 2271 Å. The resolution is typically 4.5/6.0 arcsec (FWHM) for FUV/NUV band (Madore 2005). At optical wavelengths, we take SDSS images at u ( ~3551 Å), g ( ~4686 Å), r ( ~6166 Å), i ( ~7480 Å), and z ( ~8932 Å) bands. The spatial resolution of the SDSS images is about 1.5″. The values are estimated using the effective FWHM of the PSF fitting by a double-Gaussian profile1 . For the IR part, Mrk 848 has been observed by Spitzer (AOR key is 12318720). The mean FWHM of the PSF for the Spitzer/IRAC is about 2′′ (Fazio et al. 2004; Aniano et al. 2011). The longest wavelength used in this work is 8 μm from the IRAC observation. For even longer wavelengths in IR, the two interacting galaxies can not be spatially resolved. The images in these bands are shown in Fig. 3.
To obtain the UV-to-IR SED of each region, we calculate the fluxes in each band within the radius of each region. We estimate the background using an annulus 30′′ away from the center with a width of 5″. The flux of each region is obtained by summing up the fluxes for the pixels in each region with the background subtracted. The SEDs obtained from the photometry are shown in Fig. 4.
Since the spatial resolution of these bands are inhomogeneous, to match the photometry in different bands, the images of each band shouldbe converted into the same resolution. Here we use the GALEX NUV image (with the worst resolution, 6′′ ) as the reference.
The following steps are taken for these images:
- 1.
Align all the images to WCS, and rescale the pixel size to the GALEX NUV pixel size (1.5′′) while keeping the surface brightness of the images unchanged.
- 2.
Degrade all the images to the GALEX NUV point spread function (PSF) using the large set of kernels presented by Aniano et al. (2011).
Then we calculate the SED of each region again. The results are overplotted in Fig. 4. It appears that the difference caused by the PSF in such a radius (5′′ ) is small (the median difference for each region is < 15%, Fig. 4). Hereafter, we adopt the SEDs derived from the PSF-convolved images.
As shown in Fig. 4, the SED shapes of the core regions (R3 & R4) are apparently steeper than the tail regions. The infrared emission is much brighter in core regions than in tail regions, indicating that the core regions have more active star formation and heavier dust extinction (active galactic nuclei (AGN) contribution is negligible as we discuss in Sect. 3.6).
UV to IR images used in this work and their resolutions.
 |
Fig. 3 Images of Mrk 848 from GALEX, SDSS, and Spitzer, respectively. The size of each image is 1′ × 1′ . All the images are rotated north-up. |
3 Dust attenuation in Mrk 848
Since Mrk 848 is very bright in the IR band (the total luminosity in 8–1000 μm LTIR > 1012L⊙), it is expected to have high dust attenuation. To explore the stellar populations in each region, we first examine their dust attenuation properties. We begin with the UV-to-IR broadband SED fitting. The long wavelength coverage of data can constrain the thermal emission by dust. In combination with the UV-optical data, these data provide strong constains on the dust attenuation. Then we compare the results with the dust attenuation derived from the LTIR∕LFUV ratio (infrared excess, IRX), the slope of the UV continuum (β), the optical continuum fitting and the Balmer decrement, respectively.
 |
Fig. 4 SEDs of the six regions in Mrk 848. Triangles show SEDs derived from the images with their original resolution. Squares show SEDs derived from the images after degrading the resolution to 6′′ by convolving with the NUV PSF. |
3.1 UV to IR broadband SED fitting
We use CIGALE (Code Investigating GALaxy Emission) to fit the multiwavelength SED from UV to IR. CIGALE can fit the UV to IR data simultaneously by balancing the dust absorption in UV/optical bands and the dust emission in IR bands. This code has been widely used in literature to derive the star formation and dust attenuation in galaxies from the UV to IR multiwavelength SEDs (e.g., Giovannoli et al. 2011; Buat et al. 2012). A detailed description of the code can be found in Noll et al. (2009).
Here we describe the main features in our fitting. For the stellar emission, we adopt the stellar population synthesis models of (Bruzual & Charlot 2003, hereafter BC03) and the Salpeter IMF (Salpeter 1955). We consider a two-exponentially decreasing SFH, that is, an older stellar population with an exponentially decreasing SFH added with a younger stellar population that indicates a later starburst. The ages and e-folding time of the two components are free parameters. The later burst can be used as an indication of the merging-induced star formation (e.g., Hernquist 1989; Torrey et al. 2012; Patton et al. 2013). The two components are linked by the mass fraction of the burst fburst. The metallicity is fixed to solar metallicity during the SED fitting. Other metallicities have also been tested.The changes of the results caused by the metallicity are not significant and do not affect our conclusions.
The dust attenuation is modeled assuming the Calzetti extinction curve with 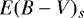 as a free parameter. A reduction factor of the visual attenuation, fatt, is applied to the stars older than 10 Myr to account for the distributions of stars of different ages (Charlot & Fall 2000; Panuzzo et al. 2007; Buat et al. 2012; Lo Faro et al. 2017). Here we fix the value of fatt to 0.5.
as a free parameter. A reduction factor of the visual attenuation, fatt, is applied to the stars older than 10 Myr to account for the distributions of stars of different ages (Charlot & Fall 2000; Panuzzo et al. 2007; Buat et al. 2012; Lo Faro et al. 2017). Here we fix the value of fatt to 0.5.
To simultaneously fit the IR part of the data, the dust emission is modeled using the templates of Dale et al. (2014). The templates are based on the star-forming-SED models modified with a certain fraction of AGN contribution. Here we ignore the contributionfrom AGN (see Sect. 3.6). The star-forming-SED models are governed by the parameter α, which relates the dust mass to the heating intensity. The parameter α is an exponent indicating the contribution of a series of “local” SEDs representing the emission from dust exposed to a wide range of heating intensities (Dale & Helou 2002). In general, active star forming regions have a smaller value of α than quiescent regions. The total energy emitted by dust is estimated to balance the extincted energy from the stellar emission.
The main parameters and the input values for CIGALE are reported in Table 3. CIGALE creates models according to these input values and finds the best-fit model by χ2 minimization. To probe a large parameter space while saving the computing time, we adopt a similar approach with Buat et al. (2011). We start with a wide range of input parameters, and then reduce it by removing values never chosen during the χ2 minimization. The output values are estimated by building the probability distribution function (PDF) and then taking the mean and standard deviation of the PDF. We derive the color excess of the stars 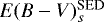 from AB − AV calculated from the SED fitting. It is an effective
from AB − AV calculated from the SED fitting. It is an effective 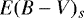 taking account of both the old stellar population and the young stellar population. The results of the
taking account of both the old stellar population and the young stellar population. The results of the 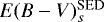 for each region in Mrk 848 are listed in Table 4.
for each region in Mrk 848 are listed in Table 4.
We use mock data to test how well the fitting can constrain the output parameters, with the method described by Giovannoli et al. (2011) and Boquien et al. (2012). The mock photometry in each region is created from the best-fit model of each region by deviating the best-fit model flux with a random error σ, which follows Gaussian distribution with a standard deviation of 10% flux. For each region, we generate 20 sets of mock SEDs. Thenwe do the SED fitting for the mock SEDs with the same input parameters described above. The fitting results are compared with the intrinsic values of the best-fit model (Fig. 5). For the dust attenuation the mock results are scattered approximately around our best-fit parameters (correlation coefficient r > 0.9), indicating that they are well constrained by the SED fitting.
Parameters used in the SED fitting.
Color excess 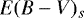 in each region derived from different methods.
in each region derived from different methods.
3.2 Dust attenuation estimated from the UV/IR indicators
Although the fitting method is quite efficient at deriving several physical parameters of galaxies at one time, it can bring uncertainties caused by the degeneracy of parameters. It also depends on the assumptions of the SFH and the dust extinction of the young and the old stellar populations. To investigate the reliability of the fitting method, we calculate the dust attenuation directly using two indicators. First, we examine the LTIR∕LFUV ratio (infrared excess, IRX), where LTIR is the total infrared luminosity in 8–1000 μm, and the LFUV is the νLν calculated in the FUV band. The IRX is widely recognized to be a robust measurement of dust attenuation. The IR and the UV emission together canprovide good constraints on the dust attenuation of galaxies. Here we adopt the formula derived by Buat et al. (2005):
![\begin{equation*} A_{\textrm{FUV}}^{\textrm{IRX}}\textrm{[mag]}=-0.0333x^3+0.3522x^2+1.1960x+0.4967, \end{equation*}](/articles/aa/full_html/2018/05/aa31865-17/aa31865-17-eq11.png) (1)
(1)
The IR luminosity LTIR is estimated using the 8 μm flux. We adopt the median value of the calibrations given by Wu et al. (2005), Reddy et al. (2006), Bavouzet et al. (2008) and Nordon et al. (2012). The standard deviation of these calibrations is taken as the uncertainty of the value. Assuming that the extinction obeys the Calzetti Law, the attenuation in the FUV band is related to the color excess of the stars 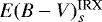 as
as
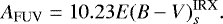 (3)
(3)
The results of 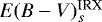 are listed in Table 4. The comparison between the
are listed in Table 4. The comparison between the 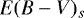 derived from the IRX and those derived from the SED shows that they are in agreement with each other (Fig. 6).
derived from the IRX and those derived from the SED shows that they are in agreement with each other (Fig. 6).
Another option to measure the dust attenuation is to use the slope of the UV continuum. It is commonly used as a proxy to estimate dust attenuation when the IR data are not available. Using the GALEX NUV and FUV data, we can derive the slope β from the formula given by Kong et al. (2004):
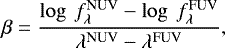 (4)
(4)
where 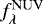 and
and 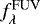 are the NUV and FUV fluxes, respectively (in ergs cm2 s−1 Å−1).
are the NUV and FUV fluxes, respectively (in ergs cm2 s−1 Å−1).
Assuming the IRX-β relation given by Meurer et al. (1999), β is related to AFUV as
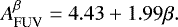 (5)
(5)
Recent studies have shown that this relation has a large dispersion for different types of galaxies (e.g., Kong et al. 2004; Buat et al. 2005; Burgarella et al. 2005; Cortese et al. 2006; Boissier et al. 2007; Boquien et al. 2012; Takeuchi et al. 2012). A blind use of this relation will cause either underestimation or overestimation of the dust attenuation. Figure 7 shows the IRX-β relation for the six regions of Mrk 848. The core regions (R3 and R4) obey the relation derived from starbursts by Meurer et al. (1999), while the IRX-β relation of the tail regions are more similar to that of galaxies with more quiescent star formation activities. If using Eq. (5), the dust attenuation derived from the UV slope will be larger than that derived from the IRX. However, considering the variation of the IRX-β relation and using the IRX-β relation given by Muñoz-Mateos et al. (2009), Boissier et al. (2007), Cortese et al. (2006) or Pettini et al. (1998) for the tail regions, the attenuation derived from β is consistent with that derived from the IRX.
 |
Fig. 5 Comparison of the values for six parameters of the best-fit models and their values estimated by CIGALE from the mock data based on the best-fit models. The mock results of the dust attenuation, the stellar mass and the SFR are scattered approximately around the best-fit parameters (correlation coefficient r > 0.9), indicating that they are well constrained by the SED fitting. The burst fraction fburst and the burst age tburst are weakly constrained. |
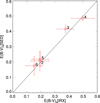 |
Fig. 6 Comparison of the |
 |
Fig. 7 IRX-β relation for the six regions of Mrk 848 (squares with error bars). The relations given by Meurer et al. (1999), Muñoz-Mateos et al. (2009), Boissier et al. (2007), Cortese et al. (2006) and Pettini et al. (1998) are overplotted. |
3.3 Dust attenuation estimated from fitting the optical continuum
The dust attenuation of each region can also be obtained by fitting the optical spectra using stellar population synthesis models. We use penalized Pixel-Fitting (pPXF; Cappellari & Emsellem 2004; Cappellari 2017) where the maximum penalized likelihood approach is adopted. We choose 96 single stellar population (SSP) models of BC03 assuming a Salpeter IMF (Salpeter 1955), with metallicity [Z/H] ranging from −2.3 to 0.4, and ages ranging from 10 Myr to 13 Gyr. To obtain the dust attenuation, we assume the Calzetti extinction curve (Calzetti et al. 2000) and allow pPXF to fit the stellar color excess 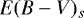 as a free parameter together with the kinematics and the weights of each SSP component. The emission lines are masked during the fitting.
as a free parameter together with the kinematics and the weights of each SSP component. The emission lines are masked during the fitting.
The results of the color excess 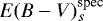 are listed in Table 4. We find that the
are listed in Table 4. We find that the 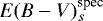 given by the pPXF optical spectral fitting is a factor of 0.5 of the
given by the pPXF optical spectral fitting is a factor of 0.5 of the 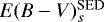 given by the UV-to-IR SED fitting (Fig. 8). This difference indicates that the optical continuum cannot probe the heavily attenuated regions as deep as the UV-to-IR data (see Sect. 3.5 for further discussion).
given by the UV-to-IR SED fitting (Fig. 8). This difference indicates that the optical continuum cannot probe the heavily attenuated regions as deep as the UV-to-IR data (see Sect. 3.5 for further discussion).
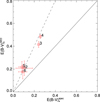 |
Fig. 8 Comparison of the |
3.4 Dust attenuation derived from the Balmer decrement
With MaNGA spectra, we can obtain the dust attenuation from the Balmer decrement, H α∕Hβ. The fluxes of emission lines can be derived from MaNGA spectra after removing the continuum by stellar population synthesis. Comparing the observed ratio Hα∕Hβ with the theoretical value of 2.86 obtained for the Case B recombination, we can derive the extinction A(H α) and the nebular color excess 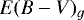 :
:
![\begin{equation*} E(B-V)_g=\frac{2.5}{k(\textrm{H}\beta)-k(\textrm{H}\alpha)}\log\left[{\frac{(\textrm{H}\alpha/\textrm{H}\beta)_{\textrm{obs}}}{2.86}}\right]. \end{equation*}](/articles/aa/full_html/2018/05/aa31865-17/aa31865-17-eq26.png) (6)
(6)
Assuming the reddening curve k(λ) of Calzetti et al. (2000), the value of k(Hβ) − k(Hα) is 1.27.
The color excess of the nebular emission lines, 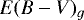 , is linked to that of the stellar continuum,
, is linked to that of the stellar continuum, 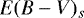 , by a factor f,
, by a factor f, 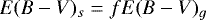 . The classical value of f derived from local galaxies is 0.44 (Calzetti 1997; Wuyts et al. 2011). The value was first derived by Calzetti (1997) by comparing the UV slope to the
. The classical value of f derived from local galaxies is 0.44 (Calzetti 1997; Wuyts et al. 2011). The value was first derived by Calzetti (1997) by comparing the UV slope to the 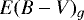 derived from Hα for a sample of starburst galaxies, and then widely used in literature. Wuyts et al. (2011) investigated a larger sample with data from UV-to-IR, and confirmed that this value is valid when correcting the SFRHα to SFR UV +IR. Pannella et al. (2015) show that f should be 0.58 if the
derived from Hα for a sample of starburst galaxies, and then widely used in literature. Wuyts et al. (2011) investigated a larger sample with data from UV-to-IR, and confirmed that this value is valid when correcting the SFRHα to SFR UV +IR. Pannella et al. (2015) show that f should be 0.58 if the 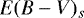 is derived from the Calzetti extinction curve rather than the extinction curve of Fitzpatrick (1999). Works on high-z galaxies give larger f values (e.g., Kashino et al. 2013; Koyama et al. 2015; Puglisi et al. 2016).
is derived from the Calzetti extinction curve rather than the extinction curve of Fitzpatrick (1999). Works on high-z galaxies give larger f values (e.g., Kashino et al. 2013; Koyama et al. 2015; Puglisi et al. 2016).
In Fig. 9 we plot the 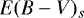 of the regions of Mrk 848 derived from the SED fitting and the spectra fitting compared with the
of the regions of Mrk 848 derived from the SED fitting and the spectra fitting compared with the 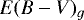 . The SED fitting gives f ~ 1 while the spectral fitting gives f ~ 0.5. The physical mechanism that may explain the varying f factor is discussed in the following section.
. The SED fitting gives f ~ 1 while the spectral fitting gives f ~ 0.5. The physical mechanism that may explain the varying f factor is discussed in the following section.
 |
Fig. 9 Comparison of the |
3.5 Physical interpretation
From the above analysis, we find that the stellar color excess derived from the SED fitting 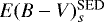 is larger than that derived from the optical spectra fitting
is larger than that derived from the optical spectra fitting 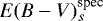 , especially inthe core regions (R3 and R4). We used the mock data (Sect. 3.1) and tested that the
, especially inthe core regions (R3 and R4). We used the mock data (Sect. 3.1) and tested that the 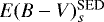 are well constrained. We also showed in Sect. 3.2 that the
are well constrained. We also showed in Sect. 3.2 that the 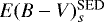 is consistent with that obtained using the IR/UV indicators. However, using the
is consistent with that obtained using the IR/UV indicators. However, using the 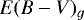 given by the Balmer decrement, the results from SEDs put
given by the Balmer decrement, the results from SEDs put 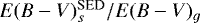 to have a ratio of ~1, which is inconsistent with the classical f value of 0.44 (or the local value 0.58 given by Pannella et al. 2015). On the other hand, the
to have a ratio of ~1, which is inconsistent with the classical f value of 0.44 (or the local value 0.58 given by Pannella et al. 2015). On the other hand, the 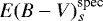 to
to 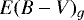 ratio is 0.5, consistent with the classical f value.
ratio is 0.5, consistent with the classical f value.
The difference among these results can be explained by the two-component dust model (e.g., Calzetti et al. 1994; Charlot & Fall 2000; Wild et al. 2011; Price et al. 2014), corresponding to the similar implementation in our broadband SED fitting. As illustrated in Charlot & Fall (2000), this model contains a diffuse dust component in the interstellar medium (ISM) and a dust component in the stellar birth clouds. The former affects both the old diffuse stellar populations and the young stellar populations, whereas the latter affects only the young stellar populations which are still embedded in the birth clouds. Since Mrk 848 is a merger, the gas inflow into the center would lead to starbursts, making it necessary to consider the two-component dust model. For galaxies with high specific SFRs (SFR/M*) as in our case (see Table 5), both the emission lines and the UV-to-IR continuum emission, which is dominated by the recently formed stars in the birth cloud, are attenuated by both dust components. Therefore, the attenuation of emission lines and that of the stars dominating UV-to-IR SED would be similar.
In the framework of the two-component dust model, the 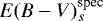 would be lower than
would be lower than 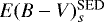 . In the stellar birth cloud, the optical radiation from both stars and gas will mostly be absorbed by the dense cloud before escaping from the galaxy. Therefore, what we observed in optical bands will be dominated by the diffuse radiation from older stars in the diffused regions outside of the birth clouds. In contrast, the UV and IR SED detects emissions from more attenuated parts inside the birth clouds. Therefore, the two quantities measure different dust attenuation.
. In the stellar birth cloud, the optical radiation from both stars and gas will mostly be absorbed by the dense cloud before escaping from the galaxy. Therefore, what we observed in optical bands will be dominated by the diffuse radiation from older stars in the diffused regions outside of the birth clouds. In contrast, the UV and IR SED detects emissions from more attenuated parts inside the birth clouds. Therefore, the two quantities measure different dust attenuation.
Wild et al. (2011) and Price et al. (2014) suggest that the star to gas attenuation ratio is larger in higher SSFR galaxies, in agreement with our interpretation above – that the UV-to-IR SED detects dusty, high SSFR parts of Mrk 848, whereas the optical continuum is dominated by the emission in the diffuse, low SSFR region.
It is interesting that the tail regions also show some discrepancy between optical- and UV/IR-derived dust attenuation, implying similar dust geometry in the tail regions. A possible explanation is that there are channels in the tail regions from which gas inflows to the center, and during the inflow path, the gas also cools down and forms stars. Figure 10 illustrates the physical picture described above. We note that the actual situation may be more complicated than this simple picture (see Sect. 3.7).
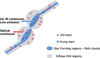 |
Fig. 10 Pictorial representation of the distribution of dust and stars in Mrk 848. The optical continuum observed is dominated by the diffuse region outside of the birth cloud. The UV/IR continuum and the line emissions are dominated by the star formation in the birth cloud that are more opaque than the diffuse region. Therefore, the UV/IR continuum and the line emissions are more attenuated than the optical continuum. |
3.6 Active galactic nuclei contribution
The X-ray observation of Mrk 848 shows that it may encompass an AGN (Brightman & Nandra 2011). We examine the emission lines obtained from MaNGA spectra, and find that the equivalent widths of the permitted emission lines (e.g., Hα and Hβ) are less than 300 km s−1. Therefore, the embedded AGN is Seyfert-2 type. The BPT diagram (Baldwin et al. 1981) shows this system is dominated by composite regions (Fig. 11), implying that the AGN contribution to emission lines is not significant. The contribution to the continuum should be even less. We also examine the AGN contribution using the SED fitting with CIGALE. We adopt the AGN models of Dale et al. (2014) and introduce the parameter “AGN fraction” in fitting. It turns out that in each region, the AGN fraction to the SED is less than 10%. Therefore, the existence of AGN does not affect our results.
 |
Fig. 11 Left: BPT diagram of Mrk 848. Right: spatial distribution of the AGN (red), composite (yellow), and star-forming (blue) regions. |
3.7 Influence of the extinction law
In Sect. 3.5, we interpreted the different values of the 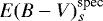 ,
, 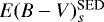 , and
, and 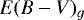 as the results of a geometrical effect that the young and old stellar populations may suffer from different dust attenuation because of their different spatial distribution. In reality, the situation may be more complicated.
as the results of a geometrical effect that the young and old stellar populations may suffer from different dust attenuation because of their different spatial distribution. In reality, the situation may be more complicated.
The derived color excess depends on the extinction law. For simplicity and considering the starburst nature of Mrk 848, we adopted the dust extinction curve of Calzetti et al. (2000) in the above study. Here we test the influence of different extinction curves using the CCM extinction curve of Cardelli et al. (1989), and varying the 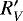 in Calzetti Law from 3.1 to 5.0. We find that the conclusion is not affected by the different implementation of extinction. The variation of the extinction curve is very complicated and beyond the scope of this work. Here the Calzetti extinction curve is a good approximation considering the starburst nature of Mrk 848.
in Calzetti Law from 3.1 to 5.0. We find that the conclusion is not affected by the different implementation of extinction. The variation of the extinction curve is very complicated and beyond the scope of this work. Here the Calzetti extinction curve is a good approximation considering the starburst nature of Mrk 848.
4 Star formation in Mrk 848
4.1 Star formation history
Measuring the SFH of a galaxy from its observed SEDs is not trivial in practice. The best approach to providing unbiased results might be to model the SEDs with non-parametric SFHs (Conroy 2013). However, the non-parametric SFH-reconstruction method requires not only data of very high quality, but also a good understanding of the dust attenuation.
In this work, the pPXF code was used to reconstruct the non-parametric SFHs. We used two different methods to treat the dust. First, we let the attenuation be a free parameter and let the pPXF fit the spectra, as described inSect. 3.3. Second, we corrected the dust attenuation of the spectra using the 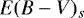 values obtained from the SED fitting in Sect. 3.1 and then conducted the spectral fitting. The resulting SFHs are shown in Fig. 12.
values obtained from the SED fitting in Sect. 3.1 and then conducted the spectral fitting. The resulting SFHs are shown in Fig. 12.
The pPXF fitting with 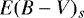 as a free parameter gives a large fraction of older stellar populations and a very low fraction of stellar populations younger than 500 Myr. In contrast, the fitting ofthe corrected spectra results in a very high fraction of young stellar populations and an extremely low fraction of stellar populations older than 1 Gyr. Neither of the two methods seem reliable considering that the observed high fluxes both in UV/FIR and in NIR imply that these regions should have considerable fractions of both young and old stellar populations. Therefore, the former method underestimates the fraction of the young stellar populations, whereas the latter overcorrects the dust attenuation and underestimates the fraction of the old stellar populations.
as a free parameter gives a large fraction of older stellar populations and a very low fraction of stellar populations younger than 500 Myr. In contrast, the fitting ofthe corrected spectra results in a very high fraction of young stellar populations and an extremely low fraction of stellar populations older than 1 Gyr. Neither of the two methods seem reliable considering that the observed high fluxes both in UV/FIR and in NIR imply that these regions should have considerable fractions of both young and old stellar populations. Therefore, the former method underestimates the fraction of the young stellar populations, whereas the latter overcorrects the dust attenuation and underestimates the fraction of the old stellar populations.
According to the two-component dust model, the attenuation of the old stellar populations and the young stellar populations should be treated differently. The young stellar populations are more attenuated by dust than the old stellar populations. Therefore, because the above two methods considered only one dust component which gives the effective dust attenuation, over the whole region they overcorrect the dust attenuation of the old stellar populations, and undercorrect that of young stellar populations.
We then attempt to conduct the spectra fitting by adopting the two-component dust model. We assume that the stellar populations younger than t0 years old are more attenuated than the older stellar populations, and that 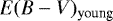 is two times as great as
is two times as great as  . Letting t0 change from 10 Myr to 50 Myr and
. Letting t0 change from 10 Myr to 50 Myr and  from 0.05 to 0.3, we search for the solution with the minimal χ2. The resulting SFHs (open histograms in Fig. 12) show both the burst populations and the old stellar populations, consistent with the picture implied by the high fluxes in both UV/IR and NIR. This is more reasonable than the results given by the one-component dust model, where only a young or old population exists.
from 0.05 to 0.3, we search for the solution with the minimal χ2. The resulting SFHs (open histograms in Fig. 12) show both the burst populations and the old stellar populations, consistent with the picture implied by the high fluxes in both UV/IR and NIR. This is more reasonable than the results given by the one-component dust model, where only a young or old population exists.
The SFHs can also be obtained from the SED fitting by CIGALE. Since we adopt the assumption of an SFH with two exponentially decreasing components for each region, the age of the burst tburst, the duration of the burst τburst and the mass fraction of the burst fburst are used to constrain the young stellar population, and the old stellar population is constrained by the parameter τmain, indicating the time scale of the star formation (see Sect. 3.1). Table 5 presents the SFH parameters derived from the SED fitting.
The UV-to-IR SED fitting provides good constraints on the dust attenuation of each region. However, since the SED fitting assumes an analytical SFH, the real SFH, which may be quite complicated and highly stochastic, cannot be well reconstructed. Some studies have shown that it is difficult to disentangle the different scenarios of the SFH because of the degeneracy of the fits (e.g. Pforr et al. 2012; Conroy 2013; Buat et al. 2014, 2015; Fernández et al. 2015, and references therein). A recent work by Smith & Hayward (2015) showed that SFHs of isolated disk galaxies can be recovered well using the Bayesian approach. However, they failed to recover the SFH of mergers because the star formation in interacting galaxies is much more complicated than in isolated disks. Our mock analysis in Sect. 3.1 (Fig. 5) shows that the stellar mass and the SFR are well constrained by the SED fitting. However, the parameters of the SFH such as fburst and tburst are weakly constrained.
Comparing the SFHs derived from the spectral fitting and the SED fitting is not straightforward, because the spectral fitting gives non-parametric and discrete SFHs while the SED fitting gives parametric and continuous SFHs. Qualitatively, we find that the SFHs derived from the SED fitting are consistent with the spectral fitting using the two-component dust model. Both methods indicate that a significant fraction ( ~15%) of masses are contributed by stellar populations less than 500 Myr. This recent star formation may be triggered by the galaxy interaction. Both methods show that there is very recent star formation ( ~100 Myr) in one of the core regions (R4). Instead the tail regions do not show a significant fraction of stellar populations younger than 100 Myr, but contain more stellar populations with ages of 500 Myr to 1 Gyr. The results may also indicate that the tail regions experience merger induced starburst earlier than the core regions, which is consistent with the scenario mentioned in Sect. 3.5 that the gas inflows from the tails to the center and cools down along the path.
 |
Fig. 12 Stellar populations of each region derived from pPXF, normalized to the total mass of each region, as a function of stellar ages. The black histograms show the results from pPXF fitting with |
Results of star formation history from broadband SED fitting.
4.2 Star formation rate
Next, we compare the SFRs obtained with the two methods. Here we take the SFR averaged in the recent 100 Myr. Figure 13 shows the comparison of the SFRs derived from the UV-to-IR SED fitting, the optical continuum stellar population fitting and the H α fluxes. If all comparing to the SFR estimated from the UV-to-IR SED method, the results from the optical continuum fitting (open diamonds) with E(B − V ) as a free parameter underestimate the SFR by ~1 dex. The consistency is improved when the two-component dust model is applied (filled diamonds). However, the SFRs are still underestimated, especially for the R4 region, which has a very high SFR, implying that the SFRs in active star-forming regions are not well constrained by the optical continuum data only. A better consistency is obtained when the E(B − V ) information from UV-to-IR is introduced in the optical continuum fitting (open circles). We also calculate the SFRs using the dust corrected H α emission. We corrected the H α luminosity using both the Balmer decrement and the 8 μm data with the relation provided in Kennicutt et al. (2009) and Kennicutt & Evans (2012). Both corrections show similar results. Figure 13 shows that the dust corrected H α derived SFRs (corrected using the 8 μm data) are lower than the UV-to-IR SED derived SFRs. If we consider that part of the Hα could be contributed by the shock excitation (Rich et al. 2011, 2015), the SFRs derived from Hα should be even lower. The discrepancy is partly due to that the IFU data do not fully cover every region. Some pixels are missed because of the limited size of the IFU and/or the bad data quality. We scale the average value of the observed pixels to the whole region whencalculating the SFRs, which may account for part of the differences from the UV-to-IR SED results that are derived from the data with full coverage of Mrk 848. Also, the wavelength coverage in our SED fitting is limited to 8 μm, which may produce large scatters in the estimated SFRs (Calzetti et al. 2007). Apart from these uncertainties, the lower SFR derived from the dust corrected Hα is consistentwith the two-component dust model with a large covering factor of the birth clouds (Wild et al. 2011).
 |
Fig. 13 Comparison of the SFRs derived from the UV-to-IR SED fitting (filled squares), the dust corrected H α fluxes (filled triangles), the optical continuum stellar population fitting using the two-component dust model (filled diamonds), the optical continuum stellar population fitting with E(B − V ) as a free parameter (open diamonds), and the optical continuum stellar population fitting with E(B − V ) from UV-to-IR data (open circles). |
5 Summary
The plentiful data compiled both from the UV-to-IR multiwavelength photometry and from the MaNGA IFU spectroscopy enable us to study the galaxy merger Mrk 848 in terms of the spatially resolved star formation properties. We divide the merger into six regions, among which two regions belong to the core area where the star formation is very intense and others belong to the tail area. In each region, we use the UV-to-IR SED and the IFU spectrum respectively to analyze the dust attenuation and the star formation ofthe merger.
The dust attenuation of stars derived from the UV-to-IR SED 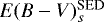 is consistent with that estimated from the UV/IR indicators, including the infrared excess (IRX) and the UV slope (β). Furthermore, we test the reliability of the
is consistent with that estimated from the UV/IR indicators, including the infrared excess (IRX) and the UV slope (β). Furthermore, we test the reliability of the 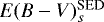 with a set ofmock SEDs generated by deviating the best-fit model SEDs, showing that the dust attenuation of the continuum can be well constrained by the UV-to-IR broadband SED fitting.
with a set ofmock SEDs generated by deviating the best-fit model SEDs, showing that the dust attenuation of the continuum can be well constrained by the UV-to-IR broadband SED fitting.
However, the dust attenuation of stars derived from the optical spectral fitting 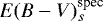 is smaller than that from the multi-band SED fitting. When compared to the
is smaller than that from the multi-band SED fitting. When compared to the 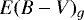 obtained from the Balmer decrement, the ratio of the
obtained from the Balmer decrement, the ratio of the 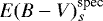 to the
to the 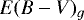 is 0.5, consistent with the local value, while the
is 0.5, consistent with the local value, while the 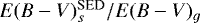 is ~ 1. The difference between the results from the UV-to-IR data and the optical data can be explained by the model with two-component dust, in which the younger stellar populations are embedded in the birth clouds and thus are attenuated by both the dust from the surrounding birth clouds and the dust from the ISM, whereas the older stellar populations are only attenuated by the diffuse dust.
is ~ 1. The difference between the results from the UV-to-IR data and the optical data can be explained by the model with two-component dust, in which the younger stellar populations are embedded in the birth clouds and thus are attenuated by both the dust from the surrounding birth clouds and the dust from the ISM, whereas the older stellar populations are only attenuated by the diffuse dust.
When adopting the two-component dust model in the spectral fitting, the resulting SFH become qualitatively consistent with that from the multi-band SED fitting. It might be a caution that the simple one-component dust model is not applicable for the mergers which are more complicated in the distribution and the properties of the dust, and that the two-component dust model is necessary toreconstruct the SFH of the galaxy merger.
By investigating the SFH of the core and tail regions in Mrk 848, we find that both the spectral fitting and the SED fitting methods indicate very recent starburst (~100 Myr) in core regions, especially in region 4 which has the most intense star formation. The tail regions also show certain sign of recent starburst, but the burst seems to have happened earlier (~ 500 Myr) than in the core regions. The high SFRs in the core regions are consistent with the interaction induced starburst.
Our results imply that, it is a non-trivial task to break the degeneracy between the stellar population and dust attenuation for the merging galaxy. Information from multiwavelength observations from the UV to the IR is necessary to constrain the dust attenuation and to reconstruct the SFH.
Acknowledgements
We thank the anonymous referee for a thorough and constructive review. This work is supported by the National Natural Science Foundation of China (NSFC) with the Project Number of 11303070 (PI: FTY), 11433003 (PI: Chenggang Shu) and 11573050 (PI: SS). FTY is sponsored by Natural Science Foundation of Shanghai (Project Number: 17ZR1435900) and the China Scholarship Council (CSC). C.J. acknowledges support from the Natural Science Foundation of Shanghai (No. 15ZR1446600), the National Natural Science Foundation of China (NSFC, No. 11773051), and the CAS Key Research Program of Frontier Sciences (No. QYZDB-SSW-SYS033). MAF is grateful for financial support from CONICYT FONDECYT project No. 3160304. MB was supported by MINEDUC-UA projects, code ANT 1655 and ANT 1656, and FONDECYT project 1170618. This research made use of Marvin, a core Python package and web framework for MaNGA data, developed by Brian Cherinka, José Sánchez-Gallego, and Brett Andrews (MaNGA Collaboration, 2017). This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
Appendix A Spectral fitting with pPXF for regions in Mrk 848
We present the best-fit models and the residuals of the optical spectral fitting with pPXF. Figure A.1 shows the results assuming one-component dust and fitting the E(B − V ) as a free parameter. Figure A.2 shows the results assuming one-component dust and adopting the E(B − V ) from UV-to-IR SED fitting. Figure A.3 shows the fitting results assuming the two-component dust model.
 |
Fig. A.1 Spectra (black lines), best-fit models, (red lines) and residuals (green dots) of pPXF fitting for the different regions in Mrk 848 with the E(B − V ) as a free parameter. The yellow vertical lines show the masked emission line regions. |
 |
Fig. A.2 Spectra, best-fit models, and residuals of pPXF fitting for the different regions in Mrk 848 with the E(B − V ) derived from the UV-to-IR data. Symbols are the same as in Fig. A.1. |
 |
Fig. A.3 Spectra, best-fit models, and residuals of pPXF fitting for the different regions in Mrk 848 with the two-component dust model, assuming that the stellar populations less than t0 Myr are attenuated twice of the stellar populations older than t0 Myr. Symbols are the same as in Fig. A.1. |
References
- Alonso, M. S., Tissera, P. B., Coldwell, G., & Lambas, D. G. 2004, MNRAS, 352, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Scoville, N. Z. 2000, ApJ, 532, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barton Gillespie, E., Geller, M. J., & Kenyon, S. J. 2003, ApJ, 582, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Bavouzet, N., Dole, H., Le Floc’h, E., et al. 2008, A&A, 479, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Shu, F. H. 1980, ApJ, 238, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., Gil de Paz, A., Boselli, A., et al. 2007, ApJS, 173, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Buat, V., Boselli, A., et al. 2012, A&A, 539, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Buat, V., & Perret, V. 2014, A&A, 571, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brightman, M., & Nandra, K. 2011, MNRAS, 413, 1206 [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Iglesias-Páramo, J., Seibert, M., et al. 2005, ApJ, 619, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Giovannoli, E., Heinis, S., et al. 2011, A&A, 533, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Heinis, S., Boquien, M., et al. 2014, A&A, 561, A39 [Google Scholar]
- Buat, V., Oi, N., Heinis, S., et al. 2015, A&A, 577, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 1997, in AIP Conf. Ser., 408, ed. W. H. Waller, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Boselli, A., Buat, V., et al. 2006, ApJ, 637, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drory, N., MacDonald, N., Bershady, M. A., et al. 2015, AJ, 149, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, AJ, 135, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Chandar, R., Whitmore, B., & Regan, M. 2006, ApJ, 644, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, M., Yuan, F., Shen, S., et al. 2015, Galaxies, 3, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannoli, E., Buat, V., Noll, S., Burgarella, D., & Magnelli, B. 2011, A&A, 525, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1989, Nature, 340, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Kashino, D., Silverman, J. D., Rodighiero, G., et al. 2013, ApJ, 777, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, X., Charlot, S., Brinchmann, J., & Fall, S. M. 2004, MNRAS, 349, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Kodama, T., Hayashi, M., et al. 2015, MNRAS, 453, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Groves, B., Schinnerer, E., et al. 2013, ApJ, 771, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Yan, R., Bershady, M. A., et al. 2015, AJ, 150, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F. 2005, in AIP Conf. Ser., Vol. 761, eds. C. C. Popescu, & R. J. Tuffs, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Melnick, J., & Mirabel, I. F. 1990, A&A, 231, L19 [NASA ADS] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., Vigroux, L., Charmandaris, V., et al. 1998, A&A, 333, L1 [NASA ADS] [Google Scholar]
- Moreno, J., Torrey, P., Ellison, S. L., et al. 2015, MNRAS, 448, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordon, R., Lutz, D., Genzel, R., et al. 2012, ApJ, 745, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Panuzzo, P., Granato, G. L., Buat, V., et al. 2007, MNRAS, 375, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Torrey, P., Ellison, S. L., Mendel, J. T., & Scudder, J. M. 2013, MNRAS, 433, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Kellogg, M., Steidel, C. C., et al. 1998, ApJ, 508, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Pforr, J., Maraston, C., & Tonini, C. 2012, MNRAS, 422, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. H., Kriek, M., Brammer, G. B., et al. 2014, ApJ, 788, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Puglisi, A., Rodighiero, G., Franceschini, A., et al. 2016, A&A, 586, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Kraljic, K., & Duc, P.-A. 2014, MNRAS, 442, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, J. A., Kewley, L. J., & Dopita, M. A. 2011, ApJ, 734, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, J. A., Kewley, L. J., & Dopita, M. A. 2015, ApJS, 221, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sánchez, S. F., & González-Serrano, J. I. 2003, A&A, 406, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D. B., Soifer, B. T., Scoville, N. Z., & Sargent, A. I. 1988, ApJ, 324, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, K. B., Rix, H.-W., da Cunha, E., et al. 2013, MNRAS, 432, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Smith, D. J. B., & Hayward, C. C. 2015, MNRAS, 453, 1597 [Google Scholar]
- Takeuchi, T. T., Yuan, F.-T., Ikeyama, A., Murata, K. L., & Inoue, A. K. 2012, ApJ, 755, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Matsubayashi, K., Kajisawa, M., et al. 2012, ApJ, 753, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Tojeiro, R., Wilkins, S., Heavens, A. F., Panter, B., & Jimenez, R. 2009, ApJS, 185, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Torrey, P., Cox, T. J., Kewley, L., & Hernquist, L. 2012, ApJ, 746, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Wild, V., Charlot, S., Brinchmann, J., et al. 2011, MNRAS, 417, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Wild, V., Rosales-Ortega, F., Falcón-Barroso, J., et al. 2014, A&A, 567, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, H., Cao, C., Hao, C.-N., et al. 2005, ApJ, 632, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Lutz, D., et al. 2011, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Domingue, D., Cheng, Y.-W., et al. 2010, ApJ, 713, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, R., Tremonti, C., Bershady, M. A., et al. 2016, AJ, 151, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F.-T., Takeuchi, T. T., Matsuoka, Y., et al. 2012, A&A, 548, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, H.-X., Gao, Y., & Kong, X. 2010, MNRAS, 401, 1839 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Center coordinates of each region and the signal-to-noise ratio (S/N) of the binned MaNGA spectra in each region.
All Figures
 |
Fig. 1 Regions (cores: R3 and R4, tails: R1, R2, R5 and R6) of Mrk 848 used for analysis in this work, overplotted on the r band image of SDSS. The radius of each region is 5″. This image is rotated north-up. |
| In the text | |
 |
Fig. 2 Left panel: coverage of MaNGA IFU bundle on Mrk 848. Right panel: S/N distribution of MaNGA spectra. |
| In the text | |
 |
Fig. 3 Images of Mrk 848 from GALEX, SDSS, and Spitzer, respectively. The size of each image is 1′ × 1′ . All the images are rotated north-up. |
| In the text | |
 |
Fig. 4 SEDs of the six regions in Mrk 848. Triangles show SEDs derived from the images with their original resolution. Squares show SEDs derived from the images after degrading the resolution to 6′′ by convolving with the NUV PSF. |
| In the text | |
 |
Fig. 5 Comparison of the values for six parameters of the best-fit models and their values estimated by CIGALE from the mock data based on the best-fit models. The mock results of the dust attenuation, the stellar mass and the SFR are scattered approximately around the best-fit parameters (correlation coefficient r > 0.9), indicating that they are well constrained by the SED fitting. The burst fraction fburst and the burst age tburst are weakly constrained. |
| In the text | |
 |
Fig. 6 Comparison of the |
| In the text | |
 |
Fig. 7 IRX-β relation for the six regions of Mrk 848 (squares with error bars). The relations given by Meurer et al. (1999), Muñoz-Mateos et al. (2009), Boissier et al. (2007), Cortese et al. (2006) and Pettini et al. (1998) are overplotted. |
| In the text | |
 |
Fig. 8 Comparison of the |
| In the text | |
 |
Fig. 9 Comparison of the |
| In the text | |
 |
Fig. 10 Pictorial representation of the distribution of dust and stars in Mrk 848. The optical continuum observed is dominated by the diffuse region outside of the birth cloud. The UV/IR continuum and the line emissions are dominated by the star formation in the birth cloud that are more opaque than the diffuse region. Therefore, the UV/IR continuum and the line emissions are more attenuated than the optical continuum. |
| In the text | |
 |
Fig. 11 Left: BPT diagram of Mrk 848. Right: spatial distribution of the AGN (red), composite (yellow), and star-forming (blue) regions. |
| In the text | |
 |
Fig. 12 Stellar populations of each region derived from pPXF, normalized to the total mass of each region, as a function of stellar ages. The black histograms show the results from pPXF fitting with |
| In the text | |
 |
Fig. 13 Comparison of the SFRs derived from the UV-to-IR SED fitting (filled squares), the dust corrected H α fluxes (filled triangles), the optical continuum stellar population fitting using the two-component dust model (filled diamonds), the optical continuum stellar population fitting with E(B − V ) as a free parameter (open diamonds), and the optical continuum stellar population fitting with E(B − V ) from UV-to-IR data (open circles). |
| In the text | |
 |
Fig. A.1 Spectra (black lines), best-fit models, (red lines) and residuals (green dots) of pPXF fitting for the different regions in Mrk 848 with the E(B − V ) as a free parameter. The yellow vertical lines show the masked emission line regions. |
| In the text | |
 |
Fig. A.2 Spectra, best-fit models, and residuals of pPXF fitting for the different regions in Mrk 848 with the E(B − V ) derived from the UV-to-IR data. Symbols are the same as in Fig. A.1. |
| In the text | |
 |
Fig. A.3 Spectra, best-fit models, and residuals of pPXF fitting for the different regions in Mrk 848 with the two-component dust model, assuming that the stellar populations less than t0 Myr are attenuated twice of the stellar populations older than t0 Myr. Symbols are the same as in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.