| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731478 | |
| Published online | 04 June 2018 | |
A hot Saturn on an eccentric orbit around the giant star K2-132★
1
European Southern Observatory,
Alonso de Córdova 3107,
Casilla
19001,
Santiago,
Chile
e-mail: mjones@eso.org
2
Millennium Institute of Astrophysics,
Santiago,
Chile
3
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile,
Av. Vicuña Mackenna 4860,
7820436
Macul,
Santiago,
Chile
4
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
5
Center of Astro-Engineering UC, Pontificia Universidad Católica de Chile,
Av. Vicuña Mackenna 4860,
7820436
Macul,
Santiago,
Chile
6
Departamento de Astronomía, Universidad de Chile,
Camino El Observatorio 1515,
Las Condes,
Santiago,
Chile
7
Instituto de Física y Astronomía, Universidad de Vaparaíso,
Casilla
5030,
Valparaíso,
Chile
8
Department of Astronomy, Stockholm University,
11419,
Stockholm,
Sweden
Received:
30
June
2017
Accepted:
18
December
2017
Although the majority of radial velocity detected planets have been found orbiting solar-type stars, a fraction of them have been discovered around giant stars. These planetary systems have revealed different orbital properties when compared to solar-type star companions. In particular, radial velocity surveys have shown that there is a lack of giant planets in close-in orbits around giant stars, in contrast to the known population of hot Jupiters orbiting solar-type stars. It has been theorized that the reason for this distinctive feature in the semimajor axis distribution is the result of the stellar evolution and/or that it is due to the effect of a different formation/evolution scenario for planets around intermediate-mass stars. However, in the past few years a handful of transiting short-period planets (P ≲ 10 days) have been found around giant stars, thanks to the high-precision photometric data obtained initially by the Kepler mission, and later by its two-wheel extension K2. These new discoveries have allowed us for the first time to study the orbital properties and physical parameters of these intriguing and elusive substellar companions. In this paper we report on an independent discovery of a transiting planet in field 10 of the K2 mission, also reported recently by Grunblatt et al. (2017, AJ, 154, 254). The host star has recently evolved to the giant phase, and has the following atmospheric parameters: Teff = 4878 ± 70 K, log g = 3.289 ± 0.004, and [Fe/H] = −0.11 ± 0.05 dex. The main orbital parameters of K2-132 b, obtained with all the available data for the system are: P = 9.1708 ± 0.0025 d, e = 0.290 ± 0.049, Mp = 0.495 ± 0.007 MJ and Rp = 1.089 ± 0.006 RJ. This is the fifth known planet orbiting any giant star with a < 0.1, and the most eccentric one among them, making K2-132 b a very interesting object.
Key words: techniques: radial velocities / planet-star interactions / planets and satellites: general
Tables of the photometry and of the radial velocities are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/613/A76
© ESO 2018
1 Introduction
To date, more than 3000 planetary companions have been discovered1 orbiting stars other than the Sun, and this number is rapidly evolving as more and more new planets are routinely detected by different groups. Strictly speaking, the first extrasolar planetary system was found around a stellar remnant, namely the pulsar PSR 1257+12 (Wolszczan & Frail 1992). However, a few years later, Mayor & Queloz (1995) announced the detection of a periodic signal in the radial velocity (RV) observations of the solar-type star 51 Pegasi. The signal was caused by the presence of a giant planet in a four-day orbit, confirming the existence of extrasolar planets. This discovery marked the beginning of the exoplanet observational area, which is currently living a golden age.
Afterward, new RV measurements allowed the detection of several hot Jupiters and a large fraction of eccentric planetary companions (e.g., Marcy et al. 2005); this completely changed our knowledge of planetary formation and evolution, which had been mainly restricted to the study of the solar system. These discoveries severely challenged the planet formation theories, bringing back to life the importance of dynamical processes like planet migration (Papaloizou & Lin 1984) and eccentricity excitation via planet–star (e.g Kozai 1962; Lidov 1962) and planet–planet interactions (e.g., Rasio & Ford 1996; Weidenschilling & Marzari 1996; Lin & Ida 1997). Moreover, as soon as instruments like HARPS (Mayor et al. 2003) capable of reaching ≲1 m s−1 precision were developed, a large population of small rocky planets was unveiled, whose RV signals were hidden behind the instrumental noise and the stellar jitter (e.g., Mayor et al. 2009). Similarly, pioneering studies aimed at detecting transiting planets from ground-based photometric data (Charbonneau et al. 2000, Henry et al. 2000) led to the discovery of a multitude of short-period giant planets (e.g., Bakos et al. 2004; Pollacco et al. 2006) that provided direct information of their physical properties, such as density, radius, and atmospheric composition (Seager & Deming 2010; Crossfield 2015). Moreover, when combined with RV data, the planet mass can be directly inferred as can the spin-orbit angle from the Rossiter-McLaughlin effect (e.g., Queloz et al. 2000; Brown et al. 2012). However, only the advent of dedicated space-based missions like CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010) has allowed us to efficiently detect transiting rocky planets, whose transit depths are as small as ~100 ppm. Similarly, space-based observations have more recently permitted the detection of transiting planets orbiting around giant stars, which is incredibly challenging from the Earth, due to the small transit depth and long duration of the transit. However, these systems are of great importance for several reasons. First, by studying the planet radius as a function of the stellar irradiation (see Demory & Seager 2011), it is possible to discriminate between the direct inflation scenario due to the increasing stellar irradiation as the host star evolves through the giant phase (Grunblatt et al. 2016) or due to delayed thermal contraction (Lopez & Fortney 2016). Second, RV surveys have found an intriguing lack of short-period (P < 10 days) giant planets around evolved stars (e.g., Johnson et al. 2007; Döllinger et al. 2011; Jones et al. 2014) in direct contrast to what is observed in solar-type host stars. In fact, even though over a thousand ofsuch post main-sequence (MS) stars have been targeted by different groups (Frink et al. 2001; Setiawan et al. 2003; Hatzes et al. 2005; Sato et al. 2005; Niedzielski et al. 2009; Jones et al. 2011; Wittenmyer et al. 2011), only one short-period planet has been detected by means of RV measurements (Johnson et al. 2010). Therefore, the detection of new giant transiting planets around giant stars provides us with valuable information about the properties of these elusive substellar companions.
In this paper we present the discovery of a Saturn-mass planet in a short-period and eccentric orbit around the evolved star K2-132. The transit signal was detected from K2 (Howell et al. 2014) photometric data taken in Campaign 10 as part of a Chilean-based effort aimed at the detection and characterization of transiting exoplanetary systems (see Brahm et al. 2016, Espinoza et al. 2016, Espinoza et al. 2017). Additionally, we performed a spectroscopic follow-up using HARPS and FEROS. From these datasets we computed precision RVs that confirm the transit signal of the companion. From the combined transit and photometric data we obtained the following planet parameters: P = 9.171 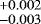 d, e = 0.29
d, e = 0.29 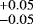 , Mp = 0.495
, Mp = 0.495 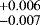 MJ, and Rp = 1.089
MJ, and Rp = 1.089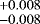 . The paper is structured as follows. In Sect. 2 we present the photometric analysis and RV measurements. In Sect. 3 we describe the host star properties, including the asteroseismic analysis, and the global modeling of the photometric and RV data. Finally, the discussion and summary are presented in Sect. 4.
. The paper is structured as follows. In Sect. 2 we present the photometric analysis and RV measurements. In Sect. 3 we describe the host star properties, including the asteroseismic analysis, and the global modeling of the photometric and RV data. Finally, the discussion and summary are presented in Sect. 4.
2 Observations
2.1 K2 Photometry
Photometry for the star K2-132 was obtained in the long-cadence mode with the Kepler spacecraft during Campaign 10 of the repurposed K2 mission. As described in previous works (Espinoza et al. 2016; Brahm et al. 2016), photometry was obtained for all stars in the field using our own implementation of the EVEREST algorithm (Luger et al. 2016) as soon as the data was available at MAST. A box least-squares (BLS) algorithm was used in order to search for planetary signals in each of the light curves after they were detrended, i.e., any long-term trends were removed using a median filter smoothed with a Gaussian filter. Our algorithm detected transit-like features with depths of ~1000 ppm and a period of ~9 days in the light curve of K2-132, and thus it entered our list of transiting planet candidates and was selected for further spectroscopic follow-up in order to confirm or reject its possible planetary nature. In the reminder of this paper, we prefer to use the light curves of Vanderburg & Johnson (2014) because they attain better precisions than our light curves obtained using our implementation of the EVEREST algorithm. Figure 1 shows this photometry where the transits can be spotted by eye. The first two transits of the planet candidate observable in this light curve showed strong systematics, and we decided to not include them in our analysis.
 |
Fig. 1 Top panel: Light curve of K2-132 (black points) along with the smoothed median filter used to model its long-term trend (orange solid line). Bottom panel: Light curve detrended of the long-term trend. The transits detected by our BLS analysis are indicated with red arrows. |
2.2 Precision radial velocities
To confirm the planetary nature of the transiting candidate K2-132 identified from the K2 photometry, we obtained high-resolution spectra using two different environment stabilized instruments. These observations were used i) to perform a fast spectral classification of the star in order to determine the expected size of the planet and the expected amplitude of the radial velocity signal; ii) to identify whether the observed spectrum is composed of more that one stellar spectrum, which could imply that the photometric signal is produced by a blended eclipsing binary; and iii) to measure precise radial velocities in order to rule out the presence of stellar companions and to determine the orbital parameters of the planetary system.
We obtained the first spectra of K2-132 using the HARPS spectrograph mounted on the ESO 3.6 m telescope at the ESO La Silla Observatory on April 23, 2017. From this first spectrum we were able to identify that the star was an early K-type star (Teff = 4900 ± 200 K) with relatively low surface gravity (log g = 3.25 ± 0.3 dex) consistent with a red giant star, which implied that the transits could have been produced by a giant planet. We obtained another seven HARPS spectra for K2-132 between April and May 2017 to measure the radial velocity variations. We used exposure times of 1200 s to achieve a typical signal-to-noise ratio (S/N) of ~30, which produces photon noise dominated errors in RV on the order of 7 m s−1. Given that the nightly instrumental velocity drift of this spectrograph is significantly smaller than the expected errors in RV, we did not use the simultaneous comparison fiber. The spectra were reduced and analyzed with the CERES pipeline (Brahm et al. 2017a), which performs the optimal extraction and wavelength calibration of the spectra before computing the corresponding RVs, bisector spans, and a rough spectral classification.
We obtained six additional spectra of K2-132 between May and June of 2017, using the FEROS spectrograph (Kaufer et al. 1999) mounted on the 2.2 m MPG telescope at the ESO La Silla Observatory. In this case, the amplitude of the instrumental drift during one night is on the order of ~200 m s−1, and thereforewe used the comparison fiber to trace the instrumental velocity drift by using a ThAr lamp. We used exposure times of 1200 seconds, which delivered radial velocity errors of ~7 m s−1. The FEROS spectra were also reduced and analyzed using CERES.
During the final writing phase of this article, Grunblatt et al. (2017) announced the discovery and characterization of this same target, and published radial velocities obtained with Keck/HIRES. For completeness, we also include their data in our analysis, which allowed us to further refine the system parameters (see Sect. 3).
As shown in Fig. 2, the radial velocity variations measured by HARPS, FEROS, and Keck/HIRES are consistent with a Keplerian orbit produced by a giant planet (K ~ 40 m s−1), and consistent with the photometric ephemeris of the K2 light curve. We also computed the degree of correlation between RVs and bisector span values for HARPS and FEROS (the analysis of the Keck/HIRES data can be seen in Grunblatt et al. 2017) in order to rule out the possibility that the observed RV variations are due to a blended scenario (Santerne et al. 2015). We used a bootstrap algorithm to determine the distribution of the error weighted Pearson correlation coefficient, finding that the data is consistent with no correlation at the 95% confidence interval (see Fig. 3).
 |
Fig. 2 Top panel: Phased-folded radial velocities of K2-132 obtained with HARPS (red dots), FEROS (gray dots), and Keck/HIRES (blue dots). The red line corresponds to the Keplerian model using the posterior parameters of the MCMC analysis of Sect. 3.5. Bottom panel: Residuals for the observed radial velocities. The small blue band around zero has a width equal to the fitted jitter term of 5.1 m s−1. |
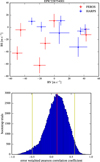 |
Fig. 3 Top panel: observed radial velocities vs. bisector span measurements for HARPS (blue) and FEROS (red). Bottom panel: bootstrap distribution of the weighted Pearson correlation coefficient between radial velocities and bisector span measurements. FEROS and HARPS velocity points are consistent with no correlation. |
3 Analysis
3.1 Atmospheric parameters
To determinethe atmospheric parameters of K2-132, we used the Zonal Atmospheric Stellar Parameters Estimator (ZASPE; Brahm et al. 2017b) code. Briefly, ZASPE matches the observed stellar spectrum with a set of synthetic spectra generated from the ATLAS9 model atmospheres (Kurucz 1993). This procedure is performed via a global χ2 minimizationin a set of selected spectral regions that are highly sensitive to small changes in Teff, log g, and [Fe/H]. In addition, reliable errors in the parameters are obtained by considering the degree of systematic mismatch present between the observed spectrum and the optimal synthetic spectrum. In this specific case, we run ZASPE with a HARPS high S/N spectrum, which was built by combining eight individual spectra taken at different epochs after correcting by their relative Doppler shift. The results are summarized in Table 1. In addition, we obtained the atmospheric parameters by matching the curve of growth, using the equivalent width of a set of carefully selected Fe I and Fe II lines (Jones et al. 2011), and by imposing excitation and ionization equilibrium. For this purpose we used the Spectroscopic Parameters and atmosphEric ChemIstriEs of Stars (SPECIES; Soto & Jenkins 2018) code, which implements an automated version of MOOG2 (Sneden 1973) to iterate through the atmospheric parameters until the equilibrium condition is reached. The uncertainties in the results are derived by considering the contribution from the uncertainty in the excitation and ionization equilibrium, and from the correlations among the parameters. These results are also listed in Table 1. As can be seen, we obtained very good agreement between the results from ZASPE and SPECIES.
Stellar parameters of K2-132.
3.2 Planet scenario validation
To validate the planetary nature of K2-132 b, we ran the Validation of Exoplanet Signals using a Probabilistic Algorithm (VESPA; Morton 2012). Since we do not detect any radial velocity consistent with a non-blended eclipsing binary system (see Sect. 2.2), we set the likelihood of this event to zero in these calculations, modeling then the possibility that our planet candidate could be produced by either a bona fide planet, a blended eclipsing binary system, or a hierarchical triple system. Assuming an occurrence rate of giant planets around giant stars similar to that of hot Jupiters around solar-type stars (~1%; Marcy et al. 2005; Wang et al. 2015), we find a false-positive probability (FPP) for our system of 0.01%. If we consider a lower occurrence rate for giant stars of ~0.1%, then we obtain a FPP of 0.09%. This validates our system as a genuine exoplanet system.
3.3 Asteroseismology
In Fig. 4 we show the power spectral density (PSD) of the K2 light curve shown in Fig. 1 with the transits removed. This shows a clear power excess with regularly spaced peaks at a frequency of ≈240 μHz, corresponding to a period of ≈70 min. Oscillations in that range are expected for a low-luminosity giant (Bedding et al. 2010), and an estimation of the frequency of maximum power, νmax, and the large frequency separation, Δ ν, allow in turn precise estimations of the stellar density and log g. We estimate these parameters from the power spectrum using a method similar to that of Huber et al. (2009). To estimate νmax we smoothed the power spectrum with a Gaussian kernel with σ = 10 μHz and take the maximum of the smoothed power spectrum as the estimate. The value of Δ ν was estimated from the autocorrelation function (ACF) in the range 14–20 μHz, a broad region that should contain the Δν value as expected from the known relation between νmax and Δ ν (Stello et al. 2009). We find two regions showing broad and structured power peaks; we took the maximum of the ACF in each of those regions as trial Δν values and examined the resulting échelle diagram (power spectral density versus {ν∕Δ ν mod 1}) and required that the l = 0 modes appear at ≈0.4 as expected (White et al. 2011). This criterion is satisfied by a local maximum of the ACF at Δ ν = 18.55 μHz, which we take as our estimate. We use the breadth of the broad power peak to assign an uncertainty of 0.25 μHz, so our final estimate is Δ ν = 18.55 ± 0.25 μHz. The uncertainty on νmax was estimated by recalculating this parameter on realizations of the power spectrum, where correlated noise is added with properties estimated from the background away from the peaks. The value we obtain is νmax = 240 ± 6 μHz. We used Eqs. (1) and (2) in Grunblatt et al. (2016) in order to obtain estimates for the density ρ = 0.0269 ± 0.0009 gr cm−3 and surface gravity log g = 3.29 ± 0.02. We note that given the similarity between K2-132 and K2-97 it is appropriate to use the value of fΔν assumed in Eq. (1) by Grunblatt et al. (2016).
 |
Fig. 4 Power spectral density of the K2 light curve. |
3.4 Physical parameters
To compute the physical parameters and evolutionary status of K2-132 we used the Yonsei-Yale isochrones by searching for the stellar age and mass of the model that most closely resembles the observed properties of the host star. We used the Teff and [Fe/H] derived with ZASPE, but given that the stellar log g is not tightly constrained by spectroscopy, we used the ρ⋆ derived from our asteroseismic analysis as a luminosity indicator for the isochrones.
We ran a Markov chain Monte Carlo (MCMC) analysis using the emcee Python package for exploring the parameter space. In this process we held fixed the [Fe/H] to the spectroscopic value, while the stellar age and mass were considered as free parameters. To compute the model Teff and ρ⋆, we interpolated the original isochrones in mass, age, and [Fe/H] using the algorithm provided with the isochrones. Figure 5 displays some of the Yonsei-Yale isochrones for the ZASPE determined metallicity for K2-132 in the Teff – ρ⋆ plane, along with the corresponding assumed values for the host star.
 |
Fig. 5 Stellar density as a function of the stellar Teff for the Yonsei-Yale isochrones. From left to right the plotted isochrones correspond to ages of 0.1, 2, 4, 6, 8 Gyr. The blue dot corresponds to the assumed parameters of the host star. |
3.5 Global Modeling
The K2 photometry along with the radial velocity measurements were fitted simultaneously with the exonailer algorithm3, whose main characteristics are detailed in Espinoza et al. (2016). In summary, we use a transit model using the batman package (Kreidberg 2015) and fit the transit light curve by resampling the transit model with the method of selective resampling described in Kipping (2013). We follow Espinoza & Jordán (2016) and select the quadratic limb darkening as the optimal law for this case because it provides the lowest mean-squared error in the planet-to-star radius ratio, which in this case is the most interesting parameter to retrieve. For the RVs, a different systemic velocity is fitted for each instrument, and a common jitter value is fitted simultaneously for every dataset, which is added in quadrature to the error bars of each RV data point. We then use the emcee MCMC package to explore the parameter space and to obtain reliable estimates of the uncertainties of each parameter.
As described in Sect. 3.3, the star clearly shows a correlated structure in the observed K2 photometry, which is typical of red giant stars. In order to account for this structure, in our modeling we use the physically motivated Gaussian process (GP) model described in Foreman-Mackey et al. (2017), which assumes that the power spectrum of the K2 photometry can be described by two sets of terms. The first is a term that modulates the granulation “background” of the process, which takes care of the power at lower frequencies. Assuming an oscillator with a quality factor 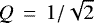 (e.g., Kallinger et al. 2014), its PSD is given by
(e.g., Kallinger et al. 2014), its PSD is given by
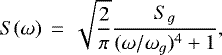 (1)
(1)
where ωg corresponds to the frequency of the undamped oscillator and Sg is proportional to the power at the frequency ω = ωg. The second set of terms accounts for the power excess at higher frequencies due to the asteroseismic oscillations described in Sect. 3.3. The idea is to model the “peaks” observed at and around νmax. These terms are given by
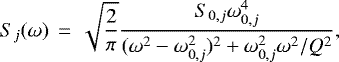 (2)
(2)
where ω0,j = 2π(νmax + jΔν + ϵ) and S0,j = (A∕Q2) exp 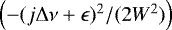 . Here, A and W are free parameters that are shared by all of the terms in Eq. (2). The number of terms j is somewhat arbitrary, and define the number of peaks one would want to capture. Based on the number of peaks in the periodogram around νmax, we chose a total of seven terms (j =−3, −2, …, 2, 3). Finally, we also fit for a photometric jitter term σw, which in the time domain allows us to estimate the underlying photon noise in addition to this stochastic process.
. Here, A and W are free parameters that are shared by all of the terms in Eq. (2). The number of terms j is somewhat arbitrary, and define the number of peaks one would want to capture. Based on the number of peaks in the periodogram around νmax, we chose a total of seven terms (j =−3, −2, …, 2, 3). Finally, we also fit for a photometric jitter term σw, which in the time domain allows us to estimate the underlying photon noise in addition to this stochastic process.
To model this correlated structure in the time domain, we used the celerite package4, which we have implemented as part of exonailer. Given that the transits only occupy a small portion of the light curve, we decided to first analyze the light curve with the transits removed, estimate the parameters of the noise model defined above, and then use those parameters to account for the correlated structure in the transit and RV fitting. For this purpose, 500 walkers with 1000 steps each are used, 500 of which are used as burn-in. The starting point of each of the parameters is based on a previous maximum-likelihood estimation of the parameters, and emcee is used to explore the parameter space in order to obtain parameter uncertainties. Table 2 summarizes the results of this fit. Figure 6 shows a three-day portion of the light curve. It can be seen that our modeling captures the variability observed in the K2 photometry in the time-domain. Figure 7 shows the corresponding PSD of the lightcurve and our model in the frequency-domain.
Having parametrized the noise in the light curve with the above-mentioned modeling, we proceeded to fit the transit and radial velocities simultaneously using these noise parameters as inputs for the photometric modeling. We used the estimated stellar density in Sect. 3.3 in order to put a prior on a∕R* through the relation 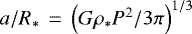 , where P is the period of the orbit that has been very well constrained with our BLS analysis. We use 500 walkers with 1000 steps each in order to perform this simultaneous fit, where the first 500 steps are discarded as burn-in. Figures 2 and 8 show the results of this simultaneous modeling, with the former presenting the transit light curve modeling and the latter presenting the modeling of our high-precision RV measurements. Table 3 summarizes the results of our global modeling.
, where P is the period of the orbit that has been very well constrained with our BLS analysis. We use 500 walkers with 1000 steps each in order to perform this simultaneous fit, where the first 500 steps are discarded as burn-in. Figures 2 and 8 show the results of this simultaneous modeling, with the former presenting the transit light curve modeling and the latter presenting the modeling of our high-precision RV measurements. Table 3 summarizes the results of our global modeling.
Our modeling predicts a quite interesting eccentricity of 0.29± 0.05. In order to test how well this non-zero eccentricity matches the observed data, we repeated our modeling assuming a circular orbit and computed an estimate of the evidence of both models by using the Bayesian information criterion (BIC). The difference in the BIC values between the circular and eccentric models is Δ BIC = 15.8 in favor of the eccentric model. This implies that the eccentric model is exp(ΔBIC∕2) ≈ 2700 times more likely than the circular model, which is strong evidence against this latter model. For comparison, we recomputed the orbital solution using a jitter for each instrument as a free parameter. We obtained a semi-amplitude and eccentricity of 43.0 ± 2.0 m s−1 and 0.30 ± 0.05, respectively, in excellent agreement with the values obtained from the common jitter analysis.
Noise parameters for the light curve of K2-132.
 |
Fig. 6 Top panel: portion of the K2 photometry of the target star. The error bars correspond to the fitted value of σw using our noise model. The blue line with bands shows the posterior prediction of our GP modeling at the given times and the 2-σ credibility interval, respectively. Bottom panel: Residuals between the fitted GP and the K2 photometry. No obvious structure is observed in the residuals. |
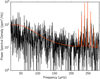 |
Fig. 7 Power spectral density (PSD) of the light curve shown in Fig. 6 (black) along with our noise model on top (red). Our ad hoc model model captures the low-frequency (≲200 μHz) and the high-frequency components of the PSD. |
 |
Fig. 8 Top panel: transits of K2-132 b (black points) along with the best-fit transit model (red solid line) and GP (blue line), along with the 3-σ credibility interval for the posterior predictive GP regression (blue bands). Middle panel: phase-folded light curve with the GP model removed (black points) along with the best-fit transit light curve model (red). Bottom panel: residuals of the phase-folded light curve after removal of the best-fit transit and GP model. |
Parameters obtained from the global modeling.
4 Discussion
4.1 Short-period planets around giant stars
One of the most intriguing results from RV surveys is the observed scarcity of relatively close-in (a ≲ 0.5 AU) planets around post-MS stars. This observational trend has been attributed to the strong tidal torque exerted by the star as its radius grows during the giant phase. As a result, planets are expected to lose orbital angular momentum, thus moving inward until they are evaporated in the stellar atmosphere (Livio & Soker 1983; Sato et al. 2008; Villaver & Livio 2009; Kunitomo et al. 2011). On the other hand, the majority of the giant stars targeted by RV surveys are intermediate-mass stars (M⋆ ~ 1.5–3.0 M⊙), thus they are the post-MS counterpart of A and early F main-sequence stars. Therefore, their companions should not be directly compared to those orbiting solar-type stars. Based on this analysis, known planets orbiting field giant stars are expected to be born in different conditions from those around low-mass stars. In particular, these planets are formed in more massive disks (since Md ∝ M⋆; Andrews et al. 2013), from which they can efficiently accrete a significant amount of gas, becoming gas giants (e.g., Kennedy & Kenyon 2008). In addition, due to the higher gas accretion rate (Muzerolle et al. 2005) and higher irradiation, these disks have shorter dissipation timescales (Currie 2009; Kennedy & Kenyon 2009) and the snow line is located at a greater distance from the central star (Kennedy & Kenyon 2008). As a consequence, these planets are most likely formed at greater orbital distances and, due to the shorter disk timescale, inward migration is halted; they thus reach their final position at a relatively large distance from the parent star. For comparison, Currie (2009) predicted that only ~1.5% of intermediate-mass stars host giant planets with a ≲ 0.5 AU, while ≳7.5% of them host at least one gas giant at a ≳ 0.5 AU. Fig. 9 shows the mass versus the orbital distance of planets detected around giant stars (log g ≲ 3.5), via RV measurements (black dots) and by the transit method (red open circles). We note that values of the RV detected systems correspond to the minimum planet mass (Mp sini). The dotted line represents a radial velocity semi-amplitude of K = 30 m s−1 for a 1.5 M⊙ star, (corresponding to a 3-σ detection; e.g., Hekker et al. 2006). As can be seen, there is only one companion detected via RVs interior to 0.1 AU, and the rest of them reside at an orbital distance a ≳ 0.4 AU. As discussed above, this observational result might be explained by the engulfment of the innermost planets as the parent star evolves off the MS and becomes a giant star. However, since a similar trend is observed in less evolved subgiants whose radii have not yet reached a value where tidal interactions are strong enough to affect the orbits of their companions, Johnson et al. (2007) argued that this is probably explained by a different formation scenario between planets around low-mass stars and those formed in more massive disks. From Fig. 9 it is also evident that planets residing interior to ~0.1 AU are significantly less massive (Mp ≲ 1 MJ) than those orbiting at a greater distance. In fact, two of these transiting planets are well below the 3-σ detection threshold, thus they are not detectable via radial velocities. A similar trend is also observed in MS stars (Zucker & Mazeh 2002), which might be caused by a decrease in the type II migration speed with increasing planetary mass, i.e., d a∕dt ∝ M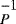 (Mordasini et al. 2009). This theoretical prediction naturally explains why the most massive planets are found at a ≳ 0.4 AU. On the other hand, the mass distribution of the parent stars of these two populations of planets are different. While the mean stellar mass of the RV detected planets is 1.78 M⊙, this value is only 1.38 M⊙ for the transiting systems and thus two distinct planet mass distributions are expected to be found. Moreover, a similar result is observed between the mass of planets orbiting subgiant and giant stars (planets around giant stars being significantly more massive than those around subgiants; see Jones et al. 2014). In fact, the mean mass of the subgiant parent stars is 1.5 M⊙, significantly lower than giant host stars. These results provide further observational support of a different formation and migration scenario for planets at different host star mass. This result suggest that the observed lack of planet around giant stars is mainly due to the primordial distinct formation scenario proposed by Johnson et al. (Johnson et al. (2007)).
(Mordasini et al. 2009). This theoretical prediction naturally explains why the most massive planets are found at a ≳ 0.4 AU. On the other hand, the mass distribution of the parent stars of these two populations of planets are different. While the mean stellar mass of the RV detected planets is 1.78 M⊙, this value is only 1.38 M⊙ for the transiting systems and thus two distinct planet mass distributions are expected to be found. Moreover, a similar result is observed between the mass of planets orbiting subgiant and giant stars (planets around giant stars being significantly more massive than those around subgiants; see Jones et al. 2014). In fact, the mean mass of the subgiant parent stars is 1.5 M⊙, significantly lower than giant host stars. These results provide further observational support of a different formation and migration scenario for planets at different host star mass. This result suggest that the observed lack of planet around giant stars is mainly due to the primordial distinct formation scenario proposed by Johnson et al. (Johnson et al. (2007)).
 |
Fig. 9 Semimajor axis vs. planetary mass of companions detected around giant stars. The black dots and open red circles correspond to planets detected via the RV and transit method, respectively. The blue triangle corresponds to the position of K2-132 b. The dotted line corresponds to a RV amplitude of K = 30 m s−1 for a 1.5 M⋆ star. |
4.2 Orbital evolution
Short-period planets are known to be strongly affected by tidal interactions with their host stars. Observationally, this result is supported by the low orbital eccentricities of planetary companions with a ≲ 0.1 AU when compared to planets that are farther out (Marcy et al. 2005). While the parent star is on the main sequence, tides raised on the planet are thought to be the main mechanism responsible for the eccentricity damping, which at the same time produce significant internal heating, and thus might explain the large observed radii of many transiting short-period planets (Jackson et al. 2008a). However, after the host star evolves to the giant phase, its radius rapidly increases, and tides raised on the stellar envelope become stronger, eventually dominating over tides within the planet (Schlaufman & Winn 2013). We used Eq. (1) from Jackson et al. (2008b) to compute the eccentricity damping timescale τe for K2-132 b, including the contribution from tides raised both in the planet and in the star. We adopted the tidal quality factors of Q⋆ = 106.5 and Qp = 105.5 derived by Jackson et al. (2008b). Given the current radius of the host star, we obtained a circularization timescale of τe ~ 3 Gyr. We note that at this point the tides raised in the planet slightly dominate over tides in the star. Also, since τe is on the order of the age of the system, K2-132 b has probably not suffered from significant eccentricity damping in the past. However, since the host star is rapidly climbing the red giant branch (RGB), its radius is growing in timescales much shorter than τe. For comparison, if we recompute τe when the star has reached about ~8 R⊙ (~150 Myr from now), then the tides raised in the star completely dominate over tides in the planet, and we obtain a much shorter value of τe ~ 250 Myr. This means that tidal circularization is expected to happen in a few hundred Myr. Similarly, we computed the tidal decay timescale τa, using Eq. (2) in Jackson et al. We obtained τa ~ 10 Gyr, which is longer than the age of the system. By comparing τa with τe, it is clear that circularization is expected to occur well before tidal engulfment, thus we should expect to find two different populations of short-period planets around first ascending RGB stars, those in which the host star is close to the base of the RGB, and so have retained their primordial eccentricity, and those that are located around more evolved stars that are expected to have nearly circular orbits. The discovery of new planets like the one presented here will allow us to confirm this prediction, while at the same time we can use them to calibrate the tidal efficiencies in fully convective RGB stars. Unfortunately, detecting transiting planets around more evolved stars whose radii are significantly larger is still very challenging due to the reduced transit depth and longer duration of the transit.
4.3 Summary
In this paper we present the discovery of a 9.2-day orbit transiting planet around the giant star K2-132, from the high-precision photometric data taken by the K2 mission. A further spectroscopic follow-up allowed us to confirm the planetary nature of the periodic transit observed in the K2 data. Our discovery was made independently by Grunblatt et al. (2017), who announced their result as we were writing up this paper. Based on the combined photometric and RV analysis, which includes all radial velocities available including the Keck/HIRES RVs of Grunblatt et al. (2017), we derive a planetary mass of 0.50 ± 0.01MJ and an eccentricity of 0.29 ± 0.05, making K2-132 b the most eccentric planetary companion among all known short-period (P ≲ 50 days) planet orbiting giant stars. Using high-precision photometric data, we performed an asteroseismic analysis, from which we derived a stellar mass and radius of 1.19 ± 0.04 and 4.11 ± 0.05, respectively.
In addition, we put this planet into context by comparing its orbital properties to those systems that have been found around giant stars. We conclude that transiting systems like K2-132 b provide observational support for a different formation and migration scenario for planets in more massive protoplanetary disks around more massive stars. Finally, we discussed the orbital evolution (circularization and tidal decay timescales) for this system. From this analysis, we concluded that more eccentric systems like this one might be found by transit surveys around giant stars close to the base of the RGB, while a population of planets in nearly circular orbits is expected to be found around stars that are slightly more evolved than K2-132.
Acknowledgements
We thank S. Grunblatt and D. Huber for helpful feedback, in particular with respect to the estimation of stellar properties through asteroseismology. R. B., N. E., and A. J. acknowledge support from the Ministry for the Economy, Development and Tourism Programa Iniciativa Científica Milenio through grant IC 120009, awarded to the Millenium Institute of Astrophysics. A. J. acknowledges support from Fondecyt grant 1171208 and partial support by CATA-Basal (PB06, CONICYT). N. E. acknowledges support from Financiamiento Basal PFB06. J. J. acknowledges support from Fondecyt grant 1161218 and partial support from CATA-Basal (PB06, Conicyt).
References
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, COSPAR Scientific Assembly, 36, 3749 [Google Scholar]
- Bakos, G. A., Noyes, R. W., Kov?cs, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Huber, D., Stello, D., et al. 2010, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brahm, R., Jones, M. I., Espinoza, N., et al. 2016, PASP, 128, 124402 [NASA ADS] [CrossRef] [Google Scholar]
- Brahm, R., Jordán, A., & Espinoza, N. 2017a, PASP, 129, 3 [Google Scholar]
- Brahm, R., Jordán, A., Hartman, J., & Bakos, G. 2017b, MNRAS, 467, 971 [NASA ADS] [Google Scholar]
- Brown, D. J. A., Collier C. A., Anderson, D. R., et al. 2012, MNRAS, 423, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M. 2015, PASP, 127, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T. 2009, ApJ, 694, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Döllinger, M., Hatzes, A., Pasquini, L., et al. 2011, AIPC, 1331, 79 [NASA ADS] [Google Scholar]
- Espinoza, N., & Jordán, A. 2016, MNRAS, 457, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., Brahm, R., Jordán, A., et al. 2016, ApJ, 830, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., Rabus, M., Brahm, R., et al. 2017, MNRAS, 471, 4374 [NASA ADS] [CrossRef] [Google Scholar]
- Frink, S., Quirrenbach, A., Fischer, D., Röser, S., & Schilbach, E. 2001, PASP, 113, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Grunblatt, S. K., Huber, D., Gaidos, E., et al. 2016, AJ, 152, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Grunblatt, S. K., Huber, D., Gaidos, E., et al. 2017, AJ, 154, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Reffert, S., Quirrenbach, A., et al. 2006, A&A, 454, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, D., Stello, D., Bedding, T. R., et al. 2009, CoAst, 160, 74 [NASA ADS] [Google Scholar]
- Henry, G. W. Marcy, G. W., Butler, R. P., & Vogt, S. S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B., Barnes, R., Greenberg, R. 2008a, MNRAS, 391, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B., Greenberg, R., & Barnes, R. 2008b ApJ, 681, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Bowler, B. P., Howard, A. W., et al. 2010, ApJ, 721, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. I., Jenkins, J. S., Rojo, P., & Melo, C. H. F. 2011, A&A, 536, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, M. I., Jenkins, J. S., Bluhm, P., Rojo, P., & Melo, C. H. F. 2014, A&A, 566, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2009, ApJ, 695, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Kunitomo, M., Ikoma, M., Sato, B., et al. 2011, ApJ, 737, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog, VI/39 [Google Scholar]
- Lidov, M. L. 1962, Planet Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Ida, S. 1997, ApJ, 477, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 1983, A&A, 125, L12 [NASA ADS] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2016, ApJ, 818, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Agol, E., Kruse, E., et al. 2016, AJ, 152, 100 [Google Scholar]
- Marcy, G. W., & Butler, R. P., Fischer, D. A., et al. 2005, Progr. Theor. Phys. Suppl., 158, 24 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, T. 2012, ApJ, 761, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Luhman, K. L., Bricenõ, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Niedzielski, A., Nowak, G., Adamów, M., & Wolszczan, A. 2009, ApJ, 707, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J., & Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Salasnich, B., Girardi, L., Weiss, A., & Chiosi, C. 2000, A&A, 361, 1023 [NASA ADS] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2015, MNRAS, 451, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Kambe,E., Takeda, Y., et al. 2005, PASJ, 57, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Izumiura, H., Toyota, E., et al. 2008, PASJ, 60, 539 [NASA ADS] [Google Scholar]
- Schlaufman, K. C., & Winn, J. N. 2013, ApJ, 772, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Deming, D., 2010, ARA&A, 48, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Setiawan, J., Pasquini, L., da Silva, L., von der Lühe, O., & Hatzes, A. 2003, A&A, 397, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, M. G., & Jenkins, J. S. 2018, A&A, in press, DOI: 10.1051/0004-6361/201731533 [Google Scholar]
- Stello, D., Chaplin, W. J., Basu, S., et al. 2009, MNRAS, 400, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderburg, A., & Johnson, J. A. 2014, PASP, 126, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Villaver, E., & Livio, M. 2009, ApJ, 705, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fischer, D. A., Horch, E. P., & Huang, X. 2015, ApJ, 799, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Marzari, F. 1996, Nature, 384, 619 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al., 2011, ApJ, 743, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Endl, M., Wang, L., et al. 2011, ApJ, 743, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., & Mazeh, T. 2002, ApJ, 568, L113 [NASA ADS] [CrossRef] [Google Scholar]
As of June 2017; source: http://exoplanets.org
All Tables
All Figures
 |
Fig. 1 Top panel: Light curve of K2-132 (black points) along with the smoothed median filter used to model its long-term trend (orange solid line). Bottom panel: Light curve detrended of the long-term trend. The transits detected by our BLS analysis are indicated with red arrows. |
| In the text | |
 |
Fig. 2 Top panel: Phased-folded radial velocities of K2-132 obtained with HARPS (red dots), FEROS (gray dots), and Keck/HIRES (blue dots). The red line corresponds to the Keplerian model using the posterior parameters of the MCMC analysis of Sect. 3.5. Bottom panel: Residuals for the observed radial velocities. The small blue band around zero has a width equal to the fitted jitter term of 5.1 m s−1. |
| In the text | |
 |
Fig. 3 Top panel: observed radial velocities vs. bisector span measurements for HARPS (blue) and FEROS (red). Bottom panel: bootstrap distribution of the weighted Pearson correlation coefficient between radial velocities and bisector span measurements. FEROS and HARPS velocity points are consistent with no correlation. |
| In the text | |
 |
Fig. 4 Power spectral density of the K2 light curve. |
| In the text | |
 |
Fig. 5 Stellar density as a function of the stellar Teff for the Yonsei-Yale isochrones. From left to right the plotted isochrones correspond to ages of 0.1, 2, 4, 6, 8 Gyr. The blue dot corresponds to the assumed parameters of the host star. |
| In the text | |
 |
Fig. 6 Top panel: portion of the K2 photometry of the target star. The error bars correspond to the fitted value of σw using our noise model. The blue line with bands shows the posterior prediction of our GP modeling at the given times and the 2-σ credibility interval, respectively. Bottom panel: Residuals between the fitted GP and the K2 photometry. No obvious structure is observed in the residuals. |
| In the text | |
 |
Fig. 7 Power spectral density (PSD) of the light curve shown in Fig. 6 (black) along with our noise model on top (red). Our ad hoc model model captures the low-frequency (≲200 μHz) and the high-frequency components of the PSD. |
| In the text | |
 |
Fig. 8 Top panel: transits of K2-132 b (black points) along with the best-fit transit model (red solid line) and GP (blue line), along with the 3-σ credibility interval for the posterior predictive GP regression (blue bands). Middle panel: phase-folded light curve with the GP model removed (black points) along with the best-fit transit light curve model (red). Bottom panel: residuals of the phase-folded light curve after removal of the best-fit transit and GP model. |
| In the text | |
 |
Fig. 9 Semimajor axis vs. planetary mass of companions detected around giant stars. The black dots and open red circles correspond to planets detected via the RV and transit method, respectively. The blue triangle corresponds to the position of K2-132 b. The dotted line corresponds to a RV amplitude of K = 30 m s−1 for a 1.5 M⋆ star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


