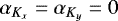| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201731204 | |
| Published online | 16 May 2018 | |
Generation and evolution of anisotropic turbulence and related energy transfer in drifting proton-alpha plasmas
Center for mathematical Plasma Astrophysics, KU Leuven,
Celestijnenlaan 200B,
3001
Leuven, Belgium
e-mail: yana.maneva@kuleuven.be, stefaan.poedts@kuleuven.be
Received:
19
May
2017
Accepted:
16
January
2018
The power spectra of magnetic field fluctuations in the solar wind typically follow a power-law dependence with respect to the observed frequencies and wave-numbers. The background magnetic field often influences the plasma properties, setting a preferential direction for plasma heating and acceleration. At the same time the evolution of the solar-wind turbulence at the ion and electron scales is influenced by the plasma properties through local micro-instabilities and wave-particle interactions. The solar-wind-plasma temperature and the solar-wind turbulence at sub- and sup-ion scales simultaneously show anisotropic features, with different components and fluctuation power in parallel with and perpendicular to the orientation of the background magnetic field. The ratio between the power of the magnetic field fluctuations in parallel and perpendicular direction at the ion scales may vary with the heliospheric distance and depends on various parameters, including the local wave properties and nonthermal plasma features, such as temperature anisotropies and relative drift speeds. In this work we have performed two-and-a-half-dimensional hybrid simulations to study the generation and evolution of anisotropic turbulence in a drifting multi-ion species plasma. We investigate the evolution of the turbulent spectral slopes along and across the background magnetic field for the cases of initially isotropic and anisotropic turbulence. Finally, we show the effect of the various turbulent spectra for the local ion heating in the solar wind.
Key words: turbulence / waves / plasmas / solar wind / acceleration of particles
© ESO 2018
1 Introduction
In-situ observations of the power spectra of magnetic fluctuations in the collisionless solar wind exhibit power-law behavior with different spectral slopes as we move from large fluid to small kinetic scales. The original theory for isotropic hydrodynamic turbulence by Kolmogorov (1941) and its extension for magnetized fluids by Iroshnikov (1963) and Kraichnan (1965) suggest that the spectral slope for a self-sustained turbulent system should take the value of −3/2 or −5/3, respectively. Derived under the assumptions of incompressible and isotropic plasma, these original fluid predictions could well explain and fit many of the observed solar-wind data within the so-called inertial range (Kiyani et al. 2015). From the inertial range, the turbulent cascade transfers the fluctuation power further towards smaller scales, where the available electromagnetic energy can be dissipated and transferred to the particles via stochastic processes, wave-particle interactions, or acceleration at small-scale current sheets. The solar corona is strongly magnetized, which leads to the formation of anisotropic temperatures with different components along and across the background magnetic field. These features can be advected or locally generated in the solar wind and frequently observed there; for example, see Maruca et al. (2012). The original Kolmogorov turbulence theory does not include the information related to anisotropic pressure tensor which naturally develops in magnetized plasmas with strong background field. The preferential direction set by the magnetic field adds an extra layer of complexity, especially when compressibility and multiple species are considered. The first attempt of including the effects of anisotropic pressure as presented by Chew et al. (1956) has lead to the further development of various anisotropic turbulence theories; see, for example, Goldreich & Sridhar (1997); Schekochihin et al. (2009); Passot et al. (2012). Including all the relevant factors which influence the evolution of a turbulent system is a rather challenging task, requiring the combined efforts of analytical and numerical modeling, together with detailed analysis of observational data. Observations of the magnetic power spectra at the dissipation scales in the solar wind suggest a power-law scaling with a highly variable spectral index, which can take values between −2 and −4.2 (e.g., Leamon et al. 1998, 1999; Smith et al. 2006; Sahraoui et al. 2009; Chen et al. 2010; Alexandrova et al. 2012; Lion et al. 2016). Combining observations from the sub-ion to the smallest electron dissipation scales initiated the concept of a converging spectral index of −2.8 in the dissipation range (Kiyani et al. 2009; Alexandrova et al. 2009; Sahraoui et al. 2010). Simultaneously, several teams pursued the possibility of a “universal” power-law scaling with spectral slope of −8/3, which is further exponentially damped at the sub-electron scales (Alexandrova et al. 2012, 2013). Still, the precise values of the spectral indices at the ion and electron scales and their scale-dependence in the solar wind are the subject of further investigations. In-situ measurements from various solar-wind spacecraft also indicate the presence of anisotropic turbulence with different spectral slopes of the magnetic-field power spectra in parallel with and perpendicular to the orientation of the background magnetic field (Leamon et al. 1998; Sahraoui et al. 2010; Wicks et al. 2010, 2011; Chen et al. 2010, 2012; Kiyani et al. 2013). In addition, both the parallel and the perpendicular energy spectra steepen as we reach the dissipation range and we observe multiple spectral breaks from the injection range towards the ion and electron scales (Sahraoui et al. 2009, 2010; Alexandrova et al. 2009; Alexandrova et al. 2013; Bruno & Carbone 2013; Bruno & Telloni 2015). The turbulent dissipation at the sub-ion scales is believed to add to local ion heating and acceleration, so that the spectral breaks are typically associated with particle energization. This gained energy can be in the form of anisotropic heating, formation of nonthermal features in the particle velocity distributions functions, and preferential and differential acceleration between the different ion populations; see, for example, Passot et al. (2014); Franci et al. (2015b); Servidio et al. (2015); Maneva et al. (2015b, 2016c); Valentini et al. (2016). Similar to observational data, existing analytical and numerical models of the turbulent cascade from the large MHD scales down to the small ion and electron dissipation scales in the solar wind also predict the steepening of the spectral slopes with various spectral brakes; for example, see Howes et al. (2008, 2011); Wan et al. (2012, 2015); Servidio et al. (2015); Ofman et al. (2014); Franci et al. (2015b); Valentini et al. (2016). Nevertheless, the exact nature of the spectral breaks, the generation of anisotropic turbulence with different fluctuation power along and across the background magnetic field, and the related conversion of the available electromagnetic energy to kinetic and thermal energy, as well as the energy distribution among the different particle species, are tedious problems requiring multiple complementary studies to gain a better understanding. To study the relation between the evolution of the anisotropic turbulent spectra and the particle heating at the ion and sub-ion scales we perform a series of two-and-a-half-dimensional (2.5D) hybrid simulations in a drifting proton-α plasma. Within the hybrid approach we neglect the fast electron dynamics and treat the electrons as an isothermal fluid, whereas the protons and the minor ion population are evolved in a fully kinetic manner. Previous hybrid-PIC (particle-in-cell) and full PIC simulation studies have investigated the behavior of the fluctuation spectra in the inertial and dissipation ranges in an electron–proton plasma (Franci et al. 2015a,b; Hellinger et al. 2015; Wan et al. 2015). The influence of solar-wind turbulence on the behavior of minor ions was previously studied by, for example, Hellinger et al. (2005); Hellinger & Trávníček (2006, 2013); Maneva et al. (2013b, 2014, 2015a,b); Ofman et al. (2014) within a hybrid-PIC approach and by Perrone et al. (2013); Servidio et al. (2015); Valentini et al. (2016) within a hybrid-Vlasov simulation setup. These studies looked into various aspects of minor ion evolution in the presence of waves, instabilities, and current sheets, including the effects of the solar-wind expansion.
Maneva et al. (2015a) performed 2.5D hybrid numerical simulations to study the effect of the solar-wind expansion on the preferential heating and acceleration of minor ions in the solar wind. The authors provided evidence that local short-scale wave-particle interactions can overcome the expected perpendicular cooling related to the large-scale solar-wind expansion and consequently slow down the generation of firehose-unstable populations. Similar results were previously found by Maneva et al. (2013b) who studied the fluctuation power transfer from parallel to oblique wave numbers and demonstrated the generation of oblique fluctuations. The paper showed that the differential streaming between the protons and the minor ions can play an important role in the re-distribution of the wave power from parallel to perpendicular scales. Maneva et al. (2015b) introduced a data-based solar-wind modeling for which the initial conditions for the numerical simulations were partially provided by Wind spacecraft data. The proton and electron densities, temperatures, anisotropies and plasma beta were taken from a specific solar-wind interval. The magnetic field fluctuations and their spectral slope were also provided by observations. Based on these, Maneva et al. (2015b) followed the procedure given in Viñas et al. (2014) in order to generate initial magnetic-field and velocity fluctuations corresponding to Alfvénic fluctuations with different angles of propagation from 0° until 60°. The initial fluctuations had anisotropic spectra with steeper spectral slopes in parallel direction. The study focused on the evolution of the ion bulk properties and the ion velocity distribution functions and investigated the generated wave types and their dispersion at the final stage of the simulations. In the present paper we focus on the spectral properties of the magnetic fluctuations and their nonlinear evolution. We have introduced the comparison between initially anisotropic fluctuations with different indices in parallel and perpendicular direction and isotropic spectra with equal flat spectral slopes at the beginning. To better understand the scale-dependence of the nonlinear evolution and the turbulent cascade, the initial isotropic spectra are shifted towards larger scales. Finally we have included the case of highly oblique wave propagation at θ ≈ 80°, which was not considered before.
The goal of this paper is to extend our previous works on 2.5D hybrid simulations of parallel and oblique wave propagation in a multi-ion-species plasma as presented in Maneva et al. (2015a,b). Here we study the evolution of the magnetic power spectra, the bulk particle response, and the electromagnetic energy cascade with anisotropic energy transfer between the parallel and perpendicular scales in the presence of a drifting proton-α population in a β < 1 collisionless solar-wind plasma. We investigate the development and evolution of anisotropic spectral indices with different values along and across the background magnetic field. Simultaneously we examine the dependence of the spectral slopes on the direction and the scales at which the energy is initially deposited.
The paper is organized as follows: Sect. 2 describes the initial conditions and provides the model setup, Sect. 3 presents the model results, and, finally, Sect. 4 provides a summary of the main findings, discusses the applications, and ends with concluding remarks.
2 Model setup
The current model is based on 2.5D hybrid simulations with isothermal massless fluid electrons and two kinetic ion species – protons and α particles. The model has been previously used to study the effects of minor ions such as α particles and oxygen 5+ and the related wave-particle interactions in decaying monochromatic waves and broad-band spectra in homogeneous collisionless plasmas (Maneva et al. 2013a,b, 2015a,b, 2016c), or the effects of a gradual solar-wind expansion for the evolution of two-stream instability in a multi-ion component plasma (Maneva et al. 2016b). The model neglects the effects of the electron inertia and is best suited for plasma dynamics at sub-ion and ion scales. Respectively, we are looking at fluctuation power and wave propagation at frequencies below the electron-cyclotron frequency. The model neglects the electron kinetic properties, such as the presence of strahl and temperature anisotropies, and is limited to moderate plasma conditions for which the electron and ion scales are well-separated. If the electrons are prone to strong kinetic instabilities which manifest themselves at the ion scales, such separation is no longer possible; see Maneva et al. (2016a) for an example.
The model setup is based on initially isotropic drifting Maxwellian velocity distributions initialized with equal temperatures 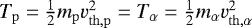 . The relative drift speed between the two ion species is fixed to V αp = 0.44V A and the plasma beta for all simulation cases is set to βp = βα = 0.33, where
. The relative drift speed between the two ion species is fixed to V αp = 0.44V A and the plasma beta for all simulation cases is set to βp = βα = 0.33, where 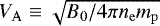 is the Alfvén speed, B0 is the magnitude of the background magnetic field, ne is the electron density, mp is the proton mass and
is the Alfvén speed, B0 is the magnitude of the background magnetic field, ne is the electron density, mp is the proton mass and 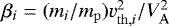 . These initialparameters represent a subset of the in situ observed, undisturbed, fast solar-wind conditions as described in Maneva et al. (2015b).
. These initialparameters represent a subset of the in situ observed, undisturbed, fast solar-wind conditions as described in Maneva et al. (2015b).
Figure 7 presents similar 2D plots to the ones shown on Fig. 6 with the temporal evolution of the parallel magnetic field normalized to the background value. The simulation setup corresponds to the case of initially isotropic flat spectra at θ ≤ 30° and θ ≤ 60° imposed at slightly larger scales as presented on Fig. 2. The magnetic field at the final stage of the fluctuations is less structured than in the case of smaller scale fluctuations presented on Fig. 6. The reason for this is presumably the fact that at larger scales it takes a longer time for the turbulence to develop. We should also note that the damping rate of the two-stream instability-driven waves is smaller at larger scales, hence we could expect a higher level of fluctuations in this case. The evolved fields are shown at the end of the simulations at Ω p t = 800.
All variables throughout this paper are normalized to the proton cyclotron frequency Ω p and the Alfvén speed V A as defined above. The wave-numbers are expressed in units of inverse proton inertial length di. The size of the simulation box is the same in both spatial directions, Lx = Ly = 384di, with the same spatial resolution dx = dy = 1.5di and number of grid points nx = ny = 256. The time step chosen for the simulations is a tiny fraction of the proton cyclotron frequency 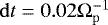 .
.
We should note that the selected value of the relative drift speed can be considered as stable with respect to linear multi-fluid and kinetic Alfvén/magnetosonic instabilities for parallel wave propagation. The initial spectrum is damped when oblique wave propagation in a finite-temperature warm-plasma Vlasov theory is taken into account. In this sense, from the point of view of linear kinetic instability theory the imposed wave spectra are expected to damp and transfer their energy to the particles, while the relative drift speed is expected to remain unchanged. Below we will see that nonlinear effects can make the initial drift unstable as discussed in the results in Sect. 3. Note that the initial state might be unstable from the point of view of quasi-linear parametric instabilities as observed in previous simulation works; see for example Fig. 9 from Maneva et al. (2014).
Apart from the differential streaming, the other energy source in the system is a broad-band spectrum of Alfvénic fluctuations.The input fluctuations for all simulation cases are initialized with a total amplitude which amounts to 20% of the background magnetic field, δBtot = 0.2B0. To model the initial fluctuations we perform Vlasov linear instability analysis and calculate the magnetic field and velocity fluctuations,corresponding to parallel propagating dispersive Alfvén waves. The reconstruction of the magnetic field follows the approach given in Viñas et al. (2014) and the oblique spectra have been generated by rotation of the parallel fluctuations at various angles as described in Maneva et al. (2015b). This is performed to adopt the magnetic field reconstruction scheme, which is currently developed for strictly parallel wave propagation.
The resulting various broad-band spectra used for the simulations are represented in Figs. 1 and 2. The initial states correspond to various propagation angles and the initial spectra are shifted in wave-number space. We consider two types of initial setups. Figure 1 represents the case of initially anisotropic turbulence with different spectral slopes along the magnetic field 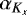 and in perpendicular direction
and in perpendicular direction 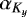 . For the anisotropic turbulent states we have fixed the parallel spectral index to resemble the observed values within the inertial range,
. For the anisotropic turbulent states we have fixed the parallel spectral index to resemble the observed values within the inertial range, 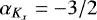 , and assumed a flat spectra in perpendicular direction
, and assumed a flat spectra in perpendicular direction 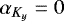 . The second group of simulation setups is based on isotropic spectral slopes and slightly larger scale fluctuations. For the isotropic case studies we have used flat spectra in both parallel and perpendicular directions. The fluctuation power for these cases has been shifted to smaller wave-numbers. For more information on the initial parameters confer with Table 1. To limit the influence of resonant interactions on the observed plasma heating, all input fluctuation spectra are chosen below the ion inertial length for the α particles. Unlike other previous turbulence studies, for example, Perrone et al. (2013); Franci et al. (2015a,b); Hellinger et al. (2015), our physical setup is based on in-plane configuration for which the background magnetic field and the velocity fluctuations are initialized within the same plane. Figure 1 describes the initial power spectral density for magnetic field fluctuations for the case of anisotropic spectral slopes. The same type of spectra was previously used in Maneva et al. (2015b) to study the preferential heating of α particles. In this study we focus on the spectral properties of the fluctuations and their turbulent evolution. The three different spectra correspond to various angles of propagation, starting with parallel propagating waves and increasing the propagation angle to 30° and 60°. Although below the ion inertial length for the minor ions, the spectra are within the dispersive range, where weak turbulence behavior is expected. Figure 2 shows the initial magnetic field power spectral density for the case of isotropic slopes with equal flat spectra in parallel and perpendicular direction. The spectra have also been shifted towards larger scales and enter a regime where strong turbulence could be expected. The different spectra correspond to parallel and oblique propagation up to 80°. In the next section we follow the evolution of the spectral slopes corresponding to these two types of initial spectra (anisotropic and isotropic) and study the dynamical interactions in relation to the different turbulence regimes. Simultaneously we investigate the evolution of the bulk plasma properties, such as the relative drift speed, the temperatures, and the related temperature anisotropies.
. The second group of simulation setups is based on isotropic spectral slopes and slightly larger scale fluctuations. For the isotropic case studies we have used flat spectra in both parallel and perpendicular directions. The fluctuation power for these cases has been shifted to smaller wave-numbers. For more information on the initial parameters confer with Table 1. To limit the influence of resonant interactions on the observed plasma heating, all input fluctuation spectra are chosen below the ion inertial length for the α particles. Unlike other previous turbulence studies, for example, Perrone et al. (2013); Franci et al. (2015a,b); Hellinger et al. (2015), our physical setup is based on in-plane configuration for which the background magnetic field and the velocity fluctuations are initialized within the same plane. Figure 1 describes the initial power spectral density for magnetic field fluctuations for the case of anisotropic spectral slopes. The same type of spectra was previously used in Maneva et al. (2015b) to study the preferential heating of α particles. In this study we focus on the spectral properties of the fluctuations and their turbulent evolution. The three different spectra correspond to various angles of propagation, starting with parallel propagating waves and increasing the propagation angle to 30° and 60°. Although below the ion inertial length for the minor ions, the spectra are within the dispersive range, where weak turbulence behavior is expected. Figure 2 shows the initial magnetic field power spectral density for the case of isotropic slopes with equal flat spectra in parallel and perpendicular direction. The spectra have also been shifted towards larger scales and enter a regime where strong turbulence could be expected. The different spectra correspond to parallel and oblique propagation up to 80°. In the next section we follow the evolution of the spectral slopes corresponding to these two types of initial spectra (anisotropic and isotropic) and study the dynamical interactions in relation to the different turbulence regimes. Simultaneously we investigate the evolution of the bulk plasma properties, such as the relative drift speed, the temperatures, and the related temperature anisotropies.
 |
Fig. 1 Initial two-dimensional (2D) PSD of the magnetic field fluctuations in Fourier space with anisotropic spectral slopes in Kx and Ky. The simulation setup is the same as in Fig. 3. From left to right the plots correspond to parallel and oblique wave propagation at θ = 0°, θ ≤ 30° and θ ≤ 60°. |
 |
Fig. 2 Initial 2D PSD of the magnetic field fluctuations in Fourier space corresponding to various propagation angles with initially isotropic spectral slopes in Kx and Ky. The simulation setup corresponds to Fig. 4. From left to right the plots represent propagation at θ = 0°, θ ≤ 30°, θ ≤ 60° and θ ≤ 80°. |
 |
Fig. 3 One-dimensional plots of the initial and evolved power spectra of the magnetic field fluctuations as a function of parallel Kx di and perpendicular Kydi normalized wave numbers as a function of the propagation angle. From left to right the plots correspond to parallel θ = 0°, quasi-parallel θ ≤ 30°, and highly oblique propagation at θ ≤ 60°. All cases are initialized with anisotropic spectral slope with different values along Kx and Ky; see Table 1. |
Parameter values for the simulations.
3 Simulated spectral slopes and related ion response
The initial fluctuation power spectra described in the previous section are imposed as initial conditions for the magnetic field and the velocity fluctuations. Once imposed, the various spectra decay and evolve differently acquiring diverse final spectral slopes. All simulations are performed until Ω p t = 800, except for the case of θ ≈ 80°, where the system was evolved until Ω p t = 1600. All wave-numbers are normalized to the inverse proton inertial length 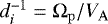 . For the given spatial resolution and the size of the box the available range of wave-numbers in each direction is Kdi = [0.016, 4.18]. Due to the limitations of the hybrid approach and the sub-proton physics considered here in all plots below we have limited the maximum wave-number range to a single proton inertial length. In this respect the system allows for nonlinear interactions at smaller scales, but such interactions do not occur for the selected low-frequency initial spectra considered here.
. For the given spatial resolution and the size of the box the available range of wave-numbers in each direction is Kdi = [0.016, 4.18]. Due to the limitations of the hybrid approach and the sub-proton physics considered here in all plots below we have limited the maximum wave-number range to a single proton inertial length. In this respect the system allows for nonlinear interactions at smaller scales, but such interactions do not occur for the selected low-frequency initial spectra considered here.
Figure 3 describes the initial (top panels) and late-stage evolution (bottom panels) of the parallel 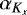 and perpendicular
and perpendicular 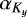 components of the magnetic-field-power spectral slopes. The figure corresponds to the case of initially anisotropic turbulence with fluctuations in the range of dispersive wave-numbers; see Table 1. To compute the one dimensional (1D) evolution of the parallel and perpendicular spectral slopes shown in Figs. 3 and 4 we averaged the 2D magnetic field fluctuations in the perpendicular and parallel directions, respectively. In this respect our notations
components of the magnetic-field-power spectral slopes. The figure corresponds to the case of initially anisotropic turbulence with fluctuations in the range of dispersive wave-numbers; see Table 1. To compute the one dimensional (1D) evolution of the parallel and perpendicular spectral slopes shown in Figs. 3 and 4 we averaged the 2D magnetic field fluctuations in the perpendicular and parallel directions, respectively. In this respect our notations 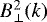 and
and 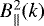 refer to B2 (k) averaged over kx or ky, respectively. Within our notations
refer to B2 (k) averaged over kx or ky, respectively. Within our notations 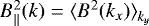 and
and 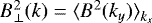 . It is important to note that the components of the averaged magnetic-field power spectra as defined by these notations differ from the actual power of the individual parallel and perpendicular magnetic field components. In this sense the plots should be seen as an averaged 1D magnetic-field power spectra. The figure shows the steepening of the initial spectral slopes related to the evolution and dissipation of the initial broad band spectra. For the case of strictly parallel propagating waves within a very short time, Ω p t < 100, the initial spectral slope steepens from
. It is important to note that the components of the averaged magnetic-field power spectra as defined by these notations differ from the actual power of the individual parallel and perpendicular magnetic field components. In this sense the plots should be seen as an averaged 1D magnetic-field power spectra. The figure shows the steepening of the initial spectral slopes related to the evolution and dissipation of the initial broad band spectra. For the case of strictly parallel propagating waves within a very short time, Ω p t < 100, the initial spectral slope steepens from 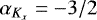 to
to 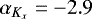 . This case is prone to parametric processes with dynamic wave–wave transfer. In this sense the turbulence is not fully developed and the spectral slopes undergo various changes towards the end of the simulation at Ω p t = 800. After a few hundred gyro periods the averaged magnetic spectra in parallel direction exhibit a combination of several pronounced peaks with no distinct spectral slope and at the end of the simulation the peak of the fluctuation power is concentrated at larger scales than the initially imposed spectra. In the case of oblique wave propagation at θ ≈ 30° the parametric instabilities are suppressed and the fluctuation power remains within the initially imposed spectral range (see the second panels at the top and bottom). Although the fluctuations evolve differently, the spectral slope at the end of the simulation looks similar to the early stage of the evolution in the case of parallel propagation. This means that the oblique spectral slopes at a certain time of their evolution resemble the spectral slopes of the initially strictly parallel propagating waves at early times. Thus if we compare the spectral slopes for the parallel propagating waves at an early time, Ω p t ≤ 120, and the quasi-parallel case of θ ≈ 30° at a later time, Ω p t = 800, the spectra show similar spectral slopes of
. This case is prone to parametric processes with dynamic wave–wave transfer. In this sense the turbulence is not fully developed and the spectral slopes undergo various changes towards the end of the simulation at Ω p t = 800. After a few hundred gyro periods the averaged magnetic spectra in parallel direction exhibit a combination of several pronounced peaks with no distinct spectral slope and at the end of the simulation the peak of the fluctuation power is concentrated at larger scales than the initially imposed spectra. In the case of oblique wave propagation at θ ≈ 30° the parametric instabilities are suppressed and the fluctuation power remains within the initially imposed spectral range (see the second panels at the top and bottom). Although the fluctuations evolve differently, the spectral slope at the end of the simulation looks similar to the early stage of the evolution in the case of parallel propagation. This means that the oblique spectral slopes at a certain time of their evolution resemble the spectral slopes of the initially strictly parallel propagating waves at early times. Thus if we compare the spectral slopes for the parallel propagating waves at an early time, Ω p t ≤ 120, and the quasi-parallel case of θ ≈ 30° at a later time, Ω p t = 800, the spectra show similar spectral slopes of 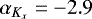 ; see Table 1. We should note that in the case of parallel propagating waves the fluctuation power cascades towards higher wave-numbers, which is not observed in the quasi-parallel case for angles θ ≤ 60°. Neither case, θ = 0° or θ ≈ 30°, shows significant evolution of the power spectra in perpendicular direction, hence it is not shown on the figure. On the contrary, in the case of θ ≤ 60°, both the parallel and the perpendicular spectral slopes evolve and steepen. Once again the fluctuation power remains mainly within the initially imposed spectral range, although we observe the onset of direct cascade towards smaller scales in the perpendicular direction. The spectral slopes in parallel direction steepen slightly less than in the previous cases of smaller propagation angles
; see Table 1. We should note that in the case of parallel propagating waves the fluctuation power cascades towards higher wave-numbers, which is not observed in the quasi-parallel case for angles θ ≤ 60°. Neither case, θ = 0° or θ ≈ 30°, shows significant evolution of the power spectra in perpendicular direction, hence it is not shown on the figure. On the contrary, in the case of θ ≤ 60°, both the parallel and the perpendicular spectral slopes evolve and steepen. Once again the fluctuation power remains mainly within the initially imposed spectral range, although we observe the onset of direct cascade towards smaller scales in the perpendicular direction. The spectral slopes in parallel direction steepen slightly less than in the previous cases of smaller propagation angles  . In the perpendicular direction the spectral slope of the averaged magnetic-field power spectra obtains the expected values for Iroshnikov-Kraichnan turbulence
. In the perpendicular direction the spectral slope of the averaged magnetic-field power spectra obtains the expected values for Iroshnikov-Kraichnan turbulence 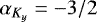 .
.
Similar to Fig. 3, Fig. 4 shows the evolution of the 1D magnetic-field power spectra this time for the case of initially isotropic spectral slopes and larger-scale fluctuations. The initial spectra for all fluctuations are flat for all simulated propagation angles and are plotted in the top panel. The bottom panel depicts the evolved spectra. For clarity, the various propagation angles and different simulation times are included in the plots. The left panels describe strictly parallel-propagating spectra at θ = 0°. One can see that the parallel spectra decreases at a similar rate with respect to the previous case of imposed anisotropic spectral slopes (see the left panels of Fig. 3). For these cases the difference between the evolved and the initial parallel spectral slopes looks similar, 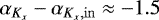 at Ωpt = 120. Nevertheless, the plot suggests that defining a distinct spectral slope for the case of flat isotropic spectra at larger scales is even more difficult than in the case of anisotropic fluctuations. Additionally the fluctuations in the isotropic case are imposed at larger scales, which impedes the direct cascade. This suggests that the cascade processes operate differently at larger and smaller scales. Another difference between the two conditions of parallel propagating waves with isotropic and anisotropic spectral slopes at larger and smaller scales respectively, is that in the case of isotropic fluctuations at larger scales, the direct cascade operates slower and does not transfer wave energy to the smaller sub-proton scales. Once again parametric processes are expected to operate in this case and the final spectrum at the end of the simulations at Ω p t = 800 consists of individual peaks and retains a shallower slope with
at Ωpt = 120. Nevertheless, the plot suggests that defining a distinct spectral slope for the case of flat isotropic spectra at larger scales is even more difficult than in the case of anisotropic fluctuations. Additionally the fluctuations in the isotropic case are imposed at larger scales, which impedes the direct cascade. This suggests that the cascade processes operate differently at larger and smaller scales. Another difference between the two conditions of parallel propagating waves with isotropic and anisotropic spectral slopes at larger and smaller scales respectively, is that in the case of isotropic fluctuations at larger scales, the direct cascade operates slower and does not transfer wave energy to the smaller sub-proton scales. Once again parametric processes are expected to operate in this case and the final spectrum at the end of the simulations at Ω p t = 800 consists of individual peaks and retains a shallower slope with 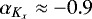 . The available fluctuation power is also shifted towards larger scales and the initially imposed power above Ky di = 0.2 is well depleted. We should note that the parallel cascade in the case of θ = 0° is partially reversible as the spectra is dominated by individual peaks. At a later stage the parallel spectra goes through inverse cascade, so that at Ω p t = 800 the parallel fluctuations are confined approximately within the range of kx ∈ [0.08, 0.45]. This inverse cascade at a later stage is probably due to a decay instability, which brings wave power at wave-numbers lower than the initially imposed ones. Such processes are not so prominent in the quasi-parallel case with θ = 30°, where the fluctuations remain within the initially imposed spectral range.
. The available fluctuation power is also shifted towards larger scales and the initially imposed power above Ky di = 0.2 is well depleted. We should note that the parallel cascade in the case of θ = 0° is partially reversible as the spectra is dominated by individual peaks. At a later stage the parallel spectra goes through inverse cascade, so that at Ω p t = 800 the parallel fluctuations are confined approximately within the range of kx ∈ [0.08, 0.45]. This inverse cascade at a later stage is probably due to a decay instability, which brings wave power at wave-numbers lower than the initially imposed ones. Such processes are not so prominent in the quasi-parallel case with θ = 30°, where the fluctuations remain within the initially imposed spectral range.
The second panel at the bottom on Fig. 4 describes the evolved averaged 1D magnetic spectra in the parallel direction for wave propagation at θ ≤ 30°. Unlike the case of parallel wave propagation, there is no clear signature for parametric processes in the parallel direction and the magnetic spectrum evolves smoothly reaching a parallel spectral slope of 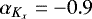 . There is some transfer of fluctuation power with direct cascade towards smaller scales in the perpendicular direction. Yet, the initial spectral slope imposed in the perpendicular direction does not change significantly and the spectrum remains flat with
. There is some transfer of fluctuation power with direct cascade towards smaller scales in the perpendicular direction. Yet, the initial spectral slope imposed in the perpendicular direction does not change significantly and the spectrum remains flat with 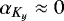 . Since the spectrum remains flat we have chosen not to include it in the plots.
. Since the spectrum remains flat we have chosen not to include it in the plots.
The last two panels of Fig. 4 illustrate the evolution of the averaged power spectra for the case of oblique wave propagation at θ ≤ 60°. In this case the magnetic spectrum shows similar evolution in parallel and perpendicular direction with rather shallow isotropic slopes 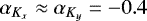 . We observe some cascade towards smaller scales in the perpendicular direction with the formation of different spectral slope there. The turbulence is still not well-developed at the final stage of the simulations at Ω p t = 800 and it is expected that at a later time the two spectra would further evolve possibly merging into a single power law. Figure 5 shows the case of initially isotropic flat spectra for highly oblique propagation at θ ≈ 80°. The magnetic field power remains almost flat in parallel direction with
. We observe some cascade towards smaller scales in the perpendicular direction with the formation of different spectral slope there. The turbulence is still not well-developed at the final stage of the simulations at Ω p t = 800 and it is expected that at a later time the two spectra would further evolve possibly merging into a single power law. Figure 5 shows the case of initially isotropic flat spectra for highly oblique propagation at θ ≈ 80°. The magnetic field power remains almost flat in parallel direction with  towards the end of the simulations at Ωpt = 800. In the perpendicular direction the power spectra forms a break close to the upper range of the initially imposed perpendicular wave-numbers and develops two distinct spectral slopes with
towards the end of the simulations at Ωpt = 800. In the perpendicular direction the power spectra forms a break close to the upper range of the initially imposed perpendicular wave-numbers and develops two distinct spectral slopes with  at large scales and
at large scales and  at small scales beyond the ion inertial length for the alpha particles Ky dα = 0.5. Similar to the case of isotropic fluctuations at θ ≤ 60° described above, the turbulence is not well-developed within the simulation time of Ω p t = 800.
at small scales beyond the ion inertial length for the alpha particles Ky dα = 0.5. Similar to the case of isotropic fluctuations at θ ≤ 60° described above, the turbulence is not well-developed within the simulation time of Ω p t = 800.
We should note that, depending on the simulation setup, the turbulent spectra discussed throughout this paper might not necessarily represent a state of fully developed turbulence. Fully developed turbulence in the solar wind is usually referred to in the context of strong turbulence studies, for which the nonlinear interactions are carried out by vortexes and structures that develop predominantly in the perpendicular plane (transverse to the background magnetic field). To study the evolution of strong turbulence within a 2.5D setup, one would require an out-of-plane background magnetic-field configuration. Such studies have previously been performed (see, e.g., Perrone et al. 2013; Valentini et al. 2016; Franci et al. 2015a,b), revealing relatively quick formation of the developed turbulence within one or two hundred proton gyro-periods. Within our study, on the other hand, we consider an in-plane magnetic-field geometry, which can reveal the evolution and the possible nonlinear interactions in the perpendicular-parallel plane. The scope of this paper is to study the system evolution in the case of weak turbulence, where the nonlinear interactions are carried out predominantly by waves. Furthermore it is interesting to follow the evolution of the spectra as we transition from strictly parallel towards highly oblique angles of propagation.
Figure 6 presents 2D plots with the evolution of the spatial distribution of the parallel component of the magnetic field for the cases of oblique wave propagation at θ ≤ 30° and θ ≤ 60°. The upper panels show the initial conditions and the bottom panels show the evolved states at the end of the simulations at Ω p t = 800. The simulation setup corresponds to the case of initially anisotropic spectral slopes at smaller scales as presented on Fig. 1. The magnetic fluctuations at the final stage exhibit structured features, typical for the saturation stage of plasma instabilities; in this case the Alfvén-magnetosonic two-stream instability driven by the relative drift speed.
Figure 8 shows the temporal evolution of the 2D magnetic field spectra for the same case as described inFigs. 1 and 6. The plot shows the evolution at different times, Ω p t = 10, 150, 400, and 800, increasing from left to right starting from the upper left panel towards the lower right panel. As visible from the plots, the case of θ ≤ 60° anisotropic fluctuations imposed at the dispersive scales is prone to parametric instabilities and three wave couplings. Within several proton gyro-periods, Ωpt = 10, we observe strong beating with the generation of oblique modes at higher wave-numbers than the original spectrum with Ky di ∈ [0.6–0.8] and extended parallel wave-numbers from Kxdi ∈ [0.3, 0.45]. At a later stage the nonlinearly generated fluctuations at higher Kx di and Ky di are dissipated, and the magnetic power is concentrated at lower Kxdi, at or below the range of the original spectrum. Simultaneously, the spectrum expands in Ky di with both direct and inverse cascades generating more power in oblique direction.
Figure 9 presents the temporal evolution of the normalized 2D magnetic field spectra for the case of isotropic fluctuations at θ≤ 60°. The initial spectrum is the same as the one presented in Figs. 1 and 7. Unlike the previous evolution of the spectrum described in Fig. 8, here we do not observe evidence for beating or three wave interactions, mainly due to the fact that the fluctuations are imposed at larger scales. The fluctuations instead show a direct cascade and evolve towards higher perpendicular wave-numbers before being dissipated by the particles.
Figure 10 complements the magnetic spectra evolution presented above. The figure illustrates the final state of the magnetic field spectra at the end of the simulations at Ω p t = 800. From left to right we have the cases of θ = 0° and θ = 30° in the upper panel and the cases of θ = 60° and θ = 80° in the lower panel. The evolved spectra correspond to the initially isotropic cases presented in Fig. 2. The plot illustrates that the parallel spectrum remains predominantly parallel, while in the case of θ = 30° the oblique spectrum quickly evolves towards isotropic turbulence with similar fluctuation power in parallel and perpendicular directions. At higher propagation angles, a direct cascade operates primarily in the perpendicular direction, bringing energy to higher wave-numbers and reaching the proton gyration scales in the case of θ = 80°.
In an attempt to understand the evolution of the imposed spectra we performed linear instability analysis for the different angles of propagation. Figure 11 shows the linear dispersion relation for the simulated isotropic drifting proton-α plasma. Thereal frequency is drawn on the left panel and the predicted damping rates are presented in the right-hand panel. For the purpose of the this study we are interested in the evolution of the Alfvénic fluctuations since together with the relative drift speed the Alfvén waves represent the primary energy source in our model. Focusing on the Alfvén modes we have plotted their predicted damping rates and have left out the other solutions from the dispersion plots, such as slow waves, proton-cyclotron waves, fast modes, and so on. In general, the Alfvén wave phase speed decreases as the waves transition from Alfvén ion-cyclotron at parallel propagation to kinetic Alfvén waves (KAWs) at highly oblique angles (see the left panel). As a general trend we observe stronger damping rate as we progress from larger to smaller scales. This holds true for the individual angles of propagation. Yet we can see that for the selected spectral range of the initial fluctuations in our study the fluctuations at θ = 60° are expected to damp quicker than the cases of θ = 30° and θ = 80°, which is in partial agreement with the evolution of the 2D spectra described in Fig. 10. Nevertheless, the linear damping rate cannot be directly correlated with the steeping of the spectral slopes, which suggests that nonlinear processes influence the evolution of the system.
As discussed in the model setup introduced in Sect. 2, apart from the initial fluctuation spectra there is an additional energy source in the system in the form of relative drift speed between the protons and the α particles. The relative drift is stable for the case of large-scale parallel fluctuations with zero imaginary part of the frequency. Furthermore the relative drift is not expected to drive magnetosonic or Alfvén instability even when oblique propagation is considered. Instead, in the case of oblique propagation, the Alfvén modes are essentially damped at all scales, as discussed above. Nevertheless, as the system evolves, the initial relative drift speed decreases and the α particles are being decelerated. The evolution of the relative drift speed and the ion temperature anisotropies is presented in Fig. 12. The relative speed between the two species monotonously decreases and does not reach saturation within the simulation time for all propagation angles considered here. The decrease is probably a nonlinear effect of destabilization of the two-stream instability in the presence of the imposed broad-band spectra. It is interesting to note that the relative drift is most unstable for the case of θ ≤ 60°. For this initial spectrum the relative drift at the end of the simulation reduces with more than 50%. The initial apparent anisotropies for the protons and the α particles are due to the bulk velocity fluctuations related to the initial wave spectra. The temperature anisotropy here is defined as T⊥∕T∥ and the apparent anisotropies for both species depend on the angle of propagation. For strictly parallel propagation, the broad-band spectrum of Alfvénic fluctuations induces strictly perpendicular bulk velocity fluctuations with random phases and varying amplitudes, which lead to an apparent increase in the perpendicular temperature for the ions and hence generate an apparent anisotropy. As we move towards oblique wave propagation the initial spectrum introduces both perpendicular and parallel components in the bulk velocity. In the case of highly oblique propagation at θ = 80° the induced fluctuations for the protons are predominantly in parallel direction, which leads to an inverse apparent anisotropy with T⊥ ∕T∥ < 1. Similar to the relative drift speed the temperature anisotropy for the protons also decreases throughout the simulation time. The temperature anisotropy of the α particles on the other hand passes through several different stages. In the case of θ ≤ 30° the anisotropy decreases until Ωpt ≈ 350 after which it saturates. Similar behavior with saturation at slightly later time is observed for the case of θ ≤ 80°. The intermediate case of θ ≤ 60° does not fully saturate within the simulated time, as the anisotropy towards the end of the simulations starts to increase.
Figure 13 tackles the details of the evolution of the temperature anisotropy and presents the related response of the individual parallel and perpendicular components of the ion temperatures. The proton temperatures are plotted in the top row, while the temperature components for the α particles are presented at the bottom. The propagation angle is varied from left to right for the same cases shown in the temperature anisotropy plots above. Initially the two ion species have the same temperature and in the course of evolution the α particles are preferentially heated and can become more than twice hotter than the protons. The perpendicular temperature component for the protons monotonously decreases for all cases, which determines the reduction of their temperature anisotropy. The extent of the anisotropy is mainly determined by the extent of the parallel proton heating and the value of the apparent temperatures induced by the initial spectra. The strongest parallel proton heating appears for the case of θ ≤ 30° and θ ≤ 60°, while in the case of θ ≈ 80° we observe strongest apparent parallel temperature for the protons. The strongest parallel heating for the α particles is observed for θ ≤ 60° where the αs are most efficiently decelerated, while the strongest perpendicular heating is in the case of θ ≈ 80°, where the initial spectrum has cascaded towards the smaller sub-proton sup-α scales; see Fig. 5. In the cases of θ ≤ 30° and θ ≤ 80° the parallel and perpendicular temperatures for the minor ions increase at the same rate, which determines the saturation of their temperature anisotropy described above.
 |
Fig. 4 One-dimensional plots of the initial and evolved power spectra of the magnetic field fluctuations at θ = 0°, θ ≤ 30°, and θ ≤ 60° for flat spectra with initially isotropic spectral slopes α = 0. The magnetic field fluctuations are initialized at larger scales in comparison to the ones shown in Fig. 3. |
 |
Fig. 5 Evolution of the averaged magnetic field fluctuations in parallel (left) and perpendicular directions (right). The upper panel describes the imposed flat spectra with initially isotropic spectral slopes α = 0 at θ ≈ 80°. The bottom panel shows the evolved power spectra of the magnetic field fluctuations with two distinct spectral slopes. |
 |
Fig. 6 Initial (upper panel) and final (lower panel) stages of the normalized parallel component of the magnetic-field fluctuations δBx ∕B0 in real space for two cases with initial propagation angles θ ≤ 30° (left) and θ ≤ 60° (right). The initial spectral slopes are anisotropic and correspond to Figs. 3 and 1. |
 |
Fig. 7 Snapshots with the initial (upper panel) and final (lower panel) stages of the normalized parallel component of the magnetic field fluctuations for the cases of isotropic spectral slopes at θ ≤ 30° (left) and θ ≤ 60° (right); see Figs. 4 and 2. |
 |
Fig. 8 Example evolution of the 2D PSD of the magnetic-field fluctuations in Fourier space for the case of obliquely propagating waves at θ ≤ 60°. The snapshots from left to right in the upper and lower panel show the magnetic-field PSD at Ω p t = 10, 150, 400 and 800. The wave numbers are normalized to the ion inertial length di. |
 |
Fig. 9 Evolution of the 2D PSD of the magnetic-field fluctuations in Fourier space for the case of initially flat spectrum with obliquely propagating waves at θ ≤ 60°. The time for snapshots and the normalization are the same as in Fig. 8. |
 |
Fig. 10 Evolved 2D PSD of the magnetic-field fluctuations in Fourier space at Ωpt = 800 corresponding to various propagation angles from θ = 0° till θ = 80° with initially flat spectra |
 |
Fig. 11 Solutions of the warm plasma oblique linear dispersion relation for Alfén modes at different propagation angles in the presence of relative drift speed between the two ion species, V αp = 0.44V A. Real frequencies are shown in the left panel and the damping rates are depicted to the right. |
 |
Fig. 12 Evolution of the temperature anisotropy associated with obliquely propagating waves at various angles θ ≤ 30°, 60° and 80°. Alpha particles are shown in the left panel and proton temperature anisotropies are drawn in the middle one. The right panel describes the evolution of the relative drift speed between the two ion species for the three propagation cases. |
4 Summary and conclusion
We have performed 2.5D hybrid numerical simulations to study the evolution of initial broad-band spectra of Alfvénic fluctuations (initialized in the magnetic field and the bulk velocity fluctuations). We have focused on two main groups of fluctuation spectra: one with initially isotropic slopes imposed at large scales and one with initially anisotropic spectral slopes shifted to the more dispersive scales, closer to the ion inertial length for the α particles. Within these two major groups we have considered fluctuations at various propagation angles and studied the influence of the propagation angles on the evolution of the spectral slopes.
The results of the study show an isotropic behavior of the turbulent power spectra with generally steeper slopes in the direction of the predominant wave power initially imposed in the system. In the case of parallel wave propagation the spectral slopes evolve steeper in the parallel direction, while in the perpendicular direction the spectral slopes remain almost unchanged. Similarly, in the case of highly oblique propagation at θ ≈ 80°, the fluctuations evolve predominantly in the perpendicular direction and the parallel spectral slopes are only slightly affected. Hence from the analyzed cases we can conclude that the spectral slopes are expected to be steeper in the perpendicular direction for highly oblique waves and vice versa for parallel propagating fluctuations. Apart from the direction of the initial spectrum and the initially imposed spectral slopes the other relevant factor for the evolution of the spectra is the wavelength of the imposed fluctuations. Generally at longer wavelengths we observe shallower spectral slopes and more “dissipation” is observed at the higher wavelength dispersive and dissipative scales. This reflects the that the fluctuations at these scales can be transferred to the particles through various scattering processes and wave-particle interactions.
We have calculated the expected damping rates based on warm-plasma Vlasov linear theory calculations and have compared them with the evolution of the initially imposed wave spectra and the initial value of the relative drift speed. We find no correlation between the observed damping rates and the steepening of the initial spectral slopes for the various propagation angles. The evolution of the relative drift speed shows some anti-correlation with the calculated damping rate at large scales. This suggests that the evolution of the system is dominated by nonlinear processes and does not follow the linear instability predictions. The steepening of the initially imposed spectra is predominantly related to nonlinear cascade towards smaller scales as well as particle heating, with parallel heating for the protons and preferential heating of the minor ions in both parallel and perpendicular directions.
We should note that all initial fluctuations considered here are within the so-called inertial range (some of them approach the dissipation range for the α particles). Nevertheless, we do not observe a single unique spectral slope for the different cases. In this sense the evolution of the turbulent fluctuations presented here does not represent a state of fully developed turbulence. It is interesting to note that even when we impose a broad-band spectra with Iroshnikov-Kraichnan spectral slopes, the spectra evolve in time and the spectral slopes steepen. Furthermore, when a flat spectrum is imposed, the spectral slopes of the fluctuations rarely reach the expected values for the inertial range. This could be related to the fact that the regular turbulence usually develops in the 2D plane perpendicular to the background magnetic field, where the nonlinear time is smaller and the turbulence develops much faster. On the other hand it could also be related to the changes of the turbulent evolution in the presence of relative drifts. To answer these questions we need to compare the in-plane and out-of-plane turbulent evolution and perform more parameter studies of the effects of the differential streaming. The spectral slopes within our study evolve differently for the various angles of propagation, which suggests another possible dependence to look for in the solar-wind data.
As a final remark we should note that the weak turbulence and the steepening of the spectral slopes in the perpendicular-parallel plane develop much slower than the strong turbulence, which evolves predominantly in the perpendicular-perpendicular plane. Another factor which influences the evolution of the turbulence is the imposed initial broad-band spectra. The broad-band spectra are expected to show different evolution in comparison to the evolution of a single or a couple of monochromatic modes, which are often imposed in decaying turbulence studies. The interrelation of the plasma properties, the spectral slopes, and the various wave properties in a multi-species plasma environment poses a problem of great interest for the solar-wind community. Our research is the first attempt to address these connections. The study is extremely relevant to the upcoming space missions such as Solar Probe Plus, Solar Orbiter, and the newly proposed ESA mission THOR, whose main objective is to study the various energization mechanisms in the solar wind.
 |
Fig. 13 Evolution of the parallel (blue dash-dotted line) and perpendicular (in solid purple) temperature components for protons (upper panels) and alpha particles (lower panels) for the three cases of oblique wave propagation shown in Fig. 12 with initially flat power spectra in Kx and Ky. |
Acknowledgements
Y.M. would like to acknowledge A. F. Viñas and P. Moya for various fruitful discussions throughout the early stages of this work. This study has been funded under FWO – Research Foundation Flanders: Postdoctoral Fellowship grant 12K1416N. The work had also received funding from projects C 90347 (ESA Prodex), GOA/2015-014 (KU Leuven) and G.0A23.16N (FWO-Vlaanderen).
References
- Alexandrova, O., Saur, J., Lacombe, C., et al. 2009, Phys. Rev. Lett., 103, 165003 [NASA ADS] [CrossRef] [Google Scholar]
- Alexandrova, O., Lacombe, C., Mangeney, A., Grappin, R., & Maksimovic, M. 2012, ApJ, 760, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Alexandrova, O., Chen, C. H. K., et al. 2013, Space Sci. Rev., 178, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bruno, R., & Carbone, V. 2013, Living Rev. Sol. Phys., 10, 2 [Google Scholar]
- Bruno, R., & Telloni, D. 2015, ApJ, 811, L17 [Google Scholar]
- Chen, C. H. K., Horbury, T. S., Schekochihin, A. A., et al. 2010, Phys. Rev. Lett., 104, 255002 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H. K., Mallet, A., Schekochihin, A. A., et al. 2012, ApJ, 758, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Chew, G. F., Goldberger, M. L., & Low, F. E. 1956, Proc. R. Soc. London Ser. A, 236, 112 [Google Scholar]
- Franci, L., Landi, S., Matteini, L., Verdini, A., & Hellinger, P. 2015a, ApJ, 812, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Franci, L., Verdini, A., Matteini, L., Landi, S., & Hellinger, P. 2015b, ApJ, 804, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1997, ApJ, 485, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., & Trávníček, P. 2006, J. Geophys. Res. (Space Phys.), 111, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., & Trávníček, P. M. 2013, J. Geophys. Res. (Space Phys.), 118, 5421 [Google Scholar]
- Hellinger, P., Velli, M., Trávníček, P., et al. 2005, J. Geophys. Res., 110, 12109 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., Matteini, L., Landi, S., et al. 2015, ApJ, 811, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Howes, G. G., Dorland, W., Cowley, S. C., et al. 2008, Phys. Rev. Lett., 100, 065004 [NASA ADS] [CrossRef] [Google Scholar]
- Howes, G. G., Tenbarge, J. M., Dorland, W., et al. 2011, Phys. Rev. Lett., 107, 035004 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iroshnikov, P. S. 1963, AZh, 40, 742 [NASA ADS] [Google Scholar]
- Kiyani, K. H., Chapman, S. C., Khotyaintsev, Y. V., Dunlop, M. W., & Sahraoui, F. 2009, Phys. Rev. Lett., 103, 075006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kiyani, K. H., Chapman, S. C., Sahraoui, F., et al. 2013, ApJ, 763, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kiyani, K. H., Osman, K. T., & Chapman, S. C. 2015, Philos. Trans. Royal Soc. London Ser. A, 373, 20140155 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Kraichnan, R. H. 1965, Phys. Fluids, 8, 1385 [Google Scholar]
- Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., & Wong, H. K. 1998, J. Geophys. Res., 103, 4775 [NASA ADS] [CrossRef] [Google Scholar]
- Leamon, R. J., Smith, C. W., Ness, N. F., & Wong, H. K. 1999, J. Geophys. Res., 104, 22331 [NASA ADS] [CrossRef] [Google Scholar]
- Lion, S., Alexandrova, O., & Zaslavsky, A. 2016, ApJ, 824, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Ofman, L., & Viñas A. F. 2013a, AIP Conf. Ser., eds. G. P. Zank, J. Borovsky, R. Bruno, et al. 1539, 34 [NASA ADS] [Google Scholar]
- Maneva, Y. G., Viñas, A. F., & Ofman, L. 2013b, J. Geophys. Res., 118, 2842 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Araneda, J.-A., & Marsch, E. 2014, ApJ, 783, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Ofman, L., & Viñas, A. 2015a, A&A, 578, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maneva, Y. G., Viñas, A. F., Moya, P. S., Wicks, R. T., & Poedts, S. 2015b, ApJ, 814, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y., Lazar, M., Viñas, A., & Poedts, S. 2016a, ApJ, 832, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Poedts, S., & Araneda, J. A. 2016b, AIP Conf. Ser., 1714, 030004 [Google Scholar]
- Maneva, Y. G., Viñas, A., Araneda, J., & Poedts, S. 2016c, AIP Conf. Ser., 1720, 040011 [Google Scholar]
- Maruca, B. A., Kasper, J. C., & Gary, S. P. 2012, ApJ, 748, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Viñas, A.-F., & Maneva, Y. G. 2014, J. Geophys. Res., 119, 4223 [CrossRef] [Google Scholar]
- Passot, T., Sulem, P. L., & Hunana, P. 2012, Phys. Plasmas, 19, 082113 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., Henri, P., Laveder, D., & Sulem, P.-L. 2014, Eur. Phys. J. D, 68, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrone, D., Valentini, F., Servidio, S., Dalena, S., & Veltri, P. 2013, ApJ, 762, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Sahraoui, F., Goldstein, M. L., Robert, P., & Khotyaintsev, Y. V. 2009, Phys. Rev. Lett., 102, 231102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., & Rezeau, L. 2010, Phys. Rev. Lett., 105, 131101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Dorland, W., et al. 2009, ApJS, 182, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Servidio,S., Valentini, F., Perrone, D., et al. 2015, J. Plasma Phys., 81, 325810107 [CrossRef] [Google Scholar]
- Smith, C. W., Hamilton, K., Vasquez, B. J., & Leamon, R. J. 2006, ApJ, 645, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Valentini, F., Perrone, D., Stabile, S., et al. 2016, New J. Phys., 18, 125001 [Google Scholar]
- Viñas, A. F., Moya, P. S., Araneda, J. A., & Maneva, Y. G. 2014, ApJ, 786, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, M., Matthaeus, W. H., Karimabadi, H., et al. 2012, Phys. Rev. Lett., 109, 195001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wan, M., Matthaeus, W. H., Roytershteyn, V., et al. 2015, Phys. Rev. Lett., 114, 175002 [NASA ADS] [CrossRef] [Google Scholar]
- Wicks, R. T., Horbury, T. S., Chen, C. H. K., & Schekochihin, A. A. 2010, MNRAS, 407, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Wicks, R. T., Horbury, T. S., Chen, C. H. K., & Schekochihin, A. A. 2011, Phys. Rev. Lett., 106, 045001 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Initial two-dimensional (2D) PSD of the magnetic field fluctuations in Fourier space with anisotropic spectral slopes in Kx and Ky. The simulation setup is the same as in Fig. 3. From left to right the plots correspond to parallel and oblique wave propagation at θ = 0°, θ ≤ 30° and θ ≤ 60°. |
| In the text | |
 |
Fig. 2 Initial 2D PSD of the magnetic field fluctuations in Fourier space corresponding to various propagation angles with initially isotropic spectral slopes in Kx and Ky. The simulation setup corresponds to Fig. 4. From left to right the plots represent propagation at θ = 0°, θ ≤ 30°, θ ≤ 60° and θ ≤ 80°. |
| In the text | |
 |
Fig. 3 One-dimensional plots of the initial and evolved power spectra of the magnetic field fluctuations as a function of parallel Kx di and perpendicular Kydi normalized wave numbers as a function of the propagation angle. From left to right the plots correspond to parallel θ = 0°, quasi-parallel θ ≤ 30°, and highly oblique propagation at θ ≤ 60°. All cases are initialized with anisotropic spectral slope with different values along Kx and Ky; see Table 1. |
| In the text | |
 |
Fig. 4 One-dimensional plots of the initial and evolved power spectra of the magnetic field fluctuations at θ = 0°, θ ≤ 30°, and θ ≤ 60° for flat spectra with initially isotropic spectral slopes α = 0. The magnetic field fluctuations are initialized at larger scales in comparison to the ones shown in Fig. 3. |
| In the text | |
 |
Fig. 5 Evolution of the averaged magnetic field fluctuations in parallel (left) and perpendicular directions (right). The upper panel describes the imposed flat spectra with initially isotropic spectral slopes α = 0 at θ ≈ 80°. The bottom panel shows the evolved power spectra of the magnetic field fluctuations with two distinct spectral slopes. |
| In the text | |
 |
Fig. 6 Initial (upper panel) and final (lower panel) stages of the normalized parallel component of the magnetic-field fluctuations δBx ∕B0 in real space for two cases with initial propagation angles θ ≤ 30° (left) and θ ≤ 60° (right). The initial spectral slopes are anisotropic and correspond to Figs. 3 and 1. |
| In the text | |
 |
Fig. 7 Snapshots with the initial (upper panel) and final (lower panel) stages of the normalized parallel component of the magnetic field fluctuations for the cases of isotropic spectral slopes at θ ≤ 30° (left) and θ ≤ 60° (right); see Figs. 4 and 2. |
| In the text | |
 |
Fig. 8 Example evolution of the 2D PSD of the magnetic-field fluctuations in Fourier space for the case of obliquely propagating waves at θ ≤ 60°. The snapshots from left to right in the upper and lower panel show the magnetic-field PSD at Ω p t = 10, 150, 400 and 800. The wave numbers are normalized to the ion inertial length di. |
| In the text | |
 |
Fig. 9 Evolution of the 2D PSD of the magnetic-field fluctuations in Fourier space for the case of initially flat spectrum with obliquely propagating waves at θ ≤ 60°. The time for snapshots and the normalization are the same as in Fig. 8. |
| In the text | |
 |
Fig. 10 Evolved 2D PSD of the magnetic-field fluctuations in Fourier space at Ωpt = 800 corresponding to various propagation angles from θ = 0° till θ = 80° with initially flat spectra |
| In the text | |
 |
Fig. 11 Solutions of the warm plasma oblique linear dispersion relation for Alfén modes at different propagation angles in the presence of relative drift speed between the two ion species, V αp = 0.44V A. Real frequencies are shown in the left panel and the damping rates are depicted to the right. |
| In the text | |
 |
Fig. 12 Evolution of the temperature anisotropy associated with obliquely propagating waves at various angles θ ≤ 30°, 60° and 80°. Alpha particles are shown in the left panel and proton temperature anisotropies are drawn in the middle one. The right panel describes the evolution of the relative drift speed between the two ion species for the three propagation cases. |
| In the text | |
 |
Fig. 13 Evolution of the parallel (blue dash-dotted line) and perpendicular (in solid purple) temperature components for protons (upper panels) and alpha particles (lower panels) for the three cases of oblique wave propagation shown in Fig. 12 with initially flat power spectra in Kx and Ky. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.