EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 612 (April 2018) A&A, 612 (2018) A49 Full HTML
Free Access
Issue
A&A
Volume 612, April 2018
Article Number A49
Number of page(s) 63
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/201732054
Published online 20 April 2018

© ESO 2018

1 Introduction

Spectroscopy of M dwarfs has become a very active research field because potentially habitable planetary companions cause Doppler variations that are more easily detectable around stars of lower mass (Martín et al. 2005; Scalo et al. 2007; Tarter et al. 2007). These stars also constitute the vast majority of potential planet hosts in our immediate vicinity, and a detailed characterization of their planets is believed to be easier than in the more massive, brighter, and more distant Sun-like stars (see, e.g., Anglada-Escudé et al. 2016).

The first radial velocity (RV) surveys for extrasolar planets focused on objects in orbit around Sun-like stars (see, e.g., Udry & Santos 2007). The lower end of the mass range of the discovered planets was continuously extended until measurement precision reached a level of about 1 m s−1 (Mayor et al. 2009b; Fischer et al. 2016). At this precision, a 10 M⊕ planet can be discovered on a 1 yr orbit in the liquid-water habitable zone around a 1 M⊙ star. The shortcut to potentially habitable planets similar to Earth is to look around lighter stars; at the same RV precision, a 2 M⊕ planet can be found in the habitable zone around a 0.3 M⊙ star (see, e.g., Rivera et al. 2005; Mayor et al. 2009a; Bonfils et al. 2013; Anglada-Escudé et al. 2013, 2014, 2016).

The CARMENES M-dwarf survey began operations on Jan 1, 2016. The instrument is located at Calar Alto observatory in Almeria, Southern Spain (37°13′25″N, 2°32′46″W). It provides nearly continuous wavelength coverage from 520 to 1710 nm from its two channels: the visual channel (VIS) with a spectral resolution of R = 94 600 covers the range λ = 520–960 nm, and the near-infrared channel (NIR) operates at R = 80 400 and λ = 960–1710 nm (Quirrenbach et al. 2016). For the M-dwarf survey, we regularly observe about 300 M dwarfs across all M-spectral subtypes. A total amount of 750 useful nights is reserved as Guaranteed Time Observations (GTO) with the goal to collect approximately 70 spectra for each target over the course of the program (Garcia-Piquer et al. 2017).

The main motivation for building an optical and near-infrared spectrograph with this large wavelength coverage is to measure RVs in very cool stars (e.g., Martín et al. 2006) and to understand the amount of RV information and stellar RV jitter as a function of wavelength. It is well known that Sun-like stars provide most RV information at blue optical wavelengths where astronomical spectrographs already reached the 10 m s−1 level in the 1980s (Campbell & Walker 1979; Merline 1985). However, cooler low-mass stars provide more flux at near-infrared wavelengths, while their spectrum is extremely rich in molecular features at optical wavelengths, which makes detailed predictions about measurable RV precisions difficult. There has not been a final answer so far to the question in which spectral range the RV method is most sensitive for low-mass stars (see Sect. 4).

Radial velocity jitter can be caused by corotating active regions, magnetic cycles, variations in stellar granulation, stellar oscillations, and other mechanisms (e.g., Lagrange et al. 2010; Meunier et al. 2010a,b; Cegla et al. 2014; Lanza et al. 2016). Its amplitude is expected to depend on wavelength (e.g., Desort et al. 2007; Reiners et al. 2010; Marchwinski et al. 2015). A spectrograph with large wavelength coverage can help to distinguish between Keplerian signals from an orbiting planet and RV variations caused by the star itself (e.g., Saar & Donahue 1997; Barnes et al. 2011, 2017; Jeffers et al. 2014; Korhonen et al. 2015). Furthermore, the pattern of RV variation as a function of wavelength can itself provide important information about the star, for example, about spot temperatures and Zeeman broadening (Reiners et al. 2013), or about a modal identification for pulsating stars (Amado et al. 2007; Amado 2007).

While stellar atmosphere models have improved significantly over the past decade and instruments are being designed for 10 cm s−1 precision (Pepe et al. 2010), there is a need for empirical calibration of the possible RV precision across optical and near-infrared wavelengths for M dwarfs. The growing amount of transiting-planet candidates discovered by photometry missions such as Kepler, MEarth, APACHE, and future missions like TESS and PLATO, requires a substantial infrastructure for spectroscopic follow-up. A host of red optical and near-infrared spectrographs are currently planned or under constructionthat will provide the required data to determine down the mass of our nearest transiting neighbors (e.g., Mahadevan et al. 2014; Artigau et al. 2014; Kotani et al. 2014; Seifahrt et al. 2016; Crepp et al. 2016; Claudi et al. 2016; Jurgenson et al. 2016; Gibson et al. 2016). For an efficient planning of RV follow-up in low-mass stars, and for new or extended RV surveys of our closest neighbors, empirical information on the RV performance across different wavelengths is important. With our data from the CARMENES program, we are in an excellent position to address this question.

In this paper, we introduce the CARMENES sample and provide detailed information about the 324 target stars that we are surveying for planets. After more than a year of observations, we have amassed several thousand spectra with both CARMENES channels, enough to draw statistically significant conclusions about the spectroscopic properties and RV precision across the entire CARMENES wavelength range. CARMENES is the first spectrograph that routinely delivers high-resolution spectra of low-mass stars at infrared wavelengths. Before CARMENES, spectroscopic information of low-mass stars could only be provided by a few instruments, most of them requiring multiple settings and/or access to 10 m class telescopes (e.g., Lebzelter et al. 2012). As a service to the community, with this paper we also publish one CARMENES spectrum for each survey star.

We introduce the CARMENES GTO sample stars and the library of CARMENES spectra in Sect. 2, and we derive spectroscopic information about rotation and radial velocities for each star. In Sect. 3 we take a detailed look into our atlas of high-resolution spectra for three example stars that represent different M subtypes. The atlas itself is published in Appendix A. We investigate the RV information content of M dwarfs from our observations in Sect. 4. Finally, our results are summarized in Sect. 5.

2 Library of M-type CARMENES spectra

The CARMENES spectral format covers the wavelength range 520–1710 nm. In the telescope front-end, a beam splitter sends light at wavelengths shorter than 960 nm into the VIS channel and longer wavelengths into the NIR channel. The two channels operate independently, but see light from the same object. Data are reduced with our automatic pipeline using the method of optimal extraction (Zechmeister et al. 2014). Reduced spectra are stored at the Calar Alto archive and analyzed for their RVs (Zechmeister et al. 2018); see also Caballero et al. (2016).

The NIR detector is an array of two detectors that are separated by a small gap. The spectral coverage is almost continuous, with additional small gaps that grow toward long wavelengths; gaps are between zero and 15 nm large from the very blue to the very red end. The spectral format cannot be changed. An overview of the CARMENES spectral range and telluric contamination is presented in Fig. 1. The normalized spectrum is shown logarithmically on both axes. It shows the telluric contamination of the spectrum and the three main atmospheric windows, that is, the z, J, and H bands, that are covered by the NIR channel.

As part of the GTO agreement, we provide early access to one CARMENES spectrum for each of our sample targets (Table B.1). They can be downloaded from the CARMENES GTO Data Archive (Caballero et al. 2016)1. Each spectrum is a single exposure obtained between Jan. 1, 2016, and Aug. 31, 2017, and has a signal-to-noise ratio (S/N) typical for our survey (see below). Details on how the S/N is calculated are given in Zechmeister et al. (2018).

thumbnail Fig. 1

Overview of the CARMENES spectral range. The spectrum covered by the VIS channel is shown in blue, and the NIR channel in red. The target shown is the A2V star 50 Cas. The stellar spectrum only exihibits a few hydrogen lines, all strong features are from Earth’s atmosphere.

2.1 Sample

To define our sample of M dwarfs, we selected the brightest members of every spectral subtype that are visible from Calar Alto (δ >−23°) and that are not known to be members of multiple systems at separations closer than 5″. We carried out extensive preparatory observations and characterization to define our survey sample. For more details on target preselection and characterization, we refer to Alonso-Floriano et al. (2015), Cortés-Contreras et al. (2017), and Jeffers et al. (2017). In contrast to other M-dwarf planet surveys, we explicitly did not bias our sample with regard to age or chromospheric activity. One of the expected advantages of the long-wavelength coverage of CARMENES is that RV variations caused by stellar activity can to some extent be distinguished from orbital motion. Learning about the RV signature from starspots and stellar activity as a function of wavelength is one of the science goals of the CARMENES M-dwarf survey. We also did not exclude stars with planets that were already known. Our sample therefore has some overlap with other RV programs. Analyses of CARMENES RVs for seven stars with known planets were presented in Trifonov et al. (2018).

After a few observations were taken for each star, we discovered several double-lined spectroscopic binaries (SB2s) that will be presented in a separate paper. After cleaning for SB2s, we ended up with a survey sample of 324 stars; all stars are presented in Table B.1. With only a few exceptions, the spectral types we used were adopted from the works of Reid et al. (1995); Hawley et al. (1996); Gizis et al. (2002); Lépine et al. (2013); Alonso-Floriano et al. (2015). For details about spectral types we refer to Alonso-Floriano et al. (2015). J-band magnitudes are taken from the Two Micron All Sky Survey (Skrutskie et al. 2006). The typical limit for the J-band magnitude for our survey is J = 10 mag, and it is brighter for earlier spectral types. Some targets with known transiting planets were added to the sample although they are fainter than our typical survey targets. The distribution of the sample stars in spectral type, mass, and J-band magnitude is shown in Fig. 2. As a consequence of the steep decrease in luminosity toward late-type stars, only very few stars of our sample are later than M5. On the other hand, the distribution of our sample stars in mass is flatter and reaches down to the brown dwarf limit. This is mainly because there is only little difference in mass between dwarf stars in the spectral type range M6–M9. Individual values of J-band magnitude and mass are shown versus spectral types in Fig. 3. As a rule of thumb, for a mid-M J = 9 mag star, CARMENES reaches a S/N of 150 per pixel in the I band after 25 min exposure time.

We also report masses and activity level in terms of Hα luminosity relative to bolometric luminosity in Table B.1. Masses are computed from Ks-band magnitudes according to the relations provided in Delfosse et al. (2000) and Benedict et al. (2016). We caution that masses below 0.1 M⊙ may be underestimated because these relations lose predictive utility for MK >10 mag (Benedict et al. 2016). Hα luminosities are computed from measuring equivalent widths and converting them into luminosities (see, e.g., Reiners & Basri 2008). More details on Hα measurements and other chromosperic lines in the CARMENES spectral range will be provided in a forthcoming paper.

thumbnail Fig. 2

From top to bottom: distribution of the CARMENES survey sample in spectral type, mass, and J-band magnitude. The subsample of stars with Hα emission is shown in red.
thumbnail Fig. 3

J-band magnitude (left panel) and mass (right panel) for all stars of the CARMENES survey sample.

2.2 Stellar rotation

We calculated the projected rotation velocities, v sini, from our spectra taken with CARMENES-VIS with the cross-correlation method. We computed the cross-correlation function (CCF) and calibrated the width of the CCF against artificially broadened spectra of a reference star (see, e.g., Reiners et al. 2012; Jeffers et al. 2017). We used coadded spectra from all observations for each star if more than five exposures were available (see Zechmeister et al. 2018). For cross-correlation reference, we selected stars that were observed frequently (at least ten times), which guarantees a very high S/N reference (coadded) spectrum, and for which information on the rotation period from photometry is available. We used three different reference stars to minimize systematic errors caused by spectral mismatch (Table 1). All reference stars are relatively slow rotators, and their equatorial rotation velocity, v, is estimated from the rotation period, P, and radius, R, to lie well below our detection limit.

For each star, we computed a set of CCFs for individual orders of the CARMENES spectral format. The adopted v sin i is the average of values from orders that we found to provide reliable information about stellar rotation. Our criteria for the selected orders are the absence of significant telluric contamination and chromospheric emission lines, high S/N, and small influence from strong spectroscopic features, such as molecular band heads. The latter can introduce substantial systematic errors for relatively small differences in the spectral characteristics of our stars. The spectral regions that we chose cover the wavelength ranges 592–610 nm, 650.5–654 nm, and 660–685 nm in stars more massive than M = 0.125M⊙, and 741–757 nm, 774–810 nm, 840–843 nm, and 847–885 nm in less massive stars. As uncertainties, we report the standard deviations of the set of values calculated in these spectral chunks. All values of v sin i measured from the CARMENES spectra are given in Table B.1.

Table 1

Refererence stars used for the calculation of vsini.

2.2.1 Fast and slow rotation

Many of the stars in our sample are relatively slow rotators. If Doppler broadening from stellar rotation is too small compared to the spectral resolution (and other broadening mechanisms), the effect cannot be reliably detected. In the case of M stars, turbulence and thermal broadening are on the order of 1–2 km s−1 in the lines of heavy ions and molecules, so that instrumental resolution determines the detection limit. For a criterion to reliably detect stellar rotation, we estimate that its Doppler effect must broaden thespectral lines by at least half a resolution element. In the case of CARMENES-VIS with R = 94 600, this means that v sin i = 2 km s−1 is a conservative lower detection limit. For stars where we could not determine rotational broadening in excess of 2 km s−1, we report this value as an upper limit for vsini in Table B.1.

We find that 75 of our 324 sample stars (23%) show significant rotational broadening. A detailed investigation of the fraction of active stars in our sample and a comparison to volume-limited M-dwarf samples is carried out in Jeffers et al. (2017). In that paper, a larger sample of stars was observed in preparation of the CARMENES survey. In the final CARMENES sample, we included 40 stars for which no information on v sin i was available before. We also compiled a list of rotation periods, P, measured from photometry. These values are reported together with the expected equatorial rotation velocity vEq . To calculate vEq from P, we determined the radius of each star according to the mass-radius relation for 4 Gyr old stars of solar metallicity from Baraffe et al. (1998).

The CARMENES results for vsini are shown as a function of mass in Fig. 4. In this figure, we plot all stars with Hα emission as filled circles and those without Hα emission as open circles. All stars with significant rotational broadening and masses below M = 0.55M⊙ are also Hα-emitters; there is no inactive fast rotator below that mass limit. The fraction of active stars is higher at lower mass, a result that was found previously by other investigations (cf. Jeffers et al. 2017).

A handful of inactive stars with high masses (M >0.55M⊙) also show significant line broadening. The absence of Hα emission in these stars deserves some deeper discussion. One possible explanation is that the spectra of these stars, in particular the wings of their atomic lines, are intrinsically different from “normal” M0 star spectra. The masses of these targets are relatively high for spectral type M0, which may point to peculiarities in the composition or age of these stars. This could lead to systematic differences between the spectra of our template M0 star and these apparently massive M0 stars, which cause a systematic offset in our determination of v sin i. A second plausible explanation is that these stars are in fact rotating significantly faster than the inactive stars that are less massive, but here rotation is still not fast enough to produce Hα emission. The left panel of Fig. 8 in Jeffers et al. (2017) shows that normalized Hα emission is proportional to rotation period in all M stars of spectral type M0–M4.5. Hα emission, however, becomes undetectable at a level of log LHα∕Lbol = −4.5 in these stars. While all stars rotating faster than P = 10 d show Hα in emission, activity in a growing fraction of the slower rotators falls below that threshold and cannot be detected anymore. In other words, at rotation periods of P = 10 d and slower, not all stars exhibit Hα in emission. For our measurements, this means that the critical value of v sin i above which we always expect to find Hα emission is a function of radius (or mass). We plot the critical value of v sin i that corresponds to P = 10 d as a red dashed line in Fig. 4. The critical value is below v sin i = 2 km s−1 in stars less massive than M = 0.45M⊙ but rises above our detection limit towards higher masses. The five stars with detected surface rotation but no Hα emission are rotating at rates around the critical rate of P = 10 d or slower. We therefore conclude that our measurements of v sin i >2 km s−1 are consistent with the lack of Hα emission in these stars.

thumbnail Fig. 4

Projected rotation velocity vsini as a functionof stellar mass. Stars with detected Hα emission are shown as filled circles, and stars with no Hα emission are shown as open circles. Colors indicate the level of Hα emission as shown in the legend. Slow rotators are plotted at our detection limit of v sin i = 2 km s−1. The red dashed line indicates values of vEq for stars with rotation periods P = 10 d. Above this line, Hα is always expected in emission (see text).

2.2.2 Comparing photometric period to surface rotation

For many of our target stars we have information on rotational periods that we can combine with our measurements of projected surface rotation, v sin i (see Reiners et al. 2012). We plot vsini against the expected equatorial rotation velocity according to photometric period and stellar radius in Fig. 5. We also show lines indicating v sin i as expected for a given vEq observed under inclination angles of i = 90°, 50°, 30°, and 10°. We include our estimate on the inclination values from this comparison in Table B.1.

The majority of the stars with available P and vsini follow the relation for i = 90° or a little below. Useful estimates of the inclination angle i can be given in cases where a photometric period and a measurement of surface rotation above the detection limit are available. Of these stars, about one half (15) have values of v sin i higher than vEq . Most of them are consistent with inclination angles i = 90 deg within the measurement uncertainties. We find only one star with a very small uncertainty in v sin i, but with a photometric period indicating much slower rotation (RX J0506.2); its rotation period of 0.89 d is inconsistent with the line broadening seen in our spectra. Nevertheless, we do not expect such high a fraction of stars observed nearly equator-on in a sample of stars in which inclination angles should be randomly distributed (uniform distribution in cos i). Possible reasons for a bias toward largeinclination angles include i) underestimated stellar radii, perhaps caused by a systematic bias in metallicity; ii) overestimated rotational periods, perhaps caused by misidentifying harmonics of P as the true rotational period or by differential rotation; iii) a systematically higher detection efficiency for photometric periods in stars observed under high inclination angles; and iv) overestimated values of v sin i. For the latter, spectral mismatch between the targes and their reference stars is one obvious candidate. This may be particularly important for the three stars with v sin i >vEq that have surface rotation velocities between 2 and 4 km s−1 and belong to the group of relatively massive stars discussed above (see Sect. 2.2.1).

One way to adjust the distribution of inclination angles is to select a different set of reference stars. We have experimented with other reference stars, and as expected, found other choices that can produce systematically lower values for v sin i. Our principal requirement for the set of reference stars, however, was that spectral line broadening should be negligible and that external information from photometric measurements should be available. We conclude that the absolute values of v sini need to be interpreted with great care, in particular when they are compared to photometric periods.

thumbnail Fig. 5

Comparison between vsini and equatorial velocity v estimated from photometric period and radius. Active stars are indicated as filled circles as in Fig. 4. Dashed lines show expected relations between v sin i and v for inclination angles i = 90°, 50°, 30°, and 10°.

2.3 Absolute radial velocities

For our sample stars, we computed absolute radial velocities from the same data as were used for the calculation of v sini. From the CCFs that were calculated for a set of spectral orders, we derived RV offsets between each star and the reference. Because we here use coadded spectra, our results represent the mean radial velocities averaged over all observations for each star. An analysis of the RV variability of each target will be performed in detail for our planet search, but this is beyond the scope of this paper.

From our cross-correlation analysis, we obtained RVs for each star relative to its reference according to spectral type (see Table 1). Before coadding, all observed spectra were corrected for barycentric motion. Thus, the radial velocities are the true differences between the motion of the stars with respect to the solar system. The absolute values of the radial velocities, however, are unknown. We shifted our RVs to the absolute scale of the Gaia pre-launch catalog of RV standard stars provided by Soubiran et al. (2013). Our samples have three targets in common: Gl 450, Gl 514, and Gl 526. We computed the relative radial velocity shift between Gl 514 and our three reference stars, and shifted all our RVs such that the RVs of Gl 514 match the value from Soubiran et al. (2013, vrad = 14.386 km s−1). After calibration, the RVs of the two other stars, Gl 450 and Gl 526, also agree with the literature values within approximately 100 m s−1 (vrad = 0.221 km s−1 and 15.570 km s−1, respectively; Soubiran et al. 2013).

Absolute RVs for all our stars are provided in Table B.1. The typical relative uncertainties for our measurements are on the order of 10 m s−1; they are dominated by spectral differences between the stars (note that we compute the radial velocity from the CCF relative to observed spectra of our reference stars). Faster rotators typically have larger uncertainties for the same reasons as discussed in Sect. 2.2.

3 Spectral atlas

We present a spectral atlas of three representative M dwarfs of spectral types M1 (GX And), M3.5 (Luyten’s star), and M7 (Teegarden’s star). The three objects are among the brightest targets of their spectral type and providehigh-quality M-dwarf data at very different effective temperatures. One spectrum of each star is shown in the spectral atlas in Fig. A.1. We show the entire wavelength range from Hα up to the red end of our spectral format (645–1710 nm). Information on the individual observations is summarized in Table 2. Each figure of the atlas covers an increase of approximately 2.3% in wavelength, that is, ~ 2100 resolution elements. The top panels show a spectrum of the telluric standard star 50 Cas as in Fig. 1. In the other three panels, we present the three M-dwarf spectra in black, together with a PHOENIX model spectrum from Husser et al. (2013) in red, calculated for approximately the atmospheric parameters we expect for the stars’ spectral types, that is, 3700 K (M1), 3400 K (M3.5), and 2600 K (M7). We chose log g = 5.0 and solar metallicity for this comparison. Model spectra are artificially broadened to match the spectral resolution of our observations. In the top panel of the atlas figures, the spectrum of the telluric standard is shown with annotations of the most prominent absorption features. The hydrogen H I lines are stellar features, positions are taken from The Atomic Line List v2.042 . In the second panel, we show the spectrum of GX And together with annotations of the most prominent atomic and molecular absorption features seen in M dwarfs. Line positions of atomic lines are taken from VALD (Ryabchikova et al. 2015), information on molecular bands was compiled from Cushing et al. (2005). We chose to show our observed spectra without applying any Doppler shift so that telluric lines appear at the same position in all panels of our atlas. Because of barycentric motion and the stars’ radial velocities, the spectral features are therefore slightly shifted. In order to match the features of the model spectra to our observations, we Doppler-shifted the model spectra accordingly. The values that we applied are given in Table 2.

Our wavelength range covers parts of the range shown in the atlas from Tinney & Reid (1998), which contains the spectral range up to 920 nm. In the following, we discuss the spectroscopic features observed at wavelengths redward of 920 nm only. For a discussion of M-dwarf spectra at shorter wavelengths, we refer to Tinney & Reid (1998), for instance.

Table 2

Basic information about spectra shown in the spectral atlas.

3.1 Y band

The spectral range around 970 nm contains a number of strong Ti lines that are very useful for the study of M-dwarf magnetic fields (e.g., Kochukhov & Lavail 2017; Shulyak et al. 2017). These lines are embedded in telluric water absorption, which needs to be corrected for. The strong water absorption ends at around 980 nm, just before the well-known Wing-Ford band of molecular FeH sets in (see, e.g., Reiners & Basri 2006). The wavelength range 985–1100 nm is virtually free of telluric absorption. It contains mostly FeH lines, several strong atomic Ti lines, a prominent Ca line, and a handful of weaker lines from other atoms. Absorption from the FeH band has intensively been used to measure rotation and magnetic fields in M dwarfs. The great advantage of the Wing-Ford band is that it contains a large number of relatively isolated absorption lines that are not as densely packed as the TiO or VO lines in the visual wavelength range, which allows a line profile analysis of individual lines at least in early- and mid-M stars (e.g., Reiners 2007). FeH lines have very different Landé g-factors that are useful for differential investigation of Zeeman broadening or stellar metallicity (Shulyak et al. 2011).

Some visual spectrographs based on CCDs can reach out to this wavelength range, such as UVES/VLT, HIRES/Keck, or ESPADONS/CFHT. They have been used to provide spectral quality that so far was superior to most of the spectra taken with infrared detectors. CARMENES NIR also covers this range with an infrared detector, but here the efficiency was optimized to reach high throughput at these wavelengths. Therefore, CARMENES has become one of the most efficient instruments specifically in this wavelength range.

Our comparison between observations and model spectra at all three spectral types shows that many molecular and atomic lines are well reproduced by the models. However, the intensity of the FeH molecular lines is often overestimated, and a set of strong absorption features appears in the M7 model at wavelengths around 1050 nm that are not detected in the observed spectrum. We did not make an attempt to find the models that are most similar to our observed spectra, but the physical setup of these particular models is clearly either lacking adequate input data (e.g., better molecular line data) or the models inappropriately simulate the physical situation at very low effective temperatures (at least for this wavelength region), or both3 .

Heavy water absorption between 1100 nm and 1200 nm separates the Y band from the J band. At high spectral resolution, we can identify stellar absorption lines from Na, K, Fe, Cr, and Mg embedded in the forest of water lines. Some of them are strong and isolated enough, so that they might be useful for a line profile analysis.

3.2 J band

The J band starts around 1200 nm, where the water absorption band becomes much weaker. The transparent atmospheric window extends until water is again detected redward of 1300 nm. The region in between is not as free of telluric lines as the Y band because there is an additional molecular band from O2 around 1270 nm. The M-dwarf spectra in the J band are very poor in absorption lines compared to the other spectral regions in the visual and near-infrared range. There are no substantial molecular bands similar to the TiO, VO, or FeH bands at shorter wavelengths. The two K I lines near 1250 nm stand out prominently, and there are a few lines from Ca, Ti, Fe, and Mn around 1286 nm. A Na I line is buried in telluric O2 absorption, and two Al I lines appear at the red end of the J band, wherewater absorption is relevant again (the two Al I lines are unfortunately lost in a gap of the CARMENES spectral format). Another line of Mn I is visible around 1330 nm before very strong water absorption separates the J from the H band. We do not showthe wavelength range between 13 850 and 1480 nm because almost no starlight passes through the dense water features.

The spectral models show good agreement with the observed spectra. In the J band, no prominent features seem to be missing in the models, and none of the features predicted by the models are missing in the spectra. The long exposure of the M7 star shows a number of sky emission lines from OH airglow (Oliva et al. 2015).

3.3 H band

At the blue end of the H band, water absorption is significantly reduced at around 1500 nm until the end of our spectral format at 1710 nm. Additional telluric absorption bands from CO2 are visible at 1540 nm, 1570 nm, 1600 nm, and 1640 nm (Herzberg 1950).

Around 1480 nm, a series of stellar molecular OH absorption lines appears among the water lines. The set of OH lines covers the entire H band and adds a significant number of stellar absorption features. In terms of atomic lines, the situation is similar to the J band, with only a few scattered weak lines throughout the entire band. These lines are Mg I at 1505 nm (partially lost in spectral format gaps), very weak lines of K I 1517 nm, a handful of lines from Fe I and Ti I throughout the band, and a set of Ca I lines at 1615 nm. Overall, these lines are all relatively weak, which implies that the amount of information available for line profile analysis using a high-resolution spectrograph is limited.

Another component of stellar absorption that becomes stronger toward later spectral types appears throughout the entire H band. This component is significantly above the noise level and is also predicted by the models. The absorption is probably due to FeH, but the lines are too dense for an individual line analysis.

4 Radial velocity information content

The RV precision that can be achieved in a spectroscopic RV measurement depends on the number of photons that can be collected at some particular wavelength, that is, on the S/N and also on the amount of spectroscopic information that is available to measure the Doppler shift, that is, the RV information content (Connes 1985; Butler et al. 1996; Bouchy et al. 2001). At stellar photospheric temperatures, electronic transitions from atoms and molecules typically generate many spectral lines at optical wavelengths, but fewer at longer wavelengths. In low-mass stars, ro-vibrational transitions add molecular bands at red optical and near-infrared wavelengths. Thus, the RV information content is typically higher at short optical wavelengths, but toward laterspectral types, the photon-dominated S/N grows dramatically from blue optical toward infrared wavelengths.

Detailed simulations of the photon-limited RV precision in M dwarfs were carried out by Reiners et al. (2010); Rodler et al. (2011); Bottom et al. (2013); Plavchan et al. (2015); Figueira et al. (2016). With only very few exceptions, these studies relied on synthetic spectra from model atmosphere simulations. These works agree with the general picture that more RV information is available at short wavelengths, but about the details of which spectral range is better than another, after taking into account also the available number of photons, there are discrepancies by a factor of two or more. One reason for the discrepancies is that different models were used; model predictions for the occurrence of molecular bands depend on input parameters about the stellar atmosphere and molecular physics. Another reason is the treatment of telluric lines, which becomes a very significant factor at near-infrared wavelengths.

The spectra from our survey provide empirical information on the RV precision that is achievable in M dwarfs across the wavelength range 520–1710 nm. A major motivation to observe M dwarfs at longer wavelengths is that the measurement uncertainty in any spectral bin, (S/N)−1, decreases dramatically from V band to J band. Nevertheless, there are far fewer spectroscopic features, that is, spectroscopic RV information, at longer wavelengths. The ratio of the two is the RV precision that can be achieved in an observation. In the following, we provide the first empirical information on the wavelength dependence of the RV precision in M dwarfs from a significant number of observations.

We follow the definition of Bouchy et al. (2001); the RV precision that can be reached in an observation of a star in a given wavelength range can be written as 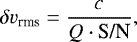(1)

where c is the speed of light and Q is the quality factor. The latter is essentially the cumulative spectral gradient across the wavelength range that is used for analysis. It depends on the intrinsic spectral features of the star, but also on additional line broadening, in particular, spectral resolution and stellar surface rotation, v sini.

4.1 Empirical radial velocity information

For all CARMENES observations, we have empirical values of δvrms for each individual spectral order. For details on the calculation of δvrms, we refer to Zechmeister et al. (2018), where it is called ϵv. In short, our pipeline fits each individual spectrum to a coadded template calculated from all our observations of that star. The value of δvrms is the uncertainty of the optimal radial velocity in this fit. We begin our analysis of the RV precision by looking into its dependence on wavelength for different M-star spectral types. For this analysis, we used 6625 observations that were taken with both CARMENES channels simultaneously. Observations were only considered for the 261 stars that were observed more than five times with each of the channels. Of these data, the values of δvrms differ even for stars of the same spectral types because the individual stars are not equally bright and they are observed under varying sky conditions, which results in different S/Ns. Furthermore, the quality factor can differ between stars of the same spectral type because of rotation. In order to make our observations comparable, we rescaled the RV precisions δvrms for each individual spectrum according to S/N and v sini. Before doing so, we checked in the individual values that δvrms could be described as a function of both S/N and v sini. In both cases, we found clear relations for all stars of a given spectral type by comparing δvrms in one order. The relations are identical between the different spectral types. As expected, we find that δvrms is directly proportional to S/N−1. For the dependence on v sini, we find a relation of 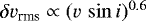. We scaled the values of δvrms between different stars and observations to a fiducial observation of a slowly rotating star observed at an S/N of 150 per resolution element in the J band.

We show in Fig. 6 the rescaled RV precision δvrms for all individual spectral orders for which RVs were calculated by our analysis procedure (excluding orders with very heavy telluric contamination or too low S/N). The wavelength range we considered for this analysis is 550–1700 nm. From the rescaled values, we computed for each order the median value from all observations of stars with similar spectral types. These are the black points plotted in the individual panels of Fig. 6. The error bars shown are the 25th and the 75th percentile of all observations, that is, half of all observations for any given spectral type and spectral order fall within the range of the error bars. The number of observations used for each spectral type plot is given in upper right corner of each panel.

The information from individual orders is very useful to assess the amount of information in small spectral regions. To gain a better idea about the RV precision calculated from larger wavelength areas, we quadratically added the RV information from different spectral orders in 100 nm (VIS) or 200 nm (NIR) bands. This choice is rather arbitrary, but it partially reflects the fact that at constant spectral resolution, and at wavelengths that are longer by a factor of two, the same number of resolution elements are contained in a range that is a factor of two longer in units of wavelength. In the NIR channel, our 200 nm chunks are also similar to the Y , J, and H bands. Their values are shown as gray circles with horizontal lines that mark the wavelength ranges covered in each band. Finally, we quadratically added RV information across the wavelength ranges that are covered by the CARMENES VIS and NIR channels in blue and red, respectively.

From our general considerations about S/N and the distribution of spectroscopic features (Sect. 1), we expect that in early-M type stars the larger amount of spectroscopic information at shorter wavelengths leads to better RV precision at visual wavelengths than at infrared wavelengths. In late-M type stars, however, the general lack of photons at visual wavelengths must lead to a severe loss of information so that the RV precision at infrared wavelengths improves relative to the performance at visual wavelengths. This picture is consistent with the empirical results we obtain from Fig. 6. In all stars of spectral type M0–M5, the RV precision improves from the shortest wavelengths at 550 nm toward 700 nm, where much RV information is contained in the TiO band that starts at 706 nm. The next spectral orders up to about 900 nm perform somewhat worse, but still relatively well. We find another region of excellent RV precision around 770 nm, where the TiO system that sets in around 760 nm is no longer contaminated by the oxygen A band. Spectral orders at wavelengths longer than 900 nm carry significantly less RV information than those at shorter wavelengths in stars of spectral types M0–M5. Specifically, when we combined all RV information in the wavelength ranges covered by CARMENES VIS and NIR (550–960 nm and 960–1700 nm, respectively), we found that in stars of spectral type M5, the RV information content is about a factor of 2.5 higher in the VIS channel than in the NIR channel.

For stars of spectral type M6 and later, we can observe in Fig. 6 the influence of the spectral energy distribution on RV precision. Inour M6 and M7 stars, we can still compute RVs at wavelengths down to 550 nm, but the poor S/N leads to typical RV precisions exceeding 20m s−1 (the spectral orders at wavelengths shorter than 650 nm are no longer computed in M8 and M9 stars). Nevertheless, the RV precision we observe in stars of spectral types M6–M9 is still relatively high (the values are low) at red visual wavelengths. In M6 and M7 stars, most RV information is available at wavelengths 700–900 nm, and the combined VIS channel information outperforms the NIR channel information by approximately 50%. In our combined sample of M8 and M9 stars, the VIS and the NIR channel are roughly equal in terms of RV information.In particular, these stars still show a high RV signal at 800–900 nm. Similar performance is reached in the Y and H bands; the J band provides slightly less information.

thumbnail Fig. 6

Empirical RV precision (δvrms) for individual spectral orders of CARMENES observed in the sample stars. Each panel shows for each order the median value for all observations taken of stars with spectral types M0 and M0.5 (upper left panel), M1 and M1.5 (upper right panel), and so forth. Error bars mark the 25th and 75th percentile of all observations. Gray points show quadratically added δvrms for 100 or 200 nm wide spectral windows, as indicated by the horizontal bars. Blue and red symbols show the CARMENES VIS and NIR spectral ranges. The number of observations per spectral type is given in the upper right corner of each panel.

4.2 Spectroscopic information and signal-to-noise ratio

As next step, we aim to distinguish the factors of δvrms, Q, and S/N, and individually show them as a function of wavelength. Our goal here is to see in which way the influence of S/N and the amount of spectral information,Q, determines the RV precision in M dwarfs. As an example of the S/N as a function of wavelength, we show normalized S/N curves for three stars in the top panel of Fig. 7 as observed with CARMENES. For our example, we again selected the three stars shown in our spectroscopic atlas: M1: GX And (black), M3.5: Luyten’s star (orange), and M7: Teegarden’s star (red). The S/N curves are normalized to S/N = 150 at J band. We clearly see the lack of signal at short wavelengths in the very cool M7 star. For the S/N curve, we used all available spectral orders, including those with strong telluric absorption. Thus, the S/N here is a combination of the stellar flux and telluric absorption.

In the center panel of Fig. 7, we visualize the amount of spectroscopic information (c∕Q) that we calculated from observed spectra of the three example stars. We computed this value as the cumulative spectral gradient across the wavelength ranges, see Eq. (6) in Butler et al. (1996). The wavelength regions are the same 100 nm and 200 nm wide windows as in Fig. 6. For this computation, we used the coadded spectra from all observations of our three example stars; see Zechmeister et al. (2018) for details. During coadding, wavelength regions contaminated by telluric lines were masked. As discussed below, this is a potential source of uncertainty particularly at long wavelengths, where telluric contamination is significant. For the computation of c∕Q, the photon noise in the coadded spectra is negligible. The number of observations used per star at VIS/NIR are GX And: 181/163; Luyten’s star: 691/677; and Teegarden’s star: 48/43. In all three example stars, there is significantly more RV information at shorter wavelengths. Furthermore, the spectra of cooler stars carry more RV information than the spectra from early-M dwarfs because they exhibit more spectral features from molecular absorption.

In the bottom panel of Fig. 7, we compare RV uncertainties for CARMENES spectra following two different approaches: a) assuming a signal-to-noise ratio of S∕N = 150 at the J band, we calculate the amount of spectroscopic RV information, (c∕Q)∕S∕N, using a coadded high-quality spectrum for each of our example stars (filled circles; see Eq. 1); and b) from a large number of observations (e.g., 2041 CARMENES observations of M3 and M3.5 stars), we calculated the median of their internal RV uncertainties, δvrms, (open stars) from fitting every individual spectrum to a coadded template of the observed star as shown in Fig. 6 (scaled to S∕N = 150 at the J band and slow rotation, see above). With this comparison, we aim to reveal any systematic problems in our RV determination. In general, the values calculated following the two different approaches compare very well; for all wavelength bands and spectral types, they agree within a factor of two; most of the values agree even better. Consistent with our calculations from spectral fitting, our analysis of the S/N and the amount of spectrosopic features shows that in all M dwarfs down to M7, the highest RV precision can be reached at around 700 nm or 800 nm. At 600 nm, observations of M dwarfs show considerably lower RV precision because of their very low S/N. At 700 and 800 nm, however, the signal is still high enough to provide higher RV precision than regions at longer wavelengths (it levels out only in M8/9 stars, see Fig. 6). The reason for this is the substantial loss in spectroscopic features from VIS to NIR wavelengths.

One important source of uncertainty in our calculation of Q is the occurrence of telluric features, in particular, at infrared wavelengths. In the bottom panel of Fig. 7, we observe that the values of (c∕Q)∕S∕N are lower than our measured RV precision, in particular in the J band. A possible explanation is that our coadded spectra are contaminated by telluric features. These features can contribute to Q because they introduce additional spectral gradients. They also increase the value of our empirically measured RV uncertainty because the individual observations and the coadded spectra do not resemble each other at these features. The result of poorly treated telluric lines is therefore a bias toward higher values in our empirical RV uncertainty and toward lower values in the uncertainty estimate (c∕Q)∕S∕N. We identify the treatment of telluric lines as one of the main areas where infrared (and also red visual) RV precision can be improved, but we also note that in the presence of a sufficient amount of spectroscopic features like in our M7 star, this appears to be a negligible problem.

There are a number of instrumental effects that can affect our analysis of precision vs. λ from the CARMENES data. These effects include global efficiency offsets between the VIS and the NIR, varying spectrograph throughput and detector efficiency, or λ-dependent read noise. The difference in spectral resolution between the VIS and the NIR channel slightly penalizes the NIR channel RV precision, but the expected effect is on the order of only 10% and not significant for our conclusions. Although our analysis was carried out using observed data and S/N values that were determined empirically, we note that instrumental effects may be hidden. However, the two CARMENES channels are very similar in their optical design and performance, and our results can probably be taken as fairly typical for other high-resolution spectrographs.

thumbnail Fig. 7

Comparison between empirical values for RV precision δvrms and its constituents S/N and c∕Q. Top panel: normalized S/N from individual spectra of GX And (M1), Luyten’s star (M3.5), and Teegarden’s star (M7). Middle panel: cumulative spectroscopic information c∕Q calculated from coadded spectra of the three example stars. Bottom panel: ratio between c∕Q and S/N (filled circles) together with empirical values of δvrms (open stars, see Fig. 6).

5 Summary

After all targets of the CARMENES survey were observed at least once, we derived basic spectroscopic information for each target about radial velocity, Hα emission, and projected surface rotation. We provide this information together with the list of the 324 targets of our CARMENES M-dwarf survey in this work. For each star, we provide one spectrum observed with the two CARMENES channels, which cover the wavelength range 550–1700 nm. This is the first large library of high-resolution near-infrared spectra of low-mass stars. We also show a spectroscopic atlas of three example M dwarfs (M1, M3.5, M7) and compare their spectra to a telluric standard and synthetic models at very high spectral resolution. We find that the synthetic spectra in general succeed in predicting the main features in M-dwarf spectra, but the amount of spectroscopic features is sometimes higher than in the models.

Our analysis of stellar rotation and activity adds precise v sin i measurements to the available catalogues of M-dwarf rotation. Several of our stars rotate as fast as v sin i = 20 km s−1 and more. Our values are included in the more detailed analysis of rotation and activity by Jeffers et al. (2017). They are consistent with the general picture of M-dwarf activity. We find some very early M-dwarfs that exhibit significant rotation but no Hα emission. These stars have rotation periods close to P = 10 d, and they are probably rotating slowly enough to explain the lack of Hα emission (see also Jeffers et al. 2017).

We employed several thousand observations of M dwarfs taken at visual and near-infrared wavelengths to calculate the RV uncertainty as a function of wavelength for individual spectral subtypes. We conclude that the wavelength range 700–900 nm provides an excellent source of RV information for all M dwarfs. At shorter wavelengths, the RV precision is lower and deteriorates toward later spectral types. At longer wavelengths, the RV precision is significantly lower up to spectral types M6/M7. The turnover point where RV information content at NIR wavelengths becomes comparable to the one at VIS wavelengths is located at spectral types as late as M8/M9.

Our results answer the question at which wavelength the best RV precision can be reached in observations of M dwarfs with a stabilized spectrograph: the optimal range for M-dwarf RV spectroscopy is the spectral range 700–900 nm. Calculating the spectroscopic quality factor Q and the S/N for three example stars, we showed that our conclusions about the RV uncertainties are consistent with the spectroscopic information we find in the spectra. At wavelengths shorter than 700 nm, the lack of photons limits the RV precision; at wavelengths longer than 900 nm, the amount of spectroscopic information is so much lower than at shorter wavelengths that the advantage in S/N cannot compensate for the loss in RV precision. Only in the latest spectral types (M8 and M9) did we find the RV precision at near-infrared wavelengths to match the amount of information at shorter wavelengths.

Our result is especially interesting for other planned M-dwarf surveys and the spectroscopic follow-up of transiting M dwarfs. Instruments used for this purpose are often mounted at 4m class telescopes that have a similar performance as the 3.5m telescope at Calar Alto that is used for the CARMENES survey. For these, very late-M dwarfs are difficult to observe because they are extremely faint (at all wavelengths), and the limited RV precision is further affected by their often high rotation rates. Thus, instruments at 4m class telescopes will typically reach an RV precision on the order of 1 m s−1 only in early- and mid-M dwarfs, where the spectral range 700–900 nm is the most efficient. However, an RV precision of 2 m s−1 can be reached at 4m class telescopes within reasonable times in many stars of spectral type M6 and earlier. Here, NIR RV data cannot outperform red visual RV observations, but NIR RVs can reach below the typical limit of radial velocity jitter in M dwarfs that is on the order of 3–4 m s−1 (Bonfils et al. 2013). The main reasons for this jitter are corotating active regions (including their effect on convective blueshift) and granulation, and their RV signal is expected to be wavelength dependent. The combination of RV observations at visual and near-infrared wavelengths is ideal to distinguish between Keplerian signals and stellar variability. CARMENES delivers these data across a very large wavelength range. It is therefore optimally suited to search for low-mass planets around mid-type M dwarfs where variability is a serious concern.

Acknowledgements

We thank an anonymous referee for prompt attention and helpful comments that helped to improve the quality of this paper. CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Economy, the German Science Foundation through the Major Research Instrumentation Programme and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. We acknowledge the following funding programs: European Research Council (ERC-279347), Deutsche Forschungsgemeinschaft (RE 1664/12-1, RE 2694/4-1), Bundesministerium für Bildung und Forschung (BMBF-05A14MG3, BMBF-05A17MG3), Spanish Ministry of Economy and Competitiveness (MINECO, grants AYA2015-68012-C2-2-P, AYA2016-79425-C3-1,2,3-P, AYA2015-69350-C3-2-P, AYA2014-54348-C03-01, AYA2014-56359-P, AYA2014-54348-C3-2-R, AYA2016-79425-C3-3-P and 2013 Ramòn y Cajal program RYC-2013-14875), Fondo Europeo de Desarrollo Regional (FEDER, grant ESP2016-80435-C2-1-R, ESP2015-65712- C5-5-R), Generalitat de Catalunya/CERCA programme, Spanish Ministerio de Educación, Cultura y Deporte, programa de Formación de Profesorado Universitario (grant FPU15/01476), Deutsches Zentrum für Luft- und Raumfahrt (grants 50OW0204 and 50OO1501), Office of Naval Research Global (award no. N62909-15-1-2011), Mexican CONACyT grant CB-2012-183007.

Appendix A Atlas of near-infrared spectra

In Fig. A.1 we plot spectra of a telluric standard star and three survey targets in black and the synthetic model spectra in red. See Sect. 3 for details.

thumbnail Fig. A.1

CARMENES spectral atlas.

Appendix B Table of targets

Basic data for the CARMENES GTO targets are provided in Table B.1. Columns are discussed in the main text. Uncertainties for estimates of the inclination angle i are computed only from the uncertainties in v sini.

Table B.1

Basic data of the CARMENES GTO sample.

References

  1. Alonso-Floriano, F. J., Morales, J. C., Caballero, J. A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Amado, P. J. 2007, Commun. Asteroseismol., 151, 57 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amado, P. J., Suárez, J. C., Garrido, R., Moya, A., & Martín-Ruiz, S. 2007, Commun. Asteroseismol., 150, 311 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anglada-Escudé, G., Tuomi, M., Gerlach, E., et al. 2013, A&A, 556, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Anglada-Escudé, G., Arriagada, P., Tuomi, M., et al. 2014, MNRAS, 443, L89 [NASA ADS] [CrossRef] [Google Scholar]
  6. Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Artigau, É., Kouach, D., Donati, J.-F., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914715 [CrossRef] [Google Scholar]
  8. Baliunas, S. L., Hartmann, L., Noyes, R. W., et al. 1983, ApJ, 275, 752 [NASA ADS] [CrossRef] [Google Scholar]
  9. Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
  10. Barnes, J. R., Jeffers, S. V., & Jones, H. R. A. 2011, MNRAS, 412, 1599 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barnes, J. R., Jeffers, S. V., Anglada-Escudé, G., et al. 2017, MNRAS, 466, 1733 [NASA ADS] [CrossRef] [Google Scholar]
  12. Benedict, G. F., Henry, T. J., Franz, O. G., et al. 2016, AJ, 152, 141 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bottom, M., Muirhead, P. S., Johnson, J. A., & Blake, C. H. 2013, PASP, 125, 240 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
  17. Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, in Observatory Operations: Strategies, Processes, and Systems VI, Proc. SPIE, 9910, 99100E [Google Scholar]
  18. Campbell, B., & Walker, G. A. H. 1979, PASP, 91, 540 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cegla, H. M., Stassun, K. G., Watson, C. A., Bastien, F. A., & Pepper, J. 2014, ApJ, 780, 104 [CrossRef] [Google Scholar]
  20. Chugainov, P. F. 1974, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 52, 3 [NASA ADS] [Google Scholar]
  21. Claudi, R., Benatti, S., Carleo, I., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 99081A [Google Scholar]
  22. Connes, P. 1985, Ap&SS, 110, 211 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cortés-Contreras, M., Béjar, V. J. S., Caballero, J. A., et al. 2017, A&A, 597, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Crepp, J. R., Crass, J., King, D., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990819 [CrossRef] [Google Scholar]
  25. Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
  26. Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
  27. Desort, M., Lagrange, A.-M., Galland, F., Udry, S., & Mayor, M. 2007, A&A, 473, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Fekel, F. C., & Henry, G. W. 2000, AJ, 120, 3265 [NASA ADS] [CrossRef] [Google Scholar]
  29. Figueira, P., Adibekyan, V. Z., Oshagh, M., et al. 2016, A&A, 586, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Fischer, D. A., Anglada-Escude, G., Arriagada, P., et al. 2016, PASP, 128, 066001 [NASA ADS] [CrossRef] [Google Scholar]
  31. Garcia-Piquer, A., Morales, J. C., Ribas, I., et al. 2017, A&A, 604, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gibson, S. R., Howard, A. W., Marcy, G. W., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990870 [CrossRef] [Google Scholar]
  33. Gizis, J. E., Reid, I. N., & Hawley, S. L. 2002, AJ, 123, 3356 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hartman, J. D., Bakos, G. Á., Noyes, R. W., et al. 2011, AJ, 141, 166 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hawley, S. L., Gizis, J. E., & Reid, I. N. 1996, AJ, 112, 2799 [NASA ADS] [CrossRef] [Google Scholar]
  36. Herzberg, G. 1950, Molecular spectra and molecular structure, Vol. 1: Spectra of diatomic molecules [Google Scholar]
  37. Houdebine, E. R., & Mullan, D. J. 2015, ApJ, 801, 106 [NASA ADS] [CrossRef] [Google Scholar]
  38. Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
  40. Jeffers, S. V., Barnes, J. R., Jones, H. R. A., et al. 2014, MNRAS, 438, 2717 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jeffers, S. V., Schöfer, P., Lamert, A., et al. 2017, A&A, submitted [Google Scholar]
  42. Jurgenson, C., Fischer, D., McCracken, T., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 99086T [Google Scholar]
  43. Kiraga, M. 2012, Acta Astron., 62, 67 [NASA ADS] [Google Scholar]
  44. Kiraga, M., & Stȩpień K. 2013, Acta Astron., 63, 53 [NASA ADS] [Google Scholar]
  45. Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
  46. Kochukhov, O., & Lavail, A. 2017, ApJ, 835, L4 [NASA ADS] [CrossRef] [Google Scholar]
  47. Korhonen, H., Vida, K., Husarik, M., et al. 2010, Astron. Nachr., 331, 772 [NASA ADS] [CrossRef] [Google Scholar]
  48. Korhonen, H., Andersen, J. M., Piskunov, N., et al. 2015, MNRAS, 448, 3038 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Kotani, T., Tamura, M., Suto, H., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914714 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Lanza, A. F., Molaro, P., Monaco, L., & Haywood, R. D. 2016, A&A, 587, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lebzelter, T., Seifahrt, A., Uttenthaler, S., et al. 2012, A&A, 539, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Lépine, S., Hilton, E. J., Mann, A. W., et al. 2013, AJ, 145, 102 [NASA ADS] [CrossRef] [Google Scholar]
  54. Mahadevan, S., Ramsey, L. W., Terrien, R., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471G [Google Scholar]
  55. Marchwinski, R. C., Mahadevan, S., Robertson, P., Ramsey, L., & Harder, J. 2015, ApJ, 798, 63 [NASA ADS] [CrossRef] [Google Scholar]
  56. Martín, E. L., Guenther, E., Barrado y Navascués, D., et al. 2005, Astron. Nachr., 326, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  57. Martín, E. L., Guenther, E., Zapatero Osorio, M. R., Bouy, H., & Wainscoat, R. 2006, ApJ, 644, L75 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mayor, M., Bonfils, X., Forveille, T., et al. 2009a, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Mayor, M., Udry, S., Lovis, C., et al. 2009b, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Merline, W. J. 1985, in Stellar Radial Velocities, eds. A. G. D. Philip, & D. W. Latham, Proc. IAU Colloq., 88, 87 [NASA ADS] [Google Scholar]
  61. Meunier, N., Desort, M., & Lagrange, A.-M. 2010a, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Meunier, N., Lagrange, A.-M., & Desort, M. 2010b, A&A, 519, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Newton, E. R., Irwin, J., Charbonneau, D., et al. 2016, ApJ, 821, 93 [NASA ADS] [CrossRef] [Google Scholar]
  64. Norton, A. J., Wheatley, P. J., West, R. G., et al. 2007, A&A, 467, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Oliva, E., Origlia, L., Scuderi, S., et al. 2015, A&A, 581, A [Google Scholar]
  66. Pepe, F. A., Cristiani, S., Rebolo Lopez, R., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77350 [Google Scholar]
  67. Plavchan, P., Latham, D., Gaudi, S., et al. 2015, ArXiv e-prints [arxiv:1503.01770] [Google Scholar]
  68. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990812 [Google Scholar]
  69. Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
  70. Reiners, A. 2007, A&A, 467, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Reiners, A., & Basri, G. 2006, ApJ, 644, 497 [NASA ADS] [CrossRef] [Google Scholar]
  72. Reiners, A., & Basri, G. 2008, ApJ, 684, 1390 [NASA ADS] [CrossRef] [Google Scholar]
  73. Reiners, A., Homeier, D., Hauschildt, P. H., & Allard, F. 2007, A&A, 473, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
  75. Reiners, A., Joshi, N., & Goldman, B. 2012, AJ, 143, 93 [NASA ADS] [CrossRef] [Google Scholar]
  76. Reiners, A., Shulyak, D., Anglada-Escudé, G., et al. 2013, A&A, 552, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Rivera, E. J., Lissauer, J. J., Butler, R. P., et al. 2005, ApJ, 634, 625 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rodler, F., Del Burgo, C., Witte, S., et al. 2011, A&A, 532, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
  80. Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
  81. Scalo, J., Kaltenegger, L., Segura, A. G., et al. 2007, Astrobiology, 7, 85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  82. Seifahrt, A., Bean, J. L., Stürmer, J., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 990818 [CrossRef] [Google Scholar]
  83. Shulyak, D., Seifahrt, A., Reiners, A., Kochukhov, O., & Piskunov, N. 2011, MNRAS, 418, 2548 [NASA ADS] [CrossRef] [Google Scholar]
  84. Shulyak, D., Reiners, A., Engeln, A., et al. 2017, Nat. Astron., 1, 0184 [NASA ADS] [CrossRef] [Google Scholar]
  85. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  86. Soubiran, C., Jasniewicz, G., Chemin, L., et al. 2013, A&A, 552, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
  88. Suárez Mascareño, A., Rebolo, R., & González Hernández J. I. 2016, A&A, 595, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Tarter, J. C., Backus, P. R., Mancinelli, R. L., et al. 2007, Astrobiology, 7, 30 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  90. Testa, P., Drake, J. J., & Peres, G. 2004, ApJ, 617, 508 [NASA ADS] [CrossRef] [Google Scholar]
  91. Tinney, C. G., & Reid, I. N. 1998, MNRAS, 301, 1031 [NASA ADS] [CrossRef] [Google Scholar]
  92. Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
  94. Wang, J., & Ford, E. B. 2011, MNRAS, 418, 1822 [NASA ADS] [CrossRef] [Google Scholar]
  95. West, A. A., Weisenburger, K. L., Irwin, J., et al. 2015, ApJ, 812, 3 [NASA ADS] [CrossRef] [Google Scholar]
  96. Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
3

We note that observations and models also disagree in several strong alkali lines where the models predict too wide damping wings (see, e.g., Reiners et al. 2007), and the models overpredict the strength of the lithium line at 670.8 nm because lithium depletion was not taken into account.

All Tables

Table 1

Refererence stars used for the calculation of vsini.

In the text
Table 2

Basic information about spectra shown in the spectral atlas.

In the text
Table B.1

Basic data of the CARMENES GTO sample.

In the text

All Figures

thumbnail Fig. 1

Overview of the CARMENES spectral range. The spectrum covered by the VIS channel is shown in blue, and the NIR channel in red. The target shown is the A2V star 50 Cas. The stellar spectrum only exihibits a few hydrogen lines, all strong features are from Earth’s atmosphere.
In the text
thumbnail Fig. 2

From top to bottom: distribution of the CARMENES survey sample in spectral type, mass, and J-band magnitude. The subsample of stars with Hα emission is shown in red.
In the text
thumbnail Fig. 3

J-band magnitude (left panel) and mass (right panel) for all stars of the CARMENES survey sample.
In the text
thumbnail Fig. 4

Projected rotation velocity vsini as a functionof stellar mass. Stars with detected Hα emission are shown as filled circles, and stars with no Hα emission are shown as open circles. Colors indicate the level of Hα emission as shown in the legend. Slow rotators are plotted at our detection limit of v sin i = 2 km s−1. The red dashed line indicates values of vEq for stars with rotation periods P = 10 d. Above this line, Hα is always expected in emission (see text).
In the text
thumbnail Fig. 5

Comparison between vsini and equatorial velocity v estimated from photometric period and radius. Active stars are indicated as filled circles as in Fig. 4. Dashed lines show expected relations between v sin i and v for inclination angles i = 90°, 50°, 30°, and 10°.
In the text
thumbnail Fig. 6

Empirical RV precision (δvrms) for individual spectral orders of CARMENES observed in the sample stars. Each panel shows for each order the median value for all observations taken of stars with spectral types M0 and M0.5 (upper left panel), M1 and M1.5 (upper right panel), and so forth. Error bars mark the 25th and 75th percentile of all observations. Gray points show quadratically added δvrms for 100 or 200 nm wide spectral windows, as indicated by the horizontal bars. Blue and red symbols show the CARMENES VIS and NIR spectral ranges. The number of observations per spectral type is given in the upper right corner of each panel.
In the text
thumbnail Fig. 7

Comparison between empirical values for RV precision δvrms and its constituents S/N and c∕Q. Top panel: normalized S/N from individual spectra of GX And (M1), Luyten’s star (M3.5), and Teegarden’s star (M7). Middle panel: cumulative spectroscopic information c∕Q calculated from coadded spectra of the three example stars. Bottom panel: ratio between c∕Q and S/N (filled circles) together with empirical values of δvrms (open stars, see Fig. 6).
In the text
thumbnail Fig. A.1

CARMENES spectral atlas.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.