| Issue |
A&A
Volume 612, April 2018
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201731932 | |
| Published online | 13 April 2018 | |
Model-independent and model-based local lensing properties of CL0024+1654 from multiply imaged galaxies
1
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik,
Philosophenweg 12,
69120
Heidelberg, Germany
e-mail: j.wagner@uni-heidelberg.de
2
Heidelberg Institute for Theoretical Studies,
69118
Heidelberg, Germany
3
Expertisecentrum voor Digitale Media, Universiteit Hasselt,
Wetenschapspark 2,
3590
Diepenbeek, Belgium
e-mail: jori.liesenborgs@uhasselt.be
4
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester,
Alan Turing Building, Oxford Road,
Manchester
M13 9PL, UK
e-mail: nicolas.tessore@manchester.co.uk
Received:
11
September
2017
Accepted:
11
December
2017
Context. Local gravitational lensing properties, such as convergence and shear, determined at the positions of multiply imaged background objects, yield valuable information on the smaller-scale lensing matter distribution in the central part of galaxy clusters. Highly distorted multiple images with resolved brightness features like the ones observed in CL0024 allow us to study these local lensing properties and to tighten the constraints on the properties of dark matter on sub-cluster scale.
Aim. We investigate to what precision local magnification ratios, 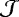 , ratios of convergences, f, and reduced shears, g = (g1, g2), can be determined independently of a lens model for the five resolved multiple images of the source at zs = 1.675 in CL0024. We also determine if a comparison to the respective results obtained by the parametric modelling tool Lenstool and by the non-parametric modelling tool Grale can detect biases in the models. For these lens models, we analyse the influence of the number and location of the constraints from multiple images on the lens properties at the positions of the five multiple images of the source at zs = 1.675.
, ratios of convergences, f, and reduced shears, g = (g1, g2), can be determined independently of a lens model for the five resolved multiple images of the source at zs = 1.675 in CL0024. We also determine if a comparison to the respective results obtained by the parametric modelling tool Lenstool and by the non-parametric modelling tool Grale can detect biases in the models. For these lens models, we analyse the influence of the number and location of the constraints from multiple images on the lens properties at the positions of the five multiple images of the source at zs = 1.675.
Methods. Our model-independent approach uses a linear mapping between the five resolved multiple images to determine the magnification ratios, ratios of convergences, and reduced shears at their positions. With constraints from up to six multiple image systems, we generate Lenstool and Grale models using the same image positions, cosmological parameters, and number of generated convergence and shear maps to determine the local values of 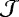 , f, and g at the same positions across all methods.
, f, and g at the same positions across all methods.
Results. All approaches show strong agreement on the local values of 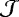 , f, and g. We find that Lenstool obtains the tightest confidence bounds even for convergences around one using constraints from six multiple-image systems, while the best Grale model is generated only using constraints from all multiple images with resolved brightness features and adding limited small-scale mass corrections. Yet, confidence bounds as large as the values themselves can occur for convergences close to one in all approaches.
, f, and g. We find that Lenstool obtains the tightest confidence bounds even for convergences around one using constraints from six multiple-image systems, while the best Grale model is generated only using constraints from all multiple images with resolved brightness features and adding limited small-scale mass corrections. Yet, confidence bounds as large as the values themselves can occur for convergences close to one in all approaches.
Conclusions. Our results agree with previous findings, support the light-traces-mass assumption, and the merger hypothesis for CL0024. Comparing the different approaches can detect model biases. The model-independent approach determines the local lens properties to a comparable precision in less than one second.
Key words: dark matter / gravitational lensing: strong / methods: data analysis / methods: analytical / galaxies: clusters: individual: CL0024+1654 / galaxies: luminosity function, mass function
© ESO 2018
1 Motivation and related work
The Frontier Fields Lens Modelling Comparison Project (Meneghetti et al. 2017) is the most encompassing systematic comparison of lens modelling approaches so far. It employs simulated data of unresolved multiple images in two artificially generated galaxy clusters. From this comparison we know that the mass enclosed in the critical curves of a galaxy cluster is determined to only a few percent inaccuracy and imprecision by any lens modelling approach. In contrast, the accuracy and precision of local convergence and shear values strongly depend on the number and positions of the multiple images observed. This, in turn, sets the limits on the accuracy and precision by which the distribution and properties of small-scale compact dark matter can be determined, for example, in Diego et al. (2017).
Simulations of multiple images showing distinctive features in their brightness distributions are yet to be developed. So far, real galaxies extracted from deep HST observations have been employed to model the brightness distributions of sources in simulations, as, for example, in Meneghetti et al. (2017). Hence, the multiple images appear unstructured in current simulations because the high magnification regions in the strong lensing regime require a resolution beyond that of the HST cameras for the sources to obtain images with resolved brightness features. Thus, we rely on the galaxy cluster CL0024 to compare the model-independent reconstruction of local ratios of convergences and reduced shear values developed in Tessore (2017) with the parametric lens modelling approach Lenstool, and the non-parametric lens modelling approach Grale. The model-independent approach was tested using simulations in Wagner & Tessore (2018). Lenstool was developed in Kneib et al. (1996); Jullo et al. (2007), and Grale in Liesenborgs et al. (2006, 2010).
CL0024 is a well-studied cluster, whose strong lensing properties have been investigated, for example, in Broadhurst et al. (2000); Colley et al. (1996); Jee et al. (2007); Liesenborgs et al. (2008); Richard et al. (2011); Umetsu et al. (2010); Zitrin et al. (2009). Therefore, we do not develop more advanced models but focus on the model comparison with the model-independent approach. The cluster contains one system of five multiple images. Each of them shows six distinctive features in the brightness distribution which can be used to determine ratios of convergences and reduced shears at the positions of the multiple images without the use of a lens model, as described in Tessore (2017) and Wagner & Tessore (2018). In addition, a multitude of systems of non-resolved multiple images are proposed in this cluster, for example, in Zitrin et al. (2009), which we also employ here to set up the Lenstool and Grale lens models.
Using the same cosmological parameter values and positions of multiple-image systems, we calculate the Lenstool and Grale lens models. We retrieve the local ratios of convergences and reduced shears from the respective maps at the same positions to compare them to the same lens properties calculated from the model-independent approach at these positions. This direct comparison between the two model-based and the model-independent local lens properties allows us to investigate differences and similarities between the different lens reconstruction ansatzes. Furthermore, we investigate whether or not the comparison can determine if the light-traces-mass assumption usually employed in parametric lens modelling is fulfilled, and whether or not we can set a scale below which further refinements of a non-parametric lens model may overfit the model to the data. This may generate dark matter artefacts, as possibly found in Jee et al. (2007) and discussed in Ponente & Diego (2011).
We also investigate the robustness of the local convergence ratios and reduced shear values of the model-based approaches when we reduce the number of multiple-image systems that are used for the lens modelling. This analysis shows how strong constraints from multiple images of one system influence the convergence ratios and reduced shear values at the positions of neighbouring multiple images of other systems. It also determines whether the multiple-image positions of one system suffice as input constraints for the lens model in order to yield the local convergence ratios and reduced shears at these positions.
The paper is organised as follows: After the introduction of the multiple-image systems in CL0024 that we employ in Sect. 2, we describe how the model-independent information is calculated in Sect. 3. Then, we generate the Lenstool and Grale model-based reconstructions of CL0024 in Sect. 4 and extract the same information from their convergence and shear maps as can be retrieved from the model-independent approach. Based on this information, a comparison of all three approaches is performed in Sect. 5, of which the results are summarised in Sect. 6.
2 Multiple-image systems in CL0024
In CL0024, a multitude of multiple-image-system candidates has been detected and used to reconstruct the lensing properties of the galaxy cluster (see Sect. 1). However, only for one five-image system has a spectroscopic redshift been measured so far (Broadhurst et al. 2000), corroborating the lensing hypothesis for these images. The most systematic collection of multiple-image-system candidates together with photometric redshift estimates was published in Zitrin et al. (2009), which we use in the following. As none of the candidate systems 2–11 of Zitrin et al. (2009) are confirmed spectroscopically, not all of them need to be true multiple-image systems. Therefore, we employ only a subset of those candidate systems close to system 1, guided by an initial Lenstool reconstruction as detailed in Sect. 4.1.
To make the reconstructed local lens properties as comparable as possible, the model-based approaches employ the same positions of the six multiple-image systems listed in Table 1. In addition to the points in system 1 listed in Table 1, the model-independent reconstruction and Grale use the positions of up to five additional identifiable bright spots in all images of system 1 listed in Table 2. These points were determined by eye of the HST ACS/WFC image in the F475W band (PI:Ford 20041 ), in which these resolved features are most prominent.
Systems of multiple images employed in the model-based lens reconstructions.
3 Model-independent lens reconstruction
In Tessore (2017), it was shown how properties of strong gravitational lenses can be recovered in a model-independent fashion from the mapping of multiple images onto one another. Given n multiple images, the image maps φi are functions that map the arbitrarily chosen reference image 1 onto the multiple image i = 2, …, n. The Jacobian matrix of the image map φi is the relative magnification matrix 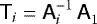 between images 1 and i, where A is the usual magnification matrix,
between images 1 and i, where A is the usual magnification matrix,
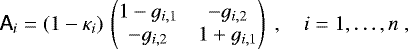 (1)
(1)
in terms of the convergence κ and the two components of the reduced shear g
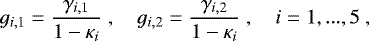 (2)
(2)
with γi,1 and γi,2 denoting the shear components for each image i, as defined in the usual notation by Schneider et al. (1992) with respect to the RA/Dec coordinate system.
Explicitly writing out the entries of Ti, i = 2, …, n,
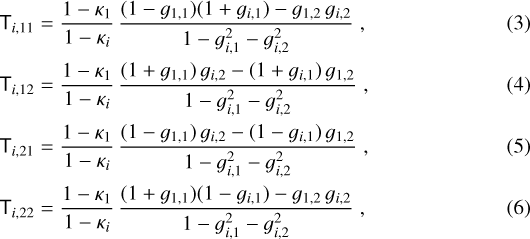
the reduced shears g1,j and gi,j, j = 1, 2, are generally recoverable, while the convergences κ1 and κi only appear in the form of a convergence ratio,
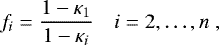 (7)
(7)
that scales all components of Ti equally. Therefore, neither κ1 nor κi can be recovered individually (this is also implied by the mass sheet degeneracy), and only the convergence ratios and reduced shears g1,1, g1,2, f2, g2,1, g2,2, … are observable properties of strong gravitational lenses at first order in the image mapping and hence second order in the deflection potential.
To reconstruct the values of f and g from a given relative magnification matrix T, it is useful to construct combinations of the entries (3)–(6),
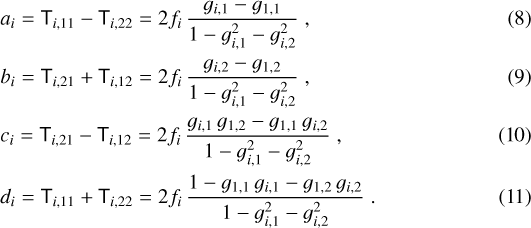
We note that ci and di are the curl and divergence of the image map, respectively. When at least three images 1, i, j are observed, the system of Eqs. (8)–(11) can be solved for the reduced shear of the reference image,

as well as the convergence ratio and shear of multiple image i,
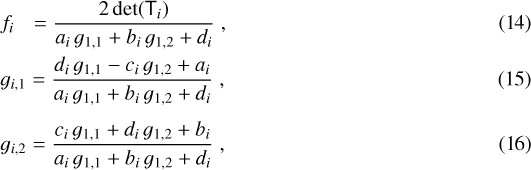
where det(Ti) is the determinant. The same expressions hold for multiple image j.
we relate the determinant of the transformation matrix to the magnification ratio between image i, μi, and image 1, μ1, which yields the relative parities between those images and can be compared to the respective measured flux ratios. Using Eqs. (3) to (6), the 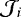 can be expressed in terms of the fi, gi,1, and gi,2, so that they do not yield additional information.
can be expressed in terms of the fi, gi,1, and gi,2, so that they do not yield additional information.
By constructing the image maps φi, i = 2, …, n, from observations and evaluating their Jacobian matrices, it is possible to measure the relative magnification matrix Ti directly from data. This in turn makes it possible to reconstruct the magnification ratios (17), convergence ratios (14), and reduced shears (15)–(16) – that is, the observable properties – of the gravitational lens in a completely model-independent manner.
Equations (2), (7), and (17) define lens properties that can also be extracted from model-based convergence and shear maps and thus be compared between all three lens reconstruction methods.
3.1 Linear image mapping by point matching
We assume that an observer has found a family of m points, also referred to as reference points in the following, individually labelled from 1 to m, that reliably show the same features across all multiple images. In addition, we require that convergence and shear do not vary significantly over the area covered by the family of points in each multiple image. Then, it is possible to approximate the image maps as linear transformations of conjugate points between the multiple images.
Let xij denote the point with index j = 1, …, m in multiple image i = 2, …, n, and x1j the corresponding point in the reference image 1. If the assumption of linearity holds, the image mapping is described by a matrix, which in this case is the relative magnification matrix Ti. Mapping the observed points x11, x12, … from reference image 1 to multiple image i should recover the observed points xij,
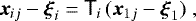 (18)
(18)
where ξi, ξ1 are anchor points for the affine transformation between multiple images 1 and i. Lens reconstruction by point matching amounts to finding a relative magnification matrix Ti that solves this equation for all points j in a given image i.
As the reconstructed Ti is the solution of the linearised mapping over the entire area covered by the family of points in a multiple image, it is not necessarily the same as the relative magnification matrix that would be obtained from a fully non-linear image map at the points ξi and ξ1. The anchor point ξ1 of the reference image is arbitrary, since it can be absorbed into the left-hand side of Eq. (18). However, it makes sense to pick ξ1 within the observed image, for example as the centroid of the points x1j. The locations of the remaining anchor points ξ2, ξ3, …, which are additional free parameters of the reconstruction, can then be understood as the images of ξ1 under the linearised image mapping.
In observations, the images xij of the reference points x1j will be localised with some level of uncertainty. The difference between an observed position xij and the prediction (18) can be modelled as a bivariate normal random variable,
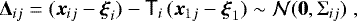 (19)
(19)
where the uncertainty in the observed position xij is described by a covariance matrix Σij. No uncertainty is associated with the reference points x1j, which are fixed by the observer. For given relative magnification matrices Ti, the quality of the reconstruction is then quantified by the χ2-value,
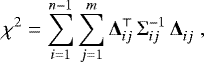 (20)
(20)
where the sum extends over n − 1 multiple images of the reference image 1 and their m observed points. Minimising the χ2 -term (20) returns best-fit values for the relative magnification matrices Ti and anchor points ξi, which are the degrees of freedom of the reconstruction. Figure 1 visualises the point matching using the six reference points in system 1 of Table 2 as example (left) and it shows a schematic of how the linear transformation is derived from the magnification matrices of two images with two reference points and one anchor point in each image (right).
 |
Fig. 1 CL0024 with detailed pictures of the five multiple images of system 1 (left). The user-defined reference points in the reference image 1 are marked by red circles, while the red-encircled regions in the remaining images denote 95% confidence bounds of the locations of the transformed reference points by the best-fit linear transformations. (Image credits: NASA, ESA, M. J. Jee (Johns Hopkins University)). Also shown is a diagram of the principle of extracting local lens properties from the linear transformation between multiple images from the same source (right). |
3.2 Parametrisation of the matrices
When more than three multiple images of a source are observed, the system of constraints for the convergence ratios and reduced shears is overdetermined, since the n − 1 relative magnification matrices have 4n − 4 coefficients, for 3n − 1 lens quantities (Tessore 2017). In this case, the relative magnification matrices Ti cannot directly be used as the parameters of the reconstruction: Each pair i, j of images could yield a different reduced shear over the reference image (12)–(13), leading to an inconsistent reconstruction.
To circumvent the problem, a suitable parametrisation of the matrices Ti can be adopted. A natural choice are the convergence ratio fi and reduced shear components gi,1, gi,2, so that the relative magnification matrices are given by expressions (3)–(6). In practice, this leads to a numerically difficult reconstruction: Due to the non-linear form of the expressions, the parameters fi, gi,1, gi,2 are strongly correlated, which makes the exploration of the parameter space difficult with simple numerical methods.
A more practical parametrisation keeps the optimisation problem as nearly linear as possible. This can be achieved by noting that for every relative magnification matrix Ti, there exists a relation between the ai, bi and ci coefficients (8)–(10) and the reduced shear g1,1, g1,2 over the reference image,
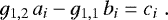 (21)
(21)
Hence it is possible to use the coefficients ai, bi, di for multiple images i = 2, …, n, together with the reduced shear g1,1, g1,2 over the reference image as the parameters of the reconstruction and write the relative magnification matrices as
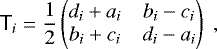 (22)
(22)
where the coefficient ci must be computed from the relation in Eq. (21). With this parametrisation, the reconstruction remains consistent and, at the same time, easy to handle with standard numerical methods.
3.3 Implementation
An implementation of the image mapping technique presented here is publicly available2 . The ptmatch routine will take a list of reference points with optional uncertainties and perform the point matching described above. Also provided are converters between relative magnification matrices and lens quantities, as well as utilities for producing mapped images and a source reconstruction.
The C implementation of the MPFIT routine Markwardt (2009) is used to minimise the χ2 - term (20) and returns the best-fit values for the reduced shear g1,1, g1,2 of the reference image, the coefficients ai, bi, di of the relative magnification matrices, and the components ξi,1, ξi,2 of the anchor points, resulting in a total number of 5n − 3 parameters. The number of constraints from m points in n − 1 multiple images is 2 m (n − 1). Hence a minimum of three points in three images is necessary, in which case the system is solvable, as expected (Tessore 2017).
MPFIT requires the χ2-term (20) to be the sum of squares of uncorrelated random deviates 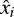 of unit variance,
of unit variance,
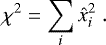 (23)
(23)
To bring the difference terms (19) into the required form, a whitening transform Wij with 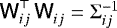 is applied to the random variables,
is applied to the random variables,
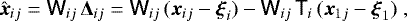 (24)
(24)
so that the two components of the result are uncorrelated with unit variance. For a covariance matrix Σ with variances 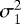 ,
, 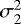 and correlation coefficient ρ, a possible whitening transform is given by the Cholesky decomposition of the inverse matrix Σ−1,
and correlation coefficient ρ, a possible whitening transform is given by the Cholesky decomposition of the inverse matrix Σ−1,
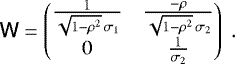 (25)
(25)
It is clear that the χ2-value of the transformed variables,
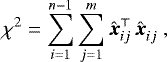 (26)
(26)
is formally the same as the original term (20), and at the same time of the required form (23) for MPFIT.
Besides the best-fit values, MPFIT also allows us to estimate the covariance matrix of the parameters near the minimum by numerical differentiation3. Both results can be used together to sample the parameter space using importance sampling from a normal distribution with the estimated covariance matrix and centred on the maximum-likelihood parameters. This process yields a full likelihood distribution and allows for the estimation of robust confidence bounds for the reconstructed lens quantities. As examples, Figs. 2 and 3 show these likelihood distributions for the two model-independent reconstructions of  , and g using all six and the last four reference points of Table 2, respectively.
, and g using all six and the last four reference points of Table 2, respectively.
 |
Fig. 2 Likelihood distributions of the model-independently determined |
 |
Fig. 3 As in Fig. 2 but using the last four reference points of Table 2. Dark-grey shaded areas mark the region between the 16th and 84th percentiles. |
3.4 Testing and application to CL0024
For lensing by a simulated singular isothermal, elliptical lens, Wagner & Tessore (2018) showed that this approach becomes inaccurate when the reference points are spread over distances of 10% of the distance between the closest multiple images. Then, the prerequisite that convergence and shear variations over the image areas are negligible breaks down. Comparing the spread of the six reference points for the first image around their centre, which is approximately 1″, with the distance of this image to the second one, which is approximately 10″, we observe that this limit may be reached for CL0024.
Therefore, we perform one reconstruction of the local lens properties using all six reference points in each image and compare it to the results obtained by discarding the first two reference points in each image. While the former reconstruction may become inaccurate due to the large area covered by the reference points, we reduce the area over which the reference points are spread in the latter reconstruction (see Fig. 1 left).
As the approach assumes that variations of convergence and shear are negligible over the area covered by the reference points, all image points in the convex hull of the reference points are assigned the same f-, g-, and  -values determined by the linear transformation between the multiple images.
-values determined by the linear transformation between the multiple images.
Using all six reference points for all five images listed in Table 2, we obtain the mean fi -, gi,1 -, and gi,2 -values and their standard deviations from 10 000 samples as shown in Table 5 in the ninth column block. Discarding the first two reference points and repeating the evaluation for another 10 000 samples, the results are listed in the tenth column block of Table 5. The likelihood distributions with the median values and the confidence levels from the 16th and 84th percentile determined from the 10 000 samples are shown in Figs. 2 and 3.
4 Lens models for CL0024
To investigate the influence of the number of strong lensing constraints on the local magnification ratios, ratios of convergences, and reduced shear values (Eqs. (7) to (17)) for the parametric and non-parametric lens modelling methods, we generate lens models
-
using all six systems of multiple images (as selected according to Sect. 4.1.1) with Grale and Lenstool;
-
using only the constraints from system 1 of Table 1 with Grale and Lenstool; and
-
using the positions of all six resolved features of system 1 as constraints4 with Grale.
For the last configuration of the list, we generate one Grale model with small-scale mass corrections and one without, in order to also investigate possible overfitting to the multiple images at the cost of unrealistic mass distributions, as found in Ponente & Diego (2011) for another non-parametric lens modelling approach.
As cosmological parameters, both lens modelling methods use
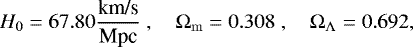 (27)
(27)
for the Hubble constant, the matter, and dark energy density parameters, respectively, in agreement with the Planck measurements (Planck Collaboration XIII 2016).
To ensure that all models have the least human-induced bias possible, the parametric and non-parametric models are simultaneously and independently generated by two of the authors based on the multiple image positions determined by Zitrin et al. (2009) and the positions of the six resolved features in system 1 determined by the third author prior to modelling.
The quality of the lens models can be compared by the root-mean-square deviations (RMSI) between the model-generated images and the observed ones, which are calculated in the same way for both lens model approaches (see Sects. 4.1 and 4.2).
From the analytical models, we produce convergence and shear maps at the resolution of 0.05″ per pixel and determine the 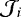 -, fi -, gi,1 -, and gi,2 -values, i = 1, ..., 5, and their confidence bounds at the positions of system 1 listed in Table 1 to compare these local lens properties for all three lens description approaches in Sect. 5.
-, fi -, gi,1 -, and gi,2 -values, i = 1, ..., 5, and their confidence bounds at the positions of system 1 listed in Table 1 to compare these local lens properties for all three lens description approaches in Sect. 5.
4.1 Parametric reconstruction by Lenstool
Lenstool is a software package that models gravitational lenses as a superposition of smooth, analytical, large-scale dark matter halo profiles of a specific type previously selected by the user and takes into account the luminous cluster member galaxies with their smaller-scale dark matter halos5. The parameters of the latter are determined as an ensemble with the same mass profile from the light-traces-mass assumption and the Tully–Fisher and Faber–Jackson scaling relations.
As further detailed in Jullo et al. (2007), the optimum lens model for given ranges of parameter values of the predefined dark matter halo profiles, the catalogue of the brightest member galaxies, and the constraints from the systems of multiple images is obtained by source plane optimisation or image plane optimisation.
For all Lenstool lens models, we choose the pseudo-isothermal mass distribution (PIEMD) as the analytic large-scale dark matter halo profile, which is also used for the latest Lenstool reconstruction of CL0024 employing strong lensing constraints performed by Richard et al. (2011; see references therein). As catalogue of brightest member galaxies, we use the one from the Lenstool homepage6 , also employed in Richard et al. (2011).
We assess the quality of our Lenstool models by three goodness-of-fit estimators, as described in Jullo et al. (2007): the RMSI between the model-generated multiple images and the observed ones, the logarithm of the evidence for that model, 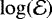 , and its χ2-value.
, and its χ2-value.
The parameters of the optimum lens model and their confidence bounds are determined by a Bayesian Markov-Chain-Monte-Carlo (MCMC) approach, as detailed in Jullo et al. (2007). In the same manner, the redshifts for all systems without a spectroscopic redshift are predicted, to be compared with the measured photometric ones and the ones from the model by Zitrin et al. (2009).
To obtain magnification ratios, ratios of convergences, and reduced shear values at the positions of system 1 listed in Table 1 according to Eqs. (7) to (17) with confidence bounds, we generate 30 convergence and shear maps and use the average of the retrieved values and their standard deviations for the comparison in Sect. 5.
4.1.1 Selection of multiple-image systems and number of dark matter halos
We generate Lenstool models with one, two, and three PIEMD large-scale dark matter halos employing all multiple-image systems of Zitrin et al. (2009) and the catalogue of the 85 brightest member galaxies from the Lenstool homepage. Since these models are only used for selection purposes, we optimise them using the fast source plane optimisation. Appendix A shows the configuration file for one PIEMD dark matter halo. In agreement with Richard et al. (2011), we find that the minimal most likely number of dark matter halos is two, taking into account the uncertainty limits of the optimisation procedure. Appendix C shows the critical curves and caustics of the three models, their goodness-of-fit measures, and the positions of all multiple images on the HST ACS/WFC image in the F475W band (PI:Ford 2004).
With the same three lens models, we select the set of multiple image systems to generate the best-fit Lenstool model by considering the RMSI for all individual multiple image systems and keep the multiple image systems with the lowest RMSI that sample the vicinity of system 1. Further details about the selection process leading to the set of employed multiple image systems in Table 1 can be found in Appendix C.
4.1.2 Reconstruction with six multiple image systems
The best-fit Lenstool model is thus calculated using the multiple images of Table 1, two PIEMD large-scale dark matter halo profiles, and the catalogue of the 85 brightest member galaxies. Since the model-independent approach employs image plane observables to retrieve local lens properties at the position of the multiple images, we optimise this model in the image plane. Appendix B shows the configuration file to obtain this model.
Lenstool also solves for the unknown redshifts of the five multiple image systems that have not been analysed spectroscopically. We obtain the following mean values and standard deviations from the implemented MCMC sampling.
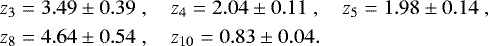 (28)
(28)
Comparing these results to those obtained by Zitrin et al. (2009) in Table 1, we observe that they agree within their uncertainty bounds except for system 3, which Lenstool estimates as being much higher. Figure 4 (left) shows the critical curves and caustics that this best-fit Lenstool model produces.
To determine the quality of the set of 30 lens models, as shown in Table 3, we determine the average and standard deviation of the total RMSI, 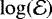 , and χ2 over all models. In addition, we calculate the RMSI per multiple image system as listed in the second column of Table 4, and observe that all systems show an RMSI lower than
, and χ2 over all models. In addition, we calculate the RMSI per multiple image system as listed in the second column of Table 4, and observe that all systems show an RMSI lower than 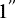 , yielding the overall RMSI of
, yielding the overall RMSI of 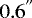 . Subsequently, we extract the lens properties of Eqs. (2), (7), and (17) from their convergence and shear maps and list the average and standard deviation in the second column block of Table 5.
. Subsequently, we extract the lens properties of Eqs. (2), (7), and (17) from their convergence and shear maps and list the average and standard deviation in the second column block of Table 5.
We employ a constant mass-to-light ratio for the catalogue of brightest cluster member galaxies, as is usually done; see, for example, Meneghetti et al. (2017). In order to test the influence of a non-constant mass-to-light ratio, we change the default slope for the cut radius of the galaxies in the configuration file of Appendix B from 4 to 2.5 to reproduce the fundamental plane (see Caminha et al. 2017 and references therein). We generate one model by image plane optimisation and employ the bayesMap utility to calculate 30 convergence and shear maps from the MCMC data of this model.
Compared to the values listed in the second column of Table 3, 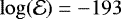 , RMSI = 0.72, and χ2 = 246 indicate that the quality of the model with non-constant mass-to-light ratio is worse. Yet, the estimated redshifts,
, RMSI = 0.72, and χ2 = 246 indicate that the quality of the model with non-constant mass-to-light ratio is worse. Yet, the estimated redshifts,
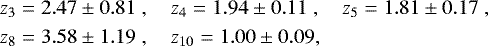 (29)
(29)
are closer to the ones found in Zitrin et al. (2009) and are also in agreement with the photometric measurements within their ranges of uncertainties. The averages and standard deviations of 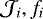 , gi,1, and gi,2, i = 1, ..., 5, according to Eqs. (2), (7), and (17) are shown in the third column block of Table 5.
, gi,1, and gi,2, i = 1, ..., 5, according to Eqs. (2), (7), and (17) are shown in the third column block of Table 5.
Degrees of freedom (DOF), average logarithmic evidence (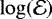 ), RMSI in arcseconds over all image systems, and total χ2 and their standard deviations for all lens models.
), RMSI in arcseconds over all image systems, and total χ2 and their standard deviations for all lens models.
4.1.3 Reconstruction with system 1
Reducing the number of strong lensing constraints to system 1 listed in Table 1, the free lens model parameters of only one PIEMD large-scale dark matter halo and of the catalogue of the brightest member galaxies can be determined, if we additionally fix the PIEMD cut radius, chosen to be 1000″. Adapting the configuration file in Appendix B accordingly, we determine the most likely lens model by image plane optimisation, as in Sect. 4.1.2 and show its critical curves and caustics in Fig. 4 (right). We generate 30 of these lens models and list the resulting average values of the quality measures and their standard deviations below the ones for the model of Sect. 4.1.2 in Table 3. Analogously, the 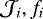 , gi,1, and gi,2, i = 1, ..., 5, according to Eqs. (2), (7), and (17) are shown in the fourth column block of Table 5.
, gi,1, and gi,2, i = 1, ..., 5, according to Eqs. (2), (7), and (17) are shown in the fourth column block of Table 5.
 |
Fig. 4 Lenstool models employing the 85 brightest member galaxies and two large-scale PIEMD dark matter halos and all multiple image systems of Table 1 detailed in Sect. 4.1.2 (left), or only one large-scale PIEMD dark matter halo and system 1 of Table 1 detailed in Sect. 4.1.3 (right). The critical curves for zs = 1.675 determined by the marching squares algorithm (see Appendix B) are marked in red, the caustics in yellow and the multiple images in blue. |
4.2 Non-parametric reconstruction by Grale
Contrary to parametric lens reconstruction techniques like Lenstool, so-called non-parametric or free-form lens reconstruction algorithms make no assumptions about any correlation between the dark and luminous matter distributions. Instead of fitting specific lens models to a given set of multiple image systems and bright cluster member galaxies, they reconstruct the lensing mass distribution in terms of basis functions whose number, location, and parameters are determined by the constraints that the set of multiple image systems provides. For our comparison, we employ Grale by Liesenborgs et al. (2006, 2010), which divides the region of interest into a uniform grid and assigns a Plummer mass profile (Plummer 1911), as basis function to each grid cell. Inspired by the work of Brewer & Lewis (2005), a genetic algorithm determines the weight for each basis function by maximising the overlap of the back-traced images of all sets of multiple images in the source plane. Subdividing the grid into comparably more massive regions, the lens model is refined iteratively until the desired level of detail is reached, that is, the highest achievable given the strong lensing constraints. Hence, similar to Lenstool, the same multiple-image positions are employed, which set the scale down to which the dark matter distribution is reconstructed.
Contrary to Lenstool, this method optimises the lens model only in the source plane and no information on the brightest cluster member galaxies is used. Instead, nullspace information is employed as a further constraint, that is, the lens model should not generate images in regions not containing any observed images.
As goodness-of-fit measure, the overlap of the back-traced multiple images for all sets of multiple images in the source plane is used. Furthermore, we check whether a caustic intersects the back-traced multiple images of system 1 and that the model does not produce any further images for the source of system 1.
Running the genetic algorithm as further detailed in Appendix D multiple times produces lens models that differ from one another due to the dependency of the optimisation procedure on its initial conditions and due to the lens model degeneracies in sparsely constrained regions. To obtain the best-fit Grale lens model, we average over all of these lens models. The RMSI between the model-generated multiple images and the observed ones is calculated in the same way as done by Lenstool. For our comparison in Sect. 5, 30 individual models are used to determine the average and the standard deviation of their magnification ratios, ratios of convergences, and reduced shear maps according to Eqs. (2), (7), and (17) at the positions of system 1 in Table 1. To be consistent with the model-independent approach and Lenstool, we convert the Grale results from the world coordinate system to the pixel coordinates used by the other methods by interchanging the sign of gi,2, i = 1, ..., 5.
4.2.1 Reconstruction with six multiple-image systems
Contrary to Lenstool, Grale cannot solve for the unknown redshifts of the five multiple-image systems without spectroscopic redshift, but requires them as input parameters. As the photometric redshift estimates are subject to high uncertainties and a large scatter between the individual images of one set, we use the well-constrained model-predicted redshifts of Zitrin et al. (2009), listed in the right-most column of Table 1. They are in good agreement with the photometric redshifts. The redshifts predicted by our Lenstool models are not employed at this stage in order to keep our lens models independent. After the comparison, we investigate the influence of the Lenstool-predicted redshifts on the Grale modelling in Sect. 5.3.
As the sources of the multiple image systems lie at different redshifts, the mass-sheet degeneracy should be broken sufficiently by the observations, and therefore the weight of a mass-sheet basis function is determined in addition to the weights of the Plummer basis functions. Running Grale 30 times with these specifications, we obtain the mean values of the lens properties and their standard deviations at the positions of system 1 (see Table 1) as listed in the fifth column block of Table 5.
By considering the magnification ratios, ratios of convergences, and reduced shears, any effect due to breaking the mass-sheet degeneracy is divided out again. However, including the mass-sheet component as an overall mass offset is necessary for the genetic algorithm to achieve the good reconstruction quality shown in Table 3. Figure 5 (left) shows the critical curves of the resulting model, analogously to Fig. 4.
To compare the quality of fit for the Grale models with those of Lenstool, we also list the RMSI for all multiple images in the fourth row of Table 3 and the RMSI for the individual multiple image systems in Table 4. As can be observed, both approaches are able to reconstruct the multiple images with an overall RMSI below 1″, which is also true for the individual systems except system 3.
 |
Fig. 5 Grale models employing all multiple image systems of Table 1 detailed in Sect. 4.2.1(left), and only system 1 of Table 1 detailed in Sect. 4.2.2 (right). The critical curves for zs = 1.675 determined by the sign change of the determinant of the magnification matrix are marked in red, the multiple images are marked in blue. |
4.2.2 Reconstruction with system 1
Next, we reduce the six systems of multiple images used in Sect. 4.2.1 to system 1 of Table 1. Now, the mass-sheet degeneracy cannot be broken and the additional mass-sheet component introduced in the optimisation process for the Grale model of Sect. 4.2.1 is dropped. Using these specifications and running Grale 30 times, we obtain the results at the positions of system 1 (see Table 1) listed in the sixth column block of Table 5 and shown in Fig. 5 (right).
As for the previous Grale model, we also determine the RMSI for system 1 and add it to Table 3. With fewer constraints to meet, the RMSI drops significantly, as expected.
4.2.3 Reconstruction with all reference points of system 1
As Grale is able to selectively refine the resolution of the lens model in more massive regions, we also generate a Grale lens model using all reference points of Table 2, keeping all other specifications as described in the previous Section, that is, without a mass-sheet basis function. The resulting values for the magnification ratios, ratios of convergences, and reduced shears at the positions of system 1 from Table 1 are shown in the seventh column block of Table 5 and in Fig. 6 (left).
Due to the increasing number of constraints compared to the Grale model of Sect. 4.2.2, the RMSI of all reference points, shown in the sixth row of Table 3, increases.
 |
Fig. 6 Grale models employing all reference points of Table 2 as detailed in Sect. 4.2.3 (left), and including small-scale mass corrections as detailed in Sect. 4.2.4 (right).The critical curves and caustics are analogous to the ones in Fig. 5. |
4.2.4 Reconstruction with all reference points of system 1 including small-scale mass corrections
For the last Grale model, we use the same configuration as for Sect. 4.2.3. But before averaging over all models, we employ a 48 × 48 uniform grid to add small-scale mass corrections to each of the 30 individual solutions generated by the genetic algorithm (see Liesenborgs et al. 2008 for further details). This causes the RMSI to decrease compared to the model of Sect. 4.2.3, as shown in Table 3. In Sect. 5, we analyse whether or not this step introduces unrealistic small-scale dark matter clumps by comparing the local 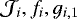 , and gi,2, as listed in the eighth column block of Table 5, to the results from the other approaches. Checking for overfitting is necessary, as, for instance, Ponente & Diego (2011) discovered that their algorithm generated unphysical dark matter structures in the lensing mass distribution when forced to optimally match the constraints from the multiple images. Thus, they concluded that the ring-like dark matter structure in CL0024 proposed by Jee et al. (2007) might be caused by overfitting. To avoid overfitting, we limit the total amount of small-scale mass corrections to 10% of the mass already assigned to the cluster. This procedure is able to reproduce the observed images, as shown in Fig. 7, in which we overlay the observed multiple images with the multiple images generated by Grale. The latter are determined by back-projecting the first image of system 1 to the source plane and then mapping this source to the image plane again, using the model discussed in this section. The model-generated images are shown with an offset to the left of the observed ones.
, and gi,2, as listed in the eighth column block of Table 5, to the results from the other approaches. Checking for overfitting is necessary, as, for instance, Ponente & Diego (2011) discovered that their algorithm generated unphysical dark matter structures in the lensing mass distribution when forced to optimally match the constraints from the multiple images. Thus, they concluded that the ring-like dark matter structure in CL0024 proposed by Jee et al. (2007) might be caused by overfitting. To avoid overfitting, we limit the total amount of small-scale mass corrections to 10% of the mass already assigned to the cluster. This procedure is able to reproduce the observed images, as shown in Fig. 7, in which we overlay the observed multiple images with the multiple images generated by Grale. The latter are determined by back-projecting the first image of system 1 to the source plane and then mapping this source to the image plane again, using the model discussed in this section. The model-generated images are shown with an offset to the left of the observed ones.
The critical curves and caustics for this lens model are shown in Fig. 6 (right).
 |
Fig. 7 Overlay between the observed multiple images of system 1 in Table 1 (Image credits: NASA, ESA, M. J. Jee (Johns Hopkins University)) and the images generated by the Grale model of Sect. 4.2.4 using the back-projected first image as source (for visualisation purposes, the model-generated images are displayed with an offset to the left of the observed images). |
5 Comparison of the approaches
The comparison is performed by an automated script after all data have been collected and the evaluation scheme has been defined. As detailed in Sects. 3 and 4, all results of the model-independent and model-based approaches are summarised in Table 5. First, we compare the different lens reconstructions for each approach before we compare the reconstructions among the different approaches. The lens models are of comparable good quality, which can be read off Tables 3 and 4, meaning that effects due to varying quality are negligible.
5.1 Comparison of model-independent approaches
Comparing the 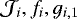 , and gi,2, i = 1, ..., 5, using four and six reference points, we find that both reconstructions agree within their standard deviations and the confidence level bounds set by the 16th and 84th percentiles (see Figs. 2 and 3). This implies that the convergence and shear can still be approximated as constant over the area enclosed by the six reference points. The strong disagreement between the mean values for the second image implies steep changes in the convergence and shear fields in the vicinity of the critical curve. Using the four reference points, the larger standard deviations occur because these four reference points cover a smaller area of the image and are more aligned than all six reference points, which increases the uncertainty in the transformation between the reference points that confines the
, and gi,2, i = 1, ..., 5, using four and six reference points, we find that both reconstructions agree within their standard deviations and the confidence level bounds set by the 16th and 84th percentiles (see Figs. 2 and 3). This implies that the convergence and shear can still be approximated as constant over the area enclosed by the six reference points. The strong disagreement between the mean values for the second image implies steep changes in the convergence and shear fields in the vicinity of the critical curve. Using the four reference points, the larger standard deviations occur because these four reference points cover a smaller area of the image and are more aligned than all six reference points, which increases the uncertainty in the transformation between the reference points that confines the 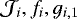 , and gi,2. Evidence supporting this hypothesis can be found in Appendix E, in which we calculate the
, and gi,2. Evidence supporting this hypothesis can be found in Appendix E, in which we calculate the 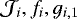 , and gi,2 using four of the six reference points that form a tetragon such that the same area is covered. Hence, the area covered by the reference points and not the number of reference points is decisive for the width of the confidence bounds of the local lens properties.
, and gi,2 using four of the six reference points that form a tetragon such that the same area is covered. Hence, the area covered by the reference points and not the number of reference points is decisive for the width of the confidence bounds of the local lens properties.
Thus, the 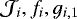 , and gi,2 determined from the six reference points are best suited for the comparison to the model-based approaches. The model-independent approach makes the least amount of assumptions about the lensing configuration. The resulting local lens properties therefore set limits on the precision of the local
, and gi,2 determined from the six reference points are best suited for the comparison to the model-based approaches. The model-independent approach makes the least amount of assumptions about the lensing configuration. The resulting local lens properties therefore set limits on the precision of the local 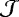 -, f-, and g-values obtainable in a purely data-driven way. We assume that the true magnification ratios, ratios of convergences, and reduced shear values lie within these confidence bounds, as supported by the simulations of Wagner & Tessore (2018). Further accuracy tests using realistically simulated lenses are currently under development.
-, f-, and g-values obtainable in a purely data-driven way. We assume that the true magnification ratios, ratios of convergences, and reduced shear values lie within these confidence bounds, as supported by the simulations of Wagner & Tessore (2018). Further accuracy tests using realistically simulated lenses are currently under development.
5.2 Comparison of Lenstool approaches
The three Lenstool models agree in 13 out of 18 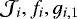 , and gi,2, i = 1, ...5 within their confidence bounds. Comparing the first two models using all multiple-image systems of Table 1, we find that they agree in all parameters within their confidence bounds. The first model with constant mass-to-light ratio for the cluster member galaxies has mostly larger confidence bounds than the second model. Using only system 1 of Table 1, we observe larger confidence bounds than when employing all multiple image systems of Table 1.
, and gi,2, i = 1, ...5 within their confidence bounds. Comparing the first two models using all multiple-image systems of Table 1, we find that they agree in all parameters within their confidence bounds. The first model with constant mass-to-light ratio for the cluster member galaxies has mostly larger confidence bounds than the second model. Using only system 1 of Table 1, we observe larger confidence bounds than when employing all multiple image systems of Table 1.
Given this high degree of agreement, the parametric lens modelling approach yields robust local ratios of convergences and reduced shears, taking into account that the number of constraints from system 1 only suffices to determine the parameters of one large-scale dark matter halo and of the parameters for the smaller-scale dark matter clumps belonging to the brightest member galaxies, while the models employing all six multiple-image systems constrain two large-scale dark matter halos and the parameters of the smaller-scale dark matter clumps underneath the brightest member galaxies. In addition, the low number of parameters to be adjusted (8 when using system 1 and 21 (22, when changing the mass-to-light ratio) when using all six multiple image systems) avoids overfitting to the constraints and the generation of small-scale mass artefacts.
As the difference in the first two Lenstool models is not significant, we compare both of them to the model-independent approach.
5.3 Comparison of Grale approaches
The Grale models with their many degrees of freedom also have broad confidence bounds. All Grale models yield highly unreliable 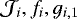 , and gi,2 for i = 2 and 4, for which κ ≈ 1. To investigate the reason for the broad confidence bounds, we generate 100 models by the genetic algorithm using only system 1 of Table 1 as detailed in Sect. 4.2.2. Averaging over ns = 10, 25, 50, 75, 100 individual models, five different Grale models are obtained. If the size of the confidence bounds is dominated by statistical uncertainties, we expect the standard deviations to shrink when averaging over an increasing number of individual models. Plotting the standard deviations for these five Grale models for each of the multiple images of system 1 in Fig. 8, we observe that the deviations do not decrease when averaging over an increasing number of individual models. Hence, the size of the confidence bounds is mainly determined by the variation between the different models fulfilling the same (sparse) constraints set by the multiple images. This hypothesis is supported by the fact that the Grale models using all six reference points (see Sects. 4.2.3 and 4.2.4) yield tighter confidence bounds on the
, and gi,2 for i = 2 and 4, for which κ ≈ 1. To investigate the reason for the broad confidence bounds, we generate 100 models by the genetic algorithm using only system 1 of Table 1 as detailed in Sect. 4.2.2. Averaging over ns = 10, 25, 50, 75, 100 individual models, five different Grale models are obtained. If the size of the confidence bounds is dominated by statistical uncertainties, we expect the standard deviations to shrink when averaging over an increasing number of individual models. Plotting the standard deviations for these five Grale models for each of the multiple images of system 1 in Fig. 8, we observe that the deviations do not decrease when averaging over an increasing number of individual models. Hence, the size of the confidence bounds is mainly determined by the variation between the different models fulfilling the same (sparse) constraints set by the multiple images. This hypothesis is supported by the fact that the Grale models using all six reference points (see Sects. 4.2.3 and 4.2.4) yield tighter confidence bounds on the 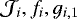 , and gi,2 than the models with only one constraint per multiple image. Hence, to obtain the tightest confidence bounds on local lens properties, Grale requires as many constraints as possible in the vicinity of the point where the lens properties are to be determined.
, and gi,2 than the models with only one constraint per multiple image. Hence, to obtain the tightest confidence bounds on local lens properties, Grale requires as many constraints as possible in the vicinity of the point where the lens properties are to be determined.
For the comparison shown in Table 5, we employed the redshifts from Zitrin et al. (2009) for the Grale model of Sect. 4.2.1 to avoid introducing a bias between the Lenstool and Grale models. After the independent lens model comparison, we now investigate the influence of the Lenstool redshifts on the Grale model. We employ the redshifts determined by Lenstool in the configuration of Appendix B (see Sect. 4.1.2) and rerun the model generation procedure detailed in Sect. 4.2.1. The resulting overall RMSI is 1.16± 0.59 and thus worse than for the model of Sect. 4.2.1. As further detailed by the RMSI for the individual multiple image systems and the 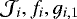 , and gi,2 in Appendix F, the Lenstool redshifts do mainly increase the size of the confidence bounds compared to the Grale model of Sect. 4.2.1 and the large overlap of their confidence bounds does not hint at significant differences between both models. Thus, the redshifts of additional multiple images used for the Grale lens modelling have a minor impact on the
, and gi,2 in Appendix F, the Lenstool redshifts do mainly increase the size of the confidence bounds compared to the Grale model of Sect. 4.2.1 and the large overlap of their confidence bounds does not hint at significant differences between both models. Thus, the redshifts of additional multiple images used for the Grale lens modelling have a minor impact on the 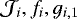 , and gi,2 at the positions of system 1 of Table 1.
, and gi,2 at the positions of system 1 of Table 1.
As for the other approaches, all Grale models agree within their confidence bounds. This is expected because, as stated in Ponente & Diego (2011), non-parametric lens modelling approaches can reproduce the multiple images to any accuracy level. Yet, overfitting is prevented in our models by not adding any small-scale mass corrections for the models detailed in Sects. 4.2.1, 4.2.2 and 4.2.3. But, as Table 5 shows, even adding small-scale mass corrections as detailed in Sect. 4.2.4, does not significantly change the resulting 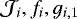 , and gi,2, nor the overall smooth shape of the critical curves (see Fig. 6). Thus, we can conclude that local constraints suffice to obtain local lens properties using Grale. The best Grale model is that of Sect. 4.2.4 due to its tightest confidence bounds.
, and gi,2, nor the overall smooth shape of the critical curves (see Fig. 6). Thus, we can conclude that local constraints suffice to obtain local lens properties using Grale. The best Grale model is that of Sect. 4.2.4 due to its tightest confidence bounds.
 |
Fig. 8 Dependency of the size of the confidence bound, that is, the standard deviation of the fi, gi,1, and gi,2, i = 1, ..., 5, for all multiple images of system 1 of Table 1 determined by the Grale model detailed in Sect. 4.2.2, on the number of individual models, ns, generated by the genetic algorithm and averaged over to obtain the final Grale model. |
5.4 Comparison between all approaches
All approaches show confidence bounds as large as the ratios of convergences and reduced shear values, except for the Lenstool models generated from six multiple image systems, in which the largest confidence bound is 83% of g4,1 for the model with constant mass-to-light ratio of the brightest member galaxies and 50% of g4,1 for the model with non-constant mass-to-light ratio. Hence, Lenstool yields the most robust local lens properties, also in the vicinity of the critical curve, comparing, for example, the confidence bounds of f2 among the approaches.
To obtain the 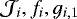 , and gi,2, i = 1, ..., 5, with the tightest confidence bounds, Lenstool requires several multiple image systems as constraints, while Grale best uses several reference points from a single resolved multiple image system in the vicinity of the point at which the lens properties are to be retrieved. For the model-independent approach, the area over which the reference points are spread is anticorrelated with the size of the confidence bounds. Hence, the area should be maximised, adhering to the approximation that
, and gi,2, i = 1, ..., 5, with the tightest confidence bounds, Lenstool requires several multiple image systems as constraints, while Grale best uses several reference points from a single resolved multiple image system in the vicinity of the point at which the lens properties are to be retrieved. For the model-independent approach, the area over which the reference points are spread is anticorrelated with the size of the confidence bounds. Hence, the area should be maximised, adhering to the approximation that 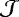 , f, and g are constant.
, f, and g are constant.
We thus find that the three methods require complementary constraints from the multiple images and obtain similar local lens properties with comparable precision.
Comparing the 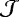 -, f-, and g-values of the model-independent approach from six reference points to the respective values obtained by the optimum Lenstool models of Sect. 4.1.2 and the optimum Grale model of Sect. 4.2.4, we find that for Lenstool, 12 (11, for non-constant mass-to-light ratio) of all 18
-, f-, and g-values of the model-independent approach from six reference points to the respective values obtained by the optimum Lenstool models of Sect. 4.1.2 and the optimum Grale model of Sect. 4.2.4, we find that for Lenstool, 12 (11, for non-constant mass-to-light ratio) of all 18 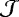 -, f-, and g-values agree with the values obtained independently from the lens model, within their confidence bounds, and for Grale, the agreement is found in 17
-, f-, and g-values agree with the values obtained independently from the lens model, within their confidence bounds, and for Grale, the agreement is found in 17 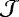 -, f- and g-values. Lenstool deviates in
-, f- and g-values. Lenstool deviates in 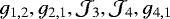 , (
, (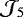 ), and g5,1, while Grale deviates in g5,2.
), and g5,1, while Grale deviates in g5,2.
As the first Lenstool model with constant mass-to-light ratio agrees to the majority of 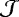 -, f- and g-values of the model-independent approach and only deviates in g1,2 and g5,1 from the best Grale model, our results are in agreement with the assumption that light traces mass in CL0024.
-, f- and g-values of the model-independent approach and only deviates in g1,2 and g5,1 from the best Grale model, our results are in agreement with the assumption that light traces mass in CL0024.
The second Lenstool model with non-constant mass-to-light ratio and tighter confidence bounds disagrees in 8 of the 18 parameters with the best Grale model. Hence, we can conclude that a non-constant mass-to-light ratio for the cluster member galaxies is less consistent with the model-independent approach and the best Grale model, therefore a constant mass-to-light ratio is favoured in CL0024. The best-fit Lenstool model is thus the one using six multiple-image systems and a constant mass-to-light ratio for the brightest member galaxies.
Comparing all results gained in Sects. 4.1.1, 4.1.2, 4.2.1, and Appendix F, the question arises whether or not system 3 of Table 1 is a real multiple-image system because its RMSI is higher than the ones of the other multiple image systems in most of the lens models, and the redshift predicted by the best-fit Lenstool model is much higher than the one obtained by Zitrin et al. (2009) and their photometric redshift estimates. Furthermore, two authors independently arrive at the result that system 3 is hard to model with Grale and Lenstool. Hence, spectroscopic measurements are required to corroborate or reject the lensing hypothesis for this multiple-image system.
Finally, we use the results obtained in Sects. 4.1.2 and 4.2.1 to investigate the merger hypothesis for CL0024. In the Lenstool and Grale models discussed in these sections, we find deviations from a symmetric, relaxed cluster structure, as can be observed in the convergence maps of the models from Sects. 4.1.2 and 4.2.1 shown in Fig. 9: Inspecting the isocontour κ = 1 (yellow curves) in both convergence maps, the asymmetric shape is clearly seen. While the convergence map reconstructed by Grale shows only a few closed curves of κ = 1, several more are observed in the convergence map obtained by Lenstool due to the dark matter halos of the brightest cluster member galaxies. Both convergence maps show regions of κ = 1 close to image 2, as expected from the relatively broad confidence bounds for this image and tend to a similar stretching around the central image 5. The differences in the shape of the isocontour for the convergence maps of Lenstool and Grale once again (see also Fig. 8) show the freedom lens models have to extend the lens reconstruction beyond the vicinity of multiple images.
The estimation of redshifts is degenerate with the parameters of the dark matter halos in Lenstool. Thus, beyond a corroboration of the merger hypothesis, more quantitative statements about the merger masses and geometry cannot be made without spectroscopic redshift measurements.
 |
Fig. 9 Convergence maps of the Lenstool model of Sect. 4.1.2 (left) and the Grale model of Sect. 4.2.1 (right). The positions of system 1 of Table 1 are marked in red, the yellow curves delineate the isocontour κ = 1. |
6 Conclusion
We performed the most direct comparison between the model-independent local lens reconstruction approach for multiple images with resolved brightness features as described in Tessore (2017); Wagner & Tessore (2018), the parametric lens modelling software Lenstool (Kneib et al. 1996; Jullo et al. 2007), and the non-parametric lens modelling approach Grale (Liesenborgs et al. 2006, 2010): Using the same positions of multiple images, the same cosmological parameter values, and the same number of model-predicted convergence and shear maps for the evaluation statistics, we determined magnification ratios, ratios of convergences, and reduced shears at the positions of the five multiple images of the source at redshift zs = 1.675 in the galaxy cluster CL0024 (Colley et al. 1996) from both lens modelling approaches, and compared these local lens properties to their model-independent counterparts.
Summarising the results detailed in Sect. 5, we arrive at the following conclusions:
-
The local lens properties, that is, the magnification ratios, ratios of convergences, and reduced shear values (
 -,
f-,
and g-values)
at the five positions obtained by the model-independent approach, Lenstool, and Grale coincide in the majority of
cases within their confidence bounds, supporting the validity of the light-traces-mass assumption in CL0024 and
favouring a constant mass-to-light ratio for the brightest cluster member galaxies.
-,
f-,
and g-values)
at the five positions obtained by the model-independent approach, Lenstool, and Grale coincide in the majority of
cases within their confidence bounds, supporting the validity of the light-traces-mass assumption in CL0024 and
favouring a constant mass-to-light ratio for the brightest cluster member galaxies. -
Our results are in agreement with the merger hypothesis assumed in Kneib et al. (1996); Zhang et al. (2005); Zitrin et al. (2009) because, according to our Lenstool models, the smallest, most probable number of large-scale dark matter halos for the strong lensing region is two and the convergence maps generated by Grale also suggest perturbations to a symmetric, relaxed cluster structure (see Fig. 9).
-
Our Lenstool and Grale models mostly encountered high root-mean square deviations between the observed and model-predicted positions of the multiple images of system 3 in Table 1 compared to all other multiple image systems employed. The best-fit Lenstool model also predicted a much higher redshift for this system (3.49 ± 0.39) than Zitrin et al. (2009) (
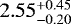 )
and the photometric redshift estimates (between 2.48
and 2.76,
see Zitrin et al. 2009). Hence, spectroscopic observations are necessary to further investigate whether these
observations really originate from the same source galaxy.
)
and the photometric redshift estimates (between 2.48
and 2.76,
see Zitrin et al. 2009). Hence, spectroscopic observations are necessary to further investigate whether these
observations really originate from the same source galaxy. -
All three approaches show broad confidence bounds for the f-, and g-values that can become as large as the values themselves, especially close to regions where the convergence equals one and the denominator in the fs and gs approaches zero. This is in agreement with the findings made by Meneghetti et al. (2017) employing unresolved multiple-image systems.
-
From a methodological point of view, we discovered that the model-independent approach yields
 -,
f-,
and g-values
that are of the same quality as the model-generated ones, if there are at least four resolved brightness
features forming a tetragon that covers an image region of approximately constant convergence and shear.
While Lenstool is well-suited to reconstruct the global cluster structure including the member galaxies,
local lens properties on (sub-)galaxy scale are better determined by Grale when reconstructing the local
f-
and g-values
from all resolved brightness features close to the position of interest and adding limited small-scale mass corrections.
This is very advantageous because, in this way, no unconfirmed additional multiple image systems with uncertain
photometric redshifts have to be taken into account. Limiting the mass corrections to 10% of the total mass, Grale
shows no sign of unrealistically oscillating mass distributions.
-,
f-,
and g-values
that are of the same quality as the model-generated ones, if there are at least four resolved brightness
features forming a tetragon that covers an image region of approximately constant convergence and shear.
While Lenstool is well-suited to reconstruct the global cluster structure including the member galaxies,
local lens properties on (sub-)galaxy scale are better determined by Grale when reconstructing the local
f-
and g-values
from all resolved brightness features close to the position of interest and adding limited small-scale mass corrections.
This is very advantageous because, in this way, no unconfirmed additional multiple image systems with uncertain
photometric redshifts have to be taken into account. Limiting the mass corrections to 10% of the total mass, Grale
shows no sign of unrealistically oscillating mass distributions. -
For the run times, we find that the model-independent approach takes about 0.23 s to determine the values in the last two column blocks of Table 5 using a Linux-PC with 8 × Intel Core i7-4710MQ CPU @ 2.50GHz and 31.1 GiB RAM. On the same machine, Lenstool, Version 6.8.1., takes about 24 h for each of the 40 models of Sect. 4.1.2 and around 4 h for each of the 40 models of Sect. 4.1.3 including the calculations for the convergence and shear maps. The Grale algorithm takes about 45 min to obtain one individual model of the genetic algorithm for the specifications of Sect. 4.2.1, 10 min for one individual model for Sects. 4.2.2 and 4.2.3, and 30 min to determine the small-scale mass corrections for one individual model in Sect. 4.2.4, running on a single computing node with 2 × 12-core “Haswell” processors of type Xeon E5-2680v3. Thus, the model-independent approach employs the miminum set of assumptions about the lensing configuration and is by far the fastest way to extract the local lens properties. This is to be expected because the model-based approaches provide a more encompassing picture and require more runtime for this.
Acknowledgements
JW would like to thank Mauricio Carrasco, Matteo Maturi, Massimo Meneghetti, Sven Meyer, Juan Remolina, Sebastian Stapelberg, Rüdiger Vaas, and Adi Zitrin for helpful discussions, and Johan Richard for helpful discussions and providing the information on his lens model. JW gratefully acknowledges the support by the Deutsche Forschungsgemeinschaft (DFG) WA3547/1-1. JL acknowledges the use of the computational resources and services provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation - Flanders (FWO) and the Flemish Government – department EWI. NT acknowledges support from the European Research Council in the form of a Consolidator Grant with number 681431.
Appendix A Lenstool configuration file for the model in Sect. 4.1.1
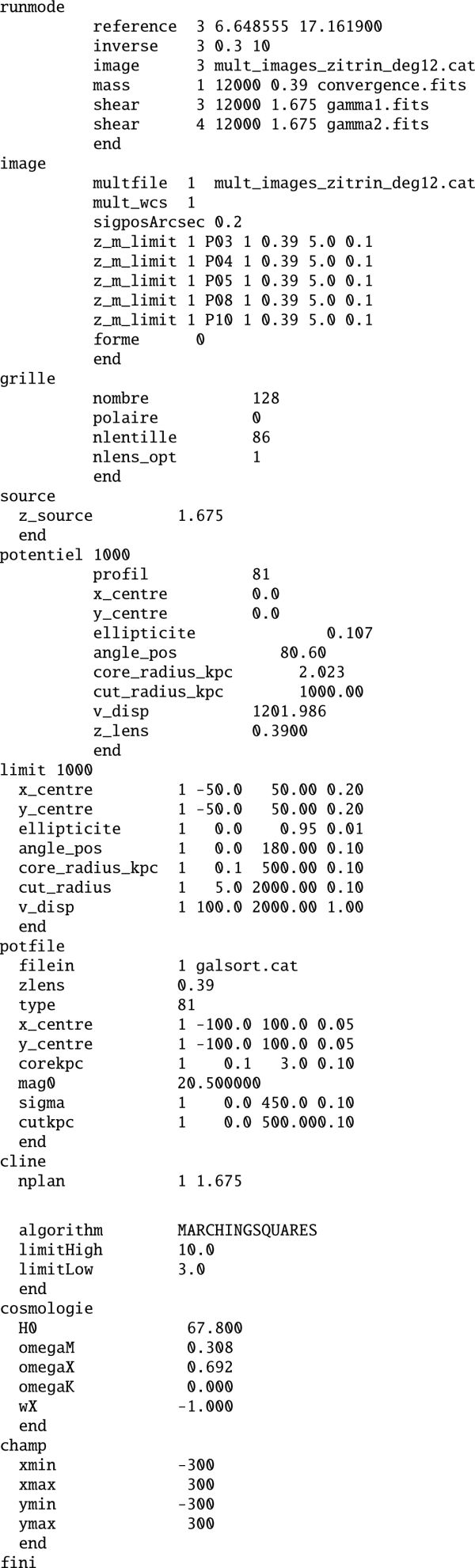
 |
Fig. A.1 Lenstool lens models employing the 85 brightest member galaxies, system 1 of Table 1 and systems 2–11 of Zitrin et al. (2009), and one large-scale PIEMD dark matter halo (left), and two large-scale PIEMD dark matter halos (centre), and three large-scale PIEMD dark matter halos (right). The critical curves determined by the marching squares algorithm (see Appendix A for its configuration) are marked in red, the caustics in yellow and the multiple images in the notation of Zitrin et al. (2009) in blue. |
Appendix B Lenstool configuration file for the model in Sect. 4.1.2
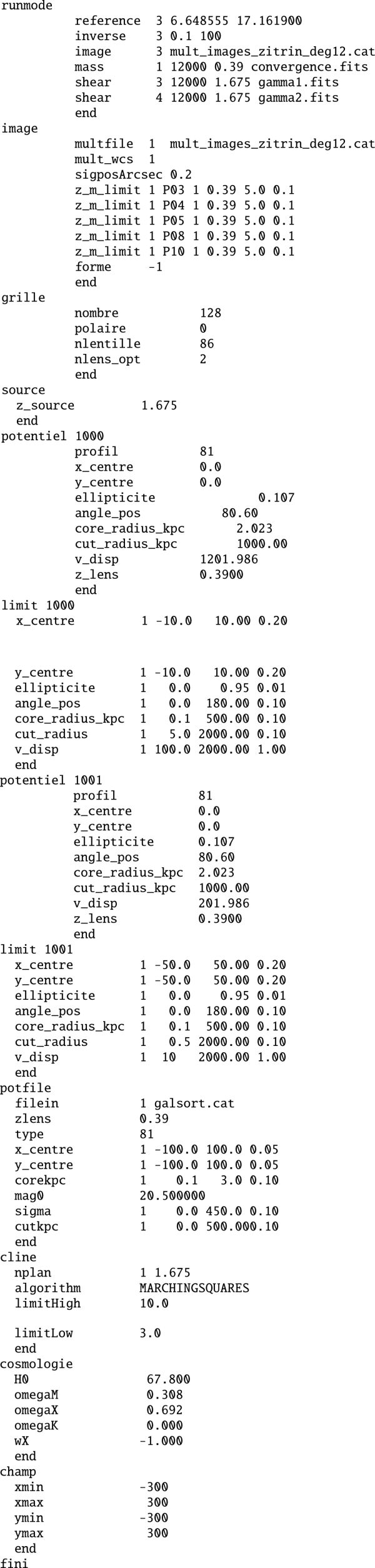
Appendix C Lenstool models used in Sect. 4.1.1
Using the configuration file of Appendix A with one PIEMD dark matter halo, system 1 of Table 1 and systems 2–11 of Zitrin et al. (2009), and the catalogue of the brightest cluster member galaxies, we arrive at a lens model whose critical curves and caustics are shown in Fig. A.1 (left). Adapting the configuration file to two and three PIEMD dark matter halos for the same remaining specifications, we obtain the critical curves and caustics of Fig. A.1 (centre) and A.1 (right), respectively.
For all models, the results for the goodness-of-fit measures and the degrees of freedom, that is, the number of constraints minus the number of lens model parameters, are summarised in Table C.1.
With the same three lens models considered in Table C.1, we select the set of multiple image systems to generate the best-fit Lenstool model by considering the RMSI for the single multiple image systems, as shown in Table C.2. Systems 6 and 7 are eliminated from our set, as they are not real multiple image systems or require further smaller-scale substructure fine-tuning because at least two lens models cannot determine their source positions within the required precision. We also eliminate systems 9 and 11, due to their non-decreasing, high RMSI-values. As the central part of the cluster is already probed by systems 4 and 10 and the remaining image of system 2 is far from all images of system 1, it is also discarded from the set. Although system 3 shows high RMSI, it is kept in the set, as its RMSI decreases quickly with increasing number of PIEMDs and with its far-spread images 3.2, 3.3, and 3.4, it constrains the lensing potential around image 1.4. Thus, the set of multiple image systems as shown in Table 1 is obtained.
Goodness-of-fit values over all image systems of Lenstool models for CL0024 for varying numbers of dark matter halo PIEMDs (# PIEMDs) using system 1 in Table 1 and systems 2–11 of Zitrin et al. (2009) as constraints.
Individual RMSI in arcseconds for system 1 in Table 1 and systems 2–11 of Zitrin et al. (2009) in the lens models with one, two, and three PIEMD dark matter halos.
Appendix D Grale configurations for the models used in Sect. 4.2
We employ a 60″ squared region around the reference point in the Lenstool configuration files (see Appendix B). As an initial grid, 15 × 15 uniformly distributed squared grid cells are generated and the grid is refined to the level that the number and positions of the constraints permit. The prediction of images relatively far from the cluster centre is avoided by introducing a 200″ squared nullspace grid, centred at the same reference point.
For the reconstruction using six multiple image systems, about 600 basis functions are used, while for the remaining Grale models, about 300 basis functions are taken into account.
Appendix E Influence of the area spanned by the reference points on the confidence bounds in the model-independent approach
Instead of discarding the first two reference points as done in Sect. 3, we now discard points 3 and 5 in Table 2 to obtain the following mean and median 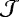 -, f-, and g-values, their confidence intervals set by the 16th and 84th percentiles, and their standard deviations:
-, f-, and g-values, their confidence intervals set by the 16th and 84th percentiles, and their standard deviations:
Comparing the size of the confidence intervals with those using six reference points (eighth column block of Table 5) we see that they are of comparable size and smaller than the ones using four reference points spanning a smaller area(last column block of Table 5).
Mean and median 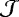 -, f-, and g-values with their confidence bounds using four reference points spanning the same area as the six reference points.
-, f-, and g-values with their confidence bounds using four reference points spanning the same area as the six reference points.
Appendix F Influence of redshifts in the Grale model of Sect. 4.2.1
Instead of employing the model-predicted redshifts of Zitrin et al. (2009), we now use the model-predicted redshifts as determined by Lenstool in Sect. 4.1.2 to generate the Grale model detailed in Sect. 4.2.1. The RMSI per multiple image system are as follows, for comparison, we list the RMSI for the Grale model of Sect. 4.2.1in the last column of Table F.1.
From the convergence and shear maps, we obtain the following mean 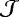 -, f-, and g-values and their standard deviations; for comparison, we add the respective values for the model of Sect. 4.2.1 in the fourth and fifth columns of Table F.2.
-, f-, and g-values and their standard deviations; for comparison, we add the respective values for the model of Sect. 4.2.1 in the fourth and fifth columns of Table F.2.
Comparison of RMSI obtained by Grale per multiple image system when using the Lenstool redshifts of Sect. 4.1.2 as input (second column) and the RMSI per multiple image system using the model-predicted redshifts by Zitrin et al. (2009).
Comparison of local lens properties using the Lenstool redshifts determined in Sect. 4.1.2 (second and third columns) and using the model-predicted redshifts from Zitrin et al. (2009) as input for Grale (last two columns).
References
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Ford, H., Bouwens, R., et al. 2004, ApJS, 150, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brewer, B. J., & Lewis, G. F. 2005, PASA, 22, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T., Huang, X., Frye, B., & Ellis, R. 2000, ApJ, 534, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coe, D., Benítez, N., Sánchez, S. F., et al. 2006, AJ, 132, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Colley, W. N., Tyson, J. A., & Turner, E. L. 1996, ApJ, 461, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J. M., Kaiser, N., Broadhurst, T., et al. 2017, Phys. Rev. Mater., 1, 054006 [Google Scholar]
- Jee, M. J., Ford, H. C., Illingworth, G. D., et al. 2007, ApJ, 661, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., & Kneib, J.-P. 2009, MNRAS, 395, 1319 [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Liesenborgs, J., De Rijcke, S., & Dejonghe, H. 2006, MNRAS, 367, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Liesenborgs, J., de Rijcke, S., Dejonghe, H., & Bekaert, P. 2008, MNRAS, 389, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Liesenborgs, J., de Rijcke, S., & Dejonghe, H. 2010, Astrophysics Source Code Library [record ascl:1011.021] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
- Meneghetti, M., Natarajan, P., Coe, D., et al. 2017, MNRAS, 472, 3177 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Ponente, P. P., & Diego, J. M. 2011, A&A, 535, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Jones, T., Ellis, R., et al. 2011, MNRAS, 413, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses, Astronomy and Astrophysics Library (New York: Springer) [Google Scholar]
- Tessore, N. 2017, A&A, 597, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umetsu, K., Medezinski, E., Broadhurst, T., et al. 2010, ApJ, 714, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, J., & Tessore, N. 2018, A&A, in press, DOI: 10.1051/0004-6361/201730947 [Google Scholar]
- Zhang, Y.-Y., Böhringer, H., Mellier, Y., Soucail, G., & Forman, W. 2005, A&A, 429, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zitrin, A., Broadhurst, T., Umetsu, K., et al. 2009, MNRAS, 396, 1985 [NASA ADS] [CrossRef] [Google Scholar]
Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).
There is a Lenstool version combining parametric and non-parametric lens modelling (Jullo & Kneib 2009), which is not considered here, as it is computationally more intensive.
All Tables
Degrees of freedom (DOF), average logarithmic evidence (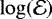 ), RMSI in arcseconds over all image systems, and total χ2 and their standard deviations for all lens models.
), RMSI in arcseconds over all image systems, and total χ2 and their standard deviations for all lens models.
Goodness-of-fit values over all image systems of Lenstool models for CL0024 for varying numbers of dark matter halo PIEMDs (# PIEMDs) using system 1 in Table 1 and systems 2–11 of Zitrin et al. (2009) as constraints.
Individual RMSI in arcseconds for system 1 in Table 1 and systems 2–11 of Zitrin et al. (2009) in the lens models with one, two, and three PIEMD dark matter halos.
Mean and median  -, f-, and g-values with their confidence bounds using four reference points spanning the same area as the six reference points.
-, f-, and g-values with their confidence bounds using four reference points spanning the same area as the six reference points.
Comparison of RMSI obtained by Grale per multiple image system when using the Lenstool redshifts of Sect. 4.1.2 as input (second column) and the RMSI per multiple image system using the model-predicted redshifts by Zitrin et al. (2009).
Comparison of local lens properties using the Lenstool redshifts determined in Sect. 4.1.2 (second and third columns) and using the model-predicted redshifts from Zitrin et al. (2009) as input for Grale (last two columns).
All Figures
 |
Fig. 1 CL0024 with detailed pictures of the five multiple images of system 1 (left). The user-defined reference points in the reference image 1 are marked by red circles, while the red-encircled regions in the remaining images denote 95% confidence bounds of the locations of the transformed reference points by the best-fit linear transformations. (Image credits: NASA, ESA, M. J. Jee (Johns Hopkins University)). Also shown is a diagram of the principle of extracting local lens properties from the linear transformation between multiple images from the same source (right). |
| In the text | |
 |
Fig. 2 Likelihood distributions of the model-independently determined |
| In the text | |
 |
Fig. 3 As in Fig. 2 but using the last four reference points of Table 2. Dark-grey shaded areas mark the region between the 16th and 84th percentiles. |
| In the text | |
 |
Fig. 4 Lenstool models employing the 85 brightest member galaxies and two large-scale PIEMD dark matter halos and all multiple image systems of Table 1 detailed in Sect. 4.1.2 (left), or only one large-scale PIEMD dark matter halo and system 1 of Table 1 detailed in Sect. 4.1.3 (right). The critical curves for zs = 1.675 determined by the marching squares algorithm (see Appendix B) are marked in red, the caustics in yellow and the multiple images in blue. |
| In the text | |
 |
Fig. 5 Grale models employing all multiple image systems of Table 1 detailed in Sect. 4.2.1(left), and only system 1 of Table 1 detailed in Sect. 4.2.2 (right). The critical curves for zs = 1.675 determined by the sign change of the determinant of the magnification matrix are marked in red, the multiple images are marked in blue. |
| In the text | |
 |
Fig. 6 Grale models employing all reference points of Table 2 as detailed in Sect. 4.2.3 (left), and including small-scale mass corrections as detailed in Sect. 4.2.4 (right).The critical curves and caustics are analogous to the ones in Fig. 5. |
| In the text | |
 |
Fig. 7 Overlay between the observed multiple images of system 1 in Table 1 (Image credits: NASA, ESA, M. J. Jee (Johns Hopkins University)) and the images generated by the Grale model of Sect. 4.2.4 using the back-projected first image as source (for visualisation purposes, the model-generated images are displayed with an offset to the left of the observed images). |
| In the text | |
 |
Fig. 8 Dependency of the size of the confidence bound, that is, the standard deviation of the fi, gi,1, and gi,2, i = 1, ..., 5, for all multiple images of system 1 of Table 1 determined by the Grale model detailed in Sect. 4.2.2, on the number of individual models, ns, generated by the genetic algorithm and averaged over to obtain the final Grale model. |
| In the text | |
 |
Fig. 9 Convergence maps of the Lenstool model of Sect. 4.1.2 (left) and the Grale model of Sect. 4.2.1 (right). The positions of system 1 of Table 1 are marked in red, the yellow curves delineate the isocontour κ = 1. |
| In the text | |
 |
Fig. A.1 Lenstool lens models employing the 85 brightest member galaxies, system 1 of Table 1 and systems 2–11 of Zitrin et al. (2009), and one large-scale PIEMD dark matter halo (left), and two large-scale PIEMD dark matter halos (centre), and three large-scale PIEMD dark matter halos (right). The critical curves determined by the marching squares algorithm (see Appendix A for its configuration) are marked in red, the caustics in yellow and the multiple images in the notation of Zitrin et al. (2009) in blue. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.