| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732163 | |
| Published online | 29 March 2018 | |
High-precision broad-band linear polarimetry of early-type binaries
II. Variable, phase-locked polarization in triple Algol-type system λ Tauri★
1
Tuorla Observatory, Department of Physics and Astronomy, University of Turku,
Väisäläntie 20,
21500
Kaarina, Finland
e-mail: andber@utu.fi
2
FINCA, University of Turku,
Väisäläntie 20,
21500
Kaarina, Finland
3
Kiepenheuer-Institut für Sonnenphysik,
79104
Freiburg, Germany
4
Graduate School of Science, Tohoku University,
Aoba-ku,
Sendai
980-8578, Japan
Received:
24
October
2017
Accepted:
23
December
2017
Aim. To study the binary geometry of the classic Algol-type triple system λ Tau, we have searched for polarization variations over the orbital cycle of the inner semi-detached binary, arising from light scattering in the circumstellar material formed from ongoing mass transfer. Phase-locked polarization curves provide an independent estimate for the inclination i, orientation Ω, and the direction of the rotation for the inner orbit.
Methods. Linear polarization measurements of λ Tau in the B, V , and R passbands with the high-precision Dipol-2 polarimeter have been carried out. The data have been obtained on the 60 cm KVA (Observatory Roque de los Muchachos, La Palma, Spain) and Tohoku 60 cm (Haleakala, Hawaii, USA) remotely controlled telescopes over 69 observing nights. Analytic and numerical modelling codes are used to interpret the data.
Results. Optical polarimetry revealed small intrinsic polarization in λ Tau with ~0.05% peak-to-peak variation over the orbital period of 3.95 d. The variability pattern is typical for binary systems showing strong second harmonic of the orbital period. We apply a standard analytical method and our own light scattering models to derive parameters of the inner binary orbit from the fit to the observed variability of the normalized Stokes parameters. From the analytical method, the average for three passband values of orbit inclination i = 76° + 1°∕−2° and orientation Ω = 15°(195°) ± 2° are obtained. Scattering models give similar inclination values i = 72–76° and orbit orientation ranging from Ω = 16°(196°) to Ω = 19°(199°), depending on the geometry of the scattering cloud. The rotation of the inner system, as seen on the plane of the sky, is clockwise. We have found that with the scattering model the best fit is obtained for the scattering cloud located between the primary and the secondary, near the inner Lagrangian point or along the Roche lobe surface of the secondary facing the primary. The inclination i, inferred from polarimetry, agrees with the previously made conclusion on the semi-detached nature of the inner binary, whose secondary component is filling its Roche lobe. The non-periodic scatter, which is also present in the polarization data, can be interpreted as being due to sporadic changes in the mass transfer rate.
Key words: polarization / scattering / binaries: eclipsing / techniques: polarimetric / circumstellar matter
The polarization data for λ Tauri are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/611/A69
© ESO, 2017
1 Introduction
The scattering of light in a close binary system often results in variable linear polarization which is synchronous with the orbital motion. Studying this polarization allows us to draw conclusions on the properties of the binary system and the structure of the circumbinary environment. A detected variable polarization gives an independent estimate of the orbit inclination i and orientation of the orbit Ω (see Brown et al. 1978; Drissen et al. 1986). The direction of orbital motion on the plane of the sky is also revealed. Although the inclination of the eclipsing system can be readily found from the model fit to the light variability curve, the last two parameters (Ω and direction of motion), apart from polarimetry, can be currently directly determined only via interferometry (cf. Kemp et al. 1981; Baron et al. 2012).
In the above-mentioned context, the original study of Algol serves as the example of the diagnostic power of high-precision polarimetry for triple systems with a semi-detached inner binary. Analysis of the Algol polarization data yielded the orientation of the inner orbit at 47°± 4° (Kemp et al. 1981), which is almost exactly orthogonal to the orientation of the outer orbit, inferred from speckle interferometry. Moreover, the direction of motion on the inner orbit, derived from polarimetry, has been found to be counter-revolving with respect to the outer one. The nearly orthogonal orientation of the inner and outer orbits in Algol has been considered as highly unlikely and was conceivably rejected (Söderhjelm 1975, 1980). However, recent H-band interferometry performed by Baron et al. (2012) has resolved Algol’s inner orbit, yielding the orientation of 43.4° ± 0.3°, which is in remarkably good agreement with that obtained from polarimetry more than 30 years ago. Near-IR interferometry also confirmed the counter-rotation of Algol’s inner orbit motion.
In Algol-type binaries, variable phase-locked polarization may arise due to the electron scattering (Thomson scattering) in the disk around a mass-gaining primary and/or in the stream of gas flowing from a secondary that is filling its Roche lobe. The amplitude of variability depends, in general, on the amount of light-scattering material. In Algol-type systems the presence and strength of Hα emission is a reliable indicator for the ongoing mass transfer activity and existence of disks and streams (Peters 1989). However, most classical Algols show only weak Hα emission in their spectra. In many cases, this emission can only be seen in the differential synthetic profile after modelling and subtracting profiles which are produced in the atmospheres of primary and secondary components (cf. Vesper et al. 2001).
Indeed, the few classical Algol systems which have been observed polarimetrically show only small-amplitude polarization variability at best, i.e. ≈0.025% in Algol itself, and ≈0.125% in U Sge (see Rudy & Kemp 1978). To detect and study the variation in polarization in such systems, high-precision measurements and extensive orbital phase coverage are needed.
To study the small-amplitude polarization variability, we have developed and built the Dipol-2 polarimeter (Piirola et al. 2014). The accuracy of this instrument is limited mostly by the number of registered photons and it is capable in practice of measuring linear polarization simultaneously in the B, V , and R bands at a precision of 10−5. In 2012, we started an observational campaign on high-precision polarimetry of binary systems, employing the remotely controlled 60 cm KVA telescope (La Palma, Spain). Starting from the end of 2014, a second copy of Dipol-2 was installed on the Tohoku 60 cm (T60) telescope at Haleakala Observatory, Hawaii. One of the first results of this polarimetry campaign was a detection of the variable phase-locked polarization in the detached O-type non-eclipsing system HD 48099 with peak-to-peak amplitude of ≤0.10% (Berdyugin et al. 2016).
Here we report the outcome of our study of polarization in the classical Algol-type eclipsing binary λ Tau, which, like an Algol itself, is a triple system.
2 λ Tau
The eclipsing variable λ Tau is a bright (mV = 3.4) system consisting of a double-line eclipsing binary with a period of 3.952948 days and an unseen tertiary component with a rotational period of 33 days (see Fekel & Tomkin 1982, and references therein). The light curve shows only partial eclipses, with the depth of the primary eclipse ≃ 0m44 (Grant 1959). The more massive component is a B3 V star with the mass of 7.2 M⊙ and radius of RA = 6.4 R⊙. The secondary star, which is filling its Roche lobe, has a mid-A spectral type with a mass of 1.9 M⊙ and radius of RB = 5.3 R⊙. The lines of the tertiary component are not visible in the spectrum and its orbit is reconstructed by detection of periodic residuals in variation in radial velocities of the primary and secondary (Fekel & Tomkin 1982). The estimated mass of the third star is 0.7 ± 0.2 M⊙ and, according to Fekel & Tomkin (1982), it is most probably a K dwarf.
Although the Hα line in the spectrum of λ Tau is seen in absorption (cf. Grant 1959), subtraction of synthetic atmospheric profiles has revealed the presence of double-peaked emission (Vesper et al. 2001). Examination of the residual profile has showed a signature of central emission arising in the region between the components, and the presence of a rapidly rotating disk (Vesper et al. 2001). This evidence of mass transfer taking place in the inner binary is in agreement with extreme UV observations by Polidan & Peters (1980), which showed the presence of a gas stream.
Despite the very low period ratio in λ Tau, which is only slightly greater than 8:1, no observational evidence for nodal precession has been found. The variations in eclipse depths, which can reveal the nodal motion, have not been detected over a period of ≥30 years. The inner and outer orbits in this triple system are apparently co-planar and remarkably stable over the time span of at least several decades (see Fekel & Tomkin 1982, and discussion therein). The stability of the λ Tau system on larger timescales has been addressed several times (see e.g. Kiseleva et al. 1994, 1998). It was found that the outcome of numeric simulations of the component motions on large timescales depends significantly on the initial conditions, such as the mutual orientation of inner and outer orbit (co-planar or orthogonal), the direction of orbital motions (co-rotation or counter-rotation), and the type of the mass exchange (conservative or non-conservative).
One of the reasons why we targeted this triple system is the possibility of employing high-precision polarimetry to address this issue. The orientation and direction of rotation for the inner orbit can be derived from the analysis of polarization data in the same way as was done for the Algol.
From the period ratio ≈ 8 : 1 and separation of the inner binary components = 21.3 R⊙ (Fekel & Tomkin 1982), one can obtain an estimate for maximum separation of the outer orbit ≈ 85 R⊙ = 0.4 AU. At the distance of 148 pc forλ Tau this value converts to maximum angular separation between positions of the tertiary on the plane of the sky ≈ 2.7 mas. Interestingly, this is fairly close to the projected major semi-axis of the inner orbit in Algol, a = 2.15 mas, as revealed by the CHARA H-band interferometry (Baron et al. 2012).
The quoted maximum resolution of the CHARA interferometer in the H-band is ≈0.5 mas, and is even better in the optical (Baron et al. 2012). Unfortunately, the tertiary star in the λ Tau system is much fainter than the primary and secondary at optical wavelengths. However, because the third component is a K star, the difference in brightness is much less pronounced in the H and K bands. In addition, a relatively short period of motion for the outer orbit (33 days) could make λ Tau a good potential target for near-IR interferometry.
3 Optical polarimetry
3.1 Polarimetric observations
Polarimetry of λ Tau was performed with the Dipol-2 on the 60 cm KVA telescope at the Observatorio del Roque de los Muchachos, La Palma (Dec 2012–Feb 2013, Jan 2014), and the T60 telescope at Haleakala Observatory, Hawaii (Jan 2015, Aug–Dec 2015, Oct–Nov 2016). Both telescopes are operated in remote mode.
Removalof the instrumental polarization Pinst was done by observations of zero-polarized standard stars. More than 20 stars were measured on both telescopes and the average values of instrumental polarization in the B, V , and R bands were computed. The zero point of the polarization angle was determined by the observations of highly polarized standards HD 25443 and HD 204827. For both telescopes Pinst < 0.01%, and we wereable to determine it with an accuracy of 0.0002–0.0003% (see Berdyugin et al. 2016, Tables 1 and 2). This allowed us to calibrate our measurements with a high level of precision and guaranteed consistency between the data sets obtained on two different telescopes. Details of our data calibration and reduction techniques can also be found in Kosenkov et al. (2017).
The total exposure duration of polarization measuring cycle for λ Tau was about 20–30 min per night. During this time, from 48 to 64 single measurements of normalized Stokes parameters q and u were obtained and the average nightly values of linear polarization (69 in total) were computed. Typical measuring errors, calculated from the internal scatter of individual observations, are in the range of 0.001–0.003%, attributable mostly to photon noise in the given passband and sky conditions.
3.2 Polarization variability
To plot a dependence of polarization against the phase of the orbital period of the eclipsing inner binary, the following ephemeris was used: JD(pr. min) = 245 5577.3203 + 3.9529482 . Our measurements clearly reveal low-amplitude (ΔP ≤ 0.07%) phase-locked variability ofpolarization in λ Tau. The variations in the Stokes parameters q and u with the orbital phase are shown in Fig. 1, and the original data are available at the CDS. In the earlier publication (Piirola et al. 2014), we note that the panels in the figure showing polarization variability for λ Tau and HD 165052 are swapped.
Figure 1 also shows the best Fourier fits to the data, including first and second harmonics of the orbital period. As can be seen, the second harmonic variations clearly dominate. According to the analytic scattering model of Brown et al. (1978, hereafter BME model), a dominant second harmonic is expected for a binary system where the light scattering material is symmetrically distributed about the orbital plane. Interestingly, the behaviour of the intrinsic polarization in λ Tau appears to be in strong contrast with Algol itself, where the variations in the Stokes parameter q are predominated by the first harmonic. The average values of polarization are small in all passbands: P ≤ 0.15%. This shows that the interstellar polarization in the direction of λ Tau is small, but not entirely negligible. The small value of interstellar polarization is in agreement with the λ Tau galactic latitude b = −29° (away from galactic plane) and distance d ≃ 150 pc.
The amplitude of variations decreases from ≃0.07% in the B to ≃0.05% in the R band. Thomson scattering is a grey process, but this decrease in polarization can be explained as being due to dilution effects of unpolarized free-free emission and radiation from the secondary increasing towards longer wavelengths. As seen in Fig. 1, the amplitude of variations in the Stokes q is noticeably larger then in Stokes u. This suggests a rather high inclination i of the binary orbit in the λ Tau system (see Fig. 4 in Brown et al. 1978), as expected from the eclipses seen in the light curve.
 |
Fig. 1 Normalized Stokes parameters q and u in the BV R bands of λ Tau plotted against the phase of the orbital period. Phase 0.0 corresponds to the primary minimum. The best Fourier fits with two harmonics are shown as solid lines. Error bars ( ± σ) are shown, or are less than the size of the symbol. |
4 Analysis of polarization data
In λ Tau, the intrinsic linear polarization must be associated with the mass transfer in the semi-detached inner binary. Considering all available data, we can convincingly propose the light scattering on the matter flowing from the Roche-lobe filling secondary as the most probable mechanism which is responsible for the observed phase-locked polarization variability.
There are other mechanisms which may operate in a hot O-spectral type binary system, i.e. reflection of light from the atmospheres of stars and scattering of light in the dense stellar wind (Berdyugin & Harries 1999; Berdyugin et al. 2016). The analysis of variable polarization arising due to these mechanisms would require an explicit numerical modelling of the light scattering processes (Berdyugin et al. 2016). However, given the spectral types of primary and secondary (B3V and mid-A), determined with a high level of confidence, we can consider it unlikely that both reflection and stellar wind have significant contribution to the intrinsic polarization in λ Tau.
This allows us, in addition to the scattering model, to apply the analytical solution proposed by Brown et al. (1978) and derive the parameters of the inner orbit for λ Tau from the coefficients of the best Fourier fits to the normalized Stokes parameters q and u. Since we have polarization data obtained in three passbands, we can derive three sets of orbital parameters independently and compare them with each other.
Following this approach, we have fitted our observational data with Fourier series up to second-order terms, using the standard equations

where λ = 2πϕ and ϕ is the orbital phase. The best fits are shown in Fig. 1. The terms of the best Fourier fits q0 , …, q4 and u0 , …, u4 are given in Table 1. As is seen from this table, the second harmonic terms clearly dominate the observed variability of the Stokes parameters. The contribution from the first harmonic terms (q1 , q2, u1, u2) is marginal and the statistical significance of their coefficients is low, ≤ 3σ (with the exception of u2 ). Figure 2 shows ellipses of the second harmonic for the B, V , and R bands on the (q, u) plane. The ellipse is swept twice per orbit and the direction of circumvention, which is clockwise, corresponds to the direction of orbital motion on the inner orbit in system of λ Tau.
There is a noticeable scatter of the data points around the fitting curves. This scatter, as we believe, is real and demonstrates that apart from periodic phase-locked variability, there are non-periodic polarization variations in λ Tau. As the intrinsic polarization in λ Tau is directly related to mass transfer in the inner binary, this non-periodic component most likely arises from non-stationary processes influencing distribution and concentration of light scattering material.
We would like to point out that a significant change in rotational velocity of the primary mass-gaining star in λ Tau has been reported by Olson (1984) from comparison of the measurements taken in 1968 and 1970. This was interpreted as the consequence of sporadic mass flows occurring in the inner binary. Interpretation of our polarization data supports a scenario with ongoing (permanent) mass flow with sporadic or irregular changes in the mass transfer rate.
Harmonic coefficients of the best Fourier fits to the data obtained for the BV R bands.
 |
Fig. 2 Variations in polarization of λ Tau on the (q, u) plane. The solid lines show the second harmonic fits in the BV R bands. Phases of the orbital period 0.0, 0.25, 0.50, and 0.75 are indicated for the B-band ellipse. Arrows show the direction of circumvention, which is clockwise. The eccentricity of ellipse e gives the inclination of a binary orbit i (e = sin 2i∕(1 + cos2i)) and the angle between the major axis and the q-axis gives the orientation of orbit Ω. |
 |
Fig. 3 Best fits of the observed variations in Stokes parameters q and u in λ Tau with theRoche cloud scattering model for the B band. The dashed lines show the values of the interstellar polarization from the model fit. |
4.1 Parameters of the binary orbit from the analytical solution
To derive orbital parameters from the coefficients of the Fourier fits, we used the formulas given by Drissen et al. (1986, Appendix). The inclination of orbit i and orientation of orbit Ω (i.e. the longitude of ascending node) were computed for each passband separately and are presented in Table 2; as can be seen, the agreement between the values of i and Ω obtained from the best fits for the different passbands is remarkably good. There is an ambiguity in the direction of longitude of ascending node Ω which is determined polarimetrically, and the value of Ω + 180° is equally possible (cf. Drissen et al. 1986).
Table 2 also gives the value of parameter A =H∕G, where H is the measure of effective concentration of material toward the orbital plane and G is the measure of effective degree of asymmetry about the orbital plane (cf. Brown et al. 1978). Table 2 gives two values of A, independently determined from the set of Fourier coefficients for Stokes q and Stokes u. As the derived value of A ≫ 1 for all passbands, there is a high degree of concentration and symmetry of light scattering material with respect to the plane of orbital motion in the inner binary of λ Tau.
As was shown by Aspin et al. (1981), Simmons et al. (1982), and Wolinski & Dolan (1994), there is a bias in the polarimetrically derived orbit inclination i. Because of the unavoidable noise in polarization data (i.e. due to the finite precision of measurements), the inclination of orbit derived from the best Fourier fit is always biased towards higher values. The amount of bias depends notonly on the level of noise, but also on the true inclination: it is higher for the lower true values of i. A bias of the same nature can also be induced by stochastic noise, arising due to intrinsic non-periodic component in polarization variability (see Manset& Bastien 2000).
Since the inner pair in λ Tau is an eclipsing binary, we can expect that the true inclination is comfortably high and the bias is small. There are several estimates of inner orbit inclination obtained from the modelling of the binary light curve: i = 86° (Grant 1959), i = 81.3° ± 0.3° (Hutchings &Hill 1971), and i = 76.0° ± 0.5° (Cester et al. 1978). As was shown by Fekel & Tomkin (1982), among these estimates only that determined by Cester et al. (1978) is consistent with the requirement that the secondary should fill its Roche lobe.
As is seen from Table 2, the values of i obtained from our polarization data for the B, V , and R bands are very close to each other. Moreover, they are in excellent agreement with the inclination of orbit i = 76° derived by Cester et al. (1978). In order to define the confidence intervals for i and Ω we used the method proposed in the paper by Wolinski & Dolan (1994). It utilizes the special merit parameter γ defined as
 (2)
(2)
where A is the fraction of the amplitude of polarization variability defined as
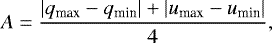 (3)
(3)
N is the number of observations, and σP is the error of polarization measurements. In the case of λ Tau, the typical error of observation is several times smaller than the amplitude of non-periodic scatter. Therefore, we use in Eq. (2) the value of σP, which corresponds to the variance of non-periodic noise determined from the scatter of the observed Stokes parameters around the best fit curves. The weighted σP, derived in this way, is the highest for the B band ( ≈0.006%), and lowest for the R band ( ≈0.004%). The resulting values of γ computed for the B, V , and R bands via Eqs. (2) and (3) are 750, 970, and 990, respectively.
To estimate 1σ confidence intervals for i and Ω we employed the plots presented in the paper by Wolinski & Dolan (1994, Figs. 4 and 6 therein) for γ = 300. Because our values of γ are at least 2.5–3 times higher, these estimates are rather conservative, and actual confidence intervals must be even smaller. The resulting values of inclination and orbit orientation, averaged for all passbands, are i = 76° + 1°∕−2° and Ω =15°(195°) ± 2°.
Parameters of binary orbit in λ Tau derived from coefficients of the Fourier fits for the BV R bands.
4.2 Scattering model
The analytical solutions do not take into account the finite size of the stars and eclipses of the scattering material which unavoidably take place in close binary stars seen at high inclination. Numerical modelling has the obvious advantage that it allows inclusion explicitly into the model various scattering components: e.g. stream, disk, shells, etc. Thus, it gives more information on the possible location of light scattering material than the analytical solution does. We have modelled polarization in λ Tau with a scattering code that is based on the approach outlined in Piirola (1980) and Piirola et al. (2005, 2006). Single Thomson scattering of photons by an optically thin medium, and spherical illuminating stars are assumed. For λ Tau we have considered five possible scattering geometries:
-
1.
Scattering from a cloud approximating the shape of the Roche lobe of the secondary star surface facing the primary component;
-
2.
Scattering cloud near the inner Lagrangian point L1;
-
3.
Spherical scattering shell around the secondary component;
-
4.
Stream between the components;
-
5.
Flattened disk around the primary.
Model fits were made for each of these models separately, assuming one dominant scattering component. In our models we fixed the stellar and orbital parameters to those given in Sect. 2. The results of our modelling for each scattering scenario are combined in Table 3. This table gives the value of the (unweighted) RMS scatter σ of observed points from the fitted model curves, orbital inclination i, the longitude of ascending node Ω, the parameter W (which is proportional to the total number of scattering electrons), and the parameters of the interstellar polarization determined by the model qis, uis. These results are presented separately for each passband. The error estimates of the parameters given in Table 3 are providedby the least-squares fitting procedure described in detail in the Appendix of Piirola et al. (2005). The best fitting inclination was found by running the model code for a range of inclinations, and then choosing the inclination where the RMS scatter reaches the minimum.
The best fit (see Figs. 3–5) is obtained with the Roche cloud model (Table 3); nearly as good is the fit by the L1 cloud. The spherical shell around the secondary and the stream between the components give somewhat worse fits, i.e. larger RMS scatter of the observed points from the model curves. The disk is clearly inferior, and no statistically significant disk around the primary is seen in polarized light. Therefore, no useful orbital parameters are provided by the disk model.
Illustrations of the Roche and L1 cloud models are given in Figs. 6 and 7. The Roche cloud is shifted by 5°, as seen from the centre of the secondary star, into the direction of the orbital motion of the secondary star. The L1 cloud is shifted in longitude by 0.2RA (where RA is the radius of primary star) into the orbital motion direction of the secondary star. The Shell B and Stream models are shown together in Figs. 8 and 9, where the amount of the polarized flux from the scattering points is also indicated. The length of the bars is proportional to the polarized flux and the direction of the bars gives the position angle of the maximum electric vector. The maximum polarized flux is observed near the quadratures, phases 0.25 and 0.75, where scattering angles are favourable (near 90°). At the primary eclipse (phase 0.0) the intrinsic polarization goes to zero as the scattering material is not visible. Another minimum of the phase-locked polarization takes place near the secondary minimum where the scattering angles are low (backscattering). Actually a polarization reversal occurs at phase 0.5 where the direction of polarization becomes perpendicular to the predominant polarization direction (Figs. 8 and 9). This is also seen in Figs. 3–5 where the values of q and u momentarily cross the interstellar polarization levels at phase 0.5, i.e. the intrinsic q and u change signs.
The value of interstellar polarization, as derived from the model fits, is in the range of 0.11–0.12% with the maximum in the V band. This wavelength dependence is to be expected for the “typical” diffuse interstellar dust which has a mean λmax ≈ 0.55 nm (cf. Whittet 1991).
The orbital inclination values, i ~ 76°, and the orientation, Ω ~ 16°, obtained from the Shell B model agree very well with those given by the analytic solution (Sect. 4.1). This is expected as the model is perfectly symmetric. The other models converge at somewhat lower inclination (i ~ 72°–74°). This would require a corresponding modification of the binary parameter solution adopted earlier for λ Tauri. The slightly lower inclination values are still consistent with the secondary filling its Roche lobe. According to Fekel & Tomkin (1982) this condition is i ≤ 76°.
As shown in Fig. 10, the disk around the primary would be visible throughout the orbital cycle, except just before and after the primary eclipse, where sharp changes of intrinsic polarization would take place. This is inconsistent with the observed polarization curves and puts quite tight upper limits for the amount of disk-like scattering material in the system. If the disk is put as a second component together with one of the better fitting scattering models, the weighting factor is reduced to Wdisk ~ 0.01, and the fit is not improved. Applying Eqs. (2) and (3) in Piirola et al. (2005), this value of W corresponds to the mass of fully ionized hydrogen in the disk, MH ~ 0.8 × 10−13 M⊙. For the better fitting models (Table 3) the scattering cloud masses are 30–40 times larger. However, if the disk is optically thick, multiple scattering reduces the net polarization, and the disk may become invisible in polarized light.
 |
Fig. 6 Modelfor λ Tau with a scattering cloud near the Roche lobe surface of the secondary facing the primary. The numbers give the orbital phase. |
 |
Fig. 7 Modelfor λ Tau with a scattering cloud near the inner Lagrangian point L1. |
 |
Fig. 8 Scattering models for λ Tau with a spherical shell around the secondary and a stream between the components. The length of the ticks is proportionalto the polarized flux, and the orientation gives the position angle of the maximum electric vector. See Sect. 4.2 for details. |
 |
Fig. 10 Scattering model for λ Tau with anequatorial disk around the primary component. |
5 Conclusions
Our high-precision polarization measurements of the triple system λ Tau have revealed intrinsic linear polarization which is variable with the phase of inner binary orbital period. The amplitude of this variability, ~0.05%, is typical for classical Algol-type semi-detached systems. We show that the most likely mechanism responsible for this polarization is light scattering in the circumstellar material which is formed due to ongoing mass transfer. The presence of a non-periodic component in variations in the observed Stokes parameters q and u can be explained by sporadic changes in the mass transfer rate.
From the Fourier fit to the observed variations in the Stokes parameters, the estimates for the inclination i = 76° + 1°∕−2°, and orientation Ω =15°(195°) ± 2° of the inner orbit have been found. The direction of motion on this orbit, as seen on the sky, is clockwise. The inclination of orbit derived from polarimetry, i = 76°, is in good agreement with the value determined by Cester et al. (1978) from the light curve. This provides additional support to the conclusion that the secondary star in λ Tau system is filling the Roche lobe.
The best fits for the numerical scattering model have been obtained for the light scattering cloud located between the primary and secondary components. The inclination of binary orbit, i = 72°–76°, derived from the numerical model fits agrees within the errors with the i obtained from the analytical solution. The scattering model fits give slightly different values of the orbit orientation, Ω =16°(196°)–19°(199°), depending on the location of the scattering material.
Since for λ Tau the orientation and direction of rotation on the inner orbit have now been determined polarimetrically, this triple system with low period ratio can be considered a promising potential target for high-resolution IR interferometry. If the orbital motion on the outer orbit is resolved, all the parameters necessary for drawing conclusions on the long-term stability of λ Tau will be known. Our results show the power of high-precision polarimetry to provide important information on the structure of interacting binaries and multiple stellar systems.
Acknowledgements
This work was supported by the ERC Advanced Grant HotMol ERC-2011-AdG-291659 (www.hotmol.eu). DIPOL-2 was built in cooperation by the University of Turku, Finland, and the Kiepenheuer Institut fuer Sonnenphysik, Germany, with support from the Leibniz Association grant SAW-2011-KIS-7. We are grateful to the Institute for Astronomy, University of Hawaii for the observing time allocated for us on the T60 telescope. We are also grateful to the AAVSO and, personally, to Bob Nelson for maintaining and regularly updating his very useful o-c web page.
References
- Aspin, C., Simmons, J. F. L., & Brown, J. C. 1981, MNRAS, 194, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, F., Monnier, J. D., Pedretti, E., et al. 2012, ApJ, 752, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugin, A. V., & Harries, T. J. 1999, A&A, 352, 177 [NASA ADS] [Google Scholar]
- Berdyugin, A., Piirola, V., Sadegi, S., et al., 2016, A&A, 591, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C., McLean, I. S., & Emslie, A. G. 1978, A&A, 68, 415 [NASA ADS] [Google Scholar]
- Cester, B., Fedel, B., Giuricin, G., Mardirossian, F., & Mazzetti, M., 1978, A&A, 62, 291 [NASA ADS] [Google Scholar]
- Drissen, L., Lamontagne, R., Moffat, A. F. J., Bastien, P., & Seguin, M. 1986, ApJ, 304, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., & Tomkin, J., 1982, ApJ, 263, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, G. 1959, ApJ, 129, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hutchings, J. B., & Hill, G. 1971, ApJ, 166, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Kemp, J. C., Barbour, M. S., McBirney, R. E., & Rudy, R. J. 1981, ApJ, 243, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Orlov, V. V. 1994, MNRAS, 270, 936 [NASA ADS] [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenkov, I. A., Berdyugin, A. V., Piirola, V., et al. 2017, MNRAS, 468, 4362 [NASA ADS] [CrossRef] [Google Scholar]
- Manset, N., & Bastien, P. 2000, AJ, 120, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, E. C. 1984, PASP, 96, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, G. J. 1989, Space Sci. Rev., 50, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Piirola, V. 1980, A&A, 90, 48 [NASA ADS] [Google Scholar]
- Piirola, V., Berdyugin, A., Mikkola, S., & Coyne, G. V. 2005, ApJ, 632, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Piirola, V., Berdyugin, A., Coyne, G. V., Efimov, Y. S., & Shakhovskoi, N. M. 2006, A&A, 454, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piirola, V., Berdyugin, A., & Berdyugina, S. 2014, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 9147, 8 [Google Scholar]
- Polidan, R. S., & Peters, G. J., 1980, in Close Binary Stars: Observations and Interpretation, eds. M. J. Plavec, D. M. Popper, & R. K. Ulrich (Dordrecht: Reidel), IAU Symp., 88, 293 [Google Scholar]
- Rudy, R. J., & Kemp, J. C. 1978, ApJ, 221, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, J. F. L., Aspin, C., & Brown, J. C. 1982, MNRAS, 198, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Söderhjelm, S., 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
- Söderhjelm, S., 1980, A&A, 89, 100 [Google Scholar]
- Vesper, D., Honeycutt, K., & Hunt, T. 2001, AJ, 121, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., 1991, in Dust in the Galactic Environment, eds. R. J. Tayler, & R. F. White (Cambridge: Cambridge University Press, IOP Publishing Ltd) [Google Scholar]
- Wolinski, K. G., & Dolan, J. F. 1994, MNRAS, 267, 5 [NASA ADS] [CrossRef] [Google Scholar]
The latest ephemeris can be found at https://www.aavso.org/bob-nelsons-o-c-files. It is based on the O–C data collected up to the year 2011.
All Tables
Harmonic coefficients of the best Fourier fits to the data obtained for the BV R bands.
Parameters of binary orbit in λ Tau derived from coefficients of the Fourier fits for the BV R bands.
All Figures
 |
Fig. 1 Normalized Stokes parameters q and u in the BV R bands of λ Tau plotted against the phase of the orbital period. Phase 0.0 corresponds to the primary minimum. The best Fourier fits with two harmonics are shown as solid lines. Error bars ( ± σ) are shown, or are less than the size of the symbol. |
| In the text | |
 |
Fig. 2 Variations in polarization of λ Tau on the (q, u) plane. The solid lines show the second harmonic fits in the BV R bands. Phases of the orbital period 0.0, 0.25, 0.50, and 0.75 are indicated for the B-band ellipse. Arrows show the direction of circumvention, which is clockwise. The eccentricity of ellipse e gives the inclination of a binary orbit i (e = sin 2i∕(1 + cos2i)) and the angle between the major axis and the q-axis gives the orientation of orbit Ω. |
| In the text | |
 |
Fig. 3 Best fits of the observed variations in Stokes parameters q and u in λ Tau with theRoche cloud scattering model for the B band. The dashed lines show the values of the interstellar polarization from the model fit. |
| In the text | |
 |
Fig. 4 As in Fig. 3, but for the V band. |
| In the text | |
 |
Fig. 5 As in Fig. 3, but for the R band. |
| In the text | |
 |
Fig. 6 Modelfor λ Tau with a scattering cloud near the Roche lobe surface of the secondary facing the primary. The numbers give the orbital phase. |
| In the text | |
 |
Fig. 7 Modelfor λ Tau with a scattering cloud near the inner Lagrangian point L1. |
| In the text | |
 |
Fig. 8 Scattering models for λ Tau with a spherical shell around the secondary and a stream between the components. The length of the ticks is proportionalto the polarized flux, and the orientation gives the position angle of the maximum electric vector. See Sect. 4.2 for details. |
| In the text | |
 |
Fig. 9 As in Fig. 8, but for the orbital phases 0.50 to 0.0. |
| In the text | |
 |
Fig. 10 Scattering model for λ Tau with anequatorial disk around the primary component. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


