| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731991 | |
| Published online | 29 March 2018 | |
CHANG-ES
IX. Radio scale heights and scale lengths of a consistent sample of 13 spiral galaxies seen edge-on and their correlations
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
e-mail: mkrause@mpifr-bonn.mpg.de
2
Dept. of Physics, Engineering Physics, & Astronomy, Queen’s University,
Kingston,
Ontario
K7L 3N6, Canada
e-mail: irwin@astro.queensu.ca
3
Astronomisches Institut, Ruhr Universität Bochum,
44780
Bochum, Germany
4
Department of Astronomy, University of Michigan,
311 West Hall, 1085 S. University Ave,
Ann Arbor,
MI
48109-1107, USA
5
CSIRO Astronomy and Space Science,
26 Dick Perry Avenue,
Kensington,
WA
6151, Australia
6
Department of Physics and Astronomy, University of New Mexico, 800 Yale Boulevard, NE,
Albuquerque,
NM
87131, USA
7
Universität Hamburg, Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg, Germany
8
Department of Astronomy, New Mexico State University, PO Box 30001, MSC 4500,
Las Cruces,
NM
88003, USA
9
Department of Physics and Astronomy, University of Manitoba,
Winnipeg,
Manitoba
R3T 2N2, Canada
10
National Radio Astronomy Observatory,
520 Egmont Road,
Charlottesville,
VA
22903, USA
Received:
25
September
2017
Accepted:
27
November
2017
Aim. The vertical halo scale height is a crucial parameter to understand the transport of cosmic-ray electrons (CRE) and their energy loss mechanisms in spiral galaxies. Until now, the radio scale height could only be determined for a few edge-on galaxies because of missing sensitivity at high resolution.
Methods. We developed a sophisticated method for the scale height determination of edge-on galaxies. With this we determined the scale heights and radial scale lengths for a sample of 13 galaxies from the CHANG-ES radio continuum survey in two frequency bands.
Results. The sample average values for the radio scale heights of the halo are 1.1 ± 0.3 kpc in C-band and 1.4 ± 0.7 kpc in L-band. From the frequency dependence analysis of the halo scale heights we found that the wind velocities (estimated using the adiabatic loss time) are above the escape velocity. We found that the halo scale heights increase linearly with the radio diameters. In order to exclude the diameter dependence, we defined a normalized scale height h˜ which is quite similar for all sample galaxies at both frequency bands and does not depend on the star formation rate or the magnetic field strength. However, h˜ shows a tight anticorrelation with the mass surface density.
Conclusions. The sample galaxies with smaller scale lengths are more spherical in the radio emission, while those with larger scale lengths are flatter. The radio scale height depends mainly on the radio diameter of the galaxy. The sample galaxies are consistent with an escape-dominated radio halo with convective cosmic ray propagation, indicating that galactic winds are a widespread phenomenon in spiral galaxies. While a higher star formation rate or star formation surface density does not lead to a higher wind velocity, we found for the first time observational evidence of a gravitational deceleration of CRE outflow, e.g. a lowering of the wind velocity from the galactic disk.
Key words: galaxies: spiral / galaxy: halo / galaxies: magnetic fields / galaxies: ISM / radio continuum: general / radio continuum: galaxies / radio continuum: galaxies
© ESO 2018
1 Introduction
The halo around spiral galaxies is the interface between the bright disk with star formation activity and the intergalactic medium and can best be observed in edge-on galaxies. Halos of star-forming galaxies are formed of stars, gas, cosmic rays, and magnetic fields. The star formation in the galactic disk is generally regarded to be the source of cosmic-ray electrons (CRE) accelerated in the shock fronts of supernova (SN) explosions. Together with the magnetic field, CRE are responsible for non-thermal radio emission. The gravitational force is balanced by thermal, non-thermal, and kinetic pressures. Models assuming hydrostatic equilibrium are used to describe the global state of the multi-phase interstellar medium (ISM) in galactic halos (Fletcher & Shukurov 2001; Boulares & Cox 1990). The assumption of hydrostatic equilibrium appears to be valid when considering the average state of the ISM over large scales or times. Magnetic fields and cosmic rays are generally thought to be important contributors to the pressure balance of galaxy halos (Boulares & Cox 1990), while the role of gas outflows and their kinetic pressure is unclear.
The distributions of gas density, cosmic rays, and magnetic fields with distance from the galaxy plane can be described by at least two exponential functions, one with a small scale height (typically a few 100 pc) for the disk itself and one with a larger scale height (1–2 kpc) for the halo. Magnetohydrodynamic models of evolving galaxies indicate that another very extended component with a scale height of 10–40 kpc may exist (Pakmor et al. 2017).
The best tool for measuring the energy densities of the magnetic fields and cosmic rays is non-thermal (synchrotron) emission, which is strongest in the radio range. The intensity of synchrotron emission is proportional to the magnetic field strength to the power of about two and the number density of CRE in the relevant energy range. CRE with energies of a few GeV emit radio waves in the GHz range in magnetic fields of about 10 μG strength. The total radio continuum emission of a galaxy halo is dominated by this synchrotron emission.
The extent of a radio halo perpendicular to the disk of a spiral galaxy, as we observe it in the radio continuum, is related to the extent of magnetic fields and CRE and to the sensitivity level of a radio map. Usually, the magnetic field extends far out into the halo and further into the intergalactic medium (IGM). Under the assumption of energy equipartition between cosmic rays and magnetic fields, the extent of magnetic fields is larger than that of cosmic rays by a factor of about 2 (Beck 2007).
In addition, the CRE lose their energy while they travel outwards into the halo and their volume density decreases due to adiabatic expansion into the IGM. Both effects lead to a “halo boundary” which is frequency dependent. Beyond this boundary synchrotron emission is no longer detectable because CRE are not energetic enough or not sufficiently numerous. Depending on which process dominates, we distinguish between a synchrotron energy loss-dominated (low energy) or an escape-dominated halo (a few CRE).
The transport of the CRE themselves can happen by diffusion or by convective outflow. These processes have different frequency dependences which can be used to identify them. They also depend on the total magnetic field strength and field ordering (Tabatabaei et al. 2013).
From pioneering observations of edge-on galaxies by Hummel & van der Hulst (1989) and Hummel et al. (1991a,b) it is clear that radio continuum emission can extend far into galaxy halos up to vertical heights of many kpc. As the simple extent of a radio halo depends on the sensitivity of the observations, a better suited and more physical quantity is usually taken to describe the halo size. This is the radio scale height of the halo, sometimes also referred to as scale height of the thick disk (Dumke et al. 1995).
Until now, the radio scale heights of the halos could only be determined for a few bright and extended nearby spiral galaxies (see Dumke & Krause 1998; Krause 2009; Heesen et al. 2016). With the Continuum HAlos in Nearby Galaxies – an EVLA Survey (CHANG-ES) observations (Irwin et al. 2012), we significantly increased the number of observed edge-on galaxies, as well as the sensitivity of the radio maps. In this paper we present the scale heights of thirteen galaxies of this sample in C-band and L-band (with central frequencies of 6 GHz and 1.5 GHz) by which the number of observed edge-on galaxies increases significantly, especially towards smaller or more distant objects. We describe the sample selection in Sect. 2 and present the method used for the scale height determination in Sect. 3. The results are presented in Sect. 4 and compared with other structural properties of the galaxies in Sect. 5. We also determined the magnetic field strengths for the galaxies, given in Sect. 6, and discuss the frequency dependence of the halo scale heights in Sect. 7. Finally, the radio scale heights were tested for correlations with e.g. the magnetic field strengths and star formation in Sect. 8 and discussed in Sect. 9, followed by the summary and conclusion in Sect. 10.
2 Galaxy sample
CHANG-ES (Irwin et al. 2012) is an unprecedented deep radio continuum survey of a sample of 35 nearby spiral galaxies seen edge-on and observed with the Karl G. Jansky Very Large Array (hereafter Expanded VLA or EVLA) in its commissioning phase. The sample galaxies are selected from the Nearby Galaxies Catalog (NBGC; Tully 1988) according to their radio flux density at 1.4 GHz (S1.4 > 20 mJy), blue isophotol diameter (4′ < d25 < 15′), declination (δ > −23°), and inclination (i > 75°) (see Table 1 in Irwin et al. 2012). In addition, three well-known edge-on galaxies just outside the size limits were also added: NGC 4244, NGC 4565, and NGC 5775. These are 35 galaxies in total which enable us, for the first time, to observe radio halos and determine vertical scale heights in a statistically meaningful sample of nearby spiral galaxies. The galaxies were observed in C- and L-band at B- (only L-band), C-, and D-array configurations (see Irwin et al. (2012) for details). The total and polarized intensity maps at D-array are published in Paper IV (Wiegert et al. 2015) and are available in the CHANG-ES Data Release I1 . The observations at C-array are also reduced and will be published by Walterbos et al. (in prep.). As we need high sensitivity and high resolution for the determination of the vertical radio scale heights, we analyse in this paper C-band (6 GHz with 2 GHz bandwidth) D-array and L-band (1.5 GHz with 500 MHz bandwidth) C-array maps of total intensity with an (untapered) angular resolution between 9′′ and 16′′ .
Missinglarge-scale flux density for extended structures larger than 4′ is expected at C-band. As we do not yet have corresponding single-dish observations to combine with our CHANG-ES data, we excluded eight galaxies from our sample with angular sizes larger than 12′ (as determined from the plots in Paper IV; Wiegert et al. 2015). We omitted five more galaxies which do not show extended disk emission and are known to have strong nuclear activity and/or to be in a merger phase: NGC 660, NGC 2992, NGC 4594, NGC 4845, and NGC 5084. The initial value for the position angle of each galaxy was taken from NED and the literature. For each galaxy we checked these values with our new radio observations at C-band.
As the scale heights are meant to describe the vertical extent of the disk and halo of a galaxy, we have to restrict ourselves to strongly inclined objects. The value for the inclination given in Tully (1988) was checked for each galaxy with that given in NED and actual values in the literature. As our scale height program (see Sect. 3) is very sensitive to this parameter. It even allows us to verify the value within a certain range. Ultimately, we found that our best estimates for the inclination deviate up to 8° from the values given by Tully (1988). We also found that vertical scale heights can only properly be fitted for galaxies with inclinations i > 80° with the correction for the disk emission applied in our model (see Sect. 3). Hence, we rejected seven galaxies from our sample which we found to have inclinations i < 80°: NGC 3448, NGC 4388, NGC 4096, NGC 4438, NGC 4666, NGC 5297, and NGC 5792. This is probably also the case for twomore galaxies, NGC 2613 and NGC 2683. In addition, the latter shows a varying position angle by ~25° across the velocity field, which may indicate a strong bar viewed close to side-on (Kuzio de Naray et al. 2009). Hence, we also exclude these two galaxies. Our final galaxy sample contains 13 edge-on spiral galaxies which are listed in Table 1 together with our best estimates for the inclination (i) and position angles (p.a.). The values for the distance are taken from Paper IV (Wiegert et al. 2015). The coordinates given in Table 1 are the central positions of the galaxies as given in Wiegert et al. (2015) except for NGC 4013, for which we determined the location of the strong nuclear source from our 9.1′′ resolution map to be α2000 = 11h58m31.s4 and δ2000 = 43°56′50′′. All maps (at C- and L-band) were smoothed to a circular beam with HPBW given in Table 1 together with their rms noise values in our maps. The rms values listed in Cols. 8 and 10 were measured from our slightly smoothed primary beam corrected maps. They are thus different from the values given in Wiegert et al. (2015) for C-band and Walterbos et al. (in prep.) for L-band, which were measured from the maps without primary beam correction and far from the source.
Galaxy sample.
3 Method
The determination of the vertical radio scale heights of spiral galaxies seen edge-on goes back to the method initially described and applied by Dumke et al. (1995). We determined the scale heights with the new NOD3 program package (Müller et al. 2017). The task is called “BoxModels” and works with total intensity maps in fits-format smoothed to a circular beam.
Within the task, the galaxy is rotated by an angle given by the position angle of the galaxy to a horizontally orientated major axis. Then strips are chosen perpendicular to the major axis (hence in the z-direction) positioned with respect to the centre of the galaxy. As an example we use our 6 GHz map of NGC 5775 (Fig. 1) with the strips on top of the rotated galaxy in Fig. 2. Each strip consists of a number of rectangular boxes, specified by the width ofthe strip and a certain height within which the radio intensities are averaged. The uncertainties in the intensities were derived from the standard deviation around the mean in each box. In order to exclude the intensity gradient in the z-direction from the standard deviation, the standard deviation is calculated separately along each row within a box parallel to the galaxy’s major axis, and averaged over all rows within each box. The averaged intensity in each box forms a distribution with z that is fitted to determine the scale height along each individual strip. For inclinations i < 90° the observed intensity distribution is the superposition of the intrinsic vertical distribution of the disk and halo emission and the inclined disk emission (even if we assumed that the disk is infinitesimally thin), convolved with the beam ofthe telescope. As we are only interested in the vertical intensity distribution, the contribution of the disk hasto be estimated. It depends only on the disk’s diameter and inclination. The disk is assumed to be circular in shape with a diameter given by its radio emission along the major axis. Its inclined values are used for a diameter-dependent geometrical correction for the contribution of the disk on the scale heights by defining an effective beam size HPBWeff which is largest at the central strip and decreases in the strips further outwards along the major axis approaching the value of the HPBW at the edges.
As an exact deconvolution of the observed intensity distribution with HPBWeff cannot be applied, we assume different possible vertical distributions convolved with the corresponding HPBWeff for each strip and compare them with the observed distributions by least-square fits. Similar to Dumke et al. (1995), we assume an intrinsic exponential
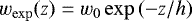 (1)
(1)
or an intrinsic Gaussian distribution
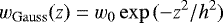 (2)
(2)
with peak intensity w0 and scale height h. This is convolved with the effective telescope beam 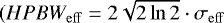 )
)
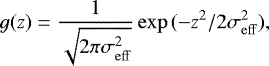 (3)
(3)
which describes the contribution of the telescope’s beam and the projected emission of the infinitesimally thin disk. The convolved emission profile has the form
![\begin{align}\vspace*{-8pt} W_{\mathrm{exp}}(z) &=&\frac{w_{0}}{2}\exp{(-z^{2}/2\sigma_{\mathrm{eff}}^{2})} \\* &&\times \left[\exp{\left(\frac{\sigma_{\mathrm{eff}}^{2}-{zh}}{\sqrt{2}\sigma_{\mathrm{eff}}h}\right)}^{2}\mathrm{erfc}\left(\frac{\sigma_{\mathrm{eff}}^{2}-{zh}}{\sqrt{2}\sigma_{\mathrm{eff}} h}\right) \right.\\* && + \left. \exp{\left(\frac{\sigma_{\mathrm{eff}}^{2}+{zh}}{\sqrt{2}\sigma_{\mathrm{eff}} h}\right)}^{2}\mathrm{erfc}\left(\frac{\sigma_{\mathrm{eff}}^{2}+zh}{\sqrt{2}\sigma_{\mathrm{eff}} h}\right) \right] \vspace*{-8pt} \end{align}](/articles/aa/full_html/2018/03/aa31991-17/aa31991-17-eq7.png) (4)
(4)
in the case of an exponential intrinsic distribution (Sievers 1988), where erfc is the complementary error function, defined as
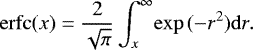 (5)
(5)
For a Gaussian intrinsic distribution, the convolution yields (Dumke 1994)
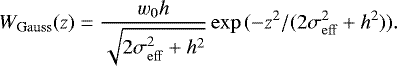 (6)
(6)
The vertical radio scale heights h can be determined by fitting one or two convolved exponential or Gaussian functions of the form given in Eq. (4) or Eq. (6) to the averaged radio intensities along each strip of a galaxy. The least-squares fits are made using the Levenberg–Marquardt method. Single boxes along a strip with mean values smaller than 2× the rms-noise intensity level of the map are omitted by the fitting procedure. The quality of the fit along each strip is determined by a reduced χ2 test.
4 Application to our sample and results
4.1 Scale heights
The vertical scale heights were determined for all galaxies in our sample, as defined in Sect. 2 for C- and L-band. We applied the program to the untapered but primary beam corrected maps of total intensity which had been cleaned with a robust 0 weighting, as described in Paper IV (Wiegert et al. 2015). The strip width had to be adapted for each galaxy and band in such a way that first they are broader than the beam size in order to gain sensitivity and to have independent points between neighbouring strips, and second they are small enough to avoid strong intensity variation parallel to the major axis which would increase the intensity dispersion within one box. The vertical box size (box height) was taken as 4′′ , which is smaller than half the beam size. Otherwise, the sampling along the intensity profile would not be sufficient to fit the maximum of the vertical intensity distribution well enough. This means that neighbouring points along one strip are not independent from each other. As the errors of the individual points are only determined along the strip length, not the strip height (see Sect. 3), the selected box height does not affect the errors of the individual points.
Figure 3 presents the plots together with the results for each strip of our example galaxy NGC 5775 shown in Figs. 1 and 2. The parameters used for the fits of all galaxies in our sample are summarized in Table 2. Generally within our sample, the intensity distribution along the strips can be better fitted by exponential functions than by Gaussian functions. First, the data in each strip was fitted by a two component exponential function, as shown in Fig. 3. Then the scale heights determined in each strip of a galaxy were averaged together (except for some strongly deviating values with large errors which have been omitted). The averaged scale heights for each galaxy together with their standard deviations at both frequency bands are listed in Table 3 as h0 for the thin disk exponential component and h for the exponential thick disk/halo component. In the following, we will refer to h as scale height of the halo.
In NGC 3079, the scale heights of the central strips have also been omitted in the averaging procedure because of the strong nuclear source. Similarly, in UGC 10288 only strips which do not contain the background radio galaxy CHANG-ES A (Irwin et al. 2013)are considered.
Generally, the relative errors of the scale heights of the halo are between 5% and 20%, whereas those of the thin disk are much larger (50–100%). Hence, the scale heights of the thin disk are not well determined. This is partly because the expected scale heights for the thin disks are small (2.5′′ corresponds to about 300 pc for galaxies at a distance of 25 Mpc) compared to the angular beam size of about 10′′ of the observations (see Table 1). Another problem, especially for the values for the thin disk, are the errors in the inclination, which are about ±2°. However, only the nearest galaxies with distances ≲20 Mpc have the smallest scale heights fitted for the thin disk in Table 3 with values corresponding to only 50 ± 50 pc in C-band. This could hint at smaller scale heights for the thin disks than previously known.
The values for the halo scale heights are in general ≳10′′ (i.e. larger than the beam size), which is large enough to be reliably estimated. In this paper from now on we only discuss the results for the halo. For two galaxies, NGC 3877 and UGC 10288, we found the same results for two fit components. Hence, one component is enough to fit their vertical distributions. As these values are larger than expected for the thin disk, we refer to them as halo scale heights.
The halo scale heights of the total radio emission are given in kpc in Table 4. The variation within our sample is far greater than that of the scale heights determined earlier for five large and more nearby edge-on galaxies at 4.8 GHz (1.8 ± 0.2 kp; Krause 2015). Our new values range between 0.7 kpc and 1.5 kpc in C-band, and between 0.9 kpc and more than 3 kpc in L-band. The value for NGC 5775 in C-band (which is in both samples) is also smaller than the values given in Soida et al. (2011). However, when corrected to the distance of 26.7 Mpc as taken in Soida et al. (2011), we derive 1.6 ± 0.14 kpc for the C-band halo scale height instead of 2.0 ± 0.2 as given in Soida et al. (2011). The remaining difference may be due to a higher angular resolution of our new maps (11′′ instead of 16′′) and to the more sophisticated method of our new scale height determination which may be important for this small object (in angular size). We already note here that other bright and more nearby galaxies (hence larger in angular and/or physical size) like NGC 891, NGC 4565, and NGC 4631 from the CHANG-ES sample have larger halo scale heights when determined with the same new method (see Schmidt et al., in prep.; Mora-Partiarroyo et al., in prep.) than the galaxies in our sample.
Our averaged values for the halo scale heights are 1.1 ± 0.3 kpc in C-band and 1.4 ± 0.7 kpc in L-band. As the averaged L-band value is also below the previous value determined at 4.8 GHz, our smaller values for the scale heights cannot be explained by missing large-scale flux density as this affects mainly the C-band values (see Sect. 4.2).
 |
Fig. 1 Total intensity colourized map of NGC 5775 at 6 GHz. The rms noise is 10 μJy beam−1 with the beam size (10.7′′) given in bottom left corner. |
 |
Fig. 2 Rotated total intensity colourized map of NGC 5775 at 6 GHz with the strips and boxes for the scale height determination superimposed. In this case we used seven strips of 30′′ in width, with 21 boxes of 4′′ in height each. The beam size (10.7′′) is given in bottom left corner. |
Fit parameters.
 |
Fig. 3 Averaged radio intensities of NGC 5775 within the boxes along the seven strips shown in Fig. 2 and their two-component exponential fits according to Eq. (4). |
Fit results.
Halo scale heights and normalized (halo) scale heights.
4.2 Radial extents and possible effects of missing spacings
Before we discuss our scale height values physically we have to make sure whether they suffer from missing large-scale flux density in the map. As mentioned in Sect. 2, we excluded galaxies which are larger in angular size than 6′ from our sample.
Missing large-scale flux density for extended structures larger than 240′′ is expected at C-band and only larger than 970′′ at L-band. For comparison, we determined the angular sizes of all sample galaxies in C- and L-band within the 2 × rms contours along the major axis (see Cols. 2 and 3 (diameter) in Table 5). While in L-band all sample galaxies are much smaller than 970′′ in angular size, in C-band there are several galaxies with angular diameters near or above 240′′ . Missing large-scale flux density in these galaxies could lead to underestimated scale heights. In order to test this, we determined the radio diameter of each galaxy as the angular size of the radio intensity within 2× the rms contours along the major axis (see Table 1) and plotted the scale heights for C- and L-band against this quantity (both measured in arcsec), as shown in Fig. 4.
In contrast to what would be expected for missing large-scale structure (namely a decrease in scale heights with diameter when both are measured in arcsec), the scale heights determined at C-band increase with diameter. At larger diameters the scale heights at L-band also increase, similarly to the C-band data. Hence, we conclude that we have no obvious missing spacing problem for our sample galaxies. However, we cannot exclude them. In this case the C-band scale heights would give lower limits for the radio scale heights.
Diameters.
 |
Fig. 4 Halo scale heights vs. the galaxy’s radio continuum diameter, both in arcsec in order to exclude errors in the distance determination. C-band data are represented by black asterisks, L-band data by blue triangles. |
5 Radial scale lengths, distances, and diameters
In addition to the vertical scale heights we also determined the radial scale lengths of all sample galaxies. As learned from the analysis of stellar disks in edge-on galaxies, the line-of-sight integration of an exponential distribution in radius results in a Bessel function that can be closely approximated by an exponential with the same scale length (van der Kruit & Searle 1981). The evaluation was done with the same task in the NOD3 package (Müller et al. 2017), similar to that of the scale height determination (see Sect. 3) except that the strip is now parallel to the major axis with a width of about 1–2.5× HPBW. The distribution is again corrected for the beam size. However, no correction for the inclination is necessary. We fitted a one-component exponential fit to the radial intensity distribution. For the galaxies with a strong nuclear source, we made a two-component fit (for NGC 3079) or subtracted the central source before the fitting (for NGC 4013). No reasonable fit for the scale length could be made for UGC 10288 because of the bright radio galaxy CHANG-ES A located asymmetrically behind the disk. The scale lengths for C- and L-band are given in Table 6 together with their L- to C-band ratios. They vary over a much larger range than the scale heights.
The distances used (as given in Table 1) are taken from CHANGES Paper IV (Wiegert et al. 2015). In order to test all distances we plotted the scale heights as well as the diameters (see Sect. 4.2) with distance in Figs. 5 and 6. The indication in Fig. 6 that the radio diameters dr increase with distance is understandable as a result of the interplay of the selection criteria of the CHANG-ES galaxies. The sample is flux density limited (at the lower end) and fixed in angular size range (see Sect. 2). This range is even smaller for our subsample (4′ < d < 6′) and means that our sample is biased such that large but nearby galaxies are omitted (due to the upper size limit), while with increasing distances only larger galaxies are extended enough to fulfil the lower size limit. On the other hand, their flux densities decrease quadratically with distance, which restricts the detectability of the outer parts of their disks to a given sensitivity of the observations. The lower limit for the flux density, however, prefers brighter galaxies. Even so, we stress that our sample also contains galaxies with low star formation rate surface density (SFRSD ; taken from Wiegert et al. 2015) at large distances, as shown in Fig. 7.
The halo scale heights (measured in kpc) increase slightly with distance as shown in Fig. 5. The only exception is UGC 10288, which is not surprising since the CHANG-ES observations revealed the presence of a strong, double-lobed extragalactic radio source (CHANG-ES A) located almost directly behind this edge-on galaxy (Irwin et al. 2013). UGC 10288 would have fallen well below the CHANG-ES flux density cut-off had it been considered without the dominant contribution of what has now been shown to be the background source CHANG-ES A. The values for UGC 10288 presented in this paper are determined after the separation of the two objects.
Scale lengths and normalized scale lengths.
 |
Fig. 5 Halo scale heights vs. the assumed distances. C-band data are represented by black asterisks, L-band data by blue triangles. |
 |
Fig. 6 Observed radio diameter vs. the assumed distance. C-band data are represented by black asterisks, L-band data by blue triangles. |
 |
Fig. 7 Star formation rate surface density SFRSD vs. the distances of the sample galaxies. |
6 Magnetic field strengths
We determined the galaxy-averaged total magnetic field strength in all galaxies from the C-band images with the assumption of energy equipartition between the magnetic field and the cosmic rays according to Beck & Krause (2005). The line of sight (L) through the galaxy was estimated using 80% of the measured diameter of each galaxy within 5× the rms contour of the total power image. The non-thermal spectral index αn was estimated from the flux densities given in Paper IV (Wiegert et al. 2015) (except for NGC 3079) with the assumption that the thermal fraction at C-band is 20% and negligible at L-band. The determined values for αn are all close to 1 (see Table 7). As the determined spectral index value for NGC 3079 is strongly influenced by the nucleus and its outflow, we simply assumed a value of 1.0 for this galaxy. We further assumed a proton-to-electron number density K = 100.
We determined the average magnetic field strengths for the total galaxy Bt and for the disk Bt(disk) separately. For the calculation of Bt we used the intensity at C-band averaged over the entire galaxy within 5× the rms contour, whereas for Bt(disk) we averagedthe radio intensity over that same extent projected along the minor axis at the inclination of the galaxy. For our sample, the uncertainty in the non-thermal spectral index α is the dominant contribution to the error in the magnetic field strengths which is ≲1 μG for Δα ≲ 0.1. The adopted values of L, non-thermal spectral indices, and determined magnetic fields strengths are summarized in Table 7 together with the star formation rates (SFR) and the star formation rate surface density (SFRSD ) taken from Paper IV (Wiegert et al. 2015).
The averaged total field strengths Bt for all galaxies are in the narrow range of 9–11 μG, except for the very faint galaxy UGC 10288. This can be easily understood by our selection criteria of the sample galaxies with respect to the size (d25 > 4′ and dr < 5′) and flux density (S1.4 > 20 mJy) (see Sect. 2) and the fact that the equipartition magnetic field strengths depends on the radio surface brightness of the galaxies with a small exponent of about 1/4. Hence, our galaxy sample just includes the spiral galaxies with the highest surface brightness, except for UGC 10288. The averaged magnetic field strengths of the disk Bt(disk) are slightly larger and vary over a somewhat wider range, between 10 μG and 15 μG, again except for UGC 10288. In contrast, the SFR of the sample galaxies is spread over quite a large range ((0.5–5.3) M⊙ yr−1), similar to SFRSD which is in the range of (1.1–6.6) 10−3 M⊙ yr−1 kpc−2 (Wiegert et al. 2015).
Magnetic field strengths, star formation rates, and total mass surface densities.
7 Frequency dependence of radio scale heights
The shape of a radio halo and the variation of the radio scale heights with frequency can tell us a lot about the possible loss or transport mechanisms of the CRE in the halo (see Sect. 1). Hence, we plotted the C- and L-band scale heights in Fig. 8. Most of the sample galaxies are located near to the one-to-one-line with one strong outlier, NGC 3003. The L-band values for NGC 3079 may be underestimated because of the poor quality of the map (see Table 1). Hence, altogether the scale heights at L-band are larger or about equal to those at C-band.
The ratio of the radio scale heights as measured in L- and C-band are given in Table 4 together with its errors as calculated by error propagation. For NGC 3079 the uncertainty due to the high noise error of the L-band map is not included. The ratio of the scale lengths at both bands is about 1 within 10% for most of the galaxies (see Table 6).
NGC 3003 reveals the largest difference between the two bands. However, its inclination is not well determined and was very difficult to estimate even with our scale height fits (as described in Sect. 2). It is described as a disturbed galaxy with asymmetric spiral arms (Karthick et al. 2014) with indications for a starburst superwind (Hoopes et al. 1999). Hence, the inclination may be smaller than 85° and we cannot fully trust our scale height values for this galaxy.
For both synchrotron loss- and escape-dominated halos the CR transport from the disk into the halo is assumed to be due to diffusive or convective propagation which lead to different frequency dependencies of the radio scale heights. In a synchrotron energy loss-dominated halo the outer halo boundary is observationally determined where the CRE have lost their energy by a sufficient amount that its radiation is below the detection limit of our observations. In an escape-dominated halo the halo boundary is observed where the number of CRE and the magnetic field strengths are too small to emit detectable radio emission, which is also dependent on the sensitivity of the observations. In practice both processes can occur simultaneously along the line of sight. In the following, we estimate the frequency and magnetic field strength dependencies of the synchrotron energy loss-dominated halo (a) and the escape-dominated halo (b), each for diffusive and convective CRE propagation.
(a) Following Heesen et al. (2009), based on e.g. Longair (2011), the synchrotron cooling timescale for CRE is given by
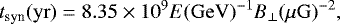 (7)
(7)
where E is the CRE energy and B⊥ the field strength perpendicular to the CRE motion where we can assume 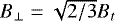 for an isotropic distribution of magnetic field orientations. Synchrotron emission at frequency ν comes from CRE with the average energy
for an isotropic distribution of magnetic field orientations. Synchrotron emission at frequency ν comes from CRE with the average energy
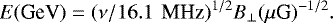 (8)
(8)
For a field strength of 10 μG this is about 6 GeV at C-band and 3 GeV at L-band.
Using Eqs. (7) and (8) the synchrotron timescale for the CRE can be expressed by 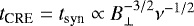 . The CRE diffusion length
. The CRE diffusion length 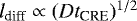 , where D is the diffusion coefficient. Mulcahy et al. (2016) found no evidence for an energy dependence of D in M 51 in a similar CRE energy range of our observations, hence we obtain for a synchrotron energy loss-dominated halo
, where D is the diffusion coefficient. Mulcahy et al. (2016) found no evidence for an energy dependence of D in M 51 in a similar CRE energy range of our observations, hence we obtain for a synchrotron energy loss-dominated halo
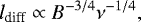 (9)
(9)
while Murphy (2009) suggested D ∝ E1∕2, leading to D ∝ B−1∕4ν1∕4 (Tabatabaei et al. 2013) and hence to
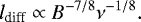 (10)
(10)
Synchrotron intensity depends on the product of CRE number density and the magnetic field strength to the power of about 2. Consequently, the exponential scale height of the synchrotron emission hz depends on the exponential CRE scale height hCRE and the exponential scale height of the magnetic field hB as
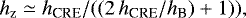 (11)
(11)
where hCRE is given by the diffusion length ldiff. Magnetic fields are expected to extend far above the disk, much further than CRE can propagate by diffusion, so that ldiff ≪ hB and hz ≈ ldiff.
In the above case of diffusion in a synchrotron energy loss-dominated halo we get
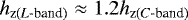 (12)
(12)
if D is energy dependent (D ∝ E1∕2), and
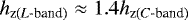 (13)
(13)
if D is not energy dependent.
For convection the CRE propagation length lcon is determined by the convection velocity, assumed to be the wind velocity vwind, hence
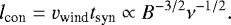 (14)
(14)
In the case of streaming, vwind has to be replaced by the Alfvén velocity vA. Both velocities are expected to increase with distance from the galactic plane, but the detailed dependencies could not yet be measured. Assuming that lcon is proportional to the radio scale height hz, we obtain for convection in a synchrotron energy loss-dominated halo
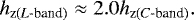 (15)
(15)
(b) In the case of an escape-dominated halo (i.e. tesc ≪ tsyn) the CRE confinement time is expected to be equal to the CRE escape time tesc and to be roughly constant. Here, the CRE scale height hCRE is probably determined by energy equipartition between cosmic rays and magnetic fields, so that hCRE = hB∕2 and, according to Eq. (11), hz = hCRE∕2 = hB∕4. Hence, hCRE is larger than in the case of a synchrotron energy loss-dominated halo.
Using the different energy dependencies of the diffusion length D as given in Eqs. (9) and (10), the exponential synchrotron scale height only weakly depends on the observed frequency and for an escape-dominated halo with diffusion we obtain
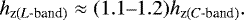 (16)
(16)
For convection, the wind velocity may only depend on the magnetic field and not on the observed frequency, hence we conclude for an escape-dominated halo with convective propagation
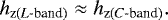 (17)
(17)
From the estimates above we see that a distinction between diffusion in a synchrotron energy loss-dominated halo and diffusion in an escape-dominated halo using the frequency dependence of the radio scale heights alone is hardly possible. The ratio of the determined exponential scale heights for the halo in L-band and C-band are given in Table 4 and graphically presented in Fig. 9, together with their errors.
Remarkably, the ratios for all galaxies range between 1 and 2, except for the outliers NGC 3003 and NGC 3079, mentioned already at the beginning of this section. The coloured areas in Fig. 9 indicate the expected ranges for an escape-dominated halo with convection (in yellow), a synchrotron energy loss-dominated or escape-dominated halo both with diffusion (in green), and a synchrotron energy loss-dominated halo with convection (in blue). Including the errors, only NGC 3003 could be a galaxy with a synchrotron energy loss-dominated halo with convective propagation. The others seem to have either escape-dominated halos or synchrotron energy loss-dominated halos with diffusion, between which a separation on the basis of the ratios alone is difficult due to their errors. Nevertheless, from the frequency analysis the clearest candidates for having an escape-dominated halo with convective propagation are NGC 4157, NGC 4217, and NGC 4302.
 |
Fig. 8 Radioscale heights in C- and L-band. |
 |
Fig. 9 Ratio of the scale heights in L- and C-band with errors for all galaxies. The coloured areas indicate the expected ranges for an escape-dominated halo with convection (yellow), a synchrotron energy loss-dominated or escape-dominated halo with diffusion (green), and a synchrotron loss-dominated halo with convection (blue). |
8 Correlations
As star formation in the disk is thought to be the source of the accelerated CRE in the disk and halo, we tested our data sets for possible correlations of the radio scale heights with the star formation activity in the disk (SFR and SFRSD ), and further with the total magnetic field strength (Bt, and that in the disk Bt(disk)). We found no clear dependence of the halo scale heights and SFRSD (as shown in Fig. 10) or SFR, nor with Bt(disk) (see Fig. 11) or Bt.
As discussed in Sect. 5, we found that both the diameter and the halo scale heights increase with distance. A direct comparison of the scale heights with the diameters (both measured in kpc) shows that the scale heights increase linearly with the galaxy’s size (radio diameter) (see Fig. 12). This cannot be explained by any selection effect due to our selection criteria, as discussed in Sect. 5. We fitted the radio data of C-band and L-band together with a weighted linear fit with a slope of 0.05± 0.01 and an intercept of about zero (reduced χ2 = 4.1). The outlier is again NGC 3003 in L-band. UGC 10288 has the smallest scale heights in both bands compared to its large diameter. The radio scale heights also increase with the optical diameter (see Table 5) in the blue light, as given by the 25th mag arcsec2 (Tully 1988), even though less significant. Table 5 already shows that the optical diameters are not tightly correlated with the radio diameters.
A similar trend is visible between the scale lengths and the radio diameters in our sample galaxies (see Fig. 13), though the spread of the scale lengths is larger than that in scale height. We consider these relations to be physical.
A comparison between the scale heights and scale lengths is presented in Fig. 14 for both bands. It also shows a linear correlation.
In order to exclude a bias due to the size of the galaxy, we determined the ratios between the radio scale heights from Table 4, for C- and L-band each, and the radio diameters dr as given in Table 5. We define this quantity as the normalized scale height 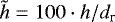 which is presented in Table 4 for C- and L-band together with its error
which is presented in Table 4 for C- and L-band together with its error 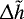 according toerror propagation. We choose the radio diameters instead of the optical diameters, as the radio diameters also correct for spectral index effects between the observations at C-band and L-band.
according toerror propagation. We choose the radio diameters instead of the optical diameters, as the radio diameters also correct for spectral index effects between the observations at C-band and L-band.
The normalized scale heights 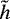 are – different from the scale heights – independent of the diameters of the galaxies. A closer look at the
are – different from the scale heights – independent of the diameters of the galaxies. A closer look at the 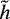 values reveals that they are about constant, except for the outliers NGC 3003 at L-band and UGC 10288: the mean value in C-band (L-band) of 5.22 (5.58) has a spread of only 0.77 (0.80) which is smaller than most of their individual errors
values reveals that they are about constant, except for the outliers NGC 3003 at L-band and UGC 10288: the mean value in C-band (L-band) of 5.22 (5.58) has a spread of only 0.77 (0.80) which is smaller than most of their individual errors 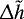 in Table 4. Plots of the normalized scale heights against the SFR, SFRSD , Bt , and Bt(disk) do not show further correlations of the normalized scale heights with one of these parameters.
in Table 4. Plots of the normalized scale heights against the SFR, SFRSD , Bt , and Bt(disk) do not show further correlations of the normalized scale heights with one of these parameters.
We also determined the total mass surface density of each galaxy by 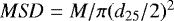 where d25 is the blue isophotol diameter as given in Table 5 and M is the total mass (Irwin et al. 2012). The values for the total mass surface densities vary significantly within the galaxy sample and are presented in Table 7. While the halo scale heights do not correlate with MS D, we found an anticorrelation between the normalized scale heights and MS D as presentedin Fig. 15 for C-band and in Fig. 16 for L-band. Remarkably, the fit parameters for C-band and L-band (without the strongly deviating L-band value for NGC 3003) are equal within their errors, hence we could have fitted them together but decided to present them separately. UGC 10288 was not included into the fit as its flux density was found to be below the flux density limits of the CHANG-ES sample, as discussed in Sect. 5. The fitted parameters of the linear fit to the values of both bands together is m = −0.19 ± 0.03 (slope) and b = 7.50 ± 0.44 (intercept) with a reduced χ2 = 0.72.
where d25 is the blue isophotol diameter as given in Table 5 and M is the total mass (Irwin et al. 2012). The values for the total mass surface densities vary significantly within the galaxy sample and are presented in Table 7. While the halo scale heights do not correlate with MS D, we found an anticorrelation between the normalized scale heights and MS D as presentedin Fig. 15 for C-band and in Fig. 16 for L-band. Remarkably, the fit parameters for C-band and L-band (without the strongly deviating L-band value for NGC 3003) are equal within their errors, hence we could have fitted them together but decided to present them separately. UGC 10288 was not included into the fit as its flux density was found to be below the flux density limits of the CHANG-ES sample, as discussed in Sect. 5. The fitted parameters of the linear fit to the values of both bands together is m = −0.19 ± 0.03 (slope) and b = 7.50 ± 0.44 (intercept) with a reduced χ2 = 0.72.
We conclude that the radio scale heights h of the halo depend mainly and linearly on the radio diameter of the galaxy. If this dependence is eliminated by taking the normalized scale heights 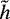 instead, we detected a tight and linear anticorrelation of
instead, we detected a tight and linear anticorrelation of 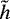 with the mass surface density of the galaxy. This will be further discussed in Sect. 9.
with the mass surface density of the galaxy. This will be further discussed in Sect. 9.
Similar to the normalized scale height, we defined the normalized scale length 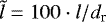 . The values are presented in Table 6 for C- and L-band, together with their errors according to error propagation. Their values vary, however, over a wider range. Their spread in C-band (L-band) is 7.5 (7.6), hence much greater than the individual errors
. The values are presented in Table 6 for C- and L-band, together with their errors according to error propagation. Their values vary, however, over a wider range. Their spread in C-band (L-band) is 7.5 (7.6), hence much greater than the individual errors 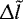 in Table 6.
in Table 6.
When measuring the radio scale heights in units of scale lengths they systematically decrease with scale lengths (and also with the normalized scale lengths) as shown in Fig. 17. The same trend is visible when plotting the scale heights in units of scale length against the normalized scale lengths (Fig. 18). There, diameter effects are eliminated for both coordinates. We conclude from these figures that galaxies with smaller scale lengths are more spherical in the radio emission than those with larger scale lengths. We tested whether this relation also depends on the SFRSD or the Hubble type of the galaxies without a positive result.
The question remains: what determines the scale lengths in a galaxy? We tested whether the scale lengths depend on the star formation or magnetic field strength, similar to the test for the scale heights. The dependence of the scale lengths on SFRSD is shown in Fig. 19 and thaton Bt(disk) in Fig. 20. While no clear correlation of the scale lengths with SFR, SFRSD , or Bt is visible, a linear increase in the scale lengths with Bdisk ≳ 11.5μG is indicated. The outlier N3044 in Fig. 20 shows an outstanding ordered X-shaped magnetic field with strong vertical components above and below its central region in our sample (Wiegert et al. 2015) which may easily have caused an overestimation of Bt(disk) by (1–2) μG.
 |
Fig. 10 Radio scale heights vs. star formation rate surface density. C-band data are represented by black asterisks, L-band data by blue triangles. The L-band outlier is again NGC 3003. No clear correlation is visible. |
 |
Fig. 11 Scaleheight vs. the total magnetic field strength in the disk Bt(disk). C-band data are represented by black asterisks, L-band data by blue triangles. UGC 10288 was not included in the plot because of its significantly lower magnetic field strength Bdisk = 6.7μG. |
 |
Fig. 12 Halo scale height vs. the radio diameter. C-band data are represented by black asterisks, L-band data by blue triangles. A weighted linear fit to all data together has a slope of 0.05 ± 0.01 with intercept of about zero ( − 0.15 ± 0.29). For clarity, only the errors in scale height are presented; those in diameter are identical with Fig. 13. |
 |
Fig. 13 Scale length vs. the radio diameter. C-band data are represented by black asterisks, L-band data by blue triangles. A weighted linear fit to all data together has a slope of 0.16 ± 0.04 with intercept of about zero ( − 0.15 ± 0.89). UGC 10288is omitted (see note a of Table 6). |
 |
Fig. 14 Haloscale lengths vary over a wider range of values than scale heights, especially in C-band. C-band data are represented by black asterisks, L-band data by blue triangles. |
 |
Fig. 17 Scale heights in units of scale lengths vs. scale lengths. C-band data are represented by black asterisks, L-band data by blue triangles. |
 |
Fig. 18 Scaleheights in units of scale lengths vs. scale length divided by the radio diameter (i.e. normalized scale length). C-band data are represented by black asterisks, L-band data by blue triangles. The outlier is again NGC 3003 in L-band. This plot is free of diameter dependence. |
9 Discussion
Within this work we detected for the first time that the radio scale height increases linearly with radio diameter, which is surprising. We could not find an obvious physical explanation that would not simultaneously imply a correlation of the halo scale height with SFR or SFRSD.
In order to exclude this correlation from the further analysis we defined the normalized scale height 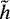 and normalized scale length
and normalized scale length 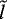 as describedin Sect. 8. We found that the normalized scale heights are very similar and that the radio scale height depends mainly on the radio diameter of the galaxy. Even though our sample may be biased towards brighter galaxies due to the selection criteria of the CHANG-ES sample (as discussed in Sect. 5), our sample contains galaxies with low SFR and SFRSD, also at large distances. We found, remarkably, that neither the scale height h nor
as describedin Sect. 8. We found that the normalized scale heights are very similar and that the radio scale height depends mainly on the radio diameter of the galaxy. Even though our sample may be biased towards brighter galaxies due to the selection criteria of the CHANG-ES sample (as discussed in Sect. 5), our sample contains galaxies with low SFR and SFRSD, also at large distances. We found, remarkably, that neither the scale height h nor 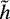 depend on SFR or SFRSD. We conclude that the radio halo properties are not simply dictated by the star formation activity.
depend on SFR or SFRSD. We conclude that the radio halo properties are not simply dictated by the star formation activity.
However, we found a tight and linear anticorrelation of the normalized scale height 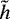 with the mass surface density MS D of the galaxies. The mass surface density is a measure of the gravitational potential of the galaxy with the baryonic mass being mainly concentrated in the disk of a galaxy. A similar decrease in
with the mass surface density MS D of the galaxies. The mass surface density is a measure of the gravitational potential of the galaxy with the baryonic mass being mainly concentrated in the disk of a galaxy. A similar decrease in 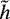 with an increase of MS D at both frequency bands as shown in Figs. 15 and 16 can be regarded as an observational indication for a gravitational deceleration of the CRE outflow on its way up into the halo.
with an increase of MS D at both frequency bands as shown in Figs. 15 and 16 can be regarded as an observational indication for a gravitational deceleration of the CRE outflow on its way up into the halo.
The radio-weak galaxy UGC 10288 with its radio intensity well below the CHANG-ES flux density limit has a significantly lower magnetic field strength than the sample average (see Sect. 6). Though it does not deviate from the sample with respect to its value for the halo scale height or to its SFR or SFRSD , it has the smallest value for the normalized scale height 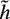 . The reason for this surprising result could be an observational bias of our sample towards radio-bright galaxies. UGC 10288 may represent a class of radio-weak galaxies that still have a significant level of star formation. Although there is general consensus that star formation drives the amplification of turbulent magnetic field (called the small-scale dynamo), other still unexplored factors may affect the efficiency of field amplification.
. The reason for this surprising result could be an observational bias of our sample towards radio-bright galaxies. UGC 10288 may represent a class of radio-weak galaxies that still have a significant level of star formation. Although there is general consensus that star formation drives the amplification of turbulent magnetic field (called the small-scale dynamo), other still unexplored factors may affect the efficiency of field amplification.
From the frequency dependence as discussed in Sect. 7 we conclude that the clearest candidates for an escape-dominated halo are NGC 4157, NGC 4217, and NGC 4302. Their scale heights are similar at both frequencies. In this case, the CRE leave the halo so fast that no significant frequency dependence due to synchrotron losses can be observed. This means that the adiabatic loss time of CRE is smaller than their synchrotron life time within the observed distances from the galactic plane. Using Eq. (7), the synchrotron life time of CRE is tsyn ≃ 1.39 × 107 yr for C-band and B = 10μG. In escape-dominated halos, we can assume equipartition between magnetic fields and cosmic rays, so that the scale height of the cosmic-ray electrons hCRE is about twice the observed synchrotron scale height hz, which is about 1 kpc for the three galaxies mentioned above (see Table 4). Hence, we can estimate a mean cosmic-ray bulk speed vCRE (corresponding to the velocity of a galactic wind) of vCRE = 2hz∕tesc > 2hz∕tsyn ≃ 140 km s−1.
The adiabatic loss time depends only on the reciprocal velocity gradient: 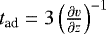 (Heesen et al. 2009). Assuming a constant increase in the CRE velocity with height gives vwind = 6hz∕tad = 420 km s−1, significantly higher than 140 km s−1 and above the escape velocity from the disk, which is about 280 km s−1 for a rotation speed of 200 km s−1 (Heesen et al. 2009).
(Heesen et al. 2009). Assuming a constant increase in the CRE velocity with height gives vwind = 6hz∕tad = 420 km s−1, significantly higher than 140 km s−1 and above the escape velocity from the disk, which is about 280 km s−1 for a rotation speed of 200 km s−1 (Heesen et al. 2009).
On the other hand, if the scale heights mainly depend on the diameters of the galaxy, we should multiply the L–C-band scale height ratio of Table 4 by the inverse of the L- to C-band diameter ratio of Table 5 before performing the frequency analysis. This correction for the diameters leads, however, to about equal scale heights in C- and L-band, as indicated already in Fig. 12 by the fact that the values in C- and L-band can be fitted together well by one linear fit. This directly leads to the conclusion that all galaxies have an escape-dominated halo with convective CRE propagation (see Sect. 7).
As discussed in Sect. 7 the scale height hz of a synchrotron energy loss-dominated halo depends not only on the observing frequency, but also on the strength of the total magnetic field. According to Eqs. (9), (10), and (14), hz would decrease with increasing magnetic field strength for a synchrotron energy loss-dominated halo. This is not visible in Fig. 11. The CRE in the halos of our sample galaxies are not dominated by synchrotron losses, consistent with the lack of frequency dependence as discussed above.
The magnetic field strength may be another important parameter for the evolution of a radio halo. The galaxy with the smallest magnetic field strength in the sample by far is UGC 10288. It is the galaxy whose values lie significantly beyond the fitted curve in Fig. 12 and hence has the smallest normalized scale height within the sample (see Table 4) significantly outside the mean normalized scale height of 5.22± 0.77. We recall here that UGC 10288 deviates only in its magnetic field strength (and radio intensity) from the other sample galaxies, but not in its radio scale height nor its star formation activity.
Furthermore, NGC 3044 can be regarded as an outlier in Fig. 20. Its scale length is relatively small for its large Bdisk. In comparison with the other sample galaxies, NGC 3044 shows strongly polarized intensity indicating a well-ordered X-shaped magnetic field with strong vertical components above and below its central region (Wiegert et al. 2015). Such a field configuration should help the CRs to escape from the disk into the halo. Even here, the radio scale height is comparable to the othersample galaxies, but the scale length is smaller. With this single galaxy we cannot clarify whether this is just an accidental coincidence or if it indicates a causal influence on the development on the radio scale lengths. However, this finding fits into the given interpretation of Figs. 19 and 20in Sect. 8 that the scale lengths grow with increasing magnetic field strength in the disk and SFRSD unless the field configuration supports the CR escape directly by strongly ordered, vertical magnetic field components.
This suggests that especially the magnetic field strength in the disk Bt(disk) and the field structure of an ordered or large-scale magnetic field in the halo are important parameters for the evolution of a radio halo, e.g. by supporting the CR outflow or increasing the wind velocity.
For the estimates of the total magnetic field strengths we assumed energy equipartition between the CRE and the magnetic field in the halo. This is not necessarily a given. A faster decrease in the magnetic field strength than expected by equipartition would also decrease the observed radio emission. This possibility has been included and can be modelled by the “SPINNAKER” code of Heesen et al. (2016) which also needs spectral indices as inputs. On the other hand, strong synchrotron losses increase the ratio K of cosmic-ray protons and electrons. Our assumption of the standard value of K = 100 would then underestimate the field strength in the halo. The analysis of the CHANG-ES galaxies with this method is planned and will be published in a forthcoming paper.
 |
Fig. 15 Normalized scale heights in C-band vs. the mass surface density measured in solar masses kpc−2. The weighted linear fit to the data (excluding GC 10288) has a slope of − 0.21 ± 0.03 (reduced χ2 = 0.37). |
 |
Fig. 16 Normalized scale heights in L-band vs. the mass surface density measured in solar masses kpc−2. The weighted linear fit to the data (excluding UGC 10288 and NGC 3003) has a slope of − 0.16 ± 0.10 (reduced χ2 = 0.96). |
 |
Fig. 19 Scalelength vs. the star formation rate density SFRSD without UGC 10288. C-band data are represented by black asterisks, L-band data by blue triangles. |
 |
Fig. 20 Scalelength vs. the total magnetic field strength in the disk Bt(disk) without UGC 10288. C-band data are represented by black asterisks, L-band data by blue triangles. |
10 Summary and conclusions
Within this work we defined a subsample of the 35 CHANG-ES galaxies as being smaller than 4.5′ in diameter with an inclination larger than 80° with extended disk emission not severely disturbed or dominated by nuclear activity and/or interaction. This leads to a sample of 13 galaxies in total. For these galaxies we determined the vertical scale heights for the thin disk and halo from C- and L-band observations with an angular resolution of about 10′′ in a consistent way with a more sophisticated method than used before. Different from the halo scale heights, the relative errors of the values for the thin disk are too high to be discussed further.
We checked our results for possible systematic effects of missing large-scale flux density which could play a role mainly at C-band, but we found no indication of a significant effect. We determined the scale height ratios of the results at both frequency bands and discussed the frequency dependence of the halo scale heights with respect to the CR transport and energy loss mechanisms.
Assuming energy equipartition between the magnetic field and cosmic rays we determined the total magnetic field strengths Bt for the whole galaxy and for the disk alone Bt(disk) for all sample galaxies. Finally, we tested our data sets for possible correlations.
Our main results are as follows:
-
The averaged values for the radio scale heights of the halo are 1.1 ± 0.3 kpc in C-band and 1.4 ± 0.7 kpc in L-band.
-
The halo scale height and scale length increase linearly with the radio diameters.
-
In order to correct for a bias due to the radio size of the galaxy, we defined a normalized scale height
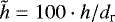 and a normalized scale length
and a normalized scale length 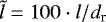 .
The normalized scale heights
.
The normalized scale heights 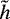 are equal within the scale height errors for our sample galaxies; only UGC 10288 has a slightly lower value.
are equal within the scale height errors for our sample galaxies; only UGC 10288 has a slightly lower value. -
Those spiral galaxies in our sample with smaller scale lengths are more spherical in the radio emission, while those with larger scale heights are flatter.
-
The total magnetic field strengths Bt (Bt(disk)) are in the small range of 9–11 μG (11–15 μG). Only UGC 10288 has a weaker field of about 6 μG.
From the analysis of the frequency dependence, the clearest candidates for an escape-dominated halo are NGC 4157, NGC 4217, and NGC 4302, for which the wind velocities are estimated using the adiabatic loss time to be up to about 420 km s−1 at the height of 1 kpc (the halo scale height). This value seems to be rather high and may reduce to up to 1/3 of this value if adiabatic losses occur not only in z-direction, but are also significant in all three dimensions. In this case the velocity would be equal to 140 km s−1 which is the velocity required for a synchrotron energy loss-dominated halo. We conclude that the adiabatic losses are mainly in the z-direction and the wind speeds are ≫140 km s−1, up to 420 km s−1, hence they may exceed the typical escape velocity of 300 km s−1.
The scale height ratios between L-band and C-band range mainly between 1 and 2. This range is expected for synchrotron energy loss-dominated or escape-dominated halos. However, if the scale height ratios are corrected for the diameter dependence, they reduce to unity. This is expected for escape-dominated halos with convective propagation. As the scale height–magnetic field dependence also does not fit to synchrotron energy loss-dominated halos, we conclude that the sample galaxies (except possibly UGC 10288) have an escape-dominated halo with convective propagation.
In summary we make the following conclusions:
-
The halo scale height of our sample galaxies increases mainly with the radio diameter of the galaxies. The physical reason for this remarkable result remains unexplained.
-
When corrected for the diameter effect, the radio scale height shows a tight and linear anticorrelation with the mass surface density, indicating a gravitational deceleration of the CRE outflow from the galactic disk, e.g. a lowering of the wind velocity.
-
All sample galaxies are consistent with an escape-dominated halo with convective propagation.
-
A higher SFR or SFRSD does not lead directly to a faster CR transport (i.e. larger wind velocity).
In contrast to the scale heights, neither the scale lengths l nor the normalized scale length 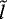 are constant within our sample galaxies. We found that
are constant within our sample galaxies. We found that 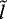 does not depend on SFR, SFRSD, or Bt. A linear increase in the scale lengths with the magnetic field strength in the disk for Bt(disk) ≳ 11.5μG is indicated.
does not depend on SFR, SFRSD, or Bt. A linear increase in the scale lengths with the magnetic field strength in the disk for Bt(disk) ≳ 11.5μG is indicated.
Acknowledgements
We thank Andrew Fletcher and Aritra Basu for fruitful discussions, and Aritra Basu also for helpful comments on the manuscript. We acknowledge a helpful suggestion of the anonymous referee. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. RAMW acknowledges support from the National Science Foundation through grant AST-1615594.
References
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Dumke, M. 1994, Diploma thesis, University of Bonn, Germany [Google Scholar]
- Dumke, M., & Krause, M. 1998, in Lect. Notes Phys., eds. D. Breitschwerdt, M. J. Freyberg, & J. Truemper (Berlin: Springer Verlag), IAU Colloq. 166, The Local Bubble and Beyond, 506, 555 [Google Scholar]
- Dumke, M., Krause, M., Wielebinski, R., & Klein, U. 1995, A&A, 302, 691 [NASA ADS] [Google Scholar]
- Fletcher, A., & Shukurov, A. 2001, MNRAS, 325, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009, A&A, 494, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heesen, V., Dettmar, R.-J., Krause, M., Beck, R., & Stein, Y. 2016, MNRAS, 458, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Hoopes, C. G., Walterbos, R. A. M., & Rand, R. J. 1999, ApJ, 522, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, E., & van der Hulst, J. M. 1989, A&AS, 81, 51 [NASA ADS] [Google Scholar]
- Hummel, E., Beck, R., & Dahlem, M. 1991a, A&A, 248, 23 [NASA ADS] [Google Scholar]
- Hummel, E., Beck, R., & Dettmar, R.-J. 1991b, A&AS, 87, 309 [NASA ADS] [Google Scholar]
- Irwin, J., Beck, R., Benjamin, R. A., et al. 2012, AJ, 144, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Krause, M., English, J., et al. 2013, AJ, 146, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Karthick, M. C., López-Sánchez, Á. R., Sahu, D. K., Sanwal, B. B., & Bisht, S. 2014, MNRAS, 439, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. 2009, in Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 25 [NASA ADS] [Google Scholar]
- Krause, M. 2015, Highlights of Astronomy, 16, 399 [NASA ADS] [Google Scholar]
- Kuzio de Naray, R., Zagursky, M. J., & McGaugh, S. S. 2009, AJ, 138, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 2011, High Energy Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Mulcahy, D. D., Fletcher, A., Beck, R., Mitra, D., & Scaife, A. M. M. 2016, A&A, 592, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, P., Krause, M., Beck, R., & Schmidt, P. 2017, A&A, 606, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J. 2009, ApJ, 706, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Gómez, F. A., Grand, R. J. J., et al. 2017, MNRAS, 469, 3185 [NASA ADS] [CrossRef] [Google Scholar]
- Sievers, A. 1988, Ph.D. Thesis, University of Bonn, Germany [Google Scholar]
- Soida, M., Krause, M., Dettmar, R.-J., & Urbanik, M. 2011, A&A, 531, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Berkhuijsen, E. M., Frick, P., Beck, R., & Schinnerer, E. 2013, A&A, 557, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B. 1988, Nearby galaxies catalog (Cambridge: Cambridge University Press) [Google Scholar]
- van der Kruit,P. C. & Searle, L. 1981, A&A, 95, 105 [NASA ADS] [Google Scholar]
- Wiegert, T., Irwin, J., Miskolczi, A., et al. 2015, AJ, 150, 81 [NASA ADS] [CrossRef] [Google Scholar]
The CHANG-ES data release I is available at: www.queensu.ca/changes
All Tables
Magnetic field strengths, star formation rates, and total mass surface densities.
All Figures
 |
Fig. 1 Total intensity colourized map of NGC 5775 at 6 GHz. The rms noise is 10 μJy beam−1 with the beam size (10.7′′) given in bottom left corner. |
| In the text | |
 |
Fig. 2 Rotated total intensity colourized map of NGC 5775 at 6 GHz with the strips and boxes for the scale height determination superimposed. In this case we used seven strips of 30′′ in width, with 21 boxes of 4′′ in height each. The beam size (10.7′′) is given in bottom left corner. |
| In the text | |
 |
Fig. 3 Averaged radio intensities of NGC 5775 within the boxes along the seven strips shown in Fig. 2 and their two-component exponential fits according to Eq. (4). |
| In the text | |
 |
Fig. 4 Halo scale heights vs. the galaxy’s radio continuum diameter, both in arcsec in order to exclude errors in the distance determination. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 5 Halo scale heights vs. the assumed distances. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 6 Observed radio diameter vs. the assumed distance. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 7 Star formation rate surface density SFRSD vs. the distances of the sample galaxies. |
| In the text | |
 |
Fig. 8 Radioscale heights in C- and L-band. |
| In the text | |
 |
Fig. 9 Ratio of the scale heights in L- and C-band with errors for all galaxies. The coloured areas indicate the expected ranges for an escape-dominated halo with convection (yellow), a synchrotron energy loss-dominated or escape-dominated halo with diffusion (green), and a synchrotron loss-dominated halo with convection (blue). |
| In the text | |
 |
Fig. 10 Radio scale heights vs. star formation rate surface density. C-band data are represented by black asterisks, L-band data by blue triangles. The L-band outlier is again NGC 3003. No clear correlation is visible. |
| In the text | |
 |
Fig. 11 Scaleheight vs. the total magnetic field strength in the disk Bt(disk). C-band data are represented by black asterisks, L-band data by blue triangles. UGC 10288 was not included in the plot because of its significantly lower magnetic field strength Bdisk = 6.7μG. |
| In the text | |
 |
Fig. 12 Halo scale height vs. the radio diameter. C-band data are represented by black asterisks, L-band data by blue triangles. A weighted linear fit to all data together has a slope of 0.05 ± 0.01 with intercept of about zero ( − 0.15 ± 0.29). For clarity, only the errors in scale height are presented; those in diameter are identical with Fig. 13. |
| In the text | |
 |
Fig. 13 Scale length vs. the radio diameter. C-band data are represented by black asterisks, L-band data by blue triangles. A weighted linear fit to all data together has a slope of 0.16 ± 0.04 with intercept of about zero ( − 0.15 ± 0.89). UGC 10288is omitted (see note a of Table 6). |
| In the text | |
 |
Fig. 14 Haloscale lengths vary over a wider range of values than scale heights, especially in C-band. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 17 Scale heights in units of scale lengths vs. scale lengths. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 18 Scaleheights in units of scale lengths vs. scale length divided by the radio diameter (i.e. normalized scale length). C-band data are represented by black asterisks, L-band data by blue triangles. The outlier is again NGC 3003 in L-band. This plot is free of diameter dependence. |
| In the text | |
 |
Fig. 15 Normalized scale heights in C-band vs. the mass surface density measured in solar masses kpc−2. The weighted linear fit to the data (excluding GC 10288) has a slope of − 0.21 ± 0.03 (reduced χ2 = 0.37). |
| In the text | |
 |
Fig. 16 Normalized scale heights in L-band vs. the mass surface density measured in solar masses kpc−2. The weighted linear fit to the data (excluding UGC 10288 and NGC 3003) has a slope of − 0.16 ± 0.10 (reduced χ2 = 0.96). |
| In the text | |
 |
Fig. 19 Scalelength vs. the star formation rate density SFRSD without UGC 10288. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
 |
Fig. 20 Scalelength vs. the total magnetic field strength in the disk Bt(disk) without UGC 10288. C-band data are represented by black asterisks, L-band data by blue triangles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


