| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731604 | |
| Published online | 01 February 2018 | |
Equation of state of dense nuclear matter and neutron star structure from nuclear chiral interactions
1 Dipartimento di Fisica “E. Fermi”, Università di Pisa, Largo B. Pontecorvo, 3, 56127 Pisa, Italy
e-mail: ignazio.bombaci@unipi.it; domenico.logoteta@infn.pi.it
2 INFN, Sezione di Pisa, Largo B. Pontecorvo, 3, 56127 Pisa, Italy
Received: 19 July 2017
Accepted: 3 October 2017
Aims. We report a new microscopic equation of state (EOS) of dense symmetric nuclear matter, pure neutron matter, and asymmetric and β-stable nuclear matter at zero temperature using recent realistic two-body and three-body nuclear interactions derived in the framework of chiral perturbation theory (ChPT) and including the Δ(1232) isobar intermediate state. This EOS is provided in tabular form and in parametrized form ready for use in numerical general relativity simulations of binary neutron star merging. Here we use our new EOS for β-stable nuclear matter to compute various structural properties of non-rotating neutron stars.
Methods. The EOS is derived using the Brueckner–Bethe–Goldstone quantum many-body theory in the Brueckner–Hartree–Fock approximation. Neutron star properties are next computed solving numerically the Tolman–Oppenheimer–Volkov structure equations.
Results. Our EOS models are able to reproduce the empirical saturation point of symmetric nuclear matter, the symmetry energy Esym, and its slope parameter L at the empirical saturation density n0. In addition, our EOS models are compatible with experimental data from collisions between heavy nuclei at energies ranging from a few tens of MeV up to several hundreds of MeV per nucleon. These experiments provide a selective test for constraining the nuclear EOS up to ~4n0. Our EOS models are consistent with present measured neutron star masses and particularly with the mass M = 2.01 ± 0.04 M⊙ of the neutron stars in PSR J0348+0432.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2018
1. Introduction
With central densities exceeding the density of atomic nuclei (2.6 × 1014 g/cm3) several times over, neutron stars (NSs) are the densest macroscopic objects in the universe. They thus represent incomparable natural laboratories that allow us to investigate the constituents of matter and their interactions under extreme conditions that cannot be reproduced in any terrestrial laboratory, and to explore the phase diagram of quantum chromodynamics (QCD) in a region that is presently inaccessible to numerical calculations of QCD on a space–time lattice (D’Elia & Lombardo 2003; Gupta 2010; Fukushima & Hatsuda 2011).
The global properties of NSs (mass, radius, maximum mass, maximum spin frequency, etc.) and their internal composition (constituent particle species and possible different phases of matter) primarily depend on the equation of state (EOS) of strong interacting matter (Prakash et al. 1997; Lattimer & Prakash 2016) i.e., on the thermodynamical relation between the matter pressure, energy density, and temperature. The EOS of dense matter is also a basic ingredient for modeling various astrophysical phenomena related to NSs, such as core-collapse supernovae (SNe; Oertel et al. 2017) and binary neutron star (BNS) mergers.
Determining the correct EOS model that describes NSs is a fundamental problem of nuclear and particle physics and of astrophysics, and major efforts have been made during the last few decades to solve it by measuring different NS properties using the data collected by various generations of X-ray and γ-ray satellites and by ground-based radio telescopes.
The recent detection of four gravitational wave events (Abbott et al. 2016a,b, 2017a,b) caused by binary black hole mergers, but in particular the very recent detection of gravitational wave signals from a binary neutron star merger (Abbott et al. 2017c), is giving a big boost to the research on dense matter physics. The gravitational wave signal, especially from the BNS post-merger phase, offers a unique opportunity to test different dense matter EOS models (Shibata et al. 2005; Bauswein & Janka 2012; Takami et al. 2014; Bernuzzi et al. 2015; Sekiguchi et al. 2016; Rezzolla & Takami 2016; Bauswein et al. 2016; Endrizzi et al. 2016; Maione et al. 2016; Ciolfi et al. 2017; Radice et al. 2017; Piro et al. 2017). Thus, gravitational wave astronomy will open a new window to explore matter under extreme conditions.
As mentioned before, due to their large central densities, various “exotic” constituents, for example hyperons (Glendenning 1985; Vidaña et al. 2011a; Chatterjee & Vidaña 2016; Haidenbauer et al. 2017) or a quark deconfined phase of matter (Glendenning 1996; Bombaci et al. 2008, 2016; Logoteta et al. 2012; Bombaci & Logoteta 2013), are expected in neutron star interiors.
In the present work, we consider the more traditional view where the core of a NS is modeled as a uniform charge-neutral fluid of neutrons, protons, electrons, and muons in equilibrium with respect to the weak interaction (β-stable nuclear matter). Even in this “simplified” picture, the determination of the EOS from the underlying nuclear interactions remains a challenging theoretical problem. In fact, it is necessary to calculate the EOS to extreme conditions of high density and high neutron-proton asymmetry, i.e., in a regime where the EOS is poorly constrained by nuclear data and experiments. The nuclear symmetry energy is thus one of the most important quantities that controls the composition and the pressure of β-stable nuclear matter (Bombaci & Lombardo 1991; Zuo et al. 2014), and consequently many NS attributes such as the radius, moment of inertia, and crustal properties (Lattimer 2014; Lattimer & Prakash 2016).
Another important issue is related to the role of three-nucleon forces (TNFs) on the EOS, particularly at high density. In fact, it is well known that TNFs are essential in order to reproduce the experimental binding energy of few-nucleon systems (A = 3, 4) and the empirical saturation point (n0 = 0.16 ± 0.01 fm-3, E/A | n0 = −16.0 ± 1.0 MeV) of symmetric nuclear matter. As shown by several microscopic calculations (Wiringa et al. 1988; Baldo et al. 1997; Akmal et al. 1998; Li & Schulze 2008) of the EOS of β-stable nuclear matter based on realistic nucleon-nucleon (NN) interactions supplemented with TNFs, it is possible to obtain NSs with maximum mass1Mmax ~ 2 M⊙, thus in agreement with currently measured masses. However, the value of Mmax depends in a sensitive manner on the TNFs strength at high density (Li & Schulze 2008), thus indicating that the properties of few-body nuclear systems and of nuclear matter saturation cannot be used to constrain TNFs at high density.
Recent years have witnessed a significant progress in the description of nuclear interactions. In fact, the chiral effective field theory (ChEFT) has opened a new avenue for the description of nuclear interactions (Weinberg 1979, 1990, 1991, 1992; Epelbaum et al. 2009; Machleidt & Entem 2011) and nuclear systems consistent with QCD, the fundamental theory of the strong interaction. The significant advantage of using this method consists in the fact that two-body, three-body, and even many-body nuclear interactions can be calculated perturbatively, i.e., order by order, according to a well-defined scheme based on a low-energy effective QCD Lagrangian that retains the symmetries of QCD and in particular the approximate chiral symmetry. Within this chiral perturbation theory (ChPT) the details of the QCD dynamics are contained in parameters known as the low-energy constants (LECs), which are fixed by low-energy experimental data.
Recently, Piarulli et al. (2016) have formulated a fully local in coordinate-space two-nucleon chiral potential which includes the Δ(1232) isobar (hereafter the Δ isobar) intermediate state. This new potential represents the fully local version of the minimally non-local chiral interaction reported in Piarulli et al. (2015). It has been pointed out by various authors (Kaiser et al. 1998; Krebbs et al. 2007) that a Δ-full ChPT has an improved convergence with respect to the Δ-less ChPT. In addition, the Δ-full ChPT naturally leads to TNFs induced by two-pion exchange with excitation of an intermediate Δ, the celebrated Fujita–Miyazawa three-nucleon force (Fujita & Miyazawa 1957).
In this work, we present a new microscopic EOS of dense symmetric nuclear matter (SNM), pure neutron matter (PNM), and asymmetric and β-stable nuclear matter at zero temperature using the local chiral potential by Piarulli et al. (2016) supplemented with TNFs (Logoteta et al. 2016b) and employing the Brueckner–Bethe–Goldstone (BBG; Day 1967; Baldo & Burgio 2012) many-body theory within the Brueckner–Hartree–Fock (BHF) approximation. This zero temperature EOS is provided both in tabular form and in parametrized form ready for use in numerical general relativity simulations of binary neutron star merging after being supplemented by a thermal contribution as described in e.g., Shibata et al. (2005), Bauswein & Janka (2012), Takami et al. (2014), Bernuzzi et al. (2015), Rezzolla & Takami (2016), Bauswein et al. (2016), Endrizzi et al. (2016), Maione et al. (2016), Ciolfi et al. (2017).
In addition, we use our new EOS for β-stable nuclear matter to compute various structural properties of non-rotating neutron stars. The present work represents a development and an extension to high nuclear baryon densities (n> 2.5n0) relevant for astrophysical applications with respect to our previous works (Logoteta et al. 2015, 2016a,b) where ChPT nuclear interactions are used in BHF calculations of nuclear matter properties around the empirical saturation density.
The paper is organized as follows: in Sect. 2 we present the nuclear interactions we have considered; in Sect. 3 we describe the BBG many-body theory and discuss the inclusion of TNFs in this framework; in Sect. 4 we present our results for the EOS of SNM and PNM; in Sect. 5 we report the calculated symmetry energy and the EOS for asymmetric and β-stable nuclear matter; in Sect. 6 we present various neutron star properties, as calculated with our new EOS; in the last section we summarize our main results.
2. Nuclear interactions in chiral perturbation theory
In this section we briefly describe the specific interactions we have employed in the present work. Among the wide variety of nuclear interactions derived in the framework of ChPT, for the two-body nuclear interaction, we have used the fully local chiral potential at the next-to-next-to-next-to-leading-order (N3LO) of ChPT, including Δ isobar excitations in intermediate state (hereafter N3LOΔ) recently proposed by Piarulli et al. (2016). This potential was originally presented in Piarulli et al. (2015) in a minimal non-local form. We note that Piarulli et al. (2016) report different parametrizations of the local potential obtained by fitting the low-energy NN experimental data using different long- and short-range cutoffs. In the calculations presented in this work, we use the model b described in Piarulli et al. (2016; see their Table II), which fits the Granada database (Navarro et al. 2013) of proton-proton (pp) and neutron-proton (np) scattering data up to an energy of 125 MeV in the laboratory reference frame and has a χ2/datum ~1.07.
There is a great deal of experimental evidence that the Δ isobar plays an important role in nuclear processes. For instance the excitation of the Δ isobar is needed to reproduce the observed energy spectra of low-lying states in s- and p-shell nuclei and to reproduce the correct spin-orbit splitting of P-wave resonances in low-energy n-α scattering (Pieper et al. 2001; Nollett et al. 2007; Carlson et al. 2015). It is consequently very important to test this new chiral nuclear potential (Piarulli et al. 2016) also in nuclear matter calculations at high density for astrophysical applications.
For the TNF, we have used the potential by Epelbaum et al. (2002) calculated at the next-to-next-to-leading-order (N2LO) of ChPT in its local version given by Navratil (2007). The N2LO TNF depends on the parameters c1, c3, c4, cD, and cE, i.e., the LECs. The N2LO three-nucleon interaction keeps the same operatorial structure, including or not the Δ degrees of freedom (Krebbs et al. 2007). We note that the constants c1, c3, and c4 are already fixed at the two-body level by the N3LO interaction. However, when including the Δ isobar in the three-body potential, the parameters c3 and c4 take additional contribution from the Fujita–Miyazawa diagram. This diagram appears at the next-to-leading-order (NLO) of ChPT and it is clearly not present in the theory without the Δ (see discussion in Logoteta et al. 2016b for more details).
The values of the LECs ci in the TNF used in the present work are reported in Table 1 for two different parametrizations. As mentioned previously, the parameters c1, c3, and c4 are already fixed by the NN and πN (pion–nucleon) interaction, while the parameters cD and cE are not determined at the two-body level and thus have to be set by reproducing some specific observable of few-body nuclear systems or by reproducing the empirical saturation point of SNM.
The first TNF parametrization (hereafter N2LOΔ1) was determined in Logoteta et al. (2016b), fitting the LECs cD and cE to get a good saturation point for SNM. For the second TNF parametrization (hereafter N2LOΔ2) the values of cD and cE were set in order to reproduce the 3H binding energy (Logoteta et al. 2016b).
Values of the low-energy constants (LECs) of the TNF models used in the present calculations.
3. The Brueckner–Bethe–Goldstone many-body theory
The Brueckner–Bethe–Goldstone (BBG) many-body theory is based on a linked cluster expansion (the hole-line expansion) of the energy per nucleon 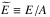 of nuclear matter. The various terms of the expansion can be represented by Goldstone diagrams grouped according to the number of independent hole-lines (i.e., lines representing empty single particle states in the Fermi sea). The basic ingredient in this approach is the Brueckner reaction matrix G, which sums, in a closed form, the infinite series of the so-called ladder-diagrams and takes into consideration the short-range strongly repulsive part of the nucleon-nucleon interaction.
of nuclear matter. The various terms of the expansion can be represented by Goldstone diagrams grouped according to the number of independent hole-lines (i.e., lines representing empty single particle states in the Fermi sea). The basic ingredient in this approach is the Brueckner reaction matrix G, which sums, in a closed form, the infinite series of the so-called ladder-diagrams and takes into consideration the short-range strongly repulsive part of the nucleon-nucleon interaction.
In the general case of asymmetric nuclear matter with neutron number density nn, proton number density np, total nucleon number density n = nn + np, and isospin asymmetry (asymmetry parameter), 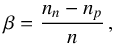 (1)the reaction matrix depends on the isospin 3rd components τ and τ′ of the two interacting nucleons. Thus, there are different G-matrices describing the nn, pp, and np in medium effective interactions. They are obtained by solving the generalized Bethe–Goldstone equations
(1)the reaction matrix depends on the isospin 3rd components τ and τ′ of the two interacting nucleons. Thus, there are different G-matrices describing the nn, pp, and np in medium effective interactions. They are obtained by solving the generalized Bethe–Goldstone equations 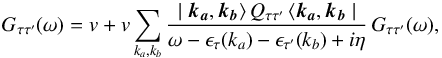 (2)where v is the bare NN interaction (or a density dependent two-body effective interaction when three-nucleon forces are introduced; see next section) and the quantity ω is the so-called starting energy. In the present work we consider spin unpolarized nuclear matter, thus in Eq. (2) and in the following equations we drop the spin indices to simplify the formalism2. The operator |ka,kb ⟩ Qττ′ ⟨ ka,kb| (Pauli operator) projects on intermediate scattering states in which the momenta ka and kb of the two interacting nucleons are above their respective Fermi momenta
(2)where v is the bare NN interaction (or a density dependent two-body effective interaction when three-nucleon forces are introduced; see next section) and the quantity ω is the so-called starting energy. In the present work we consider spin unpolarized nuclear matter, thus in Eq. (2) and in the following equations we drop the spin indices to simplify the formalism2. The operator |ka,kb ⟩ Qττ′ ⟨ ka,kb| (Pauli operator) projects on intermediate scattering states in which the momenta ka and kb of the two interacting nucleons are above their respective Fermi momenta ![\hbox{$k_{F}^{[\tau]}$}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq54.png) and
and ![\hbox{$k_{F}^{[\tau^\prime]}$}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq55.png) since states with momenta smaller that these values are occupied by the nucleons of the nuclear medium. Thus the Bethe–Goldstone equation describes the scattering of two nucleons in the presence of other nucleons, and the Brueckner G matrix represents the effective interaction between two nucleons in the nuclear medium and properly takes into account the short-range correlations arising from the strongly repulsive core in the bare NN interaction.
since states with momenta smaller that these values are occupied by the nucleons of the nuclear medium. Thus the Bethe–Goldstone equation describes the scattering of two nucleons in the presence of other nucleons, and the Brueckner G matrix represents the effective interaction between two nucleons in the nuclear medium and properly takes into account the short-range correlations arising from the strongly repulsive core in the bare NN interaction.
The single-particle energy ϵτ(k) of a nucleon (τ = n,p) with momentum k and mass mτ is given by 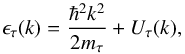 (3)where Uτ(k) is a single-particle potential that represents the mean field felt by a nucleon due to its interaction with the other nucleons of the medium. In the BHF approximation of the BBG theory, Uτ(k) is calculated through the real part of the on-energy-shell G-matrix (Bethe et al. 1963; Hüfner & Mahaux 1972) and is given by
(3)where Uτ(k) is a single-particle potential that represents the mean field felt by a nucleon due to its interaction with the other nucleons of the medium. In the BHF approximation of the BBG theory, Uτ(k) is calculated through the real part of the on-energy-shell G-matrix (Bethe et al. 1963; Hüfner & Mahaux 1972) and is given by ![\begin{equation} U_{\tau}(k) = \sum_{\tau^\prime} \sum_{k'\leq k_{F}^{[\tau^\prime]}} \mbox{Re} \ \langle \vec{k},\vec{k^\prime} \mid G_{\tau\tau^\prime}(\omega^*) \mid \vec{k},\vec{k^\prime} \rangle_a , \label{spp} \end{equation}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq62.png) (4)where the sum runs over all neutron and proton occupied states, ω∗ = ϵτ(k) + ϵτ′(k′), and the matrix elements are properly antisymmetrized. We make use of the so-called continuous choice (Jeukenne et al. 1976; Grangè et al. 1987; Baldo et al. 1990, 1991) for the single-particle potential Uτ(k) when solving the Bethe–Goldstone equation. As shown by Song et al. (1998) and Baldo et al. (2000), the contribution of the three-hole-line diagrams to the energy per nucleon E/A is minimized in this prescription and a faster convergence of the hole-line expansion for E/A is achieved with respect to the gap choice for Uτ(k).
(4)where the sum runs over all neutron and proton occupied states, ω∗ = ϵτ(k) + ϵτ′(k′), and the matrix elements are properly antisymmetrized. We make use of the so-called continuous choice (Jeukenne et al. 1976; Grangè et al. 1987; Baldo et al. 1990, 1991) for the single-particle potential Uτ(k) when solving the Bethe–Goldstone equation. As shown by Song et al. (1998) and Baldo et al. (2000), the contribution of the three-hole-line diagrams to the energy per nucleon E/A is minimized in this prescription and a faster convergence of the hole-line expansion for E/A is achieved with respect to the gap choice for Uτ(k).
In this scheme Eqs. (2)–(4) have to be solved self-consistently using an iterative numerical procedure. Once a self-consistent solution is achieved, the energy per nucleon of asymmetric nuclear matter is 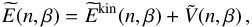 (5)where
(5)where ![\begin{eqnarray} \widetilde{E}^{\rm kin}(n,\beta) &=& \frac{1}{A} \sum_{\tau}\sum_{k \leq k_{F}^{[\tau]} } \frac{\hbar^2k^2}{2m_{\tau}} \nonumber \\ &=& \widetilde{E}^{\rm kin}_{0}(n) \, \frac{1}{2} \bigg\{ \frac{m_p}{m} (1+\beta)^{5/3} + \frac{m_n}{m} (1-\beta)^{5/3} \bigg\} \label{ekin} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq66.png) (6)is the total kinetic energy per nucleon. In the previous expression, mn and mp respectively denote the neutron and proton masses, m = (mn + mp)/2 the average nucleon mass, and
(6)is the total kinetic energy per nucleon. In the previous expression, mn and mp respectively denote the neutron and proton masses, m = (mn + mp)/2 the average nucleon mass, and 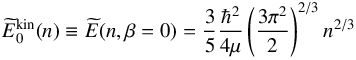 (7)the kinetic energy per nucleon of SNM, with μ = mnmp/ (mn + mp) being the reduced nucleon mass. The second term in Eq. (5) gives the potential energy contribution to total energy per nucleon. In the BHF approximation it can be written as
(7)the kinetic energy per nucleon of SNM, with μ = mnmp/ (mn + mp) being the reduced nucleon mass. The second term in Eq. (5) gives the potential energy contribution to total energy per nucleon. In the BHF approximation it can be written as ![\begin{equation} \widetilde{V}(n,\beta) = \frac{1}{2} \frac{1}{A}\sum_{\tau}\sum_{k \leq k_{F}^{[\tau]} } U_{\tau}(k) \ . \label{epot} \end{equation}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq72.png) (8)In this approach the two-body interaction v is the only physical input for the numerical solution Bethe–Goldstone equation.
(8)In this approach the two-body interaction v is the only physical input for the numerical solution Bethe–Goldstone equation.
As is well known, within the most advanced non-relativistic quantum many-body approaches it is not possible to reproduce the empirical saturation point of symmetric nuclear matter when using two-body nuclear interactions only. In fact, the saturation points obtained using different NN potentials lie within a narrow band called the Coester band (Coester et al. 1970; Day 1981), with either a too large saturation density or a too small binding energy (B = −E/A) compared to the empirical values. In particular, SNM turns out to be overbound with a too large saturation density when using modern high-precision NN potentials, fitting NN scattering data up to energy of 350 MeV, with a χ2 per datum next to 1 (Li et al. 2006). As in the case of few-nucleon systems (Kalantar-Nayestanak et al. 2012; Hammer et al. 2013; Binder et al. 2016) and also for the nuclear matter case, TNFs are considered to be the missing physical effect of the whole picture. The inclusion of TNF is thus required in order to reproduce a realistic saturation point (Friedman & Pandharipande 1981; Baldo et al. 1997; Akmal et al. 1998; Li et al. 2008; Taranto et al. 2013; Zuo et al. 2014). In addition, TNFs are crucial in the case of dense β-stable nuclear matter to obtain a stiff EOS (Baldo et al. 1997; Akmal et al. 1998; Li & Schulze 2008; Chamel et al. 2011) compatible with the measured masses M = 1.97 ± 0.04 M⊙ (Demorest et al. 2010) and M = 2.01 ± 0.04 M⊙ (Antoniadis et al. 2013) of the neutron stars in PSR J1614–2230 and PSR J0348+0432, respectively.
Within the BHF approach TNFs cannot be used directly in their original form because it would be necessary to solve three-body Faddeev equations in the nuclear medium (Bethe–Faddeev equations; Bethe 1965; Rajaraman & Bethe 1967), and currently this is a task still far from being achieved. To circumvent this problem an effective density dependent two-body force 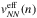 is built starting from the original three-body force by averaging over one of the three nucleons (Loiseau et al. 1971; Grangé et al. 1989).
is built starting from the original three-body force by averaging over one of the three nucleons (Loiseau et al. 1971; Grangé et al. 1989).
In the present work, following Holt et al. (2010), we derive a density dependent effective NN force averaging the chiral N2LOΔ1 and N2LOΔ2 TNFs in the nuclear medium, as described in more detail in Logoteta et al. (2016b).
The Bethe–Goldstone Eq. (2) is then solved adding this effective density dependent two-body force to the bare NN interaction (the N3LOΔ interaction in our case). It is important to note that when the original N2LOΔ1 and N2LOΔ2 TNFs are reduced to an effective density dependent two-body interaction 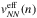 , the only terms that survive in PNM after the average are those proportional to the LECs c1 and c3 (Logoteta et al. 2016b). Thus, the calculations using the models N3LOΔ+N2LOΔ1 and N3LOΔ+N2LOΔ2 give the same results in PNM because they are not affected by the values of the LECs cD and cE, and they have the same values for the LECs c1 and c3 (see Table 1).
, the only terms that survive in PNM after the average are those proportional to the LECs c1 and c3 (Logoteta et al. 2016b). Thus, the calculations using the models N3LOΔ+N2LOΔ1 and N3LOΔ+N2LOΔ2 give the same results in PNM because they are not affected by the values of the LECs cD and cE, and they have the same values for the LECs c1 and c3 (see Table 1).
4. Equation of state for symmetric nuclear matter and pure neutron matter
 |
Fig. 1 Energy per particle of pure neutron matter (triangles) and symmetric nuclear matter (squares and circles) as a function of the nucleon number density for the interaction models considered in this work. The various symbols represent the results of our microscopic BHF calculations, whereas the lines represent the energy per particle obtained using the parametrization given by Eqs. (18) and (19) for the potential energy contribution to E/A for SNM and PNM. |
In this section we present and discuss the results of our calculations for the equation of state, i.e., the energy per nucleon E/A as a function of the baryon number density n, for SNM (β = 0) and PNM (β = 1) using the chiral nuclear interaction models and the BHF approach described in the previous pages. In this section of our work, we extend the nuclear matter calculations reported in Logoteta et al. (2016b) to high nucleon densities (n> 0.4 fm-3) relevant for neutron star physics, binary neutron star merging, and core-collapse supernovae.
We note that we have to solve the general Eqs. (2)–(4) even when we consider the case of SNM since the N3LOΔ two-nucleon interaction contains charge-independence breaking (CIB) and charge-symmetry breaking (CSB) terms (for a review, see, e.g., Miller et al. 2006) and since we consider the experimental values of the neutron and proton masses, i.e., we do not consider the approximation mn = mp.
Properties of nuclear matter for the interaction models used in this work.
Making the usually adopted angular average of the Pauli operator and of the energy denominator (Grangè et al. 1987; Baldo et al. 1991), the Bethe–Goldstone Eq. (2) can be expanded in partial waves. In all the calculations performed in the present work, we have considered partial wave contributions up to a total two-body angular momentum Jmax = 8. We have verified that the inclusion of partial waves with Jmax> 8 does not appreciably change our results. For example, the relative change in the calculated BHF potential energy per nucleon (Eq. (8)) in SNM at density n = 1.0 fm-3 when including partial wave contributions up to Jmax = 10 is 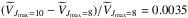 .
.
In Fig. 1 we show the energy per nucleon of SNM obtained using the two parametrizations (see Table 1) of the chiral N2LOΔ TNF, namely N2LOΔ1 (squares) and N2LOΔ2 (circles). The different symbols represent the results of our microscopic BHF calculations, whereas the lines represent the energy per particle obtained using the parametrization given by Eqs. (18) and (19) for the potential energy contribution to E/A for SNM and PNM discussed in the next section. It is apparent that at low density (n< 0.3 fm-3) the two models produce almost identical results. At n = 0.4 fm-3 the difference between the energy per nucleon originating from the two TNF models is ~ 3 MeV. This energy difference increases for increasing nucleon densities and is equal to ~ 41.5 MeV at n = 1.0 fm-3. In the case of PNM the energy per particle (triangles in Fig. 1) for the two TNF models coincide because, as discussed in the previous section, neutron matter is not affected by terms proportional to the LECs cE and cD.
In Table 2 we list the calculated values of the saturation points of SNM for the two interaction models considered in the present work. As we can see, the empirical saturation point of SNM, n0 = 0.16 ± 0.01 fm-3, E/A | n0 = −16.0 ± 1.0 MeV, is fairly well reproduced by our microscopic calculations. In Table 2 we also report the nuclear symmetry energy, calculated as 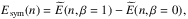 and the symmetry energy slope parameter,
and the symmetry energy slope parameter, 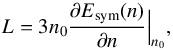 (9)at the calculated saturation density n0 (Col. 2 in Table 2). Our calculated Esym(n0) and L are in a satisfactory agreement with the values obtained by other BHF calculations with two- and three-body interactions (Li et al. 2006; Li & Schulze 2008; Vidanã et al. 2009, 2011b) and with the values extracted from various nuclear experimental data (Lattimer 2014).
(9)at the calculated saturation density n0 (Col. 2 in Table 2). Our calculated Esym(n0) and L are in a satisfactory agreement with the values obtained by other BHF calculations with two- and three-body interactions (Li et al. 2006; Li & Schulze 2008; Vidanã et al. 2009, 2011b) and with the values extracted from various nuclear experimental data (Lattimer 2014).
The incompressibility of SNM 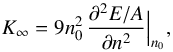 (10)at the calculated saturation point for the interaction models used in the present work is given in the last column of Table 2. Our calculated values for K∞ underestimate the empirical value K∞ = 210 ± 30 MeV (Blaizot et al. 1976) or more recently K∞ = 240 ± 20 MeV (Shlomo et al. 2006) extracted from experimental data of giant monopole resonance energies in medium-mass and heavy nuclei. This is a common feature with many other BHF nuclear matter calculations with two- and three-body nuclear interactions (Li & Schulze 2008; Vidanã et al. 2009).
(10)at the calculated saturation point for the interaction models used in the present work is given in the last column of Table 2. Our calculated values for K∞ underestimate the empirical value K∞ = 210 ± 30 MeV (Blaizot et al. 1976) or more recently K∞ = 240 ± 20 MeV (Shlomo et al. 2006) extracted from experimental data of giant monopole resonance energies in medium-mass and heavy nuclei. This is a common feature with many other BHF nuclear matter calculations with two- and three-body nuclear interactions (Li & Schulze 2008; Vidanã et al. 2009).
 |
Fig. 2 Pressure of symmetric nuclear matter for the two interaction models used in this work. The red hatched area represents the region in the pressure–density plane for SNM which is consistent with the measured elliptic flow of matter in collision experiments between heavy atomic nuclei (Danielewicz et al. 2002). |
In addition to the empirical constraints at density around the saturation density n0, the nuclear EOS can be tested using experimental data from collisions between heavy nuclei at energies ranging from a few tens of MeV up to several hundreds of MeV per nucleon. These collisions can compress nuclear matter up to ~ 4n0, thus giving valuable empirical information on the nuclear EOS at these supranuclear densities. Based on numerical simulations that reproduce the measured elliptic flow of matter in collision experiments between heavy nuclei, Danielewicz et al. (2002) have been able to obtain a region in the pressure–density plane for SNM which is consistent with these elliptic flow experimental data. This region is represented by the red hatched area in Fig. 2. These collision experiments between heavy nuclei thus provide a selective test for constraining the nuclear EOS up to ~ 4n0. In the same figure, we show the pressure for our two EOS models for SNM obtained from the calculated energy per nucleon and using the standard thermodynamical relation 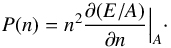 (11)As we can see our results are fully compatible with the empirical constraints given by Danielewicz et al. (2002).
(11)As we can see our results are fully compatible with the empirical constraints given by Danielewicz et al. (2002).
We want to emphasize that our BHF code, when used in conjunction with the N3LOΔ NN interaction plus our two parametrizations of the N2LOΔ TNF, reaches numerical convergence in the self-consistent scheme within a reasonable number of iterations (between ~ 7 and 14) and up to the largest densities (n ~ 1.2 fm-3) typical of neutron star maximum mass configurations. Thus, the nuclear matter EOS can be calculated fully microscopically up to these large densities. On the other hand, our BHF code does not reach convergence, already at density ~ 0.5 fm-3, when used in conjunction with other interaction models derived at the same order of the Δ-less ChPT (Logoteta et al. 2016b). Thus, in order to use these other interaction models for neutron star structure calculations, it is necessary to make a questionable extrapolation of the EOS to large densities.
This important difference in the convergence of the BHF scheme with chiral interactions is related to the inclusion of the Δ isobar both in the two- and three-nucleon potentials used in our present calculations. In fact, the Δ-full ChPT has an improved convergence (Kaiser et al. 1998; Krebbs et al. 2007) with respect to the Δ-less ChPT.
5. Symmetry energy and EOS for asymmetric and β-stable nuclear matter
The EOS of asymmetric nuclear matter can be calculated solving numerically Eqs. (2)–(4) and (8) for various values of the asymmetry parameter (0 ≤ β ≤ 1) and for various densities (0.5 ≤ n/n0 ≤ 8). These systematic calculations are not particularly demanding from a computational point of view; however, the use of these EOS tables is not ideal for applications to numerical simulations in general relativistic hydrodynamics. Thus, in the present work, in addition to providing EOS in tabular forms, we derive an EOS for asymmetric and β-stable nuclear matter at zero temperature in parametrized forms ready to be used in numerical simulations of binary neutron star merging.
To this end, instead of using the general expression given in Eq. (8) for the BHF potential energy contribution 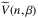 to the energy per nucleon of asymmetric nuclear matter, we employ the so-called parabolic approximation in the asymmetry parameter β (Bombaci & Lombardo 1991)
to the energy per nucleon of asymmetric nuclear matter, we employ the so-called parabolic approximation in the asymmetry parameter β (Bombaci & Lombardo 1991) 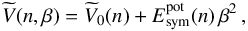 (12)with
(12)with 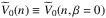 and
and 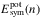 being the potential energy contribution to the energy per nucleon of SNM and to the total symmetry energy Esym, respectively. Using Eq. (12),
being the potential energy contribution to the energy per nucleon of SNM and to the total symmetry energy Esym, respectively. Using Eq. (12), 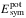 can be written as the difference between the potential energy contribution to the energy per nucleon of PNM and SNM, i.e.,
can be written as the difference between the potential energy contribution to the energy per nucleon of PNM and SNM, i.e., 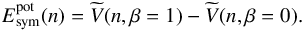 (13)It is important to note that the presence of tiny CSB and CIB terms in the nuclear interaction used in the present calculations could invalidate Eq. (12). For example, a CSB component in the NN interaction produces a linear (and more generally odd-power) β-term in Eq. (12) (Haensel 1997). We have numerically checked the accuracy of Eq. (12) for the N3LOΔ nucleon-nucleon interaction up to the high densities considered in the present calculations. Thus, in agreement with the results of Haensel (1997) and Müther et al. (1999), the effects on the EOS of asymmetric nuclear matter and on the nuclear symmetry energy of CSB and CIB terms in the NN interaction are essentially negligible.
(13)It is important to note that the presence of tiny CSB and CIB terms in the nuclear interaction used in the present calculations could invalidate Eq. (12). For example, a CSB component in the NN interaction produces a linear (and more generally odd-power) β-term in Eq. (12) (Haensel 1997). We have numerically checked the accuracy of Eq. (12) for the N3LOΔ nucleon-nucleon interaction up to the high densities considered in the present calculations. Thus, in agreement with the results of Haensel (1997) and Müther et al. (1999), the effects on the EOS of asymmetric nuclear matter and on the nuclear symmetry energy of CSB and CIB terms in the NN interaction are essentially negligible.
The nucleon chemical potentials μτ (τ = n,p), inclusive of the rest mass of the particle, can be thus written as 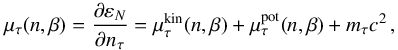 (14)with
(14)with 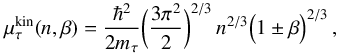 (15)
(15)![\begin{equation} \mu_{\tau}^{\rm pot}(n,\beta) = \widetilde{V}_{0}(n) + n \frac{\partial \widetilde{V}_{0}}{\partial n} \pm 2 E^{\rm pot}_{\rm sym}(n) \, \beta + \bigg[ n \frac{\partial E^{\rm pot}_{\rm sym}(n)}{\partial n} - E^{\rm pot}_{\rm sym}(n) \bigg] \, \beta^2 \, , \label{chempot-4} \end{equation}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq121.png) (16)where the partial derivatives of the nucleonic energy density
(16)where the partial derivatives of the nucleonic energy density 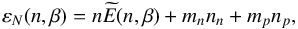 (17)are taken at zero temperature and constant volume, and the upper and lower sign in Eqs. (15) and (16) refers to neutrons and protons, respectively.
(17)are taken at zero temperature and constant volume, and the upper and lower sign in Eqs. (15) and (16) refers to neutrons and protons, respectively.
Subsequently, we parametrize the potential energy contribution to the energy per nucleon of SNM and PNM as 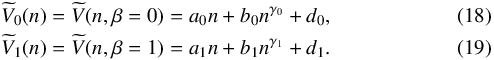 We have fixed the values of the coefficients in Eqs. (18) and (19) fitting the results of our microscopic BHF calculations for SNM and PNM in the density range 0.10–1.20 fm-3. The coefficients given in Table 3 fit the BHF results with a root mean square relative error (RMSRE) = 0.0069 for both interactions in the case of SNM, and RMSRE = 0.0104 in the case of PNM. The energy per particle E/A corresponding to this parametrization is represented by the different lines in Fig. 1.
We have fixed the values of the coefficients in Eqs. (18) and (19) fitting the results of our microscopic BHF calculations for SNM and PNM in the density range 0.10–1.20 fm-3. The coefficients given in Table 3 fit the BHF results with a root mean square relative error (RMSRE) = 0.0069 for both interactions in the case of SNM, and RMSRE = 0.0104 in the case of PNM. The energy per particle E/A corresponding to this parametrization is represented by the different lines in Fig. 1.
Thus, using Eq. (13) the potential part of the symmetry energy can be written as 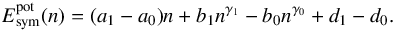 (20)Equations (12), (18), and (20), together with Eqs. (6) and (7) giving the kinetic energy per nucleon, provide our parametrized EOS for asymmetric nuclear matter.
(20)Equations (12), (18), and (20), together with Eqs. (6) and (7) giving the kinetic energy per nucleon, provide our parametrized EOS for asymmetric nuclear matter.
We next calculate the composition of β-stable nuclear matter, solving the equations for chemical equilibrium in neutrino-free matter (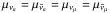 ) (Prakash et al. 1997) at a given total nucleon density n
) (Prakash et al. 1997) at a given total nucleon density n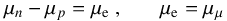 (21)and for charge neutrality
(21)and for charge neutrality 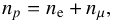 (22)with electrons and muons treated as relativistic ideal Fermi gases.
(22)with electrons and muons treated as relativistic ideal Fermi gases.
The potential energy contribution to the nucleon chemical potential can thus be written as ![\begin{eqnarray} \mu_{\tau}^{\rm pot} &=& 2 a_0 n + (\gamma_0 + 1) b_0 n^{\gamma_0} + d_0 \pm 2 E^{\rm pot}_{\rm sym}(n) \beta \nonumber \\ &&\quad+ [(\gamma_1 - 1) b_1 n^{\gamma_1} - (\gamma_0 - 1) b_0 n^{\gamma_0} - (d_1 - d_0)] \beta^2 \, , \label{chempot-5} \end{eqnarray}](/articles/aa/full_html/2018/01/aa31604-17/aa31604-17-eq140.png) (23)where the upper and lower sign refers to neutrons and protons, respectively. Consequently, the difference between the neutron and proton chemical potentials entering in the β-equilibrium condition (21) can be written as
(23)where the upper and lower sign refers to neutrons and protons, respectively. Consequently, the difference between the neutron and proton chemical potentials entering in the β-equilibrium condition (21) can be written as 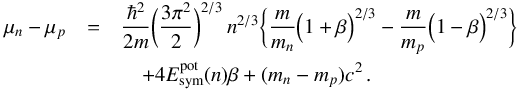 (24)The composition of β-stable matter, i.e., the particle fractions xi = ni/n (with i = n, p, e−, μ−) calculated using the parametrization (18) and (19) of our microscopic calculations, is shown in Fig. 3. The continuous (dashed) lines refer to the model N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2). These results are in agreement with various other microscopic BHF calculations based on realistic nuclear interactions (Baldo et al. 1997; Burgio et al. 2011).
(24)The composition of β-stable matter, i.e., the particle fractions xi = ni/n (with i = n, p, e−, μ−) calculated using the parametrization (18) and (19) of our microscopic calculations, is shown in Fig. 3. The continuous (dashed) lines refer to the model N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2). These results are in agreement with various other microscopic BHF calculations based on realistic nuclear interactions (Baldo et al. 1997; Burgio et al. 2011).
When the proton fraction xp = np/n is larger than a threshold value, denoted as 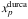 , the direct URCA processes
, the direct URCA processes 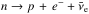 , p + e− → n + νe can occur in neutron star matter (Lattimer et al. 1991).
, p + e− → n + νe can occur in neutron star matter (Lattimer et al. 1991).
In β-stable nuclear matter we can easily show that 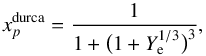 (25)where Ye = ne/ (ne + nμ) is the leptonic electron fraction.
(25)where Ye = ne/ (ne + nμ) is the leptonic electron fraction.
The threshold proton fraction for direct URCA processes is depicted in Fig. 3 by the continuous line labeled 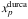 . Below the muon threshold density
. Below the muon threshold density 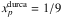 .
.
The calculated values for the threshold nucleon number density ndurca for the occurrence of direct URCA processes, for the corresponding proton fraction xp(ndurca) together with the corresponding neutron star gravitational mass Mdurca = M(nc = ndurca) are reported in Table 4.
 |
Fig. 3 Particle fractions of β-stable nuclear matter for the models described in the text. |
Threshold values for the occurrence of direct URCA processes in dense β-stable nuclear matter.
Once we have determined the particle fractions xi(n) in β-stable matter, the corresponding nucleonic contribution εN(n) to the total energy density ε(n) = εN(n) + εL(n) can be obtained using Eq. (17). In addition, the nucleonic contribution PN(n) to the total pressure P(n) = PN(n) + PL(n) can be calculated using the thermodynamic relation 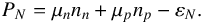 (26)Finally, the leptonic contributions εL and PL to the total energy density and total pressure, respectively, are computed using the expressions for relativistic ideal Fermi gases with me = 0.511 MeV/c2 and mμ = 105.658 MeV/c2.
(26)Finally, the leptonic contributions εL and PL to the total energy density and total pressure, respectively, are computed using the expressions for relativistic ideal Fermi gases with me = 0.511 MeV/c2 and mμ = 105.658 MeV/c2.
The resulting EOS for β-stable matter for the two considered nuclear interaction models is shown in Fig. 4. These results are consistent with those reported in Fig. 1.
The EOS for β-stable matter is also reported in tabular form in the Appendix, where in addition to the baryon number density, energy density, and pressure, we also list the proton fraction xp and the electron fraction xe. The muon fraction is given by xμ = xp−xe.
Our tabular EOS for β-stable matter can be reproduced in a simple and very accurate parametrized form. To this end we parametrize the total energy density ε (second column in Tables A.1 and A.2) as a function of the nucleon number density n using the simple equation 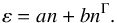 (27)Then the total pressure can be deduced using the thermodynamical relation
(27)Then the total pressure can be deduced using the thermodynamical relation 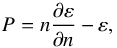 (28)and is given by the polytrope
(28)and is given by the polytrope 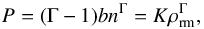 (29)where ρrm = (a/c2)n is the rest-mass density (c is the speed of light) and
(29)where ρrm = (a/c2)n is the rest-mass density (c is the speed of light) and 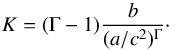 (30)The energy density can thus be written as
(30)The energy density can thus be written as 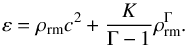 (31)The coefficients reported in Table 5 fit the tabular EOS for β-stable matter in the density range 0.08–1.30 fm-3 with a RMSRE = 0.00018 in the case of the N3LOΔ+N2LOΔ1 interaction and RMSRE = 0.00047 in the case of the N3LOΔ+N2LOΔ2 interaction. The curves representing these parametrized EOS in Fig. 4 are indistinguishable from those obtained from the tabular EOS reported in the Appendix.
(31)The coefficients reported in Table 5 fit the tabular EOS for β-stable matter in the density range 0.08–1.30 fm-3 with a RMSRE = 0.00018 in the case of the N3LOΔ+N2LOΔ1 interaction and RMSRE = 0.00047 in the case of the N3LOΔ+N2LOΔ2 interaction. The curves representing these parametrized EOS in Fig. 4 are indistinguishable from those obtained from the tabular EOS reported in the Appendix.
 |
Fig. 4 Equation of state of β-stable nuclear matter for the models described in the text. |
 |
Fig. 5 Speed of sound vs/c (in units of the speed of light c) in β-stable nuclear matter as a function of the baryon number density n. The heavy dots on the two curves represent the central density of the neutron star maximum mass configuration for the corresponding EOS model. |
In Fig. 5 we plot the speed of sound vs in β-stable matter as a function of the baryon number density n. The plotted curves were obtained performing the numerical derivative of our tabular EOS according to the definition vs/c = (dP/ dε)1/2. Using our parametrization (Eqs. (27) and (29)) for the EOS of β-stable matter, we obtain 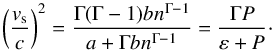 (32)The corresponding curves in Fig. 5 are indistinguishable from those obtained using the the numerical derivative from the tabular EOS. The heavy dots on both curves in Fig. 5 represent the central density of the neutron star maximum mass configuration for the corresponding EOS model (see next section). Thus, our EOS models fulfill the causality condition vS/c< 1 up to the highest densities reached in the corresponding neutron star configurations (see next section).
(32)The corresponding curves in Fig. 5 are indistinguishable from those obtained using the the numerical derivative from the tabular EOS. The heavy dots on both curves in Fig. 5 represent the central density of the neutron star maximum mass configuration for the corresponding EOS model (see next section). Thus, our EOS models fulfill the causality condition vS/c< 1 up to the highest densities reached in the corresponding neutron star configurations (see next section).
6. Neutron star structure
The structural properties of non-rotating neutron stars can be obtained integrating numerically the equation for hydrostatic equilibrium in general relativity (Tolman 1934; Oppenheimer & Volkoff 1939) 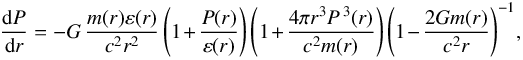 (33)and
(33)and 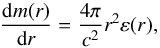 (34)where G is the gravitational constant and m(r) is the gravitational mass enclosed within a sphere of radial coordinate r (surface area 4πr2).
(34)where G is the gravitational constant and m(r) is the gravitational mass enclosed within a sphere of radial coordinate r (surface area 4πr2).
 |
Fig. 6 Mass–radius relationship (panel a) and mass–central baryon density relationship (panel b) for the two nuclear interaction models considered in this work. The hatched region in panel a represents the mass–radius constraints obtained by Steiner et al. (2010, 2013b). The strip with boundaries marked with orange lines stands for the measured mass M = 2.01 ± 0.04 M⊙ (Antoniadis et al. 2013) of the neutron stars in PSR J0348+0432. |
Starting with a central energy density εc ≡ ε(r = 0), we integrate out Eqs. (33) and (34) until the energy density equals the one corresponding to the density of iron εsurf/c2 = 7.86 g/cm3. This condition determines the stellar surface and specifies the neutron star radius R (through the surface area 4πR2) and the stellar gravitational mass 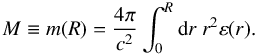 (35)The total baryon number of a star with central baryon density nc = n(r = 0) is given by
(35)The total baryon number of a star with central baryon density nc = n(r = 0) is given by 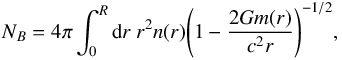 (36)and the baryonic mass (or “rest mass”) of the neutron star is
(36)and the baryonic mass (or “rest mass”) of the neutron star is 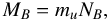 (37)where mu is a baryonic mass unit that we take equal to mu = m(12C)/12 = 1.6605 × 10-24 g. Other choices for mu are sometimes used in the literature as mu = mn or mu = m(56Fe)/56. These choices for mu only make small changes in the calculated stellar binding energy since ΔEbind/ (MBc2) ~ 0.01.
(37)where mu is a baryonic mass unit that we take equal to mu = m(12C)/12 = 1.6605 × 10-24 g. Other choices for mu are sometimes used in the literature as mu = mn or mu = m(56Fe)/56. These choices for mu only make small changes in the calculated stellar binding energy since ΔEbind/ (MBc2) ~ 0.01.
The total binding energy of the star is thus 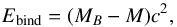 (38)which represents the total energy liberated during the neutron star’s birth.
(38)which represents the total energy liberated during the neutron star’s birth.
The stellar structure Eqs. (33), (34), and (36) have been integrated using the microscopic EOS (in tabular form) for β-stable nuclear matter described in the previous sections to model the neutron star core, whereas to model the stellar crust (i.e., for nucleonic density ≤0.08 fm-3) we have used the Baym–Pethick–Sutherland (Baym et al. 1971) and the Negele & Vautherin (1973) EOS. The results are shown in Fig. 6, where we plot the mass-radius (panel (a)) and mass-central density (panel (b)) relations for the considered EOS models. We note that our EOS models are both compatible with current measured neutron star masses and particularly with the mass M = 2.01 ± 0.04 M⊙ (Antoniadis et al. 2013) of the neutron stars in PSR J0348+0432. The hatched regions in Fig. 6 represent the mass–radius constraints based on the analysis of recent observations of both transiently accreting and bursting X-ray sources obtained by Steiner et al. (2010, 2013b). Manifestly, the neutron star configurations calculated with our EOS models are able to fulfill these empirical constraints on the mass–radius relationship.
Maximum mass configuration properties for the interaction models considered in this work.
 |
Fig. 7 Gravitational redshift at the neutron star surface as a function of the stellar gravitational mass for the two considered EOS models. The horizontal lines represent the measured gravitational redshift z = 0.35 for the X-ray burst source in the low-mass X-ray binary EXO 07482−676 (Cottam et al. 2002) and |
 |
Fig. 8 Neutron star binding energy versus the stellar gravitational mass (left panel) and fractional binding energy Ebind/ (Mc2) = (MB−M) /M as a function of the surface gravitational redshift zsurf (right panel) for the two considered EOS models. |
Various structural properties of the maximum mass configuration for the two considered EOS models are listed in Table 6. Our present results are in good agreement with the results of other calculations (Baldo et al. 1997; Akmal et al. 1998) based on microscopic approaches.
The gravitational redshift of a signal emitted from the stellar surface is 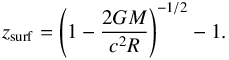 (39)Thus, measurements of zsurf of spectral lines can give direct information on the stellar compactness parameter
(39)Thus, measurements of zsurf of spectral lines can give direct information on the stellar compactness parameter 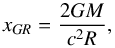 (40)and consequently can place limits on the EOS for dense matter. The surface gravitational redshift calculated for our two EOS models is presented in Fig. 7. The two horizontal lines in the same figure represent the measured gravitational redshift z = 0.35 for the X-ray bursts source in the low-mass X-ray binary EXO 07482−676 (Cottam et al. 2002) and
(40)and consequently can place limits on the EOS for dense matter. The surface gravitational redshift calculated for our two EOS models is presented in Fig. 7. The two horizontal lines in the same figure represent the measured gravitational redshift z = 0.35 for the X-ray bursts source in the low-mass X-ray binary EXO 07482−676 (Cottam et al. 2002) and 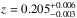 for the isolated neutron star RX J0720.4−3125 (Hambaryan et al. 2017).
for the isolated neutron star RX J0720.4−3125 (Hambaryan et al. 2017).
In Fig. 8 (left panel) we plot the binding energy Ebind versus the stellar gravitational mass M. Various empirical formulae have been given to describe the dependence Ebind(M) or Ebind(MB) (Lattimer & Yahil 1989; Prakash et al. 1997; Lattimer & Prakash 2001). In particular many numerical calculations have shown that there is a narrow band of possible values of the stellar binding energy for a given mass implying the existence of a universal relation Ebind(M) or Ebind(MB).
Our calculated binding energy for neutron stars in the mass range 1.0 M⊙ ≤ M ≤ Mmax can be fitted with very high accuracy using the simple relation 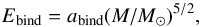 (41)with abind = 1.055 × 1053 erg (abind = 1.073 × 1053 erg) for the N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2) EOS model.
(41)with abind = 1.055 × 1053 erg (abind = 1.073 × 1053 erg) for the N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2) EOS model.
Next, in Fig. 8 (right panel) we plot the quantity Ebind/ (Mc2) as a function of the surface gravitational redshift zsurf. The results for the stellar binding energy from the numerical integration of the TOV equation for neutron stars in the mass range 1.0 M⊙ ≤ M ≤ Mmax can be fitted with very high accuracy using the simple relation 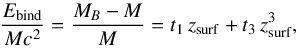 (42)with t1 = 0.4505 (t1 = 0.4509) and t3 = −0.4207 (t3 = −0.4832) for the N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2) EOS model.
(42)with t1 = 0.4505 (t1 = 0.4509) and t3 = −0.4207 (t3 = −0.4832) for the N3LOΔ+N2LOΔ1 (N3LOΔ+N2LOΔ2) EOS model.
The binding energy of a neutron star could be deduced from the detection of neutrinos from a nearby supernova. In addition, a possible measurement of zsurf for the neutron star left behind by the same supernova event will give very strong constraints on the EOS of stellar matter. We note that a few minutes after its birth a neutron star can be described using the EOS of cold (i.e., at zero temperature) and neutrino-free matter (Prakash et al. 1997).
7. Summary
In this work we derived a new microscopic EOS of dense SMN, PNM, as well as asymmetric and β-stable nuclear matter at zero temperature using modern two-body and three-body nuclear forces determined in the framework of chiral perturbation theory and including the Δ isobar intermediate state. To this end, we employed the BHF many-body approach, which properly takes into account the short-range correlations arising from the strongly repulsive core in the bare NN interaction. This feature is particularly relevant in the case of matter at supranuclear densities. Our EOS models are able to reproduce the empirical saturation point of symmetric nuclear matter, the symmetry energy Esym, and its slope parameter L at the empirical saturation density n0 and are compatible with experimental data from collisions between heavy nuclei at energies ranging from a few tens of MeV up to several hundreds of MeV per nucleon. We used our EOS for β-stable nuclear matter to compute various structural properties of non-rotating neutron stars. The calculated neutron star configurations are consistent with present measured neutron star masses and particularly with the mass M = 2.01 ± 0.04 M⊙ of the neutron stars in PSR J0348+0432.
We provided our new EOS both in tabular form and in parametrized form ready to be used in numerical general relativity simulations of binary neutron star merging. To this purpose our zero temperature EOS needs to be supplemented by a thermal contribution that accounts for the sizeable increase in the internal energy at the merger. This is usually done by adding an ideal-fluid component to the zero temperature EOS, which accounts for the shock heating (Rezzolla & Zanotti 2013).
In a more consistent thermodynamical approach the EOS relevant for core-collapse SNe and BNS mergers simulations should be derived within a finite temperature many-body approach (Shen et al. 1998; Hempel & Schaffner-Bielich 2010; Steiner et al. 2013a; Oertel et al. 2017; Togashi et al. 2017). We are presently working on the extension of our microscopic nuclear matter EOS based on nuclear chiral interactions to the case of finite temperature for applications to numerical simulations of the above-mentioned astrophysical phenomena.
In future studies we also plan to extend our present calculations to the case of β-stable hyperonic matter, based on nucleon-hyperon (Haidenbauer et al. 2013), and hyperon-hyperon (Haidenbauer et al. 2016) interactions derived in the framework of ChPT, and to include hyperonic three-body interactions within this formalism.
Spin polarized nuclear matter within the BHF approach has been considered by, e.g., Vidaña & Bombaci (2002) and Bombaci et al. (2006).
Acknowledgments
This work has been partially supported by “NewCompstar”, COST Action MP1304.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2016a, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2016b, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017a, Phys. Rev. Lett., 118, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017b, Phys. Rev. Lett., 119, 141101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017c, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 1233232 [Google Scholar]
- Baldo, M., & Burgio, G. F. 2012, Rep. Progr. Phys., 75, 026301 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Bombaci, I., Giansiracusa, G., et al. 1990, Phys. Rev. C, 41, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Bombaci, I., Ferreira, L. S., Giansiracusa, G., & Lombardo, U. 1991, Phys. Rev. C, 43, 2605 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Bombaci, I., & Burgio, G. F. 1997, A&A , 328, 274 [NASA ADS] [Google Scholar]
- Baldo, M., Giansiracusa, G., Lombardo, U., & Song, H. Q. 2000, Phys. Lett. B, 473, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bauswein, A., & Janka, H.-T. 2012, Phys. Rev. Lett., 108, 011101 [Google Scholar]
- Bauswein, A., Stergioulas, N., & Janka, H.-T. 2016, Eur. Phys. J. A, 52, 56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, D. 1971, ApJ, 170, 299 [Google Scholar]
- Bernuzzi, S., Dietrich, T., & Nagar, A. 2015, Phys. Rev. Lett., 115, 091101 [Google Scholar]
- Bethe, H. A. 1965, Phys. Rev., 138, 804B [NASA ADS] [CrossRef] [Google Scholar]
- Bethe, H. A., Brandow, B. H., & Petschek, A. G. 1963, Phys. Rev., 129, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Binder, S., et al. (LENPIC Collaboration) 2016, Phys. Rev. C, 93, 044002 [NASA ADS] [CrossRef] [Google Scholar]
- Blaizot, J. P., Gogny, D., & Grammaticos, B. 1976, Nucl. Phys. A, 265, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., & Logoteta, D. 2013, MNRAS, 433, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., & Lombardo, U. 1991, Phys. Rev. C, 44, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Polls, A., Ramos, A., Rios, A., & Vidaña, I. 2006, Phys. Lett. B, 632, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Panda, P. K., Providência, C., & Vidaña, I. 2008, Phys. Rev. D, 77, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Logoteta, D., Vidaña, I., & Providência, C. 2016, Eur. Phys. J. A, 52, 58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgio, G. F., Schulze, H.-J., & Li, A. 2011, Phys. Rev. C, 83, 025804 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, J., Gandolfi, S., Pederiva, F., et al. 2015, Rev. Mod. Phys., 87, 1067 [Google Scholar]
- Chamel, N., Fantina, A. F., Paearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802(R) [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., & Vidaña, I. 2016, Eur. Phys. J. A, 52, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciolfi, R., Kastaun, W., Giacomazzo, B., et al. 2017, Phys. Rev. D, 95, 063016 [NASA ADS] [CrossRef] [Google Scholar]
- Coester, F., Cohen, S., Day, B., & Vincent, C. M. 1970, Phys. Rev. C, 1, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Cottam, J., Paerels, F., & Mendez, M. 2002, Nature, 420, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Day, B. D. 1967, Rev. Mod. Phys., 39, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Day, B. D. 1981, Phys. Rev. Lett., 47, 226 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, M., & Lombardo, M. P. 2003, Phys. Rev. D, 67, 014505 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P., Pennucci, T., Ransom, S., Roberts, M., & Hessels, J. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Endrizzi, A., Ciolfi, R., Giacomazzo, B., Kastaun, W., & Kawamura, T. 2016, Class. Quant. Grav., 33, 164001 [NASA ADS] [CrossRef] [Google Scholar]
- Epelbaum, E., Nogga, A., Glocklë, W., et al. 2002, Phys. Rev. C, 66, 064001 [NASA ADS] [CrossRef] [Google Scholar]
- Epelbaum, E., Hammer, H.-W., & Meißner, U.-G. 2009, Rev. Mod. Phys., 81, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, J., & Miyazawa, H. 1957, Prog. Theor. Phys., 17, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, K., & Hatsuda, T. 2011, Rept. Prog. Phys., 74, 014001 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 1985, ApJ., 293, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 1996, Compact Stars: Nuclear Physics, Particle Physics, and General Relativity (Springer Verlag) [Google Scholar]
- Grangé, P., Cugnon, J., & Lejeune, A. 1987, Nucl. Phys. A, 473, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Grangé, P., Lejeunne, A., Martzolff, B., & Mathiot, J.-F. 1989, Phys. Rev. C, 40, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S. 2010, PoS LATTICE2010, 007 [arXiv:1101.0109] [Google Scholar]
- Haensel, P. 1997, J. Phys. G, 3, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Haidenbauer, J., Petschauer, S., Kaiser, N., et al. 2013, Nucl. Phys. A, 915, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Haidenbauer, J., Meißner, U.-G., & Petschauer, S. 2016, Nucl. Phys. A, 954, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Haidenbauer, J., Meißner, U.-G., Kaiser, N., & Weise, W. 2017, Eur. Phys. J. A, 53, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hambaryan, V., Suleimanov, V., Haberl, F., et al. 2017, A&A, 601, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, H. W., Nogga, A., & Schenk, A., 2013, Rev. Mod. Phys., 85, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Hempel, M., & Schaffner-Bielich, J. 2010, Nucl. Phys. A, 837, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J. W., Kaiser, N., & Weise, W. 2010, Phys. Rev. C, 81, 024002 [NASA ADS] [CrossRef] [Google Scholar]
- Hüfner, J., & Mahaux, C. 1972, Ann. Phys., 73, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Jeukenne, J. P., Lejeunne, A., & Mahaux, C. 1976, Phys. Rep., 25, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Gerstendörfer, S., & Weise, W. 1998, Nucl. Phys. A, 637, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Kalantar-Nayestanaki, N., Epelbaum, E., Messchendorp, J. G., & Nogga, A. 2012, Rep. Prog. Phys., 75, 016301 [Google Scholar]
- Krebs, H., Epelbaum, E., & Meißner, U.-G. 2007, Eur. Phys. J. A, 32 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattimer, J. M. 2014, Gen. Rel. Grav., 46, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J., & Prakash, M. 2001, ApJ, 550, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J., & Prakash, M. 2016, Phys. Rep., 621, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J., & Yahil, A. 1989, ApJ, 340, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. H., & Schulze, H.-J. 2008 Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. H., Lombardo, U., Schulze, H.-J., et al. 2006, Phys. Rev. C, 74, 047304 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. H., Lombardo, U., Schulze, H.-J., & Zuo, W. 2008, Phys. Rev. C, 77, 034316 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D., Bombaci, I., Providência, C., & Vidaña, I. 2012, Phys. Rev. D, 85, 023003 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D., Vidaña, I., Bombaci, I., & Kievsky, A. 2015, Phys. Rev. C, 91, 064001 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D., Bombaci, I., & Kievsky, A. 2016a, Phys. Lett. B, 758, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D., Bombaci, I., & Kievsky, A. 2016b, Phys Rev. C, 94, 064001 [NASA ADS] [CrossRef] [Google Scholar]
- Loiseau, B. A., Nogami, Y., & Ross, C. K. 1971, Nucl. Phys. A, 401, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Machleidt, R., & Entem, D. R. 2011, Phys. Rep., 503, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Maione, F., De Pietri, R., Feo, A., & Löffler, F. 2016, Class. Quant. Grav., 33, 175009 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, G. A., Opper, A. K., & Stephenson, E. J. 2006, Ann. Rev. Nucl. Part. Sci., 56, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Müther, H., Polls, A., & Machleidt, R. 1999, Phys. Lett. B, 445, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro Pérez, R., Amaro, J. E., & Ruiz Arriola, E., 2013, Phys. Rev. C, 88, 064002; 2015; Erratum, Phys. Rev. C, 91, 029901 [NASA ADS] [CrossRef] [Google Scholar]
- Navratil, P. 2007, Few-Body Syst., 41, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Negele, J. W., & Vautherin, D. 1973, Nucl. Phys. A, 207, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Nollett, K. M., Pieper, S. C., Wiringa, R. B., Carlson, J., & Hale, G. M. 2007, Phys. Rev. Lett, 99, 022502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oertel, M., Hempel, M., Klahn, T., & Typel, S. 2017, Rev. Mod. Phys., 89, 015007 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, J., & Volkoff, G. 1939, Phys. Rev, 55, 374 [Google Scholar]
- Piarulli, M., Girlanda, L., Schiavilla, R., et al. 2015, Phys. Rev. C, 91, 024003 [NASA ADS] [CrossRef] [Google Scholar]
- Piarulli, M., Girlanda, L., Schiavilla, R., et al. 2016, Phys. Rev. C, 94, 054007 [NASA ADS] [CrossRef] [Google Scholar]
- Pieper, S. C., Pandharipande, V. R., Wiringa, R. B., & Carlson, J. 2001, Phys. Rev. C, 64, 014001 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., Giacomazzo, B., & Perna, R. 2017, ApJ, 844, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Prakash, M., Bombaci, I., Prakash, M., et al. 1997, Phys. Rep., 280, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Bernuzzi, S., Del Pozzo, W., Roberts, L. F., & Ott, C. D. 2017, ApJ, 842, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Rajaraman, R., & Bethe, H. A. 1967, Rev. Mod. Phys., 39, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Takami, K. 2016, Phys. Rev. D, 93, 124051 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Zanotti, O. 2013, Relativistic Hydrodynamics (Oxford, UK: Oxford University Press) [Google Scholar]
- Sekiguchi, Y., Kiuchi, K., Kyutoku, K., Shibata, M., & Taniguchi, K. 2016, Phys. Rev. D, 93, 124046 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, H., Toki, H., Oyamatsu, K., & Sumiyoshi, K. 1998, Nucl. Phys. A, 637, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., Taniguchi, K., & Uryu, K. 2005, Phys. Rev. D, 71, 084021 [NASA ADS] [CrossRef] [Google Scholar]
- Shlomo, S., Kolomietz, V. K., & Colò, G. 2006, Eur. Phys. J. A, 30, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, H. Q., Baldo, M., Giansiracusa, G., & Lombardo, U. 1998, Phys. Rev. Lett., 81, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Hempel, M., & Fischer, T. 2013a, ApJ, 774, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2013b, ApJ, 765, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, K., Rezzolla, L., & Baiotti, L. 2014, Phys. Rev. Lett., 113, 091104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taranto, G., Baldo, M., & Burgio, G. F. 2013, Phys. Rev. C, 87, 045803 [NASA ADS] [CrossRef] [Google Scholar]
- Togashi, H., Nakazato, K., Takehara, Y., et al. 2017, Nucl. Phys. A, 961, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Tolman, R. C. 1934, Proc. Nat. Acad. Sci. (USA), 20, 3 [Google Scholar]
- Vidaña, I., & Bombaci, I. 2002, Phys. Rev. C, 66, 045801 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Providência, C., Polls, A., & Rios, A. 2009, Phys. Rev. C, 80, 045806 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Logoteta, D., Providência, C., Polls, A., & Bombaci, I. 2011a, Europhys. Lett., 94, 11002 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Polls, A., & Providência, C. 2011b, Phys. Rev. C, 84, 062801(R) [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1979, Physica A, 96, 327 [Google Scholar]
- Weinberg, S. 1990, Phys. Lett. B, 251, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1991, Nucl. Phys. B, 363, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1992, Phys. Lett. B, 259, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Wiringa, R. B., Fiks, V., & Fabrocini, A. 1998, Phys. Rev. C, 38, 1010 [Google Scholar]
- Zuo, W., Bombaci, I., & Lombardo, U. 2014, Eur. Phys. J. A, 50, 12. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Tables for the equation of state of β-stable matter
Equation of state for β-stable matter. Model N3LOΔ+N2LOΔ1.
Equation of state for β-stable matter. Model N3LOΔ+N2LOΔ2.
All Tables
Values of the low-energy constants (LECs) of the TNF models used in the present calculations.
Threshold values for the occurrence of direct URCA processes in dense β-stable nuclear matter.
Maximum mass configuration properties for the interaction models considered in this work.
All Figures
 |
Fig. 1 Energy per particle of pure neutron matter (triangles) and symmetric nuclear matter (squares and circles) as a function of the nucleon number density for the interaction models considered in this work. The various symbols represent the results of our microscopic BHF calculations, whereas the lines represent the energy per particle obtained using the parametrization given by Eqs. (18) and (19) for the potential energy contribution to E/A for SNM and PNM. |
| In the text | |
 |
Fig. 2 Pressure of symmetric nuclear matter for the two interaction models used in this work. The red hatched area represents the region in the pressure–density plane for SNM which is consistent with the measured elliptic flow of matter in collision experiments between heavy atomic nuclei (Danielewicz et al. 2002). |
| In the text | |
 |
Fig. 3 Particle fractions of β-stable nuclear matter for the models described in the text. |
| In the text | |
 |
Fig. 4 Equation of state of β-stable nuclear matter for the models described in the text. |
| In the text | |
 |
Fig. 5 Speed of sound vs/c (in units of the speed of light c) in β-stable nuclear matter as a function of the baryon number density n. The heavy dots on the two curves represent the central density of the neutron star maximum mass configuration for the corresponding EOS model. |
| In the text | |
 |
Fig. 6 Mass–radius relationship (panel a) and mass–central baryon density relationship (panel b) for the two nuclear interaction models considered in this work. The hatched region in panel a represents the mass–radius constraints obtained by Steiner et al. (2010, 2013b). The strip with boundaries marked with orange lines stands for the measured mass M = 2.01 ± 0.04 M⊙ (Antoniadis et al. 2013) of the neutron stars in PSR J0348+0432. |
| In the text | |
 |
Fig. 7 Gravitational redshift at the neutron star surface as a function of the stellar gravitational mass for the two considered EOS models. The horizontal lines represent the measured gravitational redshift z = 0.35 for the X-ray burst source in the low-mass X-ray binary EXO 07482−676 (Cottam et al. 2002) and |
| In the text | |
 |
Fig. 8 Neutron star binding energy versus the stellar gravitational mass (left panel) and fractional binding energy Ebind/ (Mc2) = (MB−M) /M as a function of the surface gravitational redshift zsurf (right panel) for the two considered EOS models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


