| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 9 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201731461 | |
| Published online | 09 January 2018 | |
COSMOGRAIL: the COSmological MOnitoring of GRAvItational Lenses
XVI. Time delays for the quadruply imaged quasar DES J0408−5354 with high-cadence photometric monitoring⋆
1 Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: vivien.bonvin@epfl.ch
2 Fermi National Accelerator Laboratory, PO Box 500, Batavia, IL 60510, USA
3 Department of Physics, University of California, Davis, CA 95616, USA
4 Kavli Institute for Cosmological Physics, University of Chicago, Chicago, IL 60637, USA
5 Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94035, USA
6 Max Planck Institute for Astrophysics, Karl-Schwarzschild-Strasse 1, 85740 Garching, Germany
7 Physik-Department, Technische Universität München, James-Franck-Straße 1, 85748 Garching, Germany
8 Institute of Astronomy and Astrophysics, Academia Sinica, PO Box 23-141, 10617 Taipei, Taiwan, PR China
9 Department of Physics and Astronomy, University of California, Los Angeles, CA 90095, USA
10 Departamento de Ciencias Físicas, Universidad Andres Bello Fernandez Concha 700, Las Condes, Santiago, Chile
11 Millennium Institute of Astrophysics, Santiago, Chile
12 Instituto de Física y Astronomía, Universidad de Valparaíso, Avda. Gran Bretaña 1111, Playa Ancha, 2360102 Valparaíso, Chile
13 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
14 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei Munchen, Germany
15 Centro de Astroingeniería, Facultad de Física, Pontificia Universidad Católica deChile, Av. Vicuña Mackenna 4860, Macul 7820436, Santiago, Chile
16 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
17 Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, Casilla 603, La Serena, Chile
18 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
19 Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
20 LSST, 933 North Cherry Avenue, Tucson, AZ 85721, USA
21 CNRS, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
22 Department of Physics & Astronomy, University College London, Gower Street, London, WC1E 6BT, UK
23 Sorbonne Universités, UPMC Univ. Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
24 Kavli Institute for Particle Astrophysics & Cosmology, PO Box 2450, Stanford University, Stanford, CA 94305, USA
25 SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
26 Laboratório Interinstitucional de e-Astronomia – LIneA, Rua Gal. José Cristino 77, Rio de Janeiro, RJ – 20921-400, Brazil
27 Observatório Nacional, Rua Gal. José Cristino 77, Rio de Janeiro, RJ – 20921-400, Brazil
28 Department of Astronomy, University of Illinois, 1002 W. Green Street, Urbana, IL 61801, USA
29 National Center for Supercomputing Applications, 1205 West Clark St., Urbana, IL 61801, USA
30 Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, 08193 Bellaterra (Barcelona), Spain
31 Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA 19104, USA
32 George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, and Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843, USA
33 Department of Physics, IIT Hyderabad, Kandi, Telangana 502285, India
34 Institut de Ciències de l’Espai, IEEC-CSIC, Campus UAB, Carrer de Can Magrans, s/n, 08193 Bellaterra, Barcelona, Spain
35 Instituto de Fisica Teorica UAM/CSIC, Universidad Autonoma de Madrid, 28049 Madrid, Spain
36 Department of Astronomy, University of California, Berkeley, 501 Campbell Hall, Berkeley, CA 94720, USA
37 Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
38 Center for Cosmology and Astro-Particle Physics, The Ohio State University, Columbus, OH 43210, USA
39 Department of Physics, The Ohio State University, Columbus, OH 43210, USA
40 Astronomy Department, University of Washington, Box 351580, Seattle, WA 98195, USA
41 Australian Astronomical Observatory, North Ryde, NSW 2113, Australia
42 Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA
43 Departamento de Física Matemática, Instituto de Física, Universidade de São Paulo, CP 66318, São Paulo, SP, 05314-970, Brazil
44 Institució Catalana de Recerca i Estudis Avançats, 08010 Barcelona, Spain
45 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Dr., Pasadena, CA 91109, USA
46 Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), 28040 Madrid, Spain
47 Department of Physics, University of Michigan, Ann Arbor, MI 48109, USA
48 School of Physics and Astronomy, University of Southampton, Southampton, SO17 1BJ, UK
49 Instituto de Física Gleb Wataghin, Universidade Estadual de Campinas, 13083-859 Campinas, SP, Brazil
50 Computer Science and Mathematics Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
Received: 28 June 2017
Accepted: 5 October 2017
We present time-delay measurements for the new quadruple imaged quasar DES J0408−5354, the first quadruple imaged quasar found in the Dark Energy Survey (DES). Our result is made possible by implementing a new observational strategy using almost daily observations with the MPIA 2.2 m telescope at La Silla observatory and deep exposures reaching a signal-to-noise ratio of about 1000 per quasar image. This data qualityallows us to catch small photometric variations (a few mmag rms) of the quasar, acting on temporal scales much shorter than microlensing, and hence making the time delay measurement very robust against microlensing. In only seven months we very accurately measured one of the time delays in DES J0408−5354: Δt(AB) = −112.1 ± 2.1 days (1.8%) using only the MPIA 2.2 m data. In combination with data taken with the 1.2 m Euler Swiss telescope, we also measured two delays involving the D component of the system Δt(AD) = −155.5 ± 12.8 days (8.2%) and Δt(BD) = −42.4 ± 17.6 days (41%), where all the error bars include systematics. Turning these time delays into cosmological constraints will require deep Hubble Space Telescope (HST) imaging or ground-based adaptive optics (AO), and information on the velocity field of the lensing galaxy.
Key words: methods: data analysis / gravitational lensing: strong / cosmological parameters
Lightcurves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/609/A71
© ESO, 2018
1. Introduction
Accurate and precise measurements of the time delay(s) between multiple images of gravitationally lensed quasars offer an independent way of constraining cosmology. The method is simple and is mostly sensitive to H0 with weak dependence on other cosmological parameters (Refsdal 1964). For this reason, the time-delay method has the potential to alleviate the degeneracies between cosmological parameters other than H0. In addition, it provides helpful input to resolve the tension between H0 as measured by Planck assuming a flat Lambda cold dark matter (ΛCDM) model (Planck Collaboration XIII 2016) and the local distance ladder, i.e. Cepheid stars (Freedman 2017; Freedman et al. 2001) and type Ia supernovae (e.g. Riess et al. 2016). Quasar time delays offer an opportunity to measure H0 completely independently of any of the above probes.
The method requires several ingredients: i) time-delay measurements; ii) models constraining the mass and light distribution in the lensing galaxy; and iii) an estimate of the contribution of objects along the line of sight to the overall potential well. The first point has been addressed by the COSMOGRAIL programme, which was started in 2004 and has delivered since then some of the best quality time-delay measurements (e.g. Bonvin et al. 2017; Rathna Kumar et al. 2013; Tewes et al. 2013b; Courbin et al. 2011; Vuissoz et al. 2008; Courbin et al. 2005; Eigenbrod et al. 2005). In parallel, detailed modelling techniques have been developed and used on deep Hubble Space Telescope (HST) images in combination with spectroscopic data providing crucial constraints on the dynamics of the lensing galaxy (Treu & Koopmans 2002; Suyu et al. 2006, 2009). Such models, in combination with an estimate of the overall mass along the line of sight (e.g. Hilbert et al. 2009; McCully et al. 2017, 2014; Collett et al. 2013) allow one to measure the time-delay distance and consequently the Hubble parameter, H0 (e.g. Suyu et al. 2010).
In order to perform precise cosmological measurement with strongly lensed quasars, these three ingredients must be accurately constrained. This has become possible only recently with the joint efforts of the COSMOGRAIL (e.g. Courbin et al. 2005) and H0LiCOW programmes (H0 Lenses in COSMOGRAIL’s Wellspring; Suyu et al. 2017), focussing on five well-selected bright lensed quasars. Recent results can be found in Bonvin et al. (2017), Wong et al. (2017), Rusu et al. (2017), Sluse et al. (2016) who infer 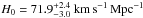 from three of the H0LiCOW lenses in a flat ΛCDM Universe.
from three of the H0LiCOW lenses in a flat ΛCDM Universe.
The H0LiCOW sample currently under study includes five lenses with an expected H0 measurement to <3.5% including systematics (Suyu et al. 2017). Going beyond this requires mass production of time delays. With 55 new time delays and dynamical measurements for the lensing galaxy, Jee et al. (2015) estimated that H0 can be measured to close to 1%. An independent study by Shajib, Agnello & Treu (in prep.) has shown that with resolved kinematics of the lens (e.g. with JWST or ground-based adaptive optics; AO) 1% accuracy on H0 can be reached with 40 lenses. This requires the discovery of new lenses, which is underway in the Dark Energy Survey (DES) (Ostrovski et al. 2017; Lin et al. 2017; Agnello et al. 2015), deep spectroscopy, characterisation of the line-of-sight matter distribution, and measurement of the time delays to a few percents for each individual system. The latter is the goal of the present work.
Because the slow intrinsic variations of the quasar occur roughly at the same timescale as the extrinsic variations (i.e. microlensing), measuring time delays requires years of monitoring. As the future of time delay cosmography resides in the measurement of several tens of new time delays, each time delay must be measured shortly after the start of the monitoring campaign, i.e. much faster than the typical 10 yrs it takes with current lens monitoring data. Current lens monitoring campaigns, including COSMOGRAIL, use 1 m class telescopes with a monitoring cadence of about 1 epoch per 3–4 days. The typical photometric accuracy with such data is limited to about 0.01 mag rms for many targets, hence allowing us to catch only the most prominent features of the quasar variations. It is difficult, and sometimes impossible, to sufficiently disentangle these features from extrinsic variations related to microlensing unless very long light curves are available (e.g. Bonvin et al. 2016; Liao et al. 2015).
In the present work, we implement a new high-cadence and high signal-to-noise (high-S/N) lens monitoring programme, with the goal of measuring time delays in only one single observing season. With on average one observing point per day and a S/N of the order of 1000 per quasar component, we can now catch much faster variability in the intrinsic light curve of the quasar (e.g. Mosquera & Kochanek 2011). In almost all cases, these features on timescales of a few days to a few weeks are more than an order of magnitude faster than the extrinsic variations. This difference in signal frequencies makes it possible to disentangle much better between extrinsic and intrinsic quasar variations. As the small and fast quasar variations are frequent (see e.g. Kepler data for AGNs in Mushotzky et al. 2011), only a short monitoring period is required to measure time delays, i.e. catching significant quasar variations is guaranteed in a one-year period provided high-S/N and high-cadence data are available. This achieved with the MPIA 2.2 m telescope and the Wide Field Imager (WFI) at ESO La Silla Observatory daily, through a dedicated monitoring programme.
We present here our first time delay measurement obtained with the MPIA 2.2 m telescope for the quadruply imaged quasar DES J0408−5354, at zq = 2.375. DES J0408−5354 was identified as a quadruple imaged quasar by Lin et al. (2017). The lensing galaxy has a redshift of zl = 0.597, measured by (Lin et al. 2017) using the Gemini-South telescope. Agnello et al. (2017) provide simple models for DES J0408−5354 using a deep image of the lens obtained from WFI data and predict time delays for a ΛCDM cosmology and different mass distributions including potential companions to the lensing galaxy, which influence the time-delay predictions.
 |
Fig. 1 Part of the field of view around DES J0408−5354 as seen with the 2.2 m MPIA/ESO telescope at La Silla observatory. The image is a stack of 150 frames totaling 25 h of exposure. The 6 PSF stars used to obtain the photometric light curves with deconvolution photometry are indicated in red. The 6 stars used for the frame-to-frame calibration of the relative photometry are indicated in green. The inset shows a 10′′ zoom on DES J0408−5354 and is extracted from a single 640 s exposure with 0.6′′ seeing with the same labelling for the quasar images as in Fig. 1 of Lin et al. (2017). Image C is blended with a foreground lensing galaxy labelled G2 in Agnello et al. (2017) and Lin et al. (2017). |
2. Observations and photometry
The observational material for the present time-delay measurement consists of almost daily imaging data with the MPIA 2.2 m telescope and of bi-weekly imaging with the 1.2 m Euler Swiss telescope, both at ESO La Silla.
We started the observations on 1 October 2016 with the MPIA 2.2 m telescope at ESO La Silla to monitor DES J0408−5354 through the Rc filter. The WFI instrument, mounted in the 2.2 m telescope, has a total field of view of 36′× 36′, covered by eight CCDs with a pixel size of 0.2′′. For our monitoring purpose we use only one chip to ensure a stable night-to-night calibration. This chip has a field of view of 9′× 18′. Part of this chip is shown in Fig. 1.
The WFI was used almost daily until 8 April 2017, i.e. over a total of seven months of visibility of the object, except for 14 consecutive nights between 10 December 2016 and 24 December 2016 due to technical problems and for one week in January 2017 due to an extended period of poor weather. For each observing epoch, four dithered exposures of 640 s each were taken in the Rc filter. A total of 459 images were taken in seven months, of which 398 images have adequate seeing and point spread function (PSF) quality. More precisely, we removed the images with 1- a seeing above 3.0′′, 2- a mean ellipticity above e = 0.4, 3- a sky level about 10 000 electrons, and 4- obvious failure in the PSF modelling. On average, the resulting temporal sampling was one observing point every 1.96 day. The median seeing over this period was 1.1′′. Thanks to flexible scheduling of the observations at the telescope it was possible to observe DES J0408−5354 most of the time at low airmass. The seeing and airmass distributions of the observations are given in Fig. 2.
The high cadence and high S/N (2–3 mmag rms per quasar image) obtained with the 2.2 m telescope allow us to catch much smaller and much shorter photometric variations than the COSMOGRAIL observations obtained with smaller 1 m telescopes. We can typically see signals as small as a few mmags and as short as a 15–20 days, which is crucial to avoid contamination by extrinsic variations, as illustrated in Sect. 3.
The data from the 1.2 m Euler telescope were obtained in the R band with the ECAM instrument from July 2016 to April 2017. The pixel size of the camera is 0.238′′, providing a field of view of 14′ on a side. We took, for each of the 45 observing epochs six exposures of 360 s each, i.e. 36 min in total. The mean temporal sampling for the Euler observations is of only one point every 5 days, but the Euler observations started about 100 days before the WFI observations, hence extending the length of the light curves.
 |
Fig. 2 Seeing and airmass distributions for the 7 months of observations of DES J0408−5354 with the WFI instrument on the MPIA 2.2 m telescope. |
The data reduction procedure applied to the images follows the standard COSMOGRAIL pipeline, as applied to the data obtained with the 1.2 m Euler telescope for RX J1131−123 (Tewes et al. 2013b) and HE 0435−1223 (Bonvin et al. 2017). It includes subtraction of a bias level and flat-fielding using sky flats taken on average every few nights. Each frame is then sky-subtracted using the GLOBAL option in the Sextractor package (Bertin & Arnouts 1996). The data from the 2.2 m telescope have significant fringe patterns on bright nights. We therefore constructed a fringe image by iteratively sigma-clipping the four dithered exposure of each night and by taking the median. This image was then subtracted from the individual dithered exposures taken each night, which are subsequently registered to the same pixel grid.
We carried out the photometric measurements using the deconvolution photometry with the so-called MCS image deconvolution algorithm (Magain et al. 1998; Cantale et al. 2016). This algorithm first computes a deconvolution kernel from the images of stars. The kernel is chosen so that the PSF in the deconvolved images is a circular Gaussian function with a full width half maximum (FWHM) of 2 pixels. The pixel size in the deconvolved images is half that of the original data, i.e. the resolution in the resulting images is 0.2′′ for WFI and the pixel size is 0.1′′. We show the PSF stars and the reference stars used for the image-to-image flux calibration in Fig. 1.
The MCS algorithm deconvolves all the registered images simultaneously, i.e. each one with its own PSF. However, all images share the same deconvolved model, which is decomposed into a point-source channel (quasar images) and an extended-channel (lensing galaxy and faint quasar host galaxy). In this process, the position of the point sources is the same for all images and the extended channel, but the intensities of the point sources vary from image to image, hence leading to the photometric light curves. The latter are presented for the three brightest lensed images of DES J0408−5354 in Fig. 3, which shows the striking difference in depth and sampling between the 2.2 m data and the Euler data. Yet, the two data sets agree and complement each other well and exhibit fine structures in the light curves of A and B. The D component, however, has much shallower variations given the larger photometric error bars and will need further monitoring.
3. Time delay measurement
We used PyCS1, which is a toolbox containing several algorithms, to measure time delays from quasar light curves and account for the intrinsic variations (from the lensed source) and extrinsic variations (microlensing) in the data. The (public) algorithm was proposed by Tewes et al. (2013a) and tested on simulated data from the time delay challenge (Bonvin et al. 2016; Liao et al. 2015) with overall excellent performances.
3.1. Time delay measurement with PyCS
PyCS is the standard curve-shifting toolbox of the COSMOGRAIL project. We applied this technique to the WFI light curves and to the combination of Euler and WFI data. We did not attempt to measure a time delay using the Euler data on their own as they contain only 45 epochs over the duration of the observations. However, used in combination with the WFI images, the Euler data increase the time baseline with observations between July 2016 and October 2016.
We used the two best algorithms of the PyCS toolbox: the free-knot spline technique and regression difference technique (Tewes et al. 2013a). In the former, the intrinsic and extrinsic variations in the light curves are modelled explicitly as spline functions. In doing so, we give more flexibility to the spline representing the intrinsic variations of the quasar than to the spline representing extrinsic variations. This flexibility is varied through a parameter η representing the initial knot spacing in the splines (Tewes et al. 2013a). The value of η is optimized using simulated light curves that mimic the properties of the data. These simulated light curves are produced using the same toolbox as in Sect. 3.2. However, our results depend little on the exact value for η and, for a fixed choice of η, the position of the knots can change during the fit. This avoids many of the traditional “oscillation” problems with spline fit using fixed (and possibly badly placed) knots. To fit the present data, we used splines with only three knots to represent microlensing. We further imposed that the central knot stays centred on the temporal axis between the light curve extrema during the minimization process. Adding knots to the microlensing splines does not significantly change the results.
In the regression difference technique, we minimized the variability of the difference between Gaussian-process regressions performed on each light curve individually. This second method has no explicitly parametrized form for the extrinsic variability, which makes the two techniques fundamentally different and independent. We applied the two methods to our data in the same way as in Bonvin et al. (2017) and Tewes et al. (2013a), who also gave the procedure to derive the random and systematic errors from simulated light curves. As the results may depend on some of the key parameters that characterize each method, we performed robustness checks identical to those in Bonvin et al. (2017); we used PyCS with a large range of method parameters, namely the number of knots of the spline technique and covariance function of the regression difference technique (see Tewes et al. 2013a, for a full description of these parameters). We do not find significant differences in the mean time-delay values among the results obtained for the various tests, although the precision might vary.
 |
Fig. 3 Top: light curves for DES J0408−5354 obtained in the Rc filter with the MPIA 2.2 m telescope and the WFI instrument. The points obtained with the 1.2 m Euler telescope are also shown with larger and thicker symbols. To guide the eye, the structure constraining the most the AB time delay is indicated between black solid lines. Bottom left: spline-fitting of the intrinsic quasar variations (with an initial knot step of η = 15 days) and time delay determination when neglecting extrinsic variation due to microlensing. The time delay values do not depend much on the choice of this η parameter, which is only an initial value optimized during the fit. Bottom right: same as bottom left but now including extrinsic variations (colour curves). For more clarity the lower S/N Euler data are only shown in the top panel. Our light curves are available at the CDS and on cosmograil.org. |
 |
Fig. 4 Time delay measurements for the 3 brightest quasar images of DES J0408−5354 using the data shown in Fig. 3. The time delay measurements are carried out in 3 different ways. Results using the WFI data with the spline fitting method are shown in blue and those in purple show the regression difference method. Results for the combined WFI+Euler data set using the spline fitting method are shown in green. For comparison we also show, in black, the spline fitting result when using only the high-cadence WFI data and no model for the microlensing extrinsic variations. A negative Δt(AB) means that the signal from image A reaches the observer’s plane before B. |
 |
Fig. 5 Error estimates for the time-delay measurements performed on 1000 simulated light curves. The colour code is the same as in Fig. 4. The x-axis of each panel shows the values for the true time delay in the mock light curves. For each time-delay value, the random error bars are shown as thin lines and systematic errors as thick lines. The values for the time delays, as measured on the real data correspond to the centre of each panel. |
The time-delay measurements are summarized in Fig. 4 for different data sets, i.e. with and without the Euler data. The longer-baseline Euler data improve the time-delay estimates involving the D image when used in combination with the 2.2 m WFI data. The latter have strong constraining power as high-frequency structures are captured in the curves, i.e. mostly the A and B components that display two strong features, including two inflection points in the case of B. For the much fainter D image, the situation is more complex as it displays only one shallow inflection point and no clear feature that can be matched to the other light curves.
3.2. Error estimates
In PyCS, the error estimates are carried out by running the curve-shifting techniques on mock light curves created from a generative model (see Tewes et al. 2013a). In these mocks, the intrinsic and extrinsic variations of the quasar are the same as that inferred from the real data and the temporal sampling and photometric errors. What changes from mock to mock are the correlated extrinsic variability (whose statistical properties mimic the observations), photometric noise, true time delays, and value of the simulated data points. The mock curves are drawn so that they have the same “time-delay constraining power” as the original data, i.e. the properties of the residuals after fitting the mock with a spline are statistically the same as in the real data.
We carried out simulations for a broad range of true input time delays around the measured value. This error analysis is summarized in Fig. 5 which, for each of the true time delay tested, provides random and systematic errors. The final error for the delay is taken as the worst random error over all the bins, combined in quadrature with the worst systematic error. Obviously, the size of the bins and the range of true time delays explored when drawing the simulated light curves can have an impact on the final error. Part of the robustness checks we performed are intended to ensure that we do not overestimate or underestimate the errors by choosing inappropriate bin sizes and ranges in true time delays. In the present case, our choice of possible true time delays ranges up to ±10 days from our initial estimation obtained by running our point estimator on the original data. Such a wide range encompasses our uncertainty regarding the time delays of DES J0408−5354 that have never been measured before, yet this uncertainty is also small enough to make sure that simulated light curves (especially A and D) are sufficiently overlapping. We can note from the bottom panels of Fig. 5, that the large systematic errors of the spline optimizer (in blue and green) come mostly from the simulations with extreme values of true delays.
For the A and B light curves, which benefit from high-S/N data, the time delay is very accurate, whatever true delay is tested. This illustrates the importance of catching as many faint and short-duration structures in the light curves and the impact of high-cadence and high-S/N data. As a robustness test, we carry out the time-delay measurements without modelling explicitly extrinsic variations when using the spline technique. These results are indicated in black in Figs. 4 and 5 and show that the value of the time delays do not depend much on the extrinsic variations for the AB delay. Future observations of other objects will show if this is specific to DES J0408−5354 or a more general behaviour of the results with high-cadence and high-S/N light curves. Our final time delay value for AB is Δt(AB) = −112.1 ± 2.1 days (1.8%), as obtained with the free-knot spline method using only the WFI data and extrinsic variations explicitly included. We make this choice because the time-delay measurement is precisely determined mostly thanks to the finely modelled peak in the WFI light curves (around mhjd = 57710 in A and 57820 in B). This peak is only crudely visible in the Euler data. Thus, adding the latter data set in the present case would only increase the overall noise. Also, including extrinsic variations explicitly only slightly shifts the result while keeping the precision unchanged, as shown in Fig. 4. We chose nevertheless to include extrinsic variations explicitly since they are physically motivated and since the data speak in favour of such variations: microlensing and the subsequent extrinsic variations are present at some level in almost every lensed quasar known to date (Mosquera & Kochanek 2011).
In contrast to AB, the precision on the AD and BD delays depends on how extrinsic variations are modelled. Because of the lack of fine and sharp structures in the D light curve and with only one shallow inflection point, the intrinsic and extrinsic variations are almost fully degenerate. We chose as our final results for these two delays the values obtained with the free-knot spline techniques for the combined Euler and WFI data sets. These times delay estimates are Δt(AD) = −155.5 ± 12.8 days (8.2%) and Δt(BD) = −42.4 ± 17.6 days (41%).
Finally, it is worth noting that the delays obtained with the regression difference technique applied only to WFI are consistent with those from the free-knot spline techniques and the AD and BD delays are even more precisely measured. We however prefer to stick to the results of the free-knot splines since they are much more precise for AB, which is currently – and by far – the most constraining delay to be used in future modelling of this lensed system. We also explicitly avoid cherry-picking the best technique per delay, i.e. in the present case the free-knot splines for AB and the regression difference for AD and BD. Such an ad hoc choice may introduce a bias that is difficult to quantify. Finally, the free-knot splines technique is that giving the smallest systematics according to Fig. 5.
3.3. Comparison with simple models
Simple lens models are provided by Agnello et al. (2017) and are useful to design the monitoring strategy. They show that DES J0408−5354 is challenging in terms of measuring time delays, as the longest time delay is half the visibility window of the object. Even under these difficult conditions, the MPIA 2.2 m data allow us to measure it to 1.8% accuracy and precision, by unveiling short and small photometric variations of the quasar images A and B.
The time delay we find for AB is in marginal agreement with the predictions of Agnello et al. (2017) but a detailed comparison between our measurement and the model predictions for DES J0408−5354 would be hazardous at this stage. Indeed, two values of the delay are possible as quasar image C has a possible companion in its vicinity. The predicted delays are Δt(AB) ~ −85 days for a model with a companion and Δt(AB) ~ −125 days for a model without a companion galaxy, which introduces degeneracies in the models that cannot be lifted with the current imaging data, which only provide the relative positions of the quasar images relative to the lensing galaxy. Until deep HST or ground-based AO images are available it will impossible to discriminate between models with or without this companion object.
Independent of the characterization of the companion, the minimum information required to constrain lens models, even with few degree of freedom, are 1- sharp images of the lensed quasar host galaxy and 2- dynamics of the main lensing galaxy, as is used for all objects in the H0LiCOW programme (Suyu et al. 2017; Bonvin et al. 2017). Suyu et al. (2014) illustrate how a radially thick Einstein ring can lift most model degeneracies in combination with the central velocity dispersion of the lens. Acquisition of both HST images of the Einstein ring and spectra of the lens are under way.
4. Conclusions
We demonstrate a new observational strategy for measuring time delays in lensed quasars, using high-cadence and high signal-to-noise monitoring photometry. The data, obtained almost daily over seven months with the MPIA 2.2 m telescope at ESO La Silla, allow us to measure Δt(AB) = −112.1 ± 2.1 days (1.8%), Δt(AD) = −155.5 ± 12.8 days (8.2%) and Δt(BD) = −42.4 ± 17.6 days (41%), where the error bars include systematics due to residual extrinsic variations. For the AB time delay, the time-delay values depend little on the way extrinsic variations are modelled, hence indicating that the high-frequency signal in the light curves from the WFI instrument on the 2.2 m telescope is dominated by the intrinsic variations of the quasar, as expected. For the D component, however, we only report a tentative delay due to the lack of fast variations seen in the light curve of this faint lensed image.
With the current imaging data for DES J0408−5354 it is too early to compare in detail the model predictions for the time delays (Agnello et al. 2017) and our measurements. Imaging with the HST or with ground-based AO is mandatory before drawing any conclusions and before carrying out any cosmological inference with DES J0408−5354. Fortunately, the object has several bright stars in its immediate vicinity, making it an excellent prey for VLT and AO, for example with the MUSE integral field spectrograph, providing the required dynamical information on the lensing galaxy(ies). In the near-IR observations with the VLT and the Hawk-I imager and the GRAAL AO system would both allow us to measure the dynamics of the lens and probe the mass along the line of sight on a 7′× 7′ field of view.
With the many wide-field surveys taking place at the moment (DES, KiDS, CFIS, DECals, and HSC) and with LSST and Euclid coming in a fairly near future, the available number of lensed quasars will increase dramatically (e.g. Oguri & Marshall 2010). We show how daily and very high signal-to-noise observations during 1 single season can match and potentially surpass long-term monitoring carried out at a lower rate (e.g. weekly) over many years. This should be accounted for when planning synoptic surveys such as the LSST. Although the latter will definitely yield very high signal-to-noise images, the full benefit of monitoring data with a 8 m telescope will be much enhanced in combination with a daily cadence or very close to a daily cadence.
We currently have been monitoring four objects since October 2016 with the MPIA 2.2 m. From a preliminary analysis of these four targets, we anticipate that reliable (i.e. to a few percents) time delays will be measured for three of these targets. We show here our results for DES J0408−5354, for which the observing season is finished.
PyCS can be obtained from http://www.cosmograil.org
Acknowledgments
The authors would like to thank R. Gredel for his help in setting up the programme at the MPIA 2.2 m telescope. This work is supported by the Swiss National Science Foundation (SNSF). S. H. Suyu and D. C. Y. Chao thank the Max Planck Society for support through the Max Planck Research Group for SHS. T. Treu acknowledges support by the National Science Foundation through grant 1450141, by the Packard Foundation through a Packard Research Fellowship and by the UCLA Dean of Physical Sciences. K.Rojas is supported by Becas de Doctorado Nacional CONICYT 2017. T. Anguita and M. Chijani acknowledge support by proyecto FONDECYT 11130630 and by the Ministry for the Economy, Development, and Tourism’s Programa Inicativa Científica Milenio through grant IC 12009, awarded to The Millennium Institute of Astrophysics (MAS). M. Tewes acknowledges support from the DFG grant Hi 1495/2-1. J. Garcia-Bellido is supported by the Research Project FPA2015-68048 [MINECO-FEDER], and the Centro de Excelencia Severo Ochoa Program SEV-2012-0249. C. D. Fassnacht acknowledges support from the National Science Foundation grant AST-1312329 and from the UC Davis Physics Department and Dean of Math and Physical Sciences. Funding for the DES Projects has been provided by the US Department of Energy, the US National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical Astronomy Observatory, the University of Nottingham, The Ohio State University, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, Texas A&M University, and the OzDES Membership Consortium. The DES data management system is supported by the National Science Foundation under Grant Number AST-1138766. The DES participants from Spanish institutions are partially supported by MINECO under grants AYA2015-71825, ESP2015-88861, FPA2015-68048, SEV-2012-0234, SEV-2012-0249, and MDM-2015-0509, some of which include ERDF funds from the European Union. IFAE is partially funded by the CERCA programme of the Generalitat de Catalunya.
References
- Agnello, A., Treu, T., Ostrovski, F., et al. 2015, MNRAS, 454, 1260 [Google Scholar]
- Agnello, A., Lin, H., Buckley-Geer, L., et al. 2017, MNRAS, 472, 4038 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonvin, V., Tewes, M., Courbin, F., et al. 2016, A&A, 585, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonvin, V., Courbin, F., Suyu, S. H., et al. 2017, MNRAS, 465, 4914 [NASA ADS] [CrossRef] [Google Scholar]
- Cantale, N., Courbin, F., Tewes, M., Jablonka, P., & Meylan, G. 2016, A&A, 589, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collett, T. E., Marshall, P. J., Auger, M. W., et al. 2013, MNRAS, 432, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Courbin, F., Eigenbrod, A., Vuissoz, C., Meylan, G., & Magain, P. 2005, in Gravitational Lensing Impact on Cosmology, eds. Y. Mellier, & G. Meylan, IAU Symp., 225, 297 [Google Scholar]
- Courbin, F., Chantry, V., Revaz, Y., et al. 2011, A&A, 536, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eigenbrod, A., Courbin, F., Vuissoz, C., et al. 2005, A&A, 436, 25 [Google Scholar]
- Freedman, W. L. 2017, Nature Astron., 1, 0121 [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jee, I., Komatsu, E., & Suyu, S. H. 2015, J. Cosmology Astropart. Phys., 11, 033 [Google Scholar]
- Liao, K., Treu, T., Marshall, P., et al. 2015, ApJ, 800, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Buckley-Geer, E., Agnello, A., et al. 2017, ApJ, 838, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P., Courbin, F., & Sohy, S. 1998, ApJ, 494, 472 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Keeton, C. R., Wong, K. C., & Zabludoff, A. I. 2014, MNRAS, 443, 3631 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Keeton, C. R., Wong, K. C., & Zabludoff, A. I. 2017, ApJ, 836, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Mosquera, A. M., & Kochanek, C. S. 2011, ApJ, 738, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Mushotzky, R. F., Edelson, R., Baumgartner, W., & Gandhi, P. 2011, ApJ, 743, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
- Ostrovski, F., McMahon, R. G., Connolly, A. J., et al. 2017, MNRAS, 465, 4325 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathna Kumar, S., Tewes, M., Stalin, C. S., et al. 2013, A&A, 557, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Fassnacht, C. D., Sluse, D., et al. 2017, MNRAS, 467, 4220 [NASA ADS] [CrossRef] [Google Scholar]
- Sluse, D., Sonnenfeld, A., Rumbaugh, N., et al. 2016, MNRAS, 470, 4838 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Hobson, M. P., & Blandford, R. D. 2006, MNRAS, 371, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Marshall, P. J., Blandford, R. D., et al. 2009, ApJ, 691, 277 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Auger, M. W., et al. 2010, ApJ, 711, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
- Tewes, M., Courbin, F., & Meylan, G. 2013a, A&A, 553, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tewes, M., Courbin, F., Meylan, G., et al. 2013b, A&A, 556, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2002, MNRAS, 337, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Vuissoz, C., Courbin, F., Sluse, D., et al. 2008, A&A, 488, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wong, K. C., Suyu, S. H., Auger, M. W., et al. 2017, MNRAS, 465, 4895 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Part of the field of view around DES J0408−5354 as seen with the 2.2 m MPIA/ESO telescope at La Silla observatory. The image is a stack of 150 frames totaling 25 h of exposure. The 6 PSF stars used to obtain the photometric light curves with deconvolution photometry are indicated in red. The 6 stars used for the frame-to-frame calibration of the relative photometry are indicated in green. The inset shows a 10′′ zoom on DES J0408−5354 and is extracted from a single 640 s exposure with 0.6′′ seeing with the same labelling for the quasar images as in Fig. 1 of Lin et al. (2017). Image C is blended with a foreground lensing galaxy labelled G2 in Agnello et al. (2017) and Lin et al. (2017). |
| In the text | |
 |
Fig. 2 Seeing and airmass distributions for the 7 months of observations of DES J0408−5354 with the WFI instrument on the MPIA 2.2 m telescope. |
| In the text | |
 |
Fig. 3 Top: light curves for DES J0408−5354 obtained in the Rc filter with the MPIA 2.2 m telescope and the WFI instrument. The points obtained with the 1.2 m Euler telescope are also shown with larger and thicker symbols. To guide the eye, the structure constraining the most the AB time delay is indicated between black solid lines. Bottom left: spline-fitting of the intrinsic quasar variations (with an initial knot step of η = 15 days) and time delay determination when neglecting extrinsic variation due to microlensing. The time delay values do not depend much on the choice of this η parameter, which is only an initial value optimized during the fit. Bottom right: same as bottom left but now including extrinsic variations (colour curves). For more clarity the lower S/N Euler data are only shown in the top panel. Our light curves are available at the CDS and on cosmograil.org. |
| In the text | |
 |
Fig. 4 Time delay measurements for the 3 brightest quasar images of DES J0408−5354 using the data shown in Fig. 3. The time delay measurements are carried out in 3 different ways. Results using the WFI data with the spline fitting method are shown in blue and those in purple show the regression difference method. Results for the combined WFI+Euler data set using the spline fitting method are shown in green. For comparison we also show, in black, the spline fitting result when using only the high-cadence WFI data and no model for the microlensing extrinsic variations. A negative Δt(AB) means that the signal from image A reaches the observer’s plane before B. |
| In the text | |
 |
Fig. 5 Error estimates for the time-delay measurements performed on 1000 simulated light curves. The colour code is the same as in Fig. 4. The x-axis of each panel shows the values for the true time delay in the mock light curves. For each time-delay value, the random error bars are shown as thin lines and systematic errors as thick lines. The values for the time delays, as measured on the real data correspond to the centre of each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


