| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201730843 | |
| Published online | 05 February 2018 | |
The Carnegie Supernova Project I
Methods to estimate host-galaxy reddening of stripped-envelope supernovae ⋆
1 Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: max@phys.au.dk
2 The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
3 Observatories of the Carnegie Institution for Science, 813 Santa Barbara St., Pasadena, CA 91101, USA
4 Carnegie Observatories, Las Campanas Observatory, Casilla 601, La Serena, Chile
5 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque S/N, B1900 FWA La Plata, Argentina
6 Instituto de Astrofísica de La Plata (IALP), CONICET, Argentina
7 Kavli Institute for the Physics and Mathematics of the Universe, Todai Institutes for Advanced Study, University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8583, Japan
8 Department of Physics, Florida State University, 77 Chieftain Way, Tallahassee, FL 32306, USA
9 Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot 7610001, Israel
10 George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843, USA
Received: 22 March 2017
Accepted: 31 July 2017
We aim to improve upon contemporary methods to estimate host-galaxy reddening of stripped-envelope (SE) supernovae (SNe). To this end the Carnegie Supernova Project (CSP-I) SE SN photometry data release, consisting of nearly three dozen objects, is used to identify a minimally reddened sub-sample for each traditionally defined spectroscopic sub-type (i.e., SNe IIb, SNe Ib, SNe Ic). Inspection of the optical and near-infrared (NIR) colors and color evolution of the minimally reddened sub-samples reveals a high degree of homogeneity, particularly between 0 d to +20 d relative to B-band maximum. This motivated the construction of intrinsic color-curve templates, which when compared to the colors of reddened SE SNe, yields an entire suite of optical and NIR color excess measurements. Comparison of optical/optical vs. optical/NIR color excess measurements indicates the majority of the CSP-I SE SNe suffer relatively low amounts of reddening (i.e., E(B−V)host< 0.20 mag) and we find evidence for different RVhost values among different SE SN. Fitting the color excess measurements of the seven most reddened (i.e., E(B−V)host> 0.20 mag) objects with the Fitzpatrick (1999, PASP, 111, 63) reddening law model provides robust estimates of the host visual-extinction AVhost and RVhost. In the case of the SE SNe with relatively low amounts of reddening, a preferred value of RVhost is adopted for each sub-type, resulting in estimates of AVhost through Fitzpatrick (1999) reddening law model fits to the observed color excess measurements. Our analysis suggests SE SNe reside in galaxies characterized by a range of dust properties. We also find evidence that SNe Ic are more likely to occur in regions characterized by larger RVhost values compared to SNe IIb/Ib and they also tend to suffer more extinction. The later finding is consistent with work in the literature suggesting SNe Ic tend to occur in regions of on-going star formation.
Key words: supernovae: general
© ESO, 2018
1. Introduction
Stripped-envelope (SE) core-collapse (CC) supernovae (SNe) mark the terminal endpoint in the lives of massive stars that have shed their hydrogen (Type IIb/Ib) and possibly helium (Type Ic) layers over their evolutionary lifetimes. The majority of mass loss for single massive stars is due to line-driven winds, while for massive stars in binary systems the majority of mass loss is likely due to mass transfer to the companion via Roche lobe overflow and/or through common envelope evolution. Recent studies of samples of SE SNe (Drout et al. 2011; Cano 2013; Taddia et al. 2015; Lyman et al. 2016; Prentice et al. 2016) indicate Type IIb/Ib/Ic exhibit a range of 56Ni mass (MNi) and explosion energy (EK), while ejecta mass (Mej) estimates are found to span a more narrow range. For example, Lyman et al. (2016) found from an extended sample of SE SNe that key explosion parameters range as: ⟨ MNi ⟩ = 0.14−0.29 M⊙, ⟨ Mej ⟩ = 2.6−3.9 M⊙ and ⟨ EK ⟩ = (2.7−5.2) × 1051 erg. Only the more extreme SNe Ic-BL (broad-line) exhibit significantly higher values of EK and MNi.
The low ejecta masses typically inferred for the current samples of SE SNe, along with the direct progenitor detection for a handful of events (e.g., SN 1993J, SN 2008ax, SN 2011dh, SN 2013df, iPTF13bvn, see Smartt 2015, and references therein) and the rates of the various sub-types (Smith et al. 2011), suggest their progenitors are linked to binary star systems (see Yoon 2015, for a review). However, single massive stars may account for the brightest and most energetic SE SNe, including those associated with long-duration gamma-ray bursts and some superluminous supernovae. To date no progenitor detections exist of any SN Ic.
An important requirement to accurately estimate the luminosity and explosion parameters of any type of SN is an estimate of its reddening due to dust along the line-of-sight to the observer. Assuming the extinction of any given SN can be defined by a dust law that has a wavelength dependence, the level of reddening experienced by two passbands will differ. Reddening is typically parameterized by the E(B−V) color excess and the absorption coefficient, RV. The absorption coefficient dictates the total-to-selective absorption and is defined as RV = AV/E(B−V). In this parameterization E(B−V) sets the optical depth of the intervening dust and gas and RV is dependent on the average dust grain size (Weingarter & Draine 2001). In practice large values of RV lead to shallow extinction curves and are associated with larger than normal size dust grains, while low values of RV lead to steep extinction curves due to smaller than normal size dust grains.
Reddening is typically split between two components. The first component accounts for reddening due to dust within the Milky Way (defined by 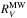 and E(B−V)MW) and the second component accounts for reddening external to the Milky Way (defined by
and E(B−V)MW) and the second component accounts for reddening external to the Milky Way (defined by  and E(B−V)host). Reddening along any particular line-of-sight in the Milky Way can be approximately corrected for using the reddening maps of Schlafly & Finkbeiner (2011) and Schlafly et al. (2016). However, accounting for reddening external to our own galaxy is significantly more challenging. In principle, light traveling from an extragalactic source may be reddened by dust located in its immediate vicinity, dust located in the host galaxy of the source, and potentially by dust encountered within the intergalactic medium. Typically the combined effect of reddening due to dust associated with these locations is lumped together and labeled as E(B−V)host. In principle, this could lead to potential problems as dust at any of these locations could have different properties, leading to significantly different values of RV and hence various levels of reddening. Indeed even in the MW the dust in the bulge shows significant variations of
and E(B−V)host). Reddening along any particular line-of-sight in the Milky Way can be approximately corrected for using the reddening maps of Schlafly & Finkbeiner (2011) and Schlafly et al. (2016). However, accounting for reddening external to our own galaxy is significantly more challenging. In principle, light traveling from an extragalactic source may be reddened by dust located in its immediate vicinity, dust located in the host galaxy of the source, and potentially by dust encountered within the intergalactic medium. Typically the combined effect of reddening due to dust associated with these locations is lumped together and labeled as E(B−V)host. In principle, this could lead to potential problems as dust at any of these locations could have different properties, leading to significantly different values of RV and hence various levels of reddening. Indeed even in the MW the dust in the bulge shows significant variations of 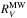 (Nataf et al. 2016).
(Nataf et al. 2016).
Efforts to devise robust methods to estimate 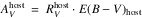 for SE SNe have largely been hampered by a lack of well-observed and homogeneous samples, and as a result, the inability to identify well-defined intrinsic SN colors. Typically, host extinction values of SE SNe are inferred from empirically-derived relations between the measured equivalent width of Na i D (hereafter EWNa i D) and E(B−V)host, and assuming a typical Galactic reddening law characterized by RV = 3.1. These relations often rely on calibrations determined from observations within the Milky Way (e.g., Munari & Zwitter 1997; Poznanski et al. 2012) and their use to determine reddening in the hosts of extragalactic SNe is suspect as dust properties are known to vary among galaxies (Poznanski et al. 2011). Indeed, these relations are associated with significant scatter, providing extinction values with uncertainties of ~68% of the inferred value of AV (Phillips et al. 2013). When combined with extinction estimates computed from Balmer decrement measurements of the immediate environment of a SN (cf. Xiao et al. 2012) and/or other less direct indicators, such as the position within the respective host galaxy and/or the SN peak colors, one can arrive at an estimate of
for SE SNe have largely been hampered by a lack of well-observed and homogeneous samples, and as a result, the inability to identify well-defined intrinsic SN colors. Typically, host extinction values of SE SNe are inferred from empirically-derived relations between the measured equivalent width of Na i D (hereafter EWNa i D) and E(B−V)host, and assuming a typical Galactic reddening law characterized by RV = 3.1. These relations often rely on calibrations determined from observations within the Milky Way (e.g., Munari & Zwitter 1997; Poznanski et al. 2012) and their use to determine reddening in the hosts of extragalactic SNe is suspect as dust properties are known to vary among galaxies (Poznanski et al. 2011). Indeed, these relations are associated with significant scatter, providing extinction values with uncertainties of ~68% of the inferred value of AV (Phillips et al. 2013). When combined with extinction estimates computed from Balmer decrement measurements of the immediate environment of a SN (cf. Xiao et al. 2012) and/or other less direct indicators, such as the position within the respective host galaxy and/or the SN peak colors, one can arrive at an estimate of  , but with significant uncertainty.
, but with significant uncertainty.
Drout et al. (2011) constructed an intrinsic V−R color curve template from a small sample of SE SNe. With this template they were then able to define an intrinsic V−R color at +10 d relative to V-band maximum with a scatter of only a few tenths of a magnitude. This intrinsic color allows for the inference of the E(V−R)host color excess for reddened objects, and when adopting a reddening law, the host extinction. Unfortunately the photometry of the objects in the Drout et al. sample was computed from images obtained with various telescopes, which is known to lead to considerable calibration issues (e.g. Stritzinger et al. 2002). They also adopted host extinction values for some of the literature-based objects that were estimated from different Na i D vs. E(B−V)host relations. A similar approach was employed by Taddia et al. (2015) to estimate the host-galaxy reddening for a sample of SE SNe, but in this case a g−r intrinsic color template was constructed from photometry of a number of objects from the literature.
Ideally, one should identify intrinsic SE SN colors from photometry obtained on a single, stable and well-understood photometric system, in addition to expanding the analysis to include various color combinations extending over a range of wavelength in order to facilitate a robust estimate of both  and
and  .
.
In this paper we build upon the work of Drout et al. and in doing so present methods to infer E(B−V)host,  , and in some instances, a preferred value of
, and in some instances, a preferred value of  for SE SNe. To realize these aims we make use of high-quality, multi-color light curves of over thirty SE SNe observed by the first phase of the Carnegie Supernova Project (CSP-I; Hamuy et al. 2006). The full CSP-I sample of SE SNe is presented in a companion paper (Stritzinger et al. 2018)1, and consists of optical (ugriBV) photometry of 34 objects, with a subset of 26 of these having at least some near-infrared (NIR, i.e. YJH) photometry. The CSP-I sample is ideal for the present purpose as it has been obtained on a well-understood photometric system (Stritzinger et al. 2011; Krisciunas et al., in prep.), and consists of photometry measured from high signal-to-noise images typically taken under excellent observing conditions. Furthermore, the CSP-I has put forth a considerable effort to define accurate local sequences of stars, calibrated relative to standard star fields observed over multiple photometric nights. Combined with host-galaxy template-image subtraction of each science image, our SN magnitudes have been measured differentially to the local sequence, yielding photometry with typical (statistical and systematics) uncertainties ranging between 0.01 to 0.03 mag. Analysis of the full the CSP-I photometric light curves and spectroscopy are presented in additional companion papers by Taddia et al. (2018) and Holmbo et al. (in prep.), respectively. From these works we adopt for each object (i) estimates of the epoch of maximum for each filtered light curve, (ii) K-corrections, and (iii) the spectral classification of each object.
for SE SNe. To realize these aims we make use of high-quality, multi-color light curves of over thirty SE SNe observed by the first phase of the Carnegie Supernova Project (CSP-I; Hamuy et al. 2006). The full CSP-I sample of SE SNe is presented in a companion paper (Stritzinger et al. 2018)1, and consists of optical (ugriBV) photometry of 34 objects, with a subset of 26 of these having at least some near-infrared (NIR, i.e. YJH) photometry. The CSP-I sample is ideal for the present purpose as it has been obtained on a well-understood photometric system (Stritzinger et al. 2011; Krisciunas et al., in prep.), and consists of photometry measured from high signal-to-noise images typically taken under excellent observing conditions. Furthermore, the CSP-I has put forth a considerable effort to define accurate local sequences of stars, calibrated relative to standard star fields observed over multiple photometric nights. Combined with host-galaxy template-image subtraction of each science image, our SN magnitudes have been measured differentially to the local sequence, yielding photometry with typical (statistical and systematics) uncertainties ranging between 0.01 to 0.03 mag. Analysis of the full the CSP-I photometric light curves and spectroscopy are presented in additional companion papers by Taddia et al. (2018) and Holmbo et al. (in prep.), respectively. From these works we adopt for each object (i) estimates of the epoch of maximum for each filtered light curve, (ii) K-corrections, and (iii) the spectral classification of each object.
In Sect. 2 we examine the optical and NIR colors of the CSP-I SE SN sample. This is followed by Sect. 3 where we define intrinsic color-curve templates for the different spectroscopic SE SN sub-types, i.e., Type IIb, Type Ib, and Type Ic. In Sect. 4 the intrinsic color templates are compared to the observed colors of reddened SE SNe to compute optical and NIR color excesses. These inferred color excesses are then used to derive host-extinction  for all reddened SE SNe in our sample and to constrain
for all reddened SE SNe in our sample and to constrain  for the most reddened objects. Finally in Sect. 5 the results obtained from various techniques and color-excess combinations are compared and discussed.
for the most reddened objects. Finally in Sect. 5 the results obtained from various techniques and color-excess combinations are compared and discussed.
2. Color curves of CSP stripped-envelope supernovae
Shown in each of the sub-panels of Fig. 1 are various optical and optical/NIR colors plotted vs. time relative to maximum light for the CSP-I SE SN sample. All colors have been corrected for Milky Way extinction using values listed in NED that originate from the Schlafly & Finkbeiner (2011) re-calibration of the Schlegel et al. (1998) extinction maps of the Milky Way, assuming a Fitzpatrick (1999, hereafter F99) reddening law characterized by 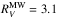 . The plotted SN colors also include time-dilation corrections and K corrections (see Taddia et al. 2018). To facilitate the construction of optical/NIR colors the NIR light curves were first interpolated as described by Taddia et al. (2018) and Stritzinger et al. (2018), and then evaluated on the epochs that optical observations were obtained.
. The plotted SN colors also include time-dilation corrections and K corrections (see Taddia et al. 2018). To facilitate the construction of optical/NIR colors the NIR light curves were first interpolated as described by Taddia et al. (2018) and Stritzinger et al. (2018), and then evaluated on the epochs that optical observations were obtained.
The overall shape of the color evolution for each color combination is quite similar. In the epochs preceding maximum brightness the colors of SE SNe are typically at their bluest values (e.g., Stritzinger et al. 2002; Gal-Yam et al. 2004). As the SNe evolve through maximum light and the temperature of their photosphere drops, the colors evolve towards the red almost linearly. The increase in colors observed in Fig. 1 during this time can exceed (over) two magnitudes for nearly all color combinations except for the V−i color curves which exhibit a color change of no more than 1.5 mag. Upon reaching their maximum red color between two to three weeks past maximum, the color curves make an abrupt turn and evolve back towards the blue, following a linear evolution with a shallow slope out to later times.
Turning to NIR colors, shown in Fig. 2 (from top to bottom) are the Y−J, Y−H, and J−H color curves for the CSP-I SE SN sample. Inspection of the Y−J and Y−H colors reveals an evolution similar to the optical and optical/NIR colors shown in Fig. 1, albeit with more complex behavior. At early phases the colors are blue, and as the SN evolve over the next fortnight their colors move towards the red. This is followed by a turnover to the blue that is significantly more prevalent than in the case of the optical and optical/NIR color curves. The J−H color curves, on the other hand, show blue SN colors at early times, which then evolve consistently towards the red over the entire duration of our photometric coverage.
 |
Fig. 1 Various optical and optical/NIR colors plotted as a function of days relative to maximum for the CSP SE SN sample. Symbols are color coded here and largely throughout this manuscript based on the different sub-types. Specifically, green, blue, red and magenta correspond to SNe IIb, Ib, Ic and Ic-BL, respectively. |
To obtain a continuous representation of the color evolution, the optical and optical/NIR color curves of each SN are fit with an analytic function. The color curves shown in Fig. 1 largely mimic the color evolution of normal SNe Ia. We therefore opted to fit each color curve with the same analytical function employed by Burns et al. (2014) to study the color properties of the CSP-I sample of SNe Ia. The Burns et al. (2014) analytical function is nearly linear with positive slope at early times, subsequently reaches a maximum value, and then makes a transitions back to a linear function with negative slope. The functional form is as follows: ![\begin{eqnarray} y(t)& = &\frac{\left(s_{0}+s_{1}\right)}{2}t+ \frac{\tau}{2}\left(s_{1}-s_{0}\right)\ln\left[\cosh\left(\frac{t-t_{1}}{\tau}\right)\right] \nonumber \\ & &+\,c+f(t,t_{0}), \label{eq:gifit} \end{eqnarray}](/articles/aa/full_html/2018/01/aa30843-17/aa30843-17-eq44.png) (1)where s0 is the initial slope, s1 is the final slope, τ is the length scale over which the transition occurs, and c sets the overall normalization of the function. The location of the color maximum is defined as tmax = t1 + τ tanh-1((s0 + s1)/(s0−s1)). In order to capture the color evolution at the earliest epochs, a second-order polynomial, f(t,t0), for t < t0 and equal to 0 for t > t0, completes Eq. (1). An example fit of Eq. (1) to the B−V color curve of the Type IIb SN 2006T is shown in Fig. 3. The function provides an objective representation of the color evolution, and the various fit parameters are well-determined for all optical and optical/NIR color combinations.
(1)where s0 is the initial slope, s1 is the final slope, τ is the length scale over which the transition occurs, and c sets the overall normalization of the function. The location of the color maximum is defined as tmax = t1 + τ tanh-1((s0 + s1)/(s0−s1)). In order to capture the color evolution at the earliest epochs, a second-order polynomial, f(t,t0), for t < t0 and equal to 0 for t > t0, completes Eq. (1). An example fit of Eq. (1) to the B−V color curve of the Type IIb SN 2006T is shown in Fig. 3. The function provides an objective representation of the color evolution, and the various fit parameters are well-determined for all optical and optical/NIR color combinations.
For some objects the photometric coverage is poor and does not cover the pre-peak phase or does not extend to the epoch(s) when maximum color is reached. In these cases the polynomial describing the early color evolution is removed from Eq. (1) before the observed colors are fit. In some other instances the color coverage only extends over several days, and when so, the colors are fit with a low-order polynomial.
3. Intrinsic color-curve templates and temperature constraints from hydrodynamical explosion models
3.1. Color-curve templates
The construction of intrinsic color-curve templates requires the identification of a sub-set of objects believed to suffer minimal to no reddening. To identify such objects we implemented selection criteria based on several factors. The two main criteria in identifying a minimally reddened SE SN is little to no Na i D absorption in the optical spectrum and relatively blue optical colors. If an object fulfilled these two criteria we then also sought confirmation by considering the location of the SN in its host galaxy and the host’s inclination. Objects that fulfilled the first two criteria and were located in the outskirts of their hosts and/or in minimally inclined galaxies are considered to suffer minimal to no reddening.
In principle, EWNa i D can provide an indication of the host-galaxy color excess (e.g., Munari & Zwitter 1997; Poznanski et al. 2012), although the relations used are associated with large scatter (Phillips et al. 2013). With this caveat in mind, plotted in Fig. 4 (left panel) is EWNa i D measured from near-maximum light spectra for each member of our sample (Holmbo et al., in prep.) vs. the B−V color at +10 d relative to Vmax (hereafter B−V+ 10 d). We report the EWNa i D values in Table 1 and note that no time variations in the measured EWNa i D values are found for objects with multiple epochs of spectra available. For objects with minimal to no EWNa i D a 3σ upper limit was computed based on the noise of the spectrum in the region of the Na i D line. These limits are plotted as arrows in Fig. 4. The two quantities exhibit a linear trend accompanied with scatter. The best fit linear function between the EWNa i D and B−V+ 10 d (including the upper limits) is given by 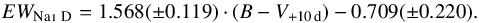 (2)The fact that those SE SNe with minimal to no EWNa i D are also the bluest objects within our sample is encouraging in the perspective of using SE SN colors to estimate host extinction. The small region in the lower left corner of Fig. 4 (left panel) defined by two dashed lines (B−V+ 10 d< 1.05 mag, EWNa i D< 0.4 Å) contains the objects characterized by both blue color and minimal to no EWNa i D. These objects can be used to construct intrinsic color-curve templates for each of the SE SN sub-types. Specifically, contained within the region are three objects for each spectroscopic sub-type and they correspond to the Type IIb SN 2005Q, SN 2008aq, and SN 2009Z; the Type Ib SN 2004ew (this SN is actually not observed at +10 d but its color at epochs earlier than +20 d are as blue as those of the other two unreddened SNe Ib), SN 2007Y, and SN 2007kj; and the Type Ic SN 2004fe, SN 2005em, and SN 2008hh. These SNe are also marked in the right-panel of Fig. 4, where plotted are the de-projected and normalized SN distances from their respective host galaxy centers vs. their respective host galaxy inclinations (cf. Taddia et al. 2018). For eight of the nine objects we have the necessary host-galaxy information to place them in the right panel of Fig. 4 (black circles). Each of these SNe appear relatively far from the center of their host, and none of their respective hosts are significantly inclined. This provides an additional measure of confidence these objects suffer minimal host reddening.
(2)The fact that those SE SNe with minimal to no EWNa i D are also the bluest objects within our sample is encouraging in the perspective of using SE SN colors to estimate host extinction. The small region in the lower left corner of Fig. 4 (left panel) defined by two dashed lines (B−V+ 10 d< 1.05 mag, EWNa i D< 0.4 Å) contains the objects characterized by both blue color and minimal to no EWNa i D. These objects can be used to construct intrinsic color-curve templates for each of the SE SN sub-types. Specifically, contained within the region are three objects for each spectroscopic sub-type and they correspond to the Type IIb SN 2005Q, SN 2008aq, and SN 2009Z; the Type Ib SN 2004ew (this SN is actually not observed at +10 d but its color at epochs earlier than +20 d are as blue as those of the other two unreddened SNe Ib), SN 2007Y, and SN 2007kj; and the Type Ic SN 2004fe, SN 2005em, and SN 2008hh. These SNe are also marked in the right-panel of Fig. 4, where plotted are the de-projected and normalized SN distances from their respective host galaxy centers vs. their respective host galaxy inclinations (cf. Taddia et al. 2018). For eight of the nine objects we have the necessary host-galaxy information to place them in the right panel of Fig. 4 (black circles). Each of these SNe appear relatively far from the center of their host, and none of their respective hosts are significantly inclined. This provides an additional measure of confidence these objects suffer minimal host reddening.
 |
Fig. 2 NIR colors for our sample of SE SNe. |
 |
Fig. 3 An example of the B−V color curve of SN 2006T fit with the analytical function described by Eq. (1). |
 |
Fig. 4 Left panel: Na i D EW versus the galactic-extinction corrected B−V at +10 d for the CSP-I sample of SE SNe. Arrows indicate upper limits. The best linear fit is shown by a dashed-dotted line. The area in the low-left corner contained within the borders of the square dashed box includes 9 objects (SN 2004aw is not reported because it was not observed at +10 d but its color within +20 d is as blue as that of the other 8 events) whose host extinction is considered to be negligible. Right panel: de-projected and normalized SN offset from the host center versus host galaxy inclination. The objects suspected of suffering low extinction are circled in black, and they never appear in both strongly inclined galaxies and at locations close to their host center (i.e., they always sit outside the box delimited by dashed lines in the figure). Symbols are color coded based on the different sub-types: green, blue, red and magenta for SNe IIb, Ib, Ic and Ic-BL, respectively. |
Equivalent width measurements of Na i D.
With a minimally-reddened subsample identified, intrinsic color-curve templates for each of three canonical SE SN subtypes were constructed. An example is provided in Fig. 5 where the B−V color curves of each of the minimally-reddened Type IIb, Type Ib and Type Ic SNe (hereafter SNe IIb, SNe Ib, SNe Ic) are plotted, along with the intrinsic B−V color templates derived from fitting simultaneously the colors of each SE SN sub-type with Eq. (1). Also shown is a comparison between each of the three template color curves. The templates are slightly different among the three sub-types, with the SNe Ic showing redder colors during the 20 days post maximum and bluer colors after the peak of B−V. This is most likely due to differences in the spectral features.
Plotted in Fig. 6 are visual-wavelength spectra for 8 of the 9 objects selected as representative of the intrinsic color evolution of the three sub-types. This includes post maximum spectra of the Type IIb SN 2005Q, SN 2008aq and SN 2009Z, the Type Ib SN 2007Y and SN 2007kj, and the Type Ic SN 2004fe, SN 2005em and SN 2008hh. The spectra of the various spectral types are broadly similar though clear differences between line strengths and line ratios are apparent between the different SN sub-types, particular around the location of Hα and the He i features, with the latter feature being absent in SNe Ic (see Holmbo et al., in prep.).
 |
Fig. 5 Intrinsic B−V color-curve templates for SNe IIb, Ib and Ic, as obtained from the best fit (solid lines) of Eq. (1) to the observed colors of nine minimally-reddened objects. Dashed lines are the associated 1σ uncertainties. The three templates are over-plotted in the bottom-right panel, showing that there are differences among the SE SN sub-types at all phases. The template uncertainties (highlighted in the bottom-right sub-panel) are lower in the first month after maximum, and then increase over time. |
 |
Fig. 6 Post V-band maximum visual-wavelength spectroscopy of eight of the nine minimally-reddened objects identified in the CSP-I SE SN sample. Overall the spectra are similar for each individual sub-type, through differences between line strengths and line ratios are apparent, particular at the location of Hα and the He i features which evolve considerably as a function of phase. |
We next proceed to construct intrinsic color-curve templates extending over various optical and optical/NIR color combinations for each SE SN sub-type. Plotted in Fig. 7 are the intrinsic color-curve templates for eight color combinations: u−V, B−V, g−V, V−r, V−i, V−Y, V−J, and V−H, along with their accompanying 1σ uncertainties computed by adding in quadrature the photometry errors. Color-curve templates were constructed by fitting Eq. (1) to the various color combinations of each of the SE SN subtypes. In general between 0 d and +20 d the different SE SN sub-types exhibit similar –though not identical– colors and temporal morphology, while at earlier and later epochs color differences are more pronounced. The average dispersion of our V−X color templates between 0 d and +20 d is in the range 0.02–0.15 mag for SNe Ib, 0.01–0.14 mag for SNe IIb, 0.02–0.09 mag for SNe Ic. The intrinsic V−X colors at +10 d since Vmax are given in Table 2. Drout et al. (2011) report a V−R color at +10 d since Vmax of 0.26 ± 0.06 mag, which is very close to our SN IIb value for V−r at that phase, and as well is consistent within the errors with the V−r colors of the SN Ib and SN Ic minimally reddened sub-samples at the same phase. The intrinsic V−X color templates for each subtype as well as the B−X, g−X and r−X templates (see Sect. 4.5) are provided in electronic format2.
Intrinsic values of 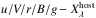 colors at +10 d since V/r/B/g maximum.
colors at +10 d since V/r/B/g maximum.
3.2. Minimal post maximum color dispersion
SE SNe potentially arise from multiple progenitors ranging from single to binary star systems and do exhibit a (modest) range of inferred key explosion parameters. Nevertheless, the low dispersion in colors around +10 d as demonstrated by Drout et al. (2011), Taddia et al. (2015), and the present CSP-I sample is observed and an explanation is warranted if we are to define and employ intrinsic colors to estimate host-galaxy reddening. For guidance we turn to hydrodynamical explosion models. In Taddia et al. (2018) a grid of hydrodynamical models are presented (see Bersten et al. 2011, for details on the code) that reproduces the bolometric light curves and velocity evolution of our SE SN sample. The explosion models represent He-rich progenitor stars that cover a range of mass, yielding SNe with MNi values ranging between 0.034 and 1.8 M⊙, Mej values ranging between 1.0 and 6.2 M⊙, and explosion energies ranging between (0.6−4) × 1051 erg. Plotted as diamonds in the left panel of Fig. 8 are the +10 d photospheric temperatures for our series of models vs. the ratio between each model’s MNi and Mej values. The parameters clearly correlate and are well fit by a power law as indicated with a dashed black line. Also shown in Fig. 8 (left panel) is the range of the MNi to Mej ratio inferred from simple analytical model fits to the bolometric light curves of several dozen SE SNe (Lyman et al. 2016). These regions are defined by the median and standard deviation values of the MNi to Mej ratio for each sub-type (Lyman et al. 2016, see their Table 4), and when compared to the hydrodynamical modeling, imply for each sub-type a rather narrow range in the +10 d photospheric temperature (e.g., for SNe Ib we find 0.027 <MNi/Mej< 0.076).
Assuming SE SNe can be treated as black-body sources, we compute the +10 d B−V color for each model and plot it versus the corresponding MNi to Mej ratio in the right panel of Fig. 8. The parameters show a trend that is well fit by a power law function. Over-plotted as vertical lines is the range of the MNi to Mej ratio as inferred by Lyman et al. (2016), while the empty dotted points represent the corresponding mean B−V color value for each sub-type. Taking the standard deviation of the B−V colors for each sub-type in the allowed range of the MNi to Mej ratio, the uncertainty in the intrinsic B−V color is estimated to be σB−V = 0.09,0.09,0.05 and 0.09 mag for SNe IIb, Ib, Ic and Ic-BL, respectively. In the case of SNe Ic-BL, given the dearth of available models, σB−V was taken to be half the difference between the B−V values of the best fit function (black dashed curve) at the two extremes (magenta dashed lines) of the MNi to Mej ratio.
If we consider the standard deviation of B−V without distinguishing among SN sub-types, we obtain σB−V = 0.19 mag. This suggests it is prudent to consider different intrinsic colors for each SE SN sub-type. Note that the average uncertainty for our three B−V color templates between 0 and +20 d is 0.02–0.03 mag and that the uncertainty quoted for the +10 d V−R color by Drout et al. (2011) is 0.06 mag, which is consistent with our estimates of σB−V for each SE SN sub-type. This implies that the intrinsic color-curve templates can provide E(B−V)host color excess estimates with a systematic accuracy of ≤0.1 mag. Finally, we note that recently Dessart et al. (2016) have published an extended set of SE SN models which also exhibit +10 d V−R colors characterized by minimal dispersion.
 |
Fig. 7 Intrinsic color-curves templates for SNe IIb, Ib, and Ic for eight different color combinations. Each template is constructed by averaging the best fit of Eq. (1) to the observed colors of minimally-reddened SE SNe. Dashed lines are the associated 1σ uncertainties. Note that the thick portion of the color curves corresponds to the epochs used to infer color excesses. |
 |
Fig. 8 Left panel: plotted as diamonds is the temperature at +10 d calculated from an extended set of hydrodynamical explosion models that best-fit the bolometric light curves of our sample (see Taddia et al. 2018) vs. the ratio of the 56Ni mass and Mej for each model. The models indicate SE SNe with higher 56Ni to Mej ratios tend to exhibit higher temperatures, and the correlation between these parameters is well described by a power-law fit (black dashed line). Dashed vertical lines indicate the range of the 56Ni mass to Mej ratio inferred by Lyman et al. (2016) based on a large observational sample of SE SNe. The range of the 56Ni mass to Mej ratio for the each SE SN sub-type is relatively narrow, and implies a narrow range of ~1000° in temperature at +10 d. Right panel: inferred B−V color at +10 d determined from hydrodynamical models, plotted versus the ratio between 56Ni mass and Mej. The parameters are fit with a power law function plotted as black dashed line. Dashed vertical lines indicate the range in parameter space inferred by Lyman et al. (2016) for the various SE SN sub-types, while color circles are mean values obtained from the explosion models contained within each of the indicated regions with errorbars corresponding to 1σ uncertainty. This plot indicates a rather narrow range of intrinsic B−V colors are expected for the span of 56Ni to Mej ratios observed in the various SE SN sub-types. B−V color uncertainties are found to be lower than 0.1 mag for each SE SN sub-type. |
 |
Fig. 9 Observed color curves (yellow triangles) of the Type IIb SN 2006T compared to the SNe IIb intrinsic color-curves templates (green lines) for eight different color combinations. The color excesses are computed for the various color combination by taking the difference between the observed and intrinsic colors (black lines) between 0 d and +20 d (thick lines). |
 |
Fig. 10 Comparison of E(B−V)host color excesses with E(V−X)host (for X = i, Y, J, H) color excesses of 18 reddened SE SN. Color excess values are computed by taking the difference between the intrinsic color-curve templates and the observed colors of the reddened SE SNe from 0 d and +20 d. Over-plotted as solid lines are the best |
E(V−Xλ)host color excesses inferred from post maximum colors.
Best-fit  and
and  values for the seven most reddened SE SNe with eight color excess combinations.
values for the seven most reddened SE SNe with eight color excess combinations.
Best-fit  values of 15 low reddened SE SNe obtained from E(V−Xλ)host, E(r−Xλ)host, E(B−Xλ)host and E(g−Xλ)host assuming a universal
values of 15 low reddened SE SNe obtained from E(V−Xλ)host, E(r−Xλ)host, E(B−Xλ)host and E(g−Xλ)host assuming a universal  value for each SE SN sub-type.
value for each SE SN sub-type.
Given the clear correlation between the MNi to Mej ratio and the B−V color at +10 d, we also checked to see if the minimally-reddened objects identified in this section are also characterized by a high MNi to Mej ratio as compared to the reddened objects. If this were the case the minimally-reddened objects should appear blue due to a higher MNi to Mej ratio and not for being minimally reddened. However, in Taddia et al. (2018) the minimally reddening objects are found to cover the full phase space of the MNi to Mej ratio for each sub-type, suggesting the color templates are representative of the intrinsic colors of SE SNe.
4. Host-galaxy color excess, host-galaxy extinction and constraints on RV
With intrinsic color-curve templates in hand various color excesses can be inferred. In the following section we describe how this is done and how color excesses are used to estimate the host-extinction  , and constrain
, and constrain  for the most heavily reddened objects.
for the most heavily reddened objects.
4.1. Color excess estimates via intrinsic color-curve templates
To compute the color excess for any particular optical or optical/NIR color combination the observed SN color curve (corrected for Galactic reddening) is compared to its corresponding intrinsic color-curve template. As already noted, Drout et al. (2011) used +10 d as their fiducial epoch to infer the E(V−R)host color excess. We on the other hand have elected to compute color excesses by taking the difference between the observed and intrinsic colors between 0 d and + 20 d. This temporal interval was chosen for several reasons. Firstly, the majority of our light curves have their best time sampling in the two to three weeks just after maximum. Secondly, during this period the different SE SN sub-types follow a similar evolution in most colors, and thirdly, the overall scatter in the various intrinsic colors is minimal (see Fig. 7). To confirm this is an appropriate manner to proceed we experimented with making templates extending from 0 d to +10 d and from +10 d to +20 d. In short, these two sets of templates give results consistent with one another and with the results obtained using the 0 d to +20 d templates.
The technique used to infer the various 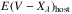 (where Xλ = u, B, g, r, i, Y, J, H) color excess values is demonstrated in Fig. 9. Here the observed V−Xλ color curve of SN 2006T (yellow triangles) is fit with Eq. (1) (black line) and this fit is compared to the corresponding SN IIb intrinsic-color template (green line). Specifically, the difference between the two curves in the interval between 0 and +20 d (where the line representing the template is plotted more thick in Fig. 9) represents the
(where Xλ = u, B, g, r, i, Y, J, H) color excess values is demonstrated in Fig. 9. Here the observed V−Xλ color curve of SN 2006T (yellow triangles) is fit with Eq. (1) (black line) and this fit is compared to the corresponding SN IIb intrinsic-color template (green line). Specifically, the difference between the two curves in the interval between 0 and +20 d (where the line representing the template is plotted more thick in Fig. 9) represents the 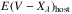 color excess.
color excess. 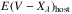 is computed by taking a weighted average of the difference between the intrinsic color template and the observed colors of the reddened SNe. The adopted weights correspond to the uncertainties associated with the measured observed colors and the estimated epoch of maximum light.
is computed by taking a weighted average of the difference between the intrinsic color template and the observed colors of the reddened SNe. The adopted weights correspond to the uncertainties associated with the measured observed colors and the estimated epoch of maximum light.
Armed with three sets of intrinsic color-curve templates, one for each of the SE SN sub-types, the various 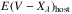 color-excess combinations are computed for the entire sample of reddened SE SNe. The results are provided in Table 3 with accompanying uncertainties computed by adding in quadrature (i) the weighted standard deviation of the difference between the observed and template colors, (ii) the average color uncertainty of the template, (iii) the average uncertainty of the observed color, and (iv) the uncertainty related to the temporal phase. Below in Sect. 4.5 this approach is extended to estimate color excess values for the entire suite of B−Xλ, g−Xλ and r−Xλ color combinations.
color-excess combinations are computed for the entire sample of reddened SE SNe. The results are provided in Table 3 with accompanying uncertainties computed by adding in quadrature (i) the weighted standard deviation of the difference between the observed and template colors, (ii) the average color uncertainty of the template, (iii) the average uncertainty of the observed color, and (iv) the uncertainty related to the temporal phase. Below in Sect. 4.5 this approach is extended to estimate color excess values for the entire suite of B−Xλ, g−Xλ and r−Xλ color combinations.
4.2. Optical-NIR color excesses
Assuming the dust contained within the host-galaxies of our SE SN sample follows a F99 reddening law, a universal value of  can be derived for each of the SE SN spectral sub-types by comparing the color excesses between the optical and NIR bands. Plotted in Fig. 10 are the measured E(B−V)host color excess values compared with the measured E(V−Xλ)host color excess values (for Xλ = i,Y,J,H) of 18 SE SN. Over-plotted as lines are the best-fit linear functions for each of the SE SN sub-types where the corresponding slopes have been converted to the
can be derived for each of the SE SN spectral sub-types by comparing the color excesses between the optical and NIR bands. Plotted in Fig. 10 are the measured E(B−V)host color excess values compared with the measured E(V−Xλ)host color excess values (for Xλ = i,Y,J,H) of 18 SE SN. Over-plotted as lines are the best-fit linear functions for each of the SE SN sub-types where the corresponding slopes have been converted to the  values reported in each panel. To convert the E(V−i,V−Y,V−J,V−H)host/E(B−V)host slopes to
values reported in each panel. To convert the E(V−i,V−Y,V−J,V−H)host/E(B−V)host slopes to  , we adopt the method described by Krisciunas et al. (2006) and Folatelli et al. (2010). This requires the calculation of the appropriate aλ and bλ coefficients (see Folatelli et al. 2010, their Appendix B), which is done using a +10 d spectral template constructed for each SE SN sub-type (see Holmbo et al., in prep.). A summary of this work and a list of the resulting coefficients is provided in Appendix B.
, we adopt the method described by Krisciunas et al. (2006) and Folatelli et al. (2010). This requires the calculation of the appropriate aλ and bλ coefficients (see Folatelli et al. 2010, their Appendix B), which is done using a +10 d spectral template constructed for each SE SN sub-type (see Holmbo et al., in prep.). A summary of this work and a list of the resulting coefficients is provided in Appendix B.
The best-fit  value for each SE SN sub-type is found to be strongly dependent on the color-excess combination considered and this is particularly the case of the SNe Ic. As the majority of the reddened objects in the sample suffer relatively moderate amounts of reddening only weak constraints can be placed on
value for each SE SN sub-type is found to be strongly dependent on the color-excess combination considered and this is particularly the case of the SNe Ic. As the majority of the reddened objects in the sample suffer relatively moderate amounts of reddening only weak constraints can be placed on  . Nevertheless, the comparison of optical with NIR color excess measurements in Fig. 10 suggests that the various SE SN sub-types are not well represented by a universal
. Nevertheless, the comparison of optical with NIR color excess measurements in Fig. 10 suggests that the various SE SN sub-types are not well represented by a universal  value, and this simple analysis suggests SNe Ic favor
value, and this simple analysis suggests SNe Ic favor  values that are on average larger than those inferred form the SNe IIb and SNe Ib. These results are based on small number statistic and conclusions should be taken with some caution, however this type of analysis demonstrates the potential to understand the relationship between SE SN and dust reddening.
values that are on average larger than those inferred form the SNe IIb and SNe Ib. These results are based on small number statistic and conclusions should be taken with some caution, however this type of analysis demonstrates the potential to understand the relationship between SE SN and dust reddening.
4.3. Host-extinction A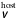 from multi-color fits and preferred values of R
from multi-color fits and preferred values of R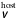
The comparison of optical and NIR color excess values in Sect. 4.2 highlights the difficulty to fit for  separately for objects suffering little-to-moderate amounts of reddening. In principle accurate estimates of both
separately for objects suffering little-to-moderate amounts of reddening. In principle accurate estimates of both  and
and  are best obtained from optical and NIR color excess measurements of SNe suffering appreciable levels of reddening, i.e., E(B−V)host≳ 0.20 mag. Seven objects meet the criteria and have both optical and NIR photometry. These are: SN 2014gt (Ic), SN 2005aw (Ic), SN 2006T (IIb), SN 2006ep (Ib), SN 2007C (Ib), SN 2009bb (Ic-BL), and SN 2009dt (Ic). The E(V−Xλ)host color excess values of each of these SNe are fit with the F99 reddening law with
are best obtained from optical and NIR color excess measurements of SNe suffering appreciable levels of reddening, i.e., E(B−V)host≳ 0.20 mag. Seven objects meet the criteria and have both optical and NIR photometry. These are: SN 2014gt (Ic), SN 2005aw (Ic), SN 2006T (IIb), SN 2006ep (Ib), SN 2007C (Ib), SN 2009bb (Ic-BL), and SN 2009dt (Ic). The E(V−Xλ)host color excess values of each of these SNe are fit with the F99 reddening law with  set as a free parameter. The best non-linear least-squares fit for each object is plotted in Fig. 11 and the corresponding
set as a free parameter. The best non-linear least-squares fit for each object is plotted in Fig. 11 and the corresponding  and
and  values are listed in each sub-panel and in Table 4. In general, the shape of the color excess vs. wavelength relations for the most highly reddened SE SN exhibit similar morphology, and this holds irrespective of spectroscopic subtype. Figure 11 is encouraging and demonstrates the importance of NIR photometry to estimate the reddening parameter. As of today we are limited by small number statistics and an expanded sample is required to confidently determine the intrinsic properties of SE SNe at NIR wavelengths.
values are listed in each sub-panel and in Table 4. In general, the shape of the color excess vs. wavelength relations for the most highly reddened SE SN exhibit similar morphology, and this holds irrespective of spectroscopic subtype. Figure 11 is encouraging and demonstrates the importance of NIR photometry to estimate the reddening parameter. As of today we are limited by small number statistics and an expanded sample is required to confidently determine the intrinsic properties of SE SNe at NIR wavelengths.
 |
Fig. 11 E(V−Xλ)host as a function of wavelength for seven objects whose E(V−B)host< −0.20 mag and with 8 different E(V−Xλ)host combinations extending from E(V−u)host to E(V−H)host (except for SN 2009dt where u−V is missing). Diamonds correspond to E(V−Xλ)host values obtained by comparison with the intrinsic color-curve templates for each object’s spectroscopic sub-type. Solid lines represent the best reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. The SN names are color coded with respect to their spectroscopic sub-type, i.e. SNe IIb in green, SNe Ib in blue, SNe Ic in red, and SNe Ic-BL in magenta. |
 |
Fig. 12 E(V−Xλ)host plotted as a function of wavelength for 14 SE SNe affected by 0 <E(B−V)host< 0.2 or with a limited set of E(V−Xλ)host combinations. Note that the nine minimally-reddened objects are not included and that due to limited photometric coverage, SN 2006fo, SN 2008gc, and SN 2009ca are also omitted. Black diamonds indicate the E(V−Xλ)host color excess values obtained by taking the difference between the intrinsic color-curve template and the observed colors of each reddened SE SN from 0 d to +20 d. Solid lines correspond to the best reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. Shown in red is the best fit for |
 |
Fig. 13 Cumulative distribution of peak absolute magnitudes of the CSP-I SE SN sample with (blue) and without (dashed red) host-extinction corrections. The actual distributions are shown by segmented lines, their best fit assuming kernel distributions are shown by curves of the same color. |
 |
Fig. 14 Right panel: visual-extinction |
 |
Fig. 15 E(V−Xλ)host plotted as a function of wavelength for 17 reddened SE SN. The full sample was culled down to these objects due to omission of the nine minimally-reddened objects, SN 2006fo, SN 2008gc, and SN 2009ca due to poor photometric coverage, and also SN 2004gq, SN 2007hn, SN 2007ag, and SN 2007rz as the G08 reddening law provides a poor fit. Black diamonds indicate the E(V−Xλ)host color excess values obtained by minimizing the difference between the intrinsic color-curve template and the observed colors of each spectroscopic sub-type. Solid orange lines correspond to the best G08 reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. The corresponding best-fit |
 |
Fig. 16
|
Among the objects with significant reddening a range of  values are obtained. This includes an
values are obtained. This includes an 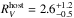 for the Type Ib SN 2007C, an
for the Type Ib SN 2007C, an 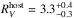 for the Type Ic BL SN 2009bb and an
for the Type Ic BL SN 2009bb and an 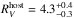 for the normal Type Ic SN 2009dt. Interestingly, this is consistent with the findings in Sect. 4.2 suggesting SNe Ib and SNe IIb tend to occur in low
for the normal Type Ic SN 2009dt. Interestingly, this is consistent with the findings in Sect. 4.2 suggesting SNe Ib and SNe IIb tend to occur in low  hosts compared to SNe Ic. The only SN IIb with sufficient reddening to determine
hosts compared to SNe Ic. The only SN IIb with sufficient reddening to determine  is SN 2006T, and as indicated in Fig. 11, it is found to exhibit the low value of
is SN 2006T, and as indicated in Fig. 11, it is found to exhibit the low value of 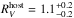 .
.
The E(B−V)host color excess values presented in Sect. 4.2 reveal that the majority of the objects in our sample suffer relatively low amounts of reddening (i.e., E(B−V)host< 0.20 mag). For these events it is not possible to obtain reliable estimates of  from our fitting method as the associated error is exceedingly large. This also holds true for objects lacking NIR photometry. For these objects we therefore assume their host-galaxy dust properties are similar to those characterizing the dust of the hosts of the most reddened objects in each of the SE SN sub-type samples. In doing so we adopt
from our fitting method as the associated error is exceedingly large. This also holds true for objects lacking NIR photometry. For these objects we therefore assume their host-galaxy dust properties are similar to those characterizing the dust of the hosts of the most reddened objects in each of the SE SN sub-type samples. In doing so we adopt 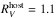 for all SNe IIb (as derived from SN 2006T),
for all SNe IIb (as derived from SN 2006T), 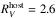 for all SNe Ib (as derived from SN 2007C), and
for all SNe Ib (as derived from SN 2007C), and 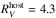 for all SNe Ic (as derived from in SN 2009dt). With
for all SNe Ic (as derived from in SN 2009dt). With  set for each SE SN sub-type each of the low reddened object’s optical and NIR E(V−Xλ)host sequences are fit with the F99 reddening law.
set for each SE SN sub-type each of the low reddened object’s optical and NIR E(V−Xλ)host sequences are fit with the F99 reddening law.
Plotted in Fig. 12 are the E(V−Xλ)host color excess values for the SE SNe suffering low extinction (where Xλ = u,B,g,R,i,Y,J,H) vs. the effective wavelength of passband Xλ3. Over-plotted as solid lines in each panel are the best-fit F99 models for the  values associated to each sub-type with the associated 1σ uncertain indicated by the dashed lines. The corresponding best-fit values of
values associated to each sub-type with the associated 1σ uncertain indicated by the dashed lines. The corresponding best-fit values of  are reported in each sub-panel and listed in Table 5. From close inspection of the various panels one is able to see the adopted
are reported in each sub-panel and listed in Table 5. From close inspection of the various panels one is able to see the adopted  values generally provide a good fit to the various color excess values plotted as a function of wavelength.
values generally provide a good fit to the various color excess values plotted as a function of wavelength.
We next compute the peak absolute magnitude cumulative distribution function (CDF) for our sample. To do so CDFs are computed with and without the inclusion of host-extinction corrections. Plotted in Fig. 13 are the peak luminosity CDFs for each of the nine CSP-I bandpasses, which we fit assuming a kernel distribution to guide the eye (the best fits are shown by curves of the same color). Inspection the CDFs of the blue bands (i.e., u, B, g) reveals that host-extinction corrected CDFs (in blue) are steeper compared to the uncorrected CDFs (in red), indicating their distributions are narrower. Following the discussion of Faran et al. (2014), this is an encouraging results as a reduction in the dispersion of peak luminosities of the sample population after application of reddening corrections suggests the validity of the extinction corrections.
We now examine the distribution of inferred extinction values for the different SE SN subtypes. Plotted in Fig. 14 (left-hand panel) are the best-fit  cumulative distribution functions (CDFs) based on the fits shown in Figs. 11 and 12. Comparing the different CDFs suggests that on average SNe Ic are characterized by larger
cumulative distribution functions (CDFs) based on the fits shown in Figs. 11 and 12. Comparing the different CDFs suggests that on average SNe Ic are characterized by larger  values than SNe IIb and SNe Ib. A Kolmogorov-Smirnov test indicates the significance of these differences is larger than 2σ for the comparison between SNe Ic and SNe IIb (p-value = 0.0013). This is true also when we assume RV = 3.1 for all the objects suffering low extinction, rather than different RV based on their subclass. This is demonstrated in the right-hand panel of Fig. 14, where SNe Ic and SNe IIb are different in their AV distributions, with p-value = 0.0465.
values than SNe IIb and SNe Ib. A Kolmogorov-Smirnov test indicates the significance of these differences is larger than 2σ for the comparison between SNe Ic and SNe IIb (p-value = 0.0013). This is true also when we assume RV = 3.1 for all the objects suffering low extinction, rather than different RV based on their subclass. This is demonstrated in the right-hand panel of Fig. 14, where SNe Ic and SNe IIb are different in their AV distributions, with p-value = 0.0465.
4.4. Host-extinction A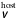 from Goobar model
from Goobar model
Up to here we have assumed the color excess values of our SE SN sample are well reproduced by a F99 reddening law. However, close inspection of the E(V−u)host color excess values and the best fits shown in Figs. 11 and 12 reveal that in a number of cases (e.g., SN 2004gt, SN 2004gv, SN 2005aw, SN 2006ir, SN 2006lc, and SN 2009dp) the E(V−u)host color excess values are not perfectly reproduced by the F99 law. This inspired us to fit an alternative reddening law to the observed optical and NIR color excess values. In this instance we adopt the Goobar (2008, hereafter G08) reddening law, which corresponds to a power law taking the functional form: 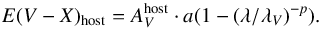 (3)Here
(3)Here  is the host-dust extinction, λV is the central wavelength of the V filter, and a and p correspond to the power-law fit parameters. The power-law function described by Eq. (3) was originally crafted to describe the effects of reddening of SN light produced by multiple scatters off a shell of dust located in the circumstellar environment of SNe Ia. To break the degeneracy between
is the host-dust extinction, λV is the central wavelength of the V filter, and a and p correspond to the power-law fit parameters. The power-law function described by Eq. (3) was originally crafted to describe the effects of reddening of SN light produced by multiple scatters off a shell of dust located in the circumstellar environment of SNe Ia. To break the degeneracy between  and a we adopt a = 1 (see Amanullah et al. 2015). As a caveat we note the inferred
and a we adopt a = 1 (see Amanullah et al. 2015). As a caveat we note the inferred  values from the power-law fits cannot be taken explicitly as the extinction in the V band, and as well in such a model where part of the extinction is due to scattering of light off of CSM one can infer a large range of
values from the power-law fits cannot be taken explicitly as the extinction in the V band, and as well in such a model where part of the extinction is due to scattering of light off of CSM one can infer a large range of  values. If such scattering is common among the SE SN population would then suggest SE SN subtypes do not favor a preferred
values. If such scattering is common among the SE SN population would then suggest SE SN subtypes do not favor a preferred  value.
value.
Plotted in Fig. 15 are the best fit power-law functions (blue line) to 17 SE SNe where the G08 reddening law is found to provide a good match to the E(V−Xλ) color excess values. In each of the instances where the E(V−u)host color excess points are poorly fit by a F99, the G08 model provides superior fits.
We now examine the p values obtained from the best G08 model fits of the seven (see Fig. 11) most highly reddening objects. Of these objects the best-fit p values of SN 2005aw, SN 2006T, SN 2006ep, and SN 2009dt are found to be inconsistent with the expected p values between − 1.5 to − 2.5 (Goobar 2008), while SN 2004gt, SN 2007C, and SN 2009bb are found to have best-fit p value confidence intervals that overlap with the range between − 1.5 and − 2.5 (see Fig. 15). This suggests these later three objects might have CSM dust driving multiple scatterings of light. We note, however, that the best F99 model fits to the color excesses of these objects also fit quite well (see Fig. 11).
4.5. Reddening constraints from additional color excess combinations: E(B – X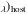 , E(g – Xλ)host and E(r – Xλ)host
, E(g – Xλ)host and E(r – Xλ)host
Most of the current SN follow-up programs do not necessarily observe objects in both SDSS and Johnson passbands. Therefore, we want to consider alternatives to the V−Xλ color combinations to infer  and
and  . This will, for example, allow one to use our intrinsic color templates also for SNe only observed in the SDSS passbands and not in Johnson passbands. Specifically, in the following the B−Xλ, g−Xλ, and r−Xλ color combinations are considered.
. This will, for example, allow one to use our intrinsic color templates also for SNe only observed in the SDSS passbands and not in Johnson passbands. Specifically, in the following the B−Xλ, g−Xλ, and r−Xλ color combinations are considered.
Following the procedure used to construct V−Xλ intrinsic color-curve templates, intrinsic color-curve templates are constructed for each of the B−Xλ, g−Xλ, and r−Xλ color combinations. These intrinsic color-curve templates are used to infer color excess values of reddened SE SNe relying on the methodology described in Sect. 4.3. The results of this exercise are summarized in Tables 4 and 5.
In the case of the seven most heavily reddened objects, best-fit  and
and  values are determined for each color combination. The best-fit results for these objects are listed in Table 4, as well as the average
values are determined for each color combination. The best-fit results for these objects are listed in Table 4, as well as the average  and
and  values obtained from each color combination. The average values are characterized by relatively small standard deviations ranging between 0.1–1.1 and 0.03–0.15 for
values obtained from each color combination. The average values are characterized by relatively small standard deviations ranging between 0.1–1.1 and 0.03–0.15 for  and
and  , respectively.
, respectively.
Reported in Table 5 are the best-fit  values for each color combination of the 14 SE SNe suffering relatively low reddening. To obtain the best-fit value a universal
values for each color combination of the 14 SE SNe suffering relatively low reddening. To obtain the best-fit value a universal  value was assumed for each SE SN sub-type as determined from the most reddened objects (see Sect. 4.3). In addition, the average of the best-fit
value was assumed for each SE SN sub-type as determined from the most reddened objects (see Sect. 4.3). In addition, the average of the best-fit  values obtained from each of the four color combinations is also given. Comparing the
values obtained from each of the four color combinations is also given. Comparing the  values obtained from the four different color combinations reveals that for most of the objects the
values obtained from the four different color combinations reveals that for most of the objects the  standard deviation is relatively small. We therefore conclude that when applied to different color combinations the method gives consistent results.
standard deviation is relatively small. We therefore conclude that when applied to different color combinations the method gives consistent results.
5. Discussion
The CSP-I SE SN light-curve sample has enabled us to devise improved methods to quantify host-galaxy dust extinction, and with the addition of our NIR photometry the added ability to constrain  . We now examine the consistency of the results obtained from the methods presented in Sects. 4.1 and 4.3. Plotted in Fig. 16 are comparisons between the best-fit
. We now examine the consistency of the results obtained from the methods presented in Sects. 4.1 and 4.3. Plotted in Fig. 16 are comparisons between the best-fit  values obtained from fits of the F99 law to each object’s set of color excesses (see the last column of Tables 4 and 5) and the
values obtained from fits of the F99 law to each object’s set of color excesses (see the last column of Tables 4 and 5) and the  values inferred from individual E(V−Xλ)host color excess measurement and the F99 law (see Table 3). In doing so these comparisons are made for each of the four color excess combinations: E(V−Xλ)host (top-left panel), E(B−Xλ)host (top-right panel), E(g−Xλ)host (bottom-left panel), and E(r−Xλ)host (bottom-right panel). Included in each panel’s sub-plots is the root-mean-square (rms) difference between the two methods. In general the
values inferred from individual E(V−Xλ)host color excess measurement and the F99 law (see Table 3). In doing so these comparisons are made for each of the four color excess combinations: E(V−Xλ)host (top-left panel), E(B−Xλ)host (top-right panel), E(g−Xλ)host (bottom-left panel), and E(r−Xλ)host (bottom-right panel). Included in each panel’s sub-plots is the root-mean-square (rms) difference between the two methods. In general the  values obtained by the two methods are in good agreement, as indicated by the fact that the data follow the black lines in the plots.
values obtained by the two methods are in good agreement, as indicated by the fact that the data follow the black lines in the plots.
 |
Fig. 17
|
We find that the optical and NIR color combinations providing the smallest dispersion among the suite of E(V−Xλ)host, E(B−Xλ)host, E(g−Xλ)host, and E(r−Xλ)host color combinations considered in this work are as follows. In the case of E(V−Xλ)host and time relative to Vmax the V−r and V−H colors exhibit minimal dispersion in  , while for E(B−Xλ)host and time relative to Bmax the B−i and B−H colors exhibit minimal dispersion. Moreover, for E(g−Xλ)host and time relative to gmax the g−r and g−H colors exhibit minimal dispersion in
, while for E(B−Xλ)host and time relative to Bmax the B−i and B−H colors exhibit minimal dispersion. Moreover, for E(g−Xλ)host and time relative to gmax the g−r and g−H colors exhibit minimal dispersion in  , while for E(r−Xλ)host and time relative to rmax the r−g/V and r−H colors exhibit minimal dispersion. Discrepancies between the two methods are largely due to different spectral lines affecting the
, while for E(r−Xλ)host and time relative to rmax the r−g/V and r−H colors exhibit minimal dispersion. Discrepancies between the two methods are largely due to different spectral lines affecting the  measurement from a single V/B/g/r−Xλ color combination more than the global V/B/g/r−Xλ fit value.
measurement from a single V/B/g/r−Xλ color combination more than the global V/B/g/r−Xλ fit value.
We now compare the  value derived for each object in the sample to their EWNa i D measurement obtained from visual-wavelength spectra (Holmbo et al., in prep.). Specifically,
value derived for each object in the sample to their EWNa i D measurement obtained from visual-wavelength spectra (Holmbo et al., in prep.). Specifically,  average values given in Tables 4 and 5 are plotted in Fig. 17 vs. EWNa i D. Over-plotted in the figure is the relation (solid blue line) found between these parameters by Poznanski et al. (2012), as well as a linear fit (dashed line) to the data assuming EWNa i D = 0 when
average values given in Tables 4 and 5 are plotted in Fig. 17 vs. EWNa i D. Over-plotted in the figure is the relation (solid blue line) found between these parameters by Poznanski et al. (2012), as well as a linear fit (dashed line) to the data assuming EWNa i D = 0 when 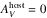 . The latter of these is given by
. The latter of these is given by ![\hbox{$A_V^{\rm host}[{\rm mag}] = 0.78(\pm0.15) \cdot EW_{\ion{Na}{i}~\rm D}[{\rm \AA}]$}](/articles/aa/full_html/2018/01/aa30843-17/aa30843-17-eq274.png) . As expected there is significant scatter between the two quantities (cf. Poznanski et al. 2011).
. As expected there is significant scatter between the two quantities (cf. Poznanski et al. 2011).
Returning to the  CDFs shown in Fig. 14, it is interesting to note that the SNe Ic consistently exhibit higher extinction values compared to SNe IIb and SNe Ib, and this holds independent of the assume value of
CDFs shown in Fig. 14, it is interesting to note that the SNe Ic consistently exhibit higher extinction values compared to SNe IIb and SNe Ib, and this holds independent of the assume value of  . This is consistent with the findings of Anderson et al. (2015) whom used pixel statistics based on Hα emission to study the environments of SNe by tracing on-going (<16 Myr old) star formation within SN host galaxies. Anderson et al. found that SNe Ic show a statistically significant preference for being located in regions of on-going star formation, while SNe Ib are located in regions that do not as closely follow ongoing star formation. The implications are that the progenitors of SNe Ic have shorter lifetimes and are more massive compared to the progenitors of SNe Ib. Being preferentially located in on-going star forming regions could therefore explain why SNe Ic experience (on average) more dust extinction compared with SNe Ib. As a caveat to the SNe Ic, we stress this subtype contains a mixed bag of transient phenomena, and assuming intrinsic colors based on more normal examples may not be appropriate to apply to more extreme cases such as the broad-line SN 2009bb and SN 2009ca. Unfortunately, we are limited by small number statistics though this will hopefully change in the future.
. This is consistent with the findings of Anderson et al. (2015) whom used pixel statistics based on Hα emission to study the environments of SNe by tracing on-going (<16 Myr old) star formation within SN host galaxies. Anderson et al. found that SNe Ic show a statistically significant preference for being located in regions of on-going star formation, while SNe Ib are located in regions that do not as closely follow ongoing star formation. The implications are that the progenitors of SNe Ic have shorter lifetimes and are more massive compared to the progenitors of SNe Ib. Being preferentially located in on-going star forming regions could therefore explain why SNe Ic experience (on average) more dust extinction compared with SNe Ib. As a caveat to the SNe Ic, we stress this subtype contains a mixed bag of transient phenomena, and assuming intrinsic colors based on more normal examples may not be appropriate to apply to more extreme cases such as the broad-line SN 2009bb and SN 2009ca. Unfortunately, we are limited by small number statistics though this will hopefully change in the future.
The findings of Sect. 4 indicate SE SNe appear to reside in host galaxies characterized by a range of dust properties. Although the sample size of heavily reddened objects is small, hosts of SNe Ic are found to be characterized by standard MW  values, while SNe IIb and SNe Ib tend to favor lower
values, while SNe IIb and SNe Ib tend to favor lower  values.
values.
Low  values have been inferred from the study of some core-collapse SNe. For example, Folatelli et al. (2014) recently inferred reddening parameters of
values have been inferred from the study of some core-collapse SNe. For example, Folatelli et al. (2014) recently inferred reddening parameters of 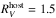 and E(B−V)host = 0.41 mag for the flat-velocity Type IIb SN 2010as. Additionally in the process of constructing a low red-shift Hubble diagram populated with SNe IIP, Olivares et al. (2010) obtained a global value of
and E(B−V)host = 0.41 mag for the flat-velocity Type IIb SN 2010as. Additionally in the process of constructing a low red-shift Hubble diagram populated with SNe IIP, Olivares et al. (2010) obtained a global value of 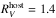 .
.
Low  values are also obtained from the study of individual and samples of moderate-to-heavily reddened SNe Ia, suggesting
values are also obtained from the study of individual and samples of moderate-to-heavily reddened SNe Ia, suggesting  values ranging from 1.1 (Tripp 1998) to 2.2 (Kessler et al. 2009; Guy et al. 2010; Mandel et al. 2011; Burns et al. 2014) to somewhere between
values ranging from 1.1 (Tripp 1998) to 2.2 (Kessler et al. 2009; Guy et al. 2010; Mandel et al. 2011; Burns et al. 2014) to somewhere between 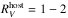 (Folatelli et al. 2010). Plotted in Fig. 18 is the RV CDF obtained for the most reddened SE SNe in our sample compared to the RV CDF obtained from an extended sample of CSP-I SNe Ia characterized by E(B−V)host ≥ 0.2 mag (see Burns et al. 2014). In general, compared to reddened SNe Ia, SE SNe tend to exhibit larger
(Folatelli et al. 2010). Plotted in Fig. 18 is the RV CDF obtained for the most reddened SE SNe in our sample compared to the RV CDF obtained from an extended sample of CSP-I SNe Ia characterized by E(B−V)host ≥ 0.2 mag (see Burns et al. 2014). In general, compared to reddened SNe Ia, SE SNe tend to exhibit larger 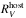 values.
values.
As noted in Sect. 4.3 a handful of objects exhibit E(V−u)host color excess values not reproduced by the fits obtained using the F99 reddening law. This motivated us to fit each set of color excess values of our sample with the CSM-motivated reddening law of G08 (see Fig. 15). This model was originally introduced to explain the abnormally low  values implied from the study of some heavily reddened SNe Ia. Although the G08 reddening law provides superior fits to the u colors of some objects it does not necessarily imply this is due to dust in the SN’s immediate circumstellar environment. For example, Burns et al. (2014) found for several highly reddened SNe Ia with abnormal blue colors that they were spectroscopically peculiar objects exhibiting high-velocity features. This implies the anomalous V−u colors could be driven by the prominent Ca ii H&K feature rather than related to the circumstellar environment. Unfortunately, the spectral coverage of our sample does not allow us to investigate the nature of this spectral feature given the wavelength cut-off at the blue end of the spectrum for the majority of the objects occurs at ~4000 Å (see Holmbo et al., in prep.).
values implied from the study of some heavily reddened SNe Ia. Although the G08 reddening law provides superior fits to the u colors of some objects it does not necessarily imply this is due to dust in the SN’s immediate circumstellar environment. For example, Burns et al. (2014) found for several highly reddened SNe Ia with abnormal blue colors that they were spectroscopically peculiar objects exhibiting high-velocity features. This implies the anomalous V−u colors could be driven by the prominent Ca ii H&K feature rather than related to the circumstellar environment. Unfortunately, the spectral coverage of our sample does not allow us to investigate the nature of this spectral feature given the wavelength cut-off at the blue end of the spectrum for the majority of the objects occurs at ~4000 Å (see Holmbo et al., in prep.).
In summary, we have identified a minimally-reddened sample of SE SNe enabling us to define intrinsic color-curve templates for the main spectroscopically defined SE SN sub-types. The minimally-reddened sample is used to infer the color excess of the reddened objects, and in the case of heavily reddened objects, a constraint on  . This work demonstrates the potential of securely estimating the host reddening parameters of SE SNe and highlights the added benefits of NIR photometry when it comes to determining the host-galaxy reddening properties. In the future, significant numbers of SE SNe will be discovered, and it is our hope that this work will provide a basis for further efforts to improve upon our ability to understand their origins.
. This work demonstrates the potential of securely estimating the host reddening parameters of SE SNe and highlights the added benefits of NIR photometry when it comes to determining the host-galaxy reddening properties. In the future, significant numbers of SE SNe will be discovered, and it is our hope that this work will provide a basis for further efforts to improve upon our ability to understand their origins.
 |
Fig. 18 RV distribution for our most reddened events as compared to those of SNe Ia from Burns et al. (2014), where we have selected objects characterized by E(B−V)host ≥ 0.2 mag and RV obtained from fitting a F99 reddening law. On average, SNe Ia prefer smaller values of RV. |
Published CSP-I photometry is readily available in electronic format at our Pasadena-based webpage: http://csp.obs.carnegiescience.edu/
The intrinsic color-curve templates are available in electronic format on our CSP Pasadena-based webpage: http://csp.obs.carnegiescience.edu/
The method used to compute an average effective wavelength for each of the CSP-I passbands is provided in Appendix A.
Acknowledgments
We thank R. Amanullah, E. Baron, A. Goobar, and P. Mazzali for useful discussions. M. D. Stritzinger, F. Taddia, E. Hsiao and C. Contreras gratefully acknowledge support provided by the Danish Agency for Science and Technology and Innovation realized through a Sapere Aude Level 2 grant. M. D. Stritzinger acknowledges funding by a research grant (13261) from the VILLUM FONDEN and the Instrument Centre for Danish Astrophysics (IDA). M. D. Stritzinger conducted a portion of this research at the Aspen Center for Physics, which is supported by NSF grant PHY-1066293. F. Taddia and J. Sollerman gratefully acknowledge the support from the Knut and Alice Wallenberg Foundation. This material is also based upon work supported by NSF under grants AST–0306969, AST–0607438, AST–0908886, AST–1008343, AST-1613426, AST–1613455, and AST–1613472. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Amanullah, R., Johansson, J., Goobar, A., et al. 2015, MNRAS, 453, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J. P., James, P. A., Habergham, S. M., & Galbany, L. 2015, PASA, 32, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bersten, M. C., Benvenuto, O., & Hamuy, M. 2011, ApJ, 729, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, S., Prieto, J. L., Patat, F., et al. 2009, ApJ, 693, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, C. R., Stritzinger, M. D., Phillips, M. M., et al. 2014, ApJ, 789, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cano, Z. 2013, MNRAS, 434, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Woosley, S., et al. 2016, MNRAS, 458, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Soderberg, A. M., Gal-Yam, A., et al. 2011, ApJ, 741, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Faran, T., Poznanski, D., Filippenko, A. V., et al. 2014, MNRAS, 442, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Phillips, M. M., Burns, C. R., et al. 2010, AJ, 139, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Bersten, M., Kuncarayakti, H., et al. 2014, ApJ, 792, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., Poznanski, D., Maoz, D., et al. 2012, PASP, 116, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Goobar, A. 2008, ApJ, 686, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M. A., Folatelli, G., Morrell, N., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Prieto, J. L., Garnavich, P., et al. 2006, AJ, 131, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A., Nugent, P., Fruchter, A., et al. 2005, ApJ, 624, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., Bersier, D., James, P. A., et al. 2016, MNRAS, 457, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K. S., Narayan, G., & Kirshner, R. P. 2011, ApJ, 731, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., & Zwitter, T. 1997, A&A, 318, 269 [NASA ADS] [Google Scholar]
- Nataf, D. M., Gonzalez, O. A., Casagrande, L., et al. 2016, MNRAS, 456, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, E. F., Hamuy, M., Pignata, G., et al. 2010, ApJ, 715, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Simon, J. D., Morrell, N., et al. 2013, ApJ, 779, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Ganeshalingam, M., Silverman, J., & Filippenko, A. V. 2011, MNRAS, 414, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Prochaska, J. X., & Bloom, J. S. 2012, MNRAS, 426, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Prentice, S. J., Mazzali, P. A., Pian, E., et al. 2016, MNRAS, 458, 2973 [NASA ADS] [CrossRef] [Google Scholar]
- Sahu, D. K., Anupama, G. C., & Chakradhari, N. K. 2013, MNRAS, 433, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Meisner, A. M., Stutz, A. M., et al. 2016, ApJ, 821, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2015, PASA, 32,e016 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Filippenko, A. V., & Chornock, R. 2011, MNRAS, 412, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Phillips, M. M., Boldt, L. N., et al. 2011, AJ, 142, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Anderson, J. P., Contreras, C., et al. 2018, A&A, 609, A134 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Sollerman, J., Leloudas, G., et al. 2015, A&A, 574, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Bersten, M. C., et al. 2018, A&A, 609, A136 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tripp, R. 1998, A&A, 331, 815 [NASA ADS] [Google Scholar]
- Turatto, M., Benetti, S., & Cappellaro, E. 2003, in From Twilight to Highlight: The Physics of Supernovae Proc. (Springer), 200 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, T., Wang, T., Wang, H., et al. 2012, MNRAS, 421, 486 [NASA ADS] [Google Scholar]
- Yoon, S.-C. 2015, PASA, 32, 15 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Average effective filter wavelengths
Plotted in the various panels of Fig. A.1 is the effective wavelength vs. days relative to V-band maximum for each of the CSP-I passbands. To compute the black curve the effective
wavelength of each filter is computed using the Nugent spectral templates (cf., Levan et al. 2005). The average of these values is indicated with a dashed horizontal line and this value is adopted as the effect wavelength for each passband.
 |
Fig. A.1 Temporal evolution of each passband’s effective wavelength, which is driven by the temporal evolution of the SED. Effective wavelengths were measured each CSP-I passbands using the Nugent SN Ib/c spectral templates. |
Appendix B: Deriving R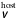 via color excess measurements
via color excess measurements
Here we describe the ax and bx reddening law coefficients are computed for the X = ugriBVYJH bands. It is these coefficients that enable us to estimate 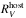 based on the slope(s) obtained by plotting E(V−X)+ 10 d vs. E(B−V)+ 10 d. Our approach follows directly the method employed by Folatelli et al. (2010) to determine the ax and bx coefficients applicable to dust studies related to Type Ia supernovae. In our case however we use template spectra computed from the CSP-I SE SN spectroscopy sample (Holmbo et al., in prep.).
based on the slope(s) obtained by plotting E(V−X)+ 10 d vs. E(B−V)+ 10 d. Our approach follows directly the method employed by Folatelli et al. (2010) to determine the ax and bx coefficients applicable to dust studies related to Type Ia supernovae. In our case however we use template spectra computed from the CSP-I SE SN spectroscopy sample (Holmbo et al., in prep.).
Following Cardelli et al. (1989), we first parameterized the reddening law as a function of wavelength in the following form: 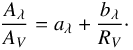 (B.1)The optical coefficients are computed by first multiplying a range of
(B.1)The optical coefficients are computed by first multiplying a range of 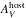 values with +10 d and +20 d spectral templates, while for the NIR coefficients we resorted to direct extrapolation from ~1.0 to 2.5 microns. Synthetic photometry is then computed from the raw spectral templates and the modified spectral templates using the CSP-I system response functions. Taking the difference between the resulting synthetic magnitudes then provides values for the observed absorption AX and AV, corresponding to bands X and V. Finally, estimates of the aλ and bλ coefficients are obtained for all the bands by fitting linear relations between AX and RV, as parameterized in Eq. (B.1).
values with +10 d and +20 d spectral templates, while for the NIR coefficients we resorted to direct extrapolation from ~1.0 to 2.5 microns. Synthetic photometry is then computed from the raw spectral templates and the modified spectral templates using the CSP-I system response functions. Taking the difference between the resulting synthetic magnitudes then provides values for the observed absorption AX and AV, corresponding to bands X and V. Finally, estimates of the aλ and bλ coefficients are obtained for all the bands by fitting linear relations between AX and RV, as parameterized in Eq. (B.1).
These calculation were performed using the Fitzpatrick (1999) reddening law and the results are summarized in Table B.1. Inspection of the various coefficients reveals quite consistent results for each passband among each of the SE SN subtypes. As explained in Folatelli et al. these coefficients allow us to convert an observed color excess measurements, as presented in Sect. 4.2, to a true value of 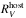 as defined in Eq. (B.1).
as defined in Eq. (B.1).
Reddening-law coefficients for SE SNe at +10 d.
All Tables
Best-fit  and
and  values for the seven most reddened SE SNe with eight color excess combinations.
values for the seven most reddened SE SNe with eight color excess combinations.
Best-fit  values of 15 low reddened SE SNe obtained from E(V−Xλ)host, E(r−Xλ)host, E(B−Xλ)host and E(g−Xλ)host assuming a universal
values of 15 low reddened SE SNe obtained from E(V−Xλ)host, E(r−Xλ)host, E(B−Xλ)host and E(g−Xλ)host assuming a universal  value for each SE SN sub-type.
value for each SE SN sub-type.
All Figures
 |
Fig. 1 Various optical and optical/NIR colors plotted as a function of days relative to maximum for the CSP SE SN sample. Symbols are color coded here and largely throughout this manuscript based on the different sub-types. Specifically, green, blue, red and magenta correspond to SNe IIb, Ib, Ic and Ic-BL, respectively. |
| In the text | |
 |
Fig. 2 NIR colors for our sample of SE SNe. |
| In the text | |
 |
Fig. 3 An example of the B−V color curve of SN 2006T fit with the analytical function described by Eq. (1). |
| In the text | |
 |
Fig. 4 Left panel: Na i D EW versus the galactic-extinction corrected B−V at +10 d for the CSP-I sample of SE SNe. Arrows indicate upper limits. The best linear fit is shown by a dashed-dotted line. The area in the low-left corner contained within the borders of the square dashed box includes 9 objects (SN 2004aw is not reported because it was not observed at +10 d but its color within +20 d is as blue as that of the other 8 events) whose host extinction is considered to be negligible. Right panel: de-projected and normalized SN offset from the host center versus host galaxy inclination. The objects suspected of suffering low extinction are circled in black, and they never appear in both strongly inclined galaxies and at locations close to their host center (i.e., they always sit outside the box delimited by dashed lines in the figure). Symbols are color coded based on the different sub-types: green, blue, red and magenta for SNe IIb, Ib, Ic and Ic-BL, respectively. |
| In the text | |
 |
Fig. 5 Intrinsic B−V color-curve templates for SNe IIb, Ib and Ic, as obtained from the best fit (solid lines) of Eq. (1) to the observed colors of nine minimally-reddened objects. Dashed lines are the associated 1σ uncertainties. The three templates are over-plotted in the bottom-right panel, showing that there are differences among the SE SN sub-types at all phases. The template uncertainties (highlighted in the bottom-right sub-panel) are lower in the first month after maximum, and then increase over time. |
| In the text | |
 |
Fig. 6 Post V-band maximum visual-wavelength spectroscopy of eight of the nine minimally-reddened objects identified in the CSP-I SE SN sample. Overall the spectra are similar for each individual sub-type, through differences between line strengths and line ratios are apparent, particular at the location of Hα and the He i features which evolve considerably as a function of phase. |
| In the text | |
 |
Fig. 7 Intrinsic color-curves templates for SNe IIb, Ib, and Ic for eight different color combinations. Each template is constructed by averaging the best fit of Eq. (1) to the observed colors of minimally-reddened SE SNe. Dashed lines are the associated 1σ uncertainties. Note that the thick portion of the color curves corresponds to the epochs used to infer color excesses. |
| In the text | |
 |
Fig. 8 Left panel: plotted as diamonds is the temperature at +10 d calculated from an extended set of hydrodynamical explosion models that best-fit the bolometric light curves of our sample (see Taddia et al. 2018) vs. the ratio of the 56Ni mass and Mej for each model. The models indicate SE SNe with higher 56Ni to Mej ratios tend to exhibit higher temperatures, and the correlation between these parameters is well described by a power-law fit (black dashed line). Dashed vertical lines indicate the range of the 56Ni mass to Mej ratio inferred by Lyman et al. (2016) based on a large observational sample of SE SNe. The range of the 56Ni mass to Mej ratio for the each SE SN sub-type is relatively narrow, and implies a narrow range of ~1000° in temperature at +10 d. Right panel: inferred B−V color at +10 d determined from hydrodynamical models, plotted versus the ratio between 56Ni mass and Mej. The parameters are fit with a power law function plotted as black dashed line. Dashed vertical lines indicate the range in parameter space inferred by Lyman et al. (2016) for the various SE SN sub-types, while color circles are mean values obtained from the explosion models contained within each of the indicated regions with errorbars corresponding to 1σ uncertainty. This plot indicates a rather narrow range of intrinsic B−V colors are expected for the span of 56Ni to Mej ratios observed in the various SE SN sub-types. B−V color uncertainties are found to be lower than 0.1 mag for each SE SN sub-type. |
| In the text | |
 |
Fig. 9 Observed color curves (yellow triangles) of the Type IIb SN 2006T compared to the SNe IIb intrinsic color-curves templates (green lines) for eight different color combinations. The color excesses are computed for the various color combination by taking the difference between the observed and intrinsic colors (black lines) between 0 d and +20 d (thick lines). |
| In the text | |
 |
Fig. 10 Comparison of E(B−V)host color excesses with E(V−X)host (for X = i, Y, J, H) color excesses of 18 reddened SE SN. Color excess values are computed by taking the difference between the intrinsic color-curve templates and the observed colors of the reddened SE SNe from 0 d and +20 d. Over-plotted as solid lines are the best |
| In the text | |
 |
Fig. 11 E(V−Xλ)host as a function of wavelength for seven objects whose E(V−B)host< −0.20 mag and with 8 different E(V−Xλ)host combinations extending from E(V−u)host to E(V−H)host (except for SN 2009dt where u−V is missing). Diamonds correspond to E(V−Xλ)host values obtained by comparison with the intrinsic color-curve templates for each object’s spectroscopic sub-type. Solid lines represent the best reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. The SN names are color coded with respect to their spectroscopic sub-type, i.e. SNe IIb in green, SNe Ib in blue, SNe Ic in red, and SNe Ic-BL in magenta. |
| In the text | |
 |
Fig. 12 E(V−Xλ)host plotted as a function of wavelength for 14 SE SNe affected by 0 <E(B−V)host< 0.2 or with a limited set of E(V−Xλ)host combinations. Note that the nine minimally-reddened objects are not included and that due to limited photometric coverage, SN 2006fo, SN 2008gc, and SN 2009ca are also omitted. Black diamonds indicate the E(V−Xλ)host color excess values obtained by taking the difference between the intrinsic color-curve template and the observed colors of each reddened SE SN from 0 d to +20 d. Solid lines correspond to the best reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. Shown in red is the best fit for |
| In the text | |
 |
Fig. 13 Cumulative distribution of peak absolute magnitudes of the CSP-I SE SN sample with (blue) and without (dashed red) host-extinction corrections. The actual distributions are shown by segmented lines, their best fit assuming kernel distributions are shown by curves of the same color. |
| In the text | |
 |
Fig. 14 Right panel: visual-extinction |
| In the text | |
 |
Fig. 15 E(V−Xλ)host plotted as a function of wavelength for 17 reddened SE SN. The full sample was culled down to these objects due to omission of the nine minimally-reddened objects, SN 2006fo, SN 2008gc, and SN 2009ca due to poor photometric coverage, and also SN 2004gq, SN 2007hn, SN 2007ag, and SN 2007rz as the G08 reddening law provides a poor fit. Black diamonds indicate the E(V−Xλ)host color excess values obtained by minimizing the difference between the intrinsic color-curve template and the observed colors of each spectroscopic sub-type. Solid orange lines correspond to the best G08 reddening law fit to each series of data and the corresponding 1σ uncertainty of the fit is indicated with dashed lines. The corresponding best-fit |
| In the text | |
 |
Fig. 16
|
| In the text | |
 |
Fig. 17
|
| In the text | |
 |
Fig. 18 RV distribution for our most reddened events as compared to those of SNe Ia from Burns et al. (2014), where we have selected objects characterized by E(B−V)host ≥ 0.2 mag and RV obtained from fitting a F99 reddening law. On average, SNe Ia prefer smaller values of RV. |
| In the text | |
 |
Fig. A.1 Temporal evolution of each passband’s effective wavelength, which is driven by the temporal evolution of the SED. Effective wavelengths were measured each CSP-I passbands using the Nugent SN Ib/c spectral templates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


