| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731759 | |
| Published online | 31 October 2017 | |
Colour variations in the GRB 120327A afterglow⋆
1 INAF–Osservatorio Astronomico di Brera, via E. Bianchi 36, 23807 Merate (LC), Italy
e-mail: andrea.melandri@brera.inaf.it
2 ICRANet-Rio, Centro Brasileiro de Pesquisas Físicas, Rua Dr. Xavier Sigaud 150, Rio de Janeiro, RJ 22290-180, Brazil
3 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
4 Department of Physics, The George Washington University, Washington, DC 20052, USA
5 Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
6 CEOU/Astronomy Program, Dept. of Physics & Astronomy, Seoul National University, Seoul, 151-742, South Korea
7 Mullard Space Science Laboratory, University College London, Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
8 Okayama Astrophysical Observatory, National Astronomical Observatory of Japan, Asakuchi, Okayama 719-0232, Japan
9 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
10 Astrophysics Research Institute, Liverpool JMU, IC2, Liverpool Science Park, 146 Brownlow Hill, Liverpool L3 5RF, UK
11 Department of Physics, University of Bath, Claverton Down, Bath, BA2 7AY, UK
12 Department of Astronomy and Astrophysics, Pennsylvania State University, University Park, PA 16802, USA
13 Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
14 Skynet Robotic Telescope Network, Dep. of Physics and Astronomy, Univ. of North Carolina, Chapel Hill, NC 27599-3255, USA
15 Department of Physics, North Carolina A&T State University, Greensboro, NC 27411, USA
16 Laboratoire Univers et Particules de Montpellier, Université Montpellier, Place Eugène Bataillon, 34095 Montpellier, France
17 INAF–Osservatorio Astronomico di Roma, via Frascati 33, 00078 Monteporzio Catone ( Roma), Italy
18 ASI Science Data Centre, via del Politecnico snc, 00133 Roma, Italy
19 Centre for Astrophysics and Cosmology, University of Nova Gorica, Vipavska 11c, 5270 Ajdovščina, Slovenia
20 Dipartimento di Fisica, Universitá di Ferrara, via Saragat 1, 44100 Ferrara, Italy
21 Ishigakijima Astronomical Observatory, NAO of Japan, 1024-1, Arakawa, Ishigaki, Okinawa 907-0024, Japan
22 University College Dublin, School of Physics UCD, Belfield, Dublin 4, Ireland
23 Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
24 Astronomical Institute, Czech Academy of Sciences, (ASU CAS), Ondřejov, Czech Republic
25 INAF–IASF Milano, via E. Bassini 15, 20133 Milano, Italy
26 GEPI,Observatoire de Paris, CNRS, Univ. Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
27 Korea Astronomy and Space Science Institute, Daejeon 34055, Korea
Received: 11 August 2017
Accepted: 21 September 2017
Aims. We present a comprehensive temporal and spectral analysis of the long Swift GRB 120327A afterglow data to investigate possible causes of the observed early-time colour variations.
Methods. We collected data from various instruments and telescopes in X-ray, ultraviolet, optical, and near-infrared bands, and determined the shapes of the afterglow early-time light curves. We studied the overall temporal behaviour and the spectral energy distributions from early to late times.
Results. The ultraviolet, optical, and near-infrared light curves can be modelled with a single power-law component between 200 and 2 × 104 s after the burst event. The X-ray light curve shows a canonical steep-shallow-steep behaviour that is typical of long gamma-ray bursts. At early times a colour variation is observed in the ultraviolet/optical bands, while at very late times a hint of a re-brightening is visible. The observed early-time colour change can be explained as a variation in the intrinsic optical spectral index, rather than an evolution of the optical extinction.
Key words: gamma-ray burst: individual: GRB 120327A / dust, extinction
Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/607/A29
© ESO, 2017
1. Introduction
The early afterglow is one of most interesting emission stages of gamma-ray bursts (GRBs). In a few tens of seconds the afterglow, X-ray, ultraviolet, optical, infrared, and radio emission begins to dominate over the fading prompt gamma-ray emission, and the timescale and intensity of the phenomenon offer powerful diagnostics of the physical processes within the outflow and the environment of the progenitor (e.g. Vestrand et al. 2006; Molinari et al. 2007; Melandri et al. 2008; Liang et al. 2013; Zaninoni et al. 2013).
Of particular interest are those few cases where a colour variation during the early optical afterglow has been singled out (Nysewander et al. 2006; Morgan et al. 2014). GRB 120327A is one of such a few events. In general, early-time colour variation can be the signature of rather different phenomena, such as the passage of a break frequency of the optical spectrum through the optical bands (e.g. Filgas et al. 2011); variation of the optical extinction due to either dust photo-destruction (Morgan et al. 2014) or the outflow progression through a wind-shaped environment (Rykoff et al. 2004); and the superposition of different emission stages, such as forward and reverse shock (Kobayashi & Zhang 2003) in the context of the “fireball” model (Piran 2004).
In this paper we report and discuss the observations of the long GRB 120327A, concentrating on the early-time colour evolution of the optical light curve. The data are reported in Sect. 2. The results are presented in Sect. 3. The possible interpretative scenarios are discussed in Sect. 4 and conclusions are drawn in Sect. 5. The respective temporal and spectral decay indices α and β are defined by fν(t) ∝ t− αν− β, and unless stated otherwise, all errors are reported at 1σ.
2. Observations
GRB 120327A was discovered by the Swift satellite (Gehrels et al. 2004) on March 27, 2012, at 02:55:16 UT (Sbarufatti et al. 2012). The bright X-ray and optical counterparts of this long gamma-ray burst (T90 ~ 63 s; Krimm et al. 2012) were observed by the X-ray Telescope (XRT) and the Ultraviolet and Optical Telescope (UVOT). In the UV it was at U ~ 18 a few minutes after the prompt event (Kuin et al. 2012). A redshift was quickly measured by Perley & Tanvir (2012) and Krühler et al. (2012) by absorption lines at z = 2.813. Several ground-based facilities observed the field and detected the counterpart in the optical and near-infrared (NIR) wavelengths. The afterglow was also detected at 34 GHz with a flux density of about 0.7 mJy (Hancock et al. 2012).
In this paper we retrieved and analysed XRT and UVOT data, together with Rapid Eye Mount (REM) telescope (Zerbi et al. 2001; Covino et al. 2004) NIR data, and IAC80, CTIO, BOOTES, PROMPT, Watcher, CQUEAN/2.1 m Otto-Struve telescope (Park et al. 2012), GROND (Greiner et al. 2008), SMARTS, MITSuME, NOT, and Liverpool Telescope (LT; Steele et al. 2004) optical data. For the analysis we also included photometric data from LT-RINGO2 imaging polarimeter (Steele et al. 2017). We reduced and analysed the data following standard procedures. Calibration was obtained by means of secondary standard stars in the field provided by the APASS1 and 2MASS2 catalogues in the optical and NIR bands, respectively. We obtained Rc and Ic magnitudes from APASS r and i magnitudes by means of suitable transformation equations. Optical SMARTS data are calibrated by means of a Landolt standard star field. ZY 2.1 m Otto-Struve telescope magnitudes are calibrated following Hodgkin et al. (2009). Optical and NIR magnitudes, not corrected for the Galactic reddening EB − V = 0.29 (Schlafly & Finkbeiner 2011), are reported in Table 2 (at the CDS). These data supersede those published in Kuin et al. (2012), Covino et al. (2012), Gorosabel et al. (2012), LaClyuze et al. (2012), Meehan et al. (2012), Im et al. (2012), Cobb (2012), Kuroda et al. (2012a,b), and Smith & Virgili (2012). We also used data from Sudilovsky et al. (2012) in our analysis.
3. Results
3.1. Light curves
In Fig. 1 the available optical/NIR data are plotted together with the X-ray light curve at 1 keV. The X-ray afterglow shows a canonical steep-flat-steep evolution with a considerable variability superposed on the general trend. The initial X-ray decay (αX,1 ~ 3) is consistent with the tail of the prompt BAT emission. Between 3 × 102 and 3 × 103 s the light curve flattens to αX,2 ~ 0.4 and then it becomes steeper to αX,3 ~ 2 up to the limit of detection.
The optical data start during the X-ray flat phase and show a colour evolution in the optical/NIR afterglow getting redder with time. The evolution is stronger in the bluer bands and more rapid at early time. We performed a multi-band fit of the UV/optical/NIR data in the time interval [200, 2×104] s (Fig. 1). Between 103 − 104 s the more densely sampled optical bands follow a decay αopt ~ 1.2. To visually emphasise the observed colour variation, in Fig. 2 we normalised all the early-time data to the better sampled R band, shifting all the UBV magnitudes in order to have good accordance at the time t ~ 103 s (as shown in Fig. 1 the afterglow temporal behaviour after that time is clearly achromatic in the UV/optical/NIR bands). As can be seen the more we move to bluer filters the larger is the deviation at early times from the estimated afterglow decay index. At late time the optical light curve shows the hint of a re-brightening that evolves from the red to the blue. However, the investigation of this late feature is beyond the purpose of this work.
 |
Fig. 1 Optical (UBgVRrIiz), NIR (YJHK), and X-ray (1 keV) light curve of GRB 120327A afterglow. Bands are artificially shifted for clarity (see Table 2 for calibrated magnitudes). Solid lines represent the best fit for the optical/NIR bands, assuming a variable optical spectral index β and fixed optical extinction. Vertical dashed lines show the Tmid of the four SEDs described in the main text. |
3.2. Spectral energy distributions
For the spectral energy distribution (SED) fit we consider the absorption in the optical and X-ray ranges both locally (i.e. in the GRB host galaxy) and arising from the Milky Way (MW). For the optical band we used the extinction laws given by Pei (1992, Eq. (20) and Table 4 therein) for the MW, the Large Magellanic Cloud (LMC), and Small Magellanic Cloud (SMC). For the X-ray data, we considered the model for the photoelectric cross section per HI-atom units for a given metallicity presented by Morrison & McCammon (1983), assuming solar metallicity (e.g. Covino et al. 2013; Zaninoni et al. 2013).
In addition, D’Elia et al. (2014) showed that the SED of GRB 120327A is characterised by a powerful Lymanα emission with log NH ~ 22. This implies that the obtained photometry in the bands including hydrogen lines has to be corrected for the line emission. Moreover, some of our data are obtained with filters that cover spectral ranges bluer than the Lymanα, i.e. about 460 nm in the observer frame. Together with the host galaxy extinction we therefore need to consider the absorption due to intergalactic medium that can only be computed in statistical sense. We followed the recipe proposed by Japelj et al. (2012).
 |
Fig. 2 Early-time UBV magnitudes normalised to the R-band light curve at t ~ 103 s (shaded region). The dashed line is the power-law decay index of the late-time optical afterglow. |
In Figs. 3 and 4 we show the results of the SEDs performed at four different time intervals between 700 and 18 000 s after the burst event. The X-ray-to-optical SEDs are best fitted using a broken power law3.
We fit the data considering two possible models (Fig. 4):
-
Variable optical extinction as AV = AV0 + k × t0.5, with AV0 = 0.04 ± 0.02, k = 6.02 ± 0.25 and t the time in seconds from the burst onset4; the optical spectral index is constant
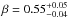 (orange area).
(orange area). -
Variable optical spectral index as β = β0 + ktα, with β0 = 0.76 ± 0.05, k = − 5.2e5,
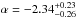 , and t the time in seconds from the burst onset;
the optical extinction is constant AV = 0.05 ± 0.02 (green
area).
, and t the time in seconds from the burst onset;
the optical extinction is constant AV = 0.05 ± 0.02 (green
area).
 for 333 d.o.f.). As said before, the X-ray light curve shows the plateau phase between 200 and ~3000 s. In this epoch the photon index ΓX rises from ~1.2 at ~300 s up to ~2.0 at ~700 s and then seems to decrease until it sets at the value of ~1.6 ± 0.1 (Fig. 4. bottom panel). This is similar to the variation of the optical spectral index, as reported in Table 1 and fitted in Fig. 4 (mid panel), strengthening the validity of our fit with a broken power-law function.
for 333 d.o.f.). As said before, the X-ray light curve shows the plateau phase between 200 and ~3000 s. In this epoch the photon index ΓX rises from ~1.2 at ~300 s up to ~2.0 at ~700 s and then seems to decrease until it sets at the value of ~1.6 ± 0.1 (Fig. 4. bottom panel). This is similar to the variation of the optical spectral index, as reported in Table 1 and fitted in Fig. 4 (mid panel), strengthening the validity of our fit with a broken power-law function.
 |
Fig. 3 The four spectral energy distributions estimated at Tmid. De-reddened optical data and unabsorbed X-ray flux are shown. Dashed lines represent our fitting model. |
 |
Fig. 4 Evolution with time of the spectral parameters. Variation of the optical extinction AV (top) and of the optical spectral index β (centre). Blue stars represent the values obtained by four SEDs as reported in Table 1. The green area refers to the model with AV fixed, while the orange area to the model with β fixed. The red squares (bottom) represent the variation of the X-ray photon index Γ, which at late times settles around the value ~1.6 ± 0.1 (grey area). |
4. Discussion
In the context of the standard fireball model (Sari et al. 1998; Chevalier & Li 2000), the GRB afterglow is related to the synchrotron emission from a decelerating relativistic shell that slows into an external medium. The observed colour variation in the
optical light curve at early time (Figs. 1 and 2) could arise from various scenarios:
-
(a)
The colour evolution could be caused by the passage of a break frequency. Considering that the spectral index β becomes shallower, the passage of the cooling frequency νc ∝ t1 / 2 in the slow cooling wind medium is the only possible case in this scenario, otherwise β becomes steeper or it changes sign (Chevalier & Li 2000). The passage of νc is expected to cause the spectral index change Δβ = 1 / 2, simultaneously with the decay index change Δα = 1 / 4 in the light curve (Sari et al. 1998). However, the observed change in the spectral index is smaller Δβ ~ 0.2 (i.e. the difference in β between the first epoch and later epochs), and no temporal breaks seem to be associated with this spectral change. Moreover, our SED analysis seems to indicate that νopt<νc<νX at the time of each SED (Fig. 3). Therefore the passage of a break frequency cannot explain the observations well, and the scenario can be discarded.
-
(b)
The colour change could be simply caused by a variation of the spectral index β. Following Morgan et al. (2014), we fit the SEDs letting β free to vary and fixing the dust parameters to the values obtained at late times. Therefore, the colour change can be modelled similar to a variation in the intrinsic spectral index β, as Fν2 = Fν1(ν2/ν1)Δβ12 (Perley et al. 2010). Indeed, as can be seen in Fig. 4 (middle panel), this possibility could explain the observed data. From our fit, the largest variation of the spectral index is expected at the very early times (green area), where it goes from β ~ − 1.4 at the time of our first UV detection (~3 × 102 s) up to β ~ − 0.7 at t ~ 103 s when in fact the observed temporal behaviour becomes achromatic.
-
(c)
Another possible source of the colour variation could be a change of the optical extinction because of the dust destruction by the jet within 10–30 pc (Draine & Salpeter 1979; Waxman & Draine 2000; Fruchter et al. 2001; Perna & Lazzati 2002; Draine & Hao 2002). This is supported by the fact that long GRBs have massive star progenitors and explode in dusty environments (Morgan et al. 2014). In this case, both the extinction AV and reddening RV are expected to change (e.g. Perna et al. 2003). Therefore, we fitted the optical/X-ray SEDs letting AV and β free to change, since the dust absorption observed at early times can have different signatures than those at late times (Morgan et al. 2014). For GRB 120327A we do not see a clear variation of the extinction in our spectral analysis. However, we find an excess of the X-ray absorbing column density at early time (NH ~ 1.6 × 1022 cm-2) that disappears after ~150 s from the burst onset, becoming consistent with the Galactic value (Willingale et al. 2013). Assuming the dust-to-gas relation reported by Covino et al. (2013) this would correspond to an AV ~ 1 mag, implying some sort of extinction variation at very early times. However, the dust destruction scenario seems a contrived explanation.
Fit parameters of the optical SED at different epochs.
5. Summary and conclusions
We analysed the temporal and spectral properties of GRB 120327A. The multi-band fit has highlighted the presence of a colour variation from early to late time that cannot be easily explained with the passage of a break frequency through the optical/NIR bands, either with the assumption of an homogenous or wind-like surrounding medium. However, in the fast-cooling case with a wind-like medium, small changes of the spectral index could be the result of the theoretical curvature of the spectrum (Granot & Sari 2006).
No evidence for a change in the absorption, AV, which could explain the observed colour variation, is clearly seen in our data; we find an average AV = 0.05 ± 0.02 for the dust content of the host galaxy. Although we cannot exclude completely the dust photo-destruction scenario, the variation of the spectral index β seems to be the favoured explanation, reproducing the observed data very well. Such a variation could be the result of small changes of the microphysical parameters (p, ϵe, and ϵB) from early to late times. In particular, a small variation of electron spectral index (of the order of ~0.4 dex) would reproduce the observed Δβ.
This function is an upgrade of the optical flux attenuation function described by Rykoff et al. (2004), assuming the bulk Lorentz factor Γ of the emitting shell free to vary.
Acknowledgments
A.M., S.Co., S.Ca., B.S., P.D.A., and G.T. acknowledge support from the ASI grant I/004/11/3. E.Z. acknowledges the support by the International Cooperation Program CAPES-ICRANet financed by CAPES – Brazilian Federal Agency for Support and Evaluation of Graduate Education within the Ministry of Education of Brazil. D.M. acknowledges support from the Instrument center for Danish Astrophysics (IDA). C.G.M. acknowledges support from the Royal Society, the Wolfson Foundation, and the Science and Technology Facilities Council. L.H. acknowledges support from SFI (07-RFP-PHYF295, 11/RFP.1/AST/3188) and the EU-FP7/GLORIA (grant No. 283783). M.I. and J.W.K. acknowledge the support from the National Research Foundation of Korea grant Nos. 2017R1A3A3001362 and 2016R1D1A1B03934815. D.K. acknowledges the financial support from the Slovenian Research Agency (P1-0188). This work has been supported by ASI grant I/004/11/0 and by PRIN-MIUR 2009 grants. This research was made possible through the use of the AAVSO Photometric All-Sky Survey (APASS), funded by the Robert Martin Ayers Sciences Fund. Partly based on observations made with the Nordic Optical Telescope (program 46-003, PI Jakobsson), operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofísica de Canarias.
References
- Chevalier, R. A., & Li, Z.-Y. 1999, ApJ, 520, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Li, Z.-Y. 2000, ApJ, 536, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Cobb, B. E. 2012, GCN, 13188, 1 [Google Scholar]
- Covino, S., Stefanon, M., Sciuto, G., et al. 2004, SPIE, 5492, 1613 [Google Scholar]
- Covino, S., Fugazza, D., & Rossi, A. 2012, GCN, 13128, 1 [Google Scholar]
- Covino, S., Melandri, A., Salvaterra, R., et al. 2013, MNRAS, 432, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Fynbo, J. P. U., Goldoni, P., et al. 2014, A&A, 564, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Hao, L. 2002, ApJ, 569, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Filgas, R., Greiner, J., Schady, P., et al. 2011, A&A, 535, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruchter, A., Krolik, J. H., & Rhoads, J. E. 2001, ApJ, 563, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gorosabel, J., Castro-Tirado, A. J., Walker, C., et al. 2012, GCN, 13130, 1 [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Hancock, P., Murphy, T., Gaensler, B., et al. 2012, GCN, 13180, 1 [Google Scholar]
- Hodgkin, S. T., Irwin, M. J., Hewett, P. C., & Warren, S. J. 2009, MNRAS, 394, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Kim, J.-W., & Kim, D. 2012, GCN, 13140, 1 [Google Scholar]
- Japelj, J., Gomboc, A., & Kopac, D. 2012, Proc. of Gamma-Ray Bursts 2012 Conference, PoS 078 [Google Scholar]
- Kobayashi, S., & Zhang, B. 2003, ApJ, 597, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Krimm, H. A., Barthelmy, S. D., Baumgartner, W. H., et al. 2012, GCN, 13137, 1 [Google Scholar]
- Krühler, T., Fynbo, J. P. U., Milvang-Jensen, B., Tanvir, N., & Jakobsson, P. 2012, GCN, 13134, 1 [Google Scholar]
- Kuin, P., & Sbarufatti, B. 2012, GCN, 13138, 1 [Google Scholar]
- Kuroda, D., Hanayama, H., Miyaji, T., et al. 2012a, GCN, 13156, 1 [Google Scholar]
- Kuroda, D., Hanayama, H., Miyaji, T., et al. 2012b, GCN, 13169, 1 [Google Scholar]
- LaCluyze, A., Haislip, J., Ivarsen, K., et al. 2012, GCN, 13127, 1 [Google Scholar]
- Liang, E.-W., Li, L., Gao, H., et al. 2013, ApJ, 774, 13 [Google Scholar]
- Meehan, S., Hanlon, L., Topinka, M., & Kubanek, P. 2012, GCN, 13144, 1 [Google Scholar]
- Melandri, A., Mundell, C. G., Kobayashi, S., et al. 2008, ApJ, 686, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, E., Vergani, S. D., Malesani, D., et al. 2007, A&A, 469, 13 [Google Scholar]
- Morgan, A. N., Perley, D. A., Cenko, S. B., et al. 2014, MNRAS, 440, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nysewander, M. C., Reichart, D. E., Park, H.-S., et al. 2006, ApJ, 651, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Park, W.-K., Pak, S., Im, M., et al. 2012, PASP, 124, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., & Tanvir, N. R. 2012, GCN, 13133, 1 [Google Scholar]
- Perley, D. A., Bloom, J. S., Klein, C. R., et al. 2010, MNRAS, 406, 2473 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., & Lazzati, D. 2002, ApJ, 580, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., Lazzati, D., & Fiore, F. 2003, ApJ, 585, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Smith, D. A., Price, P. A., et al. 2004, ApJ, 601, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 2004, RvMP, 76, 1143 [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarufatti, B., Barthelmy, S. D., Gehrels, N., et al. 2012, GCN, 13123, 1 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., & Virgili, F. 2012, GCN, 13125, 1 [Google Scholar]
- Steele, I. A., Smith, R. J., Rees, P. C., et al. 2004, SPIE, 5489, 679 [NASA ADS] [Google Scholar]
- Steele, I. A., Kopač, D., Arnold, D. M., et al. 2017, ApJ, 843, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Sudilovsky, V., Nicuesa Guelbenzu, A., & Greiner, J. 2012, GCN, 13129, 1 [Google Scholar]
- Vestrand, W. T., Wren, J. A., Wozniak, P. R., et al. 2006, Nature, 442, 172 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Waxman, E., & Draine, B. T. 2000, ApJ, 537, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Zaninoni, E., Bernardini, M. G., Margutti, R., Oates, S., & Chincarini, G. 2013, A&A, 557, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zerbi, F. M., Chincarini, G., Ghisellini, G., et al. 2001, Astron. Nachr., 322, 275 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Optical (UBgVRrIiz), NIR (YJHK), and X-ray (1 keV) light curve of GRB 120327A afterglow. Bands are artificially shifted for clarity (see Table 2 for calibrated magnitudes). Solid lines represent the best fit for the optical/NIR bands, assuming a variable optical spectral index β and fixed optical extinction. Vertical dashed lines show the Tmid of the four SEDs described in the main text. |
| In the text | |
 |
Fig. 2 Early-time UBV magnitudes normalised to the R-band light curve at t ~ 103 s (shaded region). The dashed line is the power-law decay index of the late-time optical afterglow. |
| In the text | |
 |
Fig. 3 The four spectral energy distributions estimated at Tmid. De-reddened optical data and unabsorbed X-ray flux are shown. Dashed lines represent our fitting model. |
| In the text | |
 |
Fig. 4 Evolution with time of the spectral parameters. Variation of the optical extinction AV (top) and of the optical spectral index β (centre). Blue stars represent the values obtained by four SEDs as reported in Table 1. The green area refers to the model with AV fixed, while the orange area to the model with β fixed. The red squares (bottom) represent the variation of the X-ray photon index Γ, which at late times settles around the value ~1.6 ± 0.1 (grey area). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


