EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 606 (October 2017) A&A, 606 (2017) A85 Full HTML
Free Access
Issue
A&A
Volume 606, October 2017
Article Number A85
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201731062
Published online 17 October 2017

© ESO, 2017

1. Introduction

Studies of the halo of the Milky Way and other massive galaxies show that the metallicity distribution functions (MDFs) of halo stars is very different from that of globular clusters in the same galaxy. Observations indicate that the cluster-to-star ratio is a strong function of metallicity in spiral (e.g. Carollo et al. 2010; Gratton et al. 2012; Durrell et al. 2001, 2004; Chapman et al. 2006; Kalirai et al. 2006) and elliptical galaxies (e.g. Harris & Harris 2002; Harris 2003; Beasley et al. 2008). Similar differences have also been observed for dwarf galaxies (e.g. Beasley et al. 2008; Mackey & Gilmore 2004; Sharina et al. 2010)1. The most extreme example was found in the Fornax dSph where the stars have a broad metallicity distribution with −2.5 < [M/H] < −0.2 with a peak at [M/H] = −1.0 while the globular clusters are all metal-poor with −2.6 < [M/H] < −1.4 (Larsen et al. 2012b). So the cluster-to-star ratio is very low at high metallicity and very high at low metallicity.

These trends are not expected if star formation and cluster formation trace each other as in nearby star-forming regions where a certain small fraction of the stars (typically 5–10%, Goddard et al. 2010; Kruijssen 2012; Adamo et al. 2015) are in bound clusters. If ancient clusters and stars would also trace each other, one would expect that the metallicity distributions of the old globular clusters and old stellar populations match each other (assuming no metal contamination within clusters), which is obviously not the case. One interpretation of these results is that star and cluster formation were different in the early Universe, when metal-poor GCs were formed, with separate events forming the bulk of the cluster and stellar populations. Alternatively, it is possible that evolutionary effects are responsible for the observed differences, with preferential cluster disruption or hierarchical galaxy merging influencing the ratio of clusters to field stars as a function of metallicity or location.

There has been much work done in the past few years attempting to include globular clusters in galaxy formation simulations in an attempt to place globular clusters in a more cosmological context and obtain an understanding of their MDFs. One commonly adopted method is through “particle tagging”, where certain particles in the simulations are treated as globular clusters. Such simulations have provided insight into various globular cluster population properties (e.g. Moore et al. 2006; Moran et al. 2014), although they generally make the assumption that field stars and globular clusters will share the same MDFs, whereas observations show variations over ~ 3 orders of magnitude (e.g. Kruijssen 2014). Such assumptions lead to unphysical solutions as to when globular clusters formed (i.e. z> 10 for metal poor clusters, see Brodie & Strader 2006, which is inconsistent with their ages; see e.g. Forbes & Bridges 2010), because they can only produce sufficiently extended globular cluster galactocentric radial distributions at extremely high redshift. Additionally, such simulations, often done in post-processing, do not follow the tidal history of the globular clusters meaning that the cluster dissolution cannot be taken into account in the necessary detail. Tonini (2013) got around this problem by matching the cluster-to-star ratio (or specific frequency) of each galaxy (in post-processing) to observations of present-day galaxies, with the aim of reproducing the MDFs of globular clusters. However, the origin of the adopted specific frequency cannot be tested in this way. When aiming to understand the origin of the different MDFs of globular clusters and field stars, which is equivalent to studying the cluster-to-star ratio as a function of metallicity, one must instead employ fully self-consistent models for the formation and evolution of globular cluster in galaxy formation simulations, taking into account the impact of the environment on the cluster formation efficiency and cluster mass loss.

In this paper, we aim to formulate the problem of the different MDFs of globular clusters and field stars and identify the most promising responsible physical mechanisms, particularly with an eye on the upcoming generation of self-consistent models of globular cluster formation during galaxy formation (e.g. Pfeffer et al., in prep.; Kruijssen et al., in prep.). We do this by describing the observational constraints and studying the different effects that influence both the formation and the disruption of star clusters, and may have played a role in producing different MDFs of globular clusters and halo stars within galaxies.

  • 1.

    The first is that the fraction of stars formed in bound clusters(Γ) may depend on metallicity and environment.

  • 2.

    The second, intimately related to the first, is that some internal or external process may preferentially destroy young clusters in a metallicity dependent way.

  • 3.

    The third is that the maximum cluster mass may depend on metallicity such that massive globular clusters are less likely to form in metal-rich galaxies.

  • 4.

    The fourth is environmentally dependent cluster disruption, where clusters may be destroyed more rapidly in strong and/or time-varying tidal fields, and most strongly towards high metallicities (e.g., near the centres of galaxies or in gas-rich environments).

  • 5.

    The fifth is dynamical friction, which may force massive clusters to spiral-in to the centres of galaxies.

  • 6.

    The sixth is any combination of the first five, considered in the framework of hierarchical galaxy formation.

The goal of the present work is to investigate why the cluster and star populations have different MDFs within galaxies. The paper is organized as follows. In Sect. 2 we describe the relevant observations of the distributions (spatial and metallicity) of old stars and globular clusters in halos of spiral, elliptical and dwarf galaxies. In Sect. 3 we briefly summarize these observations and mention the unexplained problems. In Sect. 4 we discuss the formation of clusters of different metallicities in different environments. In Sect. 5 the different mechanisms that may destroy the clusters are discussed. In Sect. 6 the capture of clusters from stripped dwarf galaxies are studied. The conclusions and discussion are presented in Sect. 7.

2. Observed metallicity distribution functions (MDF) of clusters and stars

The study of the MDF of stars in individual galaxy halos is possible through resolved stellar photometry, but is limited to galaxies in the Local Group and nearby groups, up to about 10 Mpc. We will use the detailed properties of stars and GCs in Cen A, M 31 and the Fornax dSphs as representative examples for ellipticals, spirals and dwarf galaxies.

2.1. Large spiral and elliptical galaxies

2.1.1. The MDF of halo stars

The stars in the halos of large spiral and elliptical galaxies show similarities in their metallicity distributions: a high metallicity component with a peak at [M/H] ≃ −0.5 to −1.5 and a lower metallicity component or a tail in more massive elliptical galaxies, with a broader peak at [M/H] ≃ −1.5 to −2.0, e.g.: MW: (Ryan & Norris 1991; An et al. 2012); M 31: (Durrell et al. 2001; Durrell et al. 2004; Chapman et al. 2006; Kalirai et al. 2006; Gilbert et al. 2014; Ibata et al. 2014; Gregersen et al. 2015); M81: (Durrell et al. 2010); NGC 891: (Mouhcine et al. 2007; Rejkuba et al. 2009); NGC 2403: (Barker et al. 2012); Sombrero: (Mould & Spitler 2010); other nearby spirals (e.g. Mouhcine et al. 2005; Mouhcine 2006); NGC 5128: (Harris et al. 1999; Harris & Harris 2000, 2002; Rejkuba et al. 2005, 2014; Crnojević et al. 2013); NGC 3377: (Harris et al. 2007a) NGC 3379: (Harris et al. 2007b; Lee & Jang 2016) NGC 3115: (Peacock et al. 2015).

The metal-rich component is concentrated more towards the inner regions and the metal-poor component becomes significant only in the outer regions. The metallicity of both the metal-rich and metal-poor components increase with increasing galaxy luminosity (Mouhcine 2006) and the stellar halo metallicity scales with stellar halo mass (Harmsen et al. 2017) with a slope that is broadly similar to the stellar mass versus stellar metallicity relation for local galaxies (Gallazzi et al. 2005; Kirby et al. 2013). Forbes et al. (1997) and Mouhcine (2006) suggested that the metal-poor component is due to the tidal disruption of dwarf-like objects whereas the metal-rich population is related to the formation of the bulge and/or disk. In elliptical galaxies, where the low-metallicity tail is weaker2, the metal-poor component may be the relic of the very earliest formation stage, whereas the metal-rich component originated in the former disks of the merged galaxies (e.g. Harris et al. 2007b; Bekki et al. 2002.

2.1.2. The MDF of globular clusters

The MDF of globular clusters in spiral galaxies and giant ellipticals is clearly bimodal with the metal-rich clusters concentrated towards the galactic center and the metal-poor clusters (which are invariably very old, t ≥ 10 Gyr) distributed over larger distances (Gebhardt & Kissler-Patig 1999; Peng et al. 2006; Brodie et al. 2012). For instance the MDF of GCs in the MW has peaks at [M/H] = −1.55 ± 0.07 and −0.55 ± 0.10 (Harris et al. 2016) and the giant elliptical Cen A has peaks at [M/H] = –1.4 and –0.4 (Beasley et al. 2008).

The peak in the MDF of the metal-poor (blue) GCs was found to be almost constant at [M/H]≃ –1.5 (Burgarella et al. 2001) and showing no correlation with the parent galaxy luminosity (Forbes et al. 1997) in several studies. However, more homogeneous samples revealed a shallow but significant correlation between the peak MDF of the blue clusters and the host galaxy luminosity (e.g. Larsen et al. 2001; Strader et al. 2004; Peng et al. 2006). By contrast, the peak of the metal-rich (red) GCs depends strongly on the mass or luminosity of the galaxies: the more massive a galaxy, the more metal-rich its red peak in the MDF (e.g. Peng et al. 2006, for the Virgo galaxies; and Liu et al. 2011, for the Fornax cluster galaxies). The radial distribution of the metal-rich GCs in the MW shows a steep decline beyond RGal ≃ 10 kpc, whereas the population of metal-poor GCs extends all the way from about 1 to 100 kpc (e.g. see the review by Harris 2001). In Cen A the majority of the clusters with [M/H]> –1 are within 20 kpc projected distance from the center, whereas the metal-poor clusters show a flatter distribution with projected distance. Also in large cD galaxies the galactic radial distribution of metal-rich clusters is much steeper than that of metal-poor clusters, see e.g. Fig. 20 of Harris et al. (2016, 2017).

Several studies have shown that the radial distribution of the metal-rich GCs follow approximately the radial distribution of the star-light and that the kinematics of the red clusters also follow that of the stars, whereas the blue GCs have a larger velocity dispersion, e.g. Schuberth et al. (2010), Strader et al. (2011), Pota et al. (2013) and the review by Brodie & Strader (2006).

thumbnail Fig. 1

Upper figure: comparison between the normalized MDF of stars (dotted) and GCs (full lines) in three distance regions of Cen A. Each MDF is normalized to 1. Lower figure: logarithmic ratio between the normalized MDFs of clusters and stars as a function of [M/H] in bins of Δ [M/H] = 0.30. The colours are the same as in the upper figure. For clarity, the points of the three regions are slightly horizontal shifted with respect to one another. The coloured dotted lines show the weighted least square fits of the three distance regions. The full black line is the least square fit of the three regions combined. It has a slope of −0.78 ± 0.05.

2.1.3. Giant elliptical galaxy NGC 5128 = Cen A

In Fig. 1 the normalized MDF of GCs and halo stars in the giant elliptical galaxy Cen A (NGC 5218) at a distance of 3.8 Mpc (Harris et al. 2010) are compared in three distance regions of the halo.

The stellar MDF is based on resolved stellar population studies in fields at projected distances of (i) 8 kpc (Harris & Harris 2002); (ii) in two field at 21 and 31 kpc (Harris et al. 1999; Harris & Harris 2000); and (iii) in the outer halo field at 38 kpc galactocentric distance (Rejkuba et al. 2005). The MDF of the 408 GCs was derived by combining the samples of (i) 207 GCs with spectroscopic metallicities from Beasley et al. (2008) and (ii) 201 spectroscopically confirmed GCs with velocities consistent with being members of the globular cluster system (GCS) of NGC 5128, whose metallicities were calculated from Washington (C–T1) photometric index (Woodley et al. 2007)3. These GCs span a range of projected distances from 0 to 45 kpc, but the large majority is located within the inner 15 kpc – this is primarily due to incomplete spectroscopic studies of the outer regions of the GCS in this galaxy.

The stellar MDF is measured by interpolating (V−I) colours of the upper Red Giant Branch (RGB) stars on a set of empirically calibrated stellar evolutionary tracks (Harris et al. 1999) assuming an alpha enhancement of [α/Fe] = + 0.3. The relative precision in MDFs of different fields is ensured by using the same filters for observations of different fields, as well as the same colour-metallicity calibration and interpolation code. While it is well known that the RGB colour varies non-linearly with metallicity and the photometric metallicities have higher errors at the metal-poor end (Saviane et al. 2000; Harris & Harris 2000), comparison of photometric MDFs with those constructed from spectroscopic measurements of individual stars shows a good agreement on the average values, as well as the overall shape of MDFs (e.g. Gonzalez et al. 2011, for a wide MDF in the Milky Way bulge)4. Kalirai et al. (2006) also found a very good agreement between photometric and spectroscopic metallicities for M 31 giants for the whole metallicity range except the most metal-poor bin ([M/H] < −1.5), where photometric measurements extend to lower values, making the photometric stellar MDF broader. The metallicity accuracy for GC measurements is of the order of ~0.15 dex (Beasley et al. 2008), depending more strongly on the quality of spectra, then on the metallicity of individual clusters.

The top panel in the upper figure compares the MDF of the field stars at 8 kpc field with that of GCs located between 6 <Rp< 15 kpc. The middle panel compares the MDF of GCs at 15 <R< 30 kpc with the stellar MDF in the combined fields at 21 and 31 kpc, which have very similar MDFs (Rejkuba et al. 2005). The lower panel compares the MDFs of stars in the 38 kpc field with GCs at R> 30 kpc. We see that the stellar MDF in the inner region of Cen A is wider and extends to slightly higher [M/H] than in the outer halo. Harris & Harris (2002) have argued that this is due to contributions by bulge stars. On the other hand, the MDFs of the GCs are flatter with the contribution of the metal-poor clusters with [M/H] < −1.5 increasing towards larger distances.

At all distances the clusters are underrepresented compared to stars at high metallicity [M/H] > −1 and overrepresented at low metallicity, [M/H] < −1 (see also Beasley et al. (2008) for a similar observation).

(The terms “underrepresented” and “overrepresented” in this respect are always relative to the “mean” cluster-to-star ratio, which is generally of the order of a percent in mass).

The lower part of Fig. 1 shows the logarithmic ratio between the normalized MDFs of clusters and stars as a function of metallicity. In all three distance ranges this ratio decreases with increasing [M/H] by about 2 dex in the range of −2.5 < [M/H] < 05. Although the absolute values of the specific frequency SN in the three distance regions is not known, the trend in the lower part of Fig. 1 shows that the decrease of SN with [M/H] appears to be independent of distance. The weighted least square fits at the inner radial distance range has a slope of dlog (Ncl/Nstars)/d [M/H] = −0.82 ± 0.06. The slopes in the other two distance ranges are –0.59 and –1.0 but are less well determined due to the large error-bars. The linear regression of the full sample has a slope of −078 ± 0.05. We conclude that the dependence of the ratio Ncl/Nstars on metallicity is independent of the galactocentric distance and has a slope of dlog (Ncl/Nstars)/d [M/H] = −0.80 ± 0.07. Further confidence in our conclusion is gained by comparing the stellar vs. GC MDFs in NGC 3115, which also show a similar dependence on metallicity that is independence of the distance, as shown in Figs. 11 and 12 of Peacock et al. (2015).

thumbnail Fig. 2

Upper figure: comparison between the normalized MDF of stars (dotted) and GCs (full lines) in two distance regions of M 31. Each MDF is normalized to 1. Lower figure: logarithmic ratio between the normalized MDFs of clusters and stars as a function of [M/H] in bins of 0.6 at two distance regions of M 31. The weighted least square fit of (Ncl/Nstars) versus [M/H] for the inner and outer regions are shown by dotted red and blue lines respectively. The black line is the fit to all data and has a slope of −0.69 ± 0.27.

2.1.4. Spiral Galaxy M 31

Figure 2 shows the normalized MDF of clusters and halo stars in M 31. The data for the clusters are taken from the Revised Bologna Catalog, the main repository of information for M 31 GCs (Galleti et al. 2004), which contains metallicity measurements for 225 GCs based on Lick indices by Galleti et al. (2009). The MDF of the halo stars is from Kalirai et al. (2006). These authors derived the metallicities of 250 halo RGB stars in 12 fields, ranging in projected distance from 12 to 165 kpc from the center. Assuming that the halo stars and the GCs are both distributed spherically around M 31, rather than ellipsoidally, we can directly compare the MDF of both samples as a function of projected galactocentric distance, by correcting for the tilt of the M 31 disk6.

The MDF of the halo stars is shown in two distance bins at R< 20 and R> 20 kpc. The GC sample was split at R = 15 kpc to have sufficient clusters in the outer region to make a meaningful MDF. The inner region contains about 200 clusters, the outer region contains only 12 GCs

The figure shows that the MDF of the halo stars of M 31 becomes wider and shifts to lower metallicity with increasing distance (see Kalirai et al. 2006, for the gradual trend). In contrast, the MDF of the clusters is approximately the same in both regions, within the statistical uncertainty. In both the inner and the outer region the mean metallicity of the GC is lower than that of the stars. The effect is strongest in the inner region which may, at least partly, be due the contribution by the bulge stars in the inner region (Kalirai et al. 2006).

The lower part of Fig. 2 shows the logarithmic ratio between the normalized MDF of clusters and stars as a function of [M/H] in bins of Δ [M/H] = 0.6. The linear weighted least square fit for the inner region has a slope of dlog (Ncl/Nstars)/d [M/H] = −0.79 ± 0.31. The trend in the outer region is much less well defined, due to the fact that most bins contain only 1 to 4 clusters, so the uncertainty is large. Combining all data we find a slope of −0.65 ± 0.27. This is compatible with the slope of −0.80 ± 0.07 found for Cen A (Fig. 1)7.

2.2. Dwarf galaxies

2.2.1. The MDF of stars in dwarf galaxies

The stellar MDFs of the dwarf elliptical M32 (Grillmair et al. 1996) and irregular galaxy LMC (Cole et al. 2000; Haschke et al. 2012) are very similar to those of the stellar halos of the giant elliptical Cen A and the spiral galaxy M 31 (Harris & Harris 2001). They all show a peak around [M/H] ~ −0.5 with a low metallicity tail extending to [M/H] ~ −2. Fainter dwarf galaxies (−14 <MV< −10), in particular dwarf elliptical (dEs) and dwarf spheroidals (dSphs), show similar shapes of their stellar MDFs, but with much lower peak metallicities of [M/H] −1.5 and extensions of their low metallicity tail to [M/H] ~ −3 (Local Group: Starkenburg et al. 2010; Cen A group: Crnojević et al. 2010; M81 group: Lianou et al. 2010). The mean metallicity of the stellar populations of dwarf galaxies shows a clear trend with galaxy mass and metallicity: the more massive or luminous a galaxy, the higher its mean stellar metallicity, indicating that more massive dwarfs had higher star formation rates or were better able to retain the enriched gas that was released by stellar winds and supernovae (Grebel et al. 2003). The same trend was also found for spirals and ellipticals.

Within dwarf galaxies, the metallicity may vary as a function of distance from the center. For dwarf galaxies in the Local Group (LG), where metallicities can be measured spectroscopically, the age-metallicity degeneracy problem in the interpretation of color-color distributions can be avoided. Leaman et al. (2013) derived the metallicity gradient in the LG dwarf irregular WLM and compared it with those in the LG dSphs and the Magellanic Clouds. The metallicity gradient is small or absent in dIrrs, d [M/H] /d(r/rc) = −0.04 ± 0.04, but clearly present in dSphs, d [M/H] /d(r/rc) ≃ −0.15 ± 0.05, where rc is the core radius, which is typically 0.2 to 0.6 kpc.

Table 1

The contribution of high and low-metallicity objects to the normalized MDFs of stars and clusters in the inner and outer halos of galaxies.

2.2.2. The MDF of globular clusters in dwarf galaxies

Dwarf galaxies have generally very small numbers of GCs so the best way to derive information about their statistical properties is the combination of results of many galaxies of similar types. This has been done for samples of 69 dwarf ellipticals in the Virgo and Fornax clusters (Miller & Lotz 2007) and 57 and 68 nearby mainly dwarf irregulars by Sharina et al. (2005) and Georgiev et al. (2009).

thumbnail Fig. 3

Comparison between the normalized MDF of stars (dotted) and GCs (full lines) in the Fornax dwarf spheroidal galaxy. Each MDF is normalized to 1.

Globular clusters in dwarf galaxies are in general very metal-poor, mostly even more metal-poor than the peak metallicity of the dwarf’s stellar MDF (e.g. Mackey & Gilmore 2004; Sharina et al. 2010). The Fornax dSph, for example, contains four GCs with [M/H] ~ −2.5 to –1.9 and one more metal-rich GC at [M/H] ~ −1.5 dex, whereas its stellar MDF peaks at [M/H] ~ −1.0 with a long tail towards lower metallicities (Strader et al. 2003; Helmi et al. 2006; Larsen et al. 2012b). A similar situation is found in the dwarf galaxy WLM, where the GCs with a metallicity of [M/H] = −2.0 are significantly more metal-poor than the average of –1.3 of the field stars in this galaxy (Leaman et al. 2013; Larsen et al. 2012a). The dwarf galaxy IKN has five GCs but only the metallicity [M/H] = −2.1 of IKN-5 is known with some confidence. The average metallicity of the field stars is between –1.5 an –1.0. (Lianou et al. 2010; Georgiev et al. 2010; Larsen et al. 2014).

Figure 3 shows the MDF of stars and GCs in the Fornax dSph, based on the data by Larsen et al. (2012b). It shows the same trend as the MDFs in the outer halo of Cen A but more extreme: the MDF of the stars peaks near [M/H] ≃ −1 with a low metallicity tail to ≃–2, but the MDF of the GCs is narrower and at lower metallicity than in Cen A. The GCs at [M/H] > −1 are conspicuously absent.

2.3. The specific frequency of clusters in different galaxies

The ratio between the number of clusters and the stellar population can be expressed in terms of the specific frequency, SN = NGC × 100.4(MV + 15) which is the number of GCs relative to the B-magnitude of the Galaxy (Harris & van den Bergh 1981) or the specific luminosity TL = 100 × LGC/LGal (Harris 1991) or the specific mass Sm = 100 × MGC/MGal, where MGal is the stellar mass (Zepf & Ashman 1993; Peng et al. 2008). The dependence of SN or T on galaxy type has been reviewed by Brodie & Strader (2006). The largest dataset of about 100 early type galaxies in the Virgo cluster, shows that the specific mass Sm has a typical low value of about 0.3 for galaxies in the mass range of 9.5 < log (MGal/M⊙) < 11.0 (Peng et al. 2008). This implies that in these galaxies the mass fraction of 0.003 is in clusters. Beyond this mass range, the mean values of Sm increase to both lower and higher mass. Galaxies with MGal ≃ 1012M⊙ reach Sm ~ 1. Galaxies with MGal < 109M⊙ have a large scatter in Sm between 0 and about 2, with nearly all dwarfs with large Sm located within 1 kpc form the cD galaxy M87. This suggests that the cluster formation in dwarfs is biased towards dense environments.

An observable that is key to the present work is the relative specific frequency of metal-poor and metal-rich GCs as a function of galaxy mass. In Peng et al. (2008), SN is derived for both subpopulations. In the mass range of 109 to 1011M⊙ the value of T, which is the total number of clusters per 109M⊙ decreases with galaxy mass from about 30 at M = 109M⊙ to 0.5 at M = 1011M⊙. Over this mass range the fraction of the blue (metal-poor) clusters is between 90 and 70%. Since the metallicity of these galaxies increases with increasing mass, it indicates a decrease of SN with increasing metallicity. This trend is similar to the one found in Cen A (Fig. 1). In galaxies with M > 1011M⊙ the metal-rich fraction flattens or even decreases somewhat, which is likely the result of a substantial fraction of the GC populations in these galaxies stemming from accreted dwarf galaxies.

In galaxies for which the radial distributions of the stellar light and the GC systems both have been measured, the stellar light overall decreases faster with radius than the GC systems. This indicates that the specific frequency or the value of T of the GCs increases with distance. If the GC system is split into red metal-rich clusters and blue metal-poor clusters, the red component always drops steeper with distance and follows the stellar light profile more closely than the blue component. This indicates that T of the blue component increases faster with distance than the red component (Brodie & Strader 2006; Pota et al. 2013). This is in comparison to total stellar light. However, Peacock et al. (2015) have shown for NGC 3115 that if the samples of GCs and stars are both split into blue and red (metal-poor and metal-rich) components, the blue GCs follow the shallow slope of the metal-poor stars. So, the metal-poor clusters follow the same radial distribution as the metal-poor stars and the metal-rich clusters follow the radial trend of the metal-rich stars. Consequently, the cluster-to-star ratio is independent of distance and only dependent on metallicity (in agreement with Figs. 1 and 2 for Cen A and M 31 respectively).

3. Summary of the observations

Table 1 summarizes the differences in the contributions of metal-poor, [M/H] < −1, and metal-rich, [M/H] > −1, stars and clusters at the inner and outer regions of the large galaxies Cen A and M 31 and in the Fornax dSph. For each group of objects (stars or clusters) the sum of the contributions of the high and low metallicity fraction is normalized to 1 in each region. The table also shows the ratio of the cluster-vs-stellar contributions to the MDF at the inner and outer regions of these galaxies, with the adopted boundary indicated. Notice the general trends that:

  • (a)

    In both the inner and outer regions the relative contribution ofthe clusters at low metallicity is larger than that of the stars.

  • (b)

    In both the inner and the outer regions the relative contributions of the clusters at high metallicity is smaller than that of the stars.

  • (c)

    The ratios of the Fornax dSph are more similar to those in the outer regions of the larger galaxies than to the inner regions, with the note that there is not a single cluster at [M/H] > −1. (Due to the low number statistics of only 5 clusters in this galaxy, the value of log(RGC/stars) would have increased to –0.5 if only 1 metal-rich cluster had been found in the Fornax dSph.)

  • (d)

    In the inner and outer regions of the halo of the large spiral galaxy M 31 the cluster-to-star ratio is high at low metallicity and low at high metallicity.

  • (e)

    In dwarf galaxies both the stellar populations and the GC populations are metal-poor, but the clusters are more metal-poor than the stars.

The observations summarized above raise the following questions:

  • Q1.

    Why are the GCs in dwarf galaxies on average moremetal-poor than the stars?

  • Q2.

    In the inner regions of the halos of large galaxies that are dominated by metal-rich stars, why are there no or very few metal-rich clusters (left)?

  • Q3.

    In the outer regions of the halos of large galaxies, that are dominated by metal-poor clusters, why is the metal-poor stellar population that should accompany the clusters absent or very weak?

  • Q4.

    Why does the cluster-to-star ratio, expressed as RGC/stars, decrease so strongly with increasing metallicity in giant elliptical (Cen A), in spiral galaxies (M 31) and dwarf ellipticals (Fornax dSph)?

  • Q5.

    Why is this trend approximately independent of projected radial distance in Cen A and M 31?

To answer these questions we have to consider the formation of clusters in different environments as well as their destruction by various effects. In Sect. 4 we first discuss the formation and in Sects. 5 and 6 we will discuss the destruction of GCs.

4. The formation of globular clusters

In Sects. 4–6 we address possible explanations for the observed differences between the MDFs of halo stars and globular clusters. In order for any explanation to be viable, it should either depend on the metallicity itself, or have an indirect dependence on metallicity due to differences in cosmological environment. We do not consider the metallicity dependence of the star formation rate, because this study concentrates on the relation between clusters and stars which depends only on the cluster formation efficiency (CFE), i.e. the fraction of star formation that ends up in bound clusters, and on cluster destruction. Because more massive clusters have a higher survival probability (see Sect. 5), any environmental dependence of the maximum cluster mass could also be important in setting the globular cluster-to-field star ratio. In this section, we first focus on the mechanisms related to globular cluster formation and any resulting environmental variation of the CFE, residual gas expulsion, and the maximum cluster mass.

Throughout Sects. 4–6, the presented calculations and arguments have been motivated by the observed physical conditions of the ISM and star formation in galaxies at high redshift (z = 1–3), obtained either through adaptive optics observations, sub-mm interferometry, or gravitational lensing (e.g. Förster Schreiber et al. 2009; Genzel et al. 2011; Swinbank et al. 2011, 2012; Livermore et al. 2015; Dessauges-Zavadsky et al. 2017). In (almost) all cases, the environmental dependences of the considered physical mechanisms have been identified and applied in this high-redshift context.

4.1. The cluster formation efficiency and its dependence on metallicity

The zeroth-order solution to the metallicity-dependence of the cluster-to-field-star mass ratio is that the fraction of star formation that results in bound stellar clusters (the cluster formation efficiency or CFE Γ, see Bastian 2008) is a function of metallicity. Specifically, the CFE should decrease with metallicity in order to simultaneously produce the observed MDFs of clusters and field stars. It is therefore relevant to address whether (and how) the CFE can be affected by metallicity or the environment.

Globular clusters are thought to have formed in high-pressure, actively star-forming environments (e.g., Ashman & Zepf 1992; Elmegreen & Efremov 1997; Elmegreen 2010; Shapiro et al. 2010; Kruijssen 2015). The observed metallicity dependence of the cluster-to-star ratio could be explained if the CFE in metal-rich star-forming galaxies is lower than in metal-poor star-forming galaxies. There is a broad relation of increasing metallicity with galaxy mass, from low to high redshift (e.g. Tremonti et al. 2004; Erb et al. 2006), which can be understood by arguing that metals cannot be retained in the shallow potential wells of low-mass galaxies (e.g. Mac Low & Ferrara 1999). This clear and systematic trend of increasing metallicity with galaxy mass has been observed out to z ~ 4 down to stellar masses of M⋆ ~ 5 × 108M⊙ and metallicities [Fe/H] ~ −1.3, with a dependence of decreasing metallicity with redshift (Mannucci et al. 2009). For this reason, metal-poor globular clusters have been proposed to originate from dwarf galaxies (Elmegreen & Efremov 1997; Muratov & Gnedin 2010), whereas metal-rich globular clusters were likely produced in more massive galaxies (Forbes et al. 1997; Shapiro et al. 2010; Kruijssen et al. 2012b). This is a reasonable argument, even if the present-day globular cluster population of a galaxy spans a broad metallicity range, because galaxies are widely thought to have formed hierarchically from a large number of lower-mass progenitors.

The CFE increases with the gas surface density of the galaxy disc Σg, because higher-pressure gas can achieve higher star formation efficiencies, resulting in a larger fraction of all star formation in bound clusters (Kruijssen 2012). In the local Universe, the gas pressure does not exhibit a strong dependence on galaxy mass, as high gas or star formation rate surface densities are observed across the galaxy mass range (see e.g. the compilation by Adamo et al. 2015). However, Kruijssen (2015, Table 1) propose that despite considerable (and possibly dominant) scatter, the higher binding energy of massive galaxies leads to a weak increase of the gas pressure with galaxy mass and (hence) metallicity at a given redshift. The predicted CFEs for globular clusters thus increase with metallicity, which for the observed galaxy mass-metallicity relation at z ~ 3 (Mannucci et al. 2009) leads to Γ = 0.38 at [Fe/H] = −2.3 (this requires an extrapolation of the mass-metallicity relation to metallicities [Fe/H] < −1.3) and Γ = 0.56 at [Fe/H] = −0.6 (Kruijssen 2015). This result cannot explain the observations mentioned in Sect. 2, because they require a higher cluster formation efficiency in low metallicity galaxies8.

In principle, one could also argue that the redshift dependence of galaxy metallicity signifies higher formation redshifts for metal-poor globular clusters than metal-rich ones. This is only partially true observationally (e.g. Forbes & Bridges 2010), but even then the dynamic range of metallicity is too limited for this idea to work. For a Milky Way progenitor galaxy of M⋆ ~ 109M⊙ at z = 4 (cf. Moster et al. 2013), the metallicity is [Fe/H] ~ −1. If the metallicity would only depend on redshift (rather than on galaxy mass during hierarchical galaxy formation), the metal-poor globular clusters should have formed at z ≫ 4, where gas pressures and CFEs were likely lower than at the peak of the cosmic star formation history (z ~ 2, e.g. Madau & Dickinson 2014), leading to a peak CFE at [Fe/H] > −1. This is again in disagreement with the trend of monotonically increasing cluster-to-star ratios towards low metallicities. Metallicity is therefore primarily a tracer of galaxy mass, and only secondarily of redshift.

These theoretical arguments imply that it is unlikely that a metallicity dependence of the CFE can explain the differences between the MDF of halo stars and globular clusters, because it is opposite to the observed metallicity trend of the cluster-to-star ratios. Additionally, the dynamic range of the observed cluster-to-star ratios across the range of GC metallicities in galaxies (spanning three orders of magnitude) is unlikely to be explained by differences in the CFE as that is only expected to vary by a factor of ~ 2.

4.2. The destruction of clusters at young age by gas expulsion (infant mortality)

It has been proposed that, after the formation of a bound stellar cluster is completed, its long-term survival is not necessarily guaranteed due to residual gas expulsion (e.g. Lada et al. 1984; Boily & Kroupa 2003; Baumgardt & Kroupa 2007). The cluster could end up unbound at an early phase if the star formation process was locally inefficient, so that a significant fraction of the cluster mass is in the form of gas. The removal of this gas by stellar winds and radiative heating may unbind the cluster. This will depend on the gas fraction that is expected to remain when feedback obstructs further star formation.

Recent observational and theoretical evidence shows that the star formation process can lead to initially virialised and gas-poor stellar systems before any significant feedback can have taken place (Kruijssen et al. 2012a; Girichidis et al. 2012; Cottaar et al. 2012; Longmore et al. 2014). This implies that newly formed massive clusters do not contain a large amount of gas and hence that the influence of gas expulsion (infant mortality) on the destruction of massive clusters is small (cf. Longmore et al. 2014)9.

Based on the current theoretical picture of cluster formation, infant mortality by gas expulsion is unlikely to explain the observed differences between the MDF of globular clusters and halo stars, provided that globular cluster formation proceeds in a similar way to massive cluster formation observed in the local Universe.

4.3. The environmental dependence of the maximum cluster mass

As we will discuss in Sect. 5, the disruption timescale of clusters in a given environment increases with the cluster mass. This means that the decreasing cluster-to-star ratio with metallicity could be explained if massive clusters are less likely to form in high-metallicity environments. This possibility is explored here.

There is a range of observational evidence showing that the cluster mass function has an exponential truncation at the high-mass end, both for young clusters (e.g. Gieles et al. 2006a; Larsen 2009; Portegies Zwart et al. 2010; Johnson et al. 2017) and globular clusters (e.g. Fall & Zhang 2001; Jordán et al. 2007; Kruijssen & Portegies Zwart 2009). At the same time, it is clear that this maximum mass scale is not universal. Across the aforementioned range of papers, the maximum cluster mass covers Mc = 8 × 103–3 × 106M⊙. It is an important question what causes this large dynamic range and how it may depend on the metallicity.

It was suggested by Kruijssen (2014) that the maximum cluster mass follows from the maximum giant molecular cloud (GMC) mass as Mc = ϵsfΓMGMC, with ϵsf the star formation efficiency (SFE) and MGMC the maximum GMC mass, which is proposed to be set by the Toomre (1964) mass, i.e. the largest self-gravitating scale in a differentially rotating disc. This hypothesis is supported by the good agreement with observed maximum GMC and cluster masses across different galactic environments (Kruijssen 2014; Adamo et al. 2015; Freeman et al. 2017). Reina-Campos & Kruijssen (2017) generalized this model by showing that in environments with low gas surface density and low angular velocity (i.e. shear), the maximum cluster mass is not limited by shear, but by feedback disrupting a collapsing cloud before it has coalesced altogether. This updated model yields excellent agreement with observations of clouds, clumps, and clusters from the local Universe out to high redshift, including the lowest maximum cluster mass observed to date (Mc = 8 × 103M⊙ in M 31, Johnson et al. 2017). Most importantly for the present work, Reina-Campos & Kruijssen (2017) demonstrated that the high-pressure conditions of globular cluster formation (almost) entirely correspond to the shear-limited regime.

In the context of globular cluster formation, Jordán et al. (2007) observed that globular cluster mass functions have maximum mass scales Mc covering a dynamic range of roughly one order of magnitude (Mc = 4 × 105–4 × 106M⊙) in Virgo cluster galaxies, in such a way that Mc increases with galaxy mass M⋆. Kruijssen (2015) combined the Mc−M⋆ relation with the relation between the globular cluster system metallicity and galaxy mass from Peng et al. (2006) to derive an approximate relation of log (Mc/M⊙) ~ 6.5 + 0.7 [Fe/H] and subsequently use this relation to constrain the ISM conditions as a function of metallicity assuming that the maximum globular cluster mass is indeed shear-limited. As a result, it is found that gas pressures, maximum GMC masses, and (as is shown by the above expression) maximum cluster masses all increase with metallicity, analogously to the CFE in Sect. 4.1. This is opposite to the required trend.

While the metallicity dependence of Mc has the wrong sign to explain the observed cluster-to-star ratios, the maximum cluster mass likely plays at least some role in setting the extremes of the globular cluster MDF relative to that of field stars. Because Mc is thought to decrease with cosmic time due to a decrease of the gas pressure (Reina-Campos & Kruijssen 2017), fewer massive (and thus long-lived) clusters per unit field star mass are formed at later times. Due to the increase of the metallicity with cosmic time, this means that the cluster-to-star ratio at high metallicities is lowered further by continued star formation after the peak epoch of globular cluster formation has passed. However, these young stars will not be co-spatial with the older stars and clusters due to differences in the scale height and scale radius of the star-forming disc and the old stellar population. Massive galaxies formed through many minor and/or major mergers and have rich haloes. We therefore do not expect continued star formation to affect the cluster-to-star ratios that we obtain for the galaxy haloes of Cen A and M 31 in several radial bins. It is most likely that the extension of the field star MDF to higher metallicities than globular clusters is simply in accordance with the monotonic (i.e. featureless) decrease of the cluster-to-star ratio towards high metallicities in these galaxies (see Sect. 2). By contrast, continued star formation may have contributed to the low cluster-to-star ratio at high metallicities seen in Fornax, because we cannot separate out the halo due to the galaxy’s dSph morphology.

The MDF of field stars does not only extend further than that of globular clusters at high metallicities, but it also extends further at the low-metallicity end – there are no known globular clusters with metallicities [Fe/H] < −3 (see Sect. 2), but extremely metal-poor field stars do exist (e.g. Frebel & Norris 2015). Because chemical enrichment proceeds extremely rapidly at low metallicity, such stars must have formed at low star formation rate surface densities and thus gas pressures, inhibiting the formation of massive and long-lived clusters. We therefore suggest that the apparent minimum globular cluster metallicity results from a strong decrease of both Mc and Γ at [Fe/H] ≲ −2.5.

The available observational and theoretical evidence suggests that the maximum cluster mass increases with metallicity at high redshift and therefore cannot explain the dearth of globular clusters at high metallicities relative to field stars, which would require the maximum cluster mass to decrease with metallicity so that fewer long-lived clusters are formed towards high metallicities.

5. The destruction of bound globular clusters

Bound clusters that survived the early destruction processes mentioned above, may later dissolve by the loss of stars due to stellar evolution, two-body relaxation with tidal evaporation, and tidal shocks. This dissolution is an important ingredient for understanding the relation between the populations of stars and clusters, because it reduces the cluster population. Cluster dissolution also contributes to the field star population, but this effect is negligible because only a very small fraction of stars is born in bound massive clusters.

The destruction of star clusters is expected to depend on (their location in) the host galaxy. Because the metallicity is a strong function of galaxy mass and since most galaxies have a radial metallicity gradient, with metallicity increasing towards the center, any environmentally-dependent cluster destruction will result in a metallicity-dependent cluster destruction. In principle this might explain qualitatively why the metal-poor and metal-rich globular cluster populations follow different spatial distributions within the halo of their host galaxy, with metal-rich clusters predominantly residing at small galactocentric distances (R< 5 kpc in the Milky Way, Harris 1996).

5.1. Cluster destruction by stellar evolution and tidal evaporation

Clusters orbiting in a galaxy lose stars by tidal evaporation. The mass evolution due to tidal evaporation and stellar evolution can be described by 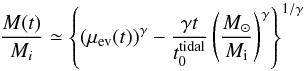(1)with masses in units of M⊙ and γ ≃ 0.65 (Baumgardt & Makino 2003; Lamers et al. 2005, 2010). In this expression μev(t) is the fraction of the mass that is lost by stellar evolution, with μev(t) ≃ 0.3 at t> 10 Gyr. Equation (1) shows that clusters with an initial mass of Mi ≃ 106M⊙ will be destroyed by tidal effect on a timescale of 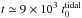. The dissolution parameter 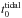for clusters orbiting the center of a galaxy with a logarithmic potential (i.e. a flat rotation curve VGal) is 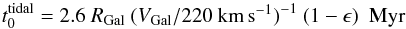(2)where R (in kpc) is the apocenter and ϵ the eccentricity of the cluster orbit (Baumgardt & Makino 2003). This results in 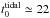Myr for Milky Way clusters on circular orbits at 8.5 kpc. Clusters with Mi = 1 × 106M⊙ will be destroyed within 12 Gyr if 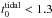Myr. Clusters on circular orbits in spiral galaxies (VGal ≃ 250 km s-1) will only be destroyed by tidal destruction if they are at RGal< 0.5 kpc and those in giant elliptical galaxies (VGal ≃ 500 km s-1) at RGal< 1.2 kpc.

Tidal evaporation and evolution alone can only explain the small metal rich cluster-to-star ratio observed in Cen A and spiral galaxies near their very center. However, the observed trend extends over a much wider distance range.

5.2. Cluster destruction by dynamical friction

In the previous section we have assumed that the orbits of clusters do not change during their lifetime. We now consider the decrease of cluster orbits due to dynamical friction.

Massive objects that are moving in a dense medium consisting of lower-mass bodies experience a gravitational drag that is caused by the gravitational attraction of these bodies towards the wake behind the massive object. Under the right conditions, this dynamical friction can cause massive globular clusters to spiral in towards the centers of their host galaxies (e.g. Chandrasekhar 1943; Tremaine et al. 1975; Capriotti & Hawley 1996; Lotz et al. 2001), where they may be destroyed by tidal evaporation. A simplified expression for the timescale on which an object spirals into the galactic center due to dynamical friction is given in Binney & Tremaine (1987) under the assumption of a flat galaxy rotation curve: 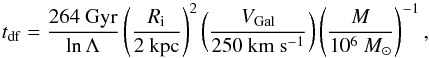(3)where ln Λ ≈ 10 is the Coulomb logarithm of the encounters, Ri is the initial galactocentric radius, VGal is the circular velocity of the host galaxy, and M is the cluster mass. As the formula shows, dynamical friction is more efficient (i.e. the dynamical friction timescale is shorter) for small initial radii, small circular velocities, and large cluster masses. This latter property of dynamical friction contrasts with the dynamical disruption that is discussed in Sect. 5.1, which favors the destruction of low-mass clusters.

Assuming a mean globular cluster mass of 5 × 105M⊙ over the course of their lifetime to account for stellar evolution and dynamical mass loss, Eq. (3) provides a critical initial galactocentric radius within which any globular clusters of age t must have spiraled-in due to dynamical friction, as a function of the circular velocity: 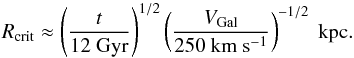(4)For our Galaxy (VGal = 220 km s-1), this expression shows that all globular clusters within a radius of 1 kpc have been lost due to dynamical friction, assuming an age of t ≃ 12 Gyr.

The present-day number density profile of globular clusters in the Milky Way follows a power law with an index of about −2.7 in the range R = 1–10 kpc. Because the profile within 1 kpc has been strongly affected by dynamical friction, to first order we can extrapolate this profile to R = 0 to obtain an initial distribution. Under this assumption, a fraction of (1/5)0.3 = 0.62 of all globular clusters within 5 kpc (where ~ 80% of the metal-rich GCs reside) were formed within a radius of 1 kpc and were thus destroyed within a Hubble time. For a mean cluster mass of 5 × 105M⊙ the critical radius is Rcrit = 0.64 kpc and the fraction of clusters within 5 kpc that are destroyed is 0.54. Metal-poor globular clusters suffered a negligible decline due to their larger average galactocentric radii.

Dynamical friction may have led to the destruction of about half of the clusters formed within RGal< 1 kpc from the center thus explaining the small cluster-to-star ratio close to the Galactic Center, but not the general trend that exists over a much larger distance range.

5.3. Cluster destruction by tidal shocks from the dense interstellar medium of high-redshift galaxies

A considerable body of work has shown that stellar clusters are efficiently destroyed by (impulsive) tidal shocks from passing gas overdensities such as GMCs (e.g. Lamers & Gieles 2006; Gieles et al. 2006b; Kruijssen et al. 2011), especially in the gas-rich environments at high redshift where globular clusters must have formed (Elmegreen 2010; Kruijssen 2015). These works have shown that tidal shocks can be more than an order of magnitude more efficient at destroying clusters than tidal evaporation. The importance of tidal shocks from the ISM is underlined by the observation that there exists a strong correlation between the median cluster age and the ISM surface density and velocity dispersion in nearby galaxies (Miholics et al. 2017).

At face value, tidal shocks could explain the strong dependence of the cluster-to-star ratio on metallicity, because destruction processes provide a large dynamic range – starting from a certain number of clusters per unit field-star mass, disruption can reduce that number by any amount until the Poisson limit of a single globular cluster is reached. In order to be a feasible explanation of the observed metallicity trends, the strength and/or duration of tidal shock-driven disruption must increase with the globular cluster metallicity. It has been proposed by Kruijssen (2015) that this is indeed the case, due to two effects. Firstly, the gas pressure increases towards higher galaxy masses (which have higher metallicities), resulting in increased cluster destruction towards high metallicities. The disruption time of a 105M⊙ cluster is estimated to decrease from a few Gyr at [Fe/H] < −2 to less than 100 Myr at [Fe/H] > −0.7, with a total dynamic range of a factor of ~ 50. Secondly, the duration of tidal-shock driven disruption is expected to weakly increase with metallicity, because the migration of clusters out of the gas-rich environment due to galaxy mergers occurs less frequently towards high galaxy masses. The duration is estimated to range from 0.1–1 Gyr at [Fe/H] < −2 to several Gyr at [Fe/H] > −0.7. By taking the ratio between the disruption timescale and the migration timescale, we find that destruction is more efficient at high metallicities by a factor of 100–1000 than at low metallicities. This agrees very well with the observed trend of the cluster-to-star ratio decreasing by a factor of 100–1000 as a function of metallicity presented in Sect. 210.

Kruijssen (2015) further argued that the migration of globular clusters away from the gas-rich environment of their host galaxies proceeds through galaxy mergers, redistributing the cluster orbits in a way that largely erases their correlation to their birth environment, even if a weak metallicity gradient remains. This may explain why the cluster-to-star ratio depends strongly on the metallicity, but only weakly on the present-day galactocentric radius – the current positions of globular clusters are only an indirect tracer of the high-redshift environment in which most of the disruption took place.

The theoretical arguments outlined here suggest that the differences between the MDF of globular clusters and halo stars may be caused by tidal shock-driven disruption, which proceeds more rapidly and over a longer timescale in higher-metallicity galaxies. The implication of this is that the cluster-to-star ratio does not reflect a formation efficiency, but a survival fraction.

6. The survival of clusters in the cosmological context

In many of the previous sections (all but Sect. 5.3), we have assumed that the clusters are formed in their present host galaxies, and that their destruction depends on the present conditions in these host galaxies. However, these conditions may have changed during the cosmological history. Most generally, the hierarchical galaxy formation process means that present-day galaxies and their haloes have a large number of progenitors at the formation redshift of globular clusters (e.g. De Lucia & Blaizot 2007). Therefore, the only way of understanding intra-galaxy variations of the cluster-to-star ratio at z = 0 is by combining inter-galaxy variations at z ~ 3, which indeed characterizes much of the discussion in this work. In this section we discuss the consequences of hierarchical galaxy growth for the survival of globular clusters.

The mass evolution of globular clusters during the cosmological growth of their host galaxies has traditionally been underemphasised, but recent studies are beginning to address the topic in more detail. Prieto & Gnedin (2008) were the first to insert globular clusters into a dark matter-only simulation of hierarchical structure formation, following their evolution with a semi-analytic model. Their method was expanded by Muratov & Gnedin (2010), who added a simple chemical model to address the emergence of the colour bimodality of globular clusters. Tonini (2013) addressed the build up of globular cluster populations in massive galaxies through semi-analytic modeling using dark-matter only merger trees. Although cluster formation and dissolution formation were not explicitly included in the simulations, the models showed that much of the metal poor globular cluster population in massive galaxies was mostly accreted from dwarf galaxies whereas the metal rich populations formed preferentially in-situ. Hence, a considerable part of the globular clusters in the Milky Way and M 31, possibly even most of the metal-poor clusters, may have originated in captured dwarf galaxies (Cote et al. 1998; Marín-Franch et al. 2009; Lee et al. 2007; Mackey et al. 2010, 2013). A similar scenario was proposed by Hilker et al. (1999) for the central Fornax cluster. So we have to consider their survival in dwarf galaxies for the first epoch of their lives and also where they are accreted into their new host galaxies.

Kruijssen (2015) has developed a semi-analytical model for the formation and evolution of globular cluster populations in a hierarchical galaxy formation context. In the following, we outline several of the main aspects of the model directly relevant to the MDFs of stars and clusters. In doing so, we distinguish between “accreted” and “in-situ” globular clusters, but we acknowledge that this represents a false dichotomy. In reality, galaxies form through hierarchical merging, implying that even the “main body” of a young galaxy is ill-defined and consists of several “ex-situ” progenitors. We use “in-situ” to refer to the globular clusters that formed during the initial collapse of the central galaxy, irrespective of the precise branch of its merger tree.

6.1. Globular clusters formed in-situ

For the globular clusters that formed within the main-body of the young massive galaxy, the conditions that they experienced during their early evolution were very different from their current conditions (i.e. within the bulge/halo of the galaxy). Given the mass-metallicity relation of galaxies, the (proto)massive galaxy is expected to be relatively metal rich, hence should preferentially form metal rich clusters. As seen in local galaxies forming massive stellar clusters (YMCs), clusters form in the gas-rich discs of galaxies, even during major mergers (e.g. Trancho et al. 2007), which likely also applies to globular clusters forming in the early Universe (e.g. Kruijssen 2015). The tidal perturbations from passing GMCs and the tidal field of the host galaxy can cause rapid mass loss amongst the young globular clusters, and if the globular clusters stay in the gas rich discs may completely dissolve. Hence, the first few Gyr of a globular cluster’s life may therefore be characterized by enhanced disruption (e.g. Elmegreen 2010; Kruijssen et al. 2012b).

However, if the young galaxy undergoes a merger, the young globular clusters can be liberated into the halo or bulge of the galaxy, away from the disruptive effects of GMCs (e.g. Kruijssen et al. 2012b). This merger can be major or minor – the globular clusters will escape the gas-rich environment as long as the host galaxy is merging with another galaxy of its own mass or higher. Given that the merger rate of galaxies was significantly higher than in the local Universe, this is expected to be an efficient mechanism in removing globular clusters from their birth-environment, i.e. outside the disk. Once in the halo, globular clusters evolve largely passively, losing mass due to two-body relaxation and (weaker) tidal perturbations (see Sect. 5).

6.2. Accreted globular clusters

As in the more massive spiral and early type galaxies, dwarf galaxies also host metallicity gradients (Tolstoy et al. 2004; Battaglia et al. 2006, 2011; Kirby et al. 2011, 2012), which implies that a metal-rich population of globular clusters will be formed more concentrated towards the centre of a dwarf galaxy, i.e. within a few kpc, than the old metal-poor population. As discussed for the more massive galaxies, the metal rich clusters near the centre of the galaxy (i.e. those within ≲2 kpc) have a lower survival probability than those outside the central regions, meaning that cluster dissolution will push the star-to-cluster ratio to higher values for the metal rich populations. In the outskirts of dwarfs, globular clusters are likely to survive for long periods meaning that their star-to-cluster ratios will be more reflective of their initial conditions than the central regions. However, the above works show that the range of metallicities of stars that formed in-situ within a single galaxy rarely exceeds more than an order of magnitude11. The more than 2 orders of magnitude in metallicity covered by globular cluster populations must therefore be obtained by merging galaxies of different masses.

When massive spirals/ellipticals accrete dwarf galaxies, they also accrete their globular cluster populations. Where the globular clusters of dwarf galaxies end up within the more massive host depends on the location of the globular clusters within the dwarf at the time of accretion and also on the mass of the dwarf galaxy. More massive dwarfs have larger binding energies, hence can survive the accretion onto the massive galaxy for a longer period. This means that they are more likely to deposit their globular clusters closer to the centre of the massive galaxy. Likewise, globular clusters on the outskirts of the dwarfs at the time of accretion (which are more likely to be metal poor) will be lost into the (outer) halo of the more massive galaxy. Hence, the majority of metal-poor globular clusters from dwarf galaxies are likely (though not required) to be contributed to the (outer) halo of the more massive galaxy and, as a result, the dissolution parameter of the accreted globular clusters hardly changes during accretion (e.g. Rieder et al. 2013). Indeed, as discussed in Sects. 2.2.1 and 3, the outer halos of the MW, M 31 and Cen-A are similar to that of dwarf galaxies in terms of the MDFs of their stars and globular clusters.

6.3. The hierarchical assembly of globular cluster systems and the role of metallicity

As discussed in Sect. 5, we expect that most of the physics governing globular cluster formation and disruption were set by their environment at the time of formation. Specifically, the host galaxy mass at formation determined the formation efficiencies, maximum cluster masses, and (most importantly) the metallicity and cluster disruption timescales. We can no longer directly measure the mass of the galaxy in which a globular cluster formed. However, in the context of the above picture of hierarchical galaxy formation and globular cluster system assembly, we see that the globular cluster metallicities are good tracers of the masses of the host galaxies in which they formed (e.g. Kruijssen 2015), thanks to the galaxy mass–metallicity relation, with a second-order dependence on the galactocentric radii in these galaxies.

Hierarchical galaxy growth weakens the relation between globular clusters and their (position within the) host galaxy, but the globular cluster metallicities are a good tracer of the host galaxy masses where globular clusters formed. Because the initial environment sets their formation and survival probability, it may not be surprising that the cluster-to-star ratio shows a clear trend with metallicity, that appears to be independent galactocentric distance in massive galaxies, and results in dissimilar MDFs of globular clusters and field stars.

7. Discussion and conclusions

We have collected and reviewed information on the globular cluster-to-star ratios, RGC/stars, in different types of galaxies as a function of galactic mass and metallicity, and as a function of metallicity and location within galaxies. The data show the following:

  • 1.

    The mean metallicity of galaxies is related to their mass, with themost massive galaxies having the highest metallicities.

  • 2.

    The cluster specific frequency, SN = Ncl/Mstars, depends on galaxy mass with the highest values in the least massive galaxies.

  • 3.

    Within a single galaxy, RGC/stars is a strong function of metallicity, with the highest ratio at low metallicity and the lowest ratio at high metallicity, and a total dynamic range as high as 2–3 orders of magnitude.

  • 4.

    One of the most extreme examples is the Fornax dSph, which has 5 clusters at [M/H] < −1 and no clusters at [M/H] > −1 although the stellar MDF peaks at [M/H] = −1. The dwarf galaxy IKN with a stellar population of [M/H] around –1.3 and one of its five clusters, viz. IKN-5 at –2.1 is another extreme example.

  • 5.

    Due to a gradient of decreasing metallicity with galactocentric distance, RGC/stars is also a function of distance, with the smallest values near the centre, but it is unclear to what extent this dependence remains after accounting for the metallicity gradient.

We acknowledge that most of these trends were already found and discussed individually in the literature (see Sect. 2). They are repeated here because we want to show the overall picture presented by the observations and try to explain them in a coherent cosmological cluster evolution framework.

For the interpretation of these observations it is important to realize that under all star forming conditions, the fraction of the mass that ends up in massive clusters with Mi> 105M⊙ is small compared to the mass of the field stars, because most of the stars end up in unbound associations or in low mass clusters that are easily dissolved by tidal evaporation and tidal shocks. This implies that RGC/stars depends on the cluster formation efficiency, CFE, of massive clusters (M> 105M⊙) and cluster destruction, and not on the star formation efficiency.

We discussed the various mechanisms that affect the cluster-to-star ratio. We first considered the dependence of the formation efficiency and early survival of clusters on the metallicity and environment.

  • (i)

    The cluster formation efficiency has a weak (and indirect)dependence on metallicity, but the predicted trend cannot explainthe observations, because the CFE is expected to be higher in highmetallicity environments, in contrast to the observed lowcluster-to-star ratio in the inner halo (Sect. 4.1).

  • (ii)

    “Infant mortality” of young clusters by gas expulsion cannot explain the observations, because in the dense environment where massive clusters are born, the amount of gas in young globular clusters is too small to unbind the clusters (Sect. 4.2).

  • (iii)

    Because GCs are typically massive, M> 104M⊙, the formation efficiency of GCs depends on the maximum mass of clusters that can be formed in various environments. Theoretical arguments, supported by observational evidence, suggest that the maximum cluster mass increases with increasing mass of giant molecular clouds, which depends on the mass and density of the galaxy and hence on the metallicity. Therefore the formation efficiency of GCs is expected to increase with increasing metallicity. This is contrary to the observed decrease of RGC/stars with increasing [M/H] (Sect. 4.3).

Considering that cluster formation does not seem to explain the observed trends, we also discussed the destruction of GCs in various environments.

  • (iv)

    Dissolution of clusters by tidal evaporation depends on thegalactic potential at the distance of their orbits. In principle, clus-ters in small orbits are destroyed faster than clusters in wide orbits.If the GCs are formed in-situ in galaxies with a radial metallicitygradient, the metal rich clusters will be destroyed more easilythan metal poor clusters on wider orbits. However, we found thattidal evaporation alone can only destroy GCs within a Hubbletime if they are on circular orbits within ~ 1 kpc (unlessthey are on highly elliptical orbits). This may explain the lack ofmetal rich GCs in the very centre of massive galaxies. Howeverthe observed trend of RGC/stars with metallicity extendsover a much wider distance range, implying that tidal evaporationcannot be responsible (Sect. 5.1).

  • (v)

    Dynamical friction leads to the inspiraling of clusters towards the galactic centre. Contrary to dissolution, the lifetimes of clusters for spiraling into the galactic centre decreases with mass, tdf ∝ RGal2 × M-1. When clusters spiral in to very small orbits, they will be destroyed by tidal evaporation and shocks. We quantified the effect due to evaporation in typical spiral galaxies and found that it will reduce the surviving number of massive clusters with M ≃ 5 × 105M⊙ on orbits smaller than about 1 kpc. This may explain the small cluster-to-star ratios of metal-rich clusters observed in the center of massive galaxies. However, the observed trend with metallicity extends over a much wider distance range (Sect. 5.2).

  • (vi)

    Clusters can also be destroyed by tidal shocks. In gas-rich galaxies at high redshift, where GCs must have formed, the destruction of GCs by tidal shocks can be orders of magnitude more efficient than tidal evaporation. We studied the environmental conditions during GC formation and found that shock-driven destruction in the environment where metal-rich clusters are formed is 100–1000 times more efficient than in the environment where metal-poor GCs are formed. This quantitatively agrees with the observed large range of RGC/stars with metallicity. It also shows that RGC/stars does not reflect the cluster formation efficiency, but the survival probability (Sect. 5.3).

Since galaxies are formed hierarchically and the present day surviving GCs have followed the history of the galaxies in which they we formed originally, we also considered the fate of clusters in the context of hierarchical galaxy formation.

  • (vii)

    GCs that formed in-situ in the high density environment ofgas-rich disks may leave their shock-destructive formationenvironment during a merger with a galaxy of the same or highermass. This is an efficient mechanism to move GCs out of the disk.Once they are in the halo, the GCs evolve passively and lose massinefficiently by tidal evaporation (Sect. 6.1).

  • (viii)

    The radial metallicity gradients in present-day spirals covers only a factor ~ 10, which is much smaller than the range in metallicity of the GCs in a galaxy, ~ 100 to 1000. Therefore the metal-poor GCs must have been captured from low-metallicity dwarf galaxies during the hierarchical growth of the central galaxy. Low-mass dwarf galaxies with low-metallicity GCs have a small binding energy, causing their clusters to be released in the low-density halo of the capturing galaxy. On the other hand, more massive dwarfs with more metal-rich GCs have stronger binding energy and will release their GCs deeper into the capturing galaxy. This explains, at least qualitatively, the radial metallicity gradient of GCs as a reflection of the host galaxy mass at GC formation (Sect. 6.2).

  • (ix)

    The merging of galaxies and the capture of GCs implies that the present-day location of the GCs is not a good indicator of their formation environment. However, combining the results presented above, in particular conclusions (vi), (vii) and (viii), imply that the RGC/stars is expected to depend strongly on metallicity and only weakly on galactocentric distance in their present host galaxy. This is qualitatively in agreement with the observed trends (Sect. 6.3).

When we discussed the observations in Sect. 3 we posed five specific questions. We can now tentatively try to answer these.

  • Q1.

    GCs in dwarf galaxies are more metal-poor than the stars,because the metal-rich clusters are formed in high densityenvironments where destruction by shocks is efficient. This maybe exacerbated by continued star and (low-mass) clusterformation in dwarfs that added metal-rich stars but no metal-richglobular clusters12.

  • Q2.

    The same arguments apply to the inner regions of the halos of large galaxies. Metal-rich clusters formed in-situ will be destroyed by shocks in their original environment. In addition, dynamical friction may have led to the destruction of the innermost clusters.

  • Q3.

    The metal-poor clusters in the outer halos of large galaxies are captured from low-mass dwarfs that had a low binding energy. The destruction rate in these dwarf galaxies and in the outer halo is small, so these clusters have a higher survival probability.

  • Q4.

    The strong dependence of the cluster-to-star ratio on metallicity is the result of the fact that the low-metallicity clusters were formed in dwarfs where the shock destruction is not efficient, whereas the more metal-rich clusters are formed in more massive galaxies (because metallicity increases with galaxy mass) where the environment is more destructive.

  • Q5.

    The present day location of GCs is only weakly related to their original location and environment. The dominant factor that sets the survival probability of clusters is the metallicity (via the relation between metallicity and galaxy mass). Hierarchical galaxy growth weakens initial radial trends. That is why the relation between RGC/stars and [M/H] is almost independent of distance.

Many of the effects proposed in this paper are only described qualitatively. In future work, we intend to quantify the framework sketched in this work using self-consistent numerical simulations of globular cluster formation and evolution during galaxy formation (Pfeffer et al., in prep.; Kruijssen et al., in prep.). Such simulations will allow us to directly follow the evolution of the cluster and field star MDFs while galaxies are forming and the cluster population is evolving due to the ongoing formation and destruction of stellar clusters.

1

The cluster-to-star ratio is the mass of stars in clusters compared to the mass of field stars in the same area of a galaxy.

2

This may be an observational selection effect due to the large effective radii, or more extended metal-poor halo components of these galaxies.

3

See Woodley et al. (2010) for the calibration from (C–T1) colour to [Fe/H] metallicity.

4

Note that Gonzalez et al. (2011) used near-IR photometric bands (J and Ks), and Streich et al. (2014) caution that metallicity determinations from RGB alone have an accuracy of 0.3 dex for simple stellar populations for [M/H] ≲−1 and 0.15 dex for [M/H] ≳−1.

5

NB: This does not mean that the cluster to star ratio Ncl/Nstars is the same in the 3 regions because we used the normalized MDFs. The absolute values are not known, because the star-counts and the cluster-counts do not cover the same region of Cen A.

6

Until more observations become available, this is presently the best one can do. Ibata et al. (2014) showed that the M 31 most metal-poor populations ([M/H] < −1.7) are distributed approximately spherically with only a relatively small fraction residing in discernible stream-like structures. More metal-rich populations contain larger fractions of stars in streams with the stream fraction reaching 86% at [M/H] > −0.6. So, actually the shape of the halo stellar distribution changes with metallicity. It should be noted that also GCs are not homogeneously distributed and appear to be more abundant in the streams.

7

A similar comparison for the Milky Way is seriously hampered by the fact that the stellar MDF can only be measured at the solar radius, RGal( ⊙ ) = 8 kpc, as a function of height | Z | above or below the Galactic plane where the sample may be contaminated by thick disk stars up to | Z | ~ 7 kpc (Jurić et al. 2008).

8

In addition, we note that the observed full dynamic range of the CFE is only a factor of 50 (e.g. Goddard et al. 2010; Adamo et al. 2015; Johnson et al. 2016). Even if one would extend this to the extreme case of Γ = 1, the total dynamic range of the CFE is two orders of magnitude. For the conditions under which GCs are likely to form (P/k = 106–109 K cm-3, Elmegreen & Efremov 1997), the CFE is only expected to vary by a factor of ~ 2 (Γ = 0.3–0.6, Kruijssen 2012). This range is considerably smaller than the required dynamic range of three orders of magnitude in the star-to-cluster ratios across the metallicity range (see Sect. 2).

9

The expulsion of residual gas may lead to the dispersal of young stellar associations, but they are irrelevant to the question at hand because we are considering massive clusters.

10

At first sight, it may seem like the large (factor of 100–1000) range in disruption timescales as a function of metallicity should result in a strong relation between metallicity and the peak mass of the globular cluster mass function (GCMF), which is thought to have been shaped by cluster disruption (e.g. Elmegreen & Efremov 1997; Fall & Zhang 2001). Such a relation is not observed (Jordán et al. 2007). However, it was shown by Kruijssen (2015, Fig. 3) that these large differences in disruption timescale lead to a range of GCMF peak masses at z = 0 that only spans a factor of 3, in quantitative agreement with the observed dependence of the peak mass on galaxy mass (Jordán et al. 2007). This weakened metallicity dependence arises for three reasons. Firstly, cluster disruption by tidal shocks becomes highly inefficient at cluster masses >106M⊙, because the crossing time of the cluster becomes shorter than the typical duration of perturbations. As a result, the GCMF peak mass hardly increases any further due to disruption. Secondly, the initial cluster mass function rapidly steepens near the maximum cluster mass scale Mc, which limits the maximum peak mass attainable by disruption. Thirdly, the remaining metallicity trend of the peak mass is largely erased during subsequent mass loss by evaporation in the galactic halo.

11

The metallicity gradient in the galactic disk, determined from Cepheids at 5 <R< 17 kpc, is about –0.05 dex/kpc (Lemasle et al. 2008) which implies a decrease in metallicity by only a factor 3 over a distance of 10 kpc.

12

This effect is most important in dwarf galaxies, because there we cannot separate the halo field stars from the younger disc field stars.

Acknowledgments

The authors thank the referee, Søren Larsen, and Bill Harris for extensive and constructive feedback that greatly improved this work. H.J.G.L.M.L. thanks ESO for a Visiting Scientist Fellowship at Garching, the LKBF for a travel grant to Liverpool, and Heidelberg University for a visiting scientist grant through Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject P1) of the German Research Foundation (DFG). J.M.D.K. gratefully acknowledges funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (grant number KR4801/1-1, PI Kruijssen), and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme via the ERC Starting Grant MUSTANG (grant agreement number 714907, PI Kruijssen). N.B. is partially funded by a Royal Society University Research Fellowship and a European Research Council (ERC) Consolidator Grant (Multi-Pop, grant agreement number 646928).

References

  1. Adamo, A., Kruijssen, J. M. D., Bastian, N., Silva-Villa, E., & Ryon, J. 2015, MNRAS, 452, 246 [NASA ADS] [CrossRef] [Google Scholar]
  2. An, D., Beers, T. C., Johnson, J. A., et al. 2012, ASP Conf. Ser., 458, 179 [Google Scholar]
  3. Ashman, K. M., & Zepf, S. E. 1992, ApJ, 384, 50 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barker, M. K., Ferguson, A. M. N., Irwin, M. J., Arimoto, N., & Jablonka, P. 2012, MNRAS, 419, 1489 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bastian, N. 2008, MNRAS, 390, 759 [NASA ADS] [CrossRef] [Google Scholar]
  6. Battaglia, G., Tolstoy, E., Helmi, A., et al. 2006, A&A, 459, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Battaglia, G., Tolstoy, E., Helmi, A., et al. 2011, MNRAS, 411, 1013 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  8. Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
  9. Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef] [Google Scholar]
  10. Beasley, M. A., Bridges, T., Peng, E., et al. 2008, MNRAS, 386, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bekki, K., Forbes, D. A., Beasley, M. A., & Couch, W. J. 2002, MNRAS, 335, 1176 [NASA ADS] [CrossRef] [Google Scholar]
  12. Binney, J., & Tremaine, S. 1987, in Galactic Dynamics (Princeton, NJ: Princeton University Press), 747 [Google Scholar]
  13. Boily, C. M., & Kroupa, P. 2003, MNRAS, 338, 665 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brodie, J. P., Usher, C., Conroy, C., et al. 2012, ApJ, 759, L33 [NASA ADS] [CrossRef] [Google Scholar]
  16. Burgarella, D., Kissler-Patig, M., & Buat, V. 2001, AJ, 121, 2647 [NASA ADS] [CrossRef] [Google Scholar]
  17. Capriotti, E. R., & Hawley, S. L. 1996, ApJ, 464, 765 [NASA ADS] [CrossRef] [Google Scholar]
  18. Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chandrasekhar, S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chapman, S. C., Ibata, R., Lewis, G. F., et al. 2006, ApJ, 653, 255 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cole, S., Lacey, C. G., Baugh, C. M., & Frenk, C. S. 2000, MNRAS, 319, 168 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cote, P., Marzke, R. O., & West, M. J. 1998, ApJ, 501, 554 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cottaar, M., Meyer, M. R., Andersen, M., & Espinoza, P. 2012, A&A, 539, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Crnojević, D., Grebel, E. K., & Koch, A. 2010, A&A, 516, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Crnojević, D., Ferguson, A. M. N., Irwin, M. J., et al. 2013, MNRAS, 432, 832 [NASA ADS] [CrossRef] [Google Scholar]
  26. De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dessauges-Zavadsky, M., Schaerer, D., Cava, A., Mayer, L., & Tamburello, V. 2017, ApJ, 836, L22 [NASA ADS] [CrossRef] [Google Scholar]
  28. Durrell, P. R., Harris, W. E., & Pritchet, C. J. 2001, AJ, 121, 2557 [NASA ADS] [CrossRef] [Google Scholar]
  29. Durrell, P. R., Harris, W. E., & Pritchet, C. J. 2004, AJ, 128, 260 [NASA ADS] [CrossRef] [Google Scholar]
  30. Durrell, P. R., Sarajedini, A., & Chandar, R. 2010, ApJ, 718, 1118 [NASA ADS] [CrossRef] [Google Scholar]
  31. Elmegreen, B. G. 2010, ApJ, 712, L184 [NASA ADS] [CrossRef] [Google Scholar]
  32. Elmegreen, B. G., & Efremov, Y. N. 1997, ApJ, 480, 235 [NASA ADS] [CrossRef] [Google Scholar]
  33. Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
  35. Forbes, D. A., & Bridges, T. 2010, MNRAS, 404, 1203 [NASA ADS] [Google Scholar]
  36. Forbes, D. A., Brodie, J. P., & Grillmair, C. J. 1997, AJ, 113, 1652 [NASA ADS] [CrossRef] [Google Scholar]
  37. FörsterSchreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  38. Frebel, A., & Norris, J. E. 2015, ARA&A, 53, 631 [NASA ADS] [CrossRef] [Google Scholar]
  39. Freeman, P., Rosolowsky, E., Kruijssen, J. M. D., Bastian, N., & Adamo, A. 2017, MNRAS, 468, 1769 [NASA ADS] [CrossRef] [Google Scholar]
  40. Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
  41. Galleti, S., Federici, L., Bellazzini, M., Fusi Pecci, F., & Macrina, S. 2004, A&A, 416, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Galleti, S., Bellazzini, M., Buzzoni, A., Federici, L., & Fusi Pecci, F. 2009, A&A, 508, 1285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gebhardt, K., & Kissler-Patig, M. 1999, AJ, 118, 1526 [NASA ADS] [CrossRef] [Google Scholar]
  44. Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [NASA ADS] [CrossRef] [Google Scholar]
  45. Georgiev, I. Y., Puzia, T. H., Hilker, M., & Goudfrooij, P. 2009, MNRAS, 392, 879 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Georgiev, I. Y., Puzia, T. H., Goudfrooij, P., & Hilker, M. 2010, MNRAS, 406, 1967 [NASA ADS] [Google Scholar]
  47. Gieles, M., Larsen, S. S., Anders, P., Bastian, N., & Stein, I. T. 2006a, A&A, 450, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006b, MNRAS, 371, 793 [NASA ADS] [CrossRef] [Google Scholar]
  49. Gilbert, K. M., Kalirai, J. S., Guhathakurta, P., et al. 2014, ApJ, 796, 76 [NASA ADS] [CrossRef] [Google Scholar]
  50. Girichidis, P., Federrath, C., Allison, R., Banerjee, R., & Klessen, R. S. 2012, MNRAS, 420, 3264 [NASA ADS] [CrossRef] [Google Scholar]
  51. Goddard, Q. E., Bastian, N., & Kennicutt, R. C. 2010, MNRAS, 405, 857 [NASA ADS] [Google Scholar]
  52. Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
  54. Grebel, E. K., Gallagher, III, J. S., & Harbeck, D. 2003, AJ, 125, 1926 [NASA ADS] [CrossRef] [Google Scholar]
  55. Gregersen, D., Seth, A. C., Williams, B. F., et al. 2015, AJ, 150, 189 [NASA ADS] [CrossRef] [Google Scholar]
  56. Grillmair, C. J., Lauer, T. R., Worthey, G., et al. 1996, AJ, 112, 1975 [NASA ADS] [CrossRef] [Google Scholar]
  57. Harmsen, B., Monachesi, A., Bell, E. F., et al. 2017, MNRAS, 466, 1491 [NASA ADS] [CrossRef] [Google Scholar]
  58. Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
  59. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  60. Harris, W. E. 2001, in Saas-Fee Advanced Course 28: Star Clusters, eds. L. Labhardt, & B. Binggeli, 223 [Google Scholar]
  61. Harris, W. E. 2003, in Extragalactic Globular Cluster Systems, ed. M. Kissler-Patig, 317 [Google Scholar]
  62. Harris, G. L. H., & Harris, W. E. 2000, AJ, 120, 2423 [NASA ADS] [CrossRef] [Google Scholar]
  63. Harris, W. E., & Harris, G. L. H. 2001, AJ, 122, 3065 [NASA ADS] [CrossRef] [Google Scholar]
  64. Harris, W. E., & Harris, G. L. H. 2002, AJ, 123, 3108 [NASA ADS] [CrossRef] [Google Scholar]
  65. Harris, W. E., & van den Bergh, S. 1981, AJ, 86, 1627 [NASA ADS] [CrossRef] [Google Scholar]
  66. Harris, G. L. H., Harris, W. E., & Poole, G. B. 1999, AJ, 117, 855 [NASA ADS] [CrossRef] [Google Scholar]
  67. Harris, W. E., Harris, G. L. H., Layden, A. C., & Stetson, P. B. 2007a, AJ, 134, 43 [NASA ADS] [CrossRef] [Google Scholar]
  68. Harris, W. E., Harris, G. L. H., Layden, A. C., & Wehner, E. M. H. 2007b, ApJ, 666, 903 [NASA ADS] [CrossRef] [Google Scholar]
  69. Harris, G. L. H., Rejkuba, M., & Harris, W. E. 2010, PASA, 27, 457 [NASA ADS] [CrossRef] [Google Scholar]
  70. Harris, W. E., Blakeslee, J. P., Whitmore, B. C., et al. 2016, ApJ, 817, 58 [NASA ADS] [CrossRef] [Google Scholar]
  71. Harris, W. E., Ciccone, S. M., Eadie, G. M., et al. 2017, ApJ, 835, 101 [NASA ADS] [CrossRef] [Google Scholar]
  72. Haschke, R., Grebel, E. K., Duffau, S., & Jin, S. 2012, AJ, 143, 48 [NASA ADS] [CrossRef] [Google Scholar]
  73. Helmi, A., Irwin, M. J., Tolstoy, E., et al. 2006, ApJ, 651, L121 [NASA ADS] [CrossRef] [Google Scholar]
  74. Hilker, M., Infante, L., & Richtler, T. 1999, A&AS, 138, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014, ApJ, 780, 128 [NASA ADS] [CrossRef] [Google Scholar]
  76. Johnson, L. C., Seth, A. C., Dalcanton, J. J., et al. 2016, ApJ, 827, 33 [NASA ADS] [CrossRef] [Google Scholar]
  77. Johnson, L. C., Seth, A. C., Dalcanton, J. J., et al. 2017, ApJ, 839, 78 [NASA ADS] [CrossRef] [Google Scholar]
  78. Jordán, A., McLaughlin, D. E., Côté, P., et al. 2007, ApJS, 171, 101 [NASA ADS] [CrossRef] [Google Scholar]
  79. Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  80. Kalirai, J. S., Gilbert, K. M., Guhathakurta, P., et al. 2006, ApJ, 648, 389 [NASA ADS] [CrossRef] [Google Scholar]
  81. Kirby, E. N., Lanfranchi, G. A., Simon, J. D., Cohen, J. G., & Guhathakurta, P. 2011, ApJ, 727, 78 [NASA ADS] [CrossRef] [Google Scholar]
  82. Kirby, E. N., Cohen, J. G., & Bellazzini, M. 2012, ApJ, 751, 46 [NASA ADS] [CrossRef] [Google Scholar]
  83. Kirby, E. N., Cohen, J. G., Guhathakurta, P., et al. 2013, ApJ, 779, 102 [NASA ADS] [CrossRef] [Google Scholar]
  84. Kruijssen, J. M. D. 2012, MNRAS, 426, 3008 [NASA ADS] [CrossRef] [Google Scholar]
  85. Kruijssen, J. M. D. 2014, Class. Quantum Grav., 31, 244006 [Google Scholar]
  86. Kruijssen, J. M. D. 2015, MNRAS, 454, 1658 [NASA ADS] [CrossRef] [Google Scholar]
  87. Kruijssen, J. M. D., & Portegies Zwart, S. F. 2009, ApJ, 698, L158 [NASA ADS] [CrossRef] [Google Scholar]
  88. Kruijssen, J. M. D., Pelupessy, F. I., Lamers, H. J. G. L. M., Portegies Zwart, S. F., & Icke, V. 2011, MNRAS, 414, 1339 [NASA ADS] [CrossRef] [Google Scholar]
  89. Kruijssen, J. M. D., Maschberger, T., Moeckel, N., et al. 2012a, MNRAS, 419, 841 [NASA ADS] [CrossRef] [Google Scholar]
  90. Kruijssen, J. M. D., Pelupessy, F. I., Lamers, H. J. G. L. M., et al. 2012b, MNRAS, 421, 1927 [NASA ADS] [CrossRef] [Google Scholar]
  91. Lada, C. J., Margulis, M., & Dearborn, D. 1984, ApJ, 285, 141 [NASA ADS] [CrossRef] [Google Scholar]
  92. Lamers, H. J. G. L. M., & Gieles, M. 2006, A&A, 455, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Lamers, H. J. G. L. M., Gieles, M., Bastian, N., et al. 2005, A&A, 441, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Lamers, H. J. G. L. M., Baumgardt, H., & Gieles, M. 2010, MNRAS, 409, 305 [NASA ADS] [CrossRef] [Google Scholar]
  95. Larsen, S. S. 2009, A&A, 494, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Larsen, S. S., Brodie, J. P., Huchra, J. P., Forbes, D. A., & Grillmair, C. J. 2001, AJ, 121, 2974 [NASA ADS] [CrossRef] [Google Scholar]
  97. Larsen, S. S., Brodie, J. P., & Strader, J. 2012a, A&A, 546, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Larsen, S. S., Strader, J., & Brodie, J. P. 2012b, A&A, 544, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Larsen, S. S., Brodie, J. P., Forbes, D. A., & Strader, J. 2014, A&A, 565, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Leaman, R., Venn, K. A., Brooks, A. M., et al. 2013, ApJ, 767, 131 [NASA ADS] [CrossRef] [Google Scholar]
  101. Lee, M. G., & Jang, I. S. 2016, ApJ, 822, 70 [NASA ADS] [CrossRef] [Google Scholar]
  102. Lee, Y.-W., Gim, H. B., & Casetti-Dinescu, D. I. 2007, ApJ, 661, L49 [NASA ADS] [CrossRef] [Google Scholar]
  103. Lemasle, B., François, P., Piersimoni, A., et al. 2008, A&A, 490, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Lianou, S., Grebel, E. K., & Koch, A. 2010, A&A, 521, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Liu, C., Peng, E. W., Jordán, A., et al. 2011, ApJ, 728, 116 [NASA ADS] [CrossRef] [Google Scholar]
  106. Livermore, R. C., Jones, T. A., Richard, J., et al. 2015, MNRAS, 450, 1812 [NASA ADS] [CrossRef] [Google Scholar]
  107. Longmore, S. N., Kruijssen, J. M. D., Bastian, N., et al. 2014, Protostars and Planets VI, 291 [Google Scholar]
  108. Lotz, J. M., Telford, R., Ferguson, H. C., et al. 2001, ApJ, 552, 572 [NASA ADS] [CrossRef] [Google Scholar]
  109. Mac Low, M.-M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
  110. Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 355, 504 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  111. Mackey, A. D., Huxor, A. P., Ferguson, A. M. N., et al. 2010, ApJ, 717, L11 [NASA ADS] [CrossRef] [Google Scholar]
  112. Mackey, A. D., Huxor, A. P., Ferguson, A. M. N., et al. 2013, MNRAS, 429, 281 [NASA ADS] [CrossRef] [Google Scholar]
  113. Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
  114. Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  115. Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
  116. Miholics, M., Kruijssen, J. M. D., & Sills, A. 2017, MNRAS, submitted [Google Scholar]
  117. Miller, B. W., & Lotz, J. M. 2007, ApJ, 670, 1074 [NASA ADS] [CrossRef] [Google Scholar]
  118. Moore, B., Diemand, J., Madau, P., Zemp, M., & Stadel, J. 2006, MNRAS, 368, 563 [NASA ADS] [CrossRef] [Google Scholar]
  119. Moran, C. C., Teyssier, R., & Lake, G. 2014, MNRAS, 442, 2826 [NASA ADS] [CrossRef] [Google Scholar]
  120. Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
  121. Mouhcine, M. 2006, ApJ, 652, 277 [NASA ADS] [CrossRef] [Google Scholar]
  122. Mouhcine, M., Rich, R. M., Ferguson, H. C., Brown, T. M., & Smith, T. E. 2005, ApJ, 633, 828 [NASA ADS] [CrossRef] [Google Scholar]
  123. Mouhcine, M., Rejkuba, M., & Ibata, R. 2007, MNRAS, 381, 873 [Google Scholar]
  124. Mould, J., & Spitler, L. 2010, ApJ, 722, 721 [NASA ADS] [CrossRef] [Google Scholar]
  125. Muratov, A. L., & Gnedin, O. Y. 2010, ApJ, 718, 1266 [NASA ADS] [CrossRef] [Google Scholar]
  126. Peacock, M. B., Strader, J., Romanowsky, A. J., & Brodie, J. P. 2015, ApJ, 800, 13 [NASA ADS] [CrossRef] [Google Scholar]
  127. Peng, E. W., Jordán, A., Côté, P., et al. 2006, ApJ, 639, 95 [NASA ADS] [CrossRef] [Google Scholar]
  128. Peng, E. W., Jordán, A., Côté, P., et al. 2008, ApJ, 681, 197 [NASA ADS] [CrossRef] [Google Scholar]
  129. Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
  130. Pota, V., Forbes, D. A., Romanowsky, A. J., et al. 2013, MNRAS, 428, 389 [NASA ADS] [CrossRef] [Google Scholar]
  131. Prieto, J. L., & Gnedin, O. Y. 2008, ApJ, 689, 919 [NASA ADS] [CrossRef] [Google Scholar]
  132. Reina-Campos, M., & Kruijssen, J. M. D. 2017, MNRAS, 469, 1282 [NASA ADS] [CrossRef] [Google Scholar]
  133. Rejkuba, M., Greggio, L., Harris, W. E., Harris, G. L. H., & Peng, E. W. 2005, ApJ, 631, 262 [NASA ADS] [CrossRef] [Google Scholar]
  134. Rejkuba, M., Mouhcine, M., & Ibata, R. 2009, MNRAS, 396, 1231 [Google Scholar]
  135. Rejkuba, M., Harris, W. E., Greggio, L., et al. 2014, ApJ, 791, L2 [NASA ADS] [CrossRef] [Google Scholar]
  136. Rieder, S., Ishiyama, T., Langelaan, P., et al. 2013, MNRAS, 436, 3695 [NASA ADS] [CrossRef] [Google Scholar]
  137. Ryan, S. G., & Norris, J. E. 1991, AJ, 101, 1865 [NASA ADS] [CrossRef] [Google Scholar]
  138. Saviane, I., Rosenberg, A., Piotto, G., & Aparicio, A. 2000, A&A, 355, 966 [NASA ADS] [Google Scholar]
  139. Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Shapiro, K. L., Genzel, R., & Förster Schreiber, N. M. 2010, MNRAS, 403, L36 [NASA ADS] [Google Scholar]
  141. Sharina, M. E., Puzia, T. H., & Makarov, D. I. 2005, A&A, 442, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Sharina, M. E., Chandar, R., Puzia, T. H., Goudfrooij, P., & Davoust, E. 2010, MNRAS, 405, 839 [NASA ADS] [Google Scholar]
  143. Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. Strader, J., Brodie, J. P., Forbes, D. A., Beasley, M. A., & Huchra, J. P. 2003, AJ, 125, 1291 [NASA ADS] [CrossRef] [Google Scholar]
  145. Strader, J., Brodie, J. P., & Forbes, D. A. 2004, AJ, 127, 3431 [NASA ADS] [CrossRef] [Google Scholar]
  146. Strader, J., Romanowsky, A. J., Brodie, J. P., et al. 2011, ApJS, 197, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  147. Streich, D., de Jong, R. S., Bailin, J., et al. 2014, A&A, 563, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  148. Swinbank, A. M., Papadopoulos, P. P., Cox, P., et al. 2011, ApJ, 742, 11 [NASA ADS] [CrossRef] [Google Scholar]
  149. Swinbank, A. M., Smail, I., Sobral, D., et al. 2012, ApJ, 760, 130 [NASA ADS] [CrossRef] [Google Scholar]
  150. Tolstoy, E., Irwin, M. J., Helmi, A., et al. 2004, ApJ, 617, L119 [NASA ADS] [CrossRef] [Google Scholar]
  151. Tonini, C. 2013, ApJ, 762, 39 [NASA ADS] [CrossRef] [Google Scholar]
  152. Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  153. Trancho, G., Bastian, N., Miller, B. W., & Schweizer, F. 2007, ApJ, 664, 284 [NASA ADS] [CrossRef] [Google Scholar]
  154. Tremaine, S. D., Ostriker, J. P., & Spitzer, Jr., L. 1975, ApJ, 196, 407 [NASA ADS] [CrossRef] [Google Scholar]
  155. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
  156. Woodley, K. A., Harris, W. E., Beasley, M. A., et al. 2007, AJ, 134, 494 [NASA ADS] [CrossRef] [Google Scholar]
  157. Woodley, K. A., Harris, W. E., Puzia, T. H., et al. 2010, ApJ, 708, 1335 [NASA ADS] [CrossRef] [Google Scholar]
  158. Zepf, S. E., & Ashman, K. M. 1993, MNRAS, 264, 611 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

The contribution of high and low-metallicity objects to the normalized MDFs of stars and clusters in the inner and outer halos of galaxies.

In the text

All Figures

thumbnail Fig. 1

Upper figure: comparison between the normalized MDF of stars (dotted) and GCs (full lines) in three distance regions of Cen A. Each MDF is normalized to 1. Lower figure: logarithmic ratio between the normalized MDFs of clusters and stars as a function of [M/H] in bins of Δ [M/H] = 0.30. The colours are the same as in the upper figure. For clarity, the points of the three regions are slightly horizontal shifted with respect to one another. The coloured dotted lines show the weighted least square fits of the three distance regions. The full black line is the least square fit of the three regions combined. It has a slope of −0.78 ± 0.05.

In the text
thumbnail Fig. 2

Upper figure: comparison between the normalized MDF of stars (dotted) and GCs (full lines) in two distance regions of M 31. Each MDF is normalized to 1. Lower figure: logarithmic ratio between the normalized MDFs of clusters and stars as a function of [M/H] in bins of 0.6 at two distance regions of M 31. The weighted least square fit of (Ncl/Nstars) versus [M/H] for the inner and outer regions are shown by dotted red and blue lines respectively. The black line is the fit to all data and has a slope of −0.69 ± 0.27.

In the text
thumbnail Fig. 3

Comparison between the normalized MDF of stars (dotted) and GCs (full lines) in the Fornax dwarf spheroidal galaxy. Each MDF is normalized to 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.