| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201730551 | |
| Published online | 27 September 2017 | |
Ultra-compact structure in intermediate-luminosity radio quasars: building a sample of standard cosmological rulers and improving the dark energy constraints up to z ~ 3
1 Department of Astronomy, Beijing Normal University, 100875 Beijing, PR China
e-mail: zhuzh@bnu.edu.cn
2 Department of Astrophysics and Cosmology, Institute of Physics, University of Silesia, Uniwersytecka 4, 40-007 Katowice, Poland
3 Key Laboratory for Computational Astrophysics, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
Received: 3 February 2017
Accepted: 10 May 2017
Context. Ultra-compact structure in radio sources (especially in quasars that can be observed up to very high redshifts), with milliarcsecond angular sizes measured by very-long-baseline interferometry (VLBI), is becoming an important astrophysical tool for probing both cosmology and the physical properties of AGN.
Aims. We present a newly compiled data set of 120 milliarcsec. compact radio sources representing intermediate-luminosity quasars covering the redshift range 0.46 < z < 2.76 and check the possibility of using these sources as independent cosmological probes. These quasars observed at 2.29 GHz show negligible dependence on redshifts and intrinsic luminosity, and thus represent a fixed comoving-length of standard ruler.
Methods. For a cosmological ruler with intrinsic length lm, the angular size–redshift relation can be written as θ(z) = lm/DA(z, where θ(z) is the angular size at redshift z, and DA(z) is the corresponding angular diameter distance. We use a compilation of angular size and redshift data for ultra-compact radio sources from a well-known VLBI survey, and implement a new cosmology-independent technique to calibrate the linear size of this standard ruler, which is also used to test different cosmological models with and without the flat universe assumption.
Results. We determine the linear size of this standard ruler as lm = 11.03 ± 0.25 pc, which is the typical radius at which AGN jets become opaque at the observed frequency ν ~ 2 GHz. Our measurement of this linear size is also consistent with the previous and recent radio observations at other different frequencies. In the framework of flat ΛCDM model, we find a high value of the matter density parameter, Ωm = 0.322+0.244-0.141, and a low value of the Hubble constant, H0 = 67.6+7.8-7.4 km s-1 Mpc-1, which is in excellent agreement with the cosmic microwave background (CMB) anisotropy measurements by Planck. We obtain Ωm = 0.309+0.215-0.151, w = -0.970+0.500-1.730 at 68.3% CL for the constant w of a dynamical dark-energy model, which demonstrates no significant deviation from the concordance ΛCDM model. Consistent fitting results are also obtained for other cosmological models explaining the cosmic acceleration, like Ricci dark energy (RDE) or the Dvali-Gabadadze-Porrati (DGP) brane-world scenario. While no significant change in w with redshift is detected, there is still considerable room for evolution in w and the transition redshift at which w departing from −1 is located at z ~ 2.0. Our results demonstrate that the method extensively investigated in our work on observational radio quasar data can be used to effectively derive cosmological information. Finally, we find the combination of high-redshift quasars and low-redshift clusters may provide an important source of angular diameter distances, considering the redshift coverage of these two astrophysical probes.
Key words: cosmological parameters / quasars: general / galaxies: active / radio continuum: galaxies
© ESO, 2017
1. Introduction
That the expansion of the Universe is accelerating at the current epoch has been demonstrated by the observations of Type Ia supernovae (SN Ia; Riess et al. 1998; Perlmutter et al. 1999) and is also supported by other independent probes into the cosmic microwave background (CMB; Pope et al. 2004) and the large scale structure (LSS; Spergel et al. 2003). Therefore, the so-called dark energy (DE), a new component driving the observed accelerated expansion of the Universe was introduced into the framework of general relativity. However, the nature of this exotic source with negative pressure has remained an enigma.
The simplest candidate consistent with current observations is the cosmological constant Λ (Peebles & Ratra 2003); however, it suffers from well-known fine tuning and coincidence problems. Other possible dark energy models with different dark energy equation of state (EoS) parametrizations (Ratra et al. 1988; Chevallier & Polarski 2001; Linder 2004) have also been the focus of investigations in recent decades. Meanwhile, it should be noted that cosmic acceleration might also be explained by possible departures of the true theory of gravity from General Relativity. From these theoretical motivations, possible multidimensionality in the brane theory gave birth to the well-known Dvali-Gabadadze-Porrati (DGP) model, while the holographic principle has generated the Ricci dark energy (RDE) model. All the above mentioned models are in agreement with some sets of observational data, e.g., the distance modulus from SNIa, or the CMB anisotropies. At this point, it is worth highlighting the issue of evolving the EoS w(z) of dark energy. Namely, a dynamical DE will be indicated by w(z) evolving across −1, rather than having a fixed value w(z) = −1, which implies an additional intrinsic degree of freedom of dark energy, and could be the smoking gun that signals the breakdown of Einstein’s theory of general relativity on cosmological scales (Zhao et al. 2012). However, the so-called “redshift desert”1 makes it very difficult to check dynamical DE from astrophysical observations. When confronted with such theoretical and observational puzzles, we have no alterative but to turn to high-precision data and develop new complementary cosmological probes at higher redshifts. In this paper we propose that compact structure measurements in radio quasars leading to calibrated standard rulers can become a useful tool for differentiating between the above-mentioned dark energy models and exploring possible dynamical evolution of w(z).
In the framework of standard cosmology, over the past decades considerable advances have been made in the search for possible candidates to serve as true standard rulers in the Universe. In particular, cosmological tests based on the angular size–distance relation have been developed in a series of papers, and implemented using various astrophysical sources. Recently, attention has been focused on large comoving length scales revealed in the baryon acoustic oscillations (BAO). The BAO peak location is commonly recognized as a fixed comoving ruler of about 105 h-1Mpc (where h is the Hubble constant H0 expressed in units of 100 km s-1 Mpc-1). However, the so-called fitting problem (Ellis & Stoeger 1987) still remains a challenge for BAO peak location as a standard ruler. In particular, the environmental dependence of the BAO location has recently been detected by Roukema et al. (2015, 2016). Moreover, Ding et al. (2015) and Zheng et al. (2016) have pointed out a noticeable systematic difference between H(z) measurements based on BAO and those obtained with differential aging techniques. Much effort has also been made to explore the sizes of galaxy clusters at different redshifts using radio observations of the Sunyaev-Zeldovich effect together with X-ray emission (De Filippis et al. 2005; Bonamente et al. 2006). However, the large observational uncertainties of these angular diameter distance measurements significantly affect the constraining power of this standard ruler. Actually, clusters alone are not able to provide a competitive source of angular diameter distance to probe the acceleration of the Universe.
In a similar spirit, radio sources constitute an especially powerful population that can be used to test the redshift–angular size relation for extended FRIIb galaxies (Daly & Djorgovski 2003), radio galaxies (Guerra & Daly 1998; Guerra et al. 2000), and radio loud quasars (Buchalter et al. 1998). For instance, it was first proposed that the canonical maximum lobe size of radio galaxies may provide a standard ruler for cosmological studies. From the mean observed separation of a sample of 14 radio lobes in combination with the measurements of radio lobe width, lobe propagation velocity, and inferred magnetic field strength, Guerra & Daly (1998) found 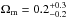 (68% confidence) for a flat cosmology.
(68% confidence) for a flat cosmology.
More promising candidates in this context are ultra-compact structure in radio sources (especially for quasars that can be observed up to very high redshifts), with milliarcsecond angular sizes measured by very-long-baseline interferometry (VLBI; Kellermann 1993; Gurvits 1994). For each source, the angular size is defined as the separation between the core (the strongest component) and the most distant component with 2% of the core peak brightness (Kellermann 1993). The original data set compiled by Gurvitset al. (1999, hereafter G99) comprises 330 milliarcsec. radio sources covering a wide range of redshifts and includes various optical counterparts, such as quasars and radio galaxies. After excluding sources with synthesized beams along the direction of apparent extension, compact sources unresolved in the observed VLBI images were naturally obtained. Finally, in order to minimize the possible dependence of angular size on spectral index and luminosity, the final sample was restricted to 145 compact sources with spectral index in the range −0.38 ≤ α ≤ 0.18 and total luminosity of Lh2 ≥ 1026 WHz-1. The possible cosmological application of these compact radio sources as a standard ruler has been extensively discussed in the literature (Vishwakarma 2001; Zhu & Fujimoto 2002; Chen & Ratra 2003). In their analysis, the full data set of 145 sources was distributed into twelve redshift bins with about the same number of sources per bin. The lowest and highest redshift bins were centered at redshifts z = 0.52 and z = 3.6, respectively. However, the typical value of the characteristic linear size lm remained one of the major uncertainties in their analysis. In order to provide tighter cosmological constraints, some authors chose to fix l at specific values (Vishwakarma 2001; Lima & Alcaniz 2002; Zhu & Fujimoto 2002), while Chen & Ratra (2003) chose to include a wide range of values for l and then integrate it over to obtain the probability distribution of the parameters of interest.
The controversy around the exact value of the characteristic linear size lm for this standard ruler or even whether compact radio sources are indeed true standard rulers still existed. Under the assumption of a homogeneous isotropic universe without cosmological constant, Gurvitset al. (1999) and Vishwakarma (2001) suggested that the exclusion of sources with extreme spectral indices and low luminosities might alleviate the dependence of lm on the source luminosity and redshift. More recently, Cao et al. (2015a) reexamined the same data in the framework of the ΛCDM cosmological model, and demonstrated that both source redshift and luminosity will affect the determination of the radio source size, i.e., the mixed population of radio sources including different optical counterparts (quasars, radio galaxies, etc.) cannot be treated as true standard rulers. In their most recent work, however, Cao et al. (2017) applied the popular parametrization lm = lLβ(1 + z)n and found that compact structure in the intermediate-luminosity radio quasars could serve as a standard cosmological ruler minimizing the above two effects (| n | ≃ 10-3, | β | ≃ 10-4), and could thus provide valuable sources of angular diameter distances at high reshifts (z ~ 3.0), reaching beyond feasible limits of supernova studies. On the other hand, through the investigation of the calibrated value for lm, we focus on the astrophysical implication of the linear size for this standard ruler. As we look into the jet of an AGN, the plasma is initially optically thin (transparent), but gets less thin as we look further in and the plasma density increases; eventually the plasma becomes optically thick (opaque), at which point we can identify the core.
The focus of this paper is on two issues. First, we extend a recent analysis by Cao et al. (2017) of compact sources as standard rulers. The extension is related to completely cosmological-model independent calibration of the linear size of standard rulers. This was not possible in a previous study where the speed of light was discussed. Second, we use the angular size measurements of 120 quasars covering redshift range z = 0.46−2.76 to constrain dynamical properties of dark energy in a way that is competitive with other probes and that reaches higher redshifts than other distance indicators. This way we demonstrate the usefulness of the sample presented. The outline of the paper is as follows. In Sect. 2 we briefly describe the quasar data and a cosmological model independent method of calibrating the linear size of this standard ruler. In Sect. 3 we report the results of constraints on the properties of dark energy obtained with the quasar data. Section 4 is devoted to constraints on other mechanisms explaining the cosmic acceleration. Finally, we give our discussion and conclusions in Sects. 5 and 6, respectively.
Compilation of intermediate-luminosity quasars.
 |
Fig. 1 Upper panel: sky distribution of the quasar sample of 120 sources detected with VLBI. Lower panel: luminosity, redshift, and angular size distribution for the quasar sample of 120 sources. |
2. Data and method
The data used here are derived from a compilation of angular size and redshift data for ultra-compact radio sources, from an well-known VLBI survey undertaken by Preston et al. (1985, hereafter P85). By employing a world-wide array of dishes forming an interferometric system with an effective baseline of about 8 × 107 wavelengths, this survey was able to detect 917 sources with compact structure out of 1398 known radio sources. The results of this survey were used initially to provide a very accurate VLBI celestial reference frame, improving precision by at least an order of magnitude compared with earlier stellar frames. An additional expectation was that the catalog would be “used in statistical studies of radio-source properties and cosmological models” (Preston et al. 1985). By considering a sample of 258 objects with redshifts z > 0.5, the possibility of applying this sample to cosmological study was first proposed by Gurvits (1994) and then extended by Jackson & Dodgson (1997), Jackson (2004), Jackson & Jannetta (2006), Cao et al. (2017). We used a revised sample comprising 613 objects with reshifts 0.0035 ≤ z ≤ 3.787, which is a recent upgrade with regard to redshift based on P85 (Jackson & Jannetta 2006)2.
All detected sources included in this comprehensive compilation were imaged with VLBI at 2.29 GHz, which involve a wide class of extragalactic objects including quasars, radio galaxies, BL Lac objects (blazars), etc. It should be noted that P85 does not give contour maps, and does not list angular sizes explicitly; however, total flux density and correlated flux density (fringe amplitude) are listed. The ratio of these two quantities is the visibility modulus Γ, which defines a characteristic angular size 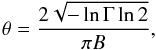 (1)where B is the interferometer baseline measured in wavelengths (Thompson et al. 1986; Gurvits 1994). The angular sizes used here were calculated using Eq. (1); it is argued in Jackson (2004) that this size is that of the core, rather than the angular distance between the core and a distant weak component.
(1)where B is the interferometer baseline measured in wavelengths (Thompson et al. 1986; Gurvits 1994). The angular sizes used here were calculated using Eq. (1); it is argued in Jackson (2004) that this size is that of the core, rather than the angular distance between the core and a distant weak component.
In our analysis, by applying two selection criteria, one on spectral index (−0.38 ≤ α ≤ 0.18) and the other on luminosity (1027 W/Hz < L < 1028 W/Hz), we focus our attention on the compact structure in 120 radio quasars with flat spectral index and intermediate luminosity. A recent study of Cao et al. (2017) suggests that they can be effectively used as standard rulers. Full information about these 120 sources can be found in Table 1, including source coordinates, redshifts, angular size, spectral index, and total flux density. The corresponding optical counterpart for each system can be found in P85. Figure 1 is an equal-area sky-distribution plot of the detected quasars. The distribution of redshifts, luminosities, and angular-sizes of the sources in our sample is also shown in Fig. 1, which simply reflects the fact that our basically luminosity-limited sample, compiled on an ad hoc basis from the literature and based on various selection criteria, is relatively homogenous both in redshifts and angular sizes. The angular sizes of the sample range from 0.424 to 2.743 milliarcsec; 15% of the quasars have angular sizes θ < 1 mas, and only a handful of quasars with larger angular sizes (θ > 2 mas) have been identified, while 75% of all quasars are located at 1.0 mas < θ < 2.0 mas. We remark here that, the final sample covers the redshift range 0.46 < z < 2.76, which indicates its potential usefulness in cosmology at high redshifts.
 |
Fig. 2 Intrinsic metric linear size lm distribution of the 120 intermediate luminosity quasars in the redshift and luminosity space. |
For a cosmological ruler with intrinsic length lm, the angular size-redshift relation can be written as (Sandage 1988) 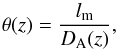 (2)whereθ(z) is the angular size at redshift z and DA(z) is the corresponding angular diameter distance. The distance DA(z) is related to H0, the Hubble constant, and E(z;p), the dimensionless expansion rate depending on redshift z and cosmological parameters p. However, the cosmological application of this technique requires good knowledge of the linear size of the standard ruler used. The possibility that a source’s linear size depends on the source luminosity and redshift should be kept in mind. In this analysis, we use a phenomenological model to characterize the relations between the projected linear size of a source and its luminosity L and redshift z (Gurvits 1994; Gurvitset al. 1999; Cao et al. 2017)
(2)whereθ(z) is the angular size at redshift z and DA(z) is the corresponding angular diameter distance. The distance DA(z) is related to H0, the Hubble constant, and E(z;p), the dimensionless expansion rate depending on redshift z and cosmological parameters p. However, the cosmological application of this technique requires good knowledge of the linear size of the standard ruler used. The possibility that a source’s linear size depends on the source luminosity and redshift should be kept in mind. In this analysis, we use a phenomenological model to characterize the relations between the projected linear size of a source and its luminosity L and redshift z (Gurvits 1994; Gurvitset al. 1999; Cao et al. 2017) 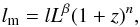 (3)where \begin{lxirformule}$l$\end{lxirformule} is the linear size scaling factor, β and n quantify the dependence of the linear size on source luminosity and redshift, respectively (Gurvits 1994). Following the analysis of Cao et al. (2017), for our quasar sample, the linear size lm is independent of both redshift and luminosity (| n | ≃ 10-3, | β | ≃ 10-4) and there is only one parameter l to be considered. The intrinsic metric linear size lm distribution of the 120 intermediate luminosity quasars in the redshift and luminosity space is shown in Fig. 2. Since both the lm (calculated from Eq. (2)) and luminosity require the knowledge of angular diameter distances, we used DA(z) values at the quasars’ redshifts inferred from the Hubble parameter (H(z)) measurements, i.e., in a cosmological model independent way (see Cao et al. 2017, for details). The measurements of H(z) are acquired by means of two different techniques: one based on cosmic chronometers (Jimenez & Loeb 2002), i.e., massive, early-type galaxies evolving passively on timescales longer than their age difference, while the other is based on the analysis of baryon acoustic oscillations (BAO). One can see from Fig. 2 that intermediate-luminosity quasars could serve as much better standard rulers than other quasar subsamples discussed in Cao et al. (2017). Therefore, if we could find a suitable method to calibrate l, then we would get stringent constraints on the angular diameter distances at different redshifs, and thus relevant cosmological parameters p. In order to check the degeneracy between p and l, we investigated our radio quasar sample in the framework of the concordance ΛCDM cosmology, which is characterized by two free parameters, the matter density Ωm, and the intrinsic linear size l. Figure 3 shows the corresponding confidence regions.
(3)where \begin{lxirformule}$l$\end{lxirformule} is the linear size scaling factor, β and n quantify the dependence of the linear size on source luminosity and redshift, respectively (Gurvits 1994). Following the analysis of Cao et al. (2017), for our quasar sample, the linear size lm is independent of both redshift and luminosity (| n | ≃ 10-3, | β | ≃ 10-4) and there is only one parameter l to be considered. The intrinsic metric linear size lm distribution of the 120 intermediate luminosity quasars in the redshift and luminosity space is shown in Fig. 2. Since both the lm (calculated from Eq. (2)) and luminosity require the knowledge of angular diameter distances, we used DA(z) values at the quasars’ redshifts inferred from the Hubble parameter (H(z)) measurements, i.e., in a cosmological model independent way (see Cao et al. 2017, for details). The measurements of H(z) are acquired by means of two different techniques: one based on cosmic chronometers (Jimenez & Loeb 2002), i.e., massive, early-type galaxies evolving passively on timescales longer than their age difference, while the other is based on the analysis of baryon acoustic oscillations (BAO). One can see from Fig. 2 that intermediate-luminosity quasars could serve as much better standard rulers than other quasar subsamples discussed in Cao et al. (2017). Therefore, if we could find a suitable method to calibrate l, then we would get stringent constraints on the angular diameter distances at different redshifs, and thus relevant cosmological parameters p. In order to check the degeneracy between p and l, we investigated our radio quasar sample in the framework of the concordance ΛCDM cosmology, which is characterized by two free parameters, the matter density Ωm, and the intrinsic linear size l. Figure 3 shows the corresponding confidence regions.
 |
Fig. 3 Degeneracy between the linear size of ultra-compact structure in radio quasars and the matter density parameter in the Universe; 68.3% and 95.4% confidence regions are shown. |
Next a cosmological-model-independent method was applied to derive the linear size of the compact structure in intermediate-luminosity radio quasars. Specifically, cosmic chronometer H(z) measurements processed using Gaussian processes (GP; Li et al. 2016) can provide angular diameter distances DA covering the quasar redshift range, and thus allows us to calibrate the angular size of milliarcsecond quasars. In the cosmic chronometers method (Jimenez & Loeb 2002), the cosmic expansion rates H(z) are measured from age estimates of red galaxies without any prior assumption of cosmology, i.e., 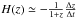 . In order to minimize the systematic effects, we used the H(z) sample following the choice of Moresco et al. (2012), Verde et al. (2014), Li et al. (2016). Currently, 30 measurements of H(z) covering the redshift range 0.070 ≤ z ≤ 1.965 have been obtained via this method (see Zheng et al. 2016, and references therein for details). However, according to the analysis of Moresco et al. (2012), the choice of stellar population synthesis model may strongly affect these estimates of Δt and thus H(z), especially at z ≥ 1.2. Therefore, we consider only 24 H(z) measurements up to z< 1.2 in this paper. Moreover, following the analysis of Verde et al. (2014), Li et al. (2014), the error bar of the highest-z point is increased by 20% to include the uncertainties of the stellar population synthesis models.
. In order to minimize the systematic effects, we used the H(z) sample following the choice of Moresco et al. (2012), Verde et al. (2014), Li et al. (2016). Currently, 30 measurements of H(z) covering the redshift range 0.070 ≤ z ≤ 1.965 have been obtained via this method (see Zheng et al. 2016, and references therein for details). However, according to the analysis of Moresco et al. (2012), the choice of stellar population synthesis model may strongly affect these estimates of Δt and thus H(z), especially at z ≥ 1.2. Therefore, we consider only 24 H(z) measurements up to z< 1.2 in this paper. Moreover, following the analysis of Verde et al. (2014), Li et al. (2014), the error bar of the highest-z point is increased by 20% to include the uncertainties of the stellar population synthesis models.
According to Holanda et al. (2013), for non-uniformly distributed H(z) data, the comoving distance integral could be obtained with a simple trapezoidal rule 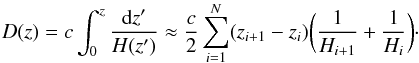 (4)Given that the number of data points and the uniformity of the spaced data will heavily influence the precision of this simple rule, we use GP, a powerful non-linear interpolating tool for reconstructing the evolution of the expansion rate with redshift, and thus integrate its inverse function to estimate distances in a cosmological model-independent way (Holanda et al. 2013). This method was first proposed to test both cosmology (Holsclaw et al. 2010a,b) and cosmography (Shafieloo et al. 2013), and then extensively applied to the derivation of the Hubble constant H0 (Busti et al. 2014), the reconstructions of the equation of state of dark energy (Seikel et al. 2013), and the distance-duality relation (Zhang 2014). The advantage of GP is that we do not need to assume a parametrized model for H(z) while reconstructing this function from the data (Holsclaw et al. 2010a,b). Moreover, with a very small and uniform step of Δz = zi + 1−zi, we may obtain more precise measurements of angular diameter distances at a certain redshift. In order to reconstruct the Hubble parameter as a function of the redshift from 24 H(z) measurements of cosmic chronometers covering z = (0.0,1.2), we used the publicly available code (Seikel et al. 2013) called the Gaussian Processes in Python (GaPP)3.
(4)Given that the number of data points and the uniformity of the spaced data will heavily influence the precision of this simple rule, we use GP, a powerful non-linear interpolating tool for reconstructing the evolution of the expansion rate with redshift, and thus integrate its inverse function to estimate distances in a cosmological model-independent way (Holanda et al. 2013). This method was first proposed to test both cosmology (Holsclaw et al. 2010a,b) and cosmography (Shafieloo et al. 2013), and then extensively applied to the derivation of the Hubble constant H0 (Busti et al. 2014), the reconstructions of the equation of state of dark energy (Seikel et al. 2013), and the distance-duality relation (Zhang 2014). The advantage of GP is that we do not need to assume a parametrized model for H(z) while reconstructing this function from the data (Holsclaw et al. 2010a,b). Moreover, with a very small and uniform step of Δz = zi + 1−zi, we may obtain more precise measurements of angular diameter distances at a certain redshift. In order to reconstruct the Hubble parameter as a function of the redshift from 24 H(z) measurements of cosmic chronometers covering z = (0.0,1.2), we used the publicly available code (Seikel et al. 2013) called the Gaussian Processes in Python (GaPP)3.
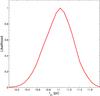 |
Fig. 4 Corrected linear size of compact quasars derived in a cosmological model independent way, using the observational H(z) data. |
Measurements of the linear size of AGN compact structure at different frequencies.
Applying the redshift-selection criterion, Δz = | zQSO−zH | ≤ 0.005, to the angular diameter distances derived from H(z), we obtain 48 measurements of DA coinciding with the quasars reshifts. Undertaking similar analysis as Cao et al. (2017), we obtain constraints on the linear size lm with the best-fit 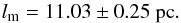 (5)The probability distribution of lm is also shown in Fig. 4, which will be used in the following cosmological analysis with quasar observations. We note that in our previous paper (Cao et al. 2017), which aimed at the estimation of the velocity of light with extragalactic sources, this calibration was not possible because of the appearance of c in the expression for DA (see, e.g., Eq. (4)). Two issues deserve attention: first, whether the rigid assumption of vanishing β and n parameters describing evolution of the comoving size lm with luminosity and redshift might introduce a bias and underestimate the uncertainties of cosmological parameters fitted and second, whether the cosmic chronometers used for calibrating QSO as standard rulers introduce a bias. These points are addressed in the following sections by modeling β and n parameters with Gaussian distributions and by comparison of the results obtained with quasars as standard rulers and with H(z) data alone.
(5)The probability distribution of lm is also shown in Fig. 4, which will be used in the following cosmological analysis with quasar observations. We note that in our previous paper (Cao et al. 2017), which aimed at the estimation of the velocity of light with extragalactic sources, this calibration was not possible because of the appearance of c in the expression for DA (see, e.g., Eq. (4)). Two issues deserve attention: first, whether the rigid assumption of vanishing β and n parameters describing evolution of the comoving size lm with luminosity and redshift might introduce a bias and underestimate the uncertainties of cosmological parameters fitted and second, whether the cosmic chronometers used for calibrating QSO as standard rulers introduce a bias. These points are addressed in the following sections by modeling β and n parameters with Gaussian distributions and by comparison of the results obtained with quasars as standard rulers and with H(z) data alone.
 |
Fig. 5 Plot of core size versus frequency (constraint on the linear size of compact structure in intermediate-luminosity quasars l at 2.16 GHz is added). The BK 79 jet model (rc ∝ ν-1 ) is used for the fitted curve from VLBI/VLBA observations in the literature. |
Now we make some comments on the physical meaning of the linear size of this standard ruler. For a long time it has been argued that active galactic nuclei (AGN) must be powered by accretion of mass onto massive black holes. Current theoretical models indicate that jets of relativistic plasma are generated in the central regions of AGN, and magnetic fields surrounding the black hole expel, accelerate, and help to collimate the jet flow outwards (Meier 2009). According to the unified classification of AGN, 10 pc is the typical radius at which AGN jets are apparently generated and there is almost no stellar contribution (Blandford & Rees 1978). In the conical jet model proposed by Blandford & Königl (1979, hereafter BK79), the base of the jet corresponds to the vertex of the cone, and the unresolved core is identified with the innermost, optically thick region of the approaching jet. For QSOs, this compact opaque parsec-scale core is located between the broad-line region (~1 pc) and narrow-line region (~100 pc) (Blandford & Rees 1978).
 |
Fig. 6 Comparison between the P15 and P85 samples concerning the angular size–redshift and angular size–luminosity diagrams based on 58 sources common to these two surveys. |
More recently, Hopkins & Quataert (2010) have investigated the correlation between the black hole’s mass accretion rate ṀBH and the star formation rate Ṁ∗. Their results from simulations showed that within the central 10 pc around the black hole the star formation rate is equal to the mass accretion rate. This conclusion is consistent with the recent observations by Silverman et al. (2009). Frey et al. (2010) has presented high-resolution radio structure imaging of five quasars (J0813+3508, J1146+4037, J1242+5422, J1611+0844, and J1659+2101) at 4.5 <z< 5 with the European VLBI Network (EVN) at 5 GHz. Although all cases have satisfied the intermediate-luminosity criterion defined in this paper, there is only one flat-spectrum source (J1611+0844) that could be used for comparison in our analysis, while the compact emission of other quasars is characterized by a steep radio spectrum (Frey et al. 2010). Moreover, we combine our constraint with the recent observation of Blazar 2200+420 from the Very Long Baseline Array (VLBA), at eight frequencies (4.6, 5.1, 7.9, 8.9, 12.9, 15.4, 22.2, 43.1 GHz) to investigate the frequency-dependent position of VLBI cores4. From the comparison presented in Fig. 5 and Table 2, we find a very good consistency between the measurements and the BK79 conical jet model, in which the position of the radio core follows r ∝ ν-1, where r is the distance from the central engine (Blandford & Königl 1979) if the core is self-absorbed and in equipartition. As noted in the analysis of Cao et al. (2017), our estimate of lm is also consistent with the results derived from recent multi-frequency VLBI imaging observations of more than 3000 compact extragalactic radio sources (Pushkarev & Kovalev 2015). In fact, 58 intermediate-luminosity quasars included in our modified P85 subsample have also been observed by recent VLBI observations based on better uv-coverage in the P15 sample. Based on these 58 sources, the P15 and P85 samples can be compared on the “angular size–redshift” and “angular size–luminosity” diagrams. They are displayed in Fig. 6, from which one can see some differences between the samples concerning estimates of the angular size. However, we checked that the characteristic linear size lm at 2 GHz estimated from P15 is consistent with the results obtained from the P85 sample. Astrophysical application of the recent multi-frequency angular size measurements of 58 intermediate-luminosity quasars from the P15 sample will be subject of a next work (Cao et al., in prep.).
If one, quite straightforwardly, attempts to construct an empirical relation DA(z) extending to higher redshifts on the basis of individual quasar angular sizes, using Eq. (2), it is possible to obtain the DA measurement and the corresponding uncertainty for each quasar. However, this procedure results in large uncertainties in DA, a problem that has already been encountered (Gurvits 1994; Gurvitset al. 1999), as can be seen from plots of the measured angular size against redshift in these works. This problem remains even after 13 systems with very large uncertainties (~50%) are removed. Therefore, in order to minimize its influence on our analysis, we have chosen to bin the remaining 107 data points and to examine the change in DA with redshift. The final sample was grouped into 20 redshift bins of width Δz = 0.10. Figure 7 shows the median values of DA for each bin plotted against the central redshift of the bin. For comparison, the two curves plotted as solid lines represent theoretical expectations from the concordance ΛCDM model and the Einstein-de Sitter model. One can see that the latter is disfavored at high confidence. More importantly, the angular diameter distance information obtained from quasars has helped us to bridge the redshift desert and extend our investigation of dark energy to much higher redshifts. It is worth noting that these 120 intermediate-luminosity QSOs are obtained in a completely cosmology-independent method, and hence can be used to constrain cosmological parameters without the circularity problems.
3. Constraints on dark energy
In this section we investigate some dark energy models and estimate their best-fitted parameters using the quasar sample. The models discussed in this section explain the accelerated expansion of the universe by introducing a hypothetical fluid whose contribution to the matter budget and equation of state are unknown parameters to be fitted.
 |
Fig. 7 Angular diameter distances DA(z) estimated from quasars as standard rulers (blue squares). Angular diameter distances from galaxy clusters (purple circles) are also added for comparison. Theoretical predictions of ΛCDM models with ΩΛ = 0.00 and ΩΛ = 0.70 are denoted by black and red solid lines, respectively. |
In Sect. 4, we discuss alternative concepts involving a departure from classical General Relativity. More specifically, the following models for dark energy will be studied in this section:
-
ΛCDM: cosmological constant in a flat universe;
-
XCDM: constant equation-of-state parameter in a flat universe;
-
wzCDM: time-varying equation-of-state parameter in a flat universe.
We determine the cosmological model parameters p using a χ2 minimization method, ![\begin{equation} \label{eq:chi2} \chi^{2}(\vec{p}) = \sum_{i}^{120}{\frac{\left[\theta(z_{i}; l_{\rm m}; \vec{p}) - \theta_{oi}\right]^{2}}{\sigma_{i}^{2}}}, \end{equation}](/articles/aa/full_html/2017/10/aa30551-17/aa30551-17-eq111.png) (6)where θ(zi;p) = lm/DA is the angle subtended by an object of proper length lm transverse to the line of sight and θoi is the observed value of the angular size with uncertainties σi. The summation is over all 120 observational data points. In computing χ2 we have also assumed additional 10% uncertainties in the observed angular sizes to account for both observational errors and the intrinsic spread in linear sizes. We note that although the best-fit values of β and n parameters describing the dependence of lm on the luminosity and redshift are negligibly small, their uncertainties could also be an important source of systematic errors on the final cosmological results. In order to address this issue, we perform a sensitivity analysis by applying Monte Carlo simulations in which β and n were characterized by Gaussian distributions, β = 0.00 ± 0.05 and n = 0.00 ± 0.05, while the uncertainty of the linear size scaling factor was taken into account with a Gaussian distribution as l = 11.03 ± 0.25 pc 5.
(6)where θ(zi;p) = lm/DA is the angle subtended by an object of proper length lm transverse to the line of sight and θoi is the observed value of the angular size with uncertainties σi. The summation is over all 120 observational data points. In computing χ2 we have also assumed additional 10% uncertainties in the observed angular sizes to account for both observational errors and the intrinsic spread in linear sizes. We note that although the best-fit values of β and n parameters describing the dependence of lm on the luminosity and redshift are negligibly small, their uncertainties could also be an important source of systematic errors on the final cosmological results. In order to address this issue, we perform a sensitivity analysis by applying Monte Carlo simulations in which β and n were characterized by Gaussian distributions, β = 0.00 ± 0.05 and n = 0.00 ± 0.05, while the uncertainty of the linear size scaling factor was taken into account with a Gaussian distribution as l = 11.03 ± 0.25 pc 5.
 |
Fig. 8 Cosmological constraints on the flat ΛCDM model from the quasar sample without (left panel) and with systematical uncertainties (right panel). Fitting results from recent H(z) measurements (black dashed lines) and Planck observations (green dot represents the best fit with 1σ errors denoted by green solid lines) are also added for comparison. |
In a similar manner to other papers introducing new compilations of cosmologically important data sets (e.g., Amanullah et al. 2010), we constrain the properties of dark energy first using QSO alone (with and without the systematic uncertainty of l, β, and n), and then perform a combined analysis using the latest CMB data from Planck Collaboration XIV (2016) and the BAO data from 6dFGS, SDSS-MGS, BOSS-LOWZ, and BOSS-CMASS (Beutler et al. 2011; Ross et al. 2015; Anderson et al. 2014). Moreover, considering that there is no strong evidence for the departure from spatially flat geometry at the current data level, which is known from and strongly supported by other independent and precise experiments (Planck Collaboration XIII 2016; Planck Collaboration XIV 2016), we assume spatial flatness of the Universe in the analyses throughout the paper. The results for each of the models are listed in Table 2 and are discussed in turn in the following sections. Unless stated otherwise, the uncertainties represent 68.3% confidence limits and include both statistical uncertainties and systematic errors. In addition, we add the prior for the Hubble constant H0 = 67.3 km s-1 Mpc-1 after Planck Collaboration XVI (2014). The exceptions are the ΛCDM and the DGP models (see next section), where H0 is treated as a free parameter.
 |
Fig. 9 Cosmological constraints on the flat ΛCDM model from the quasar sample without and with different systematical uncertainties: sys1 denotes the systematics with l = 11.03 ± 0.25 pc, β = 0.00 ± 0.05, and n = 0.00 ± 0.05, while sys2 represents the systematics with l = 11.03 ± 0.25 pc, β = 0.00 ± 0.10, and n = 0.00 ± 0.10. |
3.1. ΛCDM
If flatness of the Friedman-Robertson-Walker (FRW) metric is assumed, the only cosmological parameter of this model is p = {Ωm}. However, in order to check the constraining power of our quasar data on the Hubble constant, we chose to take H0 as the other free parameter and obtained 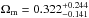 and
and 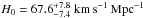 . After including systematics due to uncertainties on l, β, and n, the matter density parameter and Hubble constant respectively change to
. After including systematics due to uncertainties on l, β, and n, the matter density parameter and Hubble constant respectively change to 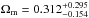 and
and 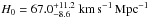 . These results are presented in Fig. 8. Now one issue which should be discussed is how much the cosmological parameters are affected by larger uncertainties of β and n. For this purpose, we changed the uncertainty of the luminosity-dependence parameter to β = 0.00 ± 0.10 and the redshift-dependence parameter to n = 0.00 ± 0.10. The comparison of the resulting constraints on Ωm and H0 based on different systematical uncertainties is shown in Fig. 9. We were able to easily check that reduction of the error of β and n lead to more stringent cosmological fits, which motivated us to improve constraints on the two parameters with a larger quasar sample from future VLBI observations based on better uv-coverage (Pushkarev & Kovalev 2015).
. These results are presented in Fig. 8. Now one issue which should be discussed is how much the cosmological parameters are affected by larger uncertainties of β and n. For this purpose, we changed the uncertainty of the luminosity-dependence parameter to β = 0.00 ± 0.10 and the redshift-dependence parameter to n = 0.00 ± 0.10. The comparison of the resulting constraints on Ωm and H0 based on different systematical uncertainties is shown in Fig. 9. We were able to easily check that reduction of the error of β and n lead to more stringent cosmological fits, which motivated us to improve constraints on the two parameters with a larger quasar sample from future VLBI observations based on better uv-coverage (Pushkarev & Kovalev 2015).
 |
Fig. 10 Probability distribution of the matter density parameter in the flat ΛCDM model, which is derived from the quasar sample without (red solid line) and with systematical uncertainties (red dashed line) with the prior on the Hubble constant H0 = 70 km s-1 Mpc-1. Fitting result from recent H(z) measurements (black dashed lines) is also added for comparison. |
Another important issue is the comparison of our cosmological results with those of earlier studies done using alternative probes. We start by comparing our results with fits obtained using H(z) measurements from cosmic chronometers. Respective likelihood contours obtained with the latest H(z) data comprising 30 data points (Zheng et al. 2016) are also plotted in Fig. 8. We see that 1σ confidence regions from these two techniques overlap very well with each other. This means that the results obtained on the sample of quasars are consistent with the H(z) fits, although with larger uncertainties due to systematic uncertainties of the parameters characterizing this standard ruler. Central fits, however, are almost the same. Furthermore, looking at the constraints obtained with QSO and H(z) data, we find a similar degeneracy between Ωm and H0. Moreover, the constraint on Ωm derived from the mean observed separation of the radio lobes (Daly & Djorgovski 2003; Guerra & Daly 1998; Guerra et al. 2000) is in broad agreement with the results we report. Then, gravitational lensing systems with QSO acting as sources may provide us with another probe of angular diameter distance data in cosmology since strong gravitational lensing statistics depend on the angular diameter distances between the source, the lens, and the observer. Using the redshift distribution of radio sources, Chiba & Yoshii (1999) calculated the absolute lensing probability for both optical and radio lenses. The best-fit mass density obtained in their analysis in a flat cosmology, 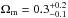 , is consistent with our results. Constraints on cosmological models using strong lensing statistics have been obtained (e.g., Biesiada et al. 2010; Cao et al. 2012a,b, 2015b). Finally, based on the first-year Planck results, Planck Collaboration XVI (2014) gave the best-fit parameters Ωm = 0.315 ± 0.017 and H0 = 67.3 ± 1.2km s-1Mpc-1 for the flat ΛCDM model, which is in perfect agreement with our standard ruler result. In contrast, compared with our quasar sample, recent combined SNLS SNe Ia data favors a lower value of Ωm and thus smaller matter density in the ΛCDM model than our quasar data (Conley et al. 2011). We note that the cosmological probe inferred from CMB anisotropy measured by Planck is also a standard ruler: the comoving size of the acoustic horizon. Therefore, appreciable consistency between the same type of probes (standard rulers) could be expected and indeed is revealed here.
, is consistent with our results. Constraints on cosmological models using strong lensing statistics have been obtained (e.g., Biesiada et al. 2010; Cao et al. 2012a,b, 2015b). Finally, based on the first-year Planck results, Planck Collaboration XVI (2014) gave the best-fit parameters Ωm = 0.315 ± 0.017 and H0 = 67.3 ± 1.2km s-1Mpc-1 for the flat ΛCDM model, which is in perfect agreement with our standard ruler result. In contrast, compared with our quasar sample, recent combined SNLS SNe Ia data favors a lower value of Ωm and thus smaller matter density in the ΛCDM model than our quasar data (Conley et al. 2011). We note that the cosmological probe inferred from CMB anisotropy measured by Planck is also a standard ruler: the comoving size of the acoustic horizon. Therefore, appreciable consistency between the same type of probes (standard rulers) could be expected and indeed is revealed here.
 |
Fig. 11 XCDM model: 68.3% and 95.4% confidence regions in the (Ωm, w) plane from QSO, BAO, CMB, and H(z). The left panel shows the QSO confidence region with the best-fit value for l only, while the right panel shows the confidence region including systematical uncertainties of l, β, and n. We note that CMB and QSO constraints are orthogonal, making this combination of cosmological probes very powerful for investigating the nature of dark energy. |
We emphasize that the value of the Hubble constant obtained in our analysis is in excellent agreement with the findings based on the Planck CMB data. Many previous studies have determined its present value with other probes. For example, the final results of the Hubble Space Telescope (HST) key project suggested the Hubble constant as H0 = 72 ± 8km s-1 Mpc-1 (Freedman et al. 2001). Then, the observations of 240 HST Galactic Cepheid variables gave H0 = 74.2 ± 3.6km s-1 Mpc-1 (Riess et al. 2009). A much lower value has been suggested by Tammann et al. (2008) who independently calibrated Cepheids and SN Ia and obtained H0 = 62.3 ± 1.3km s-1 Mpc-1. Two more recent measurements of the Hubble constant are H0 = 69.6 ± 0.7 km s-1Mpc-1 (Bennett et al. 2014) and that obtained from local Cepheids distance ladder, H0 = 73.24 ± 1.74km s-1 Mpc-1 (Riess et al. 2016). It is also worth noting that according to the meta-analysis of existing literature based on median statistics (Gott et al. 2001; Chen & Ratra 2003) the value of H0 = 68km s-1Mpc-1 can be considered the most likely value for the Hubble constant. In order to check the cosmological constraint power of the quasar sample derived in this analysis, we set the H0 = 70 km s-1 Mpc-1 prior and obtain a very stringent fit on the present-day matter density Ωm = 0.297 ± 0.027 (without systematics) and Ωm = 0.300 ± 0.055 (with systematics). This is shown in Fig. 10. For comparison, the fitting result from the H(z) data is also plotted with black dashed line. It is obvious that the current quasar observations could provide consistent and comparable cosmological constraints with respect to the cosmic chronometers.
3.2. XCDM model
Allowing for a deviation from the simple w = −1 case, an alternative is dynamical energy based exclusively on a scalar field (Ratra et al. 1988). In this case, accelerated expansion is obtained when w< −1/3, while scalar field models typically have time varying w with w ≥ −1. When flatness is assumed, it is a two-parameter model with the parameter set: p = { Ωm,w }. From the fitting results shown in Table 2 one can see that 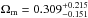 ,
, 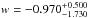 (without systematics) and
(without systematics) and 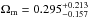 ,
, 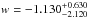 (with systematics). In order to illustrate the performance of QSO data, we also present the constraints resulting from H(z) data, which clearly indicates that the current quasar observations confronted with the cosmic chronometers could provide consistent and comparable cosmological constraints. In particular, the w coefficient obtained from our quasar sample agrees very well with the respective value derived from the Planck results. Figure 11 shows the contours for Ωm and w, with and without systematical uncertainties. It can be seen that the concordance ΛCDM model (w = −1) is consistent with the quasar method applied here. Our results demonstrate that the method extensively investigated in our work on observational radio quasar data can be used in practice to effectively derive cosmological information.
(with systematics). In order to illustrate the performance of QSO data, we also present the constraints resulting from H(z) data, which clearly indicates that the current quasar observations confronted with the cosmic chronometers could provide consistent and comparable cosmological constraints. In particular, the w coefficient obtained from our quasar sample agrees very well with the respective value derived from the Planck results. Figure 11 shows the contours for Ωm and w, with and without systematical uncertainties. It can be seen that the concordance ΛCDM model (w = −1) is consistent with the quasar method applied here. Our results demonstrate that the method extensively investigated in our work on observational radio quasar data can be used in practice to effectively derive cosmological information.
Cosmological parameters Ωm, w0, wa, and the Hubble constant H0 fitted to the QSO data.
Angular diameter distances for intermediate-luminosity radio quasars obtained using the method described in this paper may also contribute to testing the consistency between luminosity and angular diameter distances known as the distance–duality relation. Recent discussions of the Etherington reciprocity relation can be found in Cao & Zhu (2011,?, 2014). Concerning the latest Union2.1 compilation comprising 580 SN Ia data points (Suzuki et al. 2012), the results obtained from our quasar sample are fully consistent with the SNIa fits: 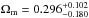 ,
, 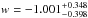 . More importantly, from the comparison between Fig. 6 in Suzuki et al. (2012) and Fig. 11 in this paper, one can clearly see that principal axes of confidence regions obtained with SNe and quasars are inclined at very high angles. This creates hopes for more stringent constraints in a combined analysis of these two data sets. Considering the big difference between the sample sizes of the two data sets, we hope intermediate-luminosity quasars would eventually serve as a complementary probe breaking the degeneracy in the (Ωm,w) plane at much higher redshifts.
. More importantly, from the comparison between Fig. 6 in Suzuki et al. (2012) and Fig. 11 in this paper, one can clearly see that principal axes of confidence regions obtained with SNe and quasars are inclined at very high angles. This creates hopes for more stringent constraints in a combined analysis of these two data sets. Considering the big difference between the sample sizes of the two data sets, we hope intermediate-luminosity quasars would eventually serve as a complementary probe breaking the degeneracy in the (Ωm,w) plane at much higher redshifts.
It is now crucial to pin down the uncertainties of each approach and employ multiple independent probes to account for unknown systematics. For comparison, we also plot the likelihood contours with the latest measurements of BAO and CMB. For the BAO data, we use the latest measurements of acoustic-scale distance ratio DV(z) /rs(zd) from the 6dFGS (rs(zd) /DV(z = 0.106) = 0.336 ± 0.015), SDSS-MGS (DV(z = 0.15) /rs(zd) = (664 ± 25)/152.66), BOSS-LOWZ (DV(z = 0.32) /rs(zd) = (1264 ± 25)/153.19), and BOSS-CMASS (DV(z = 0.57) /rs(zd) = (2056 ± 20)/153.19) (Beutler et al. 2011; Ross et al. 2015; Anderson et al. 2014)6. The parameter DV(z) in the distance ratio is the volume-averaged effective distance defined as ![\begin{equation} D_V(z)=\left[(1+z)^2D_{\rm A}^2(z)\frac{cz}{H(z)}\right]^{1/3} \end{equation}](/articles/aa/full_html/2017/10/aa30551-17/aa30551-17-eq210.png) (7)and \begin{lxirformule}$r_{\rm s}(z_{d})$\end{lxirformule} is the comoving sound horizon
(7)and \begin{lxirformule}$r_{\rm s}(z_{d})$\end{lxirformule} is the comoving sound horizon 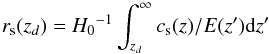 (8)at the baryon-drag epoch, zd, which can be calculated as (Eisenstein et al. 1998)
(8)at the baryon-drag epoch, zd, which can be calculated as (Eisenstein et al. 1998) ![\begin{equation} z_{\rm d}=\frac{1291(\Omega_{\rm m}h^2)^{0.251}}{1+0.659(\Omega_{\rm m}h^2)^{0.828}}[1+b_1(\Omega_{b}h^2)^{b_2}] , \end{equation}](/articles/aa/full_html/2017/10/aa30551-17/aa30551-17-eq213.png) (9)whereb1 = 0.313(Ωmh2)-0.419 [1 + 0.607(Ωmh2)0.674] and b2 = 0.238(Ωmh2)0.223. For the CMB data, we use the distance priors derived from the recent Planck data (Planck Collaboration XIV 2016), which include the measurements of the derived quantities, such as the acoustic scale (lA), the shift parameter (ℛ), and the baryonic fraction parameter (Ωbh2). The acoustic scale at recombination can be parametrized as
(9)whereb1 = 0.313(Ωmh2)-0.419 [1 + 0.607(Ωmh2)0.674] and b2 = 0.238(Ωmh2)0.223. For the CMB data, we use the distance priors derived from the recent Planck data (Planck Collaboration XIV 2016), which include the measurements of the derived quantities, such as the acoustic scale (lA), the shift parameter (ℛ), and the baryonic fraction parameter (Ωbh2). The acoustic scale at recombination can be parametrized as 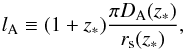 (10)wherethe comoving sound horizon expresses as
(10)wherethe comoving sound horizon expresses as 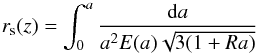 (11)with R = 31500(TCMB/ 2.7K)-4Ωbh2,TCMB = 2.7255 K. The redshift of photo-decoupling period, z∗, can be calculated as (Hu & Sugiyama 1996)
(11)with R = 31500(TCMB/ 2.7K)-4Ωbh2,TCMB = 2.7255 K. The redshift of photo-decoupling period, z∗, can be calculated as (Hu & Sugiyama 1996) ![\begin{equation} z_*=1048[1+0.00124(\Omega_{b}h^2)^{-0.738}][1+g_1(\Omega_{\rm m}h^2)^{g_2}] \end{equation}](/articles/aa/full_html/2017/10/aa30551-17/aa30551-17-eq224.png) (12)where
(12)where 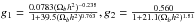 . The ℛ quantity is the least cosmological model-dependent parameter that can be extracted from the analysis of the CMB and takes the form
. The ℛ quantity is the least cosmological model-dependent parameter that can be extracted from the analysis of the CMB and takes the form 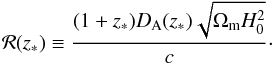 (13)Combined with the inverse covariance matrix
(13)Combined with the inverse covariance matrix 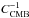 from Planck Collaboration XIV (2016), the contribution of CMB to the χ2 value can be written as
from Planck Collaboration XIV (2016), the contribution of CMB to the χ2 value can be written as 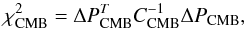 (14)where ΔPCMB is the difference between the theoretical distance prior and the observational one. In Fig. 11, we show the confidence contours of Ωm and w from QSO, BAO, and CMB. Both the individual constraints and the combined constraint are shown. The QSO constraint is almost orthogonal to that of the CMB and BAO. Adding the constraints from BAO and CMB reduces the uncertainty. Under the assumption of a flat Universe, the three probes together yield
(14)where ΔPCMB is the difference between the theoretical distance prior and the observational one. In Fig. 11, we show the confidence contours of Ωm and w from QSO, BAO, and CMB. Both the individual constraints and the combined constraint are shown. The QSO constraint is almost orthogonal to that of the CMB and BAO. Adding the constraints from BAO and CMB reduces the uncertainty. Under the assumption of a flat Universe, the three probes together yield 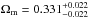 ,
, 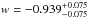 and
and 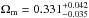 ,
, 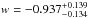 without and with systematical uncertainties, respectively. From Fig. 11 and Table 2, it is easy to see that the combined angular diameter distance data favors slightly higher values of both Ωm and w, while QSOs data favors a relatively higher Ωm and a lower w.
without and with systematical uncertainties, respectively. From Fig. 11 and Table 2, it is easy to see that the combined angular diameter distance data favors slightly higher values of both Ωm and w, while QSOs data favors a relatively higher Ωm and a lower w.
3.3. Time dependent equation of state
Next, we examined models with the DE equation of state allowed to vary with time. Considering that the quasar data alone do not tightly constrain w, even for spatially flat models, more data are added to break the strong geometrical degeneracy.
 |
Fig. 12 68.3% and 95.4% confidence regions of the (w0,wa) plane from QSO, BAO, CMB, and their combination. Zero curvature has been assumed. Points above the dotted line (w0 + wa> 0) violate early matter domination and are disfavored by the data. |
Among a wide range of dark energy models, we consider the commonly used Chevalier-Polarski-Linder (CPL) model involving certain dynamical scalar field models (Chevallier & Polarski 2001; Linder 2004), in which, to a good approximation, the equation of state of dark energy is parametrized as 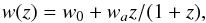 (15)where w0 and wa are constants and the ΛCDM model is recovered when w0 = −1 and wa = 0. Adding Planck CMB and BAO to the quasar data gives the 68.3% constraints:
(15)where w0 and wa are constants and the ΛCDM model is recovered when w0 = −1 and wa = 0. Adding Planck CMB and BAO to the quasar data gives the 68.3% constraints: 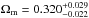 ,
, 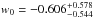 ,
, 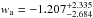 (without systematics) and
(without systematics) and 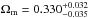 ,
, 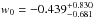 ,
, 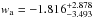 (with systematics). The constraints on w0 and wa are shown in Fig. 12 and Table 2. We note that the combined angular diameter distance data favors a w0> −1 and a negative wa, which means that dark energy was phantom-like (w< −1) in the past; then its EoS crossed the phantom divide, and recently became quintessence-like (w> −1); finally, its EoS will become positive in the future. On the contrary, QSO data with l prior favors a w0< −1 and a positive wa, which means that dark energy was quintessence-like (w> −1) in the past; then its EoS crossed the phantom divide, and recently became phantom-like (w< −1); finally, the Universe will end in a big rip.
(with systematics). The constraints on w0 and wa are shown in Fig. 12 and Table 2. We note that the combined angular diameter distance data favors a w0> −1 and a negative wa, which means that dark energy was phantom-like (w< −1) in the past; then its EoS crossed the phantom divide, and recently became quintessence-like (w> −1); finally, its EoS will become positive in the future. On the contrary, QSO data with l prior favors a w0< −1 and a positive wa, which means that dark energy was quintessence-like (w> −1) in the past; then its EoS crossed the phantom divide, and recently became phantom-like (w< −1); finally, the Universe will end in a big rip.
An accurate reconstruction of w(z) can considerably improve our understanding of the nature of both dark energy and gravity. In order to reconstruct the evolution of w(z) without assuming a specific form, this model will inevitably include more parameters than w0−wa, the number of dark energy equation-of-state parameters depending on the number of redshift bins (Kowalski et al. 2008). Confined to the sample size of our available quasar data, we carry out the analysis by dividing the full sample into different subsamples given their redshifts and fitting a constant w in each subsample. The redshifts of the QSOs span from z = 0.462 to z = 2.73, so we divide the QSOs into five groups with z< 1.0, 1.0 <z< 1.5, 1.5 <z< 2.0, 2.0 <z< 2.5, and z> 2.5. The first group has 30 QSOs with redshifts z< 1.0, the second group has 51 QSOs with redshifts 1.0 <z< 1.5, the third group has 25 QSOs with redshifts 1.5 <z< 2.0, the fourth group has 11 QSOs with redshifts 2.0 <z< 2.5, and the fifth group contains 3 QSOs with z> 2.5. We then fit the cosmic equation of state to each group of QSOs, while the remaining cosmological parameters are fixed at the best-fit values determined by Planck results. The constraints are shown in Fig. 13 and Table 4.
The first group shows a well-constrained EoS parameter from redshift 0.5 to 1.0. Therefore, no evidence of deviation from w = −1 is detected from low-redshift quasars, which is in good agreement with the previous findings from Union2.1 SN Ia constraints (Amanullah et al. 2010). The deviation from ΛCDM is also not obvious in the second and fifth redshift groups. Interestingly, our quasar data favors a transition from w< −1 at low redshift to w> −1 at higher redshift, a behavior that is consistent with the quintom model allowing w to cross −1. A redshift bin shifts the confidence interval for w(2.0 <z< 2.5) towards higher w, which is typically favored by many scalar field models. As shown in Fig. 13, the transition redshift for w departing from −1 is apparently located at z ~ 2.0 – which might be overlooked by the recent analysis – with a joint data set including Union2.1 SN, CMB, H(z), RSD (redshift space distortion), and BAO while fixing w = −1 at z> 1.5 (Zhao et al. 2012). More data extending above redshift z = 3 will be necessary to investigate the dark energy EoS parameter in this high-redshift region where the uncertainty is still very large.
 |
Fig. 13 Best-fitted w with marginalized 68.3% CL error. The results were obtained assuming a flat universe for the joint data set of QSO, BAO, CMB, with (left panel) and without (right panel) QSO systematics. The QSOs are divided into five groups with z< 1.0, 1.0 <z< 1.5, 1.5 <z< 2.0, 2.0 <z< 2.5, and z> 2.5, while BAO and CMB are added to constrain the value of Ωm, considering the well-known “geometrical degeneracy” problem. We emphasize that the results are still consistent with the cosmological constant (red dashed line) at the 68.3% confidence level. |
Constraints on equation of state w from the redshift-divided radio quasar data.
 |
Fig. 14 2D regions and 1D marginalized distribution of RDE model parameters from the quasar sample, without (left panel) and with systematical uncertainties (right panel). |
 |
Fig. 15 2D regions and 1D marginalized distribution of DGP model parameters from the quasar sample, without (left panel) and with systematical uncertainties (right panel). |
4. Beyond dark energy
As is well known, there is a physically profound question that should be addressed in the empirical cosmological studies: does the cosmic acceleration arise from a new energy component with repulsive gravity or a breakdown of General Relativity (GR) on cosmological scales? In this section, we investigate the constraining power of our quasar sample, concerning different approaches to explain the accelerated expansion of the Universe based on the departure from classical GR. Here we lay the framework for such options and give some examples. In particular we will consider two models:
-
RDE: Ricci dark energy model in a flat universe;
-
DGP: Dvali-Gabadadze-Porrati brane-world model in a flat universe.
4.1. Ricci dark energy
Other cosmological approaches to describe the dark component have received considerable attention in the past, one of which is holographic dark energy, proposed in the context of the fundamental principle of quantum gravity (Bekenstein 1981; Gao et al. 2009). Compared with the cosmological constant model, this mechanism may alleviate the well-known coincidence problem and fine tuning problem. The idea here is that the scale of dark energy is set by a cosmological Hubble horizon scale instead of the Planck length. Choosing an infrared (IR) cutoff of the quantum field theory as | R | − 1/2, where R = 6(Ḣ + 2H2) is the Ricci scalar of the flat Friedman-Robertson-Walker metric, an effective equivalent of the dark energy density can be derived (Gao et al. 2009), 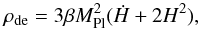 (16)where β is a constant parameter larger than zero. The Hubble parameter can be derived from the Friedman equation:
(16)where β is a constant parameter larger than zero. The Hubble parameter can be derived from the Friedman equation: ![\begin{equation} H^2 = H_0^2 \left[\frac{ 2\Omega_{\rm m}}{2-\beta}(1+z)^{3}+\left(1-{2\Omega_{\rm m}\over 2 -\beta}\right)(1+z)^{(4-{2\over\beta})}\right] . \end{equation}](/articles/aa/full_html/2017/10/aa30551-17/aa30551-17-eq276.png) (17)This is a two-parameter model with p = {Ωm,β}. Testing the RDE model with the quasar data, we obtain the following best fits:
(17)This is a two-parameter model with p = {Ωm,β}. Testing the RDE model with the quasar data, we obtain the following best fits: 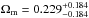 ,
, 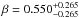 (without systematics) and
(without systematics) and 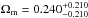 ,
, 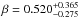 (with systematics). These results are presented in Fig. 14 and Table 4 and are in agreement with the previous analysis using galactic-scale strong gravitational lensing systems (Biesiada et al. 2011; Cao et al. 2012b), and with the previous work based on the SNe Ia Constitution compilation, the BAO measurement from the SDSS and the Two Degree Field Galaxy Redshift Survey, and the CMB measurement given by the five-year WMAP observations (Li et al. 2010).
(with systematics). These results are presented in Fig. 14 and Table 4 and are in agreement with the previous analysis using galactic-scale strong gravitational lensing systems (Biesiada et al. 2011; Cao et al. 2012b), and with the previous work based on the SNe Ia Constitution compilation, the BAO measurement from the SDSS and the Two Degree Field Galaxy Redshift Survey, and the CMB measurement given by the five-year WMAP observations (Li et al. 2010).
4.2. Higher dimension theories
Past decades have witnessed considerable advances in the modification of General Relativity as a possible explanation for the accelerated expansion of the Universe. One radical proposal is to introduce extra dimensions and allow gravitons to leak off the brane representing the observable universe. Embedding our 4D spacetime into a higher dimensional bulk spacetime, Dvali & Poratti (2000) proposed the well-known Dvali-Gabadadze-Porrati (DGP) brane-world model, in which the leaking of gravity above a certain cosmological scale rc might be responsible for the increasing cosmic expansion rate. Inspired by the DGP example, a general class of “galileon” and massive gravity models has been proposed in the literature (Mortonson et al. 2014). The length at which gravity leaking occurs defines an omega parameter, 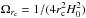 , which the Friedman equation modified as
, which the Friedman equation modified as 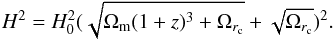 (18)The flat DGP model only contains one free model parameter, θ = { Ωm }, which is related to
(18)The flat DGP model only contains one free model parameter, θ = { Ωm }, which is related to 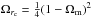 under assumption of a flat Universe. In order to make a comparison with the ΛCDM model, we also take the Hubble constant as a free parameter. The best-fit value for the mass density parameter in the DGP model is
under assumption of a flat Universe. In order to make a comparison with the ΛCDM model, we also take the Hubble constant as a free parameter. The best-fit value for the mass density parameter in the DGP model is 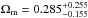 (without systematics) and
(without systematics) and 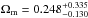 (with systematics), while the best-fit Hubble constant is
(with systematics), while the best-fit Hubble constant is 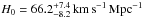 (without systematics) and
(without systematics) and 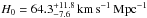 (with systematics). These results are presented in Fig. 15 and Table 4. The DGP model is the one for which we obtained the tightest constraints in our analysis thanks to the simplicity of the model, which depends on only one parameter. In this respect, this is the simplest model, together with the standard flat ΛCDM. In general, as we already discussed in (Cao & Zhu 2014), it is to be expected that models with fewer parameters perform better.
(with systematics). These results are presented in Fig. 15 and Table 4. The DGP model is the one for which we obtained the tightest constraints in our analysis thanks to the simplicity of the model, which depends on only one parameter. In this respect, this is the simplest model, together with the standard flat ΛCDM. In general, as we already discussed in (Cao & Zhu 2014), it is to be expected that models with fewer parameters perform better.
From the above considerations, two crucial consequences arise: first, given the current status of cosmological observations including QSOs, there is no strong reason to go beyond the simple, standard cosmological model with zero curvature and a cosmological constant, and second, a low value of the Hubble constant is preferred by both the new Planck data and our quasar observations. This consistency between fundamental cosmological parameters constrained from the high-redshift CMB measurements z ~ 1000 and those from the observations at relatively low redshifts z ~ 3 may alleviate the tension between Planck and the SN Ia observations at z = 0 (Marra et al. 2013; Xia et al. 2013; Li et al. 2014). In fact, projected parameters should presumably be the same from measurements at all z in a given model.
 |
Fig. 16 Best-fit confidence regions in the Ωm-w and w0−wa plane from quasars combined with angular diameter distance measurements from cluster observations. |
Best fits for different cosmological models from the radio quasar data.
5. Discussion: improving cosmological constraints by efficiently adding low-redshift clusters
The redshift of intermediate-luminosity quasars ranges between z = 0.46 and z = 2.73. Therefore, we also added to the data a set of 25 well-measured angular diameter distances from the galaxy clusters. They were obtained by considering Sunyaev-Zeldovich effect (SZE) together with X-ray emission of galaxy clusters (De Filippis et al. 2005), where an isothermal elliptical β model was used to describe the clusters. The enlargement of DA(z) sample at lower redshifts (0.142 <z< 0.890) improves the assessment of the w parameter that describes the properties of dark energy.
As shown in Fig. 11, adding the cluster data tightens the constraints substantially, giving the improved fitting results on the XCDM model: 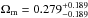 ,
, 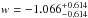 . Speaking in terms of the figure of merit (FoM) – a measure proposed by the Dark Energy Task Force (Albrecht et al. 2006), which is equal to the inverse of the area of the 95% confidence contour in the parameter plane – we find that this combined data set improves the constraint on w by 30%. Considering the redshift coverage of these two astrophysical probes, the combination of high-redshift quasars and low-redshift clusters may provide an important source of angular diameter distances, in addition to the previously studied probes including strongly gravitationally lensed systems (Biesiada et al. 2010, 2011; Cao et al. 2012a, 2015b) or X-ray gas mass fraction of galaxy clusters (Allen et al. 2004, 2008).
. Speaking in terms of the figure of merit (FoM) – a measure proposed by the Dark Energy Task Force (Albrecht et al. 2006), which is equal to the inverse of the area of the 95% confidence contour in the parameter plane – we find that this combined data set improves the constraint on w by 30%. Considering the redshift coverage of these two astrophysical probes, the combination of high-redshift quasars and low-redshift clusters may provide an important source of angular diameter distances, in addition to the previously studied probes including strongly gravitationally lensed systems (Biesiada et al. 2010, 2011; Cao et al. 2012a, 2015b) or X-ray gas mass fraction of galaxy clusters (Allen et al. 2004, 2008).
Now we show how the combination of most recent and significantly improved cosmological observations can be used to study the cosmic EoS. We consider four background probes which are directly related to angular diameter distances: intermediate-luminosity quasar data (QSO), Sunyaev-Zeldovich effect (SZE) together with X-ray emission of galaxy clusters, baryonic acoustic oscillations (BAO), and CMB observations. The first two probes are always considered as individual standard rulers, while the other two probes are treated as statistical standard rulers in cosmology. Results concerning the constraints on the CPL model parameters are displayed in Fig. 16, with the best-fit 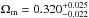 ,
, 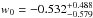 ,
, 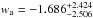 (without systematics) and
(without systematics) and 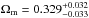 ,
, 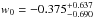 ,
, 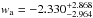 (with systematics). At 68.3% confidence level, we find that this model is still compatible with ΛCDM, i.e., the case (w0 = −1; wa = 0) typically lies within the 1σ boundary. In this context, it is clear that the collection of more complete observational data concerning angular diameter distance measurements plays a crucial role (Cao & Zhu 2014).
(with systematics). At 68.3% confidence level, we find that this model is still compatible with ΛCDM, i.e., the case (w0 = −1; wa = 0) typically lies within the 1σ boundary. In this context, it is clear that the collection of more complete observational data concerning angular diameter distance measurements plays a crucial role (Cao & Zhu 2014).
6. Summary and conclusions
In this paper, we have presented a newly compiled data set of 120 milliarcsecond compact radio-sources representing intermediate-luminosity quasars covering the redshift range 0.46 <z< 2.76. These quasars show negligible dependence of their linear size on the luminosity and redshift (| n | ≃ 10-3, | β | ≃ 10-4) and thus represent, in the standard model of cosmology, a fixed comoving-length of standard ruler. We implemented a new cosmology-independent technique to calibrate the linear size of this standard ruler. In particular, we used the technique of Gaussian processes to reconstruct the Hubble function H(z) as a function of redshift from 15 measurements of the expansion rate obtained from age estimates of passively evolving galaxies. This reconstruction enabled us to derive the angular diameter distance to a certain redshift z, and thus calibrate the liner size of radio quasars. More importantly, we found lm = 11.03 ± 0.25 pc is the typical radius at which AGN jets become opaque at the observed frequency ν ~ 2 GHz. Our measurement of this linear size is also consistent with both the previous and most recent radio observations at other different frequencies in the framework of the BK79 conical jet model.
Then this new quasar sample was used to investigate the properties of dark energy. In the framework of flat ΛCDM model, a high value of the matter density parameter, 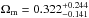 , and a low value of the Hubble constant,
, and a low value of the Hubble constant, 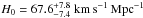 are obtained, which is in excellent agreement with the CMB anisotropy measurements by Planck. For the constant w of a dynamical dark-energy model, we obtained
are obtained, which is in excellent agreement with the CMB anisotropy measurements by Planck. For the constant w of a dynamical dark-energy model, we obtained 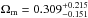 ,
, 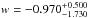 at 68.3% confidence level, which demonstrates no significant deviation from the concordance ΛCDM model. Consistent fitting results were also derived for other cosmological mechanisms explaining the cosmic acceleration, including the Ricci dark energy model and Dvali-Gabadadze-Porrati (DGP) brane-world model. Moreover, we reconstructed the dark-energy EoS parameter from different quasar subsample, and investigated the evolution of w in the redshift range 0.46 < z < 2.76. No evidence of deviation from w = −1 was detected from low-redshift quasars, which is in good agreement with the previous findings from SN Ia constraints (Amanullah et al. 2010; Suzuki et al. 2012). Interestingly, the most likely reconstruction using our quasar data favors the transition from w < −1 at low redshift to w > −1 at higher redshift, a behavior that is consistent with the quintom model which allows w to cross −1. The transition redshift at which w departs from -1 is located at z ~ 2.0, which might be overlooked by the previous analysis fixing w = −1 at z > 1.5. After adding constraints from the galaxy cluster measurements (0.142 <z< 0.890), we provide a much tighter limit on the EoS parameter:
at 68.3% confidence level, which demonstrates no significant deviation from the concordance ΛCDM model. Consistent fitting results were also derived for other cosmological mechanisms explaining the cosmic acceleration, including the Ricci dark energy model and Dvali-Gabadadze-Porrati (DGP) brane-world model. Moreover, we reconstructed the dark-energy EoS parameter from different quasar subsample, and investigated the evolution of w in the redshift range 0.46 < z < 2.76. No evidence of deviation from w = −1 was detected from low-redshift quasars, which is in good agreement with the previous findings from SN Ia constraints (Amanullah et al. 2010; Suzuki et al. 2012). Interestingly, the most likely reconstruction using our quasar data favors the transition from w < −1 at low redshift to w > −1 at higher redshift, a behavior that is consistent with the quintom model which allows w to cross −1. The transition redshift at which w departs from -1 is located at z ~ 2.0, which might be overlooked by the previous analysis fixing w = −1 at z > 1.5. After adding constraints from the galaxy cluster measurements (0.142 <z< 0.890), we provide a much tighter limit on the EoS parameter: 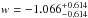 . Considering the redshift coverage of these two astrophysical probes, the combination of high-redshift quasars and low-redshift clusters may provide an important source of angular diameter distances. In order to asses the reliability of the above results with intermediate-luminosity quasars, the effects of several systematics on the final cosmological fits (due to the uncertainties of the linear size scaling factor (l) and the dependence of lm on the luminosity and redshift (β, n)) were also extensively studied in our cosmological analysis. Our findings revealed that the reduction of the above uncertainties will lead to more stringent cosmological fits, which motivates the future use of VLBI observations based on better uv-coverage to improve constraints on l, β, and n (Pushkarev & Kovalev 2015).
. Considering the redshift coverage of these two astrophysical probes, the combination of high-redshift quasars and low-redshift clusters may provide an important source of angular diameter distances. In order to asses the reliability of the above results with intermediate-luminosity quasars, the effects of several systematics on the final cosmological fits (due to the uncertainties of the linear size scaling factor (l) and the dependence of lm on the luminosity and redshift (β, n)) were also extensively studied in our cosmological analysis. Our findings revealed that the reduction of the above uncertainties will lead to more stringent cosmological fits, which motivates the future use of VLBI observations based on better uv-coverage to improve constraints on l, β, and n (Pushkarev & Kovalev 2015).
As a final remark, we point out that the sample discussed in this paper is based on VLBI images observed with various antenna configurations and techniques for image reconstruction. Our analysis potentially suffers from this systematic bias; it will be taken fully into account and included in our future work. To fully utilize the potential of current and future VLBI surveys to constrain cosmology, it will be necessary to reduce systematic errors significantly. The largest current source of systematic uncertainty is calibration. Calibration uncertainties can be split into uncertainties related to the primary standard, and uncertainties in the determination of the value of l, the linear size of this standard ruler. In principle, the first uncertainty can be reduced by multi-frequency VLBI observations of more compact radio quasars with higher sensitivity and angular resolution (Cao et al. 2017), while the reduction of the second uncertainty should turn to more efficient distance reconstruction technique. In this paper, we have applied only one particular non-parametric method based on Gaussian processes in order to reconstruct angular diameter distances from 24 cosmic chronometer measurements at z ≤ 1.2. The application of new distance-reconstruction techniques to future VLBI quasar observations of high angular resolutions will allow us to cross-calibrate the quasar systems and significantly reduce the systematic errors.
The QSO data set presented here and future complementary data sets will help us to explore these possibilities. The approach introduced in this paper, would make it feasible to build a significantly larger sample of standard rulers at much higher redshifts. With such a sample, we will be able to further investigate constraints on the cosmic evolution as well as possible evidence for dynamical dark energy.
SN Ia are commonly accepted standard candles in the Universe and from their observed distance moduli we are able to recover luminosity distances covering the lower redshift range z ≤ 1.40. On the other hand, CMB measurements, e.g., the latest results from Planck, probe very high redshift z ~ 1000 corresponding to the last scattering surface. Therefore, the redshift range 1.40 ≤ z ≤ 1000 is sometimes called the “redshift desert” because of fundamental difficulties in obtaining observational data in this range.
A full listing of all 613 objects, with appropriate parameters, is available in electronic form via http://nrl.northumbria.ac.uk/13109/
We use the term “core” as the apparent origin of AGN jets that commonly appears as the brightest feature in VLBI images of blazars (Lobanov 1998).
As discussed in Planck Collaboration XIII (2016), because the WiggleZ volume partially overlaps that of the BOSS-CMASS sample and the correlations have not been quantified, we chose not to use the recent WiggleZ results in our analysis.
Acknowledgments
The authors would like to thank the referee for the careful and critical reading and for valuable comments and suggestions which improved our paper significantly. We are grateful to John Jackson for his kind provision of the data used in this paper and for useful discussions. We thank Zhengxiang Li and Meng Yao for helpful discussions. This work was supported by the National Key Research and Development Program of China under Grants No. 2017YFA0402603; the Ministry of Science and Technology National Basic Science Program (Project 973) under Grants No. 2014CB845806; the National Natural Science Foundation of China under Grants Nos. 11503001, 11373014, and 11690023; the Fundamental Research Funds for the Central Universities and Scientific Research Foundation of Beijing Normal University; China Postdoctoral Science Foundation under grant No. 2015T80052; and the Opening Project of Key Laboratory of Computational Astrophysics, National Astronomical Observatories, Chinese Academy of Sciences. X.Z. was supported by the China Scholarship Council. This research was also partly supported by the Poland-China Scientific & Technological Cooperation Committee Project No. 35-4. M.B. was supported by Foreign Talent Introducing Project and Special Fund Support of Foreign Knowledge Introducing Project in China.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006, arXiv e-print [arXiv:astro-ph/0609591] [Google Scholar]
- Allen, S. W., Schmidt, R. W., Ebeling, H., et al. 2004, MNRAS, 353, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2014, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 1981, Phys. Rev. D, 23, 287 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., & Hinshaw, G. 2014, ApJ, 794, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Biesiada, M., Piórkowska, A., & Malec, B. 2010, MNRAS, 406, 1055 [NASA ADS] [Google Scholar]
- Biesiada, M., Malec, B., & Piórkowska, A. 2011, Res. Astron. Astrophys., 11, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Rees, M. J. 1978, Some comments on radiation mechanisms in Lacertids, in BL Lac Objects (ed. A.M. Wolfe), University of Pittsburgh, Pittsburgh, 328 [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Chapman, S. C., Ibata, R. A., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Buchalter, A., Helfand, D. J., Becker, R. H., & White, R. L. 1998, ApJ, 494, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Busti, V. C., Clarkson, C., & Seikel, M. 2014, MNRAS, 441, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., & Liang, N. 2011, Res. Astron. Astrophys., 11, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., & Zhu, Z.-H. 2011, China Series G, 54, 2260 [CrossRef] [Google Scholar]
- Cao, S., & Zhu, Z.-H. 2014, Phys. Rev. D, 90, 083006 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Chuntonov, G. A., & Shavrina, A. V. 2012a, JCAP, 55, 140 [Google Scholar]
- Cao, S., Covone, G., & Zhu, Z.-H. 2012b, ApJ, 755, 516 [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Zheng, X., & Zhu, Z.-H. 2015a, ApJ, 806, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Gavazzi, R., Piórkowska, A., & Zhu, Z.-H. 2015b, ApJ, 806, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Jackson, J., et al. 2017, JCAP, 02, 012 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., & Ratra, B. 2003, ApJ, 582, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallier, M., & Polarski, D. 2001, Int. J. Mod. Phys. D, 10, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Chiba, M., & Yoshii, Y. 1999, ApJ, 510, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daly, R. A., & Djorgovski, S. G. 2003, ApJ, 597, 9 [NASA ADS] [CrossRef] [Google Scholar]
- De Filippis, E., Sereno, M., Bautz, W., Longo, G. 2005, ApJ, 625, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, X., Biesiada, M., Cao, S., Li, Z. X., & Zhu, Z.-H., 2015, ApJ, 803, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Dvali, G., Gabadadze, G., & Porrati, M. 2000, Phys. Lett. B, 485, 208 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eisenstein, D. J., & Hu, W., 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F. R., & Stoeger, W. 1987, Class. Quant. Grav., 4, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Frey, S., Paragi, Z., Gurvits, L. I., Cseh, D., & Gabányi, K. É. 2010, A&A, 524, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, C., Wu, F., Chen, X., & Shen, Y. 2009, Phys. Rev. D, 79, 043511 [NASA ADS] [CrossRef] [Google Scholar]
- Gott, J. R., III, Vogeley, M. S., Podariu, S., & Ratra, B. 2001, ApJ, 549, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, E. J., & Daly, R. A. 1998, ApJ, 493, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, E. J., Daly, R. A., & Wan, L. 2000, ApJ, 544, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Gurvits, L. I. 1994, ApJ, 425, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Gurvits, L. I., Kellerman, K. I., & Frey, S. 1999, A&A, 342, 378 [NASA ADS] [Google Scholar]
- Holanda, R. F. L., Carvalho, J. C., & Alcaniz, J. S. 2013, JCAP, 04, 027 [NASA ADS] [CrossRef] [Google Scholar]
- Holsclaw, T., Alam, U., Sansó, B., et al. 2010a, Phys. Rev. D, 82, 103502 [NASA ADS] [CrossRef] [Google Scholar]
- Holsclaw, T., Alam, U., Sansó, B., et al. 2010b, Phys. Rev. Lett., 105, 241302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Sugiyama, N. 1996, ApJ, 471, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. C. 2004, JCAP, 11, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. C., & Dodgson, M. 1997, MNRAS, 285, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. C., & Jannetta, A. L. 2006, JCAP, 11, 002 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., & Loeb, A. 2002, ApJ, 573, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I. 1993, Nature, 361, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Li, M., Li, X. D., & Zhang, X. 2010, Sci. China Phys. Mech. Astron., 53, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. X., Wu, P. X., Yu, H. W., & Zhu, Z. H. 2014, Sci. China Phys. Mech. Astron., 57, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. X., Gonzalez, J. E., Yu, H. W., Zhu, Z.-H., & Alcaniz, J. S. 2016, Phys. Rev. D, 93, 043014 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, J. A. S., & Alcaniz, J. S. 2002, ApJ, 566, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. V. 2004, Phys. Rev. D, 68, 083503 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Marra, V., Welchman, A. E., Blake, A., & Fleming, R. W. 2013, Phys. Rev. Lett., 110, 241305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meier, D. L., 2009, in Approaching Micro-Arcsecond Resolution with VSOP-2: Astrophysics and Technology, eds. Y. Hagiwara, E. Fomalont, M. Tsuboi, & Y. Murata (San Francisco: ASP Conf. Ser.), 402, 342 [Google Scholar]
- Moresco, M., Cimatti, A., Jimenez, R., et al. 2012, JCAP, 1208, 006 [Google Scholar]
- Mortonson, M. J., Weinberg, D. H., & White, M. 2014, arXiv e-print [arXiv:1401.0046] [Google Scholar]
- O’Sullivan, S. P., & Gabuzda, D. C. 2009, MNRAS, 400, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 567 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2016, A&A, 594, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pope, A. C., Matsubara, T., Szalay, A. S., et al. 2004, ApJ, 607, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, R. A., Morabito, D. D., Williams, J. G., et al. 1985, AJ, 90, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Pushkarev, A. B., & Kovalev, Y. Y. 2015, MNRAS, 452, 4274 [NASA ADS] [CrossRef] [Google Scholar]
- Ratra, B., & Peebles, P. J. E. 1988, Phys. Rev. D, 37, 3406 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Li, W., et al. 2009, ApJS, 183, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Roukema, B., Buchert, T., Ostrowski, J. J., & France, M. J. 2015, MNRAS, 448, 1660 [NASA ADS] [CrossRef] [Google Scholar]
- Roukema, B., Buchert, T., Fuji, H., & Ostrowski, J. J. 2016, MNRAS, 456, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. 1988, ARA&A, 26, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Seikel, M., Clarkson, C., & Smith, M. 2012, JCAP, 6, 36 [Google Scholar]
- Shafieloo, A., Kim, A. G., & Linder, E. V. 2013, Phys. Rev. D, 87, 023520 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Kovač, K., Knobel, C., et al. 2009, ApJ, 695, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, AJS, 148, 175 [CrossRef] [Google Scholar]
- Suzuki, N., Rubin, D., Lidman, C., et al. 2012, ApJ, 746, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2008, A&ARv, 15, 289 [NASA ADS] [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson G. W. 1986, in Interferometry and Synthesis in Radio Astronomy (New York: John Wiley & Sons), 13 [Google Scholar]
- Verde, L., Protopapas, P., & Jimenez, R. 2014, Phys. Dark Univ., 5, 307 [CrossRef] [Google Scholar]
- Vishwakarma, R. G. 2001, Class. Quant. Grav., 18, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, J.-Q., Li, H., & Zhang, X. M. 2013, Phys. Rev. D, 88, 063501 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. 2014, arXiv e-print [arXiv:1408.3897] [Google Scholar]
- Zhao, G. B., Crittenden, R. G., Pogosian, L., & Zhang, X. M. 2012, Phys. Rev. Lett., 109, 171301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zheng, X., Ding, X., Biesiada, M., Cao, S., & Zhu, Z.-H. 2016, ApJ, 825, 1 [CrossRef] [Google Scholar]
- Zhu, Z.-H., & Fujimoto, M. K. 2002, ApJ, 581, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Measurements of the linear size of AGN compact structure at different frequencies.
Cosmological parameters Ωm, w0, wa, and the Hubble constant H0 fitted to the QSO data.
All Figures
 |
Fig. 1 Upper panel: sky distribution of the quasar sample of 120 sources detected with VLBI. Lower panel: luminosity, redshift, and angular size distribution for the quasar sample of 120 sources. |
| In the text | |
 |
Fig. 2 Intrinsic metric linear size lm distribution of the 120 intermediate luminosity quasars in the redshift and luminosity space. |
| In the text | |
 |
Fig. 3 Degeneracy between the linear size of ultra-compact structure in radio quasars and the matter density parameter in the Universe; 68.3% and 95.4% confidence regions are shown. |
| In the text | |
 |
Fig. 4 Corrected linear size of compact quasars derived in a cosmological model independent way, using the observational H(z) data. |
| In the text | |
 |
Fig. 5 Plot of core size versus frequency (constraint on the linear size of compact structure in intermediate-luminosity quasars l at 2.16 GHz is added). The BK 79 jet model (rc ∝ ν-1 ) is used for the fitted curve from VLBI/VLBA observations in the literature. |
| In the text | |
 |
Fig. 6 Comparison between the P15 and P85 samples concerning the angular size–redshift and angular size–luminosity diagrams based on 58 sources common to these two surveys. |
| In the text | |
 |
Fig. 7 Angular diameter distances DA(z) estimated from quasars as standard rulers (blue squares). Angular diameter distances from galaxy clusters (purple circles) are also added for comparison. Theoretical predictions of ΛCDM models with ΩΛ = 0.00 and ΩΛ = 0.70 are denoted by black and red solid lines, respectively. |
| In the text | |
 |
Fig. 8 Cosmological constraints on the flat ΛCDM model from the quasar sample without (left panel) and with systematical uncertainties (right panel). Fitting results from recent H(z) measurements (black dashed lines) and Planck observations (green dot represents the best fit with 1σ errors denoted by green solid lines) are also added for comparison. |
| In the text | |
 |
Fig. 9 Cosmological constraints on the flat ΛCDM model from the quasar sample without and with different systematical uncertainties: sys1 denotes the systematics with l = 11.03 ± 0.25 pc, β = 0.00 ± 0.05, and n = 0.00 ± 0.05, while sys2 represents the systematics with l = 11.03 ± 0.25 pc, β = 0.00 ± 0.10, and n = 0.00 ± 0.10. |
| In the text | |
 |
Fig. 10 Probability distribution of the matter density parameter in the flat ΛCDM model, which is derived from the quasar sample without (red solid line) and with systematical uncertainties (red dashed line) with the prior on the Hubble constant H0 = 70 km s-1 Mpc-1. Fitting result from recent H(z) measurements (black dashed lines) is also added for comparison. |
| In the text | |
 |
Fig. 11 XCDM model: 68.3% and 95.4% confidence regions in the (Ωm, w) plane from QSO, BAO, CMB, and H(z). The left panel shows the QSO confidence region with the best-fit value for l only, while the right panel shows the confidence region including systematical uncertainties of l, β, and n. We note that CMB and QSO constraints are orthogonal, making this combination of cosmological probes very powerful for investigating the nature of dark energy. |
| In the text | |
 |
Fig. 12 68.3% and 95.4% confidence regions of the (w0,wa) plane from QSO, BAO, CMB, and their combination. Zero curvature has been assumed. Points above the dotted line (w0 + wa> 0) violate early matter domination and are disfavored by the data. |
| In the text | |
 |
Fig. 13 Best-fitted w with marginalized 68.3% CL error. The results were obtained assuming a flat universe for the joint data set of QSO, BAO, CMB, with (left panel) and without (right panel) QSO systematics. The QSOs are divided into five groups with z< 1.0, 1.0 <z< 1.5, 1.5 <z< 2.0, 2.0 <z< 2.5, and z> 2.5, while BAO and CMB are added to constrain the value of Ωm, considering the well-known “geometrical degeneracy” problem. We emphasize that the results are still consistent with the cosmological constant (red dashed line) at the 68.3% confidence level. |
| In the text | |
 |
Fig. 14 2D regions and 1D marginalized distribution of RDE model parameters from the quasar sample, without (left panel) and with systematical uncertainties (right panel). |
| In the text | |
 |
Fig. 15 2D regions and 1D marginalized distribution of DGP model parameters from the quasar sample, without (left panel) and with systematical uncertainties (right panel). |
| In the text | |
 |
Fig. 16 Best-fit confidence regions in the Ωm-w and w0−wa plane from quasars combined with angular diameter distance measurements from cluster observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


