| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201630051 | |
| Published online | 11 October 2017 | |
Maximum mass of planetary embryos that formed in core-accretion models
Physikalisches Institut & Center for Space and Habitability, Universitaet Bern, 3012 Bern, Switzerland
e-mail: alibert@space.unibe.ch
Received: 13 November 2016
Accepted: 14 May 2017
Context. In the core-accretion model, the typical size of solids that are accreted to form planetary embryos and planetary cores is debated. First, models assumed that the main part of planetary cores came from large-sized planetesimals, but other more recent models are based on the accretion of small-sized pebbles.
Aims. The goal of this paper is to compute the maximum mass a growing planetary embryo can reach depending on the size of accreted planetesimals or pebbles, and to infer the possibility of growing the cores of giant planets and giant planets themselves.
Methods. We computed the internal structure of the gas envelope of planetary embryos to determine the core mass that is necessary to bind an envelope large enough to destroy planetesimals or pebbles while they are gravitationally captured. We also considered the effect of the advection wind originating from the protoplanetary disk, following the results of Ormel et al. (2015, MNRAS, 447, 3512).
Results. We show that for low-mass pebbles the envelope is large enough to destroy and vaporize pebbles completely before they can reach the core once the planetary embryo is larger than a fraction of the Earth mass. The material constituting pebbles is therefore released in the planetary envelope and is later on dispersed in the protoplanetary disk if the advection wind is strong enough. As a consequence, the growth of the planetary embryo is stopped at a mass that is so low that Kelvin-Helmholtz accretion cannot lead to the accretion of significant amounts of gas. For larger planetesimals, a similar process occurs but at much higher mass, on the order of ten Earth masses, and it is followed by rapid accretion of gas.
Conclusions. If the effect of the advection wind is as efficient as described in Ormel et al. (2015), the combined effect of the vaporization of accreted solids in the envelope of forming planetary embryos and of this advection wind prevents the growth of the planets at masses lower than or similar to the Earth mass in the case of formation by pebble accretion, up to a distance on the order of 10 AU. In the case of formation by accretion of high-mass planetesimals, the growth of the planetary core is limited at masses on the order of ten Earth masses. However, in contrast to the case of pebble accretion, further growth is still possible and proceeds either through the accretion of gas or through the accretion of solids that are destroyed in the planetary envelope when the effect of the advection wind has ceased and the planetary Hill radius becomes comparable to the disk scale height.
Key words: planets and satellites: formation / planets and satellites: composition / planets and satellites: general
© ESO, 2017
1. Introduction
In the core-accretion model, planetary embryos grow from the accretion of solids until they are massive enough to start accreting noticeable amounts of gas in a runaway process (Pollack et al. 1996; Ida & Lin 2004; Alibert et al. 2005, 2013; Benz et al. 2014). However, before this phase of runaway accretion, planetary embryos already start to gravitationally bind a small envelope when they are rather small (smaller than the Earth). Even if the envelope is tiny at this stage and therefore does not contribute noticeably to the total planetary mass, it is important for the planetary growth. Solids in the protoplanetary disk interact with this tiny envelope through gas drag and heating, and this enlarges the cross-section of the planet and therefore the accretion rate of solids (see, e.g., Podolak et al. 1988; Pollack et al. 1996; Inaba & Ikoma 2003; Alibert et al. 2005). The effect of the envelope strongly depends on the mass and density of accreted solids, and generally speaking is stronger for smaller accreted bodies (we show below, however, that this general rule has some exceptions).
One point that is currently highly debated in the context of the core-accretion model is the typical size and mass of accreted bodies. In the first models, the most important mass carriers were planetesimals, whose typical size can be intermediate (on the order of some kilometers, see Ida & Lin 2004; Fortier et al. 2013) or large (on the order of one hundred kilometers, see Pollack et al. 1996; Alibert et al. 2005). One problem of these models is that the growth of the planetary core can be slow, especially at large distances from the star, with an accretion rate that is typically on the order of 10-6M⊕/yr (see, e.g., Alibert et al. 2013). We note that even if core accretion begins with planetesimals larger than one kilometer, collisional fragments can contribute greatly to core formation (Inaba et al. 2003; Kobayashi et al. 2010, 2011).
Recently, it has been proposed that the main component (in terms of total accreted mass) of captured solids could be much smaller solids, called pebbles, whose typical size is on the order of some centimeters. These pebbles are therefore strongly coupled to the gas, as their Stockes number (the product of the Keplerian frequency and the stopping time due to gas drag) is on the order of 0.1 (e.g., Ormel & Klahr 2010; Lambrechts & Johansen 20122014; Bitsch et al. 2015a,b, Levison et al. 2015). In this case, the accretion cross-section of planetary embryos is strongly increased by the presence of the gas envelope, and the growth of planetary cores can be very rapid. The accretion rate for embryos around one Earth mass is typically one order of magnitude higher than in the case of planetesimals, which have rates on the order of 10-5M⊕/yr (see, e.g., Lambrechts et al. 2014).
The presence of the planetary envelope, however, does not only increase the cross-section of planetary embryos, it also strongly affects accreted solids. Incoming solids suffer gas drag, heating from the ambient gas and from the high post-shock temperature (in case of supersonic trajectories), and, in some cases, mechanical destruction (when the difference between the pressure in front of the incoming body and the pressure on the sides is larger than the tensile strength of the body). If the gas envelope is hot and massive enough, incoming solids are destroyed, and their material is vaporized and lost in the gas envelope before they can reach the core (Podolak et al. 1988; Mordasini et al. 2006). Beyond this point, the growth of the planetary core stops, but not the growth of the whole planet, as accreted solids increase the metal content of the planetary envelope. In addition, the end of core growth coincides with a strong decrease of the core luminosity, which triggers accretion of H/He gas from the protoplanetary disk on a Kelvin-Helmholtz (hereafter KH) timescale (Ikoma et al. 2000; Hubickyj et al. 2005). As the metal and H/He content of the envelope increase, the planet can eventually become super-critical, and runaway H/He accretion occurs (see Venturini et al. 2016, for formation calculations that self-consistently take the enrichment of the planetary envelope into account).
The previous framework is based on the fact that the planetary envelope is a closed system that practically can only gain mass (solids or H/He) from the protoplanetary disk. However, recent calculations show that this may not always be the case. Using 3D hydrodynamical models, Ormel et al. (2015) have shown that the envelope of the growing planets is constantly replenished by gas coming from the protoplanetary disk, on a timescale that depends on the planetary and disk properties. When this effect is dominant, the growth of a planet beyond the point where solids are destroyed in the envelope encounters two problems. First, the Kelvin-Helmholtz contraction can be hindered (if the KH timescale is longer than the replenishment timescale, see Ormel et al. 2015). Second, the material lost by solids in the envelope may be lost to the protoplanetary disk if the deposition rate of such material is lower than the loss rate by the advection wind. This occurs if the pollution timescale (the time in which the composition of the envelope is noticeably changed) is longer than the replenishment timescale. The first effect prevents the increase of the H/He component of the envelope, the second prevents the increase of the metal content of the envelope. Altogether, the mass growth of the planet is stopped. If the replenishment is efficient enough, the destruction of accreted solids therefore results in the end of the planetary growth, and consequently in the existence of a maximum mass of planetary embryos. Any further growth must proceed either by collision of such planetary embryos or must wait until the conditions have changed (e.g., the replenishment timescale, which depends on the properties of the protoplanetary disk, becomes longer).
2. Theoretical model
2.1. Planetary envelope
We compute the planetary structure by solving the planetary internal structure equations, assuming the luminosity is only given by the accretion rate of solids, L = GMcoreṀcore/Rcore. This means that we de facto assume that the solids reach the solid core. This is true until the point where solids are destroyed in the envelope (beyond this point, we do not use the internal structure equations any longer). 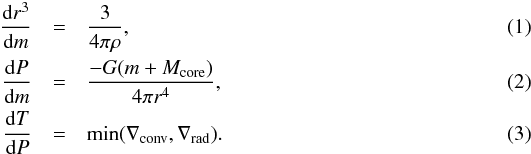 In these equations, r,P,T are the radius, the pressure, and the temperature inside the envelope, respectively. These three quantities depend on the gas mass m between the surface of the core and the sphere of radius r, the distance in the planetary envelope toward the planetary center. ρ is the mass density given as a function of T and P by the equation of state (EOS) of Saumon et al. (1995), and Mcore the mass of the solid core. The temperature gradient is given either by the radiative gradient (∇rad),
In these equations, r,P,T are the radius, the pressure, and the temperature inside the envelope, respectively. These three quantities depend on the gas mass m between the surface of the core and the sphere of radius r, the distance in the planetary envelope toward the planetary center. ρ is the mass density given as a function of T and P by the equation of state (EOS) of Saumon et al. (1995), and Mcore the mass of the solid core. The temperature gradient is given either by the radiative gradient (∇rad), 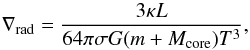 (4)or by the convective gradient, which is equal to the adiabatic one. In these formulas, σ is the Stefan-Boltzman constant and G is the gravitational constant. Finally, the luminosity L, which enters the computation of the radiative gradient, is given by the accretion energy of solids, and the opacity κ used here is taken to be equal to the opacity of the interstellar medium (ISM, Bell & Lin 1994). When the planetary envelope is small enough so that accreted solids are not destroyed (the phase during which we use the internal structure equations), the planetary envelope is constantly replenished by gas coming from the protoplanetary disk, and pollution by accreted solids is negligible. The population of grains in the planet is therefore close to the population in the protoplanetary disk, which is assumed to be similar to the population in the interstellar medium.
(4)or by the convective gradient, which is equal to the adiabatic one. In these formulas, σ is the Stefan-Boltzman constant and G is the gravitational constant. Finally, the luminosity L, which enters the computation of the radiative gradient, is given by the accretion energy of solids, and the opacity κ used here is taken to be equal to the opacity of the interstellar medium (ISM, Bell & Lin 1994). When the planetary envelope is small enough so that accreted solids are not destroyed (the phase during which we use the internal structure equations), the planetary envelope is constantly replenished by gas coming from the protoplanetary disk, and pollution by accreted solids is negligible. The population of grains in the planet is therefore close to the population in the protoplanetary disk, which is assumed to be similar to the population in the interstellar medium.
These equations are solved by using as boundary conditions the pressure and temperature in the protoplanetary disk at the position of the planetary embryo and by defining the planetary radius as a combination of the Hill and Bondi radii (Lissauer et al. 2009), 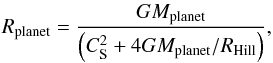 (5)where
(5)where  is the square of the sound velocity in the protoplanetary disk at the planet location aplanet, and
is the square of the sound velocity in the protoplanetary disk at the planet location aplanet, and 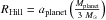 .
.
We note that, although the envelope is replenished on a timescale that can be rather short, we can still use the equations quoted above to determine the internal structure of the envelope. The internal structure equations are valid for timescales that are long compared to the dynamical timescale, which is much shorter than the replenishment timescale. In addition, the equation giving the temperature gradient is valid only when the planetary envelope is optically thick. For the opacity we consider (Bell & Lin 1994) this occurs for a planetary core equal to a fraction of an Earth mass (see also Bodenheimer & Pollack 1986).
2.2. Protoplanetary disk model
The thermodynamical properties of the disk are computed using the model of Bitsch et al. (2015a,b). This model is based on fits of 2D radiative transfer calculations including the effect of irradiation from the star. The choice of the disk model is not very important for the results we present in this paper (the disk model is more important, for example, when planetary migration is included, which strongly depends on the local disk structure). This models allows the determination of the temperature structure in the protoplanetary disk as a function of distance to the star and accretion rate in the disk. The accretion rate in the disk evolves with time on a 1 Myr timescale (Hartmann et al. 1998), 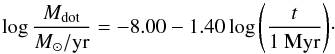 (6)From the value of the accretion rate Mdot, we compute the temperature in the solar nebula using the formulas presented in Bitsch et al. (2015a,b). The surface density and the other properties of the protoplanetary disk (scale height, mid-plane density) are computed after the value of the turbulent parameter αSS is chosen. Our reference value is αSS = 10-3, this value does not have a strong influence on our results.
(6)From the value of the accretion rate Mdot, we compute the temperature in the solar nebula using the formulas presented in Bitsch et al. (2015a,b). The surface density and the other properties of the protoplanetary disk (scale height, mid-plane density) are computed after the value of the turbulent parameter αSS is chosen. Our reference value is αSS = 10-3, this value does not have a strong influence on our results.
2.3. Timescales
Four timescales are important in the problem considered here. The first is the replenishment timescale, which we compute using the formulas of Ormel et al. (2015): 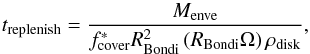 (7)where RBondi is the Bondi radius of the planetary embryo, Ω is the Keplerian frequency, Menve is the mass of the planetary envelope computed using the method presented in Sect. 2.1, and
(7)where RBondi is the Bondi radius of the planetary embryo, Ω is the Keplerian frequency, Menve is the mass of the planetary envelope computed using the method presented in Sect. 2.1, and  is a numerical parameter that quantifies the fraction of the planetary envelope that is directly part of streamlines coming from the protoplanetary disk and is found from numerical simulations to be in the range [0.1–1] (see Ormel et al. 2015). We use here a value of 0.1, which leads to an upper boundary of the likely value of treplenish.
is a numerical parameter that quantifies the fraction of the planetary envelope that is directly part of streamlines coming from the protoplanetary disk and is found from numerical simulations to be in the range [0.1–1] (see Ormel et al. 2015). We use here a value of 0.1, which leads to an upper boundary of the likely value of treplenish.
The simulations of Ormel et al. (2015) have been performed for an embedded planet, where RBondi is smaller than the scale height of the disk Hdisk. In our simulations, we therefore consider that the replenishment process stops when the planet is no longer embedded, namely when Hdisk<RBondi.
The second important timescale is the Kelvin-Helmoltz timescale, which governs the growth of the planet after the supply of energy source at the planetary core has ceased (this energy comes from the accretion of pebbles or planetesimals). Lee et al. (2014) have shown that for dust-free envelopes, the Kelvin-Helmoltz timescale is given by 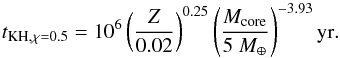 (8)This scaling is derived for a gas-to-core ratio χ of 0.5 and is based on calculations taking into account the gas opacity, but no dust opacity (see Lee et al. 2014). We note that this timescale is longer than the timescale derived by Hori & Ikoma (2010). We return in Sect. 3.3 to the consequences of a much reduced KH timescale.
(8)This scaling is derived for a gas-to-core ratio χ of 0.5 and is based on calculations taking into account the gas opacity, but no dust opacity (see Lee et al. 2014). We note that this timescale is longer than the timescale derived by Hori & Ikoma (2010). We return in Sect. 3.3 to the consequences of a much reduced KH timescale.
In the case of dusty envelopes (assuming ISM-like dust grains, see Lee et al. 2014), the KH timescale scales with Z0.72 and the pre-factor is one order of magnitude larger. Following Ormel et al. (2015), the Kelvin-Helmholtz timescale scales with the square of the gas-to-core ratio. We therefore obtain the following timescale in the case of dust-free gas: 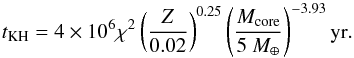 (9)In the case of a dusty atmosphere, the corresponding timescale is
(9)In the case of a dusty atmosphere, the corresponding timescale is 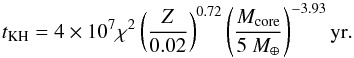 (10)We note that these timescales are valid for not too high values of Z (Lee et al. 2014 quote a value on the order of Z ~ 0.5) because for higher values of Z, the increased mean molecular weight can decrease the KH timescale (see Hori & Ikoma 2011).
(10)We note that these timescales are valid for not too high values of Z (Lee et al. 2014 quote a value on the order of Z ~ 0.5) because for higher values of Z, the increased mean molecular weight can decrease the KH timescale (see Hori & Ikoma 2011).
Finally, we emphasize that throughout this paper, we assume that the composition of the envelope is uniform. This is probably the case if convection is vigorous enough in the envelope. However, if convection is not efficient enough, the polluted portions of the envelope (the innermost parts at the beginning of the formation) may contract more rapidly, whereas the non-polluted parts (outermost regions of the envelope at the beginning of formation) would contract slowly. This may mean that the innermost region resists more strongly to the replenishment than the outermost regions. The precise determination of the envelope contraction as well as of the accurate efficiency of the replenishment is beyond the scope of this paper and will be the subject of future studies.
The third important timescale is the accretion timescale of planets. This is defined as 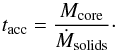 (11)The accretion rate of solids is taken to be either 10-5M⊕/yr in the case of pebble accretion, or 10-6M⊕/yr in the case of planetesimal accretion (see below).
(11)The accretion rate of solids is taken to be either 10-5M⊕/yr in the case of pebble accretion, or 10-6M⊕/yr in the case of planetesimal accretion (see below).
Finally, the fourth important timescale is the pollution timescale, which quantifies on which timescale the planetary envelope is polluted when accreted solids are completely destroyed in the envelope: 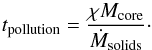 (12)
(12)
2.4. Destruction of accreted solids
When accreted solids enter the gas envelope of the planetary embryo, four mechanisms act on them:
-
the gravitational interaction with the planet;
-
the gas drag, which depends on the thermodynamical properties in the envelope and the characteristics of solids (essentially the size and density);
-
thermal mass loss by melting or vaporization (Podolak et al. 1988; Lozovsky et al. 2017);
-
mechanical destruction when the pressure difference on the solid is larger than its internal strength. For the solids we consider here, self-gravity is not important, and the internal strength is only due to material tensile strength.
Taking these four processes into account, Mordasini et al. (2006, MAB06) computed the mass of the envelope needed to destroy an incoming stony body during a central impact before it reaches the core. A detailed description of this model can be found in Mordasini et al. (2015), where the main assumptions behind the model are presented together with the main equations solved in order to compute the solid-envelope interaction. As shown in MAB06, two main effects lead to the destruction of planetesimals. For small bodies (smaller than 300 m to 1 km) thermal ablation is the main process leading to the destruction, whereas for larger bodies, mechanical destruction is the main effect. Interestingly enough, and as noted in MAB06, these two effects lead to the fact that intermediate bodies (around 300 m to 1 km) are very resistant to the destruction and can reach a core surrounded by and envelope as large as ~1–3 M⊕. For the case considered in this paper, the envelope mass needed to destroy solids of size s before they reach the core is approximately given by the following fit of the numerical results of MAB06:
-
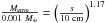 for s< 20 m;
for s< 20 m; -
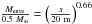 for 20 m <s< 300 m;
for 20 m <s< 300 m; -
Menve ~ 3 M⊕for 300 m <s< 1.5 km;
-
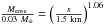 for s> 1.5 km.
for s> 1.5 km.
The first and second regime correspond to thermal destruction (ambient gas and shock heating), the fourth regime corresponds to mechanical destruction (sizes larger than 1.5 km). In this latter case (largest planetesimals), self-gravity is important and is included in our code (see Mordasini et al. 2015). We note that these fits correspond to central impacts (impact parameter equal to 0). For more general impacts (off-axis), the effect of gas drag is stronger during the incoming trajectory. As a consequence, the masses quoted above correspond to maximum values: if we consider all the possible impacts, solids will be destroyed by lower envelope masses.
In the case of mechanical destruction, matter is released in the envelope as small particles. If the temperature in the envelope is not high enough, these small particles may sink toward the core. If the temperature is high enough (higher than ~1600 K, corresponding to the sublimation of silicates, see Thiabaud et al. 2014), all the material of accreted solids is released as gas in the planetary envelope and may be subject to the recycling back to the protoplanetary disk (see Sect. 2.3). This material will in this situation not contribute to the mass growth of the planet. We plot in Fig. 4 the temperature at the base of the envelope for planets with an envelope equal to 10-4M⊕ for different epochs and different locations. As can be seen in the plot, the temperature is always high enough to vaporize silicates if they are released as small dust particles.
As we mentioned above, the luminosity of the core is computed by assuming that the accreted solids reach the core. This may a priori seem contradictory to the fact that we are interested in the destruction of the solids during their travel toward the core. However, until the envelope is massive enough to destroy the solids (the mass we wish to compute precisely), this assumption is justified. Moreover, the maximum core mass that the planetary embryo can attain before solids are destroyed does not depend very strongly on the value of the core luminosity. We discuss this aspect in more detail in Sect. 3.3.
3. Results
3.1. Envelope mass and timescales
We first consider an accretion rate of solids of 10-6M⊕/yr, which is typical for planetesimals, and the state of the protoplanetary disk at 1 Myr. Figure 1 shows the mass of planetary envelopes as a function of core mass and distance to the star, and Fig. 2 shows the replenishment timescales for the same planetary embryos.
As can be seen in Fig. 1, the higher the core mass, the higher the envelope mass, as we expect as a result of the increased core gravity. In addition, we note that the envelope mass for a given core mass increases for larger semi-major axis. This is also expected because the gas entropy is lower at a larger semi-major axis. The structure seen for a semi-major axis equal to a few AU is due to the change in the disk structure at the ice line. The replenishment timescale (Fig. 2) also depends on the core mass and the semi-major axis. The structure that can be seen in the figure results from the change in envelope mass as a function of the core mass and semi-major axis, and it also depends on the disk properties that in turn depend on the distance to the star (see Bitsch et al. 2015a,b).
 |
Fig. 1 Mass of the planetary envelope as a function of semi-major axis and core mass. The boundary conditions used for the internal structure calculations are those in the protoplanetary disk at 1 Myr, and the accretion rate of solids is equal to 10-6M⊕/yr. The contours represent the typical values quoted in Sect. 2.4, namely, from left to right, 0.001 M⊕, 0.03 M⊕, 0.5 M⊕, and 3 M⊕. |
 |
Fig. 2 Replenishment timescale for the same planetary embryos as in Fig. 1. The contours represent the location where the timescale is equal to 200 yr (solid line) and 1000 yr (dotted line), values typical of the settling and growth timescale of dust, according to Mordasini (2014). |
In the case of higher accretion rates like those encountered during the accretion of pebbles (~10-5M⊕/yr, Lambrecht et al. 2014), the results obtained are similar, the envelope mass is slightly lower and the replenishment timescale slightly shorter.
3.2. Maximum core mass
3.2.1. Accretion of pebbles
We now turn to the computation of the maximum core mass that is needed to bind an envelope large enough to destroy pebbles. We first consider pebbles as stony bodies of 10 cm in size. For these, an envelope mass of 0.001 M⊕ is high enough to destroy them. When we consider that pebbles are a mixture of icy and stony grains, they are less resistant to high temperature, and we can assume that as soon as the temperature at the base of the envelope is higher than 1600 K, they are destroyed in the envelope. Figures 3 and 4 show the core mass that is required to match either the first (envelope mass high enough to destroy incoming solids) or the second (temperature at the base of the envelope higher than 1600 K) criterion for semi-major axes ranging from 0.1 AU to 30 AU and at an epoch ranging from 0 to 3 Myr. For this calculation, the accretion rate of solids is equal to 10-5M⊕/yr, which is a typical value for pebble accretion (Lambrecht et al. 2014). Using the first criterion, the maximum mass obtained is on the order ~1 Earth masses, except very close to the star and at very early epochs. With the second criterion, the maximum mass obtained is a fraction of one Earth mass. We recall that the first criterion is derived from central impacts of stony bodies, which probably are much more resistant than pebbles. Therefore, it is likely that at masses lower than the mass shown in Fig. 3, pebbles are vaporized in the envelope. We finally note that the temperature at the base of the envelope in the case shown in Fig. 3 is always higher than 1600 K. In the case of radiative envelopes (as is the case here), these high temperature are the result of integrating the diffusion equation for the radiative flux (see Stevenson 1982). As we mentioned above (Sect. 2.1), these equations are valid for optically thick envelopes, which themselves require a core mass higher than a fraction of an Earth mass. As shown in Fig. 3, the core mass for pebble destruction is on the order of ~1 M⊕, which validates our approach.
 |
Fig. 3 Core mass required to bind an envelope mass of 0.001 M⊕, for different semi-major axes and at different epochs. The contours represent core masses equal to 2 M⊕ (solid line), 3 M⊕ (dotted line), and 4 M⊕ (dashed line). |
 |
Fig. 4 Core mass required to reach a temperature of 1600 K at the base of the envelope for different semi-major axes and at different epochs. The contour represents a core mass equal to 0.2 M⊕ (solid line) and 0.3 M⊕ (dotted line). |
Regardless of the criterion used, when the mass of the protoplanetary core is higher than ~0.5−3 M⊕, pebbles are vaporized in the atmosphere. As a consequence, the growth of the protoplanetary core stops at a mass that is on the order of the mass of Earth. We use this value in the following. Any further growth must therefore result from either Kelvin-Helmholtz contraction (accretion of H/He in the envelope) or from the ability of the planet to retain vaporized heavy material (replenishment timescale longer than the accretion timescale).
3.2.2. Accretion of planetesimals
We now consider large planetesimals. In this case, the accretion rate used to compute the planetary envelope structure is equal to 10-6M⊕/yr (e.g. Alibert et al. 2005), and an envelope mass of 1 M⊕ is required to completely destroy a stony body of 40 km (MAB06), which is much higher than in the case of pebbles (see previous section). The core mass that is required to bind such a massive envelope is correspondingly higher than in the case of pebbles, as shown in Fig. 5, and reaches more than 15 M⊕. We note that in great ranges of the parameter space (white regions in the figure), the disk scale-height is smaller than the Bondi radius of the planet, and this latter is not embedded. In this case, it is not clear if the replenishment process actually works. If it does not, there is no limit to the growth of the core through the destruction of accreted solids.
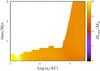 |
Fig. 5 Core mass required to bind an envelope mass of 1 M⊕, for different semi-major axes and at different epochs. The white regions in the plot correspond to planets that are not embedded in the disk (Hdisk<RBondi). |
3.3. Evolution after the maximum core mass
3.3.1. Accretion of pebbles
An important question that arises from our results is the fate of planets after the maximum core mass has been attained. First, we must wonder whether the process responsible for this maximum mass (the vaporization of pebbles) still holds after this point. When pebbles are destroyed in the envelope, they no longer heat the base of the envelope, and the temperature at this location could decrease, which would then allow the pebbles to reach the core again. However, the planets we consider here are radiative, and it is known that in this case, the temperature at the base of the envelope depends on the mass of the planet and on the mean molecular weight of the gas (Stevenson 1982), 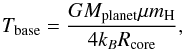 (13)where Rcore is the radius of the planetary core. It is important to note that this temperature does not depend on the luminosity of the core (which comes from the accretion of pebbles).
(13)where Rcore is the radius of the planetary core. It is important to note that this temperature does not depend on the luminosity of the core (which comes from the accretion of pebbles).
After pebbles are destroyed in the envelope, the mean molecular weight increases, which leads to an increase in temperature at the base of the envelope. We can therefore conclude that after pebbles start to be vaporized in the envelope, the process does not stop even if the pebbles no longer deposit their energy at the planetary core.
Then, the energy supply at the base of the planet envelope is suppressed, and the planet evolves by KH contraction. The pollution time (see above) can in certain cases become comparable to the replenishment time, however, which implies that the planetary envelope may rapidly become heavily polluted. The ratio of the KH timescale to the replenishment timescale is plotted in Fig. 6 as a function of the location and the time. The white solid line shows the planets for which the pollution timescale is equal to the replenishment timescales. For planets on the left side (semi-major axis smaller than ~10 AU), the replenishment timescale is shorter than the pollution timescale. The material that is released from the vaporization of pebbles is therefore lost to the protoplanetary disk before it can accumulate in the envelope. The total amount of heavy elements in the planets stops growing, and mass growth can only result from the accretion of H/He from the disk on a KH timescale. The replenishment is very fast, the timescale being shorter than ~100 yr in general (see Fig. 2). This timescale is shorter that the dust growth timescale (see Mordasini 2014), and as a consequence, the KH timescale has to be evaluated for dusty envelopes (the grains have the same size and composition as in the ISM, following Lee et al. 2014). In addition, and for the same reason, the KH timescale has to be evaluated for the metallicity of the disk (assumed to be equal to 0.02): 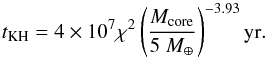 (14)For planets located farther out (right side of the white line on Fig. 6, semi-major axes larger than ~10 AU), the replenishment timescale is longer than the pollution timescale, and the metallicity in the planet increases. Taking Z = 0.5 as a typical value1, the Kelvin-Helmoltz timescale is given by
(14)For planets located farther out (right side of the white line on Fig. 6, semi-major axes larger than ~10 AU), the replenishment timescale is longer than the pollution timescale, and the metallicity in the planet increases. Taking Z = 0.5 as a typical value1, the Kelvin-Helmoltz timescale is given by 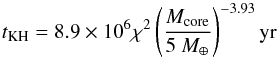 (15)for the dust-free case (it is more than one order of magnitude larger for dusty envelopes).
(15)for the dust-free case (it is more than one order of magnitude larger for dusty envelopes).
 |
Fig. 6 Ratio of the Kelvin-Helmholtz timescale to the replenishment timescales at the onset of pebble vaporization as a function of time and semi-major axis. The white solid line shows the planets for which the replenishment and the pollution timescales are equal. Planets on the left side have a replenishment timescale shorter than the pollution timescale, meaning that their envelope composition is similar to that of the disk. The replenishment timescale of the planets on the right side is longer than the pollution timescale, and the envelope is highly enriched in heavy elements. The white dotted line shows planets whose envelope enrichment exceeds 0.8, and the white dashed line shows planets whose envelope enrichment exceeds 0.9. |
As can be seen in Fig. 6, the KH timescale is longer than the replenishment timescale for nearly all planets below 10 AU (except very close planets and planets at very early epochs). In this case, and as demonstrated in Ormel et al. (2015), the accretion of H/He gas is prevented. As the core cannot grow and the metallicity of the planetary envelope is maintained at low values by the replenishment, the mass growth of the planet is stopped altogether.
For planets located at larger distance, the KH accretion occurs and increases the amount of H/He in the planetary envelope. As the pollution timescale is shorter than the replenishment timescale2, the accreted H/He rapidly becomes polluted. For example, on the right side of the lines shown in Fig. 6, the envelope enrichement exceeds 0.8 (white dotted line) or 0.9 (white dashed line). In these regions, the KH timescale could become very short as a result of the increased mean molecular weight, triggering gas accretion, at least if dilution due to this latter does not again decrease the metallicity (Hori & Ikoma 2011; Venturini et al. 2016).
In these parts of the diagram, the planetary envelope then grows on the KH timescale, the metallicity being kept high. As stated in Ormel et al. (2015) and following the analytical estimates of Piso & Youdin (2014), the KH timescale scales with the square of χ2 (the ratio of envelope to total mass). This scaling results from the fact that the energy content of the envelope scales with the pressure at the radiative-convective boundary, itself scaling with the envelope mass. In addition, the luminosity of the planet is inversely proportional to this latter pressure. The KH timescale is therefore quadratic in the envelope mass, therefore in χ. We emphasize that this scaling results from the simplified two-layer model of Piso & Youdin (2014) and that numerical simulations are necessary in order to more accurately derive the evolution of a planet after the core growth has stopped. Adopting this scaling for the rest of the paper, we see that since thereplenishment timescale scales with χ, the two timescales become equal for some value of the envelope mass. Beyond this point, the replenishment prevents the cooling of the envelope, and H/He accretion no longer occurs (Ormel et al. 2015). As the core cannot grow anymore (solids are destroyed in the envelope) and the accretion of H/He from the disk is prevented by the replenishment timescale, the growth of the planet stops altogether. The envelope mass that the planet can accrete is plotted in Fig. 7 as a function of location and time. As explained above, its value is equal to 10-3 for planets inside ~10 AU (the KH timescale is longer than the replenishment timescale at the onset of pebble vaporization), and grows to a fraction of one Earth mass for planets farther away. We note that we did not considered the time required to accrete this final envelope mass. If this time is longer than the disk lifetime, the final envelope would be even smaller.
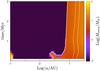 |
Fig. 7 Maximum envelope mass as a function of location in the disk and epoch. The white contours have the same meaning as in Fig. 6. |
Finally, if the planet succeeds in reaching a very high metallicity (on the order of 1) in the envelope, the KH timescale can be substantially reduced (Hori & Ikoma 2011). For example, a core of one Earth mass surrounded by an envelope of Z = 0.8 metallicity has an accretion timescale of 1 Myr, which is comparable to the disk lifetime. Any planet whose envelope metallicity is higher than this threshold could therefore accrete a substantial amount of H/He from the disk before the disk has disappeared. This process, however, can only take place in the outer regions of the disk.
The dotted and dashed white lines in Figs. 6 and 7 show planets with an envelope metallicity equal to 0.8 and 0.9, respectively. In our nominal model, this corresponds to planets located at a distance larger than ~20 AU, but the location of these lines sensitively depends on the value of the solid accretion rate. For example, for an accretion rate of solids ten times lower than our nominal value, the solid white line would be translated to the right and would be located close to the dashed white line.
In addition, as H/He accretion proceeds, the metallicity in the envelope can be reduced by dilution (Hori & Ikoma 2011), which could re-increase the KH timescale, and therefore slow accretion down. Taking these effects into account requires computing the planet evolution in a way similar to Venturini et al. (2016) and is beyond the scope of this paper.
The result and discussion we presented in this section depend on the value of the KH timescale. Interestingly enough, the value of the KH timescale derived by Hori & Ikoma (2010) appears to be lower than the values of Lee et al. (2014) that we use in this paper. If the KH timescale is shorter than the values assumed here, planets could acquire a large envelope at a distance smaller than the distances presented in Fig. 7.
3.3.2. Accretion of planetesimals
In the case of planetesimal accretion, we can make the same estimations. However, as the limiting core mass is much higher, the KH timescale is much shorter. As a consequence, after the maximum core mass is reached, the planet will start accreting gas, and depending on the remaining lifetime of the disk, become a Neptune-like planet or a gas giant.
Interestingly enough, for an envelope mass of ~1 M⊕ and an accretion rate of 10-6M⊕/yr, the pollution timescale is much longer than the replenishment timescales. As a consequence, the heavy elements released by the destruction of solids cannot accumulate in the envelope, whose metallicity remains low. We therefore expect in this scenario that the planetary envelope is made of nearly pure H/He (because the metallicity is the metallicity of the gas in the protoplanetary disk), at least as long as the replenishment is efficient. We note that some planets are likely to contain a very high mass of heavy elements (e.g., HD149026b, see Ikoma et al. 2006; Guillot et al. 2006). The formation of such a planet by accretion of planetesimals is not hindered by the replenishment process if this high mass of planetesimals is accreted after the replenishment has ceased, when the planet Hill radius is larger than the disk scale height.
4. Discussion
The maximum core mass that a planetary embryo can reach before its envelope is so large that accreted solids are vaporized strongly depends on the size of these solids. In the case of pebbles of ~10 cm in size, the maximum core mass is on the order of one Earth mass. In the case of planetesimals that are a few kilometers in size, the maximum core mass is higher than ~15 M⊕. These results have strong implications: if the replenishment timescale is shorter than the accretion timescale, as shown by Ormel et al. (2015) in their simulations, the material vaporized in the planetary envelope is lost on a timescale that is shorter than the timescale on which solids are accreted. This means that the material originating in accreted solids does not accumulate in the planet and cannot contribute to its mass growth. The interplay between the disruption of solids through their interaction with the gas envelope and the strong advection wind originating from the protoplanetary disk therefore lead to the end of planetary growth for a core mass that depends on the size of the accreted bodies. In the case of pebble accretion, the growth stops at approximately the mass of the Earth or at lower masses. For the case of planetesimals, the growth stops at a mass higher than 15 M⊕. As we demonstrated above, further growth by accretion of H/He from the protoplanetary disk is negligible when the planets are small (Earth mass). In this case, the growth of planetary embryos is stopped by the process of solid destruction in the envelope. Any further planetary growth must proceed by collision between planetary embryos, or must wait until the thermodynamical conditions have changed in the protoplanetary disk. When the accreted solids are much larger, and the core that is needed to bind an envelope large enough to destroy them is also large, the planetary growth is not stopped because accretion of H/He from the protoplanetary disk is allowed by the short KH timescale.
For pebble accretion, the maximum core mass is very low, the accretion of gas after the core growth has ceased is very small, and no noticeable accretion of gas can proceed during typical disk lifetimes. As a consequence, the growth of planetary embryos by pebble accretion is not possible for masses beyond ~1 M⊕, at least in the innermost regions of the disk (semi-major axis smaller than ~20 AU). The formation of Jupiter and Saturn in the innermost 20 AU of the disk by pebble accretion, for example, would require either that they form by the collision between bodies of ~1 M⊕, or that some of the assumptions used in this paper are not fulfilled. The first hypothesis would mean that the planetary embryos collide on a short timescale because a mass of ~10 M⊕ must be reached before the gas disk has disappeared in order for the planet to have enough time to accrete gas. This poses a problem because when a protoplanetary disk is present, planetary embryos should be kept on quasi-circular orbits as a result of disk-embryo interactions. In this case, one expect that substantial collision would occur only when the disk has nearly disappeared, at a time when there is probably not enough gas to form the envelopes of Jupiter and Saturn. The formation of Jupiter and Saturn in this model should therefore occur at distances larger than ~20 AU, followed by, or simultaneously with, a phase of migration.
Another possibility is that some of the assumptions used in this work are not fulfilled during the formation of planets. For example, the calculations performed by Ormel et al. (2015) are based on the isothermal equation of state and we have assumed a value of  that does not depend on the planetary mass or on the semi-major axis (we have adopted a value that is on the lower end of the range derived by Ormel et al. (2015), the replenishment timescales we obtain are therefore upper limits). If more realistic models were to show that the replenishment timescale is much longer (longer than the accretion timescale), the replenishment of planetary envelopes would be negligible. In this case, the growth of planets after pebbles are disrupted in the core could continue by simultaneously growing the core and increasing the metallicity of the envelope (see Venturini et al. 2015, 2016).
that does not depend on the planetary mass or on the semi-major axis (we have adopted a value that is on the lower end of the range derived by Ormel et al. (2015), the replenishment timescales we obtain are therefore upper limits). If more realistic models were to show that the replenishment timescale is much longer (longer than the accretion timescale), the replenishment of planetary envelopes would be negligible. In this case, the growth of planets after pebbles are disrupted in the core could continue by simultaneously growing the core and increasing the metallicity of the envelope (see Venturini et al. 2015, 2016).
We also note that the simulations performed by Ormel et al. (2015) assume an isothermal and inviscid gas. On the other hand, other simulations by D’Angelo & Bodenheimer (2013), for instance, who included the effect of radiation transport and viscosity, found that material from the deep regions of the envelope are gravitationally bound to the planet. The two simulations predict different efficiency of the replenishment, as well as differences in the region of the envelope that can actually be replenished. If the material from incoming solids is dissolved in the innermost regions of the planet and if this region is not replenished, as shown in D’Angelo & Bodenheimer (2013), the core growth would continue until a higher mass is reached. As the core grows, the envelope mass also grows, and incoming solids are destroyed at increasingly higher envelope levels. The termination of core growth would in this case occur at higher core masses.
5. Conclusion
Using the results of MAB06, we have derived an approximate fit that describes the envelope mass that is necessary to destroy stony solids of different mass before they reach the core of a forming protoplanet. The results of MAB06 are derived under the assumption of non-porous stony material, during a central impact. As impacts are in general non-central and solids are probably porous and/or made of a mixture of silicates and ices (this is especially the case for pebbles that drift in from the outer part of the protoplanetary disk, see Bitsch et al. 2015), the envelope masses obtained by MAB06 are upper limits of the envelope mass. In other words, under more realistic conditions, the envelope mass that is needed to disrupt and vaporize accreted solids is probably lower than the mass we used. As a consequence, because for a given location in the disk the envelope mass is a growing function of the core mass, the maximum core mass we derived in the previous sections is probably overestimated.
We showed that because of the interplay between the destruction of solids in the protoplanetary envelope and the replenishment process, the core growth can be stopped at a mass that strongly depends on the typical size of accreted solids. For pebble accretion, this size is on the order of the mass of Earth, whereas in the case of massive planetesimals (hundreds of meters at least), the limiting mass is at least ten times higher. After the core growth is stopped, any further growth must be the result of gas accretion, which depends on the ability of the planet to cool down. We discussed this possibility using arguments based on the KH timescale, but definitive conclusion will have to wait until the development of new formation calculations that take in a self-consistent way 1) solid destruction; 2) the consecutive enrichment in heavy elements; and 3) the replenishment process into account.
Another conclusion of our work is that in the case of planetesimal accretion, the pollution timescale of the planetary envelope is much longer than the replenishment timescale. This imply that as long as the process of replenishment is active, the gas envelope remains of low metallicity. Interestingly, the envelope of all the giant planets we know is enriched in heavy elements, and this enrichment is very strong for Uranus and Neptune (e.g., Helled et al. 2011). In the framework of the models presented here, this implies that a substantial fraction of solids is accreted after the replenishment process has ceased, for example, when the disk scale-height becomes smaller than the Bondi radius of the planet (white regions in Fig. 5). We note that this is very likely for planets forming at large distance from the star because in planetesimal-based planet formation, the accretion rate of solids is rather slow. It is therefore likely that large portions of heavy elements are accreted at a stage when the replenishment of the envelope is ineffective.
Finally, we point out that the results presented in this paper are to be taken as proof-of-principle of the interplay between the advection wind and the vaporization of accreted solids in forming planets. For example, one assumption of the calculations presented here is that core growth completely ceases when solids are destroyed in the envelope. If some of the material were to somehow reach the core, however, the picture would be changed, the efficiency of core growth being reduced and not suppressed3. Moreover, the actual maximum core mass that a planet can reach in any given formation scenario depends on the precise internal properties of accreted solids (porosity, tensile strength, composition, and size), as well as on the dynamics of their accretion and then on the behavior of the material constituting the accreted solids at high temperature and pressure. These factors govern the solid-gas interaction in the planetary envelope and ultimately the release of accreted material as gaseous species. Finally, we did not consider in this work the possibility that after high enough metallicities are attained in the planetary envelope, solids may condense fast enough to be able to sink to the core. The computation of this effect requires determining the kinetics of condensation and of sinking, and the knowledge of the thermodynamical properties of highly enriched material at high pressure. This is beyond the scope of this paper.
We finally note that Levison et al. (2015) presented a scenario for the formation of the solar system based on pebble accretion. This scenario, which is specific to the formation of our system, seems to fit many of its dynamical constraints. However, this model did not include the replenishment process of Ormel et al. (2015), and as a consequence, it should be revisited taking the possible effects described here into account.
Despite the shortcomings outlined above, the destruction of solids during the growth of planets, a process that is especially important in the case of pebble accretion, coupled with the replenishment of planetary envelopes has strong implications on the growth of planets. If the assumptions made in this work indeed hold (e.g., on the efficiency of replenishment), the process described in this paper therefore represents a serious bottleneck in the formation by pebble accretion of planets that are more massive than a few Earth masses, in particular in the innermost regions (below ~10 AU) of the disk.
The actual value of Z results from the competition between accretion and replenishment and is given by 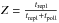 . The value of Z = 0.5 therefore corresponds to the white solid line in Fig. 6.
. The value of Z = 0.5 therefore corresponds to the white solid line in Fig. 6.
Acknowledgments
We thank Willy Benz for insightful discussions. This work was supported in part by the European Research Council under grant 239605. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation. The author acknowledges the financial support of the SNSF.
References
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerfer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Ida, S., Alibert, Y., Lin, D., & Mordasini, C. 2014, Protostars and Planets VI (University of Arizona Press), 691 [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015a, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015b, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., & Bodenheimer, P. 2013, ApJ, 778, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2011, ApJ, 726. 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2011, MNRAS, 416, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D.N.C. 2004, ApJ, 604, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Guillot, T., Genda, H., Tanigawa, T., & Ida, S. 2006, A&A, 650, 1150 [Google Scholar]
- Inaba, S., & Ikoma, M. 2003, A&A, 410, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inaba, S., Wetherill, G. W., & Ikoma, M. 2003, Icarus, 166, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Tanaka, H., Krivov, A. V., & Inaba, S. 2010, Icarus, 209, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Tanaka, H., & Krivov, A. V. 2011, ApJ, 738, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H, Kretke, K & Duncan, M. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Lissauer, J.J., Hubickyj, O., D’Angelo, G., & Bodenheimer, P. 2009, Icarus, 199, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Lozovsky, M., Helled, R., Rosenberg, E., & Bodenheimer, P. 2017, ApJ, 836, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies. Colloquium held at Observatoire de Haute Provence, France, August 22–25, 2005. eds. L. Arnold, F. Bouchy, & C. Moutou [Google Scholar]
- Mordasini, C., Mollière, P., Dittkrist, K.-M., Jin, S., & Alibert, Y. 2015, Int. J. Astrobiol., 14, 201 [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R., 2015, MNRAS, 447, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Piso, A.-M., & Youdin, A., 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M., Pollack, J.B., & Reynolds, R.T., 1988, Icarus 73, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. 1982, Planet Space Sci., 30, 755 [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Alibert, Y., Benz, W., & Ikoma, M. 2015, A&A, 576, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Alibert, Y., & Benz, W. 2016, A&A, 596, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Mass of the planetary envelope as a function of semi-major axis and core mass. The boundary conditions used for the internal structure calculations are those in the protoplanetary disk at 1 Myr, and the accretion rate of solids is equal to 10-6M⊕/yr. The contours represent the typical values quoted in Sect. 2.4, namely, from left to right, 0.001 M⊕, 0.03 M⊕, 0.5 M⊕, and 3 M⊕. |
| In the text | |
 |
Fig. 2 Replenishment timescale for the same planetary embryos as in Fig. 1. The contours represent the location where the timescale is equal to 200 yr (solid line) and 1000 yr (dotted line), values typical of the settling and growth timescale of dust, according to Mordasini (2014). |
| In the text | |
 |
Fig. 3 Core mass required to bind an envelope mass of 0.001 M⊕, for different semi-major axes and at different epochs. The contours represent core masses equal to 2 M⊕ (solid line), 3 M⊕ (dotted line), and 4 M⊕ (dashed line). |
| In the text | |
 |
Fig. 4 Core mass required to reach a temperature of 1600 K at the base of the envelope for different semi-major axes and at different epochs. The contour represents a core mass equal to 0.2 M⊕ (solid line) and 0.3 M⊕ (dotted line). |
| In the text | |
 |
Fig. 5 Core mass required to bind an envelope mass of 1 M⊕, for different semi-major axes and at different epochs. The white regions in the plot correspond to planets that are not embedded in the disk (Hdisk<RBondi). |
| In the text | |
 |
Fig. 6 Ratio of the Kelvin-Helmholtz timescale to the replenishment timescales at the onset of pebble vaporization as a function of time and semi-major axis. The white solid line shows the planets for which the replenishment and the pollution timescales are equal. Planets on the left side have a replenishment timescale shorter than the pollution timescale, meaning that their envelope composition is similar to that of the disk. The replenishment timescale of the planets on the right side is longer than the pollution timescale, and the envelope is highly enriched in heavy elements. The white dotted line shows planets whose envelope enrichment exceeds 0.8, and the white dashed line shows planets whose envelope enrichment exceeds 0.9. |
| In the text | |
 |
Fig. 7 Maximum envelope mass as a function of location in the disk and epoch. The white contours have the same meaning as in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


