| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629560 | |
| Published online | 12 October 2017 | |
A hydrodynamic mechanism of meteor ablation
The melt-spraying model⋆
Odesa National Maritime University, Mechnikova str., 34, 65029 Odesa, Ukraine
e-mail: club21@ukr.net
Received: 20 August 2016
Accepted: 26 June 2017
Context. Hydrodynamic conditions are similar in a molten meteoroid and a liquid drop in a high-speed airflow. Despite the fact that the latter is well-studied, both experimentally and theoretically, hydrodynamic instability theory has not been applied to study the fragmentation of molten meteoroids.
Aims. We aim to treat quasi-continuous spraying of meteoroid melt due to hydrodynamic instability as a possible mechanism of ablation. Our objectives are to calculate the time development of particle release, the released particle sizes and their distribution by sizes, as well as the meteoroid mass loss law.
Methods. We have applied gradient instability theory to model the behaviour of the meteoroid melt layer and its interaction with the atmosphere. We have assumed a spherical meteoroid and that the meteoroid has a shallow entry angle, such that the density of the air stream interacting with the meteoroid is nearly constant.
Results. High-frequency spraying of the molten meteoroid is numerically simulated. The intermediate and final size distributions of released particles are calculated, as well as the meteoroid mass loss law. Fast and slow meteoroids of iron and stone compositions are modelled, resulting in significant differences in the size distribution of melt particles sprayed from each meteoroid. Less viscous iron melt produces finer particles and a denser aerosol wake than a stony one does.
Conclusions. Analysis of the critical conditions for the gradient instability mechanism shows that the dynamic pressure of the air-stream at heights up to 100 km is sufficient to overcome surface tension forces and pull out liquid particles from the meteoroid melt by means of unstable disturbances. Hence, the proposed melt-spraying model is able to explain quasi-continuous mode of meteoroid fragmentation at large heights and low dynamic pressures. A closed-form solution of the meteoroid ablation problem is obtained due to the melt-spraying model usage, at the meteoroid composition, initial radius and velocity being given.
Key words: hydrodynamics / atmospheric effects / methods: numerical / methods: analytical / meteorites, meteors, meteoroids / instabilities
The movies associated to Figs. 6 and 7 are available at http://www.aanda.org
© ESO, 2017
1. Introduction
The dust content of air is able to strongly influence the state of the high atmosphere and the processes which occur there. A number of phenomena that take place in the high atmosphere are associated with cosmic dust influx, such as an increase in intensity of the scattered solar radiation field, natural radiation and resonance scattering in the lines of different atoms and ions, and the specular reflection of radio waves from ionized meteor trails (Lebedinets 1981; Bronshten 1983). Cosmic dust particles also serve as the condensation nuclei in the noctilucent cloud formation (Bronshten 1984). It is known that heating even a small number of dust particles (up to 5 × 104) can generate an upward air flow with an ascending velocity of 1 cm s-1; the dust cloud at mid day can create a stratospheric cyclone, as well (Astapovich 1958; Hsu et al. 1997). The influence of aerosol on climate changing predictions is reflected in the review of Kahn (2012).
 |
Fig. 1 Scheme of the flow in case of outstripping ablation (a) and in case of outstripping melting (b). Scheme of flow in disturbed boundary layer (c): solid thin lines indicate melt particles’ streamlines; thick dashed lines indicate undisturbed boundary layer limits. AB is the curvature radius of disturbed streamlines; Fcf is the centrifugal force acting at moving melt particle. |
The kinetics of these processes depend strongly on the dust volume concentration, as well as the number distribution of particles by sizes. These quantities are determined by the underlying physics of the particle generation process. Ablation of meteoroids penetrating the Earth’s atmosphere at hypersonic velocities is one of the origins of the dust particles (Bronshten 1983; Ceplecha et al. 1998; Williams 2002). Meteoroids are responsible for the influx of thousands of tons of tiny particles into the Earth’s upper atmosphere annually (Mathews et al. 2001; Janches & Chau 2005). The passage of high-velocity meteoroids through the atmosphere is believed to affect the overall aerothermochemistry.
Ablation is the most complicated process in the meteor phenomenon, in which the mass loss kinetics depends on all the parameters used in calculations (Stober & Jacobi 2008). The simple theory of meteors can evaluate only the total ablating mass influx (Bronshten 1983). However, the most important characteristics of ablation are the particle sizes, the frequency at which the particles are released, number density and size distribution, which influence processes in the meteor wake and the whole meteor phenomenon. These parameters are determined by the mechanics of the particle formation and release from the meteoroid body, so it is of prime importance to investigate the release mechanism and to quantify the particle generation. We investigate meteoroid ablation through modelling constrained by observations, as direct study of the meteoroid fragmentation and the resultant particle size distributions are not practical.
There are several mechanisms that contribute to meteoroid ablation, including evaporation, sputtering, fragmentation, disruption, shelling, spallation, husking (Borovička et al. 2007; Bronshten 1983), and dispersion of the unstable fusion film (Girin 1992). Moreover, the meteoroid fragmentation can proceed in several hypothetical ways (Borovička et al. 2007; Bronshten 1983): progressive fragmentation into parts, which continue to crumble, quasi-continuous detachment of small particles from the main body, and sudden disruption into a number of particles.
It is generally recognized that quasi-continuous fragmentation is one of the main modes of ablation (Lebedinets & Shushkova 1970). Mechanisms of quasi-continuous fragmentation include hydrodynamic instability of the liquid fusion film formed on a solid meteor body (Bronshten 1983), which has not been investigated in detail. Careful consideration of the aerodynamic interaction between an air stream and molten layer of meteoroid has led us to the conclusion that the high-frequency droplet spraying from the molten layer due to the hydrodynamic instability of the melt surface is actual. This hypothesis was originally declared in Girin (1992) and it was based upon the similarity in hydrodynamics of the meteoroid fusion film and a liquid drop in a speedy gas flow. Indeed, values of the hydrodynamic forces, as well as the main criterion for a liquid dispersion (i.e. Weber number), are close for meteoroids and for liquid drops. In its turn, drop shattering is well-studied theoretically and experimentally as a dispersion of the smallest daughter droplets from the parent drop surface (see, for instance, Reinecke & Waldman 1975).
The instability of a thin molten film of a meteoroid was examined in (Girin 1992; Girin & Kopyt 1994) as a mechanism of melt spraying, so that the estimations for the droplet sizes and frequency of their release were obtained. Though, such important characteristics of the meteor phenomenon as transient distributions of the released droplets by sizes, the meteoroid ablation and deceleration laws were not found. Similarly, the ablation of small planetesimals due to the unstable dispersion of fusion film was used as the basic mechanism of spherical chondrules formation by Genge (2000).
The mechanism of the meteoroid melt spraying due to the hydrodynamic gradient instability is considered in the present paper for the particular class of molten meteoroids, leading to the closed mathematical model of the sprayed mass losses. Peculiarities of the gradient instability are described in Sects. 2 and 3; determination of the sprayed particles’ number and sizes are given in Sect. 4, while the model results for three specific meteoroids are considered in Sect. 5. Supplementary material, including the nomenclature list, is in the Appendix.
Generally, the melt instability performance is determined by the balance between meteoroid heating and aerodynamics. Depending on meteoroid velocity, size and substance, two regimes of meteoroid ablation due to instability are possible. When the aerodynamic interaction dominates over the rate of heating, the mass loss overtakes fusion. Conversely, melting outstrips mass losses when the heating dominates over aerodynamics. In the former case the rate of mass loss exceeds the rate of melting, so that the molten layer thickness b is less than the thickness δm of the velocity boundary layer in the melt should be. The unstable disturbances are then affected by the stabilizing influence of the meteoroid rigid core (Fig. 1a). In this case, droplets that result from disruption of the molten layer have a size corresponding to a thickness of the layer itself. The results obtained in Girin & Kopyt (1994) are thus valid for the case of dominant ablation.
In the opposite case of the dominant fusion, the molten layer is essentially thicker than the velocity boundary layer induced by the airstream viscous stresses in the melt: b>δm. Then, the velocity profile in the melt acquires the form of the completed boundary layer obeying the boundary layer relationships (Schlichting 1960). Thus, the flow near air–melt interface becomes different in this case, consisting of free conjugated boundary layers, in air, δa, and in the melt, δm, independent from the solid core Fig. 1b). This fact changes principally the mechanism of the instability, compelling the fragmented particles have a size distribution that must be modelled.
2. The instability of a gradient flow near liquid-gas interface
The flow near the liquid − gas interface depends on the media properties. The effect of the velocity profile peculiarities on the liquid − gas interface instability was studied in (Girin 1985). It was established that variations of the media inertial and viscous properties modify the profile, transforming the flow within the conjugated liquid – gas boundary layers. For a linear approximation of the profile (Fig. 2), it was shown that the instability mechanism can differ from the classical Kelvin − Helmholtz type. Namely, the latter type is in action only when the liquid kinematic viscosity is greater than that one of the gas: νm>νa. In this case the liquid boundary layer is much thicker than the gas one, while the surface velocity, Vs, is much less than the airstream velocity: Vs ≪ Va. Thus, the velocity profile is close to the discontinuous one (tangential discontinuity) which is the base for the Kelvin − Helmholtz mechanism (Fig. 2a, see Eqs. (2)).
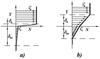 |
Fig. 2 Linear fit of velocity profile in conjugated boundary layers; case νm>νa(a) and νa>νm(b); δa, δm – air and melt boundary layer thicknesses. |
But when the inverse inequality takes place, νa>νm, the boundary layer thicknesses become comparable, δm = O(δa), as well as the velocities: Vs = O(Va) (see Eqs. (2)). Thus, the velocity profile becomes inflated (Fig. 2b) changing the dispersion relation of the boundary-value problem for disturbances. In this case the mechanism of instability becomes completely different from the Kelvin − Helmholtz one, because it is determined now by the unstable root of another dispersion relation, given below as Eq. (1). The instability investigation (Girin 1985) mentioned above resulted in the algebraic dispersion relation of the fourth power with respect to the frequency ω of the disturbance of the form E = E0exp(ihx − iωt). In the case of liquid − gas systems (i.e. α = ρa/ρm ≪ 1) it can be simplified to the third-power equation: ![\begin{equation} (\Omega-\Delta)\left[ (\Omega-\Delta)(\Omega+K\Delta) + (1 - K)\Delta \right] = \Delta^3 {\rm{We}}_{\rm{s}}^{ - {\rm{1}}} (\Omega-K\Delta), \end{equation}](/articles/aa/full_html/2017/10/aa29560-16/aa29560-16-eq21.png) (1)here Ω = ωδm/Vs, Vs – velocity at the liquid-gas interface (Fig. 2),
(1)here Ω = ωδm/Vs, Vs – velocity at the liquid-gas interface (Fig. 2), 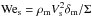 is “surface” Weber number, ρa , m are the air and melt densities, Σ is surface tension of the melt, Δ = 2πδm/λ is dimensionless wavenumber, λ is disturbance wavelength, K = [1 − exp( − 2Δ)] / (2Δ), α is the air-to-melt density ratio.
is “surface” Weber number, ρa , m are the air and melt densities, Σ is surface tension of the melt, Δ = 2πδm/λ is dimensionless wavenumber, λ is disturbance wavelength, K = [1 − exp( − 2Δ)] / (2Δ), α is the air-to-melt density ratio.
The unstable root of Eq. (1) defines a different type of periodical instability, called the gradient instability (Girin 1985; 2012), the mechanism of which is generated within the liquid boundary layer by the huge velocity gradient, ∂Vm x/∂y ≈ Vs/δm, which ranges up to (104 − 105)s-1 for liquid drops as well as for meteoroids. This will be demonstrated later with Eqs. (2). The cause of the gradient instability is the inertial (centrifugal) forces of disturbed curvilinear motion (see Fig. 1c), as explained in Appendix A. As the dispersion relation Eq. (1) contains none of the air parameters ρa,Va,δa, the air flow has a weak influence on the disturbances, just transferring momentum to the liquid by means of viscous shear stresses, as it was noted in (Gordillo et al. 2001; Girin 2011a).
The gradient instability mechanism explains the “stripping” mode of a liquid atomization as a quasi-continuous, high-frequency periodic spraying from the unstable part of a liquid surface (Girin 2011a,b). It is known for this mechanism that ablation largely increases the evaporated mass due to the rapid increase of the total liquid surface of the sprayed particles (up to 100 times, Girin 2011b), which would be a significant effect for meteors.
A certain class of middle-sized meteoroids exist, which melt completely because meteoroid heating dominates over ablation. The initial radii of these meteoroids range from 3 × 10-3 cm to 0.7 cm for iron and from 6 × 10-3 cm to 0.3 cm for stony meteoroids (Bronshten 1983). Meteoroids larger than these are melted to some depth less than the radius; smaller sized meteoroids decelerate faster than they are totally melted and evaporated (Bronshten 1983). On the other hand, the conclusions of Rogers et al. (2005) show that the smallest of these meteoroids can lose a significant part of their mass due to sputtering. This turns out to have a negligible effect on our meteoroid size considerations, as Fig. 6 of Rogers et al. (2005) shows that sputtering can be neglected for meteoroids with initial radii greater than R 0> 8 × 10-3 cm for stony meteoroids, and R 0> 5 × 10-3 cm for iron meteoroids. At the same time, the upper size limit for the meteoroids modelled here can also be raised, because the condition b>δm does not require that the meteoroid be totally molten. Consequently, in this paper we will consider initial radii ranging from 5 × 10-3 cm to more than 1 cm for iron and from 8 × 10-3 cm to 0.5 cm for stony meteoroids.
Thus, the theory of the molten meteoroid spraying can be elaborated in the same way as the theory of drop atomization in a high-speed airflow was constructed (Girin 2011a,b, 2014b). The gradient instability theory is applied below to the class of molten meteoroids in the form of main relationships, which are listed in the next section. A direct extension of this theory, which was validated for a drop in a steady uniform airstream, to meteoroid flight is impossible, as the air density variation with altitude must be taken into account. Therefore, we will consider here the case of a shallow entry angle trajectory (i.e. a small angle γ between the trajectory and the horizon), when the ambient air density is changing gradually with time. In this case, γ ≪ π, we are able to calculate the main kinetic parameters of the sprayed melt droplets: radii r and period tper of their release from the meteoroid surface, which govern the meteor phenomenon as a whole and the meteor aerosol wake formation in particular.
The meteoroid trajectory in the Earth’s atmosphere can be divided onto two parts: a heating stage, when evaporation and sputtering can be neglected, and an ablation stage, when a meteor itself already exists (Krinov 1960); only the latter stage is considered here. Meteoroid flight proceeds with hypersonic velocities, when the Mach number is large (Ma∞ ≫ 1), but the air flow behind the detached shock wave is subsonic due to the air compression (Courant & Friedriechs 1976), so that Maa ≈ 0.4 (Loitsyanskiy 1995) (Fig. 3). Moreover, the vapour influx increases density in the vicinity of a meteoroid by more than 100 times (Boyd 2000; Popova et al. 2000), further decreasing the Mach number. The role of compressibility is increased only at the lateral sides of a meteoroid, where the gas-stream velocity has some growth. This means that the incompressible medium model is applicable here as a first-order approximation since the compressibility exhibits itself only when the Mach number becomes comparable with unity and greater.
More important is the fact that the gas phase density growth due to the evaporation decreases Knudsen number drastically. Figure 9 of Boyd’s (2000) paper shows that vapour density exceeds the air density near the meteoroid surface by ≈500 times for H-chondrite meteoroid ablating below ≈100 km. That text also states: The mean free path of the flow immediately adjacent to the meteoroid is about 10-5 m giving a local Knudsen number based on the meteoroid diameter of 0.001 which is in the near-continuum regime. So, following Boyd, the vapours together with the air compression are solely able to diminish the local Knudsen number for meteoroid by 4000 times, which raises the height of the continuum regime by ≈30 km (see Fig. 1 of Campbell-Brown & Koschny 2004 paper). Our usage of the continuum model is thus in agreement with Boyd’s findings. Some other studies, for example, Zinn et al. (2004) use the fluid hydrodynamics equations up to 90 km.
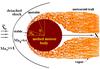 |
Fig. 3 Flow scheme around meteoroid body. Stable and unstable parts of molten meteoroid surface are shown. |
3. The mechanics of particle release
Despite large values of the melt dynamic viscosity, μm, the inequality νa>νm takes place for meteoroids due to the low air density at meteor altitudes. Therefore, the real velocity profile across surface of a completely molten meteoroid is close to that shown in Fig. 2b. For this reason, the gradient instability of the flow in the conjugated air-melt boundary layers is assumed as the mechanism of a particle breakaway from the molten meteoroid surface. The model of a molten meteoroid spraying is built below on the basis of this assumption.
The process of liquid particle generation at some arbitrary elementary area Δli is shown in Fig. 4, which is the result of growth of the unstable wave amplitude. It illustrates the natural assumption that the size of a released droplet is determined uniquely by the wavelength λ, while the periodicity of the fragmentation process is given by the characteristic time tper ≈ Im-1(ω). When applying theoretical results of an instability treatment to practical problems, the fastest unstable wave is of prime interest, as it is the very wave that will separate a droplet from the meteoroid melt layer. It is sufficient thus for the droplet release description to use the values of the fastest disturbance wavelength, λf, and characteristic time tf (or the growth rate factor, 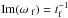 , Chandrasekhar 1960).
, Chandrasekhar 1960).
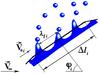 |
Fig. 4 Particle release process at ith area element of meteoroid surface. |
Within the gradient instability theory, these parameters are uniquely determined by the unstable periodic root Ωf of the dispersion relation Eq. (1). In view of the one-parameter character of the Eq. (1), it appears that the fastest wave parameters only depend on the surface Weber number, Wes. The dimensionless wavenumber Δf = 2πδm/λf and growth rate factor Im(Ωf) were calculated in (Girin 1985) and are given in Fig. 5 as functions of Wes. The plots show that there exists a critical value Wes.cr. = 3.08 such that the air–melt interface is unstable if Wes> Wes.cr.. At Wes ≥ 20 the parameters become independent from Wes and equal to Δf = 1.225, Im(Ωf) = 0.24. Additionally, the relation between the real and imaginary parts of the unstable root, Re(Ωf) = 1.5Im(Ωf), means that periodicity of the particles release is comparable with the characteristic time of e-fold growth of the disturbance amplitude. The behaviour of the wavenumber and growth rate factor depicted in Fig. 5 are applied below to calculate the molten particle release mechanics.
The unstable wave growth depends essentially on the media interaction at the liquid – gas interface. In high-speed flows the interaction occurs within the conjugated boundary layers. On the basis of the general boundary layer theory (Schlichting 1960), the relations between the main boundary-layer flow parameters δm, δa, Vs, Va (Fig. 2) can be derived (see Appendix B), which are important in the gradient instability analysis: 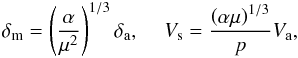 (2)where μ = μa/μm is air-to-melt viscosity ratio, p = 1 + (αμ)1 / 3.
(2)where μ = μa/μm is air-to-melt viscosity ratio, p = 1 + (αμ)1 / 3.
The flow geometry around the meteoroid is determined by the meteoroid body shape. Assuming the spherical shape of the body and the velocity potential of the air flow around a sphere in the form Va(ϕ) = 1.5(V∞ − w)sinϕ (Kochin et al. 1964), we can apply the boundary layer thickness distribution along the meteoroid surface in Ranger’s (1972) form: 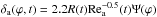 . The latter is valid for a gas over a liquid sphere, here Ψ(ϕ) = ((6ϕ − 4sin2ϕ + 0.5sin4ϕ) / sin5ϕ)0.5, ϕ is the polar angle of a surface area element (Figs. 1b and 3). Together with Eq. (B.1) this yields the geometry factor for a liquid sphere:
. The latter is valid for a gas over a liquid sphere, here Ψ(ϕ) = ((6ϕ − 4sin2ϕ + 0.5sin4ϕ) / sin5ϕ)0.5, ϕ is the polar angle of a surface area element (Figs. 1b and 3). Together with Eq. (B.1) this yields the geometry factor for a liquid sphere: 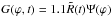 ,
, 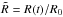 . Taking into account Eq. (2), the necessary condition for the gradient instability performance, Wes ≥ 3.08, can be written at an arbitrary area element ϕ of the meteoroid surface in the following form (see Appendix B):
. Taking into account Eq. (2), the necessary condition for the gradient instability performance, Wes ≥ 3.08, can be written at an arbitrary area element ϕ of the meteoroid surface in the following form (see Appendix B): 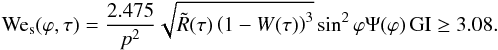 (3)Here
(3)Here 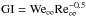 appears as the gradient instability criterion,
appears as the gradient instability criterion, 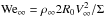 and Re∞ = ρ∞2R0V∞/μ∞ are the Weber and Reynolds numbers for the meteoroid, w is the meteoroid velocity deficit due to deceleration, so that V∞ − w is the relative air – meteoroid velocity, W = w/V∞, τ = t/tch; tch = 2R0/α0.5V∞ is the characteristic timescale, V∞ is meteoroid entry velocity.
and Re∞ = ρ∞2R0V∞/μ∞ are the Weber and Reynolds numbers for the meteoroid, w is the meteoroid velocity deficit due to deceleration, so that V∞ − w is the relative air – meteoroid velocity, W = w/V∞, τ = t/tch; tch = 2R0/α0.5V∞ is the characteristic timescale, V∞ is meteoroid entry velocity.
Applying the function behaviour shown in Fig. 5 to the meteoroid surface, we find out that there exists a critical angle along the surface, ϕcr(t), where Wes(ϕcr) = Wes.cr. = 3.08. This critical point divides the surface into stable, ϕ<ϕcr, and unstable, ϕ>ϕcr, parts (Fig. 3). Equality in Eq. (3) defines the value of ϕcr(τ). As the normalized meteoroid radius, 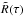 , and the relative meteoroid speed, 1 − W(τ), decrease with time, the initial moment τ = 0 (when
, and the relative meteoroid speed, 1 − W(τ), decrease with time, the initial moment τ = 0 (when 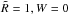 ) is the most favourable for the fulfillment of inequality (3). At τ = 0 we will have ϕcr<π/ 2 in Eq. (3) when
) is the most favourable for the fulfillment of inequality (3). At τ = 0 we will have ϕcr<π/ 2 in Eq. (3) when 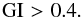 (4)This indicates that the part of the surface adjacent to the meteoroid edge, ϕcr<ϕ<π/ 2, is unstable at GI > 0.4, providing a possibility of the high-frequency periodic spraying of the molten substance from the meteoroid surface. This is depicted in Fig. 3. Equation (3) indicates that when GI increases, ϕcr decreases, so for large GI ≫ 0.4, the values of ϕcr are small, ϕcr ≪ π (see the calculated data in Table 1). Thus, the majority of the meteoroid surface generates a mist of the molten particles quasi-continuously, as shown in Fig. 4.
(4)This indicates that the part of the surface adjacent to the meteoroid edge, ϕcr<ϕ<π/ 2, is unstable at GI > 0.4, providing a possibility of the high-frequency periodic spraying of the molten substance from the meteoroid surface. This is depicted in Fig. 3. Equation (3) indicates that when GI increases, ϕcr decreases, so for large GI ≫ 0.4, the values of ϕcr are small, ϕcr ≪ π (see the calculated data in Table 1). Thus, the majority of the meteoroid surface generates a mist of the molten particles quasi-continuously, as shown in Fig. 4.
Parameters of calculated spraying meteoroids of radius R0 = 0.3 cm.
The inequality 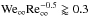 was first found empirically by Rabin et al. (1960) as a condition for the stripping mode of a liquid drop breakup. For the standard air conditions, α = 1.3 × 10-3, it was revealed and grounded theoretically in (Girin 1985) as the criterion for the gradient instability existence at a drop surface. While Eq. (3) expresses the critical conditions locally at every meteoroid surface area ϕ, the criterion GI determines the possibility of instability existence in a whole meteoroid flight.
was first found empirically by Rabin et al. (1960) as a condition for the stripping mode of a liquid drop breakup. For the standard air conditions, α = 1.3 × 10-3, it was revealed and grounded theoretically in (Girin 1985) as the criterion for the gradient instability existence at a drop surface. While Eq. (3) expresses the critical conditions locally at every meteoroid surface area ϕ, the criterion GI determines the possibility of instability existence in a whole meteoroid flight.
The inequality Eq. (4) reflects the critical condition for air-melt instability rigorously. We note that the near-critical conditions in the vicinity of the critical point at meteoroid surface yield long wavelengths, which are greater than the meteoroid radius, coupled with large values of the induction period of the instability, which is greater than the period of meteor existence. In practice, this suggests modifying the condition of instability up to GI ≥ 0.6 (or equally Wes ≥ 4.62), see Girin (2011a).
The two Weber numbers, surface Wes and meteoroid We∞, have the same general sense: the ratio of the hydrodynamic forces to the surface tension forces. But the surface Weber number Wes specifically relates hydrodynamic pressure 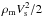 of the melt motion in the liquid boundary layer (which defines the centrifugal force scale) to the surface tension forces δm/ Σ of the disturbed interface, whose curvature radius Rc is proportional to δm (Fig. 1c). The former force creates the destabilizing effect, defining the centrifugal force scale; the latter force defines a stabilizing effect. Thus, the surface Weber number reflects locally, at a disturbance level, the ratio of destabilizing forces to the stabilizing ones, governing the disturbance development.
of the melt motion in the liquid boundary layer (which defines the centrifugal force scale) to the surface tension forces δm/ Σ of the disturbed interface, whose curvature radius Rc is proportional to δm (Fig. 1c). The former force creates the destabilizing effect, defining the centrifugal force scale; the latter force defines a stabilizing effect. Thus, the surface Weber number reflects locally, at a disturbance level, the ratio of destabilizing forces to the stabilizing ones, governing the disturbance development.
The existence of the critical value Wes.cr. has a simple physical meaning, which is explained in Appendix C. This critical value, when applied to a meteoroid, yields the critical hydrodynamic pressure of the airstream running against the meteoroid, 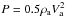 , which is sufficient to pull out the droplets from the meteoroid melt by means of the unstable disturbances. These values are calculated in Appendix C for the three particular meteoroids considered in the present paper:
, which is sufficient to pull out the droplets from the meteoroid melt by means of the unstable disturbances. These values are calculated in Appendix C for the three particular meteoroids considered in the present paper: 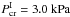 ,
, 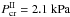 ,
, 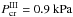 .
.
 |
Fig. 5 Basic dependencies Δf(Wes) (solid line) and Im [ Ωf(Wes) ] (dashed line) of gradient instability. |
Previously, it has been noted (Borovička et al. 2007) that dynamic pressure of the airstream does not exceed the meteoroid strength and therefore the fragmentation cannot be explained by the direct action of the airstream. The dynamic pressure is on the order of 5 − 20 kPa at heights just below 100 km, which is too small to prevail over the meteoroid strength. Conversely, the critical values of 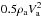 , derived above, which correspond to the value Wes.cr., show that the dynamic pressure of the airstream at heights up to 100 km, is sufficient to overcome surface tension forces and pull out liquid particles from the meteoroid melt by means of unstable disturbances. Hence, this model is able to explain meteoroid fragmentation at large heights and low dynamic pressures.
, derived above, which correspond to the value Wes.cr., show that the dynamic pressure of the airstream at heights up to 100 km, is sufficient to overcome surface tension forces and pull out liquid particles from the meteoroid melt by means of unstable disturbances. Hence, this model is able to explain meteoroid fragmentation at large heights and low dynamic pressures.
On the other hand, the melt spraying mechanism resembles models of quasi-continuous meteoroid fragmentation (such as dustball, thermal erosion, and thermal disruption models, see Campbell-Brown et al. 2013), but is able to provide theoretical predictions of the fragmentation frequency, and fragment size distributions. These are based on the rigorous mathematical treatment of the instability problem, which was carried out in Girin (1985).
4. The quantification of the melt spraying
Because of the small values of ρ∞ at higher altitudes, Eq. (4) is satisfied only below the altitude z0, where the air density becomes large enough to produce a mechanical effect. Above that, the meteoroid interaction with the atmosphere has thermal nature and leads to the meteoroid heating and the molten layer formation (Krinov 1960). Values of z0 are calculated for specific meteoroids and given in Table 1.
The values of z0 reflect the critical condition in Eq. (4) for gradient instability, but there are some additional necessary conditions. For instance, the meteoroid must first become molten for the gradient instability itself to work. According to Bronshten’s (1983) data for R0 = 1 cm, the heights zm, where the meteoroid attains a melt temperature Tm, for the considered in present paper three variants are as follows: 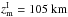 ,
, 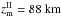 ,
, 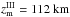 . In each case we have zm ≤ z0, so, the spraying process starts well below z0, where the melt layer grows sufficiently and the gradient instability mechanism is able to start. The altitude, where the meteoroid is molten through the characteristic depth of its half-radius, can be estimated with the use of the Lebedinets & Portniagin (1966) solution for the temperature distribution inside a rapidly and randomly rotating sphere. According to this solution, the ratio of densities at the heights where the meteoroid surface attains the melt temperature first, ρm, and where the meteoroid body is melted by the depth of half radius, ρh.r., is:
. In each case we have zm ≤ z0, so, the spraying process starts well below z0, where the melt layer grows sufficiently and the gradient instability mechanism is able to start. The altitude, where the meteoroid is molten through the characteristic depth of its half-radius, can be estimated with the use of the Lebedinets & Portniagin (1966) solution for the temperature distribution inside a rapidly and randomly rotating sphere. According to this solution, the ratio of densities at the heights where the meteoroid surface attains the melt temperature first, ρm, and where the meteoroid body is melted by the depth of half radius, ρh.r., is: 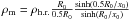 , where
, where 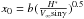 is the characteristic depth of heating. So, the ratio ρh.r./ρm depends on the meteoroid substance, size and velocity. With the use of data for x0 (Bronshten 1983), we have R0/x0 = 3.33;1.76;6.58 consecutively for the meteoroids considered in the present paper. Making calculations with the formula above, we will have: ρh.r./ρm = 2.75;1.41;6.74 consecutively. Then the difference in the two heights may be determined assuming the uniform atmosphere density distribution with altitude. In this way we obtain: zh.r. = zm − 7.1 km;2.4 km;13.4 km consecutively. The height at which the melt depth is sufficient for the spraying process beginning can be estimated as zh.r. = 97.9 km;85.6 km;98.6 km consecutively for the meteoroids considered in the present paper. Thus, the meteoroid spraying will start at heights smaller than z = z0 in all of the variants considered here.
is the characteristic depth of heating. So, the ratio ρh.r./ρm depends on the meteoroid substance, size and velocity. With the use of data for x0 (Bronshten 1983), we have R0/x0 = 3.33;1.76;6.58 consecutively for the meteoroids considered in the present paper. Making calculations with the formula above, we will have: ρh.r./ρm = 2.75;1.41;6.74 consecutively. Then the difference in the two heights may be determined assuming the uniform atmosphere density distribution with altitude. In this way we obtain: zh.r. = zm − 7.1 km;2.4 km;13.4 km consecutively. The height at which the melt depth is sufficient for the spraying process beginning can be estimated as zh.r. = 97.9 km;85.6 km;98.6 km consecutively for the meteoroids considered in the present paper. Thus, the meteoroid spraying will start at heights smaller than z = z0 in all of the variants considered here.
Once the critical condition in Eq. (4) is fulfilled for a meteoroid, each elementary area, where the inequality Eq. (3) is satisfied, can be considered as a high-frequency source of the molten meteoroid particles. In our analysis we must consider the air flow variability along the curved meteoroid surface, which causes the dependence of λ f, tf and Wes on the polar angle ϕ (Fig. 3). We divide the meteoroid surface into a system of plane elementary areas (more exactly − spherical belts in the axially symmetrical flow) of the width Δli = R(t) Δϕi (Fig. 4), so that at every small time interval Δt the flow parameters may be treated as constant at every ith area element. The problem of the breakaway droplet parameters determination is then reduced to the application of the above mentioned instability regularities to this local-plane flow. Only the windward part of a meteoroid surface is considered further since the flow past the meteoroid leeward part is weak.
As the droplets are generated by the fastest unstable disturbance, it is natural to assume that the droplet sizes and period of their release from the main body are proportional to the disturbance wavelength and characteristic time of e-fold growth of the disturbance amplitude at a given ith area element, correspondingly: 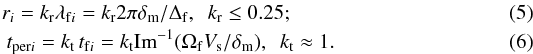 The model coefficients, kr = 0.17 and kt = 1.1, were determined in Girin (2011a) by constraining the model with experimental data.
The model coefficients, kr = 0.17 and kt = 1.1, were determined in Girin (2011a) by constraining the model with experimental data.
Having the main parameters of the spraying process, ri and tperi, expressed via the main parameters of the air flow, δa and Va in Eqs. (5) and (6) with the use of Eq. (2), we are able to quantify the spraying process. The number of wavelengths which are confined within ith area element, is equal to ni = Δli/λ f i. Due to the axial symmetry of the flow past the meteoroid, this is the number of tori of radius R(t)sinϕi, which have been broken away from the spherical belt corresponding to Δli. The toroidal breakaway structures were observed in LIF-experiments (Laser Induced Fluorescence) of Theofanous & Li (2008) on a liquid drop breakup.
When the disturbance has grown in amplitude by e, or τindi = ∫dt/tperi ≥ 1, we suppose that separation of ntori = ni tori of cross-section radius ri occurs at that moment from that area element. Assuming that the liquid tori rapidly break up into droplets of radius ri in the airstream, and taking the overall volume of the tori, 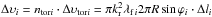 , divided by the single droplet volume, υi = 4 / 3πri3, we obtain the differential equation for the number Δni of the newborn particles:
, divided by the single droplet volume, υi = 4 / 3πri3, we obtain the differential equation for the number Δni of the newborn particles: 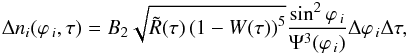 (7)which are released during period Δτ = tindi/tch from the area element Δli = RΔϕi. In accord with Eq. (5) and expression Δf = 2πδm/λf, the newborn particle radius can be written as follows:
(7)which are released during period Δτ = tindi/tch from the area element Δli = RΔϕi. In accord with Eq. (5) and expression Δf = 2πδm/λf, the newborn particle radius can be written as follows: 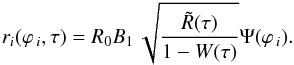 (8)
(8)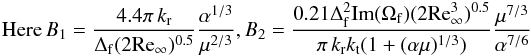 have the sense of scaling parameters for the particle sizes and number, respectively (Girin 2011a). For large values of Wes, Wes> 20, B1 and B2 are constants. The derivation of Eqs. (7) and (8) can be found in Appendix D.
have the sense of scaling parameters for the particle sizes and number, respectively (Girin 2011a). For large values of Wes, Wes> 20, B1 and B2 are constants. The derivation of Eqs. (7) and (8) can be found in Appendix D.
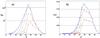 |
Fig. 6 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant I: fast iron meteoroid. Blue indicates the final distribution at τ = 2.72; brown, red, light green, and crimson indicate, respectively, the intermediate distributions at τ = 0.44, 0.89, 1.39, and 1.80; tch = 2.16 × 10-3 s. See Movie 1. |
 |
Fig. 7 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant II: slow iron meteoroid. Blue indicates the final distribution at τ = 3.11; brown, red, light green, and crimson indicate, respectively, the intermediate distributions at τ = 0.30, 0.93, 1.88, and 2.48; tch = 5.15 × 10-3 s. See Movie 2. |
In general, the intricacy of Δf and Im(Ωf) dependencies on ϕ and t via surface Weber number Wes(ϕ,t) together with the transiency and complexity of the air flow geometry makes it necessary to carry out numerical study of the ablation process (though in part two of this paper we will present the approximate analytical solution to the problem). As previously done for a drop atomizing in a speedy gas stream (Girin 2014b), the values for Va,Vs ,δa,δm, Wes, Δf, Im(Ωf),r,τind and Δn are computed here with Eqs. (2), (3), (5)–(8) and results of Fig. 5. Then, the melt mass 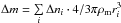 , which is released as breakaway particles, is subtracted from the meteoroid mass m(t) as the outcome of ablation; the current meteoroid radius R(t) is thus found.
, which is released as breakaway particles, is subtracted from the meteoroid mass m(t) as the outcome of ablation; the current meteoroid radius R(t) is thus found.
 |
Fig. 8 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant III: stony meteoroid. Blue indicates the final distribution at τ = 105; purple, orange, light-blue, green, brown, red, light green, and crimson indicate, respectively, the intermediate ones at τ = 2.05, 3.88, 5.94, 9.96, 16.8, 29.9, 48.7, and 73.0;tch = 1.45 × 10-3 s. |
5. Results and discussion
The model of melt spraying presented here allows us to determine the most important parameters of the ablation process, including the distribution of all sprayed particles by sizes, as well as evolution of the sprayed mist in space and time. Here we consider three particular cases of spherical meteoroids of initial radius R0 = 0.3 cm and different velocities and substances, which begin to ablate when moving in the continuum regime. The six-fold air compression and flow deceleration behind the detached shock front ahead of the meteoroid (Fig. 3) are taken into account. The density of air flow and meteoric material around the meteoroid is assumed to be large enough, so that the gas species density value, ρa = 10-7 g cm-3, is much greater than the ambient atmosphere density ρ∞ and corresponds to almost 30 km lower height (see the end of Sect. 2).
Results of the calculations in the form of transient number, Δn(r), and mass, ΔM(r), distributions of the sprayed droplets by sizes are given in Figs. 6–8. In addition, two video files, Movie 1 and Movie 2 illustrate the transient dynamics of the particle size distribution for the considered meteoroids. During flight, the meteoroid velocity is assumed to change in accordance with empirical law: W = 1 − exp( − Cτ) (Girin 2011a), where parameter C = 2α0.5 has the sense of meteoroid deceleration, as the derivative dW/ dτ shows. In this case, the meteoroid velocity decrease is negligible along most of the trajectory till the end of meteoroid ablation, because the characteristic time of meteoroid deceleration is much greater than the one of spraying: C-1 ≫ τch. The calculated dependence of meteoroid radius on the count-down time, ts.d. − t, is close to linear, so that the ablation law is close to the form M = (1 − t/ts.d.)3; here ts.d. is the overall time of the spraying process duration.
Some general information is given in Table 1, where the initial meteoroid velocity, V∞, is given in km s-1 and the ablation coefficient, 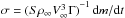 , is in s2 cm-2; here Γ is the drag coefficient. The media properties are: ρir = 7.8 g cm-3, ρst = 3.5 g cm-3, μ∞ = 6.8 × 10-5 kg m-1 s-1, μir = 5.8 × 10-3 kg m-1 s-1, μst = 0.174 kg m-1 s-1, Σir = 1.2 N m-1, and Σst = 0.36 N m-1. The values of Reynolds criterion Re∞ indicate that the regime of air streamlining past meteor body provides in each case the development of boundary layer in a liquid melt, while GI-criterion values are large enough to provide a full-strength working of the gradient instability mechanism. The minimum value of the growth time tf of the disturbance amplitude, taken along the meteoroid surface, is shown as the characteristic time of the breaking-away periodicity of the molten droplets. Compared with the overall spraying time ts.d., the calculated values of tf indicate the intensity of the spraying mechanism, since the ratio tf/ts.d. is small, ranging from 0.001 to 0.002 in the considered cases of meteoroids.
, is in s2 cm-2; here Γ is the drag coefficient. The media properties are: ρir = 7.8 g cm-3, ρst = 3.5 g cm-3, μ∞ = 6.8 × 10-5 kg m-1 s-1, μir = 5.8 × 10-3 kg m-1 s-1, μst = 0.174 kg m-1 s-1, Σir = 1.2 N m-1, and Σst = 0.36 N m-1. The values of Reynolds criterion Re∞ indicate that the regime of air streamlining past meteor body provides in each case the development of boundary layer in a liquid melt, while GI-criterion values are large enough to provide a full-strength working of the gradient instability mechanism. The minimum value of the growth time tf of the disturbance amplitude, taken along the meteoroid surface, is shown as the characteristic time of the breaking-away periodicity of the molten droplets. Compared with the overall spraying time ts.d., the calculated values of tf indicate the intensity of the spraying mechanism, since the ratio tf/ts.d. is small, ranging from 0.001 to 0.002 in the considered cases of meteoroids.
One can see that the ablation coefficient for the iron meteoroids falls into the range of the values generally accepted in the physical theory of meteors, σ = (10-12 − 10-11) s2 cm-2 (Bronshten 1983), while the value for the stone meteoroid is two orders lower than this range.
But this low value correlates with the intrinsic values of ablation coefficient, which were revealed and obtained recently (Ceplecha & ReVelle 2005; Borovička 2006). Indeed, when the fragmentation mode of ablation proceeds, the fragments ablate simultaneously, so that two different values of ablation coefficient, intrinsic and apparent, must be considered. Specifically, the former lies in the range from 10-13 to 8 × 10-13 s2 cm-2, while the latter has considerably greater values. The intrinsic ablation coefficient is calculated here.
Calculations reveal a large number, N = 1.5 × 106, of the particles produced by the fast iron meteor, which are two orders smaller by sizes than the parent meteoroid. Their sizes range from 4 μm to 135 μm, with the median radius rmed = 26.9 μm (Fig. 6); however, the mass fraction of those particles which have radii larger than rmed, constitutes 0.76m0. A few particles have sizes greater than 45 μm. These values can be compared with those obtained in Campbell-Brown et al. (2013) for meteor 20101106_065820 (velocity V∞ = 69.5 km s-1, radius R0 = 0.4 mm) with the use of the thermal disruption model. Specifically, the particle sizes were ranged from 31 μm to 144 μm.
As the expressions for the scaling parameters B1, B2 show, the particle sizes vary generally as 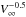 , while their total number N varies as
, while their total number N varies as 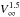 . For the slower iron meteoroid, V∞ = 25 km s-1, the sizes are larger and range from 16 μm to 265 μm, with the median radius rmed = 41.6 μm; a few particles have sizes greater than 70 μm. The mass fraction of those particles which have a radius greater than rmed, constitutes 0.78m0. The dynamics of the transient distributions of the slow and fast iron meteoroids are reflected in the supplementary video files (Movie 1 and Movie 2).
. For the slower iron meteoroid, V∞ = 25 km s-1, the sizes are larger and range from 16 μm to 265 μm, with the median radius rmed = 41.6 μm; a few particles have sizes greater than 70 μm. The mass fraction of those particles which have a radius greater than rmed, constitutes 0.78m0. The dynamics of the transient distributions of the slow and fast iron meteoroids are reflected in the supplementary video files (Movie 1 and Movie 2).
The rate of ablation varies along the meteoroid surface. In all calculations it had its minimum at the angle ϕ 1 near the critical angle and then increased towards ϕ = π/ 2. The larger droplets are always generated at the beginning of the ablation process, while the smaller droplets are released at the end, when the meteoroid radius is small. This means that, when the molten meteoroid moves along a gently sloped trajectory, the beginning of its aerosol trail consists of more coarse particles than the end.
The melt of iron meteoroid has boundary layer nearly 13 times thinner than that of a stony meteoroid, along with an interface velocity Vs that is 2.5 times larger as formulae in Eq. (2) show. This yields a more that 30-fold increase in velocity gradient in the iron melt (as it is directly proportional to μ, see Eq. (2)) and a consequently stronger destabilization of the iron-melt flow. This consideration leads to the conclusion regarding the significant role of thermal influx to the melt, which must be taken into account in instability applications, as the melt viscosity depends considerably on temperature.
The stony meteoroid disintegrates much more slowly than the iron ones due to the 30-fold larger viscosity, which agrees with conclusions of Bronshten (1983). This leads to large increase in the total ablation time, ts.d., and to a difference in the breakaway particle sizes of more than an order, in comparison with the iron meteor of the same velocity. The particle sizes range from 100 μm to 570 μm, with the median radius rmed = 336 μm, as seen in Fig. 8. The mass fraction of those particles, which have radii greater than rmed, constitutes 0.74m0. These values can be compared with those obtained with the use of the thermal disruption model in Campbell-Brown et al. (2013) for meteor 20101103_053624, which had a little greater velocity (V∞ = 66.4 km s-1) and less radius (R0 = 0.7 mm). Namely, the particle sizes ranged from 81 μm to 272 μm.
The fragmentation of the stony meteoroid is not terminated by the gradient instability mechanism. As seen in Eq. (2), this is due to the thick boundary layer, which for a high-viscosity stony melt becomes comparable with the radius of the meteoroid remnant. Thus, the fastest unstable disturbance wavelength, λf, becomes comparable with the remnant radius 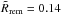 . We note that this terminal fragmentation has little effect on the overall meteoroid ablation since the remnant meteoroid mass is mrem = 2.7 × 10-3m0. However, the molten remnant can be fragmented afterwards by the mechanism of the Rayleigh − Taylor instability, since the current Weber number value is sufficiently large at that moment, We∞ ≈ 100, to provide the “claviform” or “multibag” mode of the remnant breakup (Reinecke & Waldman 1975; Zhao et al. 2010; Girin 2012, 2014a). Some ending meteor flashes can be explained thus as the delayed bursting of their remnants (Girin 1992; Girin & Kopyt 1994), since the low-Weber modes of breakup consist in a sudden rupture of a vast thin “bag” film into the tiny droplets.
. We note that this terminal fragmentation has little effect on the overall meteoroid ablation since the remnant meteoroid mass is mrem = 2.7 × 10-3m0. However, the molten remnant can be fragmented afterwards by the mechanism of the Rayleigh − Taylor instability, since the current Weber number value is sufficiently large at that moment, We∞ ≈ 100, to provide the “claviform” or “multibag” mode of the remnant breakup (Reinecke & Waldman 1975; Zhao et al. 2010; Girin 2012, 2014a). Some ending meteor flashes can be explained thus as the delayed bursting of their remnants (Girin 1992; Girin & Kopyt 1994), since the low-Weber modes of breakup consist in a sudden rupture of a vast thin “bag” film into the tiny droplets.
Two−mode particle distribution may exist at small values of the gradient instability criterion GI due to the influence of the “hump” in Δf(Wes) dependence shown in Fig. 5. This feature causes a shift towards smaller particle sizes near the critical point ϕcr on the meteoroid surface. At smaller GI values this effect becomes more distinct, as Fig. 7 shows, since ϕcr becomes greater at smaller GI (see Table 1), approaching ϕ = π/ 2. As a result, most part of the meteoroid surface produces smaller particles, creating the bi−modal distribution in droplet sizes. The two−mode distribution can be seen in paper Campbell-Brown et al. (2013) in the analysis of low-speed meteor 20101016_070052.
Table 1 shows that the meteor path, l, for the iron meteoroid is shorter than for the stony one. Together with the difference in the total number of generated particles this gives significantly different aerosol density in the meteor wakes.
6. Conclusions
We have presented the theory of a molten meteoroid spraying, which allowed an investigation of the details of ablation kinetics. The theory is based on the mechanism of the gradient instability, which generated high-frequency quasi-continuous spraying of the liquid melt particles constituting a meteor aerosol wake.
The analysis shows that the dynamic pressure of the airstream at heights 80–100 km is sufficient to pull out the liquid melt droplets via the mechanism of gradient instability, which provides a simple and natural explanation of the quasi-continuous fragmentation of small (≈1 cm) meteoroids at similar heights.
The problem of meteoroid ablation is solved theoretically in a closed form for the case of a shallow entry angle, the physical properties, initial radius and velocity of the meteoroid being given. The sizes of molten, sprayed droplets and transient distributions for the iron and stony meteoroids are calculated. Differences in iron and stony meteoroid mechanical properties cause significant changes in the generated particles: meteor wake lengths, particle size distributions, and aerosol number densities differed by more than an order of magnitude for iron and stony meteoroids of the same entrance velocity. Less viscous iron melt yielded finer particles and a denser aerosol wake than the stony one. The fast iron meteoroid with the entry velocity V∞ = 60 km s-1 gradually burst into more than a million particles with radii ranging from 4 μm to 135 μm when the meteoroid radius was 0.3 cm. Generally, the radii of the sprayed droplets are comparable with sizes of the “grains” obtained within the theories based on the “dustball” hypothesis. However, the parameters of sprayed droplets depended essentially on a meteoroid radius, velocity and substance. A future effort may involve modelling the luminosity of the meteoroid and sprayed droplets to compare with observed meteor light curves or trail lengths.
During the spraying process the largest droplets are generated at the beginning of the ablation, while the smallest droplets are generated towards the end, as the present results show. The ablating meteoroid radius varies almost linearly with time. The influence of the meteoroid entry velocity on the number and sizes of breakaway particles is estimated.
This paper presents a quantitative application of the gradient instability theory to meteoroid fragmentation. Based on the results of this study, the next steps are investigation of the dynamic structure of the meteoric aerosol wake and meteor luminosity under the increasing rate of vapour production caused by the increased liquid surface of sprayed droplets, as well as investigating the case of an arbitrary meteoroid entry angle.
Movies
Movie of Fig. 6 Access here
Movie of Fig. 7 Access here
References
- Astapovich, I. S. 1958, Meteoric Events in Earth’s Atmosphere (Moscow: Fizmatgiz) [Google Scholar]
- Borovička, J. 2006, in Asteroids, Comets and Meteors, eds. D. Lazzaro, S. Ferraz-Mello, & J. Fernandez, Proc. IAU Symp., 229, 249 [Google Scholar]
- Borovička, J., Spurný, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyd, I. D. 2000, Earth Moon Planets, 82-83, 93 [Google Scholar]
- Bronshten, V. A. 1983, Physics of Meteor Phenomena (Dordrecht: Reidel) [Google Scholar]
- Bronshten, V. A. 1984, Noctilusent Clouds and their Observation (Moscow: Nauka) [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell-Brown, M. D., Borovička, J., Brown, P. G., & Stokan, E. 2013, A&A, 557, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceplecha, Z., & ReVelle, D. O. 2005, Meteorit. Planet. Sci., 40, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z., Borovička, J., & Elford, W. G. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Hydrodynamic and Hydromagnetic Instability (Oxford: Clarendon Press) [Google Scholar]
- Courant, R., & Friedriechs, K. O. 1976, Supersonic Flow and Shock Waves (New York: Springer-Verlag) [Google Scholar]
- Genge, M. J. 2000, Meteor. & Planet. Sci., 35, 1143 [CrossRef] [Google Scholar]
- Girin, A. G. 1985, J. Eng. Phys. Thermophys., 48, 560 [CrossRef] [Google Scholar]
- Girin, A. G. 1992, Astronomicheskiy Vestnik (Astron. Herald), 26, 85 [in Russian] [Google Scholar]
- Girin, A. G. 2011a, J. Eng. Phys. Thermophys., 84, 262 [CrossRef] [Google Scholar]
- Girin, A. G. 2011b, J. Eng. Phys. Thermophys., 84, 872 [CrossRef] [Google Scholar]
- Girin, A. G. 2012, Atom. Sprays, 22, 921 [CrossRef] [Google Scholar]
- Girin, A. G. 2014a, Atom. Sprays, 24, 349 [CrossRef] [Google Scholar]
- Girin, A. G. 2014b, Atom. Sprays, 24, 977 [Google Scholar]
- Girin, A. G., & Kopyt, N. K. 1994, J. Aeros. Science, 25, 1353 [CrossRef] [Google Scholar]
- Gordillo, J. M., Perez-Saborid, M., & Gaňán-Calvo, A. M. 2001, J. Fluid Mech., 448, 23 [CrossRef] [Google Scholar]
- Hsu, N. C., Torres, O., Seftor, C., Herman, J., & Bhartia, P. K. 1997, in Atmosp. Transparency from Satellites: Effects of Aerosol and Thin Clouds. Int. Workshop. Marathea, Italy (Consiglio Nazionale delle Ricerche), 14 [Google Scholar]
- Janches, D., & Chau, J. L. 2005, J. Atm. Sol. Terr. Phys., 67, 1196 [CrossRef] [Google Scholar]
- Kahn, R. A. 2012, Surv. Geophys., 33, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Kochin, N. E., Kibel, I. A., & Rose, N. V. 1964, Theoretical Hydrodynamics (New York: Interscience Publishers) [Google Scholar]
- Krinov, E. L. 1960, The Principles of Meteoritics (New York: Pergamon) [Google Scholar]
- Lebedinets, V. N. 1981, Aerosol in the Upper Atmosphere and Interplanetary Dust (Leningrad: IEM Gidrometeoizdat) [In Russian] [Google Scholar]
- Lebedinets, V. N., & Portniagin, Y. I. 1966, Planet. Space Sci., 13, 9 [Google Scholar]
- Lebedinets, V. N., & Shushkova, V. B. 1970, Planet. Space Sci., 18, 1653 [NASA ADS] [CrossRef] [Google Scholar]
- Loitsyanskiy, L. G. 1995, Mechanics of Liquid and Gases (New York: Begell House Inc.) [Google Scholar]
- Mathews, J. D., Janches, D., Meisel, D. D., & Zhou, Q. H. 2001, Geophys. Res. Lett., 28, 1929 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, O. P., Sidneva, S. N., Shuvalov, V. V., & Strelkov, A. S. 2000, Earth Moon Planets, 82, 109 [NASA ADS] [Google Scholar]
- Rabin, E., Schallenmuller, A. R., & Lowhead, R. B. 1960, Displacement and Shattering of Propellant Droplets, Final Summary Report AFOSR TR-60-75 [Google Scholar]
- Ranger, A. A. 1972, Astron. Acta, 17, 675 [Google Scholar]
- Reinecke, W. G., & Waldman, G. D. 1975, Shock Layer Shattering of Cloud Drops in Reentry Flight, American Inst. of Aeronautics and Astronautics, 13th Aerospace Sci. Meeting, in Pasadena (CA), paper 75-152 [Google Scholar]
- Rogers, L. A., Hill, K. A., & Hawkes, R. L. 2005, Planet. Space Sci., 53, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. 1960, Boundary Layer Theory (New York: McGraw Hill) [Google Scholar]
- Stober, G., & Jacobi, C. 2008, Wiss. Mitteil. Institute for Meteorology, Univ. Leipzig, 42, 155 [Google Scholar]
- Theofanous, T. G., & Li, G. J. 2008, Phys. Fluids, 20, 052103 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, I. P. 2002, in Meteors in the Earth’s Atmosphere, eds. E. Murad, & I. P. Williams (Cambridge, UK: Cambridge University Press), 2 [Google Scholar]
- Zhao, H., Liu, H. F., Li, W. F., & Xu, J. L. 2010, Phys. Fluids, 22, 114103 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J., Judd, O. P., & ReVelle, O. D. 2004, Adv. Space Res., 33, 1466 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The cause of the gradient instability
The cause of instability of a gradient flow in a vicinity of liquid – gas interface is the inertial forces of disturbed curvilinear motion (Fig. 1c). Indeed, in its motion along curvilinear trajectory with velocity V every liquid particle undergoes centrifugal acceleration: 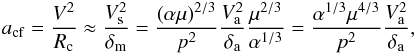 (A.1)where Eqs. (2) are used. Here the curvature radius Rc = AB (Fig. 1c) of the disturbed trajectory is proportional to ≈ λf/ 2 ≈ δm, as the expression Δf = 2πδm/λf = 1.225 shows at Wes> 20 (see Sect. 3).
(A.1)where Eqs. (2) are used. Here the curvature radius Rc = AB (Fig. 1c) of the disturbed trajectory is proportional to ≈ λf/ 2 ≈ δm, as the expression Δf = 2πδm/λf = 1.225 shows at Wes> 20 (see Sect. 3).
The centrifugal force is normal to the air-melt interface, acting on any liquid particle within the disturbance elevation (Fig. 1c). Thus, once the melt surface is disturbed, the liquid heaps are being pulled out by the centrifugal force with huge acceleration of the order of ≈104 − 105 m s-2, as Eq. (A.1) shows for meteoroids. These values are more than a thousand times greater than the terrestrial gravitation, which explains the mechanism of the ligament formation shown in Fig. 4. The same tendency has the centrifugal force acting on the moving air particles above the liquid heap, but this action at the interface is smaller because of the less air density. Indeed, the dispersal relation (Eq. (1)) of the perturbation problem contains none of the gas parameters, so, the air contributes a little force into the interface instability mechanism, its role is reduced simply to generate the shear motion in liquid by means of the viscous stresses.
The huge centrifugal force pulls out the liquid ligaments of size ≈λ/ 2, which quickly burst by the airstream into several drops of approximately the same diameter (Fig. 4), providing the mechanism of meteoroid melt spraying. The time of accelerated growth of the disturbance amplitude till the value λ/ 2, which is sufficient for the breakaway droplet formation, can be estimated as t = (λ/ 2acf)0.5< 10-4 s (when Eq. (A.1) is taken into account), assuming constant acceleration. These estimates show that the unstable disturbance develops quickly during meteoroid flight thus providing the spraying ablation mechanism.
Appendix B: The boundary layer relationships
Since an air-liquid interaction occurs in the conjugated boundary layers, a few relationships are necessary for the gradient instability analysis and its application, which have their origin in the boundary layer theory. In accordance with this theory (Schlichting 1960), the air, δa, and the melt, δm, boundary layer thicknesses are expressed via the Reynolds numbers of flows in the air, Rea, and melt, Rem, boundary layers: 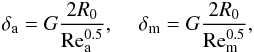 (B.1)here Rea = ρa2R0(Va − Vs) /μa, Rem = ρm2R0Vs/μm, μa is the air dynamic viscosity, Va is the air velocity, Vs is velocity at the air-melt interface (Fig. 2,b), R0 is the initial meteoroid radius. Characteristic values of the velocity gradients in boundary layers are bounded by the requirement of equality of the viscous shear stresses at the interface y = 0: μmVs/δm = μa(Va − Vs) /δa. Eliminating geometry factor G, we obtain the important relations:
(B.1)here Rea = ρa2R0(Va − Vs) /μa, Rem = ρm2R0Vs/μm, μa is the air dynamic viscosity, Va is the air velocity, Vs is velocity at the air-melt interface (Fig. 2,b), R0 is the initial meteoroid radius. Characteristic values of the velocity gradients in boundary layers are bounded by the requirement of equality of the viscous shear stresses at the interface y = 0: μmVs/δm = μa(Va − Vs) /δa. Eliminating geometry factor G, we obtain the important relations: 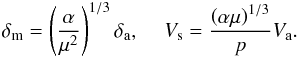 (B.2)Assuming the spherical shape of the meteoroid and the velocity potential of the air flow around a sphere in the form Va(ϕ) = 1.5(V∞ − w)sinϕ (Kochin et al. 1964), let us apply the boundary layer thickness distribution along the meteoroid surface in Ranger’s (1972) form:
(B.2)Assuming the spherical shape of the meteoroid and the velocity potential of the air flow around a sphere in the form Va(ϕ) = 1.5(V∞ − w)sinϕ (Kochin et al. 1964), let us apply the boundary layer thickness distribution along the meteoroid surface in Ranger’s (1972) form: 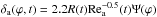 ; the latter is valid for a gas over a liquid sphere, here Ψ(ϕ) = ((6ϕ − 4sin2ϕ + 0.5sin4ϕ) / sin5ϕ)0.5, ϕ is the polar angle of a surface area element (Figs. 1b and 3). The latter together with Eq. (B.1) yields the geometry factor for a liquid sphere:
; the latter is valid for a gas over a liquid sphere, here Ψ(ϕ) = ((6ϕ − 4sin2ϕ + 0.5sin4ϕ) / sin5ϕ)0.5, ϕ is the polar angle of a surface area element (Figs. 1b and 3). The latter together with Eq. (B.1) yields the geometry factor for a liquid sphere: 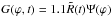 ,
, 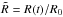 .
.
Let us transform the necessary condition for the gradient instability, Wes ≥ 3.08, rewriting it for an arbitrary area element ϕ at meteoroid surface: 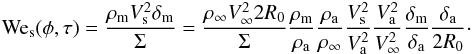 (B.3)The right-hand side can be further transformed to:
(B.3)The right-hand side can be further transformed to: 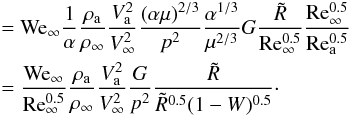 (B.4)When
(B.4)When 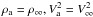 , and in the virtue of relationships
, and in the virtue of relationships 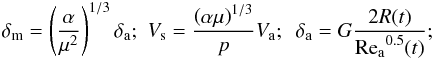 Va = 1.5V∞(1 − w(t))sin(ϕ), we will have:
Va = 1.5V∞(1 − w(t))sin(ϕ), we will have: 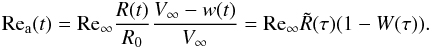 Eventually, we obtain Eq. (3):
Eventually, we obtain Eq. (3): 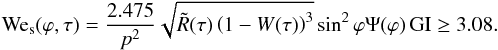 (B.5)Thus, the local condition for the gradient instability proceeding, Wes> Wes.cr. = 3.08, can be rewritten in the whole problem velocity and length scales, V∞ and R0:
(B.5)Thus, the local condition for the gradient instability proceeding, Wes> Wes.cr. = 3.08, can be rewritten in the whole problem velocity and length scales, V∞ and R0: 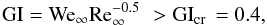 (B.6)which exhibits the necessary condition for the melt surface instability for the whole meteoroid flight. Expression (B.6) is obtained from the inequality in (B.5) at τ = 0 since
(B.6)which exhibits the necessary condition for the melt surface instability for the whole meteoroid flight. Expression (B.6) is obtained from the inequality in (B.5) at τ = 0 since 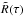 , 1 − W(τ) are the decreasing functions, so that initial moment is preferable for instability performance. Value ϕ = π/ 2 was also used since δm,Vs, Wes have the uppermost values at a liquid body periphery, ϕ = π/ 2.
, 1 − W(τ) are the decreasing functions, so that initial moment is preferable for instability performance. Value ϕ = π/ 2 was also used since δm,Vs, Wes have the uppermost values at a liquid body periphery, ϕ = π/ 2.
Appendix C: The meaning of the surface Weber number criterion
The two Weber numbers, surface Wes and meteoroid We∞, have the same general sense: the ratio of the hydrodynamic forces to the surface tension forces. But the surface Weber number Wes specifically relates hydrodynamic pressure 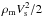 of the melt motion in the liquid boundary layer to the surface tension forces δm/ Σ of the disturbed interface, whose curvature radius Rc = AB (Fig. 1c) is proportional to δm; the latter follows from the relation Δf = 2πδm/λf = 1.225 at Wes> 20. The former force creates the destabilizing effect, defining the centrifugal force scale, see Eq. (A.1); the latter force defines a stabilizing effect. Thus, the surface Weber number reflects locally, at a disturbance level, the ratio of destabilizing forces to the stabilizing ones, governing the disturbance development. At Wes> 3.08 the inertial forces prevail over the surface tension and the disturbance becomes unstable, growing in amplitude. The role of viscous forces is to form the gradient flow of characteristic depth δm in a liquid melt.
of the melt motion in the liquid boundary layer to the surface tension forces δm/ Σ of the disturbed interface, whose curvature radius Rc = AB (Fig. 1c) is proportional to δm; the latter follows from the relation Δf = 2πδm/λf = 1.225 at Wes> 20. The former force creates the destabilizing effect, defining the centrifugal force scale, see Eq. (A.1); the latter force defines a stabilizing effect. Thus, the surface Weber number reflects locally, at a disturbance level, the ratio of destabilizing forces to the stabilizing ones, governing the disturbance development. At Wes> 3.08 the inertial forces prevail over the surface tension and the disturbance becomes unstable, growing in amplitude. The role of viscous forces is to form the gradient flow of characteristic depth δm in a liquid melt.
The existence of the critical value Wes.cr. has a simple hydrodynamic sense. In order to reveal the meaning of Wes.cr for a meteoroid flight, let us go over to the air flow parameters in the inequality 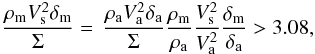 (C.1)or, using Eqs. (2) (or equally (B.2)):
(C.1)or, using Eqs. (2) (or equally (B.2)): 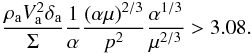 (C.2)The inequality (C.2) can be resolved with respect to the dynamic pressure P of the airstream past meteoroid:
(C.2)The inequality (C.2) can be resolved with respect to the dynamic pressure P of the airstream past meteoroid: 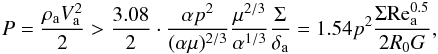 (C.3)with the use of Eqs. (B.1). With the value G(π/ 2,0) = 3.38, which follows from the Ranger expression for δa (see Appendix B), we consecutively obtain the values for the three variants of meteoroids: PI> 3.0 kPa, PII> 2.1 kPa, PIII> 0.9 kPa, the notation in Sect. 3 regarding the value Wes.cr. = 4.62 being taken into account.
(C.3)with the use of Eqs. (B.1). With the value G(π/ 2,0) = 3.38, which follows from the Ranger expression for δa (see Appendix B), we consecutively obtain the values for the three variants of meteoroids: PI> 3.0 kPa, PII> 2.1 kPa, PIII> 0.9 kPa, the notation in Sect. 3 regarding the value Wes.cr. = 4.62 being taken into account.
In some publications (Borovička et al. 2007) it has been noted that meteoroid fragmentation can not be explained by the direct action of the dynamic pressure of airstream. The latter has an order of (5 − 20) kPa at heights of about 90–100 km, which is too small to prevail over the solid meteoroid strength. But the critical values of the dynamic pressure P, obtained above, which correspond to the value Wes.cr. = 4.62, show that the dynamic pressure of airstream at heights up to 100 km, which is too low with respect to a solid meteoroid body strength, is sufficient, however, to overcome surface tension forces and to pull out liquid particles from the meteoroid melt by means of unstable disturbances, providing thus the quasi-continuous spraying mechanism of meteoroid ablation. The gradient instability pulls out ligaments from the liquid (Fig. 4) by means of centrifugal forces imposed at moving liquid layer, when the unstable disturbances appear on a liquid surface (Fig. 1c).
Appendix D: The differential equation for the sprayed droplets’ number
The rate of the tori production (see Sect. 4) can be expressed as the ratio of the number ntor of the tori that were broken away by the time period tper, to this time period: 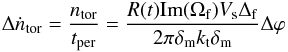
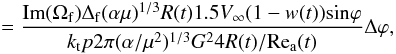 (D.1)with the use of the expressions
(D.1)with the use of the expressions 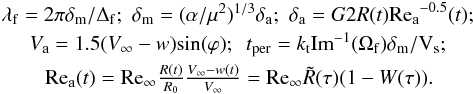 The single torus volume is υtor = 2π2(krλf)2R(t)sinϕ, so that the melt volume gone with the tori by the time period tper is
The single torus volume is υtor = 2π2(krλf)2R(t)sinϕ, so that the melt volume gone with the tori by the time period tper is 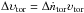 . Assuming that the liquid tori are quickly breaking up into droplets of radius r in the airstream and dividing this volume by the single droplet volume, υdr = 4 / 3π(krλf)3, we obtain the number of droplets broken away by the time tper:
. Assuming that the liquid tori are quickly breaking up into droplets of radius r in the airstream and dividing this volume by the single droplet volume, υdr = 4 / 3π(krλf)3, we obtain the number of droplets broken away by the time tper: 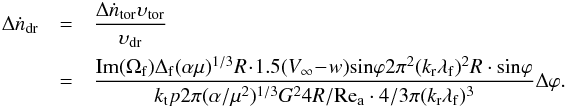 (D.2)Using the above expressions for λf, δm, δa, Rea, and G = 1.1Ψ(ϕ), we can simplify this expression to the form:
(D.2)Using the above expressions for λf, δm, δa, Rea, and G = 1.1Ψ(ϕ), we can simplify this expression to the form: 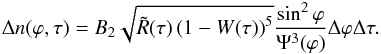 (D.3)Here
(D.3)Here 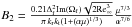 has the sense of the scaling parameter for the number of breakaway particles (Girin 2011a).
has the sense of the scaling parameter for the number of breakaway particles (Girin 2011a).
Equation (D.3) is the differential Eq. (7) for the number Δn of the newborn particles, which are released during the period Δτ = tper/tch from the area element Δl = R(t)Δϕ.
In accord with Eq. (5) and the expressions given above, the newborn particle radius can be written as follows: ![\appendix \setcounter{section}{4} \begin{eqnarray} r (\varphi ,\tau ) = k_{\rm{r}} \frac{2\pi \delta_{\rm{m}}}{\Delta_{\rm{f}}} = k_{\rm{r}} \frac{2\pi \cdot 2 R_0\cdot1.1 \Psi(\varphi)}{\Delta_{\rm{f}}{\rm{Re_\infty}^{0.5}}} \frac{\tilde{R}(\tau)^{0.5}}{[1\!-\!W(\tau)]^{0.5}} \frac{\alpha^{1/3}}{\mu^{2/3}}. \end{eqnarray}](/articles/aa/full_html/2017/10/aa29560-16/aa29560-16-eq359.png) (D.4)This expression can be rewritten in the form of Eq. (8):
(D.4)This expression can be rewritten in the form of Eq. (8): 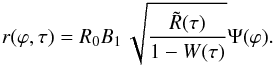 (D.5)Here
(D.5)Here 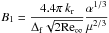 has the sense of the scaling parameter for the breakaway particle sizes (Girin 2011a). For large values of Wes, when Wes> 20, B1 and B2 are constants since Δf and Ωf are constants (Fig. 5).
has the sense of the scaling parameter for the breakaway particle sizes (Girin 2011a). For large values of Wes, when Wes> 20, B1 and B2 are constants since Δf and Ωf are constants (Fig. 5).
Appendix E: Nomenclature
| b | – molten layer thickness; |
| B 1 , B 2 | – scaling parameters; |
| E | – disturbance amplitude; |
| G | – boundary layer geometry factor; |
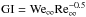
|
– gradient instability criterion; |
| Im-1(ω) | – growth rate factor; |
| k r , k t | – coefficients in Eqs. (5) and (6); |
| l | – meteoroid path; |
| m | – meteoroid mass; |
| M = m/m0 | |
| Ma | – Mach number; |
| N | – total number of particles; |
| p = 1 + (αμ)1 / 3 | |
| P | – dynamic pressure; |
| R | – current meteoroid radius; |
|
|
| r | – breakaway droplet radius; |
|
|
| Re∞ = ρ∞2R0V∞/μ∞ | – Reynolds number for meteoroid; |
| S | – meteoroid surface area; |
| t | – elapsed time; |
| tch = 2R0/α0.5V∞ | – characteristic timescale; |
| V | – velocity; |
| w | – meteoroid velocity deficit due to |
| deceleration; | |
| W = w/V∞ | |
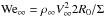
|
– Weber number for meteoroid; |
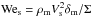
|
– surface Weber number; |
| x,y | – coordinates within boundary layer; |
| z | – meteor altitude. |
| Greek symbols: | |
| α = ρa/ρm | – air-to-melt density ratio; |
| γ | – angle between trajectory and horizon; |
| Γ | – aerodynamic drag coefficient; |
| δ | – boundary layer thickness; |
| μ a ,m | – dynamic viscosity; |
| μ = μa/μm | |
| ρ | – density; |
| Δl | – area element length; |
| Σ | – melt surface tension; |
| σ | – ablation coefficient; |
| τ | – dimensionless time; |
| ν | – kinematic viscosity; |
| λ | – disturbance wavelength; |
| ϕ | – polar angle (Figs. 1b, 3); |
| Δn | – number of newborn droplets; |
| Δ = 2πδm/λ | – dimensionless wavenumber; |
| Δυtor | – torus volume; |
| τ ind | – disturbance induction time; |
| ω | – disturbance complex frequency; |
| Ω = ωδm/Vs |
| Indices: | |
| a | – air near meteoroid surface; |
| c | – curvature; |
| cf | – centrifugal; |
| cr | – critical; |
| f | – fastest disturbance; |
| h.r. | – half radius; |
| ind | – induction; |
| ir | – iron; |
| m | – melt; |
| med | – median; |
| per | – period; |
| rem | – remnant; |
| s | – surface; |
| st | – stone; |
| s.d. | – spraying duration; |
| 0 | – initial values; |
| ∞ | – ambient air. |
| Super-index I-III is the calculated | |
| meteoroid number. |
All Tables
All Figures
 |
Fig. 1 Scheme of the flow in case of outstripping ablation (a) and in case of outstripping melting (b). Scheme of flow in disturbed boundary layer (c): solid thin lines indicate melt particles’ streamlines; thick dashed lines indicate undisturbed boundary layer limits. AB is the curvature radius of disturbed streamlines; Fcf is the centrifugal force acting at moving melt particle. |
| In the text | |
 |
Fig. 2 Linear fit of velocity profile in conjugated boundary layers; case νm>νa(a) and νa>νm(b); δa, δm – air and melt boundary layer thicknesses. |
| In the text | |
 |
Fig. 3 Flow scheme around meteoroid body. Stable and unstable parts of molten meteoroid surface are shown. |
| In the text | |
 |
Fig. 4 Particle release process at ith area element of meteoroid surface. |
| In the text | |
 |
Fig. 5 Basic dependencies Δf(Wes) (solid line) and Im [ Ωf(Wes) ] (dashed line) of gradient instability. |
| In the text | |
 |
Fig. 6 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant I: fast iron meteoroid. Blue indicates the final distribution at τ = 2.72; brown, red, light green, and crimson indicate, respectively, the intermediate distributions at τ = 0.44, 0.89, 1.39, and 1.80; tch = 2.16 × 10-3 s. See Movie 1. |
| In the text | |
 |
Fig. 7 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant II: slow iron meteoroid. Blue indicates the final distribution at τ = 3.11; brown, red, light green, and crimson indicate, respectively, the intermediate distributions at τ = 0.30, 0.93, 1.88, and 2.48; tch = 5.15 × 10-3 s. See Movie 2. |
| In the text | |
 |
Fig. 8 Distributions of breakaway droplets by sizes: Δn(r)(a) and ΔM(r)(b). Variant III: stony meteoroid. Blue indicates the final distribution at τ = 105; purple, orange, light-blue, green, brown, red, light green, and crimson indicate, respectively, the intermediate ones at τ = 2.05, 3.88, 5.94, 9.96, 16.8, 29.9, 48.7, and 73.0;tch = 1.45 × 10-3 s. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


