| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201731270 | |
| Published online | 01 September 2017 | |
Isotope exchange reactions involving HCO+ with CO: A theoretical approach
1 Université Paris-Est, Laboratoire Modélisation et Simulation Multi Echelle, MSME UMR 8208 CNRS, 5 bd Descartes, 77454 Marne-la-Vallée, France
e-mail: Mirjana.Mladenovic@u-pem.fr
2 LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, 92190 Meudon, France
e-mail: evelyne.roueff@obspm.fr
Received: 29 May 2017
Accepted: 6 July 2017
Aims. We aim to investigate fractionation reactions involved in the 12C/13C, 16O/18O, and 17O balance.
Methods. Full-dimensional rovibrational calculations were used to compute numerically exact rovibrational energies and thermal equilibrium conditions to derive the reaction rate coefficients. A nonlinear least-squares method was employed to represent the rate coefficients by analytic functions.
Results. New exothermicities are derived for 30 isotopic exchange reactions of HCO+ with CO. For each of the reactions, we provide the analytic three-parameter Arrhenius-Kooij formula for both the forward reaction and backward reaction rate coefficients, that can further be used in astrochemical kinetic models. Rotational constants derived here for the 17O containing forms of HCO+ may assist detection of these cations in outer space.
Key words: ISM: general / ISM: molecules / ISM: abundances
© ESO, 2017
1. Introduction
The 18O and 17O isotopic variants of CO are routinely detected in interstellar galactic and extragalactic environments and are used to determine the evolution trend of the corresponding 18O/17O ratio through the galactic disk. However, HC17O+ has, to our knowledge, only been detected in two sources, SgB2 by Guélin et al. (1982) and in the molecular peak of the L1544 pre-stellar core by Dore et al. (2001a), who also refined the spectroscopic constants and the hyperfine coupling constants as the 17O nucleus has a spin of 5/2. With the advent of sensitive receivers and large collecting areas available in modern observational facilities, such as ALMA and NOEMA, there is no doubt that more observations of these molecular ions will become available. However, the chemical reactions which may occur and possibly enhance the abundance of this rare molecular ion through isotopic exchange reactions, such as those occurring for HC18O+ (Mladenović & Roueff 2014), have not yet been reported. The purpose of the present study is to derive accurate values of the exothermicities involved in isotopic exchange reactions and to propose the corresponding reaction rate coefficients which can further be used in astrochemical models.
The fractionation of stable isotopes can be ascribed to a combination of the mass dependent thermodynamic (equilibrium) partition functions, the mass dependent diffusion coefficients, and the mass dependent reaction rate coefficients. This is in accordance with quantum mechanics, which predicts that mass affects the strength of chemical bonds and the vibrational, rotational, and translational motions, so that temperature dependent isotope fractionations may arise from quantum mechanical effects on rovibrational motion. For a given vibrational state, the vibrational energy is lower for a bond involving a heavier isotope. The extent of isotopic fractionation varies inversely with temperature and is large at low temperatures.
Smith & Adams (1980) measured the forward kf and reverse kr rate coefficients for three isotopic variants of the reaction HCO+ with CO at 80, 200, 300, and 510 K using a selected ion flow tube (SIFT) technique. Langer et al. (1984) extrapolated the experimental values of Smith & Adams (1980) to temperatures below 80 K toward the limit of the average dipole orientation model of ion-polar molecule capture collisions (Su & Bowers 1975), producing the total rate coefficients kT = kf + kr for nine temperatures over the range 5–300 K. Langer et al. employed a common reduced mass for three isotopic variants of HCO++CO studied by Smith & Adams (1980). The values for kT were used in combination with theoretical spectroscopic parameters calculated for the isotopic variants of HCO+ by Henning et al. (1977) in order to model cosmochemical carbon and oxygen isotope fractionations. From the total mass-independent rate coefficients kT and the theoretical zero point energy differences ΔE, Langer et al. (1984) estimated the rate coefficients kf and kr for six reactions HCO++CO involving isotopologues containing 12C, 13C, 16O, and 18O.
Recently, we have investigated in some detail the isotope fractionation reactions of HCO+/HOC+ with CO and of N2H+ with N2 (Mladenović & Roueff 2014), hereafter called Paper I. In Paper I, we employed the global three-dimensional potential energy surfaces developed by Mladenović & Schmatz (1998) for the isomerizing system HCO+/HOC+ and by Schmatz & Mladenović (1997) for the isoelectronic species N2H+ in combination with a numerically exact method for the rovibrational calculations (Mladenović & Bačić 1990; Mladenović 2002). For the reaction HCO++CO, we pointed out inaccuracies of previous exothermicity values, which have been commonly used in chemical networks. The new exothermicities are found to affect significantly the rate coefficients derived at 10 K, corresponding to the temperature of dark interstellar cloud environments.
The isotopes H, D, 12C, 13C, 16O, and 18O were considered in our previous work (Mladenović & Roueff 2014), resulting in six reactions HCO++CO involving hydrogen and six reactions DCO++CO involving deuterium. In the present work, we extend our analysis with the stable isotope 17O. The possible isotopic variants of HCO+ and CO are connected by 15 reactions for the hydrogenic forms and 15 reactions for the deuterated counterparts. All 30 were studied here. Nominal abundances of oxygen isotopes 16O, 17O, and 18O are 99.76, 0.04, and 0.20%, respectively (Mills et al. 1993).
Our theoretical approach is described in Sect. 2. In Sect. 3, we report the energies involved in all possible exchange reactions between CO and HCO+ (HOC+) isotopologues and their deuterium variants, as well as the rate coefficients for the reaction of HCO+ with CO in the 5–300 K temperature window. We summarize our finding in Sect. 4.
2. Methods
Isotopic exchange reactions can occur according to different types as discussed in Roueff et al. (2015). However, the equilibrium constant Ke, which provides the ratio of the forward reaction rate coefficient kf and the backward (reverse) reaction rate coefficient kr, is uniquely defined under thermal equilibrium conditions.
We considered the exchange between an heavy (H) and light (L) isotope in the reaction 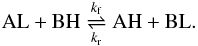 (1)Under thermal equilibrium conditions, the equilibrium constant Ke is given by
(1)Under thermal equilibrium conditions, the equilibrium constant Ke is given by 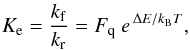 (2)using
(2)using 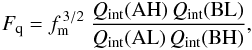 (3)and
(3)and 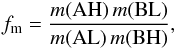 (4)where m(X) stands for the mass of the species X. In Eq. (2), ΔE is the zero point energy difference between the reactants and the products,
(4)where m(X) stands for the mass of the species X. In Eq. (2), ΔE is the zero point energy difference between the reactants and the products, 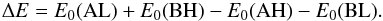 (5)To express ΔE in Kelvin, we used ΔE/kB, where kB is the Boltzmann constant. The zero point energy E0(X) for the species X is measured on an absolute energy scale. In practical applications, E0(X) is given relative to the respective potential energy minimum. The electronic states are not changed in the course of the reaction of Eq. (1), so that the ratio of the electronic partition functions is unity in Eq. (3). The term fm arises from the translational contribution. For the internal partition function Qint, we used
(5)To express ΔE in Kelvin, we used ΔE/kB, where kB is the Boltzmann constant. The zero point energy E0(X) for the species X is measured on an absolute energy scale. In practical applications, E0(X) is given relative to the respective potential energy minimum. The electronic states are not changed in the course of the reaction of Eq. (1), so that the ratio of the electronic partition functions is unity in Eq. (3). The term fm arises from the translational contribution. For the internal partition function Qint, we used 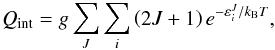 (6)where
(6)where 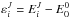 denotes the rovibrational energy for a total angular momentum J. The factor 2J + 1 accounts for the degeneracy with respect to the space-fixed reference frame and g for the nuclear spin degeneracy. Additional care is required for the nuclear spin degeneracy factor when different spin states (e.g., ortho or para) are involved either in the reactants or in the products, as discussed in Terzieva & Herbst (2000). The rovibrational energies
denotes the rovibrational energy for a total angular momentum J. The factor 2J + 1 accounts for the degeneracy with respect to the space-fixed reference frame and g for the nuclear spin degeneracy. Additional care is required for the nuclear spin degeneracy factor when different spin states (e.g., ortho or para) are involved either in the reactants or in the products, as discussed in Terzieva & Herbst (2000). The rovibrational energies 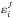 are measured relative to the corresponding zero point energy
are measured relative to the corresponding zero point energy 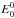 .
.
For all the species involved in the reaction considered, the rovibrational energies 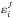 are computed by theoretical means, considering explicitly the quantum mechanical effects due to vibrational anharmonicities and rovibrational couplings. The energies
are computed by theoretical means, considering explicitly the quantum mechanical effects due to vibrational anharmonicities and rovibrational couplings. The energies 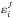 are used to evaluate the partition functions Qint of Eq. (6) for a given temperature and then to compute the equilibrium constant Ke of Eq. (2). This approach has been pursued also in Paper I.
are used to evaluate the partition functions Qint of Eq. (6) for a given temperature and then to compute the equilibrium constant Ke of Eq. (2). This approach has been pursued also in Paper I.
If the exchange proceeds through the formation of an adduct which can dissociate both backwards and forwards, we can define a total rate coefficient kT, which is often expressed as the capture rate constant, 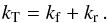 (7)We then readily have
(7)We then readily have 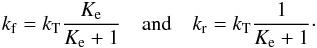 (8)Such a mechanism takes place for the isotopic exchange reaction of 13C+ with CO and isotopologues as well as for proton transfer reactions of the type
(8)Such a mechanism takes place for the isotopic exchange reaction of 13C+ with CO and isotopologues as well as for proton transfer reactions of the type 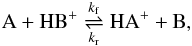 (9)where A and B are isotopologues of CO.
(9)where A and B are isotopologues of CO.
At low temperatures, the dominant term in the expression of Eq. (2) for the equilibrium constant Ke is the exponential term. Approximating Fq ≈ 1, so that Ke ≈ e ΔE/kBT, it follows that 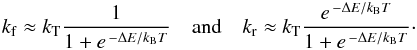 (10)The partition function factor Fq of Eq. (3) provides thus a quantitative estimate of the goodness of the approximation of Eq. (10), which is often employed in kinetic models at low temperatures.
(10)The partition function factor Fq of Eq. (3) provides thus a quantitative estimate of the goodness of the approximation of Eq. (10), which is often employed in kinetic models at low temperatures.
3. Results and discussion
All the isotopic variants of 12C, 13C, 16O, 17O, and 18O for CO, HCO+/HOC+, and DCO+/DOC+ are considered in this work. Using the global three-dimensional potential energy surface of Mladenović & Schmatz (1998) for the isomerizing system HCO+/HOC+, we calculate the rovibrational level energies for six isotopologues of HCO+ and six isotopologues of DCO+, as well as for HOC+ and DOC+. For isotopologues of CO, we employ the CCSD(T)/cc-pVQZ potential energy curve, developed previously (Mladenović & Roueff 2014). From these results, the zero point energy differences are readily determined for the proton transfer reactions of Eq. (9) involving HCO+ with CO and HOC+ with CO. The equilibrium constants Ke as a function of temperature are evaluated according to Eq. (2) for the isotope exchange reactions HCO++CO, which have already been studied experimentally (Smith & Adams 1980).
The spectroscopic properties for the isotopologues of HCO+ are summarized in Table A.1. The mode labels ν1,ν2,ν3 refer respectively to the higher-frequency (CH) stretching vibration, the bending vibration, and the lower-frequency stretching (CO) vibration, whereby the bending vibration is doubly degenerate. By fitting the calculated ground state vibrational energies obtained for 0 ≤ J ≤ 15 to the standard polynomial expression, ![\begin{equation} E_{0}(J) ~=B_0~J(J+1)-D_{0}~[J(J+1)]^2, \label{rot.ef} \end{equation}](/articles/aa/full_html/2017/09/aa31270-17/aa31270-17-eq41.png) (11)we have derived the effective rotational constant B0 and the quartic centrifugal distortion constant D0 for the ground vibrational state. The ground state vibrational correction ΔB0 to the equilibrium rotational constant Be is given by
(11)we have derived the effective rotational constant B0 and the quartic centrifugal distortion constant D0 for the ground vibrational state. The ground state vibrational correction ΔB0 to the equilibrium rotational constant Be is given by 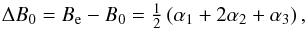 (12)where αi is a vibration-rotation interaction constant for the ith vibration (Herzberg 1991). In this expression, we substitute our Be values with the best estimate
(12)where αi is a vibration-rotation interaction constant for the ith vibration (Herzberg 1991). In this expression, we substitute our Be values with the best estimate 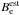 of the equilibrium rotational constant, computed employing the best estimate of the equilibrium geometry re(HC) = 1.09197 Å and re(CO) = 1.10546 Å due to Puzzarini et al. (1996). This approach yields our best estimate
of the equilibrium rotational constant, computed employing the best estimate of the equilibrium geometry re(HC) = 1.09197 Å and re(CO) = 1.10546 Å due to Puzzarini et al. (1996). This approach yields our best estimate 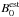 of the rotational constant for the ground vibrational state as
of the rotational constant for the ground vibrational state as 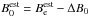 . As seen in Table A.1, all of the theoretical values for
. As seen in Table A.1, all of the theoretical values for 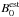 agree with the available experimental B0 values within 11 MHz. Similar accuracy can also be expected for other HCO+ isotopologues that are not yet experimentally detected. For the fundamental vibrational transitions, our theoretical results agree within 5 cm-1 with the experimental findings. In the case of the quartic centrifugal distortion constants D0, the agreement is within 4.5 kHz.
agree with the available experimental B0 values within 11 MHz. Similar accuracy can also be expected for other HCO+ isotopologues that are not yet experimentally detected. For the fundamental vibrational transitions, our theoretical results agree within 5 cm-1 with the experimental findings. In the case of the quartic centrifugal distortion constants D0, the agreement is within 4.5 kHz.
Direct proton transfer via the collinear approach from the carbon or oxygen side of CO to HCO+/HOC+ was studied in Paper 1 using the CCSD(T)/aug-cc-pVTZ electronic structure method. In all the cases analyzed there, the reaction was found to proceed through a stable intermediate proton-bound complex A-H-B+ (see Eq. (9)), such that the reaction is barrierless in this description. In the case of the reaction involving HOC+, it appears that the CO-catalyzed isomerisation is a more likely event than the proton transfer reaction, as seen in Fig. 2a of Paper 1.
3.1. Zero point energies
The ground state vibrational energies calculated in this work for isotopic variants of CO, HCO+, and HOC+ are collected in Table A.2. They are given relative to the corresponding potential energy minimum. On the potential energy surface for HCO+/HOC+, the global potential energy minimum is at −1.86 cm-1. In assembling Table A.2, we noticed that Table 1 of Paper I did not incorporate the energy shift of 1.86 cm-1 for the zero point energies of D12C16O+, D12C18O+, D13C16O+, and D13C18O+. Accordingly, we list the zero point energies for all of the isotopologues of CO, HCO+, and HOC+ in Table A.2 of this work. We note that the other results of Paper I are not affected by this misprint.
 |
Fig. 1 Relative positions of the ground state vibrational energies of six isotopologues of CO and HCO+. |
The zero point energies are graphically displayed in Fig. 1 for the isotopic 12C, 13C, 16O, 17O, and 18O variants of CO and HCO+. The largest difference ΔEmax seen there is between the zero point energies for the lightest and heaviest forms, yielding ΔEmax = 72.8 K for carbon monoxide and ΔEmax = 97.0 K for the formyl cation. The species containing 17O possess zero point energies lying between the zero point energies of the 18O and 16O forms in Fig. 1 and Table A.2.
3.2. Reactions of HCO+ and HOC+ with CO
The zero point energy differences for the proton transfer reactions CO+HCO+/HOC+ are presented in Table A.3. In accordance with the notation of Paper I, the reactions involving the formyl cation HCO+ are labeled with F and the reactions involving the isoformyl cation HOC+ with I. The deuterium variant of the reaction Fn is denoted by Fn(D), where n = 1–15, and similar for the other cases. The reactions F1-F6 involving the isotopes 16O and 18O were studied in some detail in Paper I. Inclusion of the isotope 17O leads to nine additional reactions, which are denoted by F7-F15 and similar for the other variants. A complete list of possible reactions for the isotopes H, D, 12C, 13C, 16O, 17O, and 18O is given in Table A.3. The exothermicities for the reactions F1-F6, F1(D)-F6(D), I1-I6, and I1(D)-I6(D) were already shown in Table 2 of Paper I. The proton transfer reactions I1 and I1(D) involving HOC+ were also considered by Lohr (1998).
The largest ΔE in Table A.3 is associated with the reactions F5 and F5(D) in the case of HCO+ and with the reactions I6 and I6(D) in the case of HOC+. From Table A.3, we easily deduce that 13C is preferentially placed in H/DCO+ and a heavier O in H/DOC+. The reactions involving the same isotope of C in HCO+ and CO possess smaller exothermicities than the reactions involving different C isotopes, as seen by comparing for example, reaction F3 (ΔE = 6.4 K) with reaction F5 (ΔE = 24.2 K), which involve 18O. The corresponding 17O counterparts have somewhat smaller ΔE values, for example reaction F7 of ΔE = 3.4 K versus reaction F11 of ΔE = 21.2 K. In all cases, reactions involving deuterium possess slightly higher exothermicities, for example, ΔE for reactions F15 and F15(D) are 20.8 K and 25.3 K, respectively. The reactions with the isoformyl isomers have lower exothermicities than the reactions with the formyl forms. In several cases, the reactions HOC++CO proceed in the direction opposite to the direction of the corresponding HCO++CO reaction in accordance with the fact that the isotopic substitution of the central atom is thermodynamically favored. Table A.3 clearly exemplifies this effect.
The partition function factors Fq, the isotope exchange equilibrium constants Ke, and the rate coefficients (kf,kr) for several temperatures between 5 and 300 K are given in Table A.4 for reactions F7-F15 and F7(D)-F15(D). This table complements Table 5 of Paper I, which provides analogous information for reactions F1-F6 and F1(D)-F6(D). The values of Ke are obtained using Eq. (2) by direct evaluation of the internal partition functions Qint from the computed rovibrational energies. The forward reaction kf and backward reaction kr rate coefficients are calculated according to Eq. (8) using our ΔE values of Table A.2 in combination with the total temperature dependent rate coefficients kT given by Langer et al. (1984).
In Eq. (2), Fq is a mass and temperature dependent factor, defined by Eq. (3). Its temperature dependence is due to the temperature dependence of Qint. The mass dependence of Fq comes from the translational contribution fm. In addition, the mass affects the effective rotational constants for a given vibrational state, as well as the reduced mass specifying the vibrational motion, yielding thus the mass dependent Qint. In the low temperature limit relevant for dark cloud conditions, the discrete rotational structure of the ground vibrational state provides the major contribution to Qint. For 30 reactions HCO++CO, given here in Table A.4 and before in Table 5 of Paper I, the factor Fq differs from 1 at most by 3.5%. Using Fq = 1 to compute (kf,kr) by means of Eq. (10), we obtain rate coefficients which differ by at most 4% from the values listed in Table A.4.
3.3. Analytic representations of the rate coefficients
For the reaction HCO++CO, the total rate coefficients derived by Langer et al. (1984) are available for nine temperatures: 5, 10, 20, 40, 60, 80, 100, 200, and 300 K. Using these values, the forward and backward rate coefficients are determined (see Table A.4) and fit via the popular Arrhenius-Kooij formula (Kooij 1893), 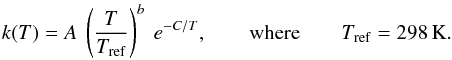 (13)
(13)
This analytical expansion has one nonlinear parameter, so that we employ a nonlinear least-squares technique (the Levenberg-Marquardt algorithm) to obtain optimum values for the fitting parameters (Press et al. 1985). The resulting values for A, b, and C are given in Table A.5. The statistical uncertainties are given as root-mean-square (rms) fitting errors, 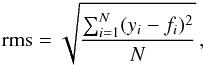 (14)
(14)
where N is the number of the known (input) data (xi,yi) fit by a function f = f(x), so that fi = f(xi).
 |
Fig. 2 Temperature dependence of the rate coefficients kT, kf, and kr obtained in the fitting procedures. |
The forward reaction rate coefficients kf and the backward reaction rate coefficients kr are fit separately since they represent elementary chemical processes. The difference between the parameters Cr for kr and Cf for kf is equal to the exothermicity for the corresponding isotopic exchange reaction, Cr−Cf = ΔE. This is easy to verify by comparing Tables A.3 and A.5. The fitting parameters in Table A.5 reproduce the values of the rate coefficients kf and kr at nine temperatures (Table A.4 of this work and Table 5 of Paper I) with rms deviations better than 2 × 10-11 cm3 s-1. Mean absolute percentage deviations are better than 4%.
The variation with temperature of the rate coefficients kf and kr obtained in the fitting procedures are graphically displayed in Fig. 2 for all 30 isotopic variants of the reaction HCO++CO. At temperatures above 50 K, kf and kr exhibit a weak temperature dependence. The forward reaction becomes faster and the backward reaction slower as the temperature decreases, so that kr tends to zero as T → 0 K. In Fig. 2, kf and kr are most different for reaction F5(D), associated with the largest ΔE value of 29.4 K in Table A.3. They are least different for reactions F9 and F10, attributed the smallest ΔE value of 3.0 K (Table A.3). The experimental results of Smith & Adams (1980) available for the reaction F1 at 80, 200, and 300 K are also shown (yellow circles).
In Fig. 2, the total rate coefficients kT (blue lines) are obtained as kf + kr for each of the 30 reactions considered. The values of Langer et al. (1984) (red circles) are additionally shown along with their estimated uncertainties (vertical bars). Even though kf and kr are noticeably different for different reactions, the resulting kT functions are similar, as expected from the model used. Our kT results for reaction F5(D) best approximate the values of Langer et al. (1984) and can be used as an analytic representation for their values if/when needed.
The estimates of Langer et al. (1984) cover temperatures between 5 and 300 K. The analytic expressions of Table A.5 are accordingly valid only over this temperature range. Since the modified Arrhenius function of Eq. (13) goes always to zero when T → 0 K, the functional representations derived for kf will also tend to zero at temperatures below 5 K. Prior to elaborating on other forms more suitable for kinetic applications close to 0 K, one may consider the inclusion in astrochemical kinetic networks of the analytic three-parameter representations for the rate coefficients kf and kr, derived here for the isotope exchange reactions HCO++CO (Table A.5).
4. Summary
In the present work, we have employed the full-dimensional quantum mechanical methods to calculate the rovibrational energies for all isotopologues of CO, HCO+, and HOC+ involving the isotopes H, D, 16O, 17O, 18O, 12C, and 13C. These results are used to derive accurate values of the exothermicities for possible isotopic exchange reactions. For the reaction of HCO+ with CO, all possible isotope fractionation variants are subsequently considered (in total 30 reactions). Values corresponding to the 17O isotope are reported for the first time. The energy defects arising for the 17O cases are found to be slightly smaller than those involved with 18O.
For each of the reactions considered, the analytic three-parameter expressions are derived for the isotopic exchange rate coefficients kf and kr. These analytic representations can straightforwardly be introduced in astrochemical kinetic models in order to better understand the isotopic chemical evolution.
For all of the isotopologues of HCO+ involving H, D, 16O, 17O, 18O, 12C, and 13C, we provide the fundamental vibrational transitions and the rotational constants. Our best estimates of the rotational constants can provide useful assistance in analyzing expected observations of the rare forms of this cation.
Acknowledgments
We thank Professor Lewerenz for critical reading of the manuscript. This work was partially supported by the French program Physique et Chimie du Milieu Interstellaire (PCMI) funded by the Conseil National de la Recherche Scientifique (CNRS) and Centre National d’Études Spatiales (CNES).
References
- Amano, T. 1983, J. Chem. Phys., 79, 3595 [NASA ADS] [CrossRef] [Google Scholar]
- Bensch, F., Pak, I., Wouterloot, J. G. A., Klapper, G., & Winnewisser, G. 2001, ApJ, 562, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, P. B., & Rothwell, W. J. 1984, J. Chem. Phys., 81, 5239 [NASA ADS] [CrossRef] [Google Scholar]
- Dore, L., Cazzoli, G., & Caselli, P. 2001a, A&A, 368, 712 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dore, L., Puzzarini, C., & Cazzoli, G. 2001b, Can. J. Phys., 79, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, S. C., McKeller, A. R. W., & Sears, T. J. 1984, J. Chem. Phys., 81, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., & Langer, W. D. 1981, J. Chem. Phys., 74, 6990 [NASA ADS] [CrossRef] [Google Scholar]
- Guélin, M., Cernicharo, J., & Linke, R. A. 1982, ApJ, 263, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, P., Kraemer, W. P., & Diercksen, G. H. F. 1977, Internal Report, MPI/PAE Astro 135, Max-Planck Institut, München [Google Scholar]
- Herzberg, G. 1991, Molecular Spectra & Molecular Structure Vol. II, Infrared and Raman Spectra of Polyatomic Molecules (corrected reprint of 1945 edition) (Malabar FL: Krieger) [Google Scholar]
- Hirota, E., & Endo, Y. 1988, J. Mol. Spectr., 127, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Kooij, D. M. 1893, Zeitschr. Phys. Chemie B, 12, 155 [Google Scholar]
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H.-K., Zhang, J.-S., Liu, Z.-W., et al. 2016, RA&A, 16, 047 [Google Scholar]
- Lohr, L. L. 1998, J. Chem. Phys., 108, 8012 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, I., Cvitaš, T., Homann, K., Kallay, N., & Kuchitsu, K. 1993, Quantities, Units and Symbols in Physical Chemistry, 2nd edn. (Oxford: Blackwell Scientific Publications) [Google Scholar]
- Mladenović, M. 2002, Spectrochim. Acta, Part A, 58, 795 [CrossRef] [Google Scholar]
- Mladenović, M., & Bačić, Z. 1990, J. Chem. Phys., 93, 3039 [NASA ADS] [CrossRef] [Google Scholar]
- Mladenović, M., & Roueff, E. 2014, A&A, 566, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mladenović, M., & Schmatz, S. 1998, J. Chem. Phys., 109, 4456 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1985, Numerical Recipes, Example Book (Fortran) (Cambridge: Cambridge University Press) [Google Scholar]
- Puzzarini, C., Tarroni, R., Palmieri, P., Carter, S., & Dore, L. 1996, Mol. Phys., 87, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmatz, S., & Mladenović, M. 1997, Ber. Bunsenges. Phys. Chemie, 101, 372 [CrossRef] [Google Scholar]
- Smith, D., & Adams, N. G. 1980, ApJ, 242, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Su, T., & Bowers, M. T. 1975, Int. J. Mass. Spec. Ion. Phys., 17, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J. S., Sun, L. L., Riquelme, D., et al. 2015, ApJS, 219, 28 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tables
Computed anharmonic fundamental vibrational transitions νi (in cm-1), estimated ground state vibrational corrections ΔB0 (in MHz), best estimates of the rotational constant 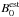 (in MHz), and quartic centrifugal distortion rotational constants D0 (in kHz) for the isotopologues of HCO+.
(in MHz), and quartic centrifugal distortion rotational constants D0 (in kHz) for the isotopologues of HCO+.
Zero point vibrational energies (in cm-1) of the isotopologues of CO, HCO+, and HOC+.
Zero point energy differences ΔE between the reactants and products for the isotope fractionation reactions of H/DCO+ and H/DOC+ with CO.
Equilibrium constants Ke, partition function factors Fq, and rate coefficients kf,kr (in 10-10 cm3 s-1) for the reactions of H/DCO+ with CO involving the isotope 17O.
Fitting parameters A (in 10-10 cm3 s-1), b, and C (in K) for the forward rate coefficients kf and the reverse rate coefficients kr for the reactions of HCO+ with CO.
All Tables
Computed anharmonic fundamental vibrational transitions νi (in cm-1), estimated ground state vibrational corrections ΔB0 (in MHz), best estimates of the rotational constant 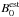 (in MHz), and quartic centrifugal distortion rotational constants D0 (in kHz) for the isotopologues of HCO+.
(in MHz), and quartic centrifugal distortion rotational constants D0 (in kHz) for the isotopologues of HCO+.
Zero point vibrational energies (in cm-1) of the isotopologues of CO, HCO+, and HOC+.
Zero point energy differences ΔE between the reactants and products for the isotope fractionation reactions of H/DCO+ and H/DOC+ with CO.
Equilibrium constants Ke, partition function factors Fq, and rate coefficients kf,kr (in 10-10 cm3 s-1) for the reactions of H/DCO+ with CO involving the isotope 17O.
Fitting parameters A (in 10-10 cm3 s-1), b, and C (in K) for the forward rate coefficients kf and the reverse rate coefficients kr for the reactions of HCO+ with CO.
All Figures
 |
Fig. 1 Relative positions of the ground state vibrational energies of six isotopologues of CO and HCO+. |
| In the text | |
 |
Fig. 2 Temperature dependence of the rate coefficients kT, kf, and kr obtained in the fitting procedures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


