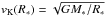| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201730847 | |
| Published online | 01 September 2017 | |
The vertical structure of the boundary layer around compact objects
Institut für Astronomie und Astrophysik, Abt. Computational Physics, Auf der Morgenstelle 10, 72076 Tübingen, Germany
e-mail: marius.hertfelder@gmail.com
Received: 22 March 2017
Accepted: 10 May 2017
Context. Mass transfer due to Roche lobe overflow leads to the formation of an accretion disk around a weakly magnetized white dwarf (WD) in cataclysmic variables. At the inner edge of the disk, the gas comes upon the surface of the WD and has to get rid of its excess kinetic energy in order to settle down on the more slowly rotating outer stellar layers. This region is known as the boundary layer (BL).
Aims. In this work we investigate the vertical structure of the BL, which is still poorly understood. We shall provide details of the basic structure of the two-dimensional (2D) BL and how it depends on parameters such as stellar mass and rotation rate, as well as the mass-accretion rate. We further investigate the destination of the disk material and compare our results with previous one-dimensional (1D) simulations.
Methods. We solve the 2D equations of radiation hydrodynamics in a spherical (r-ϑ) geometry using a parallel grid-based code that employs a Riemann solver. The radiation energy is considered in the two-temperature approach with a radiative flux given by the flux-limited diffusion approximation.
Results. The BL around a non-rotating WD is characterized by a steep drop in angular velocity over a width of only 1% of the stellar radius, a heavy depletion of mass, and a high temperature (~500 000 K) as a consequence of the strong shear. Variations in Ω∗,M∗, and Ṁ influence the extent of the changes of the variables in the BL but not the general structure. Depending on Ω∗, the disk material travels up to the poles or is halted at a certain latitude. The extent of mixing with the stellar material also depends on Ω∗. We find that the 1D approximation matches the 2D data well, apart from an underestimated temperature.
Key words: accretion, accretion disks / hydrodynamics / methods: numerical / white dwarfs / binaries: close
© ESO, 2017
1. Introduction
Accretion of matter onto a non-magnetized star is accompanied by the formation of a boundary layer (BL) where the Keplerian rotation rate of the disk smoothly connects to the stellar rotation rate, that is, in general, much smaller. In the BL, up to ~ 50% of the total accretion luminosity is liberated in a spatially very confined region. In this publication we focus on the BL around a white dwarf (WD) that resides in a cataclysmic variable (CV) system. The BL around a WD typically has a radial extent of ≲ 1% of the stellar radius (Lynden-Bell & Pringle 1974; Hertfelder et al. 2013). The extent of the energy released in the BL depends on the rotation rate of the WD. When the gas enters the BL from the outer parts of the disk, it gradually gets rid of one half of the accretion energy during its inward drift through the disk. The other half of the energy gained by falling into the gravitational potential of the star is stored in terms of kinetic energy. The difference of the kinetic energy at this point and on the surface of the star of each gas particle is liberated in the BL and radiated away in the form of soft and hard X-ray and UV emission (e.g., Cordova et al. 1981a,b; Cordova & Mason 1984). Therefore, the slower the star spins, the higher the energy output of the BL. Apart from the stellar mass and radius, another parameter that heavily influences the radiation characteristics of the BL is the mass-accretion rate Ṁ, which can vary over a wide range for CVs. If it is relatively low, Ṁ ≤ 10-10M⊙/ yr (Warner 1987), the BL is optically thin and very high temperatures of the order 108 K are reached, resulting in soft and hard X-ray emission (e.g., Mukai & Patterson 2004; Pandel et al. 2003, 2005; King & Shaviv 1984; Shaviv 1987; Narayan & Popham 1993; Popham 1999). Higher mass-accretion rates lead to optically thick BLs with lower temperatures of about 105 K (Pringle 1977; Syunyaev & Shakura 1986; Popham & Narayan 1995) in which case the radiation is mostly thermalized (see e.g., Cordova et al. 1980; Mauche 2004).
From a numerical point of view, the BL problem has initially been approached by timescale estimates and stationary calculations (Lynden-Bell & Pringle 1974; Pringle 1977; Tylenda 1977, 1981; Pringle & Savonije 1979; Regev 1983). With increasing computational power, evolutionary simulations became viable and made the investigation of the temporal evolution and non-stationary phenomena possible (Robertson & Frank 1986; Kley & Hensler 1987; Kley 1989a,b, 1991). Godon et al. (1995) performed one-dimensional simulations, where axial symmetry is assumed and the equations are integrated over the vertical (z) direction. This procedure is known as the thin-disk approach and provides a good first approximation for the BL problem. In a previous paper series we performed (one-dimensional) 1D simulations including vertical cooling, radiation transport, and the treatment of the radiation energy, and calculated detailed emergent spectra from these models (Hertfelder et al. 2013; Suleimanov et al. 2014).
In this paper we consider the problem in two-dimensional (2D) spherical coordinates. As in the 1D case, we still assume axisymmetry in order to get rid of the ϕ-coordinate. We conduct full radiation hydrodynamics simulations, where the radiation energy is treated in the two-temperature approximation (Kuiper et al. 2010; Commerçon et al. 2011), which means that an additional evolutionary equation for the radiation energy is considered. Since the BLs we study here are mostly optically thick, we employ the flux-limited diffusion approximation (Levermore & Pomraning 1981; Levermore 1984) for the radiative flux. We use realistic boundary conditions with a vertically spread mass inflow at the outer edge of the simulation domain (disk) and a sophisticated initial model, which is constructed from different 1D codes (see Sect. 3.2). Our studies are hence related to the work by Kley (1989a,b, 1991) but can span much longer dynamic timescales and feature a much higher resolution due to the parallel code and the available computing power. Multidimensional simulations of the BL have also been done by Fisker & Balsara (2005), Fisker et al. (2006), although only for the adiabatic case, or Balsara et al. (2009), who used a simplified energy dissipation function without radiation transport. Kley & Lin (1996, 1999) also did full radiation hydrodynamics simulations for protostars and studied the evolution of FU Orionis outbursts in protostellar disks, and Babkovskaia et al. (2008) studied the BL around neutron stars in low-mass X-ray binaries. Magnetic fields have been included in 2D by Küker et al. (2003) and in three dimensions (3D) by Armitage (2002). In both cases, however, only low resolution and short dynamical timescales have been presented. Romanova et al. (2012), for example, performed 3D magnetohydrodynamical simulations and also considered magnetospheric accretion but did not include radiation transport.
Simulations in the disk plane have been performed by Belyaev et al. (2012, 2013a,b), Hertfelder & Kley (2015), Philippov et al. (2016), Belyaev (2017) in order to investigate the transport of mass and angular momentum (AM) in the BL. Since it has been shown that due to the increase of the angular velocity Ω with radius, the magnetorotational instability (MRI, Velikhov 1959; Chandrasekhar 1960) is ineffective in the BL (Godon 1995; Abramowicz et al. 1996; Pessah & Chan 2012), alternative concepts are currently being looked into. A promising candidate is the AM transport by acoustic waves excited by the sonic instability (Glatzel 1988; Belyaev & Rafikov 2012).
A different approach to describe the interface between the star and the disk was pursued by Inogamov & Sunyaev (1999, 2010) who introduced the concept of the spreading layer (SL). The SL is a 1D, vertical approximation for the deceleration of disk material on the stellar surface, which is connected to the disk by a 2D transition region. The main difference with the radial BL model is, that the rotating gas is spread on the star where it is then decelerated by turbulent interaction with colder stellar layers beneath it. As a consequence, the SL radiation emerges from two rings on the northern and southern hemisphere of the star. This concept was originally developed for neutron stars and later adapted to WDs in CVs (Piro & Bildsten 2004b,a). (Suleimanov & Poutanen 2006) extended the model for the effects of general relativity and different chemical compositions of the accreted matter.
In this publication, we want to study the vertical structure and the long-term evolution of the BL around a WD. A high resolution is employed in order to monitor the polar spreading and mixing of the disk material on the stellar surface. We decipher whether or not the results show indications of a SL and compare the midplane profiles with 1D simulations as presented in Hertfelder et al. (2013).
The paper is organized as follows. In Sect. 2 we present the basic physical model and list the equations used for production and postprocessing. Section 3 is dedicated to the numerical background of our work. We describe the code, boundary and initial conditions and how we constructed the models, which are shown and detailed in Sect. 4. We finish with Sect. 5, where we discuss the results and come to a conclusion.
2. Physics
In this section, we present the physical foundations for the simulations we have performed and that are described later in this publication. In order to investigate the vertical structure of the BL we use the Navier-Stokes equations in spherical coordinates (r, ϑ, ϕ) and assume symmetry in the azimuthal direction. We therefore drop all derivatives with respect to the azimuthal coordinate ϕ but do hold on to the momentum equation in the corresponding direction.
2.1. Vertical structure equations
The conservation of mass is represented by the continuity equation, which is given by 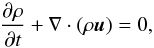 (1)where ρ and u = (ur,uϑ) are the gas density and velocity, respectively. The equations for the momentum conservation are conveniently expressed in terms of the physically conserved quantities s, g, and h. We therefore introduce the radial momentum density s = ρur, the polar momentum density g = ρruϑ and the angular momentum density h = ρruϕsinϑ = Ωr2sin2ϑ. With regards to these variables, the momentum equations read
(1)where ρ and u = (ur,uϑ) are the gas density and velocity, respectively. The equations for the momentum conservation are conveniently expressed in terms of the physically conserved quantities s, g, and h. We therefore introduce the radial momentum density s = ρur, the polar momentum density g = ρruϑ and the angular momentum density h = ρruϕsinϑ = Ωr2sin2ϑ. With regards to these variables, the momentum equations read 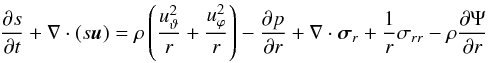 (2)for the radial direction,
(2)for the radial direction, 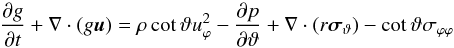 (3)for the polar direction and
(3)for the polar direction and 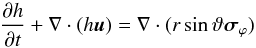 (4)for the azimuthal direction. In the above equations p denotes the gas pressure
(4)for the azimuthal direction. In the above equations p denotes the gas pressure 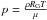 , where
, where 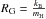 with Boltzmann’s constant kB and the mass of hydrogen mH, T is the gas temperature and μ is the mean molecular weight.
with Boltzmann’s constant kB and the mass of hydrogen mH, T is the gas temperature and μ is the mean molecular weight. 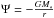 is the gravitational potential and G and M∗ are the gravitational constant and the mass of the star, respectively.
is the gravitational potential and G and M∗ are the gravitational constant and the mass of the star, respectively.
The viscous stress tensor is denoted by σ and can be displayed in a coordinate-system-independent way by means of the covariant formulation 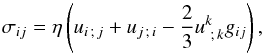 (5)where um ; n and
(5)where um ; n and 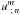 are the co- and contravariant derivative of the mth component of the velocity with respect to n, while gij is the metrical tensor of the coordinate system and η is the dynamic viscosity. We note that Eq. (5) gives the covariant components of the stress tensor that have to be translated to physical components by employing the metric coefficients. The same applies for the co- and contravariant formulation of the velocity. For details of this procedure as well as an insight into tensor calculus we refer the interested reader to classical textbooks such as Arfken & Weber (2005) or Mihalas & Mihalas (1984). The latter book also contains a summary of the individual physical components of σ in spherical coordinates. The vector representations of the stress tensor in Eqs. (2)−(4) are given by σr = (σrr,σrϑ,σrϕ) (σϑ and σϕ similarly) and the divergence is calculated accordingly.
are the co- and contravariant derivative of the mth component of the velocity with respect to n, while gij is the metrical tensor of the coordinate system and η is the dynamic viscosity. We note that Eq. (5) gives the covariant components of the stress tensor that have to be translated to physical components by employing the metric coefficients. The same applies for the co- and contravariant formulation of the velocity. For details of this procedure as well as an insight into tensor calculus we refer the interested reader to classical textbooks such as Arfken & Weber (2005) or Mihalas & Mihalas (1984). The latter book also contains a summary of the individual physical components of σ in spherical coordinates. The vector representations of the stress tensor in Eqs. (2)−(4) are given by σr = (σrr,σrϑ,σrϕ) (σϑ and σϕ similarly) and the divergence is calculated accordingly.
The equation for the conservation of energy is given by 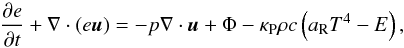 (6)where e = ρε = ρcVT is the internal energy of the gas (ε and cV are the specific internal energy and heat capacity, respectively), and Φ is the viscous dissipation function which relates to the stress tensor via
(6)where e = ρε = ρcVT is the internal energy of the gas (ε and cV are the specific internal energy and heat capacity, respectively), and Φ is the viscous dissipation function which relates to the stress tensor via 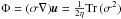 (see e.g., Mihalas & Mihalas 1984). The last term in brackets on the right-hand side of equation Eq. (6) accounts for the heating and cooling through the energy exchange between the gas and the radiation field due to emission and absorption processes, and E denotes the radiation energy density, which is also evolved in time in our model. The according equation reads:
(see e.g., Mihalas & Mihalas 1984). The last term in brackets on the right-hand side of equation Eq. (6) accounts for the heating and cooling through the energy exchange between the gas and the radiation field due to emission and absorption processes, and E denotes the radiation energy density, which is also evolved in time in our model. The according equation reads: 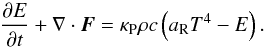 (7)Here, F is the radiative flux and κP,c, and aR are the Planck mean opacity, the speed of light, and the radiation constant. The approach that incorporates two coupled equations for the gas energy (6) and the radiation energy density (7), respectively, is called the two-temperature approximation (Kuiper et al. 2010; Commerçon et al. 2011).
(7)Here, F is the radiative flux and κP,c, and aR are the Planck mean opacity, the speed of light, and the radiation constant. The approach that incorporates two coupled equations for the gas energy (6) and the radiation energy density (7), respectively, is called the two-temperature approximation (Kuiper et al. 2010; Commerçon et al. 2011).
In order to close the set of equations, we need an assumption for the radiative flux F. Here we use the flux-limited diffusion approximation (Levermore & Pomraning 1981; Levermore 1984, FLD) where the radiative flux is given by 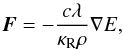 (8)with the Rosseland mean opacity κR and the flux limiter λ. The flux limiter mediates between optically thick regions, where radiation and matter are in thermal equilibrium, and optically thin regions, where photons can travel much farther before they interact with matter. In our simulations we utilize the formulation of the flux limiter given by Minerbo (1978) where λ is calculated by
(8)with the Rosseland mean opacity κR and the flux limiter λ. The flux limiter mediates between optically thick regions, where radiation and matter are in thermal equilibrium, and optically thin regions, where photons can travel much farther before they interact with matter. In our simulations we utilize the formulation of the flux limiter given by Minerbo (1978) where λ is calculated by 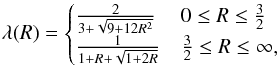 (9)with
(9)with 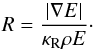 (10)The Rosseland mean opacity is further determined following Kramer’s law,
(10)The Rosseland mean opacity is further determined following Kramer’s law, 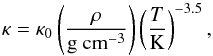 (11)where κ0 = 5 × 1024 cm2 g-1, which we also use for the Planck mean opacity (see also Bitsch et al. 2013). As a lower threshold, we consider a constant opacity κThomson = 0.4 cm2 g-1 which accounts for free-electron scattering processes at very high temperatures (Thomson scattering).
(11)where κ0 = 5 × 1024 cm2 g-1, which we also use for the Planck mean opacity (see also Bitsch et al. 2013). As a lower threshold, we consider a constant opacity κThomson = 0.4 cm2 g-1 which accounts for free-electron scattering processes at very high temperatures (Thomson scattering).
2.2. Viscosity
As has been discussed in Sect. 1, the driving mechanism for angular momentum transport in the BL is still a matter of ongoing research. We do not yet have a suitable prescription to implement the wave-mediated AM transport in the equations of hydrodynamics without directly simulating it. This, however, is not feasible for the kind of simulations presented in this publication, considering the huge demand of computational resources for highly resolved, three dimensional radiation hydrodynamics simulations (see e.g., Hertfelder & Kley 2015). We therefore employ the classic α-prescription by Shakura & Sunyaev (1973), which considers turbulent stresses in the accretion disk responsible for the observed AM transport and parametrizes them according to 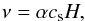 (12)where ν = η/ρ is the kinematic viscosity and
(12)where ν = η/ρ is the kinematic viscosity and 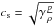 is the sound speed. H is a length scale that stands for the maximum eddy size of the turbulence. We define it according to Papaloizou & Stanley (1986):
is the sound speed. H is a length scale that stands for the maximum eddy size of the turbulence. We define it according to Papaloizou & Stanley (1986):  (13)By employing Eq. (13) for the length scale, we account for the fact that in the BL the radial pressure scale height Hr becomes smaller than the vertical one. The relations for the scale heights read
(13)By employing Eq. (13) for the length scale, we account for the fact that in the BL the radial pressure scale height Hr becomes smaller than the vertical one. The relations for the scale heights read 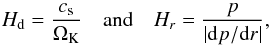 (14)where
(14)where 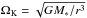 is the Keplerian angular velocity. Inside the star, which is included, to a lesser extent, in our simulations, we apply a constant small viscosity νconst = 1012 cm2/ s. In the low-density region above the disk, no viscous heating occurs.
is the Keplerian angular velocity. Inside the star, which is included, to a lesser extent, in our simulations, we apply a constant small viscosity νconst = 1012 cm2/ s. In the low-density region above the disk, no viscous heating occurs.
2.3. One-dimensional disks and stellar structure equations
In Sect. 3 we describe in detail the workflow we used in order to create the vertical models of the BL. Apart from the actual 2D simulations, the initial conditions also involve 1D disk profiles as well as a simple representation of the star. The underlying equations shall be presented here in short.
The 1D disk profiles are created using the thin disk approximation where the Navier-Stokes equations are vertically integrated and azimuthal symmetry is assumed. The 3D equations are thus reduced to depend only on the time t and the cylindrical radius R = rsinϑ. The mass density ρ is replaced by the surface density Σ during the vertical integration. Since a Gaussian profile is assumed for the vertical density stratification of the disk, we can recalculate the midplane mass density from the results of the 1D simulations and approximate the vertical density and temperature structure. The equations of the slim disk approach and details about the code we used to obtain the 1D profiles can be found in Hertfelder et al. (2013).
The outermost layers of the star are obtained from the radial hydrostatic equilibrium and flux conservation: Here, F = Frad + Fconv is the stellar flux, which consists of a radiative and a convective part, T∗ is the effective temperature of the star (i.e., T at the optical depth τ = 1) and σSB is the Stefan-Boltzmann constant. All other quantities are identical to the ones described earlier. We neglect the convective flux in Eq. (16) since we found that it is sufficient to only use the radiative flux to obtain a robust starting model for the star that can be plugged into the full 2D simulation. The two stellar structure equations are coupled ordinary differential equations that can be solved for ρ(r) and T(r). The radius of the star R∗ is determined from the mass-radius relation for WDs by Nauenberg (1972).
3. Numerics
3.1. General remarks
We mainly used the code PLUTO (Mignone et al. 2007) for the simulations presented in this publication. In PLUTO, the conservation laws Eqs. (1), (2)–(4), (6) are discretized on a static grid using the finite volume (FV) formalism where volume averages evolve in time. A high-resolution shock-capturing (HRSC) scheme is applied, with the algorithm being based on a reconstruct–solve–average (RSA) strategy. This means, that the variables are interpolated to the cell interfaces where subsequently a Riemann problem is solved for the two discontinuous states. Finally, the system is evolved in time using the fluxes computed by the Riemann solver. In order to approximate the variables at the cell interfaces, we used the piecewise parabolic method (PPM, 5th order), which is known to handle curvilinear coordinates and non-uniform grid spacing more correctly than other implemented methods1. The code retains a global 2nd-order accuracy as fluxes are computed at the interface midpoints. PLUTO offers a variety of slope limiters for the reconstruction step that differ in diffusivity. We have found that for our problem it is adept to start with a more diffusive limiter (minmod-limiter) and switch to the least diffusive monotonized central difference limiter (MC-limiter) once the simulation converges to the equilibrium. The Riemann problem is solved using the approximative HLLC solver, which is a Harten, Lax, Van Leer method that also considers the contact discontinuity. Finally, a dimensionally unsplit third-order TVD Runge-Kutta scheme with a variable time step based on the Courant-Friedrichs-Lewy condition (Courant et al. 1928) is employed for the temporal integration. The code has been tested and used extensively for a variety of applications2.
Since we also considered the evolution of the radiation energy density (Eq. (7)), we made use of the additional module by Kolb et al. (2013). Here, an additional step is performed after the non-radiative part has been accomplished. In this step, the radiation energy is solved together with the corresponding absorption-emission term in the gas energy equation. This results in a system of two coupled differential equations (see also Commerçon et al. 2011). Since radiation processes typically happen on much shorter timescales than hydrodynamical processes, an explicit treatment of these equations would confine the time step severely and render the method impractical. Therefore, an implicit scheme is applied to handle the radiative part. The resulting system of equations, which is partially linearized following Commerçon et al. (2011), is solved using the matrix solver from the PETSc library. For our problem, the improved stabilized version of the biconjugate gradient squared method (KSPIBCGS) in connection with a block jacobian or hypre preconditioner has turned out to be a fast and reliable combination. A variety of tests have been performed in order to confirm the correctness of the implementation and applicability of the method (Kolb et al. 2013). Due to the fact that the radiation module as described above can only handle 3D problem setups, we have modified it to support one and two dimensions, as well, and have redone the test cases.
3.2. Initial conditions
During the preparations and the first runs we noticed that PLUTO is quite susceptible to crashes due to negative density or pressure. In the BL problem, large density contrasts appear between the star-disk system and the virtually empty space above the disk, where high radial infall velocities are reached. However, the closer the initial model3 matches the equilibrium state, the more stable the simulations are. Thus, we developed a strategy where we build the full problem step by step from smaller subproblems and perpetually construct initial models from the results of the preceding step. We outline this approach below:
We begin by constructing the very outer layers of the star. For that purpose the stellar structure Eqs. (15), (16) are solved for ρ(r) and T(r) using a fourth-order Runge-Kutta integrator. The integration starts at r = 1 and is performed outwards. The initial density ρ(r = 1) is varied until we obtain T = T∗ at optical depth τ = 1. Then, the integration starts at r = 1 again and is performed inwards. The simulation domain of the star spans [0.99,1.01] and a large number of grid cells is needed due to the large gradients.
The following step entails calculating a radial 1D profile for the disk; we use our self-developed code, which solves the partial differential equations on a fixed Eulerian, staggered grid using a semi-implicit-explicit time stepping scheme with operator splitting (see also Stone & Norman 1992). In contrast to the simulations performed in Hertfelder et al. (2013) we do not simulate the BL, but only the disk for this step. Therefore we shift the inner boundary to r = 1.1 and require the azimuthal velocity to be Keplerian while we impose zero-gradient boundary conditions for all other variables. The outer boundary resides at r = 5 and the BCs remain unchanged. After the 1D disk has reached its equilibrium state we switch to the PLUTO code, load in the 1D profiles and extrapolate them by using a Gaussian vertical stratification. The disk simulation is now 2D with a domain that spans from ϑ = 0 to π/ 2. We run the PLUTO code until the 2D disk has reached a stationary state.
Finally, we join together the ingredients mentioned above. The domain now ranges from 0.99 to 5 in radius with 1118 logarithmically spaced grid cells and from 0 to π/ 2 with 1000 grid cells in polar angle. The number of cells has been chosen such that each cell is approximately quadratic. The stellar structure model and the 2D disk are loaded in and the small region [1,1.1] in radius that has no yet been simulated is simply extrapolated from the disk. In this region, the BL starts to build immediately after starting the full 2D simulation.
We have chosen the aforementioned procedure since it minimizes the time effort and maximizes the chances for a successful run without crashes. Another obvious way to pursue would be to simulate 1D BL profiles and attach these to the star and extend them to 2D. This approach is, however, much more time consuming and the initial model is less stable.
3.3. Boundary conditions and density floor
At the outer boundary at r = 5, mass is continuously entering the domain, representing the mass flux Ṁ through the disk. Numerically this is accomplished by manipulating the flux into the outermost active cells that is actually calculated by the Riemann solver. We spread the mass influx over a vertical extent assuming a Gaussian profile whose width is determined through the disk height that comes out of the 1D disk simulation. The influx is realized such that the mass-accretion rate Ṁ is a simple runtime input parameter. The inflowing matter further receives an azimuthal momentum so that uϕ matches the Keplerian velocity at the outer boundary. The radiation energy density at the outer boundary is fixed at a value corresponding to T = 100 K. In the disk, we impose a no-flux condition since the radial transport is very small. The other quantities are implemented with zero-gradient BCs. Above the disk, the outer radial boundary is closed to prevent additional mass from falling in.
The inner boundary at r = 0.99 is a rigid wall where the radial and polar velocities equal zero. The azimuthal velocity is implemented as an input parameter so we can easily change the rotation rate of the star Ω∗. For the radiation energy density, the radiative flux of the star at the inner domain edge is used as a boundary condition. All other variables are again implemented using zero-gradient or Neuman-type boundary conditions, which means that the normal derivative at the boundary vanishes. At the polar axis (ϑ = 0) and in the equatorial plane (ϑ = π/ 2) we apply symmetry conditions (vanishing gradients) as boundary conditions.
We apply a lower threshold for the density of 5 × 10-14 g / cm3, which is approximately ten orders of magnitude smaller than the disk midplane density. It is effective in the empty area above the disk and prevents negative densities due to infalling material. The density floor, however, also causes a flat density structure in this region. Along with the small radiation energy density above the disk, the computation of the flux-limiter becomes inaccurate and flux barriers develop that prevent the cooling of the disk. Since this process is unphysical, we reset the flux-limiter to 1 / 3 in areas of low ρ and E in order to maintain a radiative flux towards the domain boundary. Since the ambient region is dynamically unimportant due to its low density, this intervention does not affect the validity of the model.
3.4. Model parameters
In this publication, we are interested in the structure of the BL around a weakly magnetized WD, a situation that is frequently found in CV systems. White dwarf in CVs typically have masses in the range of one solar mass and effective temperatures of T∗ ~ 50 000 K (e.g., Sion et al. 2010, for SS Cygni). We leave the effective temperature fixed at 50 000 K. The radial scale height of the star grows with T∗ and it is easier to simulate a star with a larger scale height since a lower resolution may be chosen. The mass of the WD, on the other hand, is one parameter that we have varied during our research. Analogous to Hertfelder et al. (2013), we considered three masses, M∗ = 0.8 M⊙, 1.0 M⊙ and 1.2 M⊙. Alongside the mass, the radius of the WD is the crucial parameter that determines the strength of the gravitational pull. We used the mass-radius relation from Nauenberg (1972) in order to calculate R∗, which, for instance, yields R∗ ≈ 5.6 × 108 cm for M∗ = 1.0 M⊙. An equatorial radius increase for rapidly rotating WDs is automatically taken into account in the simulations. The WD rotation rate Ω∗ itself is an important parameter that we vary from 0.0ΩK (non-rotating) up to 0.9ΩK for fast rotating stars. Ω∗ determines the amount of kinetic energy that the gas loses before meeting the star and therefore the total luminosity of the BL. The last parameter that we modify is the mass-accretion rate Ṁ , which can comprise several orders of magnitude in CVs. We consider mass-accretion rates of Ṁ = (10-8−10-10) M⊙/ yr. Furthermore, we took α = 0.01 for the viscosity parameter and γ = 5 / 3 (monoatomic ideal gas) for the adiabatic index. The gas is assumed to consist of completely ionized hydrogen, so we adopt μ = 0.5 for the mean molecular weight.
4. Results
4.1. The basic structure of the 2D BL
We begin the presentation of the results by discussing the general structure and basic properties of the 2D BL. For this purpose we adopt the parameter set of M∗ = 0.8 M⊙,Ṁ = 10-8M⊙/ yr,Ω∗ = 0.0ΩK as our reference model which serves as the starting point for our analysis. The measured mass-accretion rate of the reference model is nearly constant throughout the domain. The maximum deviation from the imposed value is below 10%. This also applies to the simulations mentioned later in the text. Typically the models reach a state where the general flow structure remains steady after some tens of orbits. It does, however, take a few hundred orbits for the temperature to settle down to the equilibrium value and for the mass-accretion rate to exactly match the imposed value. All models presented in this paper are virtually in a steady state.
 |
Fig. 1 Density (a) and temperature (b) for the reference model as a function of radius r and vertical coordinate z in cgs units at orbit 688. Contour lines for the levels (0.8,5,10,20,30) × 10-6 g / cm3 are overlaid in the plot of the density a). The white line in panel b denotes the points where the optical depth is unity, τ = 1. |
The thermal structure of the BL after 688 orbits is illustrated in Fig. 1 with the mass density ρ on the left hand side (a) and the temperature T on the right hand side (b). Additional contour lines are added to panel (a) in order to clarify the structure of the disk. We first discuss the density structure of the reference model. A heavy depletion of mass is observed directly in front of the stellar equator and the density decreases by approximately two orders of magnitude compared to the disk. This region, which connects the disk with the stellar surface, is called the BL. Due to the decreasing density and increasing infall velocity, it resembles a bottleneck where matter has to go through before it can come to rest on the star. At the surface of the star, the density rises rapidly with decreasing distance from the center and is several orders of magnitude larger than in the disk, which begins on the other side of the BL. The density in the disk is highest in the equatorial plane and decreases like a Gauss function in the vertical direction until it reaches the density floor. This area is represented in the plot by the dark blue color-coding. The gas from the disk accumulates in an equatorial shell around the star, which is barely visible since it is very thin. This is an indication for efficient radiative cooling of the gas that is heated up in the BL. The thin layer of disk material floats on the stellar surface and slowly spreads towards the poles. After almost 700 orbits it reaches a latitude of ~ 35° and continues to crawl towards the pole. One orbit is given by the time needed for a point on the stellar surface to make a full rotation, T = 2π/ ΩK(R∗) ≈ 11.5 s.
 |
Fig. 2 Radiation energy density E of the reference model in g / (cm s2) as a function of radius and height for the inner part of the accretion disk at orbit 688. The arrows denote the direction of the radiative flux as specified in Eq. (8). |
The temperature distribution of the gas is visualized in Fig. 1b. The main feature is the peak in the equatorial plane at r ≈ 1 with a temperature of almost 550 000 K. It is the consequence of the strong shearing in the BL due to the abrupt drop of the angular velocity. The shearing component of the stress tensor is the dominant part for the dissipation, and the heat production is proportional to the square of the shear. At the maximum of the angular velocity at r = 1.0065, the shear vanishes since the gradient is zero, ∂Ω /∂r = 0 (zero-torque point). Thus the heat production declines for greater radii r ≳ 1 before it rises again in the accretion disk. This minimum of T is visible at r ≈ 1.1 in the equatorial plane in Fig. 1b. The location of the minimum does, however, not coincide with the zero-torque point because of the transport of energy mainly through radiation. Moreover, the cooling rate strongly depends on the density, which changes drastically in this region and thus also influences the temperature distribution. Another important point is that due to the high radial velocities in this area, the components σrr and σϕϕ also become important concerning the heat production. It is therefore a complex interplay of several factors that arranges the temperature here. In the disk, beyond r = 1.1, the midplane temperature increases again because of the ever-present shear of a differentially rotating accretion disk. It peaks at r = 1.51 and T = 495 857 K and decreases again for larger radii with a slope approximately proportional to r− 1 / 2 due to the influence of the BL. For larger radii r ≫ 1, T approaches the r− 3 / 4 variation of the standard disk solution. In the vertical direction, the disk can cool efficiently and hence the temperature drops rapidly to a few thousand K. The temperature of the low-density material above the disk decreases with radius.
 |
Fig. 3 Panel a: Density as shown in Fig. 1 as an orientation for the over plotted velocity vectors. The color-bar indicates the absolute value of the velocity of each vector in units of vK(R∗). Only the radial and polar component of the velocity vector have been taken into account. Panel b: Angular velocity Ω = uϕ/r (blue) and the radial velocity ur (red) in the equatorial plane as a function of the radius r. The y-axis on the left-hand side refers to Ω and the y-axis on the right-hand side refers to ur. All velocities are normalized to the Keplerian (angular) velocity at the surface of the star, |
The radiation energy density E shows the same features as the gas temperature since the medium is mainly optically thick in the disk and BL. The energy dissipation in the BL also leads to a drastic increase in radiation energy density. In addition to E, Fig. 2 visualizes the radiative flux F which is computed according to Eq. (8). At around r ≈ 1.1 there is also a minimum in E that lies between the BL and the disk in the equatorial plane. Due to the gradient of the radiation energy density inwards and outwards from this minimum, there is considerable radiation transport towards the point r ≈ 1.1. The energy produced in the BL is therefore transported outwards by radiation. Also some part of the energy produced in the disk is transported inwards. Thus there is a significant redistribution of energy both from the BL and from the disk to a wider region of about 10 percent of the stellar radius in radial extent. This region is called the thermal BL (Regev & Bertout 1995; Popham & Narayan 1995). In the disk, the cooling from the surface is accounted for by the radiation transport in the vertical direction, which is indicated by the nearly vertical arrows pointing upwards in Fig. 2. Directly above the BL, the radiative flux is very strong and pushes the disk surface flux outwards. At higher stellar latitudes, Fig. 2 shows that the flux is directed towards the star. This unexpected behavior is probably a consequence of the small density in the corona and the numerical problems for the radiation transport associated with the density floor. However, this region does not influence the structure or the thermodynamics of the BL.
In Fig. 3a the dynamic structure of the star-BL-disk system is displayed. The density is shown as an orientation for the velocity vectors that visualize the direction and the magnitude of the flow. The disk shows a steady slow inflow towards the star. The inflow velocity is larger near the disk surface than in the midplane. As the gas approaches the stellar surface it is considerably sped up. This is clearly visible in Fig. 3b, where the radial velocity ur in the disk midplane is shown in red. The infall of material is accelerated until r ≈ 1.05 and then rapidly decelerated as the matter comes to the surface of the star. The peak of ur corresponds to a Mach number of approximately 0.25, so the infall occurs subsonically for our chosen value of α, which is important for causality reasons (e.g., Pringle 1977). Due to the friction in the disk, the gas loses angular momentum and its stabilizing force so that the infall velocity increases. As a consequence, the density in this region must decrease accordingly in order to maintain a constant mass-accretion rate through the disk. The mass flux through concentric spherical shells of radius r is given by 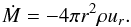 (15)Thus, if the velocity becomes larger, the density must decrease. Ṁ can be derived from Eq. (1) assuming a stationary state (∂t = 0). Also shown in Fig. 3b is the angular velocity Ω, which describes the rotation of the gas around the star. In the disk, the gas rotates with Keplerian frequency and there is a force balance between the gravitational force of the star and the centrifugal force of the circular motion. Additional forces arising through pressure gradients are, in general, small in the disk and influence Ω only slightly. As the gas approaches the stellar surface, it is decelerated and smoothly connects to the rotation rate of the star, which is zero in this case. The deceleration happens very fast and causes a supersonic velocity drop over a range of less than one percent of the stellar radius. Here, the stabilization of the gas switches from centrifugal to pressure support. The large gradient of Ω during the velocity drop is responsible for the heat production in the BL and drives the high temperature observed in the thermal BL. In contrast, by definition the dynamical BL is the region from the stellar surface to the maximum of Ω (zero-torque point) and it is extremely small for BLs around WDs. In this case, the width amounts to Δr = 0.01. We begin to measure the BL width when the angular velocity deviates by more than 1% from the stellar-rotation rate. Only the velocities, especially ur and uϕ, vary considerably on a scale of the order of the dynamical BL width (~ 1%R∗). For the other quantities, it is usually not necessary to resolve the dynamical BL in the figures since no rapid changes happen (see e.g., Fig. 3b vs. Fig. 6, lower panels). From an observational point of view, the thermal BL is the essential region. However, if we compare the dynamics or the width of the BL, we refer to the dynamical BL.
(15)Thus, if the velocity becomes larger, the density must decrease. Ṁ can be derived from Eq. (1) assuming a stationary state (∂t = 0). Also shown in Fig. 3b is the angular velocity Ω, which describes the rotation of the gas around the star. In the disk, the gas rotates with Keplerian frequency and there is a force balance between the gravitational force of the star and the centrifugal force of the circular motion. Additional forces arising through pressure gradients are, in general, small in the disk and influence Ω only slightly. As the gas approaches the stellar surface, it is decelerated and smoothly connects to the rotation rate of the star, which is zero in this case. The deceleration happens very fast and causes a supersonic velocity drop over a range of less than one percent of the stellar radius. Here, the stabilization of the gas switches from centrifugal to pressure support. The large gradient of Ω during the velocity drop is responsible for the heat production in the BL and drives the high temperature observed in the thermal BL. In contrast, by definition the dynamical BL is the region from the stellar surface to the maximum of Ω (zero-torque point) and it is extremely small for BLs around WDs. In this case, the width amounts to Δr = 0.01. We begin to measure the BL width when the angular velocity deviates by more than 1% from the stellar-rotation rate. Only the velocities, especially ur and uϕ, vary considerably on a scale of the order of the dynamical BL width (~ 1%R∗). For the other quantities, it is usually not necessary to resolve the dynamical BL in the figures since no rapid changes happen (see e.g., Fig. 3b vs. Fig. 6, lower panels). From an observational point of view, the thermal BL is the essential region. However, if we compare the dynamics or the width of the BL, we refer to the dynamical BL.
Once the gas has reached the surface of the star, it has lost almost all of its angular and radial momentum and has settled to a dense shell in the equatorial plane. It is slowly driven to the poles of the star. Above the disk we set the velocities to zero whenever the density floor is applied. We thus limit the velocity of the inevitably infalling gas since it dissipates energy when it shocks on the surface of the star or the disk and heats up the low-density regions. Therefore, no velocity arrows are visible in the dark blue regions of Fig. 3.
 |
Fig. 4 Midplane temperature T as a function of radius. We compare the results from 1D (red) and 2D (blue) simulations. A general deviation of about 10% is due to an insufficient approximation of the vertical optical depth in the 1D approach. |
We now compare the reference model with the results of the 1D approach where the BL equations in cylindrical coordinates are vertically integrated and axisymmetry is assumed (see Hertfelder et al. 2013). The vertically integrated density (surface density), which is extracted from the 2D data by integrating vertically at constant spherical radius, is similar for the two approaches. In the disk, the differences are small (≲ 5%). The only significant deviation (~ 40%) is given in the BL where the 1D model predicts a surface density that is slightly too low. The temperature deviates by approximately 50 000 K or 10% throughout the domain, see Fig. 4. In order to be sure that the reason for this mismatch is not given by a non fully relaxed 2D midplane temperature, we looked at snapshots of different times and found that in the equatorial plane, the model is in thermal equilibrium. We conclude that the 1D approximation slightly underestimates the disk temperature. Apart from the general deviation, the overall trend is well reproduced. The 1D approach insufficiently approximates the vertical structure of the disk. This leads to a lower temperature as well as a lower disk height. In the 1D model, thus, the disk is too thin. This is a consequence of the vertical cooling, which relies on an approximation of the vertical optical depth analog to a gray atmosphere. If the estimate for the vertical optical depth is too low, the cooling is more efficient and, hence the temperature in the equatorial plane lower. The dynamical structure of the 1D model matches the 2D simulation very well. The shape of Ω and the width of the BL are virtually identical for the two different approaches. The infall velocity is also a close match, though it is slightly larger in the BL since the surface density is smaller (see Eq. (15)).
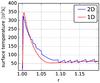 |
Fig. 5 Surface temperature as a function of radius for the 1D radial model and the 2D model. In the latter, the radiation temperature Trad is calculated following Eq. (17) and the surface temperature of the disk and BL is given by Trad at an optical depth of τ = 1. |
Figure 5 shows the surface temperature of the BL and the disk. In the 1D radial approximation, the surface temperature is derived from the midplane temperature by employing the estimate for the vertical optical depth τeff by Hubeny (1990): ![\begin{equation} T_\text{c}^{\text{1D}} = \sqrt[4]{\tau_\text{eff}} T_\text{surface}^{\text{1D}} . \end{equation}](/articles/aa/full_html/2017/09/aa30847-17/aa30847-17-eq162.png) (16)For the 2D model, the radiation temperature is computed according to
(16)For the 2D model, the radiation temperature is computed according to 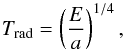 (17)where a is the radiation constant. The surface temperature is then obtained by evaluating Trad in an optical depth of τ = 1. Since the line of constant τ = 1 approximately equals the visible surface, the surface temperature is a measure for the radiation emitted by the system. The 1D and the 2D approaches yield remarkably similar values of Tsurf (Fig. 5). The peak of the 2D surface temperature is slightly shifted towards the star since the BL of the 2D model lies closer to the star than in the 1D case (see also Fig. 4). The peak is marginally lower and the descent less steep. In the 2D model, the thermal BL is thus slightly wider and less hot than in the 1D approximation. In the disk, both models decrease to about 55 000 K and the radiation is comparable to the WD. The 2D surface temperature is not as smooth as the 1D counterpart and shows frequent edges and small spikes. The reason is, that, coming from above, the density in the disk rapidly rises to the point where τ = 1 and the number of grid cells in this region is limited. By increasing the resolution at the transition to the disk, the smoothness of the profile could be improved.
(17)where a is the radiation constant. The surface temperature is then obtained by evaluating Trad in an optical depth of τ = 1. Since the line of constant τ = 1 approximately equals the visible surface, the surface temperature is a measure for the radiation emitted by the system. The 1D and the 2D approaches yield remarkably similar values of Tsurf (Fig. 5). The peak of the 2D surface temperature is slightly shifted towards the star since the BL of the 2D model lies closer to the star than in the 1D case (see also Fig. 4). The peak is marginally lower and the descent less steep. In the 2D model, the thermal BL is thus slightly wider and less hot than in the 1D approximation. In the disk, both models decrease to about 55 000 K and the radiation is comparable to the WD. The 2D surface temperature is not as smooth as the 1D counterpart and shows frequent edges and small spikes. The reason is, that, coming from above, the density in the disk rapidly rises to the point where τ = 1 and the number of grid cells in this region is limited. By increasing the resolution at the transition to the disk, the smoothness of the profile could be improved.
4.2. The influence of the WD rotation
 |
Fig. 6 Angular velocity Ω and radial velocity ur (both in dimensionless units) and density ρ and temperature T in cgs units. All variables show the radial dependency in the equatorial plane. The different colors denote the different stellar rotation rates of 0,0.3,0.5,0.7 and 0.9 times the Keplerian angular velocity at the stellar surface. The snapshots are taken after 688, 251, 248, 263 and 253 orbits. The blue lines correspond to the reference model. |
The rotation rate of the WD is an important parameter since it determines the amount of energy released in the BL. With increasing stellar rotation rate, the amount of kinetic energy that is transformed into heat in the BL decreases. The luminosity of the BL decreases quadratically with increasing stellar rotation rate, 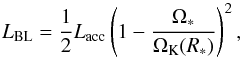 (18)where Lacc = GM∗Ṁ/R∗ is the total accretion luminosity. Equation (18) can be derived theoretically (Popham & Narayan 1995) and has been verified numerically (Hertfelder 2017).
(18)where Lacc = GM∗Ṁ/R∗ is the total accretion luminosity. Equation (18) can be derived theoretically (Popham & Narayan 1995) and has been verified numerically (Hertfelder 2017).
We considered five different stellar rotation rates ranging from non-rotating up to nearly break-up rotation velocity. The differences between these models are illustrated in Fig. 6 where the midplane radial dependency of the angular velocity, radial velocity, density and temperature are shown. The angular velocity Ω decreases smoothly from Keplerian rotation in the disk to the stellar-rotation rate. The faster the star spins, the more the dynamical BL is shifted to greater radii since the star increases its equatorial radius due to the centrifugal force imposed by its rotation. For a WD that spins at 70% of ΩK, the equatorial radius increase amounts to already ~ 4% of the stellar radius. Also, the dynamical BL width becomes larger with increasing stellar rotation; Δr = 0.01,0.015,0.016,0.025 for Ω∗ = 0.0,0.3,0.5,0.7ΩK(R∗). The reason for the increasing BL width is the complex interplay of density and temperature, both of which influence the viscosity, which ultimately governs the width of the BL. In the disk, the angular velocity of all models is nearly Keplerian, with a small deviation due to the outward pointing pressure gradient, which adds as a stabilizing force.
The infall velocity ur shows a behavior which is not expected from 1D BL simulations where the maximum of the radial velocity decreases with rising rotation rate (e.g., Hertfelder et al. 2013). In contrast, the 2D simulations propose a trend where the peak of ur first increases significantly before decreasing again. The turnaround point seems to be in the range of Ω∗ ≈ 0.3 and only for a high stellar rotation rate of Ω∗ = 0.7 is the peak smaller than in the non-rotating model. Here it would certainly be interesting to run additional models with different Ω∗ to investigate the trend in depth. Apart from the peak behavior, the shape of ur reflects our expectations. Coming from the disk, ur is small and increases as the BL is approached. In the BL, it peaks and then decreases rapidly as the stellar surface is encountered. Although two models peak at a higher infall velocity than the reference model, the infall is still well sub-sonic.
The unexpected behavior of the rotating models continues to occur in the density and the temperature. While in 1D models there is a clear trend that the (surface) density increases and the temperature decreases as the star spins up, Fig. 6 points towards a different picture. The density in the BL for the Ω∗ = 0.3 case is smaller than in the non-rotating model. The same applies for the model where the star rotates at half of the break-up velocity. The trend of each ρ(r) curve, however, is in perfect agreement with the non-rotating model. The temperature, instead of decreasing with increasing rotation rate, seems to rise at first glance. Important, though, is the BL temperature which corresponds to the region directly in front of the steep rise as we enter the star. Here, the non-rotating model has a higher temperature than the 0.3 and 0.5 cases, which is in agreement with Eq. (18). The 0.7 model deviates from this picture since the equatorial radius increase is already very pronounced. The cause for the increased infall velocity in the rotating models is unclear. Perhaps the lack of a stabilizing pressure force due to a lower BL temperature is responsible for the accelerated inflow. As has been mentioned earlier, ρ will adjust to the radial velocity such that the mass flux remains constant, see Eq. (15). This could also explain the lower density in these cases. In general, however, the inflow velocity should be proportional to the loss of angular momentum and thus be higher for lower Ω∗. This point remains to be clarified through further investigation. The temperature of the Ω∗ = 0.9 model is not visible in Fig. 6 since it is larger than 800 000 K throughout the plotted region due to the high density.
A special case is given by the model with a stellar rotation rate of 0.9. Due to the high rotation rate of the star, the system has reached a state where matter is fed into the disk by the star and transported outwards by the disk. This phenomenon is called a decretion disk. The radial velocity is pointing outwards throughout the disk. Due to this exotic state of the disk, no BL is formed and the density and temperature are much higher than in the other cases since the hot stellar material is transported outwards. We find that a decretion disk is formed in each model that has a rotation rate of 0.9 and therefore exclude those cases from our further analysis.
For the models with a rotating star we found that the material does not continue its journey to the poles unhindered as was the case for the non-rotating star. We investigate the polar spreading of the material, which depends on the stellar rotation rate, in detail in Sect. 4.4.
4.3. Dependency on stellar mass and mass-accretion rate
 |
Fig. 7 Density and temperature in the equatorial plane as a function of radius. In the upper two panels the variables are displayed for three different mass-accretion rates. The plot of the temperature has an additional zoom box to make the thin peaks in the BL more visible. Lower two panels: ρ and T for three different stellar masses. |
We now investigate to what extent the stellar mass and the mass-accretion rate of the system influence the structure of the BL. To this end, we consider the following models (see also Table 1): For the Ṁ-study, we leave the stellar mass fixed at M∗ = 0.8 M⊙ and compare three different mass-accretion rates, 10-8,10-9 , and 10-10M⊙/ yr. We then fix Ṁ at 10-8M⊙/ yr and change the stellar mass to 0.8,1.0, and 1.2 M⊙. All models feature a non-rotating WD.
The upper two panels of Fig. 7 show the density ρ and the temperature T in the equatorial plane as a function of radius for three different mass-accretion rates. With decreasing Ṁ the density also drops significantly. A difference of two orders of magnitude in mass-accretion rate leads to a density drop of one and 1.5 orders of magnitude in the disk and in the BL, respectively. A similar trend applies to the temperature, which also decreases with ceasing mass-accretion rate. Here we find a factor of more than three between the temperature in the disk with an accretion rate of 10-10 and 10-8 solar masses per year. While the hottest model reaches over 500 000 K in the BL, the coldest model lies at only roughly 150 000 K, apart from the interesting peak, which we discuss later. The more mass is transported through the disk, the more massive the disk will grow and hence the density increases with Ṁ. This behavior is also reflected in the disk height, which increases along with Ṁ. Due to the higher disk density, the depletion of mass in the boundary layer is less severe for the high Ṁ case as well. There are two major reasons for the increasing temperature: On the one hand, the total accretion luminosity scales linearly with the mass-accretion rate: 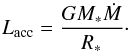 (19)It describes the total amount of energy the gas loses in the disk and the BL around a non-rotating star per time. Thus, the higher the mass-accretion rate, the higher the energy production and also the temperature, since there is simply more material in the disk, which produces heat through shearing. On the other hand, a higher disk density amplifies the energy dissipation. In the BL, again, the increase in temperature is more distinct than in the disk.
(19)It describes the total amount of energy the gas loses in the disk and the BL around a non-rotating star per time. Thus, the higher the mass-accretion rate, the higher the energy production and also the temperature, since there is simply more material in the disk, which produces heat through shearing. On the other hand, a higher disk density amplifies the energy dissipation. In the BL, again, the increase in temperature is more distinct than in the disk.
Width of the boundary layer for a parameter variation of the stellar mass and the mass-accretion rate.
With decreasing mass-accretion rate, an interesting feature arises for the temperature in the BL. In the zoom-in box of Fig. 7, which magnifies the BL region [0.99,1.03], small peaks for 10-9 and 10-10M⊙/ yr are visible, which seem to grow larger with decreasing Ṁ. Those temperature peaks directly reflect the heat production in the BL where the dissipation rate has its maximum and are also observed in 1D simulations (e.g., Hertfelder et al. 2013). Since at this location the density is very low due to the peak of the radial velocity, the matter cannot cool efficiently enough. The radiation transport depends on the opacity, which strongly depends on the density and the temperature. The lower the mass-accretion rate, the smaller also the density and the transport of energy away from this region by radiation, thus cooling this region down, becomes more and more difficult. Therefore this peak grows more pronounced with decreasing Ṁ.
In the lower two panels of Fig. 7, the midplane density and temperature for the three different stellar masses are presented. The density plot confirms, that a higher stellar mass leads to higher density in the disk and in the BL. The variation is roughly exponentially and equally pronounced in the disk and the BL. With increasing stellar mass, the radius of the WD decreases due to the inverse mass-radius relation. This causes a non-linear variation of gravity and the disk height for high-mass WDs is considerably smaller than for lower-mass WDs. Since the mass-accretion rate remains fixed, the amount of mass transported through the disk also remains constant and thus the density increases with M∗. According to Eq. (19) and in combination with the higher density, the temperature also increases strongly. For the case of a very massive 1.2 solar mass WD, the one million K temperature mark is reached. Again, the temperature in the BL grows stronger than in the disk with increasing M∗. A peak in the BL is not visible due to the high mass-accretion rate and the effective radiative cooling. For reference, we state the radii for the WDs of masses 0.8,1.0, and 1.2 M∗ which amount to 7.1 × 108,5.6 × 108 , and 4 × 108 cm, respectively.
The dynamical structure does not significantly change with the stellar mass or the mass-accretion rate and can be described by the general flow structure of the reference model (see Sect. 4.1). The width of the BL, however, depends on Ṁ and M∗ as can be extracted from Table 1. There is a clear trend for all stellar masses that the BL shrinks with decreasing mass-accretion rate. The width further decreases with increasing stellar mass. High mass-accretion rates lead to broader BLs since the density and the temperature are larger and consequently the BL hotter. This effect is reinforced by the inefficient radiation transport in the BL for low mass-accretion rates, which prevents a more distinct expansion. When considering the stellar masses, however, higher densities and temperatures cause quite the opposite, namely a shrinking BL width. Here, we have to take into account the increased gravitational pull, which dominates in this case and drags the disk as close as possible to the stellar surface. Several factors contribute to the width of the BL and it is therefore difficult, to come to a unique conclusion without running simulations. The radial velocities and Mach numbers are almost identical, apart from the slight radial shift due to the different BL widths. We also observe an unhindered, slow polar spreading of the disk material shell in all models.
4.4. Polar spreading and mixing
 |
Fig. 8 Black and white image of the tracer, which has been inserted in the equatorial plane in order to visualize the mixing and polar spreading of the disk material of a 0.8 M⊙ WD with Ṁ = 10-8M⊙/ yr. The plots differ in the stellar-rotation rate, which is given by 0.0 (a), orbit 688), 0.3 (b), orbit 251), 0.5 (c), orbit 248) and 0.7ΩK(R∗) (d), orbit 263). The dotted black line denotes the optical depth of τ = 2 / 3. |
In Fig. 8, the destination of the disk material on the stellar surface is visualized. To this purpose, we have added a tracer in the equatorial plane just short of the stellar surface in the simulations. The tracer behaves like a scalar quantity for which an advection equation is solved. It thus illustrates in which direction the material from the disk is going. Along with the tracer we have added the line of constant τ = 2 / 3 with a dotted black line that is approximately the visible surface of the star. Four different stellar rotation rates are given.
 |
Fig. 9 Maximum latitude reached by the disk material on its way to the pole as a function of the stellar-rotation rate. The different curves correspond to different choices of stellar mass and mass-accretion rate (see legend). The maximum latitude angle is measured towards the equatorial plane and is given in degrees. |
In Fig. 8a the situation is shown for the reference model with the non-rotating WD. As was mentioned earlier, the disk material is gathered in a very thin shell that slowly moves to the poles. Since the WD is not rotating and the material has been completely depleted of its angular momentum near the midplane, the surface of the WD is an equipotential area. The gas is pushed up towards the poles by the pressure that has developed in the midplane at r ≈ 1 due to the deceleration of the disk. On the WD surface, the movement is slowed down by friction. If the viscosity νconst of the WD is reduced, we observe that the material reaches the poles faster than in the reference model. In these cases, we can actually follow the simulation for the time that is needed for the gas to reach the pole. However, the choice of an overly small νconst is problematic since it prevents the BL from building up in the first place. For the rotating models it is especially important that νconst is large enough so that the WD rotates like a solid body. We have found that νconst = 1012 cm2/ s is a good choice for this purpose.
The picture changes when the star begins to rotate. In this case, there is a centrifugal barrier that initially prevents the gas from leaving the midplane. However, the pressure force in the equatorial plane is large enough to overcome this barrier and push the material towards the pole. At a certain latitude, an equilibrium of pressure and centrifugal force is established and the movement is halted. This situation is illustrated in panels (b)−(d) of Fig. 8, where the WD rotates with 30%,50%, and 70% of ΩK(R∗). Since with increasing stellar rotation rate the centrifugal force increases and the pressure force decreases, the maximum latitude shrinks considerably.
The mixing of the stellar and disk material also becomes more pronounced with increasing rotation rate. In all three cases where the WD spins at a non-zero rate, the τ = 2 / 3 is engulfed in a mixture of material from the disk and the star. Therefore it is to be expected that the radiation of the star is reprocessed in regions partly dominated by disk material; material that might have a composition different from the stellar mixture in some cases. This situation occurs, however, only for a part of the star and two caps at the poles, which increase in size as the star spins up and remain untouched by the disk material.
Figure 9, where the maximum latitude as a function of Ω∗ is shown, visualizes how the spreading is influenced by M∗ and Ṁ. The trend of the polar spreading of material decreasing with stellar radius from Fig. 8 is confirmed by Fig. 9 for various combinations of stellar mass and mass-accretion rate. The gas faces a centrifugal barrier when traveling to the poles due to the fact that it retains an increasing amount of angular momentum with growing stellar rotation rate when reaching the stellar surface. The viscosity on the stellar surface on regions off the equatorial plane is far too low to decelerate the material efficiently and rid it of its excess angular momentum. This also explains the unhindered slow movement of the disk gas in the non-rotating case.
Figure 9 further suggests that an increase in stellar mass leads to a considerable growth of the maximum latitude. The rotational velocity on the surface of the star is proportional to 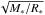 and thus is growing with increasing stellar mass. This means that a point on the equator of a 1.2 M⊙ WD that rotates with 30% of the break-up velocity moves at almost 2000 km s-1, whereas for a 0.8 M⊙ WD the velocity is only about 1200 km s-1. The important quantity for the polar spreading, however, is the angular momentum, which scales
and thus is growing with increasing stellar mass. This means that a point on the equator of a 1.2 M⊙ WD that rotates with 30% of the break-up velocity moves at almost 2000 km s-1, whereas for a 0.8 M⊙ WD the velocity is only about 1200 km s-1. The important quantity for the polar spreading, however, is the angular momentum, which scales 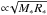 on the surface and thus decreases with increasing stellar mass due to the inverse mass-radius relation of WDs. The material can therefore reach higher latitudes on the WD. The mass-accretion rate, on the contrary, does not seem to influence the polar spreading at all. The small deviations between the blue, cyan, and magenta curves in Fig. 9 are probably due to inaccuracies in measurement. There is therefore no increased pressure force to drive the material further to the poles for increasing mass-accretion rate. The angular momentum of the gas remains the key issue in the polar spreading. It would be interesting to investigate the shape of the Ω∗ dependence of the maximum latitude further, however, with only three data points per curve we feel that an interpretation beyond the general trend is too speculative. We leave that issue for future studies.
on the surface and thus decreases with increasing stellar mass due to the inverse mass-radius relation of WDs. The material can therefore reach higher latitudes on the WD. The mass-accretion rate, on the contrary, does not seem to influence the polar spreading at all. The small deviations between the blue, cyan, and magenta curves in Fig. 9 are probably due to inaccuracies in measurement. There is therefore no increased pressure force to drive the material further to the poles for increasing mass-accretion rate. The angular momentum of the gas remains the key issue in the polar spreading. It would be interesting to investigate the shape of the Ω∗ dependence of the maximum latitude further, however, with only three data points per curve we feel that an interpretation beyond the general trend is too speculative. We leave that issue for future studies.
In all of the simulations we have performed, the disk material is decelerated in the midplane and the radiation of the BL emerges in proximity to the stellar equator. The situation depicted in Fig. 2 also holds true for increasing stellar rotation rate Ω∗ and only the amount of dissipated energy decreases. The disk material that finally spreads towards the poles has the same rotational velocity as the stellar surface. Therefore, we do not observe a spreading layer (SL) as mentioned in Inogamov & Sunyaev (1999, 2010), where the rotating material first spreads on the star and is decelerated and radiates within two rings above and beyond the equator. The latitude of these rings depends on the mass-accretion rate. However, we also do not detect any such changes in the BL when the mass-accretion rate is varied (for instance Fig. 9).
5. Summary and conclusion
For this publication we have performed 2D simulations of the non-magnetic BL around WDs in CVs in a spherical geometry assuming axisymmetry. The hydrodynamical model based on the Navier-Stokes equations is extended by an additional equation for the radiation energy, which is closed using the flux-limited diffusion approach. We employ Kramer’s opacity, which suits the temperatures found in the inner disk around WDs and utilize a modified α-prescription for the viscosity, which also takes into account the radial scale height in the BL. A total of 45 models have been prepared in a complex way (see Sect. 3.2) and run with varied M∗ (0.8,1.0,1.2 M⊙), Ṁ (10-8,10-9,10-10M⊙/ yr) and Ω∗ (0.0,0.3,0.5,0.7,0.9ΩK(R∗)). Each model features a high resolution (~ 1.1 million cells) and has been run for several hundred orbits, both of which are unprecedented, especially when considering the elaborate physics included in the model. The downside of this advanced setup are simulation times of ≳ 1 week with 560 parallel cores on the most recent cluster hardware. However, this can be coped with thanks to the availability of high-performance computing centers in Baden-Württemberg, Germany.
We found that in the BL the angular velocity of the gas decreases smoothly from the Keplerian rotation in the disk towards the non-rotating stellar surface. Due to the loss of stabilization by angular momentum, the infall velocity of the gas increases and peaks in the BL. This goes along with a severe depletion of mass which is characteristic for the BL and suggests the picture of a bottleneck. Since the gas loses a great amount of energy before coming to rest on the star, very high temperatures of ~ 550 000 K for a 0.8 M∗ WD with a mass accretion of 10-8M∗/ yr are reached. Whereas the dynamical BL, that is, the region where Ω drops to Ω∗, is very small (≲ 1%R∗), the area over which the dissipated energy is radiated away is considerably larger (~ 10% R∗). This is of particular interest for the observational appearance of the BL, since a wider region means less hard radiation. The radiative flux further reveals that the hottest (i.e., closest to the star) part of the disk also contributes to the thermal BL. This might lead to an overestimated Ω∗ since the BL dissipation is assumed slightly too large when comparing observations with synthetic BL models.
By increasing the stellar-rotation rate, the general structure of the BL does not change. The angular velocity still smoothly connects to the surface velocity and the density and temperature in the BL are small and large, respectively. The dynamical width, however, increases due to the changing viscosity which is governed by the temperature. One open question remains with the infall velocity that, against our expectations, increases with rising Ω∗ at first and decreases only for Ω∗ ≳ 0.3. An interesting case is found for the high stellar-rotation rate of 0.9ΩK(R∗) throughout the M∗,Ṁ parameter space. Here, a decretion disk is formed and material from the star is transported outwards through the disk. In general, the stellar-rotation rate is an important parameter since it determines the amount of energy liberated and radiated away in the BL and can in principle be identified by analyzing the BL luminosity from observations. There is, however, an ambiguity in that different choices of Ω∗,M∗ , and Ṁ can lead to similar luminosities, which complicates this process. One way to circumvent this difficulty entails measuring the BL X-ray luminosity along with the bolometric luminosity since Hertfelder (2017) has recently shown that the X-ray luminosity scales 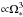 as opposed to the
as opposed to the 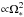 dependency of the total luminosity.
dependency of the total luminosity.
The mass-accretion rate and the stellar mass both affect the BL such that a higher value leads to an increase in density and temperature. In the first case, the higher amount of mass in the disk due to the higher accretion rate and hence the increased dissipation is responsible for the rise in density and temperature. In the other case, a higher M∗ intensifies the gravitational pull on the material. A process which is supported by the inverse mass-radius relation of WDs. The width of the BL decreases with increasing stellar mass or decreasing mass-accretion rate for the same reasons. The height of the disk also follows this trend. Intriguingly, with decreasing mass-accretion rate a thin but pronounced temperature peak within the dynamical BL becomes visible due to an inefficient radiative cooling under these conditions. At these mass-accretion rates, the BL starts to become optically thin. The value matches other studies, which give a threshold of about 10-10M⊙/ yr for an optically thin BL (e.g., Warner 1987). Whether or not the peak becomes higher and more pronounced with further decreasing mass-accretion rate, as well as whether or not this finally results in soft and hard X-ray emission from the BL, should be investigated through future studies.
Due to its complexity and resource consumption, the BL is still frequently treated in a 1D approximation (see for instance Hertfelder et al. 2013; Hertfelder 2017). We found that this approach is well justified if the right conclusions are drawn from the results. Insight into the vertical structure or the interplay between BL and star is clearly inaccessible by this method. The radiation and luminosity, however, can be deduced even from 1D models, especially since the surface temperatures are almost identical. One must bear in mind, though, that the 1D model predicts an overly low midplane temperature and disk height due to an insufficient approximation of the vertical optical depth. Apart from this drawback and a small artificial radial shift, the midplane profiles are amazingly similar between the two different approaches. Because of the vastly reduced simulation time (~hours), 1D models are to be preferred for luminosity calculations, for instance.
The results further indicate that the polar spreading, that is, the motion of the disk material in the direction of the poles of the star, depends on the rotation rate. For a non-rotating star, a dense shell creeps towards the poles and does not come to rest before reaching them. With increasing rotation rate, the maximum latitude reached by the gas recedes due to the angular momentum that the gas is not able to get rid of on the slippery stellar surface at higher latitudes. Also, the mixing with the stellar material becomes more pronounced with increasing stellar rotation and the gas from the disk comes to rest on and around the observable surface. As a consequence, the stellar radiation might be reprocessed in a mixture of star and disk material and carry away the spectral features of both. We note, however, that in our setup, differences in the mean molecular weight of the accreted and WD material and gravitational settling are not taken into account. While variations in mass-accretion rate have little or no influence on the polar spreading, a higher stellar mass leads to higher maximum latitudes. The angular momentum at the stellar surface for a fixed rotation rate (e.g., 0.3ΩK(R∗)) decreases with increasing stellar mass due to the inverse mass-radius relations of WDs. Thus for regular relations, as for instance in young stars, the maximum latitude is likely to decrease with increasing stellar mass. Our simulations show no indication of a deceleration of the disk material above (or beyond) the stellar equator for any chosen parameter set. Therefore, we can rule out the concept of the SL for our setup. It remains to be investigated whether or not this picture changes when a different mechanism for the viscosity is employed (e.g., Belyaev & Rafikov 2012).
In general, our results are in good agreement with Kley (1991) who performed simulations of the BL around a solar mass WD. We find a slightly smaller BL width for comparable parameters. This is, however, probably a consequence of small differences in the applied viscosity prescription. Furthermore, we do not detect the extremely hot corona (~ 108 K) above the disk found in Kley (1991). In contrast, this region has a temperature of only ~ 104 K, which is probably too low and a consequence of the simplified radiation treatment in the optically thin corona. The author also mentions that if a turbulent ansatz for the viscosity is taken (similar to Eq. (12)), the flow shows a strong time variability with an irregular and eddy-like structure. The question is raised of whether this is a consequence of inconsistencies with initial conditions or a general feature of accretion disk flows. Analyzing our simulations, we believe now that this is a transient phenomenon due to some involuntary initial perturbations, which disappears after several orbits of simulation time. A higher numerical resolution also mitigates this problem. We can, however, not rule out that, for a specific choice of parameters, a real physically unstable state develops. Instabilities are more likely found in the disk plane though (e.g., Hertfelder & Kley 2015). More recently, Balsara et al. (2009) conducted simulations of the BL around a WD with a strong focus on the outer stellar layers. They varied the α parameter and found optically thick BLs that extend to more than 30° to either side of the disk plane after a short time. While we also find optically thick BLs for α = 0.01 and high mass-accretion rates, the inflation of the BL is absent in our simulations and both the disk and the BL are rather thin, as is expected around a compact object. The unphysical treatment of the dissipated energy most likely causes the behavior observed in Balsara et al. (2009). We also did not detect gravity waves or Kelvin-Helmholtz instabilities although the outer stellar layers are included and are highly resolved in our setup.
The non-magnetic BL has been investigated in a 1D radial approximation (Hertfelder et al. 2013), in a 2D cylindrical approach in order to examine the instabilities in the disk plane (Hertfelder & Kley 2015), and finally in the current paper in a 2D spherical geometry that reveals the vertical structure. The mammoth task that still remains to be accomplished is the combination of the latter two. Full 3D simulations will reveal how the AM transport by the BL instability influences the vertical structure and vice versa. Sadly, this lies beyond what is computationally feasible at this time since a high resolution in all three coordinate directions is necessary (especially in the azimuthal direction) and particularly the 3D radiation transport will slow down the simulations considerably. There are, however, other open questions in connection with the BL such as the influence of magnetic fields or the role of the BL around protoplanets in disks which can be tackled in a 1D or 2D approach.
Acknowledgments
Marius Hertfelder received financial support from the German National Academic Foundation (Studienstiftung des deutschen Volkes). This work was performed on the computational resource ForHLR II funded by the Ministry of Science, Research and the Arts Baden-Württemberg and DFG (“Deutsche Forschungsgemeinschaft”). Preprocessing of the production runs has been carried out on the BwForCluster BinAC and the authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant No. INST 39/963-1 FUGG. M.H. wants to thank Hartmut Häfner of the Steinbuch Centre for Computing (SCC) at KIT and Volker Lutz at the Zentrum für Datenverarbeitung (ZDV) in Tübingen, for their support. We further made use of matplotlib (Hunter 2007), a python module for data visualization. We also thank the referee for his/her constructive comments which helped to improve this paper.
References
- Abramowicz, M., Brandenburg, A., & Lasota, J.-P. 1996, MNRAS, 281, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Arfken, G. B., & Weber, H. J. 2005, Mathematical Methods for Physicists, 6th edn. (Academic Press) [Google Scholar]
- Armitage, P. J. 2002, MNRAS, 330, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Babkovskaia, N., Brandenburg, A., & Poutanen, J. 2008, MNRAS, 386, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., Fisker, J. L., Godon, P., & Sion, E. M. 2009, ApJ, 702, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A. 2017, ApJ, 835, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A., & Rafikov, R. R. 2012, ApJ, 752, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A., Rafikov, R. R., & Stone, J. M. 2012, ApJ, 760, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A., Rafikov, R. R., & Stone, J. M. 2013a, ApJ, 770, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A., Rafikov, R. R., & Stone, J. M. 2013b, ApJ, 770, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1960, Proc. National Academy of Science, 46, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordova, F. A., & Mason, K. O. 1984, MNRAS, 206, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Nugent, J. J., Klein, S. R., & Garmire, G. P. 1980, MNRAS, 190, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Jensen, K. A., & Nugent, J. J. 1981a, MNRAS, 196, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Mason, K. O., & Nelson, J. E. 1981b, ApJ, 245, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Math. Ann., 100, 32 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fisker, J. L., & Balsara, D. S. 2005, ApJ, 635, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Fisker, J. L., Balsara, D. S., & Burger, T. 2006, New Astron. Rev., 50, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzel, W. 1988, MNRAS, 231, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P. 1995, MNRAS, 277, 157 [NASA ADS] [Google Scholar]
- Godon, P., Regev, O., & Shaviv, G. 1995, MNRAS, 275, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Hertfelder, M. 2017, ArXiv e-prints [arXiv:1702.06726] [Google Scholar]
- Hertfelder, M., & Kley, W. 2015, A&A, 579, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hertfelder, M., Kley, W., Suleimanov, V., & Werner, K. 2013, A&A, 560, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Computing In Science & Engineering, 9, 90 [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 1999, Astron. Lett., 25, 269 [NASA ADS] [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 2010, Astron. Lett., 36, 848 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., & Shaviv, G. 1984, Nature, 308, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1989a, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1989b, A&A, 222, 141 [NASA ADS] [Google Scholar]
- Kley, W. 1991, A&A, 247, 95 [NASA ADS] [Google Scholar]
- Kley, W., & Hensler, G. 1987, A&A, 172, 124 [NASA ADS] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1996, ApJ, 461, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1999, ApJ, 518, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, S. M., Stute, M., Kley, W., & Mignone, A. 2013, A&A, 559, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuiper, R., Klahr, H., Dullemond, C., Kley, W., & Henning, T. 2010, A&A, 511, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Küker, M., Henning, T., & Rüdiger, G. 2003, ApJ, 589, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D. 1984, J. Quant. Spec. Radiat. Transf., 31, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 20, eds. G. Tovmassian, & E. Sion, 174 [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Minerbo, G. N. 1978, J. Quant. Spec. Radiat. Transf., 20, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., & Patterson, J. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 20, eds. G. Tovmassian, & E. Sion, 244 [Google Scholar]
- Narayan, R., & Popham, R. 1993, Nature, 362, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Pandel, D., Córdova, F. A., & Howell, S. B. 2003, MNRAS, 346, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Pandel, D., Córdova, F. A., Mason, K. O., & Priedhorsky, W. C. 2005, ApJ, 626, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Stanley, G. Q. G. 1986, MNRAS, 220, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., & Chan, C.-K. 2012, ApJ, 751, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Philippov, A. A., Rafikov, R. R., & Stone, J. M. 2016, ApJ, 817, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2004a, ApJ, 616, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2004b, ApJ, 610, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R. 1999, MNRAS, 308, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., & Narayan, R. 1995, ApJ, 442, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1977, MNRAS, 178, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Savonije, G. J. 1979, MNRAS, 187, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Regev, O. 1983, A&A, 126, 146 [NASA ADS] [Google Scholar]
- Regev, O., & Bertout, C. 1995, MNRAS, 272, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, J. A., & Frank, J. 1986, MNRAS, 221, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2012, MNRAS, 421, 63 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shaviv, G. 1987, Ap&SS, 130, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., Godon, P., Myzcka, J., & Blair, W. P. 2010, ApJ, 716, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., Hertfelder, M., Werner, K., & Kley, W. 2014, A&A, 571, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Syunyaev, R. A., & Shakura, N. I. 1986, Sov. Astron. Lett., 12, 117 [NASA ADS] [Google Scholar]
- Tylenda, R. 1977, Acta Astron., 27, 235 [NASA ADS] [Google Scholar]
- Tylenda, R. 1981, Acta Astron., 31, 267 [NASA ADS] [Google Scholar]
- Velikhov, E. 1959, Zhur. Eksptl. i Teoret. Fiz., 36 [Google Scholar]
- Warner, B. 1987, MNRAS, 227, 23 [NASA ADS] [Google Scholar]
All Tables
Width of the boundary layer for a parameter variation of the stellar mass and the mass-accretion rate.
All Figures
 |
Fig. 1 Density (a) and temperature (b) for the reference model as a function of radius r and vertical coordinate z in cgs units at orbit 688. Contour lines for the levels (0.8,5,10,20,30) × 10-6 g / cm3 are overlaid in the plot of the density a). The white line in panel b denotes the points where the optical depth is unity, τ = 1. |
| In the text | |
 |
Fig. 2 Radiation energy density E of the reference model in g / (cm s2) as a function of radius and height for the inner part of the accretion disk at orbit 688. The arrows denote the direction of the radiative flux as specified in Eq. (8). |
| In the text | |
 |
Fig. 3 Panel a: Density as shown in Fig. 1 as an orientation for the over plotted velocity vectors. The color-bar indicates the absolute value of the velocity of each vector in units of vK(R∗). Only the radial and polar component of the velocity vector have been taken into account. Panel b: Angular velocity Ω = uϕ/r (blue) and the radial velocity ur (red) in the equatorial plane as a function of the radius r. The y-axis on the left-hand side refers to Ω and the y-axis on the right-hand side refers to ur. All velocities are normalized to the Keplerian (angular) velocity at the surface of the star, |
| In the text | |
 |
Fig. 4 Midplane temperature T as a function of radius. We compare the results from 1D (red) and 2D (blue) simulations. A general deviation of about 10% is due to an insufficient approximation of the vertical optical depth in the 1D approach. |
| In the text | |
 |
Fig. 5 Surface temperature as a function of radius for the 1D radial model and the 2D model. In the latter, the radiation temperature Trad is calculated following Eq. (17) and the surface temperature of the disk and BL is given by Trad at an optical depth of τ = 1. |
| In the text | |
 |
Fig. 6 Angular velocity Ω and radial velocity ur (both in dimensionless units) and density ρ and temperature T in cgs units. All variables show the radial dependency in the equatorial plane. The different colors denote the different stellar rotation rates of 0,0.3,0.5,0.7 and 0.9 times the Keplerian angular velocity at the stellar surface. The snapshots are taken after 688, 251, 248, 263 and 253 orbits. The blue lines correspond to the reference model. |
| In the text | |
 |
Fig. 7 Density and temperature in the equatorial plane as a function of radius. In the upper two panels the variables are displayed for three different mass-accretion rates. The plot of the temperature has an additional zoom box to make the thin peaks in the BL more visible. Lower two panels: ρ and T for three different stellar masses. |
| In the text | |
 |
Fig. 8 Black and white image of the tracer, which has been inserted in the equatorial plane in order to visualize the mixing and polar spreading of the disk material of a 0.8 M⊙ WD with Ṁ = 10-8M⊙/ yr. The plots differ in the stellar-rotation rate, which is given by 0.0 (a), orbit 688), 0.3 (b), orbit 251), 0.5 (c), orbit 248) and 0.7ΩK(R∗) (d), orbit 263). The dotted black line denotes the optical depth of τ = 2 / 3. |
| In the text | |
 |
Fig. 9 Maximum latitude reached by the disk material on its way to the pole as a function of the stellar-rotation rate. The different curves correspond to different choices of stellar mass and mass-accretion rate (see legend). The maximum latitude angle is measured towards the equatorial plane and is given in degrees. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.