| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201730486 | |
| Published online | 29 August 2017 | |
A new approach for modelling chromospheric evaporation in response to enhanced coronal heating
II. Non-uniform heating
1 School of Mathematics and Statistics, University of St. Andrews, St. Andrews, Fife, KY16 9SS, UK
e-mail: cdj3@st-andrews.ac.uk
2 Space and Atmospheric Physics, The Blackett Laboratory, Imperial College, London, SW7 2BW, UK
Received: 23 January 2017
Accepted: 25 April 2017
We proposed that the use of an approximate “jump condition” at the solar transition region permits fast and accurate numerical solutions of the one dimensional hydrodynamic equations when the corona undergoes impulsive heating. In particular, it eliminates the need for the very short timesteps imposed by a highly resolved numerical grid. This paper presents further examples of the applicability of the method for cases of non-uniform heating, in particular, nanoflare trains (uniform in space but non-uniform in time) and spatially localised impulsive heating, including at the loop apex and base of the transition region. In all cases the overall behaviour of the coronal density and temperature shows good agreement with a fully resolved one dimensional model and is significantly better than the equivalent results from a 1D code run without using the jump condition but with the same coarse grid. A detailed assessment of the errors introduced by the jump condition is presented showing that the causes of discrepancy with the fully resolved code are (i) the neglect of the terms corresponding to the rate of change of total energy in the unresolved atmosphere; (ii) mass motions at the base of the transition region and (iii) for some cases with footpoint heating, an over-estimation of the radiative losses in the transition region.
Key words: Sun: corona / Sun: magnetic fields / magnetohydrodynamics (MHD) / Sun: chromosphere
© ESO, 2017
1. Introduction
By using one-dimensional (1D) hydrodynamic (field-aligned) models to study the physics of magnetically confined coronal loops (see e.g. Reale 2014, for a review), we have learned a great deal about the temporal response of coronal loop plasma to heating. If the corona is heated by impulsive energy releases, both the temperature and density increase and then decline, with the time of peak temperature preceding that of the peak density. The changes in density are the result of an enthalpy flux to and from the chromosphere, through the transition region (TR), to the corona. An upward enthalpy flux first increases the coronal density, often called (chromospheric) “evaporation” (e.g. Antiochos & Sturrock 1978), then after the time of peak density a downward enthalpy flux drains the loop in order to power the TR radiation (Bradshaw & Cargill 2010a,b).
However, one of the main difficulties encountered with 1D hydrodynamic computational models is the need to implement a grid that fully resolves the steep TR, which is also very dynamic, moving in response to the coronal heating and cooling. The temperature length scale (LT = T/ | dT/ dz |, where T is the temperature and z the spatial coordinate along the magnetic field) is very small in the TR. LT can be less than 1km for a loop in thermal equilibrium and even shorter in hot flaring loops, because of the steep temperature dependence of thermal conduction and the location of the peak of the radiative losses between 105 and 106 K. Resolving these small length scales is essential in order to obtain the correct coronal density in response to time dependent heating (Bradshaw & Cargill 2013, hereafter BC13). Otherwise, the heat flux from the corona “jumps” over an under-resolved TR to the chromosphere, where the incoming energy is then radiated away, rather than going into driving the evaporation. BC13 showed that major errors in the coronal density were likely with a lack of spatial resolution.
Furthermore, in order to achieve numerical stability, the thermal conduction timestep scales as the minimum of 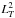 over the whole grid implying long computation times for fully resolved 1D simulations. The problem is more severe in multi-dimensional magnetohydrodynamic (MHD) models where computational resources place significant constraints on the achievable resolutions. Therefore, there is a need for a simple and computationally efficient method that can be employed in both 1D hydrodynamic and multi-dimensional MHD models to help obtain the correct coronal response to impulsive heating events.
over the whole grid implying long computation times for fully resolved 1D simulations. The problem is more severe in multi-dimensional magnetohydrodynamic (MHD) models where computational resources place significant constraints on the achievable resolutions. Therefore, there is a need for a simple and computationally efficient method that can be employed in both 1D hydrodynamic and multi-dimensional MHD models to help obtain the correct coronal response to impulsive heating events.
Johnston et al. (2017, hereafter Paper I) present a physically motivated approach to deal with this problem by using an integrated form of the energy equation that essentially treats the unresolved region of the lower TR as a discontinuity. The response of the TR to changing coronal conditions is then determined through the imposition of a jump condition, which compensates for the energy lost when the heat flux jumps over an unresolved TR by imposing a local velocity correction. In Paper I we demonstrate that this new approach obtains coronal densities comparable to fully resolved 1D models (e.g. BC13) but with computation times that are between one and two orders of magnitude faster, since the computational timestep is not limited by thermal conduction in the TR.
However, in Paper I we consider only the case of spatially uniform heating. The purpose of this paper is two-fold. Firstly, it is important to consider how the jump condition performs for different (spatially non-uniform) heating functions and initial plasma conditions in order for future users to have confidence in the model. The latter is addressed through consideration of a nanoflare train. The former involves studies of highly localised heating pulses, including a challenging case where the heating is located at the base of the TR. Secondly, it has become clear that the coronal plasma parameters, in particular the density, show systematic deviations from those in fully resolved simulations. A full analysis of the terms in the jump condition (both retained and neglected) has been undertaken to understand the cause of this. This paper is not intended as a physical comparison between the different heating models but is intended to demonstrate the wide applicability of the jump condition used.
We derive the jump condition and describe the implementation of the method in Sect. 2. In Sects. 3 and 4, we demonstrate the application of our approach through a series of examples. A detailed discussion of the quantities associated with the jump condition is presented in Sect. 5. We present our conclusions in Sect. 6.
2. Numerical method and experiments
2.1. Numerical method
The full details of the numerical method are discussed in Paper I and so they are just restated briefly here. We solved the 1D field-aligned MHD equations using two different methods, a Lagrangian remap (Lare) approach, as described for 3D MHD in Arber et al. (2001), adapted for 1D field-aligned hydrodynamics (Paper I) and the adaptive mesh refinement code HYDRAD (Bradshaw & Mason 2003; Bradshaw & Cargill 2006, BC13).
For the initial condition we used a magnetic strand (loop) in static equilibrium of total length 2L that includes a 5 Mm model chromosphere (acting mainly as a mass reservoir) at the base of each TR. The corresponding temperature and density profiles were derived using the same base quantities (T = 104 K and n = 1017 m-3) and method that was described in Paper I.
2.2. Overview of the unresolved transition region jump condition
The 1D energy conservation equation is given by 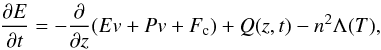 (1)where E = P/ (γ − 1) + 1 / 2ρv2 (gravity is neglected for this discussion but is included in the 1D field-aligned MHD equations that we solve), v is the velocity, P is the gas pressure, ρ is the density, n is the number density, Fc = − κ0T5 / 2∂T/∂z is the heat flux and Q(z,t) is a heating function that includes background uniform heating and a time dependent component that can be dependent on position. Λ(T) is the radiative loss function in an optically thin plasma, which we approximate using the piecewise continuous function defined in Klimchuk et al. (2008).
(1)where E = P/ (γ − 1) + 1 / 2ρv2 (gravity is neglected for this discussion but is included in the 1D field-aligned MHD equations that we solve), v is the velocity, P is the gas pressure, ρ is the density, n is the number density, Fc = − κ0T5 / 2∂T/∂z is the heat flux and Q(z,t) is a heating function that includes background uniform heating and a time dependent component that can be dependent on position. Λ(T) is the radiative loss function in an optically thin plasma, which we approximate using the piecewise continuous function defined in Klimchuk et al. (2008).
We define the unresolved transition region (UTR) as the region of thickness ℓ that extends from the final location in the TR at which the temperature length scale (LT) is resolved (z0, i.e. where the criteria LR/LT ≤ δ< 1 is satisfied, with LR denoting the simulation resolution and δ = 1 / 4 is used throughout this paper) downwards to the base of the TR (zb, which is the location where the temperature first reaches or falls below the chromospheric temperature of 104 K), as outlined in Paper I. Integrating Eq. (1)over the UTR, from the base of the TR (zb) upwards to the top of the UTR (z0), we obtain, 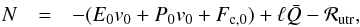 (2)where N is defined as
(2)where N is defined as 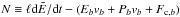 and the subscripts 0 and b indicate quantities evaluated at the top and base of the UTR respectively. The overbars indicate spatial averages over the UTR, ℛutr is the integrated radiative losses and
and the subscripts 0 and b indicate quantities evaluated at the top and base of the UTR respectively. The overbars indicate spatial averages over the UTR, ℛutr is the integrated radiative losses and 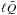 is the volumetric heating rate in the UTR.
is the volumetric heating rate in the UTR.
We assume that the left-hand side (LHS) of Eq. (2)can be neglected based on the arguments presented in Paper I (see also, e.g. Klimchuk et al. 2008; Cargill et al. 2012a,b), so that N represents the neglected terms. Hence, we obtain the UTR jump condition, 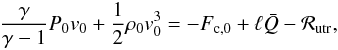 (3)where the terms on the LHS are the enthalpy (Fe,0) and kinetic energy (Fke,0) fluxes, respectively. The terms on the RHS are the heat flux, the integrated volumetric heating rate and the radiative losses (
(3)where the terms on the LHS are the enthalpy (Fe,0) and kinetic energy (Fke,0) fluxes, respectively. The terms on the RHS are the heat flux, the integrated volumetric heating rate and the radiative losses (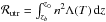 ) in the UTR respectively.
) in the UTR respectively.
The lower TR is modelled as a discontinuity that responds to changing coronal conditions through the imposition of the jump condition (3)which in turn implies a local velocity correction (v0), as discussed in Paper I. We reiterate here that to calculate this velocity correction based on the equilibrium results, the integrated radiative losses (IRL) in the UTR (ℛutr) are approximated using the radiative loss integral from the resolved part of the upper atmosphere 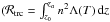 where za represents the loop apex), that is ℛutr = ℛtrc. This approximation of ℛutr is used only in the calculation of v0. It remains necessary to solve the full set of equations in the UTR (see Appendix A, Paper I) in order to retain the structure of the TR. Moreover, to accommodate the case of spatially non-uniform heating, the integrated volumetric heating rate (
where za represents the loop apex), that is ℛutr = ℛtrc. This approximation of ℛutr is used only in the calculation of v0. It remains necessary to solve the full set of equations in the UTR (see Appendix A, Paper I) in order to retain the structure of the TR. Moreover, to accommodate the case of spatially non-uniform heating, the integrated volumetric heating rate (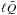 ) is now calculated as,
) is now calculated as, 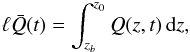 (4)which reduces to ℓQ for uniform heating (as used in Paper I). This new formalism (4)can also be used to incorporate other energy deposition methods such as that from electron or ion beams (e.g. Reep et al. 2013b).
(4)which reduces to ℓQ for uniform heating (as used in Paper I). This new formalism (4)can also be used to incorporate other energy deposition methods such as that from electron or ion beams (e.g. Reep et al. 2013b).
Using HYDRAD results, a detailed comparison of the magnitude of all the terms that appear in Eq. (2)shows that in the neglected term N, 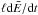 and the mass motions at the base of the TR (Fe,b + Fke,b) can have a measurable impact on the coronal plasma response. For uniform heating this led to larger coronal densities than HYDRAD. One objective of this paper is to quantify the role of these neglected terms further, and this is carried out in Sect. 5. We note here that the difficulty of including the
and the mass motions at the base of the TR (Fe,b + Fke,b) can have a measurable impact on the coronal plasma response. For uniform heating this led to larger coronal densities than HYDRAD. One objective of this paper is to quantify the role of these neglected terms further, and this is carried out in Sect. 5. We note here that the difficulty of including the 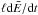 term remains as discussed in Paper I. In particular, if we could calculate
term remains as discussed in Paper I. In particular, if we could calculate 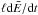 and the base motion terms accurately, with coarse spatial resolutions, then it would not be necessary to implement the jump condition.
and the base motion terms accurately, with coarse spatial resolutions, then it would not be necessary to implement the jump condition.
2.3. Experiments
To appreciate the usefulness of the UTR jump condition method, we assess its performance for a much wider range of examples than those presented in Paper I. Specifically, the experiments considered in this work explore nanoflare trains and spatially non-uniform heating events. The examples studied cover spatially symmetric and asymmetric heating for both short and long loops.
For each experiment, we assess the performance of the UTR jump condition method (referred to as LareJ) by comparing the results with Lare1D (1D code run without using the jump condition but with the same grid) and HYDRAD (fully resolved 1D model). LareJ and Lare1D use 500 uniformly spaced grid points. This choice of the number of grid points is motivated by what is routinely used in current multi-dimensional MHD models (Bourdin et al. 2013; Hansteen et al. 2015; Hood et al. 2016; Dahlburg et al. 2016; O’Hara & De Moortel 2016), so that the simulations run in a realistic time.
The HYDRAD code is run in single fluid mode with a largest grid cell width of 400 km and 12 levels of refinement employed, so that in the most highly resolved regions the grid cells are of width 98 m (BC13). In this paper we use HYDRAD as a benchmark solution.
3. Uniform heating: nanoflare trains
We consider first the case of a nanoflare train (a sequence of heating events or nanoflares e.g. Reep et al. 2013a; Cargill et al. 2015; Bradshaw & Viall 2016; Barnes et al. 2016). The aim is to investigate how the jump condition copes with heating events in loops that start with a range of densities and temperatures because they have not undergone a full evaporation and draining cycle. We model a coronal loop of total length 90 Mm and use the same nanoflare train as in Cargill et al. (2015), consisting of 23 square wave heating pulses over an 8 h period, as shown in the upper panel of Fig. 1. This set up is representative of the modelling challenge faced when trying to understand the heating of the core loops found in active regions (e.g. Warren et al. 2011, 2012). Each nanoflare lasts 200 s and they cover a range of magnitudes of heating, each with an energy dependent waiting time between events. The spatial profile of the heating is uniform along the loop.
Figure 1 shows the coronal response of the loop to the nanoflare train together with the volumetric heating rate as a function of time (upper panel). The central and lower panels show the temporal evolution of the coronal averaged temperature (T) and density (n), respectively. The coronal averages are calculated by spatially averaging over the uppermost 50% of the loop. The details of the plasma evolution are described in Cargill et al. (2015). Here we focus just on the comparison between the LareJ, Lare1D and HYDRAD solutions.
Comparing first LareJ and HYDRAD, we see that their densities follow the same basic evolution, with the LareJ density larger only by about 15–20%, due to the neglect of 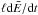 and the base motion terms as discussed above. The temperature evolution also shows good agreement. On the other hand, the Lare1D density is systematically lower than HYDRAD throughout the nanoflare train, on average by around a factor of 2 during small heating events or periods of no heating and a factor of 3 during larger events. Often there is a premature density peak and no substantial draining phase. Moreover, the density being lower has two important consequences for the Lare1D temperature evolution: (1) the peak temperature is higher during each heating event and (2) the subsequent cooling is more rapid. The first of these happens because, when releasing the same total amount of energy, a lower coronal density is heated to a higher temperature. The second arises because thermal conduction is more effective at lower density and with the temperature being higher, the conductive cooling timescale which scales as n/T5 / 2 is shorter. This is a generic feature of the Lare1D solution.
and the base motion terms as discussed above. The temperature evolution also shows good agreement. On the other hand, the Lare1D density is systematically lower than HYDRAD throughout the nanoflare train, on average by around a factor of 2 during small heating events or periods of no heating and a factor of 3 during larger events. Often there is a premature density peak and no substantial draining phase. Moreover, the density being lower has two important consequences for the Lare1D temperature evolution: (1) the peak temperature is higher during each heating event and (2) the subsequent cooling is more rapid. The first of these happens because, when releasing the same total amount of energy, a lower coronal density is heated to a higher temperature. The second arises because thermal conduction is more effective at lower density and with the temperature being higher, the conductive cooling timescale which scales as n/T5 / 2 is shorter. This is a generic feature of the Lare1D solution.
Figure 1 thus shows that the application of the jump condition approach is not limited to a single heating and cooling cycle. The approach deals equally well with periods of both low and high nanoflare frequency. (Low (high) frequency nanoflares are those where the waiting time between events is longer (significantly shorter) than a characteristic cooling timescale.) This is because the underlying physics that drives the evaporation (e.g. Klimchuk et al. 2008) is the same in each regime, for loops that have cooled and drained to sub-million degree temperatures and low densities between heating events (low frequency) and those that have not (high frequency).
We have also tested nanoflare trains in loops of total length 60 Mm (short) and 180 Mm (long). These simulations show the same fundamental properties as those discussed for the 90 Mm loop.
 |
Fig. 1 Coronal response of the plasma to a nanoflare train in a loop of total length 90 Mm over an 8 h period. The duration of each nanoflare is 200 s. The panels show the volumetric heating rate and the coronal averaged temperature and density as functions of time. The dashed blue line is the LareJ solution (computed with 500 grid points along the length of the loop with the jump condition employed), the solid blue line is the Lare1D solution (computed with the same spatial resolution as the LareJ solution but without the jump condition employed) and the dot-dashed orange line corresponds to the fully resolved HYDRAD solution. |
4. Non-uniform heating
Having considered the case of uniform heating in Paper I and Sect. 3, we now turn our attention to studying spatially non-uniform heating (e.g. Lionello et al. 2009; Mikić et al. 2013; Reale 2016; Reale et al. 2016). In this section we explore both symmetric and asymmetric heating events within short (60 Mm) and long (180 Mm) loops. The results are summarised in Table 1 and the individual events are described below.
For each case we present key metrics in the table that enable a comparison between the density and temperature attained by the different methods (LareJ, Lare1D and HYDRAD). The latter uses the maximum averaged temperature while the former, in contrast to Paper I, uses the coronal averaged density at the time of the HYDRAD peak value. This is a better metric for the density than using the maximum averaged value (as was done in Paper I) because in many cases the Lare1D density maximum occurs prematurely in the initial response, after which time the accuracy of the solution fails.
Using the metrics it can be seen that the discrepancies between the LareJ and HYDRAD results vary from being small to significant while there is always significant discrepancy between both these methods (LareJ and HYDRAD) and the Lare1D density. Our discussion focusses primarily on the most difficult cases where typically the discrepancies are largest but it should not be ignored that the jump condition method in fact works very well (the errors are smaller) in the majority of the other cases.
The events considered are based on a subset of the cases that were previously studied in Paper I (Cases 3, 5, 9 and 11 there) now referred to as Cases 1–4 respectively. The energy deposition is now localised to one of three distinct spatial locations. These are concentrated at the loop apex and the footpoints, as illustrated for both the short and long loop in Fig. 2. For footpoint heating, we consider profiles that release the energy at the base of the corona (above the top of the TR) and at the base of the TR (i.e. z = zb in the initial equilibrium), which we refer to as fp1 and fp2 heating, respectively.
 |
Fig. 2 Symmetric non-uniform heating profiles Q(z) /QH (left-hand axis), for apex (solid red line), fp1 (base of corona, dashed red line) and fp2 (base of TR, dot-dashed red line) heating (see Sect. 4), imposed on top of the temperature initial condition (solid blue line, right-hand axis). The upper (lower) panel corresponds to a 60 Mm (180 Mm) loop for which we take zH = 0.75 Mm (zH = 1.5 Mm) as the length scale of heat deposition. |
The temporal profile of the energy release is triangular, over a total duration of τH, and the spatial profile is given by, 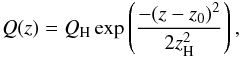 (5)where z0 is the location of maximum heating, zH is the length scale of heat deposition and QH is the maximum heating rate. We relate the results to Paper I by releasing the same total amount of energy in the symmetric non-uniform heating events as was released in the corresponding uniform heating (QU) cases. Hence, the maximum heating rate is calculated as,
(5)where z0 is the location of maximum heating, zH is the length scale of heat deposition and QH is the maximum heating rate. We relate the results to Paper I by releasing the same total amount of energy in the symmetric non-uniform heating events as was released in the corresponding uniform heating (QU) cases. Hence, the maximum heating rate is calculated as, 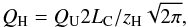 (6)where 2LC is the total coronal length between the TR bases.
(6)where 2LC is the total coronal length between the TR bases.
Asymmetric heating is studied by adjusting the symmetric footpoint heating profiles to release energy only at the left-hand leg of the loop. Thus, the total energy deposited in the asymmetric heating events (referred to as afp1 and afp2 heating) is only 50% that of the symmetric heating counterparts, but the heating at the left footpoint is the same.
4.1. Case 1
Case 1 is representative of a small flare in a short loop. For uniform heating (Paper I), this case proved to be the most challenging one for obtaining agreement between LareJ and HYDRAD. Figure 3 shows the temporal evolution of the coronal averaged temperature (T), density (n) and the corresponding temperature versus density phase space plot, in response to apex, fp1, fp2, afp1 and afp2 heating (Cols. 1–5).
Figure 3 demonstrates the level of agreement between the LareJ and HYDRAD solutions. Starting with the plasma response to apex heating, Col. 1 of Fig. 3 shows that the LareJ density has the same generic evolution with respect to the evaporation required by the heating, the time of peak density and the subsequent decay phase. The discrepancy between the LareJ density and the HYDRAD density is about 30% at the density peak, the source of which will be discussed in detail in Sect. 5 but we note that this is of the same order as found in Paper I. Furthermore, any differences in the temperature are smaller than those in the density, because of its weaker dependency on the spatial resolution for this class of problem (BC13). It can also be seen that LareJ represents a considerable improvement on the Lare1D solution, whose temperature and density suffer from rapid cooling and a premature density peak as noted in Sect. 3.
A summary of the parameter space used and results from the non-uniform heating simulations.
 |
Fig. 3 Results for Case 1. The panels show the coronal averaged temperature and density as functions of time, and the temperature versus density phase space plot. The sub-panels show the time evolution of the coronal averaged temperature over a shorter time interval (the first 200 s). Columns 1–5 correspond to apex, fp1 (base of corona), fp2 (base of TR) afp1 and afp2 (asymmetric) heating, respectively. The dashed blue line is the LareJ solution (computed with 500 grid points along the length of the loop with the jump condition employed), the solid blue line is the Lare1D solution (computed with the same spatial resolution as the LareJ solution but without the jump condition employed) and the dot-dashed orange line corresponds to the fully resolved HYDRAD solution. The total energy deposited in the asymmetric heating events (afp1 and afp2) is only 50% that of the symmetric heating events (apex, fp1 and fp2) because only the left-hand leg of the loop is heated. |
Due to the fact that thermal conduction is very efficient at coronal temperatures, the density response to fp1 heating is similar to apex heating (and both are similar to uniform heating). Following the energy release in fp1 heating there is an upward propagating conduction front that heats the coronal plasma (so the peak temperature is lower than for apex heating) and a downward propagating front that drives the evaporation from the TR. Figure 3 and Table 1 shows that the agreement obtained between the LareJ and HYDRAD solutions (for the fp1 heating event) is similar to apex heating. The Lare1D solution has the same problems as before.
For fp2 heating, the energy deposition is centred on the base of the TR and so is deposited in the chromosphere and UTR. Hence, the coronal plasma is heated by an upward propagating conduction front while simultaneously the evaporation (density front) from the TR is driven by a combination of the local energy release and conductive heating. Therefore, fp2 heating poses different challenges from apex and fp1 heating. In particular a difficulty with fp2 heating is that part of the energy released may be lost to artificially large radiation within the UTR (see Sect. 5.2).
However, Col. 3 in Fig. 3 shows that for the fp2 heating event considered in Case 1, the agreement between the temporal evolution of the LareJ temperature and density and the corresponding HYDRAD quantities is respectable and still significantly better than Lare1D. The fact that the HYDRAD peak temperature now marginally exceeds that of the LareJ solution demonstrates that energy was lost lower down in the UTR (usually the reverse is true, see Table 1), although it was only a small amount for this particular heating event.
The response of the TR to afp1 and afp2 asymmetric footpoint heating is different for each loop leg. On one hand the initial response at the left-hand leg of the loop is equivalent to the symmetric footpoint heating events, while on the other hand the response at the right-hand leg is consistent with a weakened apex heating event because it only undergoes heating following the arrival of the conduction front that is launched from the left-hand leg. In accordance with these differences in the TR response, Fig. 3 shows that for the afp1 and afp2 heating events, the coronal temperature and density peaks are lower than the equivalent symmetric heating quantities. However, the level of agreement between the LareJ and HYDRAD solutions is similar to that discussed above for the symmetric heating events. Thus, the jump condition model can be employed to capture the coronal response to both symmetric and asymmetric non-uniform heating events.
In summary, for Case 1, the jump condition solutions (LareJ) obtain a coronal density comparable to HYDRAD (fully resolved 1D model) but with a significantly faster computation time (the gains are consistent with those presented in Paper I, the speed-up is between one and two orders of magnitude) and the approach significantly improves the accuracy of both the coronal density and temperature evolution when compared to the equivalent simulations run without the jump condition (Lare1D, the solid blue lines). So despite the complexity of the type of heating considered, the jump condition still produces acceptable results when using coarse resolution.
4.2. Case 2
Figure 4 shows the results for Case 2. Here, the total amount of energy released is the same as Case 1 but the heating is slower, taking place over a longer timescale (600 s). When compared with HYDRAD, the performance of the LareJ solution once again shows good agreement, for the apex, fp1 and afp1 heating events. This is expected because the terms that control the evaporation are essentially the same as those in Case 1, but acting over longer timescales.
On the other hand, for the fp2 heating event the LareJ solution has its largest discrepancies (in response to symmetric energy deposition) when compared over the complete heating and cooling cycle with the fully resolved 1D model (HYDRAD). Column 3 in Fig. 4 shows that the temperature is lower and while the density gives a good description up until the time of the maximum, the draining phase begins slightly early. These discrepancies are related to energy losses in the UTR with LareJ. This will be discussed in detail in Sect. 5.2. Similar problems are also observed in the afp2 heating event but the energy losses are more significant for asymmetric footpoint heating (afp2) because there is only one upward propagating conduction front.
However, when we compare the LareJ solution with the equivalent simulation run without the jump condition (Lare1D), it remains clear that we still significantly improve the accuracy of the coronal density. Hence, we capture a more realistic evolution in response to the heating by employing the jump condition (LareJ), despite the energy losses in the UTR.
4.3. Cases 3 and 4
We present the results for the long (180 Mm) loop simulations in Figs. 5 and 6. In all of the ten heating events considered in Cases 3 and 4, the figures show that the LareJ solutions significantly improve the Lare1D results to accurately capture the coronal response of the fully resolved 1D model (HYDRAD). The details are analogous to the short loop simulations previously discussed with only one exception. Namely, in the fp2 and afp2 heating events, the LareJ density peak somewhat underestimates the HYDRAD value whereas in general the reverse is true (see Table 1). The explanation for these two different types of behaviour, over and under-evaporating, will be discussed next in Sect. 5.
5. Discussion of the quantities associated with the UTR jump condition
We now turn to a more detailed discussion of the results obtained with the different methods used in each experiment. The principal issue to be addressed is the discrepancy between the density evolution in LareJ and HYDRAD. In most cases the LareJ peak density exceeds that obtained by HYDRAD (referred to as over-evaporation), although for some footpoint heating cases, the opposite is true (under-evaporation). (The causes for the differences between the under-resolved Lare1D and the other simulations have been discussed earlier and in Paper I and will not be considered further.) This comparison of the models is undertaken through an analysis of the terms associated with the UTR jump condition (3), in particular the various terms in the definition of the terms neglected in LareJ (N: Eq. (2)). The cases where the LareJ density exceeds (falls below) the HYDRAD value are discussed in Sect. 5.1 (5.2).
In general, there are two important terms in N. One is the rate of change of total energy in the UTR (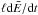 ) and when this is positive (negative), the corrected upflow (v0) in LareJ is enhanced (decreased) over the upflow at the same point in the HYDRAD solution. The second important term in N involves the mass motions at the base of the TR (Fe,b + Fke,b). When the TR moves downwards (upwards) the neglect of this motion in LareJ leads to enhanced (decreased) values of v0. The heat flux at the base of the TR (Fc,b) is negligible for all cases.
) and when this is positive (negative), the corrected upflow (v0) in LareJ is enhanced (decreased) over the upflow at the same point in the HYDRAD solution. The second important term in N involves the mass motions at the base of the TR (Fe,b + Fke,b). When the TR moves downwards (upwards) the neglect of this motion in LareJ leads to enhanced (decreased) values of v0. The heat flux at the base of the TR (Fc,b) is negligible for all cases.
An analysis of the resolved HYDRAD results enables us to quantify the importance of the terms neglected in LareJ, and Fig. 7 shows the quantities obtained by HYDRAD that are present in the UTR equations. The left column shows the various terms from Eq. (2)and the right breaks down N into its important components. Figure 8 shows quantities in Eq. (3)obtained from the HYDRAD and LareJ simulations. The definition of the “UTR” is based on the time evolution of the temperature from the LareJ solution, though of course it is fully resolved in HYDRAD. Apex heating for Cases 1 and 3 are shown in the upper two rows, only for the first 50 s in Case 1 and the first 200 s in Case 3. The lower two rows show the fp2 heating events for Cases 3 and 4 where the LareJ density peak falls below that given by HYDRAD. The first 200 s are shown for Case 3 in row 3 and the first 800 s for Case 4 in row 4. We only consider the time evolution until the first density peak because this time interval is the main source of error in the subsequent peak density.
5.1. Sources of error: over-evaporation (apex & fp1 heating)
For the Case 1 apex heating event, the HYDRAD solution (first row of Fig. 7) shows that following an initial phase where the TR retains its pre-heating properties, the arrival of the coronal conduction front leads to a short interval (12–15s) when the downward heat flux (Fc,0) is balanced by the terms neglected in LareJ (N). This interval is also associated with a small downward enthalpy flux (Fc,0 ≈ 50 | Fe,0 |) that leads to enhanced radiative losses in the UTR. The components of N (right panel) show that in the early phase, the base terms remain unimportant, and the 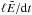 term (change of UTR total thermal energy) dominates. Looking at Fig. 8, we see that with LareJ the initial 12s is similar to HYDRAD, though the radiative losses decrease in the corona and hence our estimate of ℛutr decreases, leading to a small upward enthalpy flux. Then, between 12–15s, LareJ shows a premature upflow with the enthalpy flux being driven immediately by the conductive losses, a direct consequence of the neglect of
term (change of UTR total thermal energy) dominates. Looking at Fig. 8, we see that with LareJ the initial 12s is similar to HYDRAD, though the radiative losses decrease in the corona and hence our estimate of ℛutr decreases, leading to a small upward enthalpy flux. Then, between 12–15s, LareJ shows a premature upflow with the enthalpy flux being driven immediately by the conductive losses, a direct consequence of the neglect of 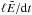 in the jump condition.
in the jump condition.
 |
Fig. 7 Analysis of quantities associated with the UTR jump condition based on fully resolved HYDRAD simulations. Rows 1, 2, 3 and 4 correspond to Case 1 apex, Case 3 apex, Case 3 fp2 and Case 4 fp2 heating, respectively. The left-hand panels show the terms in Eq. (2)that control the plasma response, namely the volumetric heating rate in the UTR ( |
 |
Fig. 8 Comparison of the dominant quantities in the UTR jump condition obtained from the HYDRAD and LareJ solutions. Rows 1, 2, 3 and 4 correspond to Case 1 apex, Case 3 apex, Case 3 fp2 and Case 4 fp2 heating, respectively. From left to right the columns show the heat flux at the top of UTR (Fc,0), volumetric heating rate in the UTR ( |
With HYDRAD, from 15s until the time of the first density peak (100 s), both N and radiative losses decline and become negligible after 50 s, with the downward heat flux driving an upward enthalpy flux. However, it should be noted that up to 40 s, N is still under an order of magnitude smaller than Fe,0 so the retention of these terms in HYDRAD leads to a smaller upflow than in LareJ, as shown in Fig. 8. At later times the HYDRAD values of N are negligible.
The apex and fp1 examples all show broadly similar behaviour: for fp1 heating the UTR is still driven by a downward heat flux. We have provided a summary of this general scenario in Table 2, which breaks down the atmospheric response to impulsive heating into 4 distinct phases that are listed by their time of importance: (i) the initial atmosphere is undisturbed; (ii) a short phase when the UTR internal energy changes are important; (iii) an evaporative phase with the components of N being of diminishing importance leading to (iv) the first and subsequent density peaks. We also note that for stronger (weaker) heating events the terms neglected in LareJ are more (less) important so the errors at the peak density are larger (smaller): see Table 1 in Paper I.
However, within this framework, there are some subtle differences between short and long loops for apex and fp1 heating. One is that in the long loop examples, the heat flux that hits the UTR is systematically smaller because the total energy released is chosen to be lower. Therefore, there is less reaction at the base to the incoming heat flux which in turn means that the neglect of N in LareJ is less important and smaller errors in the peak density arise (Table 1). This suggests that an important parameter is the “thermal energy impulse” on the UTR, defined as 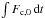 .
.
The second minor (and related) exception arises for the Case 3 apex example (short heating pulse in a long loop). In this case, the conductive travel time along the loop is longer than the half width duration of the heating pulse. From the second row of Figs. 7 and 8, as well as Table 3, we see that the LareJ upflow is no longer enhanced over that obtained by HYDRAD because the energy input into the UTR is not sustained. What is seen in Fig. 7 is not in fact a decrease in the importance in N, but instead a deficit in the dominant terms from the jump condition. A similar argument also applies to the fp1 heating event for Case 3 but for the return time of the upward propagating conduction front.
5.2. Sources of error: under-evaporation (fp2 heating)
As already noted, footpoint heating at the base of the TR (fp2) is the most challenging case but a broad outline of the results is as follows. There is over-evaporation in a number of cases but we also now find cases with LareJ with (1) under-evaporation and (2) an underestimation of the coronal temperature. An important aspect of this is the update calculation of radiation within the UTR in LareJ (see Appendix A, Paper I, and Sect. 2) which can lead to artificially high radiative losses in the UTR that are consistent with the coarse spatial resolution used (e.g. BC13, Paper I). The HYDRAD solutions enable us to quantify this error which is limited to only the fp2 heating examples.
So the difficulty with fp2 heating is that part of the energy released during the heating event (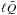 ) may be lost due to (artificially high) radiation in the UTR rather than transported to the corona by heat conduction, and the LareJ solutions indeed have a spurious reduction of the heat flux into the corona (Fc,0). This also provides the explanation for the underestimation of the coronal temperature. Furthermore, it is clear from Eq. (3)that any reductions in Fc,0 may then also affect the upflow.
) may be lost due to (artificially high) radiation in the UTR rather than transported to the corona by heat conduction, and the LareJ solutions indeed have a spurious reduction of the heat flux into the corona (Fc,0). This also provides the explanation for the underestimation of the coronal temperature. Furthermore, it is clear from Eq. (3)that any reductions in Fc,0 may then also affect the upflow.
For the Case 3 fp2 heating event, the HYDRAD solution shows that for a short interval (0–10 s) at the start of the heating period, the local energy released (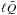 ) is balanced by N (with
) is balanced by N (with 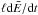 the dominant term as above). In contrast, Fig. 8 shows that the LareJ solution starts with a premature upflow (0–10 s) that is powered by
the dominant term as above). In contrast, Fig. 8 shows that the LareJ solution starts with a premature upflow (0–10 s) that is powered by 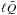 precisely because the
precisely because the 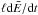 term is neglected. At 10 s an upflow begins in HYDRAD which remains present until 230 s. In this evaporation phase, the upward enthalpy flux is first driven for a short time (10–60 s) by the total local heating (
term is neglected. At 10 s an upflow begins in HYDRAD which remains present until 230 s. In this evaporation phase, the upward enthalpy flux is first driven for a short time (10–60 s) by the total local heating (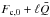 ) and then for a much longer period (60–200 s) by the terms associated with N. During this longer period,
) and then for a much longer period (60–200 s) by the terms associated with N. During this longer period, 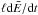 first peaks as a negative term at 60 s due to the rapid drop off in the energy release (
first peaks as a negative term at 60 s due to the rapid drop off in the energy release (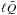 ).
). 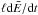 then balances Fe,0 from 60–100 s. After 100 s the enthalpy flux at the base becomes important as the TR moves back upwards (following the end of the heating) and the base motions take over the driving of the upward enthalpy flux. On the other hand, the jump condition does not model this part of the upflow. Hence, the LareJ solution underestimates Fe,0 for the duration of this period (60–200 s), as can be seen in Fig. 8.
then balances Fe,0 from 60–100 s. After 100 s the enthalpy flux at the base becomes important as the TR moves back upwards (following the end of the heating) and the base motions take over the driving of the upward enthalpy flux. On the other hand, the jump condition does not model this part of the upflow. Hence, the LareJ solution underestimates Fe,0 for the duration of this period (60–200 s), as can be seen in Fig. 8.
For the Case 4 fp2 heating, the HYDRAD solution shows generally a similar response, however, in this slower heating event, the main evaporation phase takes place between 50–600 s, with the upward enthalpy flux driven by the total local heating (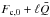 ). In contrast, these local heating mechanisms do not have equal weighting in driving the LareJ evaporation. Figure 8 shows that from 50–600 s, a somewhat overestimated
). In contrast, these local heating mechanisms do not have equal weighting in driving the LareJ evaporation. Figure 8 shows that from 50–600 s, a somewhat overestimated 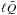 dominates a significantly underestimated Fc,0. This behaviour arises as a direct consequence of the artificial energy losses in the UTR. The outcome is that LareJ underestimates the upward enthalpy flux between 200–600 s.
dominates a significantly underestimated Fc,0. This behaviour arises as a direct consequence of the artificial energy losses in the UTR. The outcome is that LareJ underestimates the upward enthalpy flux between 200–600 s.
The quantities that control the evaporation in response to fp2 heating are predominantly the same for short and long loops. They are summarised together in Table 3 which shows additional subtleties. For example, LareJ overestimates the initial upward enthalpy flux in Cases 1 and 2 for the reasons discussed in Sect. 5.1 but underestimates Fe,0 at later times due to the behaviour described above in this section for slow and fast heating. The net effect is for a reduced over-evaporation in comparison to the corresponding apex and fp1 heating events.
6. Conclusions
We introduced the jump condition approach for 1D hydrodynamic modelling in Paper I. This is a simple method that can be employed with an under-resolved TR to deal with the difficulty of obtaining the correct interaction between a downward conductive flux and the resulting upflow. Thus, the evaporative response to a coronal heating event can be modelled without fully resolving the TR (BC13). In this further analysis of the method, the experiments presented were selected to be some of the most challenging cases.
In all of the experiments considered, the jump condition approach leads to coronal densities that are comparable to fully resolved 1D models (HYDRAD) but with computation times that are between one and two orders of magnitude faster. Therefore, the applicability of the jump condition is not limited by introducing complexities, both spatially and temporally, in the energy release (heating).
On the other hand, the densities are predominantly higher than those from a fully resolved 1D code (HYDRAD in this case) which is explained by the presence of an overestimated upward enthalpy flux. This can be attributed to the neglect of terms corresponding to the rate of change of total energy in the unresolved atmosphere and mass motions at the base of the TR. It would certainly be advantageous to include these terms in the jump condition in order to remove the over-evaporation. However, if we could calculate these neglected terms accurately then it would not be necessary to implement such an approach. Furthermore, the interaction between these terms is such that either both must be included or neither. Of course at some point diminishing returns will be reached and or the simplicity of the method weakened.
Despite the (relatively small) remaining error when comparing with a fully resolved 1D code (HYDRAD), the implementation of the jump condition leads to a significant improvement compared with the equivalent (coarse resolution) simulations run without the jump condition. Both the coronal density and temperature evolution are comparable with those obtained from fully resolved simulations, especially at the time of peak density and throughout the draining phase for both uniform (Paper I) and non-uniform heating (this paper).
Acknowledgments
The authors are grateful to Dr. Stephen Bradshaw for providing us with the HYDRAD code. We also thank the referee for their helpful comments that improved the presentation. C.D.J. acknowledges the financial support of the Carnegie Trust for the Universities of Scotland. This project has received funding from the Science and Technology Facilities Council (UK) through the consolidated grant ST/N000609/1 and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 647214).
References
- Antiochos, S. K., & Sturrock, P. A. 1978, ApJ, 220, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, W. T., Cargill, P. J., & Bradshaw, S. J. 2016, ApJ, 833, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bourdin, P.-A., Bingert, S., & Peter, H. 2013, A&A, 555, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Mason, H. E. 2003, A&A, 407, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2006, A&A, 458, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2010a, ApJ, 710, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2010b, ApJ, 717, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2013, ApJ, 770, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Viall, N. M. 2016, ApJ, 821, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Bradshaw, S. J., & Klimchuk, J. A. 2012a, ApJ, 752, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Bradshaw, S. J., & Klimchuk, J. A. 2012b, ApJ, 758, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Warren, H. P., & Bradshaw, S. J. 2015, Phil. Trans. Roy. Soc. Lond. Ser. A, 373, 20140260 [Google Scholar]
- Dahlburg, R. B., Einaudi, G., Taylor, B. D., et al. 2016, ApJ, 817, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Hansteen, V., Guerreiro, N., De Pontieu, B., & Carlsson, M. 2015, ApJ, 811, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Cargill, P. J., Browning, P. K., & Tam, K. V. 2016, ApJ, 817, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, C. D., Hood, A. W., Cargill, P. J., & De Moortel, I. 2017, A&A, 597, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klimchuk, J. A., Patsourakos, S., & Cargill, P. J. 2008, ApJ, 682, 1351 [Google Scholar]
- Lionello, R., Linker, J. A., & Mikić, Z. 2009, ApJ, 690, 902 [CrossRef] [Google Scholar]
- Mikić, Z., Lionello, R., Mok, Y., Linker, J. A., & Winebarger, A. R. 2013, ApJ, 773, 94 [NASA ADS] [CrossRef] [Google Scholar]
- O’Hara, J. P., & De Moortel, I. 2016, A&A, 594, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 94 [Google Scholar]
- Reale, F. 2016, ApJ, 826, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., Orlando, S., Guarrasi, M., et al. 2016, ApJ, 830, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Reep, J. W., Bradshaw, S. J., & Klimchuk, J. A. 2013a, ApJ, 764, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Reep, J. W., Bradshaw, S. J., & McAteer, R. T. J. 2013b, ApJ, 778, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., Brooks, D. H., & Winebarger, A. R. 2011, ApJ, 734, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., Winebarger, A. R., & Brooks, D. H. 2012, ApJ, 759, 141 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
A summary of the parameter space used and results from the non-uniform heating simulations.
All Figures
 |
Fig. 1 Coronal response of the plasma to a nanoflare train in a loop of total length 90 Mm over an 8 h period. The duration of each nanoflare is 200 s. The panels show the volumetric heating rate and the coronal averaged temperature and density as functions of time. The dashed blue line is the LareJ solution (computed with 500 grid points along the length of the loop with the jump condition employed), the solid blue line is the Lare1D solution (computed with the same spatial resolution as the LareJ solution but without the jump condition employed) and the dot-dashed orange line corresponds to the fully resolved HYDRAD solution. |
| In the text | |
 |
Fig. 2 Symmetric non-uniform heating profiles Q(z) /QH (left-hand axis), for apex (solid red line), fp1 (base of corona, dashed red line) and fp2 (base of TR, dot-dashed red line) heating (see Sect. 4), imposed on top of the temperature initial condition (solid blue line, right-hand axis). The upper (lower) panel corresponds to a 60 Mm (180 Mm) loop for which we take zH = 0.75 Mm (zH = 1.5 Mm) as the length scale of heat deposition. |
| In the text | |
 |
Fig. 3 Results for Case 1. The panels show the coronal averaged temperature and density as functions of time, and the temperature versus density phase space plot. The sub-panels show the time evolution of the coronal averaged temperature over a shorter time interval (the first 200 s). Columns 1–5 correspond to apex, fp1 (base of corona), fp2 (base of TR) afp1 and afp2 (asymmetric) heating, respectively. The dashed blue line is the LareJ solution (computed with 500 grid points along the length of the loop with the jump condition employed), the solid blue line is the Lare1D solution (computed with the same spatial resolution as the LareJ solution but without the jump condition employed) and the dot-dashed orange line corresponds to the fully resolved HYDRAD solution. The total energy deposited in the asymmetric heating events (afp1 and afp2) is only 50% that of the symmetric heating events (apex, fp1 and fp2) because only the left-hand leg of the loop is heated. |
| In the text | |
 |
Fig. 4 Results for Case 2. Notation is the same as Fig. 3. |
| In the text | |
 |
Fig. 5 Results for Case 3. Notation is the same as Fig. 3 but note the different time axis. |
| In the text | |
 |
Fig. 6 Results for Case 4. Notation is the same as Fig. 3 but note the different time axis. |
| In the text | |
 |
Fig. 7 Analysis of quantities associated with the UTR jump condition based on fully resolved HYDRAD simulations. Rows 1, 2, 3 and 4 correspond to Case 1 apex, Case 3 apex, Case 3 fp2 and Case 4 fp2 heating, respectively. The left-hand panels show the terms in Eq. (2)that control the plasma response, namely the volumetric heating rate in the UTR ( |
| In the text | |
 |
Fig. 8 Comparison of the dominant quantities in the UTR jump condition obtained from the HYDRAD and LareJ solutions. Rows 1, 2, 3 and 4 correspond to Case 1 apex, Case 3 apex, Case 3 fp2 and Case 4 fp2 heating, respectively. From left to right the columns show the heat flux at the top of UTR (Fc,0), volumetric heating rate in the UTR ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


