| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629881 | |
| Published online | 14 September 2017 | |
Comparison of different populations of granular features in the solar photosphere
1 INAF–Osservatorio Astronomico di Roma, via Frascati 33, 00078 Monte Porzio Catone, Italy
e-mail: mfalco@oact.inaf.it
2 Dipartimento di Matematica e Informatica, Università di Cagliari, via Ospedale 72, Cagliari, Italy
3 Dipartimento di Fisica e Astronomia, Sezione Astrofisica, Università di Catania, via S. Sofia 78, 95123 Catania, Italy
4 INAF–Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
Received: 11 October 2016
Accepted: 27 March 2017
Context. The granulation is the most visible manifestation of convective motions occurring in the uppermost layers of the solar convection zone. Strong magnetic fields hinder these motions, but the appearance of bright structures such as umbral dots (UDs) and light bridges (LBs) in sunspots also shows that in strong magnetic field regions, the convection is not completely suppressed.
Aims. We aim to investigate the properties of the granules identified by a new segmentation algorithm in regions characterized by different magnetic field strength, in order to improve the current knowledge of the mechanism behind the appearance of the different bright structures in sunspots.
Methods. We analyzed data acquired by the CRisp Imaging SpectroPolarimeter at the Swedish Solar Telescope on 6 August 2011 relevant to a large sunspot with a LB observed in NOAA AR 11263. We applied a new segmentation algorithm to the data acquired along the Fe I 630.15 nm line.
Results. We found that the granules in the LB have a diameter between 0.̋22 and 0.̋99, that is, smaller than the granules in a nearby plage region (PL) and similar to those of the UDs. We observed values of the mean continuum intensity between 0.42 Ic and 0.98 Ic for the LB granules, which are similar to those of the UDs. PL granules have higher values, probably reflecting different conditions of the plasma convection. Mean Doppler velocity and mean magnetic field strength have been studied and even for these physical parameters we found similar values between LB granules and UDs.
Conclusions. Different values for the physical properties analyzed have been found between the granules of the PL and LB granules of the three analyzed solar regions. In particular, we show that the granules in PL and sunspot regions have different physical properties. This clearly depends on the different physical conditions of the regions where these two kind of granular structures are embedded. We also confirm the recent findings on the similarity between granules in PL and quiet Sun regions. We show values of the various physical quantities analyzed in PL granules in agreement with those reported in the literature for quiet Sun granules. Finally, a noteworthy result is that the granules observed in the faint LB have physical properties similar to those found for UDs.
Key words: Sun: granulation / Sun: photosphere / sunspots
© ESO, 2017
1. Introduction
Properties of the quiet Sun granules reported in the literature.
High resolution observations show that the solar surface is covered by a pattern of bright cellular elements called granules, surrounded by a network of dark intergranular lanes. What we see is the convective overshoot of the heat gas flow from the solar convection zone into the atmosphere. The organization and evolution of the surface granular cells reflect the physics of the upper convective layers, but have also effects on higher solar atmospheric layers, transferring energy and momentum (Muller 1999). On the other hand, numerical simulations of solar granulation (see e.g., Nordlund et al. 2009, for a review) show that the granular pattern is mainly a surface phenomenon, driven by effective radiative cooling in the photophere.
Statistical analyses have been carried out to understand the behavior of the solar granulation and their results support the hypothesis that the solar granulation is produced by several interacting physical processes instead of being one single phenomenon: large-scale mechanisms, such as convection, and small-scale mechanisms, such as turbulence. Moreover, the geometric and thermodynamical properties are strongly dependent on the spatial scale of every single grain (Hirzberger et al. 1997).
From an observational point of view, the main problems in the study of the solar granules are: i) the necessity of high resolution observations due to the small size of the granules (of the order of few arcseconds) and ii) the identification of the single granule, which depends on the method applied. Different approaches for the segmentation of solar features are reported in literature, starting from Roudier & Muller (1986), Strous (1995), Hirzberger et al. (1997, 1999a,b), Bovelet & Wiehr (2001) to the more recent algorithm presented by Berrilli et al. (2005).
In the past a number of studies on the properties of granulation on quiet Sun regions (QSGs) have been performed. In particular, these studies concern investigation on size, continuum intensity and line-of-sight (LOS) velocity of the identified granules. Table 1 summarizes the results from the most significant published studies, and the main characteristics of the analyzed data and applied methods. If we consider the most recent results, according to Brandt (2001) the observed size of granules in the quiet Sun covers a range from approximately 0.̋2 to 3.̋4, while Hirzberger (2002) found values in the range of 0.̋17 to 1.̋9. Moreover, studies curried out by Jin et al. (2009) found that the observed size of granules in the quiet Sun have a peak at 1.̋50, while Yu et al. (2011) found values in the range 0.̋31 and 3.̋75.
A study of the brightness of the solar granulation has been done by Hirzberger (2002) who found that the mean intensity distribution in a granule is between 0.85 Ic and 1.15 Ic, with an average value at 0.99 Ic (here Ic is the mean continuum intensity). The granular relative intensity with respect to the mean intensity in the quiet Sun was also studied by Jin et al. (2009). They found that some granules are darker than the mean photosphere and that the relative intensity of granules spans the range from 0.97 Ic to 1.14 Ic, with a peak distribution at 1.07 Ic. Moreover, studies carried out by Yu et al. (2011) found that the mean intensity values of granules in the quiet Sun cover the range from 0.91 Ic to 1.13 Ic (see Table 1).
According to Hirzberger (2002), the Doppler velocities of the granules in the quiet Sun seem to be symmetrically distributed around zero. The slope toward negative velocities (indicating upward motions) is significantly steeper than toward positive velocities (referring to downflows). The velocities in the solar granulation cover a range between ± 1.5 km s-1 with a peak at −0.15 km s-1. Moreover, the intensity and the velocity distribution within the granules depend on the granular size: in small granules the maximun intensity and maximum upward velocity are located close to the granular barycenters, while in large granules the brightest parts and maximum upward velocity are shifted toward the granular boundaries (Hirzberger 2002). Jin et al. (2009) show that the granular motion ranges from −3.3 km s-1 (blueshift) to 2.0 km s-1 (redshift) with a peak at −1.0 km s-1. Yu et al. (2011) find values of the Doppler velocity in quiet Sun granules in the range between −2.16 km s-1 and 2.98 km s-1. Lagg et al. (2014) find that in quiet-Sun granules the upflow velocities in the interiors of the granules reach the maximum value of −2.0 km s-1 in the deepest layers and −1.0 km s-1 in the top layers.
Properties of the umbral dots reported in the literature.
Even if previous studies have pointed out that the solar granulation phenomenon is quite well understood, its interaction with the magnetic fields needs further investigations. According to numerical simulations of magnetoconvection (see e.g., Nordlund et al. 2009, for a review), the convective cells are prevented from expanding in presence of a magnetic field concentration (e.g., inside the umbra of a pore or sunspot). Indeed, in presence of a low field strength, the magnetic field is dominated by the convective flow and the growing convective cells push the magnetic field into narrow lanes that surround them.
Recently, Lagg et al. (2014) studied the physical properties of the granulation in a plage region (PL) and in the quiet Sun, finding similarity between the two types of granulation. According to Lagg et al. (2014), LOS velocities in the QSGs and in the PL granules (PLGs) show the typical properties of a central upflow surrounded by downflows in the intergranular lanes. The reported Doppler velocity values in the interior of PLGs are about −1.0 km s-1, while in the boundary Doppler velocity values are about 2.0 km s-1. However, Lagg et al. (2014) show that the magnetic properties of QSGs and PLGs are different. QSGs show a field-free interior and only a weak field of 100 G in the intergranular lanes. Conversely, the boundaries of PLGs show a magnetic field strength a few hundred G higher than QSGs. Moreover, in the interior of PLGs there is an enhanced horizontal magnetic field. Lagg et al. (2014) also remarked that PLGs appear smaller in size, on average, than the QSGs.
In general, the comprehension of the physical mechanisms responsible for the formation and evolution of sunspots has been greatly improved thanks to high temporal, spatial and spectral resolution data. These observations have unveiled some physical properties of several fine structures of the sunspots such as umbral dots (UDs), the small and isolated bright features often observed in the umbra. UDs are convective phenomena and observations are important in order to know whether or not the properties depend on umbral magnetic field strengths (Ji et al. 2016). Different researchers tried to study the UDs physical parameters, but this investigation is complicated due to their size at the limit of the spatial resolution achieved by current telescopes. The results of the UDs physical properties obtained in the last decade are summarized in Table 2. Taking into account the most recent results, the UDs diameters observed by Kilcik et al. (2012) cover the range between 0.̋23 and 0.̋41. A different result was found by Watanabe et al. (2012), who found diameter values between 0.̋53 and 0.̋55. Recently, investigations on UDs properties carried out by Ji et al. (2016) show diameter values between 0.̋2 and 0.̋4.
Bharti et al. (2010) carried out studies on simulated UDs and they found UDs intensity stationary values of about 0.23 Ic and 0.26 Ic. Other authors studied the mean UDs intensity referring to the adjacent umbral background. The UDs mean intensity obtained by Watanabe et al. (2012) is 1.46–1.50 Iud/Ibg, where Iud is the maximum umbral dot intensity and Ibg is the adjacent umbral background, while the results obtained by Ji et al. (2016) indicate that the UDs intensity is in the range between 1.05 Iud/Ibg and 1.15 Iud/Ibg. Among the physical properties, the study of Doppler velocities inside UDs was carried out by several authors. Sobotka & Jurčák (2009) find values of the Doppler velocities in the range −0.6 km s-1 and 0.1 km s-1. The results obtained by Ortiz et al. (2010) show that the upflows reach up to 1.4 km s-1, while the downflows show values of around 0.4 km s-1 and 1.0 km s-1 at the 80% of intensity. Downflows are observed in MHD simulation by Schüssler & Vögler (2006), but not in all the observation. Sobotka & Jurčák (2009) study the physical properties of central umbral dots (CUDs) and periferical umbral dots (PUDs) and also of penumbral granules (PGs) which become PUDs with time. They find a magnetic field strength of about 2500 G and 2700 G for CUDs, while for PUDs they found values between 1900 G and 2300 G. The values found for PG which become PUDs are in the range between 1500 G and 2000 G. Moreover, Watanabe et al. (2012) find UDs magnetic field strength in the range of about 1000 G and 2500 G and they divided relatively weak UDs (≤2000 G) from strongly magnetized UDs (≥2000 G).
Light bridges (LBs) are also fine structures observed in sunspots. These are bright and elongated features delineating the border between dark umbral cores. Granulation is also present in LBs, where the magnetic field strength is significantly reduced in photosphere and has a cusp-like configuration at higher layers (Jurčák et al. 2006). In LBs the size of the granules is used to categorize the LB in two main classes: faint light bridges (FLBs, Lites et al. 1991; Sobotka et al. 1993; Sobotka & Puschmann 2009) and granular light bridges (GLBs, Lites et al. 1991; Sobotka et al. 1994; Leka 1997; Rouppe van der Voort et al. 2010). The FLBs are elongated structures composed by granules of similar size and structure like UDs, while the GLBs show granules similar to the quiet solar granulation. Sobotka & Puschmann (2009) found similar values for the lifetime, size and horizontal velocities in UDs and in the granules of a FLB. The mean lifetime of the granules of FLBs is beetween 3.5 and 5.7 min and the average size is about 0.̋17. The Doppler velocity in SLB and FLB granules shows central upflows surrounded by downflows. According to Louis et al. (2009) and Bharti et al. (2013) the downflows can reach supersonic speeds. For instance, Lagg et al. (2014) found downflow velocities which exhibit values of 10 km s-1 in the boundaries of GLB granules. However, the study of LBs granulation properties needs a more accurate investigation.
Convective motions are of great importance for detailed structure and dynamics of many different phenomena observed in the solar surface layers, for example, the evolution of the magnetic regions, the generation and propagation of waves. Improving current knowledge of plasma properties in granulation embedded in different regions of the solar atmosphere provides to better understand the mechanisms of plasma-magnetic field interplay. In this scenario, our paper concentrates on the comparison of three different populations of granular features that are observed in the solar photosphere: the granules of the plage, the granules of a FLB observed in a decaying sunspot and the UDs observed in the umbra of the same sunspot. In Sect. 2 we present the high spatial resolution dataset used in this work. The most relevant aspect of this dataset is the presence, in the same FOV, of the three photospheric stuctures that we want to study. The data we studied were also taken under excellent seeing conditions during the acquisition of the analyzed sequence. We applied to the three regions studied the same identification algorithm which is described in Sect. 3. In Sect. 4 we show the obtained results and in Sect. 5 we draw our conclusions.
2. Observations and data reduction
We analyzed a dataset acquired on August 6, 2011 with the CRisp Imaging Spectropolarimeter (CRISP, Scharmer et al. 2008) mounted at the Swedish Solar 1-m Telescope (SST, Scharmer et al. 2003). The CRISP spectropolarimetric measurements were taken from 09:53:32 UT to 10:48:43 UT along the Fe I line pair at 630.15 nm in 15 spectral points, with steps of 4.4 pm from −26.8 pm to 34.8 pm with respect to the line center. At this wavelength, the CRISP transmission profile has a FWHM of 6.4 pm. The pixel size of the CRISP cameras at 630.15 nm was 0.̋06. The field of view (FOV) of the SST measurement was 57.̋5 × 57.̋3. For more details about the dataset, see Falco et al. (2016).
In this paper we studied the active region (AR) NOAA 11263 observed at solar coordinates (N16, W45) and we analized the best seeing sequence observed with the Fe I line at 630.15 nm. The AR, on August 6, presented a large negative polarity sunspot with a FLB dividing the umbra in two parts. This sunspot is in a decaying phase. On August 3 the sunspot presented a well-defined umbra and penumbra, while on August 4 it started to fragment. The penumbral filaments in the north-western part of the spot seem to penetrate the umbral region and on August 5 the sunspot exhibited two umbral regions inside the same penumbra: an elongated eastern umbra and another, in the western part, with a circular shape. For more details about the evolution of this sunspot, see Falco et al. (2016).
The data were processed using the CRISPRED reduction pipeline (de la Cruz Rodríguez et al. 2015). In order to achieve the highest spatial resolution in combination with the adaptive optics, the SST data have been processed using the Multi-Object Multi-Frame Blind Deconvolution (MOMFBD, van Noort et al. 2005) technique.
We applied the Very Fast Inversion of the Stokes Vector (VFISV, Borrero et al. 2011) code to the SST sequence acquired at 10:17 UT, to obtain the map of the magnetic field strength in the SST FOV. The VFISV code performs a Milne-Eddington inversion of the data using the full SST/CRISP spectropolarimetric profiles along the Fe I 630.15 nm line. The version of VFISV code that we used does not implement the option of considering straylight contamination. However, according to Scharmer et al. (2013) the straylight contamination of CRISP dataset is less than 1%.
The intensity values were normalized to the average continuum intensity of the undisturbed photosphere present in the FOV. To study the kinematics of UDs, granules in the LB region and in the quiet-Sun region, we derived the Doppler velocity of plasma motions by applying a Gaussian fit to the Fe I line profile at 630.15 nm using the MPFIT routine (Markwardt 2009) in IDL. The LOS velocity map was calibrated by subtracting the mean velocity of the pixels of a region of quiet Sun in the FOV and by appling the correction due to the convective blueshift. This correction was calculated using the tabulated values of Balthasar (1988) for the portion of the sunspot on the solar disk (μ = 0.76). In the calculation of the quiet Sun velocities the p-modes were not removed because we did not compare LOS velocities among single granules, but we analyzed the LOS velocity mean values of each sub-FOV. Therefore, we note that the velocity values may be influenced by the p-modes.
 |
Fig. 1 3D intensity image. The x and y axis are in pixels units, while the z axis is in DN. The pixel size of the CRISP camera is 0.̋06. Granules are clearly visible as peaks. |
3. Identification of the granules
 |
Fig. 2 Examples of steps of the image processing: a) overall image segmentation based on the local maxima previously located (in light blue); b) first refinement based on slope analysis; c) final labeling. The FOV of the three images is 256 × 256 pixels which corresponds to 15.̋1× 15.̋1. |
In order to identify the granules in our FOV we developed a new automatic technique. As clearly shown in Fig. 1, centers of granules correspond to peaks in the intensity image. This information has been exploited in the design of the developed algorithm. Specifically, our method consists of the following steps:
-
Gaussian filtering;
-
local maxima identification;
-
image segmentation;
-
region refinement based on slope analysis;
-
region refinement based on intensity histogram thresholding.
To reduce the noise in the original image and remove secondary local maxima, a Gaussian filtering is first applied. Once the image has been filtered, the algorithm finds local maxima. The image is then partitioned into N regions (one for each local maximum). This segmentation is performed dividing the intensity image into M sets. Specifically, these sets of points are derived from the intensity image I as follows: 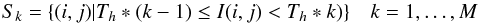 (1)where Th = max(I) /M.
(1)where Th = max(I) /M.
 |
Fig. 3 Example of average intensities of concentric annuli a) and the related differences b). A red line is overimposed to represent the adopted threshold. |
At the beginning, only local maxima are marked with different labels li ∈ { 1,2,...,N }, where N is the number of the regions to be found. Starting from the highest to the lowest set (i.e., from SM to S1), unlabeled pixels are assigned to the nearest regions considering the related boundaries. Specifically, at the generic iteration k, for each pixel p ∈ Sk, the Euclidean distance with respect to all the already assigned (i.e., labeled) pixels at the previous iteration (i.e., k−1) is exploited to perform the assignment task. Unlabeled pixels are hence assigned to the nearest region boundary.
As can be noted from Fig. 2a, the performed segmentation partitions the overall image into disjoint regions that can be used to properly identify pixels belonging to granules. Actually, each region contains both granular and background pixels. The latter correspond to pixels of the umbra which have a continuum intensity lower than 0.4 Ic in the study of FOVLB and FOVUDs, while, for the FOVPL background pixel correspond to local minimum pixels. Further refinements have hence to be applied. The first refinement is based on slope analysis. For each region, consecutive annuli with center located in the related local maximum are considered and the average intensity of pixels in each annulo is then computed (see Fig. 3a). The refinement is then performed analyzing the plot of the aforementioned intensities. Specifically, differences between the average intensity derived from consecutive annuli are computed (Fig. 3b) and are considered as granules only the pixels belonging to annuli maintainig a slope value above a fixed threshold.
As can be seen in Fig. 2b, some residual pixels belonging to background are not properly identified in the granular pattern. For example, the granule which has coordinates (250, 180) includes inside its contours also background pixels. A further step is then applied exploiting Otsu algorithm (Otsu 1979). This method, starting from the image histogram and considering two classes (i.e., granular and background pixels in our work), computes the optimal threshold that divides them. In the Otsu method an exhaustive search is performed to find the intensity threshold t that minimizes intra-class variance (maximizes inter-class variance) defined as follows: 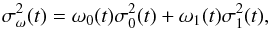 (2)where ω0 and ω1 (probabilities of the two classes) are computed from a L bins histogram:
(2)where ω0 and ω1 (probabilities of the two classes) are computed from a L bins histogram: 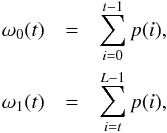 (3)and
(3)and 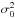 ,
, 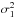 are the related variances. Moreover, p(i) = ni/N, where ni is the number of pixels of intensity i and N is the total number of pixels in the image.
are the related variances. Moreover, p(i) = ni/N, where ni is the number of pixels of intensity i and N is the total number of pixels in the image.
An example of the obtained results is reported in Fig. 2c.
4. Results
A map of the continuum intensity of the observed sunspot is shown in Fig. 4.
The sizes of the FOVs analyzed were: 391 × 191 pixels (23.̋03 × 11.̋25) for FOVUD, 136 × 46 pixels (8.̋01 × 2.̋71) for FOVLB and 166 × 361 pixels (9.̋78 × 21.̋26) for FOVPL. These FOVs have been selected with the described dimensions in order to analyze a significant statistical number of elements. The UDs, LBGs and PLGs were identified using the algorithm described in Sect. 3. We applied a treshold of 0.01 for the differences of annulus average intensities in the FOVLB and FOVUD to obtain a coherent segmentation of the elements.
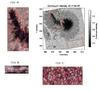 |
Fig. 4 Continuum intensity map of the preceeding sunspot of AR NOAA 11263 obtained by CRISP in the Fe I 630.15 nm line at 10:17 UT on the August 6, 2011. The solid boxes A–C indicate the FOVUD, FOVLB and FOVPL, respectively, that are analyzed in the following. North is on the top, west is at the right. The arrow labeled DC indicates the direction of disk center. |
The granules which are not located entirely inside each FOV have been omitted from the analysis. The diameter of each granule was calculated considering an ideal circular shape of the granule and using the formula: D = 2(A/π)1/2, where A is the area covered by the pixels corresponding to each granule. We considered only the granules with a diameter larger than 0.̋18, which is the spatial resolution of the SST telescope. To avoid projection effects due to the location on the solar disk of the FOV, we divided the granules area by the cosine of the heliocentric angle: μ = cos(θ) = 0.76. The number of granules studied in the FOVUD, FOVLB and in the FOVPL is 57, 41 and 217, respectively. Taking into account that the number of granules is not exactly the same in each sample we consider in the following the normalized probability distributions. In this work we study the mean continuum intensity, shown in Fig. 4, the magnetic field strength and the Doppler velocity, shown in Fig. 5, for the three regions taken into account.
 |
Fig. 5 Magnetic field strength map (left panel) and Doppler velocity map (right panel) of the preceding sunspot of AR NOAA 11263. As in Fig. 4, the solid boxes A–C indicate the FOVUD, FOVLB and FOVPL, respectively, that are analyzed in the following. |
 |
Fig. 6 Diameter (top-left panel), mean continuum intensity (top-right panel), mean Doppler velocity (bottom-left panel) and mean magnetic field strength (bottom-right panel) normalized distributions corresponding to the UDs (green), LBGs (red) and PLGs (black) analyzed. |
The magnetic field strength map (Fig. 5, left panel) shows the presence of higher magnetic filed strength inside the umbra regions, while in penumbra and in the plage regions the magnetic field strength is reduced. The magnetic field strength map indicates that in the LB region the magnetic field strength is lower than in the surroundings due to a convection re-establishment. The Doppler velocity map (Fig. 5, right panel) shows the typical upflow and downflow motions in the plage regions, the redshift and blueshif caused by the Evershed effect in the penumbra regions and an almost zero velocity in the umbra regions. In the LB and UDs regions are visible upflow and downflow motions due to plasma coming up from the convection zone. In Fig. 6 we show the normalized distribution of the physical parameters estimated for the granules analyzed in the three selected FOVs.
The distribution of the size of UDs, LBGs and PLGs is different, as shown in Fig. 6 (top-left panel). The LBGs are on average smaller than PLGs and slightly larger than UDs. In particular, the range of diameter values for the LBGs is between 0.̋25 and 1.̋14, while the range of diameter values for PLGs is larger and covers values from 0.̋31 to 2.̋36.
Properties of the umbral dots, light bridge granules and plage granules analyzed in our study.
In Fig. 6 (top-right panel) we show the normalized distribution of the mean continuum intensity studied for UDs, LBGs and PLGs. The PLGs have values of the mean continuum intensity between 0.88 Ic and 1.08 Ic with a peak around 1.0 Ic, showing a similarity with the results presented by Jin et al. (2009) for the QSGs, while the mean continuum intensity of LBGs spans between 0.42 Ic and 0.98 Ic. It is worthy of note that the LBGs show a wider range of intensity values than PLGs. A similar distribution is found for the UDs continuum intensity, but the values are between 0.23 Ic and 0.89 Ic.
The distribution of the mean Doppler velocity studied for UDs, LBGs and PLGs is shown in Fig. 6 (bottom-left panel). We stress that in each granule there are upflow (mostly in the center) and downflow (at the edges) motions and in Fig. 6 (bottom-left panel) and in our analysis we averaged the Doppler velocity inside each granule showing the mean value of these motions. The Doppler velocities of PLGs cover a range between −1.44 km s-1 and + 1.26 km s-1; the ones of UDs between −1.09 km s-1 and + 0.76 km s-1. On the other hand, the velocity of LBGs is mostly in the range −0.48 km s-1 and + 0.35 km s-1, and most of them are characterized by upward motions.
In Fig. 6 (bottom-right panel) we show also the normalized mean magnetic field strength for the different granule populations. UDs are embedded in the umbra region and their magnetic field strength is higher than the magnetic field strength observed in the PLGs, where values are lower than 600 G, with a peak at 150 G. UDs values cover a range between 850 G and 1800 G and LBGs have values of the mean magnetic field which are slightly lower than UDs values and higher than PLGs, covering a range between 750 G and 1500 G. The results of the physical properties studied for the three granular populations are summarized in Table 3.
We then studied the relation between the granular properties and their size. In Fig. 7 we compare the size of the three different populations of granules with their physical properties: mean continuum intensity, mean magnetic field strength and mean Doppler velocity.
 |
Fig. 7 Scatter plots of diameter vs. mean continuum intensity (top-left panel), diameter vs. mean magnetic field strength (top-right panel) and diameter vs. mean Doppler velocity (bottom-left panel), concerning UDs, LBGs and PLGs. The bottom-right panel shows the diameter vs. mean Doppler velocity, concerning only UDs and LBGs. The green squares correspond to UDs, the red ones to LBGs, and the black ones to PLGs. |
In Fig. 7 (top-left panel) the scatter plot shows that UDs and LBGs, which are characterized by limited value of sizes, have Ic values spanning over a relatively large interval (0.21–1.0 Ic). On the contrary, the PLGs, whose diameters span between 0.̋31 and 2.̋36, show a quite narrow distribution in Ic. PLGs have high intensity level indipendently from their diameter size, while UDs and LBGs with a diameter comparable with the small PLGs show a wide range of intensity. The scatter plot derived from PLGs shows a distribution similar to that found by Berrilli et al. (2002) and Yu et al. (2011) in their studies on quiet-Sun granulation. Indeed, the UDs distribution revealed from our study is not in agreement with the results found by Kilcik et al. (2012) and Ji et al. (2016). The LBGs distribution is similar to the UDs distribution, although for LBGs the range of intensity values is shifted into higher intensities.
In Fig. 7 (top-right panel) we show the scatter plot between the mean magnetic field strength and the diameter of the UDs, LBGs and PLGs. The range of mean magnetic field strengths of UDs and LBGs is distributed along higher values, while for the PLGs it takes values between 170 G and 700 G, that is, quite a lot lower than UDs and LBGs values. We remark that a study carried out by Ji et al. (2016) shows that UDs diameters have a decreasing distribution with increasing magnetic field strength. We do not observe such a relationship and we ascribe our result to a possible scattered light contamination in the Ji et al. (2016) measurements. In fact, the smaller the UD, the more it could be affected by scattered light from the surrounding umbra and, consequently, the larger the magnetic field would appear to be.
Figure 7 (bottom-left panel) shows the scatter plot between the mean Doppler velocity and the diameter of the UDs, LBGs and PLGs. The distribution of the mean Doppler velocity covers a larger range for UDs and PLGs than for the LBGs. In particular, the LBGs have mean Doppler velocities covering a range between −0.48 km s-1 and 0.35 km s-1 with a denser distribution at −0.1 km s-1. LBGs mean Doppler velocity are forced in a range of values that is narrower than the ranges of UDs and PLGs. To better analyze the relation between diameter and mean Doppler velocity in UDs and LBGs we plotted the two populations in the bottom-right panel of Fig. 7. The Doppler velocities observed for LBGs are concentrated in a small range around zero. UDs Doppler velocities cover a slightly wider range, while, PLGs velocities cover a wider range and reveal upflow and downflow motions for both small and larger PLGs.
5. Discussion and conclusions
In the last decades, the quiet Sun and several fine structures in the sunspots have been deeply studied thanks to observations carried out by instruments able to reach high spatial and spectral resolution. In this work we carried out a comparison of the size, the continuum intensity, the Doppler velocity and the mean magnetic field strength characterizing UDs formed in an umbra region, granules of a FLB and the granulation of a PL in a region next to the observed sunspot. These features were identified by an automated procedure on SST/CRISP observations characterized by higher resolution and wider sample of features than reported in the literature sofar.
Several studies in the literature report physical properties of granules in different solar regions, based on analysis of data taken at different positions on the solar disk, with different spatial and spectral resolution, and applying different methods to identify the analyzed granules, see Tables 1 and 2 in the Introduction. Here we discuss the main resemblances and differences between our study and the most relevant similar analyzes presented in the literature.
The new segmentation algorithm used in this work has some similarity with the one used by Bovelet & Wiehr (2001, 2007). We started from a similar algorithm, based on a multilevel tracking procedure, to avoid the clustering of closely neighboring granules and too-wide intergranular lanes. However, we added further steps to better identify the granules as the use of the Otsu method. Other algorithms, such as the one implemented by Berrilli et al. (2005), have common features with the one used in this work, but they are based on edge, while ours are based on intensity levels. The advantage of the developed identification algorithm is its flexibility, which allows us to measure the properties of granules characterized by different geometry and size, as in our case, where we want to compare the characteristics of UDs, LBGs and PLGs.
We found that the diameter of the LBGs ranges between 0.̋25 and 1.̋14. These values are lower than the values of the GLBs (by e.g., Rouppe van der Voort et al. 2010, and reference therein) and higher than the values of the FLBs (by e.g., Sobotka & Puschmann 2009, and reference therein). Recently, Lagg et al. (2014) observed a strong LB with the granule size comparable with the values of the quiet-Sun granulation (1′′ and 2′′). Instead, Sobotka & Puschmann (2009) study the physical properties of granules in a FLB and found diameters of the granules between 0.̋13 and 0.̋25, that are lower than the values found in our analysis. The range of diameter values for PLGs is larger and covers values from 0.̋31 to 2.̋36, while the range of diameter values we obtained for UDs is similar to the GLBs range and covers values from 0.̋24 and 0.̋95. These results are similar to the range of values found by Yu et al. (2011) for QSGs, while the maximum values we found for UDs size is slightly higher than in previous works. However, we cannot exclude that our method, based on the application of a threshold on the intensity of consecutive annuli, may overstimate the size of the UDs. We note that the range of the continuum intensity, of the magnetic field strength and of the LOS velocity does not vary if we change the threshold and reduce the maximum size of the UDs.
The mean continuum intensity of the LBGs that we analyzed showed a wide range of values between 0.42 Ic and 0.98 Ic. In this regard, we recall that Hirzberger et al. (2002) studied the mean continuum intensity of granules in a LB and they found a range of values between 0.8 Ic and 1.3 Ic. Moreover, they found that the UDs analyzed in the same FOV had mean continuum intensity in a range between 0.35 Ic and 0.8 Ic and suggested to use the intensity value of 0.8 Ic to separate the two types of bright structures. Actually, we found values of the mean continuum intensity of 0.23 Ic and 0.89 Ic for the UDs, which confirm and support the values found by Hirzberger et al. (2002). Moreover, it seems that some LBGs that we analyzed have an intensity similar to the typical intensity of the UDs. Although the solar region and the data analyzed, as well as the methods applied to identify the studied granules differ strongly, the range of the mean continuum intensity for the PLGs is from 0.88 to 1.08 Ic, which is similar to the results reported by Hirzberger (2002), Jin et al. (2009) and Yu et al. (2011) for the QSGs.
The Doppler velocities we detected in the LBG range between −0.48 km s-1 and 0.35 km s-1, with a peak of the frequency distribution at −0.1 km s-1, indicating that most of the LB granules are characterized by upflows. The Doppler velocity of plasma in PLGs ranges between −1.44 km s-1 and 1.26 km s-1. We found that UDs velocity values cover the range −1.09 km s-1 and 0.76 km s-1 similar to PLGs values and in agreement with the values found by Ortiz et al. (2010) for upflow and downflows motions.
We note that Doppler velocity values can be affected by the selection and analysis methods. For example Ortiz et al. (2010) were able to distinguish and measure the upflow and downflow motions inside each analyzed UD. Instead, in this work we made an average of the plasma velocity inside the entire area of the UDs identified by our algorithm. However, the values found from these two different analyzes are in agreement. In addition, the study of the granulation in the quiet Sun is also affected by the definition of granules and granular cells. According to Yu et al. (2011) a granule is the granular pattern excluding the surrounding intergranular lanes while a granular cell is the granular pattern including half of the surrounding intergranular lanes. The same definition was used by Hirzberger et al. (1997) and Jin et al. (2009). They made an average over the area of a granule, without distinguishing between upflow and downflow motions of the plasma. The values of the Doppler velocities reported by these authors are similar to those found in our analysis, although we considered the average velocity in the entire granular cell.
We also studied the mean magnetic field strength in each type of population and we found that PLGs magnetic field values are lower than 700 G with a peak at 150 G. This result is in agreement with the values of 160 G for the PL granulation studied by Lagg et al. (2014). Magnetic field in LBGs has values which are in the range of 700 G and 1500 G, similar to the range found for the UDs. This can justify the similar range of intensity between UDs and the LBGs observed in this work: the presence of magnetic field values higher in UDs and LBGs than in the PLGs inhibits the convection from sub-photospheric levels and we observe in UDs and LBGs a lower mean continuum intensity than in PLGs.
From the study of the different physical properties in the three granular populations, that depend on the granular size, we found that the main differences concern the properties of the PLGs compared to those of the LBGs and UDs. According to Parker (1979), UDs and LBs may be closely related phenomena and therefore originate from the same or similar physical mechanisms. Moreover, according to Rimmele (1997), LBs may be just a more developed state in the fragmentation process of a sunspot, in which the flux fragments have drifted far enough apart to permit more vigorous motion, most likely of convective origin, at the photospheric level. More recently, a possible common physical origin between these features was suggested by Scharmer & Spruit (2006) and Spruit & Scharmer (2006). According to Spruit & Scharmer (2006), UDs and LBs are produced by field-free convection in mostly vertical magnetic field structures and the mechanism suggested for the appearing of these structures is overturning convection in field-free gaps. In this study, we observed and analyzed a FLB formed by small granular like features, and we found similar properties between LBGs and UDs. However, the LBGs and UDs studied are not field-free, because the mean magnetic field strength is 1100 G and 1300 G, respectively. Other kind of LBs, such as GLB observed by Lagg et al. (2014), have granulation features more similar with quiet-Sun granulation. According to Lagg et al. (2014), GLBs and the quiet Sun granulation are anchored in deep layers and have common origin, while UDs and FLBs are the product of surface magneto-convection just below the local solar surface. We also found a similarity between the granules of the FLB and the UDs analyzed using a different method: we used a new identification algorithm and studied a higher number of elements observed with a higher resolution than the one used by Lagg et al. (2014). However, starting from a totally different study, we obtained a result which supports that carried out by Lagg et al. (2014). Since the study presented here was carried out on data taken on a single FLB, we plan to verify the results obtained by observing other kind of LBs also to improve our knowledge of these sunspot fine structures.
Acknowledgments
We are grateful to the University of Catania for providing the funds necessary to carry out the Observational Campaign in La Palma. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics (ISP) of Stockholm University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. We are also grateful to Professor Giovanni Gallo of the University of Catania for his contribution in the implementation of the new segmentation algorithm. This research has received funding from the EC 7th Framework Programme FP7/2007–2013 under the grant agreement SOLARNET (project No. 312495). This work was also supported by the Istituto Nazionale di Astrofisica (PRIN INAF 2014), and by the Italian Ministry of University and Research (PRIN MIUR 2012).
References
- Balthasar, H. 1988, A&AS, 72, 473 [NASA ADS] [Google Scholar]
- Berrilli, F., Consolini, G., Pietropaolo, E., et al. 2002, A&A, 381, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berrilli, F., del Moro, D., Florio, A., & Santillo, L. 2005, Sol. Phys., 228, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Bharti, L., Beeck, B., & Schüssler, M. 2010, A&A, 510, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bharti, L., Hirzberger, J., & Solanki, S. K. 2013, A&A, 552, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Bovelet, B., & Wiehr, E. 2001, Sol. Phys., 201, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2007, Sol. Phys., 243, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, P. N. 2001, Solar Photosphere: Granulation in Encyclopedia of Astronomy and Astrophysics, ed. P. Murdin (Bristol, UK: Institute of Physics Publishing, and London, UK: Nature Publishing Group), 2659 [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1977, Sol. Phys., 54, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, J. C., & Hoffman, B. D. 2007, Methods in Cell Biology, 83, 141 [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Löfdahl, M. G., Sütterlin, P., Hillberg, T., & Rouppe van der Voort, L. 2015, A&A, 573, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falco, M., Borrero, J. M., Guglielmino, S. L., et al. 2016, Sol. Phys., 291, 1939 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, S., Xu, Z., Wang, F., et al. 2014, Sol. Phys., 289, 3985 [NASA ADS] [CrossRef] [Google Scholar]
- Hamedivafa, H. 2008, Sol. Phys., 250, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J. 2002, A&A, 392, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirzberger, J., Vázquez, M., Bonet, J. A., Hanslmeier, A., & Sobotka, M. 1997, ApJ, 480, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J., Bonet, J. A., Vázquez, M., & Hanslmeier, A. 1999a, ApJ, 515, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J., Bonet, J. A., Vázquez, M., & Hanslmeier, A. 1999b, ApJ, 527, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J., Bonet, J. A., Sobotka, M., Vázquez, M., & Hanslmeier, A. 2002, A&A, 383, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ji, K., Jiang, X., Feng, S., et al. 2016, Sol. Phys., 291, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, C., Wang, J., & Zhao, M. 2009, ApJ, 690, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Jurčák, J., Martínez Pillet, V., & Sobotka, M. 2006, A&A, 453, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilcik, A., Yurchyshyn, V. B., Rempel, M., et al. 2012, ApJ, 745, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Solanki, S. K., van Noort, M., & Danilovic, S. 2014, A&A, 568, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Bida, T. A., Johannesson, A., & Scharmer, G. B. 1991, ApJ, 373, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Leka, K. D. 1997, ApJ, 484, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Louis, R. E., Bellot Rubio, L. R., Mathew, S. K., & Venkatakrishnan, P. 2009, ApJ, 704, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, Astronomical Data Analysis Software and Systems XVIII, 411, 251 [NASA ADS] [Google Scholar]
- Moga, & Gabbouj 1998, Journal of Parallel and Distributed Computing, 51 [Google Scholar]
- Muller, R. 1999, Motions in the Solar Atmosphere, 239, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, [Google Scholar]
- Ortiz, A., Bellot Rubio, L. R., & Rouppe van der Voort, L. 2010, ApJ, 713, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Otsu, N. 1979, IEEE Trans. Systems, Man and Cybernetics 9, 1, 62 [Google Scholar]
- Parker, E. N. 1979, ApJ, 234, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., Zakharov, V., & Gandorfer, A. 2008, A&A, 492, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. R. 1997, ApJ, 490, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmele, T. R. 2004, ApJ, 604, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., & Muller, R. 1986, Sol. Phys., 107, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., Coupinot, G., Hecquet, J., & Muller, R. 1985, Journal of Optics, 16, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouppe van der Voort, L., Bellot Rubio, L. R., & Ortiz, A. 2010, ApJ, 718, L78 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., & Spruit, H. C. 2006, A&A, 460, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, Proc. SPIE, 4853, 341 [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., de la Cruz Rodriguez, J., Sütterlin, P., & Henriques, V. M. J. 2013, A&A, 553, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Sobotka, M., & Jurčák, J. 2009, ApJ, 694, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Sobotka, M., & Puschmann, K. G. 2009, A&A, 504, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobotka, M., Bonet, J. A., & Vazquez, M. 1993, ApJ, 415, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Sobotka, M., Bonet, J. A., & Vazquez, M. 1994, ApJ, 426, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Martínez Pillet, V., Sobotka, M., & Vázquez, M. 2004, ApJ, 614, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Scharmer, G. B. 2006, A&A, 447, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strous, L. H. 1995, Helioseismology, 376, 213 [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Lofdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, H., Bellot Rubio, L. R., de la Cruz Rodríguez, J., & Rouppe van der Voort, L. 2012, ApJ, 757, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, D., Xie, Z., Hu, Q., et al. 2011, ApJ, 743, 58 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Properties of the umbral dots, light bridge granules and plage granules analyzed in our study.
All Figures
 |
Fig. 1 3D intensity image. The x and y axis are in pixels units, while the z axis is in DN. The pixel size of the CRISP camera is 0.̋06. Granules are clearly visible as peaks. |
| In the text | |
 |
Fig. 2 Examples of steps of the image processing: a) overall image segmentation based on the local maxima previously located (in light blue); b) first refinement based on slope analysis; c) final labeling. The FOV of the three images is 256 × 256 pixels which corresponds to 15.̋1× 15.̋1. |
| In the text | |
 |
Fig. 3 Example of average intensities of concentric annuli a) and the related differences b). A red line is overimposed to represent the adopted threshold. |
| In the text | |
 |
Fig. 4 Continuum intensity map of the preceeding sunspot of AR NOAA 11263 obtained by CRISP in the Fe I 630.15 nm line at 10:17 UT on the August 6, 2011. The solid boxes A–C indicate the FOVUD, FOVLB and FOVPL, respectively, that are analyzed in the following. North is on the top, west is at the right. The arrow labeled DC indicates the direction of disk center. |
| In the text | |
 |
Fig. 5 Magnetic field strength map (left panel) and Doppler velocity map (right panel) of the preceding sunspot of AR NOAA 11263. As in Fig. 4, the solid boxes A–C indicate the FOVUD, FOVLB and FOVPL, respectively, that are analyzed in the following. |
| In the text | |
 |
Fig. 6 Diameter (top-left panel), mean continuum intensity (top-right panel), mean Doppler velocity (bottom-left panel) and mean magnetic field strength (bottom-right panel) normalized distributions corresponding to the UDs (green), LBGs (red) and PLGs (black) analyzed. |
| In the text | |
 |
Fig. 7 Scatter plots of diameter vs. mean continuum intensity (top-left panel), diameter vs. mean magnetic field strength (top-right panel) and diameter vs. mean Doppler velocity (bottom-left panel), concerning UDs, LBGs and PLGs. The bottom-right panel shows the diameter vs. mean Doppler velocity, concerning only UDs and LBGs. The green squares correspond to UDs, the red ones to LBGs, and the black ones to PLGs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


