© ESO, 2017

1. Introduction

In order to track the star formation in galaxies and understand how gas is converted into stars, it is essential to study the prevalence and distribution of molecular gas across cosmic time. In recent years, molecular gas mass measurements have finally become feasible for normal galaxies, that is star-forming galaxies (SFGs) lying on the main sequence (MS) at redshifts z< 2.5 and featuring stellar masses of M_∗> 2.5 × 10¹⁰M_⊙ (e.g., Daddi et al. 2010; Genzel et al. 2010; Geach et al. 2011; Tacconi et al. 2010, 2013). These galaxies, following the fairly tight relation between M_∗ and star formation rate (SFR) with a dispersion of ± 0.3 dex, contribute ~80−90% of the cosmic SFR density at redshifts 0 <z< 3 (Daddi et al. 2007; Rodighiero et al. 2011; Wuyts et al. 2011; Rodighiero et al. 2015; Schreiber et al. 2015).

Fig. 1 Color-composite image of MACSJ0032-arc obtained using the HST/ACS F606W and F814W filters (left panel). The studied galaxy at zCO = 3.6314, strongly lensed by the galaxy cluster MACS J0032.1+1808, is composed of six multiple images well resolved in the HST image, labeled A, B, C, D, E, and F and encircled in white. They form a giant arc extending over 42.4′′. The right panels show, respectively, the zoom-in color-composite image obtained using the Spitzer/IRAC 3.6 and 4.5 μm bands over the multiple images B, C, D, E, and F (top) and the zoom-out color-composite image obtained using the Herschel/SPIRE 250, 350, and 500 μm bands; the white box represents a 40′′ × 40′′ area.

Fig. 2 Herschel/SPIRE 250 μm, Spitzer/IRAC 3.6 μm, PdBI 2 mm continuum, JVLA 5 GHz continuum, PdBI CO(6–5) line emission, and JVLA CO(1–0) line emission contours (in red) overlaid, from left to right and from top to bottom, on the HST/ACS F814W multiple images B, C, D, and E of MACSJ0032-arc. The contribution of the counter-image F is negligible. X refers to a galaxy member of the lensing cluster. Contour levels start at 2σ and are spaced in steps of 1σ, expect for IRAC 3.6 μm where the contours are in steps of 9, 16, 25, 36, 49σ, etc. The SPIRE detection extends beyond the multiple images B, C, D, and E, as shown in Fig. 1, but peaks at 4σ over B, C, D, and E. The rms levels of the 2 mm, 5 GHz, CO(6–5), and CO(1–0) data are 57 μJy, 1.7 μJy, 93 mJy km s-1, and 6.2 mJy km s-1, respectively. The size and orientation of the beam are indicated by the dotted (PdBI) or filled (JVLA) red ellipse in the bottom right corner.

With the increasing number of CO measurements obtained for MS SFGs, we are starting to highlight the significant role that the molecular gas plays in galaxies in general and in the implementation of the MS itself. Indeed, in the local Universe it has now been established that the location of a galaxy in the SFR–M_∗ plane is primarily governed by its supply of molecular gas, whereas variations in the star formation efficiency (SFE) only play a secondary role (Saintonge et al. 2012). Similar conclusions have been reached for high-redshift galaxies (Tacconi et al. 2013; Dessauges-Zavadsky et al. 2015), although Genzel et al. (2015) find equal contributions from the SFE and the molecular gas content for the offset of galaxies from the MS. Likewise, the observed evolution of the MS with redshift that results in the increase in the specific star formation rate (sSFR) with cosmic time (Schaerer & de Barros 2009; Rodighiero et al. 2010; Schreiber et al. 2015) is closely linked to the behavior of the molecular gas. Current observations convincingly show that the rapid rise in the sSFR of galaxies up to z ~ 2 can be explained by the comparable rise in their molecular gas fraction (f_molgas) with cosmic time and their slowly varying molecular gas depletion timescale (t_depl) (Geach et al. 2009, 2011; Genzel et al. 2010, 2015; Daddi et al. 2010; Bauermeister et al. 2013; Tacconi et al. 2010, 2013). Beyond z ≳ 2, it remains a subject of debate whether f_molgas continues to increase or whether, instead, the decrease in t_depl is steepening (Saintonge et al. 2013; Tan et al. 2013; Dessauges-Zavadsky et al. 2015), primarily due to the lack of molecular gas mass measurements available so far for MS SFGs at z> 2.5.

While determining the molecular gas content in individual MS SFGs at z> 2.5 is challenging, it is feasible with the help of strong gravitational lensing, which enables us to push beyond current instrumental sensitivity thresholds. Indeed, of the five CO measurements performed to date for z> 2.5 MS SFGs, four were obtained in strongly lensed SFGs, and the fifth was obtained in a very massive (M_∗ = 10¹¹M_⊙) unlensed SFG (Riechers et al. 2010; Johansson et al. 2012; Tan et al. 2013; Saintonge et al. 2013). Indirect estimates of the molecular gas masses in some 53 massive MS galaxies at 2.7 <z< 4 with M_∗> 2 × 10¹⁰M_⊙ were recently reported by Scoville et al. (2016) and Schinnerer et al. (2016) based on 1 mm dust continuum emissions detected with the Atacama Large Millimeter Array (ALMA).

We report here on the CO(6–5), CO(4–3), and CO(1−0) line detections for a newly discovered star-forming galaxy at z_CO = 3.6314, strongly lensed by the galaxy cluster MACS J0032.1+1808 (Ebeling et al. 2001), hereafter denoted MACSJ0032-arc. Featuring the highest redshift at which an estimate of the molecular gas mass has been obtained from CO in a normal low-mass SFG, this galaxy is of particular interest for a detailed study aimed at addressing key questions: What are the f_molgas and t_depl evolutionary trends at very high redshift? Is the CO-to-H₂ conversion factor significantly different at z ~ 3.6? Does the CO spectral line energy distribution (SLED) vary with respect to the SLEDs of lower redshift MS SFGs? Is the cold gas CO emission spatially correlated with the stellar UV emission?

Our paper is organized as follows. In Sect. 2 we introduce our target, and in Sect. 3 we describe the multiwavelength observations performed from the optical through the infrared, far-infrared, and millimeter to the radio regime. The analysis of the data including the gravitational lens modeling and the inferred stellar, dust, and CO molecular gas properties of MACSJ0032-arc can be found in Sect. 4. We discuss these results in the context of MS SFGs with CO measurements and explore the redshift evolution of both the molecular gas depletion timescale and the molecular gas fraction in Sect. 5. We also estimate the CO-to-H₂ conversion factor using two different methods and highlight their respective strengths and weaknesses. A summary and conclusions follow in Sect. 6. Throughout the paper, we assume a ΛCDM cosmology with H₀ = 70 km s^-1 Mpc^-1, Ω_M = 0.29, and Ω_Λ = 0.71, and the Chabrier (2003) initial mass function.

2. The target: MACSJ0032-arc

We report on a newly discovered galaxy, MACSJ0032-arc, identified as a bright FIR emitter in the Herschel Lensing snapshot Survey (HLS-snapshot; Egami et al., in prep.). Designed to find strongly lensed sources at high redshift, the survey used Herschel/SPIRE to image the fields around more than 300 massive galaxy clusters. Located at RA = 00:32:07.776, Dec = + 18:06:47.80, MACSJ0032-arc is strongly lensed by the galaxy cluster MACS J0032.1+1808 at z = 0.377 (Ebeling & Repp, in prep.). The redshift of the lensed system was first accessed from weak rest-frame UV interstellar medium (ISM) lines and the Lyα break detected in absorption in the spectrum we obtained with LRIS on the Keck I telescope, z_ISM = 3.626 ± 0.001 (Richard et al., in prep.). It was then confirmed with our firm detections of the CO(4–3) and CO(6–5) emission lines at z_CO = 3.6314 ± 0.0005 with the IRAM 30 m telescope. Very recently, we also detected the nebular [O iii] λ5007 and Hβ emission lines at z_neb = 3.633 ± 0.003, redshifted in the near-IR, with LUCI on the LBT (Walth et al., in prep.). The systemic redshift of MACSJ0032-arc is hence well constrained by both z_CO and z_neb, which agree within their 1σ errors. The ISM absorption lines at z_ISM appear blueshifted with respect to the systemic redshift of the galaxy by − 350 ± 65 km s^-1.

MACSJ0032-arc was also observed in the infrared (IR) as part of the Spitzer/IRAC Lensing Survey, and in the optical regime in ongoing efforts to image strong-lensing clusters with the Hubble Space Telescope (HST). It has been detected at all these wavelengths, as is shown in Fig. 1. These observations combined with millimeter (mm) and radio data obtained with the Plateau de Bure Interferometer (PdBI) and the Jansky Very Large Array (JVLA), respectively, enable us to derive the stellar, dust, and molecular gas properties of this z ~ 3.6 galaxy.

The high-quality, high-resolution rest-frame UV images obtained with HST reveal six images of this high-redshift galaxy, labeled A, B, C, D, E, and F throughout the paper, as illustrated in Fig. 1. The counter-image F is very faint and barely visible, located very close to a lensing cluster galaxy member. A seventh counter-image exists, but is de-amplified and hence invisible. All of these images originate from the same background galaxy, amplified by different magnification factors, and form a giant arc extending over 42.4′′. Moreover, the lensed galaxy is resolved into two compact, UV-bright knots, separated by ~0.8′′ in the most amplified multiple images B, C, D, and E, plus a tail attached to the brightest knot. The high-resolution JVLA observations enable us to resolve the CO(1–0) line emission and the 5 GHz radio continuum as well within the multiple images B, C, D, and E, and to compare the location of the molecular gas and dust-obscured star formation with respect to the rest-frame UV emission.

In what follows, we focus our analysis only on the brightest multiple images B, C, D, and E, covered by all our data and detected in most of them, as shown and discussed in Sect. 3.

3. Observations, data reduction, and flux estimates

3.1. HST, Spitzer, and Herschel data

The lensing cluster has been observed in two HST/ACS passbands, F606W and F814W. The astrometry of the two HST images has been adjusted to the astrometry of the interferometric JVLA 5 GHz continuum image by cross-matching positions of seven bright point-like sources detected in both the HST/ACS F606W+F814W images and in the JVLA image at more than 10σ and 8σ, respectively. Median corrections of + 0.06′′ in right ascension and − 0.17′′ in declination were applied to the HST astrometry. The resulting absolute positional error is about 45 mas for the two HST passbands.

In these high-resolution HST optical images, the multiple images of MACSJ0032-arc and the associated substructure are all resolved, and are generally unblended with foreground galaxy light in the cluster field. The sole exception is the elliptical galaxy, a cluster member labeled X, which affects the photometry of the very faint counter-image F and marginally affects image D (see Figs. 1 and 2). We fit and subtracted the light profile of galaxy X using GALFIT (Peng et al. 2002). To measure the flux of each counter-image, we first created segmentation maps by selecting, in the F814W image convolved with a 3-pixel full width half maximum (FWHM) Gaussian, all pixels above 1σ. We separate counter-images C and D, that form a continuous arc, at the location of the critical line (see Fig. 1). We use these segments to integrate the flux in the F814W band and in the properly aligned F606W image. We hence obtain clean rest-frame UV-photometry individually for each of the multiple images B, C, D, and E.

Because of the much coarser resolution of the Spitzer/IRAC IR images available in the 3.6 and 4.5 μm passbands, the multiple images C, D, E, and F are blended with each other, as well as with the cluster member X mentioned above. This can be clearly seen in Fig. 2, where we overlay the IRAC 3.6 μm contours on the HST F814W image. The IRAC flux even seems to peak at the position of galaxy X. Therefore, we derive the rest-frame optical photometry only for the well-resolved and unblended counter-image B. For this purpose, we performed prior-based photometry, as in Sklias et al. (2014). We used the reddest HST band to produce the so-called stamp image of the counter-image B. This stamp image includes only pixels within the SExtractor aperture. The pixels define the prior shape of the image B that is then convolved with the IRAC point-spread function (PSF) and scaled in flux. The photometry of the other images C, D, and E, and of the multiple images B, C, D, and E taken together, are then recovered by equally applying the IRAC 3.6 μm–F814W and IRAC 4.5 μm–F814W colors measured in B. This is fully justified, since color is conserved from one counter-image to another, which is a well-established property of gravitational lensing. In the three Herschel/SPIRE FIR images at 250, 350, and 500 μm, the multiple images B, C, D, E, and F are all blended within a single Herschel beam, with the exception of the counter-image A which falls outside the beam¹. Since MACSJ0032-arc is otherwise unblended with other SPIRE-detected sources (see Fig. 1, bottom right panel), simple aperture photometry with the standard SPIRE color and aperture corrections² yields a robust FIR flux measurement for the sum of the multiple images B, C, D, E, and F. We are confident that the contribution of the cluster member X to the Herschel flux is negligible. Indeed, at the redshift of the MACS J0032.1+1808 cluster, very few cluster galaxies besides the brightest cluster galaxies (BCGs) are likely to be detected in the SPIRE bands (Rawle et al. 2012) and the galaxy X is not a BCG. Moreover, if the contribution of the galaxy X were significant, then one would expect the combined dust peak to be wider than observed (see Fig. 4). To get the observed 250/350 μm color, any cluster galaxy contribution at 250 μm has to be small and thus its contribution to the total FIR flux negligible. Other cluster members are more than 5−10′′ away from the MACSJ0032-arc; their contribution, if any, to the Herschel flux would yield some elongation in the SPIRE point source, which is not observed.

The resulting multiwavelength photometry for the individual counter-images (when available) and the B, C, D, and E images taken together is summarized in Table 1. Because the Herschel/SPIRE photometry for the multiple images B, C, D, and E cannot be deblended (the very faint counter-image F can be neglected), we note that we are forced to work on the total B+C+D+E emission in all available bands, including the CO data, in order to get a coherent global picture.

3.2. 30 m telescope data

The IRAM 30 m telescope observations of MACSJ0032-arc were conducted on March 28 and 29, 2012, as part of a blind CO line search program in the 3 mm band aimed at identifying the redshifts of bright HLS-snapshot FIR emitters. For this purpose, we used the Eight MIxer Receiver (EMIR) combined with the 32 GHz IF system, which includes 24 fast Fourier Transform Spectrometers (FTS) working at a spectral resolution of 200 kHz. A first redshift solution of z_ISM = 3.626 ± 0.008 was obtained for MACSJ0032-arc from ISM absorption lines detected in the KeckI/LRIS spectrum (see Sect. 2). Therefore, the 32 GHz bandwidth of our EMIR observation was distributed in two 8 GHz wide IF outputs centered on the E090 band (3 mm) and the E150 band (2 mm) each, in dual polarization. The two bands were tuned to the redshifted frequencies of the CO(4−3) and CO(6–5) lines at 99.663 GHz and 149.475 GHz, respectively. The corresponding half-power beam widths are 24′′ and 16′′, respectively. All multiple images B, C, D, E, and F contribute to the observed CO(4−3) and CO(6–5) fluxes, with the exception of the counter-image A which falls outside the 30 m beam (see Fig. 1). The observations were conducted in wobbler-switching mode with a frequency of 0.5 Hz and a symmetrical azimuthal wobbler throw of 50′′ to maximize the baseline stability. The total on-source integration time was 1.4 h.

Data reduction was performed with the IRAM GILDAS software package CLASS. Since the FTS suffers from severe platforming effects, corrections were applied using a dedicated script provided by the IRAM 30 m observatory. This correction was applied individually to each scan and led to baseline-subtracted spectra. All the scans obtained with the FTS backends tuned on the CO(4–3) line and those tuned on the CO(6–5) line were averaged independently, using the temporal scan length as weight. The resulting CO(4–3) and CO(6–5) spectra were then Hanning smoothed to a resolution of 40.16 km s^-1. They reach an rms noise level of 2.4 mJy in 13.335 MHz channels and 2.2 mJy in 20 MHz channels, respectively, and reveal firm CO(4–3) and CO(6–5) emission line detections at z_CO = 3.6314 ± 0.0005 (see Fig. 7). The CO(4–3) line integrated flux listed in Table 2 is derived from a double Gaussian fit applied to the observed CO(4−3) line profile.

3.3. PdBI data

The IRAM PdBI observations of MACSJ0032-arc were carried out on November 11 and 16, 2013, in the C-configuration and in the 2 mm band, tuned to the redshifted frequency of the CO(6−5) transition at 149.300 GHz, as computed from the arc CO redshift z_CO = 3.6314 ± 0.0005. We used the WideX correlator that provides a continuous frequency coverage of 3.6 GHz in dual polarization with a fixed channel spacing of 1.95 MHz resolution. A total of 3840 visibilities were obtained during 3.2 hours of on-source integration time.

Standard data reduction was performed with the IRAM GILDAS software packages CLIC and MAPPING, with flux, bandpass, and phase calibration performed using the calibrators most suitable for our target. The data were mapped with the CLEAN procedure using the HOGBOM deconvolution algorithm and combined with “natural” weighting, thus giving priority to mapping sensitivity rather than angular resolution. The resulting synthesized beam size is 1.94′′ × 1.62′′ (PA = + 27.3°). We reach an rms noise per beam of 57 μJy in the continuum after averaging the PdBI data over the full 3.6 GHz spectral range and having excluded the channels where CO emission is detected. The resulting 2 mm continuum is then subtracted from the UV table in order to obtain the UV table for the CO(6–5) line only.

To improve the mapping accuracy for the CO(6–5) line emission, we added the short spacings from the IRAM 30 m single-dish data over the CO(6–5) detection channel interval using the UVSHORT procedure in MAPPING. This yielded an improvement of approximately 10% and an rms noise per beam of 0.7 mJy when resampling the PdBI+30 m data to a bandwidth of 20 MHz (40.16 km s^-1). Using the GO MOMENT procedure, we determine the CO(6–5) first moment map (velocity-integrated map) of the cleaned, weighted images over the nine velocity channels where the CO(6–5) emission is detected.

The resulting CO(6–5) velocity-integrated contours overlaid on the HST/ACS F814W image are shown in Fig. 2. The CO(6−5) emission is successfully detected in the four most strongly amplified multiple images of MACSJ0032-arc, namely images B, C, D, and E, with a signal-to-noise ratio (S/N) varying between 4σ and 6σ. Counter-images A and F remain undetected in CO(6–5) because of their much lower magnification factors (see Sect. 4.1). We derive the CO(6–5) line integrated fluxes of the individual images B, C, D, and E, and of their sum, using custom apertures over the velocity-integrated map, large enough to include, for each counter-image, all the signal above the background. The inferred CO(6–5) line integrated fluxes are listed in Table 1.

The 2 mm continuum emission is detected at 5.8σ in the most strongly amplified counter-image C only, as shown in Fig. 2 where the 2 mm contours are overlaid on the HST/ACS F814W image. The other images B, D, and E remain undetected. Although this is surprising, we note that their fluxes are expected to reach at most the 3σ level when scaling the observed flux in image C by the respective B, D, and E magnification factors (see Fig. 6). Emissions at this low confidence level may stochastically happen to be cancelled out, in large part by noise. Therefore, we derive a direct 2 mm continuum flux for the counter-image C, and estimate the total B+C+D+E flux by integrating the 2 mm continuum map over the same apertures as those used for the CO(6–5) emission detected over all multiple images B, C, D, and E. We find this estimate to be smaller by 38% than the total flux derived when applying the 2 mm–F814W color conservation over the multiple images of MACSJ0032-arc (see Table 1). We thus set the error on the total 2 mm continuum flux in order to match the two flux estimates within 1σ uncertainty.

3.4. JVLA data

The NRAO JVLA 5 GHz continuum observations of MACSJ0032-arc were conducted on February 9, 2014, and August 27, 2015, in the most extended A and BnA configurations (program IDs VLA/13B-358 and VLA/15A-215). The half-power beam width is 260′′, ensuring that all the multiple images are within the central area of the primary beam. We used the WIDAR correlator and the C-band receiver with the 8-bit samplers tuned to 4.20 − 6.20 GHz (1024 × 2 MHz channel, 2.0 GHz total bandwidth) to maximize the bandwidth unaffected by strong radio frequency interferences (RFI) at 4.0 − 4.2 GHz. The total on-source time was 4.5 h.

The raw data were Hanning smoothed, calibrated by the CASA pipeline provided by NRAO with appropriate calibrators used for the flux, bandpass, and phase calibration, and manually flagged to exclude any remaining strong RFI. We imaged the data using the CLEAN procedure opting for the Multi-Scale Multi-Frequency Synthesis algorithm (MS-MFS) deconvolution algorithm (Rau & Cornwell 2011), the Cottom-Schwab PSF mode, the Briggs weighting with a robust parameter of 0.5, and the tapering of baselines beyond 100 kλ to facilitate the detection of any extended components. The resulting map has a synthesized beam size of 0.87′′ × 0.62′′ (PA = + 68.0°) and an rms noise per beam of 1.7 μJy.

The detected 5 GHz continuum contours overlaid on the HST/ACS F814W image are shown in Fig. 2. All four individual counter-images B, C, D, and E are detected at 3σ and more. The corresponding 5 GHz fluxes, and that of their sum are listed in Table 1. They were derived using the PyBDSM software, performing multi two-dimensional Gaussian fits.

We observed the CO(1–0) line emission of MACSJ0032-arc on June 6, 12, 23, and 25, 2015, in the C configuration with a half-power beam width of 99′′ (program ID VLA/13A-385). We used the WIDAR correlator and the K-band receiver with the 8-bit samplers tuned to two frequencies at 24.962 GHz and 24.986 GHz (1024 × 2 MHz channel, 2.0 GHz total bandwidth; the 24 MHz gap helps mitigate the effect of the lower sensitivity at the 128 MHz bandpass edges) to cover the redshifted frequency of the CO(1–0) transition at 24.889 GHz. The total on-source time was 9.0 h.

Except for adopting no Hanning smoothing, the raw data were processed in the same way as the C-band data described above. We then used the CLEAN procedure to create an image cube and the IMCONTSUB procedure to subtract continuum emission. The resulting map has a synthesized beam size of 0.90′′ × 0.79′′ (PA = − 53.7°).

The CO(1–0) line emission is reliably detected only in the counter-image C in two velocity channels, each 144.54 km s^-1 wide. By summing over the two velocity channels using the IMMOMENTS procedure, we achieve a 4.7σ CO(1–0) detection in image C, and 2 − 3σ detections in the other images B, D, and E, as shown in Fig. 2. The CO(1–0) line integrated flux of image C, as well as the total B+C+D+E CO(1–0) line integrated flux obtained by integrating the velocity-integrated map over the same apertures as those used for the CO(6–5) emission detected over all multiple images B, C, D, and E, can be found in Table 1. The latter perfectly matches the total integrated flux derived by propagating the CO(1–0)–F814W color properly measured in image C over the sum of multiple images B, C, D, and E (see Table 1).

Fig. 3 Observed HST/ACS F814W optical image of the multiple images B, C, D, E, and F of MACSJ0032-arc with the critical line in red (left panel); simulated observation of MACSJ0032-arc resulting from the best lens model when accounting for the PSF of the HST image (middle panel); and source plane reconstruction of MACSJ0032-arc obtained by simulating the morphology of the source as the combination of three elliptical Gaussian light profiles (right panel). The two bright knots, resolved in the HST rest-frame UV images, are separated by 1.14 ± 0.28 kpc in the source plane. The simulated HST observation includes a constant Gaussian noise background matched to the F814W noise level.

3.5. Flux anomalies

A critical inspection of the fluxes measured for the individual counter-images B, C, D, and E, found in Table 1 shows that the 5 GHz continuum flux of the image E is a factor of 3 higher with respect to the expected flux from the color conservation that is supposed to hold over multiple images of a lensed object. We have carefully verified that image E is not affected by sidelobes from any bright cluster galaxy, and this is not the case. A similar failure in the color conservation is also observed for the CO(6−5) emission in image E, although this is true to a smaller extent given the lower excess of a factor of 1.6.

We have no satisfying explanation for what can induce such an excess in both the 5 GHz JVLA and CO(6–5) PdBI data. We can only speculate on two phenomena. One possible phenomenon, which can possibly break the color conservation in a single counter-image, is the micro-lensing effect, which may very locally increase the flux of a specific region of the source. If this scenario is correct, it suggests that the radio continuum and the high-J CO(6–5) transition have to be emitted from co-located regions of the MACSJ0032-arc galaxy. This is not true for either the CO(1–0) line emission or the 2 mm dust continuum; if it were true, their respective flux in image E would also be higher and this is not observed (see Table 1). Another phenomenon that may also be considered is the lensing time-delay, where the light travel time or path length for each counter-image differs. If a variable AGN were present, it is possible that image E could be boosted at a given time in comparison to the other images. The continuum may also vary differently to the line emission, such that the resulting color varies in time. Even if the AGN had an optical contribution, the variations at these wavelengths are not expected to be synchronous. However, the absence of Lyα and any other ISM lines in emission (especially C iv) in the near-UV/optical Keck I/LRIS spectrum (Richard et al., in prep.) argues quite strongly against an AGN in MACSJ0032-arc.

To overcome the anomalous flux excess in the 5 GHz continuum and the CO(6–5) line emission in image E, we consider in subsequent analyses the expected total B+C+D+E flux derived by assuming the color conservation and the fluxes measured in counter-images unaffected by the excess (see Table 2).

4. Analysis and results

4.1. Gravitational lens model

We optimize a parametric mass model of the lensing cluster MACS J0032.1+1808 based on strong-lensing constraints detected in the HST/ACS optical images. We use the positions of the five brightest multiple images A, B, C, D, and E forming the giant arc, including for each image the centroids of the two knots observed in the HST images (see Fig. 1). In addition, two triply imaged systems that we spectroscopically confirmed (Richard et al., in prep.) provide additional constraints on the large-scale mass distribution within the cluster lens. Our mass model considers components on two complementary scales: on large scales, we include two cluster-scale dark-matter haloes, parametrized by double pseudo-isothermal elliptical (dPIE) potentials (e.g., Limousin et al. 2012); and on galaxy scales, we model each member of the lensing cluster as a smaller-scale dPIE potential following a fixed scaling relation with its luminosity. We use the Lenstool software (Jullo & Kneib 2009) to optimize the lens parameters with a Bayesian Markov chain Monte Carlo (MCMC) sampler, which provides the best model by minimizing the distance between the predicted and observed locations of the counter-images, as well as a range of models sampling the parameter space of the potentials. Overall our best-fit models reproduce the location of all images with an rms of 0.17′′.

Deviating from the modeling prescription applied to all other cluster galaxies, we give special treatment to one bright cluster member, marked X in Fig. 2. As its presence splits the giant arc into multiple images C to F, additional constraints ensue that allow us to model galaxy X separately from the scaling relation. Its effect on the shape of the critical line at z ≃ 3.63 is very noticeable in Fig. 3 (left and middle panels). A counter-image F is predicted and indeed observed next to image D on the other side of the lensing galaxy X. By contrast, a seventh central counter-image is demagnified and, consequently, is not observed in our HST images. The combination of the potentials of the cluster and galaxy X leads to a very high magnification factor. To assess the value of the total magnification for the sum of the multiple images B, C, D, and E, which will be used in the rest of the paper (see Sect. 3.1), we need to properly simulate the merging pair of counter-images C and D, which experience the strongest magnification.

We simulate the morphology of the source as the combination of three elliptical Gaussian light profiles (right panel of Fig. 3) and match their flux and shape to the photometry of the observed HST images (Table 1). This was performed by inverting the location of flux peaks in the image plane to the source plane, and producing for each component a grid of elliptical Gaussians with FWHM within 100 pc to 1 kpc in each direction and varying the orientation by steps of 10 degrees. We select for each component the source model that best matches the image plane morphology once lensed and convolved by the HST PSF. The morphology is well constrained along the shear direction, but is an upper limit in the direction perpendicular to it. The simulated observation of MACSJ0032-arc, corrected for the PSF of the HST/ACS F814W image, is shown in the middle panel of Fig. 3 and globally reproduces the observed locations, shapes, and flux ratios of each counter-image, shown in the left panel of Fig. 3. We derive the total magnification of the sum of B, C, D, and E from the ratio between the total flux in the simulated image and the corresponding flux in the model image in the source plane (right panel of Fig. 3), and we get a value of μ = 62 ± 6, where the quoted uncertainty represents the statistical error from the MCMC models.

Although the respective sizes of each of the three components in our source plane model are only constrained through upper limits because they are observed as compact sources after magnification, the separation between the two brighter knots is well-constrained. We derive a physical distance of 1.14 ± 0.28 kpc, taking into account both the statistical error from the MCMC models and systematic uncertainties assessed by comparing the distances for each of the counter-images B, C, D, and E in the source plane. MACSJ0032-arc is thus found to be a compact galaxy in the source plane with a global size <2.5 kpc, after adding the three components used in our source model, each of which features a size of <500 pc. This is a typical size for SFGs at 3 <z< 4, whose stellar effective radii range from 0.4 kpc to 3 kpc with a median at 1.3 kpc (Shibuya et al. 2015).

4.2. Stellar and dust content

The combination of the available rest-frame UV, optical, and FIR photometry (see Table 1) enables constraints to be obtained on both the stellar and thermal dust spectral energy distributions (SEDs) of MACSJ0032-arc. We only consider the total photometry of the sum of the multiple images B, C, D, and E, as motivated in Sect. 3.1. The fits to these SEDs determine the physical parameters of the galaxy, such as the IR luminosity (L_IR), the extinction (A_V), SFR, M_∗, and the age of the stellar population. We perform the fits by generating 1000 Monte Carlo realizations of the observed photometric data points, which are fit and used to determine the median values and the 68% confidence intervals of the various physical parameters. The latter are then corrected for lensing effects by applying the total B+C+D+E magnification factor (Sect. 4.1).

We first model the dust-processed Herschel FIR SED using different empirical templates and the modified blackbody (MBB) function. The MBB provides the best fit to the FIR SED, with the PdBI 2 mm continuum detection giving a strong constraint on the β-slope, which we fix at 2. The best empirical template reproducing the FIR SED is the one of Vega et al. (2008), which, however, fails to reproduce the 2 mm dust continuum emission because the required β-slope is steeper than that of the template. The inferred respective total luminosities, L_IR, of the multiple images B, C, D, and E taken together are in very good agreement and only differ by 0.01 dex.

To model the stellar SED from the optical regime covered by the HST filters up to the Spitzer/IRAC IR bands, we use the energy-conserving models presented in Sklias et al. (2014). The rationale behind this approach is to decrease the number of free parameters of the usual SED fitting by fixing the attenuation using L_IR and assuming that it is due to obscuration of the SED between 0.912 μm and 3 μm. The observed L_IR/L_UV ratio is then converted into A_V using the calibration from Schaerer et al. (2013). This attenuation is entered into the updated version of the Hyperz photometric redshift code (Schaerer & de Barros 2009, 2010) to generate fits that conserve energy and alleviate the age-extinction degeneracy. Prior to this process, the stellar photometry is corrected for foreground extinction from the Galaxy, taken to be E(B − V) = 0.11 at the position of the galaxy cluster (Schlafly et al. 2011). When modeling SEDs, we consider star formation histories (SFHs) with both delayed exponential SFR (∝texp( − t/τ)) and constant SFR with a minimum age prior of t_min = 50 Myr. Either approach yields equally good best-fit SEDs with similar χ² values and comparable outputs (M_∗ and SFR) differing by about 10%. We also explore the subsolar and solar metallicities; we adopt the subsolar metallicity, since it provides the best-fit SED with a χ² of 0.40 against 1.68 for the solar fit.

The resulting best-fit FIR and stellar SEDs with a constant SFR SFH are shown in Fig. 4. The inferred physical parameters for MACSJ0032-arc are summarized in Table 2 and reveal a low-mass, luminous infrared galaxy (LIRG) with ${\mathit{M}}_{\mathrm{\ast }}\mathit{/}\mathit{\mu }\mathrm{=}\mathrm{4.}{\mathrm{8}}_{-1.0}^{\mathrm{+}\mathrm{0.5}}\mathrm{\times }{\mathrm{10}}^{\mathrm{9}}{\mathit{M}}_{\mathrm{\odot }}$. We discover that ~90% of the total SFR_{UV + IR} of this high-redshift SFG is undetected at UV wavelengths, but is seen through the thermal FIR dust emission. We find our source to lie within about − 0.1 to + 0.3 dex of the main sequence at z ~ 4, meaning at most a factor of 2 above the MS depending on the adopted MS parametrization from Tacconi et al. (2013), Speagle et al. (2014), or Tomczak et al. (2016). All these parametrizations still remain uncertain since the star formation main sequence and its scatter at z ~ 4 are not well defined yet, especially at low stellar masses comparable to MACSJ0032-arc.

Fig. 4 Observed SED of MACSJ0032-arc at zCO = 3.6314. Overlaid are the best-fit stellar SED (solid cyan line) obtained with the energy-conserving model and constant SFR SFH, as well as the best-fit FIR and mm SED obtained with the Vega et al. (2008) empirical template (solid red line) and the MBB with a β-slope fixed at 2 (dashed black line).

Finally, the combination of the Herschel FIR photometry and the PdBI 2 mm continuum allows an estimate of the dust mass (M_dust) of MACSJ0032-arc to be obtained via the flux–M_dust calibration from Kruegel (2003)${\mathit{M}}_{\mathrm{dust}}\mathrm{=}\frac{{\mathit{S}}_{\mathit{\nu }}\mathrm{\left(}{\mathit{\lambda }}_{\mathrm{obs}}\mathrm{\right)}{\mathit{D}}_{\mathit{L}}^{\mathrm{2}}}{\mathrm{(}\mathrm{1}\mathrm{+}\mathit{z}\mathrm{)}\mathit{\kappa }\mathrm{\left(}{\mathit{\lambda }}_{\mathrm{rest}}\mathrm{\right)}{\mathit{B}}_{\mathit{\nu }}\mathrm{\left(}{\mathit{\lambda }}_{\mathrm{rest}}\mathit{,}{\mathit{T}}_{\mathrm{dust}}\mathrm{\right)}}\mathit{,}$(1)where S_ν(λ_obs) is the flux at a given observed wavelength, D_L the luminosity distance, κ(λ_rest) the dust grain opacity per unit of dust mass, and B_ν(λ_rest,T_dust) the Planck function at a given rest-frame wavelength and dust temperature. For the opacities, κ(λ_rest), we follow the Li & Draine (2001) calibration. We estimate S_ν from the best-fit MBB to the FIR and 2 mm data with the β-slope fixed at 2 (see Fig. 4). The resulting values for M_dust and T_dust are given in Table 2. We propagate the error of the 2 mm continuum flux, carefully set in Sect. 3.3, on M_dust.

4.3. CO spectral line energy distribution

At z_CO = 3.6314 MACSJ0032-arc currently is the highest redshift typical LIRG with a measured CO(1–0) luminosity. The CO(1–0), CO(4–3), and CO(6–5) line detections within the arc offer the rare opportunity of characterizing the CO SLED and directly measure the CO luminosity correction factors, ${\mathit{r}}_{\mathit{J,}\mathrm{1}}\mathrm{=}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathit{J}\mathrm{-}\mathrm{(}\mathit{J}\mathrm{-}\mathrm{1}\mathrm{\left)}\mathrm{\right)}}^{\mathrm{\prime }}\mathit{/}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$, for these high-J CO transitions in a normal SFG at such a high redshift. This is of particular importance since the estimate of the molecular gas mass is based on the luminosity of the fundamental CO(1–0) line, which is rarely accessible at high redshift. In its absence, luminosity corrections have to be applied to the more readily observable rotationally excited lines.

In Fig. 5 we show the CO SLED of MACSJ0032-arc that we have corrected for the cosmic microwave background (CMB) radiation, which is becoming non-negligible at z ~ 3.6, the redshift of the arc, with a temperature of T_CMB = 12.6 K. da Cunha et al. (2013) computed the ratios between the line fluxes observed against the CMB and the intrinsic line fluxes for different CO transitions and redshifts in the local thermal equilibrium (LTE) case and in the non-LTE case. For the kinetic temperature of the gas in MACSJ0032-arc of T_kin ~ T_dust = 43 ± 5 K and the LTE case, the corresponding ratios are approximately 0.75 for CO(1–0), 0.85 for CO(4–3), and 0.9 for CO(6–5). Moreover, the total CO(6–5) line integrated flux (Table 1) was first corrected for the flux excess observed in the counter-image E³. This yields the CO(1–0), CO(4–3), and CO(6–5) luminosities corrected against CMB listed in Table 2.

Fig. 5 CMB corrected CO SLED of MACSJ0032-arc at zCO = 3.6314 (red stars) compared to the average CO SLEDs of the Milky Way (black crosses), the local (U)LIRGs (green circles), the z ~ 1 − 4 SMGs (blue squares), and the z ~ 1.5 BzK galaxies (magenta triangles). All SLEDs are normalized to the CO(1–0) flux of the average SLED for BzK galaxies, except the Milky Way normalized using CO(2–1).

The resulting CO SLED of MACSJ0032-arc is then compared to the average CO SLED of z ~ 1.5 BzK galaxies from Daddi et al. (2015), z ~ 1 − 4 submm galaxies (SMGs) from Bothwell et al. (2013), local (ultra-)LIRGs from Papadopoulos et al. (2012), and the Milky Way inner disk from Fixsen et al. (1999). We find a clear CO SLED enhancement of MACSJ0032-arc over the Milky Way CO SLED and, more specifically, this galaxy demonstrates that high-J transitions up to CO(6–5) may remain excited at least in some high-redshift normal SFGs. In fact, the CO SLED of this z ~ 3.6 galaxy appears to be similar to the SLED of high-redshift SMGs, with a turnover at J> 4, even though its IR luminosity, ${\mathit{L}}_{\mathrm{IR}}\mathit{/}\mathit{\mu }\mathrm{=}\mathrm{4.}{\mathrm{8}}_{-0.6}^{\mathrm{+}\mathrm{1.2}}\mathrm{\times }{\mathrm{10}}^{\mathrm{11}}{\mathit{L}}_{\mathrm{\odot }}$, is 10 times lower than typically observed in SMGs. Although at first glance this seems unexpected, it is still in line with the CO SLED predictions for high-redshift SFGs from theoretical modeling. Indeed, the Bournaud et al. (2015) simulations predict a turnover at only J = 5 for both disk and merger galaxies, and Narayanan & Krumholz (2014) find that the overall CO excitation is regulated by the SFR surface density, which also implies a turnover at J = 5 for MACSJ0032-arc. In addition, Papadopoulos et al. (2012) propose a toy model with no turnover at J< 6.

As a result, the CO(6–5) line detection in MACSJ0032-arc enables us to place a constraint on the CO SLED of high-redshift SFGs at a very high J rotational level. We derive the following CO luminosity correction factors: ${\mathit{r}}_{\mathrm{4}\mathit{,}\mathrm{1}}\mathrm{=}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{4}\mathrm{-}\mathrm{3}\mathrm{)}}^{\mathrm{\prime }}\mathit{/}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}\mathrm{=}\mathrm{0.60}\mathrm{\pm }\mathrm{0.17}$ and ${\mathit{r}}_{\mathrm{6}\mathit{,}\mathrm{1}}\mathrm{=}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{6}\mathrm{-}\mathrm{5}\mathrm{)}}^{\mathrm{\prime }}\mathit{/}{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}\mathrm{=}\mathrm{0.28}\mathrm{\pm }\mathrm{0.08}$⁴ (Table 2). These factors are comparable to those of high-redshift SMGs with r_4,1 = 0.41 − 0.60 and r_6,5 = 0.21 − 0.46 (Bothwell et al. 2013; Spilker et al. 2014). They are slightly higher than those of BzK galaxies at z ~ 1.5, with average r_3,1 = 0.42 ± 0.07 and r_5,1 = 0.23 ± 0.04 (Daddi et al. 2015), but formally still within the uncertainties. The trend for a somewhat more excited CO SLED in SFGs at higher redshift needs to be further confirmed.

Fig. 6 Comparison of the observed JVLA CO(1–0) line emission, PdBI CO(6–5) line emission, JVLA 5 GHz continuum, and PdBI 2 mm continuum contours, overlaid on the HST/ACS F814W multiple images B, C, D, and E of MACSJ0032-arc (left panels), with the respective simulated beam-convolved emission maps in the image plane (yellow contours in the middle and right panels) obtained for two different combinations of elliptical Gaussian light profiles in the source plane: one extended Gaussian component placed between the two HST UV-bright knots (yellow contours in the top middle panel) and two Gaussian components with locations and shapes following the two UV-bright knots (yellow contours in the top right panel). Noise realizations based on the data are added to the simulated maps, and the absolute flux scaling is obtained by matching the observed flux at the peak of the emission in the counter-image C in each of the CO(1–0), CO(6–5), 5 GHz, and 2 mm simulated maps. The critical line is in red. The size and orientation of the beams are indicated by the dashed green ellipses. Contour levels start at 2σ and are spaced in steps of 1σ (as in Fig. 2).

4.4. CO spatial distribution and kinematics

The CO(6–5) emission is successfully detected in the four most strongly amplified multiple images (B, C, D, and E) of MACSJ0032-arc (see Sect. 3.3). As shown in Fig. 2, where we overlay the velocity-integrated CO(6–5) contours on the HST/ACS F814W image, each individual counter-image is well resolved in CO(6–5), with the exception of some faint emission bridging the images C and D. However, the two knots that, at a separation of ~0.8′′ (1.14 ± 0.28 kpc in the reconstructed source plane; see Sect. 4.1), are clearly resolved in the HST rest-frame UV data within each counter-image remain blended in the PdBI 1.94′′ × 1.62′′ beam. They should be resolved in the JVLA CO(1–0) observations obtained with a beam size of 0.90′′ × 0.79′′. However, a closer look at Fig. 2, which also shows the velocity-integrated CO(1–0) contours overlaid on the HST/ACS F814W image, reveals that the peak of the CO(1–0) emission in the counter-image C falls between the two HST UV-bright knots. The JVLA radio continuum emission at 5 GHz, acquired at an even better angular resolution with a beam size of 0.87′′ × 0.62′′, also shown in Fig. 2, exhibits a very similar spatial distribution pattern to that suggested by the CO(1–0) emission: detected in images B, C, D, and E (see Sect. 3.4), it peaks between the two UV-bright knots, even in the most strongly amplified and stretched image C where it breaks into two centroids not co-spatial with the UV knots. Indeed, the observed centroid displacements between the UV and 5 GHz emissions is of ~0.25′′ in image C, which cannot be accounted for either by the JVLA positional accuracy⁵ of ~35 mas at 5σ or by the absolute HST positional error of ~45 mas (Sect. 3.1).

To ascertain the spatial origin of the CO(1–0) and CO(6−5) line emissions together with the 5 GHz and 2 mm continuum emissions with respect to the two UV-bright knots, we have searched for the best combination of elliptical Gaussian light profiles in the source plane that can reproduce all these emissions in the image plane. We are aware that forcing all the emissions to arise from exactly the same location in the source model is a strong assumption. Indeed, it is well known that the different CO lines of the rotational ladder require different physical conditions to be excited: higher density and temperature at higher J. It is therefore expected that the CO(6–5) and CO(1–0) emissions are not exactly co-spatial, as is frequently observed in the nearby galaxies such as M 82 (Ward et al. 2003) or NGC 253 (Krips et al. 2016). Also, the continuum requires the heating of the dust, and does not have the same excitation requirements as the lines, thus is likely not to be exactly co-spatial. However, modeling this complex origin of CO and continuum emissions is not possible, first because of the limited angular resolution and quality of the available CO(6–5) and 2 mm data, and second because one would quickly be hitting degeneracies in the model parameters.

The free parameters used in our source plane simulations are the number of Gaussian light profiles, their locations, shapes, and relative fluxes. To provide more realistic simulations of our observations, we have also constructed noise realizations based on the data, where all pixel values above 2.5σ were set to zero. We randomly attributed pixel values from these noise maps, convolved them with the corresponding beam, and scaled them to the same noise level as in the observations. We then follow the same procedure as in Sect. 4.1 to model the source HST rest-frame UV emission using a grid of elliptical Gaussians. We first considered a grid of three Gaussians similar to the source plane reconstruction of the HST rest-frame UV emission, then a grid of two Gaussians coincident with the two HST UV-bright knots, and finally a grid of one single Gaussian. A global flux normalization of the simulated images was, in all explored combinations, adjusted to match the observed flux at the peak of the emission in the most strongly amplified counter-image C in each of the CO(1–0), CO(6–5), 5 GHz, and 2 mm maps once convolved by their respective beams.

In Fig. 6 we show the combination of one and two elliptical Gaussian light profiles in the source plane that best reproduces the observed CO/radio/mm emissions:

• (i)

  One extended Gaussian placed between the two HST UV-bright knots (middle panels of Fig. 6): a compact elliptical Gaussian (PSF-dominated) fails to give the correct shape and orientation of the CO(1–0), CO(6–5), 5 GHz, and 2 mm emissions in the image plane, while an extended Gaussian component positioned between the two HST UV-bright knots in the source plane yields the best agreement between the simulated beam-convolved and observed maps in the image plane both in terms of spatial distribution (shape and orientation) and respective detection levels from one counter-image to the other.

• (ii)

  Two Gaussians with locations and shapes following the two HST UV-bright knots (right panels of Fig. 6): the corresponding simulated contours of the unresolved CO(6–5) and 2 mm emissions show one single blended emission in the image plane located between the two UV-bright knots, as is seen in the observations. However, the simulated contours of the 5 GHz continuum and the CO(1–0) emission in the most strongly amplified image C are resolved and show two distinct emission peaks in the image plane that fail to reproduce the observations. Bridging the two emission peaks is possible by extending the size of each Gaussian in the direction of the other UV-bright knot in the source plane, but then the simulated contours in the image plane become too extended.

In conclusion, the best simulated CO, 5 GHz, and 2 mm emissions are obtained with one extended Gaussian light profile placed between the HST UV-knots in the source plane, although some imperfections remain (see Fig. 6) such as the slight offset in the predicted locations, seen in particular in image B, which is due to the overall rms of the lens model (0.17′′, see Sect. 4.1), the overestimated 2 mm continuum emission in images B and E that can result from our too optimistic noise realization (see also Sect. 3.3), and the poor prediction of the CO(6–5) emission in image E. For this source plane reconstruction, we estimate a total magnification factor of ~65 for the sum of the CO, 5 GHz, and 2 mm emissions over the multiple images B, C, D, and E. Having derived a very similar magnification factor of μ = 62 ± 6 for the total rest-frame UV emission of images B, C, D, and E (see Sect. 4.1), this indicates that differential magnification between the UV and CO/radio/mm emissions in MACSJ0032-arc is insignificant at the precision of our current measurements.

Fig. 7 Spectra of the CO(6–5), CO(4–3), and CO(1–0) emission lines detected in MACSJ0032-arc binned in steps of 40.16 km s-1, expect for the CO(1–0) line where channels have a resolution of 144.54 km s-1. The cyan-shaded regions indicate channels where positive emission is detected. These channels are used to derive the CO line integrated fluxes and the velocity-integrated and velocity-averaged maps shown in Figs. 2 and 8, respectively. The solid red lines show the single or double Gaussian profiles that best fit the observed CO line profiles. The zero velocity is set to zCO = 3.6314.

Searching for kinematic signatures, we observe that the CO(6–5) line, extracted over all four multiple images B, C, D, and E, shows an asymmetric double-peaked emission line profile, which is similar to the CO(4–3) line, as shown in Fig. 7. Adopting a double Gaussian model for the description of the observed CO(6–5) and CO(4–3) line profiles leads to a best-fit solution that has the two velocity components separated by 185 ± 15 km s^-1, based on the nonlinear χ² minimization and the Levenberg-Marquardt algorithm. In Fig. 8 we plot, separately for the counter-images B, C+D, and E, the CO(6−5) contours integrated over, respectively, the velocity channels that define the red component and the blue component of the double-peaked CO(6−5) emission line profile. We find a clear spatial offset between the contours of the two velocity components in the counter-image C+D, while in images B and E only hints of some offset are observed. However, in all multiple images the red and blue contours follow the same inversions from one counter-image to the other as observed in the HST images and as expected from the lens model (see Figs. 1 and 3). Overall, this is suggestive of a possible signature of rotation.

The CO(1–0) line shows a single velocity component that is centered at the velocity of the strong red component of the CO(6–5) and CO(4–3) lines (see Fig. 7). The non-detection of the blue, 4 × fainter (in integrated flux) CO(1–0) component is easily explained by both the low S/N of the CO(1–0) detection and the low spectral resolution of the CO(1–0) line of 144.54 km s^-1, which implies that the blue component with FWHM = 83 ± 8 km s^-1, as derived by the Gaussian best-fitting solution of the CO(6–5) and CO(4–3) line profiles, is detected over one single velocity channel.

Fig. 8 Velocity-averaged maps of the CO(6–5) emission of the counter-images E (left panel), C+D (middle panel), and B (right panel) of MACSJ0032-arc. Overlaid are the CO(6–5) contours integrated over, respectively, the channels that define the blue component (blue contours) and the red component (red contours) of the double-peaked CO(6–5) line profile shown in Fig. 7. The color-coding is in units of integrated flux Jy km s-1 and starts at 2σ. Contour levels also start at 2σ and are spaced in steps of 1σ. A clear spatial offset between the blue and red contours is observed. The corresponding PdBI beam size of 1.94′′ × 1.62′′ is about the size of the individual counter-images themselves.

We conclude that the bulk of the molecular gas reservoir and cold dust seems, at the resolution of our data, to peak between the two UV-bright knots, while cold gas and dust still extend over the whole galaxy (see the top middle panel of Fig. 6). The fact that the radio continuum, which mostly traces the unobscured star formation through the synchrotron radiation from supernovae remnants, seems to arise from the same location indicates that most of the star formation is also taking place between the two UV-bright knots, a region which is dark at the HST rest-frame UV wavelength⁶ because it is too dusty. This is the location where ~90% of the star formation of MACSJ0032-arc occurs since SFR_UV represents only 10% of the total SFR_{UV + IR} of the galaxy (Sect. 4.2). This agrees with the lensing-corrected SFR_radio/μ = 58 ± 11 M_⊙ yr^-1 (see Table 2), as determined from the radio 5 GHz continuum flux and the SFR–1.4 GHz calibration from Bell (2003; see also Rieke et al. 2009). The 5 GHz flux was first corrected for the flux excess observed in the counter-image E (see Sect. 3.4) by propagating the 5 GHz–F814W color properly measured in images B, C, and D over the counter-image E. The spatial offset between UV clumps and the bulk of star formation has been found in many z ~ 2 SFGs, with only 5–10% of the star formation emerging in the rest-frame UV (Rujopakarn et al. 2016; Dunlop et al. 2017).

4.5. Morphology: single galaxy versus merger

Gathering all information available on MACSJ0032-arc, we now attempt to arrive at a self-consistent interpretation of its observed morphological properties summarized in the following. The arc is shown to be a fairly low-mass, normal SFG with a physical size of ~2.5 kpc or smaller, comparable to the MS galaxy population at 3 <z< 4. It is composed of two very compact rest-frame UV-bright knots with sizes <500 pc and separated by 1.14 ± 0.28 kpc in the source plane (Sect. 4.1). The bulk of the molecular gas, dust content, and star formation, found to be dust obscured, is spatially offset from the rest-frame UV emission and is located between these two UV-emission regions (Sect. 4.4). Neither the CO(1–0) emission nor the radio continuum at 5 GHz is fully resolved in the JVLA observations and may hence originate from a region with a physical size as large as the separation between the UV-bright knots or smaller (≲1.14 kpc). Our gravitational lens model suggests an extended rather than a compact CO, dust, and radio emission (Fig. 6).

Two scenarios may explain these observational facts. First, the two UV-bright knots may be two separate entities in the process of merging, creating a compression zone in their middle where most of the molecular gas mass is found, and triggering new, still dust obscured, star-bursting regions, similar to what is observed in some local galaxies (e.g., the Antennae, Whitmore et al. 1999; and NGC 6240, Rieke et al. 1985). This scenario would most easily explain the more diffuse tail seen extending from one of the UV-bright knots. On the other hand, the two very small knots with sub-kpc sizes may be two star-forming regions, or clumps, within a single gravitationally bound galaxy, whose molecular gas and star formation resides and occurs primarily in its center, similarly to the numerous high-redshift clumpy galaxies observed in HST images (e.g., Elmegreen et al. 2005; Guo et al. 2015). This scenario is supported by the arc’s main sequence and LIRG nature, and could explain both the observed double-peaked CO(4–3) and CO(6–5) emission line profiles (Fig. 7) and the spatial offset between the red and blue velocity components in the CO(6–5) velocity-averaged map (Fig. 8) as signatures of rotation. The measured velocity separation of 185 km s^-1 between the red and the blue velocity components is also compatible with this scenario.

Given the observed excited state of the CO molecular gas in MACSJ0032-arc, comparable to that of high-redshift SMGs (Sect. 4.3 and Fig. 5), we might be tempted to favor the merging scenario. However, this high excitation is more fundamentally related to the compactness of the object, irrespective of its origin (merger or not). Indeed, a compact object will, on average, have a higher molecular gas density that will lead to more excitation of CO by collisions with H₂ (see Solomon et al. 1997; Weiss et al. 2005, 2007). This compactness could reflect the general fact that galaxies are more compact at higher redshifts (z ≳ 3.5) because of their smaller sizes (e.g., Buitrago et al. 2008; Shibuya et al. 2015). Therefore, we interpret this system as a single galaxy with two UV-bright star-forming regions, but this configuration may still be the result of a recent merger or accretion event, albeit not one big enough to completely disrupt the kinematic state of the galaxy.

5. Discussion

In this section, we make use of the wealth of data we have on MACSJ0032-arc to explore the CO-to-H₂ conversion factor in this galaxy. We then add our new CO(1–0) measure to the small sample of five prior CO detections in SFGs at z> 2.5 (Riechers et al. 2010; Johansson et al. 2012; Tan et al. 2013; Saintonge et al. 2013)⁷ to study the cosmic evolution of the molecular gas depletion timescale and that of the molecular gas fraction. To place our object in the general context, we consider the compilation by Dessauges-Zavadsky et al. (2015, and references therein) of local spirals and main sequence SFGs at both z< 0.4 and z> 1 with CO measurements from the literature.

5.1. CO-to-H₂ conversion factor

A major difficulty in measuring the molecular gas mass (M_molgas) of individual galaxies is to determine the CO-to-H₂ conversion factor (α_CO) that relates M_molgas to the CO(1–0) luminosity as ${\mathit{M}}_{\mathrm{molgas}}\mathrm{=}{\mathit{\alpha }}_{\mathrm{CO}}\mathrm{\times }{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$, shown to vary with physical conditions (metallicity, temperature, density, dynamical state of the galaxy, etc.). There is a growing consensus that α_CO and metallicity are inversely correlated for galaxies with metallicities from Z ~ 0.2 Z_⊙ to Z ~ 2 Z_⊙, because of the increasing fraction of CO that is photo-dissociated at low metallicity due to the underabundance of dust that yields more intense radiation fields, resulting in molecular gas that is deficient (dark) in CO (Maloney & Black 1988; Wilson et al. 1995; Israel et al. 2000; Wolfire et al. 2010; Leroy et al. 2011; Bolatto et al. 2013; Sternberg et al. 2014).

Following Genzel et al. (2015, see their Eqs. (7), (8), (12a) and their respective justifications), we consider in what follows the metallicity-dependent CO-to-H₂ conversion function and the mass-metallicity relation calibrated to the Pettini & Pagel (2004, PP04) metallicity scale given by ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{=}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathrm{\times }\mathit{\chi }\mathrm{\left(}\mathit{Z}\mathrm{\right)}$(2)with $\mathit{\chi }\mathrm{\left(}\mathit{Z}\mathrm{\right)}\mathrm{=}{\mathrm{10}}^{\mathrm{-}\mathrm{1.27}\mathrm{(}\mathrm{12}\mathrm{+}\log \mathrm{(}\mathrm{O}\mathit{/}\mathrm{H}{\mathrm{)}}_{\mathrm{PP}\mathrm{04}}\mathrm{-}\mathrm{8.67}\mathrm{)}}$(3)and $\mathrm{12}\mathrm{+}\log \mathrm{(}\mathrm{O}\mathit{/}\mathrm{H}{\mathrm{)}}_{\mathrm{PP}\mathrm{04}}\mathrm{=}\mathit{a}\mathrm{-}\mathrm{0.087}\mathrm{(}\log \mathrm{\left(}{\mathit{M}}_{\mathrm{\ast }}\mathrm{\right)}\mathrm{-}\mathit{b}{\mathrm{)}}^{\mathrm{2}}\mathit{,}$(4)where $\begin{array}{ccc}\mathit{a}& \mathrm{=}& \mathrm{8.74}\mathrm{and}\\ \mathit{b}& \mathrm{=}& \mathrm{10.4}\mathrm{+}\mathrm{4.46}\log \mathrm{(}\mathrm{1}\mathrm{+}\mathit{z}\mathrm{)}\mathrm{-}\mathrm{1.78}\mathrm{\left(}\log \mathrm{\right(}\mathrm{1}\mathrm{+}\mathit{z}\mathrm{)}{\mathrm{)}}^{\mathrm{2}}\mathit{.}\end{array}$We assume the Milky Way CO-to-H₂ conversion factor to be α_CO,MW = 4.36 M_⊙/ (K km s^-1 pc²)⁸, which includes a correction factor of 1.36 for helium (Strong & Mattox 1996), and the solar abundance of 12 + log (O / H)_⊙ = 8.67 from Asplund et al. (2004). The resulting metallicity-dependent CO-to-H₂ conversion function is essentially a function of two physical parameters, M_∗ and redshift, as illustrated in Fig. 9 by the iso-redshift curves. The uncertainties typically are ± 0.25 dex on the inferred ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$, which is basically the scatter of the mass-metallicity relation, and ± 0.15 dex on the stellar masses. 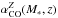The value of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{\left(}{\mathit{M}}_{\mathrm{\ast }}\mathit{,z}\mathrm{\right)}$ increases with redshift for any given M_∗, and at any given redshift increases with decreasing M_∗. Adopting these prescriptions, we find most of the CO-detected MS SFGs from our literature compilation (Dessauges-Zavadsky et al. 2015) to feature ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ values comparable to α_CO,MW, with $\mathrm{0.8}\mathit{<}{\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{<}\mathrm{1.5}$, owing to their high stellar masses (small circles in Fig. 9).

Fig. 9 Dependence of the metallicity-dependent CO-to-H2 conversion function, computed from Eqs. (2)–(4), on stellar mass and redshift. The lines are the iso-redshift curves, color-coded as a function of redshift, for z = 0.5 to z = 3.5 in steps of Δz = 0.5: the solid sections correspond to ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{<}\mathrm{1.5}$, the dashed segments to $\mathrm{1.5}\mathit{<}{\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{<}\mathrm{2}$, and the dotted portions to ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{>}\mathrm{2}$. The horizontal black line marks the Milky Way CO-to-H2 conversion factor. Small symbols represent the computed ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ values for MACSJ0032-arc (red star) as well as the compilation of MS SFGs with CO measurements from the literature (Dessauges-Zavadsky et al. 2015). Large symbols correspond to the few MS SFGs for which gas-phase metallicities have been measured from rest-frame optical nebular lines. The symbols are color-coded according to galaxy redshift and their shapes indicate ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}$ ratios (<1.5: circles, 1.5−2: triangles, and >2: squares and star).

Using the derived M_∗ (Table 2), z_CO = 3.6314, and 12 + log (O / H)_PP04 = 8.0 ± 0.2 (Z = 0.21 Z_⊙) estimated from Eq. (4), we obtain a high value of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{=}\mathrm{30}\mathrm{\pm }\mathrm{9}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ for MACSJ0032-arc, as expected for a high-redshift galaxy with a low stellar mass (star in Fig. 9). Such a high ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ value translates into a very important gas mass of M_molgas/μ = (7.6 ± 3.0) × 10¹⁰M_⊙ (lensing-corrected). Since most of this molecular gas is concentrated within a 1 − 2 kpc region (see Sect. 4.4), this also implies a very high H₂ surface density of Σ_H2/μ ≳ 2.4 × 10⁴M_⊙ pc^-2, which is about two orders of magnitude higher than the typical value of ~200 M_⊙ pc^-2 found for giant molecular clouds (GMCs) in the Milky Way, and even higher than that of GMCs in local ULIRGs of ~10⁴M_⊙ pc^-2 (Downes & Solomon 1998). In ULIRGs, however, the CO-to-H₂ conversion factor is significantly lower, typically 0.8 M_⊙/ (K km s^-1 pc²) (see below). Although there is evidence for ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{Z}}$ values of 20 − 100 M_⊙/ (K km s^-1 pc²) in dwarf galaxies like the Magellanic Clouds (Leroy et al. 2011), we argue against such a high CO-to-H₂ conversion factor for MACSJ0032-arc based on the fact that its morphology, star formation rate, and CO SLED, among other factors, represent compelling evidence of a much denser and more active environment than found in local dwarf galaxies.

The metallicity-dependent CO-to-H₂ conversion function strongly relies on the adopted mass-metallicity calibration, which has known caveats, in particular for objects at z> 2.5 and with low stellar masses. With the mass-metallicity relation specifically calibrated for SFGs at z ~ 3 − 5 and valid for galaxies with log (M_∗/M_⊙) = 9 − 11 (Troncoso et al. 2014), we find a similarly low metallicity for MACSJ0032-arc. On the other hand, the fundamental metallicity relation (FMR) calibrated for low-M_∗ galaxies (Mannucci et al. 2010, 2011; Christensen et al. 2012), characterized by μ_0.32 = log (M_∗) − 0.32log (SFR) < 9.5 (a criterion satisfied by MACSJ0032-arc with μ_0.32 = 9.1), yields a higher metallicity of 12 + log (O / H)_FMR = 8.5 ± 0.2 (Z = 0.68 Z_⊙). This higher metallicity is also supported by the low R3 = [O iii] λ5007/Hβ line flux ratio of 0.63 ± 0.07, measured in our recently acquired near-IR LBT/LUCI spectrum of MACSJ0032-arc (Walth et al., in prep.). According to the latest R3–metallicity calibration from Curti et al. (2017)⁹, although known to be very approximative, this ratio points to a metallicity of 12 + log (O / H)_neb = 8.6 − 8.7. At this higher metallicity, we obtain a much smaller ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ value of 7.1 ± 2.2 M_⊙/ (K km s^-1 pc²). Thus, the uncertainty of the metallicity of MACSJ0032-arc induces an error of at least a factor of 4 into the ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ determination.

Similar problems are encountered for the few MS galaxies at high redshift for which direct measurements of their gas-phase metallicities (large symbols in Fig. 9) have been obtained from the [N ii] λ6583/Hα λ6563 line flux ratio and the PP04 metallicity calibration¹⁰ (Teplitz et al. 2000; Hainline et al. 2009; Law et al. 2009; Richard et al. 2011; Dessauges-Zavadsky et al. 2011; Genzel et al. 2013). For most of these systems, the ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ values computed from their measured metallicities, which are higher than the metallicities estimated from Eq. (4), fall significantly below the iso-redshift curves at their M_∗ and z values (as illustrated in Fig. 9 by a redshift color-code that does not match that of the corresponding iso-redshift curve).

Magdis et al. (2011) proposed another way of determining the CO-to-H₂ conversion factor at high redshift by using the dust mass and the CO(1−0) luminosity through the relation ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\frac{\mathrm{1}}{{\mathit{\delta }}_{\mathrm{DGR}}}\mathrm{\times }\frac{{\mathit{M}}_{\mathrm{dust}}}{{\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}}\mathrm{·}$(5)This method requires the knowledge of another physical parameter that is the dust-to-gas mass ratio, defined as δ_DGR = M_dust/M_molgas¹¹. The value of δ_DGR is assumed to vary with metallicity, following the prescription derived by Leroy et al. (2011) for local galaxies ${\mathit{\delta }}_{\mathrm{DGR}}\mathrm{=}{\mathrm{10}}^{\mathrm{(}\mathrm{-}\mathrm{2}\mathrm{+}\mathrm{0.85}\mathrm{(}\mathrm{12}\mathrm{+}\log \mathrm{(}\mathrm{O}\mathit{/}\mathrm{H}{\mathrm{)}}_{\mathrm{PP}\mathrm{04}}\mathrm{-}\mathrm{8.67}\mathrm{)}\mathrm{)}}\mathit{.}$(6)From the M_dust and ${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ values listed in Table 2 and the metallicity estimate of 12 + log (O / H)_PP04 = 8.0 ± 0.2 computed using Eq. (4), we find ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\mathrm{2.8}\mathrm{\pm }\mathrm{0.9}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ for MACSJ0032-arc. This in turn yields much more reasonable M_molgas and H₂ surface density.

This ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}$ value, however, differs by a factor of 11 from the value ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{=}\mathrm{30}\mathrm{\pm }\mathrm{9}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ computed before from Eqs. (2), (3), while the two derivations of the CO-to-H₂ conversion factor, if correct, should yield the same result for any given galaxy. The cause of the discrepancy does not lie in erroneous determinations of either ${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ or M_dust (Table 2), which both enter in Eq. (5). Indeed, we detect the CO(1–0) emission, and therefore know the ${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ within the given uncertainty. Accounting for the CMB radiation leads to a higher intrinsic ${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ by approximately 25% (Sect. 4.3). The value of M_dust is notoriously more difficult to determine (Eq. (1)), and a factor of 2 uncertainty in the dust mass is commonly accepted. An underestimation of the 2 mm continuum emission could, in addition, increase the M_dust estimate, but by no more than another factor of 1.4 according to the data (see Sect. 3.3) and given the good agreement with the constant dust-to-stellar mass ratio of log (M_dust/M_∗) ≈ − 2.6 (Santini et al. 2010; Smith et al. 2012; Sklias et al. 2014). The value of δ_DGR could also vary by a factor 2 given the dispersion in the δ_DGR–metallicity relation. However, we are still far from the factor 11. The situation is less dire if we assume the higher metallicity for MACSJ0032-arc (at 12 + log (O / H)_FMR = 8.5 ± 0.2 the discrepancy falls to a factor of 7), but we are nevertheless left, in fine, with the realization that Eqs. (2), (3) and Eqs. (5), (6) cannot produce consistent results for ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ and ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}$.

There is another fundamental physical parameter that should be taken into account in the estimation of the CO-to-H₂ conversion factor, namely the gas excitation state, which depends on the galaxy temperature and density. The CO SLED analysis presented in Sect. 4.3 shows that the CO excitation in MACSJ0032-arc is much higher than that of the Milky Way, and is in fact comparable to that of high-redshift SMGs. Given this similarity in the excitation state of their molecular gas, it appears appropriate to replace, for MACSJ0032-arc, α_CO,MW in Eq. (2) by α_CO,ULIRG ≃ 0.8 M_⊙/ (K km s^-1 pc²) as observed in local ULIRGs (Solomon et al. 1997; Bolatto et al. 2013; Carilli & Walter 2013). It follows that our target’s ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ value is likely to be about 5 × lower. With this alternative ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ of reference, it becomes possible to reconcile ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ with ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}$ for MACSJ0032-arc down to a small factor between 1.3 and 2 depending on the adopted metallicity (12 + log (O / H)_FMR = 8.5 ± 0.2 and 12 + log (O / H)_PP04 = 8.0 ± 0.2, respectively).

Since we have, at present, no way to constrain the CO-to-H₂ conversion factor more tightly in MACSJ0032-arc (and in general), in the following we consider the two extreme but still reasonable α_CO values for the arc (see Table 2):

• ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{\simeq }\mathrm{7.1}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$, corresponding to an ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ along with a metallicity of 12 + log (O / H)_FMR = 8.5 ± 0.2 computed using the FMR calibrated for low-M_∗ galaxies;

• ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{\simeq }\mathrm{2.8}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$, corresponding to an ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}$ along with a metallicity of 12 + log (O / H)_PP04 = 8.0 ± 0.2 derived from Eq. (4).

These two α_CO values yield a range of lensing-corrected molecular gas masses in MACSJ0032-arc of M_molgas/μ = (7.1 − 18) × 10⁹M_⊙ (see Table 2) and lensing-corrected H₂ surfaces densities of Σ_H2/μ ≳ 2200 − 5800 M_⊙ pc².

Although it is clearly ill-constrained, we note that this range of α_CO values for MACSJ0032-arc is consistent with results from studies of z ~ 1 − 2 BzK and MS SFGs in which α_CO was found to vary between 2 and 20 M_⊙/ (K km s^-1 pc²). Indeed, Magdis et al. (2012) obtained an average ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\mathrm{5.5}\mathrm{\pm }\mathrm{0.4}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ computed for 6 BzK galaxies at z ~ 1.5 using the same Eqs. (5), (6), whereas for the same BzK galaxy sample Daddi et al. (2010) argued for ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dyn}}\mathrm{=}\mathrm{3.6}\mathrm{\pm }\mathrm{0.8}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ in a work based on the dynamical masses. Magnelli et al. (2012) obtained, on average, a much higher value of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\mathrm{14}\mathrm{\pm }\mathrm{4}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ for seven MS SFGs at z ~ 1. In another study, Genzel et al. (2012) used the Kennicutt-Schmidt (KS) relation in reverse to estimate M_molgas from the SFR and reported, for 44 SFGs at two median redshifts of ⟨ z ⟩ = 1.2 and ⟨ z ⟩ = 2.2, a range of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{KS}}$ values of 2 − 20 M_⊙/ (K km s^-1 pc²) at metallicities from 12 + log (O / H) = 8.4 to 8.9. 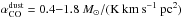Finally, our adopted α_CO values do not agree as closely with those of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\mathrm{0.4}\mathrm{-}\mathrm{1.8}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ estimated for dusty starburst galaxies at 2.5 <z< 5.7 by Aravena et al. (2016) using a constant δ_DGR.

For our compilation of CO-detected MS SFGs from the literature (Dessauges-Zavadsky et al. 2015), in the following we adopt ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$, as computed from Eqs. (2)–(4) and, when available, we consider the measured gas phase metallicities. Special attention was paid to galaxies at z> 2.5 and/or with log (M_∗/M_⊙) < 10 because of the expected larger uncertainty in their metallicities when derived from the assumed mass-metallicity relation (Eq. (4)). We therefore retain these galaxies only when direct measurements of their gas phase metallicities are available (two galaxies at z = 1.5859 and z = 2.7793, respectively, were thus removed from our compilation).

Fig. 10 Molecular gas depletion timescale as a function of redshift for our compilation of CO-detected MS SFGs from the literature (Dessauges-Zavadsky et al. 2015) and MACSJ0032-arc at zCO = 3.6314 (star). The encircled data points correspond to MS SFGs with measured gas-phase metallicities. Five redshift bins are considered: z ~ 0, z = [ 0.055,0.4 ], z = [ 1,1.6 ], z = [ 2,2.5 ], and z = [ 2.7,3.6 ]. The corresponding mean values of tdepl are shown as large black crosses with the associated 1σ dispersion as standard deviation. Magenta crosses represent tdepl values from Béthermin et al. (2015) derived from the FIR dust continuum and by adopting the same mass-metallicity relation (Eq. (4)). The observed evolution of tdepl with redshift is parametrized by a power law; the best fit, 1.15(1 + z)-0.85, is shown as a solid line.

5.2. Molecular gas depletion timescale

The depletion timescale, defined as t_depl = M_molgas/SFR, describes how long each galaxy could sustain star formation at the current rate before running out of fuel, assuming that the gas reservoir is not replenished. Models predict the depletion of the molecular gas in galaxies over cosmic time (e.g., Davé et al. 2011, 2012). More precisely, t_depl has been shown to scale as (1 + z)^-1.5 for the canonical disk model (Mo et al. 1998; Bouché et al. 2010; Genel et al. 2010). The decrease in t_depl with redshift is amply supported by CO observations of SFGs (e.g., Combes et al. 2013; Tacconi et al. 2013; Saintonge et al. 2013), but with growing evidence of a more modest redshift evolution of (1 + z)^γ, with γ possibly as low as − 0.16 (Genzel et al. 2015). Genzel et al. (2015), Béthermin et al. (2015), and Schinnerer et al. (2016) also find t_depl(z) to be only slowly evolving when estimating t_depl from the FIR dust continuum.

In Fig. 10 we show t_depl as a function of redshift for MACSJ0032-arc, and for our compilation of CO-detected galaxies from the literature (Dessauges-Zavadsky et al. 2015), which we restrict to SFGs lying within the accepted thickness of the MS (0.3 <sSFR/sSFR_MS< 3), a condition also satisfied by MACSJ0032-arc (see Sect. 4.2). The underlying CO-to-H₂ conversion factors are uniformly derived for the sample of SFGs as explained in Sect. 5.1. We extend the redshift range explored by Genzel et al. (2015) by adding the measured depletion times from CO of 5 MS SFGs in the z = [ 2.7,3.6 ] bin to the analysis, including that of MACSJ0032-arc. The new best-fit power law description of t_depl(z) is then given by the (1 + z)^-0.85 scaling and is on average steeper than that determined by Genzel et al. (2015) only for galaxies at z ≲ 2.5. With t_depl declining from ~1.0 Gyr at z ~ 0 to ~270 Myr at z ~ 3.2, the observed t_depl evolution is very similar to that inferred from the FIR dust continuum, which yields only moderate redshift evolution up to z ~ 2.5 followed by more rapid evolution at higher redshift (Béthermin et al. 2015). We almost invoke a two-step power law for the redshift evolution of t_depl, with a turnover around z ~ 2.8, but this still needs to be confirmed with more t_depl measurements at z> 2.5.

Overall, t_depl shows a more modest redshift evolution than predicted by galaxy evolution models. This may be partly due to the metallicity-dependent CO-to-H₂ conversion function we have adopted (${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ computed using Eqs. (2)–(4)). As discussed in Sect. 5.1 and shown in Fig. 9, ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ increases with redshift for all M_∗. Adopting this 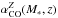${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{\left(}{\mathit{M}}_{\mathrm{\ast }}\mathit{,z}\mathrm{\right)}$ may thus artificially flatten the redshift evolution of t_depl. A steeper evolution is indeed observed when a simple α_CO,MW conversion factor is applied to MS SFGs. In this case, the power law index γ is found to vary between − 1.5 and − 1 (see Tacconi et al. 2013; Dessauges-Zavadsky et al. 2015). In any event, the lower t_depl average observed at the highest redshifts, i.e., in the z = [ 2.7,3.6 ] bin, as well as the resulting evolution of t_depl with cosmic time only become the more solid results.

5.3. Molecular gas fraction

The molecular gas fraction is defined as ${\mathit{f}}_{\mathrm{molgas}}\mathrm{=}\frac{{\mathit{M}}_{\mathrm{molgas}}}{{\mathit{M}}_{\mathrm{molgas}}\mathrm{+}{\mathit{M}}_{\mathrm{\ast }}}\mathrm{\equiv }\frac{\mathrm{1}}{\mathrm{1}\mathrm{+}\mathrm{(}\mathit{sSFR}\mathrm{\times }{\mathit{t}}_{\mathrm{depl}}{\mathrm{)}}^{-1}}\mathrm{·}$(7)Here, f_molgas depends on both sSFR and t_depl. The monotonic rise of sSFR with redshift, commonly parametrized as (1 + z)^γ, where γ = 1.5 − 3, is now well established observationally and theoretically (e.g., Schaerer & de Barros 2009; Schreiber et al. 2015; Tacchella et al. 2016; Faisst et al. 2016). Combined with the modest redshift evolution of t_depl discussed in Sect. 5.2, an increase in f_molgas with redshift is similarly expected. This f_molgas evolution with cosmic time is in line with various model predictions (e.g., Obreschkow & Rawlings 2009; Lagos et al. 2011, 2014), and could partly be at the origin of the steep decline in the star formation rate density after the peak of activity around z = 1.5 − 2 (Madau et al. 1998; Hopkins & Beacom 2006) as the molecular gas is the fuel for star formation.

In Fig. 11 we show f_molgas as a function of redshift for MACSJ0032-arc, and for our compilation of CO-detected galaxies from the literature (Dessauges-Zavadsky et al. 2015), the latter having again been restricted to SFGs lying within the accepted thickness of the MS. We assume for the SFGs from the literature the same underlying CO-to-H₂ conversion factors as for t_depl measurements (see Sect. 5.1). Extending the compilation of CO measurements to higher redshifts, the observed evolution of f_molgas with redshift is well reproduced by the scaling law 1 / (1 + (0.12(1 + z)^2.8 × (1 + z)^-0.85)^-1) (Eq. (7)), composed of the (1 + z)^γ best-fit descriptions of, respectively, sSFR(z) (e.g., Tacconi et al. 2013) and t_depl(z) (Sect. 5.2). This scaling law predicts an increase of f_molgas with redshift, which is at odds with the flattening of f_molgas(z) beyond z ≳ 2 previously claimed for CO-detected MS SFGs (Saintonge et al. 2013; Dessauges-Zavadsky et al. 2015), and for FIR dust continuum f_molgas estimates (Troncoso et al. 2014; Béthermin et al. 2015; Schinnerer et al. 2016). Nevertheless, currently, taking the few available CO measurements at z ≳ 2 at face value, we cannot exclude either the increase in or the flattening of f_molgas at high redshifts, since the two molecular gas fraction means, ⟨ f_molgas ⟩ = 0.44 ± 0.08 at z = [ 2,2.5 ] and ⟨ f_molgas ⟩ = 0.61 ± 0.22 at z = [ 2.7,3.6 ], agree within their 1σ errors defined as the standard deviation of the respective f_molgas dispersions.

Fig. 11 Same as Fig. 10, but for the molecular gas fraction. A clear evolution of fmolgas with redshift is observed, in good agreement with 1 / (1 + (0.12(1 + z)1.95)-1) (solid line).

Moreover, the adopted metallicity-dependent ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ function may artificially boost the redshift evolution of f_molgas for the same reasons that it may lessen the redshift evolution of t_depl (see Fig. 9). Indeed, the aforementioned plateau in f_molgas at z ≳ 2 is more clearly observed when instead a simple α_CO,MW conversion factor is applied to MS SFGs (Dessauges-Zavadsky et al. 2015). We can eliminate, in our estimate of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$, at least the uncertainty in the mass-metallicity relation (Eq. (4)) by considering only the few objects with direct gas-phase metallicity measurements (encircled data points in Fig. 11). Nevertheless, the mean f_molgas at z = [ 2.7,3.6 ], in that case, still remains above that of the z = [ 1,1.6 ] and z = [ 2,2.5 ] bins, but with the same large standard deviation. Interestingly, the new f_molgas measurement as high as 60–79% obtained in MACSJ0032-arc, which is the highest redshift object with a CO measure, favors a steady increase in f_molgas with redshift irrespective of the α_CO employed.

Finally, we would like to note that all the CO measurements at z> 2.5 (except one, the non-encircled triangle in Fig. 11) come from lensed galaxies with low stellar masses (log (M_∗/M_⊙) < 10.4), whereas CO is most commonly measured in massive galaxies at z< 2.5. Similarly, all the molecular gas mass estimates from the FIR dust continuum are derived for massive galaxies. Given the expected increase in f_molgas with decreasing M_∗ (Bouché et al. 2010; Davé et al. 2011), the possible trend for an increase in f_molgas beyond z ~ 2.5 may reflect the higher f_molgas expected to be found in low-mass galaxies (see Dessauges-Zavadsky et al. 2015) if the mass dependence of f_molgas is stronger than its dependence on redshift.

6. Summary and conclusions

For the first time, we can simultaneously characterize the stellar, dust, and molecular gas properties in a normal star-forming galaxy at a redshift as high as z_CO = 3.6314. MACSJ0032-arc has a fairly low stellar mass ${\mathit{M}}_{\mathrm{\ast }}\mathit{/}\mathit{\mu }\mathrm{=}\mathrm{4.}{\mathrm{8}}_{-1.0}^{\mathrm{+}\mathrm{0.5}}\mathrm{\times }{\mathrm{10}}^{\mathrm{9}}{\mathit{M}}_{\mathrm{\odot }}$ and a star formation rate $\mathit{SFR}\mathit{/}\mathit{\mu }\mathrm{=}\mathrm{5}{\mathrm{1}}_{-10}^{\mathrm{+}\mathrm{7}}{\mathit{M}}_{\mathrm{\odot }}\mathrm{y}{\mathrm{r}}^{-1}$ when corrected for the lensing magnification μ = 62 ± 6, placing it relatively close to the main sequence at z ~ 4 with an offset ≲+ 0.3 dex depending on the MS definition (Tacconi et al. 2013; Speagle et al. 2014; Tomczak et al. 2016). Moreover, it follows the tight correlation between IR and CO(1–0) luminosities (Dessauges-Zavadsky et al. 2015; Scoville et al. 2016). MACSJ0032-arc shows no weakening of its ${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ (see Tan et al. 2013) compared to the expectations based on the L_IR–${\mathit{L}}_{\mathrm{CO}\mathrm{(}\mathrm{1}\mathrm{-}\mathrm{0}\mathrm{)}}^{\mathrm{\prime }}$ relation satisfied by MS SFGs at z ≲ 2.5. Our findings for MACSJ0032-arc can be summarized as follows:

• 1.

  About 90% of the totalSFR_{UV + IR} of MACSJ0032-arc is inaccessible at rest-frame UV wavelengths, but is detected through thermal dust emission in the FIR regime.

• 2.

  In HST images, MACSJ0032-arc is resolved into two UV-bright knots, separated by 1.14 ± 0.28 kpc. The bulk of the molecular gas mass and star formation of the lensed galaxy is, however, decoupled from the rest-frame UV emission and comes from between these two UV knots, i.e., from a region too dusty to be detected at rest-frame UV wavelengths, shown to also host the 2 mm cold dust emission.

• 3.

  With the detection of the CO(1–0), CO(4–3), and CO(6–5) emission lines, whose fluxes have been corrected against the CMB, we can constrain the CO luminosity correction factors for the high J = 4 and J = 6 CO transitions in a normal SFG at z ~ 3.6. The derived values of r_4,1 = 0.60 ± 0.17 and r_6,1 = 0.28 ± 0.08 describe a CO SLED featuring a slightly more highly excited CO than found in lower-redshift SFGs, but in line with CO excitation levels observed in high-redshift SMGs even though the IR luminosity, ${\mathit{L}}_{\mathrm{IR}}\mathit{/}\mathit{\mu }\mathrm{=}\mathrm{4.}{\mathrm{8}}_{-0.6}^{\mathrm{+}\mathrm{1.2}}\mathrm{\times }{\mathrm{10}}^{\mathrm{11}}{\mathit{L}}_{\mathrm{\odot }}$, of MACSJ0032-arc is 10 times lower than typically observed in SMGs. The high CO excitation is likely due to the compactness of MACSJ0032-arc, that could result from the general fact that galaxies are more compact at higher redshifts because of their smaller sizes. These results are of particular interest in the context of high-redshift normal star-forming galaxies and their molecular gas mass estimates as only high CO rotational transitions (J ≥ 4) are accessible beyond z ~ 4 with the NOrthern Extended Millimeter Array (NOEMA) and ALMA.

• 4.

  We interpret the morphology of MACSJ0032-arc as indicative of it being a single system whose molecular gas and intense dusty star formation resides and occurs primarily in its center, surrounded by two UV-bright star-forming regions, possibly in rotation. This configuration may also be the result of a recent merger or accretion event, albeit not one big enough to completely disrupt the kinematic state of the galaxy, as we still observe double-peaked CO(4–3) and CO(6–5) line profiles.

• 5.

  Measurements of both the dust mass and the CO(1–0) luminosity of MACSJ0032-arc enable us to estimate its CO-to-H₂ conversion factor, α_CO, using several independent methods. First, we consider the redshift-dependent mass-metallicity relation and metallicity-dependent ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ function adopted by Genzel et al. (2015). This method yields a metallicity of 12 + log (O / H)_PP04 = 8.0 ± 0.2 and a value of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{=}\mathrm{30}\mathrm{\pm }\mathrm{9}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$. Alternatively, assuming the metallicity-dependent dust-to-gas mass ratio from Leroy et al. (2011), we obtain the markedly different value of ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{=}\mathrm{2.8}\mathrm{\pm }\mathrm{0.9}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$. Part of the discrepancy may be due to the uncertainty on the metallicity – we get a metallicity as high as 12 + log (O / H)_FMR = 8.5 ± 0.2 when using the FMR calibrated for low-M_∗ galaxies – and/or the high CO excitation observed in the arc, which may imply an additional correction factor to ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ on the order of α_CO,MW/α_CO,ULIRG ~ 5. When this high CO excitation state is accounted for, the discrepancy between ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ and ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}$ falls to a factor between 1.3 and 2 depending on the adopted metallicity. We thus assume the CO-to-H₂ conversion factor for MACSJ0032-arc to lie between ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathrm{dust}}\mathrm{\simeq }\mathrm{2.8}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ along with the 12 + log (O / H)_PP04 metallicity and ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathrm{\simeq }\mathrm{7.1}{\mathit{M}}_{\mathrm{\odot }}\mathit{/}\mathrm{\left(}\mathrm{K}\mathrm{km}{\mathrm{s}}^{-1}\mathrm{p}{\mathrm{c}}^{\mathrm{2}}\mathrm{\right)}$ along with the 12 + log (O / H)_FMR metallicity.

• 6.

  Adopting the above α_CO interval, we derive a depletion time for the molecular gas in this z ~ 3.6 star-forming galaxy of t_depl = 0.14 − 0.35 Gyr. Along with that of other high-redshift MS SFGs, generally limited to z ≲ 2.5 because of the scarce number of CO measurements existing beyond this redshift, our analysis confirms the decrease in t_depl with cosmic time, although to a lesser degree than predicted by galaxy evolution models.

• 7.

  For the same α_CO interval, we find the molecular gas fraction of MACSJ0032-arc to lie in the range f_molgas = 0.60 − 0.79. When combined with the results obtained previously for the few z ≳ 2.7 MS SFGs with available CO measurements, the corresponding f_molgas mean supports the continued increase in f_molgas with redshift; however, its large standard deviation does not enable us to exclude the possible flattening of f_molgas beyond z ~ 2. More CO measurements in MS SFGs at z> 2.5 are clearly needed to confirm the redshift evolution of f_molgas.

Acknowledgments

We thank the IRAM staff of both the Plateau de Bure Interferometer and the 30 m telescope for the high-quality data acquired and for their support during observations and data reduction. We are, in particular, grateful to Mélanie Krips, Jan Martin Winters, and Nicolas Billot. This work was supported by the Swiss National Science Foundation.

References

All Tables

All Figures

Fig. 1 Color-composite image of MACSJ0032-arc obtained using the HST/ACS F606W and F814W filters (left panel). The studied galaxy at zCO = 3.6314, strongly lensed by the galaxy cluster MACS J0032.1+1808, is composed of six multiple images well resolved in the HST image, labeled A, B, C, D, E, and F and encircled in white. They form a giant arc extending over 42.4′′. The right panels show, respectively, the zoom-in color-composite image obtained using the Spitzer/IRAC 3.6 and 4.5 μm bands over the multiple images B, C, D, E, and F (top) and the zoom-out color-composite image obtained using the Herschel/SPIRE 250, 350, and 500 μm bands; the white box represents a 40′′ × 40′′ area.

In the text

Fig. 2 Herschel/SPIRE 250 μm, Spitzer/IRAC 3.6 μm, PdBI 2 mm continuum, JVLA 5 GHz continuum, PdBI CO(6–5) line emission, and JVLA CO(1–0) line emission contours (in red) overlaid, from left to right and from top to bottom, on the HST/ACS F814W multiple images B, C, D, and E of MACSJ0032-arc. The contribution of the counter-image F is negligible. X refers to a galaxy member of the lensing cluster. Contour levels start at 2σ and are spaced in steps of 1σ, expect for IRAC 3.6 μm where the contours are in steps of 9, 16, 25, 36, 49σ, etc. The SPIRE detection extends beyond the multiple images B, C, D, and E, as shown in Fig. 1, but peaks at 4σ over B, C, D, and E. The rms levels of the 2 mm, 5 GHz, CO(6–5), and CO(1–0) data are 57 μJy, 1.7 μJy, 93 mJy km s-1, and 6.2 mJy km s-1, respectively. The size and orientation of the beam are indicated by the dotted (PdBI) or filled (JVLA) red ellipse in the bottom right corner.

In the text

Fig. 3 Observed HST/ACS F814W optical image of the multiple images B, C, D, E, and F of MACSJ0032-arc with the critical line in red (left panel); simulated observation of MACSJ0032-arc resulting from the best lens model when accounting for the PSF of the HST image (middle panel); and source plane reconstruction of MACSJ0032-arc obtained by simulating the morphology of the source as the combination of three elliptical Gaussian light profiles (right panel). The two bright knots, resolved in the HST rest-frame UV images, are separated by 1.14 ± 0.28 kpc in the source plane. The simulated HST observation includes a constant Gaussian noise background matched to the F814W noise level.

In the text

	Fig. 4 Observed SED of MACSJ0032-arc at zCO = 3.6314. Overlaid are the best-fit stellar SED (solid cyan line) obtained with the energy-conserving model and constant SFR SFH, as well as the best-fit FIR and mm SED obtained with the Vega et al. (2008) empirical template (solid red line) and the MBB with a β-slope fixed at 2 (dashed black line).
In the text

	Fig. 5 CMB corrected CO SLED of MACSJ0032-arc at zCO = 3.6314 (red stars) compared to the average CO SLEDs of the Milky Way (black crosses), the local (U)LIRGs (green circles), the z ~ 1 − 4 SMGs (blue squares), and the z ~ 1.5 BzK galaxies (magenta triangles). All SLEDs are normalized to the CO(1–0) flux of the average SLED for BzK galaxies, except the Milky Way normalized using CO(2–1).
In the text

Fig. 6 Comparison of the observed JVLA CO(1–0) line emission, PdBI CO(6–5) line emission, JVLA 5 GHz continuum, and PdBI 2 mm continuum contours, overlaid on the HST/ACS F814W multiple images B, C, D, and E of MACSJ0032-arc (left panels), with the respective simulated beam-convolved emission maps in the image plane (yellow contours in the middle and right panels) obtained for two different combinations of elliptical Gaussian light profiles in the source plane: one extended Gaussian component placed between the two HST UV-bright knots (yellow contours in the top middle panel) and two Gaussian components with locations and shapes following the two UV-bright knots (yellow contours in the top right panel). Noise realizations based on the data are added to the simulated maps, and the absolute flux scaling is obtained by matching the observed flux at the peak of the emission in the counter-image C in each of the CO(1–0), CO(6–5), 5 GHz, and 2 mm simulated maps. The critical line is in red. The size and orientation of the beams are indicated by the dashed green ellipses. Contour levels start at 2σ and are spaced in steps of 1σ (as in Fig. 2).

In the text

Fig. 7 Spectra of the CO(6–5), CO(4–3), and CO(1–0) emission lines detected in MACSJ0032-arc binned in steps of 40.16 km s-1, expect for the CO(1–0) line where channels have a resolution of 144.54 km s-1. The cyan-shaded regions indicate channels where positive emission is detected. These channels are used to derive the CO line integrated fluxes and the velocity-integrated and velocity-averaged maps shown in Figs. 2 and 8, respectively. The solid red lines show the single or double Gaussian profiles that best fit the observed CO line profiles. The zero velocity is set to zCO = 3.6314.

In the text

Fig. 8 Velocity-averaged maps of the CO(6–5) emission of the counter-images E (left panel), C+D (middle panel), and B (right panel) of MACSJ0032-arc. Overlaid are the CO(6–5) contours integrated over, respectively, the channels that define the blue component (blue contours) and the red component (red contours) of the double-peaked CO(6–5) line profile shown in Fig. 7. The color-coding is in units of integrated flux Jy km s-1 and starts at 2σ. Contour levels also start at 2σ and are spaced in steps of 1σ. A clear spatial offset between the blue and red contours is observed. The corresponding PdBI beam size of 1.94′′ × 1.62′′ is about the size of the individual counter-images themselves.

In the text

Fig. 9 Dependence of the metallicity-dependent CO-to-H2 conversion function, computed from Eqs. (2)–(4), on stellar mass and redshift. The lines are the iso-redshift curves, color-coded as a function of redshift, for z = 0.5 to z = 3.5 in steps of Δz = 0.5: the solid sections correspond to ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{<}\mathrm{1.5}$, the dashed segments to $\mathrm{1.5}\mathit{<}{\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{<}\mathrm{2}$, and the dotted portions to ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}\mathit{>}\mathrm{2}$. The horizontal black line marks the Milky Way CO-to-H2 conversion factor. Small symbols represent the computed ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}$ values for MACSJ0032-arc (red star) as well as the compilation of MS SFGs with CO measurements from the literature (Dessauges-Zavadsky et al. 2015). Large symbols correspond to the few MS SFGs for which gas-phase metallicities have been measured from rest-frame optical nebular lines. The symbols are color-coded according to galaxy redshift and their shapes indicate ${\mathit{\alpha }}_{\mathrm{CO}}^{\mathit{Z}}\mathit{/}{\mathit{\alpha }}_{\mathrm{CO}\mathit{,}\mathrm{MW}}$ ratios (<1.5: circles, 1.5−2: triangles, and >2: squares and star).

In the text

Fig. 10 Molecular gas depletion timescale as a function of redshift for our compilation of CO-detected MS SFGs from the literature (Dessauges-Zavadsky et al. 2015) and MACSJ0032-arc at zCO = 3.6314 (star). The encircled data points correspond to MS SFGs with measured gas-phase metallicities. Five redshift bins are considered: z ~ 0, z = [ 0.055,0.4 ], z = [ 1,1.6 ], z = [ 2,2.5 ], and z = [ 2.7,3.6 ]. The corresponding mean values of tdepl are shown as large black crosses with the associated 1σ dispersion as standard deviation. Magenta crosses represent tdepl values from Béthermin et al. (2015) derived from the FIR dust continuum and by adopting the same mass-metallicity relation (Eq. (4)). The observed evolution of tdepl with redshift is parametrized by a power law; the best fit, 1.15(1 + z)-0.85, is shown as a solid line.

In the text

	Fig. 11 Same as Fig. 10, but for the molecular gas fraction. A clear evolution of fmolgas with redshift is observed, in good agreement with 1 / (1 + (0.12(1 + z)1.95)-1) (solid line).
In the text