| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730822 | |
| Published online | 26 July 2017 | |
K2-111 b − a short period super-Earth transiting a metal poor, evolved old star
1 Leiden Observatory, University of Leiden, PO Box 9513, 2300 RA, Leiden, The Netherlands
e-mail:
fridlund@strw.leidenuniv.nl
2 Department of Earth, Space Sciences, Chalmers University of Technology, Onsala Space Observatory, 439 92, Onsala, Sweden
3 Department of Geology and Geophysics, University of Hawaii at Manoa, Honolulu, HI 96822, USA
4 Dipartimento di Fisica, Universitá di Torino, via Pietro Giuria 1, 10125 Torino, Italy
5 Landessternwarte Königstuhl, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
6 Institute of Planetary Research, German Aerospace Center (DLR), Rutherfordstrasse 2, 12489 Berlin, Germany
7 Department of Earth and Planetary Sciences, Tokyo Institute of Technology, Meguro-ku, Tokyo, Japan
8 Rheinisches Institut für Umweltforschung an der Universität zu Köln, Aachener Strasse 209, 50931 Köln, Germany
9 Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University, 22100 Lund, Sweden
10 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
11 Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
12 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
13 Center for Astronomy and Astrophysics, TU Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
14 Department of Astronomy and McDonald Observatory, University of Texas at Austin, 2515 Speedway, Stop C1400, Austin, TX 78712, USA
15 Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
16 Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
17 Princeton University, Department of Astrophysical Sciences, 4 Ivy Lane, Princeton, NJ 08544, USA
18 Department of Astronomy, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
19 Astrobiology Center, NINS, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
20 National Astronomical Observatory of Japan, NINS, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
21 Subaru Telescope, National Astronomical Observatory of Japan, 650 North Aohoku Place, Hilo, HI 96720, USA
Received: 20 March 2017
Accepted: 26 April 2017
Context. From a light curve acquired through the K2 space mission, the star K2-111(EPIC 210894022) has been identified as possibly orbited by a transiting planet.
Aims. Our aim is to confirm the planetary nature of the object and derive its fundamental parameters.
Methods. We analyse the light curve variations during the planetary transit using packages developed specifically for exoplanetary transits. Reconnaissance spectroscopy and radial velocity observations have been obtained using three separate telescope and spectrograph combinations. The spectroscopic synthesis package SME has been used to derive the stellar photospheric parameters that were used as input to various stellar evolutionary tracks in order to derive the parameters of the system. The planetary transit was also validated to occur on the assumed host star through adaptive imaging and statistical analysis.
Results. The star is found to be located in the background of the Hyades cluster at a distance at least 4 times further away from Earth than the cluster itself. The spectrum and the space velocities of K2-111 strongly suggest it to be a member of the thick disk population. The co-added high-resolution spectra show that that it is a metal poor ([Fe/H] = − 0.53 ± 0.05 dex) and α-rich somewhat evolved solar-like star of spectral type G3. We find Teff = 5730 ± 50 K, log g⋆ = 4.15 ± 0.1 cgs, and derive a radius of R⋆ = 1.3 ± 0.1 R⊙ and a mass of M⋆ = 0.88 ± 0.02 M⊙. The currently available radial velocity data confirms a super-Earth class planet with a mass of 8.6 ± 3.9 M⊕ and a radius of 1.9 ± 0.2 R⊕. A second more massive object with a period longer than about 120 days is indicated by a long-term radial velocity drift.
Conclusions. The radial velocity detection together with the imaging confirms with a high level of significance that the transit signature is caused by a planet orbiting the star K2-111. This planet is also confirmed in the radial velocity data. A second more massive object (planet, brown dwarf, or star) has been detected in the radial velocity signature. With an age of ≳10 Gyr this system is one of the oldest where planets are hitherto detected. Further studies of this planetary system are important since it contains information about the planetary formation process during a very early epoch of the history of our Galaxy.
Key words: planetary systems / stars: individual: K2-111 b / techniques: photometric / techniques: spectroscopic
© ESO, 2017
1. Introduction
Exoplanetary transits provide valuable information about the planetary size in terms of the host star. Very-high-precision transit photometry, preferably carried out from space, gives us access to the orbital parameters, which combined with either radial velocity (RV) data and/or transit timing variations (TTVs) enables the measurement of the planetary fundamental parameters, most notably, the planet’s radius, mass, and mean density (Charbonneau et al. 2000; Henry et al. 2000; Mayor & Queloz 1995; Marcy & Butler 1996; Ford et al. 2011). Determination of the fundamental parameters of exoplanets and their host stars is necessary in order to study the internal structure, composition, dynamical evolution, tidal interactions, system architecture, and the atmosphere of exoplanets (Madhusudhan et al. 2014; Winn & Fabrycky 2015; Hatzes 2016).
The successful CoRoT and Kepler space missions (Baglin & Fridlund 2006; Borucki et al. 2010) have found large numbers of transiting exoplanets of different types and have also led to the discovery and measurements of the fundamental parameters of the first rocky exoplanets CoRoT-7b and Kepler-10b (Léger et al. 2009; Queloz et al. 2009; Hatzes et al. 2011; Batalha et al. 2011), as well as introduced detailed modelling to the field of exoplanetary science (Moutou et al. 2013). One of the most important results of these missions is the realisation of how diverse exoplanets are. Later discoveries, primarily by the Kepler mission, have led to the understanding that small and dense planets (“super-Earths”) are quite common (Borucki et al. 2011; Mayor et al. 2011a,b; Torres et al. 2015; Marcy et al. 2014b,a), and that they may even have formed early in our Galaxy’s evolution (Campante et al. 2015).
The repurposed K2 space mission, provides long-timeline, high-precision photometry for exoplanet and astrophysics research. It is the new name given to NASA’s Kepler mission after the failure of one of its non-redundant reaction wheels in May 2013, which caused the pointing precision of the telescope to be non-compliant with the original mission. K2 was resumed in early 2014 by adopting a completely different observing strategy (Howell et al. 2014). The key difference of this new strategy with respect to the original one, is that the telescope can now only be pointed towards the same field in the sky for a period of maximum of ~80 days, and has to be confined to regions close to the ecliptic. K2 is thus limited instead to detect planets with much shorter orbital periods than Kepler. K2 observes stars that are on average 2–3 mag brighter than those targeted by the original Kepler mission (Howell et al. 2014), and in fields (designated “campaigns”), re-targeting every ~80 days along the ecliptic. This entails an opportunity to gain precious knowledge on the mass of small exoplanets via ground-based radial velocity follow-up observations. By observing almost exclusively brighter stars than the previous missions, the quality of the necessary ground-based follow-up observations (e.g. spectroscopic characterisations and radial velocity measurements) has improved significantly.
The approximately 10 000–15 000 objects observed in each field are listed in the Ecliptic Plane Input Catalogue (EPIC) of the K2 mission1. The capability of K2 to detect small (down to super-Earth size) transiting planets in short period orbits around such stars has recently been demonstrated (Vanderburg et al. 2015).
As part of our ongoing studies of individual exoplanetary candidates from the K2 mission, and using methods (Gaidos et al. 2017) we develop for the interpretation of K2 as well as the expected TESS (Ricker et al. 2015), CHEOPS (Broeg et al. 2013), and PLATO missions (Rauer et al. 2014), we have confirmed a short-period transiting super-Earth that together with a larger body with a significantly longer period, orbits the solar-like star K2-111 (EPIC 210894022)2. This star was previously designated as a false positive (Crossfield et al. 2016). As is true in this case, and as was found during the CoRoT mission, it is relatively common that automatic analysis methods give false positives for true detections; the evolution of the pipeline software during a space mission may motivate further analyses. It should also be stressed in this context that different algorithms may give differing results. The star is a metal poor, high velocity object indicative of an old age. Planets orbiting such stars are very rare and important since they provide information about the earliest phases of planetary formation in our Galaxy. In this paper we describe our follow-up study of this object, aimed at confirming the planetary nature of the transits, and modelling the evolution and age of the system, as well as the formation process.
The paper is organised in the following way. In Sect. 2 we present the K2 photometry, and in Sect. 3 we present the ground-based follow-up with spectral classification and validation of the planetary signal with a calculation of the false positive probability. In Sects. 4 and 5 we classify the host star kinematically, determine its distance, and derive the stellar mass, the radius, and age of the system. In Sect. 6 we then carry out the transit and radial velocity curve modelling and determine the exoplanetary physical parameters; the results of which make the discovery of a second body in this system increasingly probable. In Sect. 7 we model the orbital dynamics of the system and finally, in Sect. 8 we discuss and summarise the results.
2. K2 photometry of the transit signal
Observations of the K2 Field 4 took place between February 7 and April 23, 2015. This campaign included the Hyades, Pleiades, and NGC 1647 clusters. This was by intention and most selected targets were members of these clusters. A total of 15 847 long cadence (30 min integration time) and 122 short cadence (1 min integration time) targets were observed, and the data were made publicly available on September 4, 2015.
The part of the light curve containing the actual primary (and possibly also a secondary) transit provides significant information about both the transiting object and the host star (Seager & Mallén-Ornelas 2003). The actual light curve is, however, contaminated with noise caused by a number of instrumental and natural effects and needs to be processed before it can be interpreted. We used two different and independent methods to produce cleaned and interpretable light curves for all 15 969 targets. The first technique follows the methodology outlined in Grziwa et al. (2016). The K2 target pixel files were analysed for stellar targets and a mask for each target was calculated and assigned. After the light curve extraction, disturbances produced by the drift of the telescope over the sky were corrected by computing the rotation of the telescope’s CCDs. The drift is caused by the fact that the operation of the Kepler spacecraft using only two reaction wheels, requires using a combination of carefully balanced solar radiation pressure together with the fine adjustment thrusters in order to stabilize the spacecraft around the third axis. This results in a periodic rotation of the spacecraft about the bore sight of the telescope (Howell et al. 2014). The focal plane of K2 is equipped with an array of 21 individual CCD’s covering an area of ~116 deg2 on the sky. After corrections we then used the EXOTRANS-based pipeline (Grziwa et al. 2012) in order to separate stellar variability and discontinuities and to search for transit signals in the resulting light curves.
In the second method, we used circular apertures to extract the light curves. An optimal aperture size was selected in order to minimize the noise. The background was estimated by calculating the median value of the target pixel file after the exclusion of all pixels brighter than a threshold value that may belong to a source. The resulting light curves were de-correlated using the movement of the centroid as described in Vanderburg & Johnson (2014). For more details we refer to Johnson et al. (2016). We then used the Détection Spécialisée de Transits (DST) algorithm (Cabrera et al. 2012), originally developed for the CoRoT mission to search for transit signals in the resulting light curves.
Both the EXOTRANS and DST algorithms have been applied extensively to both CoRoT (Carpano et al. 2009; Cabrera et al. 2009; Fridlund et al. 2010; Erikson et al. 2012; Carone et al. 2012; Cavarroc et al. 2012) and Kepler data (Cabrera et al. 2014; Grziwa et al. 2016). These transit detection algorithms search for a pattern in the data and use statistics to decide if a signal is present in the data or not; for example, box-fitting Least Squares (BLS) algorithms (Kovács et al. 2002). DST uses an optimised transit shape, with the same number of free parameters as BLS, and an optimised statistic for signal detection. EXOTRANS uses a combination of the wavelet-based filter technique VARLET (Grziwa et al. 2016) and BLS. VARLET was originally developed to remove or reduce the impact of stellar variability and discontinuities in the light curves of the CoRoT mission.
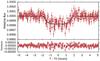 |
Fig. 1 Transit light curve folded to the orbital period of K2-111 b and residuals. The red points mark the K2 photometric data and their error bars. The integration time of the K2 data is 30 min. The solid line marks the best-fitting transit model super-sampled using ten sub-samples per K2 exposure to reduce the effects from the long integration. |
Main identifiers, optical and infrared magnitudes, and proper motion of K2-111.
When applied, both EXOTRANS and DST resulted in the discovery of a shallow transit signature in the light curve of the star designated K2-111 occurring every ~5.35 days. The depth of the signal (~0.014%), shown in Fig. 1, is compatible with a super-Earth-size planet transiting a solar-like star. Table 1 lists the main designations, optical and infrared magnitudes, and proper motion of K2-111. The detection and characterisation of the planet were then confirmed using Vanderburg & Johnson (2014)3 and EVEREST light curves (Luger et al. 2016). Together with EXOTRANS and DST, we obtained consistent parameters (e.g. period, depth, duration) within the uncertainties.
The analysis of the light curve extracted with Vanderburg’s pipeline revealed a transit-like feature close to phase 0.5 in the folded light curve with a significance of 3.6 sigma. Depending on the circumstances, the presence of secondary eclipses in the folded light curve of a planetary candidate can be a clear sign of contamination by background eclipsing binaries. Ruling out the presence of such secondary eclipses is a mandatory step in the photometric confirmation of planetary candidates. It was found that the transit-like feature was not consistent with the expected duration and dilution factor of a secondary eclipse by a background eclipsing binary. The duration and depth of the transit-like feature actually depended on the binning chosen in the folding process, which is typically not the case for genuine astrophysical signals. We concluded that the transit-like feature was either some residual of correlated noise in the light curve or simply a statistical fluctuation without astrophysical origin.
3. Ground-based follow-up
3.1. High-resolution spectroscopy
In November 2015 we obtained four reconnaissance high-resolution (R ≈ 60 000) spectra of K2-111 using the Coudé Tull spectrograph (Tull et al. 1995) at the 2.7-m telescope at the McDonald Observatory (Texas, USA). The spectra have a signal-to-noise ratio (S/N) of ~25–40 per resolution element at 5500 Å. We reduced the data using standard IRAF routines and derived preliminary spectroscopic parameters using the code Kea (Endl & Cochran 2016) and radial velocities via cross-correlation with the RV standard star HD 50692. The results from all four spectra are nearly identical and reveal a star with effective temperature Teff = 5778 ± 60 K, surface gravity, log g⋆ = 4.19 ± 0.2 dex, metallicity, [M/H] = − 0.3 ± 0.1 dex and a slow projected rotational velocity of 3.7 ± 0.3 km s-1. The spectra show no significant radial velocity variation at a level of ~150 m/s.
We started the high-precision RV follow-up of K2-111 using the Fibre-fed Echelle Spectrograph (FIES; Frandsen & Lindberg 1999; Telting et al. 2014) mounted at the 2.56-m Nordic Optical Telescope (NOT) of the Roque de los Muchachos Observatory (La Palma, Spain). We collected six high-resolution spectra (R ≈ 67 000) in November 2015, as part of the CAT observing program 35-MULTIPLE-2/15B. The exposure time was set to 2400–3600 s, leading to a S/N of 40–60 per pixel at 5500 Å. In order to remove cosmic ray hits, we split each exposure into three consecutive sub-exposures of 800–1200 s. Following the observing strategy outlined in Buchhave et al. (2010) and Gandolfi et al. (2015), we traced the RV drift of the instrument by acquiring long exposure (Texp ≈ 35 s) ThAr spectra immediately before and after the three sub-exposures. The data were reduced following IRAF and IDL routines. Radial velocities were extracted via S/N-weighted, multi-order, cross-correlation with the RV standard star HD 50692 which was observed with the same instrument set-up as the target.
Twelve additional high-resolution spectra (R ≈ 115 000) were obtained with the HARPS-N spectrograph (Cosentino et al. 2012) mounted at the 3.58-m Telescopio Nazionale Galileo (TNG) of Roque de los Muchachos Observatory (La Palma, Spain). The observations were performed between November 2015 and January 2016 as part of CAT and OPTICON programs 35-MULTIPLE-2/15B, 15B/79 and 15B/064.
We set the exposure to 1800 s and monitored the sky background using the second fibre. The data reduction was performed with the dedicated HARPS-N pipeline. The extracted spectra have a S/N of 20–60 per pixel at 5500 Å. Radial velocities were extracted by cross-correlation with a G2 numerical mask (Baranne et al. 1996; Pepe et al. 2002).
FIES and HARPS-N RV measurements of K2-111.
The FIES and HARPS-N RVs are listed in Table 2, along with the full-width at half maximum (FWHM) and the bisector span (BIS) of the cross-correlation function (CCF). Time stamps are given in barycentric Julian day in barycentric dynamical time (BJDTDB).
The FIES and HARPS-N RVs show a ~2-σ significant RV variation in phase with the K2 ephemeris, and, superimposed on a long negative linear trend (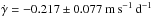 with a ~3-σ significance level), as discussed in Sect. 6. In order to assess if the observed RV variation is caused by a distortion of the spectral line profile – unveiling the presence of activity-induced RV variations and/or of a blended eclipsing binary system – we searched for possible correlations between the RV and the BIS and FWHM measurements. The linear correlation coefficient between the RV and FWHM measurements is 0.14 (p-value = 0.79) for the FIES data, and −0.13 (p-value = 0.70) for the HARPS-N data; the correlation coefficient between the RV and BIS measurements is −0.14 (p-value = 0.79) for FIES, and 0.15 (p-value = 0.64) for HARPS-N. The lack of significant correlations suggest that the observed RV variations are Doppler shifts induced by the orbiting companions. We can therefore confirm the transiting planetary candidate with a mass of 8.6 ± 3.9 M⊕ , and find support for the presence of a secondary body with a significantly longer period.
with a ~3-σ significance level), as discussed in Sect. 6. In order to assess if the observed RV variation is caused by a distortion of the spectral line profile – unveiling the presence of activity-induced RV variations and/or of a blended eclipsing binary system – we searched for possible correlations between the RV and the BIS and FWHM measurements. The linear correlation coefficient between the RV and FWHM measurements is 0.14 (p-value = 0.79) for the FIES data, and −0.13 (p-value = 0.70) for the HARPS-N data; the correlation coefficient between the RV and BIS measurements is −0.14 (p-value = 0.79) for FIES, and 0.15 (p-value = 0.64) for HARPS-N. The lack of significant correlations suggest that the observed RV variations are Doppler shifts induced by the orbiting companions. We can therefore confirm the transiting planetary candidate with a mass of 8.6 ± 3.9 M⊕ , and find support for the presence of a secondary body with a significantly longer period.
3.2. Spectral classification
The most useful method for determining the fundamental stellar parameters (e.g. M⋆, R⋆, and the stellar age), required for the interpretation of the exoplanet data, is so far to analyse the high-resolution spectra obtained in order to prepare the RV curve used for the planetary mass determination. After correcting for the RV variation, the spectra of the FIES and HARPS-N spectra were co-added to produce a high signal-to-noise ratio S/N. This resulted in one spectrum with S/N ~ 120 per pixel at 5500 Å for the co-added FIES spectrum and another with S/N ~ 150 at 5500 Å for the HARPS-N spectrum, respectively.
To determine the Teff, the profile of either of the strong Balmer line wings is then fitted to the appropriate stellar spectrum models (Fuhrmann et al. 1993; Axer et al. 1994; Fuhrmann et al. 1994, 1997b,a). This fitting procedure has to be carried out carefully since the determination of the level of the adjacent continuum can be difficult for modern high-resolution Echelle spectra where each order can only contain a limited wavelength band (Fuhrmann et al. 1997b). A suitable part of the Balmer line core is excluded since this part of the line profile originates in layers above the actual photosphere and thus would be contributing to a different value of the Teff.
K2-111 system parameters.
The analysis was then carried out as follows. We fitted the observed spectra to a grid of theoretical ATLAS12 model atmospheres from Kurucz (2013). We selected parts of the observed spectrum that contained spectral features that are sensitive to the required parameters. We used the empirical calibration equations for Sun-like stars from Bruntt et al. (2010) and Doyle et al. (2014) in order to determine the micro-turbulent (Vmic) and macro-turbulent (Vmac) velocities, respectively. The projected stellar rotational velocity v sin i was measured by fitting the profile of about 100 clean and unblended metal lines. In order to calculate the best model that fitted the different parameters, we made use of the spectral analysis package SME (Valenti & Piskunov 1996; Valenti & Fischer 2005). SME calculates synthetic spectra for a set of given stellar parameters and fits them to observed high-resolution spectra using a χ2 minimisation procedure. We used SME version 4.43 and a grid of the ATLAS12 model atmospheres (Kurucz 2013), which is a set of one-dimensional (1D) models applicable to solar-like stars.
The final adopted values are listed in Table 3. We report the individual abundances of some elements in Table 4. We find Teff = 5730 ± 50 K, log g⋆ = 4.15 ± 0.1 cgs, and an iron abundance of [Fe/H] = − 0.53 ± 0.05 dex. Crossfield et al. (2016) obtained a spectrum using the HIRES spectrograph and Specmatch. They find Teff = 5788 ± 71 K and log g⋆ = 4.224 ± 0.078, in agreement with our values. Based on an average of the Ca, Si, and Ti abundances (excluding the abundance of Mg, since that is based on only two lines), we find the [α/Fe] = + 0.2 ± 0.05 and K2-111 is thus iron-poor and moderately α-rich.
Using the Straizys & Kuriliene (1981) calibration scale for dwarf stars, the effective temperature and log g⋆ of K2-111 define the spectral type of this object as an early G-type. The low value of the log g⋆ parameter suggests that the star is evolving off the main sequence, indicating a high age and consistent with the high space velocities, as well as the low iron abundance.
3.3. Validation of the transiting planet
3.3.1. High-resolution imaging
Transits such as K2-111 b, that appear to be planetary in origin, may actually be false positives arising from the diluted signal of a fainter, unresolved eclipsing binary (EB) that is either an unrelated background system or a companion to the primary star. In order to identify this potential false alarm source, we searched for faint stars close to the target in images acquired with high spatial resolution. K2-111 was first observed on November 18, 2015 with the FastCam lucky imaging camera (Oscoz et al. 2008) at the 1.52-m Carlos Sánchez Telescope at Teide observatory, Tenerife. We acquired ten “cubes” of 1000 images through an I-band filter, each with 50 ms exposure time. Due to the 1.5′′ seeing and the relative faintness of the target, only four of these cubes could be processed successfully with the “shift and add” technique. Two processing attempts were made, using in one case the 1% and in the other the 10% of the images that have the smallest point spread function. In neither of the processed combined images, which cover an area of ≈5″ × 5″ centred on K2-111, could any further stars be discerned, up to 4 mag fainter than the target.
In order to further check if an unresolved eclipsing binary mimics planetary transits, we also performed an adaptive-optics (AO) imaging with the HiCIAO instrument on the Subaru 8.2-m telescope (Tamura et al. 2006; Suzuki et al. 2010) on December 31, 2015. Employing the AO188 (Hayano et al. 2010) and Direct Imaging (DI) mode, we observed K2-111 in the H band with 3-point dithering. To search for possible faint companions, we set each exposure time to 15 s × 10 coadds and let the target be saturated with the saturation radius being ~0.08′′. For the flux calibration, we also obtained an unsaturated image of K2-111 with an exposure time of 1.5 s × 5 coadds for each of the three dithering points using a 9.74% neutral density (ND) filter. The total integration times were 900 s for the saturated image and 22.5 s for the unsaturated one.
We reduced the HiCIAO images following the procedure described in Brandt et al. (2013) and Hirano et al. (2016). The raw images were first processed to remove the correlated read-out noises (so-called “stripes”). The hot pixels were masked and the resulting images were flat-fielded and distortion-corrected by comparing the images of the globular cluster M5 with data taken by the Hubble Space Telescope. All images in each category (saturated and unsaturated) were finally aligned and median combined. The combined unsaturated image shows that the full width at half maximum (FWHM) of K2-111 after the AO correction is 0.052′′. The images were finally aligned and median combined. With a visual inspection of the combined saturated image (see the inset of Fig. 3), we did not find any bright companion candidate up to 5′′ from the target. Two neighbouring faint objects were found to the north-east of K2-111 at a separation of ~8.5′′. These objects are, however, only partially in the photometric aperture, and too faint (flux contrasts less than 4 × 10-5 in the H band) to be a source of transit-like signals in the K2 light curve.
To draw a flux contrast curve around K2-111, we convolve the combined saturated image with an aperture equivalent to the FWHM of the object. The standard deviation of flux counts of the convolved image was computed within an arbitrary annulus as a function of separation from K2-111. After carrying out aperture photometry of the combined unsaturated image using an aperture radius of the FWHM of the point spread function and applying a correction for the integration times and the transmittance of the neutral density (ND) filter, we measure the 5σ contrast from K2-111. The solid line of Fig. 3 plots the measured 5σ contrast as a function of separation from the target in arcseconds and the 5-σ contrast is <3 × 10-4 at 1′′. Given the transit depth of ΔF/F = 1.8 × 10-4, we can exclude the presence of false alarm sources further than ~1′′ away from K2-111.
3.3.2. False-positive probability
To further exclude the possibility of a false positive due to a faint, blended eclipsing binary, we performed a Bayesian calculation based on the stellar background. This simulation does not include the probability that such a star is actually a binary on an eclipsing orbit, only the probability that an appropriate star is at the location of EPIC 210894022, and thus is an upper limit on the false-positive probability (FPP). The procedure is described in detail in Gaidos et al. (2016) and summarised here. The Bayesian prior is based on a model of the background stellar population and the likelihoods are based on observational constraints. A background stellar population equivalent to 10 square degrees (to improve counting statistics) was constructed at the location of K2-111 using TRILEGAL Version 1.6 (Vanhollebeke et al. 2009). The background was computed to Kp = 22, fainter than the faintest EB (Kp ≈ 20) that could produce the signal. The likelihood for a hypothetical background star is the product of the probabilities that (a) it can produce the observed transit depth; (b) its mean density is consistent with the observed transit duration; and (c) it does not appear in our Subaru HiCIAO H-band imaging of the K2-111 (Sect. 3.3.1). More advanced FPP calculations can take into account the precise shape of the transit but we show that such refinement is not needed in this case.
The calculation was performed by random sampling of the synthetic background population, placing the stars in a uniformly random distribution over a region with a 15′′ radius centred on K2-111. Stars that exceeded the AO contrast ratio constraint (condition c) were excluded. Given the known orbital period and mean density of the synthetic star, the probability that a binary would have an orbit capable of producing the observed transit duration (condition b) was calculated assuming a Rayleigh distribution of orbital eccentricities with a mean of 0.1. (Binaries on short-period orbits should quickly circularise.) The eclipse duration calculation uses the formula for a “small” occulting object and so is only approximate. To determine whether or not a background star could produce the observed transit signal with an eclipse depth <50% (condition a), we determined the relative contribution to the flux of K2-111 assuming a 7 × 7 pixel photometric aperture and using bilinear interpolations of the pixel response function for detector channel 48 with the tables provided in the Supplement to the Kepler Instrument Handbook4. The calculations were performed in a series of 1000 Monte Carlo iterations and a running average was used to monitor convergence. We found a FPP of ≈ 2 × 10-7.
We estimated the probability that the transit signal could be due to a companion EB or transiting planet system by using the 99.9% upper limit of the stellar density derived from the fitting of the transit light curve but without spectroscopic priors. This calculates aminimum mass and radius, and by using a stellar isochrone, the absolute brightness of a hypothetical companion with the same age and metallicity as K2-111. The contrast ratio between the hypothetical stellar companion and K2-111 can then be established via the photometric distance.
We then used an 11.5 Gyr, [Fe/H] = –0.5 isochrone (see Sect. 5) generated by the Dartmouth Stellar Evolution program (Dotter et al. 2008) to put lower limits on the companion effective temperature and mass, (Teff> 5900 K and M⋆> 0.79 M⊙) and faint limits on the magnitudes, Ks < 10.3 and a KeplerKP < 11.5 using a photometric distance of 230 pc. The predicted K-band contrast is <0.9 mag and the AO imaging we performed by Subaru-ICRS (Sect. 3.3.1) limits any such companion to within 0.095′′ (Fig. 3) or about 22 AU. Such a companion would have a typical projected RV difference of at least a few km s-1 and because of the relatively modest contrast, we would have expected to resolve a second set of lines in our FIES and HARPS-N spectra, which we do not. If the companion exists and hosts the transiting object, the object must be smaller than our estimate (and thus still a planet), because the star is hotter and thus its surface brightness is higher than K2-111.
4. The star, its distance, and space velocities
The object K2-111 is a relatively bright (Table 1) star. Based on colours and proper motion measurements, Pels et al. (1975) suggested that K2-111 is a G0 star and probably a member of the Hyades open cluster. Griffin et al. (1988) found, based on the proper motions, the object to be a likely member of the Hyades, but with incompatible photometry and radial velocities. The final conclusion of those authors was that the star is not a member of the cluster. Our observations and analysis is definitely not compatible with Hyades membership. Instead we find an old, low metallicity, early G-type star (Sect. 3.2). The low iron abundance of − 0.53 ± 0.05 dex is not in agreement with measurements of the Hyades stars, and the apparent magnitude, mV is also not consistent with that expected for a main sequence early G star in the Hyades cluster. Radial velocity measurements of K2-111 (− 16.3 km s-1) also support that it is not a Hyades star, since such stars on average have radial velocities of about +40 km s-1.
 |
Fig. 2 Spectral region encompassing the Na D doublet. The interstellar Na lines are indicated with red arrows. |
Considering the mV = 11.137 mag and colour index B − V = 0.659 mag, and assuming no or very little reddening and a main sequence star of (bolometric) absolute magnitude MV = 4.75 mag, indicative of an early G-type main sequence star, we find a lower limit to the distance of ~190 pc.
Figure 2 shows our HARPS spectrum of the Na D doublet of K2-111 where three separate components are clearly seen in each Na line: the stellar absorption profile and two (overlapping) interstellar absorption lines at different radial velocities. This is also a strong indication that the star must have a distance much larger than the Hyades cluster (45 pc). We can correct the observed B − V = 0.659 ± 0.05 for reddening using the absorption by the intervening neutral Na I along the line of sight as a measure, and the relationship between the total equivalent width of Na I absorption in both the D1 and D2 resonant lines (0.50 ± 0.05 Å) and E(B-V) reddening by Poznanski et al. (2012). This relation predicts E(B − V) = 0.055 ± 0.014, corresponding to an AV of 0.17 ± 0.04 slightly less than the upper limit one would expect from the H I column density map of Schlafly & Finkbeiner (2011) of 0.18.
We can also estimate the interstellar reddening towards K2-111 following the method outlined in Gandolfi et al. (2008). Briefly, we assume RV = 3.1 and adopt an extinction law (Cardelli et al. 1989). We fit the spectral energy distribution using synthetic colours calculated “ad hoc” from the BT-NEXTGEN low-resolution model spectrum (Allard et al. 2011) with the same parameters as we find for the star (see Sect. 3.2), resulting in a value for AV of 0.15 ± 0.03 mag, similar to what we find from Na D lines.
 |
Fig. 3 5σ flux contrast curve as a function of separation from K2-111. The inset displays the combined saturated H-band image of the target acquired with HiCIAO. The field-of-view is 4′′ × 4′′. North is up and east is left. |
An AV of 0.15 would be consistent with a distance of 210 pc if the star had the same absolute (bolometric) magnitude as the Sun. It appears, however, from our spectroscopic analysis that the star is somewhat evolved (log g⋆~ 4.15) and therefore brighter. Using the stellar parameters derived from our high-resolution high-signal-to-noise spectroscopy (see Sect. 3.2) we have Teff =5730 ± 50K, which is representative of a spectral type of G3. If we then apply the equations for M⋆ and R⋆ derived empirically by Torres et al. (2010) we can derive an upper limit to the intrinsic luminosity of 1.9 L⊙. Using the reddening derived above, this translates into a maximum distance of ~230 pc. We therefore conclude that the distance to this object is 190 pc to 230 pc with a most likely distance of 210 ± 20 pc. Applying that distance to the velocity components of the star, see Table 1, demonstrates that K2-111 is a very fast moving object, quite similar to the object Kepler-444 studied by Campante et al. (2015). Assuming a distance of 210 pc, we find the individual velocities with respect to the local standard of rest are (ULSR,VLSR,WLSR) = (130.6 ± 2.6, − 35.2 ± 1.5, − 16.3 ± 0.5 km s-1). Correcting for the Sun’s peculiar motion, this is equivalent to a space velocity of 143.8 ± 3 km s-1; almost the same as the peculiar velocity found for Kepler-444. Contrary to that object, K2-111, being of higher mass, is evolving, and therefore presumably an old object. Based on the kinematics of K2-111 and following Reddy et al. (2006) and Sperauskas et al. (2016) we can calculate the probabilities of membership in the different populations of the Galaxy. We find that these are:
-
thick disk = 96.2%;
-
halo = 3.8%;
-
thin disk < 0.1%.
Kinematically, therefore, it is most likely that K2-111 belongs to the thick disk population.
The output from the PARAM 1.3 models (da Silva et al. 2006).
 |
Fig. 4 B − V vs. stellar density (solar units). The point is EPIC 210894022 with B − V corrected for reddening based on the interstellar Na I absorption in the star’s spectrum. Dartmouth Stellar Evolution Program (DSEP; Dotter et al. 2008) isochrones for 8–13 Gyr-old stars with [Fe/H] = − 0.5 and [α/Fe] = +0.4 are plotted; heavy points are for those with Teff within 50 K of the spectroscopic value of 5730 K. The solid line is the 12.5 Gyr old isochrone, which minimizes the χ2 function. |
5. The stellar mass, radius, and age of the system
We can infer stellar parameters, including age, by comparing the observed parameters to those predicted by the Dartmouth Stellar Evolution Program (DSEP; Dotter et al. 2008). We selected isochrones for [Fe/H] = − 0.5 and [α/Fe] = +0.2 and +0.4, and compared predicted parameters to observed B − V, density ρ∗, and spectroscopic Teff and log g⋆, via a standard χ2 function, which is minimised. Applying the correction for reddening quoted in Sect. 4, we plot the reddening-corrected B − V versus the density in Fig. 4 and compared to the DSEP predictions for [Fe/H] = − 0.5 and [α/Fe] = +0.4. The dark points have predicted Teff within 50 K of the spectroscopic value of 5730 K, and the others are outside this range. The best-fit (χ2 = 2.56) isochrone of 12.5 Gyr is plotted as the heavy curve. The stellar mass is 0.88 M⊙, the radius is 1.23 R⊙, and the log g⋆ is 4.21, which is reasonably consistent with the parameters derived from the stellar spectrum (Sect. 3.2).
The 68% confidence intervals (based on Δχ2) for the posterior parameter values are: Teff = 5750–5814 K, log g⋆ = 4.20–4.25 dex, M⋆= 0.87–0.91 M⊙, R⋆= 1.13–1.33 R⊙, and an age of 11.5–13 Gyr (upper limit of isochrone models). There is a slight tension between the spectroscopically derived parameters and other parameters, that is, the errors do not overlap (Fig. 4). Using an [α/Fe] = +0.2 grid the minimum χ2 increases the discrepancy and the model age increases beyond 13 Gyr. On the other hand, a slightly higher Teff and log g would reconcile these estimates and yield a slightly younger age. Regardless, these comparisons suggest a model-dependent age of at least 10–11 Gyr, that is, at least as old as the Galactic disk itself (Martig et al. 2016).
K2-111 has a mV of 11.137 ± 0.040 (Table 1). Applying the interstellar extinction of 0.150 ± 0.025 mag found in Sect. 3.2, the de-reddened mV is 10.987 ± 0.047 mag. In order to calculate the stellar parameters, including its age, we apply the Bayesian PARAM 1.3 tool (da Silva et al. 2006)5. This tool accepts, as input, the stellar Teff, the metallicity, the de-reddened visual magnitude, mV and the parallax. Using the de-reddened mV and the distance range determined in Sect. 4 (and converting those distances to parallaxes), we ran three separate models using our observed Teff and [Fe/H] (Sect. 3.2). We find results between 8.8 Gyr and 11 Gyr, masses of 0.8–0.89 M⊙ radii between 0.85 R⊙ and 1.6 R⊙ and log g⋆ between 4.46 and 3.96 (Table 5). We then compare with the observed log g⋆ (Sect. 3.2), in order to assess which of the three distances better matches the spectroscopic parameters. Our data indicate log g⋆ = 4.15 ± 0.1 dex. This would be indicative of a distance of 210 pc. The age would in this case be 10.770 Gyr and the mass of the star would be M⋆ ~ 0.9 M⊙ but with a slightly larger R⋆ of ~ 1.3 R⊙. We note here, however, that the error bars in this particular model are large.
If we use the stellar parameters derived from our model of the observed spectrum (Teff log g⋆ and [Fe/H] Sect. 3.2) as input to derive the mass and radius based only on the equations of Torres et al. (2010), we find higher values of M⋆= 1.0 ± 0.07 M⊙, and R⋆= 1.4 ± 0.14 R⊙. These equations of Torres et al. (2010) are based on the observed high-precision M⋆ and R⋆ of 95 eclipsing binary stars of different luminosity classes where the masses and radii are known to be better than 3%, leading to a numerical relation based on the stellar parameters. It is, however, difficult to know how well these relations specifically describe K2-111. The number of stars in the generation of the numerical relation is small and of course not enough to generate “empirical” isochrones and the parameters derived in this way have to be treated with care. Specifically, the ages derived from the DSEP and PARAM 1.3 models indicate that a 1 M⊙ star would already be evolving towards the white dwarf stage and the mass of K2-111 must thus be lower. On the other hand, our observation of a lower value for log g⋆ than would be expected for a star with a M⋆ < 1 M⊙ indicates that the radius of K2-111 should be larger than 1 R⊙.
Based on the above, we conclude, that all known facts are consistent with K2-111 being a 0.86 M⊙ star that has begun to evolve off the main sequence, has a R⋆ of 1.2–1.3 R⊙, and thus a very high age. Our models are consistent with an age that is ≳10 Gyr, most likely being 10.8 Gyr or somewhat larger.
6. Transit and RV joint modelling
We performed the joint fit of the photometric and RV data using the code pyaneti, a Python/Fortran software suite based on Marcov Chain Monte Carlo (MCMC) simulations (Barragán et al., in prep.). The K2 photometry we analysed are subsets of the K2-111’s light curve extracted by Vanderburg & Johnson (2014). Here we selected ~7 h of data points around each of the 13 transits observed by K2 and de-trended each transit using a second order polynomial fitted to the out-of-transit data points. The RV data set includes the 6 FIES and 12 HARPS-N measurements presented in Sect. 3.1.
We used the equations of Mandel & Agol (2002) to fit the transit light curves and a Keplerian orbit to model the RV measurements. We adopted the Gaussian likelihood described by the equation ![\begin{equation} % \mathcal{L} = \left[ \prod_{i=1}^{n_{\mathrm{tot}}} \left (2 \pi \sigma_i^2 \right)^{- 1/2} \right] \exp \left\lbrace - \sum_{i=1}^{n_{\mathrm{tot}}} \frac{ \left(D_i - M_i \right)^2}{2 \sigma_i^2 } \right\rbrace, \label{eq:eq1} % \end{equation}](/articles/aa/full_html/2017/08/aa30822-17/aa30822-17-eq208.png) (1)where ntot = nrv + ntr is the number of RV and transit points, σi is the error associated to each data point Di, and Mi is the model associated to a given Di. We fit the same parameters as in Barragán et al. (2016) to the light curve. For the orbital period (Porb), mid-time of first transit (T0), impact parameter (b), planet-to-star radius ratio (Rp/R⋆), RV semi-amplitude variation (K), and gamma velocity, we set uniform uninformative priors, that is, we adopted rectangular distributions over given ranges of the parameters spaces. The ranges are T0 = [ 7067.9708,7067.9786 ] days for the mid-time of first transit, Porb = [ 5.3503,5.3514 ] days for the orbital period, b = [ 0,1 ] for the impact parameter, Rp/R⋆ = [ 0,1 ] for the planet-to-star radius ratio, K = [ 0,1000 ] m s-1 for the RV semi-amplitude variation, and γFIES = [ − 17, − 15 ] km s-1 and γHARPS − N = [ − 17, − 15 ] km s-1 for the systemic velocities as measured with FIES and HARPS-N, respectively.
(1)where ntot = nrv + ntr is the number of RV and transit points, σi is the error associated to each data point Di, and Mi is the model associated to a given Di. We fit the same parameters as in Barragán et al. (2016) to the light curve. For the orbital period (Porb), mid-time of first transit (T0), impact parameter (b), planet-to-star radius ratio (Rp/R⋆), RV semi-amplitude variation (K), and gamma velocity, we set uniform uninformative priors, that is, we adopted rectangular distributions over given ranges of the parameters spaces. The ranges are T0 = [ 7067.9708,7067.9786 ] days for the mid-time of first transit, Porb = [ 5.3503,5.3514 ] days for the orbital period, b = [ 0,1 ] for the impact parameter, Rp/R⋆ = [ 0,1 ] for the planet-to-star radius ratio, K = [ 0,1000 ] m s-1 for the RV semi-amplitude variation, and γFIES = [ − 17, − 15 ] km s-1 and γHARPS − N = [ − 17, − 15 ] km s-1 for the systemic velocities as measured with FIES and HARPS-N, respectively.
Given the limited number of available RV measurements and their error bars, we assumed a circular orbit (e = 0). We adopted a quadratic limb darkening law and followed the parametrisation described in Kipping (2013). To account for the K2 long integration time (~30 min), we integrated the transit models over ten steps. The shallow transit and K2’s long cadence data do not enable a meaningful determination of the scaled semi-major axis (ap/R⋆) and limb darkening coefficients u1 and u2. We thus set Gaussian priors for the stellar mass and radius (Sect. 3.2) and constrain the scaled semi-major axis using Kepler’s third law. We also used the online applet6 written by Eastman et al. (2013) to interpolate Claret & Bloemen (2011)’s limb darkening tables to the spectroscopic parameters of the host star (Sect. 3.2) and set Gaussian priors for the limb darkening coefficients u1 and u2 adopting 20% conservative error bars. We explore the parameter space with 500 chains created randomly inside the prior ranges. The chain convergence was analysed using the Gelman-Rubin statistics. The number of iterations required for the Marcov Chains to converge (“burn-in phase”) uses 25 000 more iterations with a thin factor of 50. The posterior distribution of each parameter has 250 000 independent data points.
We searched for evidence of an outer companion in the RV measurements by adding a linear trend 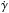 to the Keplerian model fitted to the RV data. The best fitting solution provides a linear trend of
to the Keplerian model fitted to the RV data. The best fitting solution provides a linear trend of 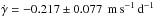 with a ~3-σ significance level. To assess if this model is better, we have to compare it with the model without linear trend. When comparing models, the one with the largest likelihood has to be preferred. At the same time, we have to check if we are not overfitting the number of parameters with the Bayesian information criteria (BIC). This is defined as BIC = kln(n) − 2lnℒ, where n is the number of data points and k the number of fitted parameters. The BIC penalises the model with more fitted parameters. When comparing models with different numbers of parameters, we have to prefer the one with the smallest BIC Gelman (2003). For our RV measurements, the model with linear trend has lnℒRV = 78 and BICRV = − 144, while the model without it gives lnℒRV = 74 and BICRV = − 139. We therefore conclude that the model with a linear trend is favoured.
with a ~3-σ significance level. To assess if this model is better, we have to compare it with the model without linear trend. When comparing models, the one with the largest likelihood has to be preferred. At the same time, we have to check if we are not overfitting the number of parameters with the Bayesian information criteria (BIC). This is defined as BIC = kln(n) − 2lnℒ, where n is the number of data points and k the number of fitted parameters. The BIC penalises the model with more fitted parameters. When comparing models with different numbers of parameters, we have to prefer the one with the smallest BIC Gelman (2003). For our RV measurements, the model with linear trend has lnℒRV = 78 and BICRV = − 144, while the model without it gives lnℒRV = 74 and BICRV = − 139. We therefore conclude that the model with a linear trend is favoured.
The final parameters are given in Table 3. They are defined as the median and 68% credible interval of the posterior distribution for each parameter. We show the folded transit light curve in Fig. 1 and the RV curves in Figs. 5 and 6.
 |
Fig. 5 Upper panel: FIES (green circles) and HARPS-N (red triangles) RV measurements versus time, following the correction for instrument offset. The best fitting Keplerian model with a linear trend is overplotted with a thick line. Lower panel: radial velocity residuals. |
 |
Fig. 6 Upper panel: FIES (green circles) and HARPS-N (red triangles) RV measurements phase-folded to the orbital period of K2-111 b, following the subtraction of the linear-trend. The best fitting circular model is overplotted with a thick black line. Lower panel: radial velocity residuals. |
 |
Fig. 7 Constraints on the third body in the K2-111 system. Solid lines show the minimum masses required to reproduce the RV trend, as a function of the third body’s orbital period and eccentricity. Dotted lines show the maximum masses allowed for dynamical stability for these periods and eccentricities (Gladman 1993; Petrovich 2015). The dashed black line shows the final masses of planets produced in the planet formation model of Bitsch et al. (2015) with a metallicity [ Fe / H ] = − 0.5. This model successfully forms super-Earths which migrate to K2-111 b’s location at the inner disc edge, and predicts that the second body would have a mass of 20–50 M⊕. K2-111 b. |
7. Orbital dynamics
The mass, orbital period, and eccentricity of the body responsible for the RV trend can be constrained by requiring that the system is dynamically stable. Bodies too close, too massive, and on overly eccentric orbits would result in an unstable system.
In Fig. 7 we show, for given periods of the outer body, the allowed mass ranges that are (a) large enough to generate the observed RV trend with P> 120 d (above the solid lines); and (b) small enough to avoid dynamical instability (below the dotted lines). For an outer body on a circular orbit, we use the criterion of Gladman (1993) while for eccentric outer bodies we use Petrovich (2015).
We show results for four values of the outer body’s eccentricity. If the outer body is on a circular orbit, it must be a gas giant planet or more massive, and the system is stable even for stellar-mass companions. If it is on a highly-eccentric orbit, gas giant planets at P ~ 1 yr are ruled out by dynamical stability. In this case, the outer planet may be a lower-mass planet on a close orbit (P ~ 1 yr) or a gas giant on a wider orbit (P > ~2 yr). We note that an eccentric orbit permits lower masses for the outer body, but this requires a specific alignment of the orbit with respect to the observer (edge-on orbit and pericentre pointing along the line of sight). In general, one can also place limits on what additional planets could be in a system between two known ones. For example, if the second planet is a Jupiter at 1 AU on a circular orbit, the separation is roughly 20 mutual Hill radii, meaning that one (or more) additional planet could be accommodated between the two planets.
We include a line in Fig. 7 that shows the final masses and orbital periods of planets formed in the planet formation model of Bitsch et al. (2015). This model makes use of the accelerated core accretion rates by pebble accretion (Lambrechts & Johansen 2014) and incorporates planet migration, meaning that the planets move through the disc as they form. Here, we use a simple power law disc model (with alpha viscosity parameter of 0.001) for the surface density and temperature following Ida et al. (2016) for sun-like stars to calculate the evolution of planets. We also make use of the metallicity measurements and evolve our planetary growth using a metallicity of [Fe/H] = − 0.5.
The dashed line marks the final mass of planets as a function of their period as predicted by our simulations of planet formation. The vertical part of the line indicates that planets with a broad range of masses have migrated to the inner edge of the disc, where they stop their accretion. Our model here predicts that the K2-111 b core has formed around 6 AU, that is, beyond the water ice line.
The results from the simulations also indicate that the potential other companion in the system should be between 20 and 50 Earth masses, provided the planets evolved independently (they did not influence each other’s growth and orbits). Follow-up observations of the planetary system can thus provide a deeper insight into the formation process of the planets in this system.
8. Discussion and summary
The K2-111 system is demonstrated to be a rare and important object among the plethora of transiting exoplanets that has been discovered by space missions in the last decade. Using adaptive optics imaging and statistical methods, and also detecting the RV signature of this planet, we have confirmed the presence of a 1.9 ± 0.2 R⊕ planet in a 5.35d orbit, as giving rise to the K2 transit signature. We find that the planet has a mass of 8.6 ± 3.9 M⊕ . The periodic RV signal is overlaid on a trend that we identify with a second more massive object. The evidence for the planet K2-111 b is strong enough for us to say that it is confirmed, while we would require more data in order to also confirm the second body.
We believe this planet to be extremely old. The reasons for this are as follows. a) The low but α-rich metal content of K2-111; b) this star has a very high space velocity of ~145 km s-1 making it a likely member of the thick disk population; and c) the modelling of the measured stellar parameters in Sect. 5. The best fit to the data is for a 0.86 M⊙ star with a most likely age of 10.8 ± 1.5 Gyr. The star appears to be beginning to move off the main sequence as indicated by both the low value of log g⋆ and the radius of the models that are most likely around 1.25 ± 0.2 R⊙.
Different populations in the Galaxy can be traced through the abundance of the α elements, O, Mg, Si, S, Ca, and Ti. In this context we note that there are similarities between K2-111 and the planet host star Kepler-444. The latter object is a metal-poor low-mass solar-like star and one of the brightest stars to be observed with Kepler. By following this object during the 4 yr of that mission, Campante et al. (2015) succeeded in detecting five transiting sub-Earth-size planets in a compact system. They were also able to record the asteroseismic signature of the host star. Interpreting the seismic data allowed a high-precision determination of mass (0.76 M⊙), radii (0.75 R⊙) and age (11.23 ± 1 Gyr) for the host star by these authors. Kepler-444 has very similar space velocities (see Sect. 4) and α element abundance as K2-111 does, something that indicates that both stars are bona-fide members of the thick disk population. It has also been suggested that Kepler-444 is a member of the Arcturus stream, a group of older iron poor stars that possibly originates from outside the Milky Way galaxy.
There exist data on a handful of other small size (super-Earth or Neptune class) planets, where there are also indications of high age. Kepler-10b and c (Batalha et al. 2011; Fressin et al. 2011), the first small planets confirmed by the Kepler mission, have been determined (asteroseismologically) to have an age of 11.9 ± 4.5 Gyr. This system has been suggested to belong to the halo population (Batalha et al. 2011). The metallicity of the star is, however, higher than K2-111 at [Fe/H] = − 0.15 ± 0.03. Also the error bars on the age are high, and no proper motions are available to kinematically determine the population of the star. The recently confirmed Kepler-510 system (Morton et al. 2016) has a host star with a metallicity of [Fe/H] = − 0.35 ± 0.1 and an asteroseismic age of 11.8 Gyr (Silva Aguirre et al. 2015). While the planet (orbital period 19.6d) has a radius of ~2.2 R⊕, no mass of this object has as yet been determined. We point out in this context that future releases of the Gaia astrometric catalogue will alleviate this situation and allow for a kinematical determination of old host star populations. There is also the case of Kapteyn’s star (GJ 191, LHS 29 or HD 33793), an M1 sub-dwarf star (Gizis 1997) with a [Fe/H] = − 0.86 ± 0.05. It is kinematically classified as a halo star and is in fact the closest such object at a distance of only 3.91 ± 0.01 pc. Two planets were detected in radial velocity measurements (Anglada-Escudé et al. 2014), with periods of 48.6d and 121.5d and mpsin i of 4.8 and 7.0 M⊕, respectively. The age of the star is very likely older than 10 Gyr because of the low metallicity and the kinematics, but exactly how old it is can not be determined at this time. Robertson et al. (2015) used a somewhat different data set, almost as large as that of Anglada-Escudé et al. (2014), and concluded that the RV signature of Kapteyn-b very likely was caused by an activity signal coming from the star. Anglada-Escudé et al. (2016) analysed this latter data set and came to the conclusion that there is no activity signal but instead most likely the bona-fide planet-b is a real planet. This demonstrates the difficulty when one is working at the limit of the sensitivity of one’s instrumentation. While it is only the three objects Kepler-444, Kepler-510, and K2-111 that have both confirmed planets and relatively well secured ages, very old stars appear to be as likely to possess planetary systems as younger systems, a not too surprising result. It is however more interesting in terms of what kind of planets form in early low-metallicity systems, as compared to the more recently formed systems where the metallicity would generally be higher. Our results are consistent with recent studies that have shown that at low metallicities Doppler-detected planethosting stars tend to have high α-content and to belong to the thick disk (Adibekyan et al. 2012a), and even suggestions that the planet incidence is greater among the thick disk population than among the thin disk for metallicities below –0.3 dex (Adibekyan et al. 2012b).
It is clear that K2-111 and its planet(s) are a welcome addition to Kepler-444 and Kepler-510. That K2-111 is abundant in α elements is interesting since the bulk of rocky planets consist of those elements (Valencia et al. 2007, 2010). Together with the five planets in the Kepler-444 system, Kepler-510 and possibly the other exoplanet systems described above, K2-111 b and its possible companion suggested here, are among the oldest planets known to date. Assuming a radius of 1.9 ± 0.2 R⊕ the planet has an average density of 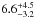 g cm-3, placing it in the same class, as far as geometrical size is concerned, as CoRoT-7b and Kepler-10b. In this context it is indeed a super-earth and the planetary density appears similar to that of Venus and the Earth itself. The errors in ρp are, at the moment, however, large enough to allow compositions that deviate from being truly “Earth-like” and more observations are required. It would have formed together with a star having a low metallicity, and more importantly at a very early epoch of our Galaxy. Although K2-111 is also iron-poor, it is moderately α-rich, in common with the planet host Kepler-444, which could be favourable for the formation of an Earth-like body. But we also have indications for a more massive planet in the same system. A number of studies so far have pointed out a correlation where metal-rich stars are more likely to harbour gas-giants (e.g. Valenti & Fischer 2005; Mortier et al. 2013), while the correlation appears to be missing for the sample of small planets discovered by Kepler (Buchhave et al. 2012). Having formed ~5–6 Gyr before the birth of the Solar System, K2-111 and its system carries information about the early stages of stellar and planetary formation in the Galaxy. It would therefore be very interesting to continue to study this system, primarily to confirm the presence of the second more massive planet and to also find its period. Finding more systems similar to K2-111 and Kepler-444 would allow us to begin to determine what implications galactic age has on planetary formation.
g cm-3, placing it in the same class, as far as geometrical size is concerned, as CoRoT-7b and Kepler-10b. In this context it is indeed a super-earth and the planetary density appears similar to that of Venus and the Earth itself. The errors in ρp are, at the moment, however, large enough to allow compositions that deviate from being truly “Earth-like” and more observations are required. It would have formed together with a star having a low metallicity, and more importantly at a very early epoch of our Galaxy. Although K2-111 is also iron-poor, it is moderately α-rich, in common with the planet host Kepler-444, which could be favourable for the formation of an Earth-like body. But we also have indications for a more massive planet in the same system. A number of studies so far have pointed out a correlation where metal-rich stars are more likely to harbour gas-giants (e.g. Valenti & Fischer 2005; Mortier et al. 2013), while the correlation appears to be missing for the sample of small planets discovered by Kepler (Buchhave et al. 2012). Having formed ~5–6 Gyr before the birth of the Solar System, K2-111 and its system carries information about the early stages of stellar and planetary formation in the Galaxy. It would therefore be very interesting to continue to study this system, primarily to confirm the presence of the second more massive planet and to also find its period. Finding more systems similar to K2-111 and Kepler-444 would allow us to begin to determine what implications galactic age has on planetary formation.
Acknowledgments
We acknowledge the very constructive comments of an anonymous referee, which have improved our paper.
We acknowledge interesting and profitable discussions with V. Adibekyan. We thank the McDonald, NOT, TNG, Subaru staff members for their unique and superb support during the observations.
Based on observations obtained a) with the Nordic Optical Telescope (NOT), operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrofísica de Canarias (IAC); b) with the Italian Telescopio Nazionale Galileo (TNG) also operated at the ORM (IAC) on the island of La Palma by the INAF – Fundación Galileo Galilei.
This research made use of data acquired with the Carlos Sánchez Telescope, operated at Teide Observatory on the island of Tenerife by the Instituto de Astrofísica de Canarias.
The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2013-2016) under grant agreement No. 312430 (OPTICON).
W.D.C., M.E. and P.M.Q. were supported by NASA grants NNX15AV58G, NNV16AE70G and NNX16AJ11G to The University of Texas at Austin.
This work has made use of SME package, which benefits from the continuing development work by J. Valenti and N. Piskunov and we gratefully acknowledge their continued support. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna (Kupka et al. 2000; Ryabchikova et al. 2015).
Sz.Cs. thanks the Hungarian National Research, Development and Innovation Office, for the NKFIH-OTKA K113117 grant.
M.F and C.M.P. gratefully acknowledge the support of the Swedish National Space Board.
M.F. acknowledges the hospitality of the Instituto de Astrofísica de Canarias where the paper was written during a 2-month stay under a Jesus Serra Foundation fellowship.
DG gratefully acknowledges the financial support of the Programma Giovani Ricercatori – Rita Levi Montalcini – Rientro dei Cervelli (2012) awarded by the Italian Ministry of Education, Universities and Research (MIUR).
A.J.M., M.B.D., A.J. and B.B. acknowledge support from the Knut & Alice Wallenberg Foundation.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012a, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., et al. 2012b, A&A, 543, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Tuomi, M., et al. 2014, MNRAS, 443, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Tuomi, M., Arriagada, P., et al. 2016, ApJ, 830, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Axer, M., Fuhrmann, K., & Gehren, T. 1994, A&A, 291, 895 [NASA ADS] [Google Scholar]
- Baglin, A., & Fridlund, M. 2006, in ESA SP, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 1306, 11 [NASA ADS] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barragán, O., Grziwa, S., Gandolfi, D., et al. 2016, AJ, 152, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Borucki, W. J., Bryson, S. T., et al. 2011, ApJ, 729, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., McElwain, M. W., Turner, E. L., et al. 2013, ApJ, 764, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, EPJ Web Conf., 47, 03005 [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Cabrera, J., Fridlund, M., Ollivier, M., et al. 2009, A&A, 506, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera, J., Csizmadia, S., Erikson, A., Rauer, H., & Kirste, S. 2012, A&A, 548, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera, J., Csizmadia, S., Lehmann, H., et al. 2014, ApJ, 781, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Barclay, T., Swift, J. J., et al. 2015, ApJ, 799, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, L., Gandolfi, D., Cabrera, J., et al. 2012, A&A, 538, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpano, S., Cabrera, J., Alonso, R., et al. 2009, A&A, 506, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavarroc, C., Moutou, C., Gandolfi, D., et al. 2012, Ap&SS, 337, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84461V [Google Scholar]
- Crossfield, I. J. M., Ciardi, D. R., Petigura, E. A., et al. 2016, ApJS, 226, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., et al. 2014, VizieR Online Data Catalog: II/328 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, A. P., Davies, G. R., Smalley, B., Chaplin, W. J., & Elsworth, Y. 2014, MNRAS, 444, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., & Cochran, W. D. 2016, PASP, 128, 094502 [NASA ADS] [CrossRef] [Google Scholar]
- Erikson, A., Santerne, A., Renner, S., et al. 2012, A&A, 539, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B., Rowe, J. F., Fabrycky, D. C., et al. 2011, ApJS, 197, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., & Lindberg, B. 1999, in Astrophysics with the NOT, eds. H. Karttunen, & V. Piirola, 71 [Google Scholar]
- Fressin, F., Torres, G., Désert, J.-M., et al. 2011, ApJS, 197, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Fridlund, M., Hébrard, G., Alonso, R., et al. 2010, A&A, 512, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997a, A&A, 323, 909 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M. J., & Bernkopf, J. 1997b, A&A, 326, 1081 [NASA ADS] [Google Scholar]
- Gaidos, E., Mann, A. W., Kraus, A. L., & Ireland, M. 2016, MNRAS, 457, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E., Kitzmann, D., & Heng, K. 2017, MNRAS, 468, 3418 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Alcalá, J. M., Leccia, S., et al. 2008, ApJ, 687, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Parviainen, H., Deeg, H. J., et al. 2015, A&A, 576, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizis, J. E. 1997, AJ, 113, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, R. F., Griffin, R. E. M., Gunn, J. E., & Zimmerman, B. A. 1988, AJ, 96, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Grziwa, S., Pätzold, M., & Carone, L. 2012, MNRAS, 420, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Grziwa, S., Gandolfi, D., Csizmadia, S., et al. 2016, AJ, 152, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2016, Space Sci. Rev., 205, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P., Fridlund, M., Nachmani, G., et al. 2011, ApJ, 743, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hayano, Y., Takami, H., Oya, S., et al. 2010, in Adaptive Optics Systems II, Proc. SPIE, 7736, 77360N [CrossRef] [Google Scholar]
- Henry, G. W., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hirano, T., Nowak, G., Kuzuhara, M., et al. 2016, ApJ, 825, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, M. C., Gandolfi, D., Fridlund, M., et al. 2016, AJ, 151, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Kurucz, R. L. 2013, Astrophysics Source Code Library [record ascl: 1303.024] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Luger, R., Agol, E., Kruse, E., et al. 2016, AJ, 152, 100 [Google Scholar]
- Madhusudhan, N., Knutson, H., Fortney, J. J., & Barman, T. 2014, Protostars and Planets VI, 739 [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., & Butler, R. P. 1996, ApJ, 464, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Isaacson, H., Howard, A. W., et al. 2014a, ApJS, 210, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Weiss, L. M., Petigura, E. A., et al. 2014b, PNAS, 111, 12655 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Minchev, I., Ness, M., Fouesneau, M., & Rix, H.-W. 2016, ApJ, 831, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Lovis, C., Pepe, F., Ségransan, D., & Udry, S. 2011a, Astron. Nachr., 332, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011b, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S., et al. 2013, A&A, 551, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, T. D., Bryson, S. T., Coughlin, J. L., et al. 2016, ApJ, 822, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Deleuil, M., Guillot, T., et al. 2013, Icarus, 226, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Oscoz, A., Rebolo, R., López, R., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701447 [CrossRef] [Google Scholar]
- Pels, G., Oort, J. H., & Pels-Kluyver, H. A. 1975, A&A, 43, 423 [NASA ADS] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovich, C. 2015, ApJ, 808, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Prochaska, J. X., & Bloom, J. S. 2012, MNRAS, 426, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, Journal of Astronomical Telescopes, Instruments, and Systems, 1, 014003 [Google Scholar]
- Robertson, P., Roy, A., & Mahadevan, S. 2015, ApJ, 805, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Davies, G. R., Basu, S., et al. 2015, MNRAS, 452, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Sperauskas, J., Bartašiūtė, S., Boyle, R. P., et al. 2016, A&A, 596, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straizys, V., & Kuriliene, G. 1981, Ap&SS, 80, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, R., Kudo, T., Hashimoto, J., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 773530 [CrossRef] [Google Scholar]
- Tamura, M., Hodapp, K., Takami, H., et al. 2006, in Proc. SPIE, Conf. Ser., 6269, 62690V [Google Scholar]
- Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Torres, G., Kipping, D. M., Fressin, F., et al. 2015, ApJ, 800, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Sasselov, D. D., & O’Connell, R. J. 2007, ApJ, 665, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Ikoma, M., Guillot, T., & Nettelmann, N. 2010, A&A, 516, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderburg, A., & Johnson, J. A. 2014, PASP, 126, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderburg, A., Montet, B. T., Johnson, J. A., et al. 2015, ApJ, 800, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Vanhollebeke, E., Groenewegen, M. A. T., & Girardi, L. 2009, A&A, 498, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Transit light curve folded to the orbital period of K2-111 b and residuals. The red points mark the K2 photometric data and their error bars. The integration time of the K2 data is 30 min. The solid line marks the best-fitting transit model super-sampled using ten sub-samples per K2 exposure to reduce the effects from the long integration. |
| In the text | |
 |
Fig. 2 Spectral region encompassing the Na D doublet. The interstellar Na lines are indicated with red arrows. |
| In the text | |
 |
Fig. 3 5σ flux contrast curve as a function of separation from K2-111. The inset displays the combined saturated H-band image of the target acquired with HiCIAO. The field-of-view is 4′′ × 4′′. North is up and east is left. |
| In the text | |
 |
Fig. 4 B − V vs. stellar density (solar units). The point is EPIC 210894022 with B − V corrected for reddening based on the interstellar Na I absorption in the star’s spectrum. Dartmouth Stellar Evolution Program (DSEP; Dotter et al. 2008) isochrones for 8–13 Gyr-old stars with [Fe/H] = − 0.5 and [α/Fe] = +0.4 are plotted; heavy points are for those with Teff within 50 K of the spectroscopic value of 5730 K. The solid line is the 12.5 Gyr old isochrone, which minimizes the χ2 function. |
| In the text | |
 |
Fig. 5 Upper panel: FIES (green circles) and HARPS-N (red triangles) RV measurements versus time, following the correction for instrument offset. The best fitting Keplerian model with a linear trend is overplotted with a thick line. Lower panel: radial velocity residuals. |
| In the text | |
 |
Fig. 6 Upper panel: FIES (green circles) and HARPS-N (red triangles) RV measurements phase-folded to the orbital period of K2-111 b, following the subtraction of the linear-trend. The best fitting circular model is overplotted with a thick black line. Lower panel: radial velocity residuals. |
| In the text | |
 |
Fig. 7 Constraints on the third body in the K2-111 system. Solid lines show the minimum masses required to reproduce the RV trend, as a function of the third body’s orbital period and eccentricity. Dotted lines show the maximum masses allowed for dynamical stability for these periods and eccentricities (Gladman 1993; Petrovich 2015). The dashed black line shows the final masses of planets produced in the planet formation model of Bitsch et al. (2015) with a metallicity [ Fe / H ] = − 0.5. This model successfully forms super-Earths which migrate to K2-111 b’s location at the inner disc edge, and predicts that the second body would have a mass of 20–50 M⊕. K2-111 b. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


