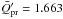| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201730455 | |
| Published online | 07 August 2017 | |
Properties of interstellar wind leading to shape morphology of the dust surrounding HD 61005
Tekov Observatory, Sokolovská 21, 934 01 Levice, Slovak Republic
e-mail: pavol.pastor@hvezdarenlevice.sk
Received: 18 January 2017
Accepted: 11 April 2017
Aims. A structure formed by dust particles ejected from the debris ring around HD 61005 is observed in the scattered light. The main aim here is to constrain interstellar wind parameters that lead to shape morphology in the vicinity of HD 61005 using currently available observational data for the debris ring.
Methods. Equation of motion of 2 × 105 dust particles ejected from the debris ring under the action of the electromagnetic radiation, stellar wind, and interstellar wind is solved. A two-dimensional (2D) grid is placed in a given direction for accumulation of the light scattered on the dust particles in order to determine the shape morphology. The interaction of the interstellar wind and the stellar wind is considered.
Results. Groups of unknown properties of the interstellar wind that create the observed morphology are determined. A relation between number densities of gas components in the interstellar wind and its relative velocity is found. Variations of the shape morphology caused by the interaction with the interstellar clouds of various temperatures are studied. When the interstellar wind velocity is tilted from debris ring axis a simple relation between the properties of the interstellar wind and an angle between the line of sight and the interstellar wind velocity exists. Dust particles that are most significantly influenced by stellar radiation move on the boundary of observed structure.
Conclusions. Observed structure at HD 61005 can be explained as a result of dust particles moving under the action of the interstellar wind. Required number densities or velocities of the interstellar wind are much higher than that of the interstellar wind entering the solar system.
Key words: protoplanetary disks / interplanetary medium / ISM: individual objects: HD 61005 / celestial mechanics
© ESO, 2017
1. Introduction
An amount of dust sufficient to produce significant infrared excess was discovered at HD 61005 during the Spitzer FEPS survey. The star was selected by Hines et al. (2007) as a promising target for HST NICMOS observations. In the scattered light, they resolved an asymmetric structure of dust at the star. Hines et al. (2007) suggested that the observed morphology could be formed as a result of an interaction between dust particles originating in the system and a gas from an interstellar medium (ISM) moving with respect to the star (interstellar wind). The fact that the star’s proper motion roughly points north (van Leeuwen 2007), while the disk’s swept-back “wings” are directed to the south, might be more than just a coincidence (Hines et al. 2007; Esposito et al. 2016). A result of the interaction was obtained numerically in Debes et al. (2009). They used a debris ring ejecting dust particles on unbound orbits varying further due to the interstellar wind (ISW) and the stellar gravity reduced by Keplerian term from Poynting–Robertson (PR) effect. Maness et al. (2009) used dust particles on bound orbits interacting with the ISM gas in order to obtain the observed morphology. Their results were based on a secular variation of dust orbits due to the ISM gas taken from Scherer (2000). According to results in Scherer (2000) the dust particles on bound orbits should undergo an increase of the semimajor axis due to the acceleration from the ISW. The increase of the semimajor axis should create the observed swept-back structure in Maness et al. (2009). However, Pástor et al. (2011) and Pástor (2012b) analytically proved that for the dust particles on bound orbits, the semimajor axis always decreases independently of an orientation of the orbit with respect to the interstellar gas velocity vector.
The debris ring ejecting the dust particles was resolved in the scattered light by Buenzli et al. (2010). According to their observations, the bulk of the debris ring with low eccentricity is roughly located between 55 and 65 AU from HD 61005 with an apparent inclination of 5.7 from edge-on. Esposito et al. (2016) suggested that dust asymmetry observed at HD 61005 can be explained as a result of secular perturbations of dust particles on bound orbits by an eccentric and inclined planet. Such an explanation requires smooth boundaries at the ends of the swept-back structure (due to the bound orbits), which are not observed as far as 350 AU from the star (Schneider et al. 2014). Moreover, scattering behavior is more consistent with smaller particles below blow-out radius (Hines et al. 2007).
In this study we use observed properties of the debris ring at HD 61005 in order to explain observed asymmetric morphology using interaction of the dust particles on unbound orbits with the ISW. We concentrate on groups of unknown properties of the ISM gas that lead to the observed morphology. We develop Debes et al. (2009) results, using the observed dimensions of the debris ring and using correct acceleration of the dust particles caused by the ISW.
2. Model
HD 61005 is the G8V star with visual magnitude 8.22 at 35.4 pc. Its position and kinematics with respect to the Sun are typical for members of the Argus association (Desidera et al. 2011). Stellar age of the Argus association is believed to be 40 Myr (Torres et al. 2008). The optical and near infrared (IR) photometry measurements suggest that the star has a temperature similar to our Sun. In far-IR the star shows IR-excess from the debris disk observed also in the scattered light (e.g., Schneider et al. 2014). We verified stellar parameters from Olofsson et al. (2016) and use them in this study. The luminosity and radius of the star used are L⋆ = 0.58 L⊙ and R⋆ = 0.84 R⊙, respectively. For the age 40 Myr and an effective temperature of 5500 K (used to scale the photometry with Kurucz library) isochrones from Siess et al. (2000) give the stellar mass 1.1 M⊙. Thus, HD 61005 is considered as a pre-main sequence star.
2.1. Electromagnetic radiation
The acceleration of moving spherical dust particles caused by the electromagnetic radiation is the PR effect (Poynting 1904; Robertson 1937; Klačka 1992, 2004; Klačka et al. 2014). The acceleration is ![\begin{equation} \label{PR} \frac{{\rm d} \vec{v}}{{\rm d}t} = \frac{\mu \beta}{r^{2}} \left [ \left ( 1 - \frac{\vec{v} \cdot \vec{e}_{\text{R}}}{c} \right ) \vec{e}_{\text{R}} - \frac{\vec{v}}{c} \right ] , \end{equation}](/articles/aa/full_html/2017/08/aa30455-17/aa30455-17-eq5.png) (1)where μ = GM⋆, G is the gravitational constant, M⋆ is the mass of the star, r is the stellocentric distance, eR is the radial unit vector directed from the star to the dust particle, v is the velocity of the particle with respect to the star, and c is the speed of light. The parameter β is defined as the ratio between the electromagnetic radiation pressure force and the gravitational force between the star and the particle at rest with respect to the star
(1)where μ = GM⋆, G is the gravitational constant, M⋆ is the mass of the star, r is the stellocentric distance, eR is the radial unit vector directed from the star to the dust particle, v is the velocity of the particle with respect to the star, and c is the speed of light. The parameter β is defined as the ratio between the electromagnetic radiation pressure force and the gravitational force between the star and the particle at rest with respect to the star  (2)Here, L⋆ is the stellar luminosity,
(2)Here, L⋆ is the stellar luminosity,  is the dimensionless efficiency factor for the radiation pressure averaged over the stellar spectrum and calculated for the radial direction (
is the dimensionless efficiency factor for the radiation pressure averaged over the stellar spectrum and calculated for the radial direction ( = 1 for a perfectly absorbing sphere), c is the speed of light in vacuum, and A′ is the geometric cross-section of the particle with mass m.
= 1 for a perfectly absorbing sphere), c is the speed of light in vacuum, and A′ is the geometric cross-section of the particle with mass m.
2.2. Mass-loss rate
The solar heliosphere is created in an interaction of the solar wind with the ISM gas incoming to the solar system. Also in the vicinity of HD 61005 its stellar wind will be influenced by an incoming ISM gas. Far outside of the astrosphere of HD 61005 we may neglect an acceleration of dust particles caused by the stellar wind (e.g., Richardson et al. 2008). For a correct description of the stellar wind at HD 61005 we need to also know the mass loss rate of this star. Recent results in Johnstone et al. (2015) enable us to approximately determine mass loss rate for a star of mass between 0.4 M⊙ and 1.1 M⊙ using the angular velocity of surface rotation, the radius, and the mass of the star. Unfortunately, in their sample, the authors only considered stars older than 100 Myr to fit parameters, although their theory also enables consideration of the pre-main sequence stars. The relation for the wind torque in Matt et al. (2012) was originally derived also for pre-main sequence stars and did not lose this applicability. Also the relation for dependence of the X-ray flux as a function of the stellar mass and the rotation period from Wright et al. (2011) is applicable for younger stars. Improvement of their fit for younger stars is beyond the scope of this study. In order to determine the mass-loss rate for HD 61005 we will simply assume that the fit obtained in Johnstone et al. (2015) can be used for this star. We will see later that the astrosphere of HD 61005 is far inside the debris ring also for much larger mass-loss rates and stellar-wind speeds. Stellar rotation with period P⋆ = 5.04 days has been determined for HD 61005 in Desidera et al. (2011) from photometric measurements. This corresponds to the angular velocity of surface rotation Ω⋆ = 2π/P⋆ ≈ 1.4 × 10-5 rad/s. For stable stars rotating with higher angular velocity than a saturation angular velocity the mass-loss rate cannot be higher (e.g., Pallavicini et al. 1981; Wright et al. 2011). The saturation angular velocity for HD 61005 can be determined from Eq. (6) in Johnstone et al. (2015) as Ωsat ≈ 5.0 × 10-5 rad/s. Since the obtained angular velocity of rotation for HD 61005 is below the saturation limit, the star is in an unsaturated regime. The angular velocity of surface rotation coupled with R⋆ = 0.84 R⊙ and M⋆ = 1.1 M⊙ gives, using Eq. (4) in Johnstone et al. (2015), the mass loss rate Ṁ⋆ ≈ 4.8 Ṁ⊙.
2.3. Stellar wind
Impinging particles of the stellar wind cause an acceleration of the dust particle that can be determined from a covariant equation of motion (Klačka et al. 2012) ![\begin{equation} \label{SW} \frac{{\rm d} \vec{v}}{{\rm d}t} = \frac{\mu \beta \eta u}{c \bar{Q}'_{\text{pr}} r^{2}} \left [ \left ( 1 - \frac{\vec{v} \cdot \vec{e}_{\text{R}}}{u} \right ) \vec{e}_{\text{R}} - \frac{\vec{v}}{u} \right ] , \end{equation}](/articles/aa/full_html/2017/08/aa30455-17/aa30455-17-eq26.png) (3)where u is the speed of the stellar wind, η is the ratio of the stellar wind energy to the stellar electromagnetic radiation energy, both radiated per unit time. For η we can write
(3)where u is the speed of the stellar wind, η is the ratio of the stellar wind energy to the stellar electromagnetic radiation energy, both radiated per unit time. For η we can write  (4)Since HD 61005 is in the unsaturated regime for the speed of the stellar wind, we obtain, according to Fig. 13 in Johnstone et al. (2015), u ≈ 1200 km s-1. Using the mass loss rate of HD 61005 we obtain η ≈ 2.4. Now, if we compare the Keplerian terms in Eqs. (1) and (3), we can neglect the Keplerian term in Eq. (3) with respect to the Keplerian term in Eq. (1) for dust particles with
(4)Since HD 61005 is in the unsaturated regime for the speed of the stellar wind, we obtain, according to Fig. 13 in Johnstone et al. (2015), u ≈ 1200 km s-1. Using the mass loss rate of HD 61005 we obtain η ≈ 2.4. Now, if we compare the Keplerian terms in Eqs. (1) and (3), we can neglect the Keplerian term in Eq. (3) with respect to the Keplerian term in Eq. (1) for dust particles with  = 1.
= 1.
2.4. ISW
Asymmetric structure observed at HD 61005 is commonly explained as result of an ISM gas affecting the dynamics of dust particles originating in the system (e.g., Debes et al. 2009; Maness et al. 2009). The acceleration used in Debes et al. (2009) was adopted from meteor theory and therefore has different handling with drag coefficients not very suitable for the ISM gas. In this work we use the correct form of acceleration causing the ISM gas to influence the dynamics of a spherical particle. The acceleration of the spherical dust moving through gas is (Baines et al. 1965)  (5)The sum in Eq. (5) runs over all particle species i. vF is the velocity of the ISM with respect to the star. cDi in Eq. (5) is the drag coefficient
(5)The sum in Eq. (5) runs over all particle species i. vF is the velocity of the ISM with respect to the star. cDi in Eq. (5) is the drag coefficient  (6)where erf(si) is the error function
(6)where erf(si) is the error function  , δi is the fraction of impinging particles specularly reflected at the surface (a diffuse reflection is assumed for the rest of the particles, see Baines et al. 1965; Gustafson 1994), Td is the temperature of the dust grain, and Ti is the temperature of the ith gas component. si in Eq. (6) is the molecular speed ratio
, δi is the fraction of impinging particles specularly reflected at the surface (a diffuse reflection is assumed for the rest of the particles, see Baines et al. 1965; Gustafson 1994), Td is the temperature of the dust grain, and Ti is the temperature of the ith gas component. si in Eq. (6) is the molecular speed ratio  (7)Here, mi is the mass of the atom in the ith gas component, k is Boltzmann’s constant, and U=| v − vF | is the relative speed of the dust particle with respect to the gas. For the collision parameter γi in Eq. (5) we obtain
(7)Here, mi is the mass of the atom in the ith gas component, k is Boltzmann’s constant, and U=| v − vF | is the relative speed of the dust particle with respect to the gas. For the collision parameter γi in Eq. (5) we obtain  (8)where ni is the number density of the ith kind of interstellar atom. We see in Sect. 3.3 that in the case of HD 61005, the ISW velocity and number densities are not affected by an interaction of the ISW with the stellar wind.
(8)where ni is the number density of the ith kind of interstellar atom. We see in Sect. 3.3 that in the case of HD 61005, the ISW velocity and number densities are not affected by an interaction of the ISW with the stellar wind.
2.5. Equation of motion
The equation of motion, which determines the dynamics of dust particles in an orbit around a star under the action of the electromagnetic radiation, the stellar wind, and ISW are calculated based on Eqs. (1), (3) and (5)  (9)Here also the approximation mentioned after Eq. (4) was considered.
(9)Here also the approximation mentioned after Eq. (4) was considered.
2.6. Distance to bow shock
The supersonic motion of a star producing a stellar wind in the local ISM creates the so-called bow shock around a direction of the star velocity in the ISM (upstream direction). The stellocentric distance to the bow shock is minimal in the upstream direction. The minimal stellocentric distance to the bow shock (stand-off distance) can be calculated from an equilibrium between ram pressures of the stellar wind and the ISM (Wilkin 1996). We have  (10)where ϱF=
(10)where ϱF= is the density of the ambient ISM. In an ideal case, the shape of the bow shock is rotationally symmetric with an axis of the symmetry going through the star in the direction of the ISW velocity. An analytical solution for the bow shock shape that is consistent with numerical solutions of magnetohydrodynamical (MHD) equations was derived in Wilkin (1996) using the assumption of momentum conservation and assuming that the material mixes and cools instantaneously (the thin shell approximation). The derived solution determines the distance to the bow shock rBS as a function of a polar angle θ measured from a bow shock surface element with the unknown distance to the upstream direction
is the density of the ambient ISM. In an ideal case, the shape of the bow shock is rotationally symmetric with an axis of the symmetry going through the star in the direction of the ISW velocity. An analytical solution for the bow shock shape that is consistent with numerical solutions of magnetohydrodynamical (MHD) equations was derived in Wilkin (1996) using the assumption of momentum conservation and assuming that the material mixes and cools instantaneously (the thin shell approximation). The derived solution determines the distance to the bow shock rBS as a function of a polar angle θ measured from a bow shock surface element with the unknown distance to the upstream direction  (11)According to Eq. (11) there is no difference in the shape of the bow shocks and their size is determined only by the stand-off distance.
(11)According to Eq. (11) there is no difference in the shape of the bow shocks and their size is determined only by the stand-off distance.
2.7. Initial conditions
We assume that the source of dust particles forming the swept-back structure at HD 61005 is in the circumstellar ring observed also in the scattered light. As the source of dust particles, we consider parent bodies in elliptical orbits with semimajor axes distributed randomly between 55 and 65 AU. We assume that the elliptical orbits have randomly distributed eccentricities smaller than 0.1. Inclinations of the orbits are distributed randomly between 0 and 2°. Arguments of pericenters, longitudes of ascending nodes, and true anomalies of the parent bodies are distributed randomly between 0 and 2π. The dust particle, after ejection from the parent body, is subjected to the radiation of the star. The position and velocity in a moment of the ejection can be used in order to calculate initial orbital elements of the dust particle. After the ejection, central Keplerian acceleration from the star is reduced by a factor 1 − β (see text after Eq. (4)) and the particle obtains a different oscular orbit. The observed swept-back structure at HD 61005 can be explained with dust particles moving in hyperbolic orbits. The dust particles in the hyperbolic orbits have also been observed in the solar system and are called β-meteoroids (Zook & Berg 1975). Calculation of initial orbital elements after an ejection to the hyperbolic orbit is shown in Appendix A.
Properties of the star HD 61005 are sufficiently well known. Unfortunately, this cannot be said about properties of the ISM gas which varies the dynamic of the observed dust. After a few numerical solutions of the equation of motion, it is easy to see that observed structure requires the acceleration caused by the ISM to be dominant in the dynamics of ejected dust particles. The dominance can be accomplished by high density, high speed and/or high temperature of the ISM gas. The observed shape morphology will be obtained for the ISW with various velocities and densities of gas components. The high temperature possibility alone requires ISM gas temperatures of more than 105 K and for such high temperatures at HD 61005 there is no observational evidence. Therefore, the gas temperature will not be considered as the primary cause for the observed morphology. The influence of the ISW with various temperatures on the shape morphology will be discussed separately. Implications for the shape morphology from the specular as well as the diffuse reflection at the surface of the dust grains will be compared.
2.8. Observations in scattered light
We numerically solved the equation of motion for 2 × 105 particles. Obtained trajectories were accumulated into a 2D grid observed from a given direction. A similar technique was used also by Debes et al. (2009) and earlier for visualization of resonant structures in debris disks by Liou & Zook (1999), Moro-Martín & Malhotra (2002), Stark & Kuchner (2008) and others. This technique enables visualization of an optical depth in a given element of the grid. In order to compare our model with observations of dust in the scattered light, we calculated an intensity of light from HD 61005 scattered on each dust particle in the given element of the grid in the observed direction using Mie scattering theory (e.g., Mie 1908; van de Hulst 1981) with an assumption that the light travels through optically thin environment. Mie theory represents one solution of Maxwell’s equations for boundary conditions used in our model.
 |
Fig. 1 An interaction of dust particles with R = 0.168 μm, ϱ = 1 g cm-3 and |
3. Results
By numerically solving the equation of motion one can easily find various properties of the ISM that lead to practically identical shape morphology. It is impossible using existing observational data to decide which properties really belong to the ISM gas at HD 61005. Instead of choosing only one property, we focus on groups of properties that give the observed structure using our dynamical model. The relative speed of HD 61005 with respect to the Sun determined from its measured proper motion is 27.0 km s-1. The ISM in the solar system arrives from the direction λecl = 254.7° (heliocentric ecliptic longitude) and βecl = 5.2° (heliocentric ecliptic latitude) and moves with a speed vF = 26.3 km s-1 (Lallement et al. 2005). If the Sun and the HD 61005 were embedded in the same interstellar cloud, the speed of the ISM gas at HD 61005 would be only 12.8 km s-1. The ISM with such a small speed requires large densities of the ISM gas in order to create the observed morphology (see further). Therefore, it is more probable that the Sun and the HD 61005 are not embedded in the same interstellar cloud.
3.1. ISW velocity perpendicular to the debris ring plane
In Fig. 1 is depicted the obtained shape morphology consistent with the observed morphology at HD 61005. The interstellar gas velocity is perpendicular to the debris ring. In order to reproduce the observed morphology we used number densities for hydrogen, helium, and plasma in the same ratios as number densities of the ISM incoming to the solar system. We have adopted the following number densities nH S = 0.2 cm-3, nHe S = 0.015 cm-3, and np S = 0.032 cm-3 from Frisch et al. (2009) for interstellar hydrogen, helium, and plasma entering the solar system, respectively. Temperatures of all ISM gas components were equal to T = 6300 K, which is approximately the temperature of interstellar helium entering the solar system that is a gas component weakly affected in the interaction of the ISW with the stellar wind. We assumed that the ISM atoms are specularly reflected at the surfaces of the dust grains (δi = 1 in Eq. (6)). Chosen speed of the ISM is vF = 30 km s-1 and the number densities found are nH = 80 cm-3, nHe = 6 cm-3, and np = 12.8 cm-3 for interstellar hydrogen, helium, and plasma, respectively. Cartesian coordinates are used in the plots with the origin in the star. The bottom-left plot is created by a rotation of a viewpoint in the top-left plot by 45° counterclockwise around the x-axis in the yz-plane. The bottom-right plot is created by the rotation of a viewpoint in the top-left plot by 95.7° counterclockwise around the x-axis in the yz-plane in order to show the shape morphology observed from the Earth (Buenzli et al. 2010). The dominance of the acceleration caused by the ISM gas enables us to use only single particle size for a creation of correct morphology shape for the given ISM parameters. In this case the shape of swept-back structure is not a function of the particle’s radius R. This can also be proved analytically using a simplified approximation that the acceleration of the dust particle sufficiently far from the star is given only by the Stark approximation. In the Stark approximation, the acceleration caused by the ISM gas depends on the velocity as CvFvF, where C is a constant (see Pástor 2012a). However, the shape of swept-back structure is a function of  . The boundary, determining the curvature of “wings”, is formed by dust particles that are most significantly influenced by the stellar radiation; hence, the particles with maximal
. The boundary, determining the curvature of “wings”, is formed by dust particles that are most significantly influenced by the stellar radiation; hence, the particles with maximal  obtained from Mie scattering theory. These particles obtain maximal variation of the velocity in approximately radial direction close to the star. The maximal
obtained from Mie scattering theory. These particles obtain maximal variation of the velocity in approximately radial direction close to the star. The maximal  is obtained for totally reflecting particles. For the effective temperature of the star 5500 K we can calculate the particle’s radius for which
is obtained for totally reflecting particles. For the effective temperature of the star 5500 K we can calculate the particle’s radius for which  is obtained. The obtained radius is 0.168 μm and corresponding maximal
is obtained. The obtained radius is 0.168 μm and corresponding maximal  is 1.663 (Fig. 2). A slightly larger radius of about 0.2 μm for the scattering particles has been suggested from observations by Hines et al. (2007). For this radius we obtain
is 1.663 (Fig. 2). A slightly larger radius of about 0.2 μm for the scattering particles has been suggested from observations by Hines et al. (2007). For this radius we obtain  , not far from the
, not far from the  . Figure 1 was obtained using icy dust particles with radius R = 0.168 μm. In Eq. (2) these parameters give β ≈ 3 for the stellar parameters of HD 61005. Scattering intensities were obtained at λ = 580 nm. This wavelength is free of any major Fraunhofer absorption lines in the stellar spectrum. The positions of dust particles are not dependent on wavelength of the observed scattered light. Therefore, the shape morphology should not depend on the chosen wavelength of scattered light in narrow visible light wavelength interval. Scattering intensities obtained using Mie theory should be exactly correct for the used model. Scattering diagram for the used particle at 580 nm is shown in Fig. 3.
. Figure 1 was obtained using icy dust particles with radius R = 0.168 μm. In Eq. (2) these parameters give β ≈ 3 for the stellar parameters of HD 61005. Scattering intensities were obtained at λ = 580 nm. This wavelength is free of any major Fraunhofer absorption lines in the stellar spectrum. The positions of dust particles are not dependent on wavelength of the observed scattered light. Therefore, the shape morphology should not depend on the chosen wavelength of scattered light in narrow visible light wavelength interval. Scattering intensities obtained using Mie theory should be exactly correct for the used model. Scattering diagram for the used particle at 580 nm is shown in Fig. 3.
3.2. Speeds and densities of the ISW
The acceleration caused by the ISM gas has such a form that smaller velocity and larger densities of the ISM gas can give the same resulting shape morphology as a larger velocity and smaller densities. In Fig. 4 are shown velocity and number densities of the ISM that produce the observed shape of the swept-back structure at HD 61005 using presented model for the dust particles with a given  . The number densities are shown as component density ratios of the interstellar matter at HD 61005 and the interstellar matter at the Sun. Temperatures of all ISM gas components were equal to T = 6300 K. Different temperatures will be taken into account in Sect. 3.4. We have used the specular reflection at the surface of the dust grains (δi = 1 in Eq. (6)). Variations of the shape morphology caused by the diffuse reflection at the surface can be neglected (see Sect. 3.5). The red line is obtained from numerical solution of the equation of motion (Eq. (9)) using a spline interpolation applied on the measured values (black circles). The shape depicted in Fig. 1 corresponds to the component density ratio
. The number densities are shown as component density ratios of the interstellar matter at HD 61005 and the interstellar matter at the Sun. Temperatures of all ISM gas components were equal to T = 6300 K. Different temperatures will be taken into account in Sect. 3.4. We have used the specular reflection at the surface of the dust grains (δi = 1 in Eq. (6)). Variations of the shape morphology caused by the diffuse reflection at the surface can be neglected (see Sect. 3.5). The red line is obtained from numerical solution of the equation of motion (Eq. (9)) using a spline interpolation applied on the measured values (black circles). The shape depicted in Fig. 1 corresponds to the component density ratio  on the red line. The observed shape morphology can be obtained with the density ratios smaller than 240 for dust particles with
on the red line. The observed shape morphology can be obtained with the density ratios smaller than 240 for dust particles with  at the ISW speed 30 km s-1. The blue line shows the Stark approximation
at the ISW speed 30 km s-1. The blue line shows the Stark approximation  kg m-1 s-2, where c0i = cDi(s0i) and
kg m-1 s-2, where c0i = cDi(s0i) and  . The dependence of cD on the speed of the ISM gas (vF) is considered in this approximation. The constant was calculated from the case depicted in Fig. 1 (vF = 30 km s-1). In the Stark approximation cD does not depend on the velocity of the dust particle. If cD were constant for all the ISW speeds, then the approximative relation would be vF=
. The dependence of cD on the speed of the ISM gas (vF) is considered in this approximation. The constant was calculated from the case depicted in Fig. 1 (vF = 30 km s-1). In the Stark approximation cD does not depend on the velocity of the dust particle. If cD were constant for all the ISW speeds, then the approximative relation would be vF= , where Cf is a constant. Such a function is depicted in Fig. 6 with the dashed line. The solution of the equation of motion is approximated fairly well by both simplified relations. The plots depicting the simplified relations were obtained only with the acceleration from the ISM gas. This demonstrates the above mentioned dominance of the ISM gas in the dynamical evolution of the dust particles farther from the star. The star’s gravity and the PR effect can by neglected in comparison with influence of the ISM gas farther from the star.
, where Cf is a constant. Such a function is depicted in Fig. 6 with the dashed line. The solution of the equation of motion is approximated fairly well by both simplified relations. The plots depicting the simplified relations were obtained only with the acceleration from the ISM gas. This demonstrates the above mentioned dominance of the ISM gas in the dynamical evolution of the dust particles farther from the star. The star’s gravity and the PR effect can by neglected in comparison with influence of the ISM gas farther from the star.
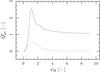 |
Fig. 2 Dimensionless efficiency factor for the radiation pressure ( |
 |
Fig. 3 Scattering diagram of light with λ = 580 nm impinging on the dust particle with R = 0.168 μm. This particle gives the maximal dimensionless efficiency factor for the radiation pressure averaged over the stellar spectrum. For xM = 2πR/λ< 1.38 scattering is predominantly back to the source. Considered situation corresponds to xM ≈ 1.820 and the scattering diagram has the usual preponderance of forward radiation over back radiation (van de Hulst 1981). |
 |
Fig. 4 Relation between the interstellar gas speed and the component ratios of the interstellar gas number densities at HD 61005 and the Sun (red lines) that give the observed morphology at HD 61005. Used interstellar gas number densities at the Sun are nH S = 0.2 cm-3, nHe S = 0.015 cm-3, and np S = 0.032 cm-3. After division of the density ratios by maximal averaged efficiency factor for the radiation pressure, we obtain the relation independent of the particle properties in our model. The blue line shows the Stark approximation with considered dependence of the drag coefficients on the velocity of the ISM gas. The dashed line shows a function |
In Debes et al. (2009), a speed of 25 km s-1 was used for the interstellar gas. Using depicted results in Fig. 4 we obtain the same observed morphology for dust particles with  at number densities nH ≈ 65.4 cm-3, nHe ≈ 4.9 cm-3, and np ≈ 10.5 cm-3. The model picture in Debes et al. (2009) was obtained with nH 100 cm-3. We found that such high densities of hydrogen alone are not necessary for three reasons: 1) Debes et al. (2009) used an assumption “that the grains originate from radii ~10 AU from the star” (see p. 324 therein). In 2009 shape of the debris ring was not yet determined. The parent bodies on such orbits produce dust particles with much larger initial velocities than the parent bodies in the observed debris ring between 55 and 65 AU. The dust particle moving with such a large initial tangential velocity requires much intensive acceleration from the ISW to be pushed up from the ring plane sufficiently fast. 2) The acceleration in Debes et al. (2009) has a different form of the drag coefficient. For the same dust particle, the same hydrogen density, and the relative particle-gas speed 25 km s-1, we obtain that the acceleration in this paper is ~1.40 times larger than the acceleration in Debes et al. (2009) at the temperature of hydrogen 6300 K. 3) It is very probable that gas components in addition to hydrogen exist in the interstellar matter at HD 61005.
at number densities nH ≈ 65.4 cm-3, nHe ≈ 4.9 cm-3, and np ≈ 10.5 cm-3. The model picture in Debes et al. (2009) was obtained with nH 100 cm-3. We found that such high densities of hydrogen alone are not necessary for three reasons: 1) Debes et al. (2009) used an assumption “that the grains originate from radii ~10 AU from the star” (see p. 324 therein). In 2009 shape of the debris ring was not yet determined. The parent bodies on such orbits produce dust particles with much larger initial velocities than the parent bodies in the observed debris ring between 55 and 65 AU. The dust particle moving with such a large initial tangential velocity requires much intensive acceleration from the ISW to be pushed up from the ring plane sufficiently fast. 2) The acceleration in Debes et al. (2009) has a different form of the drag coefficient. For the same dust particle, the same hydrogen density, and the relative particle-gas speed 25 km s-1, we obtain that the acceleration in this paper is ~1.40 times larger than the acceleration in Debes et al. (2009) at the temperature of hydrogen 6300 K. 3) It is very probable that gas components in addition to hydrogen exist in the interstellar matter at HD 61005.
If the curvature of swept-back structure were observed farther from the star, then it should be possible to determine densities of ISM components directly. The data in Fig. 4 were fitted to match available observations from Schneider et al. (2014) to distance 230 AU along the ring mid-plane with correct distance scaling from Buenzli et al. (2010).
 |
Fig. 5 Distances to the bow shock of the ISW and the stellar wind interaction in the debris ring mid-plane. The distances were obtained using Eq. (11) with θ = 90° for the ISW parameters giving the observed shape morphology for the dust particles with |
3.3. Interaction of the ISW with stellar wind
For the ISW gas considered in Fig. 4, the interaction of the ISW with the stellar wind should be supersonic (see e.g., Holzer 1989). Hence, the bow shock should be formed. Even in a case without the bow shock the equilibrium between the ram pressures of the stellar wind and the ISW gives characteristic dimensions of the interaction. For the ISW, velocity perpendicular to the debris ring holds that the plane comprising the debris ring mid-plane has the polar angle θ = 90° in Eq. (11). The shape of the bow shock varies in such away that the stellocentric distance to the bow shock in the debris ring mid-plane is  . In Fig. 5 are shown rBS for number densities and speeds corresponding in Fig. 4 to the dust particle with
. In Fig. 5 are shown rBS for number densities and speeds corresponding in Fig. 4 to the dust particle with 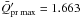 . The stand-off distances determined by the equilibrium between the ram pressures of the stellar wind and the supersonic ISM gas are much smaller than that of the debris ring. We must note that the theory in Johnstone et al. (2015) is obtained from a sample of main sequence stars. Since HD 61005 is a pre-main sequence star, then the mass loss rate and the stellar wind speed may not be accurately determined. However, as already mentioned, the theory in Johnstone et al. (2015) can be easily generalized also for the pre-main sequence stars. The calculated values of rBS for the ISW parameters giving the observed shape morphology allow even larger mass-loss rates and stellar-wind speeds to place the bow shock inside the debris ring. Moreover, in the perpendicular case the bow shock should cross the debris ring mid-plane with an inclination arctan(4 /π) ≈ 51.9° given by the shape in Eq. (11). This means that if the debris ring is located in the bow shock, the particles will leave the bow shock quickly on their trajectories giving the observed morphology. In other words, the slope of the bow shock boundary at the debris ring mid-plane is too high for the dust particle trajectories to stay in the bow shock. The calculated stellocentric distances of the bow shock in debris ring mid-plane (rBS) are significantly smaller than the stellocentric distances of the debris ring. Therefore, the debris ring is more probably located above the bow shock. Since we assume that the dust particles originate in the debris ring, the velocities and densities of the ISW should not be affected by the interaction of the ISW with the stellar wind.
. The stand-off distances determined by the equilibrium between the ram pressures of the stellar wind and the supersonic ISM gas are much smaller than that of the debris ring. We must note that the theory in Johnstone et al. (2015) is obtained from a sample of main sequence stars. Since HD 61005 is a pre-main sequence star, then the mass loss rate and the stellar wind speed may not be accurately determined. However, as already mentioned, the theory in Johnstone et al. (2015) can be easily generalized also for the pre-main sequence stars. The calculated values of rBS for the ISW parameters giving the observed shape morphology allow even larger mass-loss rates and stellar-wind speeds to place the bow shock inside the debris ring. Moreover, in the perpendicular case the bow shock should cross the debris ring mid-plane with an inclination arctan(4 /π) ≈ 51.9° given by the shape in Eq. (11). This means that if the debris ring is located in the bow shock, the particles will leave the bow shock quickly on their trajectories giving the observed morphology. In other words, the slope of the bow shock boundary at the debris ring mid-plane is too high for the dust particle trajectories to stay in the bow shock. The calculated stellocentric distances of the bow shock in debris ring mid-plane (rBS) are significantly smaller than the stellocentric distances of the debris ring. Therefore, the debris ring is more probably located above the bow shock. Since we assume that the dust particles originate in the debris ring, the velocities and densities of the ISW should not be affected by the interaction of the ISW with the stellar wind.
 |
Fig. 6 Component density ratios giving the observed shape morphology at HD 61005 for the ISW with speed 30 km s-1 and gas temperatures in the range 1000−10 000 K (red line). The component density ratios are divided by maximal averaged efficiency factor for the radiation pressure in the population of dust particles. The blue line is used for the density ratios obtained in the Stark approximation from the dependence of drag coefficients on the temperature of the ISM gas (see Eq. (6)). |
The interaction of a stellar wind with an ISM gas creates a termination shock in the stellar wind. The termination shock in the solar system was directly observed by Voyager 1 at a heliocentric distance 94 AU in 2004 and by Voyager 2 at 84 AU in 2007 (Richardson et al. 2008). Stellocentric distance to the termination shock is always smaller than that of the bow shock for a given polar angle θ (see e.g., Frisch et al. 2009). Since the stellocentric distances to the bow shock in the debris ring mid-plane at HD 61005 are smaller than 55−65 AU, the acceleration caused by the stellar wind is ignored in our model.
 |
Fig. 7 Same situation as in Fig. 1 only with different interstellar gas velocity vector and different viewpoints. The interstellar gas velocity vector lies in the xz-plane and has 45° angle between its direction and debris ring axis. Its magnitude was modified using Eq. (13) in order to obtain the same observed morphology from the Earth. The bottom-left plot shows the view on the star against the ISW. The bottom-right plot shows the view from the Earth with the same orientation as in Fig. 1. |
3.4. Temperatures of the ISW
In Fig. 6 are shown temperatures and component density ratios that give the observed morphology for the ISW speed 30 km s-1 (red line). Large variation in gas temperature requires only small variation in the density ratios in order to reproduce the observed morphology. This is a consequence of properties of the drag coefficient. For the specular reflection the dependence on the temperature is inside the Mach number and obtained Mach numbers are sufficiently large to set the drag coefficients close to 1. Therefore, the variations in the gas temperature do not have a large influence on variation of the acceleration caused by the ISW. A relation obtained from the Stark approximation is also shown (blue line). Component density ratios for the Star approximation are given by  kg m-3, where c0i = cDi(s0i) and
kg m-3, where c0i = cDi(s0i) and  . The constant corresponds to T = 6300 K for vF = 30 km s-1 (the situation depicted in Fig. 1). As in Fig. 4 the simplified relation was obtained only with the acceleration from the ISM gas without dependence on the particle’s velocity. An applicability of the Stark approximation was verified to be usable for all ISW speeds measured in Fig. 4 in the temperature range 1000−10 000 K.
. The constant corresponds to T = 6300 K for vF = 30 km s-1 (the situation depicted in Fig. 1). As in Fig. 4 the simplified relation was obtained only with the acceleration from the ISM gas without dependence on the particle’s velocity. An applicability of the Stark approximation was verified to be usable for all ISW speeds measured in Fig. 4 in the temperature range 1000−10 000 K.
3.5. Diffuse reflection at the surface
For a diffuse reflection, the drag coefficient depends on the temperature of the dust particle. At 60 AU from HD 61005, we obtain an equilibrium temperature of the dust particle ≈31 K. The equilibrium temperature should decrease with the stellocentric distance. The maximal variation of the drag coefficient due to the diffusion is according to Eq. (6)  (12)For the dust particle at 60 AU the substitution of hydrogen with the relative velocity 30 km s-1 in Eq. (12) yields the maximal variation of the drag coefficient ≈0.014. Hence, the influence of the diffusion reflection on the shape morphology should not be large. This conclusion was verified also by the numerical solution of the equation of motion with the diffuse reflection at the surface of the dust particles.
(12)For the dust particle at 60 AU the substitution of hydrogen with the relative velocity 30 km s-1 in Eq. (12) yields the maximal variation of the drag coefficient ≈0.014. Hence, the influence of the diffusion reflection on the shape morphology should not be large. This conclusion was verified also by the numerical solution of the equation of motion with the diffuse reflection at the surface of the dust particles.
3.6. ISW velocity tilted from debris ring axis
The interstellar matter velocity vector may not be perpendicular to the debris ring. Such a configuration can also produce what we observe at HD 61005. Figure 7 shows reproduced shape morphology for the case where the angle between the ISM velocity vector and the debris ring axis is 45°. The ISM velocity vector lies in the plane comprising the line of sight and the ring axis. The bottom-left plot depicts the view against the ISW with the star in the center. The bottom-right plot is created by the rotation of the viewpoint in the top-left plot by 95.7° about the x-axis counterclockwise in the yz-plane in order to show the shape morphology observed from the Earth similarly to Fig. 1. We have used the same temperature and number densities of the ISM gas components as in Fig. 1. However, simple usage of the same speed of the ISM does not give the observed morphology. To match observed morphology at this tilt of the ISM velocity vector with respect to the debris ring axis the speed must be increased. Using the same approximation as for the independence of observed morphology on the particle’s radius we can derive an equation that gives how the speed of the ISM should be modified in order to obtain the same observed morphology. A variation of the particle’s position caused by the Stark acceleration along the ISM velocity vector is  . Particle velocity perpendicular to the ISM velocity vector is conserved in the Stark approximation. Therefore, we can calculate time as t = xS/vP, where xS is the variation of the particle’s position in a direction perpendicular to the ISM velocity vector and vP is the speed of the particle in this direction. For the ISM velocity vector lying in the plane comprising the line of sight and the ring axis we obtain for two different configurations the same observed morphology if zSAsinϵA = zSBsinϵB and xSA = xSB. Here, the subscripts A and B refer to two different configurations and ϵA is an angle between the line of sight and the ISM velocity in the configuration A. The modification equation given by a substitution is
. Particle velocity perpendicular to the ISM velocity vector is conserved in the Stark approximation. Therefore, we can calculate time as t = xS/vP, where xS is the variation of the particle’s position in a direction perpendicular to the ISM velocity vector and vP is the speed of the particle in this direction. For the ISM velocity vector lying in the plane comprising the line of sight and the ring axis we obtain for two different configurations the same observed morphology if zSAsinϵA = zSBsinϵB and xSA = xSB. Here, the subscripts A and B refer to two different configurations and ϵA is an angle between the line of sight and the ISM velocity in the configuration A. The modification equation given by a substitution is  (13)When the ISM velocity vector is tilted with respect to the ring axis, the symmetry between the left and right “wings” observed from the plane comprising the ISM velocity vector and the ring axis is slightly affected. The slope of the “wings” slightly depends on whether the motion of parent bodies in the debris ring is prograde or rectograde. This is due to the fact that components of the initial dust velocity parallel and perpendicular to the ISM velocity vector vary along the mid-plane of the debris ring.
(13)When the ISM velocity vector is tilted with respect to the ring axis, the symmetry between the left and right “wings” observed from the plane comprising the ISM velocity vector and the ring axis is slightly affected. The slope of the “wings” slightly depends on whether the motion of parent bodies in the debris ring is prograde or rectograde. This is due to the fact that components of the initial dust velocity parallel and perpendicular to the ISM velocity vector vary along the mid-plane of the debris ring.
3.7. Observed morphology of ISM particles in hyperbolic orbits
Artymowicz & Clampin (1997) derived an equation of an axisymmetric paraboloidal void caused by the stellar gravity reduced by the Keplerian term from the PR effect in a flow of interstellar dust particles approaching the star in hyperbolic orbits. For the dust particles with constant β the observed morphology should be similar to tilted paraboloid z = (x2 + y2) / 4 − 1. For a boundary of the paraboloid in an orthogonal projection to a sky plane we obtain z′ = (x2/ 4 − 1 / sin2ϵ)sinϵ. Here ϵ is the angle between the line of sight and the ISM velocity (ϵ ≠ 0). At a latitude of the star (z = 0) we obtain a slope of the boundary of 45°, independently of ϵ. This result can be easily applied for a verification if an observed structure is caused by the dust particles entering the star with the ISM. For an existing application see Gáspár et al. (2008).
4. Conclusion
We have investigated the influence of ISW on the shape morphology of an observed swept-back structure originating in the debris ring at HD 61005. For explanation of the observed morphology, high velocities or densities of interstellar gas are required. On the boundary of the swept-back structure, the dust particles that are maximally influenced by stellar radiation should by present. When Debes et al. (2009) was published, no observations of the debris ring producing the dust particles existed. The assumed stellocentric distances of about 10 AU used for the location of the debris ring were much lower in comparison with today’s real observed values of 55-65 AU. Unfortunately, we were not able to reproduce Debes et al. (2009) results using the debris ring at 10 AU interacting with an interstellar hydrogen with number density nH = 100 cm-3. It is likely that low assumed stellocentric distance together with other reasons (see Sect. 3.2) lead to higher initial velocities of dust particles and consequently to higher densities and velocities of ISW required for creation of the observed shape. Required number density for the ISM with speed 25 km s-1 is 327.1 times higher than the ISM entering the solar system for the observed debris ring in comparison with the value of 500 obtained for the interstellar hydrogen in Debes et al. (2009) for the debris ring at 10 AU. For such a strong ISW the bow shock should be inside the debris ring.
The observed shape can be obtained also in the case where ISW is not perpendicular to the ring plane. Suitable configuration exists also in the case where the ISW velocity lies in a plane comprising the line of sight and the debris ring axis. A simple relation between suitable ISM speed and the angle between the line of sight and ISM velocity can be obtained.
Gas temperature does not have a large influence on the shape morphology due to larger values of Mach numbers that set the drag coefficients close to 1.
In general, we can conclude that the observed morphology created by the dust originating in the debris ring at HD 61005 can be explained if we consider dust under the action of the ISW.
Acknowledgments
I am grateful to the Nitra Self-governing Region for support. I would also like to thank the referee for suggestions that helped me improve the manuscript.
References
- Artymowicz, P., & Clampin, M. 1997, ApJ, 490, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, M. J., Williams, I. P., & Asebiomo, A. S. 1965, MNRAS, 130, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Buenzli, E., Thalmann, C., Vigan, A., et al. 2010, A&A, 524, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Debes, J. H., Weinberger, A. J., & Kuchner, M. J. 2009, ApJ, 702, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., Covino, E., Messina, S., et al. 2011, A&A, 529, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esposito, T. M., Fitzgerald, M. P., Graham, J. R., et al. 2016, AJ, 152, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Bzowski, M., Grün, E., et al. 2009, Space Sci. Rev., 146, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Gáspár, A., Su, K. Y. L., Rieke, G. H., et al. 2008, ApJ, 672, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafson, B. A. S. 1994, Annu. Rev. Earth Planet. Sci., 22, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Holzer, T. E. 1989, ARA&A, 27, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Hines, D. C., Schneider, G., Hollenbach, D., et al. 2007, ApJ, 671, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klačka, J. 1992, Earth Moon Planets, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Klačka, J. 2004, Celest. Mech. Dyn. Astron., 89, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Klačka, J., Petržala, J., Pástor, P., & Kómar, L. 2012, MNRAS, 421, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Klačka, J., Petržala, J., Pástor, P., & Kómar, L. 2014, Icarus, 232, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Quémerais, E., Bertaux, J. L., et al. 2005, Science, 307, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Liou, J.-Ch., & Zook, H. A. 1999, AJ, 118, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Maness, H. L., Kalas, P., Peek, K. M. G., et al. 2009, ApJ, 707, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Mie, G. 1908, Ann. Phys., 25, 377 [CrossRef] [Google Scholar]
- Moro-Martín, A., & Malhotra, R. 2002, AJ, 124, 2305 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Samland, M., Avenhaus, H., et al. 2016, A&A, 591, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Pástor, P. 2012a, Celest. Mech. Dyn. Astron., 112, 23 [Google Scholar]
- Pástor, P. 2012b, MNRAS, 426, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Pástor, P., Klačka, J., & Kómar, L. 2011, MNRAS, 415, 2637 [NASA ADS] [CrossRef] [Google Scholar]
- Poynting, J. M. 1904, Phil. Trans. R. Soc. Lond., Ser. A, 202, 525 [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Robertson, H. P. 1937, MNRAS, 97, 423 [NASA ADS] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Scherer, K. 2000, J. Geophys. Res., 105, A5, 10329 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Grady, C. A., Hines, D. C., et al. 2014, AJ, 148, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, C. C., & Kuchner, M. J. 2008, ApJ, 686, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, C. A. O., Quast, G. R., Melo, C. H. F., Sterzik, M. F. 2008, in Handbook of Star Forming Regions, Vol. II: The Southern Sky, ed. B. Reipurth, 757 [Google Scholar]
- van de Hulst, H. C. 1981, Light Scattering by Small Particles (New York: Dover Publications) [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilkin, F. P. 1996, ApJ, 459, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zook, H. A., & Berg, O. E. 1975, Planet. Space Sci., 23, 183 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Initial elements after an ejection to hyperbolic orbit
The positions and velocities of the parent body and the particle are equal in a moment of the ejection with zero ejection velocities. After an ejection from a parent body in an elliptical orbit the semimajor axis of the particle orbit can be calculated as follows. For the parent body we have  (A.1)where v is the speed in the moment of ejection and ap is the semimajor axis of the parent body. The subscript p will be used for quantities belonging to the parent body. For dust particle with β> 1 ejected to a hyperbolic orbit we have
(A.1)where v is the speed in the moment of ejection and ap is the semimajor axis of the parent body. The subscript p will be used for quantities belonging to the parent body. For dust particle with β> 1 ejected to a hyperbolic orbit we have  (A.2)The substitution of v2/ 2 from Eqs. (A.1) to (A.2) gives for the semimajor axis of the hyperbolic orbit
(A.2)The substitution of v2/ 2 from Eqs. (A.1) to (A.2) gives for the semimajor axis of the hyperbolic orbit  (A.3)Comparison of the angular momentum H written using the orbital elements of the parent body and the particle in the moment of ejection gives
(A.3)Comparison of the angular momentum H written using the orbital elements of the parent body and the particle in the moment of ejection gives  (A.4)If we substitute Eqs. (A.3) to (A.4), then we can determine the eccentricity of the hyperbolic orbit
(A.4)If we substitute Eqs. (A.3) to (A.4), then we can determine the eccentricity of the hyperbolic orbit  (A.5)The particle moves in the same plane as the parent body after the ejection with the zero ejection velocity. Hence, the ascending nodes and inclinations are equal
(A.5)The particle moves in the same plane as the parent body after the ejection with the zero ejection velocity. Hence, the ascending nodes and inclinations are equal  (A.6)
(A.6)
In the moment of ejection, the true longitudes of the parent body and the particle are equal. Therefore,  (A.7)where f is the true anomaly and ω is the argument of pericenter. For stellocentric distance of the dust particle with β> 1 on the hyperbolic orbit we have
(A.7)where f is the true anomaly and ω is the argument of pericenter. For stellocentric distance of the dust particle with β> 1 on the hyperbolic orbit we have  (A.8)Radial components of velocities of the parent body (vRp) and the particle (vR) are equal in the moment of ejection
(A.8)Radial components of velocities of the parent body (vRp) and the particle (vR) are equal in the moment of ejection ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{radial} v_{\text{Rp}} &= & \sqrt{\frac{\mu}{a_{\text{p}} \left ( 1 - e_{\text{p}}^{2} \right )}} e_{\text{p}} \sin f_{\text{p}} \notag \\[3mm] &= & \sqrt{\frac{\mu \left ( \beta - 1 \right )} {a \left ( e^{2} - 1 \right )}} e \sin f = v_{\text{R}} . \end{eqnarray}](/articles/aa/full_html/2017/08/aa30455-17/aa30455-17-eq160.png) (A.9)From the equality of transversal components of the velocities we obtain
(A.9)From the equality of transversal components of the velocities we obtain ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{transversal} v_{\text{Tp}} &= & \sqrt{\frac{\mu}{a_{\text{p}} \left ( 1 - e_{\text{p}}^{2} \right )}} \left ( 1 + e_{\text{p}} \cos f_{\text{p}} \right ) \notag \\[3mm] &= & \sqrt{\frac{\mu \left ( \beta - 1 \right )} {a \left ( e^{2} - 1 \right )}} \left ( e \cos f - 1 \right ) = v_{\text{T}} . \end{eqnarray}](/articles/aa/full_html/2017/08/aa30455-17/aa30455-17-eq161.png) (A.10)Using Eq. (A.4) in Eqs. (A.9) and (A.10) we can calculate the true anomaly
(A.10)Using Eq. (A.4) in Eqs. (A.9) and (A.10) we can calculate the true anomaly 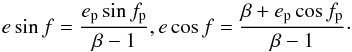 (A.11)The true anomaly substituted in Eq. (A.7) determines the argument of pericenter. For particles with β≈ 3 released from parent bodies with nearly circular orbits (ep≈ 0) the true anomaly is always close to zero, in other words, the particle is ejected close to the pericenter of the hyperbolic orbit.
(A.11)The true anomaly substituted in Eq. (A.7) determines the argument of pericenter. For particles with β≈ 3 released from parent bodies with nearly circular orbits (ep≈ 0) the true anomaly is always close to zero, in other words, the particle is ejected close to the pericenter of the hyperbolic orbit.
All Figures
 |
Fig. 1 An interaction of dust particles with R = 0.168 μm, ϱ = 1 g cm-3 and |
| In the text | |
 |
Fig. 2 Dimensionless efficiency factor for the radiation pressure ( |
| In the text | |
 |
Fig. 3 Scattering diagram of light with λ = 580 nm impinging on the dust particle with R = 0.168 μm. This particle gives the maximal dimensionless efficiency factor for the radiation pressure averaged over the stellar spectrum. For xM = 2πR/λ< 1.38 scattering is predominantly back to the source. Considered situation corresponds to xM ≈ 1.820 and the scattering diagram has the usual preponderance of forward radiation over back radiation (van de Hulst 1981). |
| In the text | |
 |
Fig. 4 Relation between the interstellar gas speed and the component ratios of the interstellar gas number densities at HD 61005 and the Sun (red lines) that give the observed morphology at HD 61005. Used interstellar gas number densities at the Sun are nH S = 0.2 cm-3, nHe S = 0.015 cm-3, and np S = 0.032 cm-3. After division of the density ratios by maximal averaged efficiency factor for the radiation pressure, we obtain the relation independent of the particle properties in our model. The blue line shows the Stark approximation with considered dependence of the drag coefficients on the velocity of the ISM gas. The dashed line shows a function |
| In the text | |
 |
Fig. 5 Distances to the bow shock of the ISW and the stellar wind interaction in the debris ring mid-plane. The distances were obtained using Eq. (11) with θ = 90° for the ISW parameters giving the observed shape morphology for the dust particles with |
| In the text | |
 |
Fig. 6 Component density ratios giving the observed shape morphology at HD 61005 for the ISW with speed 30 km s-1 and gas temperatures in the range 1000−10 000 K (red line). The component density ratios are divided by maximal averaged efficiency factor for the radiation pressure in the population of dust particles. The blue line is used for the density ratios obtained in the Stark approximation from the dependence of drag coefficients on the temperature of the ISM gas (see Eq. (6)). |
| In the text | |
 |
Fig. 7 Same situation as in Fig. 1 only with different interstellar gas velocity vector and different viewpoints. The interstellar gas velocity vector lies in the xz-plane and has 45° angle between its direction and debris ring axis. Its magnitude was modified using Eq. (13) in order to obtain the same observed morphology from the Earth. The bottom-left plot shows the view on the star against the ISW. The bottom-right plot shows the view from the Earth with the same orientation as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.