| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730506 | |
| Published online | 03 July 2017 | |
Testing connections between exo-atmospheres and their host stars
GEMINI-N/GMOS ground-based transmission spectrum of Qatar-1b⋆
1 Stellar Astrophysics Centre, Department of Physics and AstronomyAarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: cessen@phys.au.dk
2 Consejo Nacional de Investigaciones Científicas y Técnicas, Godoy Cruz 2290, C1425FQB, Ciudad Autónoma de Buenos Aires, Argentina
3 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900FWA, La Plata, Argentina
4 Instituto de Astrofísica de La Plata (CCT-La Plata, CONICET-UNLP), Paseo del Bosque, B1900FWA, La Plata, Argentina
5 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
6 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received: 27 January 2017
Accepted: 14 March 2017
Till date, only a handful exo-atmospheres have been well characterized, mostly by means of the transit method. Some classic examples are HD 209458b, HD 189733b, GJ-436b, and GJ-1214b. Data show exoplanet atmospheres to be diverse. However, this is based on a small number of cases. Here we focus our study on the exo-atmosphere of Qatar-1b, an exoplanet that looks much like HD 189733b regarding its host star’s activity level, their surface gravity, scale height, equilibrium temperature and transit parameters. Thus, our motivation relied on carrying out a comparative study of their atmospheres, and assess if these are regulated by their environment. In this work we present one primary transit of Qatar-1b obtained during September, 2014, using the 8.1 m GEMINI North telescope. The observations were performed using the GMOS-N instrument in multi-object spectroscopic mode. We collected fluxes of Qatar-1 and six more reference stars, covering the wavelength range between 460 and 746 nm. The achieved photometric precision of 0.18 parts-per-thousand in the white light curve, at a cadence of 165 s, makes this one of the most precise datasets obtained from the ground. We created 12 chromatic transit light curves that we computed by integrating fluxes in wavelength bins of different sizes, ranging between 3.5 and 20 nm. Although the data are of excellent quality, the wavelength coverage and the precision of the transmission spectrum are not sufficient to neither rule out or to favor classic atmospheric models. Nonetheless, simple statistical analysis favors the clear atmosphere scenario. A larger wavelength coverage or space-based data is required to characterize the constituents of Qatar-1b’s atmosphere and to compare it to the well known HD 189733b. On top of the similarities of the orbital and physical parameters of both exoplanets, from a long Hα photometric follow-up of Qatar-1, presented in this work, we find Qatar-1 to be as active as HD 189733.
Key words: planets and satellites: atmospheres / stars: activity / methods: observational / methods: data analysis / planets and satellites: fundamental parameters
The white light curve, the chromatic light curves, and the airmass, seeing and pixel shifts are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/603/A20
© ESO, 2017
1. Introduction
Planetary transits present a unique opportunity to study the properties of exoplanet atmospheres. During these events, a fraction of the stellar light passes through the optically thin part of the planetary atmosphere, picking up spectral features from it. The technique that reveals the composition and extent of the atmosphere of the planet is called transmission spectroscopy. To date, the chemical composition has been characterized of some systems. Some classic examples are Charbonneau et al. (2002) and Sing et al. (2008), who detected atmospheric sodium in the atmosphere of HD 209458b using the Hubble Space Telescope. This was further confirmed using high resolution ground-based observations by Snellen et al. (2008). From near-infrared observations, Deming et al. (2013) added water to the detected molecules. Redfield et al. (2008) detected sodium in the atmosphere of HD 189733b, while Sing et al. (2011a) found potassium in the X0-2 system. Bean et al. (2010) carried out the first characterization of the transmission spectrum of GJ 1214b from the ground, and Gibson et al. (2013) were pioneers in the characterization of exo-atmospheres by means of multi-object spectrographs. Although models predicted pressure-broadened absorption features of the alkali metals in cloud-free atmospheres, observational data collected at a high speed was evidencing something else: many hot Jupiter spectra were best explained by clouds or hazes in the planetary atmospheres (e.g., Pont et al. 2013; Mallonn & Strassmeier 2016). A complete overview of the exo-atmospheric zoo finally came from Sing et al. (2016), who pinpointed the richness of exo-atmospheric composition in the first comparative analysis of hot Jupiters.
To maximize the chances to detect the exoplanetary atmosphere with current ground-based instrumentation, the transiting systems need to present two distinctive features: a large transit signal to reach the signal-to-noise requirements, and low planetary surface gravity (equivalently, a prominent scale height) to ease the identification of the atmospheric signal (see, e.g., Lecavelier Des Etangs et al. 2008). In the particular case of the observing technique carried out in this work, reference stars of similar brightness as the target are also needed within the field of view. A transiting system offering all these conditions is Qatar-1. Transits in Qatar-1 (V ~ 12.8; Droege et al. 2006) were first reported by Alsubai et al. (2011), who characterized the host star as an old K-type star, with 0.85 M⊙, and 0.82 R⊙. Its hot Jupiter, Qatar-1b, has a radius of 1.16RJ and orbits the star each ~1.42 days with an inclination angle of ~ 84°. This geometry implies nearly grazing transits. For Qatar-1 the transits are ~2% deep, making them easy to detect and follow from the ground. While the parent star is smaller and cooler than the Sun, the climate of Qatar-1b is extremely hot, reaching temperatures close to 1400 K (Covino et al. 2013; Mislis et al. 2015). The proximity between exoplanet and host also means that the upper atmosphere of Qatar-1b is constantly battered by radiation whose strength is directly related to the activity of its host. Atmospheric evaporation is thought to be caused by ultraviolet and X-ray radiation from the parent star. Since Qatar-1 is relatively far away (~200 pc) an X-ray detection and further characterization of the source requires prohibitively large amounts of exposure time. Nonetheless, we and others have characterized the activity of the star (see Covino et al. 2013; Mislis et al. 2015, and Appendix A). We found that the activity levels of Qatar-1 are similar to HD 189733.
In this work, Sect. 2 details the observations and data reduction processes, Sect. 3 describes the analysis carried out over the transit light curves, Sect. 4 shows our results on the transmission spectrum of Qatar-1b, and Sect. 5 gives our discussions and conclusions. We close this work with Appendix A, containing information about the activity of Qatar-1.
2. Observations and data reduction
2.1. Observing log and instrumental setup
On the night of September 2, 2014, we observed one transit of Qatar-1b using the 8.1 m GEMINI North telescope (program Number GN-2014B-Q-47) and the instrument GMOS in multi-object spectroscopy mode. The top panel of Fig. 1 shows a pre-image of the ~7 × 7 arcmin field of view acquired some days before the date of the observations. The rectangles indicate the approximate positions of the slits. From previous photometric follow-ups (von Essen et al. 2013) we had prior information about the similarity of the brightness and spectral type between Qatar-1 and the reference star inside the central box (α = 20:13:41, δ = 65:11:33). Therefore, to maximize our chances of detecting the planetary atmosphere, the rotation angle of the instrument was chosen to center both stars in the field. To minimize flux losses we chose to use wide (15 arcsec) slitlets. The bottom panel of the same figure shows the extracted spectra of Qatar-1 (red), and the six reference stars (black). Our observations comprise 75 science frames, the last 73 acquired using an exposure time of 150 s. Adding to this the readout time, the overall cadence of our data is 165 s. The science frames were acquired between 08:10:32.7 UT and 12:03:50.0 UT, adding up to almost four hours of observing time. From the science frames, 35 were taken during transit and 40 before and after transit. The air mass ranged between 1.43 (corresponding to a stellar altitude of 44°) and 2.06 (29°). To carry out our observations we used a B600_G5303 grating centered at 589 nm, providing a wavelength coverage between 460 and 746 nm for centered stars. Figure 2 shows the environmental and observing conditions. Seeing and spatial shift changes were estimated by fitting a Gaussian profile to a spatial cut of the flux of Qatar-1 around the central wavelength. A 4 (spatial) × 2 (spectral) binning was used, giving a spatial plate scale of 0.29 arcsec/pixel; we estimated the mean seeing to be 0.6 arcsec (~ 2 binned pixels).
 |
Fig. 1 Top: field of view of our observations. Boxes indicate the approximate positions of the slits of our costumed mask. North points upward while east rightward. Both directions are indicated with arrows. The image was acquired using an R filter (r_G0303). The bright object on the very bottom is Qatar-1, which is indicated with a red box. Bottom: extracted instrumental spectra for Qatar-1 and six reference stars. The different wavelength coverage is caused by the uneven distribution of the reference stars at the sky. In both figures, Qatar-1 is indicated in red color. |
2.2. Data reduction
The data were reduced using GEMINI/GMOS IRAF tasks in combination with our own tasks. The steps of the reduction are fully described in Trancho et al. (2007), involving overscan and bias subtraction, flat fielding with Quartz-Halogen flats, and wavelength calibration using a Cu-Ar lamp spectrum. The latter was acquired using a narrow-slit mask producing fine well-resolved arc lines. In consequence, the root mean square of our wavelength solution was well contained within the resolution of the spectra. Cosmic rays were efficiently cleaned using the Laplacian Cosmic Ray Identification routine by P. van Dokkum1 (van Dokkum 2001). We performed the background subtraction by fitting the sky spectrum with a first degree polynomial across the dispersion using predetermined background regions with the IRAF task apall. Extraction of the one-dimensional spectra was interactively carried out using the same task, with apertures equal to 1, 2, 3, 5, 8, 10, and 15 times the night average full width at half maximum (FWHM), determined to be equal to two binned pixels. We ended up with 7 × 7 = 49 one-dimensional spectra for each time stamp, 7 corresponding to the 7 stars within the field of view, and 7 corresponding to the previously mentioned apertures.
3. Model parameters and transit analysis
3.1. Construction of the white light curve
The choice of the most suitable reference stars and the respective aperture was carried out by computing and further analyzing white light curves integrating the stellar fluxes between 498 and 708 nm. This wavelength range was chosen considering three main aspects: the flux of all the stars is defined, the signal of all the stars is relatively large, and atmospheric lines between 720 and 750 nm are circumvented. Extending the wavelength range would not increase the photometric precision of the data because toward smaller wavelengths the signal-to-noise ratio of the spectra decreases significantly because of the low CCD quantum efficiency, and toward larger wavelengths there are strong water and ozone absorption lines, which are expected to change with air mass. Before integrating fluxes, we checked that there were no wavelength shifts within all the spectra by analyzing both target and reference stars. To this end, we fitted Gaussian profiles to the Hα line (~656 nm), the Na doublet (~589 nm), and the most prominent Ca line (~621 nm). As a reference frame we used the one with the lowest air mass, which is coincidentally being the first frame. Averaged differences considering the values obtained from the center of these three lines between this reference frame and the remaining frames do not exceed ±0.03 nm. The computed maximum shift is well contained within one pixel because the natural resolution of the spectra is about 0.1 nm. Since we integrate in wavelength bins significantly larger than this, we left the spectra unshifted. We then produced one light curve per aperture, dividing the flux of Qatar-1 to the unweighted averaged fluxes of the reference stars combined in all possible ways. To each differential light curve we fitted a Mandel & Agol (2002) re-binned transit model (i.e., a transit model computed at a higher cadence but re-binned to our time stamps as introduced by Kipping 2010) with a quadratic limb-darkening law, simultaneously with a detrending model component that accounts for systematics over the light curve (i.e., a linear combination of time-dependent quantities such as air mass, pixel shifts, and seeing; for more details see Sect. 3.3). To minimize computing time, the choice of reference stars and aperture was carried out minimizing the standard deviation of the residual light curves which, in turn, were obtained fitting Mandel & Agol (2002) transit model times by detrending models to the data with a least-squares fit. The best reference light curve was obtained by combining stars 3, 4 and 5, counting from bottom to top (Fig. 1), and the corresponding best aperture was estimated to be 2 ×FWHM.
 |
Fig. 2 From top to bottom: air mass, seeing and spatial shift in binned pixels during observations of Qatar-1 as a function of the hours from mid-transit time. In the last two cases their mean value was subtracted to represent the variability as a function of time. The plot sizes were adjusted to display the same pixel scale. |
3.2. Determination of spectrophotometric errors
Once the most suitable reference stars were selected we computed the individual spectrophotometric errors using the formalism provided by IRAF’s photometric errors, i.e.,  (1)where Q1 and RS are the errors for Qatar-1 and the reference stars, respectively. The parameter F is the integrated flux inside the wavelength band and aperture, A the area inside the chosen band and aperture, σ the standard deviation of the sky region, N the number of sky pixels, and g the gain of the detector. The subindex i corresponds to each one of the 73 observations. It is known that errors produced in this fashion follow a photon-noise-only distribution. As a consequence, the photometric errors are underestimated (Gopal-Krishna et al. 1995). Therefore, to produce more realistic errors we scaled them up to meet the standard deviation of the residual light curve previously computed. The calculation of spectrophotometric errors in this way has two advantages: their averaged magnitudes reflect the scatter of the data and they follow the air mass trend, increasing in magnitude when air mass increases as well.
(1)where Q1 and RS are the errors for Qatar-1 and the reference stars, respectively. The parameter F is the integrated flux inside the wavelength band and aperture, A the area inside the chosen band and aperture, σ the standard deviation of the sky region, N the number of sky pixels, and g the gain of the detector. The subindex i corresponds to each one of the 73 observations. It is known that errors produced in this fashion follow a photon-noise-only distribution. As a consequence, the photometric errors are underestimated (Gopal-Krishna et al. 1995). Therefore, to produce more realistic errors we scaled them up to meet the standard deviation of the residual light curve previously computed. The calculation of spectrophotometric errors in this way has two advantages: their averaged magnitudes reflect the scatter of the data and they follow the air mass trend, increasing in magnitude when air mass increases as well.
3.3. Choice of detrending model
As shown in Fig. 2, for each time stamp we measured the air mass, the seeing, and the spatial shifts. Thus, we considered these quantities while building up the detrending model. To quantify how much these values correlate with the data, we made use of the Pearson correlation coefficient, rxy. We began subtracting a transit model to the white light curve, fixing the parameters to those computed by Mislis et al. (2015). Then, we calculated the rxy between these residuals and the air mass, giving rxy = 0.96. A similar exercise was carried out between the residuals and the seeing and the spatial shift, where in both cases rxy = 0.68. However, both quantities also vary with air mass, as a result influencing the rxy. Once the air mass trend was subtracted from these two, the new computed rxy were of 0.11 for the seeing and 0.05 for the spatial shift, corresponding to an almost null correlation.
Furthermore, we observed a time-dependent sinusoidal modulation, which can easily be seen by visual inspection of the raw white light curve. We believe this variability is not related to what Stevenson et al. (2014) nor Lendl et al. (2016) found, in which case the systematics correlated with the Cassegrain rotator position angle (CRPA) and the parallactic angle (PA) of the stars. As performed by the authors, we extracted the CRPA from the header of our images, computed the PAs, and found that the frequency at which the cosinus of these quantities changes is too low (of about a factor of 4) to represent the data. This variability also does not agree with what Sing et al. (2012) identified as slit losses, because it does not correlate with seeing. We further investigated this with GEMINI/GMOS staff, and although they are aware of this effect, they do not fully understand its origin (private communication, GEMINI Helpdesk). Therefore, since we cannot identify the source of our systematics, to define a proper detrending model and identify which combination of parameters provides the best representation of the data we made use of the Bayesian information criterion, BIC = χ2 + k ln(N), which penalizes the number k of model parameters (MP) given N = 73 data points, the reduced chi-squared statistic, 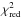 , and the standard deviation of the residual light curves, σres. Taking into consideration the environmental and instrumental variability we can measure, plus the sinusoidal time-dependent variability observed by visually inspecting the white light curve, as detrending model we considered the following eight cases:
, and the standard deviation of the residual light curves, σres. Taking into consideration the environmental and instrumental variability we can measure, plus the sinusoidal time-dependent variability observed by visually inspecting the white light curve, as detrending model we considered the following eight cases:
- 1.
- 2.
- 3.
- 4.
- 5.
A linear combination AM, plus one time-dependent sinusoidal function (SIN) with an amplitude A, a frequency ν, and a phase φ.
![\begin{equation} f_5(t) = a_0 + a_1 \text{AM}(t) + A_1 \sin[2\piup(t\nu_1 + \phi_1)].\, \label{eq:detrending5} \end{equation}](/articles/aa/full_html/2017/07/aa30506-17/aa30506-17-eq34.png) (6)
(6) - 6.
- 7.
- 8.
A linear combination between AM, SS and SG, plus one SIN.
![\begin{eqnarray} \begin{split} f_8(t) = a_0 + a_1 \text{AM}(t) + a_2 \text{SS}(t) + a_3 \text{SG}(t) \\ + A_1 \sin[2\piup(t\nu_1 + \phi_1)]. \end{split} \end{eqnarray}](/articles/aa/full_html/2017/07/aa30506-17/aa30506-17-eq37.png) (9)
(9)
Statistics (BIC, 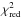 and σres) per detrending model.
and σres) per detrending model.
To begin with, the addition of the sinusoidal variability, between detrending models 5 to 8 compared to models 1 to 4, provide a significant reduction in all the statistics. This shows the relevance of its consideration. Furthermore, focusing on models 5 to 8 we evidence what we found from their respective rxy. Their statistics show again that the correlation between the data and the environmental and instrumental quantities is not strong. Overall, the model does not significantly improve results when compared to the simplest one of these four, which is just the consideration of air mass. Since the consideration of detrending function 5 (air mass) and 7 (air mass and spatial shift) provide the best representation of the data from a statistical point of view, from now on these two cases are always considered. This also gives us the chance to investigate to which extent the choice of a detrending model influences our results. Although the statistics were minimized using f7(t), the variability of the spatial shift is well contained within the fraction of a pixel and thus should not impact our results; the same goes for the variability of seeing, which is well contained within the fraction of an arcsecond.
3.4. Transit fitting
Once the white light curve was fully constructed (time stamps converted from Julian dates to Barycentric Julian Dates, BJDTDB, using the tools made available by Eastman et al. (2010), flux and spectrophotometric errors), and the detrending model components were determined (functions 5 and 7), we carried out a Markov-chain Monte Carlo (MCMC) fitting approach to determine the expectation values of the orbital and physical parameters of Qatar-1b. In this work all our MCMC calculations make use of PyAstronomy2, a collection of Python routines providing fitting and sampling algorithms implemented in the PyMC (Patil et al. 2010) and SciPy (Jones et al. 2001) packages.
Our best-fit orbital parameters for the white light curve, along with 1σ errors compared to our previous work.
For the transit we used a Mandel & Agol (2002) transit model with quadratic limb-darkening law, 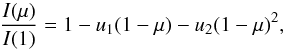 (10)re-binned to meet the cadence of our data (for motivation on the matter, see Kipping 2010). For our custom-model wavelength-dependent light curves we produced our own limb-darkening coefficients, u1 and u2. To properly account for any wavelength-dependent variability introduced by all the optical components between the source and the CCD, which could in turn affect the derived limb-darkening values, rather than considering the laboratory quantum efficiency of the CCD and the transmission of the grating we used the envelope shape of the observed spectra directly. Since this shape also includes the continuum emission of Qatar-1 we first subtracted a blackbody with parameters matching those of Qatar-1. To account for the intensity variation of the stellar source we used angle-resolved PHOENIX spectra (Hauschildt & Baron 1999; Witte et al. 2009) for a star of Teff = 4900 K, log g = 4.5 and [Fe/H] = 0.0, best matching the stellar parameters of Qatar-1 (Covino et al. 2013). The PHOENIX spectra were downloaded from the PHOENIX library3 (Husser et al. 2013). The limb-darkening coefficients were obtained fitting the quadratic law to the PHOENIX intensities, previously convolved with the shape of the observed spectra, and a box function defined as unity between the minimum and maximum considered wavelength values, and zero elsewhere. To determine the limb-darkening coefficients during the fitting procedure we neglected the data points between μ = 0 and μ = 0.1, as performed by Claret (2004). The derived limb-darkening values can be found under the third and fourth column of Table 2. A word of caution: limb-darkening values are given throughout this work with four decimals of precision. This is obtained after fitting the stellar intensities with a limb-darkening law. Therefore, this does not include errors contributed by PHOENIX spectra (errors are not computed, and therefore the impact is unknown), nor by the intrinsic errors in the stellar parameters (impact estimated to be on the third decimal). Limb-darkening values also strongly depend on the specific intensity spectra used (Csizmadia et al. 2013). Therefore, we caution against considering any values after the second decimal.
(10)re-binned to meet the cadence of our data (for motivation on the matter, see Kipping 2010). For our custom-model wavelength-dependent light curves we produced our own limb-darkening coefficients, u1 and u2. To properly account for any wavelength-dependent variability introduced by all the optical components between the source and the CCD, which could in turn affect the derived limb-darkening values, rather than considering the laboratory quantum efficiency of the CCD and the transmission of the grating we used the envelope shape of the observed spectra directly. Since this shape also includes the continuum emission of Qatar-1 we first subtracted a blackbody with parameters matching those of Qatar-1. To account for the intensity variation of the stellar source we used angle-resolved PHOENIX spectra (Hauschildt & Baron 1999; Witte et al. 2009) for a star of Teff = 4900 K, log g = 4.5 and [Fe/H] = 0.0, best matching the stellar parameters of Qatar-1 (Covino et al. 2013). The PHOENIX spectra were downloaded from the PHOENIX library3 (Husser et al. 2013). The limb-darkening coefficients were obtained fitting the quadratic law to the PHOENIX intensities, previously convolved with the shape of the observed spectra, and a box function defined as unity between the minimum and maximum considered wavelength values, and zero elsewhere. To determine the limb-darkening coefficients during the fitting procedure we neglected the data points between μ = 0 and μ = 0.1, as performed by Claret (2004). The derived limb-darkening values can be found under the third and fourth column of Table 2. A word of caution: limb-darkening values are given throughout this work with four decimals of precision. This is obtained after fitting the stellar intensities with a limb-darkening law. Therefore, this does not include errors contributed by PHOENIX spectra (errors are not computed, and therefore the impact is unknown), nor by the intrinsic errors in the stellar parameters (impact estimated to be on the third decimal). Limb-darkening values also strongly depend on the specific intensity spectra used (Csizmadia et al. 2013). Therefore, we caution against considering any values after the second decimal.
Beside the quadratic limb-darkening law we also computed non-linear limb-darkening coefficients but found no significant difference in the residual light curve after the transit fitting was performed. We also fitted the linear limb-darkening coefficient of the quadratic law to the data, fixing the quadratic coefficient to the value computed from PHOENIX intensities. Also, we fitted both limb darkening coefficients. In all cases we found no significant difference in the residuals. Since all four scenarios gave fully consistent results, we finally chose to use the simplest approach. In addition, as Müller et al. (2013) pointed out, in the case of a nearly grazing transit the planet does not cross the center of the star. Therefore, the transit light curve does not contain sufficient information concerning the limb-to-center brightness variation to fit for the limb-darkening coefficients. Hence, throughout this work we fix the coefficients to theoretical values. For the majority of exoplanet host stars the empirical limb-darkening coefficients derived from transit light curves match their theoretical counterparts reasonably well (Müller et al. 2013). However, this approach might introduce systematics in the transmission spectrum, as shown already by the significant discrepancy between fitted and theoretical limb-darkening coefficients observed by Claret (2009; HD 209458) and Mallonn et al. (2016; HAT-P-32).
For the transit model the fitting parameters are the semi-major axis scaled by the stellar radius, a/RS, the orbital inclination measured with respect to the plane of the sky, i, the mid-transit time, T0, and the planet-to-star radii ratio, RP/RS. The first three parameters are wavelength independent. The quadratic limb-darkening coefficients, u1 and u2, were considered fixed, and are considered fixed throughout this work. Since we count with one transit, the orbital period was considered as fixed to the value determined by Mislis et al. (2015). Simultaneously to the transit model we implemented the two detrending models given by f5(t) and f7(t), which are fully described in Eqs. (6) and (8).
 |
Fig. 3 White light curve of Qatar-1b. From top to bottom, the left panel of the figure shows the raw light curve in red. The air-mass model is overplotted in dashed lines. Artificially shifted below, the white light curve after subtracting the air-mass model is indicated in blue and the best-fit transit model is shown in a black continuous line. Finally, the residuals are shown in green. Error bars in all figures were enlarged to meet the standard deviation of the residuals. The right panel of the figure shows the raw white light curve in red points, along with the best-fit transit and detrending models in black dashed line for f5(t). The pink light curve corresponds to the raw data when the best-fit air-mass component has been subtracted, along with the sinusoidal time-dependent variability overplotted in a black thin continuous line. Blue points correspond to a fully detrended transit light curve; the best-fit transit model is overplotted in a black thick line. Below in green, the residual light curve obtained subtracting the best-fit transit model to the blue points (equivalently, subtracting the dashed line to the red points) can be seen. Everything has been artificially shifted. |
The fitting procedure was carried out in two stages. As starting values for the fitting parameters we used those listed in Mislis et al. (2015) for the transit model, and our custom limb-darkening coefficients. We chose conservative uniform priors for all the parameters. First, we iterated 1.5 × 106 and burned the initial 50 000 samples. Then, analyzing the posterior distributions, from their mean and standard deviations we found the expectation values of the orbital parameters and corresponding errors, respectively. Thus, throughout this work, errors on the parameters are at 1σ level. Using these values we computed a best-fit model and the residuals by simply subtracting the data to the best-fit model.
3.5. Correlated noise treatment
To quantify to which extent the residual light curve is affected by correlated noise, we followed a similar approach as described in Gillon et al. (2006), Winn et al. (2008), and Carter & Winn (2009). We started dividing the residual light curve into M bins of 15 min each, which corresponds to the approximate duration of ingress/egress. Then, we calculated the mean value of data points per bin, N. If the data are affected by correlated noise, the sample standard deviation of the binned data, σN, differ by a factor βN from its theoretical expectation (see, e.g., von Essen et al. 2013, for a more extended description). For data sets free of correlated noise, βN = 1 is expected. The consideration of f5(t) and f7(t) resulted in no measurable correlated noise. If βN had been different from 1, we would continue by enlarging the spectrophotometric errors by βN, and by carrying out the transit fitting procedure all over again. For the white light curve the amount of correlated noise was negligible and, in consequence, this step was not necessary.
3.6. Transit parameters from the white light curve
The best-fit transit parameters of Qatar-1b are summarized in Table 2 for both detrending models. The white light curves obtained considering f1(t) and f5(t), along with the model components, are plotted in Fig. 3 to stress the relevance of adding the sinusoidal term. The standard deviation of the residual white light curve is of 0.18 parts per thousand (ppt), one of the most precise ground-based white light curves ever observed.
3.7. Considerations on limb-darkening treatment
In order to test if there is an impact on the transit parameters caused by fixing the limb-darkening coefficients we repeated the exercise described here but added the linear limb-darkening coefficient as the fitting parameter, and in a further step both linear and quadratic coefficients. We found that the best-fit transit parameters are fully consistent with those shown in Table 2 when errors at 1σ level are computed. This is in good agreement with Espinoza & Jordán (2015). In this work, the authors found no significant difference in the planet-to-star radii ratio nor in the semi-major axis around 4900 Kelvin (Qatar-1’s effective temperature) when limb-darkening coefficients were either fixed or fitted (see their Fig. 10). A comparison of the transit parameters derived in this work to values published in the literature is given in Table 2. This comparison shows an unusual large discrepancy of the transit parameters among different studies. This might be caused by the different treatment of the limb-darkening coefficients, as, for example, the Covino et al. (2013) fits for the linear limb-darkening coefficients while they are fixed to theoretical values in this work. As mentioned before, the fitting of the limb-darkening coefficients for nearly-grazing planets leads to erroneous parameters. Differences in the calculation of theoretical values can cause systematic differences in the limb-darkening coefficients, too, translating into differences in the transit parameters. A homogeneous study of all transit data is beyond the scope of this work.
Values derived analyzing chromatic light curves while considering the detrending model f5(t).
4. Analysis and results
4.1. Construction of the wavelength-dependent light curves
Rather than dividing the full wavelength range in equally sized bins, we estimated the amount and extension of the wavelength channels following a quality criteria. Assuming that the probed atmosphere of the exoplanet has a maximum variability of 3 scale heights within our wavelength range (Fortney et al. 2010), considering a nominal value of RP/RS = 0.1522, and an average temperature of 1400 K (Covino et al. 2013), this would be translated into a maximum variability of RP/RS of about 1.4 ppt. If our goal is to achieve a 2σ detection, the error bars on RP/RS should be as large as 0.5 ppt. To choose the number of wavelength channels taking this into consideration we carried out the following exercise: using exactly the same time stamps as our measurements, and using as the best-fit values of the white light curve and the f5(t) detrending model as input parameters, we simulated light curves with a given amount of white noise. The first standard deviation considered in this exercise was that given by the standard deviation of the white light curve, 0.18 ppt, and 2, 4, 6, 8, and 10 times this value. To make this exercise as realistic as possible, rather than considering constant values for the error bars, we used the real errors of the white light curve but enlarged these errors to meet the noise level of the synthetic data. Then, following the approach described in Sect. 3.4, we fitted the orbital parameters a/RS, i, T0 and RP/RS. To accomplish this, we used Gaussian priors for the first three parameters, since we know them quite precisely from the white light curve analysis and they are wavelength independent, and a uniform prior distribution for RP/RS. After 105 iterations and a discard of the first 25%, we computed as usual 1σ errors on RP/RS. Our simulations show that the standard deviation that would limit our required precision is about 0.5 ppt. Since these light curves only have Gaussian noise, we consider the derived precision as an upper limit. In consequence, we defined the bin number and wavelength region so that the standard deviation of each light curve is ~0.5 ppt or lower, which leads to the 12 wavelength bins presented in this work. While following this approach we checked that the choice of wavelength channels and this integration scheme does not make a wavelength bin fall right in the middle of a Fraunhofer line, which might cause variability extrinsic to the planetary atmosphere. The first column of Table 3 shows the wavelength range for each one of the 12 wavelength bins, while the second column of the same Table indicates the bin size, both in nm. The total wavelength range was reduced forward, starting from 510 nm and ending in 708 nm, rather than the original 498–708 nm range. This was chosen to minimize correlated noise in the bluest light curve.
 |
Fig. 4 Transmission spectrum of Qatar-1b. Black circles and horizontal error bars show the derived RP/RS’s and their uncertainties. Horizontal lines are not error bars but indicate the size of the wavelength bin. Green, red and blue continuous lines correspond to Fortney et al. (2010) models for exo-atmospheres investigated in this work. Filled diamonds, squares and triangles indicate averages of the models within each wavelength bin. The models were artificially shifted to meet the data. |
 |
Fig. 5 Our 12 chromatic and detrended primary transit light curves shown in the left panel along with their respective best-fitting transit models in black continuous lines. The right panel shows the residual light curves obtained by subtracting the best-fit models (transit times detrending) to the raw data. All light curves were artificially shifted to fit the plot. |
4.2. Analysis of the chromatic light curves
Once the wavelength bins were defined, to derive the transmission spectrum of Qatar-1b we carried out a similar approach to the white light curve analysis regarding the calculation of the spectrophotometric errors, the βN factors, limb-darkening coefficients, and detrending functions, and we used the same choice of reference stars and aperture as determined in Sect. 3.1. In all cases, RP/RS were fitted with a uniform probability density function, while a/RS, i and T0 had Gaussian probability density functions with mean and standard deviation equal to the best-fit and error values obtained from the white light curve, respectively. While the RP/RS were fitted to each light curve individually, a/RS, i and T0 were fitted simultaneously to all the chromatic light curves. In other words, these three transit parameters best-fit all the light curves simultaneously. In some works, at this stage the wavelength-independent parameters are fixed. However, since it is our intention to compute reliable error bars for RP/RS, we fully used the information obtained from the white light curve and properly propagated their errors into the computation of the wavelength-dependent RP/RS’s.
With respect to the detrending coefficients, a0 and a1 for the air-mass component, and A1, ν1 and φ1 for the sinusoidal component, we tried several fitting procedures. First, we considered one set of independent detrending parameters per chromatic light curve. In this case the detrending parameters were 5 × 12 = 60. Visually inspecting our resulting light curves we found that, when placing them all together, the air mass component was the same for all the chromatic light curves. We believe this is because the colors of the brightest reference star and Qatar-1 are similar (von Essen et al. 2013) and, thus, color differences produced from the wavelength-dependent absorption of stellar light produced in our atmosphere are minimized. This similarity was not observed when the sinusoidal component of the detrending model was inspected. We fitted one a0 and one a1 simultaneously to all the light curves to reduce the parameter space in a sensible way and minimize the impact they might have over the retrieved transmission spectrum. Following Gibson et al. (2013) and Lendl et al. (2016), we also tried to subtract the common noise to all the light curves, but we found that this is not sufficient since there appears to be a wavelength dependency with the sinusoidal component of the model. When visually inspecting the residual light curves we noted that this approach was insufficient for the bluest light curve, which is where the atmosphere plays a larger role. Therefore, for this light curve we fitted a set of (a0, a1) individually, while we fitted another equivalent set of parameters to the remaining data simultaneously. As previously mentioned, all these trial exercises were carried out considering the two detrending functions f5(t) and f7(t), without influencing on the results. In this section we limit ourselves to show parameters derived from f5(t).
Table 3 summarizes our results, listing the wavelength bins and sizes, computed limb-darkening coefficients, derived RP/RS values along with 1σ errors, fitting parameters, βN values, and standard deviation of the residuals. Figure 5 shows the 12 detrended transit light curves on the left panel, their respective best-fit transit model in continuous black line, and the residual light curves for the different wavelength channels on the right panel. Each light curve has been artificially shifted to allow for visual inspection.
4.3. Transmission spectrum of Qatar-1b
Figure 4 shows the transmission spectrum of Qatar-1b obtained following the steps detailed in the previous section. When we used the detrending function f5(t), along with theoretical models. f7(t) gave fully consistent results. We compared our transmission spectrum to several theoretical models (Fortney et al. 2010) that were computed for an atmospheric temperature of 1500 K and surface gravity of 25 m/s2, and we scaled them to the planetary parameters of Qatar-1b. In the figure, continuous lines show the original models. The models were averaged within the same wavelength channels as the observed transmission spectrum of Qatar-1b. Regarding the figure, the only fitted parameter is a vertical offset necessary to match observations to models. The first model is a solar-composition model with TiO artificially removed (green triangles and dashed line). The second model is a solar composition model without TiO, which has a Rayleigh scattering component with a cross section a thousand times that of H2 (red squares and dashed line). The third model includes a gray absorber that cuts all features above a certain pressure resulting in a nearly flat spectrum (blue diamonds and dashed line). The fourth model has as main absorber TiO. Since this last model provides the poorest representation of the observed transmission spectrum and has too many features that block the rest, we did not add it into the figure. To assess which model best represents the data, we computed 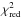 and its respective P value for each model, considering 12–1 deg of freedom. The significance level is chosen to be 5%. Both statistics are summarized in Table 4.
and its respective P value for each model, considering 12–1 deg of freedom. The significance level is chosen to be 5%. Both statistics are summarized in Table 4.
Computed statistics for the atmospheric models tested in this work.
As in the figure, the computed 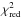 , and the P value show that the hazy and clear atmosphere models are in agreement with our data, and the flat and TiO dominant models are disfavored. Although this is not common in hot Jupiter atmospheres (Sing et al. 2016), our statistical (and very simple) analysis favors the clear atmosphere. Therefore, we caution against reaching any conclusion about the composition of the atmosphere of Qatar-1b from this data alone. We unfortunately lack the precision necessary to make a comparative study between the atmospheres of Qatar-1b and HD 189733b. More extensive wavelength coverage and space-based data are required.
, and the P value show that the hazy and clear atmosphere models are in agreement with our data, and the flat and TiO dominant models are disfavored. Although this is not common in hot Jupiter atmospheres (Sing et al. 2016), our statistical (and very simple) analysis favors the clear atmosphere. Therefore, we caution against reaching any conclusion about the composition of the atmosphere of Qatar-1b from this data alone. We unfortunately lack the precision necessary to make a comparative study between the atmospheres of Qatar-1b and HD 189733b. More extensive wavelength coverage and space-based data are required.
5. Discussion and conclusions
In this work we report GEMINI-N/GMOS spectroscopic observations carried out during one transit of Qatar-1b covering the wavelength range between 460 and 746 nm. Our main goal was to study the transmission spectrum of Qatar-1b and compare it to the well-known HD 189733b. The observations were motivated by the compatibilities in the orbital and physical parameters of both systems. It was our intention to analyze the possibility of exoplanet atmospheres to be dominated by their environments, which could be answered with follow-ups in similar systems, such as the two mentioned here.
The data collected and investigated in this work allowed us to refine the transit parameters. We derived an optical transmission spectrum of the planet that included the sodium line by creating 12 chromatic light curves. The transmission spectrum of Qatar-1b was extracted via wavelength channels whose width varied between 3.5 and 20 nm, which were chosen to minimize the standard deviation of the individual light curves and to circumvent the Fraunhofer lines. Owing to the nearly grazing orbit of Qatar-1b, during our data analysis we did not fit the limb-darkening coefficients. We customized our own limb-darkening values by convolving PHOENIX angle-resolved intensities with the transmission of the full optical setup, to have maximum control over the limb-darkening related systematics.
The observations took place around BJD~2 456 903. From the ephemeris found by our Hα photometric follow-up (see next Appendix and Fig. A.1) the transit observed here took place close to a maximum of flux which, in turn, corresponds to a minimum in spot coverage (this was cross-matched to the spot modulation observed by Mislis et al. 2015). Alsubai et al. (2011) did not find any spot crossing events in their survey photometry, nor did Mislis et al. (2015) in their high-precision photometric follow-up. The authors suggested that the planet could be crossing latitudes of the star showing low spot activity. In an attempt to better characterize the system, we carried out a photometric follow-up of the host star in Hα using the 1.2 m telescope located in Hamburg, Germany. We see clear evidence of activity correlated with what we estimated to be the rotational period of the star. From further spectroscopic observations we confirmed Qatar-1 to be a moderately active star, in agreement with Covino et al. (2013) and Mislis et al. (2015). In this context, modifications in the depth of transit light curves due to spots can occur. To quantify the amplitude of this effect, Sing et al. (2011b) have already characterized that a decrease of 1% in the stellar flux (slightly larger than the Hα variability reported here) would increase the transit depth by about 1% (their Fig. 10). This would be translated into a maximum uncertainty in the radius ratio of 0.0002. However, as calculated by, for example, Mallonn et al. (2015) for the similar host star HAT-P-19, the chromatic effect on the transmission spectrum is about an order of magnitude lower. We conclude that unocculted star spots do not significantly modify the transmission spectrum derived in this work.
After a careful analysis of our chromatic light curves, we find that the wavelength coverage and the precision of the transmission spectrum is not sufficient to either rule out or strongly favor classic atmospheric models. The simple statistical analysis carried out in this work seems to favor the clear atmosphere scenario. However, we caution against reaching any conclusions from our data alone. A larger wavelength coverage and space-based data would be required to characterize the constituents of the atmosphere of Qatar-1b.
Acknowledgments
C. von Essen acknowledges funding for the Stellar Astrophysics Centre, provided by The Danish National Research Foundation (Grant DNRF106). A special acknowledge to GEMINI Helpdesk, for replying so quickly and diligently. S. Cellone acknowledges funding from UNLP through grant 11/G127, and thanks the Stellar Astrophysics Centre (Aarhus, Denmark) for its hospitality. We acknowledge the referee for her/his positive feedback.
References
- Allen, C. W. 1973, Astrophysical quantities, 3re edn. (London: University of London) [Google Scholar]
- Alsubai, K. A., Parley, N. R., Bramich, D. M., et al. 2011, MNRAS, 417, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Miller-Ricci Kempton, E., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carter, J. A., & Winn, J. N. 2009, ApJ, 704, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2009, A&A, 506, 1335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csizmadia, S., Pasternacki, T., Dreyer, C., et al. 2013, A&A, 549, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Wilkins, A., McCullough, P., et al. 2013, ApJ, 774, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Droege, T. F., Richmond, M. W., Sallman, M. P., & Creager, R. P. 2006, PASP, 118, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Shabram, M., Showman, A. P., et al. 2010, ApJ, 709, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Barstow, J. K., et al. 2013, MNRAS, 436, 2974 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gopal-Krishna, Sagar, R., & Wiita, P. J. 1995, MNRAS, 274, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., & Miller, J. R. 1989, AJ, 97, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, http://www.scipy.org [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lendl, M., Delrez, L., Gillon, M., et al. 2016, A&A, 587, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mallonn, M., & Strassmeier, K. G. 2016, A&A, 590, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallonn, M., von Essen, C., Weingrill, J., et al. 2015, A&A, 580, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallonn, M., Bernt, I., Herrero, E., et al. 2016, MNRAS, 463, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mislis, D., Mancini, L., Tregloan-Reed, J., et al. 2015, MNRAS, 448, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Mittag, M., Hempelmann, A., González-Pérez, J. N., & Schmitt, J. H. M. M. 2010, Adv. Astron., 101502 [Google Scholar]
- Mittag, M., Hempelmann, A., González-Pérez, J. N., Schmitt, J. H. M. M., & Hall, J. C. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 1187 [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. J. 2010, J. Statistical Software, 35, 1 [NASA ADS] [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., Endl, M., Cochran, W. D., & Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Désert, J.-M., Fortney, J. J., et al. 2011a, A&A, 527, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., Pont, F., Aigrain, S., et al. 2011b, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Huitson, C. M., Lopez-Morales, M., et al. 2012, MNRAS, 426, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Fortney, J. J., Nikolov, N., et al. 2016, Nature, 529, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, K. B., Bean, J. L., Seifahrt, A., et al. 2014, AJ, 147, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Trancho, G., Bastian, N., Miller, B. W., & Schweizer, F. 2007, ApJ, 664, 284 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- von Essen, C., Schröter, S., Agol, E., & Schmitt, J. H. M. M. 2013, A&A, 555, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Johnson, J. A., Narita, N., et al. 2008, ApJ, 682, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Stellar activity
Appendix A.1: Hα photometric follow-up
The Hα chromospheric emission is known to be one of the primary indicators of activity and magnetic heating in low-mass stars (see, e.g., Cincunegui et al. 2007, for a characterization of activity indicators for spectral types from F to M). Therefore, to characterize the activity level of Qatar-1, we followed up Qatar-1 photometrically during two months using the 1.2 m Oskar Lühning Telescope (OLT) located at Hamburger Sternwarte in Hα light.
For each one of the observing nights obtained with the OLT, we calculated the mean and the dispersion of the data and considered these as representative values for the flux and the intra-night scatter. These values are shown in Fig. A.1, where differential magnitudes are plotted as a function of time. On the bottom of the figure, plotted in green is the control differential light curve, which has been artificially shifted. Plotted in red circles, on top, is the differential light curve of Qatar-1. The scatter of the two overall light curves satisfies σQatar−1 ~ 3σControl, indicating that the variability of Qatar-1 may be inherent. The horizontal dashed lines in Fig. A.1 indicates a band of 2σControl width around the mean.
 |
Fig. A.1 Hα photometric follow-up of Qatar-1. The differential light curve for Qatar-1 is indicated on the top in red circles, while the control light curve is indicated on the bottom in green squares. Horizontal lines show ± 1σ the scatter of the control light curve. The blue and pink lines show the best-fit sinusoidal to the data. The vertical dashed line shows the position at which we also acquired spectral information on Qatar-1. |
We noticed two points, indicated as black dots, which appear to be outside the data distribution. One can address this increase in the flux due to activity on the surface of the star or a color-dependent atmospheric effect. However, we can not ensure the truthfulness of the data points beyond the stability of the control light curve.
We applied a Lomb-Scargle periodogram (Lomb 1976; Scargle 1982; Zechmeister & Kürster 2009) to search for any periodicity contained in Qatar-1 light curve and to the control light curve for a sanity check. In the first case, we found a significant peak at νQ1 = 0.033 ± 0.005 c/d (PQ1 = 30 ± 7 days). The error for the frequency corresponds to the dispersion σGauss of a Gaussian function, which was fitted to the leading peak. The false-alarm probability (FAP) of the maximum power is 0.002%. Covino et al. (2013) confirmed the star to be a slow rotator (vsin(i) = 1.7 ± 0.3 km s-1). Assuming the reported vsin(i) to be the speed at the stellar equator, and considering the stellar radius estimated by Alsubai et al. (2011) (RS = 0.823 ± 0.025 R⊙), the observed velocity would translate into a rotational period of ~25 ± 5 days. Within errors, both periods seem to be consistent. We interpret νQ1 to be the rotational period of the star, which is in good agreement with that reported by Mislis et al. (2015).
Once we determined the periodicity within the data, we fitted a sinusoidal variation to Qatar-1 data in the form, 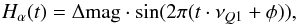 (A.1)where Δmag is the magnitude variation, φ the phase, and νQ1 considered as fixed in the value already mentioned. After fitting the complete data set first, and the data set without the points outside the distribution, we found that changes in the fitted amplitudes are contained within the precision of the data (blue and pink continuous lines, Fig. A.1). Therefore, we estimated the photometric Hα variability as Δmag = 0.009 ± 0.001. According to Pogson’s law (Allen 1973), this equates to a flux variation of ~0.8%.
(A.1)where Δmag is the magnitude variation, φ the phase, and νQ1 considered as fixed in the value already mentioned. After fitting the complete data set first, and the data set without the points outside the distribution, we found that changes in the fitted amplitudes are contained within the precision of the data (blue and pink continuous lines, Fig. A.1). Therefore, we estimated the photometric Hα variability as Δmag = 0.009 ± 0.001. According to Pogson’s law (Allen 1973), this equates to a flux variation of ~0.8%.
Appendix A.2: Stellar activity and age
Adopting our estimated rotational period for Qatar-1, PQ1 = 30 ± 7 days, we can estimate the gyrochronological age, tgyro, using the relation given by Barnes (2007), Eq. (3). Considering a Teff of 4910 K (Covino et al. 2013), the corresponding color index is (B−V) = 0.9. We obtain tgyro = 2.7 ± 1 Gyr.
Appendix A.3: The Hα equivalent width as activity indicator
We observed Qatar-1 spectroscopically using the Hamburg Robotic Telescope (HRT4) located at La Luz observatory, in Guanajuato, Mexico (Mittag et al. 2011). The telescope has a primary mirror of 1.2 m and a fibre-fed Echelle spectrograph. The spectral distribution is divided in a blue and a red channel, covering the wavelength range between ~380 to ~880 nm. The spectral resolution is estimated to be R ~ 20 000 in the blue channel.
Since Qatar-1 is intrinsically faint, we obtained 3 spectra of 30 min each to minimize the unwanted effects of cosmic ray hits. After the calibration was automatically produced (Mittag et al. 2010), we combined the three spectra to increase the signal-to-noise ratio (S/N). We estimated the final S/N of the combined spectra to be ~40. The date at which the HRT spectra was acquired is indicated in Fig. A.1 with a dashed vertical line.
Herbst & Miller (1989) carried out a detail study on the equivalent width (EW) of K- and M-type stars. These authors attempted to characterize the activity level of the stars by producing a main sequence of EW as a function of its color, representing the boundary between active and low active stars relating two observables that are trivial to obtain, i.e., 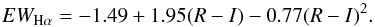 (A.2)The empirical relation is only valid for R−I> 0.4. The spectral type of Qatar-1 has been identified as K2V (Alsubai et al. 2011; Covino et al. 2013). However, the reported color information by Droege et al. (2006) (V = 12.84± 0.14 mag, I = 11.71± 0.08) is consistent with spectral types K0 to K5. Following the Calibration of MK spectral types (Allen 1973), K0 corresponds to R−I = 0.42, K2 to R−I = 0.48, and K5 to R−I = 0.63. Replacing these values into Eq. (A.2) yields EWHα = −0.806, EWHα = −0.731, and EWHα = −0.567, respectively. Using the HRT spectra we calculated the EW of the Hα line in the usual way, finding EWHα,HRT = −0.764 ± 0.064. Figure A.2 shows the EW–color index diagram of the work of Herbst & Miller (1989; their Fig. 4, black points), along with the estimation of the EW of Qatar-1 (red points) and the calculated EWHα values and their uncertainties (green rectangle). The derived quantities place Qatar-1 in the middle of the distribution of the points of Herbst & Miller (1989). In other words, Qatar-1 falls over the boundary that divides active from non-active stars. This is in agreement with the previously reported moderate activity levels by Covino et al. (2013) and Mislis et al. (2015).
(A.2)The empirical relation is only valid for R−I> 0.4. The spectral type of Qatar-1 has been identified as K2V (Alsubai et al. 2011; Covino et al. 2013). However, the reported color information by Droege et al. (2006) (V = 12.84± 0.14 mag, I = 11.71± 0.08) is consistent with spectral types K0 to K5. Following the Calibration of MK spectral types (Allen 1973), K0 corresponds to R−I = 0.42, K2 to R−I = 0.48, and K5 to R−I = 0.63. Replacing these values into Eq. (A.2) yields EWHα = −0.806, EWHα = −0.731, and EWHα = −0.567, respectively. Using the HRT spectra we calculated the EW of the Hα line in the usual way, finding EWHα,HRT = −0.764 ± 0.064. Figure A.2 shows the EW–color index diagram of the work of Herbst & Miller (1989; their Fig. 4, black points), along with the estimation of the EW of Qatar-1 (red points) and the calculated EWHα values and their uncertainties (green rectangle). The derived quantities place Qatar-1 in the middle of the distribution of the points of Herbst & Miller (1989). In other words, Qatar-1 falls over the boundary that divides active from non-active stars. This is in agreement with the previously reported moderate activity levels by Covino et al. (2013) and Mislis et al. (2015).
 |
Fig. A.2 Hα EW, as a function of R−I, obtained from Herbst & Miller (1989) in black points, the values of EWHα obtained using Eq. (A.2) from the same authors for three different color indexes in red points, and our estimated EW including the errors contained within the green rectangle. |
All Tables
Our best-fit orbital parameters for the white light curve, along with 1σ errors compared to our previous work.
Values derived analyzing chromatic light curves while considering the detrending model f5(t).
All Figures
 |
Fig. 1 Top: field of view of our observations. Boxes indicate the approximate positions of the slits of our costumed mask. North points upward while east rightward. Both directions are indicated with arrows. The image was acquired using an R filter (r_G0303). The bright object on the very bottom is Qatar-1, which is indicated with a red box. Bottom: extracted instrumental spectra for Qatar-1 and six reference stars. The different wavelength coverage is caused by the uneven distribution of the reference stars at the sky. In both figures, Qatar-1 is indicated in red color. |
| In the text | |
 |
Fig. 2 From top to bottom: air mass, seeing and spatial shift in binned pixels during observations of Qatar-1 as a function of the hours from mid-transit time. In the last two cases their mean value was subtracted to represent the variability as a function of time. The plot sizes were adjusted to display the same pixel scale. |
| In the text | |
 |
Fig. 3 White light curve of Qatar-1b. From top to bottom, the left panel of the figure shows the raw light curve in red. The air-mass model is overplotted in dashed lines. Artificially shifted below, the white light curve after subtracting the air-mass model is indicated in blue and the best-fit transit model is shown in a black continuous line. Finally, the residuals are shown in green. Error bars in all figures were enlarged to meet the standard deviation of the residuals. The right panel of the figure shows the raw white light curve in red points, along with the best-fit transit and detrending models in black dashed line for f5(t). The pink light curve corresponds to the raw data when the best-fit air-mass component has been subtracted, along with the sinusoidal time-dependent variability overplotted in a black thin continuous line. Blue points correspond to a fully detrended transit light curve; the best-fit transit model is overplotted in a black thick line. Below in green, the residual light curve obtained subtracting the best-fit transit model to the blue points (equivalently, subtracting the dashed line to the red points) can be seen. Everything has been artificially shifted. |
| In the text | |
 |
Fig. 4 Transmission spectrum of Qatar-1b. Black circles and horizontal error bars show the derived RP/RS’s and their uncertainties. Horizontal lines are not error bars but indicate the size of the wavelength bin. Green, red and blue continuous lines correspond to Fortney et al. (2010) models for exo-atmospheres investigated in this work. Filled diamonds, squares and triangles indicate averages of the models within each wavelength bin. The models were artificially shifted to meet the data. |
| In the text | |
 |
Fig. 5 Our 12 chromatic and detrended primary transit light curves shown in the left panel along with their respective best-fitting transit models in black continuous lines. The right panel shows the residual light curves obtained by subtracting the best-fit models (transit times detrending) to the raw data. All light curves were artificially shifted to fit the plot. |
| In the text | |
 |
Fig. A.1 Hα photometric follow-up of Qatar-1. The differential light curve for Qatar-1 is indicated on the top in red circles, while the control light curve is indicated on the bottom in green squares. Horizontal lines show ± 1σ the scatter of the control light curve. The blue and pink lines show the best-fit sinusoidal to the data. The vertical dashed line shows the position at which we also acquired spectral information on Qatar-1. |
| In the text | |
 |
Fig. A.2 Hα EW, as a function of R−I, obtained from Herbst & Miller (1989) in black points, the values of EWHα obtained using Eq. (A.2) from the same authors for three different color indexes in red points, and our estimated EW including the errors contained within the green rectangle. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



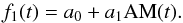
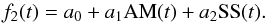
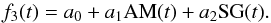
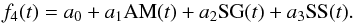
![\begin{eqnarray} \begin{split} f_6(t) = a_0 + a_1 \text{AM}(t) + a_2 \text{SS}(t) \\ + A_1 \sin[2\piup(t\nu_1 + \phi_1)]. \end{split} \end{eqnarray}](/articles/aa/full_html/2017/07/aa30506-17/aa30506-17-eq35.png)
![\begin{eqnarray} \begin{split} f_7(t) = a_0 + a_1 \text{AM}(t) + a_2 \text{SG}(t) \\ + A_1 \sin[2\piup(t\nu_1 + \phi_1)]. \label{eq:detrending7} \end{split} \end{eqnarray}](/articles/aa/full_html/2017/07/aa30506-17/aa30506-17-eq36.png)