| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629386 | |
| Published online | 03 July 2017 | |
Solar disc radius determined from observations made during eclipses with bolometric and photometric instruments on board the PICARD satellite
1 Physikalisch-Meteorologisches Observatorium Davos, World Radiation Center, 7260 Davos Dorf, Switzerland
e-mail: gerard.thuillier91@gmail.com
2 Royal Observatory of Belgium, 3 avenue circulaire, 1180 Bruxelles, Belgium
3 Max-Planck Institute for Solar System Research, 37077 Göttingen, Germany
4 Astronomy Department, Yale University, PO Box 208101, New Haven, CT 06520-8101, USA
5 Observatoire de Haute-Provence du CNRS, 04870 Saint-Michel l’ Observatoire, France
Received: 23 July 2016
Accepted: 18 February 2017
Context. Despite the importance of having an accurate measurement of the solar disc radius, there are large uncertainties of its value due to the use of different measurement techniques and instrument calibration. An item of particular importance is to establish whether the value of the solar disc radius correlates with the solar activity level.
Aims. The main goal of this work is to measure the solar disc radius in the near-UV, visible, and near-IR regions of the solar spectrum.
Methods. Three instruments on board the PICARD spacecraft, namely the Bolometric Oscillations Sensor (BOS), the PREcision MOnitoring Sensor (PREMOS), and a solar sensor (SES), are used to derive the solar disc radius using the light curves produced when the Sun is occulted by the Moon. Nine eclipses, from 2010 to 2013, resulted in 17 occultations as viewed from the moving satellite. The calculation of the solar disc radius uses a simulation of the light curve taking into account the center-to-limb variation provided by the Non-local thermodynamic Equilibrium Spectral SYnthesis (NESSY) code.
Results. We derive individual values for the solar disc radius for each viewed eclipse. Tests for a systematic variation of the radius with the progression of the solar cycle yield no significant results during the three years of measurements within the uncertainty of our measurements. Therefore, we derive a more precise radius value by averaging these values. At one astronomical unit, we obtain 959.79 arcseconds (arcsec) from the bolometric experiment; from PREMOS measurements, we obtain 959.78 arcsec at 782 nm and 959.76 arcsec at 535 nm. We found 960.07 arcsec at 210 nm, which is a higher value than the other determinations given the photons at this wavelength originate from the upper photosphere and lower chromosphere. We also give a detailed comparison of our results with those previously published using measurements from space-based and ground-based instruments using the Moon angular radius reference, and different methods.
Conclusions. Our results, which use the Moon as an absolute calibration, clearly show the dependence of the solar disc radius with wavelength in UV, visible and near-IR. Beyond the metrological results, solar disc radius measurements will allow the accuracy of models of the solar atmosphere to be tested. Proposed systematic variations of the solar disc radius during the time of observation would be smaller than the uncertainty of our measurement, which amounts to less than 26 milliarcseconds.
Key words: Sun: fundamental parameters / Sun: general / instrumentation: photometers / techniques: photometric
© ESO, 2017
1. Introduction and scientific objectives
The solar disc radius (hereafter solar radius), and its possible variation, have been the subject of increasingly accurate measurements for over 350 years. The importance of the knowledge of the radius, and its possible variation, for solar physics and climatology are briefly described as follows. Data concerning the past Sun is important for the understanding of the solar variability because they bring information to be compared with theoretical predictions. The possible link between the solar activity and the solar radius has been suggested from past observations (Ribes et al. 1987) and theoretical modelling (Sofia & Li 2001). While the solar irradiance variability on the timescales of the 11-year activity cycle and shorter is attributed to surface magnetism (see e.g. recent review by Solanki et al. 2013), the changes in the solar radius can contribute to the solar irradiance variability on longer timescales. However, the past measurements of the solar radius and irradiance are subject to uncertainties, so that an unambiguous conclusion about the possible link between the solar irradiance and radius variations is presently not possible.
Because the gaseous surface of the Sun does not have a well-defined edge, as a rocky planet or the Moon, it is not possible to define a unique and unambiguous value for the solar radius. It depends on how the solar edge is determined. Each measuring technique or analysis algorithm produces values that may have high precision, but a much lower accuracy due to systematic influences. As a consequence, while each technique can be used to establish valid values for even small radius variations, it cannot be compared with other techniques and used to derive much significance from differences between them.
The most usual definition for optical determination is based on the inflection point position (IPP) of the limb shape provided by the center-to-limb variation (CLV). In any gaseous medium the optical depth is a function of wavelength, temperature and composition. These data are provided by models of the solar atmosphere. For a given model, the CLV is calculated as a function of wavelength (see study by Thuillier et al. 2011), who have compared the CLV predictions by different models: COde for Solar Irradiance (COSI, Shapiro et al. 2010), Vernazza, Avrett, Loeser (VAL81, Vernazza et al. 1981), Solar Radiation Physical Modelling (SRPM, Fontenla et al. 2009).
In the above models the IPP depends on the opacity in the solar atmosphere. The continuum opacity increases with wavelengths in the visible domain of the spectrum so the solar radius in the continuum will increase with wavelengths (see Fig. 6 from Thuillier et al. 2011). At the same time the opacity in the solar atmosphere is dominated by millions of atomic and molecular lines (cf. Shapiro et al. 2015) so that the dependence of the IPP on the wavelength has a very complex profile (see Fig. 6 from Thuillier et al. 2011). It is important to test the model prediction with real measurements. This will require solar radius data at several wavelengths with a precision of the order of 10 milliarcseconds (mas).
While the recent measurements are of better quality than the past ones, these time series are short (a few years), and when obtained from space, instrumental difficulties make their results questionable. Furthermore, to achieve a measurement in the absolute scale, a preflight calibration should be performed. This calibration for radius measurement is very difficult to achieve with the appropriate accuracy that it is rarely done and can even be impossible to do. An angular reference could be a significant item for radius measurement, although the space environment, especially the particles, may alter its characteristics.
In recent years, different instruments have been used to make such measurements, with increasing sophistication. However, instrumental difficulties remain, which results in questionable stability of the instrument scale over time. This is why the long-term evolution of the solar radius is still an open subject, even for the 11-year solar cycle.
From the ground, the Earth’s atmosphere has an influence, which needs to be corrected with an accuracy better than 10 mas. From space, this effect vanishes, however other difficulties arise, such as the contamination by outgasing and deposition, influence of the particle precipitation, Earth’s albedo adding its contribution to the solar signal, and the thermal stability of the entire system, which is an important requirement in metrology. Nowadays, most missions aiming to measure the solar radius use imaging techniques.
In this work, we present the use of the light curves obtained during solar occultations that occur during partial eclipses, from which solar radii as a function of wavelength are derived and compared with existing values obtained via several other methods and techniques, some of which have no means of calibration and/or a different definition of the radius.
Section 2 describes techniques, methods and our approach for the solar radius determination. Section 3 describes the instruments flown on board the PICARD spacecraft. Section 4 details the data processing, Sect. 5 discusses our results, and Sect. 6 presents the uncertainty budget. The discussion and conclusions are given in Sects. 7 and 8, respectively.
2. Solar radius determination
2.1. Methods and techniques
Given the importance of accurately measuring the solar radius, the following techniques are used:
Imaging telescope. From the ground, the Earth’s atmosphereintroduces noise and spurious effects, as can be seen bycomparing different data sets obtained with different or evensimilar instruments placed at different locations. Furthermore,while the broadly used astrolabes could be considered to have anangular reference, this is not the case for all of the instruments.Furthermore, comparison of data simultaneously obtained byastrolabes have revealed inconsistent results, likely due to theatmospheric effects. Using an imaging telescope in space will avoid this effect. However, precipitating particles induce charge leakage in the CCD’s pixels especially when the detector is not at low temperature (below −40 °C), and will affect the measured limb shape, and consequently the radius determination. The imaging instruments flown to date have no means of calibration, that would help to monitor the long-term solar diameter variation in a stable scale. Indeed, this is instrumentally difficult to achieve. Furthermore, even using the IPP to define the solar diameter may raise a difficulty for comparing the solar diameter determined with the Moon as a calibration standard. The Solar disc Sextant (SDS; Sofia et al. 2013) uses a prism as angular reference. It is protected from the harsh environment of space as this instrument is operated from a high altitude stratospheric balloon, and the flights only last one day each. On the other hand, after each flight there is a strong landing impact, this requires an instrumental refurbishment which introduces its own set of problems and which are discussed in detail in their paper.
- b)
Helioseismology. The solar edge determined from helioseismologic data corresponds to the turnaround point for intermediate and high-l oscillations (Dziembowski et al. 1998; Antia et al. 2000). This turnaround point is located three to eight megametres below the photosphere, depending on the specific l value, which consequently produces radius values that are smaller than those of the other techniques. Since these measurements have a different definition of the solar radius they differ by up to 300 km (0.4 arcsec) from values obtained through the inflection point definition of the radius (Tripathy & Antia 1999; Haberreiter et al. 2008). The seismic radius values are corrected to optical depth τ = 1 depending on their characteristics (Tripathy & Antia 1999). A mean of three seismic radius determinations resulted in the nominal solar radius, RN = 695.7 Mm, adopted by the IAU (Prša et al. 2016). In order to compare this value to the observed radii of the solar disc, an additional correction, needed to take into account the difference of the apparent larger radius when observing the limb of a gaseous body with an extended atmosphere (Brown & Christensen-Dalsgaard 1998). This correction is another 333 km as given by Haberreiter et al. (2008), resulting in a value of 959.2 arcsec for the apparent radius at 500 nm of a solar sphere with the nominal radius. We compare the IAU solar radius and our results in the discussion Sect. 7.
- c)
Planets transits (Venus and Mercury). Planets transits in front the Sun also allow us to measure the solar radius; however, such events are rare (about two to three per century) and the timing of ingress and egress remains a source of uncertainty because of the black-drop effect. This technique may be used for long-term variation (e.g. Sveshnikov 2002) using Mercury transits from 1700 to 1980 to study the possible dependence of the solar diameter on the 11-year solar cycle.
- d)
Sun transit. The paper by Brown & Christensen-Dalsgaard (1998) shows the results obtained with the High Altitude Observatory Solar Diameter Monitor instrument (SDM) over more than six years (from 1981 to 1986) between a solar maximum and a minimum. The SDM is essentially a drift scan (transit or meridional circle) instrument with the advantage that rather than determining the meridional crossing visually, it is recorded with a scanning photometric instrument from which the edge is determined by means of the technique named Fast Fourier Transform Definition (FFTD, Hill & Stebbins 1975; Hill et al. 1975), which is designed to eliminate the first order effect of seeing. Because the calibration is based on the Earth’s rotation, it is known very accurately. In addition, they correct the limb location to the location of the photosphere at 800 nm by means of solar atmospheric models. From the results shown in Fig. 2 of their paper, the statistical errors for the average of the solar radius over a Carrington rotation range between approximately 0.1 and 0.3 arcsec, and they deduce an average radius value over the six years with an estimated precision of 0.009 arcsec (see their Eq. (2)) by assuming no variation from any origin (see their Fig. 2).
- e)
Use of the solar eclipses by the Moon. The lunar radius is very well known because it is a solid body, and because we can observe frequent and numerous stellar occultations. On the other hand, much less frequent eclipses of the Sun by the Moon provide opportunities to derive the solar radius from the lunar radius, and in principle would allow changes as a function of time to be measured.
-
Measurement of the eclipse duration by observers located near the centre of the area of totality.
-
Measurement of the eclipse duration by several observers placed on the north and south edges allowing the precise determination of the limits of the shadow track (see Sofia et al. 1980, for a review of these techniques and a discussion of their accuracy).
For both cases, an accurate positioning of the observers is essential (better than 50 m). The Moon topography (valleys and mountains) introduce some uncertainties, which have to be taken into account in the data processing. Furthermore, libration generates a varying profile of the surface/landscape. However, for variability studies, this effect can be almost cancelled when the eclipse events are observed in the same phase within the Saros cycle (18 years).
Using eclipses has the significant advantage of comparing the Sun radius with a stable reference provided by the Moon solid shape. The Moon’s topography was very precisely determined by the Kuguya lunar mission using spacecraft around the Moon at 100 km altitude (Araki et al. 2009). The Moon’s shape as determined by this mission is more precise than the former Watts profiles. Furthermore, eclipses provide a suitable timing (from one to three opportunities per year) for measuring a possible solar radius variation over a unique long-term. In addition, when this technique is applied from space, it can use simple photometers whose detectors are not so sensitive to degradation by particles because of the size of their detector area compared to the pixel size of an imaging telescope detector.
Because the Sun does not have a solid surface, it is not possible to define a unique radius for it. Not only is the level of the photosphere wavelength dependent, but in each case the surface of the disc is defined by a variety of algorithms that introduce their own systematic effects. For example, the surface can be defined with the IPP with a FFTD technique, and theoretically with an optical depth of 2/3, 1, etc. (see also the discussion of the nominal radius above in the introduction). For that reason, the uncertainty of precision obtained by a given method is always smaller than the (absolute) accuracy of the method. Since the probable error of each technique is obtained from the dispersion of the measurements with that technique, it does not include systematic effects. Thus, differences in the absolute radius obtained by different techniques that are significantly larger by some tens or hundreds of milliarcseconds than the quoted probable errors, cannot be excluded.
The main goal of this paper is to study the dependence of the visible solar radius on the wavelengths and compare the obtained results with the calculations performed with the Non-local thermodynamic Equilibrium Spectral SYnthesis code, a state-of-the-art radiative transfer code NESSY (Tagirov et al. 2017).
In summary:
-
Imaging telescope, either ground- or space-based, present a significant difficulty for the initial geometrical calibration of their CCD array detector.
-
In space, the long-term monitoring of the CCD performance remains a challenge given the harsh space environment.
-
The Moon in solar occultation provides a stable, well-defined calibration means, and the solar radius is scaled to the Moon radius. This opportunity can be applied by using a single (and simple) photometer.
-
On the ground, atmospheric effects have to be taken into account, however the accuracy of their correction is very uncertain.
-
For the imaging telescope, the scale is based on the IPP and on the pixels’ geometrical and photometric properties. Furthermore, the planets transits could be also working in another scale due to the definition of ingress and egress times. It would be important to precisely establish the correspondence between these scales.
2.2. Our approach to the solar radius measurement
We use data from space to avoid effects induced by the atmosphere (refraction, turbulence, and scattering). However, the space environment and especially the particles are able to alter the detectors and the optics. Our data are obtained by bolometric and photometric instruments, whose detectors are of a significantly larger size than the usual pixels of the CCD’s detectors. These instruments operated from space provide measurements by observing the change in time of the solar irradiance during the partial occultation of the Sun by the Moon. Consequently, the Moon will be used as an angular reference.
The bolometer and sunphotometers observing in several spectral domains during partial eclipses are operated simultaneously on board the PICARD spacecraft (Thuillier et al. 2006). The measurement sampling rate is high enough to precisely sample the Moon’s movement across the Sun to the spacecraft line of sight.
3. Instruments on board the PICARD microsatellite
PICARD is a spacecraft launched on 15 June 2010 on a circular sun-synchronous orbit at mean altitude of 736 km. It carries four solar instruments:
-
a bolometer, the Bolometric Oscillations Sensor (BOS) formonitoring the incoming power from the Sun and the Earth (seeSect. 3.1);
-
a set of sunphotometers, the PREcision Monitoring of Solar variability (PREMOS, Schmutz et al. 2009) for measuring the solar spectral irradiance (see Sect. 3.2);
-
a Sun sensor, the System d’Écartométrie Solaire (SES, described in Sect. 3.3) for pointing the scientific payload toward the Sun with an accuracy ±0.01 arcdegree, which will also provide useful data;
-
an imager telescope, the SOlar Diameter Imager and Surface Mapper (SODISM, Thuillier et al. 2006), which provides solar images at the set of wavelengths observed by PREMOS.
Furthermore, PICARD also carries two radiometers for total solar irradiance (TSI) measurements. These instruments could also provide data used to determine the solar radius determination. However, given the duration of the observed occultations (up to 8 min), and their sampling periodicity of about 2 min, the light curve is not appropriately sampled for solar radius determination. Nevertheless, the radiometer data will be used as explained below.
3.1. Bolometric measurements
3.1.1. Principle
The BOS (Zhu et al. 2015) consists of two concentric flat discs of surface S1 and S2 and mass m1 and m2, and painted black and white, respectively (Fig. 1). Their absorption coefficients α1 and α2 are respectively 0.97 and 0.35. Their emissivities ϵ1 and ϵ1, are close, and m1 and m2 are thermally connected to a mass mr, which consists of a small linear rod acting as a thermal shunt.
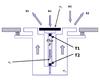 |
Fig. 1 BOS instrument. The black and white coated detectors weights are 0.8 and 160 g, respectively. The black surface integrates all electromagnetic radiation, whereas the white channel is only sensitive to the infrared radiation. m1 is fully isolated from m2 by a multilayer material. The black centre is connected to the top of the rod, which dissipates in the white ring m2. The two thermistors T1 and T2 measure the temperature at each extremity of the rod. |
The BOS provides a signal at high frequency, which is integrated over 10 s. This allows efficient rejection of the instrumental noises. When the photons either from the Sun or from the Earth, are impinging the front absorbing surfaces, they heat up m1 and m2. Given their mass ratio, which is 200, the m1 temperature increases faster than the m2 temperature. Consequently, T1 and T2 are different, and their difference T12 measures the rapid power input change while T2 provides the slow power input change.
3.1.2. Equations describing the BOS operation
Figure 1 shows the radiative inputs as well as re-emissions toward the space. The black surface (S1) absorbs and re-emits the following powers:
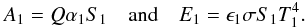 The white surface (S2) absorbs and re-emits the following powers:
The white surface (S2) absorbs and re-emits the following powers:
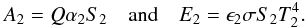 As a thermal flux F flows through the rod, the power budget provides the following relationship:
As a thermal flux F flows through the rod, the power budget provides the following relationship: 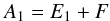 (1)F is obtained by using Fourier’s law:
(1)F is obtained by using Fourier’s law: ![\begin{equation} F = \left( \frac{C m_r}{S_r} \right) \left( \frac{\delta (T_1)}{\delta (t)} \right)+ \frac{\left[K_r (T_1 - T_2) + \sigma S_r \epsilon_r T_1^4 \right]}{S_r} \end{equation}](/articles/aa/full_html/2017/07/aa29386-16/aa29386-16-eq21.png) (2)where
(2)where
-
C is the thermal capacity of S1, S2 and the rod (aluminum);
-
Kr is the rod thermal conductivity;
-
Sr is the emissive surface of the insulation material around the rod;
-
ϵr is the emissivity coefficient of insulation material (see Fig. 1);
-
Q is the solar irradiance input.
3.1.3. Use of the BOS measurements for radius determination
Given the BOS field of view (2π), BOS gathers photons mainly from the Sun, but also from the Earth. The Earth’s contribution has to be removed. The measurements before and after the occultation are used to correct for the Earth’s radiation. Because of the displacement of the satellite (several tens of degrees), the albedo changes as the satellite passes over continents, clouds, ocean and ice of the polar caps. To account for these changes, a data set is prepared gathering measurements taken about 5 min before and after the occultation, which is interpolated during the eclipse occurrence and subtracted from the measurements. Afterward the corrected signal is normalized to unity. This may not be appropriate in the case of a rapid change in albedo. To account for this effect, we use TSI measured on board by PREMOS (Schmutz et al. 2013), which is not affected by the Earth’s radiation because of the small field of view of the radiometer. In Sect. 4.3, we explain how we keep the advantage of the BOS sampling rate and the TSI measurements free of the Earth’s contribution.
3.2. PREMOS instrument
The PREMOS consists of several filter sunphotometers and a radiometer. It operates jointly with the BOS on board PICARD. The sunphotometers are calibrated on the absolute scale and redundant channels are periodically operated to take into account the possible ageing. The spectral channels are centred at 210, 268, 535, and 782 nm (see Fig. 2 in Cessateur et al. 2016), and are sampled every 10 s as BOS. The sunphotometers have a field of view of ±1.5 arcdegree, preventing a flat-field effect at the beginning and end of the occultation. PREMOS observations extend from September 2010 to April 2014 (end of mission).
We note that the depth of the light curves is wavelength dependent in Fig. 2. This is attributed to the wavelength dependence of the CLV of the solar brightness.
 |
Fig. 2 BOS raw data are displayed with PREMOS raw data at 210, 266, 535, 607 and 782 nm together with the SES data for the 1 June 2011 occultation. The 782 nm red line shows the PREMOS data while the thin red line represents the 784 nm Sun sensor (SES) measurements. The difference is within the thickness of the lines. |
3.3. Sun Sensor
On board the PICARD spacecraft, the SES is made of a four-quadrant detector and allows us to point the spacecraft toward the Sun, with an accuracy better than a few arcminutes. It operates at 784 nm in the solar continuum within a 2.8 nm bandpass. The four-quadrant measurements sampled at 4 Hz are summed and averaged to obtain a measurement every 10 s as BOS and PREMOS sampling rate. In this way, the Sun sensor data are usable as photometric measurements. An example is shown in Fig. 2. We note the near absence of noise due to averaging over 40 measurements. Figure 2 shows the agreement between the Sun sensor data and the PREMOS measurements at 782 nm.
We note that the BOS light curve is not as deep as the others. This is due to the BOS field of view which collects photons from the Earth’s surface lit by the Sun given its 2π solid angle. This will be taken into account in Sect. 4.3.
4. Solar occultations, centre-to-limb variation and data processing
4.1. Partial solar occultations
A solar occultation occurs when the Moon passes between the Sun and the satellite, and the Moon fully or partially blocks the Sun light as viewed from the spacecraft. Since the PICARD instruments are precisely pointing to the Sun and its orbital period is smaller than the eclipse duration, typically several solar occultations occur during one eclipse. The partial occultations observed by PICARD are listed in Table 1. An eclipse occurred on 11 July 2010, but at that time the PREMOS instrument was not yet switched on. Simultaneous PREMOS and BOS measurements began for the eclipse of 1 June 2011.
List of occultations used in this study.
4.2. Partial solar occultation modelling
4.2.1. Centre-to-limb variation
The solar surface brightness is inhomogeneous. First, there are sunspots and faculae, and second there is a center to limb variation. The active regions over a large surface may not contribute more than a tenth of one per cent in the visible and near-IR. However, the CLV has to be considered in modelling. The CLV effect is taken into account for all occultations used in this study. The CLVs as a function of wavelength are calculated with NESSY (Tagirov et al. 2017), which is a further development of the Code for Solar Irradiance (COSI, Shapiro et al. 2010). NESSY has an improved treatment on the effect of non-local thermodynamic equilibrium (NLTE) effects in the chromosphere and provides a more reliable CLV at short wavelengths and chromospheric lines. The new release of the Vienna Atomic Line Database (VALD3, Ryabchikova et al. 2015) was used to take into account the contribution of Fraunhofer lines to the CLV.
The CLVs provide the change of radiance as a function of the distance from the Sun centre to the limb, and wavelength. They have been normalized to unity at the solar disc centre. For a given spectral domain, the CLV is integrated over each photometer spectral bandpass shown in Table 2. As expected for narrow bandpasses (a few nanometers), the integrated CLV is very close to the CLV at the peak transmission.
However, for BOS, which has a very large bandpass, it is important to know to which spectral domain corresponds the BOS measurements. Its bandpass extends from λ0 = 200 to λ1 = 4000 nm. The front paintings have an absorbing coefficient quasi-independent of wavelength in this spectral range (Willey et al. 1983). Consequently, for these measurements, we have used the intensity as a function of the distance (r) to the Sun centre and wavelength provided by NESSY integrated in the BOS bandpass (see Sect. 4.2.2 for the details of integration). This provides the mean CLV shown in Fig. 3. This mean CLV will be used to calculate the solar diameter as determined from the BOS measurements. Then, it is necessary to find the closest CLV to this mean CLV in order to determine the wavelength to which the BOS solar radius corresponds allowing comparison with the solar radius obtained with the photometers. For that purpose, we show in Fig. 3 the CLVs at 700, 750 and 800 nm provided by NESSY. Since the CLV of the solar brightness at 750 nm is basically identical to the CLV of the wavelength-integrated brightness, we use 750 nm as the wavelength for the BOS measurements. This is not surprising, given that most of the energy in the solar flux comes in the visible and IR spectral domains.
Width of each spectral domain at half maximun.
 |
Fig. 3 Calculated mean CLVs for the BOS (black dots) compared to CLVs predicted by NESSY at 700 nm (red) and 800 nm (green) located just below and above respectively. This shows that BOS measurements now refer to 750 nm. |
4.2.2. Geometry and calculation of the illuminated Sun surface
The light curve measured by PREMOS and BOS is a function of time t, wavelength and occultation number, first normalized to unity outside the eclipse event. Several examples are shown in Fig. 2. We denote by B(t) the irradiance value as defined above for a given wavelength and occultation number.
The light curve observed by the PICARD instruments is modelled by calculating the full Sun surface irradiance and that of the non-occulted surface by the Moon, taking into account the CLV. The difference gives the irradiance of the occulted solar surface, and taking its ratio to the full solar surface irradiance, we obtained the normalized calculated light curve C(t). The integration method taking into account the CLV is shown in Fig. 4.
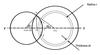 |
Fig. 4 Principle of the Sun illuminated surface calculation in polar coordinates. |
The irradiance of the non-occulted solar surface, S(t) is given by a triple integral: 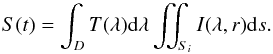 (3)The first integral corresponds to the integration over the instruments bandpass (BOS and sunphotometers). The double integral is the integration on the Sun illuminated surface Si. Since I(λ,r) is a function of r, the integration is made as shown in Fig. 4:
(3)The first integral corresponds to the integration over the instruments bandpass (BOS and sunphotometers). The double integral is the integration on the Sun illuminated surface Si. Since I(λ,r) is a function of r, the integration is made as shown in Fig. 4: 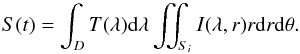 (4)Then, for a given Sun radius, the calculation is made in four steps in arbitrary units:
(4)Then, for a given Sun radius, the calculation is made in four steps in arbitrary units:
-
calculation of the solar irradiance on the partially uncovered solarsurface named {1};
-
calculation of the solar irradiance on the full solar surface named {2};
-
calculation of the difference providing the decrease in the solar irradiance {2}-{1};
-
calculation of its ratio to {2} providing the normalized decrease in the solar irradiance.
Since the relative positions of the three bodies (spacecraft, Moon and Sun) are a function of time, C(t) is a function of t, which provides the light curve (Fig. 5). C(t) depends on the Sun radius to be determined and the Moon radius, which is assumed to be constant within the precision of the present measurements.
Then, we determine the solar radius by minimizing the difference between B(t) and C(t), 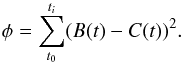 (5)The summation is carried out from t0 to ti, which is the time interval of the occultation phenomenon. A variation of the residual φ as a function of β ratio of the Sun radius to the Moon radius at the time of the occultation, is shown in Figs. 6a and b. The comparison of the measurements with the modelled light curves at the minimum residual is displayed in Figs. 7a and b.
(5)The summation is carried out from t0 to ti, which is the time interval of the occultation phenomenon. A variation of the residual φ as a function of β ratio of the Sun radius to the Moon radius at the time of the occultation, is shown in Figs. 6a and b. The comparison of the measurements with the modelled light curves at the minimum residual is displayed in Figs. 7a and b.
4.3. BOS correction of the Earth contribution
The BOS has a sampling (10 s) that provides a precise observed light curve. However, it contains the Earth’s contribution. On the other hand, the TSI has a low sampling (120 s), but is free from the Earth’s contribution. We combined the two data sets to keep the advantage of each by using the original width of the BOS light curve and the amplitude depth of the TSI light curve. The depth of the TSI light curve has always been found larger than the depth of the BOS light curve because the Earth’s contribution has its greatest effect at the maximum occultation.
 |
Fig. 5 TSI data and its Gaussian fitting. |
Figure 5 shows why a fitting is necessary in order to generate a data set that has the same sampling rate as the BOS measurements. The simplest fit was found to be Gaussian: 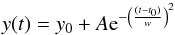 (6)where A is the amplitude coefficient (negative), y0 is the signal just before the start of the occulatation, w is the width, and t0 is the time at maximum occultation.
(6)where A is the amplitude coefficient (negative), y0 is the signal just before the start of the occulatation, w is the width, and t0 is the time at maximum occultation.
We have verified the agreement between the times of maximum occultation and the width of both TSI fitting and BOS data sets. As stated earlier, the smaller depth observed for BOS is due the upward contribution from the Earth surface and clouds.
4.4. Radius determination
The shape of the light curves shown in Fig. 2 depends on the lunar radius, the solar limb shape, the Sun-Moon distance and the Moon-PICARD distance. Using the positions of the Sun and Moon provided by the Institut de Mécanique céleste et de Calcul des Éphémérides (IMCCE), and the position of the spacecraft provided by CNES, and a given value of the Sun-to-Moon radius ratio (β), we obtain the ratio C(t) to be compared to the measured ratio B(t). The Moon radius is taken from the Kaguya mission results as 1737.1 km transformed in arcsec using the Moon to spacecraft distance. The residual φ computed using Eq. (5) is displayed in Fig. 6 as a function of β. The minimum residual provides us with β, then we obtain the solar radius in arcsec. Then it is normalysed at one Astronomical Unit.
 |
Fig. 6 The residual φ calculated by Eq. (5) is shown as a function of β for the occultation of 1 June 2011 observed by the PREMOS sunphotometer (panel a)), and BOS radiometer (panel b)). The dotted black line shows the residual φ and its polynomial fit is displayed in red. |
The minimum residual being obtained for a value βmin, we compare the measured light curve with the calculated light curve for βmin. This comparison is shown for sunphotometer at 535 nm and BOS measurements in Figs. 7a and b, respectively.
 |
Fig. 7 Upper panel a) light curve measured with the PREMOS sunphometer at 535 nm (red open circle) with the calculated light curve (solid black line) for the 1 June 2011 occultation for the value of βmin, which minimizes the residual φ. Lower panel b) as above but for the BOS data. |
The modelled light curve and the measurements are very close as shown by Figs. 7a and b. Their relative difference increases from IR to UV, likely due to the CLV precision, however, it remains below 0.01%.
This processing has been applied to the 17 occultations observed by PICARD. The results of each occultation observed by BOS and the sunphotometers are detailed in Sect. 5.
4.5. Importance of the CLV for the radius determination
To investigate the importance of using the CLV, the radius is calculated with and without CLV using the method described above. The residual is shown with and without CLV in Fig. 8a in linear coordinates and in Fig. 8b in logarithmic coordinates as a function of β to clearly present the differences around the minimum residual for the 535 nm 1 June 2011 occultation.
 |
Fig. 8 CLV and no CLV effect on the calculated residual. |
The effects of CLV are manifested as follows:
-
a)
The residual is significantly decreased.
-
b)
The β for minimum residual increases from its value with CLV leading to an increase of the calculated radius. For the case of Fig. 8, the increase is 6.3 mas.
Both effects can be understood by investigating where the CLV effect is manifested on the light curve. We show the 1 June 2011 occultation at 535 nm calculated without CLV (Figs. 9a, b) and with CLV (Figs. 9c, d). In both cases synthetic light curves are shown at the minimum residual. Figures 9a, b illustrate that light curves calculated without taking CLV into account are systematically incorrect , while calculations with CLV allow accurate reproduction of the light curve (Figs. 9c, d). Such calculations underestimate the decrease of in intensity at the maximum phase of occultation (Fig. 9a) and overestimate the decrease in the flux at the ingress and regress of the occultation when only the near-limb regions of the solar disc are covered by the Moon (Fig. 9b). Consequently the inclusion of CLV into our calculations decreases the residuals (effect a). The main contribution to the residuals in the case of calculations without CLV comes from the near-maximum phase of eclipse (see Fig. 9a) and the minimization procedure tries to compensate the systematic error arising from the omission of CLV by the increase of the solar radius (effect b).
By making the same comparison at 784 nm, these two effects almost disappear. This is consistent with the solar modelling and Fig. 8 since the CLV effect is less pronounced at 784 nm than at 535 nm.
The 17 occultations have been processed similarly. Their resulting mean shown in Table 3, is calculated to remove as much as possible the noise from the individual radius determination. The difference between CLV nad no CLV shows a significant increase toward the UV as predicted by the solar models. The CLV produced by NESSY has been shown to agree with available measurements (Shapiro et al. 2013; Bolduc 2016, priv. comm.), and we estimate that our technique properly takes the CLV effect into account. The effect of the CLV uncertainty on our radius calculations is discussed in Sect. 6.
Table 3 shows the importance of taking into account the CLV in the radius calculation. Centre-to-limb variation reduces the calculated solar radius by up to several tens of mas especially in the UV. The difference is the greatest in the UV since the CLV variation close to the limb is larger in the UV than in the visible and near-IR. The larger difference at 607 nm with respect to the other differences in the visible and near-IR is explained by the few observations made at this wavelength (noise effect in measurements).
Difference (mas) between the radius calculated without CLV and with CLV.
 |
Fig. 9 The model light curve is compared to measurements (crosses) without CLV (upper panel) with the model light curve with CLV (lower panel). |
5. Results
Seventeen solar partial occultations by the Moon were observed during the PICARD mission (Table 1). For certain eclipses, up to three occultations are observed. Table 4 provides the results of the 17 occultations as a function of wavelength.
Table 4 presents results from eclipse 14 having an uncertainty significantly above the others. The corresponding results are excluded in the means shown in Table 6. This exclusion is based on the SES pointing data showing a stable pointing before and after the eclipse and an incoherent pointing during that eclipse. This exclusion does not significantly change the mean radii, however, the mean uncertainties are affected (Tables 5 and 6).
Results at one astronomical unit (AU) provided the BOS and the PREMOS instruments.
Mean value of the 17 solar radius determinations and their standard deviation, mean value of the standars deviation between the 17 light curves and model.
Same quantities as in Table 5 calculated without occulation 14.
Table 6 shows the consistent results obtained at 782 nm by the PREMOS and the Sun sensor with 10 mas maximum difference after removing occultation 14.
The 210 nm and 266 nm spectral domains are emitted in the chromosphere. Our measurements show a larger radius at 210 nm than 266 nm, which is itself larger than in the visible continuum at 535 nm. As for 782 nm, Table 6 shows a larger value than at 535 nm. This is discussed in Sect. 7. Table 7 gathers all random uncertainties affecting the solar radius determination and their combined values.
Random uncertainties (mas) for each spectral domain.
6. The uncertainties budget of the Sun radius determination
Several sources of uncertainty affect the accuracy of the Sun radius determination. They are either of instruments origin, or satellite position, Moon topography, and centre-to-limb predictions. Each of them is estimated below.
6.1. Uncertainties affecting the radius measurements by BOS and photometers
-
a)
Spacecraft position and pointing uncertainties. The precision of the PICARD pointing is ±0.01 arcdegree, which has a negligible effect given the flat field of the instruments. The spacecraft position is known within ±7 km. This induces an uncertainty in the Sun radius determination of 10 mas.
-
b)
The Moon shape and radius. Araki et al. (2009) provided the mean radius, have also quoted the uncertainty affecting the Moon radius as ±0.01 km, which is induced by the orbit and attitude errors. The Moon topography introduces some irregularities in the light curve, which are superposed to the natural noise of the measurements obtained by the BOS and the photometers. As all channels are simultaneously operated and as there is no trend in time as seen from Fig. 10b, the mean of these RMS is calculated (Table 7, Col. 5).
-
c)
Active regions. We have examined the images recorded by SODISM on board PICARD, and verified there is no significant active region at the limb.
-
d)
The centre-to-limb variation (CLV). The light curve modelling developed here takes into account the Sun’s centre-to-limb variation. Solar models foresee the limb shape as a function of wavelength. All of them foresee an IPP displacement of about 30 mas from 400 to 800 nm, and they do not fully agree (Fig. 5 in Thuillier et al. 2011). However, the dispersion remains about ±10 mas. We have used this dispersion as an estimate of the models precision. Since our light curve model uses CLV provided by the NESSY modelling, in order to define which uncertainty is generated by the model uncertainty, we ran the same data set but changed the wavelength, which corresponds to a CLV generating an IPP change of 10 mas. We found a negligible radius difference reaching 2 mas.
6.2. Random uncertainty budget per spectral channel
Table 7 gathers all random uncertainties affecting the solar radius determination and their combined values.
The measured dispersion is extracted from Table 5 as well as the random uncertainty from the background. The random uncertainties given in Col. 3 are obtained in Sect. 5.1.a (spacecraft position and pointing uncertainties). The three random uncertainties are geometrically combined in Col. 6.
We note that the combined random uncertainties are compatible with the dispersions. The mean random uncertainty from the right column is 26 mas.
A light curve is recorded as a function of time, and thus measurement contains three variable sources of uncertainties, namely the Moon edge, the spacecraft attitude and the counting noise of the detector. The difference between the measured and modelled light curve is normalized by the measurement. This difference is the greatest when the measurement is the lowest (i.e. at the maximum occultation) indicating that the most important source of uncertainties is the noise measurement and not the attitude and Moon edge.
7. Discussion
Figure 10a displays the depth of each occultation at 535 nm (at other wavelength, the depth is very close). The middle panel (b) shows all results as a function of the occultation number and wavelength. The lower panel (c) compares the mean solar disc radius value from the PREMOS and BOS with other determinations using different techniques of calibration as a function of wavelength. Table 9 provides the reference of each data set. The 1σ uncertainties bars are indicated.
 |
Fig. 10 a) Occultation depth, b) solar radius disc for each occultation as a function of wavelength, and c) our results together with other solar disc determination. |
These results allow us to compare the solar radii as a function of wavelength for the 17 occultations in Fig. 10c. Table 5 shows the agreement between the two independent determinations of the radii at 782 and 784 nm (SES) within 14 mas, which is consistent with the uncertainty budget. The 782 nm PREMOS filter provides a radius increase (eclipse 1, 2, 3), which is not obtained with the SES filter. It could be related to the increase of the signal at the beginning of the mission (Cessateur et al. 2016). We note that the nature of the PREMOS 782 nm and SES filters are different, which may generate a different behaviour in space. We also note that the eclipse depth is not correlated with the calculated solar radius (Fig. 10a). Table 1 provides the number of sunspots per occultation. Considering the radius at 210 nm (Fig. 10b), which originates from the upper photosphere and lower chromosphere, we have searched for a dependence with the solar activity, which, if it exists, would have an effect smaller that the uncertainty of our radius determination around 30 mas as a mean (Table 7).
Figure 10c shows the radius variation with wavelength. We note the radii increase toward the short wavelength and also toward the IR. This behaviour was predicted by the solar modelling. To investigate the precision of the modelling, we compare below the theoretical values and our measurements taking into account the uncertainties. Our radius measurements refer to the Moon radius, while the Sun radius is defined from the IPP on the limb. It is likely that these two reference frames are different. For this reason, we have calculated the radius variation as a function of wavelength using the radius at 535 nm as baseline.
In the domain 535−784 nm modelling and our mean radius are in good agreement, i.e. when taking into account the uncertainty of the differences. It is of importance to note the agreement between NESSY predictions and BOS radius determination. However, Δ(“210−535”) and Δ(“266−535”) differences are close to the limit of the combined uncertainty. At this point, we note that the solar radius at 210 and 266 nm is defined by a huge number of spectrally unresolved Fraunhofer lines (and only 1% of them is measured in the laboratory, see Kurucz 2005). This might explain the uncertainty of the theoretical predictions at 210 and 266 nm PREMOS channels.
Figure 10c and Table 8 confirm the dependence of the solar diameter on wavelength calculated in Thuillier et al. (2011; see their Fig. 6). The smallest value of the radius is observed around 600 nm. It increases towards the infrared because of the increase in the continuum absorption coefficient of the negative hydrogen ion (see Gray 2005). The increase towards UV is attributed to the combined action of the Fraunhofer lines (which increases towards UV).
Using measurements from space in the EUV domain, the increase of the solar radius toward the short wavelengths has been pointed out (Rozelot et al. 2015). In the visible, Table 9 shows results between 600 and 676 nm using different techniques from space. In particular, the mean radius obtained from the seven SDS flights is in close agreement with our determination at 535 nm (959.757 versus 959.75 arcsec). Despite some noise or due to different reference scales, Table 9 suggests an increase of the solar diameter with wavelength in that spectral domain (Rozelot et al. 2015). From 607−676 nm, the radius increase is 27 mas, while we found 43 mas from 607−782 nm with PREMOS. These increases are compatible if we consider the spectral range of these measurements (607−782 nm) is larger than the previous one (607−676 nm given in Table 9). However, it is noticeable that planet transists provide higher values than the other determination with similar or close wavelength domains.
Difference (mas) with respect to the solar radius at 535 nm of the solar radius measured at all other wavelengths (Col. 3).
Solar radius (arcseconds) measurements using techniques with calibration means (planets transits 2, 4, 5), prism (3), solar occultation (1 and 7), timing (6)).
From 1715 to present, 25 solar radius determinations in white light have been carried out from ground using the Moon as calibration standard. Assuming a radius variation either absent or smaller than their precision, the mean radius calculated from the observations made since 1979 to present (Dunham et al. 1980, 2005; Fiala et al. 1985; Wan et al. 1989; Kubo 1993; Sigismondi 2008; Kilcik et al. 2009; Adassuriya et al. 2011; Lamy et al. 2015) is 959.690 arcsec, a smaller value than our results in the photospheric continuum at 535 and 607 nm. Their precision is quoted between 10 to 60 mas with a mean value of 36 mas. However, taking into account their number, and assuming that the solar radius remains constant during the entire period, it reduces to 8.5 mas. We note the effect on the precision of having a measurements time series. Furthermore comparing these results with those of Brown & Christensen-Dalsgaard (1998), we note that the two solar radius are very close (959.69 versus 959.68 arcsec), as well as their precision.
8. Conclusions
Measuring the solar disc radius and its variation remains a key undertaking for a variety of subjects ranging from solar physics to solar-terrestrial connection. These measurements, which need an accuracy of about 10 mas, require in turn very stable instruments, preferably located in space, where atmospheric effects are absent. Imaging systems that have been used for this purpose do not have adequate stability over the required lifetime (at least a decade or longer) both because of their intrinsically short lifetime, and because of the difficulty calibrating the ageing effects due to particles precipitations.
In contrast, using the light curve provided by a Moon occultation and recorded by a single detector does not appear so sensitive to the space environment, and it can be done with instruments on different space missions, which can extend the baseline of the measurements. Of course, the calibration and stability of the imaging instruments remains a challenge. In our work, because the Moon as a very stable calibration reference, we used solar occultations by the Moon to provide the long-term calibration stability. Simple instruments using large detector arrays such as sunphotometers and bolometers are able to provide measurements of the solar disc radius as a function of wavelength, as well as long-term variation. By means of occultation, light curves provided by the BOS and PREMOS instruments on board PICARD, we found that the Sun has a larger radius at 210 nm than in the visible at 535 nm, and an averaged value over the 16 occultations of 959.759 arcsec at 535 nm. It should be noted that we found 959.736 arcsec at 607 nm, a higher value than that obtained with ground-based timing measurements using solar eclipses in white light, whereas timings of planetary transits yield radius values are systematically higher. Our mean combined uncertainties is 26 mas. Correcting the 535 nm value of 959.759 ± 0.026 arcsec by 0.46 arcsec for the apparent larger radius when observing the disc, we obtain for the solar radius 959.30 arcsec, or 695.76 Mm for τ = 1 at 500 nm, which is fully consistent with the nominal solar radius adopted by IAU (959.2 arcsec). Our results as a function of wavelength show a minimum solar disc radius in the visible domain, which is consistent with the NESSY modelling.
The PICARD mission has been ended in April 2014. By keeping the PREMOS and BOS instruments in operation around the predicted occurrence time of the solar occultations, the radius variability as a function of wavelength and solar activity would have been better studied using the presented method.
Acknowledgments
Data have been obtained by the PREMOS radiometer and sunphotometers designed and built by the PMOD-WRC (CH) and supported by the Swiss PRODEX funding. PREMOS was flown on the PICARD microsatellite, a CNES mission. Ping Zhu is supported by the ESA-PRODEX program, managed by the Belgian Scientific Policy Office, PEA: 4000103202. A. I. Shapiro acknowledges funding from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007-2013) under REA grant agreement No. 624817. R. Tagirov is with PMOD-WRC Institute under contract SFN 200020-153301. S. Sofia thanks the G. Unger Vetlesen Foundation and the Brinson Foundation for their generous support of his work on solar properties and variability. The BOS instrument was designed at Royal Observatory of Belgium. We appreciate the support received from his director Ronald Van der Linden during the entire PICARD mission. Sunspot numbers were provided by the SILSO centre (Bruxelles).
References
- Adassuriya, J., Gunasekera, S., & Samarasinha, N. 2011, Sun and Geosphere, 6, 17 [NASA ADS] [Google Scholar]
- Antia, H. M., Basu, S., Pintar, J., & Pohl, B. 2000, Sol. Phys., 192, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Araki, H., Tazawa, S., Noda, H., et al. 2009, Science, 323, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., & Christensen-Dalsgaard, J. 1998, ApJ, 500, L195 [NASA ADS] [CrossRef] [Google Scholar]
- Cessateur, G., Schmutz, W., Wehrli, C., et al. 2016, A&A, 588, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, D. W., Sofia, S., Fiala, A. D., Muller, P. M., & Herald, D. 1980, Science, 210, 1243 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dunham, D. W., Thompson, J. R., Herald, D. R., et al. 2005, SORCE Science Meeting September 14−16, Durango, Colorado, http://lasp.colorado.edu/sorce/news/2005ScienceMeeting/ [Google Scholar]
- Dziembowski, W. A., Goode, P. R., di Mauro, M. P., Kosovichev, A. G., & Schou, J. 1998, ApJ, 509, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Emilio, M., Kuhn, J. R., Bush, R. I., & Scholl, I. F. 2012, ApJ, 750, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Emilio, M., Couvidat, S., Bush, R. I., Kuhn, J. R., & Scholl, I. F. 2015, ApJ, 798, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Fiala, A. D., Dunham, D. W., Dunham, J. B., & Sofia, S. 1985, in BAAS, 17, 624 [Google Scholar]
- Fontenla, J. M., Curdt, W., Haberreiter, M., Harder, J., & Tian, H. 2009, ApJ, 707, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, in The observation and analysis of stellar photospheres, 3rd edn. (Cambridge University Press) 154 [Google Scholar]
- Haberreiter, M., Schmutz, W., & Kosovichev, A. G. 2008, ApJ, 675, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hauchecorne, A., Meftah, M., Irbah, A., et al. 2014, ApJ, 783, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, H. A., & Stebbins, R. T. 1975, ApJ, 200, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, H. A., Stebbins, R. T., & Oleson, J. R. 1975, ApJ, 200, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Kilcik, A., Sigismondi, C., Rozelot, J. P., & Guhl, K. 2009, Sol. Phys., 257, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, Y. 1993, PASJ, 45, 819 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 86 [Google Scholar]
- Lamy, P., Prado, J.-Y., Floyd, O., et al. 2015, Sol. Phys., 290, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ribes, E., Ribes, J. C., & Barthalot, R. 1987, Nature, 326, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Rozelot, J. P., Kosovichev, A., & Kilcik, A. 2015, ApJ, 812, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
- Schmutz, W., Fehlmann, A., Hülsen, G., et al. 2009, Metrologia, 46, S202 [NASA ADS] [CrossRef] [Google Scholar]
- Schmutz, W., Fehlmann, A., Finsterle, W., Kopp, G., & Thuillier, G. 2013, in AIP Conf. Ser., 1531, 624 [Google Scholar]
- Shapiro, A. I., Schmutz, W., Schoell, M., Haberreiter, M., & Rozanov, E. 2010, A&A, 517, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Schmutz, W., Dominique, M., & Shapiro, A. V. 2013, Sol. Phys., 286, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, A. I., Solanki, S. K., Krivova, N. A., Tagirov, R. V., & Schmutz, W. K. 2015, A&A, 581, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sigismondi, C. 2008, in Relativistic Astrophysics, eds. C. L. Bianco, & S.-S. Xue, AIP Conf. Ser., 966, 341 [Google Scholar]
- Sofia, S., & Li, L. H. 2001, J. Geophys. Res., 106, 12969 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, S., Dunham, D. W., & Fiala, A. D. 1980, in The Ancient Sun: Fossil Record in the Earth, Moon and Meteorites, eds. R. O. Pepin, J. A. Eddy, & R. B. Merrill, 147 [Google Scholar]
- Sofia, S., Girard, T. M., Sofia, U. J., et al. 2013, MNRAS, 436, 2151 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Haigh, J. D. 2013, ARA&A, 51, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Sveshnikov, M. L. 2002, Astron. Lett., 28, 115 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tagirov, R., Shapiro, A. I., & Schmutz, W. 2017, A&A, 581, A116 [Google Scholar]
- Thuillier, G., Dewitte, S., Schmutz, W., & Picard Team. 2006, Adv. Space Res., 38, 1792 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Claudel, J., Djafer, D., et al. 2011, Sol. Phys., 268, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathy, S. C., & Antia, H. M. 1999, Sol. Phys., 186, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, L., Zhao, J.-L., Chu, Z.-Y., et al. 1989, Acta Astron. Sinica, 30, 355 [NASA ADS] [Google Scholar]
- Willey, R. R., George, R. W., Ohmart, J. G., & Walvoord, J. W. 1983, in Generation, measurement and control of stray radiation III, ed. R. P. Breault, Proc. SPIE, 384, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, P., van Ruymbeke, M., Karatekin, Ö., et al. 2015, Geoscientific Instrumentation, Methods and Data Systems, 4, 89 [Google Scholar]
All Tables
Results at one astronomical unit (AU) provided the BOS and the PREMOS instruments.
Mean value of the 17 solar radius determinations and their standard deviation, mean value of the standars deviation between the 17 light curves and model.
Difference (mas) with respect to the solar radius at 535 nm of the solar radius measured at all other wavelengths (Col. 3).
Solar radius (arcseconds) measurements using techniques with calibration means (planets transits 2, 4, 5), prism (3), solar occultation (1 and 7), timing (6)).
All Figures
 |
Fig. 1 BOS instrument. The black and white coated detectors weights are 0.8 and 160 g, respectively. The black surface integrates all electromagnetic radiation, whereas the white channel is only sensitive to the infrared radiation. m1 is fully isolated from m2 by a multilayer material. The black centre is connected to the top of the rod, which dissipates in the white ring m2. The two thermistors T1 and T2 measure the temperature at each extremity of the rod. |
| In the text | |
 |
Fig. 2 BOS raw data are displayed with PREMOS raw data at 210, 266, 535, 607 and 782 nm together with the SES data for the 1 June 2011 occultation. The 782 nm red line shows the PREMOS data while the thin red line represents the 784 nm Sun sensor (SES) measurements. The difference is within the thickness of the lines. |
| In the text | |
 |
Fig. 3 Calculated mean CLVs for the BOS (black dots) compared to CLVs predicted by NESSY at 700 nm (red) and 800 nm (green) located just below and above respectively. This shows that BOS measurements now refer to 750 nm. |
| In the text | |
 |
Fig. 4 Principle of the Sun illuminated surface calculation in polar coordinates. |
| In the text | |
 |
Fig. 5 TSI data and its Gaussian fitting. |
| In the text | |
 |
Fig. 6 The residual φ calculated by Eq. (5) is shown as a function of β for the occultation of 1 June 2011 observed by the PREMOS sunphotometer (panel a)), and BOS radiometer (panel b)). The dotted black line shows the residual φ and its polynomial fit is displayed in red. |
| In the text | |
 |
Fig. 7 Upper panel a) light curve measured with the PREMOS sunphometer at 535 nm (red open circle) with the calculated light curve (solid black line) for the 1 June 2011 occultation for the value of βmin, which minimizes the residual φ. Lower panel b) as above but for the BOS data. |
| In the text | |
 |
Fig. 8 CLV and no CLV effect on the calculated residual. |
| In the text | |
 |
Fig. 9 The model light curve is compared to measurements (crosses) without CLV (upper panel) with the model light curve with CLV (lower panel). |
| In the text | |
 |
Fig. 10 a) Occultation depth, b) solar radius disc for each occultation as a function of wavelength, and c) our results together with other solar disc determination. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


