| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628639 | |
| Published online | 19 May 2017 | |
Mass determination of K2-19b and K2-19c from radial velocities and transit timing variations⋆
1 Instituto de Astrofísica de Canarias, C/vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: dnespral@iac.es
2 Departamento de Astrofísica, Universidad de La Laguna, 38206 Tenerife, Spain
3 Dipartimento di Fisica, Università degli Studi di Trino, via Pietro Giuria 1, 10125 Torino, Italy
4 Landessternwarte Königstuhl, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
5 Dipartimento di Fisica e Astronomia, Università degli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
6 Leiden Observatory, University of Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
7 Department of Earth and Space Sciences, Chalmers University of Technology, Onsala Space Observatory, 439 92 Onsala, Sweden
8 Rheinisches Institut für Umweltforschung, Abteilung Planetenforschung an der Universität zu Köln, Aachener Strasse 209, 50931 Köln, Germany
9 Stellar Astrophysics Centre, Deparment of Physics and Astronomy, Aarhus University, Ny Munkegrade 120, 8000 Aarhus C, Denmark
10 Institute of Planetary Research, German Aerospace Center, Rutherfordstrasse 2, 12489 Berlin, Germany
11 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenberg, Germany
12 Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Spain
13 Center for Astronomy and Astrophysics, TU Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
Received: 4 April 2016
Accepted: 20 March 2017
We present radial velocity follow-up observations of K2-19, a compact planetary system hosting three planets, of which the two larger ones, K2-19b and K2-19c, are close to the 3:2 mean motion resonance. An analysis considering only the radial velocity measurements detects K2-19b, the larger and more massive planet in the system, with a mass of 54.8 ± 7.5M⊕ and provides a marginal detection of K2-19c, with a mass of Mc = 5.9+7.6-4.3 M⊕. We also used the TRADES code to simultaneously model both our RV measurements and the existing transit timing measurements. We derived a mass of 54.4 ± 8.9M⊕ for K2-19b and of 7.5+3.0-1.4M⊕ for K2-19c. For K2-19b, these masses are consistent with a previous determination that was principally based on a photodynamical analysis of the K2-19 light curve. Differences remain mainly in the mass determination of the more lightweight planet, driven likely by the limited precision of the RV measurements and possibly some as yet unrecognized systematics.
Key words: stars: individual: K2-19 / planets and satellites: fundamental parameters / techniques: radial velocities / techniques: spectroscopic / stars: fundamental parameters
RV data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/601/A128
© ESO, 2017
1. Introduction
Planets in mean-motion resonance (MMR) or commensurability have orbital period ratios that are close to integer values. Several MMRs are found in the solar system and are regarded as “tale tellers” of its dynamical evolution. For instance, the Neptune/Pluto 3:2 MMR is believed to be the result of an outward migration of Neptune (Petrovich et al. 2013). According to the Grand Tack model (Walsh et al. 2011), Jupiter and Saturn got trapped in a 3:2 (or 2:1) resonance in the early phases of the solar system formation. This would have halted and inverted the inward migration of Jupiter at ~1.5 AU, shaping the architecture of the inner terrestrial planets as we know it today (see e.g. Pierens et al. 2014).
Exoplanets can also be driven into resonant configurations through dissipative mechanisms that can change the energy of their orbits and thus the corresponding semi-major axis (Plavchan & Bilinski 2013). The MMRs most frequently found in exoplanetary systems are the 2:1 and 3:2 resonances, though others might also exist (see e.g. Holman et al. 2010; Fabrycky et al. 2012; Petrovich et al. 2013; Fabrycky et al. 2014). Current scenarios of planet formation allow for the formation of planets at any orbital radii. Therefore, it is believed that resonant configurations did not come into place during the formation of planets, but are rather the outcome of the dynamical evolution of planetary systems. Mean-motion resonances can thus provide precious insights into the evolution history of planetary systems (Kley 2010).
K2-19 (also known as EPIC 201505350) is a V = 13 mag late-type star observed by the K2 space mission (Howell et al. 2014) during its Campaign 1. It hosts three transiting planets; the orbital periods of the two larger planets are close to the 3:2 mean motion resonance: K2-19b, a sub-Saturn-size planet with an orbital period of ~7.9 days, and K2-19c, a Neptune-size planet with an orbital period of ~11.9 days. The two planets perturb each other causing transit timing variations (TTVs) that are visible in the K2 data (Armstrong et al. 2015) and in ground-based transit observations (Narita et al. 2015; Barros et al. 2015). A small inner planet with a radius of 1.14 ± 0.13 R⊕, named K2-19d, has recently been found to transit the star every ~2.5 days (Sinukoff et al. 2016). We do not consider K2-19d in the following analysis, given its expected small mass and the absence of any reported transit timing variations.
Systems such as K2-19 are precious and unique laboratories for the study of planet formation, migration, and evolution (Armstrong et al. 2015) as their orbital architectures imply a common inward migration scenario for the resonant planets (Naoz 2015). There seems to be a lack of short-period gas giants in 2:1 and 3:2 MMRs, which is likely due to the dynamical instability of these systems (Narita et al. 2015). K2-19b is to date the only gas giant planet with an orbital period shorter than 50 days known to be in a 3:2 MMR. In addition, K2-19 is a unique system compared to other resonant systems: the inner planet K2-19b is larger (and likely more massive) than the outer K2-19c, whereas outer planets in 2:1 or 3:2 MMRs tend to be larger and more massive than the inner ones. An accurate mass determination of K2-19b would be an important piece of the puzzle for understanding the dynamics of such systems (Ogihara & Kobayashi 2013).
Several attempts have been made to determine the masses of K2-19b and K2-19c. Armstrong et al. (2015) combined K2 data with ground-based transit photometry of K2-19b and used the observed TTVs to put some constraints on the mass of the two planets. Barros et al. (2015) used a more sophisticated approach to derive the masses of the planets based on a photo-dynamical model that considers transit timings and durations from transits observed by the K2 mission, as well as two additional K2-19b transits observed from the ground. They also included radial velocities obtained with SOPHIE at the Observatoire de Haute Provence (OHP) 1.9 m telescope in their analysis, although they realized that the precision of these RVs prevented the detection of the Doppler reflex motion induced by the planets. The photo-dynamical approach employed by Barros et al. (2015) models the data with an n-body dynamical integrator that takes into account the gravitational interactions of all components and derives the corresponding transit timings. Furthermore, the photo-dynamical model was executed as part of a Markov chain Monte Carlo (MCMC) method that in principle permits reliable estimates of the planet parameters, given the uncertainties of the TTVs and other input parameters. They found a mass of Mb = 44 ± 12M⊕ for K2-19b and Mc = 15.9 ± 7 M⊕ for K2-19c. Shortly afterwards, Narita et al. (2015) presented additional ground-based transit photometry of K2-19b and modelled the observed TTVs using the “synodic chopping” formulae given by Deck & Agol (2015). They found two possible solutions that are positioned above and below the 3:2 MMR. Despite the degeneracy of their solution, they estimated the mass of the outer planet K2-19c to be Mc ~ 20M⊕, in agreement with Barros et al. (2015). Although Narita et al. (2015) did not include the transit timings from Barros et al. (2015), the follow-up observations of both groups were taken at similar dates and the derived TTVs agree within the error bars. While the photo-dynamical approach by Barros et al. (2015) is in principle reliable and independent of any simplifying assumptions, we note that their analysis is based on an MCMC of no more than 3500 independents points – apparently limited by the computing requirements of the complex model calculations – and that MCMCs in highly non-linear situations (definitively the case for models where TTVs are input parameters) may easily get stuck around solutions that are only local best fits. Barros et al. (2015) in their Sect. 5.2 compare their results to a simplified analysis based solely on the K2 light curve, giving results that are in agreement but with wider posterior parameter distributions. We therefore cannot derive any conclusions on whether the presence or absence of their RV measurements had any effect in their mass determinations. We also note the work of Weiss & Marcy (2014) who studied the TTV derived masses of 65 small exoplanets (Rp ≤ 4 R⊕) and compared them with those derived with RV measurements. They found that masses from TTVs are systematically lower than masses from RVs. An independent verification of the masses of K2-19b and K2-19c from Barros et al. (2015) and Narita et al. (2015) is therefore desirable.
Here we present a high-resolution spectroscopic follow-up of K2-19 and new estimates of the masses of K2-19b and K2-19c. The paper is organized as follows: in Sect. 2 we describe the observations; in Sect. 3 we present the spectral analysis and the properties of the host star; in Sects. 4 and 5 we report on our data analysis. We present and discuss our results in Sect. 6.
2. High-resolution spectroscopic follow-up
We used the FIbre-fed Échelle Spectrograph (FIES; Frandsen & Lindberg 1999; Telting et al. 2014) mounted at the 2.56 m Nordic Optical Telescope (NOT) at Roque de los Muchachos Observatory (La Palma, Spain) to collect ten high-precision RVs of K2-19. The observations were carried out between January 2015 and January 2016 as part of the CAT and OPTICON observing programs 109-MULTIPLE-2/14B, 35-MULTIPLE-2/15B, and 15B/064. We used the FIES high-res mode, which provides a resolving power of R ≈ 67 000 in the spectral range 3600−7400 Å. Following the observing strategy described in Buchhave et al. (2010) and Gandolfi et al. (2014), we took three consecutive exposures of 900−1200 s per observation epoch to remove cosmic ray hits, and acquired long-exposed (Texp ≈ 35 s) ThAr spectra immediately before and after the three sub-exposures to trace the RV drift of the instrument. We reduced the data using standard IRAF and IDL routines, which include bias subtraction, flat fielding, order tracing and extraction, and wavelength calibration. The signal-to-noise ratio (S/N) of the extracted spectra is about ~20−25 per pixel at 5500 Å. Radial velocity measurements were derived via S/N-weighted multi-order cross-correlation with the RV standard star HD 50692 observed with the same instrument set-up as K2-19.
FIES, HARPS-N, and HARPS measurements of K2-19.
We also acquired nine high-resolution spectra (R ≈ 115 000) with the HARPS-N spectrograph (Cosentino et al. 2012) based on the 3.58 m Telescopio Nazionale Galileo (TNG) at Roque de los Muchachos Observatory (La Palma, Spain). The observations were performed between February 2015 and April 2016 as part of the same observing programs as on FIES. For each observation epoch we acquired two consecutive exposures of 1800 s, except for the last epoch when a single exposure of 3600 s was taken. The extracted spectra have a S/N per pixel of ~15−23 at 5500 Å. We monitored the Moon’s background light using the second fibre and reduced the HARPS-N data with the HARPS-N pipeline. Radial velocities were extracted by cross-correlation with a G2 numerical mask (Baranne et al. 1996; Pepe et al. 2002).
Finally, we collected five high-resolution spectra (R ≈ 115 000) with the HARPS spectrograph (Mayor et al. 2003) at the ESO 3.6 m Telescope at La Silla Observatory (Chile). The observations were performed between April and May 2016 as part of the ESO program 097.C-0948. The exposure time was set to 3000−3600 s, leading to a S/N of ~13−35 per pixel at 5500 Å on the extracted spectra. We used the second fibre to monitor the sky background and reduced the data with the online HARPS pipeline. Radial velocities were extracted by cross-correlation with a G2 numerical mask.
The FIES, HARPS-N, and HARPS-S RV measurements and their 1σ error bars are listed in Table 1, along with the barycentric Julian date in barycentric dynamical time (BJDTDB, see e.g. Eastman et al. 2010) and the cross-correlation function (CCF) bisector spans (Queloz 2001). We rejected two of the five HARPS RVs, owing to a technical problem occurred during the observations. These measurements are not listed in Table 1. The FIES and HARPS-N RVs show a possible anti-correlation with the respective CCF bisector spans, the linear Pearson correlation coefficients being −0.42 and −0.62, respectively. We followed the method described in Loyd & France (2014) to account for the uncertainties of our measurements and to quantitatively assess the significance of the possible anti-correlation. We found that the probability that the FIES and HARPS-N measurements are uncorrelated in light of their uncertainties is higher than about 48% and 24%, respectively. We therefore concluded that there is no significant correlation between the FIES and HARPS-N RVs and the respective CCF bisector spans.
3. Stellar parameters
We derived the fundamental spectroscopic parameters of K2-19 from the co-added FIES and HARPS-N spectra. Both data have a S/N of ~55 per pixel at 5500 Å. We used the Spectroscopy Made Easy (SME) package (Valenti & Piskunov 1996) along with ATLAS 9 model atmospheres (Castelli & Kurucz 2004). We fixed the microturbulent vmic and macroturbulent vmac velocities to the values given by the calibration equations of Bruntt et al. (2010) and Doyle et al. (2014), respectively. The effective temperature Teff was estimated by fitting synthetic line profiles to the observed wings of the Hα and Hβ lines. The surface gravity log g⋆ was mainly derived by analysing strong Ca I lines between 6100 and 6440 Å. We measured the projected rotational velocity v sin i⋆ fitting the spectral profiles of several unblended metal lines. The FIES and HARPS-N co-added spectra provide consistent results well within the 1σ error bars. Our final adopted values for Teff, log g⋆, [Fe/H], and v sin i⋆ are the weighted means of the values estimated by the FIES and HARPS-N spectra. Based on the Straizys & Kuriliene (1981) calibration for dwarf stars, our estimates of the spectroscopic parameters translate into a K0 V spectral type. We estimated stellar mass and radius using our values for Teff, log g⋆, [Fe/H] , and the relationship between these parameters and M⋆, R⋆, as given by Torres et al. (2010). Results are given in Table 3; our values for the mass of M⋆ = 0.918 ± 0.064 M⊙ and the radius of R⋆ = 0.881 ± 0.111 R⊙ are about 3% smaller than those derived by Barros et al. (2015), but in agreement within the error bars.
The K2 light curve of K2-19 shows periodic and quasi-periodic photometric variability with a peak-to-peak amplitude of about 1.2% (Armstrong et al. 2015). Given the spectral type of the star, the observed variability is very likely ascribable to magnetic active regions (mainly Sun-like spots) carried around by stellar rotation. We measured the rotation period of the star using the auto correlation function (ACF; see e.g. McQuillan et al. 2013) applied to the light curve of K2-19. We measured a rotation period of Prot = 20.54 ± 0.30 days (Table 3). The fast Fourier transform of the light curve shows also a significant peak at about 20.5 days (S/N = 70), in agreement with the value found by the ACF. A consistent value has also been found by Armstrong et al. (2015). Our estimates of the rotation period and stellar radius imply a value of the rotation velocity of 2.17 ± 0.27 km s-1, which agrees within ~2σ with the spectroscopically derived projected rotation velocity of 3.0 ± 0.5 km s-1.
4. RV data analysis
 |
Fig. 1 FIES (blue circles), HARPS-N (green diamonds), HARPS-S (red triangles), and RV measurements of K2-19 and Keplerian fits (solid line), phase folded to the orbital period and time of first transit of K2-19b (upper) and K2-19c (lower). For K2-19c, the fitted RVs from K2-19b have been removed. All RVs, fits and residuals (in smaller subpanels) are shown following the subtraction of the systemic velocities from the three instruments (Table 2). |
RV-derived parameters of K2-19b and K2-19c from a two-planet model.
We fitted one-planet and two-planet Keplerian models to the FIES, HARPS-N, and HARPS RV data. In the first case, we assumed that the observed Doppler shift is caused entirely by the largest transiting planet K2-19b; in the second case we assumed that both planets contribute to the observed RV variation.
The RV analysis was done using pyaneti, a Python/Fortran software suite based on MCMC sampling (Barragan et al., in prep.). The code implements the ensemble sampler with the affine invariance algorithm of Goodman & Weare (2010). It finds the best fitting parameters of the following equation RV ![\hbox{$=\gamma_i + \sum_j^N K_j \left[ \cos(\theta_j + \omega_{\star,j}) + e_j \cos \omega_{\star,j} \right]$}](/articles/aa/full_html/2017/05/aa28639-16/aa28639-16-eq72.png) , where γi are the systemic velocities as measured by the three instruments; j refers to each planet; N is the number of planets; Kj, θj, ej are the RV semi-amplitude variation, true anomaly, and orbit eccentricity of each planet j, respectively; and ω⋆,j is the argument of periapsis of the star’s orbit.
, where γi are the systemic velocities as measured by the three instruments; j refers to each planet; N is the number of planets; Kj, θj, ej are the RV semi-amplitude variation, true anomaly, and orbit eccentricity of each planet j, respectively; and ω⋆,j is the argument of periapsis of the star’s orbit.
We constrained orbital periods and mid-times of first transit to the values given by Armstrong et al. (2015), i.e. 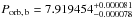 days and
days and 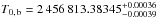 (BJDTDB) for K2-19b, and
(BJDTDB) for K2-19b, and 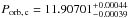 days and T0, c = 2 456 817.2759 ± 0.0012 (BJDTDB) for K2-19c. Using different ephemeris – such as those presented in Sect. 5 or those provided by Narita et al. (2015), Barros et al. (2015) or Sinukoff et al. (2016) – gives consistent results well within the error bars.
days and T0, c = 2 456 817.2759 ± 0.0012 (BJDTDB) for K2-19c. Using different ephemeris – such as those presented in Sect. 5 or those provided by Narita et al. (2015), Barros et al. (2015) or Sinukoff et al. (2016) – gives consistent results well within the error bars.
For the eccentricity and the argument of periapsis we set uninformative uniform priors using the parametrization 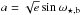 and
and 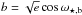 with both a and b within the range ]−1,1 [, where the reversed brackets mean that the range endpoints are excluded. To ensure that e< 1, we also impose the condition a2 + b2< 1, which was checked for all the iterations.
with both a and b within the range ]−1,1 [, where the reversed brackets mean that the range endpoints are excluded. To ensure that e< 1, we also impose the condition a2 + b2< 1, which was checked for all the iterations.
For the systemic RVs, we set uniform priors in the range γi = [7.17,7.35] km s-1, whereas the Kb,c were unconstrained, with initial values randomly set between Kb,c = [0.5,1000] m s-1. For the two-planet fit, we fixed 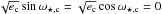 and fit only for the RV semi-amplitude variation Kc.
and fit only for the RV semi-amplitude variation Kc.
We evolved 1000 independent chains and ran 50 000 additional iterations, with a thinning factor of 50, once convergence was reached. The final parameter estimates were obtained by combining the points from all the chains, leading to a total number of 106 points for each parameter.
Assuming a stellar mass of M⋆ = 0.918 ± 0.064 M⊙ (Sect. 3), modelling the RV data with one Keplerian orbit gives a mass of Mb = 58.6 ± 4.6 M⊕ for K2-19b, with a chi-square value of 15.6. The two-planet modelling gives a similar value of Mb = 54.8 ± 7.5 M⊕ for K2-19b, and a mass of Mc = 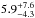 M⊕ for K2-19c, with a chi-square value of 17.5. We conclude that the RV data do not allow us to significantly detect the Doppler reflex motion induced by K2-19c. Nevertheless, two planets are known to be in this system and given the marginal RV detection of K2-19c, the two-planet fit is the preferred one. The parameter estimates, defined as the median values of the posterior probability distributions, are given in Table 2 along with the 68% credible interval.
M⊕ for K2-19c, with a chi-square value of 17.5. We conclude that the RV data do not allow us to significantly detect the Doppler reflex motion induced by K2-19c. Nevertheless, two planets are known to be in this system and given the marginal RV detection of K2-19c, the two-planet fit is the preferred one. The parameter estimates, defined as the median values of the posterior probability distributions, are given in Table 2 along with the 68% credible interval.
5. Combined RV and transit timing analysis
In a further analysis we derived masses and orbital parameters of K2-19b and K2-19c using the code TRADES (Borsato et al. 2014) to simultaneously model RV measurements and TTV data. TRADES combines the Particle Swarm Optimization (PSO; Tada 2007) with the Levenberg-Marquardt algorithm (LM; Moré et al. 1980). We used our FIES, HARPS-N, and HARPS RVs (Sect. 2) along with 20 transit mid-times (TTs) published by Narita et al. (2015)1. The ground-based observations from Barros et al. (2015) were not used in our analysis since the authors do not list the TTs, nor can the measurements be retrieved from their figures with sufficient precision. Considering the similar epochs and O−C times between the Barros et al. (2015) and Narita et al. (2015) follow-up transits, an inclusion of the Barros et al. (2015) transits is unlikely to cause significantly different results. Given the amplitude of the observed RV peak-to-peak variation (~40 m s-1; Fig. 1), we set a very conservative range of 0 <Mp< 100M⊕ for the masses of the two planets. To account for the two degenerate solutions found by Narita et al. (2015), we assumed a wide range for the orbital periods, i.e. Porb, b = 7.8−8.0 days and Porb, c = 11.5−12.5 days. We reduced the correlation between eccentricity e and argument of periapsis ω∗ of the star2 by fitting instead for the combinations ecosω∗ ,i and esinω∗ ,i, where the index i refers to planets b and c. We limited the possible eccentricities to e< 0.5, given the phased RV curve, and let the arguments of periapsis ω∗ and mean anomalies ν vary freely between 0 and 360 degrees. We used the orbital inclinations as given in Barros et al. (2015). We fixed the longitudes of nodes of both planets to zero degrees. The stellar mass was left to float around the value with Gaussian errors found in Sect. 3 (see Table 3).
The PSO simulation evolved 250 initial orbital configurations for 15 000 iterations. We used the best fitting solution as the initial guess for the LM algorithm. TRADES found a best-fit solution with a reduced chi-square 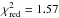 (degrees of freedom d.o.f. = 32). The parameter estimates are listed in Table 3 along with the confidence intervals at the 15.87th and 84.14th (1σ) percentiles of the residual distribution. The confidence intervals were computed with a bootstrap Monte Carlo analysis running 2000 iterations and rescaling the error bars by the quantity
(degrees of freedom d.o.f. = 32). The parameter estimates are listed in Table 3 along with the confidence intervals at the 15.87th and 84.14th (1σ) percentiles of the residual distribution. The confidence intervals were computed with a bootstrap Monte Carlo analysis running 2000 iterations and rescaling the error bars by the quantity 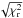 (Bruntt et al. 2006; Southworth et al. 2007; Southworth 2008). By applying the frequency map analysis method (Laskar et al. 1992), we found that the derived orbital configuration is stable. Figure 2 shows the simulated data points from the best-fit solution overlaid on the observed data. The derived planet masses are
(Bruntt et al. 2006; Southworth et al. 2007; Southworth 2008). By applying the frequency map analysis method (Laskar et al. 1992), we found that the derived orbital configuration is stable. Figure 2 shows the simulated data points from the best-fit solution overlaid on the observed data. The derived planet masses are 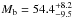 M⊕ and
M⊕ and 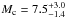 M⊕. We note that the chi-square of the TRADES RV model (which is based on both RVs and TTVs) against the radial velocity data is 19.0, which is higher than the corresponding chi-square (17.5) from the RV analysis presented in the previous section.
M⊕. We note that the chi-square of the TRADES RV model (which is based on both RVs and TTVs) against the radial velocity data is 19.0, which is higher than the corresponding chi-square (17.5) from the RV analysis presented in the previous section.
 |
Fig. 2 Upper panels: observed–calculated (O−C) times and residual plots for transit timings of K2-19b (top) and K2-19c (middle panel). O−C values were computed by subtracting a linear ephemeris from each timing measurement (black dots), taken from K2 data and from ground-based follow-up by Narita et al. (2015). Open blue circles indicate the best fitting model found by TRADES; the lower subpanels indicate the residuals of the TRADES-model. Bottom panel: radial velocity measurements from FIES (red circles), HARPS-N (green squares), and HARPS-S (black triangles), as well as the best fitting model from TRADES (blue open circles). The grey dotted line shows the TRADES RV model of both planets across the observation time window. Residuals against the model are shown in the lower subpanel. |
K2-19 system parameters.
6. Discussion
We present FIES, HARPS-N, and HARPS radial velocity follow-up observations of K2-19, with the aim to determine the masses of its planets K2-19b and K2-19c. From an analysis based only on our RV measurements and with the stellar parameters derived in Sect. 3, we estimate that K2-19b has a mass of Mb = 54.8 ± 7.5 M⊕ and K2-19c has a mass of 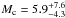 M⊕. However, a combined analysis of RV and TTV measurements (Sect. 5) resulted in a slightly lower mass of Mb = 54.4 ± 8.9M⊕ for K2-19b and higher mass of
M⊕. However, a combined analysis of RV and TTV measurements (Sect. 5) resulted in a slightly lower mass of Mb = 54.4 ± 8.9M⊕ for K2-19b and higher mass of 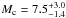 M⊕ for K2-19c. The two mass values of K2-19b are consistent with each other, deviating by less than 1σ. For K2-19c, an analysis of the RVs on their own, without prior knowledge of planet c, does not provide relevant evidence for its existence.
M⊕ for K2-19c. The two mass values of K2-19b are consistent with each other, deviating by less than 1σ. For K2-19c, an analysis of the RVs on their own, without prior knowledge of planet c, does not provide relevant evidence for its existence.
We note that the RV+TTV fits force radial velocity amplitudes that are smaller for planet b and larger for planet c, in both cases by a similar amount of ~1 m s-1 relative to the RV-only fit. Considering the known difficulties of quantifying the contribution from stellar activity to RV amplitudes on the m s-1 level, we expect that the RV amplitudes have larger uncertainties than those derived from the fits discussed in Sects. 4 and 5, which in both cases designate the RV signal as being entirely caused by the orbiting planets. Given this, the results from the two methods can be considered in agreement, implying however that no detection of planet c can be claimed from the radial velocities.
A possible concern is that the known period variation of K2-19b may affect the Keplerian fit to the RV data, which assumed constant periods. The maximum deviations from constant period during our three principal groups of RV observations, near BJDs ending in 7050, 7400, and 7500, are of 10, 70, and 90 min, respectively, based on the Barros et al. (2015) TTV prediction for these epochs (their Fig. 5; with the last value for BJDs ≈ 7500 being an extrapolation). These TTVs are not expected to significantly affect the Keplerian RV fit as they may cause only small shifts in the K2-19b phases of 0.0009, 0.006, and 0.008, respectively, implying RV variations of less than 1 m s-1. Therefore, the RV error bars of ≳ 6 m s-1 for most of our measurements will dominate over RV deviations due to phase shifts, as long as the K2-19b phases remain within 0.04 (or 8 h) relative to phases derived from an ephemeris based on the mean period given in Table 3. A similar argument can be made for K2-19c, where maximum TTVs of 250 min can be predicted, corresponding to a maximum phase shift of 0.015. Due to the small RV amplitude of K2-19c, its RV values would be affected by such a phase shift only on the cm/s level. The RV fit should therefore not be affected by the known TTVs.
Assuming a planet radius3 of 7.16 ± 0.91 R⊕ for K2-19b and of 4.34 ± 0.55 R⊕ for K2-19c, our estimate of the planets’ masses from the combined analysis of RV and TTV measurements implies mean densities of ρb = 0.85 ± 0.31 g cm-3for planet b and 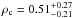 g cm-3for planet c. This density points to a likely gaseous planet with a dense core, similar to the conclusion by Barros et al. (2015). For K2-19c, our derived radius and density would imply a planet somewhat larger than Neptune, but more lightweight and without the silicate and nickel-iron core present in Neptune.
g cm-3for planet c. This density points to a likely gaseous planet with a dense core, similar to the conclusion by Barros et al. (2015). For K2-19c, our derived radius and density would imply a planet somewhat larger than Neptune, but more lightweight and without the silicate and nickel-iron core present in Neptune.
Barros et al. (2015) derived from their photo-dynamical analysis a mass of Mb = 44 ± 12M⊕ for K2-19b and of 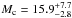 M⊕ for K2-19c, with correspondingly lower and higher densities.
M⊕ for K2-19c, with correspondingly lower and higher densities.
Considering that their planet masses were essentially derived from TTVs, and that the masses from our combined RV+TTV analysis are between their masses and ours from the RV-only analysis, we suspect that the TTVs force the mass derivation of K2-19b towards lower values than are given purely by RV data.
We also note that our TTV analysis and that by Barros et al. (2015) are not identical, with Barros et al. considering also the shapes of transits.
During the revision of this paper, a further study involving RV observations of K2-19 was published by Dai et al. (2016). With an eccentric RV model, they obtained mass estimates that are inconsistent with our work, i.e. 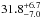 M⊕ for planet b and
M⊕ for planet b and 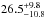 M⊕ for planet c. A revision of the RV values in their Table 7 shows that the majority of their RV data were obtained with the Carnegie Planet Finder Spectrograph (PFS) on the 6.5 m Magellan/Clay Telescope. In most of their observing nights, they obtained three nightly RV points of K2-19. Most of these nightly groups show differences between individual data points that are much larger than their quoted uncertainties of ~5 m s-1, in many cases with nightly RV variations exceeding 20 m s-1. These variations are too large to be ascribed to a physical origin in the K2-19 system and apparently arise from an unrecognized source of measurement errors. Given the strong nightly RV shifts in the PFS data, unrecognized error sources that affect frequencies longer than a single night might be present as well, with potential effects onto the planets’ RV amplitudes.
M⊕ for planet c. A revision of the RV values in their Table 7 shows that the majority of their RV data were obtained with the Carnegie Planet Finder Spectrograph (PFS) on the 6.5 m Magellan/Clay Telescope. In most of their observing nights, they obtained three nightly RV points of K2-19. Most of these nightly groups show differences between individual data points that are much larger than their quoted uncertainties of ~5 m s-1, in many cases with nightly RV variations exceeding 20 m s-1. These variations are too large to be ascribed to a physical origin in the K2-19 system and apparently arise from an unrecognized source of measurement errors. Given the strong nightly RV shifts in the PFS data, unrecognized error sources that affect frequencies longer than a single night might be present as well, with potential effects onto the planets’ RV amplitudes.
To date there are only a few planets whose masses have been derived using both methods. As examples we cite Nesvorný et al. (2013) and Barros et al. (2014), who both derived the mass of Kepler-88c (formerly known as KOI-142c) using TTVs and RV measurements, respectively. The first team measured a mass of 0.62 ± 0.03 MJup from TTVs detected on the transiting planet Kepler-88b, from which they determined the mass of the non-transiting planet Kepler-88c. The presence of Kepler-88c was later confirmed by Barros et al. (2014) using RV measurements. They derived a mass of 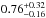 MJup for planet c, which agrees with TTV predictions of Nesvorný et al. (2013) and provides an independent validation of the TTV method.
MJup for planet c, which agrees with TTV predictions of Nesvorný et al. (2013) and provides an independent validation of the TTV method.
In the Kepler-89, system, however, Weiss et al. (2013) give RV derived masses for the planets Kepler-89c and d, with a marginal detection of the more lightweight planet c. Masuda et al. (2013) and Hadden & Lithwick (2016) each present a TTV analysis of the same system. They are able to determine the mass of planet c, found to be in the range of the Weiss et al. RV measurement, whereas their mass determinations of planet d indicate a mass ≈3 times lower than that calculated from RVs.
Another case is the reanalysis of RV and TTVs data of the Kepler-9 planetary system by Borsato et al. (2014) using the same analysis tool as in this paper (TRADES), and who estimated planet masses ~55% lower than those reported in the original discovery paper (Holman et al. 2010), which was based on a combination of RVs, transit times, and durations. In this case, Borsato et al. (2014) ascribe the discrepancy to the longer Kepler light curve that they analysed, and to different approaches in the interpretation of the TTVs.
Recently, Cubillos et al. (2017) have studied all Neptune-like planets for which both masses and radii are known, and they also note that the planets measured by TTVs typically have lower densities. Weiss & Marcy (2014) already discuss possible causes of this difference, quoting systematic underestimations for masses from TTVs (e.g. from damping of TTVs by other planets) or selection effects that make lower density planets easier to detect by TTVs. Cubillos et al. (2017) also present a hypothesis that the lower densities of TTV planets are possibly caused by high-altitude clouds or hazes that lead to inflated radii; however, this would only apply if there are systematic differences in the radii of RV and TTV measured planets caused by selection effects. Lee et al. (2016) hypothesize that such a selection may be the result of low density planets being more amenable (than denser super-Earths) to migrate to close orbits within chains of planets connected by mean-motion resonances. Consequently, such planets would preferentially be detected through TTVs. In any case, selection effects cannot account for any differences in masses if both RV and TTV masses are known.
From the results of this work, RV and TTV measurements complement each other, and create only slight discrepancies. For planet b, which is the more significant detection in the K2-19 system, the addition of RV measurements raised the mass obtained previously from TTVs by Barros et al. (2015), but within the error bars. Planet c was barely detected in our RV data, whereas we know that it exists from the transits and it is detected with much higher significance from TTV data alone or from their combination with RV data. This difference in the detection quality of a low-mass planet arises most likely from the limited precision of the RV data. We also note that RV results from different teams may vary strongly; this may be due to unrecognized issues of their calibration. To resolve such discrepancies among different results, a better understanding of the causes that may generate systematics between RV and TTV methods, but also between results obtained by the same method is desirable. More mass measurements of planets with both RVs and TTV methods should also lead to a better understanding of the origins of these differences.
We used only 20 TTs out of the 21 listed by Narita et al. (2015) because there are two TTs identified with epoch 34, observed at two different facilities, which we joined into a single data point with a smaller uncertainty.
Derived from the planet-to-star radius ratio of 0.0745 ± 0.0010 for K2-19b and 0.0451 ± 0.0007 for K2-19c from Barros et al. (2015) and our stellar radius estimate given in Table 3.
Acknowledgments
We thank the referee, Kento Masuda, for the careful revision and comments which improved this article. Also we are thankful to Jorge Melendez, Martin Kürster, François Bouchy, Nuno Santos, and Xavier Bonfils who kindly agreed to exchange HARPS time with us. This work is based on observations obtained with the Nordic Optical Telescope, operated jointly by Denmark, Finland, Iceland, Norway, and Sweden, and the HARPS-N spectrograph on the Italian Telescopio Nazionale Galileo (TNG), operated by the INAF – Fundacion Galileo Galilei. Both telescopes are on the island of La Palma in the Spanish Observatorio del Roque de Los Muchachos of the Instituto de Astrofísica de Canarias. Based also on observations made with the ESO 3.6 m Telescope at La Silla Observatory under program ID 097.C-0948. The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2013-2016) under grant agreement No. 312430 (OPTICON). D.N. acknowledges an FPI fellowship BES-2013-067287 and H.J.D. acknowledges support by grant ESP2015-65712-C5-4-R, both from the Spanish Secretary of State for R&D&i (MINECO).
References
- Armstrong, D. J., Santerne, A., Veras, D., et al. 2015, A&A, 582, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Díaz, R. F., Santerne, A., et al. 2014, A&A, 561, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Almenara, J. M., Demangeon, O., et al. 2015, MNRAS, 454, 4267 [NASA ADS] [CrossRef] [Google Scholar]
- Borsato, L., Marzari, F., Nascimbeni, V., et al. 2014, A&A, 571, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Southworth, J., Torres, G., et al. 2006, A&A, 456, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bakos, G. A., Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 1 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv eprint [arXiv:astro-ph/0405087] [Google Scholar]
- Cubillos, P., & Erkaev, V. N. 2017, MNRAS, 466, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, F., & Winn, J. N. 2016, ApJ, 823, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Deck, K. M., & Agol, E. 2015, ApJ, 802, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, A. P., Davies, G. R., Smalley, B., et al. 2014, MNRAS, 444, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Ford, E. B., Steffen, J. H., et al. 2012, ApJ, 750, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., & Lindberg, B. 1999, in Astrophysics with the NOT, Proc., eds. H. Karttunen, & V. Piirola, Anot. Conf., 71 [Google Scholar]
- Gandolfi, D., Parviainen, H., Deeg, H. J., et al. 2015, A&A, 576, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. App. Math. Comp. Sci., 5, 65 [Google Scholar]
- Hadden, S., & Lithwick, Y. 2016, ArXiv eprint [arXiv:1611.03516] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 2010, in Formation and Evolution of Exoplanets, ed. R. Barnes, 203 [Google Scholar]
- Laskar, J., Froeschlé, C., & Celletti, A. 1992, Phys. D, 56, 253 [CrossRef] [Google Scholar]
- Lee, E. J., & Chiang, E. 2016, ApJ, 817, L90 [NASA ADS] [CrossRef] [Google Scholar]
- Loyd, R. O. P., & France, K. 2014, ApJS, 211, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, K., Hirano, T., Taruya, A., Nagasawa, M., & Suto, Y. 2013, ApJ, 778, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McQuillan, A., Aigrain, S., & Mazeh, T. 2013, MNRAS, 432, 1203 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moré, J. J., Garbow, B. S., & Hillstrom, K. E. 1980, ANL-80-74, Chap. 1−3 [Google Scholar]
- Naoz, S. 2015, PNAS, 112, 4189 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, N., Hirano, T., Fukui, A., et al. 2015, A&A, 815, A47 [Google Scholar]
- Nesvorný, D., Kipping, D., Terrell, D., et al. 2013, ApJ, 777, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Kobayashi, H. 2013, ApJ, 775, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovich, C., Malhotra, R., & Tremaine, S. 2013, ApJ, 770, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., Raymond, S. N., Nesvorny, D., & Morbidelli, A. 2014, ApJ, 795, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Plavchan, P., & Bilinski, C. 2013, ApJ, 769, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., & Henry, G. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sinukoff, E., Howard, A. W., Petigura, E. A., et al. 2016, ApJ, 827, 78S [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bruntt, H., & Buzasi, D. L. 2007, A&A, 467, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straizys, V., & Kuriliene, G. 1981, Ap&SS, 80, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Telting, J. H., Avila, G., Buchhave, L., et al. 2014, AN, 335, 41 [Google Scholar]
- Tada, T. 2007, J. Jpn Soc. Hydrology & Water Res., 20, 450 [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 768, 14 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 FIES (blue circles), HARPS-N (green diamonds), HARPS-S (red triangles), and RV measurements of K2-19 and Keplerian fits (solid line), phase folded to the orbital period and time of first transit of K2-19b (upper) and K2-19c (lower). For K2-19c, the fitted RVs from K2-19b have been removed. All RVs, fits and residuals (in smaller subpanels) are shown following the subtraction of the systemic velocities from the three instruments (Table 2). |
| In the text | |
 |
Fig. 2 Upper panels: observed–calculated (O−C) times and residual plots for transit timings of K2-19b (top) and K2-19c (middle panel). O−C values were computed by subtracting a linear ephemeris from each timing measurement (black dots), taken from K2 data and from ground-based follow-up by Narita et al. (2015). Open blue circles indicate the best fitting model found by TRADES; the lower subpanels indicate the residuals of the TRADES-model. Bottom panel: radial velocity measurements from FIES (red circles), HARPS-N (green squares), and HARPS-S (black triangles), as well as the best fitting model from TRADES (blue open circles). The grey dotted line shows the TRADES RV model of both planets across the observation time window. Residuals against the model are shown in the lower subpanel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


