| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 6 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201629705 | |
| Published online | 23 March 2017 | |
Limb and gravity-darkening coefficients for the TESS satellite at several metallicities, surface gravities, and microturbulent velocities⋆
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
e-mail: claret@iaa.es
Received: 13 September 2016
Accepted: 27 October 2016
Aims. We present new gravity and limb-darkening coefficients for a wide range of effective temperatures, gravities, metallicities, and microturbulent velocities. These coefficients can be used in many different fields of stellar physics as synthetic light curves of eclipsing binaries and planetary transits, stellar diameters, line profiles in rotating stars, and others.
Methods. The limb-darkening coefficients were computed specifically for the photometric system of the space mission tess and were performed by adopting the least-square method. In addition, the linear and bi-parametric coefficients, by adopting the flux conservation method, are also available. On the other hand, to take into account the effects of tidal and rotational distortions, we computed the passband gravity-darkening coefficients y(λ) using a general differential equation in which we consider the effects of convection and of the partial derivative (∂lnI(λ) /∂lng)Teff.
Results. To generate the limb-darkening coefficients we adopt two stellar atmosphere models: atlas (plane-parallel) and phoenix (spherical, quasi-spherical, and r-method). The specific intensity distribution was fitted using five approaches: linear, quadratic, square root, logarithmic, and a more general one with four terms. These grids cover together 19 metallicities ranging from 10-5 up to 10+1 solar abundances, 0 ≤ log g ≤ 6.0 and 1500 K ≤Teff ≤ 50 000 K. The calculations of the gravity-darkening coefficients were performed for all plane-parallel ATLAS models.
Key words: planetary systems / stars: atmospheres / binaries: eclipsing
Tables 2–29 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/600/A30
© ESO, 2017
1. Introduction
The limb-darkening coefficients (LDC) are a fundamental tool in several areas of stellar physics, as for example: eclipsing binaries, measurement of stellar diameters, line profiles in rotating stars, gravitational micro-lensing, optical interferometry, or more recently, extra-solar planets’ transits. Despite the advances in the semi-empirical derivations of LDC, there is still a serious scarcity of this kind of data. Because of this, we are not yet able to perform a robust and consistent inter-comparison between observational and theoretical LDC. However, in the past few years an important effort has been carried out in this direction. For details of these comparisons related to eclipsing binaries and planetary transits see for example Claret (2008; 2009), Southworth (2008, 2012), Sing (2010), Howarth (2011), Claret & Bloemen (2011), Csizmadia et al. (2013), and Müller et al. (2013).
One of the most important sources of the semi-empirical data of LDC are the space missions such as Kepler, CoRoT, and Microvariability and Oscillations in STars (MOST) which are providing extensive observational material of high quality which is enabling a more comprehensive comparison. Complementing this set of space missions, next year the satellite Transiting Exoplanet Survey Satellite (TESS) is scheduled to launch and the data collected by all these instruments will enable the researchers to extend even further the comparison of semi-empirical data with the theoretical LDC in some favourable cases. These comparisons are crucial since they may provide some clues to the stellar atmosphere modellers which could help to improve the theoretical models. As a small contribution to this effort, we present in this paper the theoretical calculations of the limb and gravity-darkening coefficients (GDC) for the photometric system of the satellite TESS.
The paper is organized as follows. In Sect. 2 we describe briefly the objectives and main characteristics of the TESS mission. Section 3 is devoted to introducing the numerical methods and the stellar atmosphere models used to compute the LDC and GDC, while in Sect. 4 we discuss the results.
2. A brief summary of the space mission TESS
Following the successful steps by the Kepler mission, TESS is a new exo-planet finder to be launched by NASA in 2017 that will perform an all-sky survey. It is expected that this instrument will explore about 200 000 stars in the solar neighbourhood, searching for exo-planets through the planetary transit technique. The stars which are planned to be observed with TESS are brighter, on average, than those observed by Kepler and the spectral types to be surveyed range from F5 to M5. On the other hand, the sky area to be covered is 400 times larger than that covered by Kepler. The mentioned characteristics, among others, will permit the identification of a wide range of planets from the size of Earth to gas giants, in diverse orbital configurations. Therefore, it will be possible to investigate some fundamental planetary properties such as mass, radius, orbital dynamics, and details on the atmosphere (for more information on the mission, see Ricker et al. 2015; Sullivan et al. 2015, and references given therein).
Within this context the calculations of the LDC are important since they will allow the synthesis of light curves to be compared with the observational data coming from TESS. As mentioned in the Introduction, these inter-comparisons may supply new and more accurate data for the semi-empirical LDC, providing a crucial test to the stellar atmosphere models.
3. Numerical methods and the grids of stellar atmosphere models
The LDC laws adopted here are written down to facilitate the identification of the coefficients contained in the respective tables:
the linear law 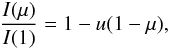 (1)the quadratic law
(1)the quadratic law 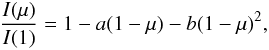 (2)the square root law
(2)the square root law 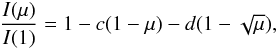 (3)the logarithmic law
(3)the logarithmic law 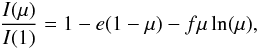 (4)and a four terms law introduced by us some time ago:
(4)and a four terms law introduced by us some time ago: 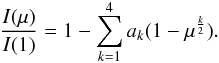 (5)In the above equations I(1) is the specific intensity at the centre of the disk and u,a,b,c,d,e,f, and ak are the corresponding LDC. The μ’s are given by cos(γ), where γ is the angle between the line of sight and the outward surface normal. The model atmosphere intensities were convolved with the transmission curve for TESS, provided by D. Latham (priv. comm.). As in the previous papers in this series, we have used the ATLAS (plane-parallel geometry), PHOENIX-COND with spherical geometry (Husser et al. 2013), and PHOENIX-DRIFT also with spherical geometry (Witte et al. 2009). These grids cover together 19 metallicities ranging from 10-5 up to 10+1 solar abundance, 0 ≤ log g ≤ 6.0 and 1500 K ≤Teff ≤ 50 000 K. The values of the microturbulent velocities (Vξ) are 0, 1, 2, 4, 8 km s-1.
(5)In the above equations I(1) is the specific intensity at the centre of the disk and u,a,b,c,d,e,f, and ak are the corresponding LDC. The μ’s are given by cos(γ), where γ is the angle between the line of sight and the outward surface normal. The model atmosphere intensities were convolved with the transmission curve for TESS, provided by D. Latham (priv. comm.). As in the previous papers in this series, we have used the ATLAS (plane-parallel geometry), PHOENIX-COND with spherical geometry (Husser et al. 2013), and PHOENIX-DRIFT also with spherical geometry (Witte et al. 2009). These grids cover together 19 metallicities ranging from 10-5 up to 10+1 solar abundance, 0 ≤ log g ≤ 6.0 and 1500 K ≤Teff ≤ 50 000 K. The values of the microturbulent velocities (Vξ) are 0, 1, 2, 4, 8 km s-1.
The LDC were computed adopting the least square method (LSM) that allows a very good description of I(μ) at any part of the disk, for any log g, effective temperature, metallicity, and microturbulent velocity, mainly if Eq. (5) is adopted. Indeed, it is desirable to handle an approach such as Eq. (5) that presents the following characteristics: (a) a single law which is valid for the whole HR (Hertzsprung-Russell) diagram; (b) is capable of reproducing well the intensity distribution and which as a consequence conserves the flux within a very small tolerance; (c) can be applicable to different pass-bands, monochromatic quantities, chemical compositions, effective temperatures, gravities, and microturbulent velocities. For the case of LSM, we adopted equally spaced μ points to prevent too large weights being applied to the limb. For completeness, we also computed the LDC adopting the flux conservation method (FCM), for bi-parametric laws and for the linear approximation; to differentiate, we used the suffixes LSM and FCM in the tables.
The dispersion of the specific intensities associated to the FCM can be as large as 1000 times those provided by the LSM when Eq. (5) is adopted. This is a serious restriction to the FCM since a good match is necessary to compute the loss and gain of light during the eclipses. Moreover, if a non-linear law is used, an extra condition must be introduced, in addition to the flux conservation. This extra condition is often arbitrary. On the other hand, the inter-comparison between the LDC computed with both numerical methods can serve as a tool to estimate the theoretical error bars. We refer interested readers to Claret (2000) for a more detailed discussion on this subject.
Due to the different input physics and numerical resolutions, the PHOENIX models are divided into two sets: 1500 K ≤ Teff ≤ 3000 K (DRIFT) and another with 2300 K ≤ Teff ≤ 12 000 K (COND). Still concerning the PHOENIX models, we have introduced in past papers the concept of quasi-spherical models for main sequence stars. For this kind of stars spherical models are constituted by a core (μ> 0.1) that behaves like a plane-parallel structure, and by an envelope that delivers the spherical part of the intensities (μ ≲ 0.1. When we compare the intensity distribution of a spherical model with one adopting the plane-parallel geometry but with the same input physics (log g, metallicity, Teff, Vξ), we detect a similar intensity distribution for both models, except in the drop-off region (μ ≲ 0.1). We define a quasi-spherical model as the model computed adopting the spherical symmetry but whose LDC are computed only for the core, that is, without considering the points inside the drop-off region. This concept allows us to compare the LDC for PHOENIX and ATLAS models (see below). It can be also used in situations where the effects of sphericity are not important.
Before discussing the results of the LDC for TESS, it is convenient to investigate an alternative to the usual quasi-spherical models. Based on the work by Wittkowski et al. (2004), Espinoza & Jordan (2015) used 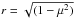 , instead of μ. They derive the LDC by searching for the maximum of the derivative of the specific intensity with respect to r and shifting the profile to this point (hereafter referred as r-method). These authors have found large differences when comparing the quadratic LDC (Kepler) computed using the r-method with the quadratic LDC using quasi-spherical models by Claret et al. (2012), mainly for cooler models as seen in their Fig. 6. However, this comparison was not performed for the same PHOENIX models: Claret, Hauschildt, & Witte used the PHOENIX-DRIFT models for effective temperatures lower than 3000 K, while Espinoza & Jordan adopted the PHOENIX-COND ones (Espinoza, priv. comm.). This important point was not considered by the mentioned authors in that comparison. The differences between PHOENIX-DRIFT and PHOENIX-COND models are large, as discussed in Claret et al. (Sect. 2). Moreover, the LDC computed for larger effective temperatures by Claret et al. are also not completely suitable for direct comparison in Fig. 6 by Espinoza & Jordan, because they also come from different stellar atmosphere models from those adopted by these authors.
, instead of μ. They derive the LDC by searching for the maximum of the derivative of the specific intensity with respect to r and shifting the profile to this point (hereafter referred as r-method). These authors have found large differences when comparing the quadratic LDC (Kepler) computed using the r-method with the quadratic LDC using quasi-spherical models by Claret et al. (2012), mainly for cooler models as seen in their Fig. 6. However, this comparison was not performed for the same PHOENIX models: Claret, Hauschildt, & Witte used the PHOENIX-DRIFT models for effective temperatures lower than 3000 K, while Espinoza & Jordan adopted the PHOENIX-COND ones (Espinoza, priv. comm.). This important point was not considered by the mentioned authors in that comparison. The differences between PHOENIX-DRIFT and PHOENIX-COND models are large, as discussed in Claret et al. (Sect. 2). Moreover, the LDC computed for larger effective temperatures by Claret et al. are also not completely suitable for direct comparison in Fig. 6 by Espinoza & Jordan, because they also come from different stellar atmosphere models from those adopted by these authors.
To try to clarify this point we compute quadratic LDC (Kepler) for PHOENIX-COND models adopting the usual quasi-spherical (μ> 0.1) and the r-method. This allows us to compare the LDC varying only the numerical methods for PHOENIX models while adopting the same input physics. Figure 1 shows such a comparison for the LDC as a function of the effective temperature, where crosses and asterisks represent the calculations adopting the usual quasi-spherical and r-method, respectively. The PHOENIX-DRIFT (x) models are also shown for comparison. The differences between the LDC for the PHOENIX-DRIFT and PHOENIX-COND models are very similar and are of the same order as those found by Espinoza & Jordan in their Fig. 6. However, the total magnitude of these differences in this case (log g = 4.5) is not fully assessed due to the different adopted methods (quasi-spherical and r) as Espinoza & Jordan argued; these differences are mainly related to the comparison between two different versions of PHOENIX models. A direct comparison between the LDC for PHOENIX-COND models adopting the usual quasi-spherical and r methods shows that both procedures provide very similar LDC (Fig. 1) presenting only small differences in the region 3.43 < log Teff< 3.65. These differences are probably related in part to the goodness of the fitting since in this interval the r-method provides the worse fittings (see third panel).
 |
Fig. 1 Quadratic LDC for PHOENIX-COND models. Quasi-spherical models are represented by a continuous line and crosses and the r method by a dashed line and asterisks. The LDC for the PHOENIX-DRIFT models from Claret et al. (2012) are denoted by a dashed-dotted line and the symbol x. In the last case and for the sake of clarity, only models with Teff< 4400 K are shown. The third panel shows the root square of the merit function χ. All calculations were performed for log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1. Kepler photometric system. LSM calculations. |
On the other hand, numerical experiments show that the goodness of fittings also depends on the local gravity (drop-off), being in general higher for the usual quasi-spherical method in the case of large log g. The opposite occurs for the r-method, at least for Kepler quadratic LDC. For the general case of bi-parametric laws, the differences between the LDC obtained using the usual quasi-spherical and r methods increase for small values of log g; these differences are, however, very small for main sequence models, that is for log g ≥ 4.0. In the case of the linear law, the mentioned differences are small and almost independent of logg. To try to minimize this problem, we redefine a quasi-spherical model as before but instead of considering the points μ> 0.1 we apply a simple algorithm to the normalized specific intensities to properly consider the exclusion of the drop-off region. We consider for LDC calculations the μ points between 1.0 and the point where the normalized intensity decays to 0.1. This method has the advantage of preserving the original core points of the PHOENIX models to effects of comparison with the other procedures. This new definition does not affect seriously the previous LDC calculations, particularly for main sequence models. Figure 1 confirms this point. Hereafter (including Table A.1) the quasi-spherical models refer to the new definition.
Despite the problems with the comparison of LDC performed by Espinoza & Jordan discussed previously and the similarities between the results from the new quasi-spherical and r methods mainly for main sequence models, the LDC for PHOENIX-DRIFT and PHOENIX-COND models are available by adopting both methods (Table A.1). We also provide the respective merit function to guide the readers when selecting the more suitable LDC. The LDC adopting PHOENIX models for other chemical compositions can be provided to the interested readers upon request.
4. Discussion of the results
4.1. Limb-darkening
As discussed extensively in the earlier papers on limb-darkening, the linear law is not a suitable approximation for most of the specific intensity distributions. This non-linearity is even more conspicuous in the case of spherical models due to the drop-off caused by the decreased matter-radiation interaction for μ ≲ 0.1. Although this law presents this problem, it can still be useful for comparing models with different geometries and/or input physics. For example, in Fig. 2 we plot the linear LDC(TESS) for PHOENIX-COND (quasi-spherical) and ATLAS models, with log[A/H] = 0.0, Vξ = 2 km s-1 and log g = 4.5. The continuous line denotes the ATLAS models while the dashed line indicates the LDC for PHOENIX-COND models. The agreement can be considered as good, except in the onset of convection, because both sets of models were computed with different mixing-length parameters. Also, for lower effective temperatures the agreement is not so good, due to the different input physics for cooler models.
 |
Fig. 2 Theoretical linear LDC for ATLAS models (continuous line) and PHOENIX-COND quasi-spherical ones (dashed line): log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1; TESS photometric system; LSM calculations. |
 |
Fig. 3 Specific intensity distribution for a [1500 K, 4.5] PHOENIX-DRIFT quasi-spherical symmetric model. Continuous line represents the model intensities (left label), while the dashed line denotes the deviations [model-fit] by adopting Eq. (5) and the dashed-dotted one represents the deviations by adopting Eq. (1) (right label): log[A/H] = 0.0, Vξ = 2 km s-1; TESS photometric system; LSM calculations. |
 |
Fig. 4 Theoretical linear LDC for ATLAS models. Continuous line denotes TESS while dashed line represents the Kepler photometric system; log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1; LSM calculations. |
 |
Fig. 5 Effects of metallicity and evolutionary status on the theoretical linear LDC for ATLAS models; TESS photometric system. Upper panel: continuous line denotes models with log[A/H] = 0.0 while dashed line indicates log[A/H] =−0.5 and dashed-dotted line those with log[A/H] =−1.0; log g = 4.5 and Vξ = 2 km s-1 for all models. Lower panel: continuous line denotes models with log g = 4.5 and dashed line represents models with log g = 3.0; log [A/H] = 0.0 and Vξ = 2 km s-1 for all models. LSM calculations for both panels. |
It is worth noticing the high values of the linear LDC (larger than 1.0) for the PHOENIX-DRIFT models at lowest effective temperatures, since it implies a negative relative intensity at the limb. This is a consequence of the not so good fit provided by Eq. (1). In Fig. 3 we show the behaviour of a PHOENIX model with Teff = 1500 K, log[A/H] = 0.0, Vξ = 2 km s-1, and log g = 4.5. The model intensity is represented by a continuous line while the dashed one denotes the deviation of the intensity [model-fitted] using Eq. (5) and the dashed-dotted line represents the deviation using Eq. (1). As a consequence of this, we recommend using the approach given by Eq. (5) or at least a bi-parametric law for the lowest effective temperatures.
A point that can be of special interest for observers is the behaviour of the LDC for the photometric systems of Kepler and TESS. Again we use the linear coefficient for the sake of clarity in the comparison. As the effective wavelengths are very different (≈630 and ≈800 nm, respectively) the corresponding LDC follow the general trend with the effective wavelength being smaller for higher λeff. The differences shown in Fig. 4 could be detected within the expected accuracy of semi-empirical LDC. Therefore, it will be very useful in the future if observers compare their respective semi-empirical LDC obtained with both instruments for similar target stars. It would also be very interesting to compare the empirical LDC with those generated using the two atmospheres’ models adopted here, given that both cover the spectral range of TESS.
Other points of interest are the metallicity and evolutionary effects on the LDC. In Fig. 5 we can see a comparison between models computed with the solar abundance and less metallic ones (upper panel, log [A/H] =−0.5 and –1.0). The differences are more pronounced for models located after the onset of convection, that is, for log Teff < 3.9. The influence of the evolutionary status is shown in the lower panel. The corresponding differences are large for the extreme ranges of effective temperatures and could be detected observationally.
4.2. Gravity-darkening
In a binary system the tides tend to elongate the stars along the line that joins them, while rotation tends to flatten them at the poles. The deviations from the spherical symmetry can be written as a function of the rotational rate and of the mass ratio. In addition to the geometrical perturbations due to the proximity effects, there is also an associated thermodynamic change. In 1924, von Zeipel established that the flux distribution in a distorted star is not uniform and is proportional to gβ1, where g is the local gravity and β1 is the gravity-darkening exponent (GDE), usually taken as 1.0 for radiative envelopes. This β1 is valid only for stars in strict radiative equilibrium and when the diffusion equation is used as a transfer equation. Recently, Claret (2015, 2016) showed that, under determined physical conditions, the theorem by von Zeipel is no longer valid.
 |
Fig. 6 Theoretical gravity-darkening coefficients for TESS, ATLAS models. The continuous line represents the calculations for log [A/H] = 0.00 and dashed line is for log [A/H] =−2.5, log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1. |
The GDE is a bolometric quantity but observations are generally performed in photometric bands. In 1959 Kopal introduced the concept of gravity-darkening coefficients (GDC, y(λ)) which connect both the bolometric and pass-band quantities. This concept is very useful to compute the light distribution of distorted configurations. If we expand in a series the ratio between the monochromatic and total radiation, we obtain the corresponding y(λ). For simplicity, it was assumed that the distorted configurations radiate as a black-body, which is not a good approximation. Often the following expression by Martynov (1973) is adopted to compute the GDC: ![\begin{eqnarray} y(\lambda, T_{\rm eff}, \log {\rm [A/H]}, \log g, V_{\xi}) = \frac{1}{4} \left(\frac{\partial\!\ln I(\lambda)} {\partial\!\ln T_{\rm eff}}\right)_{g}\cdot \end{eqnarray}](/articles/aa/full_html/2017/04/aa29705-16/aa29705-16-eq56.png) (6)In the above equation, λ denotes the wavelength and I the intensity at a given wavelength (or pass-band) at the centre of the stellar disc. This equation was improved later by Claret & Bloemen (2011) to take into account the term (∂lnI(λ) /∂lng)Teff and the effects of convection on β1. Moreover, instead of the black-body approach we use the same ATLAS atmosphere models used to compute the LDC. Therefore, the general equation which will be adopted here to compute y(λ) is:
(6)In the above equation, λ denotes the wavelength and I the intensity at a given wavelength (or pass-band) at the centre of the stellar disc. This equation was improved later by Claret & Bloemen (2011) to take into account the term (∂lnI(λ) /∂lng)Teff and the effects of convection on β1. Moreover, instead of the black-body approach we use the same ATLAS atmosphere models used to compute the LDC. Therefore, the general equation which will be adopted here to compute y(λ) is: ![\begin{eqnarray} &&\lefteqn{y(\lambda, T_{\rm eff }, \log {\rm [A/H]}, \log g, V_{\xi}) =} \nonumber \\[2mm] &&\qquad\lefteqn{\left(\frac{{ \rm d}\!\ln T_{\rm eff }}{{{\rm d}\!\ln g}}\right) \left(\frac{\partial{\ln I(\lambda)}}{{\partial{\ln T_{\rm eff }}}}\right)_{g} + \left(\frac{\partial{\ln I(\lambda)}} {\partial{\ln g}}\right)_{T_{\rm eff}}\cdot} \end{eqnarray}](/articles/aa/full_html/2017/04/aa29705-16/aa29705-16-eq59.png) (7)The effects of the convection on y(λ) are important for cooler models and (dlnTeff/ dlng) was computed considering the bolometric GDE previously calculated (see Claret 2004). For the models located in the main-sequence, the contribution of the partial derivative at constant effective temperature is not important, but it is not negligible for cool giants stars. Of course, Eq. (7) reduces to Eq. (6) if β1 = 1.0 and the partial derivative at constant effective temperature are assumed to be zero.
(7)The effects of the convection on y(λ) are important for cooler models and (dlnTeff/ dlng) was computed considering the bolometric GDE previously calculated (see Claret 2004). For the models located in the main-sequence, the contribution of the partial derivative at constant effective temperature is not important, but it is not negligible for cool giants stars. Of course, Eq. (7) reduces to Eq. (6) if β1 = 1.0 and the partial derivative at constant effective temperature are assumed to be zero.
The results for the TESS photometric system are shown in Fig. 6 for log [A/H] = 0.0 and –2.5. The effects of metallicity on y(λ) are not very large, except for two regions centred in log Teff = 3.7 and 4.5. The drop-off in y(λ) around log Teff = 3.9 is due to the effects of convection on β1. These computations supersede the old values of y(λ) based on the black-body approximation. Due to the narrowness of the basic physics input (log Teff, log g, log [A/H], Vξ) of the PHOENIX grids, we have computed y(λ) only for the ATLAS models. However, the calculations adopting PHOENIX models can be provided to interested readers upon request. Finally, Table A.1 summarizes the kind of data available at the Centre de Données Astronomiques de Strasbourg (CDS) or directly from the author.
Acknowledgments
I thank the anonymous referee for his or her comments on the original manuscript. The author would like to thank D. Latham and G. Torres for suggesting this work, for providing the transmission curve of TESS, and for helpful discussions. I acknowledge T.-O. Husser and P. Hauschildt for providing the PHOENIX models. I also would like to thank B. Rufino for her comments. The Spanish MEC (AYA2015-71718-R and ESP2015-65712-C5-5-R) is gratefully acknowledged for its support during the development of this work. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.
References
- Csizmadia, Sz., Pasternacki, Th., Dreyer, C., et al. 2013, A&A, 549, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2008, A&A, 482, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2009, A&A, 506, 1335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2015, A&A, 577, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2016, A&A, 588, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinoza, N., & Jordan, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D. 2011, MNRAS, 418, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopal, Z. 1959, Close Binary Systems (Chapman & Hall) [Google Scholar]
- Martynov, D. Ya. 1973, in Eclipsing Variable Stars, ed. V. P. Tsesevich (IPST Astrophysics Library), 128 [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astronomical Telescopes, Instruments, and Systems, 1, 014003 [Google Scholar]
- Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2012, MNRAS, 426, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K., et al. 2015, ApJ, 809, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, S., Helling, Ch., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004, A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Table
Gravity and limb-darkening coefficients for the TESS photometric system.
All Tables
All Figures
 |
Fig. 1 Quadratic LDC for PHOENIX-COND models. Quasi-spherical models are represented by a continuous line and crosses and the r method by a dashed line and asterisks. The LDC for the PHOENIX-DRIFT models from Claret et al. (2012) are denoted by a dashed-dotted line and the symbol x. In the last case and for the sake of clarity, only models with Teff< 4400 K are shown. The third panel shows the root square of the merit function χ. All calculations were performed for log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1. Kepler photometric system. LSM calculations. |
| In the text | |
 |
Fig. 2 Theoretical linear LDC for ATLAS models (continuous line) and PHOENIX-COND quasi-spherical ones (dashed line): log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1; TESS photometric system; LSM calculations. |
| In the text | |
 |
Fig. 3 Specific intensity distribution for a [1500 K, 4.5] PHOENIX-DRIFT quasi-spherical symmetric model. Continuous line represents the model intensities (left label), while the dashed line denotes the deviations [model-fit] by adopting Eq. (5) and the dashed-dotted one represents the deviations by adopting Eq. (1) (right label): log[A/H] = 0.0, Vξ = 2 km s-1; TESS photometric system; LSM calculations. |
| In the text | |
 |
Fig. 4 Theoretical linear LDC for ATLAS models. Continuous line denotes TESS while dashed line represents the Kepler photometric system; log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1; LSM calculations. |
| In the text | |
 |
Fig. 5 Effects of metallicity and evolutionary status on the theoretical linear LDC for ATLAS models; TESS photometric system. Upper panel: continuous line denotes models with log[A/H] = 0.0 while dashed line indicates log[A/H] =−0.5 and dashed-dotted line those with log[A/H] =−1.0; log g = 4.5 and Vξ = 2 km s-1 for all models. Lower panel: continuous line denotes models with log g = 4.5 and dashed line represents models with log g = 3.0; log [A/H] = 0.0 and Vξ = 2 km s-1 for all models. LSM calculations for both panels. |
| In the text | |
 |
Fig. 6 Theoretical gravity-darkening coefficients for TESS, ATLAS models. The continuous line represents the calculations for log [A/H] = 0.00 and dashed line is for log [A/H] =−2.5, log g = 4.5, log[A/H] = 0.0, Vξ = 2 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


