| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628922 | |
| Published online | 27 March 2017 | |
The nature of very low luminosity objects (VeLLOs)
1 University of Vienna, Department of Astrophysics, 1180 Vienna, Austria
e-mail: eduard.vorobiev@univie.ac.at
2 Research Institute of Physics, Southern Federal University, Stachki Ave. 194, 344090 Rostov-on-Don, Russia
3 Department of Physics, State University of New York at Fredonia, 280 Central Avenue, Fredonia, NY 14063, USA
Received: 13 May 2016
Accepted: 8 November 2016
Aims. The nature of very low luminosity objects (VeLLOs) with the internal luminosity Lobj ≤ 0.1 L⊙ is investigated by means of numerical modeling coupling the core collapse simulations with the stellar evolution calculations.
Methods. The gravitational collapse of a large sample of model cores in the mass range 0.1−2.0 M⊙ is investigated. Numerical simulations were started at the pre-stellar phase and terminated at the end of the embedded phase when 90% of the initial core mass had been accreted onto the forming protostar plus disk system. The disk formation and evolution was studied using numerical hydrodynamics simulations, while the formation and evolution of the central star was calculated using a stellar evolution code. Three scenarios for mass accretion from the disk onto the star were considered: hybrid accretion in which a fraction of accreted energy absorbed by the protostar depends on the accretion rate, hot accretion wherein a fraction of accreted energy is constant, and cold accretion wherein all accretion energy is radiated away.
Results. Our conclusions on the nature of VeLLOs depend crucially on the character of protostellar accretion. In the hybrid accretion scenario, most VeLLOs (90.6%) are expected to be the first hydrostatic cores (FHSCs) and only a small fraction (9.4%) are true protostars. In the hot accretion scenario, all VeLLOs are FHSCs due to overly high photospheric luminosity of protostars. In the cold accretion scenario, on the contrary, the majority of VeLLOs belong to the Class I phase of stellar evolution. The reason is that the stellar photospheric luminosity, which sets the floor for the total internal luminosity of a young star, is lower in cold accretion, thus enabling more VeLLOs in the protostellar stage. VeLLOs are relatively rare objects occupying 7%–11% of the total duration of the embedded phase and their masses do not exceed 0.3 M⊙. When compared with published observations inferring a fraction of VeLLOs in the protostellar stage of ~6.25%, we find that cold accretion provides a much better fit to observations than hybrid accretion (5.7% for cold accretion vs. 0.7% for hybrid accretion). Both accretion scenarios predict more VeLLOs in the Class I phase than in the Class 0 phase, in contrast to observations. Finally, when accretion variability with episodic bursts is artificially filtered out from our numerically derived accretion rates, the fraction of VeLLOs in the protostellar stage drops significantly, suggesting a causal link between the two phenomena.
Key words: stars: formation / stars: protostars / stars: low-mass / protoplanetary disks / hydrodynamics
© ESO, 2017
1. Introduction
Low-mass stars form when dense molecular cloud cores become unstable under their own self-gravity and collapse. The process of low-mass star formation has received considerable attention in the last few decades, leading to the emergence of a general picture of the evolution from dense core to star (e.g., Shu et al. 1987; McKee & Ostriker 2007). However, despite the existence of this general picture, a detailed physical understanding of the accretion process during the protostellar stage, the stage when the forming star is still embedded within and accreting from its parent dense core, remains elusive. In the simplest model of star formation, the collapse of a singular isothermal sphere (sometimes called the standard model of star formation), mass accretes from the core onto the protostar at a constant rate of ~2 × 10-6M⊙ yr-1 (Shu 1977; Shu et al. 1987). However, most protostars have luminosities significantly less than the accretion luminosity expected from accretion at this rate, as first discussed by Kenyon et al. (1990). This luminosity problem, as it is called, has been emphasized by results from Spitzer Space Telescope (Werner et al. 2004) observations of nearby star-forming regions, which find a significant population of protostars with luminosities below theoretical predictions (e.g., Dunham et al. 2008, 2013, 2014, 2015; Evans et al. 2009; Enoch et al. 2009; Kryukova et al. 2012).
There is growing evidence that the resolution of the luminosity problem lies in episodic rather than constant mass accretion, with prolonged periods of very low accretion punctuated by short bursts of rapid accretion. Vorobyov & Basu (2005, 2006, 2010, 2015) presented simulations showing that material piles up in a circumstellar disk until the disk becomes gravitationally unstable and dumps its mass in the form of gaseous clumps onto the protostar in short-lived accretion bursts. Indeed, the luminosities predicted by these simulations match the observed protostellar luminosity distribution and fully resolve the luminosity problem (Dunham et al. 2010b; Dunham & Vorobyov 2012). While other accretion models are also capable of resolving the luminosity problem without invoking variability (Offner & McKee 2011), significant indirect evidence exists in favor of episodic, variable mass accretion rates in the protostellar stage of star formation (Audard et al. 2014; Dunham et al. 2014), including infrared variability in young stars (e.g., Billot et al. 2012; Scholz et al. 2013; Rebull et al. 2014, 2015; Günther et al. 2014), outflow variability (e.g., Bachiller et al. 1991; Arce & Goodman 2001; Arce et al. 2013; Dunham et al. 2006, 2010a; Lee et al. 2010; Schwarz et al. 2012), and chemical indications of extreme temperature variations in the histories of protostellar cores (e.g., Kim et al. 2012; Visser & Bergin 2012; Visser et al. 2015; Jørgensen et al. 2013; Vorobyov et al. 2013).
The very first dense molecular cloud core to be observed by Spitzer that was classified as starless (Lynds 1014), and was in fact revealed to harbor a very low luminosity protostar (Young et al. 2004). Several other, similar detections quickly followed (e.g., Dunham et al. 2006, 2010a; Bourke et al. 2006; Lee et al. 2009), leading to the definition of a new class of objects called very low luminosity objects (VeLLOs; Di Francesco et al. 2007). Defining the internal luminosity of a protostar, Lint, as the total luminosity arising from the star and disk (including both accretion and photospheric luminosity) and excluding any luminosity arising from external heating of the surrounding dense core by the interstellar radiation field, VeLLOs are defined as protostars with Lint< 0.1 L⊙ embedded in dense cores. In a comprehensive search for VeLLOs in Spitzer observations of nearby star-forming regions, Dunham et al. (2008) found 15 total VeLLOs, 8 in isolated globules and 7 in large molecular cloud complexes. In a related study, Evans et al. (2009) identified a total of 112 protostars in these same large molecular cloud complexes. Thus VeLLOs represent 6.25% (7/112) of the total population of protostars. We, however, acknowledge that this value is likely a lower limit to the true fraction.
More recently, a number of embedded objects below the sensitivity of these large Spitzer surveys have been found, most through either interferometric detections of outflows driven by cores starless even via observations made by Spitzer, or far-infrared detections of warm dust toward such cores (Chen et al. 2010, 2012; Enoch et al. 2010; Dunham et al. 2011; Pineda et al. 2011; Pezzuto et al. 2012; Schnee et al. 2012; Murillo & Lai 2013). With typical values of Lint≤ 0.01 L⊙, these objects have been suggested as candidates for the first hydrostatic core (FHSC), a short-lived stage (0.5–50 kyr according to Omukai 2007; Tomida et al. 2010; Commercon et al. 2012) intermediate between the starless and protostellar stages that forms once the central density increases to the point where the inner region becomes opaque to radiation and lasts until the central temperature reaches 2000 K and H2 dissociates (Larson 1969). Since most of these extreme objects have been discovered serendipitously, and complete surveys with the required sensitivity to find all of them are only just starting to become available (Dunham et al. 2016), and, further, since we do not yet have clear observational methods for distinguishing between first cores and very young protostars, the total number of these objects and their input to the VeLLO fractions (FHSCs vs. protostars) remains to be understood.
While VeLLOs thus represent less than approximately 10% of the total population of protostars in nearby molecular clouds, their very low luminosities are an extreme example of the luminosity problem discussed above and are particularly challenging to explain. Assuming accretion at the standard rate of ~2 × 10-6M⊙ yr-1 (Shu et al. 1987) onto a star on the stellar/substellar boundary (0.08 M⊙) with a typical protostellar radius of 3 R⊙, the expected accretion luminosity is L = GMṀ/R = 1.6L⊙. VeLLOs, with luminosities more than an order of magnitude below this, must feature some combination of very low masses and/or mass accretion rates. While both have been indirectly inferred in detailed studies of individual VeLLOs (Dunham et al. 2006, 2010a; Lee et al. 2009, 2013), to date, no method has directly measured either their masses or mass accretion rates, since VeLLOs are too deeply embedded for optical/NIR spectroscopic measurements of accretion rates and spectral types. Thus the physical nature of VeLLOs remains unknown.
The purpose of this study is to develop a physical understanding of the nature of VeLLOs. We use the hydrodynamical simulations of Vorobyov & Basu (2005, 2006, 2010, 2015), which reproduce the full distribution of observed protostellar luminosities, including VeLLOs (Dunham & Vorobyov 2012), to investigate the characteristics of the protostars forming in these simulations with luminosities consistent with the definition of a VeLLO as given above. The organization of this work is as follows: Sect. 2 presents the description of our numerical model and adopted initial conditions. The main results are presented in Sect. 3. The model caveats are discussed in Sect. 4 and the conclusions are given in Sect. 5.
2. Model description and initial conditions
We start our numerical hydrodynamics simulations from the gravitational collapse of a starless cloud core, continue into the embedded phase of star formation, during which a star, disk, and envelope are formed, and terminate our simulations after the parental core has dissipated (0.1–0.6 Myr, depending on the core mass). Such long integration times are made possible by the use of the thin-disk approximation. This approximation is an excellent means to calculate the evolution for many models and orbital periods and its justification is discussed in Vorobyov & Basu (2010). The star, once formed, is placed in the coordinate center. The protostellar disk, once formed, occupies the inner part of the numerical polar grid (usually, several hundreds of AU), while the contracting envelope occupies the rest of the grid (which may extend to several thousands of AU). The disk, during its early evolution, is not isolated, but is exposed to intense mass loading from the infalling envelope.
To avoid overly small time steps, we introduce a “sink cell” near the coordinate origin with a radius of 5 AU and impose a free outflow boundary condition so that the matter is allowed to flow out of the computational domain into the sink cell, but is prevented from flowing in the opposite direction. During the early stages of the core collapse, we monitor the gas surface density in the sink cell and when its value exceeds a critical value for the transition from isothermal to adiabatic evolution (~1010 cm-3), we assume that a first hydrostatic core (FHSC) is formed with a size equal to that of the sink cell. The second collapse ensues and a central protostar forms when the mass of the FHSC exceeds 0.05 M⊙, as suggested by radiation transfer calculations of Masunaga & Inutsuka (2000). The mass contained in the FHSC (or in the sink cell) is then transferred to the point-sized protostar in the coordinate center over a short transition period of time (a few thousand years). A small fraction of this mass (several per cent) remains in the sink cell to guarantee a smooth transition of the gas surface density across the inner boundary. In the subsequent evolution, 90% of the gas that crosses the inner boundary is assumed to land on the protostar. The other 10% of the accreted gas is assumed to be carried away with protostellar jets.
2.1. Stellar evolution code
The evolution of the accreting protostar is based on the Lyon stellar evolution code with input physics described in Chabrier & Baraffe (1997) including accretion processes as described in Baraffe et al. (2009, 2012). The accretion rates onto the protostar Ṁ, calculated as the amount of mass passing through the sink cell during one computational time step, are derived from the hydrodynamic calculations described below. As in Baraffe et al. (2012), we assume that the fraction α of the accretion energy ϵGM∗Ṁ/R∗ is absorbed by the protostar, while the fraction (1−α) is radiated away and contributes to the accretion luminosity of the star. As in Baraffe et al. (2009), we assume a value ϵ = 1/2 characteristic of accretion from a thin disk. The current mass of the star M∗ is calculated from the mass accretion rate Ṁ, while the radius of the star R∗ is computed by the stellar evolution code.
Despite many efforts, the exact value of α in low-mass star formation is not known. In the present calculations, we consider three scenarios: a “cold” accretion model with α = 0, meaning that essentially all accretion energy is radiated away, a “hot” accretion model with α = 0.5, meaning that 50% of the accretion energy is always absorbed by the protostar, irrespective of the accretion rate, and a “hybrid” accretion model with α = 0, when accretion rates remain smaller than a critical value Ṁcr and α ≠ 0 when Ṁ>Ṁcr. More specifically, we adopt 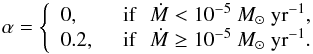 (1)The choice for the maximum value of α is based on our previous work showing that stellar properties for hybrid accretion do not change significantly as long as α is greater than 0.1–0.2 (Baraffe et al. 2009, 2012). The choice for the critical mass accretion rate of Ṁcr = 10-5M⊙ yr-1 is based on our analysis of the pressure balance at the stellar surface (see the Introduction and Appendix B in Baraffe et al. 2012). For the initial seed mass of the protostar, corresponding to the second Larson core mass, we adopt a value of 1.0MJup with an initial radius ~1.0 R⊙.
(1)The choice for the maximum value of α is based on our previous work showing that stellar properties for hybrid accretion do not change significantly as long as α is greater than 0.1–0.2 (Baraffe et al. 2009, 2012). The choice for the critical mass accretion rate of Ṁcr = 10-5M⊙ yr-1 is based on our analysis of the pressure balance at the stellar surface (see the Introduction and Appendix B in Baraffe et al. 2012). For the initial seed mass of the protostar, corresponding to the second Larson core mass, we adopt a value of 1.0MJup with an initial radius ~1.0 R⊙.
The stellar evolution code is coupled with the main hydrodynamical code in real time (no postprocessing), meaning that we simultaneously model the evolution of the star and its circumstellar disk. The input parameter to the stellar evolution code provided by disk modeling is the mass accretion rate onto the star Ṁ. The output of the stellar evolution code is the stellar radius R∗ and the photospheric luminosity L∗ ,ph, which are employed by the disk hydrodynamics simulations to calculate the total stellar luminosity and the radiation flux reaching the disk surface (see below). Due to heavy computational load, the stellar evolution code is invoked to update the properties of the protostar only every 20 yr, while the hydrodynamical time step may be as small as a few months. As a consequence, α has to be averaged over a period of 20 yr preceding the calculation of the stellar properties. This means that the actual value of α can be somewhat lower than the maximal value of 0.2.
2.2. Numerical hydrodynamics code
The main physical processes taken into account when computing the evolution of the disk and envelope include viscous and shock heating, irradiation by the forming star, background irradiation, radiative cooling from the disk surface and self-gravity. The corresponding equations of mass, momentum, and energy transport are
where subscripts p and p′ refer to the planar components (r,φ) in polar coordinates, Σ is the mass surface density, e is the internal energy per surface area, 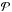 is the vertically integrated gas pressure calculated via the ideal equation of state as
is the vertically integrated gas pressure calculated via the ideal equation of state as 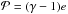 with γ = 7/5,
with γ = 7/5, 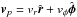 is the velocity in the disk plane, and
is the velocity in the disk plane, and 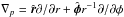 is the gradient along the planar coordinates of the disk. The gravitational acceleration in the disk plane,
is the gradient along the planar coordinates of the disk. The gravitational acceleration in the disk plane, 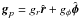 , takes into account self-gravity of the disk, found by solving for the Poisson integral (see details in Vorobyov & Basu 2010), and the gravity of the FHSC and central protostar when formed. Turbulent viscosity due to sources other than gravity is taken into account via the viscous stress tensor Π, the expression for which is provided in Vorobyov & Basu (2010). We parameterize the magnitude of kinematic viscosity ν using the alpha prescription with a spatially and temporally uniform αvisk = 5 × 10-3. The thin-disk model is complemented by a calculation of the vertical scale height h in both the disk and envelope using an assumption of local hydrostatic equilibrium (Vorobyov & Basu 2009). The resulting model has a flared structure, which guaranties that both the disk and envelope receive a fraction of the irradiation energy from the central protostar.
, takes into account self-gravity of the disk, found by solving for the Poisson integral (see details in Vorobyov & Basu 2010), and the gravity of the FHSC and central protostar when formed. Turbulent viscosity due to sources other than gravity is taken into account via the viscous stress tensor Π, the expression for which is provided in Vorobyov & Basu (2010). We parameterize the magnitude of kinematic viscosity ν using the alpha prescription with a spatially and temporally uniform αvisk = 5 × 10-3. The thin-disk model is complemented by a calculation of the vertical scale height h in both the disk and envelope using an assumption of local hydrostatic equilibrium (Vorobyov & Basu 2009). The resulting model has a flared structure, which guaranties that both the disk and envelope receive a fraction of the irradiation energy from the central protostar.
The radiative cooling Λ in Eq. (3) is determined using the diffusion approximation of the vertical radiation transport in a one-zone model of the vertical disk structure (Hubeny 1990; Johnson & Gammie 2003) 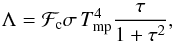 (5)where σ is the Stefan-Boltzmann constant,
(5)where σ is the Stefan-Boltzmann constant, 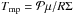 is the midplane temperature of gas, μ = 2.33 is the mean molecular weight, R is the universal gas constant, τ is the optical depth to the disk midplane, and ℱc = 2 + 20tan-1(τ)/(3π) is a function that secures a correct transition between the optically thick and optically thin regimes. We use frequency-integrated opacities of Bell & Lin (1994) to calculate the optical depth. The heating function is expressed by analogy to the cooling function as
is the midplane temperature of gas, μ = 2.33 is the mean molecular weight, R is the universal gas constant, τ is the optical depth to the disk midplane, and ℱc = 2 + 20tan-1(τ)/(3π) is a function that secures a correct transition between the optically thick and optically thin regimes. We use frequency-integrated opacities of Bell & Lin (1994) to calculate the optical depth. The heating function is expressed by analogy to the cooling function as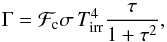 (6)where Tirr is the irradiation temperature at the disk surface determined by the stellar and background black-body irradiation as
(6)where Tirr is the irradiation temperature at the disk surface determined by the stellar and background black-body irradiation as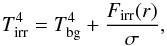 (7)where Tbg is the uniform background temperature (in our model set to the initial temperature of the natal cloud core) and Firr(r) is the radiation flux (energy per unit time per unit surface area) absorbed by the disk surface at radial distance r from the central object. The latter quantity is calculated as
(7)where Tbg is the uniform background temperature (in our model set to the initial temperature of the natal cloud core) and Firr(r) is the radiation flux (energy per unit time per unit surface area) absorbed by the disk surface at radial distance r from the central object. The latter quantity is calculated as 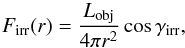 (8)where γirr is the incidence angle of radiation arriving at the disk surface at radial distance r. The incidence angle is calculated using the disk surface curvature inferred from the radial profile of the disk vertical scale height (Vorobyov & Basu 2010).
(8)where γirr is the incidence angle of radiation arriving at the disk surface at radial distance r. The incidence angle is calculated using the disk surface curvature inferred from the radial profile of the disk vertical scale height (Vorobyov & Basu 2010).
The luminosity of the central object Lobj is the sum of the accretion luminosity Laccr = (1−α)ϵGMobjṀ/Robj arising from the gravitational energy of accreted gas and the photospheric luminosity L∗ ,ph due to gravitational contraction and deuterium burning. We note that while the accretion luminosity is calculated for both the FHSC and protostar, the photospheric luminosity is calculated only for the protostar (using the stellar evolution code), but not for the FHSC (our simplistic model does not allow us to do this). The mass of the central object Mobj and accretion rate onto the central object Ṁ are determined self-consistently during numerical simulations using the amount of gas passing through the sink cell. We note that the radius of the central object is set to the radius of the sink cell in the FHSC phase and is self-consistently determined by the stellar evolution code in the protostellar phase. The numerical resolution is 512 × 512 grid points and the numerical procedure to solve hydrodynamics (Eqs. (2), (3)) is described in detail in Vorobyov & Basu (2010).
2.3. Initial setup
Our initial cloud cores are described by the gas surface density Σ and angular velocity Ω profiles of the following form:
Here, Ω0 and Σ0 are the angular velocity and gas surface density at the center of the core and 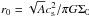 is the radius of the central plateau, where cs is the initial sound speed in the core. The gas surface density distribution described by Eq. (9) is a vertically integrated form (to within a factor of order unity) of the Bonnor-Ebert sphere with a positive density-perturbation amplitude A (Dapp & Basu 2009). The value of A is set to 1.2 and the initial gas temperature is set to 10 K. We also note that our initial conditions are typical of pre-stellar cores formed as a result of the slow expulsion of magnetic field due to ambipolar diffusion, with the angular momentum remaining constant during axially-symmetric core compression (Basu 1997).
is the radius of the central plateau, where cs is the initial sound speed in the core. The gas surface density distribution described by Eq. (9) is a vertically integrated form (to within a factor of order unity) of the Bonnor-Ebert sphere with a positive density-perturbation amplitude A (Dapp & Basu 2009). The value of A is set to 1.2 and the initial gas temperature is set to 10 K. We also note that our initial conditions are typical of pre-stellar cores formed as a result of the slow expulsion of magnetic field due to ambipolar diffusion, with the angular momentum remaining constant during axially-symmetric core compression (Basu 1997).
Our models are divided into four model sets, each characterized by a distinct ratio of the rotational to gravitational energy β. The adopted values of β lie within the limits inferred by Caselli et al. (2002) for dense molecular cloud cores. Each model is characterized by a distinct ratio rout/r0 = 6 in order to generate gravitationally unstable truncated cores of similar form, where rout is the outer radius of the cloud core. The actual procedure for generating the parameters of a specific core with a given value of β is as follows. First, we choose rout and find r0 using the adopted ratio between these two quantities. Then, we find the central surface density Σ0 from the relation 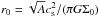 and determine the resulting cloud core mass Mc from Eq. (9).
and determine the resulting cloud core mass Mc from Eq. (9).
 |
Fig. 1 Total luminosity of the central object vs. time elapsed since the onset of core collapse in 31 models with the hybrid accretion scenario (black solid lines). The horizontal dotted lines indicate the upper luminosity for VeLLOs. The vertical dashed lines mark the instance of protostar formation. The green solid lines present the total stellar luminosity averaged over a time period of 20 kyr for models 21–24 and 29–31 and over a time period of 5 kyr for the remaining models. |
3. Model results
We have computed the evolution of our models to the end of the embedded phase, when most of the collapsing core has dissipated via accretion onto the forming disk plus star system. The numerical simulations are terminated when the mass in the infalling envelope becomes smaller than 10% of that of the initial core mass Mc. We use the obtained total (accretion plus photospheric) luminosities of the central objects to infer the nature of VeLLOs.
3.1. Hybrid accretion
Parameters for the hybrid accretion models.
In this section, we present our model results for the hybrid accretion scenario, wherein the fraction of accretion energy α absorbed by the protostar depends on the protostellar accretion rate and is determined using Eq. (1). We use 31 models, the parameters of which are presented in Table 1. Columns 2–5 give the initial mass of the core, initial ratio of rotational to gravitational energy of the core, initial outer radius of the core, and mass of the central object at the end of the embedded phase, respectively.
We start by analyzing the total luminosity of the central object Lobj in our models. The black solid lines in Fig. 1 present Lobj vs. time elapsed since the beginning of the gravitational collapse of pre-stellar cores. The horizontal dotted lines indicate, according to Dunham et al. (2006), a fiducial maximum value for the total luminosity of VeLLOs, 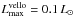 . The vertical dashed lines show the time instance when the FHSC collapses to form a protostellar/proto-brown dwarf seed.
. The vertical dashed lines show the time instance when the FHSC collapses to form a protostellar/proto-brown dwarf seed.
In the FHSC phase, the total luminosity in all models is much smaller than 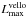 . This is because the radius of the FHSC is at least three orders of magnitude larger than that of the protostar. Although the accretion rate in the FHSC phase (a few × 10-6M⊙ yr-1) is on average comparable to or even higher than that in the later protostellar phase (10-7−10-6M⊙ yr-1), the resulting accretion luminosity in the FHSC phase is much smaller than in the protostellar phase.
. This is because the radius of the FHSC is at least three orders of magnitude larger than that of the protostar. Although the accretion rate in the FHSC phase (a few × 10-6M⊙ yr-1) is on average comparable to or even higher than that in the later protostellar phase (10-7−10-6M⊙ yr-1), the resulting accretion luminosity in the FHSC phase is much smaller than in the protostellar phase.
When the protostar forms, Lobj rises by several orders of magnitude, initially exceeding the VeLLO’s upper limit of 0.1 L⊙ in all models. In the subsequent evolution, the total stellar luminosity shows time variations with different amplitude. More specifically, Lobj in the low-Mc and low-β models (e.g., models 1–7) is characterized by an order-of magnitude flickering. On the other hand, models with higher Mc and β (e.g., models 9–13, 17–24, 27–31) demonstrate large-amplitude variations in Lobj with strong luminosity outbursts. This difference in the time behavior of Lobj stems from the different properties of protostellar disks formed from the gravitational collapse of pre-stellar cores (e.g., Vorobyov & Basu 2010). The low-Mc and low-β models produce disks of low mass and size, which are weakly gravitationally unstable and show no sign of fragmentation, while higher Mc and β models form disks that are sufficiently massive and extended to develop strong gravitational instability and fragmentation. Most of the fragments migrate onto the star owing to the loss of angular momentum via gravitational interaction with spiral arms or other fragments in the disk, producing strong accretion and luminosity bursts similar in magnitude to FU-Orionis-type eruptions (Vorobyov & Basu 2006, 2015, 2010; Machida et al. 2011).
Notwithstanding high variability, the total stellar luminosity in the protostellar phase in most models is greater than the VeLLO’s upper limit of 0.1 L⊙. Although the accretion luminosity may drop below 0.1 L⊙ following large-amplitude variations in the protostellar accretion rate, the photospheric luminosity is greater than 0.1 L⊙ in most cases. We illustrate this phenomenon in Fig. 2 for several prototype models. In particular, the thin blue lines and thick black lines show the accretion and photospheric luminosities, respectively, while the vertical red dashed line separates the FHSC and protostellar phases. The horizontal dotted lines mark the maximum luminosity of VeLLOs, 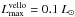 . In a few models, such as models 16 and 25, characterized by low-Mc and low-β cores, the protostellar accretion rates never exceed Ṁcr = 10-5M⊙ yr-1, implying essentially cold accretion. As a result, the protostar remains compact and its photospheric luminosity is smaller than
. In a few models, such as models 16 and 25, characterized by low-Mc and low-β cores, the protostellar accretion rates never exceed Ṁcr = 10-5M⊙ yr-1, implying essentially cold accretion. As a result, the protostar remains compact and its photospheric luminosity is smaller than 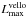 (Baraffe et al. 2009, 2012). Large variations in the accretion rate and the corresponding luminosity then lead to short episodes when the total protostellar accretion falls below the VeLLO’s upper limit.
(Baraffe et al. 2009, 2012). Large variations in the accretion rate and the corresponding luminosity then lead to short episodes when the total protostellar accretion falls below the VeLLO’s upper limit.
On the other hand, the photospheric luminosity in models 9 and 29 is always greater than 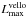 . In these (and many other) models, the protostellar accretion rates often exceed the critical value of 10-5M⊙ yr-1, resulting in absorption of part of the accretion energy by the protostar and causing the star to bloat (Baraffe et al. 2012). These models are characterized by photospheric luminosity that is greater than the upper VeLLO’s limit of
. In these (and many other) models, the protostellar accretion rates often exceed the critical value of 10-5M⊙ yr-1, resulting in absorption of part of the accretion energy by the protostar and causing the star to bloat (Baraffe et al. 2012). These models are characterized by photospheric luminosity that is greater than the upper VeLLO’s limit of 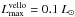 . This means that the total luminosity in these models is always greater than
. This means that the total luminosity in these models is always greater than 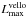 , no matter how low the accretion luminosity may actually drop.
, no matter how low the accretion luminosity may actually drop.
 |
Fig. 2 Accretion and photospheric luminosities (thin blue and thick black lines, respectively) vs. time elapsed since the onset of core collapse in four prototype models. The vertical red dashed line indicates the beginning of the protostellar phase (i.e., the onset of the collapse of a FHSC to a protostellar seed). The horizontal dotted lines indicate the upper luminosity for VeLLOs. |
3.1.1. Statistical analysis
To further clarify the nature of VeLLOs, we calculate the time spent by our models in the VeLLO state. For this purpose, we employ the method described by Dunham & Vorobyov (2012) and determine the fraction of total time fbin that all our models spend in various bins in the Lobj–tevol diagram, where tevol is the evolution time elapsed since the beginning of core collapse. To calculate this fraction, we first divide the Lobj–tevol space into 20 bins in both dimensions (in the log space) and then calculate the fraction of total time spent by the models in each bin: 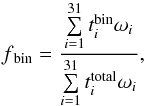 (11)where
(11)where 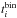 is the time spent by the ith model in the specified Lobj–tevol bin,
is the time spent by the ith model in the specified Lobj–tevol bin, 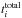 is the total duration of the ith model, ωi are the weight coefficients given to the ith model according to the adopted initial mass function (IMF), and the summation is performed over all 31 models.
is the total duration of the ith model, ωi are the weight coefficients given to the ith model according to the adopted initial mass function (IMF), and the summation is performed over all 31 models.
 |
Fig. 3 Number of models in four mass bins (dN/ dM∗ ,fin) and the calculation of the weight coefficients for the model IMF. The vertical dash-dotted lines outline the four bins, in which the final stellar masses (M∗ ,fin) are divided. The solid line presents the Kroupa IMF normalized to the total number of our models. The open squares and circles are the values of the model IMF before and after weighing, respectively, and the numbers provide the weight coefficients ωi. |
To calculate ωi, we split the range of final stellar masses M∗ ,fin into four bins (in the log space) and calculate the number of models per each mass bin, dN/ dM∗ ,fin. The resulting model IMF is shown in Fig. 3 by the open squares. The mass bins are outlined in the figure by the vertical dash-dotted lines. The solid curve shows the Kroupa IMF (Kroupa 2001), which is normalized to the total number of our models. We have also tried the Chabrier IMF (Chabrier 2005), but found that the adopted form of the IMF does not qualitatively affect our conclusions. Evidently, the model IMF and the Kroupa IMF do not match, meaning that we have taken too few low-mass model cores and too many high-mass ones in Table 1. This mismatch is caused by the fact that several models have failed due to numerical reasons. The stellar evolution code sometimes diverges, which causes the whole simulation to be terminated. We can, however, recover the Kroupa IMF by calculating the weight coefficients ωi so as to fit our model IMF to that of Kroupa. The arrows and open circles show the result of the fitting and the numbers provide the derived weights for every stellar mass bin. We note that we used the initial mass function of stars for calculating the weights, rather than the initial mass function of dense molecular cores (e.g., Alves et al. 2007). This is because the latter sample may include not only the pre-stellar, gravitationally contracting cores, as in our initial numerical setup, but also starless gravitationally stable cores. In addition, some cores in the Alves et al. sample may undergo further fragmentation when contracting to form binary/multiple stars or be partly photoevaporated/dispersed by stellar feedback. All these processes are not taken into account in our numerical simulations of isolated cores.
The fraction of total time fbin is plotted in the upper-left panel of Fig. 4 with the gray-scale mosaic. Evidently, our models spend most of the evolution time in a state with  , but VeLLOs with
, but VeLLOs with 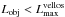 are also present. The gray-scale mosaic, however, gives little information regarding the evolutionary status of VeLLOs, that is, whether VeLLOs are FHSCs or protostars.
are also present. The gray-scale mosaic, however, gives little information regarding the evolutionary status of VeLLOs, that is, whether VeLLOs are FHSCs or protostars.
To determine the evolutionary phase to which VeLLOs belong, we split our model data into three phases: the FHSC phase, the Class 0 phase, and the Class I phase. The first phase starts from the time instance of the FHSC formation and ends when the FHSC collapses to form the protostar. The second phase starts from the moment of protostar formation and ends when 50% of the initial core mass is left in the envelope (the rest is accreted onto the star plus disk system). The third phase starts right after the Class 0 phase and ends when less than 10% of the initial core mass is left in the envelope. In all models, we assume that the Class I phase cannot last longer than 0.5 Myr, which is consistent with the lifetime of the embedded phase estimated from observations, 0.4–0.78 Myr (Dunham et al. 2015). Our adopted classification scheme is therefore based on physical properties of a young stellar object, such as envelope, disk, and stellar masses (Robitaille et al. 2006; Dunham et al. 2010a), and is more suitable for numerical simulations than observational signatures, such as submillimeter luminosity or effective temperature (André et al. 1993; Chen et al. 1995). We note that we have adopted the “Class” rather than “Stage” terminology in this paper, but the above clarification helps to avoid any confusions.
 |
Fig. 4 Total luminosity (Lobj) vs. evolutionary time (tevol) diagram. The time is counted from the onset of core collapse. The horizontal dashed lines mark the maximum VeLLO luminosity of 0.1 L⊙. The gray-scale mosaic presents the fraction of total time (in per cent) that all models spend in various bins in the Lobj–tevol diagram. The corresponding scale bar shows this fraction in per cent. The red, orange, and blue dots present the model data for the FHSC, Class 0 and Class I phases, respectively. |
Fraction of time (in per cent) spent by hybrid accretion models in each evolution phase.
The red, orange, and blue dots in Fig. 4 present the model data for the FHSC, Class 0 and Class I phases, respectively. The corresponding total luminosities are calculated every 5 yr. The dashed horizontal line shows the VeLLO’s maximum luminosity, 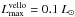 . Evidently, the FHSC phase is characterized by total luminosity that is much smaller than
. Evidently, the FHSC phase is characterized by total luminosity that is much smaller than 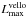 , which is not surprising considering the large radii and low accretion luminosities of the FHSCs. Indeed, for a radius of 5 AU, maximum mass of 0.05 M⊙ and maximum accretion rate of 10-5M⊙ yr-1, we obtain 1.2 × 10-2L⊙ for the maximum accretion luminosity of FHSCs, which agrees with the values in Fig. 2 (but see discussion in Sect. 4). The Class 0 and I phases, on the contrary, are mostly characterized by
, which is not surprising considering the large radii and low accretion luminosities of the FHSCs. Indeed, for a radius of 5 AU, maximum mass of 0.05 M⊙ and maximum accretion rate of 10-5M⊙ yr-1, we obtain 1.2 × 10-2L⊙ for the maximum accretion luminosity of FHSCs, which agrees with the values in Fig. 2 (but see discussion in Sect. 4). The Class 0 and I phases, on the contrary, are mostly characterized by 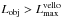 . The total luminosity drops to the VeLLO domain only episodically.
. The total luminosity drops to the VeLLO domain only episodically.
Using the constructed mosaic, we have further calculated the fractions of time (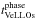 ) spent by our models in the VeLLO state with Lobj< 0.1 L⊙ during each of the three phases (FHSC, Class 0, and Class I) with respect to: a) the total time spent with L< 0.1 L⊙ during all three phases (
) spent by our models in the VeLLO state with Lobj< 0.1 L⊙ during each of the three phases (FHSC, Class 0, and Class I) with respect to: a) the total time spent with L< 0.1 L⊙ during all three phases (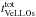 ); b) the total duration for each evolution phase (tphase); and c) the total duration for all phases (ttot). The resulting values are shown in Table 2.
); b) the total duration for each evolution phase (tphase); and c) the total duration for all phases (ttot). The resulting values are shown in Table 2.
To convert our numerically predicted time fractions to number fractions, we make a fundamental assumption of a constant star formation rate. A similar assumption is used, for example, when deriving the duration of different evolutionary phases from the observationally inferred number fractions of protostars (e.g., Dunham et al. 2015). Let us focus on the first numerical column showing the time spent in the VeLLO state for each individual phase normalized to the total time spent in the VeLLOs state (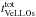 ) for all three phases. These data can be used to derive the number of VeLLOs in a given phase if the total number of VeLLOs,
) for all three phases. These data can be used to derive the number of VeLLOs in a given phase if the total number of VeLLOs, 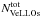 , in a given star-forming region is known:
, in a given star-forming region is known: 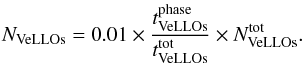 (12)Evidently, most VeLLOs are expected to be found in the FHSC phase (90.63%) and only a small fraction can be in the Class 0 (0.69%) and Class I phases (8.68%). This suggests that most VeLLOs are in fact the FHSCs, and only a minor fraction are true protostars. We note that
(12)Evidently, most VeLLOs are expected to be found in the FHSC phase (90.63%) and only a small fraction can be in the Class 0 (0.69%) and Class I phases (8.68%). This suggests that most VeLLOs are in fact the FHSCs, and only a minor fraction are true protostars. We note that 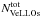 is a poorly constrained number from observations. Nevertheless, the second numerical column provides an important theoretical insight into the nature of VeLLOs.
is a poorly constrained number from observations. Nevertheless, the second numerical column provides an important theoretical insight into the nature of VeLLOs.
The second numerical column provides the time spent by our models in the VeLLO state in each individual evolution phase normalized to the duration of the phase. These data can be directly used to calculate the number of VeLLOs as follows: 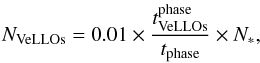 (13)where N∗ is the number of protostars in a specific phase and specific star-forming region. We note that Eq. (13) is only applicable to the protostellar phase. This quantity is much better constrained from observations than
(13)where N∗ is the number of protostars in a specific phase and specific star-forming region. We note that Eq. (13) is only applicable to the protostellar phase. This quantity is much better constrained from observations than 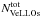 . From the third numerical column it is evident that the FHSCs spend all their time in the VeLLO state, as was already noted in Fig. 4. On the other hand, Class 0 and Class I protostars spend only a very small fraction of the lifetime of the corresponding phase in the VeLLO state, meaning that it would be unlikely (from a statistical point of view) to detect Class 0 and Class I protostars in the VeLLO state and their number count should be quite low, less than one per hundred protostars. This, however, contradicts observations. As mentioned in the Introduction, VeLLOs represent 6.25% (7/112) of the total population of protostars (and perhaps more, as discussed in Sect. 5).
. From the third numerical column it is evident that the FHSCs spend all their time in the VeLLO state, as was already noted in Fig. 4. On the other hand, Class 0 and Class I protostars spend only a very small fraction of the lifetime of the corresponding phase in the VeLLO state, meaning that it would be unlikely (from a statistical point of view) to detect Class 0 and Class I protostars in the VeLLO state and their number count should be quite low, less than one per hundred protostars. This, however, contradicts observations. As mentioned in the Introduction, VeLLOs represent 6.25% (7/112) of the total population of protostars (and perhaps more, as discussed in Sect. 5).
 |
Fig. 5 Total luminosity (Lobj) vs. central object mass (Mobj) diagram. The horizontal dashed line marks the maximum VeLLO luminosity of 0.1 L⊙. The gray-scale mosaic presents the fraction of total time (in per cent) that all models spend in various bins in the Lobj–Mobj diagram. The corresponding scale bar shows this fraction in per cent. The red, orange, and blue dots in Fig. 2 present the model data for the FHSC, Class 0 and Class I phases, respectively. |
The third numerical column indicates that VeLLOs are relatively rare objects when compared to the total duration of the embedded phase, including the FHSC phase and both Class 0 and I phases. Although the total fraction of VeLLOs in all three phases (7.3%) is similar to the observationally inferred 6.25%, this comparison is misleading because the Spitzer observations in the 3.6–8 μm cannot detect the FHSCs. After excluding the FHSCs, which in fact constitute the majority of VeLLOs according to our numerical simulations, it becomes evident that the numerically predicted number count of VeLLOs in the protostellar stage (0.68%) is again much lower than what is observationally inferred (6.25%). Finally, we note that 28 out of 31 hybrid accretion models (90%) have total luminosities always exceeding the VeLLO upper limit.
While Fig. 4 provides the information about how often and in what evolutionary phase we may expect to see VeLLOs, it tells little about the physical properties of VeLLOs, such as their mass, for example. To determine the masses of VeLLOs, we present in Fig. 5 the Ltot–Mobj diagram for the 31 models of Table 1. The horizontal dashed lines indicate the VeLLOs upper luminosity, 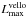 . The mosaic in the top-left panel shows the fraction of total time that all models spend in various bins in the Lobj–Mobj diagram. The red, orange, and blue dots present the data for the FHSC, Class 0 and Class I phases, respectively. Our modeling suggests that most VeLLOs are in fact brown dwarfs and/or very low-mass stars. The maximum mass of the VeLLO is found to be approximately 0.12 M⊙. Higher-mass stars are characterized by total luminosities that are gradually increasing with mass and inevitably exceed the VeLLO’s upper limit.
. The mosaic in the top-left panel shows the fraction of total time that all models spend in various bins in the Lobj–Mobj diagram. The red, orange, and blue dots present the data for the FHSC, Class 0 and Class I phases, respectively. Our modeling suggests that most VeLLOs are in fact brown dwarfs and/or very low-mass stars. The maximum mass of the VeLLO is found to be approximately 0.12 M⊙. Higher-mass stars are characterized by total luminosities that are gradually increasing with mass and inevitably exceed the VeLLO’s upper limit.
3.1.2. The effect of variable accretion
Mass accretion rates in the embedded phase of star formation often demonstrate a highly variable character (e.g. Vorobyov & Basu 2010, 2015; Elbakyan et al. 2016). Variable accretion with episodic bursts can, in particular, help to resolve the so-called luminosity problem (Dunham & Vorobyov 2012), whereby accretion luminosities typically observed for embedded protostars are factors of 10–100 lower than predicted from the spherical collapse models. In this section, we investigate to what extent variable accretion has an effect on the population of VeLLOs in the Class 0/I phases of star formation.
Many of our models also show variable accretion with episodic bursts, which is reflected in the corresponding variations of total luminosities (see Fig. 1). In order to artificially reduce the effect of variable accretion on the total luminosities, we apply the moving average to the total luminosity in models 21–24 and 29–31 over a time period of 20 kyr and in the remaining models over a time period of 5 kyr. Longer time periods are needed to smooth strong luminosity variations in models with massive disks. The resulting averaged luminosities are plotted with green solid lines in Fig. 1. The corresponding fractions of time spent in the VeLLO state are shown in Table 3. After averaging, the fraction of VeLLOs in the protostellar phase is further reduced. Now, the population of VeLLOs is almost totally dominated by FHSCs, except probably for the Class I phase, wherein we may still expect a rare occurrence of such objects.
3.2. Hot accretion
In this section, we consider the hot accretion scenario, in which α is always set to a constant value. We have recalculated 29 models shown in Table 1, but with α = 0.5, irrespective of the actual mass accretion rate onto the star. We note that two models were omitted due to numerical difficulties. The resulting total luminosities as a function of time elapsed since the onset of numerical simulations are plotted in Fig. 6. For all considered models in the protostellar phase (to the right from the vertical red dashed line), Lobj are greater than 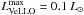 , effectively meaning no VeLLOs in the protostellar phase. This, however, contradicts the Spitzer observations (Dunham et al. 2008) indicating that VeLLOs do exist in the protostellar stage, representing 6.25% (7/112) of the total population of protostars (and perhaps more, as discussed in Sect. 5).
, effectively meaning no VeLLOs in the protostellar phase. This, however, contradicts the Spitzer observations (Dunham et al. 2008) indicating that VeLLOs do exist in the protostellar stage, representing 6.25% (7/112) of the total population of protostars (and perhaps more, as discussed in Sect. 5).
To further investigate this finding, in Fig. 7 we plot the accretion and photospheric luminosities (rather than the sum of both) for the same four models as in Fig. 2. In all four hot accretion models, the photospheric luminosity (defining the floor for the total luminosity) is always higher than 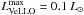 , in contrast with the corresponding hybrid accretion models, two of which having
, in contrast with the corresponding hybrid accretion models, two of which having 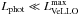 . The same tendency is found for all other hot accretion models. The star bloats in response to the constant absorption of accretion energy, which acts to increase its photospheric luminosity. We note that the accretion luminosities in the hot accretion models are systematically lower than those in the hybrid ones due to the fact that half of the accreted energy is absorbed by the protostar1. This, however, does not help to produce VeLLOs, because the photospheric luminosity is too high. To check how this finding depends on the adopted value of α, we have recalculated several models with α always set to 0.2 and found similar results.
. The same tendency is found for all other hot accretion models. The star bloats in response to the constant absorption of accretion energy, which acts to increase its photospheric luminosity. We note that the accretion luminosities in the hot accretion models are systematically lower than those in the hybrid ones due to the fact that half of the accreted energy is absorbed by the protostar1. This, however, does not help to produce VeLLOs, because the photospheric luminosity is too high. To check how this finding depends on the adopted value of α, we have recalculated several models with α always set to 0.2 and found similar results.
3.3. Cold accretion
In this section, we present our results for the cold accretion scenario, in which the fraction of accretion energy α absorbed by the protostar is set to zero independent of the actual value of the mass accretion rate. The parameters of 32 cold accretion models are listed in Table 4. The cold accretion models differ somewhat from the hybrid accretion ones, because we had to introduce several of new models instead of those that failed to run due to numerical reasons.
Parameters for the cold accretion models.
We start by examining the time evolution of the total luminosities Lobj shown in Fig. 8 by the black solid lines. The vertical red dashed line indicates the time instance of the formation of the protostellar/proto-brown dwarf seed from the FHSC. The early FHSC phase is not affected by the choice of α; the total luminosity in this phase is always below the upper VeLLO limit of 0.1 L⊙. In the protostellar phase, however, a certain difference between the hybrid and cold accretion becomes evident. The variability amplitude in Lobj is notably higher and the minimum value in Lobj is notably lower in the cold accretion scenario than in the hybrid accretion one. As a consequence, more cold accretion models now pass through the VeLLO state in the protostellar phase or at least come very close to the VeLLO state.
To illustrate this tendency, we plot in Fig. 9 the accretion and photospheric luminosities vs. time for several prototype models with cold accretion. In particular, the thin blue and thick black lines show the accretion and photospheric luminosities, respectively, while the vertical red dashed line separates the FHSC and protostellar phases. The horizontal dotted lines mark the maximum luminosity of VeLLOs, 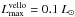 . Contrary to the hybrid accretion models shown in Fig. 2, the cold accretion models are often characterized by photospheric luminosity that is mostly lower than the VeLLOs upper limit of 0.1 L⊙, even for models with higher-Mc and β (e.g., models 22 and 24). This is because no accretion energy is absorbed by the protostar and its radius increases with time much slower than in the hybrid accretion scenario; see Fig. 4 in Baraffe et al. (2012). Smaller stellar radius means higher accretion luminosity for similar accretion rates and stellar masses. In addition, the photospheric luminosity sets the floor for the total luminosity and this floor value is lower in the cold accretion models. As a result, when variable accretion luminosity is added to the (smooth) photospheric luminosity, the cold accretion models show higher variability than the hybrid accretion models.
. Contrary to the hybrid accretion models shown in Fig. 2, the cold accretion models are often characterized by photospheric luminosity that is mostly lower than the VeLLOs upper limit of 0.1 L⊙, even for models with higher-Mc and β (e.g., models 22 and 24). This is because no accretion energy is absorbed by the protostar and its radius increases with time much slower than in the hybrid accretion scenario; see Fig. 4 in Baraffe et al. (2012). Smaller stellar radius means higher accretion luminosity for similar accretion rates and stellar masses. In addition, the photospheric luminosity sets the floor for the total luminosity and this floor value is lower in the cold accretion models. As a result, when variable accretion luminosity is added to the (smooth) photospheric luminosity, the cold accretion models show higher variability than the hybrid accretion models.
Following the method described in Sect. 3.1.1, we calculate the fraction of total time fbin that all cold accretion models spend in various bins in the Lobj–tevol diagram. The resulting time fractions are shown by the gray-scale mosaic in the top-left panel of Fig. 10. The red, orange, and blue dots present the model data for the FHSC, Class 0 and Class I phases, respectively. A visual comparison of Figs. 4 and 10 reveals that protostars with cold accretion spend more time in the VeLLO state than that with hybrid accretion. For instance, Class I objects with cold accretion can be found in the VeLLO state up to an age of 10-0.2 = 0.65 Myr, whereas the corresponding objects with hybrid accretion have total luminosities that always exceed the VeLLO’s upper limit of 0.1 L⊙ already after 10-0.75 = 0.18 Myr.
The time fractions that the cold accretion models spend in the VeLLO state are summarized in Table 5. From comparison of Tables 2 and 5 it becomes evident that the cold accretion scenario predicts more VeLLOs in the protostellar phase than does the hybrid accretion one. For instance, for the FHSCs, the combined fraction of time spent by the hybrid models in the VeLLO state (normalized to the total time spent in the VeLLOs state for all three phases) is 90.6%, while for the cold accretion models the corresponding value is only 47%. A larger fraction of time in the VeLLO state is now spent in the protostellar phase: 1.76% for the Class 0 phase and 51.2% for the Class I phase. When considering the fractions of time spent in the VeLLO state normalized to the total evolution time ttot, we see a similar tendency; the fraction of VeLLOs in the Class I phase (5.62%) slightly exceeds the corresponding value for the FHSC phase (5.16%). When comparing the fraction of VeLLOs relative to the total duration of the embedded phase (last column in Table 5), we see that the cold accretion scenario predicts most VeLLOs to actually occur in the Class I phase (5.62%), contrary to the hybrid accretion scenario wherein most VeLLOs were seen in the FHSC phase. Interestingly, the predicted fraction of VeLLOs in the Class 0 is much smaller (0.19%) than in the Class I phase (5.62%). This seems to contradict the seemingly very young age of observed VeLLOs with 73% (11/15) being Class 0 objects and only 27% (4/15) being Class I ones (Dunham et al. 2008). The existing VeLLO surveys may, however, be biased towards Class 0 sources as discussed in Sect. 5. Finally, we note that 16 out of 31 cold accretion models (50%) have total luminosities always exceeding the VeLLO upper limit.
Fraction of time (in per cent) spent by cold accretion models in each evolution phase.
Figure 11 presents the total luminosity (Lobj) vs. central object mass (Mobj) diagram for 32 cold accretion models. A comparison of the Lobj–Mobj diagram in Fig. 11 with that for the hybrid accretion models (Fig. 5) indicates that VeLLOs in the cold accretion scenario can have a significantly higher protostellar mass than in the hybrid accretion scenario. In the cold accretion scenario, the maximum mass of the protostar in the VeLLO state (for both Class 0 and Class I phases) is approximately 0.3 M⊙; at least a factor of 2 higher than in the hybrid accretion scenario.
Finally, we consider how variable accretion can affect the statistics of VeLLOs in the cold accretion scenario. The green solid lines in Fig. 8 show the total luminosities that are smoothed to reduce their time variability. We applied the same running average as was applied to the hybrid accretion models in Sect. 3.1.2. The resulting fractions of time spent in the VeLLO state are shown Table 6. After averaging, the fraction of VeLLOs in the protostellar Class 0/I phases has decreased significantly. Similarly to the hybrid accretion case, the population of VeLLOs is now totally dominated by FHSCs, except probably for the Class 0 phase, wherein we may still occasionally see such objects. We therefore conclude that accretion variability with episodic bursts holds the key to the possible frequent occurrence of VeLLOs in the protostellar phase.
4. Discussion and model caveats
To the best of our knowledge, this work is the first systematic attempt to determine the nature of VeLLOs using numerical simulations of coupled star plus disk evolution starting from the gravitational collapse of pre-stellar cores. We also want to mention the works of Tomida et al. (2010) and Commercon et al. (2012), who found that FHSCs are consistent with VeLLOs using post-processing with radiative transfer codes of 3D MHD calculations. Our numerical model, however, has limitations, which may to some extent affect our conclusions. We discuss the limitations in some detail below.
4.1. Initial conditions in pre-stellar cores
Our model cores were assumed to have a uniform and constant initial temperature of 10 K. However, an increase in the core temperature, for instance due to the presence of nearby luminous massive stars, may have a twofold effect on our results. First, this would produce an increase in the mass infall rate, Ṁinfall, onto the central object in the pre-disk phase or onto the disk in the post-disk phase, because Ṁinfall is proportional to the cube of the sound speed. For instance, a core temperature of 30 K would imply a five times higher Ṁinfall, increasing the accretion luminosity of FHSCs by the same fraction. Nevertheless, most FHSCs would still have the accretion luminosity lower than the VeLLO upper limit of 0.1 L⊙ (see Figs. 4 and 10). Second, a higher background temperature would act to weaken (however, not entirely suppressing) the gravitational instability in circumstellar disks in the early stages of star formation. For instance, a background temperature of 30 K reduces the accretion rate variability (Vorobyov & Basu 2010, 2015), which would also reduce the likelihood of a young protostar to enter the VeLLO state during quiescent, low-accretion-rate phases.
Furthermore, our model cores have the initial gas surface density distribution similar to that of the integrated Bonnor-Ebert sphere with a small initial perturbation of A = 1.2. If the initial surface density perturbation is much higher (as might be expected for the shock compressed cores), then the mass infall rate would also increase, simultaneously raising the accretion luminosity of the FHSCs. According to radiation transfer simulations of Omukai (2007), the total luminosity of the FHSC in the Shu spherical collapse model, wherein 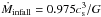 , varies in the 10-4−10-3L⊙ limits, whereas in the Larson-Penston model, in which
, varies in the 10-4−10-3L⊙ limits, whereas in the Larson-Penston model, in which 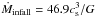 , the total luminosity is 0.01−0.1 L⊙. Therefore, variations in the initial density perturbation A may decrease the fraction of FHSCs in the VeLLO state. At the same time, a higher Ṁinfall in the post-disk formation stage would increase the strength of accretion variability and may subsequently increase the fraction of VeLLOs in the protostellar Class 0/I phases. The effect of varying initial conditions therefore requires further investigation.
, the total luminosity is 0.01−0.1 L⊙. Therefore, variations in the initial density perturbation A may decrease the fraction of FHSCs in the VeLLO state. At the same time, a higher Ṁinfall in the post-disk formation stage would increase the strength of accretion variability and may subsequently increase the fraction of VeLLOs in the protostellar Class 0/I phases. The effect of varying initial conditions therefore requires further investigation.
4.2. The lifetime of the FHSCs
As summarized in Dunham et al. (2014), the lifetime of the FHSCs may vary in wide limits, 0.5−50 kyr, depending on the amount of rotation, the mass infall rate onto the FHSC, and the strength of magnetic field in pre-stellar cores (see also Omukai 2007; Tomida et al. 2010; Commercon et al. 2012). For instance, in the spherical collapse model of Shu, the lifetime of the FHSC is 3.2 × 104 yr, assuming the gas temperature of 10 K. In the present work, we employed a toy model based on the fixed upper mass of the FHSC and the maximum gas temperature in the center of the core (see Sect. 2.2), which yielded lifetimes of between 2.8 × 103 yr and 2.2 × 104 yr. These values span a somewhat narrower range than those obtained from more realistic simulations and the construction of a more realistic model for the FHSC is needed for future work.
4.3. Internal disk luminosity
VeLLOs are observationally identified as objects with an internal luminosity ≤0.1 L⊙, the latter including the contribution from both the central object and circumstellar disk (if present). In our modeling, we calculated the total luminosity of the central object only, and neglected the internal luminosity of the disk, which may be non-zero depending on the rate of viscous and compressional heating in the disk. We currently develop disk models that include an accurate radiative transfer through the vertical disk column to estimate the internal disk luminosity.
4.4. The effect of the envelope
The envelope reprocesses the stellar radiation, which reduces the emergent flux densities at shorter wavelengths and enhances them at longer ones. Our spectral energy distributions are sufficiently well-sampled and, to first order, luminosity is conserved since the loss of the short-wavelength radiation is compensated by the increase in the long-wavelength radiation (Enoch et al. 2009; Dunham et al. 2008, 2013; Evans et al. 2009). However, the second order effects, such as geometry of the outflow cavity and external heating, can modify the emergent flux. For instance, the emergent bolometric luminosities are, on average, reduced by 20% relative to the internal luminosity Frimann et al. (in prep.) when the envelope is not spherical, but feature outflows. External heating can add from ≪0.1 L⊙ up to several tenths of a solar luminosity (e.g., Evans et al. 2001), depending on the local strength of the interstellar radiation field, how embedded a core is within its parent cloud, and the core mass. These effects were taken into account to the best of our ability, and when we compare the numbers and fractions of VeLLOs in our models to observations, we do that directly to VeLLOs as identified via internal luminosity in Dunham et al. (2008).
4.5. The fraction of ejected mass
In our models, we have assumed that 10% of the mass that passes through the sink cell is subsequently ejected by jets/outflows. The actual value is, however, a poorly constrained parameter and may vary in wide limits from 0.01% to 50% (Pelletier & Pudritz 1992; Wardle & Königl 1993; Shu et al. 1994). This may have a certain effect on our results. For instance, a value systematically higher than 10% of ejected mass would lead to a lower stellar mass and, simultaneously, a higher disk-to-star mass ratio. Lower stellar masses imply lower photospheric luminosities (under other equal conditions) and higher disk-to-star mass ratios imply stronger gravitational instability and, consequently, higher accretion variability. Both may act to increase the number of VeLLOs in the protostellar phase and focused studies are needed to assess the effect of ejected mass on the properties of stars and disks in general.
4.6. VeLLO fractions vs. initial core mass
It is interesting to know how the derived fractions of VeLLOs are related to the initial core mass in our models. Figure 12 presents the histograms showing the fraction of time spent by the cold accretion models in the VeLLO state as a function of the initial core mass (the latter represented by four mass bins). The sum of the fractions in each panel is equal to the total fraction of time spent by the corresponding objects (FHSC or Class I) in the VeLLO state. These total fractions are shown in the first and second numerical columns of Table 5. We exclude from this analysis the Class 0 objects in the cold accretion scenario because of the low statistics. We do not consider the hybrid accretion models for the same reason.
 |
Fig. 12 Fraction of time spent by the cold accretion models in the VeLLO state as a function of the initial core mass. |
Evidently, most VeLLOs in the FHSC phase are produced by low-mass cores, which is merely a reflection of the slope of the IMF (see Fig. 3). We note that the longevity of FHSCs may also depend on the initial rotation rate of the contracting pre-stellar cores (Tomida et al. 2010), which is a poorly constrained parameter. If, for instance, lower-mass cores have systematically higher ratios of rotational to gravitational energy, than they may live longer and this may further strengthen the found tendency. For the case of Class I objects, most VeLLOs are produced by cores with mass Mc ~ 0.3−0.4 M⊙. Interestingly, this is approximately the minimum mass required for contracting cores to produce gravitationally (and fragmentationally) unstable disks (Vorobyov 2013). These systems will exhibit variable accretion with episodic bursts; a necessary prerequisite for VeLLOs in the protostellar stage according to our findings. At the same time, central objects produced by these cores will have systematically lower photospheric luminosities (sometimes lower than 0.1 L⊙) than protostars produced by higher-mass cores (see Fig. 9). This combination of effects enables more VeLLOs in the Mc = 0.3−0.4 M⊙ mass range. Roughly similar results were obtained by Kim et al. (2016), who found that most VeLLO envelopes have masses ≤ 0.2 M⊙.
Observationally constrained core masses for VeLLOs are known only for a handful of objects. These are L1014 with Mcore = 1.7 M⊙ (Young et al. 2004), IRAM04191 with Mcore = 2.5 M⊙ (Dunham et al. 2006), L1521F with Mcore = 4.8 M⊙ (Bourke et al. 2006), L328 with Mcore = 0.07 M⊙ (Lee et al. 2009), and L673-7 with Mcore = 2.0 M⊙ (Dunham et al. 2010b). We note that these are current core masses and the initial core masses must have been somewhat higher. Evidently, most VeLLOs belong to rather high core masses, in disagreement with our modeling. We should emphasize, however, that the statistics in both cases (modeling and observations) is rather poor. More work is needed to understand the reason of this mismatch.
4.7. Constant star formation rate
When converting our numerically predicted time fractions to number fractions in Sect. 3.1.1, we made a fundamental assumption of a constant star formation rate. Palla & Stahler (1999, 2000) claimed that star formation in a series of star forming regions (e.g., in the Orion Nebula Cluster) shows accelerated star formation rates within the past few Myr. In Taurus, star formation shows this effect specifically in filaments while the star formation rate is declining outside filaments, after a peak approximately 2–3 Myr ago (Palla & Stahler 2002). Cores in different stages (e.g., Tafalla & Hacar 2015), Class 0 and I protostars and classical T Tauri stars co-exist, even if at different, specific locations and with different spatial spreads. This observational evidence suggests to us that star formation in active molecular clouds is ongoing for at least a couple of Myr if considered globally over the entire star formation region.
However, in our work we are predominantly interested in the evolution of the star formation rate within 1 Myr, the time scales from FHSC to protostars. Ignoring substructures and aiming at statistics of objects in molecular clouds as a whole, and assuming that cloud-to-cloud variations can be averaged out, we find it appropriate to assume, to first order, constant star formation rate over time scales of a few 100 kyr.
5. Conclusions
In this work, we have numerically studied the simultaneous evolution of protostars and protostellar disks by means of numerical hydrodynamics simulations coupled with a stellar evolution code. We consider the gravitational collapse of a large set of model cores, starting from the pre-stellar phase and terminating at the end of the embedded phase when 90% of the initial core mass has accreted onto the forming protostar plus disk system. The formation of the first hydrostatic core (FHSC) and its evolution is treated semi-analytically. Three protostellar accretion scenarios are considered: hybrid accretion, in which a fraction of accreted energy absorbed by the protostar depends on the accretion rate, hot accretion, wherein a constant fraction of the accreted energy is always absorbed by the protostar irrespective of the accretion rate, and cold accretion, wherein all accretion energy is radiated away, regardless of the actual accretion rate. We aim at determining the nature of VeLLOs, which are defined by the total luminosity Lobj not exceeding an upper limit of 0.1 L⊙. We found the following.
In the hybrid accretion scenario, most VeLLOs are expected to be FHSCs and only a small fraction are true protostars (see Table 2). When comparing the fraction of time spent by our models in the VeLLO state (Lobj< 0.1 L⊙), we found that FHSCs occupy 90.63% of the total VeLLO time, whereas Class 0 and I objects have only 0.69% and 8.68%, respectively. Furthermore, FHSCs spend all their time in the VeLLO state, whereas Class 0 and Class I protostars spend only a very small fraction of the corresponding phase duration, meaning that it would be unlikely (from a statistical point of view) to detect Class 0 and Class I protostars in the VeLLO state. Finally, VeLLOs are relatively rare objects, occupying only 7.3% of the total duration of the embedded phase (the sum of the last numerical column in Table 2), and most belong to the FHSCs (6.62%) and only a very small fraction are Class 0 (0.05%) and Class I (0.65%) protostars.
In the cold accretion scenario, the situation with VeLLOs is somewhat different (see Table 5). The majority of VeLLOs belong now to the Class I phase of stellar evolution. As with hybrid accretion, FHSCs spend all their time in the VeLLO state, but the Class I protostars now spend a modest fraction (7.91%) of the corresponding phase duration in the VeLLO state, which is much greater than a negligible value of 0.89% for the hybrid accretion models. This difference from the hybrid accretion case is caused by the reduced photospheric luminosity (and, as a consequence, reduced total luminosity) due to smaller stellar radii in the cold accretion models (Baraffe et al. 2012). However, VeLLOs are still rather rare objects, occupying only ≈11% of the embedded phase duration (the sum of the last numerical column is Table 5), but now most belong to the Class I protostars (5.62%) and FHSCs (5.16%), and only a small fraction are Class 0 protostars (0.19%).
In the hot accretion scenario, all VeLLOs belong to the FHSCs. No VeLLOs are found in either Class 0 or Class I phases. This is explained by the fact that the photospheric accretion of forming protostars is always higher than the VeLLO upper limit of 0.1 L⊙. Protostars bloat in response to the constant absorption of accretion energy and their photospheric luminosity raises above the VeLLO limit.
The most comprehensive search for VeLLOs to date was published in Dunham et al. (2008) based on the Spitzer Space Telescope Legacy Project “From Molecular Cores to Planet Forming Disks” (c2d). More recent protostar searches, summarized in Dunham et al. (2014), focused on bolometric rather than internal luminosity. Since bolometric luminosity includes external heating, and this term can dominate over internal when the internal luminosity is <0.1 L⊙, the distinction is crucial for finding VeLLOs. In Dunham et al. (2008), 15 VeLLOs were found in the c2d dataset, which contains a total of 112 protostars (Evans et al. 2009). Excluding sources from the Dunham et al. work that were not included in the Evans et al. paper, as that focused on the large molecular clouds only, there are 7 VeLLOs out of 112 protostars, suggesting a total fraction of 6.25% for VeLLOs in the protostellar stage. Here, we should note that all VeLLOs in the Dunham et al. sample belong to the protostellar stage, because the FHSCs are undetectable with the Spitzer observations at 3.6–8 μm. The obtained number is much higher than the fraction of 0.68% that we obtained in our numerical simulations for hybrid accretion, but similar to what was found for cold accretion; 5.7% (last numerical columns in Tables 2 and 5, but only for the sum of Class 0 and Class I phases). Here we should note that the observationally derived VeLLOs fraction of 6.25% may be a lower limit, because the existing surveys likely miss some objects in the tenuous Class I phase. The VeLLO sample needs to be revisited as the Herschel and SCUBA-2 core catalogs are published, since these are much deeper than the previous generation of surveys used by Dunham et al. (2008) and subsequent papers. For instance, Kim et al. (2016) inferred a VELLO fraction of <10% in the nearby star forming regions.
Most VeLLOs in the FHSC phase are produced by low-mass cores, which can be explained by the slope of the IMF. This tendency may change somewhat (strengthen or weaken) if the lifetime of the FHSCs depends systematically on the core initial rotation rate (e.g., Tomida et al. 2010). In the protostellar stage, most VeLLOs are produced by cores with mass Mc ~ 0.3−0.4 M⊙, which is in disagreement with available measurements of the core masses indicating that most VeLLOs have more massive cores. The low statistics of both numerical simulations and observations does not allow us to make definite conclusions and the reason for this disagreement remains to be understood.
VeLLOs are expected to be low-mass objects. In the hybrid accretion models, the maximum VeLLO mass is found to be 0.12 M⊙, while in the cold accretion case it is greater by a factor of approximately 2.5. For higher-mass protostars, the total luminosity in the embedded phase of star formation is inevitably greater than the VeLLO’s upper limit of 0.1 L⊙. Our work provides results that are testable with future ALMA observations that use Keplerian rotation to measure VeLLO masses. Such observations are needed to make further progress regarding the nature of VeLLOs.
Accretion variability with episodic bursts, inherent to many our models thanks to gravitational instability and fragmentation (Vorobyov & Basu 2015), has a profound effect on the calculated fractions. When variations in total luminosity caused by accretion variability are artificially reduced (by smoothing the luminosities), the fraction of VeLLOs in the Class 0/I phases greatly reduces, regardless of the accretion scenario. Without accretion variability, the population of VeLLOs would be almost totally dominated by FHSCs. We emphasize that episodic bursts and accretion variability can also be caused by mechanisms other than gravitational instability (see a review by Audard et al. 2014). It remains to be investigated how these additional sources of variability can modify our findings and hopefully improve the agreement of models with observations.
In studying the nature of VeLLOs, we have assumed that these objects have an upper luminosity of 0.1 L⊙. This value, however, has no physical motivation and is simply a result of useful convention. If the upper luminosity of VeLLOs, for instance, is increased to 0.2 L⊙, then the fraction of VeLLOs in the protostellar phase, as well as the overall fraction of VeLLOs relative to normal stars, also increases by a factor of approximately 3 for hybrid accretion and by a factor of 1.5–2.0 for cold accretion. The corresponding exact values are provided in Tables 7 and 8, respectively.
One interesting feature that can be seen in Tables 2 and 5 is that the fraction of VeLLOs in the Class 0 phase is systematically lower than in the later Class I phase. This finding seems to contradict observations, suggesting more VeLLOs in the Class 0 phase with 73% (11/15) being Class 0 objects and only 27% (4/15) being Class I objects (Dunham et al. 2008). This is likely caused by three factors. Firstly, accretion variability is lower in the early Class 0 phase (e.g., Vorobyov & Basu 2015), mainly due to lower disk masses and consequently reduced gravitational instability. Secondly, the duration of the Class 0 phase is shorter than that of the Class I phase, particularly for low-mass cores, owing to the fact that the FHSCs need to accumulate ≈0.05 M⊙ for the second collapse to ensue, which may take a sizeable fraction of the total duration of the embedded phase. We note that this argument applies strictly to the fractions calculated relative to the total time of all phases ttot and to the total time spend in the VeLLO state 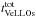 , but not to the time spend in each phase tphase. Thirdly, on the observational side, Dunham et al. (2008) may be biased against Class I sources (as discussed above) since they required evidence that the Spitzer sources were embedded in dense cores, and, for Class I sources, the cores may be tenuous enough to avoid detection.
, but not to the time spend in each phase tphase. Thirdly, on the observational side, Dunham et al. (2008) may be biased against Class I sources (as discussed above) since they required evidence that the Spitzer sources were embedded in dense cores, and, for Class I sources, the cores may be tenuous enough to avoid detection.
Finally, we note that if most VeLLOs are FHSCs, then large number detections of VeLLOs would imply long FHSC lifetimes. If rotation is not taken into account, core collapse simulations predict short lifetimes for FHSCs, in the order of several thousand years (Omukai 2007). Long lifetimes would imply that rotation and/or magnetic fields play an important role in the evolution of these objects (Tomida et al. 2010).
Acknowledgments
The authors are thankful to the anonymous referee for useful comments that helped to improve the paper. E.I.V. is thankful to Isabelle Baraffe and Gilles Chabrier for the Lyon stellar evolution code. This work is partly supported by the Austrian Science Fund (FWF) under research grant I2549-N27 and by the Russian Ministry of Education and Science Grant 3.961.2014/K. V.G.E. acknowledges Osterreichischer Austauschdienst (Austrian Agency for International Cooperation in Education and Research) for Ernst Mach grant. The simulations were performed on the Vienna Scientific Cluster (VSC-2), on the Shared Hierarchical Academic Research Computing Network (SHARCNET), and on the Atlantic Computational Excellence Network (ACEnet). This publication is supported by the Austrian Science Fund (FWF). M.M.D. acknowledges support from the Submillimeter Array (SMA) through a SMA postdoctoral fellowship, and from NASA through grant NNX13AE54G.
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., & Goodman, A. A. 2001, ApJ, 551, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., Mardones, D., Corder, S. A., et al. 2013, ApJ, 774, 39 [CrossRef] [Google Scholar]
- Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, Protostars and Planets VI, 387 [Google Scholar]
- Bachiller, R., Martin-Pintado, J., & Planesas, P. 1991, A&A, 251, 639 [NASA ADS] [Google Scholar]
- Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Vorobyov, E. I., & Chabrier, G. 2012, ApJ, 756, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S. 1997, ApJ, 485, 240 [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Billot, N., Morales-Calderón, M., Stauffer, J. R., Megeath, S. T., & Whitney, B. 2012, ApJ, 753, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bourke, T. L., Myers, P. C., Evans, N. J., II, et al. 2006, ApJ, 649, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Libr., 327, 41 [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Chen, H., Myers, P. C., Ladd, E. F., & Wood, D. O. S. 1995, ApJ, 445, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Arce, H. G., Zhang, Q., et al. 2010, ApJ, 715, 1344 [Google Scholar]
- Chen, X., Arce, H. G., Dunham, M. M., et al. 2012, ApJ, 751, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Commercon, B., Launhardt, R., Dullemond, C., & Henning, Th. 2012, A&A, 545, 98 [Google Scholar]
- Dapp, W. B., & Basu, S. 2009, MNRAS, 395, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., Evans, N. J., II, Caselli, P., et al. 2007, Protostars and Planets V, 17 [Google Scholar]
- Dunham, M. M., & Vorobyov, E. I. 2012, ApJ, 747, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Evans, N. J., II, Bourke, T. L., et al. 2006, ApJ, 651, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Crapsi, A., Evans, N. J., II, et al. 2008, ApJSS, 179, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Evans, N. J., Bourke, T. L., et al. 2010a, ApJ, 721, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M.,Evans, N. J., II, Terebey, S., Dullemond, C. P., & Young, C. H. 2010b, ApJ, 710, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Chen, X., Arce, H. G., et al. 2011, ApJ, 742, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Arce, H. G., Allen, L. E., et al. 2013, AJ, 145, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, in Protostars and Planets VI, eds. H. Beuther et al. (Tucson, AZ: Univ. Arizona Press), 195 [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, N. J., II, et al. 2015, ApJSS, 220, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Offner, S. S. R., Pineda, J. E., et al. 2016, ApJ, 823, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Elbakyan, V. G., Vorobyov, E. I., & Glebova, G. M. 2016, Astron. Rep., in press [Google Scholar]
- Enoch, M. L., Evans, N. J., II, Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Lee, J.-E., Harvey, P., Dunham, M. M., & Schnee, S. 2010, ApJ 722, L33 [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jorgensen, J. K., et al. 2009, ApJSS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Günther, H. M., Cody, A. M., Covey, K. R., et al. 2014, AJ, 148, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2003, ApJ, 597, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Visser, R., Sakai, N., et al. 2013, ApJ, 779, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., Hartmann, L. W., Strom, K. M., & Strom, S. E. 1990, AJ, 99, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, H. J., Evans, N. J., II, Dunham, M. M., Lee, J.-E., & Pontoppidan, K. M. 2012, ApJ, 758, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, M.-R., Lee, C. W., Dunham, M. M., et al. 2016, ApJSS, 225, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kryukova, E., Megeath, S. T., Gutermuth, R. A., et al. 2012, AJ, 144, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Bourke, T. L., Myers, P. C., et al. 2009, ApJ, 693, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Lee, H.-G., Shinn, J.-H., et al. 2010, ApJ, 709, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Kim, M.-R., Kim, G., et al. 2013, ApJ, 777, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S., & Matsumoto, T. 2011, ApJ, 729, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Masunaga, H., & Inutsuka, S. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Murillo, N. M., & Lai, S.-P. 2013, ApJ, 764, L15 [Google Scholar]
- Offner, S. S. R., & McKee, C. F. 2011, ApJ, 736, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K. 2007, PASJ, 59, 589 [NASA ADS] [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 2000, ApJ, 540, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 2002, ApJ, 581, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, G., Pudritz, R. E. 1992, ApJ, 394, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzuto, S., Elia, D., Schisano, E., et al. 2012, A&A, 547, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Arce, H. G., Schnee, S., et al. 2011, ApJ, 743, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Cody, A. M., Covey, K. R., et al. 2014, AJ, 148, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Cody, A. M., et al. 2015, AJ, 150, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Di Francesco, J., Enoch, M., et al. 2012, ApJ, 745, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, A., Froebrich, D., & Wood, K. 2013, MNRAS, 430, 2910 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, K. R., Shirley, Y. L., & Dunham, M. M. 2012, AJ, 144, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., & Hacar, A. 2015, A&A, 574, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomida, K., Machida, M. N., Saigo, K., Tomisaka, K., & Matsumoto, T. 2010, ApJ, 725, L239 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., & Bergin, E. A. 2012, ApJ, 754, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Visser, R., Bergin, E. A., & Jørgensen, J. K. 2015, A&A, 577, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I. 2013, A&A, 552, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, ApJ, 633, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2006, ApJ, 650, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2009, MNRAS, 393, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2010, ApJ, 719, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2015, ApJ, 805, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Baraffe, I., Harries, T., & Chabrier, G. 2013, A&A, 557, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardle, M., & Königl, A. 1993, MNRAS, 410, 218 [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Young, C. H., Jørgensen, J. K., Shirley, Y. L., et al. 2004, ApJS, 154, 396 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fraction of time (in per cent) spent by hybrid accretion models in each evolution phase.
Fraction of time (in per cent) spent by cold accretion models in each evolution phase.
All Figures
 |
Fig. 1 Total luminosity of the central object vs. time elapsed since the onset of core collapse in 31 models with the hybrid accretion scenario (black solid lines). The horizontal dotted lines indicate the upper luminosity for VeLLOs. The vertical dashed lines mark the instance of protostar formation. The green solid lines present the total stellar luminosity averaged over a time period of 20 kyr for models 21–24 and 29–31 and over a time period of 5 kyr for the remaining models. |
| In the text | |
 |
Fig. 2 Accretion and photospheric luminosities (thin blue and thick black lines, respectively) vs. time elapsed since the onset of core collapse in four prototype models. The vertical red dashed line indicates the beginning of the protostellar phase (i.e., the onset of the collapse of a FHSC to a protostellar seed). The horizontal dotted lines indicate the upper luminosity for VeLLOs. |
| In the text | |
 |
Fig. 3 Number of models in four mass bins (dN/ dM∗ ,fin) and the calculation of the weight coefficients for the model IMF. The vertical dash-dotted lines outline the four bins, in which the final stellar masses (M∗ ,fin) are divided. The solid line presents the Kroupa IMF normalized to the total number of our models. The open squares and circles are the values of the model IMF before and after weighing, respectively, and the numbers provide the weight coefficients ωi. |
| In the text | |
 |
Fig. 4 Total luminosity (Lobj) vs. evolutionary time (tevol) diagram. The time is counted from the onset of core collapse. The horizontal dashed lines mark the maximum VeLLO luminosity of 0.1 L⊙. The gray-scale mosaic presents the fraction of total time (in per cent) that all models spend in various bins in the Lobj–tevol diagram. The corresponding scale bar shows this fraction in per cent. The red, orange, and blue dots present the model data for the FHSC, Class 0 and Class I phases, respectively. |
| In the text | |
 |
Fig. 5 Total luminosity (Lobj) vs. central object mass (Mobj) diagram. The horizontal dashed line marks the maximum VeLLO luminosity of 0.1 L⊙. The gray-scale mosaic presents the fraction of total time (in per cent) that all models spend in various bins in the Lobj–Mobj diagram. The corresponding scale bar shows this fraction in per cent. The red, orange, and blue dots in Fig. 2 present the model data for the FHSC, Class 0 and Class I phases, respectively. |
| In the text | |
 |
Fig. 6 Same as Fig. 1, but for 29 models with hot accretion. |
| In the text | |
 |
Fig. 7 Same as Fig. 2, but for hot accretion. |
| In the text | |
 |
Fig. 8 Similar to Fig. 1, but for 32 models with cold accretion. |
| In the text | |
 |
Fig. 9 Similar to Fig. 2, but for models with cold accretion. |
| In the text | |
 |
Fig. 10 Similar to Fig. 4, but for models with cold accretion. |
| In the text | |
 |
Fig. 11 Similar to Fig. 5, but for models with cold accretion. |
| In the text | |
 |
Fig. 12 Fraction of time spent by the cold accretion models in the VeLLO state as a function of the initial core mass. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} \label{cont} &&\frac{{\partial \Sigma }}{{\partial t}} = - \nabla_p \cdot \left( \Sigma \bl{v}_p \right), \label{mom}\\ &&\frac{\partial}{\partial t} \left( \Sigma \bl{v}_p \right) + \left[ \nabla \cdot \left( \Sigma \bl{v_p} \otimes \bl{v}_p \right) \right]_p = - \nabla_p {\cal P} + \Sigma \, \bl{g}_p + (\nabla \cdot \mathbf{\Pi})_p, \label{energ} \\ &&\frac{\partial e}{\partial t} +\nabla_p \cdot \left( e \bl{v}_p \right) = -{\cal P} (\nabla_p \cdot \bl{v}_{p}) -\Lambda +\Gamma + \left(\nabla \bl{v}\right)_{pp^\prime}:\Pi_{pp^\prime}, \end{eqnarray}](/articles/aa/full_html/2017/04/aa28922-16/aa28922-16-eq41.png)
![\begin{eqnarray} &&\Sigma={r_0 \Sigma_0 \over \sqrt{r^2+r_0^2}}, \label{dens}\\ &&\Omega=2\Omega_0 \left( {r_0\over r}\right)^2 \left[\sqrt{1+\left({r\over r_0}\right)^2 } -1\right]. \label{omega} \end{eqnarray}](/articles/aa/full_html/2017/04/aa28922-16/aa28922-16-eq79.png)