| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628576 | |
| Published online | 22 March 2017 | |
A re-analysis of the NuSTAR and XMM-Newton broad-band spectrum of Serpens X-1
1 Universitá degli Studi di PalermoDipartimento di Fisica e Chimica, via Archirafi 36, 90123 Palermo, Italy
e-mail: marco.matranga01@unipa.it
2 Universitá degli Studi di Cagliari, Dipartimento di Fisica, SP Monserrato-Sestu KM 0.7, 09042 Monserrato, Italy
Received: 22 March 2016
Accepted: 23 December 2016
Context. High-resolution X-ray spectra of neutron star low-mass X-ray binaries (LMXBs) in the energy range 6.4−6.97 keV are often characterized by the presence of Kα transition features of iron at different ionization stages. Since these lines are thought to originate by reflection of the primary Comptonization spectrum over the accretion disk, the study of these features allows us to investigate the structure of the accretion flow close to the central source. Thus, the study of these features gives us important physical information on the system parameters and geometry. Ser X-1 is a well studied LMXB that clearly shows a broad iron line. Several attempts to fit this feature as a smeared reflection feature have been performed on XMM-Newton, suzaku, NuSTAR, and, more recently, on Chandra data, finding different results for the inner radius of the disk and other reflection or smearing parameters. High-quality broad-band NuSTAR data on Ser X-1 have recently been published. Using relativistically smeared self-consistent reflection models, a value of Rin close to 1.0 RISCO (corresponding to 6 Rg, where Rg is the Gravitational radius, defined as usual Rg = GM/c2) was found, as well as a low inclination angle of less than ~10°.
Aims. The aim of this paper is to probe to what extent the choice of reflection and continuum models (and uncertainties therein) can affect the conclusions about the disk parameters inferred from the reflection component. To this aim, we re-analyze all the available public NuSTAR and XMM-Newton observations, which have the best sensitivity at the iron line energy, of Ser X-1. Ser X-1 is a well studied source, its spectrum has been observed by several instruments, and is therefore one of the best sources for this study.
Methods. We used slightly different continuum and reflection models with respect to those adopted in the literature for this source. In particular, we fit the iron line and other reflection features with self-consistent reflection models, such as reflionx (with a power-law illuminating continuum modified with a high-energy cutoff to mimic the shape of the incident Comptonization spectrum) and rfxconv. With these models, we fit NuSTAR and XMM-Newton spectra yielding consistent spectral results.
Results. Our results are in line with those already found by Miller et al. (2013) but are less extreme. In particular, we find the inner disk radius to be ~13 Rg with an inclination angle with respect to the line of sight of ~27°. We conclude that, while the choice of the reflection model has little impact on the disk parameters, as soon as a self-consistent model is used, the choice of the continuum model can be important in the precise determination of the disk parameters from the reflection component. Hence broad-band X-ray spectra are highly preferable to constrain the continuum and disk parameters.
Key words: line: formation / line: identification / stars: individual: Serpens X-1 / stars: neutron / X-rays: binaries / X-rays: general
© ESO, 2017
1. Introduction
X-ray spectra emitted by low-mass X-ray binaries (LMXBs) of the atoll class (Hasinger & van der Klis 1989) are usually characterized by two states of emission: the soft and the hard state. During soft states, the spectrum can be well described by a soft thermal component, usually a blackbody or a disk multi-color blackbody, possibly originating from the accretion disk, and a harder component, usually a saturated Comptonization spectrum. In some cases, a hard power-law tail has been detected in the spectra of these sources during soft states both in Z sources (Di Salvo et al. 2000), and in atoll sources (e.g., Piraino et al. 2007), usually interpreted as Comptonization of a non-thermal population of electrons. On the other hand, during hard states, the hard component of the spectrum can be described by a power law with high-energy cutoff, interpreted as unsaturated Comptonization, and a weaker soft blackbody component (e.g., Di Salvo et al. 2015). The hard component is generally explained in terms of inverse Compton scattering of soft photons, coming from the neutron star surface and/or the inner accretion disk, by hot electrons present in a corona, possibly located in the inner part of the system surrounding the compact object (D’Aì et al. 2010).
In addition to the continuum, broad emission lines in the range 6.4−6.97 keV are often observed in the spectra of LMXBs (see e.g., Cackett et al. 2008; Pandel et al. 2008; D’Aì et al. 2009, 2010; Iaria et al. 2009; Di Salvo et al. 2005, 2009, 2015; Egron et al. 2013). These lines are identified as Kα transitions of iron at different ionization states and are thought to originate from reflection of the primary Comptonization spectrum over the accretion disk. These features are powerful tools to investigate the structure of the accretion flow close to the central source. In particular, important information can be inferred from the line width and profile, since the detailed profile shape is determined by the ionization state, geometry and velocity field of the emitting plasma (see e.g., Fabian et al. 1989). Indeed, when the primary Comptonization spectrum illuminates a colder accretion disk, other low-energy discrete features (such as emission lines and absorption edges) are expected to be created by photoionization and successive recombination of abundant elements in different ionizations states as well as a continuu emission caused by direct Compton scattering of the primary spectrum off the accretion disk. All these features together form the so-called reflection spectrum, and the whole reflection spectrum is smeared by the velocity-field of the matter in the accretion disk.
Ser X-1 is a persistent accreting LMXB classified as an atoll source, that shows type I X-ray bursts. The source was discovered in 1965 by Friedman et al. (1967). Li et al. (1976) firstly discovered type-I X-ray bursts from this source, which was therefore identified as an accreting neutron star. Besides type-I bursts with a typical duration of a few seconds (Balucinska & Czerny 1985), a super-burst with a duration of approximately 2 h has also been reported (Cornelisse et al. 2002). Recently, Cornelisse et al. (2013), analyzing spectra collected by the Gran Telescopio Canarias (GTC), detected a two-hour periodicity. They tentatively identified this periodicity as the orbital period of the binary and hence proposed that the secondary star might be a main-sequence K-dwarf.
Church & Balucińska-Church (2001) have performed a survey of LMXBs carried out with the ASCA satellite. The best-fit model used by these authors to fit the spectrum of Ser X-1 was a blackbody plus a cutoff power-law with a Gaussian iron line. Oosterbroek et al. (2001) have analyzed two simultaneous observations of this source collected with BeppoSAX and RXTE. The authors fitted the broad-band (0.1−200 keV) BeppoSAX spectrum with a model consisting of a disk blackbody, a reflection component described by the XSPEC model pexrav, and a Gaussian line. However, in that case, the improvement in χ2 with respect to a model consisting of a blackbody, a Comptonization spectrum modeled by compST, and a Gaussian was not significant, and therefore it was not possible to draw any definitive conclusion about the presence of a reflection continuum.
Bhattacharyya & Strohmayer (2007) carried out the analysis of three XMM-Newton observations of this system. They managed to fit the EPIC/pn spectrum with a model consisting of disk blackbody, a Comptonization continuum modeled with compTT, and a diskline, that is, a Gaussian line distorted and smeared by the Keplerian velocity field in the accretion disk (Fabian et al. 1989). They found strong evidence that the Fe line has an asymmetric profile and therefore that the line originates from reflection in the inner rim of the accretion disk. Fitted with a Laor profile (Laor 1991), the line shape gave an inner disk radius of 4−5 Rg or 16 Rg (depending on the observation) and an inclination angle to the binary system of 40−50°. Cackett et al. (2008), from data collected by suzaku, performed a study of the iron line profiles in a sample of three LMXBs including Ser X-1. From the analysis of XIS and PIN spectra, they found a good fit of the broad-band continuum using a blackbody, a disk blackbody and a power-law. Two years later, Cackett et al. (2010) re-analyzed XMM-Newton and suzaku data of a sample of ten LMXBs including Ser X-1, focusing on the iron line − reflection emission. In particular, for Ser X-1, they analyzed four spectra: three Epic-PN spectra obtained with XMM-Newton and one obtained with the XIS and the PIN instruments on board suzaku. Initially, they fitted the spectra of the continuum emission using a phenomenological model, consisting of a blackbody, a disk-blackbody, and a power-law. Then, they started the study of the Fe line adding first a diskline component and then a reflection component convolved with rdblur (that takes into account smearing effects due to the motion of the emitting plasma in a Keplerian disk). They obtained different results for the smearing parameters both for different observations and for different models used on the same observation. For the sake of clarity, these results are summarized in Table 1.
Results of spectral analysis of Ser X-1 from previous studies.
Miller et al. (2013) analyzed two NuSTAR observations carried out in July, 2013. They fitted the continuum emission using a model consisting of a blackbody, a disk blackbody and a power-law. With respect to this continuum model, evident residuals were present around 6.40−6.97 keV, suggesting the presence of a Fe line. Therefore they added a kerrdisk component to the continuum to fit the emission line, taking into account a possible non-null spin parameter for the neutron star. They also tried to fit the reflection spectrum (i.e., the iron line and other expected reflection features) with the self-consistent reflection model reflionx, a modified version of reflionx calculated for a blackbody illuminating spectrum, convolved with the kerrconv component. The addition of the reflection component gave a significant improvement of the fit. In most cases, the best fit gave low inclination angles (less than ~10°), in agreement with recent optical observations (Cornelisse et al. 2013), inner disk radii compatible with the innermost stable circular orbit (ISCO), corresponding to approximately 6 Rg for small values of the spin parameter, a ionization parameter log ξ ~ 2.3−2.6, and a slight preference for an enhanced iron abundance. The fit was relatively insensitive to the value of the adimensional spin parameter, a, of the neutron star.
More recently, Chiang et al. (2016a) analyzed a recent 300 ks Chandra/HETGS observation of the source performed in the “continuous clocking” mode and thus free of photon pile-up effects. They fitted the continuum with a combination of multicolor disk blackbody, blackbody, and power-law. The iron line was found to be significantly broader than the instrumental energy resolution and fitting this feature with a diskline instead of a broad Gaussian gave a significant improvement of the fit. They also tried self-consistent reflection models, namely the reflionx model with a power-law continuum as illuminating source and xillver (see e.g., García et al. 2013), to describe the iron line and other reflection features, yielding consistent results. In particular, this analysis gave an inner radius of ~7−8 Rg and an inclination angle of approximately 30 deg, see also Chiang et al. (2016b) for the spectral analysis of suzaku data of Ser X-1.
As described above, different continuum models were used to fit the spectrum of Ser X-1 observed with various instruments at different times. In Table 1, we summarize the results of the spectral analysis of this source obtained from previous studies, and, in particular, the results obtained for the iron line and the reflection model. Quite different values have been reported for the inclination angle (from less than 10 deg to approximately 40 deg), for the inner disk radius (from 4 to more than 100 Rg), and for the iron line centroid energy and/or the ionization parameter log ξ, indicating that the disk is formed by neutral or very highly ionized plasma.
In this paper, we re-analyze all the available public NuSTAR observations of Ser X-1, fitting the iron line and other reflection features with both phenomenological and self-consistent reflection models. These data have already been analyzed by Miller et al. (2013) using a different choice of the continuum and reflection models. We compare these results with those obtained from three XMM-Newton observations (already analyzed by Bhattacharyya & Strohmayer 2007) fitted with the same models. We choose to re-analyze NuSTAR and XMM-Newton spectra because these instruments provide the largest effective area available to date, coupled with a moderately good energy resolution, at the iron line energy, and a good broad-band coverage. Moreover, the source showed similar fluxes during the NuSTAR and XMM-Newton observations. We also note that NuSTAR is not affected by pile-up problems in the whole energy range. The spectral results obtained for NuSTAR and XMM-Newton are very similar and the smearing parameters of the reflection component are less extreme than those found by Miller et al. (2013), and in good agreement with the results obtained from the Chandra observation (Chiang et al. 2016a). In particular, we find an inner disk radius in the range 10−15 Rg and an inclination angle with respect to the line of sight of 25−30°.
Results of the fit of NuSTAR and XMM-Newton spectra of Ser X-1 using Gaussian and diskline models.
Results of the fit of NuSTAR and XMM-Newton spectra of Ser X-1 using rdblur combined with rfxconv or reflionx.
2. Observations and data reduction
In this paper, we analyze data collected by the NuSTAR satellite. Ser X-1 has been observed twice with NuSTAR, obsID: 30001013002 (12-JUL-2013) and obsID: 30001013004 (13-JUL-2013). The exposure time of each observation is approximately 40 k. The data were extracted using NuSTARDAS (NuSTAR Data Analysis Software) v1.3.0. Source data have been extracted from a circular region with 120′′ radius whereas the background has been extracted from a circular region with 90′′ radius in a region far from the source. First, we ran the “nupipeline” with default values of the parameters as we aimed to get “STAGE 2” events clean. Then spectra for both detectors, FPMA and FPMB, were extracted using the “nuproducts” command. Corresponding response files were also created as output of nuproducts. A comparison of the FPMA and FPMB spectra indicated good agreement between them. To check this agreement, we fitted the two separate spectra with all parameters tied to each other but with a constant multiplication factor left free to vary. Since the value of this parameter is 1.00319 ± 0.00145, our assumption was basically correct. Following the same approach described in Miller et al. (2013), we therefore created a single added spectrum using the “addascaspec” command. A single response file was thus created using “addrmf”, weighting the two single response matrices by the corresponding exposure time. In this way, we obtained a summed spectrum for the two NuSTAR observations and the two NuSTAR modules. We fitted this spectrum in the 3−40 keV energy range, where the emission from the source dominates over the background.
We also used non-simultaneous data collected with the XMM-Newton satellite in March, 2004. The considered obsIDs are 0084020401, 0084020501, and 0084020601. All observations are in Timing Mode and each of them has a duration of ~22 k. We extracted source spectra, background spectra, and response matrices using the (Science Analysis Software SAS) v.14 setting the parameters of the tools accordingly. We produced a calibrated photon event file using reprocessing tools “epproc” and “rgsproc” for PN and RGS data respectively. We also extracted the MOS data; these were operated in uncompressed timing mode. However, the count rate registered by the MOS was in the range 290−340 c/s, which is above the threshold for avoiding deteriorated response due to photon pile-up. The MOS spectra indeed show clear signs of pile-up and we preferred not to include them in our analysis, since these detectors cover the same energy range of the PN.
Before extracting the spectra, we filtered out contaminations due to background solar flares detected in the 10−12 keV Epic PN light-curve. In particular we have cut out approximately 600 s for obsID 0084020401, approximately 800 s for obsID 0084020501, and finally approximately 1600 s for obsID 0084020601. In order to remove the flares, we applied time filters by creating a GTI file with the task “tabgtigen”. In order to check for the presence of pile-up we ran the task “epatplot” and found significant contamination in each observation. The count-rate registered in the PN observations was in the range 860−1000 c/s that is just above the limit for avoiding contamination by pile-up. Therefore, we extracted the source spectra from a rectangular region (RAW X≥26) and (RAW X≤46) including all the pixels in the y direction but excluding the brightest columns at RAW X = 35 and RAW X = 36. This significantly reduced the pile up (pile up fraction below a few percent in the considered energy range).
We only selected events with PATTERN ≤ 4 and FLAG=0 that are the standard values to remove spurious events. We extracted the background spectra from a similar region to the one used to extract the source photons but in a region away from the source included between (RAWX ≥ 1) and (RAWX ≤ 6 ). Finally, for each observation, using the task “rgscombine” we obtained the added source spectrum RGS1+RGS2, the relative added background spectrum, along with the relative response matrices. We fitted RGS spectrum in the 0.35−1.8 keV energy range, whereas the Epic-PN in the 2.4−10 keV energy range.
Spectral analysis was performed using XSPEC v.12.8.1 (Arnaud 1996). For each fit we used the phabs model in XSPEC to describe the neutral photoelectric absorption due to the interstellar medium with photoelectric cross sections from Verner et al. (1996) and element abundances from Wilms et al. (2000). For the NuSTAR spectrum, which lacks low-energy coverage up to 3 keV, we fixed the value of the equivalent hydrogen column, NH, to the same value adopted by Miller et al. (2013), namely NH = 4 × 1021 cm-2 (Dickey & Lockman 1990), while for the XMM-Newton spectrum was left free to vary in the fit, finding a slightly higher value (see Tables 2 and 3). As a further check, we fitted the NuSTAR spectrum fixing NH to the same value found for the XMM spectrum, but the fit parameters did not change significantly.
3. Spectral analysis
3.1. NuSTAR spectral analysis
The NuSTAR observations caught the source in a high-luminosity (~1038 erg/s, Miller et al. 2013) state, therefore most probably in a soft state. As seen in other similar atoll sources, the spectrum of Ser X-1 is characterized by a soft component (i.e., blackbody), interpreted as thermal emission from the accretion disk, a hard component (i.e., a Comptonization spectrum), interpreted as saturated Comptonization from a hot corona, and often by the presence of a broad iron emission line at 6.4−6.97 keV depending on the iron ionization state. We used the Comptonization model nthComp (Życki et al. 1999) in XSPEC, with a blackbody input seed photon spectrum, to fit the hard component. We used a simple blackbody to describe the soft component. Substituting the blackbody with a multicolor disk blackbody, diskbb in XSPEC, gives a similar quality fit and the best-fit parameters do not change significantly.
To fit the iron line, we first tried simple models such as a Gaussian profile or a diskline (Fabian et al. 1989). The best-fit parameters, obtained using a Gaussian or diskline profile, alternatively, are in good agreement with each other (see Table 2). Using a diskline instead of a Gaussian profile, we get an improvement of the fit corresponding to Δχ2 = 54 for the addition of two parameters. Spectra, along with the best-fit model and residuals are shown in Fig. 1. In both cases, the fit results are poor (the relative null hypothesis probability is 2.8 × 10-8; the reduced χ2 are still relatively large, and evident residuals are present, especially above 10 keV, see Fig. 1).
 |
Fig. 1 NuSTAR spectra of Ser X-1 and best-fitting model together with residuals in units of sigma for the corresponding model. These are; top-left: “Gauss”, top-right: “diskline”, bottom-left: “rdb-reflio”, and bottom-right: “rdb-rfxconv”. Dashed lines indicate the black-body component, dotted lines indicate the reflection components (i.e., the Gaussian or Diskline profile for the iron line, top panels, or the self-consistent reflection component, bottom panels, respectively), and the dashed-dotted lines indicate the comptonized component. |
In order to fit the residuals at high energy, we added a powerlaw component (a hard tail) to all the models described above. A hard power-law tail is often required to fit high-energy residuals of atoll sources in the soft state (see e.g., Pintore et al. 2015, 2016; Iaria et al. 2001, 2002), and this component may also be present in the spectrum of Ser X-1 (see Miller et al. 2013). Unless specified otherwise, for every fit, we froze the power-law photon index to the value found by Miller et al. (2013) for Ser X-1, that is, 3.2. The new models are now called gauss-pl and diskline-pl, respectively. The new best fit parameters are reported in Table 2. While the best-fit parameters do not change significantly with the addition of this component, we get an improvement of the fit corresponding to a reduction of the χ2 by Δχ2 = 123 (for the model with a Gaussian line profile) and Δχ2 = 113 (for the model with a diskline profile) for the addition of one parameter, respectively. The probabilities of chance improvement of the fit are 8.5 × 10-24 and 8.6 × 10-23, respectively. Some residuals are still present between 10 and 20 keV, probably caused by the presence of an unmodeled Compton hump. We note that the soft blackbody component remains significant even after the addition of the power-law component. If we eliminate this component from the fitting model, we get a worse fit, corresponding to a decrease of Δχ2 = 245 for the addition of two parameters when the soft component is included in the fit, and a probability of chance improvement of the fit of ~3 × 10-44.
3.2. Reflection models
We also tried to fit the NuSTAR spectrum of Ser X-1 with more sophisticated reflection models, performing a grid of fit with self-consistent models such as reflionx or rfxconv. Reflionx and rfxconv models both include the reflection continuum, the so called Compton hump caused by direct Compton scattering of the reflected spectrum, and discrete features (emission lines and absorption edges) for many species of atoms at different ionization stages (Ross & Fabian 2005; Kolehmainen et al. 2011).
The reflionx model depends on five parameters; the abundance of iron relative to the solar value, the photon index of the illuminating power-law spectrum (Γ, ranging between 1.0 to 3.0), the normalization of reflected spectrum, the redshift of the source, and the ionization parameter ξ = LX/ (ner2) where LX is the X-ray luminosity of the illuminating source, ne is the electron density in the illuminated region, and r is the distance of the illuminating source to the reflecting medium. When using reflionx, which uses a power-law as illuminating spectrum, in order to take into account the high-energy roll over of the Comptonization spectrum, we have multiplied it by a high-energy cutoff, highecut, with the folding energy Efold set to 2.7 times the electrons temperature kTe and the cutoff energy Ecutoff tied to 0.1 keV. In this way, we introduce a cutoff in the reflection continuum, which otherwise resembles a power-law. The cut-off energy fixed at 2.7 times the electron temperature of the Comptonization spectrum (assumed to be similar to a blackbody spectrum), is appropriate for a saturated Comptonization (see e.g., Egron et al. 2013). We used the nthComp model to fit the Comptonization continuum. Moreover, we fixed the photon index of the illuminating spectrum, Γ, to that of the nthComp component. We stress that in our analysis, we use a different reflionx reflection model with respect to that used by Miller et al. (2013). In fact, we used a model that assumes an input power-law spectrum as the source of the irradiating flux, modified in order to mimic the nthcomp continuum, by introducing the model component highecut. Miller et al. (2013) instead used a modified version of reflionx calculated for a blackbody input spectrum, since that component dominates their phenomenological continuum.
rfxconv is an updated version of the code in Done & Gierliński (2006), using Ross & Fabian (2005) reflection tables. This is a convolution model that can be used with any input continuum and has therefore the advantage of taking the given Comptonization continuum as the illuminating spectrum; it depends on five parameters; the relative reflection fraction (rel-refl defined as Ω/2π, namely as the solid angle subtended by the reflecting disk as seen from the illuminating corona in units of 2π), the cosine of the inclination angle, the iron abundance relative to the Solar value, the ionization parameter Log ξ of the accretion disk surface, and the redshift of the source.
Due to its high velocities, the radiation re-emitted from the plasma located in the inner accretion disk suffers Doppler and relativistic effects (which smears the whole reflection spectrum). In order to take these effects into account, we have convolved the reflection models with the rdblur component (the kernel of the diskline model), which depends on the values of the inner and outer disk radii, in units of the Gravitational radius (Rg = GM/c2), the inclination angle of the disk (that was kept tied to the same value used for the reflection model), and the emissivity index, Betor, that is the index of the power-law dependence of the emissivity of the illuminated disk (which scales as rBetor). Finally, we also considered the possibility that the neutron star has a spin. In this case, the reflection component was convolved with the Kerrconv component (Brenneman & Reynolds 2006), that, through its adimensional spin parameter “a”, allowed us to implement a grid of models exploring different values of “a” (see Appendix A). For this model there is also the possibility to fit the emissivity index of the inner and outer parts of the disk independently, although in our fits we used the same emissivity index for the whole disk. For all the fits, we have fixed the values of Rout to 2400 Rg, the iron abundance to solar value, Fe/solar = 1, and the redshift of the source to 0. The best fit parameters are reported in Tables 2–A.2.
We started to fit the data adding a reflection component, reflionx or rfxconv, convolved with the blurring component rdblur, to the continuum model given by the blackbody and the nthcomp components (models are called rdb-reflio and rdb-rfxconv, respectively). Fit results for both models are acceptable, with 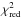 close to 1.09. There are a few differences between the best-fit parameters of the rdb-reflio model with respect to those of the rdb-rfxconv model. In particular, the rdb-rfxconv model gives a lower value of Rin, while the rdb-reflio model gives a higher ionization parameter (although with a large uncertainty). Spectra, along with the best-fit model and residuals are reported in Fig. 1. The residuals are very similar for the two models, apart from the 8−10 keV energy range, where therdb-reflio model shows flatter residuals than the rdb-rfxconv model (see Fig. 1).
close to 1.09. There are a few differences between the best-fit parameters of the rdb-reflio model with respect to those of the rdb-rfxconv model. In particular, the rdb-rfxconv model gives a lower value of Rin, while the rdb-reflio model gives a higher ionization parameter (although with a large uncertainty). Spectra, along with the best-fit model and residuals are reported in Fig. 1. The residuals are very similar for the two models, apart from the 8−10 keV energy range, where therdb-reflio model shows flatter residuals than the rdb-rfxconv model (see Fig. 1).
As before, we also tried to add a power-law component to the models obtained by the convolution of the blurring component (rdblur) with the two different reflection components (rfxconv or reflionx). The two new models are called rdb-rfxconv-pl and rdb-reflion-pl, respectively. In both cases, we get a significant improvement of the fit, with Δχ2 = 90 for the addition of two parameters and Δχ2 = 66 for the addition of one parameter, respectively. In these cases, an F-test yields a probability of chance improvement of 3.1 × 10-15 for rdb-reflion-pl and 6.1 × 10-19 for rdb-rfxconv-pl, respectively. Spectra, along with the best-fit model and residuals are reported in Fig. 2, whereas values of the best-fit parameters are listed in Table 3. Residuals are now flat (see plots reported in upper panels of Fig. 2). We also note that in this way we get more reasonable values for the best-fit parameters, especially for the ionization parameter, log ξ, which is approximately 2.7 for both models, in agreement with the centroid energy of the iron line at approximately 6.5 keV, and well below 3.7 (an ionization parameter log ξ ~ 3.7 would imply that the matter of the accretion disk would be fully ionized).
 |
Fig. 2 Top panels: NuSTAR spectra of Ser X-1 and best-fitting model together with residuals in units of sigma for the corresponding model. These are; top-left: “rdb-reflio-pl”, top-right: “rdb-rfxconv-pl”. Bottom panels: XMM-Newton spectra and best-fitting model together with residuals in units of sigma for the corresponding model. These are: bottom-left: “diskline-pl-xmm”, and bottom-right: “rdb-rfxconv-pl-xmm”. For clarity, only the first XMM-Newton observation is shown. Dashed lines indicate the black-body component, dotted lines indicate the reflection components (i.e., the Diskline profile for the iron line or the self-consistent reflection component), the solid line indicates the power-law component, and the dashed-dotted lines indicate the comptonized component. |
In summary, the best fit of the NuSTAR spectrum of Ser X-1 is obtained fitting the continuum with a soft blackbody component, a Comptonization spectrum, and a hard power-law tail and fitting the reflection features with the rfxconv model smeared by the rdblur component, since the fitting results are relatively insensitive to the value of the spin parameter “a” (see Appendix A). This fit, corresponding to a χ2(d.o.f.) = 912.5(911), gives a blackbody temperature of ≃0.54 keV, a temperature of the seed photons for the Comptonization of ≃0.93 keV, an electron temperature of the Comptonizing corona of ≃2.70 keV, and a photon index of the primary Comptonized component of ≃2.17, whereas the photon index of the hard power-law tail is steeper, at approximately 3.2. The reflection component gives a reflection amplitude (that is the solid angle subtended by the accretion disk as seen from the Comptonizing corona) of ≃0.24 and an ionization parameter of log ξ ≃ 2.7. The smearing of the reflection component gives an inner disk radius of Rin ranging between 10 and 16 Rg, an inclination angle of the disk with respect to the line of sight of i ≃27°, and the emissivity of the disk scaling as ∝r− 2.6 ± 0.2. We note that the Compton hump is highly significant. To evaluate its statistical significance, we can compare the best fit obtained with the model diskline-pl with the best fit given by the model rdb-rfxconv-pl (the main difference between the two models is, in fact, that rfxconv contains the reflection continuum and diskline does not). Using rfxconv instead of diskline, we get a decrease of the χ2 by Δχ2 = 87 for the addition of one parameter and an F-test probability of chance improvement of 8 × 10-20, which is statistically significant.
3.3. XMM-Newton spectral analysis
We also carried out the analysis of XMM-Newton observations of Ser X-1. A previous study, based only on the PN data analysis, has been reported by Bhattacharyya & Strohmayer (2007). We updated the analysis by performing the fit of the RGS spectra in the 0.35–1.8 keV energy range and the PN spectra in the 2.4–10 keV energy range. Following the same approach used for the analysis on NuSTAR data, we assumed a continuum model composed of a blackbody, a hard power-law, and the nthComp component. In addition to the continuum components described above, we also detected several discrete features present in all RGS spectra, both in absorption and in emission that were supposed to be of instrumental origin by Bhattacharyya & Strohmayer (2007). The energies of the most intense features detected in our spectra lie between 0.5 keV and 0.75 keV. To fit these features we therefore added three additional Gaussians to our model: two absorption lines at 0.528 keV and at 0.714 keV, respectively, and one in emission at 0.541 keV. The identification of these lines was not straightforward. The 0.528 keV energy is close to the neutral O Kα line, expected at a rest frame energy of 0.524 keV, while the 0.541 keV emission line is close to the expected energy of the O I edge at 0.538 keV. These two lines may, therefore, be instrumental features caused by a miscalibration of the neutral O edge in the RGS. The other absorption line at 0.714 keV is close to the O VII absorption edge expected at a rest-frame energy of 0.739 keV. Given that the identification of these lines is uncertain, we do not discuss them further here. To this continuum, we first added a diskline (model called diskline-pl-xmm, see Table 2) to fit the iron line profile. Then, we fitted the spectra substituting the diskline with the self-consistent reflection model that gave the best fit to the NuSTAR data, that is “rfxconv”, convolved with the smearing component “rdblur” (model called rdb-rfxconv-pl-xmm, results are reported in Table 3).
We have performed the fit of the spectrum obtained from these three observations simultaneously, tying parameters of the RGS with all the parameters of the PN from the same observation. The spectra of the three XMM observations are very similar to one another, except for the soft black body temperature that was left free to vary in different datasets. Values of the best-fit parameters of the model diskline-pl-xmm are in good agreement with what we have found from the fit of the NuSTAR spectra with the same model.
We also performed the fit with a model including the reflection component rfxconv, called rdb-rfxconv-pl-xmm. As before, in order to take into account structures visible in the RGS spectra, we have added three Gaussians to the model. As before, we tied parameters of the RGS to the corresponding parameters of the PN from the same observation, except for the parameter kTbb that was left free to vary among the three observations. We also note that for the these fits, the inclination angle was fixed to the corresponding values we found from the NuSTAR spectra. Results are reported in Table 3, and are in good agreement with those obtained for the NuSTAR spectrum.
4. Discussion
Ser X-1 is a well-studied LMXB showing a broad emission line at 6.4−6.97 keV interpreted as emission from iron at different ionization states and smeared by Doppler and relativistic effects caused by the fast motion of matter in the inner accretion disk. Moderately high energy resolution spectra of this source have been obtained from XMM-Newton, suzaku, NuSTAR, and Chandra. However, as described in Sect. 1, spectral results for the reflection component are quite different for different observations or for different models used to fit the continuum and/or the reflection component. While spectral differences in different observations may be, in principle, justified by intrinsic spectral variations of the source, differences caused by different continuum or reflection models should be investigated in detail in order to give a reliable estimate of the parameters of the system. For example, in a recent NuSTAR observation analyzed by Miller et al. (2013), assuming a modified version of reflionx calculated for a black-body input spectrum, the authors report a significant detection of a smeared reflection component in this source, from which they derive an inner radius of the disk broadly compatible with the disk extending to the ISCO (corresponding to 6 Rg in the case a = 0) and an inclination angle with respect to the line of sight <10°. On the other hand, Chiang et al. (2016a), analyzing a recent 300 ks Chandra/HETGS observation of the source, obtained a high-resolution X-ray spectrum that gave an inner radius of Rin ~ 7−8 Rg and an inclination angle of ~30°.
Here, we analyzed all the available NuSTAR and XMM-Newton observations of Ser X-1. These observations have already been analyzed by Miller et al. (2013) and Bhattacharyya & Strohmayer (2007), respectively, who used different continuum and reflection models and report different results for the reflection component. The same XMM-Newton observations have also been analyzed by Cackett et al. (2010), who also report different results for the reflection component, with higher inner disk radii (between 15 and more than 45 Rg) and relatively low inclination angles (<10°) when using a blurred reflection model and inclination angle between 10 and 35° when using a diskline component to fit the iron line profile (see Table 1 for more details). We have shown that we can fit the NuSTAR and XMM-Newton spectra independently with the same continuum model and with a phenomenological model (i.e., diskline) or a self-consistent reflection model (i.e., reflionx or rfxconv) for the reflection component, finding similar (compatible within the associated uncertainties) smearing parameters for the reflection component in all our fits.
To fit these spectra, we used a continuum model, composed of a blackbody component (bbody) and a comptonization continuum (nthcomp), which has been widely used in the literature to fit the spectra of neutron star LMXBs, both in the soft and in the hard state (see e.g., Egron et al. 2013). With respect to the continuum model used by Miller et al. (2013), we substituted the hottest of the two blackbody components with a Comptonization spectrum. Since this component gives the most important contribution to the source flux, especially above 5 keV, we subsequently used this component as the source of the reflection spectrum. In all our fits, the addition of a hard power-law component, with a photon index ~3 significantly improved the fit. The presence of a hard power-law component is often found in the spectra of bright LMXBs in the soft state (see e.g., Piraino et al. 2007; Pintore et al. 2015, 2016), and has been interpreted as comptonization of soft photons off a non-thermal population of electrons (see e.g., Di Salvo et al. 2000).
To fit the reflection component, which is dominated by a prominent iron line, we first used a phenomenological model consisting of a Gaussian line or a diskline, with a diskline providing a better fit than a Gaussian profile (cf. fitting results reported in Table 2). All the diskline parameters obtained from the fitting of the NuSTAR and XMM-Newton spectra are compatible with one another, except for the line flux, which appears to be lower during the XMM-Newton observations.
In order to fit the reflection spectrum with self-consistent models, which take into account not only the iron line but also other reflection features, we used both reflionx and rfxconv reflection models. In both these models, discrete emission and absorption features from the most abundant elements are included, as well as the reflected continuum. We convolved the reflection spectrum with the relativistic smearing model rdblur, taking into account Doppler and relativistic effects caused by the fast motion of the reflecting material in the inner accretion disk. We also investigated the possibility that the neutron star has a significant spin parameter. We therefore performed a grid of fits using the kerrconv smearing model, instead of rdblur, freezing the spin parameter “a” at different values (0, 0.12, and 0.14) and letting it free to vary in an additional case (see Appendix A for more details). In agreement with the results reported by Miller et al. (2013), we find that the fit is almost insensitive to the spin parameter but prefers low values of the spin parameter (a< 0.04).
The results obtained using reflionx or rfxconv are somewhat different in the fits not including the hard power-law component. However, the reflection and smearing parameters become very similar when we add this component to the continuum model (cf. results in Tables 3, A.1, A.2). The addition of this component also significantly improves all the fits. We consider “rdb-rfxconv-pl”, which includes the hard power-law component, rfxconv, as a reflection component smeared by the rbdblur component, to be our best fit model (see Table 3). The fit of the XMM-Newton spectra with the same model gave values of the parameters that agree overall with those obtained fitting the NuSTAR spectra. In this case, we found values of the ionization parameter log(ξ) ranging between 2.58 and 2.71 (slightly higher, i.e., approx. 3, for the XMM-Newton spectra) and reflection amplitudes between 0.2 and 0.3, indicating a relatively low superposition between the source of the primary Comptonization continuum and the disk (a value of 0.3 would be compatible with a spherical geometry of a compact corona inside an outer accretion disk). For the smearing parameters of the reflection component, we find values of the emissivity index of the disk ranging from −2.8 to −2.48, an inner radius of the disk from 10.6 to 16.2 Rg, and an inclination angle of the system with respect to the line of sight of 25−30°. In our results, the inclination angle is higher than that found by (Miller et al. 2013; who report an inclination angle less than 10°), but is very similar to that estimated from Chandra spectra (25−35°, see Chiang et al. 2016a). Moreover, the inner disk radius we find is not compatible with the ISCO. Assuming a 1.4 M⊙ for the neutron star, the inner radius of the disk is located at 22−34 km from the neutron star center. Note that this value is compatible to the estimated radius of the emission region of the soft blackbody component, which is in the range 19−31 km. We interpret this component as the intrinsic emission from the inner disk since this is the coldest part of the system and because the temperature of the blackbody component appears to be too low to represent a boundary layer.
5. Conclusions
The main aim of this paper is to test the robustness of disk parameters inferred from the reflection component in the case of neutron star LMXBs. To this aim, we used broad-band, moderately-high-resolution spectra of Serpens X-1, a neutron star LMXB of the atoll type with a very clear reflection spectrum that has been studied with several instruments. In particular, we carried out a broad-band spectral analysis of this source using data collected by NuSTAR and XMM-Newton satellites, which have the best sensitivity at the iron-line energy. These data have already been analyzed in literature. In particular, Miller et al. (2013) have analyzed the NuSTAR spectra and obtained a low inclination angle of approximately 8°, an inner disk radius compatible with the ISCO, an ionization parameter log ξ between 2.3 and 2.6, along with an iron abundance of approximately 3.
We performed the fitting using slightly different continuum and reflection models with respect to those used by other authors to fit the X-ray spectrum of this source. Our best fit of the NuSTAR spectrum of Ser X-1 is obtained fitting the continuum with a soft blackbody, a Comptonization spectrum, and a hard power-law tail, in addition to the reflection features. To fit the reflection features present in the spectrum, we used both empirical models and self-consistent reflection components such as reflionx and rfxconv, as well as two different blurring components that are rdblur and kerrconv. From the analysis carried out using kerconv, we have obtained that our fit is insensitive to the value assumed by the adimensional spin parameter “a”, in agreement with what was found by Miller et al. (2013) in their analysis. With regard to the reflection features, we obtain consistent results using phenomenological models (such as diskline) or self-consistent models to fit the NuSTAR spectrum of the source. In particular, the reflection component gives a reflection amplitude of Ω/2π ~ 0.2−0.3 (where Ω is the solid angle of the disk as seen from the corona in units of 2π) and an ionization parameter of log (ξ) ~ 2.6−2.7. The smearing of the reflection component gives an inner disk radius of Rin ~ 10.6−16.2 Rg, and an emissivity index of the disk in the range −(2.5−2.8), whereas the inclination angle of the disk with respect to the line of sight results in the range 25−29°. We note that the inner disk radius derived from the reflection component is compatible with the radius inferred from the soft blackbody component, which results in the range 19−31 km. The analysis of XMM-Newton spectra, carried out using the same models adopted to fit the NuSTAR spectra, gave values of the parameters compatible with those described above, although the two observations are not simultaneous. The only differences are the reflection amplitude, Ω/2π ~ 0.18−0.19, which is slightly lower, although still marginally consistent within the errors, and the ionization parameter, log (ξ) ~ 2.9−3.1, which is somewhat higher with respect to the non-simultaneous NuSTAR observations.
In conclusion, in this paper we investigated to what extent the disk parameters inferred from reflection fitting depend on the chosen spectral models for both the continuum and the reflection component. Despite the fact that several authors in previous work have used basically the same continuum model, the resulting reflection parameters, such as the inner disk radius, Rin, and the inclination angle, are scattered over a large range of values. In this paper, we re-analyzed all the available public NuSTAR and XMM-Newton observations of Ser X-1, fitting the continuum with a slightly different, physically motivated model and the iron line with different reflection models. By performing a detailed spectral analysis of NuSTAR and XMM-Newton data of the LMXB Ser X-1 using both phenomenological and self-consistent reflection models, andusing a continuum model somewhat different from that used in literature for this source, the best fit parameters derived from the two spectra are in good agreement between each other. These are also in broad agreement with the findings of Miller et al. (2013), although we find values of the inner disk and the inclination angle that are less extreme. Hence, the use of broad-band spectra and of self-consistent reflection models, together with an investigation of the continuum model, are highly desirable to infer reliable parameters from the reflection component.
Acknowledgments
We thank the anonymous referee for useful suggestions which helped to improve the manuscript. The High-Energy Astrophysics Group of Palermo acknowledges support from the Fondo Finalizzato alla Ricerca (FFR) 2012/13, project N. 2012-ATE-0390, founded by the University of Palermo. This work was partially supported by the Regione Autonoma della Sardegna through POR-FSE Sardegna 2007-2013, L.R. 7/2007, Progetti di Ricerca di Base e Orientata, Project N. CRP-60529. We also acknowledge financial contribution from the agreement ASI-INAF I/037/12/0.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Balucinska, M., & Czerny, M. 1985, Acta Astron., 35, 291 [Google Scholar]
- Bhattacharyya, S., & Strohmayer, T. E. 2007, ApJ, 664, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Brenneman, L. W., & Reynolds, C. S. 2006, ApJ, 652, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Miller, J. M., Bhattacharyya, S., et al. 2008, ApJ, 674, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Miller, J. M., Ballantyne, D. R., et al. 2010, ApJ, 720, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, C.-Y., Cackett, E. M., Miller, J. M., et al. 2016a, ApJ, 821, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, C.-Y., Morgan, R. A., Cackett, E. M., et al. 2016b, ApJ, 831, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Church, M. J., & Balucińska-Church, M. 2001, A&A, 369, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelisse, R., Kuulkers, E., in ’t Zand, J. J. M., Verbunt, F., & Heise, J. 2002, A&A, 382, 174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelisse, R., Casares, J., Charles, P. A., & Steeghs, D. 2013, MNRAS, 432, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., Iaria, R., Di Salvo, T., Matt, G., & Robba, N. R. 2009, ApJ, 693, L1 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., di Salvo, T., Ballantyne, D., et al. 2010, A&A, 516, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Salvo, T., Stella, L., Robba, N. R., et al. 2000, ApJ, 544, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Iaria, R., Méndez, M., et al. 2005, ApJ, 623, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., D’Aí, A., Iaria, R., et al. 2009, MNRAS, 398, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Iaria, R., Matranga, M., et al. 2015, MNRAS, 449, 2794 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Done, C., & Gierliński, M. 2006, MNRAS, 367, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Egron, E., Di Salvo, T., Motta, S., et al. 2013, A&A, 550, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, H., Byram, E. T., & Chubb, T. A. 1967, Science, 156, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
- Iaria, R., Di Salvo, T., Burderi, L., & Robba, N. R. 2001, ApJ, 548, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., Di Salvo, T., Robba, N. R., & Burderi, L. 2002, ApJ, 567, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., D’Aí, A., di Salvo, T., et al. 2009,A&A, 505, 1143 [Google Scholar]
- Kolehmainen, M., Done, C., & Díaz Trigo, M. 2011, MNRAS, 416, 311 [NASA ADS] [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F., Lewin, W. H. G., & Doxsey, R. 1976, IAU Circ., 2983 [Google Scholar]
- Miller, J. M., Parker, M. L., Fuerst, F., et al. 2013, ApJ, 779, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterbroek, T., Barret, D., Guainazzi, M., & Ford, E. C. 2001, A&A, 366, 138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandel, D., Kaaret, P., & Corbel, S. 2008, ApJ, 688, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Di Salvo, T., Bozzo, E., et al. 2015, MNRAS, 450, 2016 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Sanna, A., Di Salvo, T., et al. 2016, MNRAS, 457, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Piraino, S., Santangelo, A., di Salvo, T., et al. 2007, A&A, 471, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Models including kerrconv
From the spectral analysis described in Sect. 3.1, we find that our best fit obtained using rdblur as smearing component gives a soft blackbody temperature of 0.54 ± 0.06 keV and a radius of the emitting region of 25 ± 6 km, a temperature of the seed photons for the Comptonization of 0.93±0.07 keV, an electron temperature of the Comptonizing corona of 2.70 ± 0.04 keV and a photon index of the primary Comptonized component of 2.17 ± 0.04, whereas the photon index of the hard power-law tail is steeper, at approximately 3.2. The reflection component gives a reflection amplitude of 0.24±0.04 and an ionization parameter of log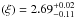 . Finally, the smearing of the reflection component gives an inner disk radius of Rin = 13.4 ± 2.8 Rg, compatible with the radius inferred from the blackbody component, and an emissivity index of the disk equal to −2.64 ± 0.16, whereas the inclination angle of the disk with respect to the line of sight is equal to 27.1 ± 1.9°. The analysis of XMM-Newton spectra, carried out using the same models adopted to fit the NuSTAR spectra, gave values of the parameters compatible to those described above, although the two observations are not simultaneous. In particular, in this case we find Rin 14.2
. Finally, the smearing of the reflection component gives an inner disk radius of Rin = 13.4 ± 2.8 Rg, compatible with the radius inferred from the blackbody component, and an emissivity index of the disk equal to −2.64 ± 0.16, whereas the inclination angle of the disk with respect to the line of sight is equal to 27.1 ± 1.9°. The analysis of XMM-Newton spectra, carried out using the same models adopted to fit the NuSTAR spectra, gave values of the parameters compatible to those described above, although the two observations are not simultaneous. In particular, in this case we find Rin 14.2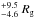 , a reflection amplitude of 0.183 ± 0.003, and an ionization parameter of log(ξ) = 3.04 ± 0.11, a temperature of the seed photons in the range 0.76−0.85 keV, and a photon index of the primary Comptonized component of 2.45 ± 0.22 keV. In other words, the XMM-Newton spectra independently confirm the results obtained for the NuSTAR spectra.
, a reflection amplitude of 0.183 ± 0.003, and an ionization parameter of log(ξ) = 3.04 ± 0.11, a temperature of the seed photons in the range 0.76−0.85 keV, and a photon index of the primary Comptonized component of 2.45 ± 0.22 keV. In other words, the XMM-Newton spectra independently confirm the results obtained for the NuSTAR spectra.
In order to check for the presence of a non-null spin parameter of the neutron star, we fitted the NuSTAR spectra using reflection components convolved with kerrconv instead of rdblur. Kerrconv convolves the spectrum with the smearing produced by a kerr disk model. It features the dimensionless “a” parameter that characterizes the spin of the system.We performed our fit first leaving “a” as a free parameter and then fixing it to the three values, 0, 0.12, and 0.14. The model with reflionx and “a” treated as a free parameter is called ker-reflio-af, whereas for a = 0, a = 0.12, and a = 0.14, the models are called ker-reflio-a0, ker-reflio-a012, and ker-reflio-a014, respectively. In the same way, the model with rfxconv and “a” treated as a free parameter is called ker-rfxconv-af, whereas for a = 0, a = 0.12, and a = 0.14, the models are called ker-rfxconv-a0, ker-rfxconv-a012, and ker-rfxconv-a014, respectively. All the models fit the data well; reduced χ2 are between 1.08 and 1.18 and residuals are basically identical. Moreover, the best-fit values of all parameters are very similar to the case with a = 0 and to the values we get using rdblur instead of kerrconv. The fit is therefore insensitive to the spin parameter, although there is a slight preference of the fit towards low values (a< 0.04). It is worth noting that in all best fit residuals, a feature is present at approximately 3.9 keV that could be the resonance line of Ca XIX (3.9 keV). Moreover, again we observe high-energy residuals (above 30 keV) indicating the presence of a hard power-law component. Also in this case, we get a very large ionization parameter using reflionx.
To avoid this problem, we therefore added a power-law component to the model obtained by the convolution of kerrconv with the two different reflection components (reflionx or rfxconv). we considered “a” free to vary or fixed it to three different values (0, 0.12, and 0.14). In all the cases, the fits are relatively good with values of the reduced χ2 from 1.0 to 1.01. Again, the addition of the power-law proved to be highly statistically significant. The F-test probability of chance improvement for the addition of two parameters is, for instance, 7.5 × 10-15 and 9 × 10-33 for the addition of a power-law to the model ker-reflio-af and ker-rfxconv-af, respectively. As before, the fit is relatively insensitive to the value assumed by the spin parameter “a”. Values of the best-fit parameters are listed in Tables A.1 and A.2.
Results of the fit of the NuSTAR spectra using kerrconv combined with rfxconv or reflionx components.
All Tables
Results of the fit of NuSTAR and XMM-Newton spectra of Ser X-1 using Gaussian and diskline models.
Results of the fit of NuSTAR and XMM-Newton spectra of Ser X-1 using rdblur combined with rfxconv or reflionx.
Results of the fit of the NuSTAR spectra using kerrconv combined with rfxconv or reflionx components.
All Figures
 |
Fig. 1 NuSTAR spectra of Ser X-1 and best-fitting model together with residuals in units of sigma for the corresponding model. These are; top-left: “Gauss”, top-right: “diskline”, bottom-left: “rdb-reflio”, and bottom-right: “rdb-rfxconv”. Dashed lines indicate the black-body component, dotted lines indicate the reflection components (i.e., the Gaussian or Diskline profile for the iron line, top panels, or the self-consistent reflection component, bottom panels, respectively), and the dashed-dotted lines indicate the comptonized component. |
| In the text | |
 |
Fig. 2 Top panels: NuSTAR spectra of Ser X-1 and best-fitting model together with residuals in units of sigma for the corresponding model. These are; top-left: “rdb-reflio-pl”, top-right: “rdb-rfxconv-pl”. Bottom panels: XMM-Newton spectra and best-fitting model together with residuals in units of sigma for the corresponding model. These are: bottom-left: “diskline-pl-xmm”, and bottom-right: “rdb-rfxconv-pl-xmm”. For clarity, only the first XMM-Newton observation is shown. Dashed lines indicate the black-body component, dotted lines indicate the reflection components (i.e., the Diskline profile for the iron line or the self-consistent reflection component), the solid line indicates the power-law component, and the dashed-dotted lines indicate the comptonized component. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


