| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201630230 | |
| Published online | 15 March 2017 | |
Frequency-dependent tidal dissipation in a viscoelastic Saturnian core and expansion of Mimas’ semi-major axis
German Aerospace Center(DLR), Institute of Planetary Research, Rutherfordstr. 2, 12489 Berlin, Germany
e-mail: Daigo.Shoji@dlr.de; Hauke.Hussmann@dlr.de
Received: 12 December 2016
Accepted: 13 February 2017
Context. Regarding tidal dissipation in Saturn, usually parameterized by Saturn’s quality factor Q, there remains a discrepancy between conventional estimates and the latest determination that has been derived from astrometric observations of Saturn’s inner satellites. If dissipation in Saturn is as large as the astrometric observations suggest, and is independent of time and tidal frequency, conventional models predict that Mimas’ initial orbit should be located inside Saturn’s synchronous orbit or even inside its Roche limit, in contradiction to formation models.
Aims. Using simple structure models and assuming Saturn’s core to be viscoelastic, we look for dissipation models which are consistent with both the latest astrometric observations and with Mimas’ orbital migration.
Methods. Firstly, using a two-layer model of Saturn’s interior structure, we constrain the ranges of rigidity and viscosity of Saturn’s core which are consistent with Saturn’s dissipation derived from astrometric observations at the tidal frequencies of Enceladus, Tethys, and Dione. Next, within the constrained viscosity and rigidity ranges, we calculate Mimas’ semi-major axis considering the frequency dependence of viscoelastic dissipation in Saturn’s core. By the two calculations, we evaluate (1) Saturnian models which can explain the astrometrically determined Saturnian dissipation, and (2) whether Mimas’ initial semi-major axis is larger than the synchronous orbit.
Results. We show that if the core is assumed to be solid with a viscosity of 1013−1014 Pa s (depending on its size), the lower boundary of the observed Saturnian dissipation at tidal frequencies of Enceladus, Tethys, and Dione (k2s/Qs ~ 4 × 10-5 where k2s is Saturn’s second degree Love number and Qs its quality factor) can be explained by our model. In this viscosity range, Mimas can stay outside the synchronous orbit and the Roche limit for 4.5 billion years of evolution.
Conclusions. In the case of a frequency dependent viscoelastic dissipative core, the lower boundary of the observed Saturnian dissipation can be consistent with the orbital expansion of Mimas. In this model, the assumption of a late formation of Mimas, discussed recently, is not required.
Key words: planets and satellites: interiors / planets and satellites: individual: Saturn / planets and satellites: individual: Mimas
© ESO, 2017
1. Introduction
Tidal dissipation in Saturn induced by its moons can be one important factor constraining the interior structure and dynamics of Saturn. The magnitude of dissipation is estimated by the quality factor, Q, which is defined as the ratio between the peak of the stored energy and the dissipated energy over one tidal cycle. A small Q value means that a large quantity of energy is dissipated in Saturn.
Although the Saturnian Q value is not constrained well, its minimum value has been evaluated by the orbital expansion of Mimas (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000). The tidal bulge on Saturn exerted by Mimas is ahead of the Saturn-Mimas axis because Saturn’s rotation period is smaller than the orbital period of Mimas. This tidal bulge adds a torque to Mimas and the semi-major axis of Mimas increases. Ignoring dissipation in Mimas, the increasing rate of semi-major axis a of Mimas is given (e.g., Murray & Dermott 2000) by 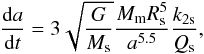 (1)where t, G, Ms, Mm, and Rs are time, the gravitational constant, Saturnian mass, Mimas’ mass, and Saturnian radius, respectively. The parameters k2s and Qs are the second degree Love number and the Q value of Saturn. By integrating Eq. (1) backwards in time, the past semi-major axis of Mimas can be calculated. As this equation shows, the change of the orbit becomes large when Qs is small. In order to move to the current orbit from a small initial semi-major axis in the past, Mimas must be located outside of the surface (and the Roche limit) of Saturn when it was formed. One of the simplest assumptions for the evaluation of Qs is that it is constant along the evolution of the planet and that it is independent of the forcing frequency (e.g., MacDonald 1964; Kaula 1964). The tidal Q of Saturn had so far been constrained by considering that Mimas took at least 4.5 billion years to move from a quasi-synchronous orbit with Saturn to its present location, yielding Qs> 18 000 (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). However, recent astrometric measurements of Saturnian satellites have indicated that the Q value of Saturn is much lower (Lainey et al. 2012, 2017). The studies reported above discuss the Saturnian dissipation by the value of Qs assuming the value of k2s derived by Gavrilov & Zharkov (1977). However, from the astrometric measurements the value of k2s/Qs can be obtained rather than Qs. Lainey et al. (2017) show that k2s/Qs of Saturn is around 10-4 (the detailed values are shown below), which implies that Qs is a few thousand only, even if we consider the latest determination of k2s = 0.413 (Wahl et al. 2017). As a mechanism of the observed dissipation of Saturn, Lainey et al. (2017) suggest a viscoelastic response of the solid core. Although a viscoelastic core can generate significant dissipation (Remus et al. 2012, 2015; Lainey et al. 2017), it contradicts the conventional estimations derived from the orbital expansion of Mimas (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). One hypothesis is that the Saturnian satellites such as Mimas were formed recently (Charnoz et al. 2011). If Mimas moved to the current position on a small timescale, strong constant dissipation inside Saturn does not contradict the orbital expansion of Mimas.
(1)where t, G, Ms, Mm, and Rs are time, the gravitational constant, Saturnian mass, Mimas’ mass, and Saturnian radius, respectively. The parameters k2s and Qs are the second degree Love number and the Q value of Saturn. By integrating Eq. (1) backwards in time, the past semi-major axis of Mimas can be calculated. As this equation shows, the change of the orbit becomes large when Qs is small. In order to move to the current orbit from a small initial semi-major axis in the past, Mimas must be located outside of the surface (and the Roche limit) of Saturn when it was formed. One of the simplest assumptions for the evaluation of Qs is that it is constant along the evolution of the planet and that it is independent of the forcing frequency (e.g., MacDonald 1964; Kaula 1964). The tidal Q of Saturn had so far been constrained by considering that Mimas took at least 4.5 billion years to move from a quasi-synchronous orbit with Saturn to its present location, yielding Qs> 18 000 (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). However, recent astrometric measurements of Saturnian satellites have indicated that the Q value of Saturn is much lower (Lainey et al. 2012, 2017). The studies reported above discuss the Saturnian dissipation by the value of Qs assuming the value of k2s derived by Gavrilov & Zharkov (1977). However, from the astrometric measurements the value of k2s/Qs can be obtained rather than Qs. Lainey et al. (2017) show that k2s/Qs of Saturn is around 10-4 (the detailed values are shown below), which implies that Qs is a few thousand only, even if we consider the latest determination of k2s = 0.413 (Wahl et al. 2017). As a mechanism of the observed dissipation of Saturn, Lainey et al. (2017) suggest a viscoelastic response of the solid core. Although a viscoelastic core can generate significant dissipation (Remus et al. 2012, 2015; Lainey et al. 2017), it contradicts the conventional estimations derived from the orbital expansion of Mimas (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). One hypothesis is that the Saturnian satellites such as Mimas were formed recently (Charnoz et al. 2011). If Mimas moved to the current position on a small timescale, strong constant dissipation inside Saturn does not contradict the orbital expansion of Mimas.
Dissipation of Saturn plays an important role for the possible activity of the Saturnian satellites. The Cassini probe has observed that Enceladus is a currently active body emanating water plumes, possibly implying liquid water in its subsurface (e.g., Porco et al. 2006). If Enceladus is in an equilibrium state of the resonance with Dione, the tidal heating rate generated in Enceladus is ~1.1 GW at Qs = 18 000 (Meyer & Wisdom 2007), which is independent of the interior structure of Enceladus. However, the equilibrium heating rate increases with decreasing Qs (Meyer & Wisdom 2007; Lainey et al. 2012), which may affect Enceladus’ structure and activity.
In this work, although the detailed structure and the state of the Saturnian core (e.g., whether the core is solid or liquid) is uncertain, we reconsider the conventional estimations derived from the orbital migration of Mimas assuming that Saturn’s core is solid and viscoelastic. In case of a viscoelastic response, both Love number and Q value depend on the frequency of the cyclic forcing. Because the tidal frequency on Saturn changes with Mimas’ semi-major axis, k2s and Qs in Eq. (1) cannot be constant. It has been demonstrated that constant Q is a strong assumption and frequency dependent Q can lead to different tidal rotational and orbital evolution (e.g., Efroimsky & Lainey 2007; Auclair-Desrotour et al. 2014). We calculate the past semi-major axis of Mimas taking into account the frequency dependence of the dissipation with the simple two-layer structure models by Remus et al. (2012, 2015). Firstly we constrain the rigidity and viscosity of the solid core, which are consistent with the latest observational results by Lainey et al. (2017), and then we calculate the semi-major axis within the range of the constrained rheological parameters. Here, we consider the value of k2s/Qs rather than Qs because k2s/Qs is the directly obtained parameter by astrometric methods. By the two calculations, we suggest the Saturnian models which can be consistent with both Mimas’ orbital evolution and the latest observational results of Saturnian dissipation.
2. Structure and rheology of Saturn
Remus et al. (2012, 2015) have explained the large dissipation of Saturn using the two layer model with fluid envelope and viscoelastic solid core. Here we assume this simple structure model because the purpose of this work is to relate the observed dissipation to Mimas’ orbital change. Mass and size of Saturn are shown in Table 1, which are consistent with Remus et al. (2012, 2015). Lainey et al. (2017) assume more detailed models with layered structure and the calculation method by Tobie et al. (2005), and mention that the viscosity range to generate the observed Qs is compatible between their complex model and the simple two layer model. In the structure models by Remus et al. (2012, 2015) and Lainey et al. (2017), the fluid envelope is assumed to be non-dissipative. Convective turbulent friction applied on fluid tidal waves (e.g., Ogilvie & Lin 2004) and the resonant-lock mechanism (Fuller et al. 2016) may contribute to the dissipation in Saturn, which can compete with the viscoelastic dissipation in the solid core (Guenel et al. 2014). Here we consider dissipation only in the solid core as an end-member model. The effect of dissipation in the envelope will be addressed in future studies. In the case of viscoelastic material, due to the delay of the response to the forcing because of viscous friction, the Love number becomes complex  , which is given (Remus et al. 2015) by
, which is given (Remus et al. 2015) by 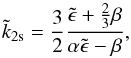 (2)where
(2)where
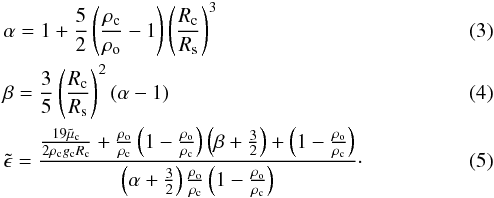 The parameters Rc, gc, ρc , and ρo are radius of the core, gravitational acceleration at the surface of the core, density of the core, and density of the envelope, respectively. We consider the value of Rc between 0.2Rs and 0.24Rs, which includes the core radius by Remus et al. (2015). gc, ρc , and ρo can be calculated from the mass of Saturn Ms, the mass of the core Mc, Rs and Rc shown in Table 1.
The parameters Rc, gc, ρc , and ρo are radius of the core, gravitational acceleration at the surface of the core, density of the core, and density of the envelope, respectively. We consider the value of Rc between 0.2Rs and 0.24Rs, which includes the core radius by Remus et al. (2015). gc, ρc , and ρo can be calculated from the mass of Saturn Ms, the mass of the core Mc, Rs and Rc shown in Table 1. 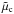 is the complex shear modulus of the viscoelastic core. In this work, we assume a Maxwell rheology in which the complex shear modulus of the Maxwell model is given by
is the complex shear modulus of the viscoelastic core. In this work, we assume a Maxwell rheology in which the complex shear modulus of the Maxwell model is given by 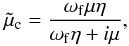 (6)where
(6)where 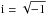 . The parameters μ, η and ω are the tidally effective rigidity and viscosity of the solid core of Saturn and the forcing frequency, respectively. For the frequency of tides on Saturn by satellites, ωf can be represented by the rotational angular velocity of Saturn Ω and the mean motion of the satellites ω as ωf = 2(Ω−ω). Because
. The parameters μ, η and ω are the tidally effective rigidity and viscosity of the solid core of Saturn and the forcing frequency, respectively. For the frequency of tides on Saturn by satellites, ωf can be represented by the rotational angular velocity of Saturn Ω and the mean motion of the satellites ω as ωf = 2(Ω−ω). Because 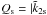 |/|Im(
|/|Im( )| (e.g., Remus et al. 2012), k2s/Qs = |Im(
)| (e.g., Remus et al. 2012), k2s/Qs = |Im( )| with
)| with 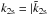 |.
|.
Physical parameters and values.
 |
Fig. 1 |Im( |
 |
Fig. 2 Evolutions of a) 2(Ω−ω) b) |Im( |
3. Method
3.1. Constraint of rigidity and viscosity for observed dissipation
Firstly we calculate the ranges of rigidity and viscosity which are consistent with the observed k2s/Qs at the tidal frequencies caused by Enceladus, Tethys, and Dione. Lainey et al. (2017) also estimated k2s/Qs at Rhea’s frequency. However, they suggest that the dissipation at Rhea’s frequency is caused by turbulent friction in the envelope, which is beyond the scope of this work. The value of k2s/Qs is (20.70 ± 19.91) × 10-5, (15.84 ± 12.26) × 10-5 and (16.02 ± 12.72) × 10-5 at the tidal frequencies of Enceladus, Tethys, and Dione, respectively, and (1.59 ± 0.74) × 10-4 in a global estimation (Lainey et al. 2017). Thus, we consider |Im( )| between 4 × 10-5 and 2.5 × 10-4. k2s/Qs is almost independent of the mean motion difference among these three satellites (Lainey et al. 2017). We set ωf = 2.5 × 10-4 rad s-1, which is between the tidal frequencies of Enceladus and Dione.
)| between 4 × 10-5 and 2.5 × 10-4. k2s/Qs is almost independent of the mean motion difference among these three satellites (Lainey et al. 2017). We set ωf = 2.5 × 10-4 rad s-1, which is between the tidal frequencies of Enceladus and Dione.
3.2. Change of Mimas’ semi-major axis
As a next step, we calculate the initial semi-major axis of Mimas with the constrained rigidity and viscosity. Assuming a Kepler orbit, the mean motion of Mimas is given by 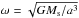 . Substituting |Im(
. Substituting |Im( )| in Eq. (1), da/ dt and dissipation of Saturn can be coupled by Eqs. (1)−(6). Integrations of a are performed backwards from the current semi-major axis a0 = 1.8552 × 108 m (Murray & Dermott 2000) with a Runge-Kutta method and 104 yr of time step. We performed additional calculations with time steps of 103 yr and 5 × 102 yr and the results did not change. For simplicity, the angular velocity of Saturn’s rotation and the mass of Mimas are fixed at Ω = 1.65 × 10-4 rad s-1 (Giampieri et al. 2006; Anderson & Schubert 2007) and Mm = 3.7493 × 1019 kg (Jacobson et al. 2006), respectively.
)| in Eq. (1), da/ dt and dissipation of Saturn can be coupled by Eqs. (1)−(6). Integrations of a are performed backwards from the current semi-major axis a0 = 1.8552 × 108 m (Murray & Dermott 2000) with a Runge-Kutta method and 104 yr of time step. We performed additional calculations with time steps of 103 yr and 5 × 102 yr and the results did not change. For simplicity, the angular velocity of Saturn’s rotation and the mass of Mimas are fixed at Ω = 1.65 × 10-4 rad s-1 (Giampieri et al. 2006; Anderson & Schubert 2007) and Mm = 3.7493 × 1019 kg (Jacobson et al. 2006), respectively.
4. Results
4.1. Rigidity and viscosity ranges for observed dissipation
Figure 1 shows |Im( )| as a function of rigidity and viscosity of Saturn’s core. The rigidity and viscosity ranges which are consistent with the observed Saturnian dissipation (Fig. 2) are compatible with the rheological values estimated by Remus et al. (2015). |Im(
)| as a function of rigidity and viscosity of Saturn’s core. The rigidity and viscosity ranges which are consistent with the observed Saturnian dissipation (Fig. 2) are compatible with the rheological values estimated by Remus et al. (2015). |Im( )| becomes maximum at around 1015 Pa s. Although rigidity and viscosity which attain the observed |Im(
)| becomes maximum at around 1015 Pa s. Although rigidity and viscosity which attain the observed |Im( )| change with the core radius, minimum viscosities for the observed dissipation should be 1013−1014 Pa s. If η ~ 1015 Pa s, |Im(
)| change with the core radius, minimum viscosities for the observed dissipation should be 1013−1014 Pa s. If η ~ 1015 Pa s, |Im( )| becomes too high to be consistent with the observed values.
)| becomes too high to be consistent with the observed values.
4.2. Evolutions of dissipation and Mimas’ orbit
Figure 2 shows the evolutions of tidal frequency 2(Ω−ω), |Im( )|, and semi-major axis a at Rc = 0.219 Rs. The rigidity μ is 5 × 1011 Pa and the viscosity η = 5 × 1013, 1014 and 1016 Pa s, which are consistent with the reasonable parameter range (Remus et al. 2015) and the observed k2s/Qs at the frequency of Enceladus, Tethys, and Dione (Fig. 1). Due to the dissipation of Saturn, the semi-major axis decreases with decreasing time (Mimas’ orbit expands with time). Because we assume
)|, and semi-major axis a at Rc = 0.219 Rs. The rigidity μ is 5 × 1011 Pa and the viscosity η = 5 × 1013, 1014 and 1016 Pa s, which are consistent with the reasonable parameter range (Remus et al. 2015) and the observed k2s/Qs at the frequency of Enceladus, Tethys, and Dione (Fig. 1). Due to the dissipation of Saturn, the semi-major axis decreases with decreasing time (Mimas’ orbit expands with time). Because we assume 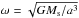 , 2(Ω−ω) also decreases as time decreases. However, once the semi-major axis decreases to the synchronous orbit with Saturn in which Mimas’ orbital period is the same as the rotational period of Saturn (Ω = ω), dissipation does not occur because 2(Ω−ω) becomes zero, and thus the migration of Mimas stops. At η = 5 × 1013 Pa s and 1014 Pa s, |Im(
, 2(Ω−ω) also decreases as time decreases. However, once the semi-major axis decreases to the synchronous orbit with Saturn in which Mimas’ orbital period is the same as the rotational period of Saturn (Ω = ω), dissipation does not occur because 2(Ω−ω) becomes zero, and thus the migration of Mimas stops. At η = 5 × 1013 Pa s and 1014 Pa s, |Im( )| decreases with decreasing time (Fig. 2b). In this viscosity range, 2(Ω−ω)/2π is smaller than the Maxwell frequency (μ/η). Thus the response of the solid core is like a fluid as a decreases (2(Ω−ω) decreases) and the core becomes less dissipative. On the other hand, at η = 1016 Pa s, |Im(
)| decreases with decreasing time (Fig. 2b). In this viscosity range, 2(Ω−ω)/2π is smaller than the Maxwell frequency (μ/η). Thus the response of the solid core is like a fluid as a decreases (2(Ω−ω) decreases) and the core becomes less dissipative. On the other hand, at η = 1016 Pa s, |Im( )| increases with decreasing time because 2(Ω−ω)/2π at t = 0 is larger than the Maxwell frequency. By the decrease of 2(Ω−ω) (increase of ω), the response of the solid core becomes viscoelastic from elastic, which results in large dissipation. Due to the large dissipation, a gets into the synchronous orbit at around −0.5 Ga (Fig. 2c).
)| increases with decreasing time because 2(Ω−ω)/2π at t = 0 is larger than the Maxwell frequency. By the decrease of 2(Ω−ω) (increase of ω), the response of the solid core becomes viscoelastic from elastic, which results in large dissipation. Due to the large dissipation, a gets into the synchronous orbit at around −0.5 Ga (Fig. 2c).
 |
Fig. 3 Comparison of semi-major axis between constant |Im( |
One important result is that, at η = 5 × 1013 Pa s, 2(Ω−ω) does not become zero and thus a does not get into the synchronous orbit at the time of solar system formation (around −4.5 Ga). Thus, if the viscosity of Saturn is around η = 5 × 1013 Pa s, the latest observational dissipation at the frequency of Enceladus, Tethys, and Dione does not contradict the conventional evaluations that Mimas must have been outside of the surface of Saturn and the synchronous orbit 4.5 billion years ago (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). In addition to the synchronous orbit, Mimas should be outside of the Roche limit. Assuming that Mimas is a rigid and spherical body, the distance of the Roche limit aL = Rs(3ρs/ρm)1/3 (Murray & Dermott 2000), while aL = 2.456 Rs(ρs/ρm)1/3 if Mimas is fluid (Chandrasekhar 1969), where ρs and ρm are the density of Saturn and Mimas, respectively. Using the values of our model (ρs = 687.3 kg m-3) and the mean density of Mimas at ρm = 1150 kg m-3 (Thomas et al. 2007), aL is ~7 × 104 km for the rigid Mimas and ~1.2 × 105 km in the case of the fluid Mimas, respectively. Even if Mimas is a fluid body, it stays outside of the Roche limit at η = 5 × 1013 Pa s (Fig. 2).
We calculated Mimas’ orbit with different rigidity within the consistent range to the observations. Although the magnitude of dissipation depends on rigidity, the value of viscosity strongly affects whether Mimas gets into the synchronous orbit because |Im( )| is relatively independent of rigidity at η ~ 1013−1014 Pa s (Fig. 1). Thus, as long as the rigidity is consistent with the observations (Fig. 1), the conclusion that Mimas does not get into the synchronous orbit at the lower boundary of the viscosity does not change.
)| is relatively independent of rigidity at η ~ 1013−1014 Pa s (Fig. 1). Thus, as long as the rigidity is consistent with the observations (Fig. 1), the conclusion that Mimas does not get into the synchronous orbit at the lower boundary of the viscosity does not change.
In addition to low viscosity, the frequency dependence of |Im( )| is another reason why Mimas does not get into the synchronous orbit and the Roche limit. In the case of η = 5 × 1013 Pa s, |Im(
)| is another reason why Mimas does not get into the synchronous orbit and the Roche limit. In the case of η = 5 × 1013 Pa s, |Im( )| is approximately 2.8 × 10-5 at t = 0 (Fig. 2b). Figure 3 compares a of the case in which |Im(
)| is approximately 2.8 × 10-5 at t = 0 (Fig. 2b). Figure 3 compares a of the case in which |Im( )| is fixed at 2.8 × 10-5 with the frequency dependent |Im(
)| is fixed at 2.8 × 10-5 with the frequency dependent |Im( )| (coupled model of dissipation and orbit). While the semi-major axis is larger than the synchronous orbit for 4.5 billion years in the coupled model, Mimas’ orbit becomes synchronous with Saturn at −3.5 Ga in the case of fixed |Im(
)| (coupled model of dissipation and orbit). While the semi-major axis is larger than the synchronous orbit for 4.5 billion years in the coupled model, Mimas’ orbit becomes synchronous with Saturn at −3.5 Ga in the case of fixed |Im(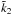 )|. As the semi-major axis decreases, due to the fluid response, |Im(
)|. As the semi-major axis decreases, due to the fluid response, |Im( )| decreases (Fig. 2b) in the coupled model. Thus, da/ dt becomes smaller as compared to the case with fixed |Im(
)| decreases (Fig. 2b) in the coupled model. Thus, da/ dt becomes smaller as compared to the case with fixed |Im( )|, which results in the slow migration of Mimas.
)|, which results in the slow migration of Mimas.
Changes of semi-major axis at Rc = 0.2 Rs and 0.24 Rs are shown in Fig. 4, respectively. Because the changing rate of the semi-major axis depends on |Im( )|, Mimas can avoid getting into the synchronous orbit regardless of core radius if the viscosity of Saturn’s core is a lower boundary for the observed k2s/Qs. It is uncertain whether the viscosity of Saturn’s solid core could be in the order of 1013 Pa s. If 1014 Pa s of viscosity is required, Saturn should have a small core at around 0.2 Rs. Future studies with ab-initio calculations of the equation of state (EOS) and observations can constrain the interior structure of Saturn more precisely (e.g., Helled & Guillot 2013; Miguel et al. 2016).
)|, Mimas can avoid getting into the synchronous orbit regardless of core radius if the viscosity of Saturn’s core is a lower boundary for the observed k2s/Qs. It is uncertain whether the viscosity of Saturn’s solid core could be in the order of 1013 Pa s. If 1014 Pa s of viscosity is required, Saturn should have a small core at around 0.2 Rs. Future studies with ab-initio calculations of the equation of state (EOS) and observations can constrain the interior structure of Saturn more precisely (e.g., Helled & Guillot 2013; Miguel et al. 2016).
 |
Fig. 4 Evolutions of semi-major axis at a): Rc = 0.2 Rs and b): Rc = 0.24 Rs and μ = 5 × 1011 Pa and viscosities consistent with the observed dissipation. |
One caveat of our results is that, although ~4 × 10-5 of |Im( )| is consistent with the observational values derived from each Saturnian satellite, it is smaller than the comprehensive evaluation at |Im(
)| is consistent with the observational values derived from each Saturnian satellite, it is smaller than the comprehensive evaluation at |Im(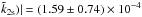 (Lainey et al. 2017). In the case of the simple two layer model, if |Im(
(Lainey et al. 2017). In the case of the simple two layer model, if |Im(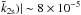 , Mimas gets into the synchronous orbit from the current position ~3 billion years ago. Calculations with more accurate core structure may solve this discrepancy, which will be addressed in future studies.
, Mimas gets into the synchronous orbit from the current position ~3 billion years ago. Calculations with more accurate core structure may solve this discrepancy, which will be addressed in future studies.
If we apply Eq. (1) to Enceladus, Tethys, and Dione, da/ dt of Tethys with the current parameters could be larger than that of Mimas. Thus Tethys can expand faster than other satellites and further discussions about Tethys’ orbital evolution may be required in future studies. The fast expansion is due to Tethys’ greater mass (as compared to Mimas and Enceladus) and its relatively small semi-major axis (as compared to Dione). It is indicated that Tethys experienced large tidal heating like Enceladus in the past (Giese et al. 2007; Chen & Nimmo 2008). Thus, the effect of dissipation in Tethys may not be negligible for its orbital evolution, which modifies Eq. (1) and requires detailed evolutions of the eccentricity and interior structure of Tethys.
5. Conclusions
Conventionally, the magnitude of Saturnian dissipation has been constrained from the orbital expansion of Mimas. Assuming a constant Love number, more than a few tens of thousands of Saturnian Q is required for Mimas to stay outside of the surface of Saturn or the synchronous orbit 4.5 billion years ago (e.g., Goldreich & Soter 1966; Gavrilov & Zharkov 1977; Murray & Dermott 2000; Meyer & Wisdom 2007). However, the latest observations of Saturnian dissipation estimated at the orbital frequency of Enceladus, Tethys, and Dione imply that the Saturnian Q is in the order of a few thousand, only (Lainey et al. 2017). We calculated the past semi-major axis of Mimas induced by tidal dissipation in Saturn’s solid core assuming a Maxwell rheology and frequency dependence of k2s/Qs (|Im( )|). If the viscosity of Saturn’s core is consistent with the lower boundary of the observed dissipation (k2s/Qs ~ 4 × 10-5) (Lainey et al. 2017) and μ/η is larger than 2(Ω−ω)/2π, due to the smaller tidal frequency in the past, Mimas can stay well outside the synchronous orbit even if it formed 4.5 billion years ago. The viscosity consistent with the observations and Mimas’ expansion changes with the radius of the Saturnian core. If the core radius is 0.2 Rs, 0.219 Rs and 0.24 Rs, ~1014 Pa s, ~5 × 1013 Pa s, and ~2.5 × 1013 Pa s of viscosities are required, respectively. In the case of these viscosity values, dissipation of Saturn is consistent with both the latest observational results and Mimas’ orbital evolution. In this model, the assumption of a late formation discussed recently (Charnoz et al. 2011) is not required.
)|). If the viscosity of Saturn’s core is consistent with the lower boundary of the observed dissipation (k2s/Qs ~ 4 × 10-5) (Lainey et al. 2017) and μ/η is larger than 2(Ω−ω)/2π, due to the smaller tidal frequency in the past, Mimas can stay well outside the synchronous orbit even if it formed 4.5 billion years ago. The viscosity consistent with the observations and Mimas’ expansion changes with the radius of the Saturnian core. If the core radius is 0.2 Rs, 0.219 Rs and 0.24 Rs, ~1014 Pa s, ~5 × 1013 Pa s, and ~2.5 × 1013 Pa s of viscosities are required, respectively. In the case of these viscosity values, dissipation of Saturn is consistent with both the latest observational results and Mimas’ orbital evolution. In this model, the assumption of a late formation discussed recently (Charnoz et al. 2011) is not required.
In this work, we assume that the solid core and the envelope are homogeneous. In addition, the envelope is assumed to be non-dissipative, and rigidity and viscosity of the core do not change with time. So far, whether a solid state core exists and its detailed structure are uncertain. We note that the Maxwell rheology used in our model would not be applicable if Saturn has a liquid core. Detailed interior structure models of Saturn and thermal evolution models can constrain the dissipation mechanisms more precisely, which should be addressed in future studies.
Acknowledgments
This work was supported by a JSPS Research Fellowship.
References
- Anderson, J. D., & Schubert, G. 2007, Science, 317, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Auclair-Desrotour, P., Le Poncin-Lafitte, C., & Mathis, S. 2014, A&A, 561, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekahr, S. 1969, Ellipsoidal Figures of Equilibrium. The Silliman Foundation Lectures (Yale Univ. Press) [Google Scholar]
- Charnoz, S., Crida, A., Castillo-Rogez, J. C., et al. 2011, Icarus, 216, 535 [Google Scholar]
- Chen, E. M. A., & Nimmo, F. 2008, Geophys. Res. Lett., 35, L19203 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M., & Lainey, V. 2007, J. Geophys. Res., 112, E12003 [Google Scholar]
- Fuller, J., Luan, J., & Quataert, E. 2016, MNRAS, 458, 3867 [NASA ADS] [CrossRef] [Google Scholar]
- Gavrilov, S. V., & Zharkov, V. N. 1977, Icarus 37, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Giampieri, G., Dougherty, M. K., Smith, E. J., & Russell, C. T. 2006, Nature, 441, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Giese, B., Wagner, R., Neukum, G., Helfenstein, P., & Thomas, P. C. 2007, Geophys. Res. Lett., 34, L21203 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Guenel, M., Mathis, S., & Remus, F. 2014, A&A, 566, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helled, R., & Guillot, T. 2013, ApJ, 767, 113 [CrossRef] [Google Scholar]
- Jacobson, R. A., Antreasian, P. G., Bordi, J. J., et al. 2006, AJ, 132, 2520 [NASA ADS] [CrossRef] [Google Scholar]
- Kaula, W. M. 1964, Rev. Geophys. Space Sci., 2, 661 [Google Scholar]
- Lainey, V., Karatekin, Ö, Desmars, J., et al. 2012, ApJ, 752, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Jacobson, R. A., Tajeddine, R., et al. 2017, Icarus, 281, 286 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, G. 1964, Rev. Geophys. Space Phys., 2, 467 [Google Scholar]
- Meyer, J., & Wisdom, J. 2007, Icarus, 188, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., Guillot, T., & Fayon, L. 2016, A&A, 596, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar system Dynamics (Cambridge University Press) [Google Scholar]
- Ogilvie, G., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Helfenstein, P., Thomas, P. C., et al. 2006, Science, 311, 1393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Remus, F., Mathis, S., Zahn, J.-P., & Lainey, V. 2012, A&A, 541, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remus, F., Mathis, S., Zahn, J.-P., & Lainey, V. 2015, A&A, 573, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, P. C., Burns, J. A., Helfenstein, P., et al. 2007, Icarus, 190, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Tobie, G., Mocquert, A., & Sotin, C. 2005, Icarus, 177, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., & Militzer, B. 2017, Icarus, 282, 183 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 |Im( |
| In the text | |
 |
Fig. 2 Evolutions of a) 2(Ω−ω) b) |Im( |
| In the text | |
 |
Fig. 3 Comparison of semi-major axis between constant |Im( |
| In the text | |
 |
Fig. 4 Evolutions of semi-major axis at a): Rc = 0.2 Rs and b): Rc = 0.24 Rs and μ = 5 × 1011 Pa and viscosities consistent with the observed dissipation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


