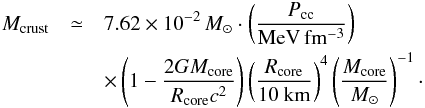| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629975 | |
| Published online | 10 March 2017 | |
Neutron star properties and the equation of state for the core
N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: jlz@camk.edu.pl; fortin@camk.edu.pl; haensel@camk.edu.pl
Received: 28 September 2016
Accepted: 3 December 2016
Context. Few unified equations of state for neutron star matter, in which core and crust are described using the same nuclear model, are available. However the use of non-unified equations of state with simplified matching between the crust and core has been shown to introduce uncertainties in the radius determination, which can be larger than the expected precision of the next generation of X-ray satellites.
Aims. We aim to eliminate the dependence of the radius and mass of neutron stars on the detailed model for the crust and on the crust-core matching procedure.
Methods. We solved the approximate equations of the hydrostatic equilibrium for the crust of neutron stars and obtained a precise formula for the radius that only depends on the core mass and radius, the baryon chemical potential at the core-crust interface, and at the crust surface. For a fully accreted crust one needs, additionally, the value of the total deep crustal heating per one accreted nucleon.
Results. For typical neutron star masses, the approximate approach allows us to determine the neutron star radius with an error ~0.1% (~10 m, equivalent to a 1% inaccuracy in the crust thickness). The formalism applies to neutron stars with a catalyzed or a fully accreted crust. The difference in the neutron star radius between the two models is proportional to the total energy release due to deep crustal heating.
Conclusions. For a given model of dense matter describing the neutron star core, the radius of a neutron star can be accurately determined independent of the crust model with a precision much better than the ~5% precision expected from the next generation of X-ray satellites. This allows us to circumvent the problem of the radius uncertainty that may arise when non-unified equations of state for the crust and core are used.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2017
1. Introduction
The interior of a neutron star (NS) consists of two main parts: the liquid core and solid crust. While the core is uniform (homogeneous), the crust is non-uniform and composed of nuclear clusters. Consequently, calculating the crust equation of state (EOS) is much less straightforward than for the core, which explains the smaller number of crust EOS available compared to those for the core. In particular, few unified EOS, i.e., those based on the same nuclear model for the crust and core, have been developed; see, for example, Douchin & Haensel (2001), Fantina et al. (2013), Pearson et al. (2014), Sharma et al. (2015), Fortin et al. (2016). Therefore non-unified EOS are often used, assuming different nuclear interaction models for the crust and core. As shown in Baldo et al. (2014), Fortin et al. (2016), for masses of astrophysical interest (M> 1 M⊙) the use of non-unified EOS can introduce an uncertainty on the radius determination on the order of 5%, which is as large as the precision expected from the next generation of X-ray telescopes: NICER (Arzoumanian et al. 2014), Athena (Motch et al. 2013), and potential LOFT-like missions (Feroci et al. 2012).
The solid crust of a NS with a mass M> 1 M⊙ contains only about one percent of the total mass of the star. However, the crust is believed to play an important role in many NS phenomena, such as pulsar glitches, X-ray bursts, gamma-ray flares of magnetars, torsional oscillations of NS, cooling of isolated NS, and cooling of X-ray transients (for review see, e.g., Chamel & Haensel 2008). A standard model of NS crust assumes that it is built of matter in nuclear equilibrium, the thermal corrections are negligibly small, and at a given baryon number density n, the crust matter is in a state of minimum energy per nucleon, E. In such a state, which defines the ground state (GS) of matter, the matter is called catalyzed. As the density n (or the mass-energy density ρ) can undergo discontinuous jumps inside the NS, a more suitable independent variable is the pressure P, which is strictly monotonous within the star. The thermodynamic potential is then the Gibbs free energy (the baryon chemical potential) μ = E + P/n, which replaces E. In the strict GS of matter both P and μ are continuous and monotonously increasing with the density when going toward the NS center.
The GS approximation is expected to be good for isolated NS born in core-collapse supernovae. However, a significant number of NS remains for 108−109 yr in low-mass X-ray binaries (LMXB), where they undergo a phase of accretion of matter from its evolved companion star. During the LMXB stage the NS is spun-up to millisecond periods; this is the so-called pulsar recycling. In such accreting NS the original crust has been replaced (fully or partially) by an accreted crust. In what follows we consider only a fully accreted crust, i.e., we assume that the NS has accreted matter with an integrated rest mass larger than the rest mass of the original GS crust.
The composition of an accreted crust (AC) is expected to be very different from that of a crust built of catalyzed matter in the GS. However, the neutron drip, dividing the whole crust into the outer (nuclei in electron gas) and inner (nuclei in neutron gas and electron gas) crusts is found at similar density for the GS and AC cases. Chamel et al. (2015) have found, using up-to-date energy density functionals and the Hartree-Fock-Bogoliubov method for solving the nuclear many-body problem, 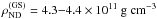 . For an accreted crust they have found some dependence on the energy density functional model and on the initial composition of ashes of X-ray bursts,
. For an accreted crust they have found some dependence on the energy density functional model and on the initial composition of ashes of X-ray bursts, 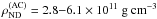 .
.
The accreted crust is, in contrast to the GS crust, a reservoir of the nuclear energy. This energy can be steadily released mainly at some 300–500 m below the NS surface, during the accretion phase, leading to deep crustal heating (Haensel & Zdunik 1990; Brown et al 1998). The EOS of an AC is stiffer than that for the GS crust, particularly for densities 5 × 1011−5 × 1012g cm-3. Consequently, the thickness of an AC is larger (Zdunik & Haensel 2011).
We present an approximate description to the NS crust structure in terms of the function relating chemical potential and pressure. Within the one-component plasma model, in Sect. 2 we derive a formula for the thickness of any layer of the crust. This formula is highly accurate and does not require any knowledge of the EOS except the values of the chemical potential at the boundaries of a given layer in the crust. The approach is then extended to describe a GS crust and we obtain formulas for the NS radius, the crust thickness and mass that only depend on the mass and radius of the NS core. Their accuracy and the dependence on the choice of the location of the core-crust transition are studied in Sect. 3. In particular it is shown that the radius and mass of a neutron star, the crust thickness, and its mass can be determined with an error smaller than 0.1%, 0.3%, 1%, and 5%, respectively. In Sect. 4 we extend the approximated approach to the case of an accreted crust, and we obtain a simple formula for the difference in the thickness of the AC and GS crusts. This only involves the total (integrated) energy release from deep crustal heating, and the mass and radius of a NS with a GS crust and is extremely accurate (<1 m). We present conclusions and perspectives in Sect. 5.
2. Crust structure: an approximation
The approximate approach to the macroscopic properties of the NS crust, based on the separation of the TOV equation into two factors dependent on stellar properties (mass and radius) and the EOS of dense matter, was discussed in Lattimer & Prakash (2007), Zdunik (2002), Zdunik et al. (2008), Zdunik & Haensel (2011).
The Tolman-Oppenheimer-Volkoff (TOV) equation of hydrostatic equilibrium in general relativity is 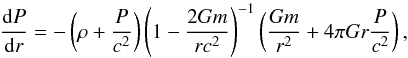 (1)with m = m(r) the gravitational mass enclosed in a sphere of radius r, P the pressure, and ρ the mass-energy density.
(1)with m = m(r) the gravitational mass enclosed in a sphere of radius r, P the pressure, and ρ the mass-energy density.
The mass of the crust Mcrust is small compared to the total mass M of the NS and thus one can assume within the crust m ≈ M. The term 4πr3P/mc2 is on the order of P/ρc2 at the bottom of the inner crust, but is three orders of magnitude smaller than P/ρc2 at the neutron drip point. For this reason, we keep the factor 1 + P/ρc2 while neglecting the term 4πr3P/mc2 as compared to one. Consequently Eq. (1) can be rewritten, in the crust, as follows: 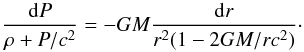 (2)Let Pcc, ncc and μcc = μ(Pcc) be the pressure, baryon density, and chemical potential at the core-crust interface, respectively. Within the crust, i.e., for 0 < P < Pcc, we define a dimensionless function of the local pressure,
(2)Let Pcc, ncc and μcc = μ(Pcc) be the pressure, baryon density, and chemical potential at the core-crust interface, respectively. Within the crust, i.e., for 0 < P < Pcc, we define a dimensionless function of the local pressure, 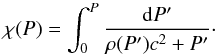 (3)The function χ(P) is determined solely by the EOS of the crust. The integral of the right-hand side of Eq. (2) then becomes
(3)The function χ(P) is determined solely by the EOS of the crust. The integral of the right-hand side of Eq. (2) then becomes ![\begin{equation} \chi\left[P\left(r\right)\right]=\frac{1}{2}\ln \left[\frac{1-r_{\rm g}/R} {1-r_{\rm g}/r}\right], \label{rap2} \end{equation}](/articles/aa/full_html/2017/03/aa29975-16/aa29975-16-eq35.png) (4)where rg ≡ 2GM/c2. Defining a = 1−rg/R, we obtain r within the crust as a function of χ,
(4)where rg ≡ 2GM/c2. Defining a = 1−rg/R, we obtain r within the crust as a function of χ, 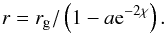 (5)In thermodynamic equilibrium one can define the baryon chemical potential μ = dρ/ dn. Thus, the first law of thermodynamics at T = 0 implies
(5)In thermodynamic equilibrium one can define the baryon chemical potential μ = dρ/ dn. Thus, the first law of thermodynamics at T = 0 implies 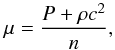 (6)which leads to the relation
(6)which leads to the relation 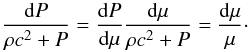 (7)The function χ is then given by exp(χ) = μ(P) /μ0, where μ0 = μ(P = 0) = m0c2 is the energy per baryon at NS surface.
(7)The function χ is then given by exp(χ) = μ(P) /μ0, where μ0 = μ(P = 0) = m0c2 is the energy per baryon at NS surface.
This allows us to determine the thickness of any shell of the crust located between two radii, r1 and r2, corresponding to the pressure P1 and P2, respectively,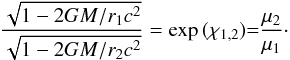 (8)A similar approach presented by Lattimer & Prakash (2007) relies on the replacement of μ in the denominator of Eq. (7) by its value at the NS surface μ0, leading to an exponential dependence in Eq. (8).
(8)A similar approach presented by Lattimer & Prakash (2007) relies on the replacement of μ in the denominator of Eq. (7) by its value at the NS surface μ0, leading to an exponential dependence in Eq. (8).
2.1. Approximate formula for the radius and crust thickness
Let Rcore be the radius of the core, i.e., at the core-crust interface, where μ = μcc. In Eq. (8), taking r1 = R and r2 = Rcore, one can obtain a formula relating R(M) to Rcore(M) as follows: 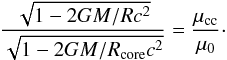 (9)The latter is equivalent to
(9)The latter is equivalent to 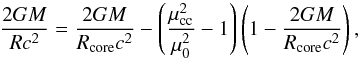 (10)which expresses the compactness of the whole star in terms of the core compactness. In this formula, the EOS of the crust enters through the ratio μcc/μ0.
(10)which expresses the compactness of the whole star in terms of the core compactness. In this formula, the EOS of the crust enters through the ratio μcc/μ0.
From Eq. (10) we find that the radius is given by 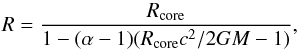 (11)where
(11)where 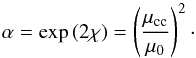 (12)Then the crust thickness lcrust = R−Rcore is
(12)Then the crust thickness lcrust = R−Rcore is 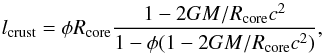 (13)where
(13)where 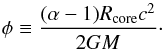 (14)It should be noted that φ defined by Eq. (14) is a nonrelativistic quantity and can be approximated for α → 1 by
(14)It should be noted that φ defined by Eq. (14) is a nonrelativistic quantity and can be approximated for α → 1 by 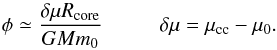 (15)The numerical formula then is written as
(15)The numerical formula then is written as 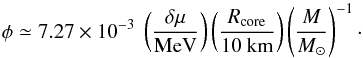 (16)The leading term in the expansion of the right-hand-side of Eq. (13) in powers of the parameter φ gives an approximate formula for the thickness of the crust proportional to δμ,
(16)The leading term in the expansion of the right-hand-side of Eq. (13) in powers of the parameter φ gives an approximate formula for the thickness of the crust proportional to δμ,  (17)where δμ is normalized to the “typical” value for the NS crust (~25 MeV, see Table 1). It should be mentioned, however, that for astrophysically relevant NS parameters (M ~ 1−2M⊙, Rcore ~ 10−12 km) one gets φ on the order of 0.15−0.25. Therefore, φ cannot be considered a very small number. Thus the accuracy of the expansion given by Eq. (17) is ~20% (see Fig. 6) and one should instead use formula in Eq. (13) to determine the thickness of the crust with a high accuracy (<1%).
(17)where δμ is normalized to the “typical” value for the NS crust (~25 MeV, see Table 1). It should be mentioned, however, that for astrophysically relevant NS parameters (M ~ 1−2M⊙, Rcore ~ 10−12 km) one gets φ on the order of 0.15−0.25. Therefore, φ cannot be considered a very small number. Thus the accuracy of the expansion given by Eq. (17) is ~20% (see Fig. 6) and one should instead use formula in Eq. (13) to determine the thickness of the crust with a high accuracy (<1%).
2.2. Approximate formula for the mass of the neutron-star crust
The crust contributes to the total mass of a NS. However the role of the mass of the crust for the total stellar mass is one order of magnitude smaller than the importance of the crust thickness for the radius of a NS. To estimate the total mass of a NS with an accuracy similar to that obtained using the approximation in Eq. (11) for the radius, we can safely use the following very crude approximation for the crust mass: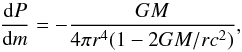 (18)which is obtained from the TOV equation by neglecting the P/c2 terms.
(18)which is obtained from the TOV equation by neglecting the P/c2 terms.
The mass of the crust is given by the formula 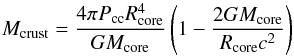 (19)and is proportional to the pressure at the bottom of the crust Pcc. The total mass of the star is then M = Mcrust + Mcore.
(19)and is proportional to the pressure at the bottom of the crust Pcc. The total mass of the star is then M = Mcrust + Mcore.
3. Neutron star parameters for a catalyzed crust
3.1. Mass and radius of a neutron star from μcc/μ0
 |
Fig. 1 NS radius R and thickness of the crust lcrust (inset) for the DH and NL3ωρ EOS as a function of the baryon density nc at the center of the star. Solid black curves indicate the exact solution calculated for the unified EOS (i.e., including the crust EOS), blue curves indicate the radius of the core (above Pcc), and dashed red lines indicate the approximation based on Eq. (11), which were obtained using the core EOS alone. |
 |
Fig. 2 NS mass M and mass of the crust Mcrust (inset) for the DH and NL3ωρ EOS as a function of the baryon central density nc. Solid black curves indicate the exact solution calculated for the unified EOS (including the crust EOS), blue curves indicate the mass of the core (P>Pcc), and dashed (red) lines indicate the approximation based on Eq. (19), which were obtained using the core EOS alone. |
Crust-core boundary for the two considered EOS DH and NL3ωρ.
The approximate formulas presented in the previous section allow us to determine the main parameters of a NS (total mass, radius, crust thickness, and mass) solely on the basis of the properties of its core, i.e., using only an EOS P(ρ) for nuclear matter below the crust-core interface (for P > Pcc). The only additional information required is the chemical potential at zero pressure μ0. For cold catalyzed matter, the minimum energy is obtained for iron 56Fe, i.e., m0c2 = μ0 = 930.4 MeV (Haensel et al. 2007).
First, for a given central density nc (or equivalently pressure Pc, given by the core EOS), and a chosen location of the core-crust transition at a density ncc or pressure Pcc, the relation between the mass and radius of the NS core Mcore(Rcore) is obtained by integrating the TOV equations outward from the center of a star with P = Pc down to Pcc. Then the mass of the crust Mcrust is determined using Eq. (19) and, consequently, so is the total mass of the star M. Using Eq. (11) the canonical M(R) relation between the mass and radius of the NS is reconstructed. The thickness of the crust is finally given by Eq. (13).
In Figs. 1 and 2 we present the result of such a procedure for two models of dense matter that fulfill the observational constraint on the maximum allowable mass Mmax > 2 M⊙: the nucleonic DH from Douchin & Haensel (2001) and the stiffer hyperonic NL3ωρ, corresponding to the EOS labeled “Y” in Fortin et al. (2016). The approximate solution (dashed lines) is almost undistinguishable from the exact solution except in the region of relatively small central density. We obtained similar conclusions for the parameters of the crust (thickness and mass) presented in the insets. In Fig. 3 various relations between masses and radii are presented. The black solid lines are the M(R) relations that are obtained when solving the TOV equations in the whole NS (core and crust) with a unified EOS, i.e., when the same nuclear models for the crust and core are used. The blue solid lines correspond to the dependence Mcore(Rcore) and are obtained by solving the TOV equations in the core, i.e., from the center at pressure Pc outward to the pressure at core-crust interface Pcc. The red dashed lines are obtained using the M(Rcore) relations in Eq. (11). In this case, we do not need any information about the crust EOS except the chemical potentials at zero pressure μ0 and at the bottom of the crust μcc in order to determine the total radius of the star. For a chosen value of the density at the core-crust transition (see Sect. 3.2), μcc can be calculated from Eq. (6) using the core EOS.
The approximate formula Eq. (11) works very well for astrophysically interesting masses of NS, i.e., M > 1M⊙. For the sake of completeness, we mention that for masses as small as 0.2M⊙ the validity of the formula breaks down because the condition Mcrust ≪ M is then obviously not fulfilled. For the NL3ωρ EOS, the difference between the exact and approximate radii is 20 m (1.0M⊙), 8 m (1.5M⊙), and 3 m (2.0M⊙). Therefore, for M> 1M⊙ the relative error is less than 0.15% of the radius of a star (or less than 1% of the thickness of the crust). The accuracy of the approximate approach is even better for the DH EOS. For the estimation of the mass of the crust, we use the simplest approximations in Eq. (20). This equation is accurate up to 6% for M > 1M⊙ and, therefore, results in a very small error in the total mass determination (less than 0.3%).
 |
Fig. 3 M(R) dependence for the exact solution of the TOV equations obtained using a unified EOS and for our approximate approach, for the DH and NL3ωρ models of dense matter. Solid black curves indicate the M(R) calculated with a unified EOS, solid blue curves indicate the Mcore(Rcore) relation, dashed red lines indicate the M(R) approximation based on Eqs. (11), (12), and the black lines indicate the exact solution of the TOV equation. |
3.2. Choice of the core-crust transition
At the core-crust interface the ground state of neutron star matter changes from a lattice of spherical nuclei in the solid crust to homogeneous matter in the liquid core. Some models predict the appearance of so-called pasta phases when the most stable shape of nuclei is no longer a sphere but, as the density increases, a rod or a slab immersed in the neutron gas (Ravenhall et al. 1983). Various approaches have been developed to determine the density of the core-crust transition, ncc; these include the study of thermodynamic spinodal or dynamical spinodal surfaces, Thomas-Fermi calculations or the random phase approximation. However for β-equilibrated matter, the values of ncc that are obtained have been shown to be similar (see, for example, Horowitz & Shen 2008; Avancini et al. 2010, 2012; Pais et al. 2016, and references therein).
The transition density is inversely proportional to the slope of the symmetry energy L (Horowitz & Piekarewicz 2001) and for typical values of 30 ≤ L ≤ 120 MeV, Ducoin et al. (2011) find for a large set of EOS based on two nuclear approaches to the many-body problem (Skyrme models and relativistic mean field calculations) 0.06 ≤ ncc ≤ 0.10 fm-3 or 0.38 ≤ ncc/n0 ≤ 0.63. Consequently, if for a given core EOS no calculation of the core-crust transition density is available, taking ncc = 0.5n0 appears reasonable.
 |
Fig. 4 Baryon chemical potential μ as a function of the pressure for the DH EOS. The points denote the value of the chemical potential at various assumed locations for the core-crust boundary used in Eqs. (11), (12) and presented in Table 1. The lowest point (DH) corresponds to the real core-crust interface in the DH model. |
 |
Fig. 5 M(R) dependence for the exact solution of the TOV equations obtained using a unified EOS and the approximate approach for the DH EOS. Different values of ncc are used (from left to right; 0.16, 0.13, 0.11, 0.09, 0.077 fm-3, see Table 1 for details). The value ncc = 0.077 fm-3 corresponds to the “real” crust-core boundary for the DH model. The solid blue curves show the M(Rcore) relation, the dashed red curves show the M(R) approximation based on Eqs. (11), (12), and the black curve shows the exact solution of the TOV equation. |
In this subsection we discuss the accuracy of our approximate approach to calculate the main parameters of a NS for different given locations of the crust-core boundary, using the DH model of dense matter as an example. In this model the “real” crust-core boundary is located at ncc = 0.077 fm-3, i.e., at about half nuclear matter density. To test the dependence of our approximations on ncc we artificially redefine the location of the core boundary to 0.09, 0.11, 0.13, 0.16 fm-3 (models DH1-DH4 in Table 1). The size of the core, which is defined by the pressure Pcc, decreases with increasing Pcc and is smallest (at given central pressure Pc) for the DH4 model. Consequently the region of the star described by the approximate formulas (outer part P < Pcc) is larger for larger Pcc, and for the DH4 model (with ncc ≃ n0) the mass of the crust is about 0.1 M⊙, which is much larger than the mass of the real crust (unified DH EOS, <0.02 M⊙).
Figure 4 shows the baryon chemical potential μ as a function of the pressure P for the DH EOS of the core. The dots correspond to the considered crust-core location (see Table 1). The lowest value is the real density of the crust-core interface for the (unified) DH model.
In Fig. 5 we present the results of our approximate approach given by Eqs. (11), (12) for the mass-radius relation for the DH EOS. For the real value of ncc the difference between the exact and approximate results is 30 m at M = 0.5 M⊙, 10 m at M = 1 M⊙, and less than 4 m at M = 1.5−2 M⊙. Even for an unrealistically high value of ncc = n0 = 0.16 fm-3 (DH4), the approximation gives a high accuracy with the uncertainty on R decreasing from ~100 m at 1 M⊙ down to 30 m at 1.5 M⊙ and 5 m at 2 M⊙.
The accuracy of the approximate approach for the thickness and mass of the crust is presented in Fig. 6 for three different locations of the bottom of the crust (models DH, DH2, and DH4). The thickness of the crust is determined very accurately by formula (13). The relative error is less than 0.7% for DH and <3.5% for DH4, which is equivalent to <10 m and <100 m inaccuracy (i.e., 0.08%, 0.7% error in the radius of the star R). Although for the presented range of masses from 1 M⊙ to Mmax the maximum relative error in Mcrust is 5–8%, the determination of the total mass M of neutron star is very accurate; i.e., 1% for ncc = n0 and 0.1% for ncc = 0.5n0 at M = 1 M⊙, where the error decreases rapidly with further increase of M.
3.3. Accuracy of the approximate approach and crust-core matching problem
In the case of a non-unified EOS the matching of the core EOS to the crust EOS is often performed by an artificial function P(ρ) or P(n) (which can be linear, polytropic, ...). In general this approach leads to thermodynamic inconsistency, which manifests itself in a discontinuity in μ (for details see Fortin et al. 2016). This discontinuity δμEOS can be as high as a few MeV, but is usually on the order of δμEOS ≃ 0.5−1.5 MeV. It results in an error in the crust thickness determination, which can be calculated with Eq. (17). The relative error in lcrust is then proportional to δμEOS/ Δμ, where Δμ is the chemical potential range in the crust (20–30 MeV). For example, for δμEOS ≃ 1 MeV the error due to inconsistent crust-core matching is larger than the accuracy given by our approximation for the crust thickness; for ncc = 0.5n0 and M = 1.4 M⊙ it is 40 m compared to the 5 m inaccuracy of our model.
As a consequence, using the approximate formulas for the radius (Eq. (11)), the crust thickness (Eq. (13)), and mass (Eq. (19)), without any further knowledge about the crust EOS, is in general more accurate than the widely used method of matching in a thermodynamically inconsistent way an EOS for the crust to a different (non-unified) EOS for the core.
 |
Fig. 6 Thickness lcrust (upper panel) and mass Mcrust (lower panel) of the crust of a NS for the DH EOS and for different values of ncc (from top to bottom; 0.16, 0.11, 0.077 fm-3). The density ncc = 0.077 fm-3 corresponds to the crust-core boundary for the DH model. Solid lines indicate the exact results calculated for the complete EOS (including the crust EOS), dashed (red) lines indicate approximations based on Eq. (13) (thickness) and Eq. (19) (mass), dotted (green) lines correspond to linearization Eq. (17) of Eq. (13). |
4. Accreted versus catalyzed crust
A characteristic feature of the EOS for an accreted crust is the existence of energy sources at pressures at which exothermic nuclear reactions are induced by the accretion of matter onto the NS surface. As a result the μ(P) relation is a discontinuous function with drops in μ equal to the energy release per one accreted nucleon. In Fig. 7 we present an example for the Mackie & Baym (1977) model of dense matter (Haensel & Zdunik 2008) of a continuous μ(GS)(P) dependence for catalyzed matter (lower continuous curve that corresponds to the minimum value of μ at a given pressure) and for an accreted crust (with energy sources located at P = Pi−1,Pi,Pi + 1).
4.1. Thickness of an accreted crust
In Sect. 2 we considered a catalyzed crust for which the function μ(P) is continuous and Eqs. ((6), (7)) hold. In this case formula (8) can be used for the whole crust, resulting in Eq. (13). In the case of an accreted crust, as shown in Fig. 7, μ(P) is not continuous and each jump in the chemical potential at a fixed pressure corresponds to an energy source. Consequently, to determine the thickness of an accreted crust one has to calculate separately the thickness of each shell located between two energy sources, for example, between Pi−1 and Pi as plotted in Fig. 7.
Using Eq. (8) the following set of equations is obtained: 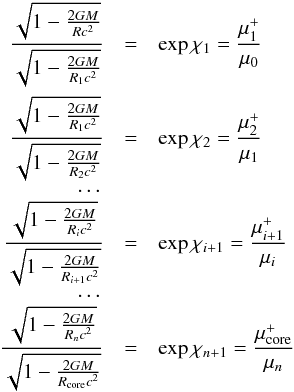 where the subscript “core” corresponds to the convergence point of the baryon chemical potential for accreted and catalyzed crusts at the bottom of the crust, i.e., where the condition
where the subscript “core” corresponds to the convergence point of the baryon chemical potential for accreted and catalyzed crusts at the bottom of the crust, i.e., where the condition 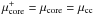 is fulfilled (see Fig. 7).
is fulfilled (see Fig. 7).
Multiplying the above equations by one another we get the final formula for the thickness of an accreted crust, 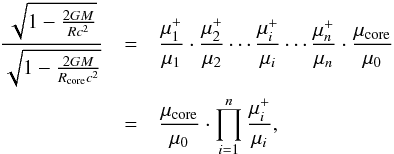 (21)where the product is calculated over all the energy sources in the accreted crust.
(21)where the product is calculated over all the energy sources in the accreted crust.
 |
Fig. 7 Baryon chemical potential μ for catalyzed (lower curve) and accreted crust (step-like curve). The Mackie & Baym (1977) model of dense matter is used in the example (for details see Haensel & Zdunik 2008). |
The energy release per one accreted nucleon at the pressure Pi is given by 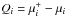 . Because Qi/μi< 10-3, one can safely approximate formula Eq. (21) by
. Because Qi/μi< 10-3, one can safely approximate formula Eq. (21) by 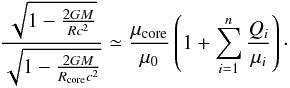 (22)The main energy sources for an accreted crust are located in the inner crust at typical pressures P ~ 0.001−0.01 MeV fm-3 (1030−1031 erg cm-3), where the chemical potential μIC ≃ 942 MeV. Replacing μi in Eq. (22) by this typical value, we get
(22)The main energy sources for an accreted crust are located in the inner crust at typical pressures P ~ 0.001−0.01 MeV fm-3 (1030−1031 erg cm-3), where the chemical potential μIC ≃ 942 MeV. Replacing μi in Eq. (22) by this typical value, we get 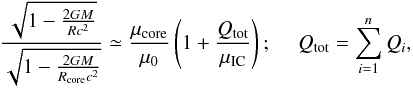 (23)where Qtot is the total energy release in the crust.
(23)where Qtot is the total energy release in the crust.
4.2. Thickness of a catalyzed crust versus an accreted crust
The formulas for the radius Rcat and Racc of a NS with a catalyzed crust and an accreted one, respectively, are 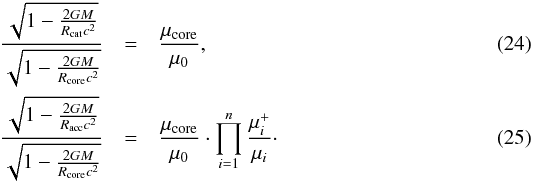 They are equivalent to
They are equivalent to 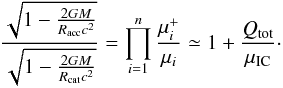 (26)Defining
(26)Defining  , Eq. (11) holds with R and Rcore replaced by Racc and Rcat respectively, i.e.,
, Eq. (11) holds with R and Rcore replaced by Racc and Rcat respectively, i.e., 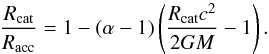 (27)The difference in the radii of NS with an accreted crust and with a catalyzed crust, ΔR = Racc−Rcat, is small compared to R and one gets the approximate relation
(27)The difference in the radii of NS with an accreted crust and with a catalyzed crust, ΔR = Racc−Rcat, is small compared to R and one gets the approximate relation ![\begin{equation} \frac{\Delta R}{R_{\rm cat}}\simeq \left[\left(\prod_{i=1}^{n}\frac{\mu_{i}^+}{\mu_i}\right)^2-1\right] \left(\frac{R_{\rm cat}c^2}{2GM}-1\right). \label{eq:raccatap} \end{equation}](/articles/aa/full_html/2017/03/aa29975-16/aa29975-16-eq165.png) (28)Using Eq. (26) we obtain
(28)Using Eq. (26) we obtain 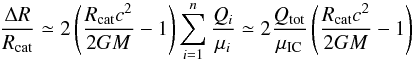 (29)which, after normalization to typical values, becomes
(29)which, after normalization to typical values, becomes  (30)where we used μIC = 942 MeV. The inaccuracy of formula (30) introduced by the approximations ((22), (23), (29)) is on the order of (Qtot/ 940 MeV), about 0.1% in ΔR (i.e., much less than 1 m).
(30)where we used μIC = 942 MeV. The inaccuracy of formula (30) introduced by the approximations ((22), (23), (29)) is on the order of (Qtot/ 940 MeV), about 0.1% in ΔR (i.e., much less than 1 m).
 |
Fig. 8 Mass-radius relation for the DH EOS for catalyzed (black, solid curve) and accreted crusts (blue, solid line). The approximation given by Eq. (30) is plotted by a dashed red curve, which can be hardly distinguished from the exact result for an accreted crust. Inset: a zoom for masses 1−2 M⊙. |
The accuracy of our approximation is visualized in Fig. 8. The exact M(R) curve is obtained for the DH EOS with catalyzed and accreted crusts based on Mackie & Baym (1977) model of nuclei (Zdunik & Haensel 2011; Haensel & Zdunik 2008). The difference in radii due to the formation scenario (i.e., accreted versus catalyzed matter) is ΔR = 80 m for 1.4 M⊙ and in the range 330−50 m for masses between 0.5 M⊙ and 1.8 M⊙, respectively. For the considered model of accreted matter the total energy release is Qtot = 1.9 MeV and the M(R) dependence obtained using Eq. (30) nearly coincides with the exact M(R). The difference in R is about 1 m for M = 1.5 M⊙.
We mentioned that when deriving Eqs. ((24), (25)) we assume the same value of μcore and μ0 for both an accreted crust and a catalyzed crust. For μcore this assumption is justified; indeed the baryon chemical potential μ for catalyzed and accreted crusts converges at pressures larger than ~0.03 MeVfm-3 (see Fig. 7). However for an accreted crust the value of μ0 actually depends on the ashes of nuclear reactions at the surface of the NS (as a result of the X-ray bursts, Haensel & Zdunik 2003). In principle it is possible that μ0acc ≠ μ0cat and the product 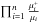 should then be multiplied by μ0acc/μ0cat. In practice the difference is smaller than 0.2 MeV/nucleon (0.02%) for the ashes considered by Gupta et al. (2007), Haensel & Zdunik (2008).
should then be multiplied by μ0acc/μ0cat. In practice the difference is smaller than 0.2 MeV/nucleon (0.02%) for the ashes considered by Gupta et al. (2007), Haensel & Zdunik (2008).
5. Conclusions
In this paper we present an approximate treatment for the crust of a NS, which allows us to calculate the mass and radius of a NS, crust thickness, and crust mass. Two limiting cases were considered: catalyzed (ground-state) crust and fully accreted crust. For a catalyzed crust R, lcrust, Mcrust, and M do not depend on the specific form of the crust EOS, but only on the crust-core transition density and EOS core. For a given core EOS and chosen density at which the core-crust transition takes places, the relation between the core radius and mass is obtained by solving the TOV equations. Then the mass and radius of the crust and the total mass and radius of the star can be obtained using simple formulas. The accuracy of this approach is higher than 1% and 5% for lcrust and Mcrust, respectively, for NS masses larger than 1 M⊙. This is equivalent to the determination of global parameters of NS (radius R and mass M) with maximum error ~0.1−0.3%. Unless the transition density ncc between the core and the crust for a given EOS of the core is available in the literature, this value is not known in advance. However for reasonable values of the symmetry energy usually ncc ≃ 0.5n0. A simple and accurate formula for the difference in the radii of a NS with a fully accreted crust with respect to that with a catalyzed crust is derived. It is proportional to the total energy release due to deep crustal heating and, in addition, depends only on the mass and radius of the model with a catalyzed crust.
The demonstrated high precision of the prediction of the radius of a NS makes the derived formulas of interest for theoretical works in particular in relation with the next generation of X-ray telescopes, which are expected to provide measurements of the NS radius with a precision of few percent.
Acknowledgments
This work was partially supported by the Polish National Science Centre (NCN) grant No. 2013/11/B/ST9/04528 and the COST Action NewCompStar. M.F. would like to thank Constança Providência for useful discussions. We also acknowledge helpful remarks of participants of the MODE-SNR-PWN 2016 Workshop (Meudon, France), after the talk by one of the authors (MF).
References
- Arzoumanian, Z., Gendreau, K. C., Baker, C. L., et al. 2014, Space Telescopes and Instrumentation, Ultraviolet to Gamma Ray, Proc. SPIE 9144, 914420 [Google Scholar]
- Avancini, S. S., Chiacchiera, S., Menezes, D. P., & Providência, C. 2010, Phys. Rev. C, 82, 055807 [NASA ADS] [CrossRef] [Google Scholar]
- Avancini, S. S., Chiacchiera, S., Menezes, D. P., & Providência, C. 2012, Phys. Rev. C, 85, 059904 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Burgio, G. F., Centelles, M., Sharma, B. K, & Viñas, X. 2014, Phys. Atom. Nuclei, 77, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., Bildsten, L., & Rutledge, R. E. 1998, ApJ, 504, L95 [Google Scholar]
- Chamel, N., & Haensel, P. 2008, Liv. Rev. Relat., 11, 10 [Google Scholar]
- Chamel, N., Fantina, A. F., Zdunik, J. L., & Haensel, P. 2015, Phys. Rev. C, 91, 055803 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ducoin, C., Margueron, J., Providência, C., & Vidaña, I. 2011, Phys. Rev. C, 83, 045810 [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 559, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroci, M., den Herder, J. W., Bozzo, E., et al. 2012, Proc. SPIE, 8443, 84432D [CrossRef] [Google Scholar]
- Fortin, M., Providência, C., Raduta, A. R., et al. 2016, Phys. Rev. C, 94, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Brown, E. F., Schatz, H., Möller, P., & Kratz, K.-L. 2007, ApJ, 662, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., Yakovlev, D. G. 2007, Neutron Stars 1, Equation of state and structure (New York: Springer) [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990, A&A, 227, 431 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horowitz, C. J., & Piekarewicz, J. 2001, Phys. Rev. Lett., 86, 5647 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Horowitz, C. J., & Shen, G. 2008, Phys. Rev. C, 78, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mackie, F. D., & Baym, G. 1977, Nucl. Phys. A, 285, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Motch, C., Wilms, J., Barret, D., et al. 2013, ArXiv e-prints [arXiv:1306.2334] [Google Scholar]
- Pearson, J. M., Chamel, N., Fantina, A. F., & Goriely, S. 2014, Eur. Phys. J. A, 50, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Pais, H., Sulaksono, A., Agrawal, B. K., & Providência, C. 2016, Phys. Rev. C, 93, 045802 [NASA ADS] [CrossRef] [Google Scholar]
- Ravenhall, D. G., Pethick, C. J., & Wilson, J. R. 1983, Phys. Rev. Lett., 50, 2066 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, B. K., Centelles, M., Viñas, X., Baldo, M., & Burgio, G. F. 2015, A&A, 584, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunik, J. L. 2002, A&A, 394, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunik, J. L., & Haensel, P. 2011, A&A, 530, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunik, J. L., Bejger, M., & Haensel, P. 2008, A&A, 491, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 NS radius R and thickness of the crust lcrust (inset) for the DH and NL3ωρ EOS as a function of the baryon density nc at the center of the star. Solid black curves indicate the exact solution calculated for the unified EOS (i.e., including the crust EOS), blue curves indicate the radius of the core (above Pcc), and dashed red lines indicate the approximation based on Eq. (11), which were obtained using the core EOS alone. |
| In the text | |
 |
Fig. 2 NS mass M and mass of the crust Mcrust (inset) for the DH and NL3ωρ EOS as a function of the baryon central density nc. Solid black curves indicate the exact solution calculated for the unified EOS (including the crust EOS), blue curves indicate the mass of the core (P>Pcc), and dashed (red) lines indicate the approximation based on Eq. (19), which were obtained using the core EOS alone. |
| In the text | |
 |
Fig. 3 M(R) dependence for the exact solution of the TOV equations obtained using a unified EOS and for our approximate approach, for the DH and NL3ωρ models of dense matter. Solid black curves indicate the M(R) calculated with a unified EOS, solid blue curves indicate the Mcore(Rcore) relation, dashed red lines indicate the M(R) approximation based on Eqs. (11), (12), and the black lines indicate the exact solution of the TOV equation. |
| In the text | |
 |
Fig. 4 Baryon chemical potential μ as a function of the pressure for the DH EOS. The points denote the value of the chemical potential at various assumed locations for the core-crust boundary used in Eqs. (11), (12) and presented in Table 1. The lowest point (DH) corresponds to the real core-crust interface in the DH model. |
| In the text | |
 |
Fig. 5 M(R) dependence for the exact solution of the TOV equations obtained using a unified EOS and the approximate approach for the DH EOS. Different values of ncc are used (from left to right; 0.16, 0.13, 0.11, 0.09, 0.077 fm-3, see Table 1 for details). The value ncc = 0.077 fm-3 corresponds to the “real” crust-core boundary for the DH model. The solid blue curves show the M(Rcore) relation, the dashed red curves show the M(R) approximation based on Eqs. (11), (12), and the black curve shows the exact solution of the TOV equation. |
| In the text | |
 |
Fig. 6 Thickness lcrust (upper panel) and mass Mcrust (lower panel) of the crust of a NS for the DH EOS and for different values of ncc (from top to bottom; 0.16, 0.11, 0.077 fm-3). The density ncc = 0.077 fm-3 corresponds to the crust-core boundary for the DH model. Solid lines indicate the exact results calculated for the complete EOS (including the crust EOS), dashed (red) lines indicate approximations based on Eq. (13) (thickness) and Eq. (19) (mass), dotted (green) lines correspond to linearization Eq. (17) of Eq. (13). |
| In the text | |
 |
Fig. 7 Baryon chemical potential μ for catalyzed (lower curve) and accreted crust (step-like curve). The Mackie & Baym (1977) model of dense matter is used in the example (for details see Haensel & Zdunik 2008). |
| In the text | |
 |
Fig. 8 Mass-radius relation for the DH EOS for catalyzed (black, solid curve) and accreted crusts (blue, solid line). The approximation given by Eq. (30) is plotted by a dashed red curve, which can be hardly distinguished from the exact result for an accreted crust. Inset: a zoom for masses 1−2 M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.